Topological Constraint Theory for Network Glasses and Glass-Forming Liquids: A Rigid Polytope Approach

1. Introduction

The deformability, entropy and even temperature-dependent disintegration modes of a random atomic network are largely determined by the network's rigidity. Seminal works by Phillips (1979), Phillips (1981), Thorpe (1983), and He and Thorpe (1985) have shown the existence of a floppy-to-rigid transition in such networks in the form of rigidity percolation. The prevailing model suggests that the network is floppy when the number of degrees of freedom per atom exceeds the number of interatomic force field constraints, and the transition to rigidity occurs when these two quantities are equal. The network's rigidity therefore depends on the average coordination number 〈r〉, and various arguments suggest that the floppy-to-rigid transition occurs at the critical value r_p = 2.4. Although Phillips (1979) and Phillips (1981) originally attempted to relate the glass-forming ability of a network to its entropy and deformability, Thorpe (1983) placed the idea of network rigidity on more formal footing by considering the number of zero-frequency vibrational modes, i.e., continuous deformations with no energy penalty. The fraction f of such modes is predicted to decrease with increasing 〈r〉 to zero at or near r_p where rigidity percolates, and increasing the connectivity further only serves to overconstrain the network.

The rigidity percolation model suggests that there could be an underlying universal dependence of the physical properties of glasses on composition that is effectively insensitive to their chemical details. The chalcogenide glasses provide an ideal testbed in this regard, being characterized by energetically similar covalent bonds and a wide range of network connectivity. As it is practically impossible to directly obtain f for these complex amorphous networks, typical studies in the literature instead report the variation of physical properties with 〈r〉 (Tanaka, 1989; Kamitakahara et al., 1991; Yang et al., 2010, 2013; Wang et al., 2014; Sen et al., 2019). However, it remains unclear what would be the signature of the rigidity percolation in the physical properties of amorphous networks as a function of the connectivity. In fact, a wide variety of physical properties including elastic moduli, refractive index and the glass transition temperature T_g of glasses in the Ge-Se system show continuous and monotonic change through r_p (Yang et al., 2013). On the other hand, Boolchand and coworkers have suggested that the floppy-to-rigid transition may not be sharp at r_p, but rather that the network is optimally constrained and therefore stress-free over a range of 〈r〉 around the threshold value of 2.4 (Wang et al., 2000; Boolchand et al., 2001, 2005; Chakravarty et al., 2004). These authors used modulated differential scanning calorimetry (MDSC) to show that Ge-Se glasses with such optimally constrained networks are characterized by vanishing non-reversing enthalpy, and identified this as a property of the “Intermediate Phase” (IP). It was further suggested that these IP glasses would be completely resistant to aging or relaxation below T_g. However, subsequent direct aging studies of IP glasses in the Ge-Se and Si-Se systems by other researchers showed the presence of both structural and enthalpy relaxation (Edwards and Sen, 2011; Zhao et al., 2013; Marple et al., 2019), thus questioning the validity of the existence of such IP.

Considering that T_g depends strongly on the connectivity of a network, its monotonic variation with 〈r〉 raises further questions about the use of the average coordination number as a governing variable for rigidity percolation. For example, the Gibbs–DiMarzio model of the chain polymer glass transition (Gibbs and DiMarzio, 1958; DiMarzio and Gibbs, 1964) predicts that T_g (along with the available free volume, chain stiffness and degree of polymerization) is described by the monotonic function T_g = T₀/(1 − κX) where X is the cross-linking density of the chains and κ is a universal constant. Note that while the chain length in chain polymers is not affected by cross-linking, this does result in progressively shorter chains for chalcogenides. Despite this difference, Sreeram et al. (1991) found that for chalcogenide networks the compositional variation of T_g could be described by the same equation if κX is replaced by β(〈r〉 − 2) where β is a system-dependent parameter. Naumis (2006) and Naumis (2015) included the effect of floppy modes on the vibrational density of states to provide theoretical justification for this observation by suggesting that the Lindemann criterion for atomic displacements at the melting point could also be applied to the glass transition. Other previous studies (Buchenau et al., 2014; Toledo-Marín and Naumis, 2017) have shown the existence of a fundamental connection between the temperature dependence of the atomic mean square displacement and viscous flow or shear relaxation in glass-forming liquids. However, the glass transition is not a true thermodynamic transition and is only significant for the fact that, by definition, the structural relaxation timescale at T_g is on the order of ~100s. Therefore, the validity of applying the Lindemann criterion to the glass transition remains questionable.

On the other hand, several studies have reported sharp changes in the activation energy of viscous flow near T_g, or in the related fragility parameter (Angell, 1991):

$\begin{array}{ll}m={\frac{\partial {\log }_{10}\eta }{\partial (T_g/T)}|}_{T=T_g}& (1)\end{array}$

where η is the viscosity, in the vicinity of T_g. That said, the original form of the rigidity percolation model cannot explain temperature-dependent dynamics in supercooled liquids because it does not include any mechanism for the thermal energy to overcome the interatomic constraints. Gupta and Mauro (2009) attempted to address this by explicitly introducing temperature-dependent network constraints in the rigidity model. This involves assigning each network constraint a switching temperature such that the constraint becomes active only when the system temperature drops below the switching point. Although this approach is used extensively in the literature to model the compositional variation of the thermophysical properties of a wide range of glass-formers, direct experimental verification of the key assumption about the switching behavior has yet to be made.

Naumis (2005) and Naumis (2015) attempted to connect the rigidity percolation model to statistical mechanics by suggesting that the floppy modes provide channels in the potential energy landscape that serve as pathways for the network to explore many local minima, and hence make a contribution S_c to the configurational entropy. This entropy was calculated as S_c = fNk_B ln Ω, where Ω is the number of accessible microstates per atomic degree of freedom and is independent of f. Floppy modes indeed provide an important source of entropy, though their connection with structural relaxation is not obvious from the standpoint of the energy landscape where metabasin hopping and vibrational excitations within the metabasins are expected to be temporally decoupled. A possible connection between the short- and long- timescale processes has been proposed by Dyre and coworkers with their elastic “shoving” model, where the rapid increase with cooling of the activation energy for structural relaxation in a fragile glass-forming liquid is attributed to a corresponding anharmonic increase of the high-frequency shear modulus (Dyre, 2006). Additionally, an exact solvable glass transition model by Toledo-Marín and Naumis (2017) has related the short-time process to the frequency of probing transition states of the energy landscape, while the long-time relaxation process represents the transition between metastable states.

The rigidity percolation model is undoubtedly useful as means to understand the behavior of random networks around the glass transition. Nevertheless, the model makes some predictions that are not consistent with experimental observations, and the average atomic coordination number 〈r〉 is not always an appropriate measure of the network connectivity (section 2.1 gives an example), at least not without qualifications described by Thorpe (1983). Moreover, a connection between the model and the statistical mechanics of glass-forming liquids has yet to be conclusively established. That is to say, the topological constraint theory of glasses should not be considered complete and inviolable.

This article proposes a variation of the topological constraint theory where, for the purposes of calculating the available degrees of freedom, the network is considered as being constructed from a collection of rigid polytopes. This view is supported by, e.g., Sidebottom's observation that the mean connectivity of a network's weakest links is more closely related to the fragility than the mean coordination number (Sidebottom, 2015, 2019), and is related to the concept of rigid unit modes in the context of negative thermal expansion materials (Evans, 1999; Fang et al., 2014). The theory is motivated and developed in section 2, along with a preliminary model that relates the available degrees of freedom to the relaxation time of a glass-forming liquid. The resulting equations are tested and evaluated for the family of chalcogenide glasses in section 3, and suggest that this variation of the topological constraint theory could be useful more generally.

2. Networks of Rigid Polytopes

This section revisits the rigidity percolation model. First, the limits of this model are explored using the example of an octahedral network, with the purpose of reinforcing that the underlying assumptions in the model are more subtle than is sometimes believed. Second, a variation on the topological constraint theory is derived where rigid polytopes are considered as the structural units of the network instead of atoms. This follows from the conceptual separation of the degrees of freedom into three classes, namely, those that are directly constrained by strong interatomic bonds, those that are constrained by the connectivity of the network, and those that are unconstrained. Apart from offering more flexibility in the application of the model, the resulting formula for the fraction of unconstrained degrees of freedom is quantitatively different from Thorpe (1983). Third, the implications of the revised model for the dynamical properties of supercooled liquids in the immediate vicinity of the glass transition are explored. The predictions of this model are compared with experiments in section 3.

2.1. Limits of the Rigity Percolation Model

Thorpe's rigidity percolation model (Thorpe, 1983) begins by classifying atoms in a random network by the number of bonds in which they participate, without distinguishing bonds of different types. If n_r is the number of atoms with r bonds, then $3\sum _r{n}_r$ is the number of degrees of freedom. Specifying the bond lengths and bond angles around an atom with r bonds imposes r/2 and 2r − 3 constraints, respectively, on the degrees of freedom. If all of these constraints are independent, then the fraction of unconstrained degrees of freedom f is given by:

$\begin{array}{ll}f=\frac{3{\displaystyle {\sum }_r{n}_r}-{\displaystyle {\sum }_r{n}_r}[r/2+(2r-3)]}{3{\displaystyle {\sum }_r{n}_r}}.& (2)\end{array}$

The average coordination number 〈r〉 is defined to be $\sum _r{n}_{r}r/\sum _r{n}_r$ (despite the misprint in Thorpe, 1983), reducing this to the standard equation:

$\begin{array}{ll}f=2-5\langle r\rangle /6.& (3)\end{array}$

Since f = 0 when 〈r〉 = 2.4, the model is often believed to predict that rigidity should percolate through the network and various properties of the system should be discontinuous around this critical value. Thorpe's original article included several qualifications to this conclusion that are unfortunately not consistently discussed in the literature, but that indicate that the situation is more nuanced than suggested by Equation (3).

Consider applying this model to the regular network of corner-sharing octahedra in a perovskite material, as shown in Figure 1A. If the formula for this material is ABO₃, then a single octahedron contains one B atom with six bonds and three O atoms with two bonds each. The average coordination number for the octahedral network is then three, and the model would seem to predict that the network is not only rigid but highly overconstrained. Nonetheless, it is widely recognized that various patterns of octahedral tilting (Glazer, 1972), including the one in Figure 1B, are low-frequency modes of the network. In fact, such soft modes are believed to be responsible for displacive phase transitions and negative thermal expansion in a number of systems (Evans, 1999; Fang et al., 2014). Possible resolutions to this apparent contradiction are considered below to help to clarify the limitations of the model as frequently interpreted, and to suggest refinements to be included in the subsequent derivation.

FIGURE 1

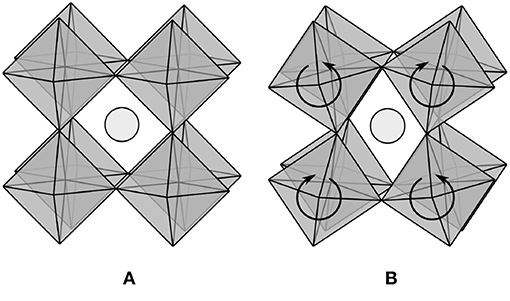
Figure 1. (A) Perovskite materials with formula ABO₃ contain a regular network of corner-sharing BO₆ octahedra, with the position of the A atom in light gray. (B) Patterns of octahedral tilting (Glazer, 1972) are low-frequency modes of the network.

Our first attempt begins with the observation that the symmetry of the ideal system allows only a constant number of octahedral tilting modes, independent of the number of atoms. Hence, as the system size approaches the thermodynamic limit, the fraction of zero-frequency modes goes to zero and the model gives the expected result. This argument is not entirely satisfying though; the number of octahedral tilting modes is constant because they extend throughout the entire network, but it is difficult to exclude the possibility of localized zero-frequency modes whose number scales with the size of a disordered system. Thorpe (1983) discussed this possibility, saying that “the number of zero frequency modes is not zero at 〈r〉 = r_p because floppy inclusions still exist”. Perhaps then the presence of localized zero-frequency modes is less relevant to the system properties than a percolating network of identical ideally rigid bonds. The difficulty with this is that bonds in physical systems are neither identical nor ideally rigid; van der Waals forces allow systems with 〈r 〉 < r_p at room temperature to solidify at low temperatures, and bond breaking allows systems with 〈r 〉 > r_p at room temperature to liquify at high temperatures. The conclusion here is the same as the one arrived at by Thorpe (1983), namely, one should neither expect to observe discontinuous behavior in the number of zero-frequency modes, nor in the properties of glass-forming liquids, at any particular value of the average coordination number.

Our second attempt considers the possibility that the number of constraints is overestimated in Equation (3). Initially observe that if the bond angles of the oxygens at the corners of the octahedra were fixed, then the octahedra would not be able to tilt. Thorpe (1983) anticipated this possibility as well: “For example in Si_xO_1−x…it is reasonable not to count the angular force at the oxygen atoms”. Since the bond angle constraints do not explicitly appear in Equation (3), such a modification needs to be performed using Equation (2). Unfortunately, excluding the oxygen bond angle constraints is insufficient to make f nonnegative, and only increases the apparent value from −0.5 to −0.25. This idea should instead be taken much further, with only independent constraints included in Equation (2) (Thorpe, 1983). The difficulty with this is that while many constraints are dependent for the octahedral network, distinguishing the dependent from the independent ones is not at all obvious due to the interactions being nonlocal (e.g., a set of bonds could form a ring). While there do exist approaches to identifying the set of independent constrains (e.g., the pebble game; Jacobs and Thorpe, 1995, 1996), these require much more detailed knowledge of the network configuration than is generally available in practice.

Perhaps since all of the quantities in Equation (2) are defined using only local information, f is more closely related to the properties of an average local environment than the overall network. Indeed, f could be interpreted as an estimate for the average fraction of unconstrained degrees of freedom per atom. A value of f = −0.25 for the octahedral network could then be rationalized as a consequence of the atoms at the centers of the octahedra being highly overconstained. If f is truly a local quantity though, one should not expect it to provide any information about the existence of nonlocal zero-frequency modes. That is, interpreting f in this way resolves the apparent contradiction introduced as motivation for this section, but raises the question of whether there is some other property that would be more relevant to the experimental properties of the system.

A revised topological constraint theory would ideally address the several concerns identified in the preceding discussion:

1. There is more than one kind of atomic interaction, and the model should distinguish rigid bond angles from flexible ones.

2. Bond angle constraints should be explicit in the model, and included only where dictated by intuition.

3. The model should suggest a connection to the nonlocal properties of the system that is explicit and consistent with experiments.

Section 2.2 proposes a revised topological constraint theory that is motivated by the first and second points, while the third is the subject of section 2.3.

2.2. Revised Topological Constraint Theory

The concept of a metabasin requires separating two types of relaxations in glass-forming liquids, namely, local rearrangements of particles and substantial structural relaxations (Stillinger, 1995). If the available kinetic energy is such that the system is confined to a single metabasin, then the system is expected to behave as a solid. Conversely, a system that often experiences the substantial structural relaxations associated with transitions between metabasins explores more of the configuration space and is expected to behave as a liquid. This suggests that characterizing the metabasins is essential to understanding the glassy state, and much effort has been expended in this direction (Doliwa and Heuer, 2003; Heuer, 2008).

Suppose that the local rearrangements in this picture can be identified with operations involving a small number of covalent bonds, and structural relaxations with changes to the network conformation or connectivity. Constraints associated with individual bonds would then be less relevant to understanding the glass transition than constraints imposed by the network connectivity on larger structural units. This serves as motivation for the topological constraint theory developed in this section, where the network is considered as being composed of rigid polytopes rather than individual atoms, and any relaxations involving bonds within a rigid polytope are explicitly not considered. While others have used rigid polytopes for this purpose before (Cooper, 1978, 1982; Gupta and Cooper, 1990), and even general networks composed of multiple types of rigid polyhedra with edge and face sharing (Gupta, 1993), those authors specifically considered the restricted question of whether topologically-disordered networks could exist. Moreover, those theories consider the number of degrees of freedom per vertex (rather than the fraction of unconstrained degrees of freedom) and require considerably more detailed knowledge of the constituent polyhedra than the theory developed here.

A polytope is a generalization of polygons and polyhedra to any nonnegative dimension. More precisely, an i-polytope is a finite region of i-dimensional space that is bounded by a finite set of (i − 1)-dimensional hyperplanes. The boundary of a polytope is itself comprised of polytopes, and a j-polytope of this type is called a j-facet¹. For example, a polyhedron (3-polytope) is bounded by faces (2-facets), the faces can join at edges (1-facets), and the edges can join at vertices (0-facets). This article only considers i-polytopes for 0 ≤ i ≤ 3, and requires two polytopes to intersect on a shared facet or not at all. For example, two tetrahedra could intersect on a 0-polytope (corner sharing), a 1-polytope (edge sharing), or a 2-polytope (face sharing), as indicated in Figure 2.

FIGURE 2

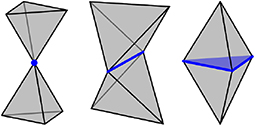
Figure 2. Two tetrahedra could intersect not at all, on a 0-polytope (Left), on a 1-polytope (center), or on a 2-polytope (Right), corresponding to corner sharing, edge sharing and face sharing.

Following the discussion above, a network of atomic bonds is represented as a network of rigid polytopes. The construction of the polytopes is flexible by design and not entirely algorithmic, but there are several general principles to follow. A polytope is usually constructed as the convex hull of a set of contiguous bonds. Substantial changes to the angles of bonds within the set should be energetically expensive since the polytopes are assumed to be rigid, and any internal degrees of freedom are explicitly ignored. This construction implies that every polytope vertex coincides with some atom; if the system contains one or more atomic species for which the bond angles are not entirely fixed (e.g., oxygen), then these should be placed at the vertices.

Figure 3 considers an example fragment of an atomic network containing two types of atoms, one 3-coordinated and the other 2-coordinated (bonds to the surroundings are omitted for simplicity). If the bond angles around the gray atoms are fixed and those around the white atoms are not, then the atomic network can be represented as a network of rods and triangles. The polytopes constructed as convex hulls of sets of atomic bonds (i.e., the rods and triangles) are called direct polytopes. The facets where direct polytopes intersect are called intersection polytopes, and encode any constraints imposed by the connectivity of the network on the motion of the direct polytopes. For example, the network in Figure 3 contains three intersection 0-polytopes, the existence of which requires the adjoining direct polytopes to share a vertex. Alternatively, one could imagine being given a collection of direct and intersection polytopes, and having to join direct polytopes along the intersection polytopes (with none left over) to create a facsimile of the atomic network.

FIGURE 3

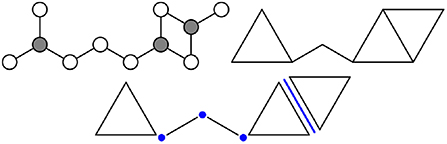
Figure 3. A portion of an atomic network (Top left) contains 2- and 3-coordinated white and gray atoms, respectively. The same network can be modeled using rigid polytopes (Top right), where the bonds around gray atoms are replaced by triangles and the remaining bonds by line segments. More precisely (Bottom), the network is composed of five direct polytopes (two 1-polytopes and three 2-polytopes) and four intersection polytopes (three 0-polytopes and one 1-polytope).

The objective of a topological constraint theory is to estimate f, the fraction of unconstrained degrees of freedom available to the network. The direct polytopes contribute degrees of freedom whereas the intersection polytopes contribute constraints; if the number of degrees of freedom contributed by a direct polytope and the number of constraints contributed by an intersection polytope are known, and every constraint is assumed to be independent, then f is straightforward to estimate. This reduces the objective of this section to the calculation of the number of degrees of freedom or constraints contributed by a given polytope.

Consider a single direct polytope. A 0-polytope requires three variables to specify the three spatial coordinates. A 1-polytope requires five variables, three for a 0-facet and two for the orientation of the attached edge. A 2- or 3-polytope requires six variables, five for a 1-facet and one for the rotation angle about that facet. For notational purposes, let d be the dimension of a direct polytope and define:

$\varphi (d)=\{\begin{array}{l}3d=0\\ 5d=1\\ 6d=2,3\end{array}.$

It is tempting to say that ϕ(d) is the number of degrees of freedom made available to the network by a direct d-polytope, but this is not necessarily the case; Figure 4 shows several situations where a direct d-polytope contributes fewer than ϕ(d) degrees of freedom. For example, the direct 3-polytope on the right constrains the distance between the connected intersection 0-polytopes, but can rotate about the relevant edge without affecting the configurations available to the network (direct polytopes not connected by intersection polytopes do not interact). That is, this direct 3-polytope effectively functions as a direct 1-polytope. Along with the other examples in Figure 4, this suggests that a direct d-polytope actually contributes only ϕ(δ) degrees of freedom, where δ ≤ d is the dimension of the convex hull of the connected intersection polytopes and is called the reduced dimension.

FIGURE 4

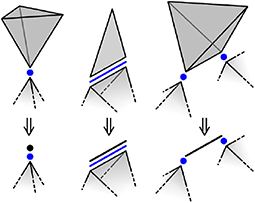
Figure 4. A direct d-polytope can contribute fewer than ϕ(d) degrees of freedom. For a direct 3-polytope connected to a single intersection 0-polytope (left), the two orientational variables do not affect the network's behavior, and the direct polytope can safely be replaced by a direct 0-polytope. More generally, only the connection of a direct polytope to an intersection polytope affects the network behavior, and the direct polytope can be replaced by the convex hull of the connected intersection polytopes.

For the intersection polytopes, the configurational variables of a single intersection d-polytope contribute ϕ(d) degrees of freedom. Connecting an intersection d-polytope to a direct polytope imposes ϕ(d) constraints on the direct polytope though, since the relevant configurational variables of the intersection and direct polytopes must be the same. There could be k additional angular constraints associated with the intersection polytope as well (counted only after reducing the dimension of the connected direct polytopes). An intersection d-polytope connected to j direct polytopes would therefore contribute a total of (j − 1)ϕ(d) + k constraints. For example, the intersection 0-polytope on the left of Figure 4 contributes three positional degrees of freedom, imposes three positional constraints on each of the connected direct polytopes, and has zero associated angular constraints for a total of three constraints.

At this point, the number of unconstrained degrees of freedom can be estimated by substracting the sum of the constraints imposed by intersection polytopes from the sum of the degrees of freedom contributed by direct polytopes. Let n_i be the number of direct polytopes with reduced dimension i, and m_ijk be the number of intersection i-polytopes with j connections to direct polytopes and k associated angular constraints. Then the proposed topological constraint theory gives the following estimate for the fraction of unconstrained degrees of freedom:

$\begin{array}{ll}f=\frac{{\displaystyle {\sum }_i{n}_i\varphi (i)}-{\displaystyle {\sum }_i{\displaystyle {\sum }_j{\displaystyle {\sum }_k{m}_{ijk}}}}[(j-1)\varphi (i)+k]}{{\displaystyle {\sum }_i{n}_i\varphi (i)}}.& (4)\end{array}$

The use of this equation can be clarified with several examples. For SiO₂, a network with n direct 3-polytopes (SiO₂ tetrahedra) would have 2n intersection 0-polytopes (oxygen atoms), each with two connections to direct polytopes and no associated angular constraints. Evaluating Equation (4) indicates that f = 0 for the SiO₂ network, in agreement with the conventional model. For the octahedral network in Figure 1, a network with n direct 3-polytopes would have 3n intersection 0-polytopes with the same properties as those for SiO₂. Evaluating Equation (4) for this network gives f = −0.5, a quantitatively different value from the −0.25 given by Equation (2) (modified to remove angular constraints on the oxygen atoms). Since the numerators of Equations (2) and (4) are both the number of unconstrained degrees of freedom (a property of the network that is independent of the model), the difference should be caused by the denominators. That is, there is a quantitative difference that results from choosing atoms or rigid polytopes as the structural units of the network. The preferred choice should depend on whether Equations (2) or (4) is more strongly correlated with the experimental data.

2.3. A Model for Entropy and Relaxation

Ideally, the relevance of the topological constraint theory developed in section 2.2 to physical systems would be established by connecting the fraction of unconstrained degrees of freedom f to an experimentally-observable quantity, and comparing the predicted and experimental values of that quantity. The purpose of this section is to motivate and derive an equation for the relaxation time τ of a glass-forming liquid that depends explicitly on f. This will imply functional dependencies of the glass transition temperature T_g and the fragility m on f that will be compared with experiments in section 3.

Given a single primary relaxation mechanism, a relaxation time τ can be modeled as having an Arrhenius dependence on temperature, at least over a limited temperature range near T_g. The relaxation time τ can then be simply written as:

$\tau ={\tau }_0\exp \left(\frac{\Delta G}{k_{B}T}\right)\text{}.$

The free energy of activation ΔG can be written in terms of an activation enthalpy and entropy. If only the activation entropy ΔS depends explicitly on f, the expression for τ can be re-written as:

$\begin{array}{ll}\tau ={\tau }_0\exp \text{}(-\frac{\Delta S(f)}{k_B})\exp \left(\frac{\Delta H}{k_{B}T}\right)\text{}.& (5)\end{array}$

This leaves only the construction of a model for ΔS(f) to be able to relate f to an experimental observable.

For this purpose, assume that the configurational entropy of a network containing chain-like moieties cross-linked by pyramidal or tetrahedral units is dominated by the conformational entropy of the chains. A simple model of such a network could contain 2-coordinated white atoms and v-coordinated gray atoms with all of the white atoms participating in chains of length n, as on the left of Figure 5. A single chain can be modeled as a self-avoiding walk (SAW), with a number of configurations approximately given by:

$\begin{array}{l}Z(n)=A{\mu }^n{n}^{\gamma -1}\end{array}$

where A, μ and γ are constants (Madras and Sokal, 1988; Schram et al., 2017). Using Boltzmann's formula S = k_B ln Z, the conformational entropy of a single chain depends on n as:

$\begin{array}{l}S(n)=k_B\left[lnA+nln\mu +(\gamma -1)lnn\right]\end{array}$

where k_B is Boltzmann's constant. Since entropy is an extensive quantity, the change in configurational entropy when breaking a bond to convert one chain of length n into two chains of length ~n/2, as on the right of Figure 5, is:

$\begin{array}{l}\Delta S=2S(n/2)-S(n)\\ =k_B[(\gamma -1)\ln (n/4)+\ln A].& (6)\end{array}$

This is interpreted as the activation entropy for the bond scission-renewal dynamics. While many distinct microscopic events are expected to contribute to the effective bond-breaking mechanism in practice, the reasoning above is intended only to motivate the form of the dependence of ΔS on n.

FIGURE 5

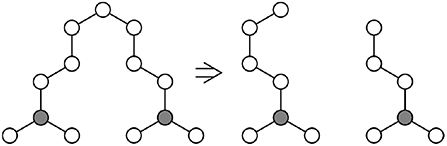
Figure 5. Consider part of a network containing only chains of length n, with v chains connected to a single gray atom (Left). One possible bond-breaking event would convert one of these chains into two chains of length ~n/2 (Right), increasing the entropy of the system.

The dependence of n on f for the system on the left of Figure 5 can be established using Equation (4). Specifically, a single chain contributes n direct 1-polytopes (n − 1), intersection 0-polytopes with two connections to direct polytopes along the chain, and 2/v intersection 0-polytopes with v connections to adjoining chains. Evaluating Equation (4) gives:

$\begin{array}{l}f=\frac{2}{5}-\frac{3-6/v}{5n}\end{array}$

for the fraction of unconstrained degrees of freedom f as a function of n. Solving instead for n gives:

$\begin{array}{ll}n=\frac{3-6/v}{2-5f}& (7)\end{array}$

which indicates that the chain length diverges as f → 0.4. Since repeating the derivation with the chain segments as 3-polytopes instead of 1-polytopes and not using the reduced dimension makes the chain length diverge as f → 0.5, a significant change is expected in the properties of most glass-forming liquids in the interval 0.4 ≤ f ≤ 0.5. Substituting Equation (7) into Equation (6) gives:

$\begin{array}{l}\Delta S(f)=-k_B\left\{(\gamma -1)\ln (0.4-f)-\left[(\gamma -1)\ln \text{}\left(\frac{3-6/v}{20}\right)+\ln A\right]\right\}\\ =-k_B[a\ln (b-f)-c]\end{array}$

for the change in configurational entropy, where a, b and c are constants. The value of a is expected to be around 0.157 from the literature (Madras and Sokal, 1988; Schram et al., 2017), and b is expected to be in the interval 0.4 ≤ b ≤ 0.5 by the above reasoning. Finally, substituting the equation for ΔS(f) into Equation (5) gives:

$\begin{array}{ll}\tau ={\tau }_0^{\prime }{(b-f)}^a\exp \text{}\left(\frac{\Delta H}{k_{B}T}\right)& (8)\end{array}$

for the relaxation time, where ${\tau }_0^{\prime }={\tau }_{0}exp(-c)$. If there is a characteristic relaxation time τ_g ≈ 100s that is a universal constant at the glass transition temperature T_g, then Equation (8) can be inverted to find T_g as a function of f:

$\begin{array}{ll}{T}_g=\frac{\Delta H/k_B}{ln({\tau }_g/{\tau }_0^{\prime })-aln(b-f)}.& (9)\end{array}$

The fragility m, on the other hand, is related by the Adam-Gibbs model of relaxation (Adam and Gibbs, 1965) to the temperature dependence of the configurational entropy S_c:

$\begin{array}{ll}m\propto {\frac{\partial S_c}{\partial T}|}_{T=T_g}.& (10)\end{array}$

Sidebottom (2015) has recently suggested that the temperature dependence of S_c is governed by the connectivity of a network. Estimating the conformational entropy of a network formed via progressive cross-linking of chains indicated an abrupt rise in m as the average chain length n between cross-linking points increased beyond ~3. Substituting this value of n into Equation (7) gives 0.30 ≤ f ≤ 0.33 for 3 ≤ v ≤ 4, values typical for chalcogenide glasses. Taken together, these results suggest that fragility m is expected to rise abruptly as f increases beyond 0.3. These predictions for the dependence of T_g and m on f are compared with experimental results for chalcogenide systems in section 3 below.

3. Connection With Experiments

For the examination of select thermophysical properties of glass-forming networks as a function of f, we restrict ourselves to binary and ternary compositions in the Ge-As-Se system ranging from pure chalcogen Se to up to the stoichiometric compositions along the GeSe₂-As₂Se₃ join. This system is chosen as it represents a simple compositional evolution from a chain-like structure for pure Se to a 3-dimensional network for the stochiometric compositions. There is the additional advantage that the nature and strength of the homopolar Se-Se and heteropolar Ge/As-Se bonds in this system are similar, which ensures that their effects on the network rigidity can be considered comparable. Although other chalcogenide systems, i.e., the sulfides and the tellurides, share similarities in the compositional variation of their physical properties, the increasingly ionic behavior in sulfides and metallic behavior in tellurides result in significant differences in the nature of the homopolar and heteropolar bonds (Wei et al., 2017). The analysis of S-rich glasses is further complicated by the presence of S₈ rings that do not participate in the network (Zhu et al., 2018). The chalcogen-deficient glass-forming compositions are not considered either, since such networks are over-constrained and the estimation of f for such networks is not physically sensible. Moreover, the structure of chalcogen-deficient Ge-As-Se networks is known to be complicated by the formation of molecular elements of the type As₄Se₃, As₄Se₄ and As₄, as well as the appearance of Ge-Ge bonds in ethane-like Se_3/2-Ge-Ge-Se_3/2 units and Ge-As bonds (Sen and Aitken, 2002; Yang et al., 2010; Kaseman et al., 2014). The quantitative estimation of the relative concentrations of these structural units and their effects on the network rigidity are not straightforward and will be considered in the future. Finally, it is well known that the GeSe_4/2 tetrahedral units in the structural network of Ge_xSe_1−x glasses over the composition range 0 ≤ x ≤ 0.33 are predominantly corner-sharing, but a small fraction (15–35%) that increases monotonically with x form edge-sharing tetrahedral units (Salmon, 2007; Edwards and Sen, 2011). Sidebottom (2015) suggested that the edge-sharing tetrahedra provide more degrees of freedom to the network compared to their corner-sharing counterparts since the shared edge does not participate in the connectivity of the rest of the network. However, this does not account for the fact that edge-sharing between tetrahedra or other rigid polytopes can severely over-constrain the local degrees of freedom of the polytope itself (Gupta and Cooper, 1990; Marple et al., 2019). Here we assume that these effects approximately cancel, and that all of the tetrahedra are corner-sharing at the concentrations considered below.

Now consider the fractional degrees of freedom f of a chalcogenide network with composition Ge_xAs_ySe_1−x−y that contains n_a atoms and n_d direct polytopes. Let α be the fraction of direct polytopes that are GeSe_4/2 tetrahedra (3-polytopes), β be the fraction that are AsSe_3/2 triangles (reduced 2-polytopes), and (1 − α − β) be the fraction that are Se_2/2 line segments (1-polytopes). The first step to calculate f is to find expressions for the direct polytope fractions α and β in terms of the atomic fractions x and y. Equating the number of Ge, As, and Se atoms with those that appear in the direct polytopes gives the following system of equations:

$\begin{array}{l}x{n}_a=\alpha n_d\\ y{n}_a=\beta n_d\\ (1-x-y)n_a=(1+\alpha +0.5\beta )n_d\end{array}$

Solving for the number of direct polytopes n_d as a function of x and y and substituting the result into the first and second equations gives:

$\begin{array}{l}\alpha =\frac{x}{1-2x-1.5y}\\ \beta =\frac{y}{1-2x-1.5y}\end{array}$

for the fractions of direct 3-polytopes and direct 2-polytopes. The second step to calculate f is to find the types and numbers of all intersection polytopes. Given the assumption that all direct polytopes are corner sharing, the network contains only intersection 0-polytopes, each with two connections to direct polytopes and no associated angular constraints. Since there is precisely one intersection 0-polytope for every Se atom, the number n_i of intersection 0-polytopes is:

$\begin{array}{l}{n}_i=(1-x-y)n_a\\ =\frac{1-x-y}{1-2x-1.5y}{n}_d.\end{array}$

Evaluating Equation (4) for a network containing αn_d direct 3-polytopes, βn_d direct 2-polytopes, (1 − α − β)n_d direct 1-polytopes, and n_i intersection 0-polytopes gives:

$\begin{array}{ll}f=\frac{2-6x-3.5y}{5-9x-6.5y}& (11)\end{array}$

for the fraction of unconstrained degrees of freedom.

The value of f is compared with the average coordination number 〈r〉 = 2x + y + 2 in Figure 6 for the binary and ternary Ge-As-Se compositions considered in this study. That f should nearly be a function of 〈r〉 is surprising, given that both f and 〈r〉 are functions of two independent variables relating to the number of tetrahedral and pyramidal cross-linking elements. It is also immediately apparent that the variation of f with 〈r〉 is quite different from that obtained by Thorpe using Equation (3), since that version of f decreases linearly with 〈r 〉 < r_p until the sharp transition at r_p = 2.4. The f obtained using Equation (11) is instead nearly a nonlinear function of 〈r〉 that goes to zero at r_p = 2.67. As a result, the model developed in section 2.2 predicts that As₂Se₃ and GeSe₄ with 〈r〉 = 2.4 are underconstrained networks, whereas Equation (3) predicts that they are isostatically rigid; the source of this difference is in the application of the angular constraints around Se atoms. This prediction of our model calls into question the existence of the IP as defined elsewhere (Wang et al., 2000; Boolchand et al., 2001, 2005; Chakravarty et al., 2004). Furthermore, one should expect a rapid increase in the elastic moduli beyond r_p = 2.67 as the network is increasingly over constrained; such behavior is indeed observed for a wide variety of binary and ternary Ge-As/Sb-S/Se chalcogenide glasses (Tanaka, 1989; Yang et al., 2013).

FIGURE 6

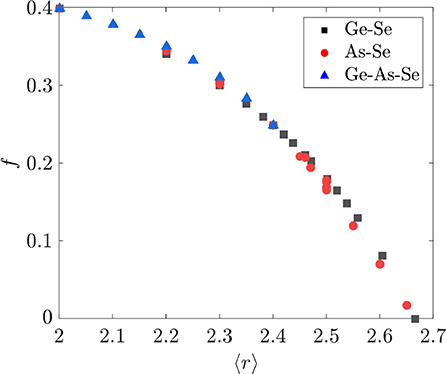
Figure 6. Fractional degrees of freedom f as a function of average coordination number 〈r〉. Composition ranges for the various systems are Ge_xSe_1−x with 0.0 ≤ x ≤ 0.33, As_xSe_1−x with 0.0 ≤ x ≤ 0.40, and Ge_xAs_ySe_1−x−y with 0.05 ≤ x ≤ 0.312 and 0.025 ≤ y ≤ 0.325.

The glass transition temperature T_g for glass-forming liquids represents an isoviscous temperature where the viscosity is ~10¹² Pa · s and the relaxation time is ~100s, and is expected to be a monotonic function of the average connectivity of a network. Since the bond strengths of the homopolar Se-Se and heteropolar Ge-Se and As-Se bonds are comparable, the T_g of Ge-As-Se glasses should monotonically decrease with f. This is borne out in Figure 7, which shows a nearly universal and linear decrease in T_g with increasing f in these glasses. The black line in Figure 7 is given by fitting Equation (9) to the data using τ_g = 100s, ${\tau }_0^{\prime }=10^{-13}\text{s}$, b = 0.45, and a standard conjugate gradient minimization algorithm for the remaining parameters. This procedure gives ΔH = 3.552 ± 0.001eV and a = 36.32 ± 0.02, with parameter uncertanties estimated by calculating the Hessian matrix at the minimum. An activation enthalpy ΔH of around twice the bond energy is reasonable enough for a scission event given the simplicity of the model developed in section 2.3, and is roughly consistent with the value of ~2.7 eV for the Ge_xSe_1−x system as reported in the literature (Gueguen et al., 2011). The deviation of a from the expected value of 0.157 is more dramatric, with the activation entropy being ~200 times larger than expected. This could be related to the number of configurations in SAW models generally being calculated for chains on lattices rather than in continuous space, or to the neglect of the effect of a scission event on the conformations available to the surrounding network components.

FIGURE 7

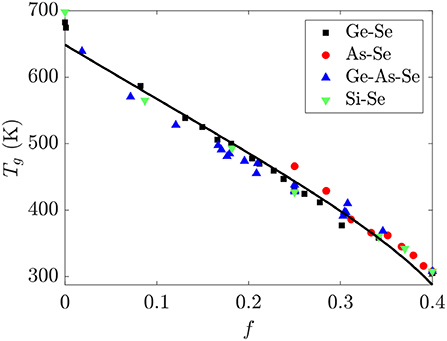
Figure 7. The glass transition temperature T_g for binary Ge-Se, As-Se, Si-Se and ternary Ge-As-Se glasses is nearly a linear function of the fractional degrees of freedom f. The black line is a fit using Equation (9) for the parameter values reported in the text. T_g data are from Bernatz et al. (2002), Yang et al. (2010), Musgraves et al. (2011), Wang et al. (2014), Marple et al. (2017), Zeidler et al. (2017).

The dependence of the fragility m on f for the same Ge-As-Se liquids is shown in Figure 8. A nearly universal functional dependence between m and f is again observed for glass-forming liquids in this system, where m is nearly constant ~30 for 0 ≤ f ≤ 0.3 and rapidly increases to ~80 for 0.3 ≤ f ≤ 0.4. Recent studies have suggested that this behavior is related to the disappearance of the conformational entropy of the selenium chain segments as their average length is reduced to ~3 (Naumis, 2015; Sidebottom, 2015), and is consistent with the prediction made in section 2.3 for the corresponding threshold value of 0.30 ≤ f ≤ 0.33. By comparison, the onset of the sharp rise in m coincides with 〈r〉 ≈ 2.3, below where the conventional topological constraint theory predicts a transition.

FIGURE 8

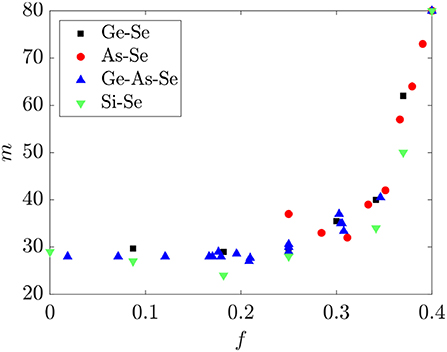
Figure 8. The fragility m for binary Ge-Se, As-Se, Si-Se and ternary Ge-As-Se glasses as a function of the fractional degrees of freedom f. Fragility data are from Bernatz et al. (2002), Koštál and Málek (2010), Gueguen et al. (2011), Musgraves et al. (2011), Wang et al. (2014), Svoboda and Málek (2015), Marple et al. (2019).

4. Conclusions

A rigid polytope model of glass structure is developed and used to calculate the relative fraction of unconstrained degrees of freedom f, the result having a fundamentally different dependence on 〈r〉 than that originally obtained by Thorpe (1983) using a mean-field approximation. The variation of T_g and m of binary and ternary chalcogenide glass-forming liquids in the Ge-As-Se system shows nearly universal dependence on f over a wide range of compositions. While T_g decreases almost linearly with f, m does not vary significantly in the range 0 ≤ f ≤ 0.3 but increases rapidly with f for 0.3 ≤ f ≤ 0.4. The variation of T_g with f can be explained by considering the change in the conformational entropy associated with the bond scission-renewal process of chain segments as the primary mode of structural relaxation of the glassy network. On the other hand, following Sidebottom (Sidebottom, 2015), the rapid increase in m for f > 0.3 is ascribed to the corresponding rise in the conformational entropy of the selenium chain segments as their average length increases beyond ~3 Se atoms.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

SS suggested the idea of using rigid polytopes to calculate topological constraints. JM developed the theoretical construct and performed all calculations. SS and JM analyzed the results and wrote the manuscript.

Funding

SS was supported by the National Science Foundation under Grant No. DMR 1855176. JM was supported by the National Science Foundation under Grant No. DMR 1839370.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Formally, a i-polytope is its own i-facet.

References

Adam, G., and Gibbs, J. H. (1965). On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 43, 139–146.

Google Scholar

Angell, C. (1991). Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems. J. Non-Crystall. Solids 131, 13–31.

Google Scholar

Bernatz, K., Echeverría, I., Simon, S., and Plazek, D. (2002). Characterization of the molecular structure of amorphous selenium using recoverable creep compliance measurements. J. Non-Crystalline Solids 307, 790–801. doi: 10.1016/S0022-3093(02)01522-3

CrossRef Full Text | Google Scholar

Boolchand, P., Georgiev, D., and Goodman, B. (2001). Discovery of the intermediate phase in chalcogenide glasses. J. Optoelectr. Adv. Mater. 3, 703–720. Available online at: https://joam.inoe.ro/arhiva/Pdf3_3/Boolchand.pdf

Google Scholar

Boolchand, P., Lucovsky, G., Phillips, J., and Thorpe, M. (2005). Self-organization and the physics of glassy networks. Philos. Magaz. 85, 3823–3838. doi: 10.1080/14786430500256425

CrossRef Full Text | Google Scholar

Buchenau, U., Zorn, R., and Ramos, M. (2014). Probing cooperative liquid dynamics with the mean square displacement. Phys. Rev. E 90:042312. doi: 10.1103/PhysRevE.90.042312

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakravarty, S., Georgiev, D., Boolchand, P., and Micoulaut, M. (2004). Ageing, fragility and the reversibility window in bulk alloy glasses. J. Phys. Conden. Matt. 17:L1. doi: 10.1088/0953-8984/17/1/L01

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper, A. R. Jr. (1982). WH Zachariasen-the melody lingers on. J. Non-Crystalline Solids 49, 1–17. doi: 10.1016/0022-3093(82)90105-3

CrossRef Full Text | Google Scholar

Cooper, A. (1978). Zachariasen's rules, Madelung constant, and network topology. Phys. Chem. Glass. 19, 60–68.

DiMarzio, E., and Gibbs, J. (1964). On the second-order transition of a rubber. J. Res. Nat. Bur. Stand. A 68, 611–617.

Google Scholar

Doliwa, B., and Heuer, A. (2003). Energy barriers and activated dynamics in a supercooled Lennard-Jones liquid. Phys. Rev. E 67:031506. doi: 10.1103/PhysRevE.67.031506

PubMed Abstract | CrossRef Full Text | Google Scholar

Dyre, J. C. (2006). Colloquium: the glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 78, 953–972. doi: 10.1103/RevModPhys.78.953

CrossRef Full Text | Google Scholar

Edwards, T., and Sen, S. (2011). Structure and relaxation in germanium selenide glasses and supercooled liquids: a Raman spectroscopic study. J. Phys. Chem. B 115, 4307–4314. doi: 10.1021/jp202174x

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, J. S. (1999). Negative thermal expansion materials. J. Chem. Soc. Dalton Trans. 19, 3317–3326.

Google Scholar

Fang, H., Dove, M. T., and Phillips, A. E. (2014). Common origin of negative thermal expansion and other exotic properties in ceramic and hybrid materials. Phys. Rev. B 89:214103. doi: 10.1103/PhysRevB.89.214103

CrossRef Full Text | Google Scholar

Gibbs, J. H., and DiMarzio, E. A. (1958). Nature of the glass transition and the glassy state. J. Chem. Phys. 28, 373–383.

Google Scholar

Glazer, A. (1972). The classification of tilted octahedra in perovskites. Acta Crystallogr. Sec. B Struct. Crystallogr. Crystal Chem. 28, 3384–3392.

Google Scholar

Gueguen, Y., Rouxel, T., Gadaud, P., Bernard, C., Keryvin, V., and Sangleboeuf, J.-C. (2011). High-temperature elasticity and viscosity of Ge x Se 1-x glasses in the transition range. Phys. Rev. B 84:064201. doi: 10.1103/PhysRevB.84.064201

CrossRef Full Text | Google Scholar

Gupta, P., and Cooper, A. (1990). Topologically disordered networks of rigid polytopes. J. Non-Crystalline Solids 123, 14–21.

Google Scholar

Gupta, P. K. (1993). Rigidity, connectivity, and glass-forming ability. J. Am. Ceram. Soc. 76, 1088–1095.

Google Scholar

Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130:094503. doi: 10.1063/1.3077168

PubMed Abstract | CrossRef Full Text | Google Scholar

He, H., and Thorpe, M. F. (1985). Elastic properties of glasses. Phys. Rev. Lett. 54:2107.

PubMed Abstract | Google Scholar

Heuer, A. (2008). Exploring the potential energy landscape of glass-forming systems: from inherent structures via metabasins to macroscopic transport. J. Phys. Conden. Matt. 20:373101. doi: 10.1088/0953-8984/20/37/373101

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobs, D., and Thorpe, M. (1996). Generic rigidity percolation in two dimensions. Phys. Rev. E 53:3682.

PubMed Abstract | Google Scholar

Jacobs, D. J., and Thorpe, M. F. (1995). Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 75:4051.

PubMed Abstract | Google Scholar

Kamitakahara, W., Cappelletti, R., Boolchand, P., Halfpap, B., Gompf, F., Neumann, D., et al. (1991). Vibrational densities of states and network rigidity in chalcogenide glasses. Phys. Rev. B 44:94.

PubMed Abstract | Google Scholar

Kaseman, D. C., Hung, I., Gan, Z., Aitken, B., Currie, S., and Sen, S. (2014). Structural and topological control on physical properties of arsenic selenide glasses. J. Phys. Chem. B 118, 2284–2293. doi: 10.1021/jp412451h

PubMed Abstract | CrossRef Full Text | Google Scholar

Koštál, P., and Málek, J. (2010). Viscosity of selenium melt. J. Non-Crystalline Solids 356, 2803–2806. doi: 10.1016/j.jnoncrysol.2010.09.032

CrossRef Full Text | Google Scholar

Madras, N., and Sokal, A. D. (1988). The pivot algorithm: a highly efficient Monte Carlo method for the self-avoiding walk. J. Statist. Phys. 50, 109–186.

Google Scholar

Marple, M., Hung, I., Gan, Z., and Sen, S. (2017). Structural and topological evolution in Si x Se1–x glasses: results from 1D and 2D 29Si and 77Se NMR spectroscopy. J. Phys. Chem. B 121, 4283–4292. doi: 10.1021/acs.jpcb.7b01307

CrossRef Full Text | Google Scholar

Marple, M. A., Yong, V., and Sen, S. (2019). Fragility and aging behavior of SixSe1-x glasses and liquids. J. Chem. Phys. 150:044506. doi: 10.1063/1.5080225

PubMed Abstract | CrossRef Full Text | Google Scholar

Musgraves, J. D., Wachtel, P., Novak, S., Wilkinson, J., and Richardson, K. (2011). Composition dependence of the viscosity and other physical properties in the arsenic selenide glass system. J. Appl. Phys. 110:063503. doi: 10.1063/1.3638122

CrossRef Full Text | Google Scholar

Naumis, G. G. (2005). Energy landscape and rigidity. Phys. Rev. E 71:026114. doi: 10.1103/PhysRevE.71.026114

PubMed Abstract | CrossRef Full Text | Google Scholar

Naumis, G. G. (2006). Variation of the glass transition temperature with rigidity and chemical composition. Phys. Rev. B 73:172202. doi: 10.1103/PhysRevB.73.172202

CrossRef Full Text | Google Scholar

Naumis, G. G. (2015). Low-frequency vibrational modes anomalies and rigidity: a key to understanding the glass and the electronic properties of flexible materials from a topological perspective. Front. Mater. 2:44. doi: 10.3389/fmats.2015.00044

CrossRef Full Text | Google Scholar

Phillips, J. (1981). Topology of covalent non-crystalline solids II: Medium-range order in chalcogenide alloys and A? Si (Ge). J. Non-Crystalline Solids 43, 37–77.

Google Scholar

Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: short-range order in chalcogenide alloys. J. Non-Crystalline Solids 34, 153–181.

Google Scholar

Salmon, P. S. (2007). Structure of liquids and glasses in the Ge–Se binary system. J. Non-Crystalline Solids 353, 2959–2974. doi: 10.1016/j.jnoncrysol.2007.05.152

CrossRef Full Text | Google Scholar

Schram, R. D., Barkema, G. T., Bisseling, R. H., and Clisby, N. (2017). Exact enumeration of self-avoiding walks on BCC and FCC lattices. J. Statist. Mech. Theory Exp. 2017:083208. doi: 10.1088/1742-5468/aa819f

CrossRef Full Text | Google Scholar

Sen, S., and Aitken, B. (2002). Atomic structure and chemical order in Ge-As selenide and sulfoselenide glasses: an x-ray absorption fine structure spectroscopic study. Phys. Rev. B 66:134204. doi: 10.1103/PhysRevB.66.134204

CrossRef Full Text | Google Scholar

Sen, S., Xia, Y., Zhu, W., Lockhart, M., and Aitken, B. (2019). Nature of the floppy-to-rigid transition in chalcogenide glass-forming liquids. J. Chem. Phys. 150:144509. doi: 10.1063/1.5092841

PubMed Abstract | CrossRef Full Text | Google Scholar

Sidebottom, D. (2019). Connecting glass-forming fragility to network topology. Front. Mater. 6:144. doi: 10.3389/fmats.2019.00144

CrossRef Full Text | Google Scholar

Sidebottom, D. L. (2015). Fragility of network-forming glasses: a universal dependence on the topological connectivity. Phys. Rev. E 92:062804. doi: 10.1103/PhysRevE.92.062804

PubMed Abstract | CrossRef Full Text | Google Scholar

Sreeram, A., Swiler, D., and Varshneya, A. (1991). Gibbs-DiMarzio equation to describe the glass transition temperature trends in multicomponent chalcogenide glasses. J. Non-Crystalline Solids 127, 287–297.

Google Scholar

Stillinger, F. H. (1995). A topographic view of supercooled liquids and glass formation. Science 267, 1935–1939.

PubMed Abstract | Google Scholar

Svoboda, R., and Málek, J. (2015). Kinetic fragility of Se-based binary chalcogenide glasses. J. Non-Crystalline Solids 419, 39–44. doi: 10.1016/j.jnoncrysol.2015.03.041

CrossRef Full Text | Google Scholar

Tanaka, K. (1989). Structural phase transitions in chalcogenide glasses. Phys. Rev. B 39:1270.

PubMed Abstract | Google Scholar

Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non-Crystalline Solids 57, 355–370.

Google Scholar

Toledo-Marín, J. Q., and Naumis, G. G. (2017). Short time dynamics determine glass forming ability in a glass transition two-level model: a stochastic approach using Kramers' escape formula. J. Chem. Phys. 146:094506. doi: 10.1063/1.4977517

CrossRef Full Text | Google Scholar

Wang, T., Gulbiten, O., Wang, R., Yang, Z., Smith, A., Luther-Davies, B., et al. (2014). Relative contribution of stoichiometry and mean coordination to the fragility of Ge–As–Se glass forming liquids. J. Phys. Chem. B 118, 1436–1442. doi: 10.1021/jp412226w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Boolchand, P., and Micoulaut, M. (2000). Glass structure, rigidity transitions and the intermediate phase in the Ge–As–Se ternary. EPL 52:633. doi: 10.1209/epl/i2000-00485-9

CrossRef Full Text | Google Scholar

Wei, S., Coleman, G. J., Lucas, P., and Angell, C. A. (2017). Glass transitions, semiconductor-metal transitions, and fragilities in Ge-V-Te (V= As, Sb) liquid alloys: the difference one element can make (vol 7, 034035, 2017). Phys. Rev. Appl. 8:049901. doi: 10.1103/PhysRevApplied.8.049901

CrossRef Full Text

Yang, G., Bureau, B., Rouxel, T., Gueguen, Y., Gulbiten, O., Roiland, C., et al. (2010). Correlation between structure and physical properties of chalcogenide glasses in the As x Se 1- x system. Phys. Rev. B 82:195206. doi: 10.1103/PhysRevB.82.195206

CrossRef Full Text | Google Scholar

Yang, G., Gueguen, Y., Sangleboeuf, J.-C., Rouxel, T., Boussard-Plédel, C., Troles, J., et al. (2013). Physical properties of the GexSe1-x glasses in the 0 <x<0.42 range in correlation with their structure. J. Non-Crystalline Solids 377, 54–59. doi: 10.1016/j.jnoncrysol.2013.01.049

CrossRef Full Text | Google Scholar

Zeidler, A., Salmon, P. S., Whittaker, D. A., Pizzey, K. J., and Hannon, A. C. (2017). Topological ordering and viscosity in the glass-forming Ge–Se system: The search for a structural or dynamical signature of the intermediate phase. Front. Mater. 4:32. doi: 10.3389/fmats.2017.00032

CrossRef Full Text | Google Scholar

Zhao, H., Koh, Y., Pyda, M., Sen, S., and Simon, S. (2013). The kinetics of the glass transition and physical aging in germanium selenide glasses. J. Non-Crystalline Solids 368, 63–70. doi: 10.1016/j.jnoncrysol.2013.02.025

CrossRef Full Text | Google Scholar

Zhu, W., Lockhart, M. J., Aitken, B. G., and Sen, S. (2018). Rheology of the λ transition in liquid sulfur: insights from arsenic sulfide liquids. J. Chem. Phys. 148:244506. doi: 10.1063/1.5037719

PubMed Abstract | CrossRef Full Text | Google Scholar