Asymmetric Dynamic Model of Temperature-Dependent Magnetorheological Damper and Application for Semi-active System

Introduction

Magnetorheological (MR) fluid is a suspension of micrometer-scale magnetic particles in non-magnetic carrier fluid. Its rheological properties can be tuned from Newtonian-like fluid state to semi-solid state by applying a magnetic field. The particles of MR fluid will be arranged in chains along magnetic induction lines. The outstanding properties of MR fluid such as fast response, reversible characteristics, and controllability depending on magnetic field have prompted a large number of studies and applications. To date, MR fluid dampers have been applied in some high-end vehicle suspensions, seat suspensions, bridges, and buildings because of the controllability and lower energy requirements (Choi et al., 2016). In general, the force of MR damper is mainly influenced by velocity and magnetic field. During the long running period, the damping force also changes with the self-induced temperature and ambient temperature (Wereley, 2013). With increment of temperature, damping force declines due to the decreased viscosity and yield stress (Wilson et al., 2009; Bahiuddin et al., 2018). Further, control performances may be deteriorated with the variation of temperature (Choi et al., 2005). The root mean square (RMS) of working space increased by 6% in single-degree-of-freedom (SDOF) with the decreasing of damping force (Batterbee and Sims, 2009). The acceleration response of the sprung mass and suspension travel in the 2-DOF tracked vehicle suspension are both degraded in a study by Zhang et al. (2013). For describing accurately damping characteristics and control performances, establishing a dynamic model is important. By a set of springs, viscous dashpots, and friction elements, parametric models are commonly analyzed, such as the bi-viscous model (Wereley et al., 1998), Bouc-wen model (Bai et al., 2015; Miah et al., 2015) and hyperbolic tangent model (Kwok et al., 2006). Considering the effect of temperature on MR damper, Jumani created an empirically derived invertible model (Jumani, 2010). Sahin improved the Bouc-wen model to capture the temperature-dependent dynamic behavior (Sahin et al., 2010).

In general, the dynamic models are established to describe symmetric hysteresis loops. In practice, some force-velocity and force-displacement loops are asymmetric due to the asymmetrical boundary conditions. These type asymmetric curves of MR dampers can be seen in the studies of Choi et al. (2001), Wang and Liao (2011), Domínguez-González et al. (2014), and Wang et al. (2007). To capture the asymmetric loops of a large-scale MR damper, García-Baños proposed an asymmetric-friction based model by modifying the viscous and Dahl model (García-Baños et al., 2017). In other fields, some dynamic models have been proposed to describe the asymmetric characteristics of piezoelectric actuator, flexible connectors, shape memory alloy, and magnetorheological elastomers. Jiang proposed a modified Prandtl-Ishlinskii model to capture the asymmetric hysteresis of piezoelectric actuators (Jiang et al., 2010). Gu also used a modified Prandtl-Ishlinskii model to describe the asymmetric hysteresis non-linearity of piezo-ceramic actuators (Gu et al., 2014). Song proposed a generalized Bouc-wen model to describe the non-centrosymmetric force-displacement loops of flexible strap connectors (Song and Der Kiureghian, 2006). In Dobson's study, the unloading stiffness reduction model was used to capture asymmetric hysteresis of a SDOF system with shape memory alloy (Dobson et al., 1997). Leng utilized artificial neural networks optimized by fuzzy algorithm (ANNOFA) model to capture the asymmetrical force characteristics of a magnetorheological elastomer isolator in shear-compression mode (Leng et al., 2018).

Based on the above analysis, the models with differential items are applied widely to capture non-linear controlled characteristics, especially the Bouc-wen model. The differential items can reduce the efficiency of parameter identification. Considering the efficiency of the algebraic model in the identification process, the algebraic model is useful to portray the asymmetric loops (Sahin et al., 2010). Therefore, an algebraic model which can describe the temperature effects and asymmetric characteristics is proposed and analyzed. The main contents are as follows. The dynamic characteristics of the MR damper are tested and analyzed in section Asymmetric Dynamic Characteristics of Temperature-Dependent MR Damper. Section Modelling and Identification displays the construction of model. Additionally, the parameters of the model are identified to track the experimental results. The semi-active system with the proposed model is simulated in section Application Case in Semi-active System. Finally, the conclusions are drawn in section Conclusion.

Asymmetric Dynamic Characteristics of Temperature-Dependent MR Damper

The mono-tube MR damper for seat suspension and its test apparatus are shown in Figure 1. The damper mainly consists of a cylinder, rod, piston, coil, and floating piston. The floating piston divides the damper into the fluid chamber and the gas accumulator. The MR fluid in the fluid chamber will generate controllable damping force under a magnetic field. The gas accumulator filled with nitrogen gas is used to compensate volumetric change. Coil spooling around the piston generates a controlled magnetic field by tuning the electrical current. To analyze the characteristics of the MR damper under different conditions, a series of experimental tests are conducted based on a computer-controlled MTS machine, electrical power supply, and incubator. The test apparatus is displayed in Figure 1C. The DC power supply is used to provide electrical energy to coil in the MR damper. Various harmonic inputs are chosen to load the MR damper. The amplitudes of sinusoidal excitation are 4, 6, and 8 mm, and the frequencies are 0.5, 0.6, and 0.7 Hz. The field-dependent characteristics are tested under current of 0, 0.4, 0.8, and 1.2 A. The MR damper is tested under fixed temperature increasing from 20 to 80°C with a step of 20°C. To ensure the stable temperature of the MR damper, it is heated in the incubator for about 3 h.

FIGURE 1

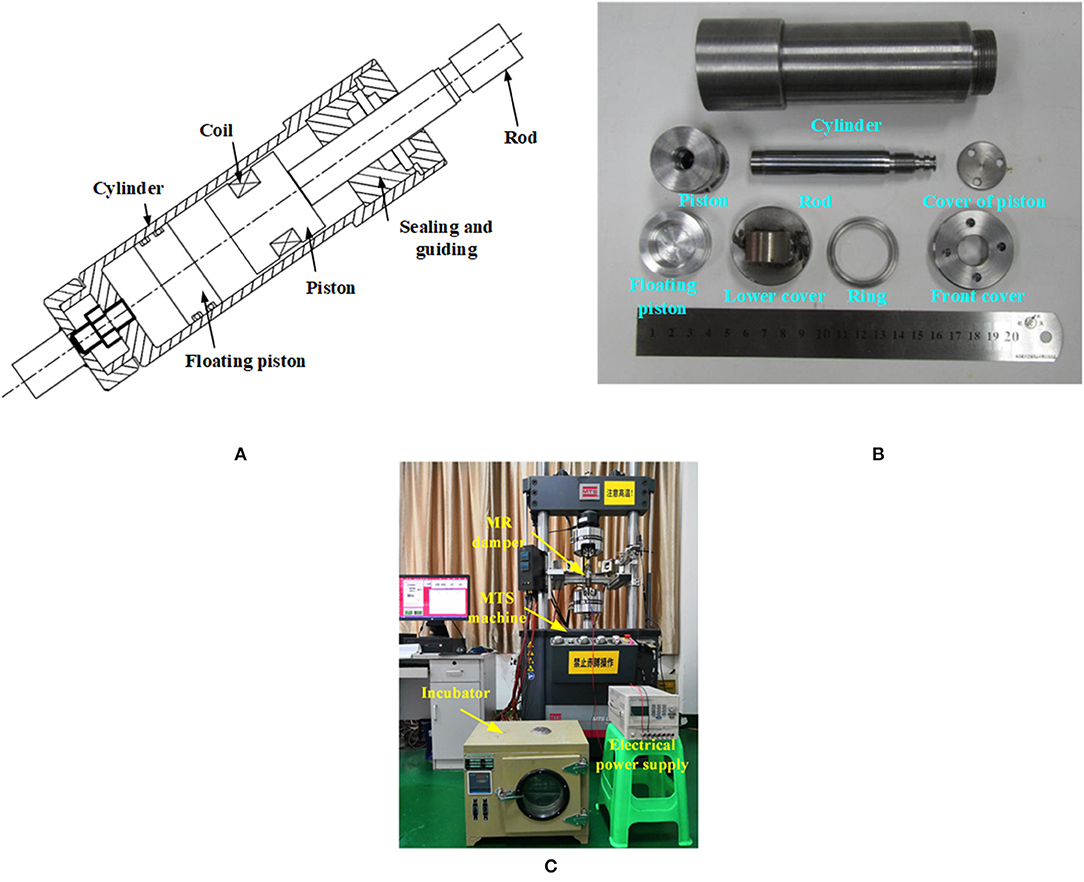
Figure 1. Experimental test of MR damper with accumulator: (A) diagram of MR damper, (B) picture of MR damper, and (C) picture of test apparatus.

The temperature-dependent characteristics are shown in Figure 2. The effects of temperature clearly show that the maximum force and area of enclosed force-displacement loop decrease with the increment of temperature. The area of the force-displacement loop means the MR damper's capability of energy dissipation. The maximum damping force and dissipated energy decline up to 33% when the temperature increases from 20 to 80°C. In general, the force-velocity loop and force-displacement loop are assumed as centrosymmetric loops. By inspecting the loops of Figure 2, the asymmetric characteristics appear in the experimental results. The asymmetrical results and ideal symmetrical loops are compared in Figure 3. The experimental results in different colors do not coincide with the ideal black loops. The non-centrosymmetric force-velocity loops and force-displacement loops cannot be captured by conventionally symmetrical models. It is also observed in Figure 3 that the maximum force and dissipated energy increase before saturation occurs when the current increases from 0 to 1.2 A. Differences of experimental results and ideal symmetric loops under different currents and temperatures are shown in Figures 4, 5. It can be seen that the difference increases with the increment of current and decreases with the increment of temperature. Normalized loops under different conditions are shown in Figure 6. The almost-identical curves show that asymmetric characteristics are the inherent properties of the designed MR damper.

FIGURE 2

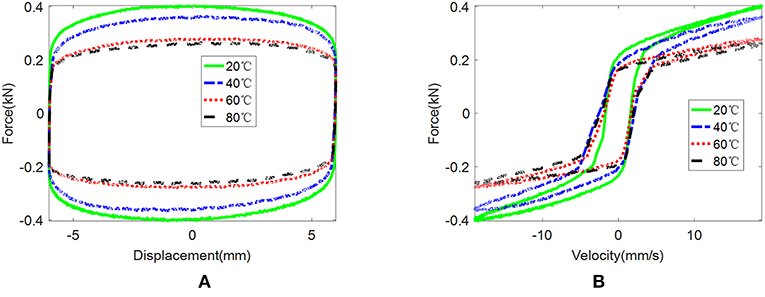
Figure 2. Experimental results at an amplitude of 6 mm, frequency of 0.5 Hz and current of 1.2 A: (A) force vs. displacement and (B) force vs. velocity.

FIGURE 3

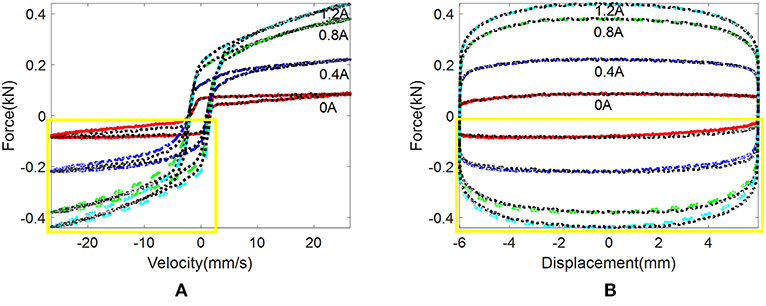
Figure 3. Comparison of experimental results and ideal symmetric loops at amplitude of 6 mm and frequency of 0.7 Hz: (A) force vs. velocity and (B) force vs. displacement.

FIGURE 4

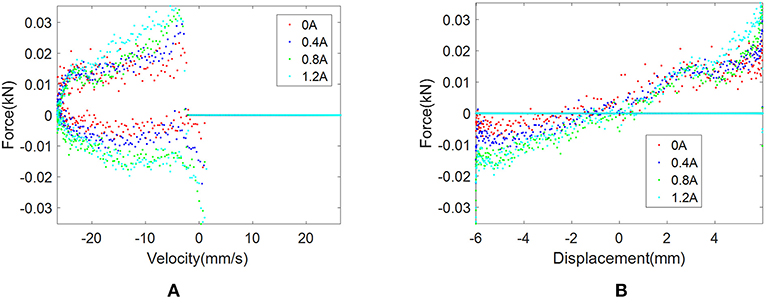
Figure 4. Differences of experimental results and ideal symmetric loops under different currents: (A) force vs. velocity and (B) force vs. displacement.

FIGURE 5

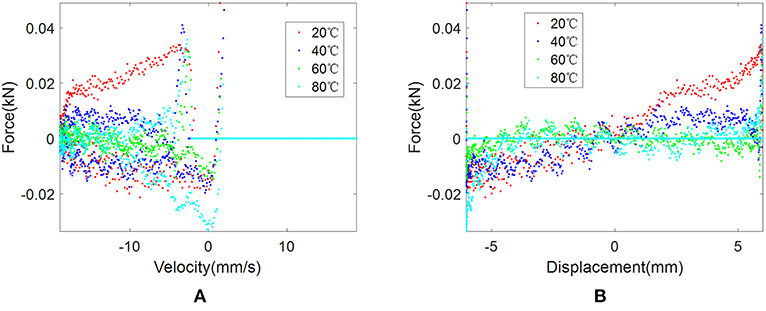
Figure 5. Differences of experimental results and ideal symmetric loops under different temperatures: (A) force vs. velocity and (B) force vs. displacement.

FIGURE 6

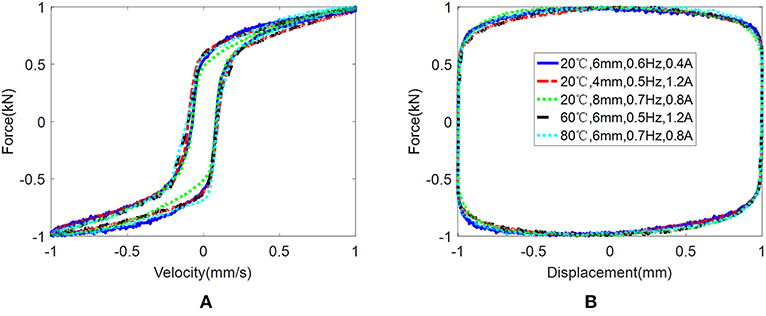
Figure 6. Normalized loops under different conditions: (A) force vs. velocity and (B) force vs. displacement.

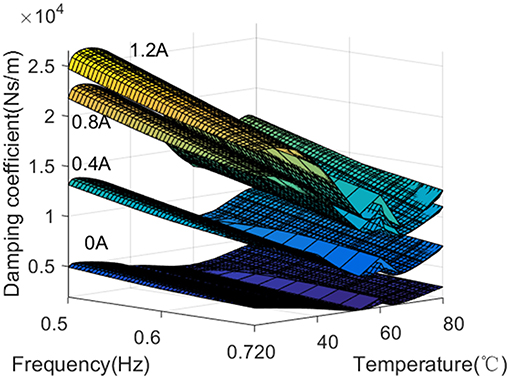
The equivalent viscous damping of MR damper is computed based on the dissipated energy per cycle (Raja et al., 2013). From Figure 7, the equivalent damping coefficient decreases with the increment of frequency and temperature. In addition, the equivalent damping coefficient increases obviously when the current increases from 0 to 1.2 A.

FIGURE 7

Figure 7. Equivalent damping characteristics.

Modeling and Identification

To predict the non-linear hysteresis loops, the dynamic models should be established (Guo and Hu, 2005; Ikhouane and Dyke, 2007; Yu et al., 2017). A typical construction of the parametric model shown in Equation (1) is used in this study.

$\begin{array}{l}{F}_d=c\dot{x}+kx+f_{hy}(1)\end{array}$

in which, c and k are the damping coefficient and stiffness coefficient, respectively. x and ẋ are the relative displacement and velocity, respectively. cẋ represents the relationship between the post-yield force and velocity. kx is related with the ends' opening of force-velocity loop. f_hy represents the hysteresis part. The basic hysteresis characteristics at lower velocities can be captured by f_hy. To describe the asymmetric characteristics in the pre-yield region and post-yield region efficiently, a developed algebraic model is proposed based on new mathematical expression of f_hy. The hysteresis part can be described by

$\begin{array}{l}{f}_{hy}=\alpha (f_{ba}+f_{br}\text{sgn}(x))(2)\end{array}$

here, α is the scale factor determining the height of the hysteresis loop. The asymmetric loop can be divided into asymmetric backbone part f_ba and branch part f_br. There are two different methods to describe asymmetric parts. One is to separate the asymmetric curve into two independent curves. Two functions are used to describe the separated curves. The other is to use one function for predicting the asymmetric characteristics directly. The functions describing the backbone curve and branch curve are shown as Equations (3) and (4), respectively.

$\begin{array}{l}{f}_{ba}=({\displaystyle \sum _{i=0}^2{p}_{pi}{\dot{x}}^{2i}})/(1+{\displaystyle \sum _{i=0}^2{p}_{pi}{\dot{x}}^{2i\text{+}2}})(\text{sgn}(\dot{x})+1)\\ +({\displaystyle \sum _{i=0}^3{p}_{ni}{\dot{x}}^i})/(1+{\displaystyle \sum _{i=1}^3{p}_{ni}{\dot{x}}^i})(1-\text{sgn}(\dot{x}))(3)\end{array}$

$\begin{array}{l}{f}_{br}=({\displaystyle \sum _{i=0}^6}{q}_i{\dot{x}}^i)/(1\text{+}{\displaystyle \sum _{i=0}^5}{q}_i{\dot{x}}^{i\text{+}1})(4)\end{array}$

here, p_pi, p_ni, and q_i are coefficients of velocity terms. The coefficients are identified by the Constriction Factor Particle Swarm Optimization (CFPSO) algorithm. To verify the accuracy of the proposed model, a conventional model is selected for performance comparisons. The mathematical function of the conventional model is shown in Equation (5) (Yu et al., 2017).

$\begin{array}{l}{F}_d=(c_{vm1}+\frac{c_{vm2}}{1+e^{c_{vm3}{\dot{x}}_m}}+c_{I1}{e}^{c_{I2}I})(\frac{1-e^{b_{ba1}\overline{\dot{x}}\text{sgn}(\dot{x})}}{1+e^{b_{ba2}\overline{\dot{x}}\text{sgn}(\dot{x})}}\text{sgn}(\dot{x})\\ +b_{br1}{e}^{-{(\frac{\overline{\dot{x}}-b_{br2}}{b_{br3}})}^2}\text{sgn}(x))(5)\end{array}$

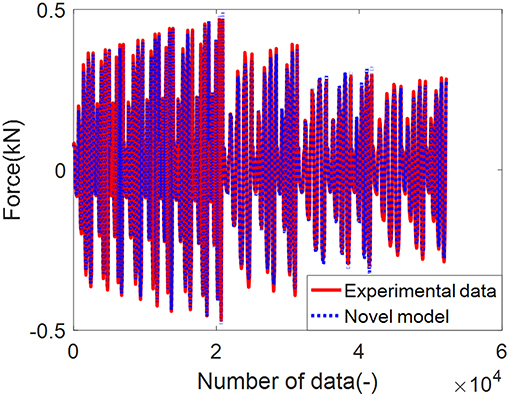
here, c_vmi, b_bai, and b_bri are coefficients needing identification. Considering the maximum velocity item in the conventional model, the calculation accuracy for random signals should be improved, while the proposed model is preferable for application under random excitation. The identified results of the proposed model and conventional model are compared in Figure 8. It can be seen that the proposed model considering the asymmetrical characteristics has more accuracy in the visual. Evaluation indices contain determination coefficient R², and mean deviation (MD) and root-mean-square error (RMSE) are used to compare experimental data and identified results. Their mathematical expressions can be seen in Equations (6)–(8). R² is used to examine the ability of the model to identify variation within the output responses. MD is used to describe the absolute difference between the experimental data and the identified results (Sahin et al., 2010). RMSE means the sample standard deviation of the differences between the identified results and the experimental data. Their values shown in Table 1 verify the trustable ability of the proposed model.

$\begin{array}{l}{R}^2=1\text{-}\frac{{\displaystyle \sum _{\text{i}=1}^N}{(F_{\text{test}}-F_{\text{model}})}^2}{{\displaystyle \sum _{\text{i}=1}^N}{(F_{\text{test}}-{\bar{F}}_{\text{test}})}^2}(6)\end{array}$

$\begin{array}{l}MD=\frac{1}{N}{\displaystyle \sum _1^N}{\displaystyle \left|\frac{F_{\text{test}}-F_{\text{model}}}{F_{\text{test}}}\right|}(7)\end{array}$

$\begin{array}{l}RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left[F_{\text{test}}-F_{\text{model}}\right]}^2}(8)\end{array}$

Here, F_test and F_model are experimental data and identified data, respectively. ${\bar{F}}_{\mathrm{\text{test}}}$ is the average value of experimental data. N is the number of experimental data groups.

FIGURE 8

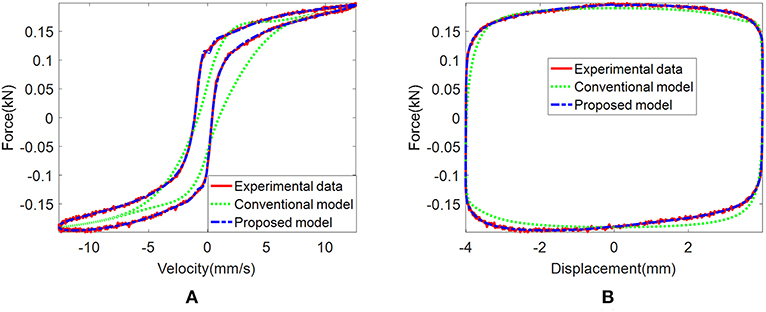
Figure 8. Comparison of the experimental data and the identified results of different models. (A) Force vs. velocity. (B) Force vs. displacement.

TABLE 1

Table 1. Evaluation criteria of accuracy.

The identified results of dynamic loops under different temperatures and currents are shown in Figure 9. It can be observed that the proposed model has the ability to capture the hysteretic loops.

FIGURE 9

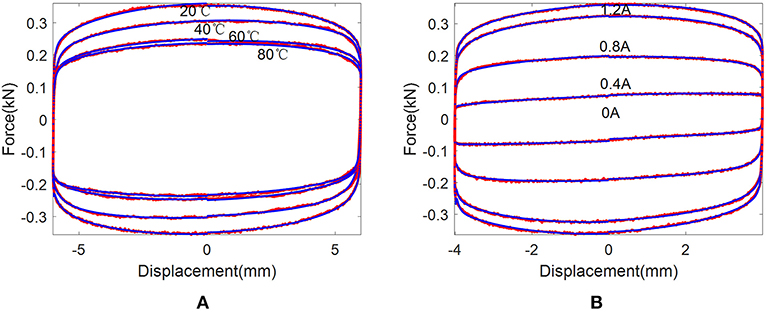
Figure 9. Comparison of the experimental data and the identified results: (A) at different temperatures and (B) at different currents (Red lines-experimental data, blue dots- identified results).

Considering that the effects of current on width and slope of the hysteretic region are not obvious, the relationships between current and parameters of f_ba and f_br are omitted in this study. Based on the identified results of c, k, and α, we can know that the variation tendencies of c, k, and α decrease with the increment of temperature. Combing the description in previous study (Dong et al., 2016; McKee et al., 2018), the mathematical expressions of identified parameters are displayed in Equations (9–11).

$\begin{array}{l}c=(c_0+c_{1}I+c_2{I}^2)e^{{\delta }_1(T-T_0)}(9)\end{array}$

$\begin{array}{l}k=(k_0+k_{1}I)e^{{\delta }_2(T-T_0)}(10)\end{array}$

$\begin{array}{l}\alpha =({\alpha }_0+{\alpha }_{1}I+{\alpha }_2{I}^2)e^{{\delta }_3(T-T_0)}(11)\end{array}$

here, α, β, and δ are temperature influence coefficients for c, k, and α, respectively. The dynamic model becomes

$\begin{array}{l}{F}_d=(c_0+c_{1}I+c_2{I}^2)e^{{\delta }_1(T-T_0)}\dot{x}+(k_0+k_{1}I)e^{{\delta }_2(T-T_0)}x\\ +({\alpha }_0+{\alpha }_{1}I+{\alpha }_2{I}^2)e^{{\delta }_3(T-T_0)}(f_{ba}+f_{br}\text{ sgn}(x))(12)\end{array}$

To verify the feasibility of the model shown in Equation (12), the comparisons between the experimental data and the identified results are shown in Figure 10. The values of R², MD and RMSE are 0.9946, 0.1703, and 16.2 N, respectively. Therefore, it can be concluded that the proposed model can accurately predict asymmetric hysteretic characteristics and temperature effects. The reverse model which is used to calculate the current value can be obtained by solving the quadratic equation.

FIGURE 10

Figure 10. Comparison of experimental data and identified results of all data.

Application Case in Semi-Active System

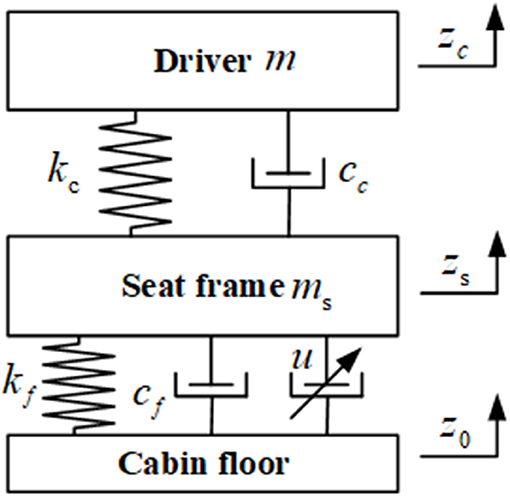
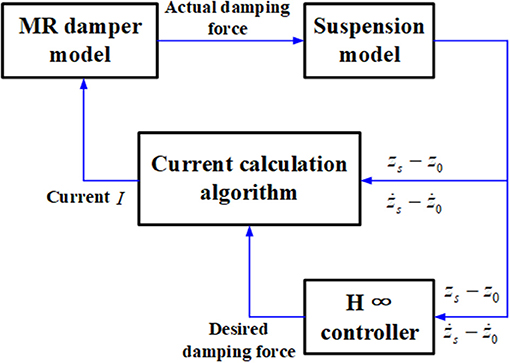
To verify the feasibility of the MR semi-active seat suspension system with the proposed model, the two degree of freedom suspension model is designed as shown in Figure 11. The mathematical expression of the dynamic model can be seen in Equations (13) and (14). For controlling the semi-active system, the H∞ control strategy is used to calculate required force. The schematic diagram of the control system is depicted in Figure 12.

$\begin{array}{l}{m}_s{\ddot{z}}_s=-k_f(z_s-z_0)-c_f({\dot{z}}_s-{\dot{z}}_0)+k_c(z_c-z_s)+\\ c_c({\dot{z}}_c-{\dot{z}}_s)-u(13)\end{array}$

$\begin{array}{l}m{\ddot{z}}_c=-k_c(z_c-z_s)-c_c({\dot{z}}_c-{\dot{z}}_s)(14)\end{array}$

here, m and m_s are mass of driver and seat frame, respectively. k_f is mixture of metal spring stiffness and gas accumulator stiffness. k_c is cushion stiffness. c_c andc_f are damping coefficient of uncontrolled suspension system and cushion, respectively.

FIGURE 11

Figure 11. Two degree of freedom suspension model.

FIGURE 12

Figure 12. Schematic diagram of control system.

Assuming x₁ = z_s–z₀, x₂ = ż_s–ż₀, x₃ = z_c–z_s, x₄ = ż_c–ż_s, $d={\left[{\ddot{z}}_0{\ddot{z}}_s\right]}^T$, the system-state equations are

$\begin{array}{l}\dot{x}(t)=Ax(t)+B_{1}d(t)+B_{2}u(t)(15)\end{array}$

$\begin{array}{l}y(t)=C_{2}x(t)(16)\end{array}$

here, $A=\left[\begin{array}{c}0100\\ -\frac{k_f}{m_s}-\frac{c_f}{m_s}\frac{k_c}{m_s}\frac{c_c}{m_s}\\ 0001\\ 00-\frac{k_c}{m}-\frac{c_c}{m}\end{array}\right]$, $B_1=\left[\begin{array}{c}0\\ -1\\ 0\\ 0\end{array}\begin{array}{c}0\\ \text{0}\\ 0\\ -1\end{array}\right]$, $B_2=\left[\begin{array}{c}0\\ \frac{1}{m_s}\\ 0\\ 0\end{array}\right]$, $C_2=\left[\begin{array}{llll}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill \end{array}\right]$. Assuming system outputs are z₁ = x₁ and $z_2={\ddot{z}}_c$, thus

$\begin{array}{l}z(t)=C_{1}x(t)(17)\end{array}$

here, $C_1=\epsilon \left[\begin{array}{c}1000\\ 00-\frac{k_c}{m}-\frac{c_c}{m}\end{array}\right]$, $\epsilon =\left[\begin{array}{ll}{\epsilon }_1\hfill & 0\hfill \\ 0\hfill & {\epsilon }_2\hfill \end{array}\right]$.

$\begin{array}{l}u(t)=\text{-}K{C}_{2}x(t)(18)\end{array}$

Thus,

$\begin{array}{l}\dot{x}(t)=(A\text{+}{B}_{2}K{C}_2)x(t)+B_{1}w(t)(19)\end{array}$

in which, w(t) = d(t). The calculating procedure is similar to the study of Ning et al. (2016); details are omitted for clarity. The value of K is [2, 2147.6]. The control performances of semi-active systems with different models of MR damper under random excitations are simulated. The results are shown in Figure 13. Model I, II, and III are symmetric model considering temperature effects, asymmetric model without temperature effects and asymmetric model considering temperature effects, respectively. Their root-mean-squares (RMS) of acceleration are 0.908, 0.965, and 0.878 m/s², respectively. The RMS of displacement are 0.0047, 0.0056, and 0.0039 m, respectively. It can be seen that the system with model III performs the lowest values of acceleration response and displacement response.

FIGURE 13

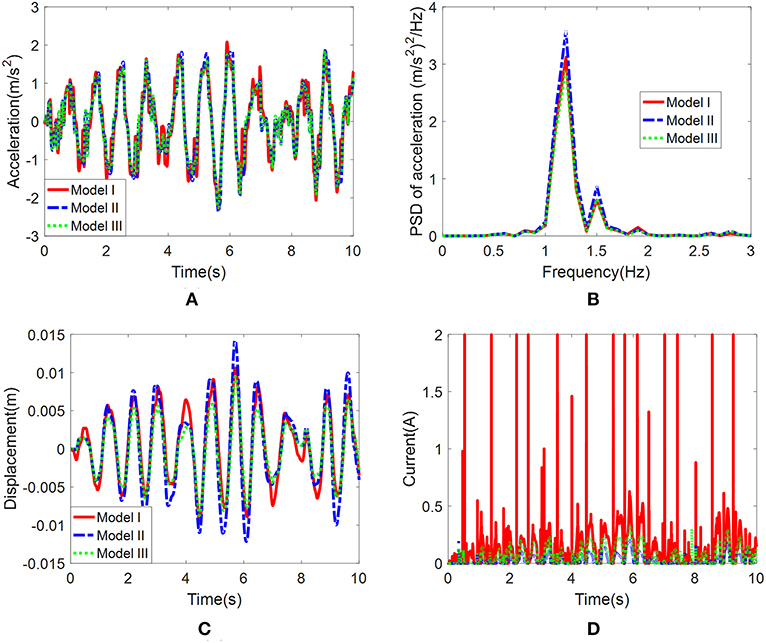
Figure 13. Control performances of semi-active system with different models under temperature of 80°C. (A) Time domain of acceleration response. (B) Frequency domain of acceleration response. (C) Time domain of displacement response. (D) Applied current.

Figure 14 shows the control performances of the semi-active system under different temperatures. It can be seen that the RMS of acceleration and RMS of displacement for the system with model II deteriorate with the increment of temperature. The acceleration responses of the semi-active system with model III have the smallest values compared to the other systems under the same conditions.

FIGURE 14

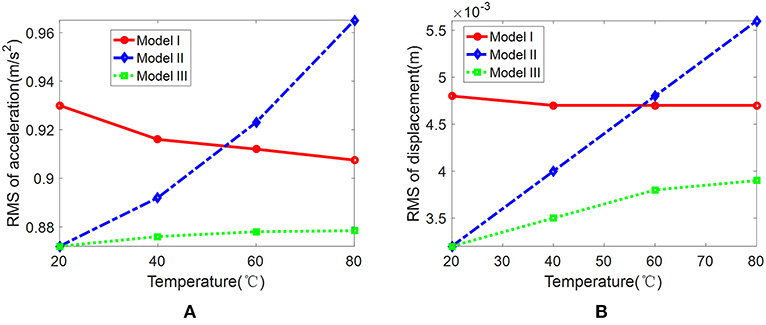
Figure 14. Control performances of semi-active system with different models under different temperatures. (A) RMS of acceleration response. (B) RMS of displacement response.

Conclusion

A dynamic model considering temperature effects and asymmetric characteristics is proposed and analyzed. The details of the conclusion are as follows.

1) Based on the experimental results of a mono-tube MR damper with accumulator, its asymmetric characteristics are analyzed. The asymmetric characteristics are inherent property of MR damper. The difference value between experimental data and ideal symmetric loop increases with the increment of current and temperature decrease.

2) A developed algebraic model is established to depict the asymmetric characteristics and temperature effects. Compared to the conventional model, the proposed model has better accuracy.

3) The performances of an MR semi-active system controlled by the H∞ strategy with three dynamic models are simulated and analyzed. The three models contain the symmetric model considering temperature effects, the asymmetric model without temperature effects, and the asymmetric model considering temperature effects. Based on the simulated results, the acceleration response, and displacement response of the semi-active system with the proposed model are better than the others.

Data Availability Statement

All datasets generated for this study are included in the manuscript/supplementary files.

Author Contributions

JY conducted the research and wrote the paper. XD supervised the research. XW and CP assisted experimental work. YZ helped to draft and revise the manuscript.

Funding

This work was financially supported by the National Natural Science Foundation of the People's Republic of China (No. 51675063) and the Fundamental Research Funds for the Central Universities (No. 2018CDGFJX0023). These support was gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the authors of the references for their enlightenment.

References

Bahiuddin, I., Mazlan, S., Shapiai, I., Imaduddin, F., and Choi, S.B. (2018). Constitutive models of magnetorheological fluids having temperature-dependent prediction parameter. Smart Mater. Struct. 27, 1–17. doi: 10.1088/1361-665X/aac237

CrossRef Full Text | Google Scholar

Bai, X. X., Chen, P., and Qian, L. J. (2015). Principle and validation of modified hysteretic models for magnetorheological dampers. Smart Mater. Struct. 24, 1–12. doi: 10.1088/0964-1726/24/8/085014

CrossRef Full Text | Google Scholar

Batterbee, D., and Sims, N. D. (2009). Temperature sensitive controller performance of MR dampers. J. Intell. Mater. Syst. Struct. 20, 297–309. doi: 10.1177/1045389X08093824

CrossRef Full Text | Google Scholar

Choi, S., Han, S., and Han, Y. (2005). Vibration control of a smart material based damper system considering temperature variation and time delay. Acta Mech. 180, 73–82. doi: 10.1007/s00707-005-0266-7

CrossRef Full Text | Google Scholar

Choi, S., Lee, S., and Park, Y. (2001). A hysteresis model for the field-dependent damping force of a magnetorheological damper. J. Sound Vibrat. 245, 375–383. doi: 10.1006/jsvi.2000.3539

CrossRef Full Text | Google Scholar

Choi, S. B., Li, W., Yu, M., Du, H., Fu, J., and Do, P. X. (2016). State of the art of control schemes for smart systems featuring magnetorheological materials. Smart Mater. Struct. 25, 1–24. doi: 10.1088/0964-1726/25/4/043001

CrossRef Full Text | Google Scholar

Dobson, S., Noori, M., Hou, Z., Dimentberg, M., and Baber, T. (1997). Modeling and random vibration analysis of SDOF systems with asymmetric hysteresis. Int. J. Nonlin. Mech. 32, 669–680. doi: 10.1016/S0020-7462(96)00090-X

CrossRef Full Text | Google Scholar

Domínguez-González, A., Stiharu, I., and Sedaghati, R. (2014). Practical hysteresis model for magnetorheological dampers. J. Intell. Mater. Syst. Struct. 25, 967–979. doi: 10.1177/1045389X13502867

CrossRef Full Text | Google Scholar

Dong, X. M., Yu, J. Q., Wang, W., and Zhang, Z. L. (2016). Robust design of magnetorheological (MR) shock absorber considering temperature effects. Int. J. Ada. Manuf. Tech. 90, 1735–1747. doi: 10.1007/s00170-016-9480-9

CrossRef Full Text | Google Scholar

García-Baños, I., Ikhouane, F., and Aguirre-Carvajal, N. (2017). An asymmetric-friction based model for magnetorheological dampers. IFAC Pap. OnLine 50, 14076–14081. doi: 10.1016/j.ifacol.2017.08.1844

CrossRef Full Text | Google Scholar

Gu, G. Y., Zhu, L. M., and Su, C. Y. (2014). Modeling and compensation of asymmetric hysteresis nonlinearity for piezoceramic actuators with a modified Prandtl–Ishlinskii model. IEEE Trans. Indus. Electron. 61, 1583–1595. doi: 10.1109/TIE.2013.2257153

CrossRef Full Text | Google Scholar

Guo, D. L., and Hu, H. Y. (2005). Nonlinear stiffness of a magnetorheological damper. Nonlin. Dyn. 40, 241–249. doi: 10.1007/s11071-005-6464-y

CrossRef Full Text | Google Scholar

Ikhouane, F., and Dyke, S. J. (2007). Modeling and identification of a shear mode magnetorheological damper. Smart Mater. Struct. 16, 605–616. doi: 10.1088/0964-1726/16/3/007

CrossRef Full Text | Google Scholar

Jiang, H., Ji, H. L., Qiu, J. H., and Chen, Y. S. (2010). A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators. IEEE Trans. Ultrason. Ferroelectr. 57, 1200–1210. doi: 10.1109/TUFFC.2010.1533

PubMed Abstract | CrossRef Full Text | Google Scholar

Jumani, S. S. (2010). An Invertible Open-Loop Nonlinear Dynamic Temperature Dependent MR Damper Model. Master of Science, Mechanical Engineering, Virginia Polytechnic Institute and State University, Virginia.

Google Scholar

Kwok, N., Ha, Q., Nguyen, T., Li, J., and Samali, B. (2006). A novel hysteretic model for magnetorheological fluid damper and parameter identification using particle swarm optimization. Sensor Actuat. A Phys. 132, 441–451. doi: 10.1016/j.sna.2006.03.015

CrossRef Full Text | Google Scholar

Leng, D. X., Xu, K., Ma, Y., Liu, G. J., and Sun, L. Y. (2018). Modeling the behaviors of magnetorheological elastomer isolator in shear-compression mixed mode utilizing artificial neural network optimized by fuzzy algorithm (ANNOFA). Smart Mater. Struct. 27, 1–14. doi: 10.1088/1361-665X/aadfa9

CrossRef Full Text | Google Scholar

McKee, M., Gordaninejad, F., and Wang, X. J. (2018). Effects of temperature on performance of compressible magnetorheological fluid suspension systems. J. Intell. Mater. Syst. Struct. 29, 41–51. doi: 10.1177/1045389X17705203

CrossRef Full Text | Google Scholar

Miah, M. S., Chatzi, E. N., Dertimanis, V. K., and Weber, F. (2015). Nonlinear modeling of a rotational MR damper via an enhanced Bouc–Wen model. Smart Mater. Struct. 24, 1–14. doi: 10.1088/0964-1726/24/10/105020

CrossRef Full Text | Google Scholar

Ning, D. H., Sun, S. S., Zhang, J. W., Du, H. P., Li, W. H., and Wang, X. (2016). An active seat suspension design for vibration control of heavy-duty vehicles. J. Low Freq. Noise Vibrat. Active Control 35, 264–278. doi: 10.1177/0263092316676389

CrossRef Full Text | Google Scholar

Raja, P., Wang, X., and Gordaninejad, F. (2013). A high-force controllable MR fluid damper–liquid spring suspension system. Smart Mater. Struct. 23, 1–10. doi: 10.1088/0964-1726/23/1/015021

CrossRef Full Text | Google Scholar

Sahin, I., Cesmeci, S., Wilson, N. L., and Wereley, N. M. (2010). “Sensitivity of magnetorheological damper behavior to perturbations in temperature via Bouc-Wen model,” in Proceedings of 12th International Conference on ER and MR Suspensions (Philadelphia, PA), 433–439.

Google Scholar

Sahin, I., Engin, T., and Çeşmeci, S. (2010). Comparison of some existing parametric models for magnetorheological fluid dampers. Smart Mater. Struct. 19, 1–11. doi: 10.1088/0964-1726/19/3/035012

CrossRef Full Text | Google Scholar

Song, J., and Der Kiureghian, A. (2006). Generalized Bouc–Wen model for highly asymmetric hysteresis. J. Eng. Mech. 132, 610–618. doi: 10.1061/(ASCE)0733-9399(2006)132:6(610)

CrossRef Full Text | Google Scholar

Wang, D. H., and Liao, W. H. (2011). Magnetorheological fluid dampers: a review of parametric modelling. Smart Mater. Struct. 20, 439–445. doi: 10.1088/0964-1726/20/2/023001

CrossRef Full Text | Google Scholar

Wang, E. R., Wang, W. J., Wang, H., Rakheja, S., and Su, C. Y. (2007). “Characterization and modeling of symmetric and asymmetric damping properties of a magnetorheological damper,” in Proceedings of the 7th WSEAS International Conference on Simulation, Modelling and Optimization (Beijing), 332–340.

Google Scholar

Wereley, N. (2013), Magnetorheology: Advances and Applications. Cambridge: Royal Society of Chemistry.

Google Scholar

Wereley, N. M., Li, P., and Kamath, G. M. (1998). Idealized hysteresis modeling of electrorheological and magnetorheological dampers. J. Intell. Mater. Syst. Struct. 9, 642–649. doi: 10.1177/1045389X9800900810

CrossRef Full Text | Google Scholar

Wilson, N. L., Wereley, N. M., Choi, Y.-T., Hiemenz, G. J., and Hu, W. (2009). “Performance robustness of a magnetorheological seat suspension to temperature variations using skyhook control,” in Active and Passive Smart Structures and Integrated Systems (San Diego, CA), 1–10.

Google Scholar

Yu, J. Q., Dong, X. M., and Zhang, Z. L. (2017). A novel model of magnetorheological damper with hysteresis division. Smart Mater. Struct. 26, 1–15. doi: 10.1088/1361-665X/aa87d6

CrossRef Full Text | Google Scholar

Zhang, J. Q., Gao, Y. Q., Yue, J., and Peng, Z. Z. (2013). Effect analysis of temperature-decay performance of magnetorheological fluid damper on tracked vehicle suspension system. Noise Vibrat. Control 33, 119–123. doi: 10.3969/j.issn.1006-1335.2013.03.027

CrossRef Full Text | Google Scholar