Topological Constraint Theory Analysis of Rigidity Transition in Highly Coordinate Amorphous Hydrogenated Boron Carbide

Introduction

Understanding the fundamental science of amorphous solids remains an essential problem in condensed matter physics (Billinge and Levin, 2007; Berthier and Biroli, 2010; Huang et al., 2013; Mauro, 2018). This problem has percolated to the forefront with the increasing demand for materials that are tunable (Baldus and Jansen, 1997; Medvedeva et al., 2017; Paquette et al., 2017; Mauro, 2018), manufacturable using gentle processing, and resilient to extreme conditions (Deb et al., 2001; Chen et al., 2003; Wilding et al., 2006; Lin et al., 2011). With expensive ab initio solutions still generally out of reach, one theory that has shown success in explaining and predicting behavior in covalently bonded random networks is topological constraint theory (TCT) or rigidity theory (Thorpe et al., 2002; Mauro, 2011; Micoulaut, 2016). As an extension to Maxwell's work on the rigidity of structural trusses (Maxwell, 1864), TCT was advanced by Phillips and Thorpe as a model for understanding the mechanical properties of amorphous glasses as a function of average atomic constraints (Phillips, 1979; Thorpe, 1983; Phillips and Thorpe, 1985; Thorpe et al., 2002). They showed that the rigidity of an amorphous network can be evaluated by comparing atomic constraints to atomic degrees of freedom, with constraints arising from bond-stretching and bond-bending forces determined by the average coordination of the network, 〈r〉, and degrees of freedom equivalent to the dimensionality of the network, i.e., three in most cases. The TCT model predicts a rigidity transition at a critical average coordination value, 〈r〉_c, when the number of atomic degrees of freedom equals the number of atomic constraints −2.4 in 3D covalent networks—demarcating a threshold between an underconstrained or “floppy” network and an overconstrained or “rigid” network, with properties scaling above the rigidity threshold as a function of network coordination (He and Thorpe, 1985).

Rigidity theory has been applied most extensively to chalcogenide glasses, such as the Ge_xSe_1−x or Ge_xAs_ySe_1−x−y systems (Boolchand et al., 2001). These systems are uniquely suitable for studying rigidity theory due to their covalent bonding and the “mix-and-match” coordination numbers of the atomic constituents (Se = 2, As = 3, Ge = 4), allowing for a range of network coordination to be achieved by varying stoichiometry. The theory has been supported computationally via the calculation of elastic constants and zero-frequency modes, which has demonstrated clear thresholds at 〈r〉 ≈ 2.4 (He and Thorpe, 1985; Franzblau and Tersoff, 1992; Plucinski and Zwanziger, 2015). The existence of a rigidity transition has been supported experimentally by probing vibrational and/or structural features in stoichiometrically varying glassy systems via Mössbauer spectroscopy (Bresser et al., 1986; Boolchand et al., 1995), Raman spectroscopy (Feng et al., 1997), and neutron scattering (Kamitakahara et al., 1991), with evidence of threshold behavior. A variety of thermal measurements probing glassy behavior have also corroborated such a threshold (Tatsumisago et al., 1990; Senapati and Varshneya, 1995). In terms of more direct experimental evidence, elastic constants/moduli have been measured, however with a vast majority of studies showing a lack of compelling support for the anticipated rigidity transition. In some cases, data sets feature no or only a small number of samples above or below the predicted threshold; in other cases, the data feature materials from different families, obscuring conclusions; and in yet other cases, the predicted effects are either not observed or are very subtle, requiring “guides to the eye” to highlight the desired interpretation (Tanaka, 1989; Yun et al., 1989; Kamitakahara et al., 1991; Sreeram et al., 1991; Srinivasan et al., 1992; Guin et al., 2009; Das et al., 2012). Some data showcase deviations from the theory which may apply to real material systems, such as a shift in 〈r〉_c (Tanaka, 1986; Duquesne and Bellessa, 1989) or the presence of multiple transitions (Wang et al., 2013), the latter being ascribed to the existence of an intermediate phase (Boolchand et al., 2001).

Rigidity threshold phenomena have also been investigated in other classes of materials wherein the incorporation of terminal hydrogen atoms or other groups is used to alter network connectivity, including a-Si:H (Kuschnereit et al., 1995), a-C:H (Boolchand et al., 1996), a-C:F (Ghossoub et al., 2010), a-SiC:H (King et al., 2013), a-SiCN:H (Gerstenberg and Taube, 1989), and a-SiOC:H (Ross and Gleason, 2005; Trujillo et al., 2010), with a few of these studies (Ross and Gleason, 2005; Trujillo et al., 2010; King et al., 2013) showing a convincing transition point, including via experimental modulus data. Finally, rigidity thresholds have been demonstrated in more complex materials such as proteins (Rader et al., 2002), zeolites (Sartbaeva et al., 2006), and cements (Bauchy et al., 2015), albeit only computationally. Overall, while the literature taken together provides plenty of evidence for rigidity threshold phenomena related to network coordination, there is only a small amount of compelling direct experimental data—particularly elastic data—corroborating the predicted result, which has been limited to a relatively small number of materials classes.

Here, we apply rigidity theory to a unique and unusually coordinated material, boron carbide. This material has garnered interest for a variety of applications, including nuclear reactor coatings (Greuner et al., 2004; Buzhinskij et al., 2009), neutron detection (Robertson et al., 2002; Caruso, 2010; Gervino et al., 2013), low-k dielectrics and related layers for integrated circuits (Han et al., 2002; Nordell et al., 2016b, 2017), and various specialized coatings (Keski-Kuha et al., 1998; Chen et al., 2006; Hu and Kong, 2014; Azizov et al., 2015; Störmer et al., 2016). The particular amorphous hydrogenated boron carbide (a-BC:H) variant described here was produced in the form of thin films by plasma-enhanced chemical vapor deposition (PECVD) from a single-source molecular ortho-carborane (o-C₂B₁₀H₁₂) precursor to form a disordered polymeric carborane-based network. The material consists of nominally 6-fold-coordinate boron (and carbon!) atoms arranged into 12-vertex icosahedral C₂B₁₀H_x subunits. These icosahedral subunits are then—we believe (Paquette et al., 2011)—cross-linked either directly to each other (Figure 1A) or via hydrocarbon linkers (Figure 1B), where the total amount of 1-fold-coordinate atomic hydrogen contained within the material correlates with decreased overall network coordination through the termination of icosahedral vertices and decreased cross-linking. By varying PECVD conditions, we have produced a substantial set of a-BC:H films with a vast range of densities, hydrogen concentrations, and effective network coordination (Figure 2A; Nordell et al., 2015, 2016a,b). We have observed a clear threshold in Young's modulus [and other properties (Nordell et al., 2015, 2016a,b)] as a function of density/hydrogen concentration (Figure 2B), which we attribute to a rigidity transition. In the present study, we describe and compare a number of constraint counting strategies and show how a-BC:H adheres to traditional TCT predictions if we apply a “superatom” approach and treat individual icosahedra as independently constrained units. Further, we discuss how TCT can be used to predict and optimize material properties of technological relevance. Importantly, the data span the “floppy,” “transition,” and “rigid” regimes, and—assuming no underlying phase transition exists—represent a direct change in network coordination and connectivity not obscured by additional chemical or structural ordering contributions. This result is an essential contribution in supporting the generality and versatility of TCT for predicting and understanding the properties of amorphous solids.

FIGURE 1

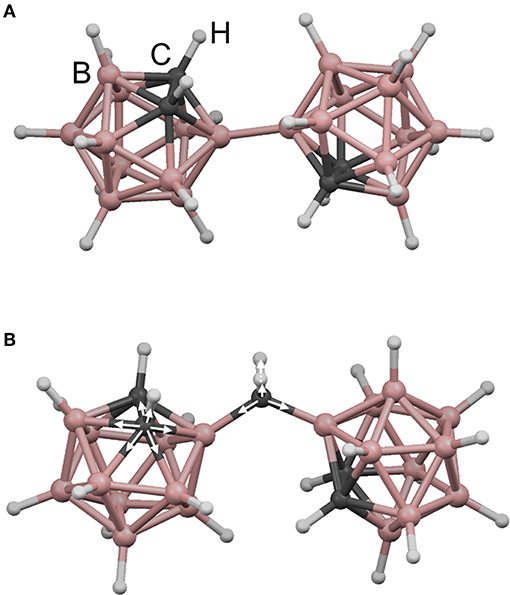
Figure 1. Illustration of possible cross-linking modes in amorphous hydrogenated boron carbide (a-BC:H): (A) directly between icosahedra and (B) via intericosahedral carbon. In (B) are shown both 6-fold-coordinate intraicosahedral carbon and 4-fold-coordinate extraicosahedral carbon environments.

FIGURE 2

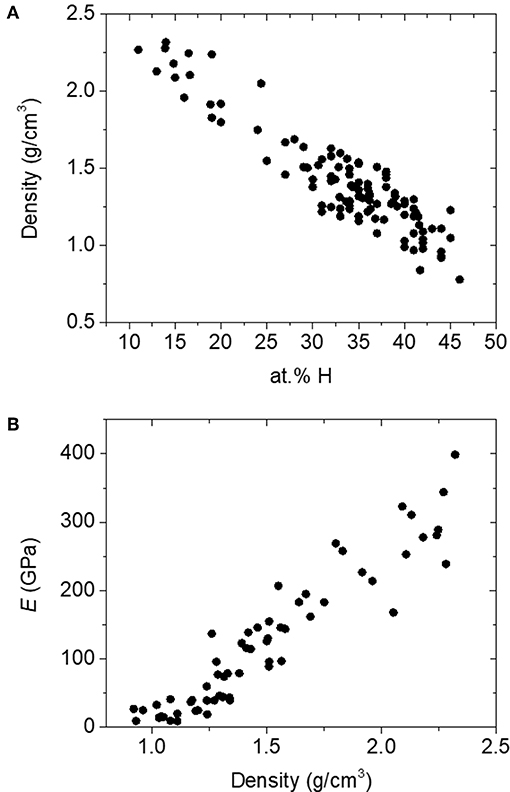
Figure 2. (A) Range of density and atomic concentration hydrogen in amorphous hydrogenated boron carbide films. (B) Young's modulus (E) as a function of density in a-BC:H films.

Results and Discussion

Topological constraint theory allows us to determine the number of zero-frequency modes or floppy modes, f, within a network—which can be related to its rigidity and glass properties—based on the difference between its atomic degrees of freedom, n_d, and atomic constraints, n_c. The constraint counting rules developed by Phillips and Thorpe can be applied with a simple knowledge of network coordination. Every r-coordinated atom accounts for r/2 bond-stretching constraints (since two atoms share each bond) and 2r – 3 bending constraints (since a 2-fold-coordinate atom involves one angle, with each additional bond introducing two new angles). If we take the average coordination number, 〈r〉, the average number of atomic constraints is then given as n_c = 〈r〉/2 + (2〈r〉 – 3). For a three dimensional network, the number of floppy modes goes to zero when n_c = n_d = 3 at a critical coordination number, 〈r〉_c, of 2.4, which represents the rigidity transition point and optimal glass-forming region.

In extending these constraint counting principles to amorphous hydrogenated boron carbide, we must first revisit the nature of the bonding in this material. The present study is based on multiple series' of a-BC:H films (Nordell et al., 2015, 2016a,b), including some fabricated as part of this work, grown by plasma-enhanced chemical vapor deposition from the single molecular precursor, ortho-carborane (o-C₂B₁₀H₁₂). We can differentiate the resulting amorphous solid from the more well-known and heavily studied crystalline B_xC variant, which is known to be comprised of B₁₂ or B₁₁C icosahedra and C–C–C or C–B–C chains within a densely packed rhombohedral lattice (Domnich et al., 2011). In contrast, evidence from previous work suggests that the PECVD carborane a-BC:H product, while still based on icosahedral units, forms a very different disordered polymeric network comprised of ortho-carborane B₁₀C₂H_x units, cross-linked to varying degrees, either directly to each other or via extraicosahedral hydrocarbon linkers (e.g., B–CH₂-B; Figure 1). Solid-state NMR and FTIR characterization (Paquette et al., 2011; Nordell et al., 2017) is consistent with the presence of hydrogenated ortho-carborane and sp³ hydrocarbon functionalities within the network. We assume that all carborane vertices that are not cross-linked are terminated by hydrogen atoms. What our previous characterization does not show evidence for are other types of boranes (e.g., partial cages), extraicosahedral boron (e.g., C–B–C chains), or B–H–B bonding. It is possible that these moieties could still be present and simply not observed due to the expected weak signal, but if so they would exist in minimal quantities.

On the basis of this information, we assume that all of the boron atoms are bonded within an icosahedral environment, and thus can be considered 6-fold coordinate. It is possible that some boron could exist in partial cages, C–B–C chains, or a form of boron oxide (Li and Qiu, 2007), but these have not been observed spectroscopically, and therefore if such compositions exist, they would most likely be present in a very small amount and would not contribute significantly to the mean coordination of the solid. The carbon within the a-BC:H network, on the other hand, exists as both intraicosahedral carbon and extraicosahedral sp³ hydrocarbon and can be considered to be in a non-traditional 6-fold-coordinate environment in the former case and a traditional 4-fold-coordinate environment in the latter (Figure 1B). Although it is possible that some sp (2-fold-coordinate) or sp² (3-fold-coordinate) hydrocarbon exists, this has not been observed by NMR and FTIR and would again be present in minimal quantities if at all. Finally, hydrogen atoms exhibit 1-fold-coordinate bonding, either terminating carborane vertices or satisfying hydrocarbon valencies. Hydrogen is known to exhibit rare bridging B–H–B bonding in amorphous boron-based solids (Anan'ev et al., 2002), but since this is not observed spectroscopically, we assume its contribution is absent or negligible. Finally, we would be remiss to not mention oxygen, which is inevitably present in these a-BC:H films in concentrations ranging from ~1–10% (Driver et al., 2012; Nordell et al., 2015). This element is found to exist in the form of OH groups, CO groups, and/or boron-oxide-based species, and is generally considered 2-fold coordinate. We have found that including oxygen in our constraint counting has a negligible effect on the result, and therefore because it is considered a contaminant we do not include it here.

Armed with knowledge of the atomic structure and coordination environments, we can calculate the mean network coordination for each film based on the concentrations of the atomic species: [B], [C], and [H]. Atomic concentrations were measured via combined Rutherford backscattering spectroscopy (RBS) and nuclear reaction analysis (NRA) methods (Nordell et al., 2015, 2016a,b). In our accounting, we assume that all boron is present within carborane units and that all carborane units maintain B₁₀C₂ stoichiometry. Therefore, for each 10 boron atoms, 2 icosahedral C atoms ([C_icosahedral]) must be accounted for, with the remaining C atoms assumed to exist as sp³ hydrocarbon species ([C_sp3]). The average coordination of the network, 〈r〉, is thus defined as:

$\begin{array}{l}\langle r\rangle =\frac{r_{\text{B}}[\text{B}]+r_{\text{C}\left(\text{icosahedral}\right)}[{\text{C}}_{\text{icosahedral}}]+r_{\text{C}\left(\text{sp3}\right)}[{\text{C}}_{sp3}]+r_{\text{H}}[\text{H}]}{\left[\text{B}\right]+\left[{\text{C}}_{\text{icosahedral}}\right]+\left[{\text{C}}_{\text{sp3}}\right]+[\text{H}]}\\ =\frac{6\left[\text{B}\right]+6\left[{\text{C}}_{\text{icosahedral}}\right]+4\left[{\text{C}}_{\text{sp3}}\right]+1[\text{H}]}{\left[\text{B}\right]+\left[{\text{C}}_{\text{icosahedral}}\right]+\left[{\text{C}}_{\text{sp3}}\right]+[\text{H}]}& (1)\end{array}$

We distinguish this first constraint counting strategy as the “atomic model,” because it considers the coordination environment of each individual atom. Figure 3 displays plots of Young's modulus (E), measured via nanoindentation (Nordell et al., 2015, 2016a,b), vs. coordination number (〈r〉) (a) as well as the associated log–log plot (b). The data appear to show three distinct regions beginning at high Young's modulus: a first region with E decreasing steadily with decreasing 〈r〉 until E ≈ 130 GPa and 〈r〉 ≈ 4.3 (light blue region), a steep fall off in E between 〈r〉 ≈ 4.3 and 4.1 centered at 4.2 (medium blue region), and a relative plateau below this with E ≈ 20 GPa (darker blue region). To assess the merit of the constraint counting model, we compare the results with two predictions from TCT: (1) the existence of a critical threshold, and (2) the observation of a power law behavior in Young's modulus as a function of 〈r〉 above the threshold.

FIGURE 3

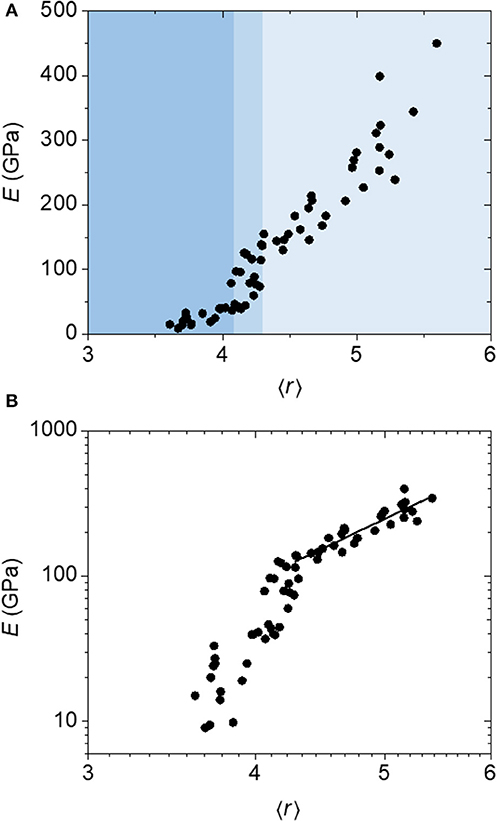
Figure 3. (A) Linear and (B) log plots of Young's modulus (E) as a function of average coordination number (〈r〉) calculated using an atomic constraint counting method for a-BC:H films. The data above the transition region is fit to a power-law function to yield an exponent of 4.4.

For a typical covalent 3D network, the predicted critical coordination is 2.4. However, for a network containing 1-fold-coordinate (OFC) atoms, a correction must be introduced to account for these as they do not impose the same constraints (Boolchand and Thorpe, 1994). The predicted threshold can thus be calculated based on the formula established by Boolchand and Thorpe, where the threshold coordination is effectively adjusted for the fraction of 1-fold-coordinate (hydrogen) atoms as:

$\begin{array}{ll}{\langle r\rangle }_{c\left(OFC\right)}=2.4-0.4\left(\frac{\left[\text{H}\right]}{\left[\text{B}\right]+\left[\text{C}\right]+\left[\text{H}\right]}\right)& (2)\end{array}$

For the a-BC:H samples, the predicted 〈r〉_c(OFC) ranges between 2.1 and 2.2 as a function of the actual H concentration of each sample. The experimental data does show a transition, but the center of this transition at 〈r〉 = 4.2 is not consistent with the value of 2.4 predicted by TCT theory. Interestingly, it is closer to the value predicted based on the bond percolation (BP) threshold, p_c, for a simple 6-fold-coordinate cubic 3D lattice (vs. that for a 4-fold-coordinate tetrahedral lattice). Assuming a p_c value of ~0.25 (Vyssotsky et al., 1961; Phillips and Thorpe, 1985; Galam and Mauger, 1996), 〈r〉_c(BP) is obtained as 〈r〉_c(BP) = z – z(p_c) = 4.5, with z = 6. Although Vyssotsky et al. (1961) do report that the lattice type does not have a significant effect relative to lattice dimensionality and coordination number, it is unclear whether a-BC:H can be appropriately modeled by this theory, not only due to it not forming a cubic lattice but also due to the nature of its bonding (vide infra).

As for the second TCT prediction, He and Thorpe demonstrated that there is a power-law type behavior in the elasticity of network glasses (He and Thorpe, 1985), where the elastic constants (C) exhibit a power law with exponent ν as a function of mean coordination above 〈r〉_c as C ∝ (〈r〉 – 〈r〉_c)^ν. Using a modified diamond lattice, they computed this exponent to be 1.5. Franzblau and Tersoff expanded on this work, showing that the exponent can range between 1.35 and 1.89 depending on the ratio of the bond-stretching and bond-bending force constants, α and β (Franzblau and Tersoff, 1992). In the a-BC:H data, the Young's modulus does exhibit a power law response above 〈r〉_{c(experimental)}; however, the calculated exponent is 4.4, which does not match the theoretical prediction. The mismatch between experiment and theory suggests that perhaps the constraint counting strategy can be improved.

In revisiting our constraint counting method, we first recognize that boron exhibits non-traditional bonding. From a valence bond perspective, boron is known to form 3 center−2 electron (3c−2e) bonds as opposed to the 2 center−2 electron (2c−2e) bonds most commonly observed. Thus, within an icosahedron, the electron density is located, not between sets of two boron atoms, but at the center of groups of three boron atoms. At the vertices of the icosahedra, we find more traditional outward-pointing 2c−2e sigma bonds (Emin, 1987). From a molecular orbital (MO) perspective, an icosahedron contains 13 internally bonding molecular orbitals and 12 externally bonding MOs. Within the internally bonding MOs, the electron density is delocalized across the surface of the icosahedron, which is considered to be aromatic (King, 2001). For an icosahedron composed of 12 boron atoms, each atom contributes three bonding electrons, for a total of 36. Twelve of these are reserved for external bonding at each vertex, which leaves 24 to fill the 13 internally bonding MOs, coming up 2 short. This explains why the C₂B₁₀ icosahedron is particularly stable (relative to the unstable B₁₂ icosahedron) as the carbon atoms contribute these two additional electrons.

Thus, from a bonding perspective, it may not be appropriate to treat the constraint counting within icosahedra based on a “ball and stick” bonding model when the electron density is not located between pairs of atoms but rather delocalized across the entire cluster. A similar breakdown in constraint counting is described by Robertson in relation to amorphous carbon (Robertson, 1992). However, between icosahedra, the connectivity is based on the more traditional sigmoidal bonding. Thus, given the overconstrained and strongly bound nature of the individual icosahedra, it is attractive to treat these as rigid “superatom” units (Castleman and Khanna, 2009), and rather than consider the degree of connectivity between individual atoms, instead consider the degree of connectivity between icosahedra (Figure 4). In this modified “superatom” constraint counting strategy, we therefore count individual icosahedra as independently constrained units with a hypothetical coordination number of 12, and then count the remaining extraicosahedral carbon atoms (recall we assume that all boron is contained within icosahedra, and that for each 10 icosahedral B atoms, there must be two associated intraicosahedral C atoms) as 4-fold coordinate, and all H atoms as 1-fold coordinate (Equation 3).

$\begin{array}{l}\langle r\rangle =\frac{r_{\text{icosahedron}}[{\text{B}}_{10}{\text{C}}_2]+r_{\text{C}\left(\text{sp3}\right)}[{\text{C}}_{\text{sp3}}]+r_{\text{H}}[\text{H}]}{\left[{\text{B}}_{10}{\text{C}}_2\right]+\left[{\text{C}}_{\text{sp3}}\right]+[\text{H}]}\\ =\frac{12\left[{\text{B}}_{10}{\text{C}}_2\right]+4\left[{\text{C}}_{\text{sp3}}\right]+1[\text{H}]}{\left[{\text{B}}_{10}{\text{C}}_2\right]+\left[{\text{C}}_{\text{sp3}}\right]+[\text{H}]} & (3)\end{array}$

The results of this constraint counting scheme are given in Figure 5. Once again we observe a clear transition region for E (medium blue shading) separating high 〈r〉 (lighter blue shading) and low 〈r〉 regions (darker blue shading), but in this case it is spanning an 〈r〉 range of 2.2–2.6, centered at 〈r〉 = 2.4 (Figure 5A). A log–log plot (Figure 5B) clearly shows a distinct linear relationship above this transition region, demonstrating a power law fit with an exponent of 1.5, exactly consistent with He and Thorpe's prediction. The distinction between the transition region and the low 〈r〉 region is less clear than in the atomic model, although there does still appear to be a rapid change in E with 〈r〉 (~30–130 GPa) in the transition region distinct from a more gradual change in E with 〈r〉 below this (~10–30 GPa). The central rigidity threshold value of 2.4 is now in line with that predicted by theory, although slightly higher than the value of 2.1–2.2 predicted for a-BC:H when applying the 1-fold-coordinate atom correction. (We note that in computing the critical coordination for the superatom network, we take the degrees of freedom for each icosahedron to be 3 as we are assuming spherical symmetry.) However, the initial onset of the steep rigidity increase is very close to the prediction.

FIGURE 4

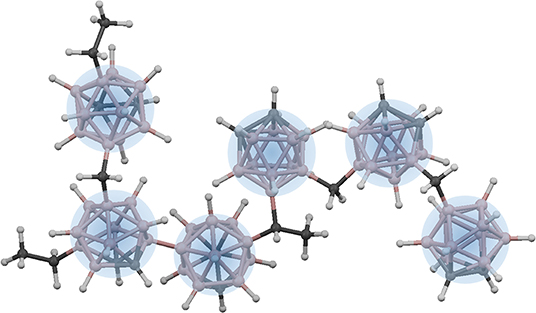
Figure 4. “Superatom”-based network in polymeric a-BC:H (with minimal cross-linking shown for simplicity). Each icosahedron is treated as a constrained superatom with a total possible coordination of 12.

FIGURE 5

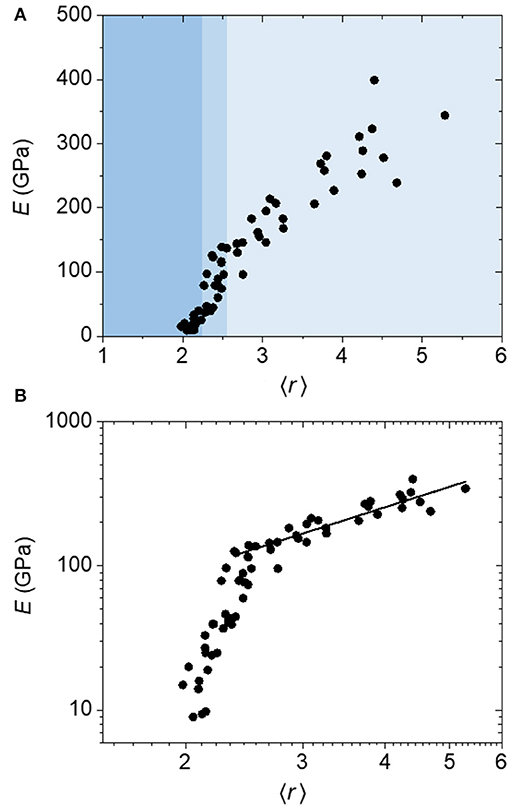
Figure 5. (A) Linear and (B) log plots of Young's modulus (E) as a function of average coordination number (〈r〉) calculated using a “superatom” constraint counting method for a-BC:H films. The data above the transition region is fit to a power-law function to yield an exponent of 1.5.

The observation of an experimental transition point slightly higher than predicted by theory is quite common, and has been shown in several amorphous systems, albeit for different reasons. Most work on topological constraint theory has focused on chalcogenide glasses, and the demonstration of a rigidity transition via the measurement of elastic properties has yielded ambiguous results. A majority of studies do not show a clear transition in elastic constants or modulus at 〈r〉 = 2.4, but many do show a transition at 〈r〉 ≈ 2.7 (or a cutoff at 2.7, which can neither confirm nor deny the existence of said transition). (Tanaka, 1986; Duquesne and Bellessa, 1989; Yun et al., 1989; Kamitakahara et al., 1991; Sreeram et al., 1991; Yang et al., 2010) Early explanations posited that this effect could be due to underlying Van der Waals (VDW) forces which are unaccounted for in the theory, that can shift and/or “wash out” the rigidity transition (Tanaka, 1986, 1989; Thorpe et al., 2002). It also became clear that these transition points corresponded to distinct changes in ordering (layers/clusters, and cross-linking thereof) of the material (Duquesne and Bellessa, 1989; Yun et al., 1989). For example, in the Ge–Se system, 〈r〉 = 2.4 corresponds to a GeSe₄ stoichiometry, at which point Se chains are fully cross-linked by Ge atoms, whereas 〈r〉 = 2.67 corresponds to a GeSe₂ stoichiometry, whereupon Ge–Ge bonds begin to form (Rouxel, 2007). These changes are still related to coordination number, though highlight distinct changes in network structure. The most current, yet still controversial (Micoulaut, 2016), interpretation of this phenomenon is that in systems where there is underlying ordering, the two transition thresholds represent the delineation of the so-called “intermediate phase” between floppy and stressed–rigid states, where the system is rigid yet optimally constrained (Boolchand et al., 2001; Sartbaeva et al., 2007). We note that although these two transitions are generally not observed in elastic modulus data, they are observed through other experimental probes such as differential scanning calorimetry and Raman spectroscopy (Boolchand et al., 2001). Of course, other effects beyond network coordination can influence elastic properties, including bond strength and packing density (Rouxel, 2007), and the changes in stoichiometry and medium-range order in chalcogenide glasses as a function of 〈r〉 therefore convolute the interpretation of network-coordination-based results for these systems to some extent. Tichý, for example, ascribes the transitions instead to chemical thresholds (Tichý and Tichá, 1994).

In terms of other material systems that demonstrate rigidity thresholds, in SiO₂ the rigidity transition is also shifted to 2.67 due to the broken bond-bending forces of the oxygen atoms (Zhang and Boolchand, 1994; Boolchand et al., 2001). The a-BC:H system studied here is perhaps most similar, however, to other partially hydrogenated networks such as a-SiC:H and a-SiOC:H, in which rigidity transitions have been observed at 〈r〉 ≈ 2.4 (Ross and Gleason, 2005; Trujillo et al., 2010; King et al., 2013). Consistently, these transition points are similarly ~0.2–0.3 coordination units higher than theoretically predicted if one accounts for the 1-fold-coordinate correction. This could potentially be due to oxygen-based bonding in the case of a-SiOC:H or VDW bonding in the case of a-SiC:H. In a-BC:H, VDW and other weak forces may likewise cause a slight shift in the experimentally observed transition threshold.

Another point of discussion concerns the region below the rigidity threshold. Although basic rigidity theory predicts that the elastic modulus goes to zero below 〈r〉_c, this is not the case in experiment due to the presence of dihedral angle and VDW forces that contribute an underlying elasticity (He and Thorpe, 1985). In other hydrogenated/fluorinated materials, the Young's modulus/hardness tends toward zero at 〈r〉_c in the case of a-C:H/a-C:F (Ghossoub et al., 2010; King et al., 2013) or finite yet very low values below 〈r〉_c in the case of a-SiC:H/a-SiOC:H (Ross and Gleason, 2005; Trujillo et al., 2010; King et al., 2013), yet in a-BC:H, it remains relatively high. This “superatom” system is unique in that, in addition to VDW and related forces, we must also consider the intrinsic rigidity of the icosahedra as well as the fact that boron-based covalent bonds are extremely strong. Further, in a-BC:H, the elastic modulus does not stabilize below 〈r〉_c but instead continues to decrease, the most straightforward reason for which is due to the decrease in network density associated with further decreases in 〈r〉. This effect is not typically captured in simulations due to these being based on the removal of bonds rather than both atoms and bonds or the substitution of atom types. Finally, regarding the transition region, it is unclear whether the behavior of the data between 〈r〉 = 2.2 and 2.6 represents some form of “intermediate phase” or is simply the experimental broadening of a sharp transition. As mentioned above, the elastic constants for simple non-ordering networks are predicted to gradually approach zero with decreasing 〈r〉 until 〈r〉_c (He and Thorpe, 1985; Plucinski and Zwanziger, 2015). Based on experimental work for materials which are said to possess an intermediate phase, we might anticipate a plateau in this region; vibrational markers tend to plateau, for example (Boolchand et al., 2001). In a rare example reported by Wang et al. where two elastic thresholds are observed experimentally in a chalcogenide glass, the data also reveal a plateau between the two (Wang et al., 2009). However, in this study the change in elastic modulus essentially mirrors the change in density, which decreases over this same region, highlighting the convolution of the effect of packing density and coordination on modulus. In a-BC:H, on the other hand, at the transition point, rather than a plateau, we instead observe a steep fall off from ~130 to ~30 GPa over a narrow range of 〈r〉. This change is not associated with an abrupt change in density, which varies smoothly with coordination number. If we base our interpretation on the assertion that it is the structural variability or the ability of a network to self-organize that leads to the intermediate phase (Micoulaut and Phillips, 2007; Sartbaeva et al., 2007), then the smooth transition in network connectivity predicted in a-BC:H may suggest that what we are observing is indeed a sharp transition associated with a significant loss in rigidity at the threshold.

Importantly, not only does a-BC:H stand out in that it demonstrates a distinct rigidity transition with a large number of data points both above and below the threshold, but it may also represent a unique example system where there is, in fact, a smooth variation in network connectivity independent from changes in medium-range ordering or chemical stoichiometry. In this way, despite its perceived complexity, the superatom a-BC:H network may actually be quite similar to the most simple theoretical network models such as the modified diamond lattice studied by He and Thorpe. One question that might arise is whether our simplified structural model of a-BC:H is truly an accurate representation of this system. To probe this question, we attempted constraint counting with several different variations. In addition to the superatom constraint counting strategy described above, we applied a second strategy where we neglected extraicosahedral carbon entirely, and only considered the ratio of 12-fold-coordinate icosahedral superatoms to 1-fold-coordinate hydrogen atoms. Using a third strategy, we assumed all extraicosahedral carbon was present in the form of CH₂ groups, and treated CH₂ groups as constrained 2-fold-coordinate units. In all three cases, the results were nearly identical to those shown in Figure 5, with the same transition point and power-law exponents, and only very slight deviations in the scatter of the data. Thus, we can conclude that the core connectivity of the lattice is by and large dependent on the degree of cross-linking between icosahedra, primarily determined by the degree of hydrogenation, and that the detailed structure and connectivity of the extraicosahedral carbon, which we admittedly do not fully understand, does not play a significant role.

In addition to investigating the relationship between Young's modulus and average network coordination, we can also look at the Young's modulus–density relationship. Here too, we see a power-law relation above a clear transition point at a density of ~1.3 g/cm³ (Figure 6). Similarly to what we have shown for a subset of this data (Nordell et al., 2016b), a power law fit above this threshold gives an exponent of 2.0, which is consistent with the quadratic scaling relationship expected for cellular solids, as well as with that observed for disordered nanoporous silica (Jain et al., 2001; Fan et al., 2007; Meza et al., 2014). At ~1.3 g/cm³, the modulus drops sharply, and below 1.2 g/cm³, the data display significantly increased scatter.

FIGURE 6

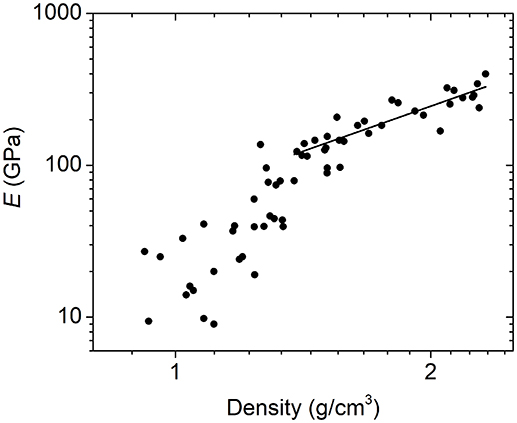
Figure 6. Logarithmic plot of Young's modulus as a function of density for a-BC:H films yielding an E ∝ D^2.0 relationship above 1.3 g/cm³.

Another property of a-BC:H that may be influenced by the rigidity regime of the a-BC:H network is its permittivity, a frequency-dependent quantity related to a material's polarizability. A material's polarization may be broken into three contributions: (1) the electronic polarization (movement of electrons) at high (optical) frequencies, (2) the distortion polarization (vibration of bonds) at moderate (infrared) frequencies, and (3) the orientation polarization (movement of permanent dipoles) at low (micro-/radio-wave) frequencies (Maex et al., 2003; Kohl, 2011). In Figure 7 is shown the high-frequency (10¹⁴ Hz) relative permittivity, ε₁, which represents the electronic contribution only, as well as the low-frequency (10⁵ Hz) or “total” permittivity, k (also commonly referred to as the dielectric constant), which represents the sum of the electronic, distortion, and orientation contributions, as a function of 〈r〉. While we observe a clear trend in ε₁ as a function of 〈r〉, which we attribute primarily to a decrease in network density (and therefore electronic density), this trend breaks down for k at low 〈r〉. This is highlighted by the k – ε₁ difference term (Figure 7, inset), which increases below 〈r〉 ≈ 2.4. We hypothesize that this is due to the expected increase in floppy modes below the rigidity transition which would contribute to distortion and orientation polarization effects (Palin, 1967). We note that we have previously found no relationship between k – ε₁ and oxygen concentration (Nordell et al., 2016b), and therefore the increased polarity of oxygen-based bonds does not appear to be the cause of this effect. For low-dielectric-constant or low-k materials, a key strategy for decreasing k involves decreasing material density, both by using lower-Z elements (containing fewer electrons) and lower volume density (i.e., higher porosity or free volume). A common challenge is the deterioration in mechanical properties associated with the latter approach (Grill et al., 2014; Michalak et al., 2015). The result described here suggests that not only does weak network connectivity decrease mechanical properties, but may also result in higher-than-anticipated k values. Thus, establishing low-density yet highly connected lattices will be essential to attaining both optimal mechanical and dielectric properties.

FIGURE 7

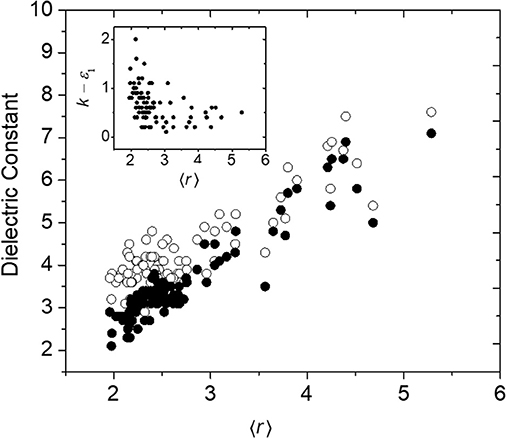
Figure 7. High- (ε₁, 4.6 × 10¹⁴ Hz, •) and low- (k, 100 kHz, ◦) frequency relative permittivity as a function of 〈r〉 for a-BC:H films. The inset displays the difference between k and ε₁ as a function of 〈r〉.

Conclusions

We have shown that amorphous hydrogenated boron carbide (a-BC:H) exhibits a transition in elastic properties as a function of average network coordination. By treating the lattice as a network of rigid icosahedral “superatoms,” the rigidity transition falls at a critical coordination of 〈r〉 = 2.4 (within a range of 2.2–2.6), essentially consistent with the Phillips–Thorpe topological constraint theory prediction with modifications for the contribution from 1-fold-coordinate atoms. Further, above the rigidity transition, the Young's modulus obeys a power law behavior as a function of 〈r〉 with an exponent of 1.5, again consistent with the original predictions by He and Thorpe and others. We have discussed how the rigidity theory framework can be used to optimize properties, such as Young's modulus and dielectric constant, for microelectronic applications. Additional analysis remains to better understand this system. In terms of constraint counting, using a molecular dynamics approach such as that described by Bauchy (2019) would be illuminating toward developing a more rigorous understanding of the constraints present in the network. Further, studying additional properties, such as glass transition temperature from differential scanning calorimetry and vibrational modes from Raman scattering, particularly in the region of 〈r〉_c, could provide valuable complementary insight into the nature of the transition. Overall, this is one of the largest and broadest sets, if not the largest/broadest, of elastic modulus data as a function of coordination number that we are aware of, and therefore represents a compelling result in directly supporting the existence of the theoretically predicted rigidity transition, in addition to supporting the generalizability of topological constraint theory to a range of materials.

Data Availability Statement

The data sets generated for this study are available on request to the corresponding author.

Author Contributions

BN and TN completed thin-film depositions and characterization. WL performed RBS/NRA measurements and analysis. PH, HL, and LR performed nanoindentation measurements and analysis. BN, MP, and SK completed data analysis and interpretation. BN and MP prepared figures. SK and AC provided technical support, both for experiment and analysis. MP wrote the manuscript, with contributions and revisions from BN and SK. All authors have approved the submission of this work.

Funding

The authors are grateful for financial support by Intel (contract no. 2012-IN-2313), the Defense Threat Reduction Agency (grant no. HDTRA1-10-1-0092), and the National Science Foundation (award no. 1729227).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anan'ev, A. S., Kon'kov, O. I., Lebedev, V. M., Novokhatski, A. N., Terukov, E. I., and Trapeznikova, I. N. (2002). Fabrication and properties of amorphous hydrogenated boron carbide films. Semiconductors 36, 941–943. doi: 10.1134/1.1500477

CrossRef Full Text | Google Scholar

Azizov, E., Barsuk, V., Begrambekov, L., Buzhinsky, O., Evsin, A., Gordeev, A., et al. (2015). Boron carbide (B₄C) coating. Deposition and testing. J. Nucl. Mater. 463, 792–795. doi: 10.1016/j.jnucmat.2015.01.015

CrossRef Full Text | Google Scholar

Baldus, H.-P., and Jansen, M. (1997). Novel high-performance ceramics—amorphous inorganic networks from molecular precursors. Angew. Chem. Int. Ed. Engl. 36, 328–343. doi: 10.1002/anie.199703281

CrossRef Full Text | Google Scholar

Bauchy, M. (2019). Deciphering the atomic genome of glasses by topological constraint theory and molecular dynamics : a review. Comput. Mater. Sci. 159, 95–102. doi: 10.1016/j.commatsci.2018.12.004

CrossRef Full Text | Google Scholar

Bauchy, M., Qomi, M. J. A., Bichara, C., Ulm, F. J., and Pellenq, R. J. M. (2015). Rigidity transition in materials: hardness is driven by weak atomic constraints. Phys. Rev. Lett. 114, 1–5. doi: 10.1103/PhysRevLett.114.125502

PubMed Abstract | CrossRef Full Text | Google Scholar

Berthier, L., and Biroli, G. (2010). Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 83:587. doi: 10.1103/RevModPhys.83.587

CrossRef Full Text | Google Scholar

Billinge, S. J. L., and Levin, I. (2007). The problem with determining atomic structure at the nanoscale. Science 316, 561–565. doi: 10.1126/science.1135080

PubMed Abstract | CrossRef Full Text | Google Scholar

Boolchand, P., Bresser, W., Zhang, M., Wu, Y., Wells, J., and Enzweiler, R. N. (1995). Lamb-Mössbauer factors as a local probe of floppy modes in network glasses. J. Non. Cryst. Solids 182, 143–154. doi: 10.1016/0022-3093(94)00540-0

CrossRef Full Text | Google Scholar

Boolchand, P., Georgiev, D. G., and Goodman, B. (2001). Discovery of the intermediate phase in chalcogenide glasses. J. Optoelectron. Adv. Mater. 3, 703–720.

Google Scholar

Boolchand, P., and Thorpe, M. F. (1994). Glass-forming tendency, percolation of rigidity, and onefold-coordinated atoms in covalent networks. Phys. Rev. B 50, 10366–10368. doi: 10.1103/PhysRevB.50.10366

PubMed Abstract | CrossRef Full Text | Google Scholar

Boolchand, P., Zhang, M., and Goodman, B. (1996). Influence of one-fold-coordinated atoms on mechanical properties of covalent networks. Phys. Rev. B 53, 11488–11494. doi: 10.1103/PhysRevB.53.11488

PubMed Abstract | CrossRef Full Text | Google Scholar

Bresser, W., Boolchand, P., and Suranyi, P. (1986). Rigidity percolation and molecular clustering in network glasses. Phys. Rev. Lett. 56, 2493–2496. doi: 10.1103/PhysRevLett.56.2493

PubMed Abstract | CrossRef Full Text | Google Scholar

Buzhinskij, O. I., Barsuk, V. A., and Otroshchenko, V. G. (2009). Renewable boron carbide coating in plasma shots of tokamak T11-M. J. Nucl. Mater. 390–391, 996–999. doi: 10.1016/j.jnucmat.2009.01.261

CrossRef Full Text | Google Scholar

Caruso, A. N. (2010). The physics of solid-state neutron detector materials and geometries. J. Phys. Condens. Matter 22:443201. doi: 10.1088/0953-8984/22/44/443201

PubMed Abstract | CrossRef Full Text | Google Scholar

Castleman, A. W. Jr., and Khanna, S. N. (2009). Clusters, superatoms, and building blocks of new materials. J. Phys. Chem. C. 113, 2664–2675. doi: 10.1016/S1571-0785(07)12010-1

CrossRef Full Text | Google Scholar

Chen, M., McCauley, J. W., and Hemker, K. J. (2003). Shock-induced localized amorphization in boron carbide. Science 299, 1563–1566. doi: 10.1126/science.1080819

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Chung, Y.-W., and Li, S.-Y. (2006). Boron carbide and boron carbonitride thin films as protective coatings in ultra-high density hard disk drives. Surf. Coatings Technol. 200, 4072–4077. doi: 10.1016/j.surfcoat.2005.02.164

CrossRef Full Text | Google Scholar

Das, C., Kiran, M. S. R. N., Ramamurty, U., and Asokan, S. (2012). Manifestation of intermediate phase in mechanical properties: Nano-indentation studies on Ge-Te-Si bulk chalcogenide glasses. Solid State Commun. 152, 2181–2184. doi: 10.1016/j.ssc.2012.09.020

CrossRef Full Text | Google Scholar

Deb, S. K., Wilding, M., Somayazulu, M., and Mcmillan, P. F. (2001). Pressure-induced amorphization and an amorphous-amorphous transition in densified porous silicon. Nature 414, 528–530. doi: 10.1038/35107036

PubMed Abstract | CrossRef Full Text | Google Scholar

Domnich, V., Reynaud, S., Haber, R. A., and Chhowalla, M. (2011). Boron carbide: structure, properties, and stability under stress. J. Am. Ceram. Soc. 94, 3605–3628. doi: 10.1111/j.1551-2916.2011.04865.x

CrossRef Full Text | Google Scholar

Driver, M. S., Paquette, M. M., Karki, S., Nordell, B. J., and Caruso, A. N. (2012). The electronic and chemical structure of the a-B₃CO_0.5:H_y-to-metal interface from photoemission spectroscopy: implications for Schottky barrier heights. J. Phys. Condens. Matter 24:445001. doi: 10.1088/0953-8984/24/44/445001

PubMed Abstract | CrossRef Full Text | Google Scholar

Duquesne, J. Y., and Bellessa, G. (1989). Ultrasonic study of percolation rigidity in Se-Ge glasses. Europhys. Lett. 9, 453–458. doi: 10.1209/0295-5075/9/5/008

CrossRef Full Text | Google Scholar

Emin, D. (1987). Icosahedral boron-rich solids. Phys. Today 40, 55–62. doi: 10.1063/1.881112

CrossRef Full Text | Google Scholar

Fan, H., Hartshorn, C., Buchheit, T., Tallant, D., Assink, R., Simpson, R., et al. (2007). Modulus–density scaling behaviour and framework architecture of nanoporous self-assembled silicas. Nat. Mater. 6, 418–423. doi: 10.1038/nmat1913

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, X., Bresser, W., and Boolchand, P. (1997). Direct evidence for stiffness threshold in chalcogenide glasses. Phys. Rev. Lett. 78, 4422–4425. doi: 10.1103/PhysRevLett.78.4422

CrossRef Full Text | Google Scholar

Franzblau, D. S., and Tersoff, J. (1992). Elastic properties of a network model of glasses. Phys. Rev. Lett. 68, 2172–2175. doi: 10.1103/PhysRevLett.68.2172

PubMed Abstract | CrossRef Full Text | Google Scholar

Galam, S., and Mauger, A. (1996). Universal formulas for percolation thresholds. Phys. Rev. E 53, 2177–2181. doi: 10.1103/PhysRevE.53.2177

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerstenberg, K. W., and Taube, K. (1989). Measurement of the Young's modulus for structural characterization of amorphous Si:C:N:H-films. Fresenius Z. Anal. Chem. 333, 313–314. doi: 10.1007/BF00572312

CrossRef Full Text | Google Scholar

Gervino, G., Balma, M., Devona, D., Lavagno, A., Palmisano, C., Zamprotta, L., et al. (2013). Preliminary results of a new boron coated neutron detector. Nucl. Instrum. Methods Phys. Res. Sect. A 718, 143–144. doi: 10.1016/j.nima.2012.08.092

CrossRef Full Text | Google Scholar

Ghossoub, M. G., Lee, J. H., Baris, O. T., Cahill, D. G., and Sinha, S. (2010). Percolation of thermal conductivity in amorphous fluorocarbons. Phys. Rev. B 82, 195441. doi: 10.1103/PhysRevB.82.195441

CrossRef Full Text | Google Scholar

Greuner, H., Balden, M., Boeswirth, B., Bolt, H., Gadow, R., Grigull, P., et al. (2004). Evaluation of vacuum plasma-sprayed boron carbide protection for the stainless steel first wall of WENDELSTEIN 7-X. J. Nucl. Mater. 329–333, 849–854. doi: 10.1016/j.jnucmat.2004.04.214

CrossRef Full Text | Google Scholar

Grill, A., Gates, S. M., Ryan, T. E., Nguyen, S. V., and Priyadarshini, D. (2014). Progress in the development and understanding of advanced low k and ultralow k dielectrics for very large-scale integrated interconnects—state of the art. Appl. Phys. Rev. 1:011306. doi: 10.1063/1.4861876

CrossRef Full Text | Google Scholar

Guin, J.-P., Rouxel, T., Sanglebœuf, J.-C., Melscoët, I., and Lucas, J. (2009). Hardness, toughness, and scratchability of germanium-selenium chalcogenide glasses. J. Am. Ceram. Soc. 85, 1545–1552. doi: 10.1111/j.1151-2916.2002.tb00310.x

CrossRef Full Text | Google Scholar

Han, L. M., Yi, X., Xie, J. Z., Zhou, M. S., and Chooi, S. (2002). Use of Boron Carbide as an Etch-Stop and Barrier Layer for Copper Dual Damascene Metallization. U.S. Patent No 6,424,044 B1. Washington, DC: U.S. Patent and Trademark Office.

Google Scholar

He, H., and Thorpe, M. (1985). Elastic properties of glasses. Phys. Rev. Lett. 54, 2107–2110. doi: 10.1103/PhysRevLett.54.2107

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, H., and Kong, J. (2014). Improved thermal performance of diamond-copper composites with boron carbide coating. J. Mater. Eng. Perform. 23, 651–657. doi: 10.1007/s11665-013-0780-z

CrossRef Full Text | Google Scholar

Huang, P. Y., Kurasch, S., Alden, J. S., Shekhawat, A., Alemi, A., a McEuen, P. L., et al. (2013). Imaging atomic rearrangements in two-dimensional silica glass: watching silica's dance. Science 342, 224–227. doi: 10.1126/science.1242248

PubMed Abstract | CrossRef Full Text | Google Scholar

Jain, A., Rogojevic, S., Gill, W. N., Plawsky, J. L., Matthew, I., Tomozawa, M., et al. (2001). Effects of processing history on the modulus of silica xerogel films. J. Appl. Phys. 90, 5832–5834. doi: 10.1063/1.1412266

CrossRef Full Text | Google Scholar

Kamitakahara, W. A., Cappelletti, R. L., Boolchand, P., Halfpap, B., Gompf, F., Neumann, D. A., et al. (1991). Vibrational densities of states and network rigidity in chalcogenide glasses. Phys. Rev. B 44, 94–100. doi: 10.1103/PhysRevB.44.94

PubMed Abstract | CrossRef Full Text | Google Scholar

Keski-Kuha, R. A., Blumenstock, G. M., Fleetwood, C. M., and Schmitt, D.-R. (1998). Effects of space exposure on ion-beam-deposited silicon-carbide and boron-carbide coatings. Appl. Opt. 37, 8038–8042. doi: 10.1364/AO.37.008038

PubMed Abstract | CrossRef Full Text | Google Scholar

King, R. B. (2001). Three-dimensional aromaticity in polyhedral boranes and related molecules. Chem. Rev. 101, 1119–1152. doi: 10.1021/cr000442t

PubMed Abstract | CrossRef Full Text | Google Scholar

King, S. W., Bielefeld, J., Xu, G., Lanford, W. A., Matsuda, Y., Dauskardt, R. H., et al. (2013). Influence of network bond percolation on the thermal, mechanical, electrical and optical properties of high and low-k a-SiC:H thin films. J. Non. Cryst. Solids 379, 67–79. doi: 10.1016/j.jnoncrysol.2013.07.028

CrossRef Full Text | Google Scholar

Kohl, P. A. (2011). Low–dielectric constant insulators for future integrated circuits and packages. Annu. Rev. Chem. Biomol. Eng. 2, 379–401. doi: 10.1146/annurev-chembioeng-061010-114137

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuschnereit, R., Fath, H., Kolomenskii, A. A., Szabadi, M., and Hess, P. (1995). Mechanical and elastic properties of amorphous hydrogenated silicon films studied by broadband surface acoustic wave spectroscopy. Appl. Phys. A 61, 269–276. doi: 10.1007/BF01538192

CrossRef Full Text | Google Scholar

Li, Y., and Qiu, T. (2007). Oxidation behaviour of boron carbide powder. Mater. Sci. Eng. A 444, 184–191. doi: 10.1016/j.msea.2006.08.068

CrossRef Full Text | Google Scholar

Lin, Y., Zhang, L., Mao, H., Chow, P., Xiao, Y., Baldini, M., et al. (2011). Amorphous diamond: A high-pressure superhard carbon allotrope. Phys. Rev. Lett. 107:175504. doi: 10.1103/PhysRevLett.107.175504

PubMed Abstract | CrossRef Full Text | Google Scholar

Maex, K., Baklanov, M. R., Shamiryan, D., Lacopi, F., Brongersma, S. H., and Yanovitskaya, Z. S. (2003). Low dielectric constant materials for microelectronics. J. Appl. Phys. 93, 8793–8841. doi: 10.1063/1.1567460

CrossRef Full Text | Google Scholar

Mauro, J. C. (2011). Topological constraint theory of glass. Am. Ceram. Soc. Bull. 90, 31–37.

Google Scholar

Mauro, J. C. (2018). Decoding the glass genome. Curr. Opin. Solid State Mater. Sci. 22, 58–64. doi: 10.1016/j.cossms.2017.09.001

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1864). On the calculation of the equilibrium and stiffness of frames. Philos. Mag. 27, 294–299. doi: 10.1080/14786446408643668

CrossRef Full Text | Google Scholar

Medvedeva, J. E., Buchholz, D. B., and Chang, R. P. H. (2017). Recent advances in understanding the structure and properties of amorphous oxide semiconductors. Adv. Electron. Mater. 3:1700082. doi: 10.1002/aelm.201700082

CrossRef Full Text | Google Scholar

Meza, L. R., Das, S., and Greer, J. R. (2014). Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 345, 1322–1327. doi: 10.1126/science.1255908

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalak, D. J., Blackwell, J. M., Torres, J. M., Sengupta, A., Kreno, L. E., Clarke, J. S., et al. (2015). Porosity scaling strategies for low-k films. J. Mater. Res. 30, 3363–3385. doi: 10.1557/jmr.2015.313

CrossRef Full Text | Google Scholar

Micoulaut, M. (2016). Concepts and applications of rigidity in non-crystalline solids: a review on new developments and directions. Adv. Phys. X 6149, 1–29. doi: 10.1080/23746149.2016.1161498

CrossRef Full Text | Google Scholar

Micoulaut, M., and Phillips, J. C. (2007). Onset of rigidity in glasses: from random to self-organized networks. J. Non. Cryst. Solids 353, 1732–1740. doi: 10.1016/j.jnoncrysol.2007.01.078

CrossRef Full Text | Google Scholar

Nordell, B. J., Karki, S., Nguyen, T. D., Rulis, P., Caruso, A. N., Purohit, S. S., et al. (2015). The Influence of hydrogen on the chemical, mechanical, optical/electronic, and electrical transport properties of amorphous hydrogenated boron carbide. J. Appl. Phys. 118:035703. doi: 10.1063/1.4927037

CrossRef Full Text | Google Scholar

Nordell, B. J., Keck, C. L., Nguyen, T. D., Caruso, A. N., Purohit, S. S., Lanford, W. A., et al. (2016a). Tuning the properties of a complex disordered material: Full factorial investigation of PECVD-grown amorphous hydrogenated boron carbide. Mater. Chem. Phys. 173, 268–284. doi: 10.1016/j.matchemphys.2016.02.013

CrossRef Full Text | Google Scholar

Nordell, B. J., Nguyen, T. D., Caruso, A. N., Purohit, S. S., Oyler, N. A., Lanford, W. A., et al. (2017). Carbon-enriched amorphous hydrogenated boron carbide films for very-low-k interlayer dielectrics. Adv. Electron. Mater. 3:1700116. doi: 10.1002/aelm.201700116

CrossRef Full Text | Google Scholar

Nordell, B. J., Nguyen, T. D., Keck, C. L., Dhungana, S., Caruso, A. N., Lanford, W. A., et al. (2016b). Conquering the low-k death curve: Insulating boron carbide dielectrics with superior mechanical properties. Adv. Electron. Mater. 2:1600073. doi: 10.1002/aelm.201600073

CrossRef Full Text | Google Scholar

Palin, G. R. (1967). “Chapter 4: electrical properties of of plastics,” in Plastics for Engineers: An Introductory Course (New York, NY: Pergamon Press), 40–48.

Google Scholar

Paquette, M. M., Li, W., Sky Driver, M., Karki, S., Caruso, A. N., and Oyler, N. A. (2011). The local physical structure of amorphous hydrogenated boron carbide: insights from magic angle spinning solid-state NMR spectroscopy. J. Phys. Condens. Matter 23:435002. doi: 10.1088/0953-8984/23/43/435002

PubMed Abstract | CrossRef Full Text | Google Scholar

Paquette, M. M., Nordell, B. J., Caruso, A. N., Sato, M., Fujiwara, H., and King, S. W. (2017). Optimization of amorphous semiconductors and low-/high-k dielectrics through percolation and topological constraint theory. MRS Bull. 42, 39–44. doi: 10.1557/mrs.2016.297

CrossRef Full Text | Google Scholar

Phillips, J., and Thorpe, M. (1985). Constraint theory, vector percolation and glass formation. Solid State Commun. 53, 699–702. doi: 10.1016/0038-1098(85)90381-3

CrossRef Full Text | Google Scholar

Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: short-range order in chalcogenide alloys. J. Non Cryst. Solids 34, 153–181. doi: 10.1016/0022-3093(79)90033-4

CrossRef Full Text | Google Scholar

Plucinski, M., and Zwanziger, J. W. (2015). Topological constraints and the Makishima-Mackenzie model. J. Non. Cryst. Solids 429, 20–23. doi: 10.1016/j.jnoncrysol.2015.08.029

CrossRef Full Text | Google Scholar

Rader, A. J., Hespenheide, B. M., Kuhn, L. A., and Thorpe, M. F. (2002). Protein unfolding: Rigidity lost. Proc. Natl. Acad. Sci. U.S.A. 99, 3540–3545. doi: 10.1073/pnas.062492699

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, B. W., Adenwalla, S., Harken, A., Welsch, P., Brand, J. I., Dowben, P. A., et al. (2002). A class of boron-rich solid-state neutron detectors. Appl. Phys. Lett. 80, 3644–3646. doi: 10.1063/1.1477942

CrossRef Full Text | Google Scholar

Robertson, J. (1992). Mechanical properties and coordinations of amorphous carbons. Phys. Rev. Lett. 68, 220–223. doi: 10.1103/PhysRevLett.68.220

PubMed Abstract | CrossRef Full Text | Google Scholar

Ross, A. D., and Gleason, K. K. (2005). Effects of condensation reactions on the structural, mechanical, and electrical properties of plasma-deposited organosilicon thin films from octamethylcyclotetrasiloxane. J. Appl. Phys. 97:113707. doi: 10.1063/1.1923163

CrossRef Full Text | Google Scholar

Rouxel, T. (2007). Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 90, 3019–3039. doi: 10.1111/j.1551-2916.2007.01945.x

CrossRef Full Text | Google Scholar

Sartbaeva, A., Wells, S. A., Huerta, A., and Thorpe, M. F. (2007). Local structural variability and the intermediate phase window in network glasses. Phys. Rev. B 75:224204. doi: 10.1103/PhysRevB.75.224204

CrossRef Full Text | Google Scholar

Sartbaeva, A., Wells, S. A., Treacy, M. M. J., and Thorpe, M. F. (2006). The flexibility window in zeolites. Nat. Mater. 5, 962–965. doi: 10.1038/nmat1784

PubMed Abstract | CrossRef Full Text | Google Scholar

Senapati, U., and Varshneya, A. K. (1995). Configurational arrangements in chalcogenide glasses: A new perspective on Phillips' constraint theory. J. Non. Cryst. Solids 185, 289–296. doi: 10.1016/0022-3093(94)00534-6

CrossRef Full Text | Google Scholar

Sreeram, A. N., Varshneya, A. K., and Swiler, D. R. (1991). Molar volume and elastic properties of multicomponent chalcogenide glasses. J. Non. Cryst. Solids 128, 294–309. doi: 10.1016/0022-3093(91)90467-K

CrossRef Full Text | Google Scholar

Srinivasan, A., Madhusoodanan, K. N., and Gopal, E. S. R. J P. (1992). Observation of a threshold behavior in the optical band gap and thermal diffusivity of Ge-Sb-Se glasses. Phys. Rev. B 45, 8112–8115. doi: 10.1103/PhysRevB.45.8112

PubMed Abstract | CrossRef Full Text | Google Scholar

Störmer, M., Siewert, F., and Sinn, H. (2016). Preparation and characterization of B₄C coatings for advanced research light sources. J. Sync. Radiat. 23, 50–58. doi: 10.1107/S1600577515020901

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, K. (1986). Elastic properties of covalent glasses. Solid State Commun. 60, 295–297. doi: 10.1016/0038-1098(86)90469-2

CrossRef Full Text | Google Scholar

Tanaka, K. (1989). Structural phase transitions in chalcogenide glasses. Phys. Rev. B 39, 1270–1279. doi: 10.1103/PhysRevB.39.1270

PubMed Abstract | CrossRef Full Text | Google Scholar

Tatsumisago, M., Halfpap, B. L., Green, J. L., Lindsay, S. M., and Angell, C. A. (1990). Fragility of Ge-As-Se glass-forming liquids in relation to rigidity percolation, and the Kauzmann Paradox. Phys. Rev. Lett. 64, 1549–1552. doi: 10.1103/PhysRevLett.64.1549

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non. Cryst. Solids 57, 355–370. doi: 10.1016/0022-3093(83)90424-6

CrossRef Full Text | Google Scholar

Thorpe, M. F., Jacobs, D. J., Chubynsky, N. V., and Rader, A. J. (2002). “Generic rigidity of network glasses,” in Rigidity Theory and Applications, eds M. F. Thorpe and P. M. Duxbury (New York, NY: Kluwer Academic/Plenum Publishers, 239–277.

Google Scholar

Tichý, L., and Tichá, H. (1994). On the chemical threshold in chalcogenide glasses. Mater. Lett. 21, 313–319. doi: 10.1016/0167-577X(94)90196-1

CrossRef Full Text | Google Scholar

Trujillo, N. J., Wu, Q., and Gleason, K. K. (2010). Ultralow dielectric constant tetravinyltetramethylcyclotetrasiloxane films deposited by initiated chemical vapor deposition (iCVD). Adv. Funct. Mater. 20, 607–616. doi: 10.1002/adfm.200900999

CrossRef Full Text | Google Scholar

Vyssotsky, V. A., Gordon, S. B., Frisch, H. L., and Hammersley, J. M. (1961). Critical percolation probabilities (bond problem). Phys. Rev. 123, 1566–1567. doi: 10.1103/PhysRev.123.1566

CrossRef Full Text | Google Scholar

Wang, R. P., Smith, A., Luther-Davies, B., Kokkonen, H., and Jackson, I. (2009). Observation of two elastic thresholds in Ge_xAs_ySe_1−x−y glasses. J. Appl. Phys. 105:056109. doi: 10.1063/1.3079806

CrossRef Full Text | Google Scholar

Wang, T., Wei, W. H., Shen, X., Wang, R. P., Davies, B. L., and Jackson, I. (2013). Elastic transition thresholds in Ge-As(Sb)-Se glasses. J. Phys. D. Appl. Phys. 46:165302. doi: 10.1088/0022-3727/46/16/165302

CrossRef Full Text | Google Scholar

Wilding, M. C., Wilson, M., and McMillan, P. F. (2006). Structural studies and polymorphism in amorphous solids and liquids at high pressure. Chem. Soc. Rev. 35, 964–986. doi: 10.1039/b517775h

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, G., Bureau, B., Rouxel, T., Gueguen, Y., Gulbiten, O., Roiland, C., et al. (2010). Correlation between structure and physical properties of chalcogenide glasses in the As_xSe_1−x system. Phys. Rev. B 82:195206. doi: 10.1103/PhysRevB.82.195206

CrossRef Full Text | Google Scholar

Yun, S. S., Li, H., Cappelletti, R. L., Enzweiler, R. N., and Boolchand, P. (1989). Onset of rigidity in Se_1−xGe_x glasses: ultrasonic elastic moduli. Phys. Rev. B 39, 8702–8706. doi: 10.1103/PhysRevB.39.8702

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., and Boolchand, P. (1994). The central role of broken bond-bending contraints in promoting glass formation in the oxides. Science 266, 1355–1357. doi: 10.1126/science.266.5189.1355

PubMed Abstract | CrossRef Full Text | Google Scholar