Signature of Coordination Defects in the Vibrational Spectrum of Amorphous Chalcogenides

1. Introduction

Chalcogenide glasses are of great technological importance due to their potential applications in rewritable optical media, electronic nonvolatile memories, electrolytes and infrared waveguides (Adam, 2014). Among such materials, As-Se systems are among the most widely studied given their use as starting material for multicomponent alloys with targeted properties (Chen et al., 2010; Yang et al., 2010; Musgraves et al., 2011; Adam, 2014). In spite of numerous studies, the structural properties of amorphous As-Se glasses are still being debated. The molecular structure in the Se-rich region between x = 0 % (pure Selenium) and x = 40 % (As₂Se₃) has been described as a network of Se chains randomly cross-linked by Arsenic atoms in a AsSe_3/2 pyramidal structure (PYR) (Adam, 2014) (Figure 1). However, while a three-fold coordination can be reliably inferred from different techniques (Bureau et al., 2003; Xin et al., 2008) and represents undoubtedly the dominant local structure, coordination defects such as quasi-tetrahedral (QT) Se=AsSe_3/2 units (Figure 1C) have been proposed to also exist (Georgiev et al., 2000), and these contain a double As=Se bond. The presence of miscoordinated species is not specific to As-Se glasses since many other chalcogenides display the tendency to form local structures that do not fully conform to the octet rule, as revealed by e.g., molecular simulation techniques. In certain chalcogenides, these defects have been used to interpret vibrational and photoelectron spectroscopic measurements (Diemann, 1979) of e.g., As₂S₅, and used subsequently for the interpretation of experimental data of As-Se glasses (Wagner and Kasap, 1996). There have been theoretical and experimental investigations (Mauro and Varshneya, 2007; Hosokawa et al., 2013) indicating that 4-fold As might be present in the glass through possible homopolar As-As defects, and a calculated coordination number was found to be larger than three (n_As = 3.29) which is another indication that such defects might be present in the glassy state. Recently, first principles molecular dynamics (FPMD) simulations (Bauchy et al., 2013, 2014) have also shown that As₂Se₃ displays a significant number of homopolar As-As and Se-Se bonds, together with the presence of QT units, albeit the fraction is rather small, typically less than 10%. Moreover, the results from such structural models lead to partial correlations seem to agree with those obtained experimentally from anomalous X-ray scattering (Hosokawa et al., 2013). Nevertheless, the question remains subject to large uncertainties given that the structural picture using QT is in contrast with the analysis of Raman spectroscopy on limited frequency range (Kostadinova, 2009) and Nuclear Quadrupole Resonance (Ahn et al., 2006).

FIGURE 1

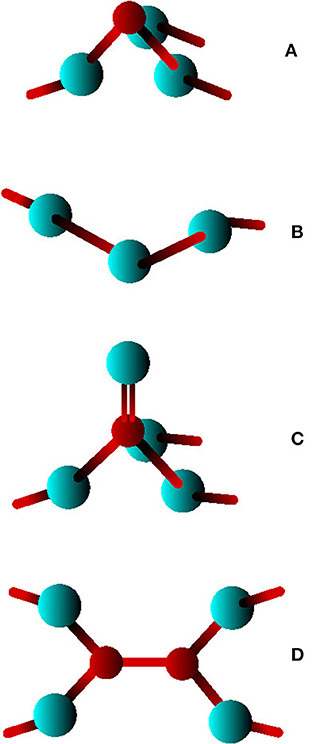
Figure 1. Possible local structures in amorphous As₂Se₃: (A) a pyramidal AsSe_3/2 (PYR), (B) a Se chain-like fragment, (C) a quasitetrahedral Se_3/2As=Se unit, (D) a homopolar As-As bond.

Experimentally, signatures of As in QT sites have been assigned to specific features of the Raman spectrum of chemical analogs such as P₂Se₅ (Georgiev et al., 2003), and different Raman peaks in As-Se were tentatively assigned (Chen et al., 2010) to vibrational modes of Se=AsSe_3/2 but their origin and thermodynamic stability has been largely overlooked. Therefore, a compelling identification of QT Arsenic has not yet been given. From a more general viewpoint, the question of coordination defects is also central for the understanding for light-induced effects which are typical of chalcogenides (Li and Drabold, 2000). Electronic excitations reduce, indeed, the HOMO-LUMO band gap, the reduction being enhanced when valence-alternation pairs (Zhang and Drabold, 1998; Simdyankin et al., 2005) can be promoted. In this respect, the question of alternative coordinations to three-fold As, their underlying stability and their behavior across the glass-liquid transition is crucial.

In the present contribution, we provide theoretical evidence that such coordination defects exist in the archetypal network former As₂Se₃. These QT units appear to be reminiscent of the liquid state where they represent the dominant local structures with a fraction of about 40%. We show that all specific local molecular structures with detectable vibrational modes such as the AsSe_3/2 (PYR) and the Se=AsSe_3/2 (QT) unit contribute to the total infrared absorption spectrum of the glass and the liquid, that is calculated using linear response theory. Such modes can be only identified from first-principles calculations permitting to obtain their typical vibrational frequency, and a complementary assignment from local clusters permits to identify typical frequencies (at ≃380 cm⁻¹) with the QT unit. The latter depends strongly on temperature and its thermal stability is examined.

2. Numerical Methods

For the simulation of the present As₂Se₃ glasses and liquids, we used density functional theory (DFT) in combination with plane wave basis sets, from the Car-Parrinello molecular dynamics (CPMD) package. The electronic scheme has been chosen after a series of methodological investigations on different liquid and amorphous chalcogenides (Ge-Se) showing that (i) a generalized gradient approximation (GGA) for the exchange-correlation energy improves substantially (Massobrio et al., 1999) the description of both short and intermediate range order when compared to the local density approximation (LDA), (ii) an alternative exchange-correlation functional (with respect to Massobrio et al., 1999), derived after PW Becke (B) for the exchange energy (Becke, 1988) and Lee, Yang and Parr (LYP) for the correlation energy (Lee et al., 1988) leads to a structure with a reduced number of miscoordinated atoms and metallic character, and improves the reproduction of vibrational spectra (Giacomazzi et al., 2011) or Nuclear Magnetic resonance (NMR) properties (Kibalchenko et al., 2010). These simulations have been found to lead to structural models able to reproduce a variety of structure functions (pair correlation, structure factor) for various compositions in the As-Se binary that have been successfully compared to experiments (Bauchy et al., 2013, 2014).

A periodically repeated cubic cell containing 200 atoms was used, corresponding to the number density (18.06 Å) of the glass (Chen et al., 2010) and the time step for the integration of the equation of motion was chosen to be 0.12 fs with a fictitious mass of 200 a.u. Valence electrons were treated explicitly, in conjunction with normconserving pseudopotentials to account for core-valence interactions. The wave functions were expanded at the Γ point of the supercell and the energy cutoff was set at 20 Ry. Finally, it should be noted that the amorphous structures result from five independent quenches (10K/ps) in order to increase the statistical accuracy of the models. The starting configurations of these independent quenches are separated by 5 ps at 1,000 K. Given the small system size of 200 atoms, there are, indeed, increased thermal history effects that can alter the overall results as highlighted by Figure 2 which shows a difference for the obtained inherent structures displaying a clear variability in short range order and manifests by a different amplitude for the As-As homopolar prepeak at 2.45 Å and different bonding distances for the second correlation (3.71–3.78 Å). By ultimately performing the averages over such inherent structures, it is implicitly assumed that the resulting “average” structure will be a more realistic model of the glassy state, as confirmed below from the inspection of the calculated structure factor or pair correlation function, and their comparison with experiments.

FIGURE 2

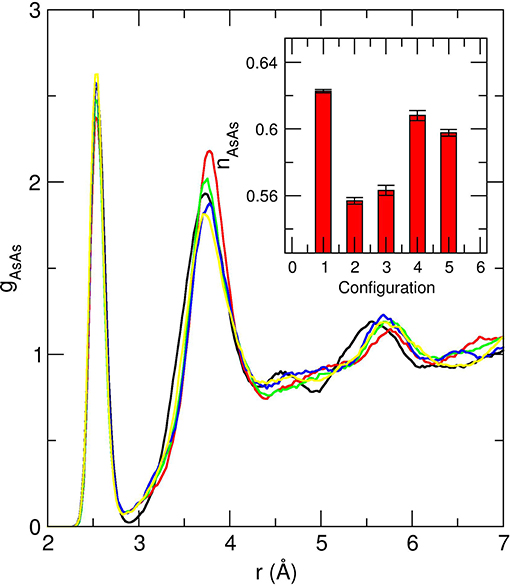
Figure 2. Calculated As-As partial pair correlation function g_AsAs for five independent quenched configurations of amorphous As₂Se₃. The inset shows the corresponding obtained AsAs coordination number n_AsAs for the five configurations.

3. Results

3.1. Structure

The obtained structural properties in real and reciprocal space are given in Figure 3. The total pair correlation function g(r) is represented in panel a. When compared to available experimental data (Xin et al., 2008; Fabian et al., 2010), one acknowledges an excellent agreement for all typical features: position, width and intensity of the principal peak at r = 2.44 Å defining the first correlation or bond distance dominated by As-Se correlations (experimentally 2.39–2.41 Å Renninger and Averbach, 1975; Mastelaro et al., 1992; Xin et al., 2008), and the secondary peak at r = 3.71 Å (experimentally 3.62–3.68 Å from various probes Renninger and Averbach, 1975; Xin et al., 2008), a slight overestimation of the bond distances being acknowledged when compared to experimental findings. The origin of the principal peak is essentially due to As-Se correlations with a moderate contributions from As-As and Se-Se bonds which is an indication of broken chemical order that has been also evidenced in another stoichiometric chalcogenide (Petri et al., 2000). The partial correlations (As-As, As-Se, Se-Se) are, indeed, also represented and two small contributions at 2.55 and 2.37 Å signal the presence of homopolar As-As and Se-Se bonds, respectively (blue curves in Figure 3A).

FIGURE 3

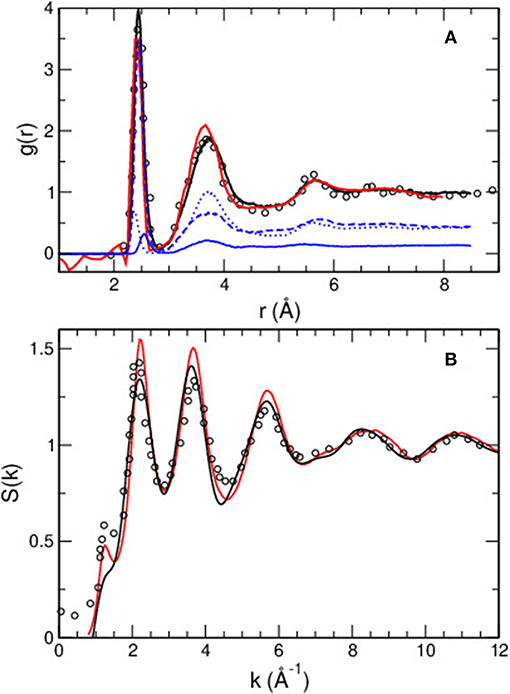
Figure 3. (A) Total calculated pair correlation function g(r) of amorphous As₂Se₃ (black curve), compared to experimental data from neutron diffusion (red curve Xin et al., 2008, circles Fabian et al., 2010). (B) Simulated structure factor S_T(k) (black curve) compared to experimental data from Fabian et al. (2010) (circles) and Xin et al. (2008) (red curve). A decomposition into partial structure factors is shown in panel a), weighted by the appropriate neutron coherence lengths and concentrations of the species: As-As (solid curve), As-Se (broken curve), Se-Se (dotted curve).

In Figure 3B the total structure factor S_T(k) is represented and compared to corresponding experimental data (Xin et al., 2008; Fabian et al., 2010). The agreement between experiments and simulation is found to be excellent for all momentum transfers k, and the two principal peaks at k_PP1=2.2 Å⁻¹ and k_PP2=3.7 Å⁻¹ are very well reproduced, as are also the peaks obtained at higher k (k > 6 Å⁻¹). Note that the first sharp diffraction peak (FSDP), while rather small in experiments (Xin et al., 2008), reduces in the simulations to a simple shoulder on the low wavevector side of the principal peak at 2.1 Å⁻¹. In contrast to similar chalcogenides (GeSe₂), we are not aware of a full resolution of partial structure factors from isotopic substituted neutron diffraction. However, it has been pointed out (Bauchy et al., 2014) that the partial resolution from anomalous X-ray scattering (Hosokawa et al., 2001, 2006) can be also very well reproduced. Such experiments reveal, furthermore, that only an As-related partial displays a FSDP at k≃1.2 Å⁻¹, which is an indication that correlations in medium range order (i.e., at low k) mainly arise from As atoms. Many other physical and chemical properties can be inferred from the simulated structure and the dynamics (Bauchy et al., 2013, 2014; Micoulaut and Bauchy, 2013).

3.2. Infrared Properties

Following a strategy developed for Ge-Se glasses (Micoulaut et al., 2013), the infrared (IR) absorption spectrum can be determined from dipole-dipole correlations. During the DFT calculation, the total dipole moment M(t) is directly calculated (Silvestrelli et al., 1997) and contributes via the Fourier transform of the dipole-dipole autocorrelation function to the IR absorption spectrum using the maximum entropy inversion method (Silver et al., 1990):

$\begin{array}{ll}\alpha (\omega )=\frac{4\pi tanh(\beta \hslash \omega /2)}{3\hslash cVn(\omega )}{\displaystyle {\int }_0^{\infty }}{e}^{-i\omega t}\langle \text{M}(t)\text{M}(0)\rangle dt,& (1)\end{array}$

where V is the volume, β=1/k_BT, and n(ω) the refractive index. Figure 4 shows the computed IR spectra α(ω)n(ω) for different temperatures. As in previous investigations of chalcogenides (Micoulaut et al., 2013), the main features are qualitatively reproduced from the simulation such as the main peak at 150-200 cm⁻¹ and the broad band between 50 and 130 cm⁻¹, these two features being detected experimentally (Lucovsky et al., 1975), as well as the shoulder peak at 250 cm⁻¹. It should be noted that the reproduction of IR properties have been found to be highly sensitive to the method employed and a previous methodological study for Ge-Se glasses has shown that a direct calculation inspired by linear response theory and the time dependence of the dipolar momentum M(t) was much more accurate than an alternative method (Giacomazzi et al., 2007, 2011). The latter builds on the response to a finite electrical field in conjunction with the computation of coupling tensors (dynamical Born charge Resta, 1994) based on the first derivative of the atomic forces with respect to the electrical field.

FIGURE 4

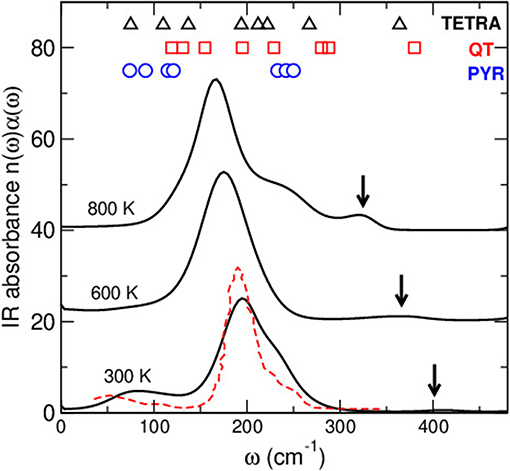
Figure 4. Calculated IR absorbance spectra in amorphous and liquid As₂Se₃, compared to the measured spectra for As₂Se₃ (Lucovsky et al., 1975) (broken red curve). On top are reminded the location of the typical vibrational modes of a pyramidal unit AsSe_3/2 (PYR), the quasi-tetrahedral unit Se=AsSe_3/2 (QT) unit and a tetrahedral As (see numbers in Table 1).

With increasing temperature, the entire spectra shifts to lower frequencies, which is consistent with an overall temperature induced softening of the vibrational motion, the main peak shifting from ≃ 180 cm⁻¹ at room temperature to about 160 cm⁻¹ at 800 K. One furthermore notes the vanishing of the low-frequency bands at 50–130 cm⁻¹ (barely detectable at 600 K) and the emergence of a shoulder peak at ≃ 300–360 cm⁻¹ which is visible at 300 K, albeit minuscule (arrows). The detail of the typical mode vibrations can be analyzed to further decode the IR spectra, in relationship with structural features.

TABLE 1

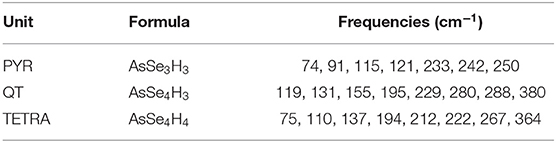
Table 1. Predicted mode frequencies of the different units present in amorphous As₂Se₃ glasses using DFT calculations.

4. Discussion

4.1. Typical Mode Frequencies

The IR spectrum can be analyzed from a vibrational cluster analysis (Table 1) on typical As-centered species. DFT based calculations of the clusters (some of them represented in Figure 1) provide a complementary indication and an assignment of the typical bands observed in Figure 4. In the present case, three typical clusters have been considered: the PYR unit which is the dominant motif of the network structure, the QT containing the double As=Se bond, and a pure tetrahedral AsSe_4/2 (TETRA) which has been suggested to be part of the structure in combination with the presence of As-As homopolar bonds (Hosokawa et al., 2013). It is seen that the PYR unit gives essentially rise to bands found in the 70–120 cm⁻¹ region, and are associated with bending/stretching and/or deformation modes of the local geometry, the modes at the largest frequencies (250 cm⁻¹) giving rise to umbrella flip modes, while smaller modes are found to be linked with breathing modes.

Interestingly, the analysis of the other clusters (TETRA, QT) indicate additional contributions at higher frequencies (180–260 cm⁻¹), consistently with the emergence of additional bands in this frequency range with increasing temperature as discussed below. The addition of an extra coordination sphere of Se atoms to As-centered unit brings the calculated frequencies somewhat closer to the experimental values found for the main peak (modes detected in the 180–220 cm⁻¹ range), although it cannot be eluded that these modes might also be the result of vibrational motions arising from linkages of elementary PYR units (Lucovsky et al., 1975). Most importantly is the fact that both QT and TETRA have an additional frequency found at ≃365 cm⁻¹ which is associated, in the case of the QT, with the vibrational motion of a double As=Se bond, as independently suggested by a Raman mode calculation (Jackson et al., 1999; Ravindren, 2014). This typical frequency is not found from the vibrational analysis of a PYR cluster (Table 1), and appears therefore to be specific of the tetrahedral defect coordination.

The calculated Raman active modes reveal, indeed, dominant vibrations at 235 cm⁻¹ and 260 cm⁻¹ are due to As-Se asymetric (in phase bond stretching) and symmetric stretching, respectively, as found experimentally (Chen et al., 2010), the only mode standing apart from the others with no possible overlap corresponding to a vibration of the Se=As double bond, expected experimentally to be near 360 cm⁻¹. It should be stressed that similar solitary modes have been determined in corresponding P-Se, P-S (Georgiev et al., 2001; Boolchand et al., 2009) and As-S glasses (Chen et al., 2008; Chakravarty et al., 2019) where the presence of P=Se and As=S double bonds could be determined independently, including from NMR (Tullius et al., 1990; Georgiev et al., 2001).

Experimentally, it has been found that the principal modes of the Raman spectrum of As₂Se₃ are spread out contiguously between 190 cm⁻¹ and 300 cm⁻¹ but with signatures of QT units found at larger frequencies (Chen et al., 2010; Ravindren, 2014) and these typical modes associated with the As=Se double bond do exist besides the main bands and have been identified at 355 cm⁻¹ and 475 cm⁻¹. In contrast to the most recent work on As-Se (Chen et al., 2010; Ravindren, 2014), previous experimental studies on Raman (Kostadinova, 2009) or IR (Lucovsky et al., 1975) have not focused (ω <330 cm⁻¹) on this high frequency domain and it would certainly be interesting to probe, at least for the IR absorption, how the present numerical results can be compared.

An inspection of the fraction of r-fold species (Figure 5) that is calculated from the network structure indicates that the 600 K and 800 K liquids can contain a large fraction of As^IV (i.e., a 4-fold As, Micoulaut and Bauchy, 2013). The structure of the liquids is, thus, at variance with the amorphous structure which is found to be mostly populated by 3-fold PYR units with minority species (≃10 %) made of As^IV that can be determined from different methods (Bauchy et al., 2014). However, as the temperature is increased across the glass transition region, the fraction of such species grows in an important fashion, leading to a fraction of about ≃40% at 1200 K, and representing the dominant motif in the stable liquid. One can thus conclude that the abrupt decrease of 4-fold coordinated As is an important structural feature driving the onset of the glass transition in As₂Se₃. These findings actually contrast those found for Ge-Se liquids where the dominant tetrahedral order prevails over extended ranges in temperature (Massobrio et al., 2001; Salmon, 2007).

FIGURE 5

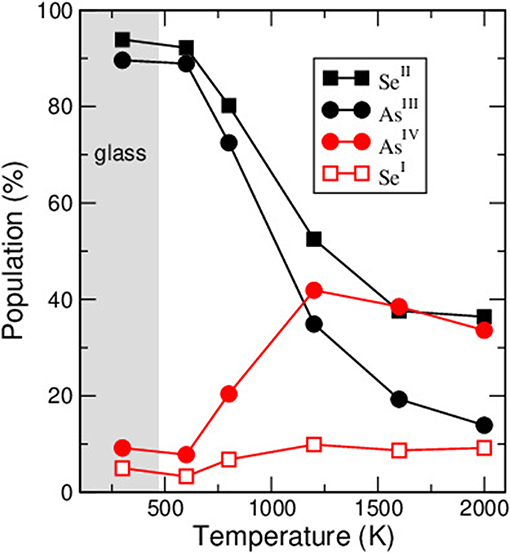
Figure 5. Calculated fraction of r-fold species in amorphous and liquid As₂Se₃ (after Micoulaut and Bauchy, 2013). The gray zone corresponds to the glass region with T_g derived from Chen et al. (2010).

4.2. Stability

In order to probe the stability of such tetrahedral motifs, we have calculated their population in the supercooled liquids as well as in the 300 K glass under special numerical preparation condition (see below).

In Figure 6A we represent the statistics of As^IV in the two target liquids at 600 K and 800 K over the picosecond time domain which corresponds to multiple bond lifetimes. Evolution with time evolves for e.g., the lowest temperature (600 K) around 8 ± 2.5 % with a bond lifetime that we have calculated to be of about 0.82 ps. The situation is somewhat different for the amorphous system. For the latter, the starting configuration at 300 K has been chosen to be a 1,000 K atomic system containing about 40% As^IV and hyperquenched (Figure 5), a Nosé-Hoover thermostat being applied with a frequency of 800 cm⁻¹ (corresponding to a relaxation time for the thermostat of 41.69 fs). A subsequent relaxation led to a modification of the structure, and the inspection of Figure 6B suggests a rapid evolution of a starting “liquid-like” network with numerous miscoordinated defects containing QT into a structure with the predominant PYR local structure, the evolution being merely fulfilled within the picosecond timescale. For the particular As^IV defect, the decrease is linked with a global decrease of As^IV having one or two homopolar As-As bonds whose initial probability is in a ratio of nearly 1:1. The trend in all defect coordinated species is found to parallel the energy of the system (not shown) which decreases with the same trend within the first picosecond.

FIGURE 6

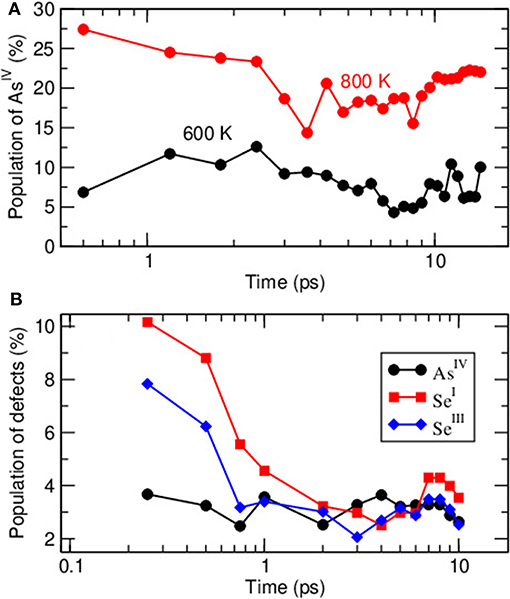
Figure 6. Calculated fraction of As^IV in liquid (600 K and 800 K) As₂Se₃ with simulation time (A) and time evolution of defect species (As^IV, Se^I, and Se^III) from a hyperquenched stable liquid to 300 K (B).

As a result, such defects represent minority species of the As₂Se₃ glass but these give rise, as evidenced from Figure 4 and Table 1, to specific spectroscopic signatures in the high frequency domain of both IR and Raman spectra, as also detected in other Group V chalcogenides (Georgiev et al., 2001; Chen et al., 2008; Boolchand et al., 2009; Chakravarty et al., 2019).

5. Summary and Conclusions

In the present contribution, we have investigated vibrational and spectroscopic properties of amorphous As₂Se₃ with a special emphasis on the signature of QT units. Results show that such units must have, like for other Group V chalcogenides, a typical mode located in the high frequency domain as revealed from the calculation of the IR absorption spectra in the glassy and liquid state. This mode is found to blueshift and to increase in amplitude as the temperature is increased, consistently with the growth of the fraction of 4-fold As that is calculated independently. It is found that such species have a large probability of occurrence in the high temperature liquid. The vibrational analysis from clusters indicates that only such higher coordinated species have a typical mode compatible with the obtained IR spectra in the region 350–400 cm⁻¹.

On a more general ground, the present numerical study shows that an amorphous system obtained from a molecular dynamics simulation represents an ultrafast quenched high-temperature liquid. In covalent chalcogenides, it is known that such liquids contain a large number of miscoordinated atoms and defect geometries which are frozen down to low temperature due, in part, to the minuscule relaxation. It would be interesting to probe such methods for other compositions in the As-Se system in order to link the probability of such QT units with documented anomalies in thermal and relaxation properties (Ravindren et al., 2014). Work in this direction is in progress.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adam, J. L. (2014). Chalcogenides: Preparation, Properties and Applications. Oxford: Woodhead.

Google Scholar

Ahn, E., Williams, G. A., and Taylor, P. C. (2006). Nuclear quadrupole resonance study of local bonding in glassy As_xSe_1x. Phys. Rev. B 74:174206. doi: 10.1103/PhysRevB.74.174206

CrossRef Full Text | Google Scholar

Bauchy, M., Kachmar, A., and Micoulaut, M. (2014). Structural, dynamic, electronic and vibrational properties of flexible, intermediate and stressed rigid As-Se glasses and liquids from first principles molecular dynamics simulations. J. Chem. Phys. 141:194506. doi: 10.1063/1.4901515

CrossRef Full Text | Google Scholar

Bauchy, M., Micoulaut, M., Boero, M., and Massobrio, C. (2013). Compositional thresholds and anomalies in connection with stiffness transitions in network glasses. Phys. Rev. Lett. 110:165501. doi: 10.1103/PhysRevLett.110.165501

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38:3098. doi: 10.1103/PhysRevA.38.3098

PubMed Abstract | CrossRef Full Text | Google Scholar

Boolchand, P., Chen, P., and Vempati, U. (2009). Intermediate phases, structural variance and network demixing in chalcogenides: the unusual case of group V sulfides. J. Non-Cryst. Solids 355:1773. doi: 10.1016/j.jnoncrysol.2008.11.046

CrossRef Full Text | Google Scholar

Bureau, B., Troles, J., Floch, M. L., Smektala, F., and Lucas, J. (2003). Medium range order studied in selenide glasses by ⁷⁷Se NMR. J. Non-Cryst. Solids 326-327:58. doi: 10.1016/S0022-3093(03)00377-6

CrossRef Full Text | Google Scholar

Chakravarty, S., Chbeir, R., Chen, P., Micoulaut, M., and Boolchand, P. (2019). Correlating melt dynamics and configurational entropy change with topological phases of As_xS_100−x glasses and the crucial role of melt/glass homogenization. Front. Mater. 6:166. doi: 10.3389/fmats.2019.00166

CrossRef Full Text | Google Scholar

Chen, P., Boolchand, P., and Georgiev, D. G. (2010). Long term aging of selenide glasses: evidence of sub-T_g endotherms and pre-T_g exotherms. J. Phys. Cond. Matt. 22:065104. doi: 10.1088/0953-8984/22/6/065104

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, P., Holbrook, C., Boolchand, P., Georgiev, D. G., Jackson, K. A., and Micoulaut, M. (2008). Intermediate phase, network demixing, boson and floppy modes, and compositional trends in glass transition temperatures of binary As_xS_1x system. Phys. Rev. B 78:224208. doi: 10.1103/PhysRevB.78.224208

CrossRef Full Text | Google Scholar

Diemann, E. (1979). Amorphous arsenic pentasulfide - structure and electronic structure. Rev. Chim. Miner. 16:237.

Google Scholar

Fabian, M., Sváb, E., Pamukchieva, V., Szekeres, A., Vogel, S., and Ruett, U. (2010). Study of As₂Se₃ and As₂Se₂Te glass structure by neutron-and X-ray diffraction methods. J. Phys. Cond. Matt. 253:012053. doi: 10.1088/1742-6596/253/1/012053

CrossRef Full Text | Google Scholar

Georgiev, D. G., Boolchand, P., Eckert, H., Micoulaut, M., and Jackson, K. (2003). The self-organized phase of bulk PxSe1-x glasses. Europhys. Lett. 62, 49–55. doi: 10.1209/epl/i2003-00361-2

CrossRef Full Text | Google Scholar

Georgiev, D. G., Boolchand, P., and Micoulaut, M. (2000). Rigidity transitions and molecular structure of As_xSe_1x glasses. Phys. Rev. B 62:R9228. doi: 10.1103/PhysRevB.62.R9228

CrossRef Full Text | Google Scholar

Georgiev, D. G., Mitkova, M., Boolchand, P., Brunklaus, G., Eckert, H., and Micoulaut, M. (2001). Molecular structure, glass transition temperature variation, agglomeration theory, and network connectivity of binary P-Se glasses. Phys. Rev. B 64:134204. doi: 10.1103/PhysRevB.64.134204

CrossRef Full Text | Google Scholar

Giacomazzi, L., Massobrio, C., and Pasquarello, A. (2007). First-principles investigation of the structural and vibrational properties of vitreous GeSe₂. Phys. Rev. B 75:174207. doi: 10.1103/PhysRevB.75.174207

CrossRef Full Text | Google Scholar

Giacomazzi, L., Massobrio, C., and Pasquarello, A. (2011). Vibrational properties of vitreous GeSe₂ with the Becke-Lee-Yang-Parr density functional. J. Phys. Cond. Matt. 23:295401. doi: 10.1088/0953-8984/23/29/295401

PubMed Abstract | CrossRef Full Text | Google Scholar

Hosokawa, S., Kawakita, Y., Pilgrim, W. C., and Hensel, F. (2001). Local structures in glassy and liquid As₂Se₃ - an anomalous X-ray scattering study. J. Non-Cryst. Solids 293–295:153. doi: 10.1016/S0022-3093(01)00665-2

CrossRef Full Text | Google Scholar

Hosokawa, S., Koura, A., Bérar, J. F., Pilgrim, W. C., Kohara, S., and Shimojo, F. (2013). Does the 8-N bonding rule break down in As₂Se₃ glass? Europhys. Lett. 102:66008. doi: 10.1209/0295-5075/102/66008

CrossRef Full Text | Google Scholar

Hosokawa, S., Wang, Y., Pilgrim, W. C., Bérar, J. F., Mamedov, S., and Boolchand, P. (2006). Partial structure analysis of glassy As₂Se₃ using anomalous X-ray scattering. J. Non-Cryst. Solids 352:1517. doi: 10.1016/j.jnoncrysol.2005.12.026

CrossRef Full Text | Google Scholar

Jackson, K., Briley, A., Grossman, S., Porezag, D. V., and Pederson, M. R. (1999). Raman-active modes of aGeSe₂ and aGeS₂: a first-principles study. Phys. Rev. B 60:R14985. doi: 10.1103/PhysRevB.60.R14985

CrossRef Full Text | Google Scholar

Kibalchenko, M., Yates, J. R., Massobrio, C., and Pasquarello, A. (2010). Structural assignments of NMR chemical shifts in Ge_xSe_1x glasses via first-principles calculations for GeSe₂, Ge₄Se₉, and GeSe crystals. Phys. Rev. B 82:020202. doi: 10.1103/PhysRevB.82.020202

CrossRef Full Text | Google Scholar

Kostadinova, O. (2009). (Ph.D. thesis). University of Patras, Patras, Greece.

Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37:785. doi: 10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., and Drabold, D. A. (2000). Direct calculation of light-induced structural change and diffusive motion in glassy As₂Se₃. Phys. Rev. Lett. 85:2785. doi: 10.1103/PhysRevLett.85.2785

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucovsky, G., Nemanich, R. J., Solin, S. A., and Keezer, R. C. (1975). Coordination dependent vibrational properties of amorphous semiconductors alloys. Solid State Commun. 17:1567. doi: 10.1016/0038-1098(75)90997-7

CrossRef Full Text | Google Scholar

Massobrio, C., Pasquarello, A., and Car, R. (1999). Intermediate range order and bonding character in disordered network-forming systems. J. Am. Chem. Soc. 121:2943. doi: 10.1021/ja9808447

CrossRef Full Text | Google Scholar

Massobrio, C., Pasquarello, A., and Car, R. (2001). Short- and intermediate-range structure of liquid GeSe₂. Phys. Rev. B 64:144205. doi: 10.1103/PhysRevB.64.144205

CrossRef Full Text | Google Scholar

Mastelaro, V., Dexpert, H., Benazeth, S., and Ollitrault-Fichet, R. (1992). Structure of the Ag-As-Se chalcogenide glasses: the AsSe-Ag₂Se line. J. Solid State Chem. 96:301. doi: 10.1016/S0022-4596(05)80263-4

CrossRef Full Text | Google Scholar

Mauro, J. C., and Varshneya, A. K. (2007). Multiscale modeling of arsenic selenide glass. J. Non-Cryst. Solids 353:1226. doi: 10.1016/j.jnoncrysol.2006.09.067

CrossRef Full Text | Google Scholar

Micoulaut, M., and Bauchy, M. (2013). Structure of As₂Se₃ and As-Se network glasses: evidence for coordination defects and homopolar bonding. J. Non-Cryst. Solids 377:34. doi: 10.1016/j.jnoncrysol.2013.01.019

CrossRef Full Text | Google Scholar

Micoulaut, M., Kachmar, A., Bauchy, M., Roux, S. L., Massobrio, C., and Boero, M. (2013). Structure, topology, rings, vibrational and electronic properties of Ge_xSe_1−x glasses across the rigidity transition: a numerical study. Phys. Rev. B 88:054203. doi: 10.1103/PhysRevB.88.054203

CrossRef Full Text | Google Scholar

Musgraves, J. D., Wachtel, P., Novak, S., Wilkinson, J., and Richardson, K. (2011). Composition dependence of the viscosity and other physical properties in the arsenic selenide glass system. J. Appl. Phys. 110:063503. doi: 10.1063/1.3638122

CrossRef Full Text | Google Scholar

Petri, I., Salmon, P. S., and Fischer, H. E. (2000). Defects in a disordered world: the structure of glassy GeSe₂. Phys. Rev. Lett. 84:2413. doi: 10.1103/PhysRevLett.84.2413

PubMed Abstract | CrossRef Full Text | Google Scholar

Ravindren, S. (2014). (Ph.D. thesis). University of Cincinnati.

Google Scholar

Ravindren, S., Gunasekera, K., Tucker, Z., Diebold, A., Boolchand, P., and Micoulaut, M. (2014). Crucial effect of glass processing and melt homogenization on the fragility of non-stoichiometric chalcogenides. J. Chem. Phys. 140:134501. doi: 10.1063/1.4869107

CrossRef Full Text | Google Scholar

Renninger, A. L., and Averbach, B. L. (1975). Atomic radial distribution functions of As-Se glasses. Phys. Rev. B 8:1507. doi: 10.1103/PhysRevB.8.1507

CrossRef Full Text | Google Scholar

Resta, R. (1994). Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66:899. doi: 10.1103/RevModPhys.66.899

CrossRef Full Text | Google Scholar

Salmon, P. S. (2007). Structure of liquids and glasses in the Ge-Se binary system. J. Non-Cryst. Solids 353:2959. doi: 10.1016/j.jnoncrysol.2007.05.152

CrossRef Full Text | Google Scholar

Silver, R. N., Silvia, D. S., and Gubernatis, J. E. (1990). Maximum-entropy method for analytic continuation of quantum Monte Carlo data. Phys. Rev. B 41:2380. doi: 10.1103/PhysRevB.41.2380

PubMed Abstract | CrossRef Full Text | Google Scholar

Silvestrelli, P. L., Bernasconi, M., and Parinello, M. (1997). Ab initio infrared spectrum of liquid water. Chem. Phys. Lett. 277:478. doi: 10.1016/S0009-2614(97)00930-5

CrossRef Full Text | Google Scholar

Simdyankin, S., Niehaus, T. A., Natarajan, G., Frauenheim, T., and Elliott, S. R. (2005). New type of charged defect in amorphous chalcogenides. Phys. Rev. Lett. 94:086401. doi: 10.1103/PhysRevLett.94.086401

PubMed Abstract | CrossRef Full Text | Google Scholar

Tullius, M., Lathrop, D., and Eckert, H. (1990). Glasses in the system phosphorus-sulfur: a phosphorus-31 spin-echo and high-speed MAS-NMR study of atomic distribution and local order. J. Phys. Chem. 94:2145. doi: 10.1021/j100368a075

CrossRef Full Text | Google Scholar

Wagner, T., and Kasap, S. O. (1996). Glass transformation, heat capacity and structure of As_xSe_1−x glasses studied by modulated temperature differential scanning calorimetry experiments. Philos. Mag. B 74:667. doi: 10.1080/01418639608241069

CrossRef Full Text | Google Scholar

Xin, S., Lu, J., and Salmon, P. S. (2008). Structure of Cu–As–Se glasses investigated by neutron diffraction with copper isotope substitution. Phys. Rev. B 78:064207. doi: 10.1103/PhysRevB.78.064207

CrossRef Full Text | Google Scholar

Yang, G., Gulbiten, O., Gueguen, Y., Bureau, B., Sangleboeuf, J. C., Roiland, C., et al. (2010). Correlation between structure and physical properties of chalcogenide glasses in the As_xSe_1x system. Phys. Rev. B 82:195206. doi: 10.1103/PhysRevB.82.195206

CrossRef Full Text | Google Scholar

Zhang, X., and Drabold, D. A. (1998). Evidence for valence alternation, and a new structural model of amorphous selenium. J. Non-Cryst. Solids 241:195. doi: 10.1016/S0022-3093(98)00807-2

CrossRef Full Text | Google Scholar