- 1State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi'an, China
- 2Shaanxi Key Laboratory of Biomedical Metal Materials, Northwest Institute for Nonferrous Metal Research, Xi'an, China
- 3School of Materials Science and Engineering, Inner Mongolia University of Technology, Hohhot, China
- 4State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China
- 5School of Material Science and Engineering, Northeastern University, Shenyang, China
The isothermal compression tests of Ti-25. 5Al-13.5Nb-2.8Mo-1.8Fe (at.%) alloys were executed under a deformation temperature range of 950–1,100°C with a strain rate range of 0.001–1 s−1 for a total height reduction of 0.5. The isothermal compression deformation behavior was investigated based on flow stress curves and dynamic model analysis. The processing map of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy was obtained for the optimum hot process parameters. The calculated value of Q (activation energy) was 634.5 kJ/mol. The constitutive model of the alloy was constructed. Based on DMM and the Prasad flow instability criteria, the hot processing map was established with a strain of 0.7. The deformation mechanisms were interpreted by microstructural observation within both stability and instability zones. A processing map showed a stable region under a deformation temperature range of 950–1,100°C with a strain rate range of 0.001–1 s−1. One certain maximum power dissipation efficiency value was ~43% and occurred at 950°C/0.001 s−1. Another peak power dissipation efficiency value was about 58% at 1,050°C/0.001 s−1. Both areas were the optimum processing regions. Furthermore, while the strain rate value exceeded 1 s−1, the alloy sustained a deformation instability phenomenon, such as a shearing band or flow localization.
Introduction
The Ti2AlNb-based alloy (Banerjee et al., 1988; Khadzhieva et al., 2014) combines low density, an improved oxidation resistance, and higher fracture toughness compared with the traditional TiAl and NiAl intermetallics (Feng et al., 2002; Yang et al., 2004; Lin et al., 2012). Therefore, Ti2AlNb intermetallics have been regarded as promising structural metals to be applied to aircraft engine components (Banerjee, 1997; Germann et al., 2005). The Ti-22Al-25Nb (at.%) and the Ti-22Al-27Nb alloys demonstrate excellent mechanical properties at high temperatures (Dey et al., 2010). Nb is an expensive and high-density additional beta-stabilizer element in Ti2AlNb alloys. The orthorhombic structure is able to dissolve most beta-stabilizer elements (Cai et al., 2018). Therefore, efforts have been made to reduce the Nb content of Ti2AlNb alloys by substituting Nb with other low-cost beta-stabilizer elements (Feng et al., 2002; Cao et al., 2006; Mao et al., 2007). The majority of the investigations were primarily concentrated on the microstructure evolution, high-temperature mechanical properties, and practical engineering application of the modified Ti2AlNb-based alloys in previous studies. Li et al. (Mao et al., 2000) studied the effects of the Ta element on the elevated-temperature comprehensive mechanical properties for Ti2AlNb-based alloys. Emura et al. (Mao et al., 2007; Emura et al., 2010) discovered that the additions of Mo and Fe elements could effectively enhance the specific strength and also improve both the tensile and creep resistance at 800°C.
In general, the formation temperature of the Ti2AlNb-based alloys ranges from 950 to 1,000°C (Boehlert et al., 1999; Yang et al., 2003). Following deformation, the workpiece is required to be heat treated within the (O+B2) phase region in order to obtain both the desired microstructures morphology and comprehensive mechanical properties. In contrast, it is proven quite difficult for the workpiece to deform at a high temperature due to both the corresponding poor workability and large deformation resistance. Moreover, the hot working technology parameters cannot be simply and accurately regulated in the course of isothermal deforming. Also, the mechanical properties are easily affected by the isothermal processing parameters and microstructure characteristics (Zong et al., 2006; Han et al., 2011a; Jia et al., 2011; Zhu et al., 2012). Both the control of accurate deformation parameters as well as an in-depth investigation of the isothermal deformation mechanisms are thus quite important. Until recently, there has been little investigation into Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy hot deformation behavior.
In previous research, Y. Mao et al. proved that the multiple additions of beta-stabilizer elements Mo and Fe are effective in decreasing Nb content as well as enhancing tensile and creep strength at high temperatures (Mao et al., 2007). However, the hot deformation behavior of multiple Mo- and Fe-composition modified Ti2AlNb-based alloys has hardly been investigated. Therefore, the purpose of this paper is to study the hot deformation behavior as well as the optimization of the processing technology parameters of the Ti2AlNb alloy with multiple additions of Mo and Fe. The flow stress curves, kinetics analysis, and processing map establishment combined with the microstructural observations of the alloy have been investigated. The influences of hot working technology parameters on the actual stress were clarified, and the Q value (deformation activation energy) was obtained. Moreover, the optimal processing technology parameters were obtained by the hot processing map and Prasad's instability criteria. The results were significant for the hot processing technology design and the flow instability phenomenon prevention.
Material And Experimental Procedures
Material Preparation
The Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy ingot (Φ 70×60 mm) was remelted three times using Cold Crucible Levitation Melting (CCLM) in order to ensure composition uniformity. The thermo-mechanical treatment route is shown in Figure 1. As shown in Figure 1, the alloy square bars (12 × 12 × L mm) was prepared by the multi-step canned forging and rolling at 1,100°C. Subsequently, the bar was solution treated under 1 100°C/1 h and consequent furnace-cooling (cooling speed: 0.03K/s) to room temperature. In the end, the bar was age treated under 800°C/100 h, AC (Air Cooling). Tβ was about 1,070°C.
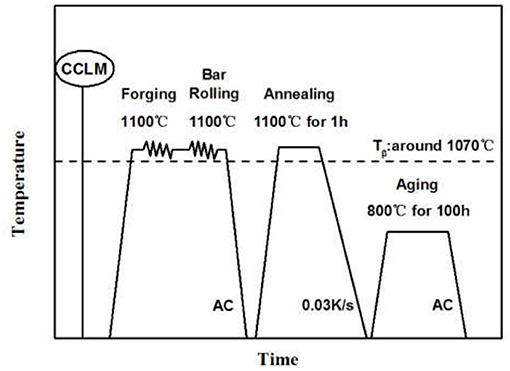
Figure 1. A schematic diagram of the thermo-mechanical treatment for the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy.
The initial microstructure of the alloy consisted of high-sized β grains. There was an aligned α2 phase colony that precipitated around the two sides of grain boundary. The grain boundaries were composed of an α2 phase (dark contrast). The fine needle-like ordered orthorhombic structure (O phase), observed with a gray contrast zone, formed inside the grains, as presented in Figure 2.
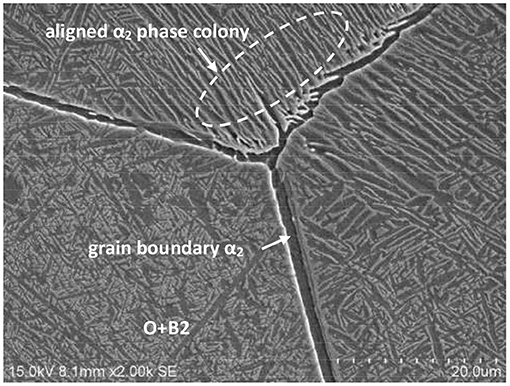
Figure 2. Initial microstructure of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy for the hot compression tests.
Hot Compression Test
The isothermal uniaxial compression testing was executed in Gleeble-3800 thermal simulator. The alloy square bars were machined into cylindrical specimens with Φ 8 × 12 mm. The specimens were deformed under the temperature range 950–1,100°C and strain rate range 0.001–1 s−1. The height reduction of each deformed specimen was 50%. Both graphite and the tantalum sheets were put between the specimen and the machine and died due to reducing friction. The deformed temperatures were monitored by a small thermocouple temperature sensor which was welded to the middle of the cylindrical specimen. The cylindrical specimens were heated to the setting temperature by using pulse current. The pre-set heating rate was 10°C/s, and the holding time was 5 min before isothermal uniaxial compression tests. Following deformation, the samples were water quenched in order for the compressed microstructures to be retained.
Microstructure Observation
In order for the microstructural evolution to be observed, the compressed deformed samples were sectioned parallel to the compression axis. The severed surface was prepared for microstructural observation. The etching solution was the HF, the HNO3, and H2O (1:2:7, vol.%). The microstructure morphology observations were conducted by OM (Olympus / PMG3) and SEM (JSM 6700).
Results And Discussions
Flow Stress Curves
The flow stress experimental data (MPa) of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloys at various deformation conditions are listed in Table 1. The typical flow curves under various isothermal conditions are illustrated in Figure 3. Similarly to other titanium alloys (Zhang et al., 2016, 2018; Gao et al., 2019; Hua et al., 2019), the mechanical properties of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy were easily affected by the working technology parameters. From Figure 3, it clearly indicated that the flow curves exhibited a peak value under a comparatively lower true strain value, and this was followed by a decrease in the true strain value gradually increased. Consequently, the true stress value retained a constant level at the high-sized strains. Furthermore, it was also discovered that, while the deformed practical temperature elevated and the strain rate decreased, the true stress value gradually reduced. The flow-softening phenomenon was observed under both of the various deformation conditions. The flow stress curves demonstrated an obviously flow-softening trend under the deformation temperature that was lower than 1,050°C. Under a fairly high deformation temperatures, while the strain value gradually rose, the flow stress curves finally reached a relatively steady state. The reason is that deformation temperature played an dominant role due to the deformed specimen under the beta single-phase zone (Han et al., 2011b). Furthermore, the flow-softening behavior was attributed to the temperature increase, which resulted from the deformed adiabatic, dynamic recrystallization (DRX), or flow instability (Murty and Rao, 2000; Zeng et al., 2008). In addition, the flow stress curves displayed a discontinuous yielding phenomenon under the strain rate values exceeding 0.1 s−1. The reason for the discontinuous yielding is associated with dislocation pile-up and motion (Wei et al., 2017). Similar phenomena were observed in Ti-22Al-25Nb alloys (Mao et al., 2000). Additionally, it was interesting to note that the curves demonstrated an obvious serrate oscillation feature under a higher strain rate value (=1 s−1). The reason for this feature was the evidence of non-uniform deformation as well as crack generation (Zeng et al., 2008).
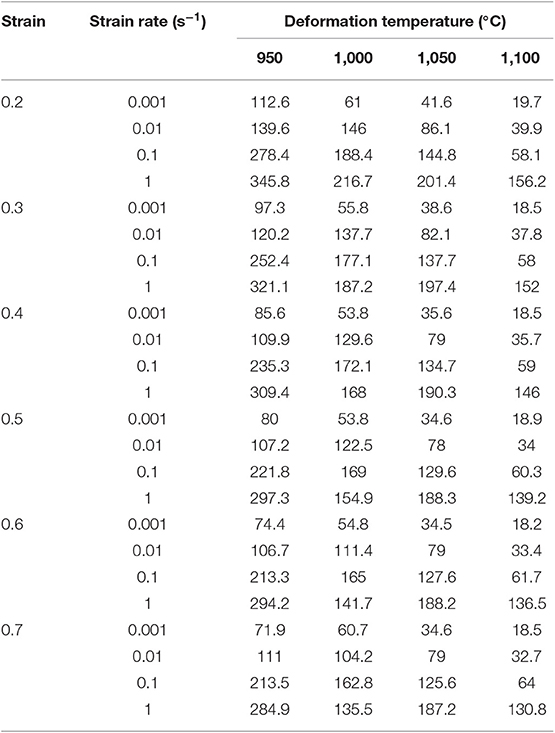
Table 1. The flow stress experimental data (MPa) of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloys at various deformation conditions.
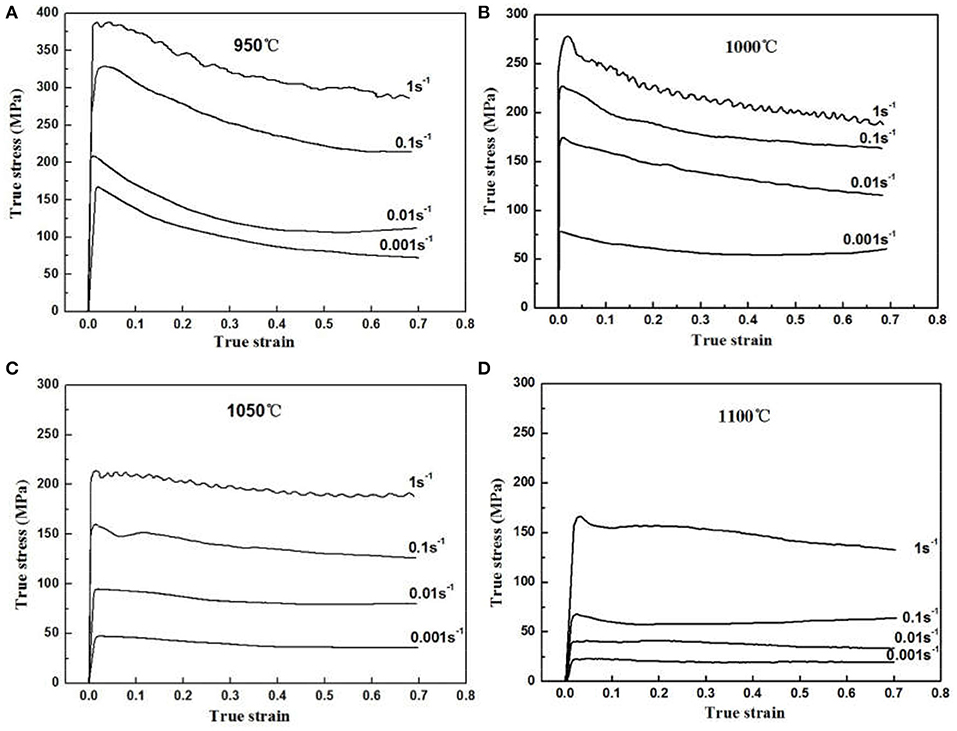
Figure 3. The flow true stress-strain curves at various isothermal compression deformation conditions for the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy: (A) 950; (B) 1,000; (C) 1,050; and (D) 1,100°C.
In general, the flow-compressed curves describe the connection between the compression strength and deformation amount. In contrast, the true stress-strain curves might demonstrate different characteristics, including steady-state flow softening or oscillation at various working parameters. In general, the steady-state flow feature of the curves exhibited a dynamic recovery (DRV) or superplasticity (Prasad and Seshacharyulu, 1998a; Prasad et al., 2001). Similarly, the flow softening was associated with adiabatic heating, lamellar globularization, or dynamic recrystallization (DRX) (Prasad et al., 2000). Subsequently, the significantly precise hot deformation mechanisms were confirmed.
Kinetic Analysis
A hyperbolic-sine Arrhenius model is utilized to reveal the connection of different working parameters description in metallic during hot plastic processing (Khamei and Dehghani, 2010; Zhang et al., 2012). This model can be presented as:
While the flow stress value is low (ασ < 0.8), Equation (1) could be simplified as:
When the flow stress value is high (ασ > 1.2), Equation (1) could be expressed as:
A1, A2, A, α, β, n, n’ are the constants; Q is the activation energy (kJ / mol); R is the gas constant (kJ / mol K−1); is the strain rate (s−1); T is the absolute temperature (K); σ is the flow stress (MPa); and α = β/n.
Equation (3) was translated into the following model by taking natural logarithm:
The plots of vs. ln σp under different temperatures are exhibited in Figure 4. It was indicated that the n value depended on two important processing parameters, which were mainly the deformation temperature and the strain rate value (Medeiros et al., 2000; Liu et al., 2009).
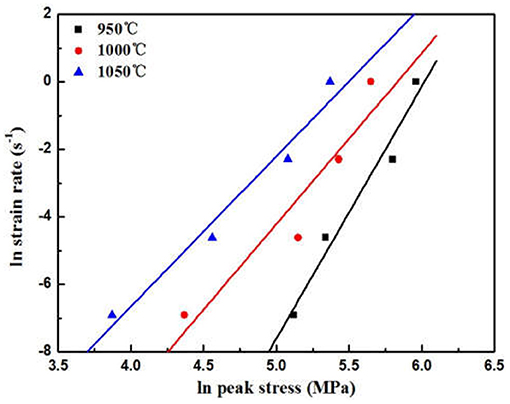
Figure 4. Variation of the peak flow stress with temperatures and strain rates for the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy.
If this relationship was ignored, the average n value was calculated as ~5.12.
The plots of the vs. the ln (sinh ασ) and the plots of the ln (sinh ασ) vs. the 1,000/T are presented in Figures 5A,B. By Equation (4), the rearrangement and differentiation to the 1/T, the activation energy of deformation could be worked out by using the Equation (5):
where is referred to the gradient of the vs. ln [sinh(ασ)] under various T (temperature) and ∂ ln [sinh(ασ)]/∂(1/T) is referred to the gradient ln [sinh(ασ)] vs. the reciprocal of 1/T under various rates of deformation. The Q value was calculated as be 634.5 kJ/mol in 950–1,050°C.
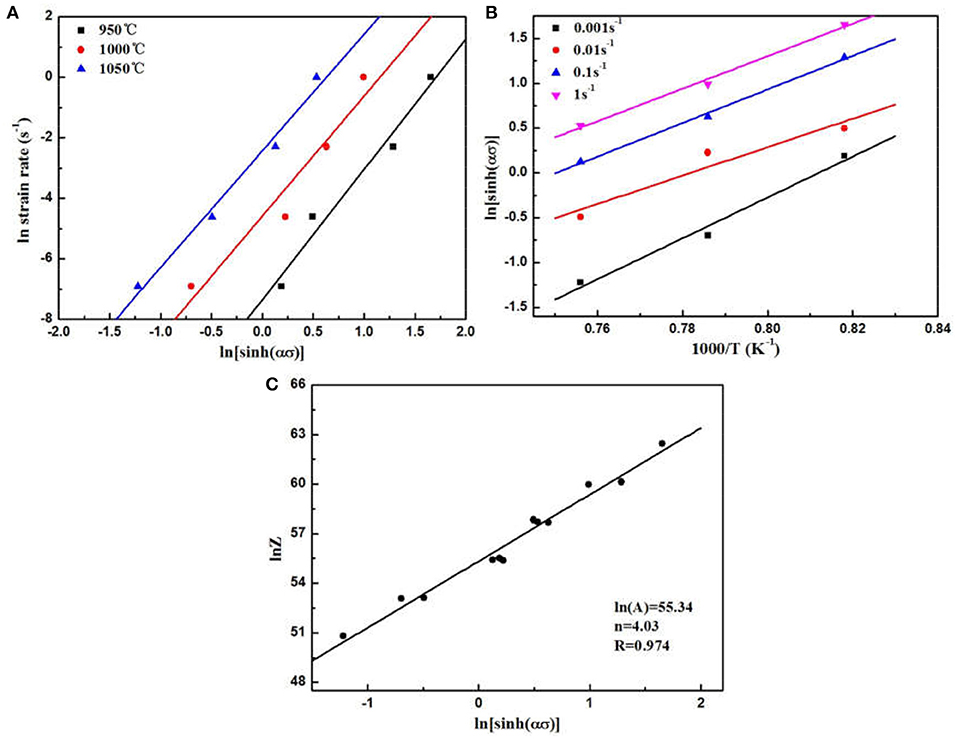
Figure 5. Variation of the peak flow stress for the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy: (A) ln (sinh ασ) vs. ; (B) ln (sinh ασ) vs. 1, 000/T; (C) ln (sinh ασ) vs. ln Z.
The activation energy value was related to the flow stress sensitivity under different working conditions. According to Equation (5), the activation energy mean value was 634.5 kJ/mol, which was just in the range of the mean values of the Ti-22Al-25Nb alloys (436.23–788.77kJ/mol) reported by Zeng et al. (Xiong et al., 2012a). It could be reasonably considered that the high Q value was associated with the globularization of the lamellar microstructures or the dynamic recrystallization. Consequently, we could reasonably predict that this material could more easily be processed at high deformation temperatures than the Ti-22Al-25Nb. The temperature compensated strain rate parameter Z (Huang and Logé, 2016) is provided by:
By the natural logarithm consideration of each side, Equation (6) was translated into the following style:
The intercept is corresponding to the value of the ln A (Figure 5C). Finally, the constitutive model of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloys could be presented as:.
Processing Map
The processing map approach is usually utilized for the purposes of hot processing of many ferrous and nonferrous metals (Sivakesavam and Prasad, 2003; Murty et al., 2005; Zeng et al., 2006; Ning et al., 2010, 2011; Jia et al., 2011), where the work piece was deemed as a power dissipater. The total absorbed power P of the deformed work piece should be decided by:
where G is the dissipater content and J is the dissipater co-content.
In general, the strain rate sensitivity parameter (m) has a close relationship with the total absorbed power (P). The total absorbed power (P) is divided into the dissipater content (G) and the dissipater co-content (J). In addition, the strain rate sensitivity parameter (m) could be provided through the equation, which is . Regarding an ideal linear dissipater (m = 1), the J is calculated to be the corresponding maximum value, using the equal . Hence, the power dissipation efficiency (η) could be defined as the J/Jmax:
The power dissipation efficiency (η) combined with the deformation temperature and the strain rate constitute a portion of the hot processing map, which is called the power dissipation map (Sakai et al., 2014). On the whole, when the value of power dissipation efficiency (η) in some regions is high, it indicates that the zone is appropriate for hot processing (Xin et al., 2016).
The flow instability map is another part of the hot processing map. In this region, the power is often consumed by the manner of heat. The typical microstructural features for the flow instability map correspond to both shear deformation bands and flow localization appearances. Generally, five instability criteria exist, and they are utilized in the description of the instability regions. These criteria are the Prasad, the Murty, the Semiatin, the Gegel and the Malas (Xiong et al., 2010). Ma et al. (Xiong et al., 2012a) discovered that the Semiatin criterion under-predicted the instability regions, while the Gegel and Malas criterion over-predicted the instability regions for the Ti-17 alloys during hot compression. The flow plastic instability maps proposed by the Prasad criteria demonstrated analogous zones to the flow instability maps of the Murty criterion. Zeng et al. (Xiong et al., 2012b) investigated the hot deformation behavior and the hot processing map of Ti-22Al-25Nb alloys based on the Murty criterion. In this work, the flow instability map was established by the procedure described by the Prasad criteria.
The flow plastic instability behavior will appear if:
In Equation (11), represents a dimensionless value. The variation of combined with the deformation temperature and the strain rate constitute another portion of the hot processing map, which is defined as an instability map.
Therefore, by the processing map utilization, the hot processing technology could be designed and controlled for the isothermal processing parameters optimization as well as the expected mechanical properties and microstructure morphology acquisition.
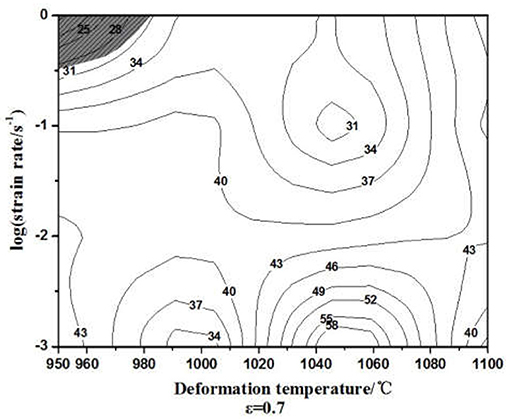
Figure 6 presented the hot processing map of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy under a strain of 0.7.
As shown in Figure 6, there were two typical regions. It is interesting to be found that the two peak η value regions easily occurred at a fairly small strain rate (<1.0 s−1). Moreover, the flow plastic instability regions also easily appeared under the same conditions.
Specially, the peak η value of ~58% occurred at 1,050°C/0.001 s−1, and these were the optimum processing conditions. Semiatin et al. (Prasad and Seshacharyulu, 1998b; Semiatin et al., 1999; Lee et al., 2008; Zhu et al., 2012) found that the Ti64 alloy with a lamellar initial microstructure was suitable for hot working under the conditions of fairly high deformation temperatures and fairly low strain rates. It could be reasonably concluded that this phenomenon had an internal relationship with the DRX (Poletti et al., 2008) or the superplasticity (Krishna et al., 1997; Khamei and Dehghani, 2010). Therefore, the region occurrence at 1,000–1,050°C and 0.001–0.1 s−1 could be explained due to dynamic recrystallization. Figure 7 presented the deformed microstructure morphology under 1,050°C/0.001 s−1. It was found that there was a mass of newly generated small recrystallized grains. Furthermore, the B2 original grain boundaries gradually transformed into a peculiar serrated characteristic. Sivakesavam and Prasad (Sivakesavam and Prasad, 2002) found that the dynamic recrystallization was composed of two competing processes: nucleation and growth. In general, the dynamic recrystallization can provide fairly excellent workability to many metallic materials through the simultaneous microstructural refinement. Therefore, the hot processability of the alloy could be enhanced under this deformation condition.
A second region with a maximum η value of 43% under 950°C/0.001 s-1 exists. It could be regarded as an optimized working domain of Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloys. Figure 8 demonstrates the hot deformed microstructure morphology received under 950°C/0.001 s−1. As seen from Figure 8, both a globularization and a kinking of the lamellar α2/O existed. The α2/O phase microstructure morphology changed from laths to the equiaxed grains as the strain increased. Therefore, the globularization mechanism of the α2/O lamellar was similar to the other Ti alloys. The lamellar globularization procedure is described here. The hot deformed microstructure is broken up into low-sized regions through either the shearing band or the sub-grain. Consequently, the β phase wedges into the lamellar boundary in order for total separation to be observed. This phenomenon could be reasonably interpreted as a kind of DRX (Semiatin et al., 1999; Prasad et al., 2001). Therefore, the globularization occurrence ability could also be deemed as an optimized working condition (Seshacharyulu et al., 1999; Song et al., 2009) during hot plastic deformation. In this work, the optimal deformation temperature consideration occurred at the (α2+β/B2+O) phase region in order for the present material to obtain a certain globularization microstructure and reach the appropriate comprehensive mechanical properties (Cowen and Boehlert, 2006). Therefore, the optimized working technology parameters were obtained at both lower temperatures (950–1,000°C) and lower strain rates (<0.01 s−1).

Figure 8. The microstructure of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloys deformed at 950°C/0.001 s−1: (A) OM image; (B) SEM image.
Previous studies (Hofmann and Blum, 1995; Prasad et al., 2001; Khamei and Dehghani, 2010) have shown that when the strain rates were higher than 1 s−1, the flow plastic instability phenomenon could be induced by shearing belts or cracks. Figures 9A–C demonstrates the hot compressed microstructures morphology under 950°C/1 s−1, 950°C/10 s−1, and 1,000°C/10 s−1. Figure 9A presents the shearing band exhibiting 45 degree toward the compressive direction due to the appearance of localized deformation temperature increase. Prasad et al. (Zhu et al., 2012) also considered that when the titanium alloys deformed at a fairly high strain rate condition, the flow plastic instabilities phenomenon could be occurred by the shearing band appearance.

Figure 9. The microstructures obtained in the instability region of the Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe alloy: (A) Shear band at 950°C/1 s−1; (B) flow localization at 950°C/10 s−1; and (C) flow localization at 1,000°C/10 s−1.
The flow localization under 950°C/10 s−1 and 1,000°C/10 s−1 is presented in Figures 9B,C. It could be concluded that the shearing band and the flow plastic localization might contribute to the occurrence of the flow plastic instability phenomenon.
Conclusions
The isothermal compression tests of Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe (at.%) alloys were executed under the deformation temperature range of 950–1,100°C with the strain rate range of 0.001–1 s−1 for a total height reduction of 0.5. The isothermal compression deformation behavior was investigated based on flow stress curves and dynamic model analysis. The processing map was obtained for the optimum hot process parameters. Several main conclusions were drawn:
1. The flow stress value was significantly sensitive to temperatures and strain rates during the hot working. When the temperature increased, or the strain rate value decreased, the flow stress value reduced accordingly.
2. The calculated value of Q (activation energy) was 634.5 kJ/mol for the alloy deformed in (α2+B2+O) and (α2+B2) phase zone, under 0.001–1 s−1. The constitutive model was constructed.
3. Based on DMM and the Prasad flow instability criteria, the hot processing map was established with strain of 0.7. The peak η value was ~58% at 1,050°C/0.001 s−1, demonstrating DRX. Also, the other appropriate hot working parameter was 950°C/0.001 s−1 in the (α2+B2+O) phase region, occurring lamellar globularization.
4. While the strain rate value exceeded 1 s−1 and the deformation temperature was lower, the alloy sustained deformation instability phenomenon, such as adiabatic shear band or flow localization. Such an instability phenomenon should be prevented.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
JC wrote the article. ZD performed the ingot melting. XZ performed the hot compression testing. WZ performed the microstructure observation. JG performed the constitutive equation and created the processing map. JL performed the technical guidance.
Funding
This work was financially supported by the National Natural Science Foundation of China (No. 51901193), the Key Research and Development Program of Shaanxi (Program No. 2019GY-151), the Science and Technology Plan Project of Weiyang District in Xi'an City (201905), and State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China (621011823). JC was the leader of the funding.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Banerjee, D. (1997). The intermetallic Ti2AlNb. Progress Mater. Sci. 42, 135–158. doi: 10.1016/S0079-6425(97)00012-1
Banerjee, D., Gogia, A. K., Nandi, T. K., and Joshi, V. A. (1988). A new ordered orthorhombic phase in a Ti3AlNb alloy. Acta Metallurgica 36, 871–882. doi: 10.1016/0001-6160(88)90141-1
Boehlert, C. J., Majumdar, B. S., Seetharaman, V., and Miracle, D. B. (1999). Part I. The microstructural evolution in Ti-Al-Nb O+Bcc orthorhombic alloys. Metallurg. Mater. Trans. A 30, 2305–2323. doi: 10.1007/s11661-999-0240-4
Cai, Q., Li, M., Zhang, Y., Liu, Y., Ma, Z., Li, C., et al. (2018). Precipitation behavior of Widmanstätten O phase associated with interface in aged Ti2AlNb-based alloys. Mater. Character. 145, 413–422. doi: 10.1016/j.matchar.2018.09.009
Cao, J., Bai, F., and Li, Z. (2006). High temperature low cycle fatigue behavior of titanium aluminide Ti−24Al−15Nb−1Mo alloy. Mater. Sci. Eng. A 424, 47–52. doi: 10.1016/j.msea.2006.02.040
Cowen, C. J., and Boehlert, C. J. (2006). Microstructure, creep, and tensile behavior of a Ti−21Al−29Nb(at.%) orthorhombic+B2 alloy. Intermetallics 14, 0–422. doi: 10.1016/j.intermet.2005.08.006
Dey, S. R., Roy, S., Suwas, S., Fundenberger, J. J., and Ray, R. K. (2010). Annealing response of the intermetallic alloy Ti−22Al−25Nb. Intermetallics 18, 1122–1131. doi: 10.1016/j.intermet.2010.02.010
Emura, S., Tsuzaki, K., and Tsuchiya, K. (2010). Improvement of room temperature ductility for Mo and Fe modified Ti2AlNb alloy. Mater. Sci. Eng. A 528, 355–362. doi: 10.1016/j.msea.2010.09.003
Feng, T., Shizuo, N., and Masuo, H. (2002). The effect of quaternary additions on the microstructures and mechanical properties of orthorhombic Ti2AlNb-based alloys. Mater. Sci. Eng. A 329–331, 492–498. doi: 10.1016/S0921-5093(01)01626-4
Gao, P., Fu, M., Zhan, M., Lei, Z., and Li, Y. (2019). Deformation behavior and microstructure evolution of titanium alloys with lamellar microstructure in hot working process: a review. J. Mate. Sci. Technol. 39, 56–73. doi: 10.1016/j.jmst.2019.07.052
Germann, L., Banerjee, D., Guédou, J. Y., and Strudel, J. L. (2005). Effect of composition on the mechanical properties of newly developed Ti2AlNb-based titanium aluminide. Intermetallics 13, 920–924. doi: 10.1016/j.intermet.2004.12.003
Han, Y., Weidong, Z., Yunlian, Q., and Yongqing, Z. (2011a). The influence of thermomechanical processing on microstructural evolution of Ti600 titanium alloy. Mater. Sci. Eng. A 528, 8410–8416. doi: 10.1016/j.msea.2011.08.007
Han, Y., Weidong, Z., Yunlian, Q., and Yongqing, Z. (2011b). Optimization of forging process parameters of Ti600 alloy by using processing map. Mater. Sci. Eng. A 529, 393–400. doi: 10.1016/j.msea.2011.09.048
Hofmann, U., and Blum, W. (1995). A simple model of deformation of Ti-48Al-2Cr-2Nb at high temperatures. Scripta Metallurg. Et Mater. 32, 371–376. doi: 10.1016/S0956-716X(99)80067-3
Hua, K., Zhang, Y., Gan, W., Kou, H., Beausir, B., Li, J., et al. (2019). Hot deformation behavior originated from dislocation activity and β to α phase transformation in a metastable β titanium alloy. Int. J. Plasticity 119, 200–214. doi: 10.1016/j.ijplas.2019.03.011
Huang, K., and Logé, R. E. (2016). A review of dynamic recrystallization phenomena in metallic materials. Mater. Design 111, 548–574. doi: 10.1016/j.matdes.2016.09.012
Jia, W., Weidong, Z., Yigang, Z., Jianrong, L., and Qingjiang, W. (2011). High-temperature deformation behavior of Ti60 titanium alloy. Mater. Sci. Eng. A 528, 4068–4074. doi: 10.1016/j.msea.2011.01.113
Khadzhieva, O. G., Illarionov, A. G., and Popov, A. A. (2014). Effect of aging on structure and properties of quenched alloy based on orthorhombic titanium aluminide Ti2AlNb. Phys. MetalsMetallograp. 115, 12–20. doi: 10.1134/S0031918X14010098
Khamei, A. A., and Dehghani, K. (2010). Modeling the hot-deformation behavior of Ni60 wt%–Ti40 wt% intermetallic alloy. J. Alloys Comp. 490, 377–381. doi: 10.1016/j.jallcom.2009.09.187
Krishna, V. G., Prasad, Y. V. R. K., Birla, N. C., and Rao, G. S. (1997). Processing map for the hot working of near-α titanium alloy 685. J. Mater. Proc. Technol. 71, 377–383. doi: 10.1016/S0924-0136(97)00102-7
Lee, K. W., Jae Sam, B., Min Geun, L., Gyu Ha, K., and Kyu Zong, C. (2008). Processing map for the hot working of Ti-8Ta-3Nb. J. Mech. Technol. 22, 931–936. doi: 10.1007/s12206-008-0106-5
Lin, P., He, Z., Yuan, S., and Shen, J. (2012). Tensile deformation behavior of Ti−22Al−25Nb alloy at elevated temperatures. Mater. Sci. Eng. A 556, 617–624. doi: 10.1016/j.msea.2012.07.036
Liu, Y., Hu, R., Li, J., Kou, H., Li, H., Chang, H., et al. (2009). Characterization of hot deformation behavior of Haynes230 by using processing maps. J. Mater. Proc. Technol. 209, 4020–4026. doi: 10.1016/j.jmatprotec.2008.09.024
Mao, Y., Hagiwara, M., and Emura, S. (2007). Creep behavior and tensile properties of Mo- and Fe-added orthorhombic Ti−22Al−11Nb−2Mo−1Fe alloy. Scripta Mater. 57, 261–264. doi: 10.1016/j.scriptamat.2007.03.053
Mao, Y., Li, S., Zhang, J., Peng, J., Zou, D., and Zhong, Z. (2000). Microstructure and tensile properties of orthorhombic Ti–Al–Nb–Ta alloys. Intermetallics 8, 659–662. doi: 10.1016/S0966-9795(99)00151-X
Medeiros, S. C., Prasad, Y. V. R. K., Frazier, W. G., and Srinivasan, R. (2000). Microstructural modeling of metadynamic recrystallization in hot working of IN 718 superalloy. Mater. Sci. Eng. A 293, 198–207. doi: 10.1016/S0921-5093(00)01053-4
Murty, S. V. S. N., and Rao, B. N. (2000). On the flow localization concepts in the processing maps of titanium alloy Ti−24Al−20Nb. J. Mater. Proc. Technol. 104, 103–109. doi: 10.1016/S0924-0136(00)00517-3
Murty, S. V. S. N., Rao, B. N., and Kashyap, B. P. (2005). Identification of flow instabilities in the processing maps of AISI 304 stainless steel. J. Mater. Proc. Technol. 166, 268–278. doi: 10.1016/j.jmatprotec.2004.09.089
Ning, Y., Zekun, Y., Hui, L., Hongzhen, G., Yu, T., and Yiwen, Z. (2010). High temperature deformation behavior of hot isostatically pressed P/M FGH4096 superalloy. Mater. Sci. Eng. A 527, 961–966. doi: 10.1016/j.msea.2009.09.011
Ning, Y., Zekun, Y., Zheng, Y., Hongzhen, G., and Fu, M. W. (2011). Flow behavior and hot workability of FGH4096 superalloys with different initial microstructures by using advanced processing maps. Mater. Sci. Eng. A 531, 91–97. doi: 10.1016/j.msea.2011.10.039
Poletti, C., Degischer, H. P., Kremmer, S., and Marketz, W. (2008). Processing maps of Ti662 unreinforced and reinforced with TiC particles according to dynamic models. Mater. Sci. Eng. A 486, 127–137. doi: 10.1016/j.msea.2007.08.077
Prasad, Y. V. R. K., and Seshacharyulu, T. (1998a). Modelling of hot deformation for microstructural control. Int. Mater. Rev. 43, 243–258. doi: 10.1179/imr.1998.43.6.243
Prasad, Y. V. R. K., and Seshacharyulu, T. (1998b). Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 243, 82–88. doi: 10.1016/S0921-5093(97)00782-X
Prasad, Y. V. R. K., Seshacharyulu, T., Medeiros, S. C., and Frazier, W. G. (2001). Influence of oxygen content on the forging response of equiaxed (α+β) preform of Ti-6Al-4V: commercial vs. ELI grade. J. Mater. Proc. Technol. 108, 320–327. doi: 10.1016/S0924-0136(00)00832-3
Prasad, Y. V. R. K., Seshacharyulu, T., Medeiros, S. C., Frazier, W. G., and Iii, J. C. M. (2000). Hot deformation mechanisms in Ti-6Al-4V with transformed β starting microstructure: commercial v. extra low interstitial grade. Metal Sci. J. 16, 1029–1036. doi: 10.1179/026708300101508829
Sakai, T., Belyakov, A., Kaibyshev, R., Miura, H., and Jonas, J. J. (2014). Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Progr. Mater. Sci. 60, 130–207. doi: 10.1016/j.pmatsci.2013.09.002
Semiatin, S. L., Seetharaman, V., and Weiss, I. (1999). Flow behavior and globularization kinetics during hot working of Ti−6Al−4V with a colony alpha microstructure. Mater. Sci. Eng. A 263, 257–271. doi: 10.1016/S0921-5093(98)01156-3
Seshacharyulu, T., Medeiros, S. C., Morgan, J. T., Malas, J. C., and Prasad, Y. V. R. K. (1999). Hot deformation mechanisms in ELI grade Ti-6A1-4V. Scripta Mater. 41, 283–288. doi: 10.1016/S1359-6462(99)00163-3
Sivakesavam, O., and Prasad, Y. V. R. K. (2002). Characteristics of superplasticity domain in the processing map for hot working of as-cast Mg−11.5Li−1.5Al alloy. Mater. Sci. Eng. A 323, 270–277. doi: 10.1016/S0921-5093(01)01392-2
Sivakesavam, O., and Prasad, Y. V. R. K. (2003). Hot deformation behaviour of as-cast Mg−2Zn−1Mn alloy in compression: a study with processing map. Mater. Sci. Eng. A 362, 118–124. doi: 10.1016/S0921-5093(03)00296-X
Song, H. W., Shi-Hong, Z., and Ming, C. (2009). Dynamic globularization kinetics during hot working of a two phase titanium alloy with a colony alpha microstructure. J. Alloys Comp 480:927. doi: 10.1016/j.jallcom.2009.02.059
Wei, D. X., Koizumi, Y., and Chiba, A. (2017). Discontinuous yielding and microstructural evolution of Ti-40 at.% Al alloy compressed in single α-hcp phase region. J. Alloys Comp. 693, 1261–1276. doi: 10.1016/j.jallcom.2016.10.080
Xin, J., Zhang, L., Ge, G., and Lin, J. (2016). Characterization of microstructure evolution in β-γ TiAl alloy containing high content of Niobium using constitutive equation and power dissipation map. Mater. Design 107, 406–415. doi: 10.1016/j.matdes.2016.06.064
Xiong, M., Weidong, Z., Bin, X., Yu, S., Chen, X., and Yuanfei, H. (2012a). Characterization of the hot deformation behavior of a Ti−22Al−25Nb alloy using processing maps based on the Murty criterion. Intermetallics 20, 1–182. doi: 10.1016/j.intermet.2011.08.027
Xiong, M., Weidong, Z., Yu, S., Kaixuan, W., Yunjin, L., and Yigang, Z. (2012b). Modeling constitutive relationship of Ti17 titanium alloy with lamellar starting microstructure. Mater. Sci. Eng. A 538, 182–189. doi: 10.1016/j.msea.2012.01.027
Xiong, M., Zeng, W., Sun, Y., Zhao, Y., Wang, S., and Zhou, Y. (2010). A comparative study of various flow instability criteria in processing map. Rare Metal Mater. Eng. 39, 756–761. doi: 10.1016/S1875-5372(10)60096-3
Yang, K. L., Huang, J. C., and Wang, Y. N. (2003). Phase transformation in the β phase of super α TiAl base alloys during static annealing and superplastic deformation at 700–1000°C. 51, 2577–2594. doi: 10.1016/S1359-6454(03)00057-0
Yang, S. J., Nam, S. W., and Hagiwara, M. (2004). Investigation of creep deformation mechanisms and environmental effects on creep resistance in a Ti2AlNb based intermetallic alloy. Intermetallics 12, 261–274. doi: 10.1016/j.intermet.2003.10.009
Zeng, W. D., Shu, Y., Zhang, X. M., Zhou, Y. G., and Zhou, L. (2008). Hot workability and microstructure evolution of highly β stabilised Ti−25V−15Cr−03Si alloy. Metal Sci. J. 24, 1222–1229. doi: 10.1179/174328407X185884
Zeng, W. D., Zhou, Y. G., Zhou, J., Yu, H. Q., and Xu, B. (2006). Recent development of processing map theory. Rare Metal Mater. Eng. 35, 673–677. doi: 10.3321/j.issn:1002-185X.2006.05.001
Zhang, J., Hongshuang, D., Hongtao, W., Kun, M., Tianjun, M., and Yu, C. (2012). Hot deformation behavior of Ti-15-3 titanium alloy: a study using processing maps, activation energy map, and Zener–Hollomon parameter map. J. Mater. Sci. 47, 4000–4011. doi: 10.1007/s10853-012-6253-1
Zhang, S. Z., Song, Z. W., Han, J. C., Zhang, C. J., Lin, P., Zhu, D. D., et al. (2018). Effect of 2–6 at.% Mo addition on microstructural evolution of Ti-44Al alloy. J. Mater. Sci. Technol. 34, 1196–1204. doi: 10.1016/j.jmst.2017.10.012
Zhang, S. Z., Zhang, C. J., Du, Z. X., Hou, Z. P., Lin, P., Kong, F. T., et al. (2016). Deformation behavior of high Nb containing TiAl based alloy in α+ γ two phase field region. Mater. Design 90, 225–229. doi: 10.1016/j.matdes.2015.10.080
Zhu, Y., Weidong, Z., Yu, S., Fei, F., and Yigang, Z. (2012). Artificial neural network approach to predict the flow stress in the isothermal compression of as-cast TC21 titanium alloy. Comp. Mater. Sci. 50, 1785–1790. doi: 10.1016/j.commatsci.2011.01.015
Keywords: titanium alloy, constitutive model, processing map, hot deformation behavior, stress-strain curves
Citation: Cheng J, Du Z, Zhang X, Zhang W, Gai J and Li J (2020) Characterization of Ti-25.5Al-13.5Nb-2.8Mo-1.8Fe Alloy Hot Deformation Behavior Through Processing Map. Front. Mater. 7:23. doi: 10.3389/fmats.2020.00023
Received: 17 December 2019; Accepted: 20 January 2020;
Published: 11 February 2020.
Edited by:
Weijie Lu, Shanghai Jiao Tong University, ChinaReviewed by:
Zhang Shuzhi, Taiyuan University of Technology, ChinaGui Wang, University of Queensland, Australia
Kelu Wang, Nanchang Hangkong University, China
Copyright © 2020 Cheng, Du, Zhang, Zhang, Gai and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Cheng, NTI0MTYxMzg2QHFxLmNvbQ==
 Jun Cheng
Jun Cheng Zhaoxin Du3
Zhaoxin Du3 Jinyang Gai
Jinyang Gai