Crystal Structure, Phase Transitions and Photoferroelectric Properties of KNbO3-Based Lead-Free Ferroelectric Ceramics: A Brief Review

Wang, Dawei; Wang, Ge; Lu, Zhilun; Al-Jlaihawi, Zaid; Feteira, Antonio

doi:10.3389/fmats.2020.00091

REVIEW article

Front. Mater., 30 April 2020

Sec. Ceramics and Glass

Volume 7 - 2020 | https://doi.org/10.3389/fmats.2020.00091

This article is part of the Research Topic Advanced Electroceramics for Energy Conversion and Storage View all 9 articles

Crystal Structure, Phase Transitions and Photoferroelectric Properties of KNbO₃-Based Lead-Free Ferroelectric Ceramics: A Brief Review

$\r\nDawei Wang$ Dawei Wang¹

Ge Wang¹

Zhilun Lu^1,2

Zaid Al-Jlaihawi³

Antonio Feteira^3*

¹Department of Materials Science and Engineering, The University of Sheffield, Sheffield, United Kingdom
²The Henry Royce Institute, Sir Robert Hadfield Building, Sheffield, United Kingdom
³Materials and Engineering Research Institute, Sheffield Hallam University, Sheffield, United Kingdom

Ferroelectric KNbO₃ (KN) ceramics were first fabricated in the 1950s, however, their use in commercial technical applications has been hampered by inherently challenging processing difficulties. In the early 1990s, the interest in KN ceramics was revived by the pursuit of Pb-free piezoceramics. More recently the search for inexpensive photovoltaic materials alternative to Si prompted bandgap engineering studies in KN-based solid solutions. If the ferroelectric and piezoelectric properties of KN-based ceramics are now well established, the understanding of chemical doping on the bandgap of KN-based ceramics is still in its infancy. Here we provide a brief review on the current understanding of the structure-property relationships in this class of materials, which successively covers crystal structures, structural phase transitions, lattice dynamics, polarization, solid solutions and bandgap engineering of KN.

Introduction

Historical Background

A combined search in the Web of Science^TM for “KNbO₃” or “potassium niobate” terms generates more than 6000 hits, as illustrated in Figure 1, reflecting the level of scientific curiosity, but also technical interest on this compound.

FIGURE 1

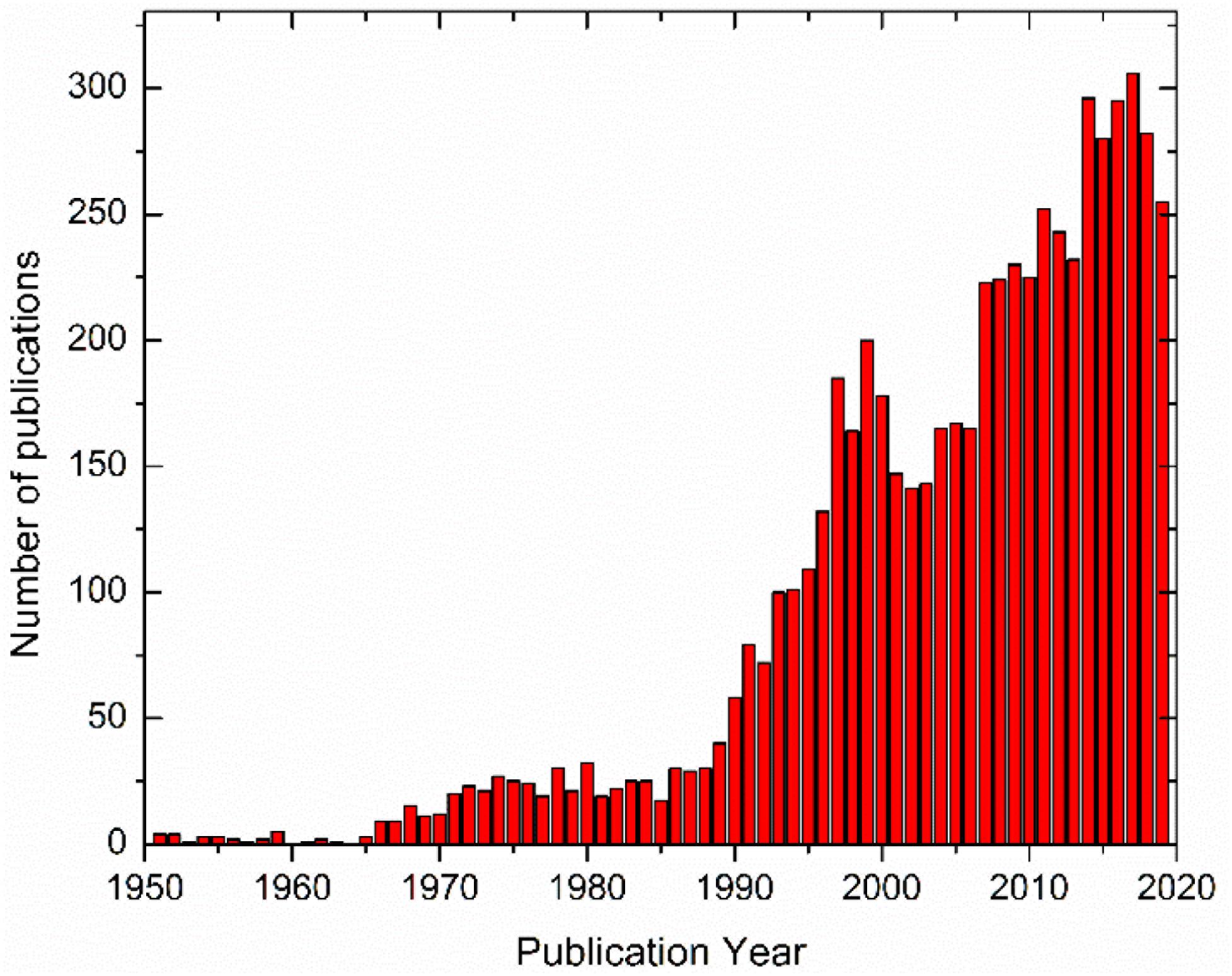
Figure 1. Evolution of the number of publications revolving around KN, as retrieved from Web of Science^TM.

Historically, the preparation of potassium metaniobate, KNbO₃ (KN), was first reported by Joly (1877) but it remained a minor scientific curiosity until 1949, when Matthias (1949) from Bell Telephone Laboratories reported the occurrence of ferroelectricity in this compound. Indeed, this discovery marked an important development in the field of ferroelectrics, because until then ferroelectricity had only been observed in Rochelle Salt, KH₂PO₄ and its isomorphous crystals, BaTiO₃ and its solid solutions. This fact led some researchers to believe that the occurrence of ferroelectricity in Rochelle Salt and BaTiO₃ was of a pure accidental nature, as no other crystals appeared to show ferroelectricity. Nevertheless, the similarity between Ti⁴⁺ and Nb⁵⁺ in terms of electronic configuration and octahedral ionic radii, encouraged Matthias (1949) to investigate the dielectric and optical properties of KN. Eventually, in 1949 he published a note (Matthias, 1949) reporting the preparation of KN crystals showing a transition point from an anisotropic to isotropic state, corresponding to the ferroelectric Curie point. Following the evidence of ferroelectricity, in 1951 Matthias and Remeika (1951) prepared multidomain KN single-crystals. Although they have successfully grown relatively large crystals (up to 1 cm edge length), those were too conductive for dielectric measurements and were only used in an optical and crystallographic study published in the same year by Wood (1951). Importantly, the latter study partly resolved the controversy concerning the exact crystal structure of KN, and provided the foundations for Katz and Megaw (1967) to determine atomic parameters and later for Hewat (1973a) to refine neutron powder diffraction data. Basically, Wood (1951) suggested that at 25°C the crystal symmetry of KN could be described by an orthorhombic cell containing two formula units, with lattice parameters given as a = 5.702, b = 5.739 and c = 3.984 ± 0.010 Å (on monoclinic axes, a = 4.045, b = 3.984 and c = 4.045 Å, β = 90°21′). At 260°C, the crystal structure is tetragonal with a = 4.0 ± 0.02 and c = 4.07 ± 0.02 Å, and finally at 500°C the structure is cubic with a = 4.024 ± 0.001 Å, as illustrated by the open circles in Figure 2.

FIGURE 2

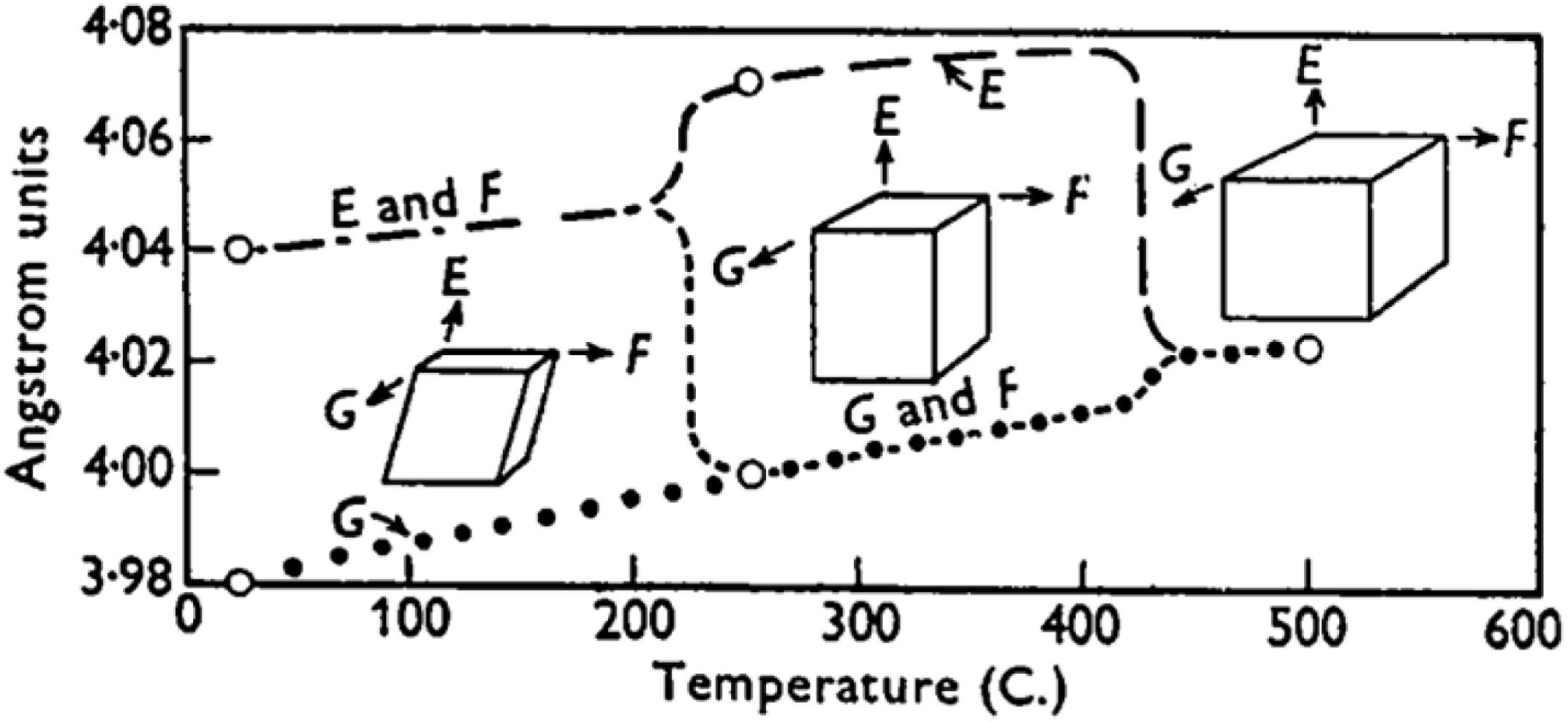
Figure 2. Polymorphism in KN (Wood, 1951) (Reproduced with permission of the International Union of Crystallography (https://journals.iucr.org/).

X-ray diffraction data were in broad agreement with polarized microscopy observations, namely, an orthorhombic-to-tetragonal transition at 225 ± 5°C and a tetragonal-to-cubic transition at 435 ± 5°C. With decreasing temperature, reversible transitions were observed at 200 ± 5°C and 420 ± 5°C, respectively. This pronounced thermal hysteresis was in agreement with the dielectric measurements carried out by Matthias and Remeika (1951) in smaller (1–3 mm) KN crystals. Nevertheless, these authors failed to detect any other dielectric anomaly down to temperatures as low as −190°C, urging them to rule out a low temperature rhombohedral phase. In comparison with BaTiO₃, the absence of a low temperature orthorhombic-to-rhombohedral structural phase transition was unexpected and prompted Pepinsky et al. (1952) at The Pennsylvania State University to revisit the dielectric behavior of KN. In 1954, they published a comprehensive dielectric study (Shirane et al., 1954a) using KN crystals prepared by Robert Newnham, who would become one of the most notable ferroelectricitians (Trolier-McKinstry and Randall, 2017). On heating, they found a dielectric anomaly at −10°C and two other dielectric anomalies at 220 and 420°C, the latter in agreement with the previous work by Matthias and Remeika (1951). On cooling, these three transitions were found at 410, 200, and −55°C, as shown in Figure 3A.

FIGURE 3

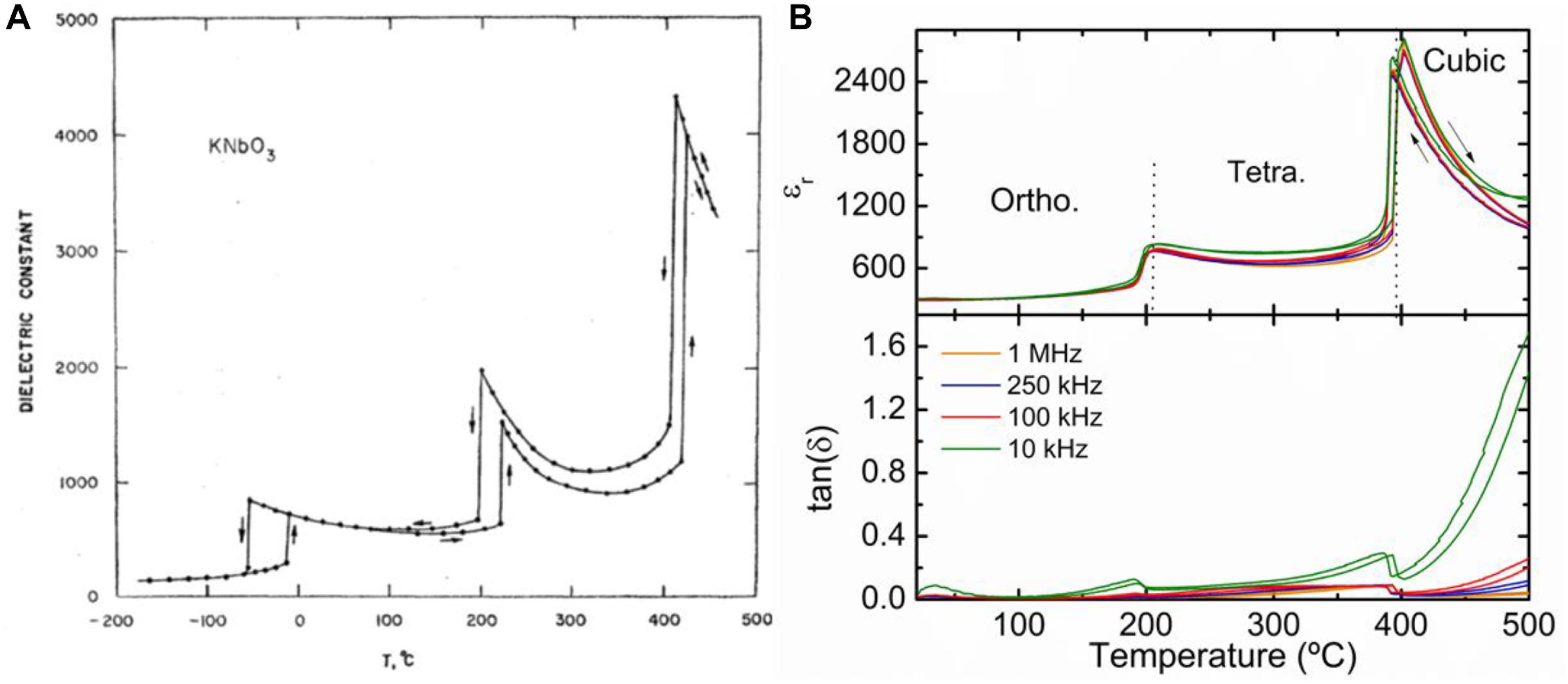
Figure 3. Temperature dependence of the dielectric permittivity of KN (A) single-crystal [Reproduced from https://doi.org/10.1103/PhysRev.96.581 (Shirane et al., 1954a)] and (B) ceramics [Published by The Royal Society of Chemistry, https://doi.org/10.1039/C6TC05515J, https://creativecommons.org/licenses/by/3.0/ (Pascual-Gonzalez et al., 2017)].

X-ray diffraction data collected at −140°C was consistent with a rhombohedral crystal structure. Hence, KN was found to be the only perovskite to exhibit the same sequence of structural phase transitions as BaTiO₃. The relative permittivity, ε_r, in the ferroelectric regime appears to increase dramatically as the crystal symmetry successively changes from rhombohedral to orthorhombic and finally to tetragonal. ε_r for the rhombohedral polymorph is in the 200–300 range, whereas for the orthorhombic is in the 800–900 range and finally for the tetragonal just slightly above 1000. A maximum ε_r of ∼4300 was observed at the tetragonal-to-cubic phase transition, as shown in Figure 3A for the single-crystal. Figure 3B shows the dependence of ε_r in the 30–500°C temperature range for stoichiometric KN ceramics with a relative density of 94%. On cooling two dielectric anomalies associated to the cubic-to-tetragonal and tetragonal-to-orthorhombic structural phase transitions are clearly visible at ∼398°C and ∼206°C, respectively. The magnitude of ε_r is lower in comparison with the values measured for the single-crystal counterpart. In literature there is a large discrepancy on the values of ε_r reported for KN ceramics. Kodaira et al. (1982) showed that depending on the relative density these values can vary from 300 (70% dense) to 800 (>90% dense).

Also in 1954, Cotts and Knight (1954) carried out a Nuclear Magnetic Resonance (NMR) study in the −196 to 460°C temperature range using KN crystals supplied by E. Wood and J. Remeika. These NMR results confirmed the occurrence of transitions at −50, 220, and 430°C, in broad agreement with the dielectric data of Shirane et al. (1954a), but in addition this study provided a further insight into the microscopic local fields giving rise to the spontaneous polarization in KN. First, the cubic-to-tetragonal transition was shown to be a first-order phase change. Second, Nb was found to form strong covalent bonds with oxygen, which had been previously suggested by Vousden (1951) to be the primary factor responsible for the origin of ferroelectricity in KN. In 2018, Skjaervø et al. (2018) revisited the thermal evolution of the crystal structure and phase transitions of KN, and their results are reproduced in Figure 4, alongside previous data by Wood (1951), Shirane et al. (1954a), Hewat (1973a), and Fontana et al. (1984).

FIGURE 4

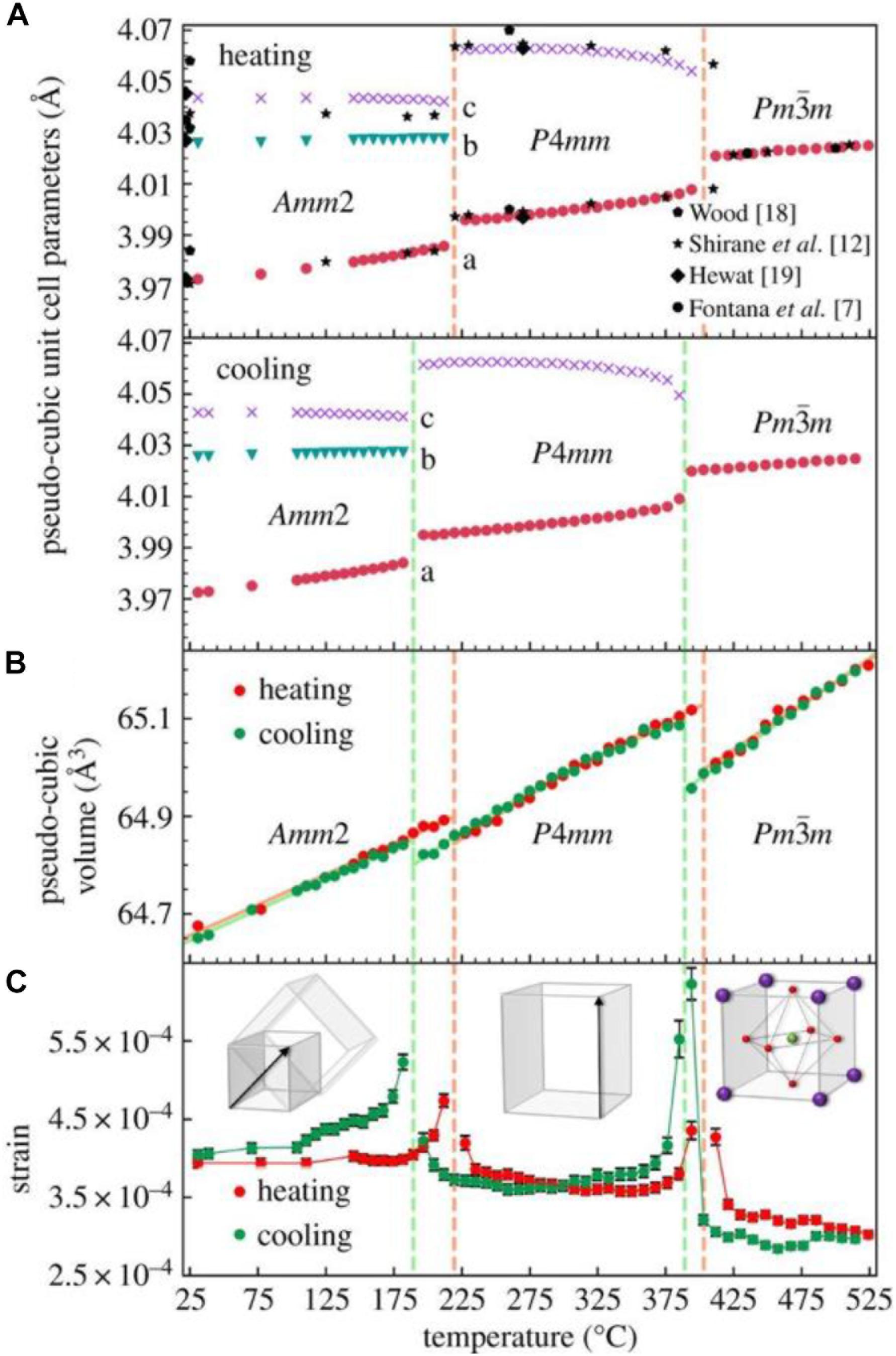
Figure 4. Pseudo-cubic (A) unit cell parameters and (B) unit cell volume of KNbO₃ upon heating and cooling measured in situ X-ray diffraction. Previous published data by Wood [18], Shirane et al. [12], Hewat [19] and Fontana et al. [7] are shown for comparison [references in Skjaervø et al. (2018)]. (C) The refined strain (Reproduced from https://doi.org/10.1098/rsos.180368, https://creativecommons.org/licenses/by/4.0/).

In the early works, KN crystals were reported to show a huge variation in color, ranging from white, yellow, blue to black, but essentially to have the same crystal structure. This was probably the first indication that the fabrication of KN would not become an easy task. Hence, color variation was believed to result from either impurities or different states of oxidation. In order to resolve this issue and to determine the optimum growing conditions for KN crystals, Reisman and Holtzberg (1955) from Watson Laboratory of International Business Machines (aka IBM) published in 1955 the first equilibrium phase diagram for the K₂O-Nb₂O₅ system, which is reproduced in Figure 5. They determined KN to melt at 1039°C. Interestingly, they stated that white KN crystals grown from a 55 mol% K₂CO₃ composition, showed the lowest electrical conductivity among crystals of any other color.

FIGURE 5

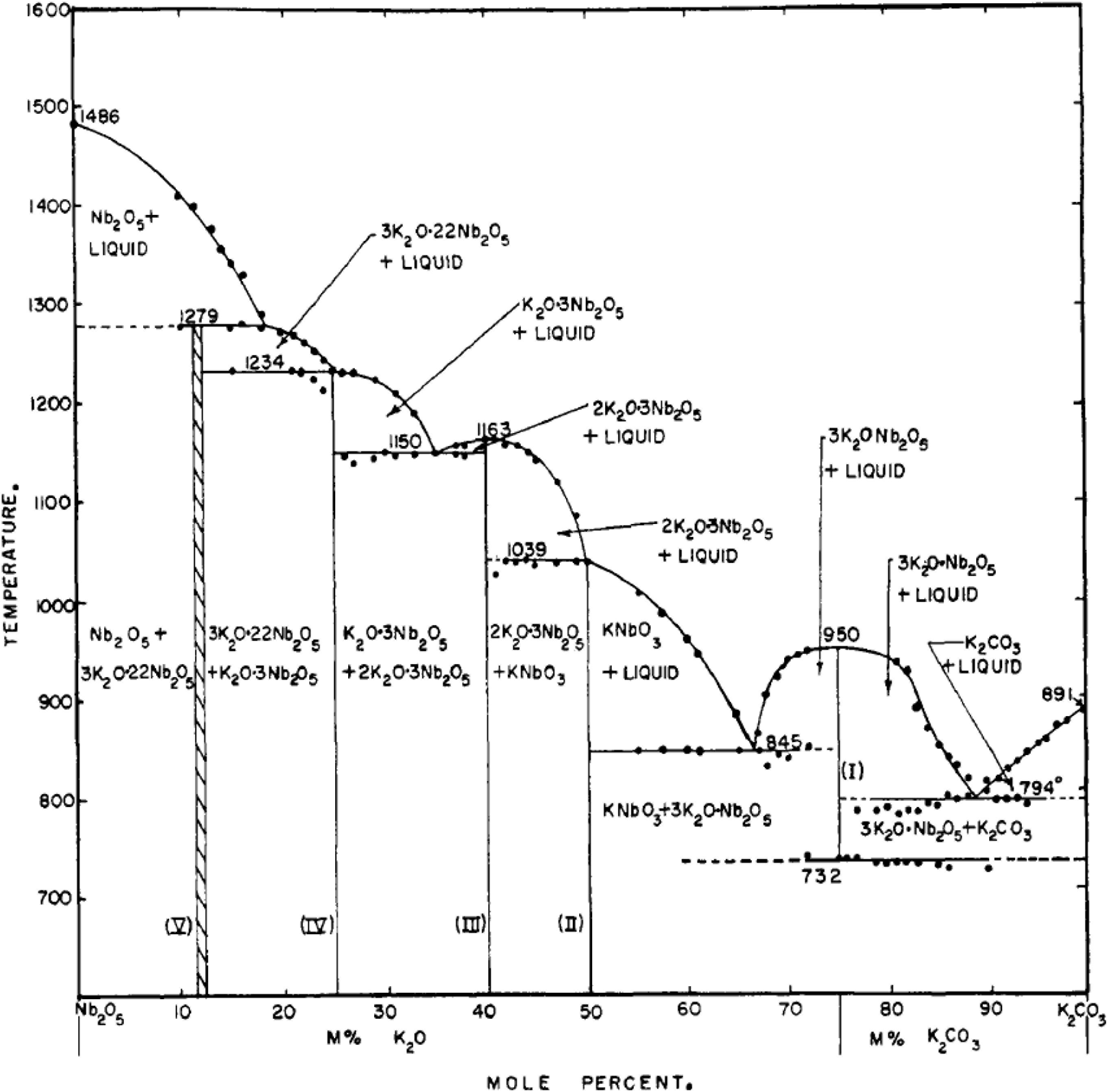
Figure 5. Phase diagram for the Nb₂O₅-K₂CO₃ system. [Adapted with permission from J. Am. Chem. Soc. 1955, 77, 8, 2115–2119 (Reisman and Holtzberg, 1955), American Chemical Society, https://doi.org/10.1021/ja01613a025].

Also in 1955, Triebwasser and Halpern (1955) reported a spontaneous polarization of 26 μC/cm² for KN crystals at the Curie point. Later, Triebwasser (1956) measured the temperature dependence of the spontaneous polarization, P_s, and of the coercive field, E_c, for KN in the temperature range from 100 to 420°C. In the orthorhombic phase, the value of polarization reported was relatively constant around 22 μC/cm², showing a sudden jump to ∼30 μC/cm² at 200°C and to remain around this value up to 380°C. Above this temperature, P_s decreased gradually to ∼26 μC/cm² at the Curie point and then it suddenly dropped to zero. The coercive field decreased with increasing temperature, showing a discontinuity at the orthorhombic-to-tetragonal phase transition. From refractive index measurements, Wiesendanger (1970) suggested that P_s should be greater than 30 μC/cm². Indeed, a larger P_s of 38 μC/cm² was deduced from measurement of ion displacements by Hewat (1973a). Further evidence for a P_s as large as 41 μC/cm² was reported by Gunter (1977) using the Camlibel pulse measurement method. This value was close to 42.9 μC/cm² as calculated by Fontana et al. (1984) and 43.3 μC/cm² as estimated by Kleemann et al. (1984). All these calculations show the tetragonal phase to have a lower P_s in comparison with the orthorhombic phase. Essentially, this large P_s value is due to cation displacement of Nb⁵⁺ within the NbO₆ octahedra, a distortion generated by the hybridization of the empty d-orbitals of Nb⁵⁺ with the O^2– p-orbitals.

Phase Transitions and Lattice Dynamics in KN

The exact nature of the phase transitions in KN was a matter of debate for decades. Two alternative models were proposed to explain the phase transitions in KN. One “displacive” model assuming that in the low temperature phases, the cations are displaced relatively to the oxygen framework along the polar axes and in the cubic phase are located in ideal perovskite positions. Another “order-disorder” or “eight-site” model, where Nb⁵⁺ are displaced along <111> directions from the center of the oxygen octahedra in all phases. Indeed, in 1973, Hewat (1973a) attributed the cubic-to-tetragonal phase transition to a condensation of a soft lattice vibrational mode in which the rigid oxygen octahedra vibrate against K⁺ and Nb⁵⁺ ions. The rigidity of the octahedra was ascribed to the strength of the O-O bonds when compared with the O-K and O-Nb bonds. Later, Hewat (1973b) also showed the oxygen octahedra to remain rigid through the low temperature phase transitions. He combined the magnitude and direction of the atomic displacements with the Cochran’s soft-mode theory of ferroelectricity to describe the temperature dependence of the dielectric permittivity of KN. Previously, in 1968 Comes et al. (1968) had suggested that the KN crystal structures (with the exception of the rhombohedral) determined by classical Bragg reflection data were de facto average structures. Their suggestion was motivated by the observation of diffuse scattering of X-rays and electrons in the cubic, tetragonal and orthorhombic phases of KN. Hence, they proposed the higher symmetry phases of KN to be intrinsically disordered phases, which in microscopic terms could be described by antiparallel correlation chains of atomic displacements extending from 40 to 100 Å (10–25 unit cells). The rhombohedral phase was deemed completely ordered due to the absence of diffuse scattering, implying that Nb⁵⁺ ions were all displaced along the same [111] direction, whereas for the other symmetries other directions were possible. The rhombohedral-to-orthorhombic phase transition was subsequently studied in detail by Fontana and Razzetti (1975) using Raman spectroscopy in the 10–310 cm^–1 frequency range. On cooling, they observed near −49°C the sudden disappearance of an anomalous broad peak at 50 cm^–1 without any appreciable sign of frequency softening or broadening. This was accompanied by the disappearance of the Breit-Wigner interference at 190 cm^–1 and the appearance of a strong narrow peak at 220 cm^–1. The temperature insensitivity of the 50 cm^–1 mode, led these authors to suggest that it cannot be due to a zone center soft mode. Nevertheless, Shigenari (1983) studied the effect of an electric field on a 56 cm^–1 mode in a KN crystal and observed as a small frequency shift, which means that the mode is not due to disorder-induced Transverse Acoustic (TA) mode with a flat dispersion but is a Brillouin zone center optical mode. However, the mode does not show clear ferroelectric soft-mode behavior as usually observed in other ferroelectrics. In comparison with BaTiO₃ the Breit-Wigner interference at 190 cm^–1 results from coupling between strongly broadened A₁ (Transverse optical, TO) modes. In KN such broad modes are absent in the rhombohedral phase, which removes the continuum necessary for the Breit-Wigner interference, and consequently it is not observed in this phase.

In 1998, Shuvaeva et al. (1998) used X-ray absorption fine structure data analysis to propose that all phase transitions are governed by both displacive and order-disorder mechanisms. The rhombohedral-to-orthorhombic structural phase transition was regarded to be essentially of a displacive type, whereas the tetragonal-to-cubic structural phase transition was dominated by the order-disorder component. They concluded that in KN a gradual crossover of displacive to order-disorder behavior occurs with increasing temperature. Vedrinskii et al. (2009) revealed that in the cubic phase, Nb ions are characterized by significant displacements from the centrosymmetric position along the threefold axes, so that they are close in the magnitude and the direction to the displacements in the low-temperatures rhombohedral phases.

In 2005, Baier-Saip et al. (2013) demonstrated that Raman spectroscopy is a powerful characterization technique to identify the different polymorphs of KN. The cubic phase displays two large and broad bands. These bands persist in the tetragonal and orthorhombic phases, and they split into narrower modes, which become sharper with decreasing temperature. Extra modes emerge in the orthorhombic and rhombohedral phase. The intensity of the sharp mode near 192 cm^–1 increases systematically with decreasing temperature. In situ Raman spectroscopy was also employed by Pascual-Gonzalez et al. (2017) and Hawley et al. (2017) to monitor the crystal symmetry in KN-based solid solutions, as exemplified in Figure 6.

FIGURE 6

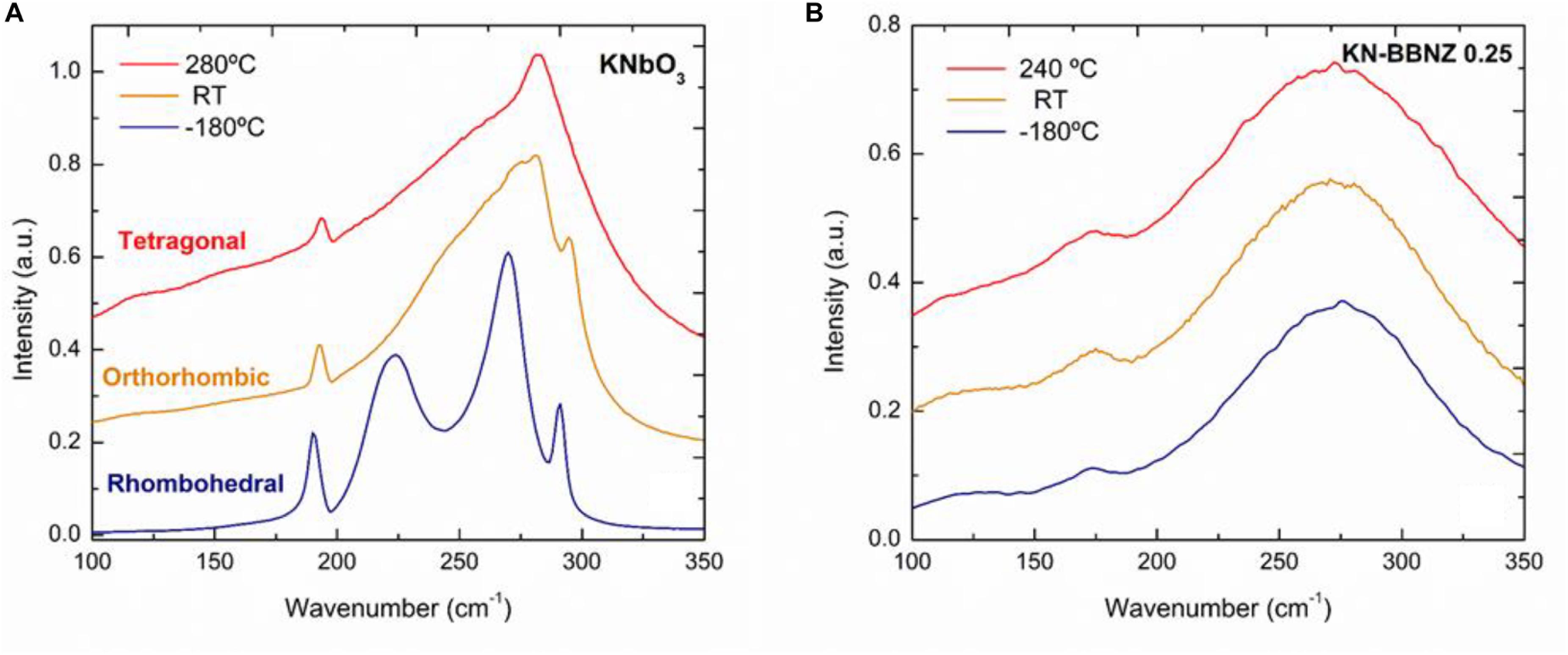
Figure 6. In situ Raman spectroscopy for (A) undoped KN and (B) pseudocubic 0.75KN-0.25Ba_0.5Bi_0.5Nb_0.5Zn_0.5O₃. [Published by The Royal Society of Chemistry, https://doi.org/10.1039/C6TC05515J, https://creativecommons.org/licenses/by/3.0/ (Pascual-Gonzalez et al., 2017)].

The three ferroelectric polymorphs of KN can be readily identified from their spectra as shown in Figure 6A, in agreement with diffraction data. The notorious absence of sharp spectral features in Figure 6B, was used by Pascual-Gonzalez et al. (2017) to rule out the occurrence of long-range polar order in 0.75KN-0.25Ba₀.₅Bi₀.₅Nb₀.₅Zn₀.₅O₃ over a wide temperature range. Gourdain et al. (1995) also employed Raman spectroscopy to investigate the stability of the ferroelectric orthorhombic KN phase under pressure. They observed a transformation to a cubic paraelectric phase above 10 GPa. The Nb⁵⁺ ion disorder decreases with increasing pressure as indicated by the disappearance of Raman activity at high pressure. Interestingly, softening of most TO modes and a progressive decrease of the Raman intensity was observed prior to that transition pressure. A comprehensive assignment of the Raman modes for orthorhombic KN was accomplished by Quittet et al. (1976), and the reader is referred to that work.

Solid Solutions and Doping Studies in KN

If by the mid-1950s, the dielectric behavior and crystallography of undoped KN was well established, little was known about the impact of doping on its properties. One of the first studies was devoted to the KNbO₃-NaNbO₃ system, which eventually became one of the most studied binary systems for Pb-free piezoceramics. In 1954, Shirane et al. (1954b) published the first phase diagram for this system, which showed a rather compositionally stable cubic-to-tetragonal and tetragonal-to-orthorhombic structural phase transition temperatures, as shown in Figure 7A.

FIGURE 7

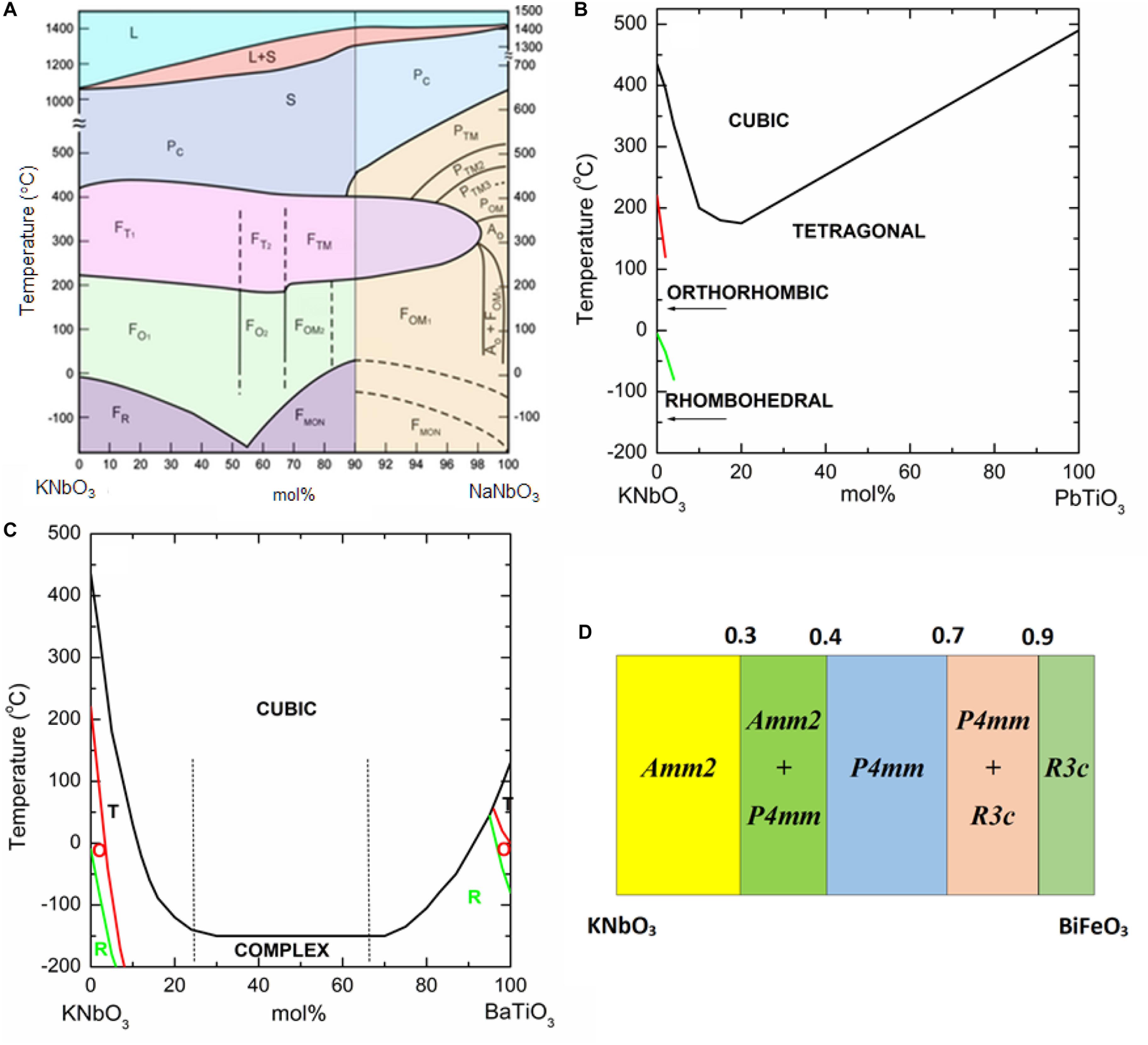
Figure 7. Phase transition temperatures in the (A) KNbO₃-NaNbO₃, (B) KNbO₃-PbTiO₃, (C) KNbO₃-BaTiO₃ systems and (D) room-temperature symmetry in the KNbO₃-BiFeO₃ system. T, tetragonal, O, orthorhombic, R, rhombohedral [Redrawn from Shirane et al. (1954b), Tien et al. (1962); Bratton and Tien (1967), Lennox et al. (2015)].

Dungan and Golding (1965) studied the electromechanical of KNbO₃-NaNbO₃ ceramics. They found the spontaneous polarization increased from ∼20 μC/cm² for KNbO₃ to ∼30 μC/cm² for NaNbO₃. The coercive field also increased continuously with NaNbO₃ content. The electromechanical coupling reached a maximum in K₀.₅Na₀.₅NbO₃ ceramics. Other studies followed, which investigated the KNbO₃-AgNbO₃, KNbO₃-KTaO₃, KNbO₃-PbTiO₃ and KNbO₃-BaTiO₃ (Reisman et al., 1955; Tien et al., 1962; Bratton and Tien, 1967; Weirauch and Tennery, 1967). These studies focused mainly in the evolution of the temperature of the phase transitions and the piezoelectric properties. Unlike KNbO₃-NaNbO₃, the KNbO₃-AgNbO₃ system shows very limited degree of solid solution between its end-members. The solubility of AgNbO₃ into KNbO₃ is slightly less than 6 mol%, as shown by Weirauch and Tennery (1967). The Curie temperature decreases by ∼ 15°C for the 6 mol% AgNbO₃. This system was revisited 3 decades later by Fu et al. (2009), who proposed a solubility as high as 20 mol% AgNbO₃. In contrast, according to Tien et al. (1962), the KNbO₃-PbTiO₃ system forms a complete solid solution. The room-temperature crystal structure is orthorhombic up to 4 mol% PbTiO₃, and above this concentration the crystal symmetry is always tetragonal. The lowest Curie temperature observed in the system was 175°C for a composition with 20% PbTiO₃, as shown in Figure 7B. The original KNbO₃–KTaO₃ phase diagram published in 1956 by Reisman et al. (1955) showed a complete solid solution, however, Hill et al. (1968) found the system to exhibit severe compositional inhomogeneity, which is rather difficult to be eliminated due to the energetically preferable phase segregation of the end members over wide compositional and temperature intervals. Hellermann et al. (1990) confirmed this immiscibility gap and used thermodynamics arguments to explain it. Dielectric measurements carried out by Triebwasser (1959) on single-crystals from KNbO₃–KTaO₃, showed (i) the Curie point to decrease, (ii) the permittivity maximum to increase and (iii) the thermal hysteresis to decrease, all with increasing KTaO₃ content. For the KNbO₃-BaTiO₃ system, the temperature for all the three structural phase transitions of KNbO₃ decreases rapidly with incorporation of BaTiO₃, as shown by Bratton and Tien (1967) as illustrated in Figure 7C. A non-homogenous distribution of Ti and Nb among different grains was detected within the 25–65 mol% BaTiO₃ compositional range. Also, interestingly, for 4 mol% BaTiO₃, only one sharp dielectric anomaly reaching an ε_r of ∼2500 at ∼350°C is observed in the temperature range from −180 to 380°C. This sharp peak was ascribed to cubic-to-tetragonal structural phase transition. In contrast, for 10 mol% BaTiO₃ a depressed and broad peak with a maximum ε_r of ∼550 at ∼50°C is detected. In 2003, Kakimoto et al. (2005) investigated the (1-x)KNbO₃-xLaFeO₃ system and found the crystal symmetry to change from orthorhombic to tetragonal at x = 0.02 and to cubic at x = 0.20. In 2015, Lennox et al. (2015) investigated the (1-x)KNbO₃-xBiFeO₃ system and found a Orthorhombic (Amm2) → Tetragonal (P4mm) → Rhombohedral (R3c) series of structural phase transitions, as shown in Figure 7D, similar to that exhibited by the PbZrO₃–PbTiO₃ solid solution. In this system, the orthorhombic symmetry is maintained at least up to 20% mol BiFeO₃ as inferred from neutron diffraction data (Lennox et al., 2015).

KN crystals exhibit unusual large mechanical coupling factors, k_t, which presents a maximum value of 0.69 at 40.51° away from the polar axis. This value is the largest k_t reported in literature among piezoelectrics, considering that the typical value for Pb(Zr,Ti)O₃ is 0.5. Even with this great mechanical coupling value, no practical applications of polycrystalline KN piezoelectric ceramics have been found due to their poor sinterability and low piezoelectric performance. A few studies dealt with minor doping of KN ceramics aiming at improving their piezoelectric performance (Matsumoto et al., 2008; Nagata et al., 2012; Kim et al., 2014; Yawata et al., 2014; Swami et al., 2018). Nowadays, KNbO₃-NaNbO₃-based solid solutions are serious contenders to replace Pb-based Pb(Zr,Ti)O₃ in some piezoelectric applications, because they can afford high piezoelectric coefficients, d₃₃, above 400 pC/N in non-textured ceramics (Li et al., 2013), and even 700 pC/N in highly textured ceramics (Li et al., 2018).

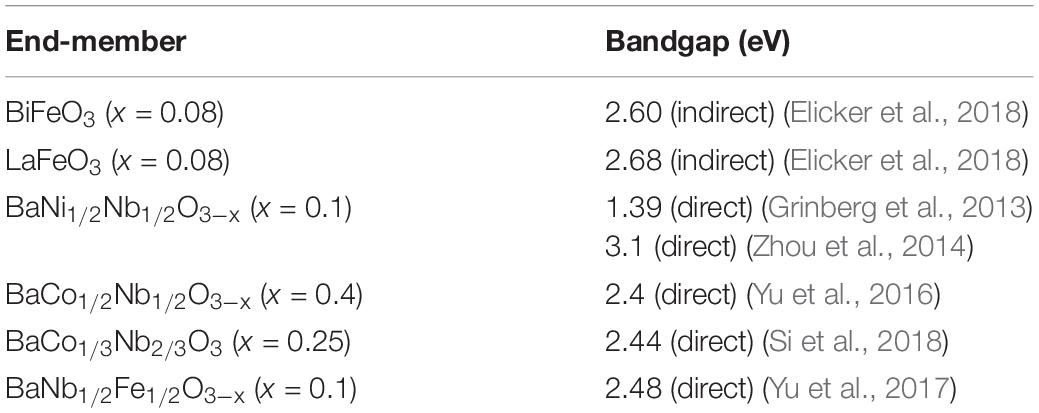
More recently solid solutions of KN with BaNi₁_/₂Nb₁_/₂O₃_–x (Grinberg et al., 2013; Zhou et al., 2014; Hawley et al., 2017), BaCo₁_/₂Nb₁_/₂O₃_–x (Yu et al., 2016, 2017), BaCo₁_/₃Nb₂_/₃O₃ (Si et al., 2018), BaNb₁_/₂Fe₁_/₂O₃_–x (Yu et al., 2017) have been investigated as potential materials for photo-induced applications, including photovoltaic applications. The photoferroelectrics characteristics of KN-based ceramics is therefore reviewed in the next section.

Photoferroelectric Characteristics of KN-Based Materials

Photoferroelectrics and Bandgaps

Photoferroelectrics are materials that exhibit simultaneously photosensitive and ferroelectric effects (Kreisel et al., 2012). The first observation of a photovoltaic effect in a ferroelectric can be traced back to 1956, when Chynoweth (1956) from Bell Telephone Laboratories reported a steady photovoltaic current in BaTiO₃ in the absence of an applied electric field. By monitoring the current response to illumination, he was able to distinguish a pyroelectric current, which decayed with time and then was followed by a photovoltaic current. In 1969, Chen (1969) observed a similar response in LiNbO₃. Both researchers attributed this phenomenon to internal fields caused by space charges at the surface of the crystals. Nevertheless, in 1974, Glass et al. (1974) concluded that photocurrents in Fe- and Cu-doped LiNbO₃ crystals were associated to the asymmetry of the lattice, thereby a bulk photovoltaic effect (BPVE), which could produce open circuit voltages (photovoltages) in excess of 1000 V. In 1977, Raevskii et al. (1977) investigated the photoferroelectric phenomenon in KN single crystals with an area of 0.5 to 1 cm². They observed a maximum photocurrent maximum at 350 nm (∼3.5 eV), which they ascribed to an intrinsic photoconductivity phenomenon, but in addition they observed other lower intensity maxima at larger wavelengths. The latter arise from impurity levels within a bandgap of 3.5 eV at room-temperature. In the same year, Raevskii et al. (1977) observed the photoconductivity in KN to decrease with increasing temperature and, moreover they noticed an anomaly of the photocurrent near the orthorhombic-rhombohedral phase transition. In 1979, Krumins and Guenter (1979) fabricated electrochemically reduced KN single-crystals with a Fe concentration of 46 ppm and studied their photovoltaic characteristics. These crystals showed a maximum absorption at 488 nm (∼ 2.5 eV), but again these investigators observed the photocurrent to decrease with increasing temperature.

After some initial excitement following the discovery of the unconventional photovoltaic effect in ferroelectrics, it rapidly became a dormant research area because most common ferroelectric materials exhibit too wide bandgaps for practical photovoltaic applications. Indeed, bandgaps of FE materials are usually greater than 3 eV, Table 1, which limits light absorption mostly to the ultraviolet (UV) region, resulting in absorbing of only 8% of the solar spectrum.

TABLE 1

Table 1. Bandgap values of ordinary FE oxides.

The interest in photoferroelectrics has been renewed by reports of an anomalous photovoltaic effect in BiFeO₃ thin films (Choi et al., 2009). Since then, there has been an intensive debate on the origin of the photovoltaic effects in ferroelectrics and how to improve their efficiency. The most significant enhancement of power conversion efficiency has been reported as 3.3% for single layers of Bi₂(Fe,Cr)O₆. In addition, it was demonstrated that it was possible to tune the bandgap of Bi₂FeCrO₆ between 1.4 and 2.1 eV, by controlling the Cr/Fe ratio (Nechache et al., 2015). This led to the design of a compositionally graded solar cell containing 3 layers, which exhibit an efficiency of 8.1%. In 2017, Alexe’s group investigated monodomain BiFeO₃ thin films possessing a single ferroelectric variant and demonstrated the photovoltaic current to exhibit a preferred direction depending on the light polarization direction and working temperature, which interestingly was found not to be along the ferroelectric polarization direction (Yang et al., 2017). This implies that the bulk photovoltaic effect arises from the non-centrosymmetric nature of ferroelectric semiconductors but is independent of the ferroelectric polarization. Moreover, it was also shown that the bulk photovoltaic effect can be tailored through the modification of the sub-band gap levels via chemical doping, thus enhancing the power conversion efficiency in ferroelectric semiconductors. Ideally, a photovoltaic material should have a bandgap in between 1.0 and 1.8 eV in order to match with the maximum of the solar spectrum. Hence, the approach for improving the power efficiency of FE materials can be based on both the narrowing of the bandgap and the induction of interband levels (Yang et al., 2017). It is worth to stress that the wide bandgaps in oxide FE perovskites (ABO₃) have been linked to the nature of the bonding between O and B ions. Basically, the large differences in electronegativity between the O and the B ions lead to the valence band to be created by the 2p O states and the conduction band by the d states of the B transition metals sitting within the O octahedra. In summary, the optical and electrooptical properties of FE ABO₃ compounds are mainly governed by the BO₆ octahedra, which determine the position of both conduction and valence bands. Hence, photovoltaic applications of photoferroelectrics have been hindered by their low efficiencies, which are directly related to their wide bandgaps.

Bandgap of Undoped KN

In 1967, Kaifu and Komatsu (1967) measured the temperature dependence of the absorption edge (based on an absorption coefficient α = 300 cm^–1) of KN, which was ascribed to transitions between 2p oxygen states and the d-like conduction states. The results are reproduced in Figure 8, which shows the bandgap to decrease from ∼3.58 eV at −173°C to ∼2.72 eV at 525°C. The temperature coefficient of the bandgap is approximately −10^–3 eV/°C. Moreover, anomalous shifts of the absorption edge are observed at temperatures similar to those of the dielectric anomalies shown in Figure 3A. Finally, it is worth to compare the thermal dependence of the pseudo-cubic unit cell volume of KN, Figure 4B, with the thermal evolution of its bandgap, Figure 8, basically the bandgap narrows as the volume of the unit cell increases. Narrowing of the bandgap with increasing temperatures does not necessarily result in higher current densities, because as shown by Raevskii et al. (1977) the photocurrent of KN decreases with increasing temperature.

FIGURE 8

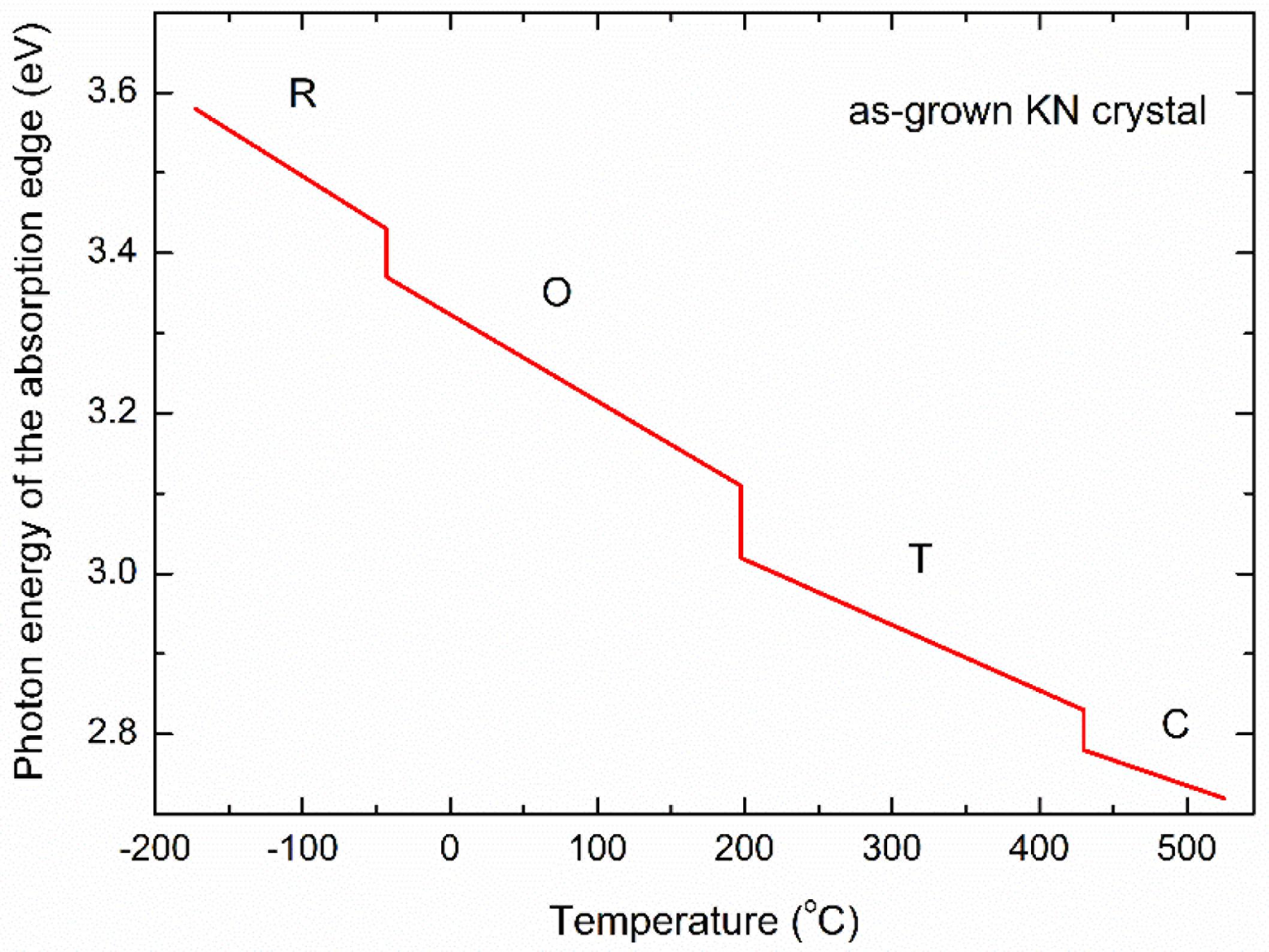
Figure 8. Temperature dependence of the forbidden band width of undoped KN crystal. [Redrawn from Kaifu and Komatsu (Kaifu et al., 1967)].

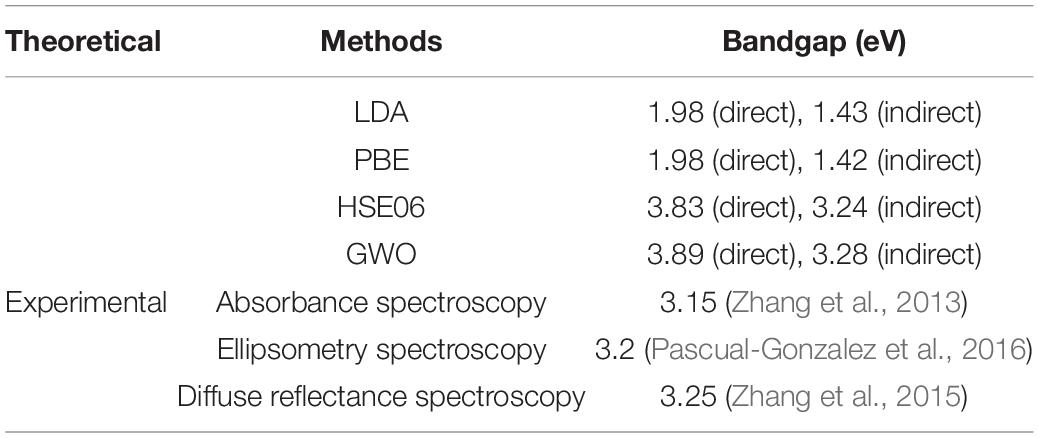
Subsequently, many other researchers reported a wide range of theoretical and experimental bandgap values for KN, as listed in Table 2.

TABLE 2

Table 2. Theoretical and experimental bandgap values for KN.

Several researchers carried out calculation of the band structure of KN. Schmidt et al. (2017) employed a Heyd-Scuseria-Ernzerhof (HSE) type hybrid functional to calculate the band structure of the different phases of KN. Their calculations for the orthorhombic phase show the valence band maximum (VBM) to be located at T symmetry point, while the conduction band minima (CBM) is positioned at Γ symmetry point, as illustrated in Figure 9. Hence, KN should be an indirect bandgap semiconductor with a transition of 3.59 eV between T and Γ symmetry points. Table 3 lists the fundamental bandgaps for the different phases of KN calculated by Schmidt et al. (2017) using the HSE-30 functional. It should be noted that these calculations correspond to electronic bandgaps, however, the trend with increasing symmetry is consistent with the experimental optical bandgap values reported by Kaifu and Komatsu (Kaifu et al., 1967), as shown in Figure 8.

FIGURE 9

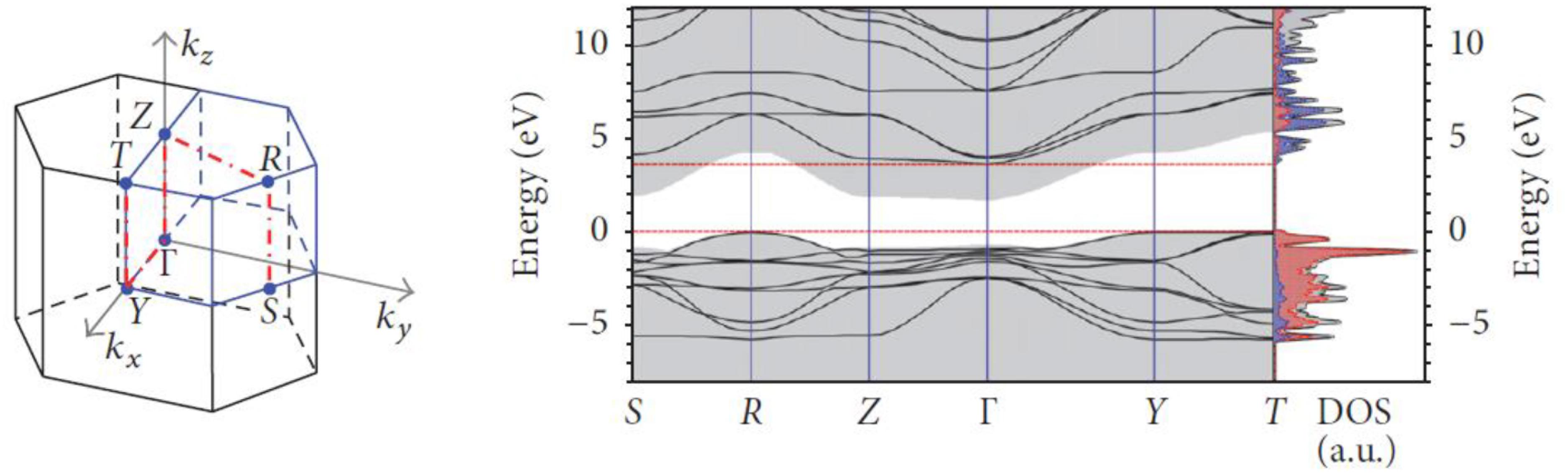
Figure 9. Band structure calculated with the HSE-30 functional for the orthorhombic phases of KN, with corresponding densities of states (DOS) in arbitrary units. The gray-shaded areas indicate the PBE band structures for comparison, and the dashed horizontal lines mark the valence-band maxima and conduction-band minima. On the left-hand side, the chosen path within the first Brillouin zone is indicated by thick dash-dotted lines. [Reproduced https://doi.org/10.1155/2017/3981317, https://creativecommons.org/licenses/by/4.0/ (Schmidt et al., 2017)].

TABLE 3

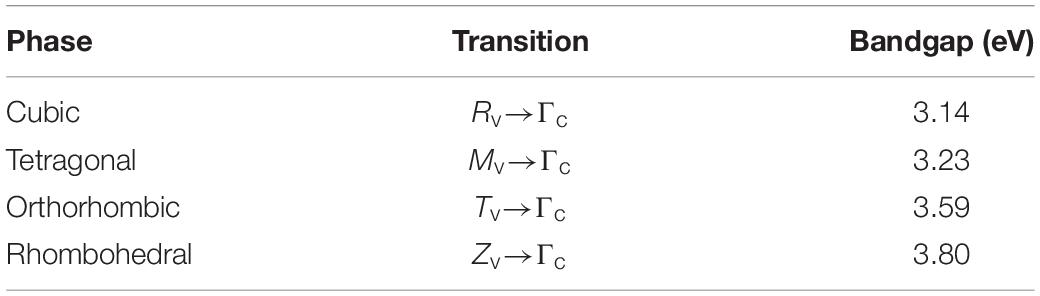
Table 3. Fundamental bandgaps for the different phases of KN using the HSE-30 functional. [After Schmidt et al. (2017)].

Impact of Doping on the Bandgap of KN

A few doping strategies have been adopted to narrow the bandgap of KN. Initial approaches for bandgap narrowing of KN relied on the simultaneous replacement of Nb⁵⁺ cations by lower valence transition metals (Me³⁺) dopants and of K¹⁺ by Ba²⁺. In principle, repulsion between non-bonding 3dⁿ orbitals of the Me³⁺ and 2p⁶ orbitals of O^2– can lead to an upshifting the VBM, resulting in bandgap narrowing. For example, Grinberg et al. (2013) investigated the K₁_–xBa_xNb₁_–x/₂Ni_x/₂O₃_{– δ} system, where charge neutrality is achieved through the creation of oxygen vacancies. For x = 0.1 these researchers reported a bandgap as low as 1.39 eV. Later, Wu et al. (2016) disputed if this narrow value of bandgap was intrinsic. They proposed that Ba, Ni co-doping of KN only slightly affects the bandgap, and the values of 1.1–1.5 eV reported by Grinberg et al. (2013) could result from misinterpretation of the 720 nm absorption band as the intrinsic bandgap. Nevertheless, these Ni induced intermediate energy levels can enhance the overall optical absorption.

Grinberg et al. (2013) measured a modest short-circuit photocurrent, J_sc, of 0.1 μA.cm^–2 and open-circuit photovoltage, V_oc, of 0.7 mV at room-temperature for a ferroelectric photovoltaic (FEPV) device based on x = 0.10. This new ferroelectric oxide based on KN has large concentration of oxygen vacancies, which can trap photo-excited carriers, consequently increasing the charge recombination rate. Basically, oxygen vacancies may have a detrimental effect on photovoltaic performance. This motivated the investigation of alternative doping strategies to lower the bandgap of KN while preserving ferroelectricity and without creating oxygen vacancies. In 2016, Pascual-Gonzalez et al. (2016) used ellipsometry to investigate the bandgap of KNbO₃-Bi(Yb,Me)O₃ (where Me = Fe or Mn) ceramics fabricated by the solid state reaction. They found that the bandgap of KN could also be narrowed by ∼30% (i.e., 1 eV) using a combination of Bi³⁺ and Yb³⁺, without the need of a Me³⁺ dopant. Remarkably, in this case bandgap narrowing was achieved without the creation of vacancies, and long-range polar order was maintained over a wide temperature range.

Wang et al. (2014) employed first principle calculations to estimate the bandgaps and spontaneous polarization for vacancy-free KNbO₃ co-doped with Zn²⁺ in B-site and A₁²⁺ and A₂³⁺ substitution on the A-site (A₁⁺² = Pb²⁺, Ba²⁺, Sr²⁺; A₂³⁺ = La³⁺, Bi³⁺) in order to achieve charge neutrality. The predicted bandgaps for those systems range between 2.92 eV and 2.11 eV. Pascual-Gonzalez et al. (2017) experimentally validated the bandgap of Ba, Zn co-doped KN, but showed the material to be non-ferroelectric.

Liang and Shao (2019) carried a first principles study for bandgap engineering of KN doped with BaNb_2/3B’_1/3O₃, where B′ is a 3d transition metal substitution. The corresponding doping concentration for the Nb sites is 12.5%. Their results are summarized in Table 4. Interestingly, Ti and Zn-doping may lead to direct bandgaps.

TABLE 4

Table 4. Summary of bandgap, transition path, gap character for KN doped with BaNb_2/3B′_1/3O₃, where B′ is a 3d transition metal. [After Liang and Shao (2019)].

In 2017, Pascual-Gonzalez et al. (2017) showed that the optical bandgap of KN could systematically narrowed by ∼1 eV via a defect-free chemical substitution mechanism based in the K₁_–xBi_xNb₁_–xFe_xO₃ (KNBF) solid solution, as illustrated in Figure 10.

FIGURE 10

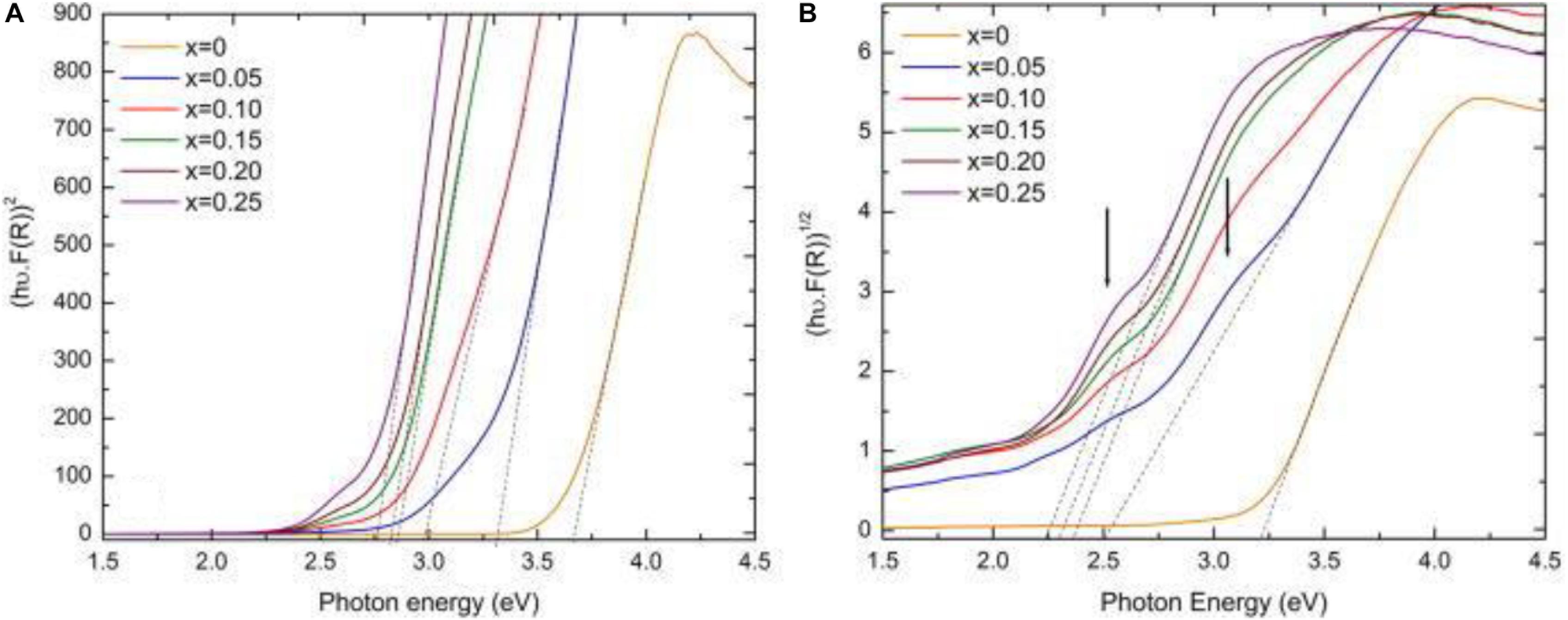
Figure 10. Tauc plot for (A) direct and (B) indirect bandgaps for KNBF (0 ≤ x ≤ 0.25) ceramics (x increases from right to left). [Reproduced from https://doi.org/10.1063/1.4982600, https://creativecommons.org/licenses/by/4.0/ (Pascual-Gonzalez et al., 2017)].

Subsequently, Elicker et al. (2018) also found a similar degree of bandgap narrowing (i.e., a 0.9–1 eV) in the K₁_–xLa_xNb₁_–xFe_xO₃ (KNLF) system, suggesting that the electronic lone-pair in Bi³⁺ may play a negligible role in the physics of bandgap narrowing of KN, as shown on Table 5. These researchers fabricated FEPV devices from KNBF and KNLF (x = 0.32), which combined with a redox couple (I^–/I^3–) exhibited a typical diode–like behavior, showing J_sc and V_oc values of 0.115 μA and 0.075 V for KNBF and 0.19 μA and 0.035 V for KNLF, respectively. More recently, Han et al studied the (1-x) KNbO₃–xBaFeO₃_{– δ} (x = 0.00–0.10) system and reported a minimum optical bandgap of approximately 1.82 eV for x = 0.10. For x = 0.07, the J_sc and V_oc values along the positive polarization direction under a standard AM1.5 illumination were measured as 0.114 μA.cm^–2 and 0.217 V, respectively. This represented an improvement in V_oc.

TABLE 5

Table 5. Experimental bandgap values for KN-based solid solutions.

In 2020, Li et al. (2020) fabricated a solar cell based on the (K,Bi)(Nb,Yb)O₃ (a material originally proposed by Pascual-Gonzalez et al. (2016) combined with TiO₂ nanoparticles, and a light-absorbing oxide hole p-type NiO conductor, which exhibits a V_oc of 1 V, which can be increased to 1.56 V by adjusting the test bias near the coercive field. Under simulated standard AM 1.5G illumination this cell shows a power conversion efficiency of 0.85%.

The high non-linear optical coefficients exhibited by KN, but also the electro-optical coefficients and high refractive indices attracted the scientific curiosity of several researchers (Fukuda and Uematsu, 1972; Uematsu, 1973; Reeves et al., 1991; Loheide et al., 1993; Ko and Hong, 2010; Schmidt et al., 2019).

Outlook

Here, the establishment of the structure-property relationships in KN, an important Pb-free ferroelectric and photoferroelectric was reviewed from an historical perspective. Special emphasis was given to the crystal structure and lattice dynamics, which determine both the high spontaneous polarization of KN and the nature of its structural phase transitions. The modification of the ferroelectric and optical properties of KN has been carried out via the formation of solid solutions. KNbO₃-NaNbO₃ is the most studied solid solution because of its potential to replace Pb-containing Pb(Zr,Ti)O₃ in piezoelectric applications. Traditionally, ferroelectrics and photovoltaics have been regarded as distinctive disciplines, however, the possibility to harvest solar energy via chemical tuning of bandgap of KN into the visible region has recently revigorated the interest in KN. Currently, the efficiency of KN-based photovoltaics is still not competitive with Si-based solar cells, however, KN may be combined with other emerging photovoltaic technologies such as lead halide perovskites or organic materials, and in photocatalytic applications (Yu et al., 2019). In addition, KN offers effects (such as photostriction, switchable photocurrents) that are not present in classical semiconductors, therefore KN may be interesting for novel non-contact sensors. The combination of photostriction and magnetostriction in photoferroelectrics can be used to achieve the optical control of magnetization, which may present potential applications in magnetic data storage and provide a novel means of all-optical switching (AOS). The impact of stress on the bandgap and photovoltaic properties of KN can also be exploited. Indeed, KN is regarded as a good candidate for photorefractive applications, electro-optic devices, optical waveguides, frequency doublers, sensing, and holographic memory storage devices.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

We wish to acknowledge the Henry Royce Institute for Advanced Materials, funded through EPSRC grants EP/R00661X/1, EP/S019367/1, EP/P02470X/1, and EP/P025285/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Baier-Saip, J., Gutierrez, M., Cabrera, A., and Baier, P. (2013). Hysteresis in the rhombohedral-orthorhombic phase transition of KNbO₃ under inhomogeneous strain. Sol. State Commun. 154, 6–10. doi: 10.1016/j.ssc.2012.10.029