A Molecular Dynamics Study on the Structure, Interfaces, Mechanical Properties, and Mechanisms of a Calcium Silicate Hydrate/2D-Silica Nanocomposite

The incorporation of nano-reinforcements is believed to be a promising method to create high performance nanocomposites, which are largely dependent on the interfacial connections. In this work, the newly emerging two-dimensional (2D) material, 2D-silica is intentionally intercalated into the interlayer defective sites of calcium silicate hydrate (C-S-H), which is the primary hydration product of ordinary portland cements. The reactive molecular simulation results indicate the nano-reinforcement can strongly interact with the inorganic matrix to form a high-ductility nanocomposite. The uniaxial tensile loading tests show the plastic stage of the C-S-H is considerably enhanced due to the intercalation of 2D-silica, which removes the intrinsic brittleness of cement-based materials at the nano-scale. It is observed that the dangling atoms at the edge of 2D-silica can react with non-bridging oxygen atoms of C-S-H, forming Si-O-Si bonds at interfaces. Those covalent bonds transform Q₁ and Q₂ in the C-S-H into high connectivity Q₃ and Q₄ species, which increases the integrity of the matrix and its resistance to crack propagation. During the tensile process, the elongation and breakage of those high-strength covalent bonds needs higher tensile stress and consumes higher energy, which leads to a strong plasticity and higher toughness. This work may shed new lights on the interaction mechanisms between 2D-materials and inorganic hosts, and provide solutions to modifying the brittleness of concrete.

Introduction

As the most widely used building material at present, nearly 30 billion tons concrete was consumed globally every year (Kim et al., 2018). The manufacturing of cement and concrete releases large amount of greenhouse gas and causes a huge adverse impact on the environment. To mitigate this effect, one path is using less concrete to achieve the same engineering requirements. Therefore, it is necessary to improve the various performance of concrete per unit mass, especially the tensile strength, which is a significant index of mechanical properties and has always been the inherent defect of cementitious materials (Mehta and Monteiro, 2014; Monteiro et al., 2017). As the main component of ordinary cement hydration products, calcium silicate hydrate (C-S-H) provides the cohesion strength and determines the durability, volume stability, mechanical properties and other engineering properties of concrete (Richardson, 2008; Zhou et al., 2016, 2018b). The C-S-H is a porous gel with an unfixed composition (calcium to silicon ratio) ranging from 0.6 to 2.0 (Jennings, 2008). It shows an amorphous nano-structure, where 3–5 nm particles are packed arbitrarily and thus pores are present in the midst among particles (Jennings, 2008). Within a particle, it is suggested that atoms are arranged in long-range disorder and short-range order. The calcium sheets attract defective silicate sheets to constitute a skeleton of a layered C-S-H molecular structure, with free calcium ions and water molecules filled into the interlayer region (Cong and Kirkpatrick, 1996a; Bauchy et al., 2014). The occurrence of large numbers of pores and defects within the C-S-H nano-structure is believed to be a main factor which limits the mechanical performance of cement-based materials (Jennings, 2008; Richardson, 2008; Mehta and Monteiro, 2014).

Previous publications have proved that an incorporation of nanomaterials into pores and defects of C-S-H such as polymers [PEG (Zhou et al., 2019a), PVA (Zhou et al., 2019b)] and carbon materials [graphene (Hou et al., 2017), carbon nanotube (Konsta-Gdoutos et al., 2010)], can effectively improve the strength, stiffness, ductility, and toughness of C-S-H gels at nano-scale and even concrete at macro-scale. Besides, nano-silica is considered as one of the extremely promising high-tech superfine inorganic materials, due to the small particle size, large specific surface area, strong surface adsorption, high surface energy, excellent thermal electrical resistance. It is widely applied in diverse industries including catalyst carrier, petrochemical, rubber reinforcing agent, plastic filling agent, printing ink thickener and so on (Liong et al., 2008; Tang et al., 2012; Tang and Cheng, 2013). Recently, nano-silica has been used to modify cement-based material (Du et al., 2014; Yu et al., 2014). It is found that nano-silica can act as a nucleation site of cement hydration and participate the pozzolanic reaction to form C-S-H, which improves the release rate of cement hydration heat, shortens hydration induction period and thus improves the early strength of concrete (Madani et al., 2012; Yu et al., 2014). On the other hand, a two-dimensional version of nano-silica (2D-silica) has emerged with the thermal, dynamical, and mechanical stabilities of two-dimensional significantly stronger than the typical bulk silica (Huang et al., 2012; Büchner and Heyde, 2017; Gao et al., 2017). It is believed that 2D-silica can be a superior reinforcement phase into C-S-H due to its high compatibility with the matrix in terms of size and composition, potentially leading to a high performance nanocomposite. However, both experimental and theoretical studies on the C-S-H/2D-silica nanocomposites are still missing, and the interaction mechanisms between the guest and matrix remain unclear.

Molecular dynamics (MD), a force filed based numerical computation method, has recently been widely used to assist the understanding of experimental results, help explain the interaction mechanisms at different phase interfaces, and provide evidence for the composition, structure, and mechanical properties of nanocomposites at the molecular scale (Sanchez and Zhang, 2008; Sakhavand et al., 2013; Duque-Redondo et al., 2014; Hou et al., 2018a, b, 2020). With the aid of molecular dynamics, Pellenq et al. (2009) proposed a molecular model of C-S-H with a calcium to silicon molar ratio (C/S) of 1.7 and a density of 2.6 g/cm³ (Monteiro et al., 2017), which conformed to the experimental data of nuclear magnetic resonance (NMR), X-ray diffraction (XRD), and small angle neutron scattering (SANS) (Cong and Kirkpatrick, 1996b; Janik et al., 2001; Allen et al., 2007). This model also accurately predict the strength and stiffness of C-S-H (Constantinides and Ulm, 2007; Ulm et al., 2007). Besides, the mechanical properties of C-S-H with different C/S ratios and its structural analogues jennite and tobermorite, calculated by MD simulations, also agreed well with the experimental results (Shahsavari et al., 2009; Manzano et al., 2013; Hou et al., 2014a, b). It implied that C-S-H exhibited an anisotropic feature when subjected to a uniaxial tensile process. C-S-H possessed the weakest tensile strength and ductility along the direction where calcium silicate sheets were aligned alternately due to the defects and pores in the interlayer region (Hou et al., 2014a). Furthermore, previous MD studies have also demonstrated that the intercalation of reinforcement phases could enhance the mechanical properties of C-S-H at the nano-scale, and the corresponding mechanisms have been elucidated. Zhou et al. (2018a) incorporated low-molecular weight polymers into the defects of C-S-H and found a significant increase in the ductility of C-S-H, which may be attributed to the bridging effect. Similarly, the addition of graphene oxide also strengthened the interlayer region of C-S-H by the formation of interfacial bonds in the study of Hou et al. (2017) Moreover, MD simulations also suggested that the stability of those interfacial bonds was highly affected by the polarity of functional groups, which determined the overall performance of the composite (Zhou et al., 2017b). However, the simulation of the mechanical behavior and mechanism of C-S-H/2D-silica nanocomposites is still lacking.

Therefore, in this work, in consideration of a high compositional and volumetric compatibility with the matrix, 2D-silica, a newly promising high-stiffness material was intercalated into the defective sites of C-S-H. With the aid of molecular dynamics, the composition, structure, and mechanical properties of C-S-H/2D-silca nanocomposites were evaluated, while the interfacial interactions between the matrix and reinforcement phase and mechanisms on the performance enhancement were investigated.

Simulation Details

Reactive Force Fields

The reactive force field ReaxFF was employed to simulate the chemical reactions occurring in both model establishment and uniaxial loading test. The ReaxFF force field (C/O/H), developed by van Duin, was originally applied in the large scale reactive chemical systems of the hydrocarbons (van Duin et al., 2001), and then another updated version (Si/O/H) was utilized to describe an inorganic system (van Duin et al., 2003). Currently, it also has extensive applications in the study of nanocrystals, silica-water interfaces, and calcium silicate hydrates (Ca/Si/O/H) (Manzano et al., 2012; Hou et al., 2015; Zhou et al., 2017a). Instead of predefining the connectivity between the atoms at a fixed state, such as ClayFF and CSHFF, the ReaxFF force field adopts a bond order-bond distance scheme. It can generate a smooth energy evolution curve, which enables the breakage and formation of chemical bonds to be captured (Schuetz and Frenklach, 2003). In the light of this philosophy, the reaction process can be tracked and the reaction can be unraveled. The fitting of quantum chemical calculations determines the parameters of ReaxFF (Ca/Si/O/H) and the specific values can be referred to previously published papers (van Duin et al., 2001; Chenoweth et al., 2008; Manzano et al., 2012).

Models

At first, an anhydrous C-S-H host model of around 44 × 44 × 44 Å was built following the procedures in Zhou et al. (2017b), and the C/S was set to be 1.3. As shown in Figure 1, the C-S-H model has a layered structure. Within a calcium silicate sheet (xy plane), and the defective chains of silicate tetrahedrons are arranged along y direction and the neighboring silicate chains are attracted by calcium sheets along x direction. The calcium silicate sheets are alternately aligned out of the xy plane along z direction. Obviously, several defects are present in the interlayer region of C-S-H.

FIGURE 1

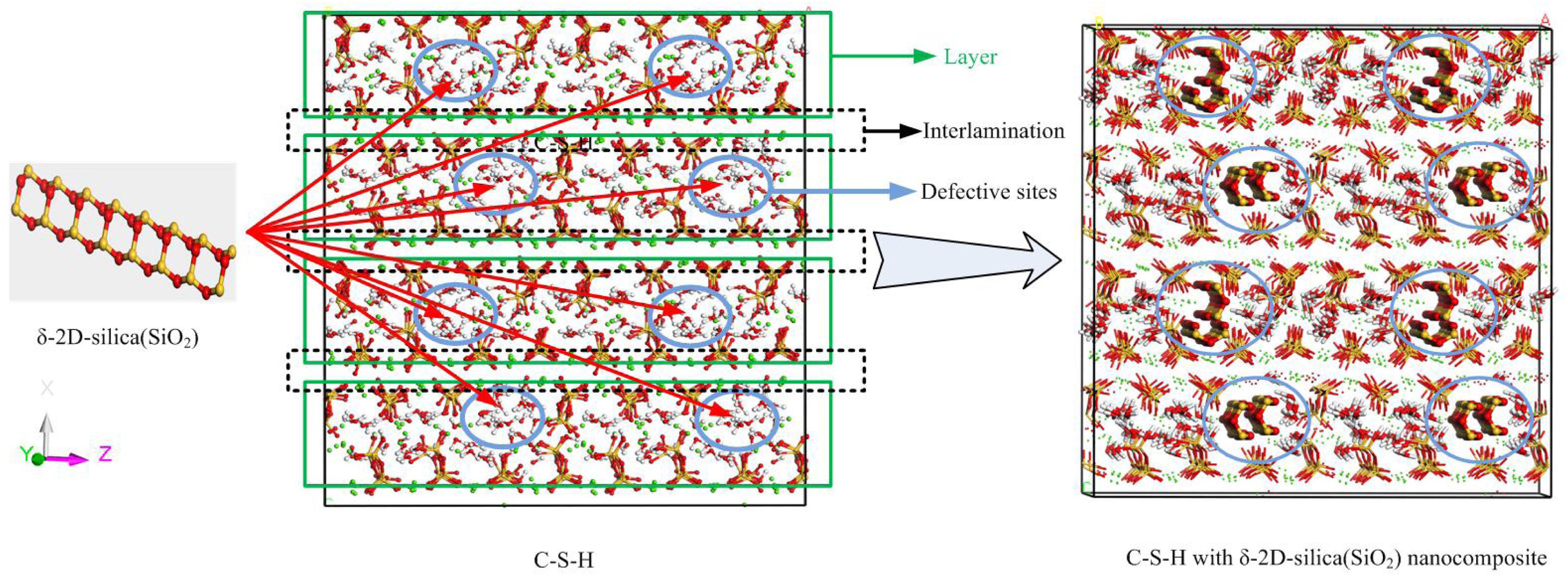
Figure 1. The schematic illustration of the δ-2D-silica (red and yellow balls denote oxygen and silicon atoms, respectively) intercalation into the interlayer defective sites of C-S-H model (green balls indicate calcium ions, red and yellow sticks indicate silicate tetrahedrons, red and white sticks denote water molecules).

Subsequently, a proper 2D-silica guest model was selected according to a previous density function theory study. Gao et al. (2017) put forward four possible structures of 2D-silica. Among those, δ-2D-silica, presented in Figure 1, is selected as the reinforcement phase to be intercalated into the interlayer region of C-S-H, due to its advantages over other structures (Gao et al., 2017). δ-2D-silica has the smallest layer thickness and high Young’s modulus as well as a negative Poisson ratio. Different dosages of 2D-silica were intercalated into the defective sites of anhydrous C-S-H model to construct the C-S-H/2D-silica model.

Finally, a Grand Canonical Monte Carlo (GCMC) water adsorption method was employed to saturate the pure C-S-H model and C-S-H/2D-silica model. By GCMC simulations, water molecules can be imbibed into the anhydrous C-S-H, until reaching an equilibrium sate with a fictitious infinite reservoir, at chemical potential μ = 0 eV and temperature T = 298 K (Bonnaud et al., 2012). In each GCMC simulation, water molecules are shifted, rotated, created or destructed in equal quantities. The equilibrium and production steps were 10⁸ and 2^∗10⁸, respectively, in a run. The final pure C-S-H and C-S-H/2D-silica models have around 8,000 atoms, which can ensure the statistical reliability of the following structural analysis and uniaxial tensile tests.

Structural Analysis and Uniaxial Tension Tests

Reactive force field molecular dynamics simulations were implemented to investigate the composition and structure of pure C-S-H and C-S-H/2D-silica models. An isothermal–isobaric (NPT) ensemble was utilized, with an equilibrium time of 100 ps and a production time of 300 ps. The C-S-H and C-S-H/2D-silica models were subjected to uniaxial tensile loading through gradual elongation at a fixed rate of 0.08/ps along x, y, z direction, respectively. An isothermal–isobaric (NPT) ensemble was also used. The model was initially relaxed at 298 K and then coupled to zero external pressure in all three dimensions for 300 ps. Subsequently, while the uniaxial test was carried out, the pressure perpendicular to the loading direction was kept at zero, to remove the influence of artificial constraint for the deformation. The maximum strain was set to 0.8 Å/Å. The stress-strain relationships can be obtained by recording the internal stress along the loading direction as a function of the applied strain.

Results and Discussion

Interactions between calcium silicate hydrate (C-S-H) and 2D-silica are presented from the following perspectives. First, the structure characteristics of pure C-S-H and C-S-H/2D-silica are investigated, respectively, and several structural parameters will be utilized to emphasize the influence of the intercalation of 2D-silica on the composition and structure of the matrix. Second, uniaxial tensile loading experiments are carried out and the effect of 2D-silica on the mechanical properties of the matrix is evaluated. At last, the interfacial reaction mechanisms are unraveled on the basis of the microstructural analysis as a function of the strain developments.

Structure

Calcium Silicate Hydrate

The pure calcium silicate hydrate, as presented in Figure 1, has a layered structure. The well-aligned calcium sheets attract the silicate sheets where silicate tetrahedrons connect with each other and are aligned in chains to form the skeleton. Between neighboring calcium silicate sheets, water molecules and calcium ions are distributed, forming the interlayer regions. In the light of different chemical environments, the calcium ions can be divided into two categories, the structural calcium ions and the interlayer calcium ions. The former represent those on the skeleton merely surrounded by silicate tetrahedron chains, attracting the oxygen atoms from silicate tetrahedrons (O_s) to achieve a specific coordination structure. The latter are those in the interlayer regions, distinct of enclosure of water molecules. Likewise, the calcium ions and the oxygen atoms from the water molecules (O_w) are attracted by electrostatic force.

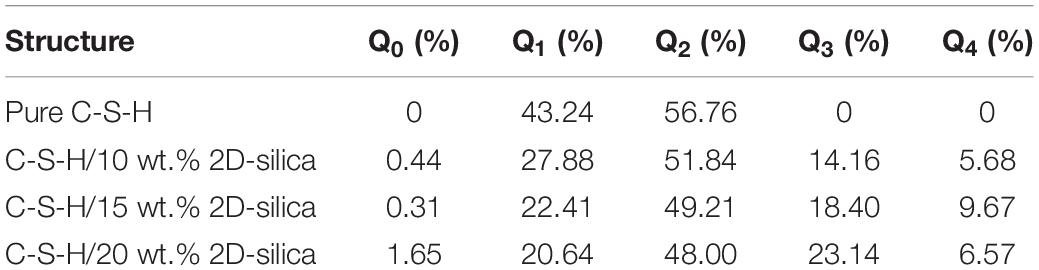
In silicate chains, the presence of bridging oxygen atoms which connect with two silicon atoms, primarily contribute to the connectivity (Figure 2). An index of Q species is put forward to analyze the structural composition and connectivity of silicate chains in C-S-H. For a certain silicon atom, Q species is defined as the number of bridging oxygen atoms it forms covalent bonds with. As illustrated in Figure 2, Q₁ represents the silicon atoms attracting merely one bridging oxygen atom, while Q₂ for two bridging atoms. Besides, the increase of the parameter n indicates higher degree of polymerization of the silicate chains. Q₁ and Q₂ is only existing Q species in the pure C-S-H, as presented in Table 1, and the calculated percentages are consistent with the (Pellenq et al., 2009) Si NMR experiments (Cong and Kirkpatrick, 1996a). As mentioned above, the interaction between the calcium ions and oxygen atoms plays an important role on the internal cohesion of C-S-H. Therefore, radial distribution function (RDF) (Zhou et al., 2018a), another structural index is proposed to describe the coordination between the calcium ions and oxygen atoms. The result, as presented in Figure 3A, indicates the interaction at a distance ranging from 2 to 3 angstroms, abundant pairs of calcium ions and oxygen atoms are present, which represent the Ca-O coordination in C-S-H. Ca-O_s (oxygen from silicate tetrahedrons) pairs constitute the calcium octahedral sheets of C-S-H, while Ca-O_w (oxygen from water molecules) pairs represent the attraction between the intralayer and interlayer region.

FIGURE 2

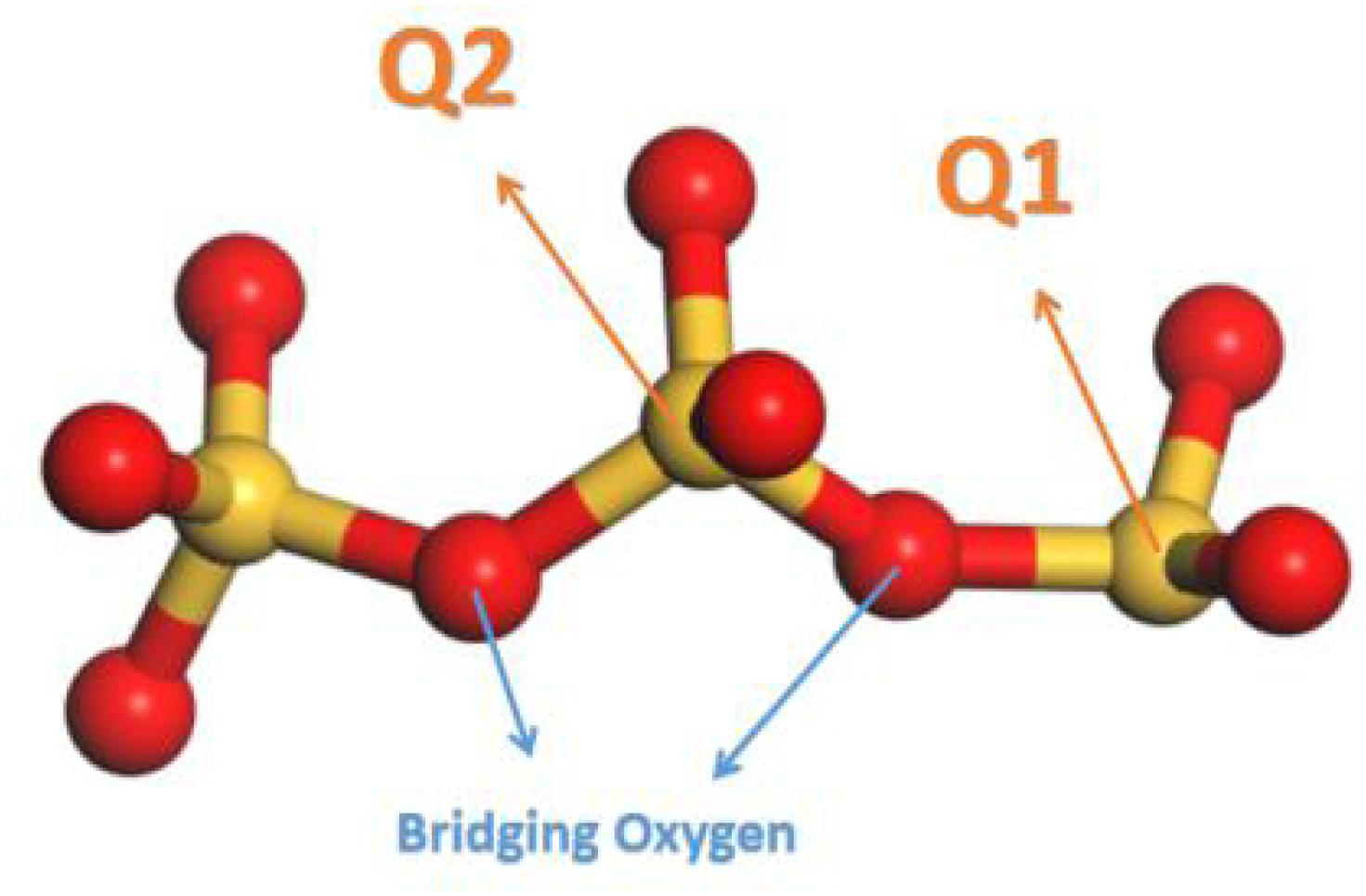
Figure 2. Schematic illustrations of Q species (red balls denote oxygen atoms and yellow balls denote silicon atoms).

TABLE 1

Table 1. Q species distribution of pure C-S-H and C-S-H/2D-silica after structural relaxation.

FIGURE 3

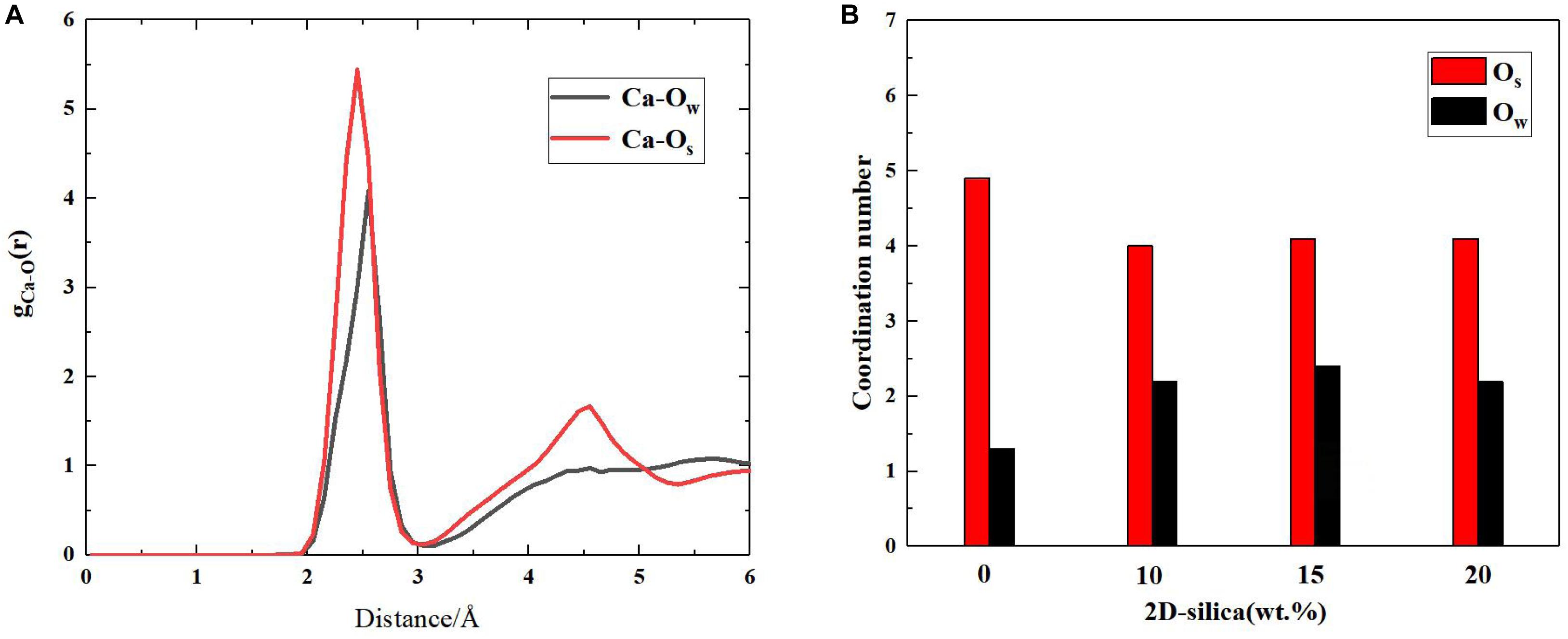
Figure 3. (A) Radial distribution function between Ca and O_w (oxygen from water molecules), O_s (oxygen from silicate tetrahedrons); (B) The coordinated oxygen number of calcium ions on average.

Calcium Silicate Hydrate With 2D-Silica Intercalated

The pure C-S-H structure and C-S-H intercalated with 2D-silica structure are shown in Figures 4A,B, respectively. In the interlayer regions of pure C-S-H, interstices induced by the defective silicate tetrahedron chains are filled up by large quantities of water molecules, which decrease the density of C-S-H and may affect the mechanical properties. With 2D-silica intercalated, the deficiencies are physically filled up. Meanwhile, owing to the surface effect of 2D-silica, the reactive dangling atoms on the boundary of 2D-silica interact with the silicate tetrahedron chains and form considerable quantities of Si-O-Si bonds (Figure 4C). Table 1 presents the distribution of Q species for pure C-S-H and C-S-H/2D-silica. It indicates that in pure C-S-H, with paucity of Q₃ and Q₄, Q₁ and Q₂ primarily dominate large fractions, respectively, 43.24 and 56.76%, which corresponds with the (Pellenq et al., 2009) Si NMR experimental values (Cong and Kirkpatrick, 1996a). In C-S-H/2D-silica, the occurrence of Q₃ and Q₄ species is observed. Q₃ denotes a silicon connected with three bridging oxygen atoms, which implies a cross-link between neighboring sheets, while Q₄ denotes a silicon network with all connecting oxygen atoms being bridged. The former is owing to the interaction between 2D-silica and the oxygen atoms in silicate tetrahedron chains. The latter, however, is confirmed to mainly derive from 2D-silica rather than C-S-H matrix, which will be explained in the next paragraph. As for Q₁ and Q₂, a drastic decrease of Q₁ is observed, along with a slight decrease of Q₂. The high reactivity of Q₁ is due to the fact that it is situated at the edge of the deficiencies, with a considerable quantity of non-bridging oxygen atoms surrounded. Thus, compared with Q₂, the polymerizations of Q₁ are susceptible to occur.

FIGURE 4

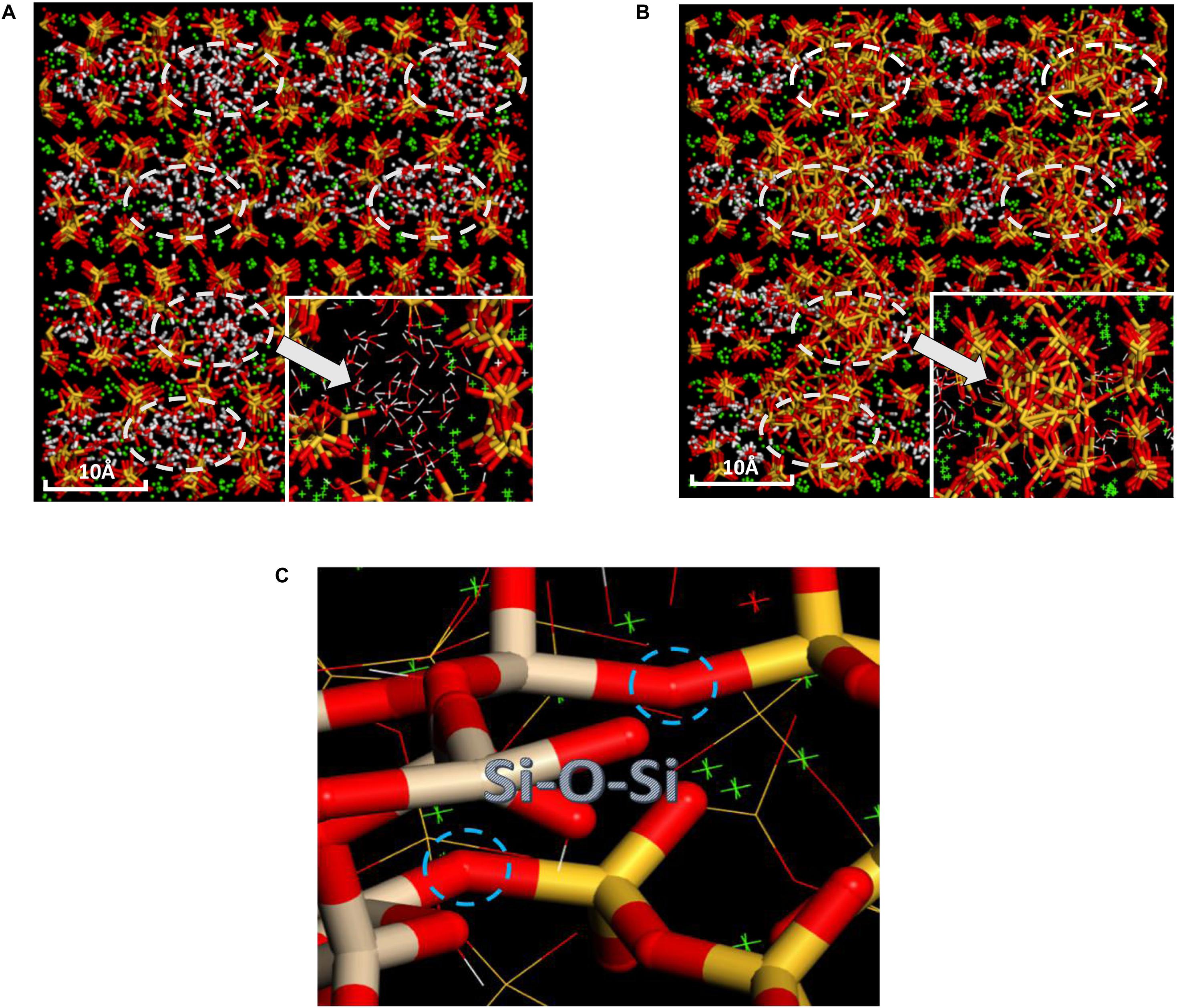
Figure 4. Comparative snapshots of (A) pure C-S-H and (B) C-S-H/2D-silica structure; (C) Schematic illustration of the interfacial Si-O-Si bonds formed between C-S-H and intercalated 2D-silica (the right red and yellow sticks indicate silicate tetrahedrons from C-S-H, while the left red and gray sticks indicate those from 2D-silica).

Further analysis is conducted to distinguish the transformation details of Q species in the C-S-H matrix (Table 2). A decline of 121 is observed for Q₁, and an increase of 22, 26, 72, 8 for Q₀, Q₂, Q₃, and Q₄, respectively. The decline of Q₁ in the C-S-H matrix again confirms the active reactivity of Q₁ at the edge of the deficiencies. Thus, improvement of cohesion of the structure is achieved with further polymerization of Q₁. For Q₂, an increase is observed in the C-S-H matrix, yet the overall structure of C-S-H/2D-silica undergoes a decline of Q₂. This means that the decline of Q₂ primarily comes from 2D-silica. It is recognized that part of the surface silicon atoms in 2D-silica are Q₂, which interacts with non-bridging oxygen atoms from the C-S-H matrix and then transformed to Q₃ and Q₄. The increase of Q₃ in the C-S-H matrix originates from the polymerization of Q₁ and occupies the largest proportion of the loss Q₁ quantities, consistent with Table 1 as demonstrated above. However, the quantity of generated Q₄ in the C-S-H matrix is relatively low. Combing Tables 1 and 2, it can be induced that Q₄ is primarily generated in 2D-silica. A possible explanation is the reorientation of Si-O bonds and transition of tetrahedron structure from δ-2D-silica to α-2D-silica (Madani et al., 2012). Apart from the polymerization, phenomenon of de-polymerization also takes place. The increase of Q₀ indicates that chemical reactions between C-S-H and 2D-silica will lead to a minor quantity of the breakage of Si-O bonds in the silicate tetrahedrons. It is concluded that the polymerization reactions of silicate tetrahedrons between C-S-H and 2D-silica reinforcements lead to an integrated nanocomposite with substantially higher connectivity than the matrix.

TABLE 2

Table 2. The number change of each Q species in the matrix of C-S-H after the intercalation of 20 wt.% 2D-silica.

The interaction between calcium ions and oxygen atoms are also altered due to the intercalation of 2D-silica. As presented in Figure 3B, in pure C-S-H, the calculated coordination environment of a calcium ion is 4.9 O_s and 1.3 O_w on average. A total coordination number of around 6 was reported by a scanning transmission X-ray microscopy study (Orozco et al., 2017), which is consistent with the MD simulation results here. While in C-S-H/2D-silica nanocomposite, the coordination oxygen number of a calcium ion is 4.0 for O_s and 2.0 for O_w. As described earlier, the intercalated 2D-silica situates in the interlayer regions and reacts with O_s atoms, which lowers the number of O_s coordinating with the calcium ions. As a consequence, more O_w atoms will be attracted by calcium ions to maintain the stability of the coordination environment.

Mechanical Properties

The uniaxial tensile experiments for pure C-S-H along x, y, z directions are conducted and the corresponding stress-strain curves are presented in Figure 5A. It can be observed that along z direction, C-S-H exhibits the weakest mechanical performance, with a maximum tensile stress of merely 4.8 GPa. As the strain level reaches 45%, a complete breakdown occurs. While along y direction, C-S-H shows the best strength and ductility. After the tensile stress reaches 10.0 GPa at the end of the elastic stage, it maintains a plateau from 20 to 45%. Subsequently, the stress keeps decreasing along with the development of strain level. Along the x direction, the C-S-H exhibits a better mechanical performance than that along z direction, though relatively weaker than y direction. The different performances of C-S-H subjected to tensile loading along three directions are closely related to the structure of pure C-S-H. The out-of-plane stiffness and ductility of C-S-H is dramatically lower than ones of xy-plane. Here, the simulated results are consistent with the previous high pressure XRD results (Geng et al., 2017, 2018) and the detailed explanations will be illustrated in section Influence of the Tensile Direction. It should be noted a minor bump still appeared even after the stress reached zero. It is caused by the computation errors in molecular dynamics simulations. For example, some approximation methods may be employed when computing long-order electrostatic, in order force to decrease the overall computation cost, which may lead to errors.

FIGURE 5

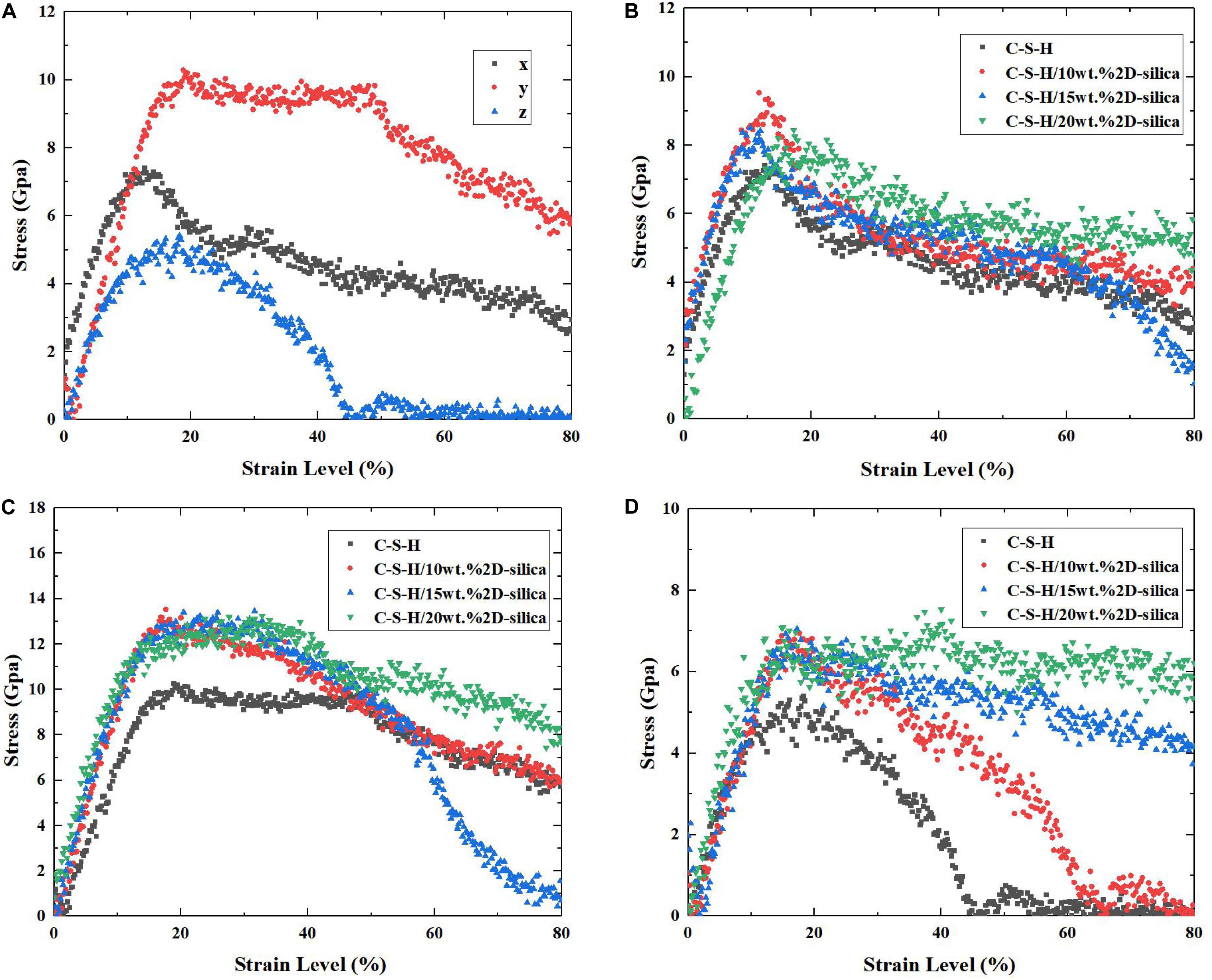
Figure 5. (A) The stress–strain curves of pure C-S-H during the uniaxial tensile process along x, y, and z directions; The stress–strain curves of pure C-S-H and C-S-H/2D-silica with different dosages during the uniaxial tensile process along (B) x direction, (C) y direction, and (D) z direction.

The influence of 2D-silica reinforcement on the stress-strain relationships of C-S-H is shown in Figures 5B–D. Overall, the matrix performs a better mechanical performance along all three directions due to the incorporation of 2D-silica, while along z direction (the originally weakest one) the enhancement efficiency is the highest. It is observed in Figure 5D that the decline of stress of pure C-S-H begins when the strain level reaches 15% and the complete fracture occurs when the strain level reaches 45%. The maximum tensile strength is 4.8 GPa and afterward the stress drops rapidly, indicating a brittle fracture. After 2D-silica is intercalated, the ductility of the structure has been greatly improved, due to the elongation of yield stage. Especially for C-S-H/20 wt.% 2D-silica, the maximum tensile strength reaches 6.8 GPa and the C-S-H remains at the yield stage until the end of tensile process with no distinct fracture observed. The improvement in the ductility can be attributed to the filling of defective pores, and the strong interaction between intercalated 2D-silica and C-S-H matrix, which will be discussed in details in section Influence of the 2D-Silica Intercalated.

The mechanical properties (tensile strength and Young’s modulus) of pure C-S-H and C-S-H/2D-silica with different dosages of reinforcements are presented in Figures 6A,B, respectively. As for tensile strength, it can be seen that intercalation of 2D-silica greatly improves the tensile strength along all three directions, while the increase of dosage of 2D-silica has a slight influence on the values. From Figure 6B, a distinct growth of Young’s modulus can also be observed along each direction. Especially along z direction, the values of Young’s modulus seem to have a positive correlation with the dosage of 2D-silica. In conclusion, the intercalation of 2D-silica has the most remarkable improvement on the mechanical performance of the C-S-H matrix along z direction, while a slight influence along x direction.

FIGURE 6

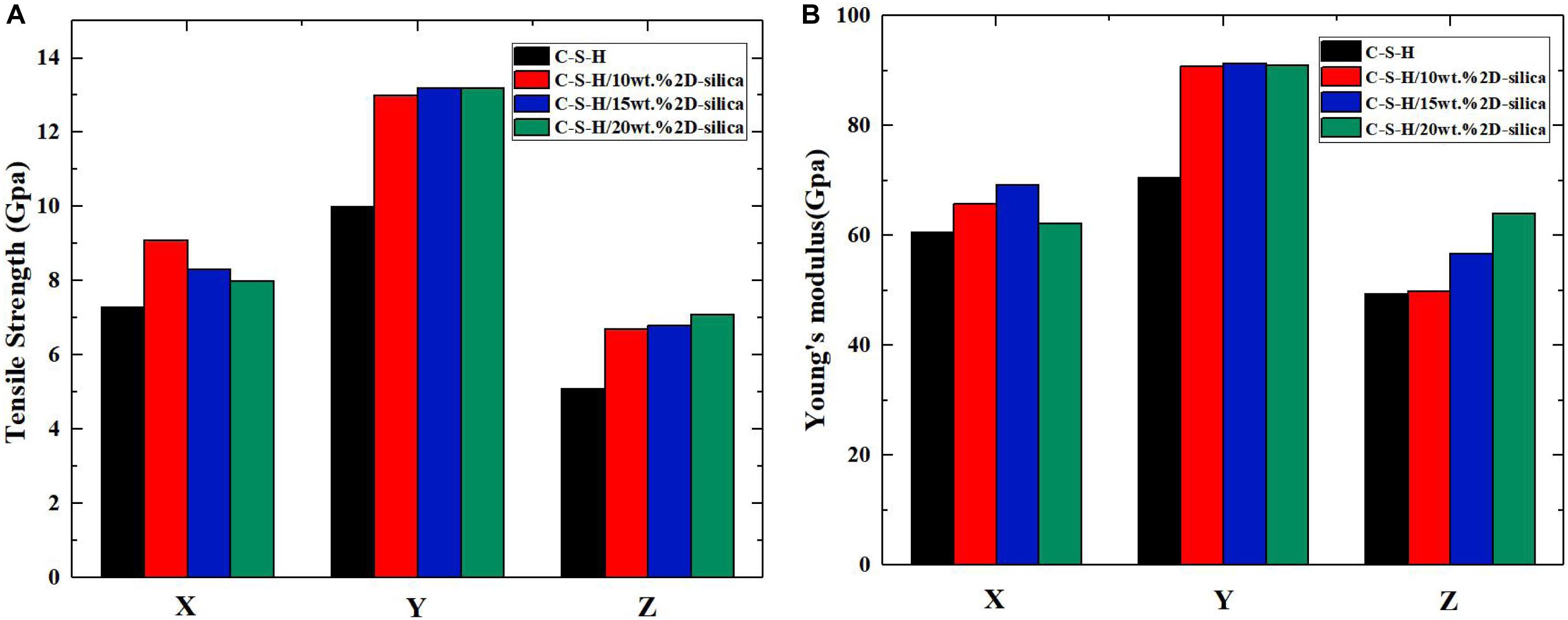
Figure 6. The calculated mechanical properties of pure C-S-H and C-S-H/2D-silica with different dosages: (A) tensile strength; (B) Young’s modulus.

Mechanism

Influence of the Tensile Direction

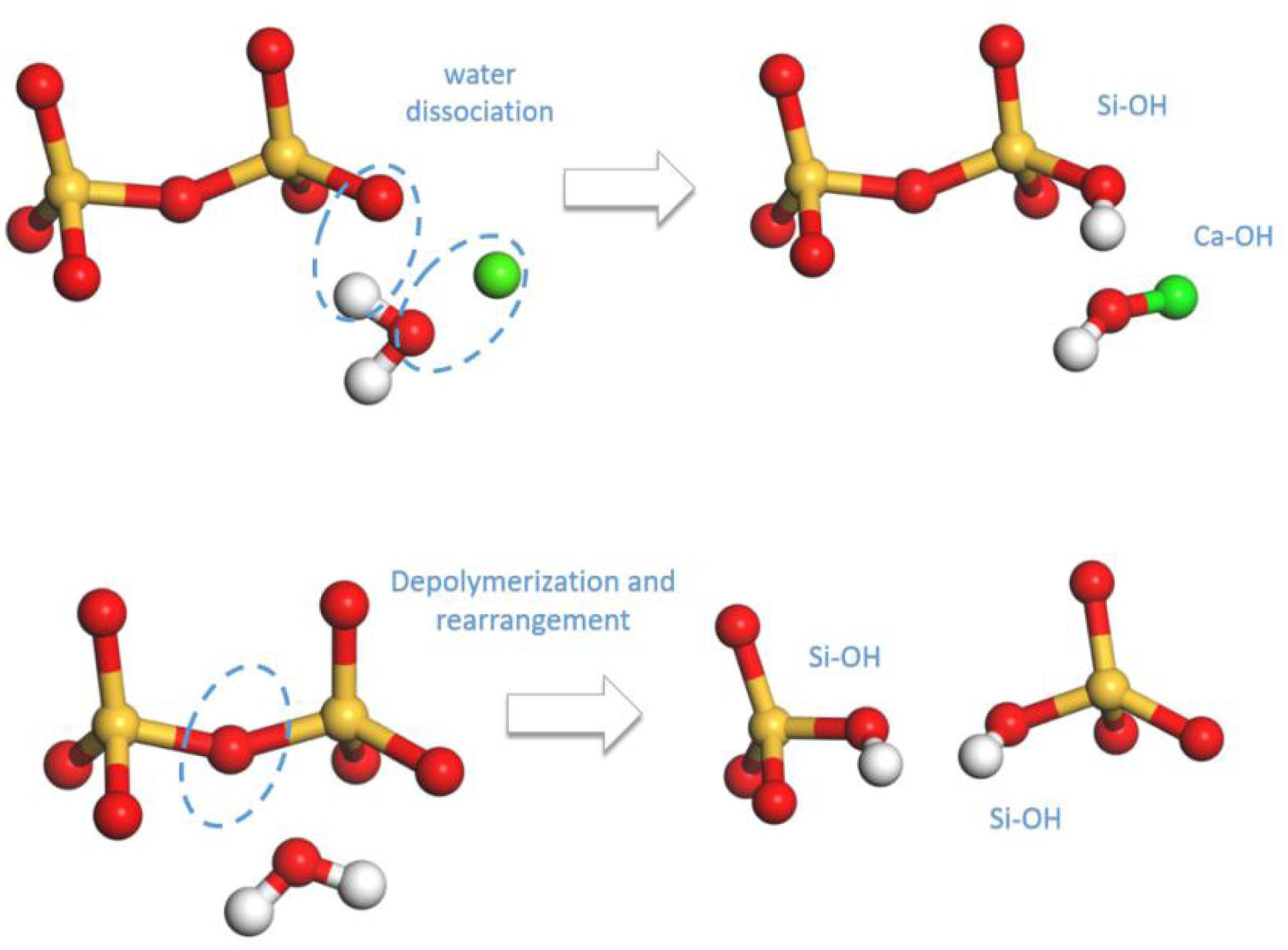
First, the mechanisms on the distinguished response of C-S-H matrix to uniaxial tensile process along x, y, and z direction are interpreted. According to the theory of Zhu et al. (2005), there exists two types of hydrolytic reactions in C-S-H model. On the other hand, during the tensile process, the internal tensile stress may reduce the activation energy of those hydrolytic reactions, leading to the dissociation of water molecules and further structural rearrangements. The two types of hydrolytic reaction can be illustrated by the following formulas, respectively:

$$Si-O\mathrm{\cdots }Ca+H_{2}O\to Si-OH+Ca-OH(1)$$

$$Si-O-Si+H_{2}O\to Si-OH+Si-OH(2)$$

In formula (1), the Si-O…Ca ionic bonds are fairly weak so that they can be easily stretched until broken. The dangling Si-O bonds will attract the water molecules and cause dissociation of water molecules to hydrogen atoms and hydroxyl groups. Subsequently, the generated hydrogen atoms and hydroxyl groups react with the Si-O bonds and calcium ions, respectively, to form the same amount of Si-OH and Ca-OH (presented in Figure 7). In formula (2), the dissociation of water molecules is based on the breakage of Si-O-Si bonds into Si-O- and Si- groups, which indicates depolymerization of the silicate tetrahedrons. The active non-bridging oxygen atoms in Si-O- will attract and dissociate the water molecules, forming double amount of Si-OH.

FIGURE 7

Figure 7. The schematic illustration of dissociation mechanisms of Si-O^… Ca and Si-O-Si bonds.

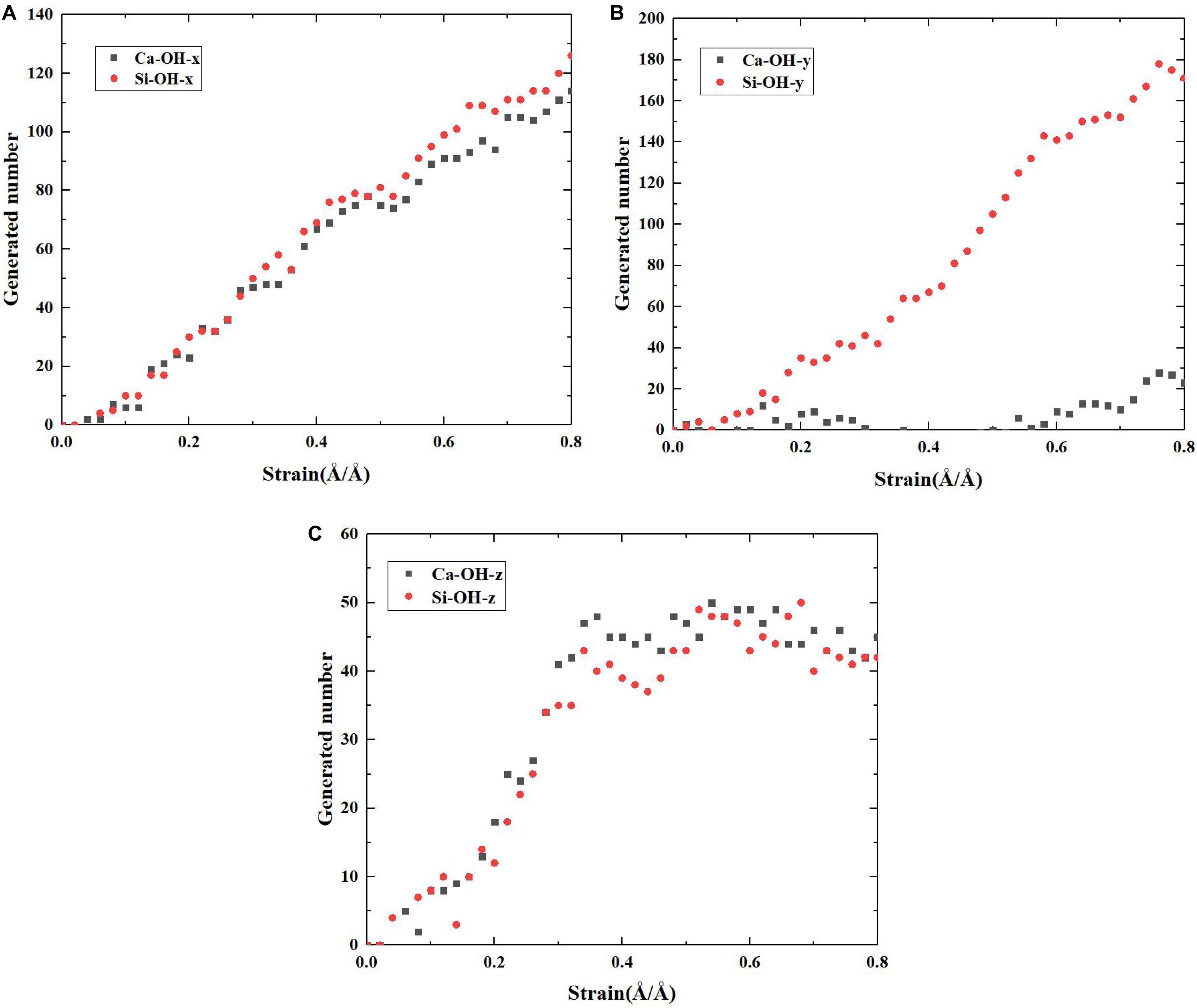
On the basis of the above reaction principles, the structural evolution mechanism of C-S-H during the tensile process can be unraveled by monitoring the number change of Ca-OH and Si-OH, as well as the distribution development of Q species. Figures 8, 9, respectively, represent the number evolution of those indicators during the tensile process. As showed in Figures 8A,C, along x and z directions, the number of Ca-OH and Si-OH exhibits a synchronous increase, indicating merely the occurrence of reaction (1) during the tensile process. The plateau in the z direction (presented in Figure 8C) corresponds with the complete fracture of C-S-H when the strain reaches 0.45 Å/Å. Besides, according to Figures 9A,C, there is no distinct evolution of Q species along the x and z directions, which well proves that the silicate tetrahedron chains are not affected in the tensile process. Thus, it is the elongation and breakage of Si-O^… Ca bonds that are responsible for the strain development. Along the y direction, the evolution of the Ca-OH and Si-OH number follows another mode, with a rapid increase of Si-OH number and almost no change of Ca-OH number. It is caused by the mere occurrence of reaction (2). As for the evolution of Q species, as presented in Figure 9B, it indicates a decrease of Q₂ and an increase of Q₀ and Q₁, which also suggests a decomposition of Q₂ to form Q₀ and Q₁. Therefore, it is concluded that mainly the high-strength Si-O-Si bonds are stretched and broken during the tensile process along y direction. Since the Si-O-Si bond owns significantly higher bond energy than Si-O…Ca, C-S-H exhibits a higher performance along y direction (Figure 5A).

FIGURE 8

Figure 8. The number evolution of generated Ca–OH, Si–OH along (A) x, (B) y, and (C) z direction.

FIGURE 9

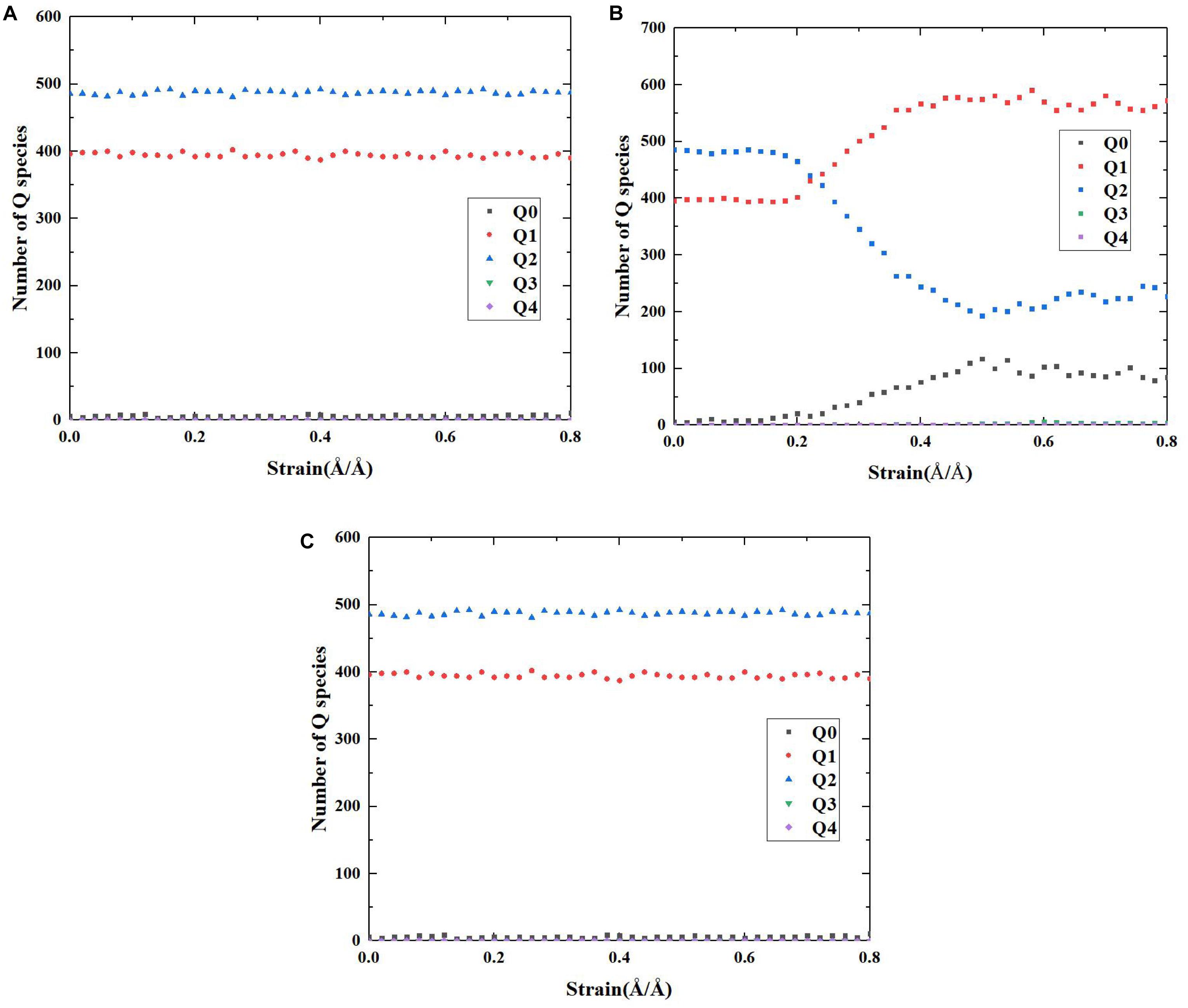
Figure 9. The number evolution of each Q species of pure C-S-H as a function of strain during the tensile process along (A) x, (B) y, and (C) z direction.

Influence of the 2D-Silica Intercalated

Since the intercalation of 2D-silica performs the highest enhancement efficiency on the mechanical properties of C-S-H along z direction, the detailed interaction mechanisms between the host and the reinforcement will be interpreted along this direction. Snapshots of pure C-S-H and C-S-H/2D-silica during the tensile process are presented in Figure 10 which are arranged on the basis of different strain levels (0.1, 0.2, 0.3, 0.4, 0.5, and 0.6 Å/Å). The initial interlayer spacings are, respectively, 8.2 and 9.5 Å for C-S-H and C-S-H/2D-silica, indicating that the intercalation of 2D-silica has enlarged the interlayer spacing. The 2D-silica molecules act as bridges in the interlayer regions, connecting the neighboring calcium silicate sheets by the formation of large quantities of Si-O-Si bonds, which is caused by the strong interaction between the 2D-silica and C-S-H matrix, as shown in Figure 4C. As described earlier, during the tensile process along z direction, for pure C-S-H, the breakage of Si-O^… Ca bonds is primarily responsible for the development of strain, generating the same amount of Ca-OH and Si-OH. However, for C-S-H/2D-silica, the presence of Si-O-Si bonds in the interlayer regions significantly changes the reaction mechanism during the tensile process.

FIGURE 10

Figure 10. The snapshots of (A) pure C-S-H and (B) C-S-H/20 wt.% 2D-silica during the tensile process along z direction at different strain levels.

With the development of the strain, the interlayer spacing of pure C-S-H is gradually enlarged, leading to distinct cracks when the strain reaches 0.3 Å/Å. On the contrary, the interlayer spacing of C-S-H/2D-silica increases continuously, with no soar of extension rate observed. The integrality of the C-S-H has not been affected owing to the formation of Si-O-Si bonds between calcium silicate sheets. Yet for the regions deficient of layer connection, the expansion of interstices can be observed. When the strain reaches 0.4 Å/Å, pure C-S-H undergoes a complete fracture (interlayer spacing of 15.2 Å/Å), while C-S-H/2D-silica still remains intact (interlayer spacing of 12.1 Å/Å). When the strain continues to develop in C-S-H/2D-silica, considerable deformation and interstices can be observed. With the connection of the strong Si-O-Si bonds, ultimate rupture is not observed even though the strain reaches 0.8 Å/Å. It is owing to the high strength of Si-O-Si bonds that contributes to the elongation of yield stage, which is consistent with the plateau of stress as presented in Figure 5D.

Besides, it is worth noting that in Zhou’s research about polymer-reinforced C-S-H (Zhou et al., 2018a), the formation of Si-O-C bonds between C-S-H and PEG, PVA, and PAA strengthens the connection of layers, which leads to similar effect of enhancement of strength and ductility. Thus, it is concluded that the interlayer bridging mechanism can effectively enhance the ductility of C-S-H matrix. In addition, in Zhou’s research, even though the intercalation of PEG shows the best enhancement of ductility comparing with other polymers, the C-S-H structure still undergoes a complete fracture when the strain reaches 0.8 Å/Å. In the opposite, as presented in Figures 5D, 10, the C-S-H/2D-silica structure still remains intact and retains a high level of tensile strength even the strain reaches 0.8 Å/Å. This proves that the strength of Si-O-Si bonds are higher than that of Si-O-C bonds, thus the breakage of bonds requires more activation energy. In other words, in terms of the enhancement efficiency, 2D-silica performs better than polymers. Besides, the enhancement effect shows a positive correlation with the amount of intercalation of 2D-silica (Figures 5D, 11). The increase of amount of 2D-silica can effectively fill up the interstices and form more Si-O-Si bonds between layers which significantly enhance the connection.

FIGURE 11

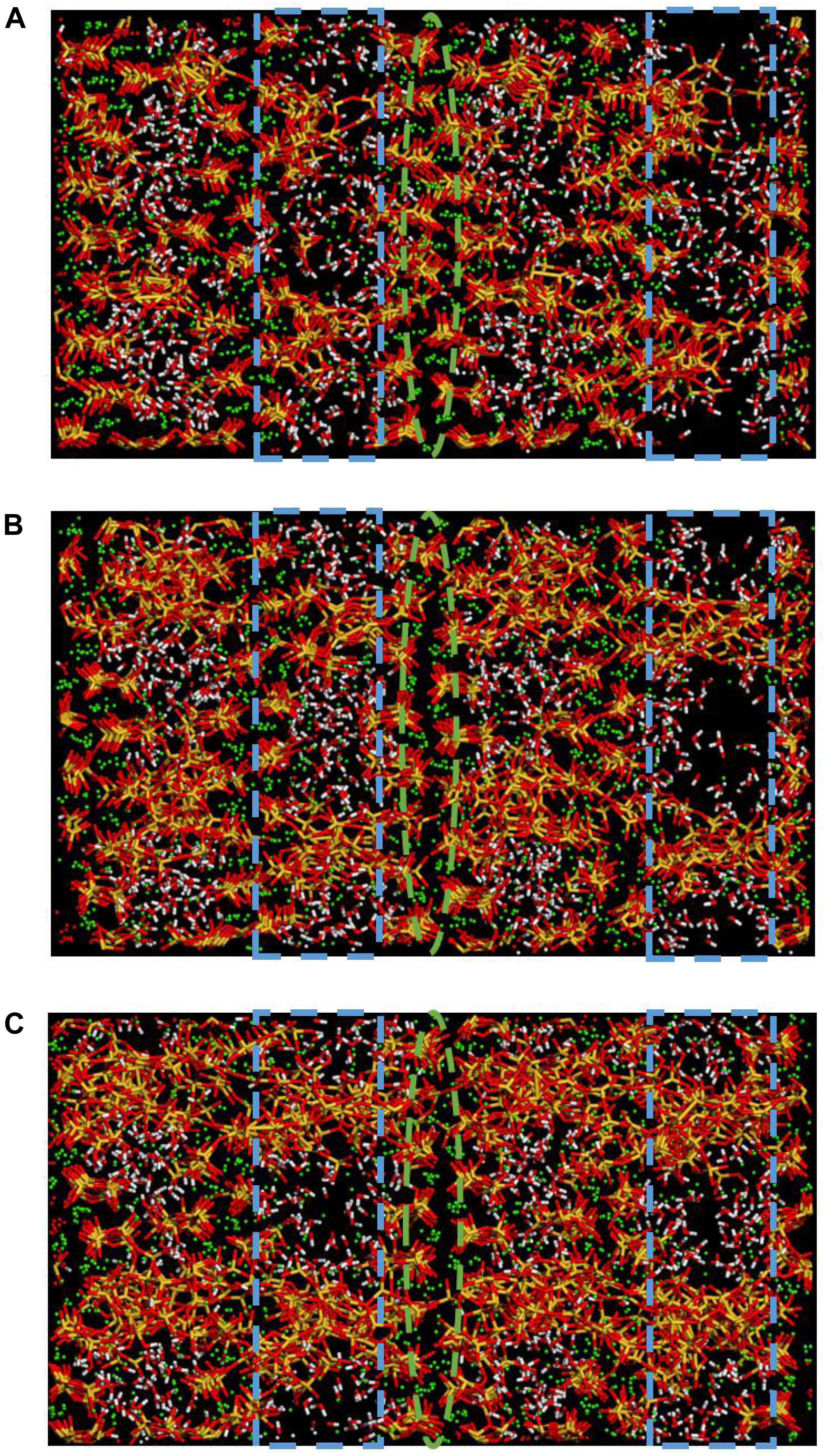
Figure 11. Snapshots of (A) C-S-H/10 wt.% 2D-silica, (B) C-S-H/15 wt.% 2D-silica, (C) C-S-H/20 wt.% 2D-silica at the strain level of 0.5 Å/Å during the z direction tensile process.

Evolution of the number of generated Ca-OH and Si-OH of pure C-S-H and C-S-H/2D-silica during the tensile process along z direction are recorded and presented in Figure 12. And on the basis of the stress -strain curve in Figure 5A, the tensile process of pure C-S-H can be categorized into elastic stage, yield stage and ultimate fracture. In the elastic stage, the evolution of Ca-OH and Si-OH keeps a synchronous correlation, indicating the occurrence of reaction (1). With the development of the strain level, a distinct increase of the slope is observed, which is an indicator for the breakage of more Si-O…Ca bonds and can be considered as the beginning of the yield age (around 0.15 Å/Å). The number of generated Ca-OH and Si-OH keeps increasing until the ultimate fracture of C-S-H (0.4 Å/Å).

FIGURE 12

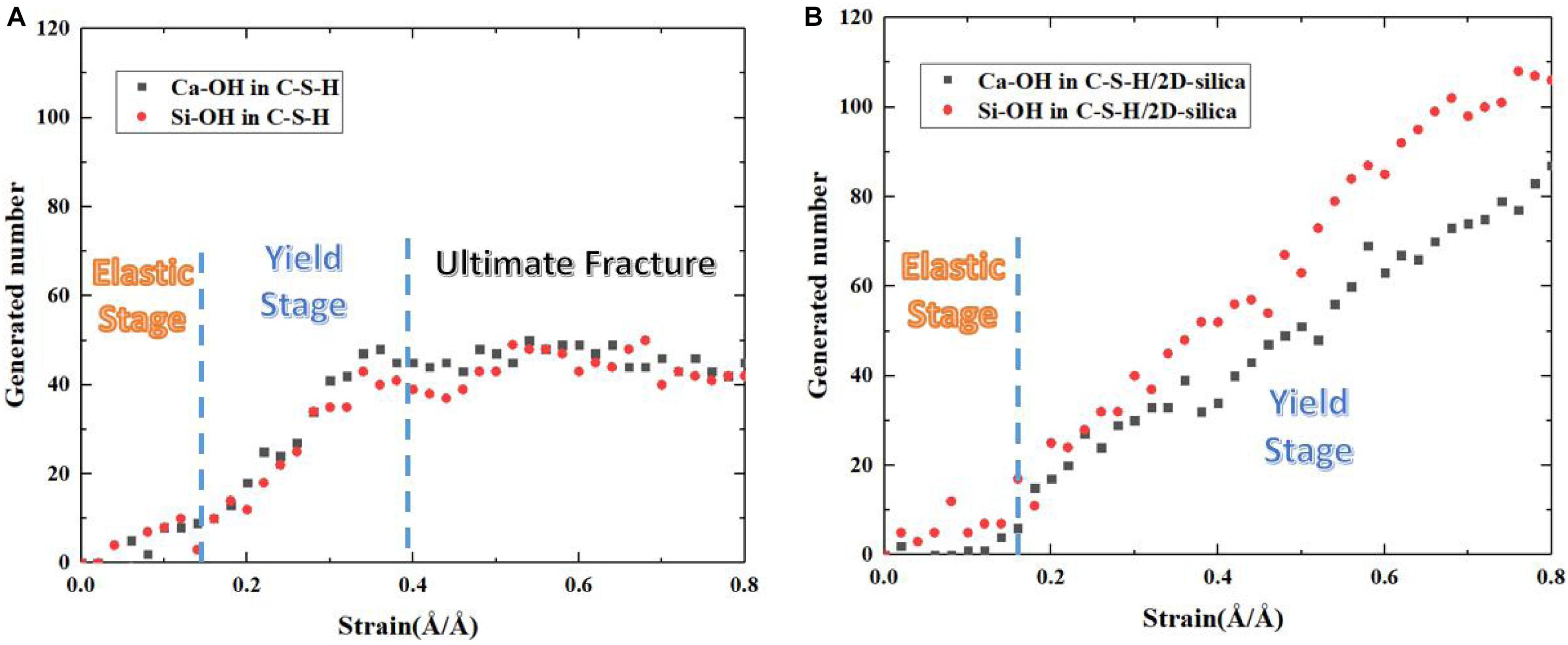
Figure 12. The evolution of generated number of Ca–OH, Si–OH of (A) pure C-S-H and (B) C-S-H/2D-silica during tensile process along z direction.

The number evolution of generated Ca-OH and Si-OH in C-S-H/2D-silica shows a similar tendency as the strain level is lower than 0.3 Å/Å. After that point, the number of hydroxyl groups keeps increasing and the rate of Si-OH surpasses that of Ca-OH, which is on account of the onset of reaction (2). From 0.3 to 0.8 Å/Å, both reaction (1) and (2) take place. The elongation and breakage of high-strength Si-O-Si bonds contribute to a higher stress level, which extends the yield stage compared with pure C-S-H. As shown in Figure 5D, the larger amount of 2D-silca is intercalated, the higher ultimate strain will be reached. For C-S-H with 20 wt.% 2D-silica intercalated, the stress still maintains as high as the yield stress until the end of the simulation. As presented in Table 3, the generated number of Ca-OH and Si-OH during the tensile process of pure C-S-H is, respectively, 45 and 42, which approximately agrees with the 1:1 correlation. While for C-S-H/2D-silica, the generated number is 87 and 106 for Ca-OH and Si-OH. From the perspective of energy dissipation, the occurrence of more chemical reactions takes in more energy, and thus increases the toughness of the matrix.

TABLE 3

Table 3. Generated number of Ca-OH and Si-OH of pure C-S-H and C-S-H/2D-silica during the tensile process along z direction.

Conclusion

In this work, 2D-silica is selected as the nano-phase reinforcement and intercalated into the interlayer regions of a C-S-H matrix, modifying the structure and thus enhancing the mechanical performance. Molecular dynamic simulation is utilized to investigate the interactions between 2D-silica and C-S-H matrix and to unravel the interfacial mechanism.

The pure C-S-H has a layered structure with only Q₁ and Q₂ silicon atoms. As the 2D-silica reinforcement is incorporated into the C-S-H matrix, the dangling silicon atoms at the edge of 2D-silica strongly interact with the reactive non-bridging oxygen atoms at the defective sites, leading to formation of interfacial Si-O-Si bonds. Those covalent bonds transform Q₁ and Q₂ in the C-S-H into high connectivity Q₃ and Q₄ species, which increases the integrity of the matrix. The uniaxial tensile loading experiments are conducted on C-S-H and C-S-H/2D-silica models along x, y, and z direction, respectively. The results show that along z direction pure C-S-H performs the weakest mechanical performance due to large numbers of defects in the interlayer, while the intercalation of 2D-silica can dramatically improve the tensile strength and ductility along this direction. The enhancement efficiency of 2D-silica on the stiffness and toughness of C-S-H xy-plane is relatively lower, since the pure C-S-H model is originally strong in the intralayer region. The enhancement mechanisms are demonstrated as follows. During the tensile process of a pure C-S-H model along z direction, it is primarily the dissociation of Si-O…Ca ionic bonds in the interlayer region that contributes to the development of strain. This relatively weak interlayer cohesion causes a brittle fracture of the matrix. However, within a C-S-H/2D-silica model, the presence of interfacial Si-O-Si bonds also shares responsibility for the strain development. The elongation and breakage of those high-strength covalent bonds needs higher tensile stress and consumes higher energy, which leads to a longer plastic stage and higher toughness. The occurrence of Q₃ and Q₄ species in the nanocomposite leads to a high-connectivity net system, increasing the resistance of crack propagation.

This work may shed new lights on the interaction mechanisms between nano-reinforcements and an inorganic host. Geopolymers also include the silicate tetrahedra, hence, such a strengthening principle may also apply to geopolymers. The dangling atoms at the edge of 2D-silica can react with non-bridging oxygen atoms of geopolymers, forming Si-O-Si bonds at interfaces. Those covalent bonds transform Q₁ and Q₂ of geopolymers into high connectivity Q₃ and Q₄ species, which increases the integrity of the matrix and its resistance to crack propagation.

Furthermore, this work provides solutions to modify the brittleness of concrete so as to achieve high performance construction materials. In this way, less cement is required for an equal bearing capacity, which promotes a low-carbon manufacturing and sustainable industry. However, the current study of 2D-silica reinforcement is still limited to a theoretical level, while further experimental research is needed to validate the simulation results.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

YZ and JH contributed conception and design of the study. HZ, YQ, and XZ organized the database and wrote sections of the manuscript. YZ and HZ performed the statistical analysis. YZ, HZ, YQ, and XZ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge support from the National Natural Science Foundation of China (Grant Nos. 51908119, 6512009004A, and U1706222) and the Natural Science Foundation of Jiangsu Province (Grant No: BK20190367).

References

Allen, A. J., Thomas, J. J., and Jennings, H. M. (2007). Composition and density of nanoscale calcium-silicate-hydrate in cement. Nat. Mater. 6, 311–316. doi: 10.1038/nmat1871

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauchy, M., Qomi, M. J. A., Ulm, F. J., and Pellenq, R. J. M. (2014). Order and disorder in calcium-silicate-hydrate. J. Chem. Phys. 140:214503. doi: 10.1063/1.4878656

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonnaud, P. A., Ji, Q., Coasne, B., Pellenq, R. J.-M., and Van Vliet, K. J. (2012). Thermodynamics of water confined in porous calcium-silicate-hydrates. Langmuir 28, 11422–11432. doi: 10.1021/la301738p

PubMed Abstract | CrossRef Full Text | Google Scholar

Büchner, C., and Heyde, M. (2017). Two-dimensional silica opens new perspectives. Progr. Surf. Sci. 92, 341–374. doi: 10.1016/j.progsurf.2017.09.001

CrossRef Full Text | Google Scholar

Chenoweth, K., van Duin, A. C. T., and Goddard, W. A. III (2008). ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 112, 1040–1053. doi: 10.1021/jp709896w

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, X., and Kirkpatrick, J. R. (1996a). 29Si MAS NMR study of the structure of calcium silicate hydrate. Adv. Cem. Based Mater. 3, 144–156. doi: 10.3390/jfb10020025

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, X. D., and Kirkpatrick, R. J. (1996b). Si-29 and O-17 NMR investigation of the structure of some crystalline calcium silicate hydrates. Adv. Cem. Based Mater. 3, 133–143.

Google Scholar

Constantinides, G., and Ulm, F.-J. (2007). The nanogranular nature of C-S-H. J. Mech. Phys. Solids 55, 64–90.

Google Scholar

Du, H., Du, S., and Liu, X. (2014). Durability performances of concrete with nano-silica. Constr. Build. Mater. 73, 705–712. doi: 10.1016/j.conbuildmat.2014.10.014

CrossRef Full Text | Google Scholar

Duque-Redondo, E., Manzano, H., Epelde-Elezcano, N., Martínez-Martínez, V., and López-Arbeloa, I. (2014). Molecular forces governing shear and tensile failure in clay-dye hybrid materials. Chem. Mater. 26, 4338–4345.

Google Scholar

Gao, Z., Dong, X., Li, N., and Ren, J. (2017). Novel two-dimensional silicon dioxide with in-plane negative poisson’s ratio. Nano Lett. 17, 772–777. doi: 10.1021/acs.nanolett.6b03921

PubMed Abstract | CrossRef Full Text | Google Scholar

Geng, G., Myers, R. J., Li, J., Maboudian, R., Carraro, C., Shapiro, D. A., et al. (2017). Aluminum-induced dreierketten chain cross-links increase the mechanical properties of nanocrystalline calcium aluminosilicate hydrate. Sci. Rep. 7:44032. doi: 10.1038/srep44032

PubMed Abstract | CrossRef Full Text | Google Scholar

Geng, G., Myers, R. J., Qomi, M. J. A., and Monteiro, P. J. M. (2018). Densification of the interlayer spacing governs the nanomechanical properties of calcium-silicate-hydrate. Sci. Rep. 7, 10986–10993. doi: 10.1038/s41598-017-11146-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., Li, T., and Wang, P. (2018a). Molecular Dynamics Study on the Structure and Dynamics of NaCl solution transport in the nanometer channel of CASH Gel. ACS Sustain. Chem. Eng. 6, 9498–9509.

Google Scholar

Hou, D., Yu, J., Jin, Z., and Hanif, A. (2018b). Molecular dynamics study on calcium silicate hydrate subjected to tension loading and water attack: Structural evolution, dynamics degradation and reactivity mechanism. Phys. Chem. Chem. Phys. 20, 11130–11144. doi: 10.1039/c7cp08634b

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., Lu, Z., Li, X., Ma, H., and Li, Z. (2017). Reactive molecular dynamics and experimental study of graphene-cement composites: Structure, dynamics and reinforcement mechanisms. Carbon N. Y. 115, 188–208.

Google Scholar

Hou, D., Ma, H., Zhu, Y., and Li, Z. (2014a). Calcium silicate hydrate from dry to saturated state: Structure, dynamics and mechanical properties. Acta Mater. 67, 81–94.

Google Scholar

Hou, D., Zhu, Y., Lu, Y., and Li, Z. (2014b). Mechanical properties of calcium silicate hydrate (C-S-H) at nano-scale: A molecular dynamics study. Mater. Chem. Phys. 146, 503–511. doi: 10.3390/ma12172837

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., Zhang, J., Pan, W., Zhang, Y., and Zhang, Z. (2020). Nanoscale mechanism of ions immobilized by the geopolymer: A molecular dynamics study. J. Nucl. Mater. 528:151841. doi: 10.1016/j.jnucmat.2019.151841

CrossRef Full Text | Google Scholar

Hou, D., Zhao, T., Ma, H., and Li, Z. (2015). Reactive molecular simulation on water confined in the Nanopores of the Calcium silicate hydrate gel: structure, reactivity, and mechanical properties. J. Phys. Chem. C 119, 1346–1358.

Google Scholar

Huang, P. Y., Kurasch, S., Srivastava, A., Skakalova, V., Kotakoski, J., Krasheninnikov, A. V., et al. (2012). Direct imaging of a two-dimensional silica glass on graphene. Nano Lett. 12, 1081–1086. doi: 10.1021/nl204423x

PubMed Abstract | CrossRef Full Text | Google Scholar

Janik, J. A., Kurdowski, W., Podsiadly, R., and Samseth, J. (2001). Fractal structure of C-S-H and tobermorite phases. ACTA Phys. Pol. A 100, 529–537.

PubMed Abstract | Google Scholar

Jennings, H. M. (2008). Refinements to colloid model of C-S-H in cement: CM-II. Cem. Concr. Res. 38, 275–289. doi: 10.1016/j.cemconres.2007.10.006

CrossRef Full Text | Google Scholar

Kim, Y., Hanif, A., Usman, M., Munir, M. J., Saleem, S. M., and Kim, S. (2018). Slag waste incorporation in high early strength concrete as cement replacement: Environmental impact and influence on hydration & durability attributes. J. Clean. Prod. 172, 3056–3065. doi: 10.1016/j.jclepro.2017.11.105

CrossRef Full Text | Google Scholar

Konsta-Gdoutos, M. S., Metaxa, Z. S., and Shah, S. P. (2010). Highly dispersed carbon nanotube reinforced cement based materials. Cem. Concr. Res. 40, 1052–1059. doi: 10.1016/j.cemconres.2010.02.015

CrossRef Full Text | Google Scholar

Liong, M., Lu, J., Kovochich, M., Xia, T., Ruehm, S. G., Nel, A. E., et al. (2008). Multifunctional inorganic nanoparticles for imaging, targeting, and drug delivery. ACS Nano 2, 889–896. doi: 10.1021/nn800072t

PubMed Abstract | CrossRef Full Text | Google Scholar

Madani, H., Bagheri, A., and Parhizkar, T. (2012). The pozzolanic reactivity of monodispersed nanosilica hydrosols and their influence on the hydration characteristics of Portland cement. Cem. Concr. Res. 42, 1563–1570.

Google Scholar

Manzano, H., Masoero, E., Lopez-Arbeloa, I., and Jennings, H. M. (2013). Shear deformations in calcium silicate hydrates. Soft Matter 9:7333. doi: 10.1103/PhysRevLett.119.035502

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzano, H., Moeini, S., Marinelli, F., van Duin, A. C. T., Ulm, F.-J., and Pellenq, R. J. M. (2012). Confined water dissociation in microporous defective silicates: Mechanism, dipole distribution, and impact on substrate properties. J. Am. Chem. Soc. 134, 2208–2215. doi: 10.1021/ja209152n

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehta, P. K., and Monteiro, P. J. M. (2014). Concrete Microstructure, Properties, and Materials, 4th Edn. New York, NY: McGraw-Hill Companies, doi: 10.1036/0071462899

CrossRef Full Text | Google Scholar

Monteiro, P. J. M., Miller, S. A., and Horvath, A. (2017). Towards sustainable concrete. Nat. Mater. 16, 688–689.

Google Scholar

Orozco, C. A., Chun, B. W., Geng, G., Emwas, A. H., and Monteiro, P. J. M. (2017). Characterization of the bonds developed between calcium silicate hydrate and polycarboxylate-based superplasticizers with silyl functionalities. Langmuir 33, 3404–3412. doi: 10.1021/acs.langmuir.6b04368

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellenq, R. J.-M., Kushima, A., Shahsavari, R., Van Vliet, K. J., Buehler, M. J., Yip, S., et al. (2009). A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. U. S. A. 106, 16102–16107. doi: 10.1073/pnas.0902180106

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, I. G. (2008). The calcium silicate hydrates. Cem. Concr. Res. 38, 137–158.

Google Scholar

Sakhavand, N., Muthuramalingam, P., and Shahsavari, R. (2013). Toughness governs the rupture of the interfacial H-bond assemblies at a critical length scale in hybrid materials. Langmuir 29, 8154–8163. doi: 10.1021/la4014015

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, F., and Zhang, L. (2008). Molecular dynamics modeling of the interface between surface functionalized graphitic structures and calcium–silicate–hydrate: interaction energies, structure, and dynamics. J. Colloid Interface Sci. 323, 349–358. doi: 10.1016/j.jcis.2008.04.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuetz, C. A., and Frenklach, M. (2003). Nucleation of soot: Molecular dynamics simulations of pyrene dimerization. Proc. Combust. Inst. 29, 2307–2314.

Google Scholar

Shahsavari, R., Buehler, M. J., Pellenq, R. J. M., and Ulm, F. J. (2009). First-principles study of elastic constants and interlayer interactions of complex hydrated oxides: Case study of tobermorite and jennite. J. Am. Ceram. Soc. 92, 2323–2330.

Google Scholar

Tang, F., Li, L., and Chen, D. (2012). Mesoporous silica nanoparticles: Synthesis, biocompatibility and drug delivery. Adv. Mater. 24, 1504–1534. doi: 10.1002/adma.201104763

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, L., and Cheng, J. (2013). Nonporous silica nanoparticles for nanomedicine application. Nano Today 8, 290–312. doi: 10.1016/j.nantod.2013.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulm, F.-J., Vandamme, M., Bobko, C., and Ortega, J. A. (2007). Statistical indentation techniques for hydrated nanocomposites: Concrete, bone, and shale. J. Am. Ceram. Soc. 90, 2677–2692.

Google Scholar

van Duin, A. C. T., Dasgupta, S., Lorant, F. A., and Goddard, A. W. (2001). ReaxFF: a reactive force field for hydrocarbonds. J. Phys. Chem. A 105, 9396–9409.

Google Scholar

van Duin, A. C. T., Strachan, A., Stewman, S., Zhang, Q., Xu, X., and Goddard, W. A. (2003). ReaxFF(SiO) reactive force field for silicon and silicon oxide systems. J. Phys. Chem. A 107, 3803–3811.

Google Scholar

Yu, R., Spiesz, P., and Brouwers, H. J. H. (2014). Effect of nano-silica on the hydration and microstructure development of Ultra-High Performance Concrete (UHPC) with a low binder amount. Constr. Build. Mater. 65, 140–150. doi: 10.1016/j.conbuildmat.2014.04.063

CrossRef Full Text | Google Scholar

Zhou, Y., Hou, D., Geng, G., Feng, P., Yu, J., and Jiang, J. (2018a). Insights into the interfacial strengthening mechanisms of calcium-silicate-hydrate/polymer nanocomposites. Phys. Chem. Chem. Phys. 20, 8247–8266. doi: 10.1039/c8cp00328a

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y., Hou, D., Jiang, J., Liu, L., She, W., Yu, J., et al. (2018b). Experimental and molecular dynamics studies on the transport and adsorption of chloride ions in the nano-pores of calcium silicate phase: The influence of calcium to silicate ratios. Microporous Mesoporous Mater. 255, 23–35.

Google Scholar

Zhou, Y., Hou, D., Jiang, J., She, W., and Yu, J. (2017a). Reactive molecular simulation on the calcium silicate hydrates/polyethylene glycol composites. Chem. Phys. Lett. 687, 184–187.

Google Scholar

Zhou, Y., Hou, D., Jiang, J., and Wang, P. (2016). Chloride ions transport and adsorption in the nano-pores of silicate calcium hydrate: Experimental and molecular dynamics studies. Constr. Build. Mater. 126, 991–1001.

Google Scholar

Zhou, Y., Hou, D., Manzano, H., Orozco, C. A., Geng, G., Monteiro, P. J. M., et al. (2017b). Interfacial connection mechanisms in Calcium-Silicate-Hydrates/Polymer nanocomposites: a molecular dynamics study. ACS Appl. Mater. Interfaces 9, 41014–41025. doi: 10.1021/acsami.7b12795

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y., Orozco, C. A., Duque-Redondo, E., Manzano, H., Geng, G., Feng, P., et al. (2019a). Modification of poly (ethylene glycol) on the microstructure and mechanical properties of calcium silicate hydrates. Cem. Concr. Res. 115, 20–30.

Google Scholar

Zhou, Y., Tang, L., Liu, J., and Miao, C. (2019b). Interaction mechanisms between organic and inorganic phases in calcium silicate hydrates/poly(vinyl alcohol) composites. Cem. Concr. Res. 125:105891.

Google Scholar

Zhu, T., Li, J., Lin, X., and Yip, S. (2005). Stress-dependent molecular pathways of silica-water reaction. J. Mech. Phys. Solids 53, 1597–1623.

Google Scholar