Smart Polymers for Advanced Applications: A Mechanical Perspective Review

Responsive materials, as well as active structural systems, are today widely used to develop unprecedented smart devices, sensors, or actuators; their functionalities come from the ability to respond to environmental stimuli with a detectable reaction. Depending on the responsive material under study, the triggering stimuli can have a different nature, ranging from physical (temperature, light, electric or magnetic field, mechanical stress, etc.), chemical (pH, ligands, etc.), or biological (enzymes, etc.) type. Such a responsiveness can be obtained by properly designing the meso- or macroscopic arrangement of the constitutive elements, as occurs in metamaterials, or can be obtained by using responsive materials per se, whose responsiveness comes from the chemistry underlying their microstructure. In fact, when the responsiveness at the molecular level is properly organized, the nanoscale response can be collectively detected at the macroscale, leading to a responsive material. In the present article, we review the enormous world of responsive polymers, by outlining the main features, characteristics, and responsive mechanisms of smart polymers and by providing a mechanical modeling perspective, both at the molecular as well as at the continuum scale level. We aim at providing a comprehensive overview of the main features and modeling aspects of the most diffused smart polymers. The quantitative mechanical description of active materials plays a key role in their development and use, enabling the design of advanced devices as well as to engineer the materials' microstructure according to the desired functionality.

Introduction

A great interest in smart and responsive materials has emerged in recent years. The materials' capability to develop autonomous functions or to provide a desired response to external actions has been recognized to be of paramount importance for the development of active devices, sensors, and actuators to be applied in advanced fields, especially those devoted to small-scale applications (Roy et al., 2010; Stuart et al., 2010; Wei et al., 2017). A commonly adopted strategy to obtain smart devices consists of harnessing a proper arrangement of several elements into a predefined pattern (metamaterials), in order to provide the assembly with the desired mechanical functionality (Grima et al., 2013; Jackson et al., 2018). The quest for smaller and smaller systems and devices to be employed in advanced technological applications has pushed forward research efforts in this direction. However, the metamaterials approach suffers from dimensional limitations. Indeed, although modern 3D printing technologies enable the fabrication of microscale size devices, they do not extend to the nano and molecular scales. This drawback can be overcome by using responsive-molecules–based materials, namely polymers (Flory, 1953), where the desired response and functionality are achieved by the collective actuation of the embedded smart molecules. Today, in modern material science, the use of a multidisciplinary approach—involving chemistry, physics, and engineering—is an unavoidable requirement to successfully design the desired components, making them suitable for specific applications (Cabane et al., 2012; Shepherd et al., 2013; Manrique-Juarez et al., 2016). Molecular switches, for instance, represent a very promising mechanism to enable the responsive capability of a bulk material via size and shape modification. In this case, responsiveness results from the transition of a molecule from one equilibrium state to another (we talk about bistable molecules or isomers), each state being characterized by distinct but different geometrical or chemical properties. In certain situations, the molecular switch does not require a conformational change of the molecule, but rather a modification in its chemical structure that can be detected at the bulk level. The transition between the two stable conformation states triggered by environmental stimuli (such as temperature, light, electric and/or magnetic fields, chemical agents, mechanical stress, biological agents, etc.) enables the development of molecular-level actuators and materials, regardless of the dimensional requirement of the application (Randolph et al., 2012; Kocak et al., 2017; Milić and Diederich, 2019). Such state of materials are ubiquitous in biology, such as in immunoglobulin (Prigogine and Nicolis, 1971), where the unfolding of molecular segments is triggered by mechanical actions (Marszalek et al., 1999).

Another effective way of obtaining smart materials is the use of liquid crystalline elastomers (LCEs), exhibiting the capability to produce a reversible mechanical actuation triggered by suitable external stimuli, such as heat, light, and electric and magnetic field, thanks to the spontaneous order embedded in their microstructure arrangement (De Gennes and Prost, 1993; Warner and Terentjev, 2007; Jiang et al., 2013; Guin et al., 2018). This property has been used in multiple applications such as artificial muscles and microelectromechanical systems (MEMS) for use in industrial and in medical applications (López-Valdeolivas et al., 2018; Shang et al., 2019). Smart polymers may also rely on a diversity of other mechanisms, which include, for instance stimulus-dependent structural rearrangement (Mayumi et al., 2012), reorganizable dynamic networks (Tanaka and Edwards, 1992), and swelling driven mechanisms typical of gels (Flory, 1950; Agarwal et al., 2019), to name a few. It is also worth mentioning the responsiveness shown by nanocomposite materials, obtained by using particular nanoparticles capable of inducing the desired response to the material in which they are embedded in; Janus nanoparticles (whose surfaces have two distinct physical properties, namely a hydrophobic part and a hydrophilic one) belong to this class of tunable interfacial nanostructures, whose response is allowed by their asymmetric character (Liu et al., 2014; Zhu et al., 2018; Dai et al., 2019). Thanks to their twofold properties the aforementioned nanocomposites have been successfully used in biological sciences, bioimaging, electronics, etc. (Su et al., 2019).

The present work aims to provide a comprehensive overview on different types of active polymers by underlining their application potential, describing the molecular mechanisms enabling their functionalities, as well as discussing current models used to describe their mechanical behavior. We hope this initiative will be useful to anyone who wish to learn and perform research in the design of smart systems and devices, and using the mathematical model to guide the tuning of their properties from a microstructural perspective. The review is organized as follows. Section Responsive Polymers: From Molecular Architecture to Emerging Response first provides a physical description of polymers at different length scales, from molecular to continuum level. Section Polymers With Conformational Instabilities, then discusses the specific class of polymers with embedded responsive molecules, i.e., those whose responsiveness comes from embedded conformational changing molecules. In section Polymers With Changing Topology, we further provide an overview of various classes of polymers with reorganizable microstructure. These include vitrimers, slide-ring gels, and liquid crystal elastomers. Section Swelling-Driven Response of Gels, finally focuses on hydrogels, in which the polymer network is able to absorb large amounts of solvent, hence triggering significant volume change (Masao, 2009). This mechanism represents an important way to get a smart response, such as in the case of temperature-dependent hydrogel swelling. Section Conclusions, concludes the review by providing closing remarks and future research perspectives in this advanced field of material science.

Responsive Polymers: From Molecular Architecture to Emerging Response

Responsive polymers belong to the class of smart materials capable of producing detectable responses under the effects of external stimuli. When properly understood and quantified, such a molecular-scale response can be conveniently exploited in various ways to obtain responsiveness at the meso- and macroscale. The response of active polymers usually consists of nanoscale changes (molecular bond rearrangement/cleavage, molecular motion, morphology change, etc.) that can induce observable changes at greater scales, such as color and/or shape changes or changes in physical properties, that can be exploited to achieve desired functionalities. Since responsiveness comes from their molecular architectures, the arrangements of polymer chains, and the nature of embedded active molecules, stimuli-responsive polymers can be tailored to have stimulus-specific chemical, physical (electrical, optical), and mechanical responses and can be engineered into different forms (thin films, micro/nanoparticles, composites, to name a few).

Molecular Mechanism in Active Polymer

In general, responsive polymers can be classified into two categories (Stuart et al., 2010; Gruhn and Emmerich, 2013): (1) covalently cross-linked polymer network that swell or shrink under a stimulus; and (2) dynamic polymer networks with a variable topology, in which cross-links or chemical bonds can be broken and formed by external stimuli. In the first category, the volume of these polymer networks can be dramatically changed by changing the pH or the chemical compositions of the solvent. Such a behavior can be understood from a multiphase mixture model, by decomposing the system into two or more phases. For instance, a pH-responsive hydrogel can be decomposed into an incompressible polymer network phase and an incompressible fluid phase. Their molecular structures can be understood by minimizing the free energy of the whole system (Nap et al., 2006), including the interaction and entropy of polymer chains, the entropy of solvent and ions in the hydrogel, the Coulomb interactions and mixing energy of polymer chains, solvent, and ions.

In the second category, the most important aspect is the network's ability to reform broken bonds and rearrange its molecular structures in a completely different topology and shape (Cho et al., 2009). During this process, the association and dissociation of dynamic bonds, as well as the diffusion of polymer chains, play the most important roles. By understanding the reaction kinetics of dynamic bonds and movement of polymer chains, it is possible to build molecular theories to relate the molecular structure to the network's mechanical behaviors (Stukalin et al., 2013). However, because of the limitations of current experimental techniques, it is still not feasible to track the molecular structure of these dynamic polymers as they deform. Molecular dynamics (MD) simulations have thus provided a useful alternative approach to understand the evolution of their internal structure and the associated molecular mechanisms.

In MD simulations, the positions and velocities of atoms and molecules can be directly obtained through the equations of motion that depend on the external and interatomic forces. This simulation tool therefore allows us to directly investigate the dynamic properties and molecular structures of stimuli-responsive polymers. Similar simulation techniques include Brownian dynamic simulations, dissipative particle dynamics (DPD) simulations, Monte Carlo simulations, and coarse-grained MD simulations. Through MD simulations, very detailed information about stimuli-responsive polymers can be obtained (Chen et al., 2019), such as the swelling behaviors of polymer networks, break and formation of dynamic bonds, changes of polymer configurations and networks, and elastic and inelastic response of polymer networks under applied strains. All of these simulations results not only help to interpret experimental observations, but also support molecular and macroscopic models. In the following sections, we will discuss current progress in MD simulations of stimuli-responsive polymers. We should emphasize that because of the limitation of the space and scope of this work, we do not separate different MD simulation techniques, such as all-atom MD and DPD simulations.

Bridging Mechanisms and Emerging Response: Continuum Mechanics

The mechanical response of a polymer originates from the elastic energy stored in the network chains due to deformation. This energy originates from the entropy of the chain's conformations measured by the end-to-end vector r between the chain's head and tail (following Gaussian or Langevin statistics). The key idea is thus to represent the physical state of a polymer network via the statistical distribution ϕ(r, t) of the chain according to their end-to-end vector (Figure 1). Indeed, if this distribution is known at any time, the deformation energy stored in the network can be evaluated by the integral $\text{Ψ}={\int }_r\varphi (r,t)\psi (r)dr$, with ψ being the energy per single chain. This equation states that the total mechanical energy stored in the network is the sum of the energies stored in each chain.

FIGURE 1

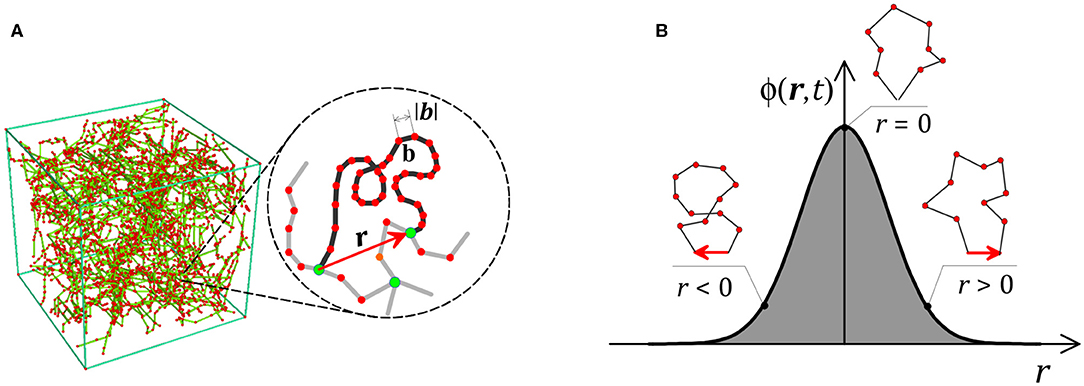
Figure 1. (A) Cross-linked polymer network and illustration of the end-to-end vector r of a single chain. The chain is assumed to consist of N Kuhn segments with length b. (B) Statistically, the chain population can be described by the distribution ϕ(r, t), for which we show a schematic example in one dimension.

The knowledge of the chain distribution provides the connection between the network structure and macroscopic quantities such as the stress, the stored elastic energy, and the average chain conformation (Vernerey et al., 2017). It is indeed possible, by enforcing the second principle of thermodynamics, to determine the stress tensor, and the average configuration of the chains via the determination of specific moments of the distribution as

$\begin{array}{ll}\sigma =\frac{1}{c}{\displaystyle {\int }_r}\varphi \frac{\partial \psi }{\partial r}\otimes rdr\text{ and }\mu =\frac{1}{c}{\displaystyle {\int }_r}\varphi r\otimes rdr,& (1)\end{array}$

where c is the chain concentration, ∂ψ/∂r is interpreted as the force in each chain, and ⊗ is the dyadic product. We note here that the tensor μ provides a description of both the average end-to-end vector (related to the trace of μ) and the average stretch directions (principal directions of μ). Furthermore, this distribution evolves in time due to chain stretch, inelastic dynamics (e.g., bond dynamic association and dissociation), or changes in molecular conformations. As a result, these relations are able to connect the molecular mechanisms and stimulus-sensitivity of a polymer to its macroscopic response, including elasticity, stress-relaxation, or self-healing. The evolution of the tensor μ under the aforementioned effects enables the determination of the deformation and the stress state in the polymer. The foregoing micromechanics model is suitable to be upscaled to the continuum level, through the homogenization of the pointwise mechanical state provided by the actual configuration of the polymer network chains. In the next sections, we will discuss the form of the distribution ϕ(r, t) based on the stimulus-sensitive molecular mechanisms, chain deformation, and dynamics. This will be done in the context of the various polymer systems listed in Table 1, so that the link between molecular mechanisms and macroscopic response becomes apparent. Table 1 summarizes the main class of responsive polymers that will be considered in the following.

TABLE 1

Table 1. Scheme of the main existing responsive polymers and their actuation mechanisms.

Polymers With Conformational Instabilities

Mechanically induced conformational change in molecules falls within so-called mechanochemistry, whose main principle is the application of a mechanical force to drive chemical reactions (Brantley et al., 2013). This technology is today used to activate molecules in materials; however, polymer mechanochemistry has not yet been adopted in industry despite the fact that laboratory-based tests have demonstrated its potentialities not achievable by traditional activation methods. This approach enables attainment of smart materials to be used in drug delivery, sensors, actuators, green applications, etc. Polymers containing active units (responsive molecules), i.e., whose collective activation provides a detectable response at the meso- or at the macroscale level, are considered. The so-called mechanophores, i.e., mechanically sensitive chemical groups built into the chemical structure of the polymer, are considered first; they usually have photochromic properties, since on mechanical stress the chemical structure of the molecule changes and so a different color light is emitted (Brown and Craig, 2015). However, other kinds of groups exist whose mechanical sensibility manifests through a geometric conformational change (Milić and Diederich, 2019).

Conformational Changing Molecules

The chemical to mechanical energy transformation is a well-known phenomenon of everyday life; however, the reverse transformation, termed mechanochemistry, allows attainment of chemical transformations through mechanical forces. Within this context, the so-called mechanophores, whose bonds or chemical functionalities are susceptible to undergoing a chemical change caused by mechanical stress, provide relevant potentialities. Mechanical stress-sensible molecules, when placed into a polymeric network, make it possible to obtain an interesting responsiveness of the polymer itself; polymeric materials whose actuation can be triggered by a mechanical stress are usually obtained by linking to the polymer network particular molecules (mechanophores) whose chemical structure or conformation (isomers) can be changed on the application of a mechanical force (Figure 2) (Caruso et al., 2009). Among the various existing compounds, spiropyran-based polymers are of particular interest since their photochromism capability—i.e., the change in the emitted light wavelength (among the mechanochromic mechanophores it is worth mentioning also diarylbibenzofuranone [DABBF], tetraarylsuccinonitrile [TASN], diarylbibenzothiophenonyl [DABBT])—enables associating the color of the emitted light to the mechanical energy transferred to the material (Klajn, 2014; Li et al., 2017). Thanks to the quantitative measurement of the amount of mechanophore activation, stress, or strain self-sensing polymers can be obtained (Früh et al., 2017). Among the wide range of applications allowed by the mechanochemistry, mechanophores have been used also for inducing self-healing capabilities in polymers (Diesendruck and Moore, 2013).

FIGURE 2

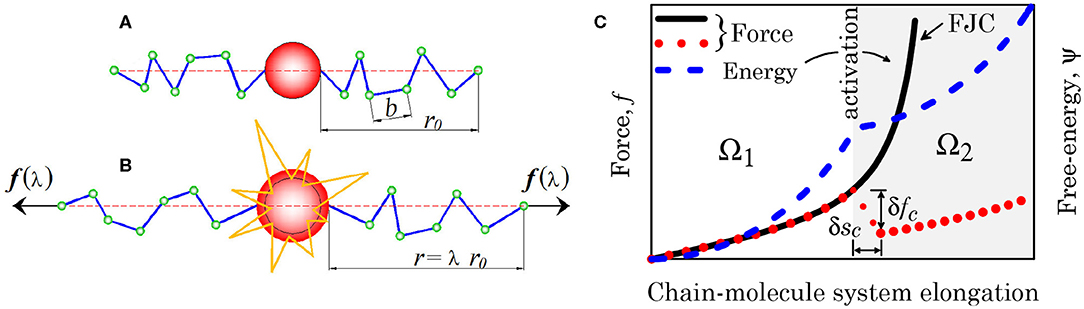
Figure 2. (A,B) Scheme of a mechanophore unit activated on mechanical force reaching the activation threshold. (C) Chain force- and energy-elongation diagrams in the presence of molecule activation.

Modeling Aspects

Mechanophore-containing polymers have been recently studied from the mechanics viewpoint in order to provide a quantitative description of their response to external stimuli (Silberstein et al., 2013, 2014; Wang et al., 2015; Takaffoli et al., 2016). In general, when dealing with a system characterized by two different stable configurational states, namely s₁ and s₂, the dynamic equilibrium quantifying how much the equilibrium of the system is closer to the state s₁ or to the state s₂ is provided by a differential equation of the form (Brighenti et al., 2018, 2019)

$\begin{array}{ll}\frac{d{\varrho }_{s_2}}{dt}=k_A{\varrho }_{s_1}-k_D{\varrho }_{s_2},& (2)\end{array}$

where ϱ_s1 and ϱ_s2 are the volume fractions of the material being in states s₁ and s₂, respectively (ϱ_s1 + ϱ_s2 = 1), while k_A, k_D are the activation and deactivation rates whose values are related to the energy barrier separating the two aforementioned states. Typically, these rates are related to the forward (ΔG_A0) and backward (ΔG_D0) energy barriers through the standard Arrhenius law, $k_A=C_A·exp\left(-\frac{\Delta G_{A0}}{k_{B}T}\right)$, $k_D=C_D·exp\left(-\frac{\Delta G_{D0}}{k_{B}T}\right),$ with C_A, C_D the frequency factors (Hänggi et al., 1990). This approach becomes useful for describing polymers whose functionality comes from active molecules or compounds, characterized by two or more states, embedded, and linked to the polymer network. In other cases, the functionality comes from a rearrangement of their backbone network or from a predefined organization of the polymer's chains, whose orientation characteristics the material may have memory.

Figure 2A schematically illustrates the occurrence of the molecule switching from one conformation to another triggered by a mechanical force, while Figure 2B provides the mechanical landscape emerging when a polymer chain contains a responsive molecule whose conformation changes upon a sufficient value of the force, leading to an expansion of the molecule; the chain force changes abruptly (by the amount δf_c) at the occurrence of the molecule conformation change by the amount δs_c (red dotted line), while the continuous black line corresponds to the standard polymer chain response [Freely Jointed Chain (FJC) model]. From the energetic viewpoint the molecule activation entails an energy vs. system deformation that is not convex any longer, indicating the occurrence of a local instability phenomenon. The mechanical effect played by the molecules activation can be easily accounted for in the expression of the deformation energy of the unit volume of the polymer; the energy difference between the initial stress-free state and the current one is expressed as

$\begin{array}{ll}\Delta \text{Ψ}={\displaystyle {\int }_r}(\varphi (r,t)-{\varphi }_0)\left[(1-{\varrho }_{s_2})\psi (r)+{\varrho }_{s_2}{\psi }_c\right]dr,& (3)\end{array}$

where ψ_c = δf_c · δs_c is the energy associated with the molecule's activation (usually negligible with respect to the deformation energy of the network). The stress state is thus provided by the expression

$\begin{array}{ll}\sigma =J^{-1}P{F}^T=\frac{\partial \Delta \text{Ψ}}{\partial F}{F}^T\cong \frac{1}{c}{\displaystyle {\int }_r}(1-{\varrho }_{s_2})\varphi \frac{\partial \psi (r)}{\partial r}\otimes rdr,& (4)\end{array}$

where it was assumed that the polymer fulfills the incompressibility condition, mathematically expressed by J = detF = 1, while F = ∂x/∂X is the deformation gradient tensor, with X, x being the position vector in the reference and in the current configuration, respectively. We note that Equation (4) is macroscopically equivalent to the stress appearing in Equation (1).

Polymers With Changing Topology

Polymers with network rearrangement capabilities have the unique properties to reorganize their chains structure in time, so leading to a continuous relaxation of their microstructure that spontaneously tends to return to the reference stress-free state (Tanaka and Edwards, 1992). A class of gels with structural rearrangement capability (slide-ring gels) coming from their movable cross-links properties (Kato et al., 2013) also belong to such a group of responsive polymers.

pH-Responsive Polymers

pH-responsive polymers can change their configurations and properties with pH variation in the solution, as illustrated in Figure 3A. Usually, these materials contain ionizable functional groups that can donate or accept protons due to the environmental pH change, presented in Figure 3B. The typical ionizable groups are weak acids and weak bases such as carboxylic acids, phosphoric acid, and amines, which can be characterized by the acid dissociation constant (pK_a) or base dissociation constant (pK_b).

FIGURE 3

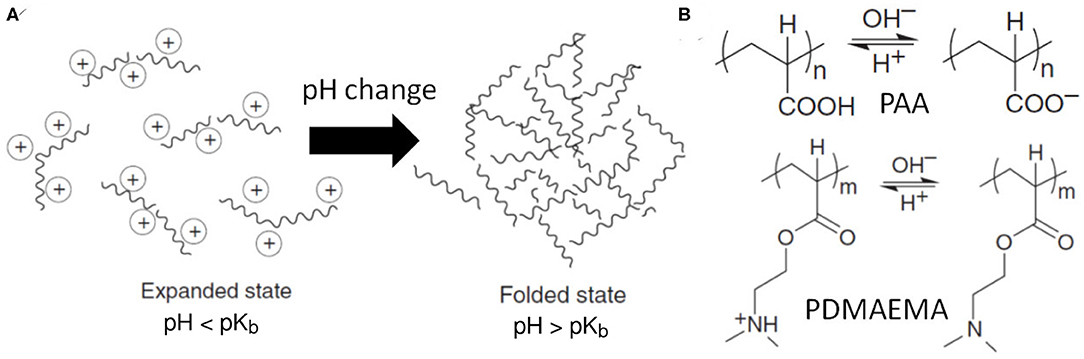
Figure 3. (A) Schematic of a pH-responsive polymer with conformation change from expanded state to folded state under pH change, depending on the ionization of the ionic chain groups. (B) Chemical structures of pH-responsive polymers with ionizable functional groups: poly(acrylic acid) (PAA) and poly(N, N-dimethylaminoethyl methacrylate) (PDMAEMA).

For example, poly(acrylic acid) (PAA) has a dissociation constant pK_a = 4.25 and above the pH value 4.25, its carboxylic group becomes ionized by denoting protons. It leads to electrostatic repulsions between polymer chains, which can then associate with water molecules for swelling. The physical properties of pH-responsive polymers, such as chain conformation, configuration, solubility, and volume, could be tailored by manipulating the charges along the backbone of polymer chains or electrolyte concentration, resulting in electrostatic repulsion forces to increase the hydrodynamic volumes of polymer chains. The transition between tightly coiled and expanded conformations can be influenced by any condition that changes the electrostatic repulsion, such as pH value, ionic strength, salt concentration, and type of counterions. The transition from collapsed state to expanded state of these polyelectrolyte chains has been explained by the change of osmotic pressure exerted by mobile counterions neutralizing the network charges (Tagliazucchi et al., 2010). Through all-atom MD simulations, Cranford et al. (2010) have studied the tunable adhesion properties of a polyelectrolyte complex consisting of PAA and poly(allylamine hydrochloride) (PAH) under different strain rates and pH values. The percent ionization of each constituent polymer has been systematically varied according to the pH range of 2.5–10 and pK_a values of carboxylate and ammonium groups in PAA and PAH, respectively. The adhesion strength is found to vary from 8 to 45 nN due to different electrostatic interactions, displaying the potential application of tunable, and mechanomutable polyelectrolyte PAA/PAH complex. In addition to adhesive strength, these pH-responsive polymers can change from a collapsed conformation to a stretched one due to the solvent pH change (Katiyar and Jha, 2017). Such a behavior can be utilized to control the transport behaviors of nanoscale fluidic channels and solid-state nanopores, as revealed by DPD simulations and theoretical studies (Tagliazucchi and Igal, 2015; Wang et al., 2018).

These pH-responsive polymers have been widely used in different fields, such as drug delivery systems, biosensors, antifouling coatings, super-hydrophilic surfaces, biomimetic membranes, and many others. To understand their conformation change under different pH environments, the mesoscale simulation technique DPD has been widely adopted. For e.g., the self-assembly process of amphiphilic copolymers (PAE-g-PEG) into vesicles, and their drug loading/release of doxorubicin drug molecules at different pH environments, have been extensively studied through MD and DPD simulations (Luo and Jianwen, 2012; Luo et al., 2016). Note that in these MD and DPD simulations, the polymers have fixed charges according to the pH condition, which ignores the charge fluctuation in reality. Nevertheless, these molecular simulation results provide quantitative understanding of the controlled drug release behaviors of pH-responsive polymers on the molecular scale.

Dynamic Network Reorganization (Vitrimers, Ionic Polymers, and Others)

The term “dynamic polymer network” refers to the class of network whose chains are not covalently bonded to the cross-links. Instead, these bonds are able to dissociate and reassociate in time under external stimuli or thermal fluctuation. Some examples of these bonds are covalently adaptable bonds (Bowman and Kloxin, 2012) or physical bonds such as hydrogen bonds and ionic interactions (Luo et al., 2014). These materials are of particular interest in several applications such as in renewable materials, self-healing, or materials with high energy dissipation. The dynamic nature of their microstructure comes from the weak nature of the bonds, such as the ionic ones, existing in some polymers (the Brownian motion induced by thermal fluctuations enables the bond exchange to occur) or can also take place in covalently bonded polymers (Leibler et al., 1991; Wojtecki et al., 2011; Jin et al., 2013; Kloxin and Bowman, 2013; Meng and Terentjev, 2018). In particular, the so-called vitrimers—a class of polymers derived from thermosetting polymers consisting of molecular covalent networks—are capable of changing their topology by thermally activated bond-exchange reactions (Capelot et al., 2012; Tellers et al., 2019). At sufficiently high temperatures they flow like viscoelastic liquids, while at low temperatures the bond-exchange reactions rate slow down, leading to a classical thermoset. Vitrimers are strong glass formers; their behavior opens new possibilities in the application of thermosets such as self-healing or simple processability in a wide temperature range.

MD Simulations of Covalent Adaptable Polymer Network

Covalent adaptable polymer networks can change their network connections through bond exchange reactions. The bond exchange reaction is usually triggered by an active unit attached to an existing bond, by kicking off its preexisting peer to form a new bond. During mechanical deformation, the bond exchange events can lead to stress relaxation and plastic deformation of the polymer network. In addition, the fractured polymer network can repair itself through the bond exchange reactions across the fractured interface. To understand the molecular structures of these covalent adaptable polymer networks and their relationship to macroscopic mechanical behaviors, Yang et al. (2015) have developed a coarse-grained MD model to study the bond exchange reactions of epoxy polymers. A numerical algorithm has been proposed for the bond exchange reactions and used to study the cross-linked network formed by epoxy resin bisphenol A diglycidyl ether (DGEBA) and tricarballylic acid curing agent. After each iteration of bond exchange reactions, the polymer network properties, such as the distance between two neighboring cross-link sites, have been analyzed to understand the evolution of molecular structures and mechanical behaviors. The MD simulation results reveal that the bond exchange reactions not only change the macroscopic shape of the polymer network, but also relax the microscopic network characteristic features back to the unstretched isotropic state. Such a simulation scheme can also be used to study the interfacial self-healing behaviors of dynamic polymer networks (Stukalin et al., 2013). For e.g., coarse-grained MD models have been recently developed to study the change of polymer networks under the influence of reversible bonds (Amin et al., 2016; Wu et al., 2019). The reversible bonds can be formed due to the dynamic covalent bonds, hydrogen bonds, metal–ligand coordination, and ionic interactions. In these coarse-grained models, the association and dissociation of reversible bonds are usually controlled by a Monte Carlo step with different energy barriers. These coarse-grained MD models can be used to further understanding of polymer chain dynamics, network change, as well as the mechanical response of the dynamic/transient polymer network on the molecular scale.

Continuum Model of a Transient Polymer Network

The distribution function ϕ(r, t) of the chains of transient polymers typically evolves over time due to attachment/detachment events. It is usually considered that a connected chain can dissociate at any configuration, but a free chain can reassociate only at the stress-free configuration (Vernerey et al., 2017). Therefore, the stored elastic energy is dissipated through a dissociation–association cycle. To quantify these dynamic events, let us define the rate of bond association as k_a and the rate of dissociation as k_d.

Due to the interplay between chain and dynamics, the evolution of the chain distribution function is determined by the following equation (Vernerey et al., 2017):

$\begin{array}{ll}\underset{\left(a\right)}{\underbrace{\frac{\partial \varphi \left(\mathit{r},t\right)}{\partial t}}}=-\underset{\left(b\right)}{\underbrace{\left(\frac{\partial \varphi \left(\mathit{r},t\right)}{\partial \mathit{r}}\otimes r\right):\mathit{L}}}+\underset{\left(c\right)}{\underbrace{k_d{\varphi }_0\left(\mathit{r}\right)}}-\underset{\left(d\right)}{\underbrace{k_d(r)\varphi \left(r,t\right)}},& (5)\end{array}$

As represented in Figure 4, this equation states that changes in the chain population (term a) are driven by the distortion of chains due to the application of a macroscopic deformation, represented by the velocity gradient L = ∂v/∂x (term b, with v the velocity vector), the attachment (at rate k_a) of new chains in a stress-free configuration, represented by the distribution ϕ₀(r) (term c), and the detachment (at rate k_d) of chains in their current configuration, represented by the distribution ϕ(r) (term d). A few important comments can be made regarding this equation: (1) this equation takes into account that chains attach in their relaxed (or stress-free) state while they detach in their current, stretched configuration. This feature is responsible for the stress-relaxation of the polymer over time (Vernerey, 2018). In addition, when bond dynamics are eliminated (k_a = k_d = 0), (Equation 5) degenerates to the evolution of an elastic network. (2) The rates k_a and k_d are understood in terms of the inverse of the average lifetime of a chain in its detached and attached states, respectively. (3) This equation, which closely resembles the Boltzmann equation in gas dynamics (Villani, 2002), has deep implications regarding the network evolution resulting from deformation and kinetics of attachment and detachment events (k_a and k_d).

FIGURE 4

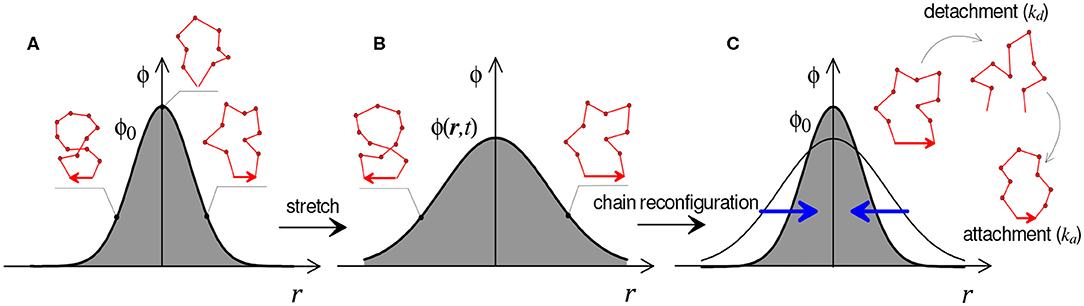
Figure 4. Graphical illustration of Equation (5) for the evolution of chain distribution function ϕ(r, t). Distribution of the chains configuration in the undeformed (A), stretched (B), and relaxed state (C).

Slide-Ring Gels: A Topological Gel With Slidable Cross-Links

Gels with high mechanical properties have found a large interest in biomedical applications. In particular, high toughness is a desirable property obtained in gels by harnessing the presence of sacrificial species enabling dissipation of energy; however, weak sacrificial chains reduce the resistance to cyclic loading (fatigue). Polymer gels are characterized by a network structure made of long entangled chains reciprocally joined at several sites termed cross-links imbibed by a fluid; an outstanding change in the mechanical properties of polymers has been obtained by making the cross-link move freely along the chains. Such a gel having movable cross-links has been obtained by adopting polyrotaxane chains cross-linked by coupling the α-cyclodextrin (CD) rings, which allows the cross-links to slide over a long distance along the network chains (Figure 5) (Karino et al., 2006).

FIGURE 5

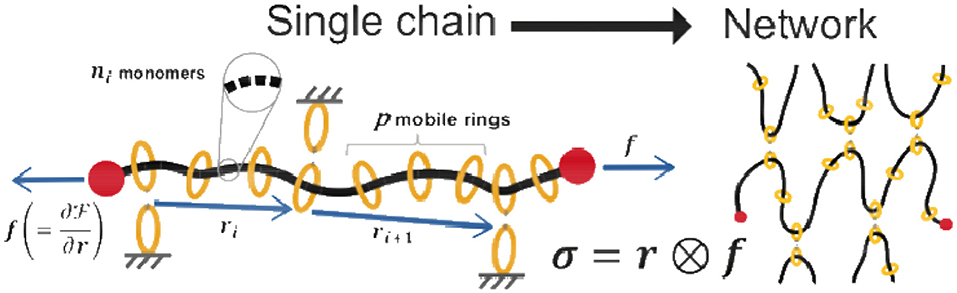
Figure 5. A chain of polyrotaxane with visual representations of the parameters used in Equation (6). The chains are cross-linked via threaded rings along the chain to form a slide-ring network. By understanding the response of a single chain, the response of a network can be achieved by statistical averaging.

This capability, from a mechanical standpoint, makes it possible to avoid the stress concentration taking place in the shortest chains—as typically occurs in standard polymers—that more easily reach their maximum extension (related to the number of Kuhn's segments per chain N and their length b as ${\lambda }_{max}=b\sqrt{N}$) and consequently fail. On the other hand, when the network possesses movable ring connections, the polymer chains can freely move through the cross-link sites, allowing the tension induced by external stress to be evenly distributed throughout the whole material (Kato et al., 2013; Jiang et al., 2018). From the mechanical viewpoint, the cross-link sites behave as a pulley, and thus the cooperative work is referred to as a pulley effect. This feature allows design of gels with unprecedented properties, such as high fracture resistance, thanks to the capability of the network to remain intact under large deformation (Liu et al., 2017).

Modeling of Slide-Ring Gels

The 2016 Nobel Prize in Chemistry (Stoddart, 2017) recognized “the design and synthesis of molecular machines,” an emerging class of synthetic molecules that can be actuated to perform mechanical work on the nanoscale. This objective is rarely achieved, however, because of challenges associated with coupling and/or scaling the directed motions of artificial molecular machines to produce a macroscopically observable response (Coskun et al., 2012). One of the most widely employed architectures for artificial molecular machines is that of a rotaxane (Bruns and Stoddart, 2016), in which one or more molecular “beads” is threaded and trapped on a molecular “string.” Because they are not chemically bonded, the molecular beads and strings can slide with respect to each other. A promising family of polyrotaxanes in which many α-cyclodextrin beads are threaded onto a polyethylene glycol (PEG) string was recently used to create a topological gel (Okumura and Ito, 2001). After polyrotaxane is synthesized, the beads are cross-linked between chains to form a slide-ring network. A pulley effect (Ito, 2007) was discovered by observing the gel's scattering patterns: homogeneity after deformation implied that the strings were able to redistribute stress evenly throughout the material using their slidable cross-links. Further experiments on slide-ring gels have elucidated their many desirable properties including high extensibility, scratch resistance, and toughness (Noda et al., 2014).

Even more interesting, the properties of slide-ring networks are highly reliant on the chemical makeup of a single chain. Typical cross-linked networks become stiffer with increasing cross-linking concentration, but one group (Mayumi et al., 2012) found that slide-ring gels start to become softer after the cross-linking concentration reaches around 3% (per unit volume). The group attributed this to the uncross-linked, mobile, rings that are left on the chains after cross-linking (Kato et al., 2015). Indeed, a novel entropy sources from these mobile rings—they have one degree of freedom (along the chain), which results in a finite permutation space defined by the contour length of the segment on which they are threaded—can be recognized. This can be thought of as a sort of built-up one-dimensional pressure between segments. Thus, a polyrotaxane chain has both an elastic and inelastic response, supported by rheological data. The elastic response arises from the classical entropic elasticity of polymer chains, which is captured in the first term of a free energy potential (describing the energy landscape and equilibrium of the chain):

$\begin{array}{ll}F={\displaystyle \underset{\text{Elastic Entropy},\psi }{{\displaystyle \underbrace{\frac{3kT}{2}\left[\sum \frac{{\displaystyle r_i^2}}{n_i{b}^2}\right]}}}}+{\displaystyle \underset{\text{Mobile Ring Entropy}}{{\displaystyle \underbrace{kT\left[\sum \frac{3-2p}{2}\text{ log }{n}_i-kT\rho \text{ log }{n}_e\right]}}}}& (6)\end{array}$

All parameters used in this expression are depicted schematically in Figure 5. In contrast with covalently cross-linked networks, the viscoelastic properties of polyrotaxane are associated with relaxation mechanisms arising from the sliding of monomers through the ring-like cross-links. With the parameters included in this free energy, the underlying physics governing a single chain can be used to understand the response of the gel using statistical averaging.

There is a promising hope for the development of smart materials and molecular motors using rotaxanes (Goujon et al., 2017). Indeed, mechanically interlocked molecules, such as rotaxanes, have a high potential for use as molecular machines. As they possess molecular components that restrict motion only along certain directions, it is possible to use them as small rotors or walkers, in analogy with the myosin heads found in biological muscles. While there is no clear answer to accomplish macroscopic work, experimental studies have shown promising directions. Scaling up of mechanical work was indeed observed in photodriven molecular rotors embedded in liquid crystal films, in monolayers of photosensitive rotaxane molecules, moving tiny droplets (Berná et al., 2005), and in LCEs for translating mechanical objects (Ikeda et al., 2007). Theoretical work on these materials is, however, still in its infancy, and the connection between the aforementioned mechanisms and the mechanical response is still to be discovered.

LCE-Based Responsive Polymers

Liquid crystals are composed of elongated rigid molecules (nematic mesogens) whose preferential orientation in space is retained (Oseen, 1933; Frank, 1958; Ericksen, 1961; Stephen and Straley, 1974; Warner and Terentjev, 2007). When embedded in a highly deformable network, they provide to the elastomer their own orientational character and the resulting material is typically identified as a liquid crystal elastomer (LCE). Such a preferential chains orientation allows exceptionally large responses to external stimuli, suitable to be exploited in a variety of applications. Within the field of responsive polymers, LCEs are of great interest because they show both the properties of a fluid and of a solid. LCEs are made of an entropically dominated rubbery network that furthermore possesses the typical order of a liquid crystal. LCEs show a large spontaneous deformation (up to 300–400% with respect to the reference configuration) when a phase transformation, from the isotropic to the nematic state, is induced by a proper stimulus. The preferential orientation of the LCEs can be easily manipulated by applying environmental stimuli, such as heat, electric/magnetic fields, or UV or visible light (Stephen and Straley, 1974), enabling a reversible response exploitable for soft actuation or sensing (Ohm et al., 2012). The change of the LCE order can induce a macroscopic change in shape, volume, etc. suitable to be harnessed for actuation purposes; LCEs can be used in several applications, ranging from artificial muscles and soft robots to deployable structures, tunable mirrors, morphing structures, stimuli-responsive surfaces, and robotic matter, to name a few (White and Broer, 2015). Their modeling requires describing the preferential orientation of the chains network and how it evolves in the material as a consequence of external actions of various natures (Warner and Terentjev, 1996; Finkelmann et al., 2001; Yakacki et al., 2015; McBride et al., 2018; Ula et al., 2018).

MD Simulations of LCE

Under light irradiation, photoresponsive LCE polymers can demonstrate conformation transition, molecular polarity, and color change. These photoresponsive polymers usually contain azobenzene, spiropyran, stilbene, and other light-responsive trigger molecules. To understand the molecular mechanisms of these photoresponsive polymers, Choi et al. (2014) have employed the MD simulations to study the structure and optomechanical behaviors of azobenzene LCE polymers. A switchable potential formalism for the N=N bond of azobenzene molecules is applied to capture the photo-switching behaviors, trans to cis and cis to trans isomerization. The influences of the isomerization ratio of these azobenzene molecules on the photostrain, elastic property, and thermal nematic–isotropic phase transition have been systematically explored. The simulation results show that the stiffness and melting temperature of these photoresponsive nematic polymer networks (PRPNs) decrease with the increment of isomerization ratio. In addition, the orientation and conformation of these PRPN can be significantly affected by the isomerization of azobenzene molecules. Very recently, they have further developed a coarse-grained MD model to study the light-induced sequential smectic–nematic–isotropic phase transition of cross-linked LCE polymers (Clarke et al., 2001; Moon et al., 2019). The overall shape of polymer network is found to be affected by the corruptions of the smectic layer and nematic orientational order. In addition to these chemistry-specific MD models, Skačej and Zannoni have developed a generic coarse-grained MD model for LCEs under electric field actuation (Skačej and Zannoni, 2011, 2012). In this model, a soft-core Gay–Berner molecular model has been adopted to represent the liquid crystal structure of polymers, which also enables the smectic–nematic and nematic–isotropic phase transitions. Through this coarse-grained model, two modes of electromechanical actuation for LCEs have been observed: (1) a transversal “semisoft” mode with director rotation resulting in orientational stripe domains of liquid crystals; and (2) a switch mode between the orientationally disordered isotropic and the aligned nematic phases.

Mechanical Aspects of LCE

LCEs store energy when deformed because of restrictions in the entropic configurations of the polymer chains (Warner and Terentjev, 1996). However, due to the orientation of the rods in these chains, they are anisotropic elastomers; i.e., the mechanical properties are dependent on the orientation order and direction (Finkelmann et al., 2001). Using concepts from statistical mechanics, the neo-classical theory describes the end-to-end vectors r of the polymer chains using an anisotropic Gaussian distribution whose directionality is characterized by the so-called step-length tensor l that represents the covariance matrix (Warner and Terentjev, 2007). The free energy of the cross-linked network can then be calculated from the entropy of the chain configurations to arrive at the Trace formula for energy density:

$\begin{array}{ll}{E}=\frac{{\mu }_s}{2}Tr\left(l^{-1}F{l}_0{F}^T\right),& (7)\end{array}$

where μ_s = ck_BT is the shear modulus of the rubbery network, and l₀ is the initial step-length tensor before deformation. Due to the coupling between the orientational order and elasticity of the chains, changes in the nematic order Q can induce deformation to several 100 percent (White and Broer, 2015) (Figure 6).

FIGURE 6

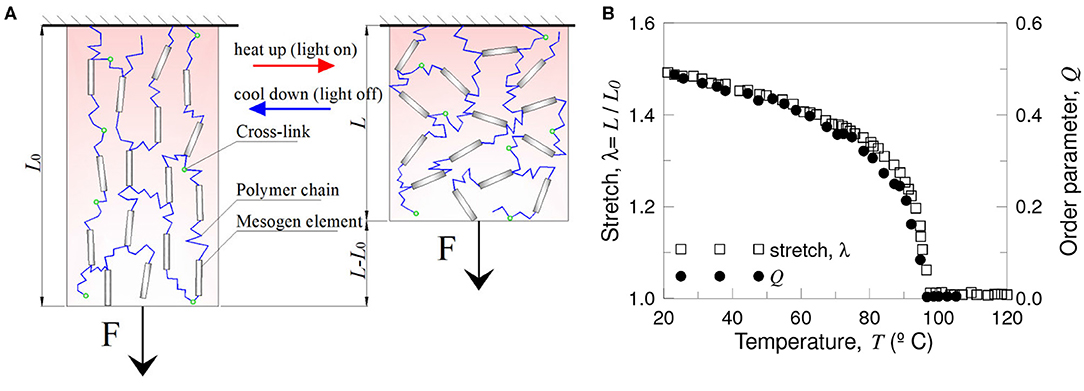
Figure 6. Thermal actuation of main chain liquid crystal elastomers to achieve work. A critical temperature produces a phase transition from nematic to isotropic state and vice-versa resulting in contraction/extension. Scheme of the network configuration in the nematic (A) and isotropic state (B). Stretch and order parameter vs. temperature (C) (figure adapted from Clarke et al., 2001).

The tensor μ, introduced in section Bridging Mechanisms and Emerging Response: Continuum Mechanics, describes the chains stretch in the 3D space and so it is related to the order parameter Q of the LCE because it represents the conformation of the chains within the network. By considering the tensor μ written in its principal directions frame of reference (μ_p) in which it assumes a diagonal form, it can be expressed as follows:

$\begin{array}{ll}{\mu }_p=\left[\begin{array}{ccc}1-Q& 0& 0\\ 0& 1-Q& 0\\ 0& 0& 1+2Q\\ \end{array}\right],& (8)\end{array}$

where it has been assumed that the nematic alignment is along the z-direction. The nematic order Q of the LCE is defined as $Q=\langle \frac{3}{2}co{s}^2\theta -\frac{1}{2}\rangle$, where θ is the angle formed by the molecular axes and their average alignment direction; in other words, it quantifies the degree of alignment of the molecular axes of the mesogens constituting the liquid crystal phase of the elastomer. The value Q = 1 indicates a perfect nematic order in which all the rods are perfectly aligned along the z-direction, while the value Q = 0 refers for randomly oriented rods, i.e., a perfectly isotropic chain arrangement. On the other hand, when 0 < Q < 1 the rods are nearly aligned with the z-axis but with an increasing dispersion whose intensity increases as Q → 0. The so-called nematic order tensor Q [or de Gennes order tensor (Warner and Terentjev, 2007)] represents the deviatoric part of the tensor μ, defined as $Q=\frac{3}{2}\left(\frac{\mu }{N{b}^2}-\frac{I}{3}\right)$ (Finkelmann et al., 2001; Warner and Terentjev, 2007).

LCEs today are designed to have the ability to produce large deformations as a response to changes in orientational order through stimuli such as heat or light (White and Broer, 2015). This has made them prime candidates for technological applications including soft robotics, artificial muscles, biomedical devices, actuators, and sensors (Ula et al., 2018). One of the key features that make reversible shape change possible in these applications is the isotropic–nematic phase transition phenomena. To achieve programmed changes in shape, the rods are first aligned permanently in their gelled state by either applying an external field (such as magnetic or electric), surface anchoring, or stretching during the polymerization stage before a second stage of cross-linking. In recent years, there has been a considerable amount of research into dynamic cross-linking reactions induced by heat or light that offer a new way to design and program LCEs (Yakacki et al., 2015; McBride et al., 2018). With a strong theoretical modeling framework, these novel materials can transform the fields of soft robotics, 3D printing, and photolithography, to name a few.

Swelling-Driven Response of GELS

Some polymers, namely gels, have the ability to make a fluid easily migrate inside their network; the fluid does not induce any modification on the material microstructure or any chemical reaction, but simply makes the polymer swell or shrink according to the in- or outflow motion of the fluid. In these problems the fluid mass transport and the network deformation are coupled phenomena (Tanaka and Fillmore, 1979; Chirani et al., 2015). Gels have been employed also for developing smart and responsive materials to be used in flexible electronics, actuation, and soft robotics (Shen et al., 2017, 2019; Rong et al., 2018). For instance, hydrogels can mimic the pressure-driven trophic motion in plants and fungi (Sridhar et al., 2018) and have been used to create light, humidity, or biological sensors capable of movement (Ionov, 2014). Although their motion is rate limited due to the slow diffusion of a solvent in the polymer mesh, it is possible to use mechanical instabilitites to trigger sudden motion, as displayed by materials inspired by the Venus flytrap (Athas et al., 2016).

Molecular-Scale Simulation of Swelling

Hydrogels often show solvent-responsive behavior due to the chemical affinity between the polymer and an external fluid. This chemical affinity is generally measured by the Flory–Huggins parameter χ. Compared with poor solvent (large χ), good solvent molecules (small χ) can easily permeate into the polymer network, stretch the chains, and swell the hydrogel. In MD simulations, the solvent-responsive behavior of polymer chains can be analyzed by radius of gyration, density profile, radial distribution function, etc. [for e.g., (Lee et al., 2009) have studied the influence of water content on the equilibrium structures and mechanical properties of poly (N-vinyl-2-pyrrolidone-co-2-hydroxyethyl methacrylate) (P(VP-co-HEMA)) hydrogel through all-atom MD simulations]. The simulation results reveal that the VP segment is more hydrophilic than the HEMA segment, and a hydrogel with random monomer sequence can be solvated more than the one with a blocky sequence. During the mechanical deformation, the VP is found to relax faster, especially in the blocky sequence, leading to the lower stress level of the hydrogel with a blocky monomer sequence. In addition to molecular structure and mechanical property, the water and polymer dynamics in hydrogels can also be studied through MD simulations (Chiessi et al., 2007). In DPD simulations, the polymer–solvent interaction is directly represented by the repulsive parameter a_ij, which is related to the Flory–Huggins parameter as a_ij = a_ii + 3.27χ. Therefore, the solvent condition in DPD simulations can be precisely controlled through adjusting the a_ij between corresponding beads. For instance, Chen and Yong (2018) have recently developed a DPD model to study hydrogel swelling under the influence of different solvent conditions and polymer network topology. The simulation results reveal that the gel swelling is a result of a mechanical balance between the elastic entropy change of the polymer network deformation and osmotic pressure originating from the mixing of polymer and solvent.

Continuum Mechanics of Swelling Hydrogels

When modeling the swelling phenomenon, the behavior of both the fluid and the solid must be considered simultaneously (Flory, 1950; Tanaka and Fillmore, 1979; Hong et al., 2008). The mechanics of gels must consider the mass balance equation to impose fluid conservation. In differential form it reads

$\begin{array}{ll}\frac{\partial C_s}{\partial t}+\nabla ·J=0,& (9)\end{array}$

where C_s is the solvent concentration (i.e., the concentration of solvent molecules per unit polymer reference volume), and J is the vector flux of solvent molecules crossing the boundary of an arbitrary volume element in the unit time (positive when entering). Both the polymer and the fluid are usually assumed to be incompressible; however, upon swelling the volume of the swollen solid increases according to J = det F = 1 + C_sv_s, where v_s is the molar volume of the fluid. The aforementioned condition provides a kinematic constraint that has to be fulfilled at any time of the fluid process. The fluid concentration is assumed to depend on the chemical potential μ and the osmotic pressure π (Hong et al., 2008, 2009), C_s(μ, π), while the constitutive relation for the fluid flow is usually adopted in the form $j=-\frac{c_{s}D}{k_{B}T}\nabla \mu$, with D, k_B, T being the diffusivity coefficient, the Boltzmann's constant, and the absolute temperature, respectively. On the other hand, from the mechanical perspective the problem is governed by the stationary condition of the following functional (Hong et al., 2008):

$\begin{array}{l}\text{Ψ}={\displaystyle {\int }_V}{\text{Ψ}}_{m}dV={\displaystyle {\int }_V}\left[\text{Ψ}(F)+{\text{Ψ}}_{mix}(C_s)\right]dV\\ +{\displaystyle {\int }_V}\pi \left[(1+v_s{C}_s)-J\right]dV=0& (10)\end{array}$

In Equation (10) the overall energy density Ψ_m, the elastic energy density Ψ, the mixing energy density (${\text{Ψ}}_{mix}=-\frac{k_{B}T}{v_s}·\left[(J-1)ln\left(\frac{J}{v_s{C}_s}\right)+\frac{\chi }{J}\right]$), and the volume change constraint can be recognized. The stationary condition for the functional (Equation 10) together with Equation (9) provide the basis for the solution of the coupled problem. Finally, the stress state in the gel is provided by $P=\partial \text{Ψ}/\partial F=(\partial {\text{Ψ}}_e/\partial F-\pi J{F}^{-T})$, with P being the first Piola (nominal) stress tensor. In gels, the solid–fluid mixture is no longer incompressible but a volume change takes place, namely J = 1+C_sv_s ≥ 1; in this case the deformation gradient associated with the swelling phenomenon assumes the simple diagonal form F_s = diag(λ_s), being ${\lambda }_s=J^{1/3}$.

Temperature-Sensitive Hydrogels

Among the family of gels, poly(N-isopropylacrylamide) (also indicated as PNIPAA or PNIPAm) forms a three-dimensional hydrogel when cross-linked with N, N′-methylene-bis-acrylamide (MBAm) or N, N′-cystamine-bis-acrylamide (CBAm) (Işikver and Saraydin, 2019). It is a gel whose fluid absorption capability is heavily influenced by the temperature; in fact, it is a temperature-responsive polymer showing a reversible lower critical solution temperature (LCST) phase transition from a swollen state to a shrunken dehydrated one (Yan and Tsujii, 2005). Thanks to its temperature-dependent swelling its application potentialities are in tissue engineering and controlled drug delivery (Yan and Tsujii, 2005). Its behavior changes from hydrophilic to hydrophobic at its LCST; i.e., below the LCST it absorbs water and dissolves in solution, while at higher temperatures it releases water and phase separation occurs.

MD Simulations of Temperature-Responsive Polymers

The temperature-responsive polymer usually has an LCST, [for e.g., poly(N-isopropylacrylamide) (PNIPAM) (LCST ~305 K)]. When the temperature is lower than LCST, the polymer chains can be miscible with water to form a highly swollen and coiled chain conformation with hydrophilicity; when the temperature is higher than LCST, the polymer chain shrinks into a curl and shows hydrophobicity with phase separation. MD simulations have been used to understand this coil–globule transition of PNIPAM at the atomic level (Deshmukh et al., 2013). The simulation results reveal that the hydrogen bonds formed between PNIPAM and water molecules play the most important role during the conformation change of PNIPAM. When the temperature is below LCST, these hydrogen bonds are strong and stable; but when above LCST, the strength of these hydrogen bonds is weakened, leading to the reduced solubility and a coil–globule transition of PNIPAM. Recently, the mesoscale modeling method DPD has been developed to further understand the phase transition dynamics of thermoresponsive polymers (Li et al., 2015). Two different mechanisms have been identified for the self-aggregation of temperature-responsive polymers during the coil-to-globule phase transition process, which is found to be dependent on the size of these polymer chains. Such a DPD model has been furthered applied to study the transport mechanisms of nanoparticles (NPs) in a thermoresponsive PNIPAM hydrogel network (Wang et al., 2020). By changing the simulation temperature across the LCTS of PNIPAM, the hydrogel network characteristics can be significantly altered, leading to the controlled release behaviors of entrapped NPs. These understandings can be adopted to guide the design of controlled drug release from stimuli-responsive hydrogels.

PNIPAm Hydrogel-Based Actuators

Hydrogels are capable of experiencing a significant change of volume by swelling/deswelling when subjected to external stimuli. For instance, thermosensitive PNIPAm hydrogels are well known for their capability to undergo a sharp volume-phase transition around the lower critical swelling temperature (LCST) of 305 K (Afroze et al., 2000; Vernerey and Shen, 2017; Shen et al., 2019). When the temperature quickly rises around the LCST, the hydrogel undergoes a reversible transition from a swollen state to a shrunken dehydrated state, losing more than 90% of its volume (Figure 7A). Due to this temperature sensitivity, the NIPAm hydrogel has found applications in a variety of applications including soft actuators (Santulli et al., 2005; Vernerey and Shen, 2017), drug delivery systems (Hoare and Kohane, 2008), and hydrogel sensors (Richter et al., 2004).

FIGURE 7

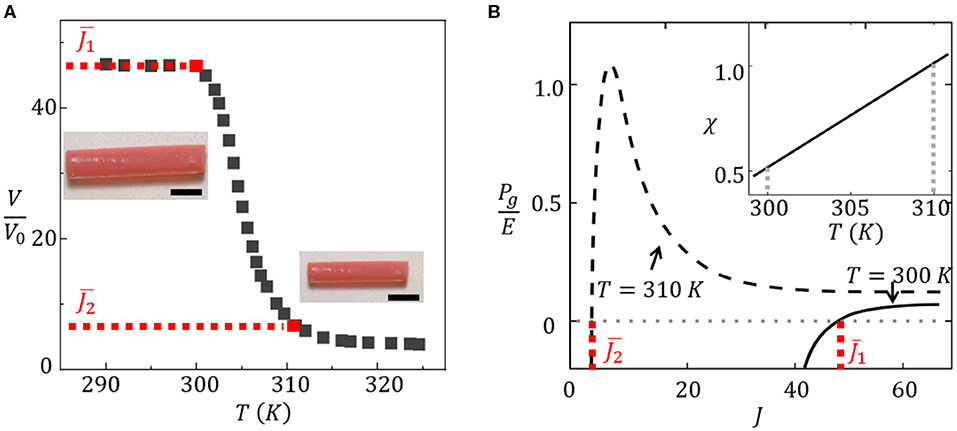
Figure 7. (A) Swelling ratio of NIPAm hydrogel as a function of temperature. (B) Curves of hydrogel pressure P_g as a function of swelling ratio J. The inset shows the linear dependency of the interaction parameter χ on temperature.

The origin of this phase transition can be explained by the interplay between two competing forces: the polymer–solvent mixing force and the elasticity of the cross-linked polymer network. At low temperatures, gel swelling arises from the affinity between a solvent and polymer and is balanced by the stretching resistance of the cross-linked chain network. The Flory–Rhener theory (Flory, 1942) has been successful at predicting this competition by decomposing the gel's Gibb's free energy ΔG into a mixing (ΔG^mix) and an elastic (ΔG^el) contribution, such that the total free energy is ΔG(J, χ) = ΔG^mix(J, χ)+ΔG^el(J), where J denotes the swelling ratio and the Flory–Huggins parameter, χ, measures the affinity between polymer and solvent [a smaller value of χ indicates a greater affinity (MacConaghy et al., 2015)]. It can be shown that the equilibrium hydrostatic pressure defined as $P_g=3(\partial \Delta G/\partial J^{})$ is split into an elastic (P_e) and an osmotic (π) contribution as follows:

$\begin{array}{l}{P}_g=P_e+\pi \text{ where }{P}_e=E(J^{-1/3}-J^{-1})\text{ and}\\ \pi =\frac{k_{B}T}{\nu }\left[ln\left(1-\frac{1}{J}\right)+\frac{1}{J}+\chi \frac{1}{J^2}\right]& (11)\end{array}$

In the above equations, E is the polymer's Young's modulus, k_BT is the thermal energy, and ν is the specific volume of solvent. The balance between osmotic and elastic pressures is achieved when the pressures in the gel are balanced (i.e., P_g = 0) for a given reduced volume V^* as shown in Figure 7A. The extreme temperature sensitivity of PNIPAm between 300 and 310 K is due to the temperature dependence of the interaction parameter χ as characterized by Afroze et al. (2000) using a series of polynomials. According to our previous work, this interaction parameter is calibrated as χ = χ₀ + χ₁T, where χ₀ = −12.917 and ${\chi }_1=0.044959K^{-1}$ (Nicodemus and Bryant, 2008). We show in Figure 7B that changes in χ drastically switch the swelling equilibrium of the gel from J ≈ 40 at T = 300 K (χ = 0.51) to J = 4 at T = 310 K (χ = 0.92). This yields a volume reduction by more than 10 times across this temperature range.

Programmable Hydrogels as Scaffolds for Tissue Engineering

Due to their high water content, hydrogels can be made to mimic most tissues of the human body. Synthetically produced hydrogels that are biomimetic and biodegradable are therefore promising platforms for cell encapsulation and tissue engineering. Hydrogels that are used to encapsulate cells are typically fabricated from hydrophilic and cytocompatible multifunctional macromolecular monomers or macromers (Nicodemus and Bryant, 2008). Many different natural and synthetic polymers have been functionalized with reactive groups to create a wide range of macromers suitable for cell encapsulation (Li et al., 2012). In particular, hydrogels that are sensitive to biological cues to undergo relaxation or degradation can be highly effective in enabling tissue growth. To create biodegradable hydrogels, chemical bonds that are susceptible to cleavage by water or enzymes can be readily introduced into the cross-links of the polymer network. Once cells are encapsulated, the hydrogel degrades to allow the transport of large extracellular matrix proteins that eventually mature into newly regenerated tissue (Bryant and Vernerey, 2018).

One of the toughest challenges is programming hydrogel degradation for optimum growth conditions. For instance, hydrogel degradation that is too fast can result in complete loss of mechanical integrity, whereas if it is too slow, it can deter growth. Understanding the physics that drive the processes of degradation and growth is therefore crucial in developing models that will help transition degradable hydrogels from the laboratory to the clinics. Supported by experiments and models, a key finding is that successful tissue growth occurs when there is a smooth transfer of mechanical properties from hydrogel to the new tissue (see Figure 8). This can be achieved by (1) matrix deposition with localized degradation and (2) ensuring overall structural connectivity of the composite gel and neo-tissue. Localized degradation is possible, for instance, with smart hydrogels whose bonds are designed to be sensitive to enzymes released from cells. This restricts transport of the extracellular matrix to the immediate vicinity of the cells where the hydrogel has degraded. The spatiotemporal behavior of hydrogel degradation and matrix deposition depend on the hydrogel properties and, often complex, cell behavior. Therefore, we have developed scaling laws that quantify these processes and potentially help tuning degradation. Localized degradation around a cell can be mathematically described by a coupled reaction–diffusion equation of the enzyme and hydrogel and characterized by the speed of advancement v and width of partially degraded gel. The local degradation speed v is given in terms of the enzyme reaction rate, κ; diffusivity, D; enzyme source concentration, c₀; and hydrogel network connectivity, β, by (Sridhar and Vernerey, 2018):

$\begin{array}{ll}v=\sqrt{\frac{D\kappa c_0}{ln\beta }}& (12)\end{array}$

This simple relationship is valuable in understanding the precise influence of each physical parameter.

FIGURE 8

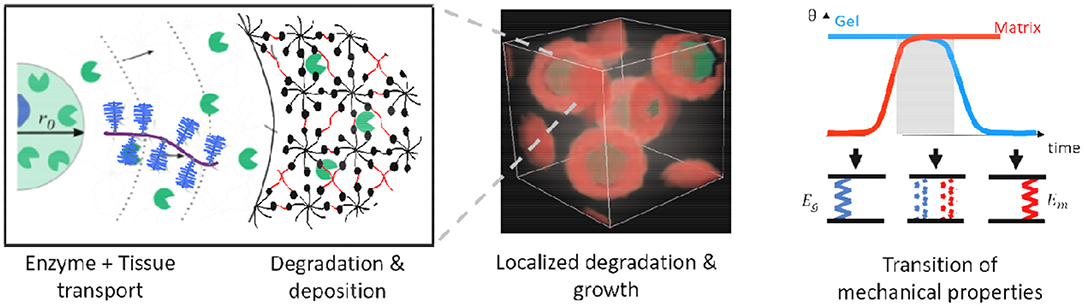
Figure 8. Degradation of enzyme-sensitive hydrogels and localized tissue deposition to ensure smooth transition of mechanical properties from gel to regenerated tissue.

With a complete 3D model (Akalp et al., 2016; Sridhar et al., 2017) that also includes cell distribution and growth deposition, one can program degradation w.r.t. to measurable cell activity of each patient to ensure mechanical integrity of the construct. As hydrogels are often amenable to in situ polymerization under direct contact with living tissue, they can be used as an injectable platform to deliver cells in vivo. Thus, programming these smart hydrogels will be a crucial step toward personalized regenerative medicine.

Conclusions

Responsive materials, as well as active structural systems, are today widely used to develop unprecedented smart devices, sensors, or actuators; their functionalities come from the ability to respond with a detectable reaction to environmental stimuli. Depending on the responsive material under study, the triggering stimuli can have a different nature, ranging from physical (temperature, light, electric or magnetic field, mechanical stress, etc.), chemical (pH, ligands, etc.), or biological (enzymes, etc.) type. Such a responsiveness can be obtained by properly designing the meso- or macroscopic arrangement of the constitutive elements, as occurs in metamaterials, or can be obtained by using responsive materials per se, whose responsiveness comes from the chemistry underneath their microstructure. In fact, when the responsiveness at the molecular level is properly organized, the nanoscale response can be collectively detected at the macroscale, leading to a so-called responsive material. In the present article we reviewed the enormous world of responsive polymers, by outlining the main features, characteristics, and responsive mechanisms of smart polymers and by providing a mechanical modeling perspective description, both at the nano as well as at the continuum scale level.

Despite extensive research conducted in computer modeling, in particular MD simulations of responsive polymers, most of these studies focus only on single stimuli-responsive polymers, such as pH, temperature, light, solvent, electric field, etc. However, dual- or multiresponsive polymers have attracted more and more attentions, as many applications of these smart materials require a combined response to several external stimuli (Zhuang et al., 2013). Thus, there is a pressing need to develop molecular models and simulations to design these dual- or multiresponsive polymers. In addition, all-atomic MD simulations can be applied to study a single polymer chain or small polymer systems at the atomistic level. However, they are not suitable to study the mesoscopic structures and properties of large and complex stimuli-responsive polymers because of the limited spatial and temporal scales of all-atomic MD simulations. To this end, the coarse-grained MD and DPD simulation techniques are more proper to study the large-scale behaviors of stimuli-responsive polymers. However, it remains a challenge to derive the effective parameters for coarse-grained MD models from the atomistic model (Li et al., 2013).

The present article aims to provide a comprehensive overview of the main features and modeling aspects of the most diffused smart polymers. In fact, the quantitative mechanical description of active materials plays a key role in their development and use, enabling the design of advanced devices as well as engineering of the materials' microstructure according to the desired functionality or responsiveness. The aim of this article, although it is not exhaustive, is to stimulate interest in this frontier field of materials science, with a preferential look at the mechanical aspects necessary for the use of intelligent polymers in unprecedented advanced applications, ranging from the macro to the nanoscale.

Author Contributions

RB was the primary investigator of this work and developed the main structure of the paper. FV and RB developed the modeling and simulations aspects of the paper related to the continuum-scale approach. YL developed the molecular scale modeling aspects of the manuscript. All authors equally contributed revising the final version of the manuscript.

Funding

RB would like to thank the support from European Union's Horizon 2020 Research and Innovation Programme (H2020-WIDESPREAD-2018, SIRAMM) under Grant Agreement No. 857124. YL would like to thank the support from National Science Foundation grants (CMMI-1762661 and CMMI-1934829).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

FV gratefully acknowledges the support of the National Science Foundation under Award No. 1761918.

References

Afroze, F., Nies, E., and Berghmans, H. (2000). Phase transitions in the system poly (N-isopropylacrylamide)/water and swelling behaviour of the corresponding networks. J. Mol. Struct. 554, 55–68. doi: 10.1016/S0022-2860(00)00559-7

CrossRef Full Text | Google Scholar

Agarwal, S., Jiang, S., and Chen, Y. (2019). Progress in the field of water and/or temperature-triggered polymer actuators. Macromol. Mater. Eng. 304:1800548. doi: 10.1002/mame.201800548

PubMed Abstract | CrossRef Full Text | Google Scholar

Akalp, U., Bryant, S. J., and Vernerey, F. J. (2016). Tuning tissue growth with scaffold degradation in enzyme-sensitive hydrogels: a mathematical model. Soft Matter. 12, 7505–7520. doi: 10.1039/C6SM00583G

PubMed Abstract | CrossRef Full Text | Google Scholar

Amin, D., Alexei, E. L., and Zuowei, W. (2016). Dynamics in supramolecular polymer networks formed by associating telechelic chains. Macromolecules 49, 7510–7524. doi: 10.1021/acs.macromol.6b00561

CrossRef Full Text | Google Scholar

Athas, J. C., Nguyen, C. P., Zarket, B. C., Gargava, A., Nie, Z., and Raghavan, S. R. (2016). Enzyme-triggered folding of hydrogels: toward a mimic of the venus flytrap. ACS Appl. Mater. Interfaces 8, 19066–19074. doi: 10.1021/acsami.6b05024

PubMed Abstract | CrossRef Full Text | Google Scholar

Berná, J., Leigh, D. A., Lubomska, M., Mendoza, S. M., Pérez, E. M., Rudolf, P., et al. (2005). Macroscopic transport by synthetic molecular machines. Nature Mater. 4, 704–710. doi: 10.1038/nmat1455

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowman, C. N., and Kloxin, C. J. (2012). Covalent adaptable networks: reversible bond structures incorporated in polymer networks. Angew. Chem. Int. Ed. 51, 4272–4274. doi: 10.1002/anie.201200708

PubMed Abstract | CrossRef Full Text | Google Scholar

Brantley, J. N., Wiggins, K. M., and Bielawski, C. W. (2013). Polymer mechanochemistry: the design and study of mechanophores. Polym. Int. 62, 2–12. doi: 10.1002/pi.4350

CrossRef Full Text | Google Scholar

Brighenti, R., Artoni, F., and Cosma, M. P. (2019). Mechanics of innovative responsive polymers. Mech. Res. Commun. 100:103403. doi: 10.1016/j.mechrescom.2019.103403

CrossRef Full Text | Google Scholar

Brighenti, R., Artoni, F., Vernerey, F., Torelli, M., Pedrini, A., Domenichelli, I., et al. (2018). Mechanics of responsive polymers via conformationally switchable molecules. J. Mech. Phys. Solids 113, 65–81. doi: 10.1016/j.jmps.2018.01.012

CrossRef Full Text | Google Scholar

Brown, C. L., and Craig, S. L. (2015). Molecular engineering of mechanophore activity for stress-responsive polymeric materials. Chem. Sci. 6, 2158–2165. doi: 10.1039/C4SC01945H

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruns, C. J., and Stoddart, J. F. (2016). The Nature of the Mechanical Bond: From Molecules to Machines. Hoboken, NJ: John Wiley & Sons. doi: 10.1002/9781119044123

CrossRef Full Text | Google Scholar

Bryant, S. J., and Vernerey, F. J. (2018). Programmable hydrogels for cell encapsulation and neo-tissue growth to enable personalized tissue engineering. Adv. Healthc. Mater. 7:1700605. doi: 10.1002/adhm.201700605

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabane, E., Zhang, X., Langowska, K., Palivan, C. G., and Meier, W. (2012). Stimuli-responsive polymers and their applications in nanomedicine. Biointerphases 7:9. doi: 10.1007/s13758-011-0009-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Capelot, M., Unterlass, M. M., Tournilhac, F., and Leibler, L. (2012). Catalytic control of the vitrimer glass transition. ACS Macro Lett. 1, 789–792. doi: 10.1021/mz300239f

CrossRef Full Text | Google Scholar

Caruso, M. M., Davis, D. A., Shen, Q., Odom, S. A., Sottos, N. R., White, S. R., et al. (2009). Mechanically-induced chemical changes in polymeric materials. Chem. Rev. 109, 5755–5798. doi: 10.1021/cr9001353

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., and Yong, X. (2018). Dissipative particle dynamics modeling of hydrogel swelling by osmotic ensemble method. J. Chem. Phys. 149:094904. doi: 10.1063/1.5045100

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Huo, J., Hao, L., and Zhou, J. (2019). Multiscale modeling and simulations of responsive polymers. Curr. Opin. Chem. Eng. 23, 21–33. doi: 10.1016/j.coche.2019.02.004

CrossRef Full Text | Google Scholar

Chiessi, E., Cavalieri, F., and Paradossi, G. (2007). Water and polymer dynamics in chemically cross-linked hydrogels of poly (vinyl alcohol): a molecular dynamics simulation study. J. Phys. Chem. B 111, 2820–2827. doi: 10.1021/jp0671143

PubMed Abstract | CrossRef Full Text | Google Scholar

Chirani, N., Gritsch, L., Motta, F. L., and Fare, S. (2015). History and applications of hydrogels. J. Biomed. Sci. 4, 1–23. doi: 10.4172/2254-609X.100013

CrossRef Full Text | Google Scholar

Cho, S. H., White, S. R., and Braun, P. V. (2009). Self-healing polymer coatings. Adv. Mater. 21, 645–649. doi: 10.1002/adma.200802008

CrossRef Full Text | Google Scholar

Choi, J., Chung, H., Yun, J. H., and Cho, M. (2014). Photo-isomerization effect of the azobenzene chain on the opto-mechanical behavior of nematic polymer: a molecular dynamics study. Appl. Phys. Lett. 105:221906. doi: 10.1063/1.4903247

CrossRef Full Text | Google Scholar

Clarke, S. M., Hotta, A., Tajbakhsh, A. R., and Terentjev, E. M. (2001). Effect of crosslinker geometry on equilibrium thermal and mechanical properties of nematic elastomers. Phys. Rev. E 64:061702. doi: 10.1103/PhysRevE.64.061702

PubMed Abstract | CrossRef Full Text | Google Scholar

Coskun, A., Banaszak, M., Astumian, R. D., Astumian, R. D., Stoddart, J. F., and Grzybowski, B. A. (2012). Great expectations: can artificial molecular machines deliver on their promise? Chem. Soc. Rev. 41, 19–30. doi: 10.1039/C1CS15262A

PubMed Abstract | CrossRef Full Text | Google Scholar

Cranford, S. W., Ortiz, C., and Buehler, M. J. (2010). Mechanomutable properties of a PAA/PAH polyelectrolyte complex: rate dependence and ionization effects on tunable adhesion strength. Soft Matter 6, 4175–4188. doi: 10.1039/c0sm00095g

CrossRef Full Text | Google Scholar

Dai, X., Chen, P., Zhu, G., Xu, Z., Zhang, X., and Yan, L. T. (2019). Entropy-mediated mechanomutable microstructures and mechanoresponsive thermal transport of nanoparticle self-assembly in block copolymers. J. Phys. Chem. Lett. 10, 7970–7979. doi: 10.1021/acs.jpclett.9b03253

PubMed Abstract | CrossRef Full Text | Google Scholar

De Gennes, P. G., and Prost, J. (1993). The Physics of Liquid Crystals, Vol. 83. Oxford, UK: Oxford University Press.

Google Scholar

Deshmukh, S. A., Li, Z., Kamath, G., Suthar, K. J., Sankaranarayanan, S. K., and Mancini, D. C. (2013). Atomistic insights into solvation dynamics and conformational transformation in thermo-sensitive and non-thermo-sensitive oligomers. Polymer 54, 210–222. doi: 10.1016/j.polymer.2012.11.009

CrossRef Full Text | Google Scholar

Diesendruck, C. E., and Moore, J. S. (2013). Mechanophores for Self-Healing Applications. Self-Healing Polymers: From Principles to Applications. Weinheim: Wiley-VCH Verlag GmbH & Co.

Google Scholar

Ericksen, J. L. (1961). Conservation laws for liquid crystals. Trans. Soc. Rheol. 5, 23–34. doi: 10.1122/1.548883

CrossRef Full Text | Google Scholar

Finkelmann, H., Greve, A., and Warner, M. (2001). The elastic anisotropy of nematic elastomers. Euro. Phys. J. E 5, 281–293. doi: 10.1007/s101890170060

CrossRef Full Text | Google Scholar

Flory, P. J. (1942). Thermodynamics of high polymer solutions. J. Chem. Phys. 10, 51–61. doi: 10.1063/1.1723621

CrossRef Full Text | Google Scholar

Flory, P. J. (1950). Statistical mechanics of swelling of network structures. J. Chem. Phys. 18, 108–111. doi: 10.1063/1.1747424

CrossRef Full Text | Google Scholar

Flory, P. J. (1953). Principles of Polymer Chemistry. New York, NY: Cornell University Press.

Google Scholar

Frank, E. C. (1958). On the theory of liquid crystals. Discuss. Faraday Soc. 25, 19–28. doi: 10.1039/df9582500019

CrossRef Full Text | Google Scholar

Früh, A. E., Artoni, F., Brighenti, R., and Dalcanale, E. (2017). Strain field self-diagnostic poly (dimethylsiloxane) elastomers. Chem. Mater. 29, 7450–7457. doi: 10.1021/acs.chemmater.7b02438

CrossRef Full Text | Google Scholar

Goujon, A., Lang, T., Mariani, G., Moulin, E., Fuks, G., Raya, J., et al. (2017). Bistable [c2] daisy chain rotaxanes as reversible muscle-like actuators in mechanically active gels. J. Am. Chem. Soc. 139, 14825–14828. doi: 10.1021/jacs.7b06710

PubMed Abstract | CrossRef Full Text | Google Scholar

Grima, J. N., Caruana-Gauci, R., Dudek, M. R., Wojciechowski, K. W., and Gatt, R. (2013). Smart metamaterials with tunable auxetic and other properties. Smart Mater. Struct. 22:084016. doi: 10.1088/0964-1726/22/8/084016

CrossRef Full Text | Google Scholar

Gruhn, T., and Emmerich, H. (2013). Simulation of stimuli-responsive polymer networks. Chemosensors 1, 43–67. doi: 10.3390/chemosensors1030043

CrossRef Full Text | Google Scholar

Guin, T., Settle, M. J., Kowalski, B. A., Auguste, A. D., Beblo, R. V., Reich, G. W., et al. (2018). Layered liquid crystal elastomer actuators. Nat. Commun. 9:2531. doi: 10.1038/s41467-018-04911-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hänggi, P., Talkner, P., and Borkovec, M. (1990). Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–341. doi: 10.1103/RevModPhys.62.251

CrossRef Full Text | Google Scholar

Hoare, T. R., and Kohane, D. S. (2008). Hydrogels in drug delivery: progress and challenges. Polymer 49, 1993–2007. doi: 10.1016/j.polymer.2008.01.027

CrossRef Full Text | Google Scholar

Hong, W., Liu, Z., and Suo, Z. (2009). Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load. Int. J. Solids Struct. 46, 3282–3289. doi: 10.1016/j.ijsolstr.2009.04.022

CrossRef Full Text | Google Scholar

Hong, W., Zhao, X., Zhou, J., and Suo, Z. (2008). A theory of coupled diffusion and large deformation in polymeric gels. J. Mech. Phys. Solids 56, 1779–1793. doi: 10.1016/j.jmps.2007.11.010

CrossRef Full Text | Google Scholar

Ikeda, T., Mamiya, J.-I., and Yu, Y. (2007). Photomechanics of liquid-crystalline elastomers and other polymers. Angew. Chem. Int. Ed. 46, 506–528. doi: 10.1002/anie.200602372

PubMed Abstract | CrossRef Full Text | Google Scholar

Ionov, L. (2014). Hydrogel-based actuators: possibilities and limitations. Materi. Today 17, 494–503. doi: 10.1016/j.mattod.2014.07.002

CrossRef Full Text | Google Scholar

Işikver, Y., and Saraydin, D. (2019). Stimuli responsive hydrogels: NIPAM/AAm/carboxylic acid polymers. Acta Chem. Iasi. 27, 155–184. doi: 10.2478/achi-2019-0012

CrossRef Full Text | Google Scholar

Ito, K. (2007). Novel cross-linking concept of polymer network: synthesis, structure, and properties of slide-ring gels with freely movable junctions. Polym. J. 39, 489–499. doi: 10.1295/polymj.PJ2006239

CrossRef Full Text | Google Scholar

Jackson, J. A., Messner, M. C., Dudukovic, N. A., Smith, W. L., Bekker, L., Moran, B., et al. (2018). Field responsive mechanical metamaterials. Sci. Adv. 4:eaau6419. doi: 10.1126/sciadv.aau6419

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, H., Li, C., and Huang, X. (2013). Actuators based on liquid crystalline elastomer materials. Nanoscale 5, 5225–5240. doi: 10.1039/c3nr00037k

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, L., Liu, C., Mayumi, K., Kato, K., Yokoyama, H., and Ito, K. (2018). Highly stretchable and instantly recoverable slide-ring gels consisting of enzymatically synthesized polyrotaxane with low host coverage. Chem. Mater. 30, 5013–5019. doi: 10.1021/acs.chemmater.8b01208

CrossRef Full Text | Google Scholar

Jin, Y., Yu, C., Denman, R. J., and Zhang, W. (2013). Recent advances in dynamic covalent chemistry. Chem. Soc. Rev. 42, 6634–6654. doi: 10.1039/c3cs60044k

PubMed Abstract | CrossRef Full Text | Google Scholar

Karino, T., Shibayama, M., and Ito, K. (2006). Slide-ring gel: topological gel with freely movable cross-links. Phys. B Condens. Matter 385, 692–696. doi: 10.1016/j.physb.2006.05.293

CrossRef Full Text | Google Scholar

Katiyar, R. S., and Jha, P. K. (2017). Phase behavior of aqueous polyacrylic acid solutions using atomistic molecular dynamics simulations of model oligomers. Polymer 114, 266–276. doi: 10.1016/j.polymer.2017.03.007

CrossRef Full Text | Google Scholar

Kato, K., Okabe, Y., Okazumi, Y., and Ito, K. (2015). A significant impact of host–guest stoichiometry on the extensibility of polyrotaxane gels. Chem. Commun. 51, 16180–16183. doi: 10.1039/C5CC07122D

PubMed Abstract | CrossRef Full Text | Google Scholar

Kato, K., Yasuda, T., and Ito, K. (2013). Viscoelastic properties of slide-ring gels reflecting sliding dynamics of partial chains and entropy of ring components. Macromolecules 46, 310–316. doi: 10.1021/ma3021135

CrossRef Full Text | Google Scholar

Klajn, R. (2014). Spiropyran-based dynamic materials. Chem. Soc. Rev. 43, 148–184. doi: 10.1039/C3CS60181A

PubMed Abstract | CrossRef Full Text | Google Scholar

Kloxin, C. J., and Bowman, C. N. (2013). Covalent adaptable networks: smart, reconfigurable and responsive network systems. Chem. Soc. Rev. 42, 7161–7173. doi: 10.1039/C3CS60046G

PubMed Abstract | CrossRef Full Text | Google Scholar

Kocak, G., Tuncer, C., and Bütün, V. J. P. C. (2017). pH-Responsive polymers. Polym. Chem. 8, 144–176. doi: 10.1039/C6PY01872F

CrossRef Full Text | Google Scholar

Lee, S. G., Brunello, G. F., Jang, S. S., and Bucknall, D. G. (2009). Molecular dynamics simulation study of P (VP-co-HEMA) hydrogels: effect of water content on equilibrium structures and mechanical properties. Biomaterials 30, 6130–6141. doi: 10.1016/j.biomaterials.2009.07.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Leibler, L., Rubinstein, M., and Colby, R. H. (1991). Dynamics of reversible networks. Macromolecules 24, 4701–4707. doi: 10.1021/ma00016a034

CrossRef Full Text | Google Scholar

Li, M., Liu, W., and Zhu, S. (2017). Smart polyolefins feeling the force: color changeable poly (ethylene-vinyl acetate) and poly (ethylene-octene) in response to mechanical force. Polymer 112, 219–227. doi: 10.1016/j.polymer.2017.02.006

CrossRef Full Text | Google Scholar

Li, Y., Abberton, B. C., Kröger, M., and Liu, W. K. (2013). Challenges in multiscale modeling of polymer dynamics. Polymers 5, 751–832. doi: 10.3390/polym5020751

CrossRef Full Text | Google Scholar

Li, Y., Rodrigues, J., and Tomas, H. (2012). Injectable and biodegradable hydrogels: gelation, biodegradation and biomedical applications. Chem. Soc. Rev. 41, 2193–2221. doi: 10.1039/C1CS15203C

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Tang, Y. H., Li, X., and Karniadakis, G. E. (2015). Mesoscale modeling of phase transition dynamics of thermoresponsive polymers. Chem. Commun. 51, 11038–11040. doi: 10.1039/C5CC01684C

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Kadono, H., Mayumi, K., Kato, K., Yokoyama, H., and Ito, K. (2017). Unusual fracture behavior of slide-ring gels with movable cross-links. ACS Macro Lett. 6, 1409–1413. doi: 10.1021/acsmacrolett.7b00729

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Guo, R., Xu, G., Huang, Z., and Yan, L. T. (2014). Entropy-mediated mechanical response of the interfacial nanoparticle patterning. Nano Lett. 14, 6910–6916. doi: 10.1021/nl5029396

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Valdeolivas, M., Liu, D., Broer, D. J., and Sánchez-Somolinos, C. (2018). 4D printed actuators with soft-robotic functions. Macromol. Rapid Commun. 39:1700710. doi: 10.1002/marc.201700710

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, F., Sun, T. L., Nakajima, T., Kurokawa, T., Zhao, Y., Ihsan, A. B., et al. (2014). Crack blunting and advancing behaviors of tough and self-healing polyampholyte hydrogel. Macromolecules 47, 6037–6046. doi: 10.1021/ma5009447

CrossRef Full Text | Google Scholar

Luo, Z., and Jianwen, J. (2012). pH-sensitive drug loading/releasing in amphiphilic copolymer PAE–PEG: Integrating molecular dynamics and dissipative particle dynamics simulations. J. Control. Release 162, 185–193. doi: 10.1016/j.jconrel.2012.06.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Z., Yan, L., Biaobing, W., and Jianwen, J. (2016). pH-sensitive vesicles formed by amphiphilic grafted copolymers with tunable membrane permeability for drug loading/release: a multiscale simulation study. Macromolecules 49, 6084–6094. doi: 10.1021/acs.macromol.6b01211

CrossRef Full Text | Google Scholar

MacConaghy, K. I., Chadly, D. M., Stoykovich, M. P., and Kaar, J. L. (2015). Optically diffracting hydrogels for screening kinase activity in vitro and in cell lysate: impact of material and solution properties. Anal. Chem. 87, 3467–3475. doi: 10.1021/acs.analchem.5b00442

PubMed Abstract | CrossRef Full Text | Google Scholar

Manrique-Juarez, M. D., Rat, S., Salmon, L., Molnár, G., Quintero, C. M., Nicu, L., et al. (2016). Switchable molecule-based materials for micro-and nanoscale actuating applications: achievements and prospects. Coord. Chem. Rev. 308, 395–408. doi: 10.1016/j.ccr.2015.04.005

CrossRef Full Text | Google Scholar

Marszalek, P. E., Lu, H., Li, H., Carrion-Vazquez, M., Oberhauser, A. F., Schulten, K., et al. (1999). Mechanical unfolding intermediates in titin modules. Nature 402, 100–103. doi: 10.1038/47083

PubMed Abstract | CrossRef Full Text | Google Scholar

Masao, D. (2009). Gel dynamics. J. Phys. Soc. Jpn. 78:052001. doi: 10.1143/JPSJ.78.052001

CrossRef Full Text

Mayumi, K., Tezuka, M., Bando, A., and Ito, K. (2012). Mechanics of slide-ring gels: novel entropic elasticity of a topological network formed by ring and string. Soft Matter 8, 8179–8183. doi: 10.1039/c2sm25508a

CrossRef Full Text | Google Scholar

McBride, M. K., Martinez, A. M., Cox, L., Alim, M., Childress, K., Beiswinger, M., et al. (2018). A readily programmable, fully reversible shape-switching material. Sci. Adv. 4:eaat4634. doi: 10.1126/sciadv.aat4634

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, F., and Terentjev, E. M. (2018). Fluidization of transient filament networks. Macromolecules 51, 4660–4669. doi: 10.1021/acs.macromol.8b00012

CrossRef Full Text | Google Scholar

Milić, J. V., and Diederich, F. (2019). The quest for molecular grippers: photo-electric control of molecular gripping machinery. Chem. A Eur. J. 25, 8440–8452. doi: 10.1002/chem.201900852

PubMed Abstract | CrossRef Full Text | Google Scholar

Moon, J., Kim, B., Choi, J., and Cho, M. (2019). Multiscale study of the relationship between photoisomerization and mechanical behavior of azo-polymer based on the coarse-grained molecular dynamics simulation. Macromolecules 52, 2033–2049. doi: 10.1021/acs.macromol.8b02535

CrossRef Full Text | Google Scholar

Nap, R., Gong, P., and Szleifer, I. (2006). Weak polyelectrolytes tethered to surfaces: effect of geometry, acid–base equilibrium and electrical permittivity. J. Polym. Sci. Part B Polym. Phys. 44, 2638–2662. doi: 10.1002/polb.20896

CrossRef Full Text | Google Scholar

Nicodemus, G. D., and Bryant, S. J. (2008). Cell encapsulation in biodegradable hydrogels for tissue engineering applications. Tissue Eng. Part B Rev. 14, 149–165. doi: 10.1089/ten.teb.2007.0332

PubMed Abstract | CrossRef Full Text | Google Scholar

Noda, Y., Hayashi, Y., and Ito, K. (2014). From topological gels to slide-ring materials. J. Appl. Polym. Sci. 131, 1–9. doi: 10.1002/app.40509

CrossRef Full Text | Google Scholar

Ohm, C., Brehmer, M., and Zentel, R. (2012). “Applications of liquid crystalline elastomers,” in Liquid Crystal Elastomers: Materials and Applications (Berlin: Springer), 49–93.

PubMed Abstract | Google Scholar

Okumura, Y., and Ito, K. (2001). The polyrotaxane gel: a topological gel by figure-of-eight cross-links. Adv. Mater. 13:485–487. doi: 10.1002/1521-4095(200104)13:7<485::AID-ADMA485>3.0.CO

CrossRef Full Text | Google Scholar

Oseen, W. C. (1933). The theory of liquid crystals. Trans. Faraday Soc. 29, 883–899. doi: 10.1039/tf9332900883

CrossRef Full Text | Google Scholar

Prigogine, I., and Nicolis, G. (1971). Biological order, structure and instabilities. Q. Rev. Biophys. 4, 107–148. doi: 10.1017/S0033583500000615

PubMed Abstract | CrossRef Full Text | Google Scholar

Randolph, L. M., Chien, M. P., and Gianneschi, N. C. (2012). Biological stimuli and biomolecules in the assembly and manipulation of nanoscale polymeric particles. Chem. Sci. 3, 1363–1380. doi: 10.1039/c2sc00857b

PubMed Abstract | CrossRef Full Text | Google Scholar

Richter, A., Howitz, S., Kuckling, D., and Arndt, K. F. (2004). Influence of volume phase transition phenomena on the behavior of hydrogel-based valves. Sens. Actuators B Chem. 99, 451–458. doi: 10.1016/j.snb.2003.12.014

CrossRef Full Text | Google Scholar

Rong, Q., Lei, W., and Liu, M. (2018). Conductive hydrogels as smart materials for flexible electronic devices. Chem. A Eur. J. 24, 16930–16943. doi: 10.1002/chem.201801302

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, D., Cambre, J. N., and Sumerlin, B. S. (2010). Future perspectives and recent advances in stimuli-responsive materials. Prog. Polym. Sci. 35, 278–301. doi: 10.1016/j.progpolymsci.2009.10.008

CrossRef Full Text | Google Scholar

Santulli, C., Patel, S. I., Jeronimidis, G., Davis, F. J., and Mitchell, G. R. (2005). Development of smart variable stiffness actuators using polymer hydrogels. Smart Mater. Struct. 14:434. doi: 10.1088/0964-1726/14/2/018

CrossRef Full Text | Google Scholar

Shang, Y., Wang, J., Ikeda, T., and Jiang, L. (2019). Bio-inspired liquid crystal actuator materials. J. Mater. Chem. C 7, 3413–3428. doi: 10.1039/C9TC00107G

CrossRef Full Text | Google Scholar

Shen, T., Font, M. G., Jung, S., Gabriel, M. L., Stoykovich, M. P., and Vernerey, F. J. (2017). Remotely triggered locomotion of hydrogel mag-bots in confined spaces. Sci. Rep. 7:16178. doi: 10.1038/s41598-017-16265-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, T., Kan, J., Benet, E., and Vernerey, F. J. (2019). On the blistering of thermo-sensitive hydrogel: the volume phase transition and mechanical instability. Soft Matter 15, 5842–5853. doi: 10.1039/C9SM00911F

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepherd, H. J., Il'ya, A., Quintero, C. M., Tricard, S., Salmon, L., Molnár, G., et al. (2013). Molecular actuators driven by cooperative spin-state switching. Nat. Commun. 4:2607. doi: 10.1038/ncomms3607

PubMed Abstract | CrossRef Full Text | Google Scholar

Silberstein, M. N., Cremar, L. D., Beiermann, B. A., Kramer, S. B., Martinez, T. J., White, S. R., et al. (2014). Modeling mechanophore activation within a viscous rubbery network. J. Mech. Phys. Solids 63, 141–153. doi: 10.1016/j.jmps.2013.09.014

CrossRef Full Text | Google Scholar

Silberstein, M. N., Min, K., Cremar, L. D., Degen, C. M., Martinez, T. J., Aluru, N. R., et al. (2013). Modeling mechanophore activation within a crosslinked glassy matrix. J. Appl. Phys. 114:023504. doi: 10.1063/1.4812581

CrossRef Full Text | Google Scholar

Skačej, G., and Zannoni, C. (2011). Main-chain swollen liquid crystal elastomers: a molecular simulation study. Soft Matter 7, 9983–9991. doi: 10.1039/c1sm05709j

CrossRef Full Text | Google Scholar

Skačej, G., and Zannoni, C. (2012). Molecular simulations elucidate electric field actuation in swollen liquid crystal elastomers. Proc. Nat. Academy Sci. U.S.A. 109, 10193–10198. doi: 10.1073/pnas.1121235109

PubMed Abstract | CrossRef Full Text | Google Scholar

Sridhar, S. L., Ortega, J. K., and Vernerey, F. J. (2018). A statistical model of expansive growth in plant and fungal cells: the case of phycomyces. Biophys. J. 115, 2428–2442. doi: 10.1016/j.bpj.2018.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Sridhar, S. L., Schneider, M. C., Chu, S., de Roucy, G., Bryant, S. J., and Vernerey, F. J. (2017). Heterogeneity is key to hydrogel-based cartilage tissue regeneration. Soft Matter 13, 4841–4855. doi: 10.1039/C7SM00423K

PubMed Abstract | CrossRef Full Text | Google Scholar

Sridhar, S. L., and Vernerey, F. (2018). Localized enzymatic degradation of polymers: physics and scaling laws. Phys. Rev. Appl. 9:031001. doi: 10.1103/PhysRevApplied.9.031001

CrossRef Full Text | Google Scholar

Stephen, M. J., and Straley, J. P. (1974). Physics of liquid crystals. Rev. Mod. Phys. 46:617. doi: 10.1103/RevModPhys.46.617

CrossRef Full Text | Google Scholar

Stoddart, J. F. (2017). Mechanically interlocked molecules (MIMs)-molecular shuttles, switches, and machines (nobel lecture). Angew. Chem. Int. Ed. 56, 11094–11125. doi: 10.1002/anie.201703216

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, M. A. C., Huck, W. T., Genzer, J., Müller, M., Ober, C., Stamm, M., et al. (2010). Emerging applications of stimuli-responsive polymer materials. Nat. Mater. 9:101. doi: 10.1038/nmat2614

PubMed Abstract | CrossRef Full Text | Google Scholar

Stukalin, E. B., Cai, L. H., Kumar, N. A., Leibler, L., and Rubinstein, M. (2013). Self-healing of unentangled polymer networks with reversible bonds. Macromolecules 46, 7525–7541. doi: 10.1021/ma401111n

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, H., Price, C. A. H., Jing, L., Tian, Q., Liu, J., and Qian, K. (2019). Janus particles: design, preparation, and biomedical applications. Mater. Today Bio. 4:100033. doi: 10.1016/j.mtbio.2019.100033

PubMed Abstract | CrossRef Full Text | Google Scholar

Tagliazucchi, M., de la Cruz, M. O., and Szleifer, I. (2010). Self-organization of grafted polyelectrolyte layers via the coupling of chemical equilibrium and physical interactions. Proc. Natl. Acad. Sci. U.S.A. 107, 5300–5305. doi: 10.1073/pnas.0913340107

PubMed Abstract | CrossRef Full Text | Google Scholar

Tagliazucchi, M., and Igal, S. (2015). Transport mechanisms in nanopores and nanochannels: can we mimic nature? Mater. Today 18, 131–142. doi: 10.1016/j.mattod.2014.10.020

CrossRef Full Text | Google Scholar

Takaffoli, M., Zhang, T., Parks, D., and Zhao, X. (2016). Mechanochemically responsive viscoelastic elastomers. J. Appl. Mech. 83, 071007-1–071007-9. doi: 10.1115/1.4033431

CrossRef Full Text | Google Scholar

Tanaka, F., and Edwards, S. F. (1992). Viscoelastic properties of physically cross-linked networks -transient network theory. Macromolecules 25, 1516–1523. doi: 10.1021/ma00031a024

CrossRef Full Text | Google Scholar

Tanaka, T., and Fillmore, D. J. (1979). Kinetics of swelling of gels. J. Chem. Phys. 70, 1214–1218. doi: 10.1063/1.437602

CrossRef Full Text | Google Scholar

Tellers, J., Pinalli, R., Soliman, M., Vachon, J., and Dalcanale, E. (2019). Reprocessable vinylogous urethane cross-linked polyethylene via reactive extrusion. Polym. Chem. 10, 5534–5542. doi: 10.1039/C9PY01194C

CrossRef Full Text | Google Scholar

Ula, S. W., Traugutt, N. A., Volpe, R. H., Patel, R. R., Yu, K., and Yakacki, C. M. (2018). Liquid crystal elastomers: an introduction and review of emerging technologies. Liq. Crystals Rev. 6, 78–107. doi: 10.1080/21680396.2018.1530155

CrossRef Full Text | Google Scholar

Vernerey, F., and Shen, T. (2017). The mechanics of hydrogel crawlers in confined environment. J. R. Soc. Interface 14:20170242. doi: 10.1098/rsif.2017.0242

PubMed Abstract | CrossRef Full Text | Google Scholar

Vernerey, F. J. (2018). Transient response of nonlinear polymer networks: a kinetic theory. J. Mech. Phys. Solids 115, 230–247. doi: 10.1016/j.jmps.2018.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Vernerey, F. J., Long, R., and Brighenti, R. (2017). A statistically-based continuum theory for polymers with transient networks. J. Mech. Phys. Solids 107, 1–20. doi: 10.1016/j.jmps.2017.05.016

CrossRef Full Text | Google Scholar

Villani, C. (2002). A review of mathematical topics in collisional kinetic theory. Handb. Math. Fluid Dyn. 1, 71–74. doi: 10.1016/S1874-5792(02)80004-0

CrossRef Full Text

Wang, C., Li, W., Jin-hao, H., and Jian, Z. (2018). Computer Simulation on the pH-responsive block copolymer membrane. Acta Polymerica Sinica 4, 515–523. doi: 10.11777/j.issn1000-3304.2017.17137

CrossRef Full Text | Google Scholar

Wang, Q., Gossweiler, G. R., Craig, S. L., and Zhao, X. (2015). Mechanics of mechanochemically responsive elastomers. J. Mech. Phys. Solids 82, 320–344. doi: 10.1016/j.jmps.2015.05.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Li, Z., Ouyang, J., and Karniadakis, G. E. (2020). Controlled release of entrapped nanoparticles from thermoresponsive hydrogels with tunable network characteristics. Soft Matter 16, 4756–4766. doi: 10.1039/D0SM00207K

PubMed Abstract | CrossRef Full Text | Google Scholar

Warner, M., and Terentjev, E. M. (1996). Nematic elastomers—a new state of matter? Prog. Polym. Sci. 21, 853–891. doi: 10.1016/S0079-6700(96)00013-5

CrossRef Full Text | Google Scholar

Warner, M., and Terentjev, E. M. (2007). Liquid Crystal Elastomers, Vol. 120. Oxford, UK: Oxford University Press.

Wei, M., Gao, Y., Li, X., and Serpe, M. J. (2017). Stimuli-responsive polymers and their applications. Polym. Chem. 8, 127–143. doi: 10.1039/C6PY01585A

PubMed Abstract | CrossRef Full Text | Google Scholar

White, T. J., and Broer, D. J. (2015). Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 14, 1087–1098. doi: 10.1038/nmat4433

PubMed Abstract | CrossRef Full Text | Google Scholar

Wojtecki, R. J., Meador, M. A., and Rowan, S. J. (2011). Using the dynamic bond to access macroscopically responsive structurally dynamic polymers. Nat. Mater. 10, 14–27. doi: 10.1038/nmat2891

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J.-B., Shu-Jia, L., Hong, L., Hu-Jun, Q., and Zhong-Yuan, L. (2019). Dynamics and reaction kinetics of coarse-grained bulk vitrimers: a molecular dynamics study. Phys. Chem. Chem. Phys. 21, 13258–13267. doi: 10.1039/C9CP01766F

PubMed Abstract | CrossRef Full Text | Google Scholar

Yakacki, C. M., Saed, M., Nair, D. P., Gong, T., Reed, S. M., and Bowman, C. N. (2015). Tailorable and programmable liquid-crystalline elastomers using a two-stage thiol–acrylate reaction. RSC Adv. 5, 18997–19001. doi: 10.1039/C5RA01039J

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, H., and Tsujii, K. (2005). Potential application of poly (N-isopropylacrylamide) gel containing polymeric micelles to drug delivery systems. Colloids Surf. B Biointerfaces 46, 142–146. doi: 10.1016/j.colsurfb.2005.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, H., Yu, K., Mu, X., Shi, X., Wei, Y., Guo, Y., et al. (2015). A molecular dynamics study of bond exchange reactions in covalent adaptable networks. Soft Matter 11, 6305–6317. doi: 10.1039/C5SM00942A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, G., Huang, Z., Xu, Z., and Yan, L. T. (2018). Tailoring interfacial nanoparticle organization through entropy. Acc. Chem. Res. 51, 900–909. doi: 10.1021/acs.accounts.8b00001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, J., Gordon, M. R., Ventura, J., Li, L., and Thayumanavan, S. (2013). Multi-stimuli responsive macromolecules and their assemblies. Chem. Soc. Rev. 42, 7421–7435. doi: 10.1039/c3cs60094g

PubMed Abstract | CrossRef Full Text | Google Scholar