A Review on Developments in Magnesium Alloys

In order to facilitate the understanding of the current research efforts and directions, this article first introduces the anomalous/problematic features of magnesium (Mg) and presents the recent approach of stacking fault energy (SFE)–based alloying element selection to lessen or eliminate this problem. Stacking fault energy computations via ab initio techniques necessitate an understanding of the free electron density distribution around atoms in a solid solution. Therefore, the assessment of the role of atoms by also considering the possibility of short range order (SRO) formation rather than a random solid solution has been revisited. Two possible types of SRO have been indicated. The relevant electronic interactions between the host Mg and the alloying element atoms are more clearly incorporated in a generally less known model by Miedema based on atomic-level thermodynamics rather than in Hume–Rothery rules. This more successful approach has also been addressed here. An evaluation founded on these premises, introducing the relatively more recent Mg alloy systems, has been given in terms of their achievements toward healing the problematic features of Mg alloys. The spectrum of alloy systems discussed ranges from doping of Mg to dilute alloy systems and to some rich alloy systems that offer remarkable properties. Among the first category, an unorthodox addition, doping with oxygen, and its implications, has been presented. The dilute alloy systems and their compositional design based on SRO and SFE together with their potentials have been reviewed. Among the rich alloy compositions, the most interesting precipitate systems, that is, the ones involving order and intermetallic formations, long-period stacking order phases, and quasi-crystals, have been discussed. Among all the alloying elements, one that deserves particular attention, calcium, with its implications such as being economical, offering environmentally friendly Mg metallurgy, and remedial effects on the shortcomings of engineering properties, and a closely related issue of calcium oxide (CaO) addition have been scrutinized. This article also makes an attempt to point out the future directions throughout the text, whenever possible.

Introduction

Several complementary reviews to the one presented here can be found in the literature. A very detailed and fascinating history of magnesium (Mg) production and its use have been presented by Witte (2015). Elegant reviews by Nie (2012) and Pekguleryuz (2013), covering the spectrum of Mg alloys up to the beginning of this decade, and the thought-provoking strong criticism by Abaspour and Cáceres (2015) on the conventional interpretation of solid solutions of Mg as random solutions are strongly recommended to the readers.

As Witte (2015) mentioned, the earliest use of Mg was for applications, such as ignition and photography flashes. Interestingly, its application as biomaterial also reaches as far back as 1878. Then, we see a large-scale use of Mg alloys in aviation prior to and during World War II for purely military purposes. During those years, only in the United States the production capacity would make up about a quarter of today's world production capacity of 950,000 tons (Albright et al., 2002; Pekguleryuz et al., 2002). The earlier association of the term “electron” with Mg alloys was said to be perhaps due to its bright white light when burning or as a tribute to the ancient alchemical term electrum (Witte, 2015). Although, this term actually originated from the geologically occurring gold and silver (Ag) alloys that were used for coinage by the inventors of money, the Lydians of the Aegean coast of Anatolia.

The review presented here does not claim to cover all aspects of alloy development efforts on Mg. For example, we will not attempt to include the consequences of alloying additions that are related to various processing methods so that the text remains within the permitted limits.

Expectations in alloying studies on Mg go beyond achieving superior engineering properties. Although such properties, if achieved, are certainly welcome, expansion of the use of Mg alloys necessitates at least lessening or, even better, remedying the anomalies/problematic attributes of Mg and its earlier commercial alloys. Without stating these issues on Mg, it would be difficult to appreciate the core aim of the efforts and the directions in the studies focusing on Mg alloys. Therefore, with the aim of serving a broader spectrum of readers, we will first introduce the problematic characteristics of Mg.

This article will next attempt to explain the current approach to recuperate those problematic properties of Mg through changing the stacking fault energy (SFE) of different planes of the hexagonal crystal. The very concept of SFE involves the changes in the free electron density distribution around atoms in solid. Thus, it also becomes necessary to evaluate how the solute atoms behave in changing this distribution in the Mg lattice. Therefore, we will, on the one hand, scrutinize the most recent approach in alloy development, that is, controlling the SFE via alloying element additions, and on the other hand, revisit a generally less known scheme of Miedema that assesses the atomic-level thermodynamic interactions in terms of electron exchange between different atoms of binary solid solutions using the electron gas model of atom. Based on the effects of alloying elements from these perspectives, the possibility of two different types of short range order (SRO) will be proposed here. We will then embark on reviewing some of the most outstanding Mg alloy systems. Although the atomic-level concepts of SFE or Miedema's model are introduced through binary systems, our review will extend beyond the binary systems into alloys that form long-period stacking order (LPSO) phases or quasi-crystals. This is so, mainly because these alloy systems appear to be the most successful ones in terms of their properties, and those concepts cannot be ignored for them. However, it should be emphasized that our purpose is neither to take on the task of implementation of those atomic-level concepts to multicomponent alloys, nor to present all the experimental alloy systems given in the literature in a comparative manner. Needless to say, some remedial contributions to change the problematic properties of Mg can be and have been sought through various processing routes as well. However, we will not shift the attention out of the fundamental solution, that is, alloying.

Revisiting the Fundamental Characteristics of Magnesium

Magnesium is the lightest structural metal. Magnesium and its earlier commercial alloys (e.g., AZ or AM series) have more than few shortcomings that generally manifest themselves together in some combinations. Some of these properties are simply inferior properties as compared to those of aluminum alloys and steels. In this respect, it suffices to recall the low elastic modulus, yield strength, and deformation capacity; sluggish and poor aging response; and inferior creep and corrosion resistance. These constitute engineering properties that may be tackled with, at least to some degree, and with a penalty of reduced final weight saving in application, through part design. Yet, some other properties may be seen as anomalies that require in-depth understanding before seeking remedies through alloying. Those may be briefly named as the tensile/compression asymmetry, pseudoelastic behavior, deformation texture, and inefficiency of recrystallization in removing it, and peculiarities in fatigue behavior.

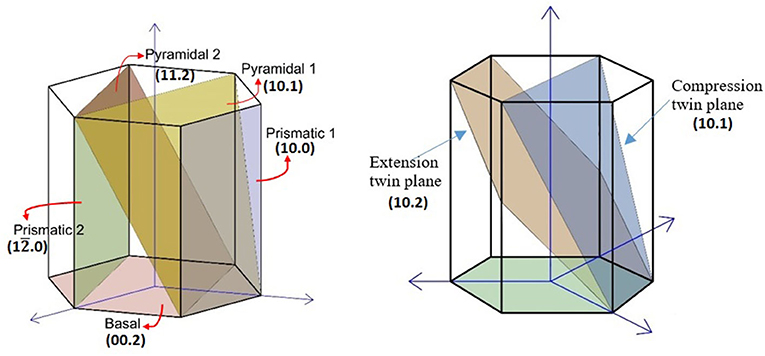
The slip and twinning systems in Mg are shown in Figure 1. Perhaps the first anomaly of Mg may be pointed out as its incompatibility with von Misses criterion due to lack of five independent slip systems. Magnesium circumvents this criterion due to twinning that operates concomitantly with the basal slip at room temperature and thus shows, although limited, some plastic deformation capacity. The other slip planes of Mg, that is, prismatic and pyramidal planes, operate sequentially, becoming active over 225°C.

FIGURE 1

Figure 1. Slip and twinning planes in magnesium crystal.

Concomitant activation of twinning with slip brings about an anomaly of Mg single crystal. Magnesium displays yield strength asymmetry in compression and tensile modes (a critical assessment given in Barnett et al., 2006), the tensile yield strength being much higher than that in compression. Both the room temperature twinning and the yield asymmetry are related to the polar nature of twinning and the critical resolved shear stress (CRSS) values of different twinning planes (Agnew, 2012). It should be noted that the terminology used for the two twinning modes may be somewhat misleading. The tensile (extension) twinning simply is the one that extends an Mg single crystal along its c-axis, while compression twinning shortens. The low CRSS value of what is known as extension (tensile) twinning and the CRSS difference between the two twinning modes and their different Schmid factors (m) (Nan et al., 2012; Kim and Park, 2018) are telling why the former predominates (CRSS ratio for basal <a> slip, {10$\overline{1}$2} extension twinning, prismatic <a> and pyramidal <c+a> slip: 1:0.7:2:15) (Barnett et al., 2006). The yield asymmetry of a single crystal, when coupled with texture, reveals itself once again in polycrystalline material, begetting an anisotropic material.

Twinning may appear to be a way to divide an existing α-Mg grain into several portions and create strengthening as in grain refinement. However, twinning cannot be activated in Mg when the grain size is well below 1μ (Wu et al., 2011; Zhu Y. T. et al., 2012). An additional consequence is that extensive basal slip followed by compression twinning can lead to strain softening as shown in experiments conducted on Mg micropillars (Yu et al., 2012). This is simply because the angular deviation created by compression twinning brings the basal planes, which has the highest Schmid factor, into a favorable orientation for further slip. Thus, twinning is also closely related to the crystallographic texture in deformed structures (Nie et al., 2013).

Twinning asserts itself once again and leads to pseudoelasticity. Upon reversing the stress direction, although not through an infinite number of cycles, detwinning creates what appears to be an elastic, that is, pseudoelastic, behavior. Because, at each cycle, the twinning is accompanied by slip in the same material, not all twins detwin together (Yu et al., 2011). Moreover, twinning is polarized (Christian and Mahajan, 1995), and twinning dislocations cannot behave in a military fashion with exact numbers during every reversal of the stress; thus, the pseudoelastic behavior peters out after some cycles (Wu et al., 2008; Brown et al., 2009; Yu et al., 2015).

Anomalies of Mg further extend into its fatigue behavior and complicated by twinning and detwinning (Yu et al., 2011), necessitating the interpretation of the stress- and strain-controlled fatigue tests separately (Sumitomo et al., 2003; Hasegawa et al., 2007; Mann et al., 2007). Because below a threshold grain size twinning ceases, such interpretations on fatigue should also consider the effect of grain size as well as the initial texture of the materials (Huppmann et al., 2011).

Deformation texture becomes particularly emphasized in Mg with a large contribution from its easy twinning. This leads to yet another anomaly in Mg. While texture can be lessened greatly or removed in other systems, once texture is created in Mg and many of its alloys, it becomes persistent even after the conventional remedial treatment of recrystallization. Cell formation during recovery stage does not happen, and consequently, newly forming “recrystallized” grains originate from the already textured parents, thus rendering the texture-removing function of recrystallization process futile. This feature is closely related to lack of dislocation populations on non-basal planes as well as to lower SFE of the basal plane, indicating that the remedial measure is also related to the SFE levels of different planes in Mg.

Critical resolved shear stress values for basal and prismatic planes of Mg show very different reduction rates with temperature, and non-monotonic changes for prismatic planes with temperature and alloy concentration in some systems, as well as anomalous changes with temperature in case of second-order pyramidal planes, have been reported (Akhtar and Teghtsoonian, 1969; Obara et al., 1973; Hosford, 1993; Christian and Mahajan, 1995; Balogh et al., 2009; Cipoletti et al., 2011). If we look at the room temperature values, CRSS ranges from 5 MPa for basal slip, 10 MPa for extension twinning (2.4 MPa in a report by Yu et al., 2011), 20 MPa for prismatic slip, 40 MPa for pyramidal slip, and 70–80 MPa (at 150°C) for compression twinning (Chapuis and Driver, 2011). Therefore, it should be remembered that, at the early stages of deformation, the tensile twins, because of lower CRSS value, are more likely to be observed rather than the compression twins. For details of twinning contribution to the total deformation, the reader should refer to the literature (Yoo, 1981; Brown et al., 2005).

Many studies relate the changes in CRSS values and/or in c/a ratio brought in by alloying additions. Indeed, via alloying, CRSS values can change through electronic effects (Masoumi et al., 2011), as well as by geometrically changing the c/a ratio of Mg crystal (Yoo, 1981; Yoo and Lee, 1991; Chen and Boyle, 2009; Wang et al., 2009). The changes in CRSS for different planes may not happen to the same extent (Kim et al., 2015) and depend on the changes incurred due to the alloying elements. Nor the changes in c/a ratio can simply be predetermined based on the atomic size differences of the constituent elements.

In a theoretical geometrical evaluation, c/a ratio undoubtedly alters the CRSS values of different slip planes as it changes the corresponding Schmid factors. Since the pioneering studies by Raynor (1959), it has come to be said that reduction in c/a ratio promotes non-basal slip activity in Mg. c/a ratio has been related to texture development as well (Styczynski et al., 2004). However, c/a ratio does not seem to be a factor fundamental enough to explain all the observed alloying effects in mechanical behavior in a consistent and a coherent manner. c/a ratio of Mg has been found to decrease for its extended solid solutions prepared via rapid solidification techniques for systems other than the binary Mg–gadolinium (Gd), Mg–yttrium (Y), and Mg–aluminum (Al) alloys (Hehmann et al., 1990). While modulus can change depending of c/a ratio, Chen and Boyle (2009) showed that the strength was not related to the modulus changes in Mg–X [X: Y, Al, zinc (Zn)]. Likewise, explanations on the ease of activation of different twinning modes based on c/a ratio changes in hexagonal close packed (HCP) metals, in general, are highly complex and sometimes even contradictory, creating a need to resort to the involvement of other additional mechanisms such as the ease of atomic shuffling or the ability of twin boundaries to act as sinks for dislocations (Yoo, 1981; Yoo and Lee, 1991; Wang et al., 2009). It is worth remembering that hcp titanium with a lower c/a ratio (c/a_Mg: 1.624 and c/a_Ti :1.58) has CRSS values lower for basal and higher for prismatic slip as compared to Mg (Raynor, 1959).

On the other hand, ab initio calculations do not treat CRSS values as a simple outcome of crystal geometry. The alloying effects go beyond changing the c/a ratio as the dislocation core structure and therefore its mobility and ability to dissociate and, in turn, to cross-slip drastically change with different solute atoms (Yasi et al., 2010; Ando et al., 2013; Liu and Li, 2015). For example, changes in c/a ratio can be attributed to atomic size changes, especially of Mg atoms, depending on the solute type. Ab initio computations by Chen and Boyle (2009) showed that a and c parameters and c/a reduce slightly in Mg–Zn, in which atomic volume of Mg and possibly of Zn also appeared to be reduced (as will be discussed further), whereas Y slightly increased the lattice volume by changing a and c, without changing the c/a ratio.

The sequential activities, based on different CRSS values and/or temperature, of different slip planes of Mg point out that some of these slip/twinning modes are “softer,” whereas the others can be described as “hard.” It then becomes obvious that the strategy to strengthen Mg or to increase its deformation capacity and even to lessen the propensity to generate deformation texture, as well as the ease of its removal through recrystallization, hinges on establishing the effects of alloying elements and their necessary quantities. If the differences in CRSS values are lessened, it would effectively mean either the “harder” modes becoming “softer” or vice versa. Another way of looking at “hard” and “soft” modes can be based on dislocation characteristics. For example, if thermal cross-slip is facilitated via increasing the SFE of the basal plane, and/or by lowering the SFE of nonbasal planes, a reduced anisotropy in deformation can be achieved (Moitra et al., 2014). If the prismatic and pyramidal slip systems, which do not contribute to deformation at room temperature, are activated, the former provides two and the latter five additional slip systems (Avedesian and Baker, 1999).

The relatively more recent efforts in resorting to the ab initio techniques together with the experimental studies focusing on dilute alloys stem from this perspective. The success of first-principles techniques (density functional theory, embedded atom model, molecular dynamics) in predicting the influences of alloying elements on dislocation behavior, and consequently on the overall mechanical behavior, lies in the fact that they allow consideration of a fundamental property, that is, free electron density distributions and the resulting bond strength and SFE changes.

In order to benefit more from the vast amount of literature involving ab initio techniques regarding the alloying, the reader should be well-versed on SFE and its influences on materials behavior. Therefore, it seems appropriate to remind ourselves the following:

Concepts of Stacking Faults and Stacking Fault Energy

It is well-known that, when stacking close packed layers of atoms to constitute an face centered cubic (FCC) or an HCP model, the difference arises by the positioning of only the third layer, thus …ABCABCABC… stacking gives FCC, whereas …ABABAB… stacking gives HCP. Thus, a mistake in these orders can convert one of these two crystals into the other locally. Such out-of-step stacking can be due to an extra atomic layer [named as “extrinsic stacking fault” (SF)] or, for example, because of condensation of vacancies, a missing layer (“intrinsic SF”). One can define a stacking disorder (SF) perpendicular to any crystal plane and in different directions in it, but for example, in prismatic plane of Mg, a stable SF cannot form as energetically prohibited (Uesugi et al., 2009).

If we make definitions based on the basal plane of Mg, the types of intrinsic SFs are two types, that is, the “growth type” and “deformation” types. The former is a missing layer with shear above it by 1/3[10$\overline{1}$0] (…ABABCBCB…– I₁ stacking), and the latter involving only shear by 1/3[10$\overline{1}$0] (…ABABCACACA…–I₂ stacking). Because SF involves a change in bond angles, a third type is also possible corresponding to stacking across a twin boundary (…ABABCBABABA…–T stacking) (Weinert, 1997). The order of increase in the energies of I₁, I₂ and extrinsic SF manifests itself in the same order in terms of the number of influenced planes neighboring the SF plane (Wang et al., 2012; Wang W. Y. et al., 2014). While I₂ SFE is directly representing an energy barrier to slip, attempt has been made also to correlate the seemingly unrelated I₁ SFE to deformation processes as will be discussed later.

Stacking fault energy, at the fundamental level, depends on the free electron density distribution, a property that changes inevitably with each alloying element, as their contribution to free electron density and/or the lattice distortion they introduce differs. Although a change in the stacking order does not change the coordination number of the atoms at and across the fault plane, at least the bond angles change. Hence, the fault plane, that is, SF, is a more energetic location compared to the planes located in the usual stacking order, in addition to being a plane where free electron density distribution in any direction from one atom to any of the neighboring atoms has also changed. An SF and its energy, as we will focus on later, not only stem from its atomic stacking configuration but also is fundamentally related to the atomic-level thermodynamics.

An SF is by definition bound by two partial dislocations, constituting a two-dimensional defect lying in between. The energy of a dislocation, being the sum of two terms, that is, the missing bond plus the strain energy due to the bent planes immediately neighboring the dislocation, also changes with SFE. Thus, dislocations on planes where SFE is low become more energetic, as the dislocation core size increases with decreasing SFE. Consequently, the ease of dissociation of a dislocation becomes closely related to SFE, getting more difficult as SFE increases, and vice versa. Hence, the prerequisite for creation of an SF is a low-enough SFE allowing dissociation of a full dislocation, relating the size of the SF area between the partials inversely to SFE.

These concepts, namely, the size of SF area and dislocation core size, change all of the mechanical responses of metals through changing the dislocation behavior. Stacking fault energy is related to the ease of birth, glide, cross-slip, and climb of dislocations. The sequential activation of the slip planes of Mg also manifests itself in the computed SFE values [SFE_basal < 50 mJ/m²; SFE_prismatic = 354 mJ/m²; SFE_pyramidal = 452 mJ/m² (Wen et al., 2009)]. These figures imply that cross-slip and climb for pyramidal slip operate more readily than those for other slip systems because of higher SFE levels (Li et al., 2013). Moreover, the initial glide of dislocations (Zhao et al., 2006), formation of twins, and movement of their boundaries (Bernstein and Tadmor, 2004; Van Swygenhoven et al., 2004) are all facilitated with lower SFEs, while climb gets slower, cross-slip restricted, and steady-state creep rate reduced (Li and Kong, 1989; Guo et al., 2006). It should also be noted that with larger core sizes, because of larger strain fields of dislocations, in a system of low SFE, while facilitating the movement of an individual dislocation, strain hardening becomes quicker, that is, dislocation movement rapidly becomes more difficult due to the larger core size of dislocations when their populations increase during deformation.

Thus, one would understand that SFE would also change whenever other players/factors are introduced. For example, if the fault plane (SF) involves foreign atoms, if near other crystal defects, when extrinsic factors such as temperature and strain are in play, we may expect SFE to change by some degree. However, all these are not to say that SFE is such an ambiguous parameter that can be ignored. On the contrary, one should remember that SFE is a relative term that can be used in a comparative way when different metals, alloys of a particular metal-base, or different planes of the same crystal are considered. Although there also exists a definition as generalized SFE (GSFE, γ surface), each crystallographic plane has, in essence, its own specific SFE value. Generalized SFEs should ideally be calculated by considering the lattice plane neighboring the SF on both sides, that is, the relaxation of the lattice perpendicular to the SF (Vitek, 1968; Yin et al., 2017). The extent of this relaxation is different when considering the SFE of different planes. Furthermore, GSFE values computed by assuming a random solid solution may contain a source of error [e.g., if SRO exists]. Thus, it becomes more useful to compare the individual SFE values of planes that are operative in slip or twinning. It should be emphasized that, in a low-symmetry system such as HCP Mg, SFE of individual crystal planes becomes more distinctive and must be considered specifically. On the other hand, GSFE values are more suitable for interpretations based on Peierls–Nabarro forces (Moitra et al., 2014).

The implications of SFE can be better interpreted through “energy change with respect to the unfaulted atomic stacking” vs. “displacement along a fault vector” plots based on ab initio calculations. These plots show an increase followed by a decrease over the full movement of the fault vector as shown schematically in Figure 2. More complex three-dimensional representations of lattice response to displacements, namely, GSFE surfaces (γ surface), are also available in the literature (Wen et al., 2009; Yasi et al., 2010; Zhang et al., 2013). In such a plot if a single curve appears, the maximum (γ_USF-unstable SF) (Figure 2A) represents the energy barrier for dislocation dissociation and implies that formation of SF is not possible. If the curve shows two maxima, the first one still shows the energy barrier for the formation of an SF, and the trough [γ_SF, also termed as γ_IS (intrinsic SF)] shows the energy of a stable SF. The second maximum in this case (Figure 2B) corresponds to the energy barrier for the formation of a twin. The minima in such plots, although very difficult, can be experimentally determined, while the maxima can be calculated only via ab initio techniques, which are also demanding tasks by any measure. The height of the peaks, that is, ratio of stable and unstable SFE levels (γ_SF/γ_USF) would indicate ease of slip, while twinning tendency diminishes as the ratio of the maxima of the two peaks (γ_UT/γ_USF) increases (Wang et al., 2011; Muzyk et al., 2012). Therefore, in order to reveal whether the birth of dislocations, dissociation into partials, or twinning is facilitated due to a particular alloying element, an evaluation of the changes in the ratios of γ_SF /γ_USF and γ_UT/γ_USF on specific crystallographic planes becomes critical. For example, Wen et al. (2009) showed that the unstable SFE for the prismatic plane {10$\overline{1}$10} is one order of magnitude higher than the (0001) basal plane, which effectively points out that creation of <c+a> dislocations is difficult on prismatic planes. It was also shown that the γ_USF for the second-order prismatic plane {11$\overline{2}$0} is one order of magnitude higher than the first-order prismatic plane {10$\overline{1}$0}.

FIGURE 2

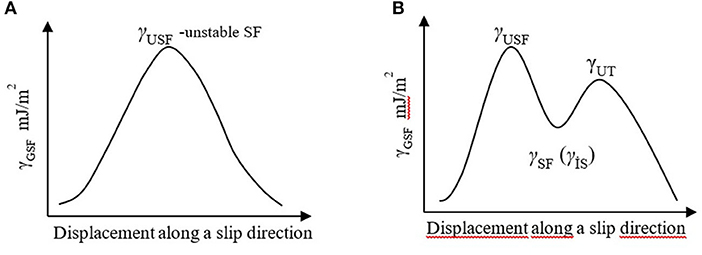
Figure 2. Typical computed GSFE curves. (A) the maximum (γ_USF, unstable SF) represents the energy barrier for dislocation dissociation and implies that formation of SF is not possible; (B) if two maxima exist, the first one still shows the energy barrier for the formation of a stacking fault, which means dissociation of dislocation is possible, and the trough (γ_SF, also termed as γ_IS, -intrinsic SF-) shows the energy of a stable SF. The second maximum in this case corresponds to the energy barrier for the formation of a twin.

As can be understood, developing alloys has reached to the point where assessment and adjustment of dislocation characteristics, and even phase stability in some other systems (e.g., new generation steels), in relation to SFE became imperative. In this regard, ab initio techniques have an exciting power in predicting the SFE changes for specific crystal planes and, in turn, all related changes for an alloy. It is obvious that ductility or strengthening considerations for Mg, in other words, adjusting the relative activities of “soft” and “hard” modes through alloying, has to involve the changes created in SFE(γ) and dislocation core properties as demonstrated in the literature (Yasi et al., 2010; Sandlöbes et al., 2011, 2012; Liu et al., 2017; Buey et al., 2018).

Effects of Individual Alloying Elements

Thermodynamic Ab initio Approach and Ab initio SFE Calculations

Because of the inherently low strength and ductility of Mg, solid solution strengthening may be regarded as the most important issue before considering the usefulness of all other strengthening mechanisms (Abaspour and Cáceres, 2015) as alloying element selection will influence all other strengthening mechanisms. Overwhelming majority of the literature is on substitutional alloying element additions, ranging in coverage from dilute systems to precipitate forming compositions. One example of much less explored area is Mg alloys containing interstitial elements, in which an interesting example now exists and will be discussed later. It is also interesting to note that those studies mostly consider the solid solutions as random solid solutions. The articles based on ab initio techniques, on the other hand, report the influence of alloying elements in solid solutions from the view of changing SFE values. The ab initio calculations, being highly important and informative, they are not exactly explaining interactions between the host and solute atoms based on atomic-level thermodynamics openly and clearly.

Therefore, we will make an attempt, by referring to the relevant literature, to point out that most of the solute elements do not form random solid solutions due to electronegativity differences, but instead they create what may be termed as electronic effects at the atomic level and consequently create SRO with strikingly different results. Thus, it can be argued that any calculation disregarding this concept and assuming random solid solutions would deviate, to some extent, from the reality.

The ultimate aim is to understand the behavior of each element and then expand this understanding toward designing multicomponent alloy systems. The fundamental approach attempting to explain the effects of individual elements in solid solutions has to be based on atomic-level thermodynamics. The theories on interatomic bond formations date back to Pauling (1960). Later, the geometrical method proposed by Miedema (1973a,b); Miedema et al. (1975) and Buey et al. (2018) following the work by Waber et al. (1963) showed better predictions for solubility or intermetallic formations.

These prediction methods were employing atomic-level thermodynamic parameters, for example, an electronegativity (equivalent to chemical potential) vs. atomic radius diagram (Waber et al., 1963), and chemical potential difference vs. electron density difference at the atomic Wigner–Seitz cell boundaries (Miedema, 1973a,c). As we will further discuss, the coordinates in these plots, for a host element of concern, indicate a specific area in the plot for a binary alloy, with great statistical correction over many binary systems, whether a solid solution and/or intermetallic compound is possible, and hence the term geometrical method is used.

On the other hand, the more recent approach in line with that of Miedema's, that is, ab initio techniques, so far based on relatively simple atomistic models and performed for 0 °K, has already proven invaluable in revealing the effects of alloying elements as a reference state. Some of such studies present the free electron density distributions (contour maps) around a foreign atom (Chen and Boyle, 2009; Wu et al., 2016) and also reveal the density of states (DOS) for electron orbitals involved in electron exchange (Chen and Boyle, 2009) and calculate the consequent SFE changes created (Sandlöbes et al., 2012, 2014; Zhang et al., 2013; Pei et al., 2015; Wu et al., 2016; Dong et al., 2018), including the influence of van der Waals forces (Ding et al., 2016) on SFEs in Mg. Moreover, some recent studies applied the same approach to dislocation–foreign atom (Yasi et al., 2010, 2011; Tsuru and Chrzan, 2015; Buey et al., 2018) or dislocation–dislocation (Fan et al., 2017) interactions with very interesting results.

It seems reasonable to say that the researchers have now a far better understanding on the effects of individual alloying elements as a result of ab initio approaches. The knowledge thus accumulated may be heralding the computer-based alloy design in some not-so-distant future. In conjunction with these efforts, experimental alloy systems started to emerge offering solutions to the shortcomings of Mg. The so-far accumulated knowledge, as Pei et al. (2015) named it, is already close to use a “theory-guided rapid alloy prototyping” approach.

Assessment of Solubility or Compound Formation

Thermodynamic assessment of solid solution hardening can be made more critically based on Miedema's model (Miedema, 1973a,b,c; Miedema et al., 1975) rather than on Hume–Rothery rules, as the former not only treats the electronegativity in physically less ambiguous way, but also takes the free electron density distribution around the atomic cells into account when calculating heat of formation. This treatment of free electron density distribution of the model also constitutes a central issue in the recent SFE calculations via ab initio techniques.

According to Miedema's model, when a solute atom is added (M-X binary), the system tries to smooth out free electron density distribution in the lattice at the atomic scale in addition to an electron charge transfer. The effect of the solute in these two terms is related to the electronegativity difference with the host and to the number of its valence electrons, that is, the chemical misfit. Moreover, in solid systems, additional energy terms are involved, that is, the misfit strains due to the size differences as well as the shear modulus misfit, thus making the assessment of solid state changes more complicated. Consequently, the bond energy, and in turn, SFE of a crystal plane, is also effected due to the presence of a solute. Computational techniques for solid state have been involving these concepts in calculating SFE values at atomic level with greater precision.

In the mathematical expression of Miedema, the formation enthalpy was expressed as follows:

$\begin{array}{l}\Delta H=f(c)[-Pe{(\Delta {\varphi }^{*})}^2+Q{(\Delta n_{WS})}^2-R]\end{array}$

(Miedema, 1973a,c)

where f (c) is a function of concentration; P and Q are assumed to be constants; e is electronic charge; Δϕ^* is the difference in chemical potential for electrons (equivalently the difference in electronegativity or difference between the work functions); and Δn_WS is the difference in the density of electrons at the boundary of the two atomic cells (i.e., Wigner–Seitz cells, which are subject to changes while atoms are changing positions from one equilibrium state to another, a point closely related to SFE; it should also be noted that Wigner–Seitz cell concept cannot be understood if one still assumes a spherical hard ball model for atoms).

The mathematical expression of the Miedema model was later modified in an empirical way for the atomic size factor (Zhang and Liu, 2002, 2005; Sun et al., 2011) and also extended to ternary systems as well (Dai et al., 2007). There may be more examples of its modifications in the literature beyond the knowledge of the author of this section.

Discrepancies in the geometrical predictions of the model when considering the case between transition and non-transition elements were attributed to a negative extra energy term R (explained to be due to hybridization of d and p orbital electrons). Unless a divalent non-transition metal is mixed with a strongly electronegative element, R was assumed to be negligible, that is, R = 0, for example, Mg, and a transition metal (Miedema, 1973a).

The heat of formation (ΔH) determines the nature of the binary mixture. Thus, it also dictates the general constitution of the binary phase diagram, indicating whether a random solid solution (ΔH = 0), a system with limited solubilities without any formations of intermetallics (+ΔH), or a system involving intermetallics (and small solubility), prevails (–ΔH) (Miedema, 1973a,b,c). Let us remember that strongly electronegative metals are those with greater tendency to form negative ions, and the weakly electronegative ones are those with a greater propensity to form positive ions. It follows that as the difference in electronegativity between the constituent elements in a binary alloy increases, a greater tendency to form intermetallic compounds is observed, with an accompanying larger heat release, that is, more negative heat of formation. In such a case, formation of a solid solution is also suppressed. This assessment would also reflect itself in the phase diagram of the mixture, in which more than a single eutectic can be expected if formation of intermetallics is probable. As pointed out by Miedema (1973a), based on an earlier work of Brewr (1967); in the extreme case when the two metals have strong affinity to each other, the mixture, as in the case of Hf and Pt, can be explosive. Albeit, as emphasized by Miedema, the very concept of electronegativity is difficult to establish for metals.

As Equation (1) shows, the two intrinsic terms, namely, the electronegativities of the constituent elements (which is shown to be linearly related to the work function in the original Miedema model) and their contributions to the free electron density of the mixture, determine the enthalpy of formation. The term Δϕ^*, created through charge transfer between the two constituent elements, makes a negative contribution to the formation enthalpy of the mixture, thus reducing the total free energy of the system. The term Δn_WS, involves rearrangement of electron density distribution at the atomic cell boundaries (Wigner–Seitz) with the need to smooth it out. This phenomenon requires a complementary change in the Wigner–Seitz atomic cell sizes of both of the elements, therefore constituting a positive contribution term, that is, making the atoms of both elements more energetic as compared to their pure state. The most problematic issue then becomes the complication arising when also taking the size (radius) of the constituent atoms into consideration especially for systems involving the transition metals due to their compressibility levels. Possibility of the two terms, Δϕ^* and Δn_WS being interdependent, was thought to be negligible and therefore ignored in the original model (Miedema, 1973a,c).

Thus, the arrived geometrical scheme is a plot of the Δϕ^* vs. Δn_WS, grouping the binary systems generally into two, with a linear line having the slope of P/Q. Nearly all the binary systems in transition metals that have a negative enthalpy are located above this line, constituting intermetallic forming binaries, and those with positive enthalpy values remaining below the border line, representing those that cannot form compounds and show low mutual solubility. This geometrical scheme was further elaborated in the same article, taking into account the fact that such a border line can be drawn for a specific element (Mg being the one in the original article) twice by crossing each other, because the absolute values of |Δϕ^*| and |Δn_WS| (Equation 1) would mathematically necessitate it. By doing so, Miedema's scheme now presents four sectors in the ϕ^* vs. n_WS diagram, with the upper and lower sectors belonging to binary systems of Mg–X that would show negative enthalpy, and the left and right sectors to those with positive values. Thus, by indicating the position of any element with its own values of ϕ^* vs. n_WS, a crossover can be generated, which geometrically reveals a crucial information, that is, upper and lower sectors involving those elements that would form intermetallics with the reference element. The graph for Mg has been given as a conceptual plot in Figure 3; for quantitative information on each element in this figure, the reader should refer to Miedema (1973a) and Abaspour and Cáceres (2015).

FIGURE 3

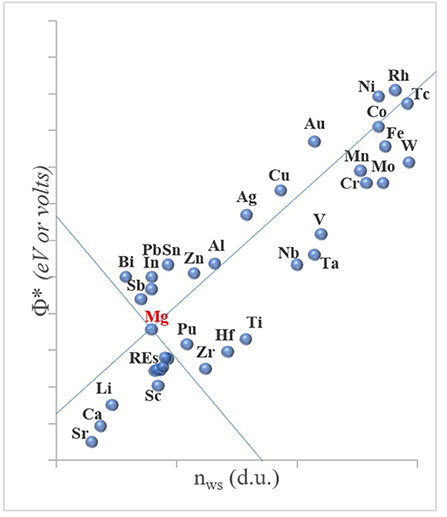
Figure 3. A conceptual illustration of Φ* (eV) the chemical potential for electrons (equivalently, electronegativity, or the work function) vs. n_WS (d.u., density unit) electron density at atomic cell (Wigner-Seitz) boundary (d.u., density units). The upper (north) and lower (south) sectors indicate the elements that can form intermetallics with Mg, and the left and right sectors involves the elements that do not (data adopted from the refs.: Miedema, 1973a; Abaspour and Cáceres, 2015).

Assessment of Solute Element Additions Based on Miedema's Scheme

The electronegativity differences between the solute and the solvent must have consequences at the atomic level and in terms of electron density distributions. Therefore, most binary systems should show some degree of resistance to form B–B bonds in a system of A–B, which may appear to be a simple solid solution on the respective phase diagram (i.e., considering the limited solubility regions at terminal sections of a phase diagram). This phenomenon was described as SRO in the early work by Cahn and Davies (1960), in which they also referred to the preceding studies of Houska and Averbach (1959) and Suzuki (1962). Short range order was also reported in earlier studies on binary Mg alloys, namely, in Mg–tin (Sn) (Henes and Gerold, 1962; van der Planken and Deruyttere, 1969), in Mg–(6.4 at%) Er and local order in Mg-(2.9 at.%) Gd (Gencheva et al., 1981), and in Mg–Zn (Akhtar and Teghtsoonian, 1969). Since then, a number of relatively recent studies on lean binary Mg alloys also focused on SRO (Blake and Cáceres, 2008; Abaspour and Caceres, 2013; Abaspour and Cáceres, 2015, 2016; Abaspour, 2014; Yang et al., 2014; Zhang et al., 2014). According to Abaspour and Caceres (2013), SRO was also claimed in previous studies (Henes and Gerold, 1962; Safranova et al., 1977) based on small-angle x-ray scattering. However, without refuting their claims, it should be borne in mind that Suzuki segregation (Suzuki, 1962) can also create similar x-ray scattering results. Many of the counter arguments on the effects of SRO were dismissed by Abaspour and Cáceres (2015). However, one that involves segregation of the solutes to dislocations does not seem to be easily dismissible. Serrated flow observed by these authors also testifies to this possibility, without going to the extreme example (Abaspour and Cáceres, 2015) of a Cottrell atmosphere.

Short range order can be viewed as a case where B–B bonds are not allowed in a binary A–B system. The phenomenon of temperature-independent flow stress in some Mg–X alloys, that is, “athermal component of solid solution strengthening,” has been attributed to SRO (Akhtar and Teghtsoonian, 1969; Abaspour and Cáceres, 2015, 2016; Abaspour et al., 2016). In essence, the phenomenon is an extra strengthening mechanism that cannot be explained based on simple solid solution strengthening (van der Planken and Deruyttere, 1969). Therefore, the physical meaning of SRO requires in-depth analysis in terms of inter atomic effects. As the term implies, SRO is limited to each A–B–A (letters representing atoms, not atomic layers) sequence in an α-Mg grain and effectively constitutes stronger obstacles to dislocation motion as compared to a case where the solute atom is just a substitution in a random solid solution. Whether the interaction of such solute atoms in SRO with dislocations can be considered as a short-range or long-range interaction is debatable as it also depends on the concentration of the solute. However, such types of obstacles would be expected to be more resistant to relatively high temperatures unlike the short-range interactions of dislocations, that is, as for the dislocation–dislocation interactions, which can be overcome readily with temperature effects. Consequently, presence of SRO can become especially useful for Mg to overcome its shortcomings such as low strength and elasticity modulus and poor creep resistance. The contribution of SRO to strength with high resistance to changes in temperature was demonstrated via compression and stress relaxation tests conducted at various temperatures (Abaspour and Caceres, 2013; Abaspour, 2014; Abaspour et al., 2016) and via creep experiments (Abaspour and Cáceres, 2015).

The following experimental observations were reported by Abaspour et al. for Mg–X [X: Y, Gd, Ca, Zn, Sn, antimony (Sb), and Al] binary systems: an initial linear strengthening at constant temperature tests; for some alloys, an increasing strength at higher temperatures and little or no stress relaxations. Studies by Abaspour (2014) and Abaspour and Cáceres (2014, 2016) showed that temperature dependence of the strength of some Mg–X [X: Al, Zn, Sn, Y, Gd, neodymium (Nd)] alloys displayed an athermal regime at low strain levels up to some different temperature range and to varying levels. The same workers further claimed that there was even a strength increase within a temperature range in the case of Mg–X (X: Y, Gd, Nd) (see Figures 2, 3 in Abaspour and Cáceres, 2016). These observations, which cannot be explained based on an ordinary solid solution, were all attributed to SRO in those alloys (Abaspour and Cáceres, 2016; Abaspour et al., 2016). The potential of these alloying elements to develop SRO in Mg was given, based on Miedema's model, in the following order (Abaspour and Caceres, 2013; Abaspour and Cáceres, 2016; Abaspour et al., 2016):

Y, Gd > Nd, calcium (Ca) > Zn, Ag, Sn > Al > Sb, strontium (Sr)… (Abaspour and Caceres, 2013; Abaspour and Cáceres, 2016)

This ranking given by Abaspour and Cáceres contradicts the implications of ab initio calculations of diffusion coefficients for the same binary systems:

D_Mg−Ca > D_Mg−Zn > D_Mg−Sn > D_Mg−Al … (Ganeshan et al., 2011)

The apparent contradiction may be due to the assumption of “random solid solutions” employed by Ganeshan et al. (2011). However, the bond strength calculations by Chen and Boyle (2009) also contradict the experimental values given by Abaspour and Cáceres (2015) for Mg–Zn. It seems that the interpretation of SRO may not be straightforward in every case and requires more detailed insight using the available ab initio calculations.

Assessment of Interatomic Bonding in Solid Solutions of Mg—Two Types of SRO

Abaspour and Cáceres (2015) disagreed with the approach to explain the solid solution strengthening incurred by Y and Gd elements (the athermal strengthening effect) in Mg–X systems via a valence mechanism as proposed by Chen and Boyle (2009). However, their objection seems unwarranted. An ab initio study by Chen and Boyle (2009) on binary systems, namely, Mg–Al, Mg–Zn, and Mg–Y, and on Mg–Li (Jin et al., 2011), showed that the interatomic bonding possessed different characteristics depending on the planes and directions in pure Mg, as well as in these lean binary alloys.

Interestingly, pure Mg was found to have, although very weak, directionality in bonds within the basal plane and perpendicular to it, the latter being stronger. The DOS (local DOS) calculations of pure Mg is consistent with several other reports (Wang et al., 2007; Peng et al., 2008; Kumari and Verma, 2018). It was shown that such directionalities were also displayed in Mg–Y (Chen and Boyle, 2009) and Mg–Al (Chen and Boyle, 2009; Ganeshan et al., 2011; Jin et al., 2011) systems, the latter being weaker than the former but both being stronger than those in pure Mg to varying degrees (Chen and Boyle, 2009). It should be stated that Mg acts weakly electronegative in Mg–Y (Stanford et al., 2015) and forming hybridized bonds with Y. Likewise, although Mg behaves electropositively in Mg–Al system, the bonding is again only weakly hybridized as the DOS calculations for Al in Mg–Al showed a reduction only for its highest energy levels (Ganeshan et al., 2011).

Mg–Zn system, on the other hand, did not show directionality as also indicated in some studies (Ganeshan et al., 2011; Garg et al., 2018). Similar cases in Mg–Li (Jin et al., 2011) and in Mg–Ca (Ganeshan et al., 2011), that is, a general depletion around the solute atoms and a general homogenization in their electron densities for all energy levels, were computed for Mg–Li and Mg–Ca, where the electronegativity differences are opposite to that in Mg–Zn, that is, Mg acting electronegatively and Li and Ca acting electropositively. Moreover, Zn slightly reduced a and c parameters and c/a ratio, whereas Y, while slightly increasing the lattice volume by changing a and c did not alter c/a ratio. The former case effectively meant a reduction in atomic volume of Mg (and possibly for that of the solute atoms as discerned from their DOS calculations), and the latter, an increase (Chen and Boyle, 2009; Stanford et al., 2015).

The studies by Chen and Boyle (2009) and by Jin et al. (2011) further showed via computational methods that the bond strength in a solid solution dominated by the shared electrons (computed as bond order–BO–). When naming the bond types, they referred to the earlier definition by Bader (1990), who suggested that all bonding interactions fall into the following categories, as has been confirmed by the recent ab initio computations: (i) the shared-electron interaction, creating covalent (localized electron sharing) and metallic bonds (dilocalized electron sharing), and (ii) the closed shell interaction, leading to ionic as well as weak bonds.

An increasing BO was interpreted to mean an increasing strength through the series Mg–Zn, Mg–Al, and Mg–Y (Chen and Boyle, 2009). In Mg–Zn system, there appeared to be no covalent bond formation specific to the presence of Zn [likewise in Mg–Li (Jin et al., 2011)] as the electron localized function (ELF) maps (also known as charge density contour maps) indicated. Furthermore, DOS calculations pointed out that all electron densities (more in p orbital than that in s) around Mg atoms neighboring Zn reduced, in addition to the removal of the mild covalency within the basal plane of Mg (existed in pure Mg) around the Zn atom. However, the mild again covalency between Mg atoms in z direction remained unchanged. The DOS calculations for Zn in Mg–Zn (Ganeshan et al., 2011), Sn in Mg–Sn, and Li in Mg–Li also showed an overall reduction and homogenization for all energy states of the solute atoms, further indicating a possible size reduction in the atomic sizes of the solutes as well. Therefore, the atomic size reduction both for Mg and the solute atoms may be interpreted as the birth of an extra strain field around the Mg atoms surrounding each solute in these binary systems. This strain field would require consideration in addition to the one that would normally exist due to the size difference of Mg and solute atoms. This reduction in the atomic size of Mg was also pointed out by Chen and Boyle (2009). However, Chen and Boyle discerned this atomic size reduction indirectly and on the basis of crystal parameter changes, without relating to their own DOS calculations, which effectively showed the electron contribution from all orbitals of Mg in Mg–Zn. The proposed extra lattice straining due to large electronegativity difference between Mg and the solute atoms was also foreseen for the system of Mg–Sn in another study (van der Planken and Deruyttere, 1969), constituting another example of SRO without covalency (hybridization).

Regarding the Mg–Y system, Chen and Boyle (2009) showed that no significant DOS change occurred in s and d orbitals of Mg, whereas its p orbital showed some increase, which was interpreted as hybridization between Mg and Y atoms, involving p and d orbitals, respectively (the calculated DOS of d orbital of Y in Mg–Y being strikingly dominant), as well as stronger directionality in the bond structure. They further confirmed through Cauchy pressure evaluation that in one direction the value was negative, also indicating directionality in the bond strength.

The proposed two SRO mechanisms also comply with the expected SFE changes in two different cases. Zn should increase I1_SFE due to reduced average atomic size (Pei et al., 2015), while Y showing an opposite trend, and indeed reported to be so (Sandlöbes et al., 2014). It may further be expected that the influence of hybridized bonds would not be uniform on the SEFs of different crystal planes, whereas the non-hybridized type would create more uniform changes, that is, either increase or decrease to similar extents. A critical evaluation of SFEs for elements representing two different SRO types showed that the expectation is largely fulfilled (Moitra et al., 2014; Shang et al., 2014; Zhang et al., 2014a; Dong et al., 2018). It seems that the implications of atomic size changes in terms of changes in a, c, and c/a ratio are also worth considering.

In one case, based on the DOS reductions in all orbitals of Mg and the consequent change in its atomic size, as in Mg–Zn and Mg–Sn, it may be interpreted that Mg behaved as a strong donor (more electropositive) as compared to the case of Mg in Mg–Y. Thus, in this SRO case, if the electronegativity difference is large enough between Mg and solute atoms, the charge transfer is stronger, leading to homogenization and an accompanying reduction in all DOS levels. Hence, the consequence is a reduction in atomic sizes, without resorting to hybridization. Such Wigner–Seitz atomic cell size changes were said to be large in Miedema's model (1973c). This can be envisaged to lead to an extra strain field (in addition to the atomic size difference of the solute) involving both the Mg and the solute atoms whenever they are neighbors and consequently additional strengthening as compared to the one expected from a random solid solution, whereas if hybridization of electron orbitals takes place, this extra strain field is absent or negligible. In this case, the SRO and accompanying strengthening are only due to the increased bond strength (covalency) between Mg and solute element.

Thus, it may be concluded that the strengthening mechanism of individual elements may depend on the way the electrons are shared. In both non-hybridized and hybridized cases, SRO forms. However, the degree of effectiveness in increasing strength differs, being stronger if hybridization exists. This view should also be taken to emphasize the importance of the purity of the alloys prepared for experimental comparisons (van der Planken and Deruyttere, 1969). In the case of Mg–Y, that is, hybridization, while increased covalency increases strength, the alloy may be expected to become more brittle according to the criteria (brittleness: R_G/B > 0.5) by Pugh (1954). However, Chen and Boyle (2009) showed that the strengthening effects in case of Al, Zn, and Y did not seem to be related to the changes in bulk moduli, and therefore despite the modulus-based criteria of Pugh, brittleness did not prevail in Mg–Y (R_G/B > 0.605).

To the best knowledge of the author, DOS calculations and ELF maps are unfortunately not available in the literature for all Mg–X binary systems to firmly conclude the presence or absence of covalency. The atomic size change is a complex phenomenon as it may be necessary to consider more than the immediate neighbors of the solute atom, in addition to the original atomic radii and concentrations. The DOS calculations and constructions of ELF maps seem indispensable for each binary system for a more complete understanding.

The phenomenon of SRO elegantly indicates the possibility for an approach to design alloy systems in a subtle and economical way. For example, α-Mg solid solutions containing only 1% addition of Y, rare earth (elements) (RE), or Ca were shown to be competitive in flow behavior with the traditional alloys, such as QE22 and ZE41, and be better than AE42 and AS21 (Abaspour and Cáceres, 2016). Abaspour and Cáceres, with reference to the studies by Zhang et al. (2014), pointed out the importance of SRO and, in turn, the selection of the alloying element, especially for cast structures showing inherent coring. The overall strength levels of such cast parts were said to dependent on the strength level of the weakest regions of what was described as percolated structures that were made up of weak solid solution regions (interiors of the cored grains) and interconnected strong grain boundary intermetallics.

When accounting for their observations, Abaspour and Cáceres (2015) disputed any role of the mechanisms, such as pinning of edge dislocations with mobile solute atoms, atomic size effect on the diffusivity, or dynamic precipitation of thermally stable precipitates. However, there exist atomic resolution imaging studies, explaining the temperature resistance of the strength on the basis of solute segregation (said to be driven by the need to reduce the twin boundary strain energy minimization) to mechanical twin boundaries in Mg–Gd, Mg–Gd–Zn (Nie et al., 2019), Mg–Y (Somekawa et al., 2017), Mg–Ca, and Mg–Zn (Somekawa et al., 2014) systems. Such solute segregations themselves were shown to be ordered along the twin boundaries and to have occurred in short annealing times. If one treats the coherent twin boundary planes as SFs, a justifiable likeness as only the bond angles change across the plane, then this segregation may be regarded as Suzuki segregation. There has been suggestions in the literature to use this type of segregation as an alloy design criterion based on ab initio calculations (Zhang et al., 2014b).

Whether this order accompanying segregation to the twin boundaries can be described as a local SRO is a subject for discussion. However, the very existence of the alloying element segregation along the twin boundaries effectively means that they diffused from the nearby matrix regions to these boundaries. Whereas, the original claim (Abaspour and Cáceres, 2015) was that SRO-forming solutes were stable to the extent that temperature changes had little effect, if at all, on their mobility. Hence was the athermal nature of the strengthening effect of SRO. However, this way of questioning is not meant to dismiss the reality of SRO. Examinations of regions away from the twin boundaries in the same α-Mg grains were not given in those reports that presented segregation to twin boundaries. Seeking the presence of SRO away from such twin boundaries would reveal if this segregation and resulting stabilization of the twins were solely responsible for the observed strengthening or were an additional contribution to an already existing SRO effect.

The explanations based on SRO alone in Mg alloys can also be strengthened via conducting some advanced imaging techniques. In such a study on Mg–Zn and Mg–Y systems (Stanford et al., 2015), the alloys were defined as random solid solutions based on tomographic atom probe maps. However, those alloys had very rich solute concentrations, and even then, the majority of solute atoms were a few atomic distance apart rather than presenting a readily noticeable solute–solute neighboring. Moreover, despite the larger atomic size of Y and much richer concentrations of Mg–Y, perhaps due to the extra strain field created by Zn in Mg–Zn, the average nearest neighbor distance between Zn–Zn was almost double compared to that of Y–Y. It is fair to say that further elaborate imaging studies would contribute to our understanding greatly.

SFE-Based Assessment on the Effects of Alloying Elements in Mg–X Systems

First, it should be recalled that SFE for a given crystal plane is strongly influenced by the interatomic electron density distribution and therefore influenced by all atomic scale parameters. It is not a priori that all the SFE values of different planes in a system will follow the suit of change in the SFE of a particular plane under the influence of a particular solute (Yin et al., 2017). As to the GSFE calculations, an important assumption in the currently employed ab initio techniques is that a random solid solution is assumed (Equation 4 in Yin et al., 2017). Considering the small size of the atomic models used in calculations, whether this makes a great difference or not is debatable but not unlikely. In this respect, individual SFE calculations may be considered more reliable than those for GSFE.

Several studies on SFE calculations are particularly comprehensive in terms of the number of alloying elements considered (Moitra et al., 2014; Shang et al., 2014; Yuasa et al., 2015; Dong et al., 2018). Pei et al. (2015), in an attempt to devise a practical guide to alloying, plotted qualitative relationships between the I_1SFE in Mg–X and the relative atomic volume, atomic number, I_1SFE of the solute, bulk modulus, and electronegativity of the solute for 18 elements. Similar reports can also be found in the literature (Wen et al., 2009).

Among the SF types, I_1SFE has been said, although not unanimously, to be indicative of the deformation capacity of the Mg–X systems based on computations as well as observations on Mg–Y (Sandlöbes et al., 2011, 2014; Agnew et al., 2015). Although, I_1SFE does not reveal an energy barrier to slip, its formation is regarded as a source for generation of nonbasal, <c+a>, dislocations, providing a step for slip at room temperature. Therefore, if I_1SFE is low I₁-type SFs form, the proposed mechanism is assumed to work and explain the ductility imparted by Y (and REs for that matter). A strong criticism to this proposal came from Yin et al. (2017), indicating that necessary number of I₁ type cannot be generated by slip, and a large population of I₁ SF prior to deformation is necessary to render the mechanism feasible. An alternative mechanism was also put forward by Kim et al. (2015) who, by using molecular dynamics simulation, suggested different level of changes in CRSS values associated with Peierls potentials for pyramidal plane and a very complex movement of leading and trailing partials in a comparative study on Mg–Y and Mg–Al.

According to the findings of Yin et al. (2017), Zn was the least effective element in reducing both basal and pyramidal I₁ and I₂ SFEs (no effect on basal types), and Al moderately reduced the basal SFEs while not changing the pyramidal types; Y created the most effective reductions as compared to Al and Zn. These findings, when considered together with the previously mentioned results by Chen and Boyle (2009), may be indicating that SFE reduction becomes more effective as the ranking of interatomic bond between the solute and Mg goes from lack of covalency, that is, Mg–Zn, to weak covalency, that is, Mg–Al, and finally to strong covalency (hybridized bonds) as in Mg–Y.

As to the computed GSFE values, the reports for a wide range of alloying elements for binary Mg alloys are unfortunately not free from contradictions, for some elements even giving opposite trends as can be seen by comparing the values given in Wang et al. (2013), Moitra et al. (2014), Shang et al. (2014), Wang W. Y. et al. (2014), Zhang et al. (2014), Yuasa et al. (2015) and Dong et al. (2018). Having summarized the effects of individual alloying elements in Mg–X systems based on the existing literature that relies on atomic scale thermodynamics, or on first-principles calculations revealing SFE values, we will now attempt to indicate the relationship between the atomic number, size, and ΔΦ^*, Δn_WS, and SFE in the periodic table. While Miedema's model considers all the elements in a single plot collectively, we will consider the elements along individual periods of the table.

In order to understand the general trend in the periodic table, several relevant plots have been given in Figures 4–6. The well-known electronegativity change by atomic number has been given in Figure 4 as a reminder that there is an overall trend of increase within each period. The intensity of increase appears to reduce as the period number increases. On the other hand, the plots of atomic number (Figure 5A) or size (Figures 5B,C) vs. n_WS or Φ^* showed clear modulations, each “inverted parabola” belonging to a period. An inverted parabolic increase in the plots of I_1SFE (SFE values from Wang W. Y. et al., 2014; Dong et al., 2018) vs. atomic number (Figure 6A) or size (Figure 6B) for each period also exists. Figure 7 shows the changes in in Φ^* (Figure 7A) and in n_WS (Figure 7A) vs. I_1SFE (Φ^* and n_WS values are from Miedema (1973a), Abaspour and Cáceres (2015), Buey et al. (2018); SFE values from Wang T. et al., 2014 and Dong et al., 2018). Although a graphical illustration has not been given here, it was found that I_2SFE also showed a similar relationship with Φ^* and n_WS, whereas GSFE did not show any specific trend (perhaps due to insufficient data). The increase in SFE as the Φ^* increased may be interpreted due to an increasing binding force between the solvent and solute atoms. On the other hand, the increase in SFE vs. n_WS plots may be attributed to a relatively more polarized electron density distribution at Wigner–Seitz atomic cell boundaries.

FIGURE 4

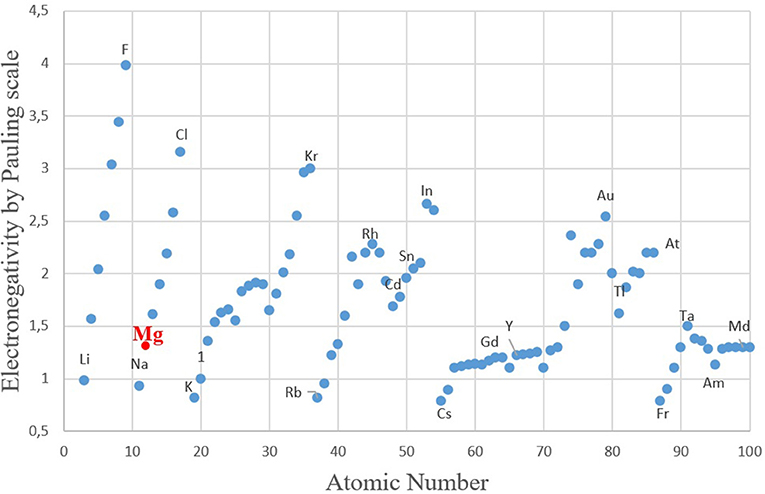
Figure 4. The relationship between the Pauling scale electronegativity values with atomic numbers (data set from: https://en.wikipedia.org/wiki/Electronegativities_of_the_elements_(data_page) with reference to: L. Pauling, The Chemical Bond, Cornell University Press, Ithaca, New York, 1967).

FIGURE 5

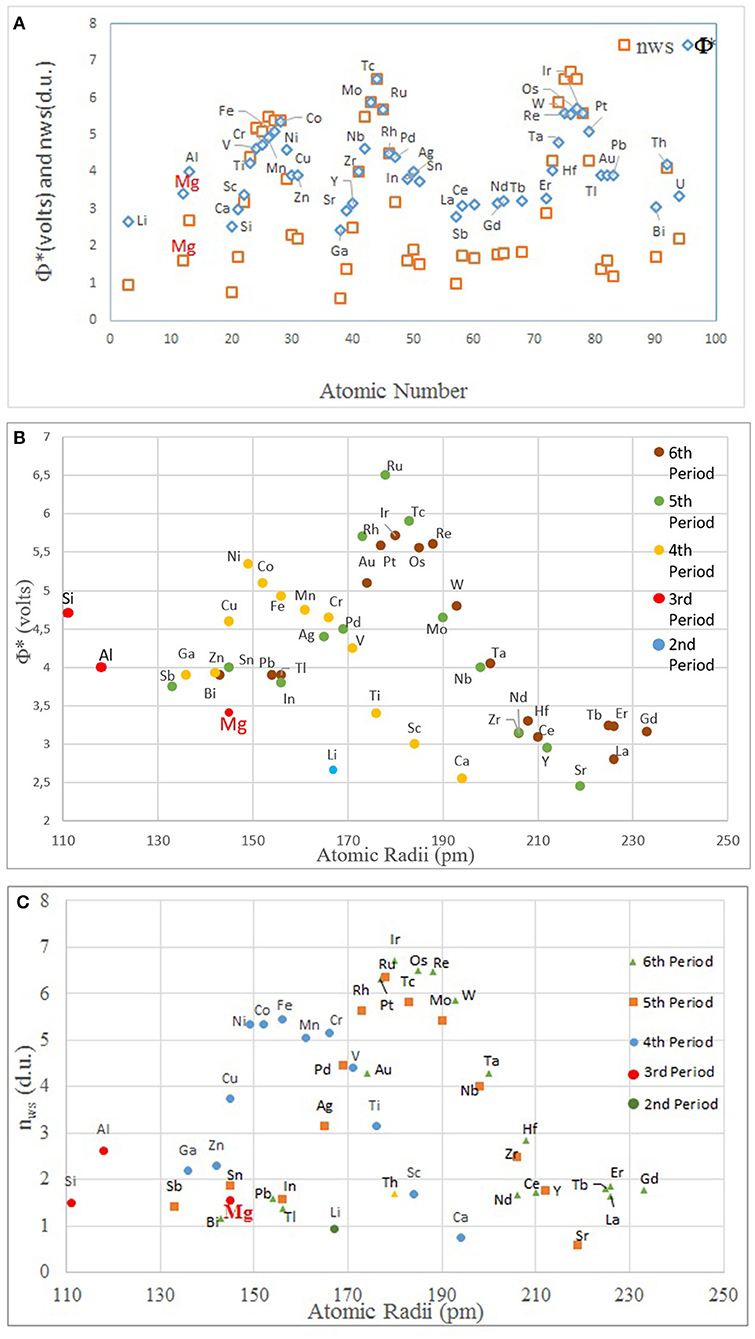
Figure 5. The plots of (A) atomic number vs. n_WS and Φ* (for clarity, the element names are only given for one data set, Φ*); (B) atomic size vs. Φ*; and (C) atomic size vs. n_WS. Note that the modulations correspond to individual periods in the periodic table (n_WS and Φ* values are from Miedema, 1973a; Abaspour and Cáceres, 2015).

FIGURE 6

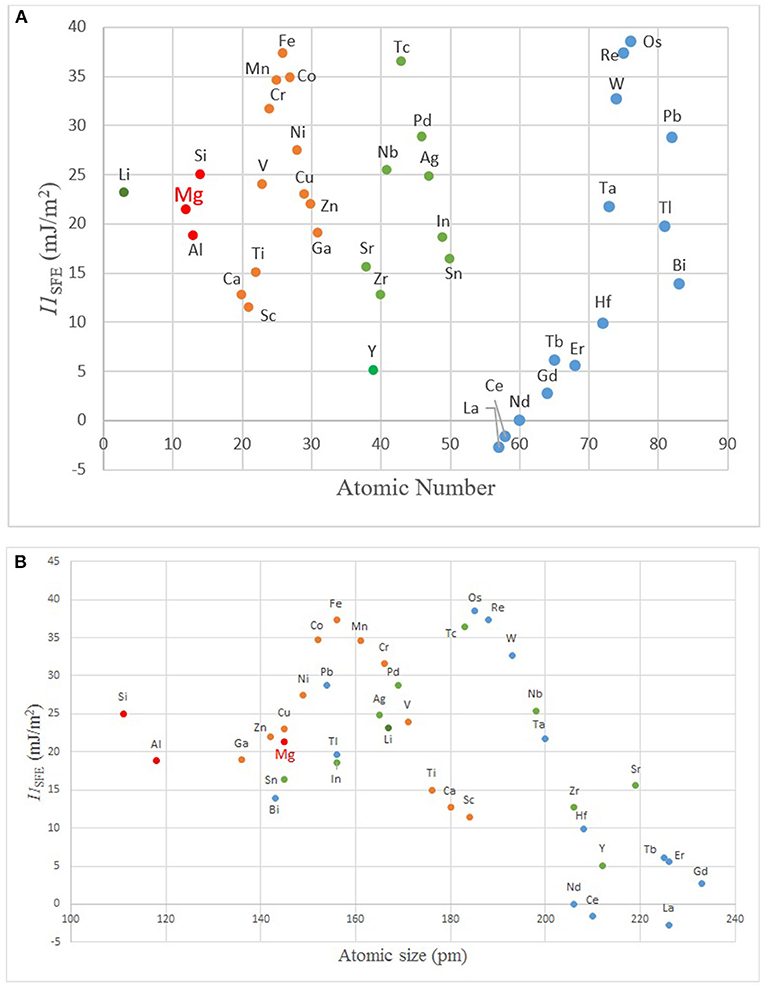
Figure 6. The plots of I1_SFE vs. (A) atomic number, and (B) size showing modulations (SFE values from Wang T. et al., 2014; Dong et al., 2018).

FIGURE 7

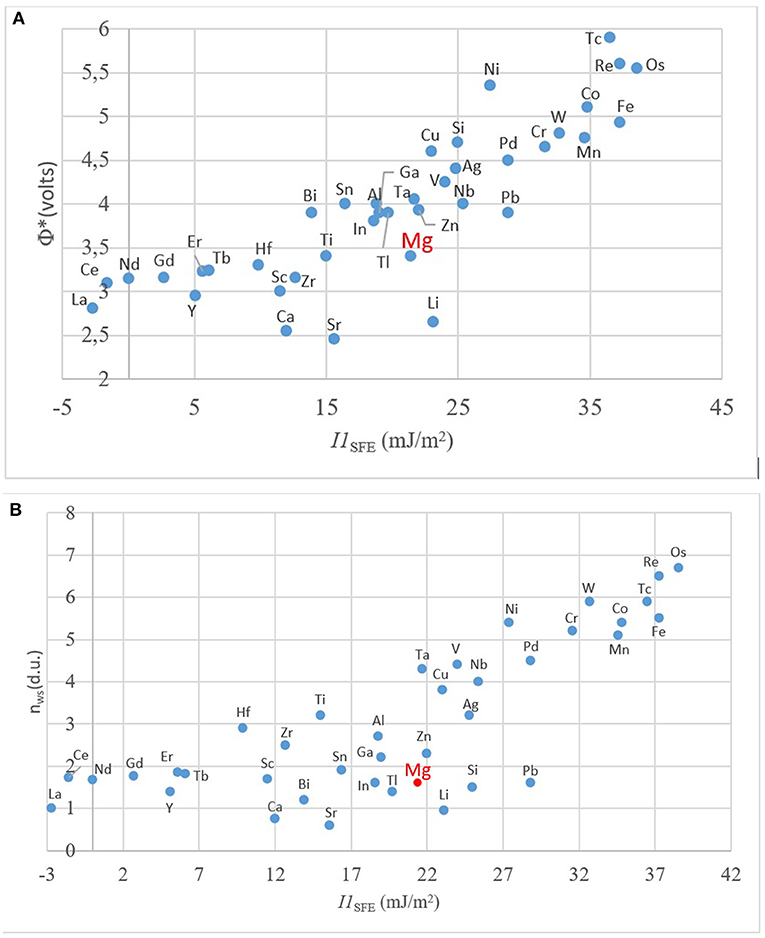
Figure 7. The relationship between the computed values of I1_SFE with (A) Φ*; and (B) n_WS. (Φ* and n_WS values are from Miedema, 1973a,b; Abaspour and Cáceres, 2015; SFE values from Wang T. et al., 2014 and Dong et al., 2018).

The parallelism between n_WS and Φ^* against the atomic number and radii further testifies Miedema's original hypothesis regarding the interdependency of the two terms. The linear relationship between the n_WS and Φ^* was already known due to Miedema. These trends also indicate the relationship between the I_1SFE and the values of n_WS and Φ^* as atomic scale thermodynamic parameters. Pei et al. (2015) have shown, for presumably a single period (elements were not stated), that I_1SFE in Mg–X increased as the electronegativity of the solute increased.

The inflection points in Figure 6 as well as in Figure 7 correspond to about the middle position in each period, that is, about the midrange in transition metals. This intriguing feature requires further evaluation. If compared with Miedema's plot (Figure 3), it can readily be noticed that all the elements of the upper (north) sector are located in the second half, namely, the decreasing part, in the Φ^*, n_WS, I_1SFE vs. atomic number plots, and reverse their side in plots vs. atomic size, whereas the elements located in the lower (south) sector of the Miedema plot reside on the reverse half of the same plot in each case. By taking into account the findings of ab initio studies (DOS calculations and the contour maps), it may be deduced that the elements that are likely to form the non-hybridized type SRO with Mg and those that form hybridized type SRO reside on the opposite sides in these “inverted parabolic” plots for each period. As such, it appears to be logical to suggest that the question of what type of SRO forms can be answered depending on the position of the candidate solute element on any of these plots involving the n_WS, Φ^* or I_1SFE. It may be suggested that if the size difference is relatively smaller and electronegativity is larger, the tendency to form non-hybridized bond type is greater, and vice versa.

Based on the interpretation of these plots, the possibility of using a currently available measurement technique, that is, Kelvin probe force microscopy (KPFM), may be suggested when assessing the SFE changes especially in studies involving multicomponent alloys (Φ^* was said to change linearly with Φ, the work function, of the constituent atoms) and that the electronegativity and chemical potential for electrons in an atomic cell were equivalent (Miedema, 1973c; Abaspour and Cáceres, 2015). Ab initio computations are rather difficult (Pei et al., 2015) and currently not capable of computing SFE in models involving several different solute atoms [few studies considered two solute atoms together (Kimizuka and Ogata, 2013)]. Kelvin probe force microscopy, because it measures work function (Φ), that is, the equivalent (Miedema, 1973c) of Φ^* in Equation (1), may be useful in understanding the SFE changes indirectly as compared to some reference materials, be it pure Mg and/or a binary alloy of known SFE. Because SFE changes are invaluable in selecting alloying elements, this practical measurement technique may prove useful in designing multicomponent alloy systems.

Relationship between electron work function (EWF) and material properties, such as strength and elastic modulus for metals and alloys, was demonstrated (Halas, 2006; Hua and Li, 2011; Lu et al., 2018). Liu and Li (2015), via ab initio calculations, showed that both I₁ and I₂ SFEs increased with EWF and that alloying Mg with the elements having lower EWF compared to Mg would impart strengthening as well as ductility and with the other elements, while increasing strength, and lower ductility.

It is thus reasonable to suggest that an understanding of alloying effects has already been established in relation to EWF, which can be measured via KPFM. Admittedly, this knowledge basis currently stems from the ab initio calculations rather than KPFM as a practical method. One impediment when employing KPFM may be the inevitable surface oxide on samples. However, if relative values are to be considered rather than seeking absolute values, KPFM readings may be promising for comparison purposes between different systems.

Doping Magnesium With Oxygen

As a counterintuitive alloying approach, intentional addition of oxygen into Mg has been arguably the most interesting attempt in the history of Mg alloys. Doping Mg with oxygen results in many interesting properties and may also be taken to indicate the potential of dilute systems involving interstitial atoms.

A recent study (Kang et al., 2016) showed that dilute concentrations of oxygen, as an interstitial element, yielded highly surprising remedial effects on the problematic properties of Mg, namely, an increased strength and deformation capacity, removal of the yield asymmetry, and even improved corrosion resistance. It has been postulated that, as a non-metallic addition, oxygen would form interatomic bonds that may be strongly ionic/covalent in character and increase strength (Kang et al., 2016).

Kang et al. (2016) succeeded in mono atomic oxygen addition to Mg by employing the dissociation tendency of nanosized TiO₂ over 400°C when in molten Mg and detected ~0.3% at. oxygen at a depth of 15–18 μ in solidified state after removing the surface oxide layer. Their first report covered pure Mg, Mg–Al, and Mg–Zn systems with oxygen additions. Among them, Mg–Zn–O system showed additional extraordinary features, such as more than 50% elongation to failure without apparent twinning, a yield drop phenomenon akin to simple low carbon steels, and, strikingly, non-basal slip in submicron-sized grains. Thermal conductivities of all oxygen containing alloys were also shown to have increased.

Two of their following studies on Mg−9Al-O alloy also reported a higher oxygen content in β-phase (~3.86% at. in Mg₁₇Al₁₂) than in α-Mg (~0.79%), leading to increased d-spacings in both phases and consequently a better match (Kang et al., 2017, 2018) and stability at the β/α interface, disappearance of the β/α eutectic, and refinement of β-phase. Presence of oxygen brought about benefits in the mechanical properties as compared to Mg−9Al, namely, 30% improved yield strength, 41% increased UTS, doubled elongation to failure, ~10% increase in elastic modulus, and fracture toughness. Albeit, their claim regarding the formation of so-called “reticular” phase during annealing treatments (Kang et al., 2018), due to lack of verification via an irrefutable method, needs substantiation. This reticular phase may turn out to be nothing more than an oxide phase.

To our best knowledge, there exist no studies yet as to the changes incurred in SFE by dissolved oxygen atoms in Mg matrix or an evaluation with actual figures of formation enthalpy of such a solid solution, although based on the evaluations by Pei et al. (2015), due to the very high electronegativity value of oxygen, a large increase at least in I₁ SFE value of Mg–O can be expected. This foreseen increase would conform to the plot given by Pei et al. (2015) that shows an increase at least in I₁ SFE with average atomic size reduction in Mg–X (Mg–O system should have a decrease in average atomic size according to Figure 3 in Pei et al. (2015). The experimental observation as to lack of twinning (Kang et al., 2016) seems to support these expectations.

Furthermore, because of the large electronegativity difference between Mg and oxygen, a dilute system of Mg–O is highly likely to form SRO. Based on the discussions earlier, directionality in bonding around oxygen atoms would not be expected. It may also be thought that, through binding, more of the available free electrons of Mg that would otherwise contribute to the corrosion potential may also be the reason for the observed (Kang et al., 2016) improvement of the corrosion resistance in Mg–O system. Such interpretations may render all the beneficial effects of this dilute binary alloy system understandable, but a demonstrated explanation through ab initio techniques could prove highly useful.

The potential beneficial effects of dissolved oxygen deserve exploration at fundamental level and in different alloy systems, be it Mg or other metals. In essence, the effect of oxygen in solid solution has long manifested its potential also in other well-known metallic systems. CP (commercial purity) titanium serves as an engineering material owing its strength level to oxygen in solid solution at ppm levels. Yet another commercially available example is oxygen-free copper, a material that would otherwise be hard and brittle. Even just these two materials clearly point out that addition of oxygen in trace amounts has the potential to create striking changes in metals including Mg. Perhaps the down side to the idea is the inherent difficulty in producing bulk quantities of materials containing controlled and dilute amounts of oxygen. Coupled with this difficulty, the highly problematic issue of finding an economical monoatomic oxygen source may continue to stand on the way to utilization of this approach. Formerly, addition of nitrogen into Mg was also attempted (Kaya et al., 2003). Despite the disappearance of the eutectic morphology in the microstructure as in oxygen addition, the attempt was probably a failure in terms of supplying monoatomic nitrogen into the molten metal due to employment of simple gas purging.

Ultrastrong Magnesium Alloys

Because comparable to the high-strength steels, the strength levels achieved in some Mg alloys deserve the definition of “ultra.” For example, owing to nanocrystalline structures containing LPSO phases, yield strength level as high as 600 MPa was reported in rapidly solidified powder metallurgy products (Inoue et al., 2001; Kawamura et al., 2001). More complex but again Y- and RE-containing, a composition [Mg−1.8 Gd−1.8 Y−0.7 Zn−0.2 zirconium (Zr) at.%] also showed a high yield strength of 473 MPa in aged condition (Homma et al., 2009).

A hot-rolled Mg−8.5 Gd−2.3 Y−1.8 Ag−0.4 Zr (wt%) with a yield strength of ~575 MPa (Wang et al., 2010; Jian et al., 2013) and Mg−8.2 Gd−3.8 Y−1.0 Zn−0.4 Zr alloy with a proof stress of 426 MPa (Xu et al., 2012) and an earlier example of alloy extrusions in the Mg–Al–Zn–Si–RE system with yield strength levels of >500 MPa (Chang et al., 1986, 1987) can also be considered in the ranks of the ultra-strength alloys, albeit these high strength levels were not accompanied by high deformation capacities, which were typically <10%.

One study, among those that reported ultrastrong levels, is particularly interesting because of its implications toward developing high-strength Mg alloys. The achieved strength level (σ_y ~575 MPa, UTS ~600 MPa, and 5.2% uniform elongation) was attributed to finely spaced SFs by Jian et al. (2013). As such, because the alloys contain abundant SFs to start with, this alloy system may also serve as a test case to show if I1-type SFs really play an important part in increasing deformation capacity as suggested in Sandlöbes et al. (2011), Sandlöbes et al. (2014), and Agnew et al. (2015). In this alloy, presence of such nanospaced SFs was proposed as an effective means to increase strength without losing the modest level of ductility even after multipass rolling. It appears that the achieved properties simply depend on the adjustment of SFE. The same study also suggested an interesting deformation mechanism, supporting the findings of an earlier work (Liao et al., 2004). The deformation was said to have changed mode and became SF-mediated instead of slip-dominated after reaching a total deformation range of 30–50% reduction as the SF widening started to operate (Jian et al., 2013). The foundation of this explanation is none other than Suzuki segregation.

The composition of this interesting alloy is akin to those that generate LPSO phases as discussed below. However, it is also worth noticing that despite the proliferation of SFs and presence of the main player elements in LPSO formation, perhaps due to the level of SFEs not being at a necessary critical range, the alloy composition with nanospaced SFs did not create LPSO phases. Considering the fact that the strength level of this structure is as high as those that contain LPSO phases leads to an intriguing question. Is the ultrastrength level achieved in composition with LPSO phases really due to these so-called strengthening particles or only a result of presence of multitude of SFs in the same structures? This view is admittedly simplifying the comparison; however, it appears that with or without LPSO phases, so long as the SFs proliferated the strength can reach to ultra levels.

A category of Mg alloys with outstanding strength levels is found within Mg–Zn–RE [or Mg–TM (transition metal)–RE] system involving LPSO phases. These may be viewed as the succession of those structures that involve nanospaced SFs without forming another phase as mentioned above. We will now embark on their discussion next.

Systems Containing LPSO Phases

The earliest observation on LPSO in Mg alloys may be ascribed to the report by Luo et al. (1994) on Mg–Zn–Zr–RE system. Many studies also refer to the report by Kawamura et al. (2001) as the precursor study on LPSO phases. Although neither the term LPSO was mentioned nor their morphology presented in that study, superior room and high temperature strengths, relatively good deformation capacity, and high strain rate superplasticity were reported for Mg–Zn–Y system. Later on, the alloys forming LPSO phases proliferated and generally expressed as Mg–TM (transition metal)–RE systems (Zhiping et al., 1994; Yokobayashi et al., 2011a,b; Kishida et al., 2012, 2013; Xu et al., 2016). Existing literature on alloys involving LPSO phases collectively reports high strength (Kawamura et al., 2001; Hagihara et al., 2010a,b) and improvement in deformation capacity, as well as in creep (Hu et al., 2016; Xu et al., 2016) and corrosion resistance as common characteristics, as compared to AZ31, WE43, ZK60, and ZX60 (Xu et al., 2016) alloys. These improved mechanical properties were generally achieved with small additions of Zn and RE, for example, 1 at.% Zn−2 at.% RE (Nie et al., 2005; Liu et al., 2008; Gao et al., 2009; Egusa and Abe, 2012).

Long-period stacking order precipitates that can exist at the grain boundaries, as well as intragranularly, are classified into two types, one that forms during solidification, and the other upon annealing (Kawamura and Yamasaki, 2007; Li et al., 2018; Sato et al., 2018). It should be noted that, alloy composition permitting, the entire grains are composed of lamella of LPSO together with bands of α-Mg, while LPSO precipitates along the grain boundaries can also be present. Thus, the material, due to formation of LPSO structures, carries many FCC layers in each grain (Kim et al., 2016). Building blocks of LPSO phases should be envisaged as SFs located between Shockley partial dislocations of α-Mg phase (Zhu et al., 2009, 2010a,b; Kim et al., 2016, 2017).

The classification of the crystal repetition of such layered structures goes back to the earlier work by Ramsdell (1947). In earlier classification of LPSO phases, the 10H (Matsuda et al., 2005; Abe et al., 2011; Hagihara et al., 2016), 18R (Kawamura et al., 2006), 14H (Itoi et al., 2004; Hagihara et al., 2010b; Abe et al., 2011; Egusa and Abe, 2012; Zhu Y. M. et al., 2012; Jin et al., 2013; Nie et al., 2014), and 24R (Abe et al., 2011) polytypes emerged, corresponding to 5, 6, 7, and 8 layers in structural blocks, each being a close-packed plane stacked in the direction of the c-axis of α-Mg crystal. Recently, an extended series have been expressed (Li et al., 2018) as 6H (now known as a building block of 18R) (Abe et al., 2002; Ping et al., 2002; Amiya et al., 2003), 10H, 14H, 15R (Mi and Jin, 2013), 18R, and 24R. Some metastable LPSO phases were also revealed by the work of Kim et al. (2016). In this notation, H stands for hexagonal, and R for rhombohedral symmetries of the Bravais systems, whereas the number refers to the number of repetitions of the structural blocks (SB) (Kim et al., 2016), each of which essentially may also be seen as having HCP stacking involving SFs. The 4 polytypes can essentially be described by a structural unit composed of AB stacking followed by a C fault layer. This fault layer is enriched in Zn and RE atoms (Egusa and Abe, 2012; Kim et al., 2017). Thus, the final ordered stacking, including the fault layer, makes up a local FCC, that is, ABCA stacking, and also shows chemical ordering perpendicular to the fault, that is, basal planes in α-Mg. As such, the workings of the system are reminiscent of Suzuki segregation and ordered segregation of the solute elements to twin boundaries as previously discussed.

The precise deciphering of the stacking sequences in 4 major types of LPSO phases in materials prepared via rapid solidification techniques has been given by Matsuda et al. (2005) and Egusa and Abe (2012) as follows: The 10H and 14H, both carrying mirror symmetry with respect to the basal plane, show stacking sequence of ABACBCBCAB and ACBCBABABABCBC, respectively. 18R and 24R, not carrying mirror symmetry with respect to the basal plane, have stacking sequence of ABABABCACACABCBCBC and ABABABABCACACACABCBCBCBC, respectively. It has been shown that 18R and 14H are stable at high and low temperatures, respectively, whereas 10H and 24R phases are not stable in every alloy system (Kim et al., 2018a). Furthermore, 14H and 18R are the most frequently observed ones (Lv et al., 2014), with the 18R showing a tendency to transform into 14H upon heat treatment or hot deformation (Oñorbe et al., 2012; Zhu Y. M. et al., 2012), as 14H appears to be energetically preferable one among the others (Kim et al., 2016). This transformation from 18R to 14H was reported to be accompanied by a decrease in SFE (Fan et al., 2011; Lv et al., 2014; Kim et al., 2016).

Long-period stacking order phases are further complicated by in-plane ordering in 14H and 18R types (Kishida et al., 2015; Kim et al., 2018b). This complication manifests itself with the presence of L1₂ type clusters, and the order is violated in one dimension, leading to the definition of order-disordered crystallographic structure in some Mg–TM-RE alloys (Yokobayashi et al., 2011a; Okamoto et al., 2014; Iwatake et al., 2015; Kishida et al., 2015, 2017). The in-plane order may be a long-range type as in Mg–Al–Gd system (Kimizuka et al., 2013; Tane et al., 2015; Kim et al., 2018b) or may be composition dependent as in Mg–Y–Zn system, being present more locally in relatively dilute alloys, and long-range type in richer Mg–Y–Zn alloys (Egusa and Abe, 2012). It has been suggested that LPSO formation is essentially governed by formation of Zn6RE8 clusters, with Mg atoms being substitutes for RE atoms (Egusa and Abe, 2012). This in-plane ordered clusters were reported to have an important effect in determining the elastic properties of the LPSO structure and, in turn, influence the properties of the alloy (Kimizuka et al., 2013; Tane et al., 2015; Kim et al., 2018b). Another important effect of LPSO phases is inhibition of the dynamic recrystallization toward maintaining small grain size. This has been attributed to the suppression of dislocation numbers due to creation of many SFs on the basal planes (Lv et al., 2014). 14H LPSO has been reported to be more effective in this regard as compared to 18R (Lv et al., 2014).

The formation and growth mechanism of LPSO structures were investigated incorporating ab initio calculations (Zhu Y. M. et al., 2012; Kim et al., 2016). Kim et al. (2017) suggested a coupled diffusional and displacive transformation mechanism involving formation of GP zones and their transformation to LPSO structures as opposed to the formerly proposed spinodal decomposition model (Iikubo et al., 2013; Narita et al., 2013). According to their model, a Zn/Y-enriched layer was defined as the precursor of LPSO structure in lean Mg–Y–Zn system and termed as GP zones. Indeed, the term fits well as these zones fulfill the criteria of being chemically ordered and coherent with the matrix. At the stage of GP zones, it was shown that no stacking alterations in the HCP arrangement of the basal planes of α-Mg took place (Kim et al., 2017). This primary step constituted the diffusional part of their suggested “coupled diffusional-displacive transformation” mechanism. In the following displacive step, LPSO structure is formed by generation and propagation of Shockley partials. Although in the original model the coherency strains were not mentioned explicitly, one can assume that the existence of such strains at precipitate–matrix interface, as in conventional GP zones, is inherent and facilitating the process. Formation of GP zones lowers the SFE paving the way for the formation of Shockley partials, at which stage the coherency stresses are substituted by the shear strains due to the partial dislocations (Kim et al., 2016). Different types of these GP zones were said to lead to different LPSO structures, in terms of both chemical and structural ordering, and to be composition dependent (Kim et al., 2017). Several other studies also reported GP zones in Mg alloys (Ping et al., 2003; Oh et al., 2005; Nishijima et al., 2007; Saito et al., 2010; Lee et al., 2011).

Quasi-Crystal Forming Systems

Formation of quasi-crystals in Mg alloys may be viewed as an extension of the assessment of the potential for intermetallics through Miedema's scheme.

Quasi-crystals were discovered by Shechtman et al. (1984) in a rapidly solidified Al–manganese alloy. This discovery in 1984 was later awarded with Nobel Prize in 2011. Since then, other systems also have been found to exhibit quasi-crystal formations.

Quasi-crystals are essentially topologically closely packed intermetallics, also known as Frank–Kasper phases. Thermodynamically stable (Abe et al., 2000) icosahedral (i-) (Kounis et al., 2000) and decagonal (d-) phases were obtained. However, they are different from the true topologically close pack structures as they do not comply with the space-filling Bravais lattices. Instead, they possess a long-range quasi-periodic order without the translational periodicity in three dimensions, showing forbidden rotational symmetry in diffraction, that is, 5-, 10-fold, and so on.

The first quasi-crystal forming Mg system, Mg–Zn–(Y, RE), was reported by Luo et al. (1993). It is now known that Mg–Zn–Al, Mg–Al–Cu/Ag/Au, Mg–Al– Zn–Cu, Mg–Al–Pd, and Mg–Cd–Yb alloy systems can form quasi-crystal phases (Yadav and Mukhopadhyay, 2018). Quasi-crystalline phases themselves have interestingly low frictional properties, high hardness and oxidation resistance, low thermal conductivity, and so on (Dubois, 2012).

It is interesting to note that once again Mg–TM–RE system, as for LPSO structures, is at the forefront in the case of quasi-crystal forming alloys. The icosahedral i-phase was obtained in Mg–Zn–Y system through normal casting conditions. Formation of quasi-crystalline phases in this system has been said to exhibit a relatively large compositional range, as well as casting process parameters (Zhang et al., 2008). Zhao and Wang (2016) reported quasi-crystalline formations with 22 kinds of different morphologies obtained through different cooling processes in Mg–Zn–Y system. High strength values up to 450 MPa were reported for this system (Bae et al., 2001).

An important outcome of their properties is that, because of their low interfacial energy, quasi-crystals are stable strengthening particles in Mg alloys (Bae et al., 2002). Therefore, we may expect to see an increasing trend in their use.

A Competitor to Rare Earth Elements? Calcium Containing Alloys

The effect of Ca in Mg is similar to REs according to Miedema's model. Benefit of Ca may be summarized as follows: reduces the tension/compression asymmetry, refines grain size (Jiang et al., 2015), increases creep resistance (Ninomiya et al., 1995; Terada et al., 2005; Amberger et al., 2009), and reduces stress relaxation (Abaspour et al., 2016) and deformation texture (Stanford, 2010; Wang T. et al., 2014). An important issue is that all these benefits of Ca addition work in AM and AZ series commercial alloys. By combined addition of Ca and Sr, some commercial alloys were also developed such as ACX or AXJ series (Suzuki et al., 2004, 2008; Luo et al., 2007; Zhu et al., 2015).

Reported ab initio calculations of GSFE due to Ca addition are again not in unison as expressed before. For example, according to the majority of the literature (Wang et al., 2013; Shang et al., 2014; Zhang et al., 2014; Yuasa et al., 2015; Dong et al., 2018), Ca decreased γ_USF of Mg. Yet, in one study (Moitra et al., 2014), Ca increased the GSFE_basal of Mg (γ_USF) in <11$\overline{2}$0> slip indicating a strengthening effect equal to that of Gd, while Ce reducing it as RE elements. Whereas for another slip direction in basal plane, although lowering the SFE of pure Mg (γ_SF) and allowing for formation of an SF, Ca is more prohibitive as compared to Gd and Ce, for dislocation dissociation with much higher GSFE_basal in <10$\overline{1}$0> slip. Reported trends were in better agreement on the effect of Ca in lowering the GSFE_prismatic of Mg (γ_USF) in the {10$\overline{1}$0} <11$\overline{2}$0> slip system, being almost equal to those of Gd and Ce, indicating facilitation of dislocation generation. As to the pyramidal slip, Zhang et al. (2014) reported a decrease in GSFE of {11$\overline{2}$2} <11$\overline{2}$3> due to Ca, Gd, and Y to varying degrees.

From the above given account based on GSFE values, Ca falls no short of RE elements. The solid solution effect of Ca may also be viewed from the perspective of SRO effects. Calcium with its low electronegativity difference with Mg is likely to form a type of SRO similar to that in Mg–Y(RE), that is, hybridized bonds. Such elements are evidently more potent in improving the strength (Abaspour et al., 2016).

When added to AZ series, it was said that Ca in the Mg₁₇Al₁₂ eutectic phase increased the melting temperature of this otherwise insufficient-for-creep-strength phase, enhancing the strength of the Mg–Al bond (Min, 2003). Depending on Al/Ca ratio, Ca addition also leads to formation of Laves phases, namely, Al₂Ca, Mg₂Ca, and (Mg, Al)₂Ca (Chai et al., 2018; Zubair et al., 2019). Among the Mg17Al12-, Al2Ca-, Mg2Sn-, and Mg2Ca-type intermetallics, based on the calculated enthalpy of formation and binding energies, Al2Ca was found to be the most stable one (Wang et al., 2016).

RE elements are expensive, and therefore, it is desirable to find alloy compositions that can perform at least to the same level as those involving REs. Calcium is the best economic alloying element that can compete with the good-for-all-illnesses-of-Mg, the RE elements, as it seems to provide remedies for a number of shortcomings and anomalies of Mg alloys (Abaspour et al., 2016; Guan et al., 2019). Furthermore, it has been shown that Ca addition conferred arguably the most attractive property to Mg, that is, protection of the melt against atmospheric corrosion, eliminating the need for a protective gas cover (Kim, 2011) during secondary melting. In fact, calcium oxide (CaO) addition for this purpose, as an easier, and if not more, equally successful metallurgical option, may further compel researchers to examine the effects of Ca in a wider spectrum of Mg alloys as CaO would open the way to Ca entry into the melts. Therefore, as one of the highlights of the past two decades, we will also scrutinize the topic of CaO addition next.

CaO Addition to Mg—Improvements in Melt Protection and Corrosion of Mg Alloys

CaO addition may just be taken as one of the most important advancements over the past two decades regarding melt protection and imparting corrosion resistance to the conventional Mg alloys. It was shown that CaO addition by 0.3–0.7 wt%, without changing the basic microstructure except for grain refinement, singlehandedly conferred perhaps the most attractive property to Mg and to its conventional alloys in the AZ series, that is, protection of the melt against burning (Kim, 2011).

Figure 8 (Rafiei et al., 2018) shows the surface of a cast Mg without any protection during melting. Without CaO addition, a severe burning and oxidation would be imminent within a matter of seconds, now resulted in a surface with silvery metallic shine, as was observed in a number of AZ series alloys (Kim, 2011). This ecologically friendly metallurgical practice, as emphasized by the foremost proponent of this method, Kim (2011), further encompasses many other additional benefits, for example, metal cleanliness, grain refinement, and, consequently, improved mechanical properties and recyclability. The outcomes of CaO addition are expected to be particularly beneficial for the wrought Mg alloys, for which the processing route starts with billet or ingot castings (Kim et al., 2007).

FIGURE 8

Figure 8. Photomicrograph showing the effect of CaO addition on melt protection. Silvery surface shine of a cast Mg-0.4Al-1CaO (wt%) alloy piece solidified without protective gas (reproduced with permission from Rafiei et al., 2018; https://www.civilica.com/Paper-IMES12-IMES12_010.html).

Exploration of the possibility of using CaO addition can be traced back to the preceding work by Sakamoto et al. (1997), reporting that Ca in pure Mg was increasing the flammability resistance. However, handling Ca industrially is a difficult and expensive operation. Moreover, Ca addition as a means for melt protection, although successful, has been reported to alter both the material properties, as well as the processing parameters employed, whereas CaO was doing the same job equally well arguably without releasing substitutional Ca into the solid solution (Kim, 2011; Lee and Kim, 2011a). Other already foreseen difficulties in Ca addition were mentioned as decreased in metal fluidity, increased die sticking, and problems related to utilization of Ca-containing scrap (Kim, 2011; Lee and Kim, 2011b).

The initial addition of CaO to Mg melt is a rather slow process, during which melt protection using a protective gas cover would still be needed (Kim et al., 2007; Lee and Kim, 2011a,b). Once added, otherwise an insufficient N₂ gas cover (Holtzer and Bobrowski, 2008) was claimed to do the job effectively in the secondary melting operations.

Initially, there was a contradiction, not on the outcomes of CaO addition but as to what happens to CaO in molten metal. First, CaO was supposed to be more stable than MgO according to Ellingham diagrams (Brain and Knacke, 1973). Second, in some reports, it was stated that CaO dispersed in pure Mg and AZ series alloys (Huang et al., 2004; Ha et al., 2008; Kondoh et al., 2011; Nam et al., 2012). It was also claimed that CaO was not to survive during solidification but to transform into Mg₂Ca phase in pure Mg (Ha et al., 2006) and into Al₂Ca, and/or (Mg,Al)₂Ca, if added to AZ series (Kim, 2011; Lee and Kim, 2011b). The first issue was resolved by a thermodynamic analysis, showing the possibility of CaO dissociation against the formation of Mg₂Ca Laves phase (Kondoh et al., 2011). The second issue, via a TEM study on AZ31 (Jeong et al., 2013), was also resolved, showing that survival of CaO particles could be attributed to the solidification rate and that the difference between Ca and CaO additions lies in the agglomeration tendency of the intermetallics in CaO-added cases. A following in situ study (Wiese et al., 2015) also confirmed CaO dissolution that even started in solid state and increased until melting.

CaO addition was also proven useful in increasing the ignition temperatures of pure Mg and AZ series alloys, lessening concerns about safe handling of machining chips (You et al., 2000; Lee and Kim, 2009a,b, 2011b; Kim, 2011), as well as paving the way for use in aviation applications. An earlier study also reported this improvement in Ca-added Mg. Although the ignition temperature decreases with increasing Al content with a corresponding decrease in melting temperatures for AZ alloys, it was shown that CaO addition in all AZ series, MRI153, MRI230, and AS21 alloys, led to increasing ignition temperatures. A noteworthy example was the remarkable figure of 1,177°C for AZ31 with 1.22 wt% CaO (Kim, 2011). In addition to the flammability findings, general corrosion resistance of Mg and AZ series alloys was also reported to have benefited greatly from the addition of CaO (You et al., 2000; Lee and Kim, 2009a,b; Kim, 2011). The conclusion arrived was that the Al content had an adverse effect, and the total amount of Ca-bearing phases was the determining figure for the ignition temperature (Lee and Kim, 2011b).

The oxide film forming on the CaO-added Mg and Mg alloys was said not to conform to the Pilling–Bedworth (Pilling and Bedworth, 1923) theory that requires no volumetric change between the unit metal and the oxide phase replacing it for formation of a protective oxide film. According to the Pilling–Bedworth theory, pure Mg forms an unprotective MgO as the related R value is less than unity, being only 0.83, whereas CaO has even a worse figure of 0.78. It appears that these figures, as they may not represent the case for a mixed oxide, are counterintuitive to explain the improvement in the case CaO addition. Although a dense oxide film formation (Lee and Kim, 2011b) was assumed to explain the protective effect of CaO addition, the nature of this phenomenon in terms of structure of the surface oxide requires further exploration.

It is fair to say that much work is still needed to understand whether such use of CaO is universally applicable for all, and especially for the potentially useful novel Mg alloys of the future, and in terms of suitability to different popular production methods. For example, a twin-roll-casting study (Li et al., 2010) showed that both Al and Ca contents deteriorated the surface quality of the product in AZ series alloys. The fact that Ca-containing complex intermetallics were found in CaO-added structures should also be taken to indicate this necessity for a more comprehensive research on alloys involving elements having the potential to form precipitates with Ca.

Conclusions and Suggestions for Future Work

Stacking fault energy changes due to addition of solute atoms into a host system are not straightforward to understand. On the other hand, Miedema's model leads to a better understanding of the free electron density distribution and the consequent SFE changes presented by the ab initio calculations. The fundamental terms of the atomic-level thermodynamic expression given by Miedema, that is, n_WS (density of electrons at the boundary of the two atomic cells, Wigner–Seitz cells) and Φ^* (the difference in chemical potential for electrons or equivalently the difference in electronegativity, or difference between the work functions), have been shown to be related to SFE in binary systems.

The qualitative relationship of those terms in Miedema's model with SFE shows that the employment of work function measurements (e.g., Kelvin Probe Force Microscopy) is possible to, at least, qualitatively assess the influence of the extra alloying elements into an alloy system with reference to a pure or binary system. Thus, a qualitative assessment of the changes in SFE in multicomponent systems can be undertaken readily when experimentally developing new alloys. This point may be appreciated better when considering the fact that ab initio calculations in multicomponent systems are currently not feasible.

Furthermore, it seems reasonable to indicate the need to extend the atomic-level thermodynamic assessment according to Miedema's approach to multicomponent systems. This difficult task would then facilitate a more complete evaluation and allow predictions in terms of precipitate forming multicomponent alloy systems, especially in terms of those that form LPSO phases or quasi-crystals.

The concept of SRO indicates the possibility of designing dilute alloy systems with desirable engineering properties. This concept also indicates the possibility to alter the freezing range of alloys with dilute additions; that is, strong SRO may expand the freezing range, as a critical parameter for casting operations such as twin roll casting. There appears to be sufficient literature that warrants further studies to explore the types of SRO through first-principles calculations, which include DOS computations. Our evaluation of the existing literature has indicated that two types of SRO can be expected depending on whether hybridization occurs in electron sharing between neighboring atoms. Miedema's geometric scheme also shows such categorization for binary alloys of Mg in terms of upper (north) and lower (south) sectors in a plot of n_WS vs. Φ^*.

The case of dilute levels of oxygen in Mg, or in other metals, presents a particularly interesting example in this regard. Presence of trace amounts of oxygen in different Mg alloy systems deserves attention.

The highly useful addition of Ca/CaO needs to be examined in a broader perspective in terms of its melt protection and the probable concomitant precipitation effects, as well as influences on castability or other processing techniques.

It should be indicated that some Mg alloy systems, such as those involving LPSO phases or quasi-crystals, and those containing Ca or dilute amount of oxygen have been developed, which offer superior engineering properties and solutions to the relatively problematic features of Mg. A steady increase in the use of Mg alloys can therefore be expected.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank to my students Sevcan Arslan, Talha Cakmak, and Ugurcan Ozogut for their help in preparation of the figures. I also extend my special thanks to my friend Prof. Dr. Ahmet Oral of Middle East Technical University for conducting the KPFM measurements at Nanomagnetics Instruments Co. The author also thankfully acknowledges the financial support provided by Scientific Research Projects (BAP) office of Mugla Sitki Kocman University toward the production of microscopy and KPFM work within the Project no: 16/070.

References

Abaspour, S. (2014). Thermodynamics-based design of creep resistant mg solid solutions using the miedema scheme (Ph.D. thesis). Queensland: The University of Queensland, Australia.

Google Scholar

Abaspour, S., and Caceres, C. H. (2013). “Creep beha viour of Mg binary solid solutions,” in Magnesium Technology 2013, eds N. Hort, S. N. Mathaudhu, N. R. Neelameggham, and M. Alderman [San Antonio, TX: The Minerals, Metals & Materials Society (TMS)], 17–20. doi: 10.1007/978-3-319-72332-7

CrossRef Full Text | Google Scholar

Abaspour, S., and Cáceres, C. H. (2014). “The athermal component of the strength of binary mg solid solutions,” in International Conference on Magnesium Technology 2014, eds N. R. Alderman, M. Manuel, M. V. Hort, and N. Neelameggham (San Diego, CA: The Minerals, Metals & Materaisl Society), 73–75.

Google Scholar

Abaspour, S., and Cáceres, C. H. (2015). Thermodynamics-based selection and design of creep-resistant cast mg alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 46, 5972–5988. doi: 10.1007/s11661-015-3128-5

CrossRef Full Text | Google Scholar

Abaspour, S., and Cáceres, C. H. (2016). High temperature strength and stress relaxation behavior of dilute binary Mg alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 47, 1313–1321. doi: 10.1007/s11661-015-3292-7

CrossRef Full Text | Google Scholar

Abaspour, S., Zambelli, V., Dargusch, M., and Cáceres, C. H. (2016). Atomic size and local order effects on the high temperature strength of binary Mg alloys. Mater. Sci. Eng. A 673, 114–121. doi: 10.1016/j.msea.2016.07.019

CrossRef Full Text | Google Scholar

Abe, E., Kawamura, Y., Hayashi, K., and Inoue, A. (2002). Long-period ordered structure in a high-strength nanocrystalline Mg-1 at% Zn-2 at% Y alloy studied by atomic-resolution Z-contrast STEM. Acta Mater. 50, 3845–3857. doi: 10.1016/S1359-6454(02)00191-X

CrossRef Full Text | Google Scholar

Abe, E., Ono, A., Itoi, T., Yamasaki, M., and Kawamura, Y. (2011). Polytypes of long-period stacking structures synchronized with chemical order in a dilute Mg-Zn-Y alloy. Philos. Mag. Lett. 91, 690–696. doi: 10.1080/09500839.2011.609149

CrossRef Full Text | Google Scholar

Abe, E., Sato, T. J., and Tsai, A. P. (2000). Structure and phase transformation of the Zn-Mg-rare-earth quasicrystals. Mater. Sci. Eng. A 294–296, 29–32. doi: 10.1016/S0921-5093(00)01312-5

CrossRef Full Text | Google Scholar

Agnew, S. R. (2012). “Advances in wrought magnesium alloys,” in Fundamentals of Processing, Properties and Applications, eds C. Bettles and M. Barnett (Pittsburgh, PA: Woodhead Publishing), 63–104.

Google Scholar

Agnew, S. R., Capolungo, L., and Calhoun, C. A. (2015). Connections between the basal I1 “growth” fault and <c+a> dislocations. Acta Mater. 82, 255–265. doi: 10.1016/j.actamat.2014.07.056

CrossRef Full Text | Google Scholar

Akhtar, A., and Teghtsoonian, E. (1969). Solid solution strengthening of magnesium single crystals-I alloying behaviour in basal slip. Acta Metall. 17, 1339–1349. doi: 10.1016/0001-6160(69)90151-5

CrossRef Full Text | Google Scholar

Albright, D. L., Bergeron, F., Neelameggham, R., Luo, A., Kaplan, H., and Pekguleryuz, M. O. (2002). Magnesium technology 2002, part II: wrought products, alloy processing, R&D strategies, corrosion, welding. JOM 54, 22–24. doi: 10.1007/BF02711862

CrossRef Full Text | Google Scholar

Amberger, D., Eisenlohr, P., and Göken, M. (2009). Microstructural evolution during creep of Ca-containing AZ91. Mater. Sci. Eng. A 510–511, 398–402. doi: 10.1016/j.msea.2008.04.115

CrossRef Full Text | Google Scholar

Amiya, K., Ohsuna, T., and Inoue, A. (2003). Long-period hexagonal structures in melt-spun Mg(97)Ln(2)Zn(1) (Ln=lanthanide metal) alloys. Mater. Trans. 44, 2151–2156. doi: 10.2320/matertrans.44.2151

CrossRef Full Text | Google Scholar

Ando, S., Kodera, A., Yagi, T., and Tsushida, M. (2013). “Alloying effects on non-basal slips in magnesum single crystals,” in Materials Science and Technology Conference and Exhibition (Montreal, CA), 1449–1454.

Avedesian, M., and Baker, H. (1999). Magnesium and Magnesium Alloys, Handbook. Cleveland, OH: ASM International.

Bader, R. F. W. (1990). Atoms in Molecules: A Quantum Theory. Oxford: Oxford University Press.

Google Scholar

Bae, D. H., Kim, S. H., Kim, D. H., and Kim, W. T. (2002). Deformation behavior of Mg-Zn-Y alloys reinforced by icosahedral quasicrystalline particles. Acta Mater. 50, 2343–2356. doi: 10.1016/S1359-6454(02)00067-8

CrossRef Full Text | Google Scholar

Bae, D. H., Kim, S. H., Kim, W. T., and Kim, D. H. (2001). High strength Mg-Zn-Y alloy containing quasicrystalline particles. Mat. Transact. 42, 2144–2147.

Google Scholar

Balogh, L., Tichy, G., and Ungár, T. (2009). Twinning on pyramidal planes in hexagonal close packed crystals determined along with other defects by X-ray line profile analysis. J. Appl. Crystallogr. 42, 580–591. doi: 10.1107/S0021889809022936

CrossRef Full Text | Google Scholar

Barnett, M. R., Keshavarz, Z., and Ma, X. (2006). A semianalytical Sachs model for the flow stress of a magnesium alloy. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 37, 2283–2293. doi: 10.1007/BF02586147

CrossRef Full Text | Google Scholar

Bernstein, N., and Tadmor, E. B. (2004). Tight-binding calculations of stacking energies and twinnability in fcc metals. Phys. Rev. B 69, 1–10. doi: 10.1103/PhysRevB.69.094116

CrossRef Full Text | Google Scholar

Blake, A. H., and Cáceres, C. H. (2008). Solid-solution hardening and softening in Mg-Zn alloys. Mater. Sci. Eng. A 483–484, 161–163. doi: 10.1016/j.msea.2006.10.205

CrossRef Full Text | Google Scholar

Brain, I., and Knacke, O. (1973). Thermochemical Properties of Inorganic Substances. Berlin; New York, NY: Springer-Verlag.

Brewr, L. (1967). A most striking confirmation of engel metallic correlation. Acta Metall. 15, 553–560. doi: 10.1016/0001-6160(67)90088-0

CrossRef Full Text | Google Scholar

Brown, D. W., Agnew, S. R., Bourke, M. A. M., Holden, T. M., Vogel, S. C., and Tom, C. N. (2005). Internal strain and texture evolution during deformation twinning in magnesium. Mater. Sci. Eng. A 399, 1–12. doi: 10.1016/j.msea.2005.02.016

CrossRef Full Text | Google Scholar

Brown, D. W., Jain, A., Agnew, S. R., and Clausen, B. (2009). Twinning and detwinning during cyclic deformation of Mg alloy AZ31B. Mater. Sci. Forum. 539–543, 3407–3413. doi: 10.4028/www.scientific.net/MSF.539-543.3407

CrossRef Full Text | Google Scholar

Buey, D., Hector, L. G., and Ghazisaeidi, M. (2018). Core structure and solute strengthening of second-order pyramidal <c+a> dislocations in Mg-Y alloys. Acta Mater. 147, 1–9. doi: 10.1016/j.actamat.2017.12.066

CrossRef Full Text | Google Scholar

Cahn, R. W., and Davies, R. G. (1960). X-ray evidence for segregation of solute to stacking faults in a copper-aluminium alloy. Philos. Mag. 5, 1119–1126. doi: 10.1080/14786436008238320

CrossRef Full Text | Google Scholar

Chai, Y., Jiang, B., Song, J., Wang, Q., He, J., Zhao, J., et al. (2018). Role of Al content on the microstructure, texture and mechanical properties of Mg-3.5Ca based alloys. Mater. Sci. Eng. A 730, 303–316. doi: 10.1016/j.msea.2018.06.011

CrossRef Full Text | Google Scholar

Chang, C. F., Das, S. K., and Raybould, D. (1987). Rapidly solidified Mg-Al-Zn-rare earth alloys. J. Mater. Eng. 9, 141–146. doi: 10.1007/BF02833703

CrossRef Full Text | Google Scholar

Chang, C. F., Das, S. K., Raybould, D., and Brown, A. (1986). Corrosion resistant high strength magnesium alloys by Rsp. Metal. Powder Rep. 41, 302–305.

Chapuis, A., and Driver, J. H. (2011). Temperature dependency of slip and twinning in plane strain compressed magnesium single crystals. Acta Mater. 59, 1986–1994. doi: 10.1016/j.actamat.2010.11.064

CrossRef Full Text | Google Scholar

Chen, K., and Boyle, K. P. (2009). Elastic properties, thermal expansion coefficients, and electronic structures of Mg and Mg-based alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 40, 2751–2760. doi: 10.1007/s11661-009-9954-6

CrossRef Full Text | Google Scholar

Christian, J. W., and Mahajan, S. (1995). Deformation twinning. Progr. Mater. Sci. 39, 1–157. doi: 10.1016/0079-6425(94)00007-7

CrossRef Full Text | Google Scholar

Cipoletti, D. E., Bower, A. F., and Krajewski, P. E. (2011). A microstructure-based model of the deformation mechanisms and flow stress during elevated-temperature straining of a magnesium alloy. Scr. Mater. 64, 931–934. doi: 10.1016/j.scriptamat.2010.12.033

CrossRef Full Text | Google Scholar

Dai, X. D., Li, J. H., and Liu, B. X. (2007). Molecular statics calculation of the formation enthalpy for ternary metal systems based on the long-range empirical interatomic potentials. Appl. Phys. Lett. 90, 6–9. doi: 10.1063/1.2716361

CrossRef Full Text | Google Scholar

Ding, Z., Liu, W., Li, S., Zhang, D., Zhao, Y., Lavernia, E. J., et al. (2016). Contribution of van der waals forces to the plasticity of magnesium. Acta Mater. 107, 127–132. doi: 10.1016/j.actamat.2016.01.026

CrossRef Full Text | Google Scholar

Dong, Q., Luo, Z., Zhu, H., Wang, L., Ying, T., Jin, Z., et al. (2018). Basal-plane stacking-fault energies of Mg alloys: a first-principles study of metallic alloying effects. J. Mater. Sci. Technol. 34, 1773–1780. doi: 10.1016/j.jmst.2018.02.009

CrossRef Full Text | Google Scholar

Dubois, J. M. (2012). Properties- and applications of quasicrystals and complex metallic alloys. Chem. Soc. Rev. 41, 6760–6777. doi: 10.1039/c2cs35110b

PubMed Abstract | CrossRef Full Text | Google Scholar

Egusa, D., and Abe, E. (2012). The structure of long period stacking/order Mg-Zn-RE phases with extended non-stoichiometry ranges. Acta Mater. 60, 166–178. doi: 10.1016/j.actamat.2011.09.030

CrossRef Full Text | Google Scholar

Fan, H., Tang, J., Tian, X., Wang, Q., Tian, X., and El-Awady, J. A. (2017). Core structures and mobility of 〉c〈 dislocations in magnesium. Scr. Mater. 135, 37–40. doi: 10.1016/j.scriptamat.2017.03.012

CrossRef Full Text | Google Scholar

Fan, T. W., Tang, B. Y., Peng, L. M., and Ding, W. J. (2011). First-principles study of long-period stacking ordered-like multi-stacking fault structures in pure magnesium. Scr. Mater. 64, 942–945. doi: 10.1016/j.scriptamat.2011.01.039

CrossRef Full Text | Google Scholar

Ganeshan, S., Hector, L. G., and Liu, Z. K. (2011). First-principles calculations of impurity diffusion coefficients in dilute Mg alloys using the 8-frequency model. Acta Mater. 59, 3214–3228. doi: 10.1016/j.actamat.2011.01.062

CrossRef Full Text | Google Scholar

Gao, Y., Wang, Q., Gu, J., Zhao, Y., Tong, Y., and Yin, D. (2009). Comparison of microstructure in Mg-10Y-5Gd-0.5Zr and Mg-10Y-5Gd-2Zn-0.5Zr alloys by conventional casting. J. Alloys Compd. 477, 374–378. doi: 10.1016/j.jallcom.2008.10.003

CrossRef Full Text | Google Scholar

Garg, P., Adlakha, I., and Solanki, K. N. (2018). Effect of solutes on ideal shear resistance and electronic properties of magnesium: a first-principles study. Acta Mater. 153, 327–335. doi: 10.1016/j.actamat.2018.05.014

CrossRef Full Text | Google Scholar

Gencheva, D. S., Katsnelson, A. A., Rokhlin, L. L., Silonov, V. M., and Khavadzha, F. A. (1981). Investigation of short-range order in magnesium alloys with erbium and gaolinium. Fiz. Metal. 51, 788–793.

Guan, D., Liu, X., Gao, J., Ma, L., Wynne, B. P., and Rainforth, W. M. (2019). Exploring the mechanism of “Rare Earth” texture evolution in a lean Mg–Zn–Ca alloy. Sci Rep. 9:7152. doi: 10.1038/s41598-019-43415-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Z., Miodownik, A. P., Saunders, N., and Schillé, J. P. (2006). Influence of stacking-fault energy on high temperature creep of alpha titanium alloys. Scr. Mater. 54, 2175–2178. doi: 10.1016/j.scriptamat.2006.02.036

CrossRef Full Text | Google Scholar

Ha, S.-H., Lee, J.-K., and Kim, S. K. (2008). Effect of CaO on oxidation resistance and microstructure of pure Mg. Mater. Trans. 49, 1081–1083. doi: 10.2320/matertrans.MC200786

CrossRef Full Text | Google Scholar

Ha, S. H., Lee, J. K., Jo, H. H., Jung, S. B., and Kim, S. K. (2006). Effect of CaO addition on ignition behavior in molten AZ31 and AZ91D Magnesium alloys. Rare Metals 25, 150–154. doi: 10.1016/S1001-0521(08)60071-6

CrossRef Full Text | Google Scholar

Hagihara, K., Kinoshita, A., Sugino, Y., Yamasaki, M., Kawamura, Y., Yasuda, H. Y., et al. (2010a). Effect of long-period stacking ordered phase on mechanical properties of Mg97Zn1Y2 extruded alloy. Acta Mater. 58, 6282–6293. doi: 10.1016/j.actamat.2010.07.050

CrossRef Full Text | Google Scholar

Hagihara, K., Okamoto, T., Izuno, H., Yamasaki, M., Matsushita, M., Nakano, T., et al. (2016). Plastic deformation behavior of 10H-type synchronized LPSO phase in a Mg-Zn-Y system. Acta Mater. 109, 90–102. doi: 10.1016/j.actamat.2016.02.037

CrossRef Full Text | Google Scholar

Hagihara, K., Yokotani, N., and Umakoshi, Y. (2010b). Plastic deformation behavior of Mg12YZn with 18R long-period stacking ordered structure. Intermetallics 18, 267–276. doi: 10.1016/j.intermet.2009.07.014

CrossRef Full Text | Google Scholar

Halas, S. (2006). 100 years of work function. Mater. Sci. Poland 24, 20–31.

Google Scholar

Hasegawa, S., Tsuchida, Y., Yano, H., and Matsui, M. (2007). Evaluation of low cycle fatigue life in AZ31 magnesium alloy. Int. J. Fatigue 29, 1839–1845. doi: 10.1016/j.ijfatigue.2006.12.003

CrossRef Full Text | Google Scholar

Hehmann, F., Sommer, F., and Predel, B. (1990). Extension of solid solubility in magnesium by rapid solidification. Mater. Sci. Eng. A 125, 249–265. doi: 10.1016/0921-5093(90)90175-3

CrossRef Full Text | Google Scholar

Henes, S., and Gerold, V. (1962). “Roentgenographic investigation of the separation process in magnesium-lead and magnesium-zinc alloys. II,” in The Separation of the Stable Equilibrium Phase (in German), ed Z. Metallk. 53, 46–51.

Google Scholar

Holtzer, M., and Bobrowski, A. (2008). Magnesium melt protection by covering gas. Arch. Found. Eng. 8, 131–136.

Google Scholar

Homma, T., Kunito, N., and Kamado, S. (2009). Fabrication of extraordinary high-strength magnesium alloy by hot extrusion. Scr. Mater. 61, 644–647. doi: 10.1016/j.scriptamat.2009.06.003

CrossRef Full Text | Google Scholar

Hosford, W. F. (1993). The Mechanics of Crystals and Textured Polycrystals. Materials Characterization, Vol. 34. Oxford: Oxford University Press.

Houska, C. R., and Averbach, B. L. (1959). Neutron irradiation effects in a copper aluminum alloy. J. Appl. Phys. 81, 1525–1532. doi: 10.1063/1.1734994

CrossRef Full Text | Google Scholar

Hu, W., Yang, Z., Liu, J., and Ye, H. (2016). “Creep of A Mg-Zn-Y alloy at elevated temperatures,” in Magnesium Technology (Hoboken, NJ: John Wiley & Sons), 169–174.

Google Scholar

Hua, G., and Li, D. (2011). Generic relation between the electron work function and young's modulus of metals. Appl. Phys. Lett. 99, 2011–2014. doi: 10.1063/1.3614475

CrossRef Full Text | Google Scholar

Huang, Y. B., Chung, I. S., You, B. S., Park, W. W., and Choi, B. H. (2004). Effect of be addition on the oxidation behavior of mg-ca alloys at elevated temperature. Met. Mater. Int. 10, 7–11. doi: 10.1007/BF03027357

CrossRef Full Text | Google Scholar

Huppmann, M., Lentz, M., Chedid, S., and Reimers, W. (2011). Analyses of deformation twinning in the extruded magnesium alloy AZ31 after compressive and cyclic loading. J. Mater. Sci. 46, 938–950. doi: 10.1007/s10853-010-4838-0

CrossRef Full Text | Google Scholar

Iikubo, S., Hamamoto, S., and Ohtani, H. (2013). Thermodynamic analysis of the Mg&ndash;RE&ndash;Zn (RE = Y, La) ternary hcp phase using the cluster variation method. Mater. Trans. 54, 636–640. doi: 10.2320/matertrans.MI201222

CrossRef Full Text | Google Scholar

Inoue, A., Kawamura, Y., Matsushita, M., Hayashi, K., and Koike, J. (2001). Novel hexagonal structure and ultrahigh strength of magnesium solid solution in the Mg–Zn–Y system. J. Mater. Res. 16, 1894–1900. doi: 10.1557/JMR.2001.0260

CrossRef Full Text | Google Scholar

Itoi, T., Seimiya, T., Kawamura, Y., and Hirohashi, M. (2004). Long period stacking structures observed in Mg97Zn 1Y2 alloy. Scr. Mater. 51, 107–111. doi: 10.1016/j.scriptamat.2004.04.003

CrossRef Full Text | Google Scholar

Iwatake, Y., Okamoto, N. L., Kishida, K., Inui, H., Ishida, J., Kai, T., et al. (2015). New crystal structure of Nd2Ni7 formed on the basis of stacking of block layers. Int. J. Hydrogen Energ. 40, 3023–3034. doi: 10.1016/j.ijhydene.2015.01.007

CrossRef Full Text | Google Scholar

Jeong, J., Im, J., Song, K., Kwon, M., Kim, S. K., Kang, Y. B., et al. (2013). Transmission electron microscopy and thermodynamic studies of CaO-added AZ31 Mg alloys. Acta Mater. 61, 3267–3277. doi: 10.1016/j.actamat.2013.02.015

CrossRef Full Text | Google Scholar

Jian, W. W., Cheng, G. M., Xu, W. Z., Yuan, H., Tsai, M. H., Wang, Q. D., et al. (2013). Ultrastrong Mg alloy via nano-spaced stacking faults. Mater. Res. Lett. 1, 61–66. doi: 10.1080/21663831.2013.765927

CrossRef Full Text | Google Scholar

Jiang, Z., Jiang, B., Yang, H., Yang, Q., Dai, J., and Pan, F. (2015). Influence of the Al2Ca phase on microstructure and mechanical properties of Mg-Al-Ca alloys. J. Alloys Compd. 647, 357–363. doi: 10.1016/j.jallcom.2015.06.060

CrossRef Full Text | Google Scholar

Jin, Q. Q., Fang, C. F., and Mi, S. B. (2013). Formation of long-period stacking ordered structures in Mg 88M5Y7 (M = Ti, Ni and Pb) casting alloys. J. Alloys Compd. 568, 21–25. doi: 10.1016/j.jallcom.2013.03.061

CrossRef Full Text | Google Scholar

Jin, Z. H., Han, J., Su, X. M., and Zhu, Y. T. (2011). Basal-plane stacking-fault energies of Mg: a first-principles study of Li- and Al-alloying effects. Scr. Mater. 2, 121–128. doi: 10.1002/9781118062142.ch15

CrossRef Full Text | Google Scholar

Kang, H., Choi, H. J., Kang, S. W., Shin, S. E., Choi, G. S., and Bae, D. H. (2016). Multi-functional magnesium alloys containing interstitial oxygen atoms. Sci. Rep. 6:23184. doi: 10.1038/srep23184

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, S. W., Kang, H., and Bae, D. H. (2017). Strengthening and toughening behaviors of a Mg-9Al alloy containing oxygen atoms. J. Alloys Compd. 725, 441–448. doi: 10.1016/j.jallcom.2017.07.190

CrossRef Full Text | Google Scholar

Kang, S. W., Kang, H., Choi, H. J., and Bae, D. H. (2018). Phase boundary sliding of a reticular-structured Mg-O-9Al alloy. J. Alloys Compd. 750, 729–740. doi: 10.1016/j.jallcom.2018.04.039

CrossRef Full Text | Google Scholar

Kawamura, Y., Hayashi, K., Inoue, A., and Masumoto, T. (2001). Rapidly solidified powder metallurgy Mg97Zn1Y2Alloys with excellent tensile yield strength above 600 MPa. Mater Trans. 42, 1172–1176. doi: 10.2320/matertrans.42.1172

CrossRef Full Text | Google Scholar

Kawamura, Y., Kasahara, T., Izumi, S., and Yamasaki, M. (2006). Elevated temperature Mg97Y2Cu1 alloy with long period ordered structure. Scr. Mater. 55, 453–456. doi: 10.1016/j.scriptamat.2006.05.011

CrossRef Full Text | Google Scholar

Kawamura, Y., and Yamasaki, M. (2007). Formation and mechanical properties of alloys with long-period stacking ordered structure. Mater. Trans. Jpn Inst. Met. 48, 2986–2992. doi: 10.2320/matertrans.MER2007142

CrossRef Full Text | Google Scholar

Kaya, A. A., Yucel, O., Eliezer, D., and Aghion, E. (2003). “An electron microscopy investigation on as-cast AZ91D alloy modified with nitrogen,” in Magnesium, The 6th International Conference on Magnesium Alloys and Their Application, ed K. U. Kainer (Wolfsburg: Wiley-VCH), 150–157.

Google Scholar

Kim, H., Ross, A. J., Shang, S. L., Wang, Y., Kecskes, L. J., and Liu, Z. K. (2018a). First-principles calculations and thermodynamic modelling of long periodic stacking ordered (LPSO) phases in Mg-Al-Gd. Materialia 4, 192–202. doi: 10.1016/j.mtla.2018.09.013

CrossRef Full Text | Google Scholar

Kim, H., Wang, W. Y., Shang, S. L., Kecskes, L. J., Darling, K. A., and Liu, Z. K. (2018b). Elastic properties of long periodic stacking ordered phases in Mg-Gd-Al alloys: a first-principles study. Intermetallics 98, 18–27. doi: 10.1016/j.intermet.2018.04.009

CrossRef Full Text | Google Scholar

Kim, J. K., Jin, L., Sandlöbes, S., and Raabe, D. (2017). Diffusional-displacive transformation enables formation of long-period stacking order in magnesium. Sci. Rep. 7:4046. doi: 10.1038/s41598-017-04343-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J. K., Ko, W. S., Sandlöbes, S., Heidelmann, M., Grabowski, B., and Raabe, D. (2016). The role of metastable LPSO building block clusters in phase transformations of an Mg-Y-Zn alloy. Acta Mater. 112, 171–183. doi: 10.1016/j.actamat.2016.04.016

CrossRef Full Text | Google Scholar

Kim, K. H., Jeon, J. B., Kim, N. J., and Lee, B. J. (2015). Role of yttrium in activation of “c + a” slip in magnesium: an atomistic approach. Scr. Mater. 108, 104–108. doi: 10.1016/j.scriptamat.2015.06.028

CrossRef Full Text | Google Scholar

Kim, S. H., and Park, S. H. (2018). Underlying mechanisms of drastic reduction in yield asymmetry of extruded Mg-Sn-Zn alloy by Al addition. Mater. Sci. Eng. A 733, 285–290. doi: 10.1016/j.msea.2018.07.063

CrossRef Full Text | Google Scholar

Kim, S. K. (2011). “Design and development of high-performance eco-mg alloys,” in Design, Processing and Properties, ed Czerwinski, F. IntechOpen. Available online at: https://www.intechopen.com/books/magnesium-alloys-design-processing-and-properties/design-and-development-of-high-performance-eco-mg-alloys (accessed January 14, 2011).

Google Scholar

Kim, S. K., Lee, J. K., Yoon, Y. O., and Jo, H. H. (2007). Development of AZ31 Mg alloy wrought process route without protective gas. J. Mater. Process. Technol. 187–188, 757–760. doi: 10.1016/j.jmatprotec.2006.11.172

CrossRef Full Text | Google Scholar

Kimizuka, H., Fronzi, M., and Ogata, S. (2013). Effect of alloying elements on in-plane ordering and disordering of solute clusters in Mg-based long-period stacking ordered structures: a first-principles analysis. Scr. Mater. 69, 594–597. doi: 10.1016/j.scriptamat.2013.07.003

CrossRef Full Text | Google Scholar

Kimizuka, H., and Ogata, S. (2013). Predicting atomic arrangement of solute clusters in dilute Mg alloys. Mater. Res. Lett. 1, 213–219. doi: 10.1080/21663831.2013.838705

CrossRef Full Text | Google Scholar

Kishida, K., Nagai, K., Matsumoto, A., Yasuhara, A., and Inui, H. (2015). Crystal structures of highly-ordered long-period stacking-ordered phases with 18 R, 14 H and 10 H-type stacking sequences in the Mg–Zn–Y system. Acta Mater. 99, 228–239. doi: 10.1016/j.actamat.2015.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Kishida, K., Yokobayashi, H., and Inui, H. (2013). The most stable crystal structure and the formation processes of an order-disorder (OD) intermetallic phase in the Mg-Al-Gd ternary system. Philos. Mag. 93, 2826–2846. doi: 10.1080/14786435.2013.790566

CrossRef Full Text | Google Scholar

Kishida, K., Yokobayashi, H., and Inui, H. (2017). A formation criterion for order-disorder (OD) phases of the long-period stacking order (LPSO)-type in Mg-Al-RE (Rare Earth) ternary systems. Sci. Rep. 7:12294. doi: 10.1038/s41598-017-12506-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kishida, K., Yokobayashi, H., Inui, H., Yamasaki, M., and Kawamura, Y. (2012). The crystal structure of the LPSO phase of the 14H-type in the Mg-Al-Gd alloy system. Intermetallics 31, 55–64. doi: 10.1016/j.intermet.2012.06.010

CrossRef Full Text | Google Scholar

Kondoh, K., Fujita, J., Umeda, J., Imai, H., Enami, K., Ohara, M., et al. (2011). Thermo-dynamic analysis on solid-state reduction of CaO particles dispersed in Mg-Al alloy. Mater. Chem. Phys. 129, 631–640. doi: 10.1016/j.matchemphys.2011.05.017

CrossRef Full Text | Google Scholar

Kounis, A., Miehe, G., and Fuess, H. (2000). Investigation of icosahedral phases in the Zn-Mg-(Y, Er) system by high resolution transmission electron microscopy. Mater. Sci. Eng. A 294–296, 323–326. doi: 10.1016/S0921-5093(00)01182-5

CrossRef Full Text | Google Scholar

Kumari, M., and Verma, U. P. (2018). Full potential study of HoMg. J. Magnes. Alloy 6, 189–196. doi: 10.1016/j.jma.2018.03.002

CrossRef Full Text | Google Scholar

Lee, J.-K., and Kim, S. K. (2011b). Effect of CaO addition on the ignition resistance of Mg-Al alloys. Mater. Trans. 52, 1483–1488. doi: 10.2320/matertrans.M2010397

CrossRef Full Text | Google Scholar

Lee, J. B., Sato, K., Konno, T. J., and Hiraga, K. (2011). Complex precipitates with long periodic stacking (LPS) phase and precipitation behaviors in the Mg97Zn1Y 1.5Nd0.5 alloy by age-annealing. Intermetallics 19, 1096–1101. doi: 10.1016/j.intermet.2010.12.003

CrossRef Full Text | Google Scholar

Lee, J. K., and Kim, S. K. (2009a). Development of novel environment-friendly magnesium alloys. Adv. Mater. Res. 47–50, 940–943. doi: 10.4028/www.scientific.net/AMR.47-50.940

CrossRef Full Text | Google Scholar

Lee, J. K., and Kim, S. K. (2009b). Thermodynamic consideration of CaO added Mg alloys in recycling process. Mater. Sci. Forum. 620–622, 615–618. doi: 10.4028/www.scientific.net/MSF.620-622.615

CrossRef Full Text | Google Scholar

Lee, J. K., and Kim, S. K. (2011a). Effect of CaO composition on oxidation and burning behaviors of AM50 Mg alloy. Trans. Nonferr. Metals Soc. China 21, s23–s27. doi: 10.1016/S1003-6326(11)61054-6

CrossRef Full Text | Google Scholar

Li, N., Huang, G., Zhong, X., and Liu, Q. (2013). Deformation mechanisms and dynamic recrystallization of AZ31 Mg alloy with different initial textures during hot tension. Mater. Des. 50, 382–391. doi: 10.1016/j.matdes.2013.03.028

CrossRef Full Text | Google Scholar

Li, X. K., Jiang, B., and Liao, J. C. (2010). Effects of Al and Ca on microstructure and surface defect of magnesium alloy thin strip. Trans. Nonferr. Metals Soc. China 20, s361–s365. doi: 10.1016/S1003-6326(10)60498-0

CrossRef Full Text | Google Scholar

Li, Y., and Kong, Q. P. (1989). Creep rate and stacking fault energy. Phys. Stat. Sol. A 113, 345–351. doi: 10.1002/pssa.2211130212

CrossRef Full Text | Google Scholar

Li, Y., Yang, C., Zeng, X., Jin, P., Qiu, D., and Ding, W. (2018). Microstructure evolution and mechanical properties of magnesium alloys containing long period stacking ordered phase. Mater. Charact. 141, 286–295. doi: 10.1016/j.matchar.2018.04.044

CrossRef Full Text | Google Scholar

Liao, X. Z., Srinivasan, S. G., Zhao, Y. H., Baskes, M. I., Zhu, Y. T., Zhou, F., et al. (2004). Formation mechanism of wide stacking faults in nanocrystalline Al. Appl. Phys. Lett. 84, 3564–3566. doi: 10.1063/1.1734689

CrossRef Full Text | Google Scholar

Liu, G., Zhang, J., Xi, G., Zuo, R., and Liu, S. (2017). Designing Mg alloys with high ductility: reducing the strength discrepancies between soft deformation modes and hard deformation modes. Acta Mater. 141, 1–9. doi: 10.1016/j.actamat.2017.09.006

CrossRef Full Text | Google Scholar

Liu, X. B., Chen, R. S., and Han, E. H. (2008). Effects of ageing treatment on microstructures and properties of Mg-Gd-Y-Zr alloys with and without Zn additions. J. Alloys Compd. 465, 232–238. doi: 10.1016/j.jallcom.2007.10.068

CrossRef Full Text | Google Scholar

Liu, Z. R., and Li, D. Y. (2015). The electronic origin of strengthening and ductilizing magnesium by solid solutes. Acta Mater. 89, 225–233. doi: 10.1016/j.actamat.2015.01.051

CrossRef Full Text | Google Scholar

Lu, H., Li, L., Huang, X., and Li, D. (2018). An electron work function based mechanism for solid solution hardening. J. Alloys Compd. 737, 323–329. doi: 10.1016/j.jallcom.2017.12.065

CrossRef Full Text | Google Scholar

Luo, A. A., Powell, B. R., and Balogh, M. P. (2007). Creep and microstructure of magnesium-aluminum-calcium based alloys. Metall. Mater. Trans. A 33, 567–574. doi: 10.1007/s11661-002-0118-1

CrossRef Full Text | Google Scholar

Luo, Z., Zhang, S., Tang, Y., and Zhao, D. (1993). Quasicrystals in as-cast Mg-Zn-RE alloys. Scr. Metall. Mater. 28, 1513–1518. doi: 10.1016/0956-716X(93)90584-F

CrossRef Full Text | Google Scholar

Luo, Z., Zhang, S., Tang, Y., and Zhao, D. (1994). J. Alloy. Comp. 209, 275–278.

Lv, B. J., Peng, J., Zhu, L., Wang, Y. J., and Tang, A. T. (2014). The effect of 14H LPSO phase on dynamic recrystallization behavior and hot workability of Mg-2.0Zn-0.3Zr-5.8Y alloy. Mater. Sci. Eng. A 599, 150–159. doi: 10.1016/j.msea.2014.01.079

CrossRef Full Text | Google Scholar

Mann, G. E., Sumitomo, T., and Griffiths, J. R. (2007). Reversible plastic strain during cyclic loading – unloading of Mg and Mg – Zn alloys. Mater. Sci. Eng. A 456, 138–146. doi: 10.1016/j.msea.2006.11.160

CrossRef Full Text | Google Scholar

Masoumi, M., Hoseini, M., and Pekguleryuz, M. (2011). The influence of Ce on the microstructure and rolling texture of Mg-1%Mn alloy. Mater. Sci. Eng. A 528, 3122–3129. doi: 10.1016/j.msea.2010.12.096

CrossRef Full Text | Google Scholar

Matsuda, M., Ii, S., Kawamura, Y., Ikuhara, Y., and Nishida, M. (2005). Variation of long-period stacking order structures in rapidly solidified Mg97Zn1Y2 alloy. Mater. Sci. Eng. A 393, 269–274. doi: 10.1016/j.msea.2004.10.040

CrossRef Full Text | Google Scholar

Mi, S. B., and Jin, Q. Q. (2013). New polytypes of long-period stacking ordered structures in Mg-Co-Y alloys. Scr. Mater. 68, 635–638. doi: 10.1016/j.scriptamat.2012.12.025

CrossRef Full Text | Google Scholar

Miedema, A. R. (1973a). A simple model for Alloys-I. rules for the alloying behaviour of transition metals. Philips Techn. Rev. 33, 149–160.

Google Scholar

Miedema, A. R. (1973b). A simple model for Alloys-II. the influence of ionicity on the stability and other physical properties of alloys. Philips Tech. Rev. 33, 196–202.

Miedema, A. R. (1973c). The electronegativity parameter for transition metals: heat of formation and charge transfer in alloys. J. Less-Common Metals 32, 117–136. doi: 10.1016/0022-5088(73)90078-7

CrossRef Full Text | Google Scholar

Miedema, A. R., Boom, R., and de Boer, F. R. (1975). On the heat of formations of solid alloys. J. Less Common Metals 41, 283–298. doi: 10.1016/0022-5088(75)90034-X

CrossRef Full Text | Google Scholar

Min, X. (2003). Analysis of EET on Ca increasing the melting point of Mg17Al12 phase. Chin. Sci. Bull. 47, 1082–1086. doi: 10.1360/02tb9243

CrossRef Full Text | Google Scholar

Moitra, A., Kim, S. G., and Horstemeyer, M. F. (2014). Solute effect on basal and prismatic slip systems of Mg. J. Phys. Condensed Matter. 26:445004. doi: 10.1088/0953-8984/26/44/445004

PubMed Abstract | CrossRef Full Text | Google Scholar

Muzyk, M., Pakiela, Z., and Kurzydlowski, K. J. (2012). Generalized stacking fault energy in magnesium alloys: density functional theory calculations. Scr. Mater. 66, 219–222. doi: 10.1016/j.scriptamat.2011.10.038

CrossRef Full Text | Google Scholar

Nam, N. D., Bian, M. Z., Forsyth, M., Seter, M., Tan, M., and Shin, K. S. (2012). Effect of calcium oxide on the corrosion behaviour of AZ91 magnesium alloy. Corros. Sci. 64, 263–271. doi: 10.1016/j.corsci.2012.07.026

CrossRef Full Text | Google Scholar

Nan, X. L., Wang, H. Y., Zhang, L., Li, J. B., and Jiang, Q. C. (2012). Calculation of schmid factors in magnesium: analysis of deformation behaviors. Scr. Mater. 67, 443–446. doi: 10.1016/j.scriptamat.2012.05.042

CrossRef Full Text | Google Scholar

Narita, K., Koyama, T., and Tsukada, Y. (2013). Phase-field simulation of spinodal decomposition on metastable hexagonal close-packed phase in magnesium–Yttrium–Zinc Alloy. Mater. Trans. 54, 661–667. doi: 10.2320/matertrans.MI201212

CrossRef Full Text | Google Scholar

Nie, A. J. F., Zhu, Y. M., Liu, J. Z., and Fang, X. Y. (2019). Periodic segregation of solute atoms in fully coherent twin boundaries. Science 340, 957–960.

Google Scholar

Nie, J. F. (2012). Precipitation and hardening in magnesium alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 43, 3891–3939. doi: 10.1007/s11661-012-1217-2

CrossRef Full Text | Google Scholar

Nie, J. F., Gao, X., and Zhu, S. M. (2005). Enhanced age hardening response and creep resistance of Mg-Gd alloys containing Zn. Scr. Mater. 53, 1049–1053. doi: 10.1016/j.scriptamat.2005.07.004

CrossRef Full Text | Google Scholar

Nie, J. F., Zhu, Y. M., Liu, J. Z., and Fang, X. Y. (2013). Periodic segregation of solute atoms in fully coherent twin boundaries. Science 340, 957–960. doi: 10.1126/science.1229369

PubMed Abstract | CrossRef Full Text | Google Scholar

Nie, J. F., Zhu, Y. M., and Morton, A. J. (2014). On the structure, transformation and deformation of long-period stacking ordered phases in Mg-Y-Zn alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 45, 3338–3348. doi: 10.1007/s11661-014-2301-6

CrossRef Full Text | Google Scholar

Ninomiya, R., Ojiro, T., and Kubota, K. (1995). Improved heat resistance of Mg-Al alloys by the Ca addition. Acta Metall. Mater. 43, 669–674. doi: 10.1016/0956-7151(94)00269-N

CrossRef Full Text | Google Scholar

Nishijima, M., Hiraga, K., Yamasaki, M., and Kawamura, Y. (2007). The structure of guinier-preston zones in an Mg-2 at%Gd-1 at%Zn alloy studied by transmission electron microscopy. Mater. Trans. 49, 227–229. doi: 10.2320/matertrans.MEP2007257

CrossRef Full Text | Google Scholar

Obara, T., Yoshinga, H., and Morozumi, S. (1973). Pyramidal slip system in magnesium. Acta Metall. 21, 837–1028. doi: 10.1016/0001-6160(73)90141-7

CrossRef Full Text

Oh, J. C., Ohkubo, T., Mukai, T., and Hono, K. (2005). TEM and 3DAP characterization of an age-hardened Mg-Ca-Zn alloy. Scr. Mater. 53, 675–679. doi: 10.1016/j.scriptamat.2005.05.030

CrossRef Full Text | Google Scholar

Okamoto, N. L., Yasuhara, A., and Inui, H. (2014). Order-disorder structure of the δ1kphase in the Fe-Zn system determined by scanning transmission electron microscopy. Acta Mater. 81, 345–357. doi: 10.1016/j.actamat.2014.08.025

CrossRef Full Text | Google Scholar

Oñorbe, E., Garcés, G., Pérez, P., and Adeva, P. (2012). Effect of the LPSO volume fraction on the microstructure and mechanical properties of Mg-Y 2X-Zn X alloys. J. Mater. Sci. 47, 1085–1093. doi: 10.1007/s10853-011-5899-4

CrossRef Full Text | Google Scholar

Pauling, L. (1960). The Nature of the Chemical Bond, 3rd Edn. Ithaca, NY: Cornell University Press.

Google Scholar

Pei, Z., Friák, M., Sandlöbes, S., Nazarov, R., Svendsen, B., Raabe, D., et al. (2015). Rapid theory-guided prototyping of ductile Mg alloys: from binary to multi-component materials. N. J. Phys. 17:93009. doi: 10.1088/1367-2630/17/9/093009

CrossRef Full Text | Google Scholar

Pekguleryuz, M. (2013). “Alloying behavior of magnesium and alloy design,” in Fundamentals of Magnesium Alloy Metallurgy, 1st Edn., eds A. A. Pekgleryuz, M. Kainer, and K. U. Kaya (Philadelphia: Woodhead Publishing), 152–196.

PubMed Abstract | Google Scholar

Pekguleryuz, M. O., Kaplan, H., Neelameggham, R., Hryn, J., Nyberg, E., Powell, B., et al. (2002). Magnesium technology 2002, part I: primary production, environmental issues, high-temperature alloys. JOM 54, 18–21. doi: 10.1007/BF02711861

CrossRef Full Text | Google Scholar

Peng, J. Z., Wang, Y. F., and Gray, M. F. (2008). First-principles study of structural stabilities and electronic properties of Mg-Nd intermetallic compounds. Phys. Condensed Matter. 403, 2344–2348. doi: 10.1016/j.physb.2007.12.016

CrossRef Full Text | Google Scholar

Pilling, N. B., and Bedworth, R. E. (1923). The oxidation of metals at high temperatures. J. Inst. Metals. 29, 529–582.

Google Scholar

Ping, D.-H., Hono, K., and Nie, J. F. (2003). Atom probe characterization of plate-like precipitates in a Mg–RE–Zn–Zr casting alloy. Scri. Mater. 48, 1017–1022. doi: 10.1016/S1359-6462(02)00586-9

CrossRef Full Text | Google Scholar

Ping, D. H., Hono, K., Kawamura, Y., and Inoue, A. (2002). Local chemistry of a nanocrystalline high-strength Mg97Y2Zn1 alloy. Philos. Mag. Lett. 82, 543–551. doi: 10.1080/0950083021000018652

CrossRef Full Text | Google Scholar

Pugh, S. F. (1954). XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond Edinburgh Dublin Philos. Mag. J. Sci. 45, 823–843. doi: 10.1080/14786440808520496

CrossRef Full Text | Google Scholar

Rafiei, S., Habibollahzadeh, A., and Wiese, B. (2018). “An insight into environment-conscious (ECO) magnesium : a review 1- introduction 2- CaO dissolution,” in IMAT 2018, 7th International Conference on Materials Engineering and Metallurgy (Tehran: MDRO), 1–10.

Ramsdell, L. S. (1947). Studies on silicon carbide. Am. Min. 32:64.

Google Scholar

Raynor, G. V. (1959). The Physical Metallurgy of Magnesium and its Alloys, Vol. 5. New York, NY: Pergamon Press.

Safranova, L. A., Kastnelson, A. A., Sveshnikov, S. V., L'Vov, S. V., and Yu, M. (1977). Short-range order in Mg-In solid solutions. Fiz. Metall. 43, 76–80.

Saito, K., Nishijima, M., and Hiraga, K. (2010). Stabilization of guinier-preston zones in hexagonal close-packed Mg-Gd-Zn alloys studied by transmission electron microscopy. Mater. Trans. 51, 1712–1714. doi: 10.2320/matertrans.M2010173

CrossRef Full Text | Google Scholar

Sakamoto, M., Akiyama, S., and Ogi, K. (1997). Suppression of ignition and burning of molten Mg alloys by Ca bearing stable oxide film. J. Mater. Sci. Lett. 16, 1048–1050. doi: 10.1023/A:1018526708423

CrossRef Full Text | Google Scholar

Sandlöbes, S., Friák, M., Zaefferer, S., Dick, A., Yi, S., Letzig, D., et al. (2012). The relation between ductility and stacking fault energies in Mg and Mg-Y alloys. Acta Mater. 60, 3011–3021. doi: 10.1016/j.actamat.2012.02.006

CrossRef Full Text | Google Scholar

Sandlöbes, S., Pei, Z., Friák, M., Zhu, L. F., Wang, F., Zaefferer, S., et al. (2014). Ductility improvement of Mg alloys by solid solution: Ab initio modeling, synthesis and mechanical properties. Acta Mater. 70, 92–104. doi: 10.1016/j.actamat.2014.02.011

CrossRef Full Text | Google Scholar

Sandlöbes, S., Zaefferer, S., Schestakow, I., Yi, S., and Gonzalez-Martinez, R. (2011). On the role of non-basal deformation mechanisms for the ductility of Mg and Mg-Y alloys. Acta Mater. 59, 429–439. doi: 10.1016/j.actamat.2010.08.031

CrossRef Full Text | Google Scholar

Sato, K., Tashiro, S., Matsunaga, S., Yamaguchi, Y., Kiguchi, T., and Konno, T. J. (2018). Evolution of long-period stacking order (LPSO) in Mg97Zn1Gd2 cast alloys viewed by HAADF-STEM multi-scale electron tomography. Philos. Mag. 98, 1945–1960. doi: 10.1080/14786435.2018.1468940

CrossRef Full Text | Google Scholar

Shang, S. L., Wang, W. Y., Zhou, B. C., Wang, Y., Darling, K. A., Kecskes, L. J., et al. (2014). Generalized stacking fault energy, ideal strength and twinnability of dilute Mg-based alloys: a first-principles study of shear deformation. Acta Mater. 67, 168–180. doi: 10.1016/j.actamat.2013.12.019

CrossRef Full Text | Google Scholar

Shechtman, D., Blech, I., Gratias, D., and Cahn, J. W. (1984). Metallic phase with longrange orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951–1953. doi: 10.1103/PhysRevLett.53.1951

CrossRef Full Text | Google Scholar

Somekawa, H., Singh, A., Inoue, T., and Tsuzaki, K. (2014). Crack propagation behaviour in magnesium binary alloys. Philos. Mag. 94, 3317–3330. doi: 10.1080/14786435.2014.956840

CrossRef Full Text | Google Scholar

Somekawa, H., Watanabe, H., Basha, D. A., Singh, A., and Inoue, T. (2017). Effect of twin boundary segregation on damping properties in magnesium alloy. Scr. Mater. 129, 35–38. doi: 10.1016/j.scriptamat.2016.10.019

CrossRef Full Text | Google Scholar

Stanford, N. (2010). The effect of calcium on the texture, microstructure and mechanical properties of extruded Mg-Mn-Ca alloys. Mater. Sci. Eng. A 528, 314–322. doi: 10.1016/j.msea.2010.08.097

CrossRef Full Text | Google Scholar

Stanford, N., Marceau, R. K. W., and Barnett, M. R. (2015). The effect of high yttrium solute concentration on the twinning behaviour of magnesium alloys. Acta Mater. 82, 447–456. doi: 10.1016/j.actamat.2014.09.022

CrossRef Full Text | Google Scholar

Styczynski, A., Hartig, C., Bohlen, J., and Letzig, D. (2004). Cold rolling textures in AZ31 wrought magnesium alloy. Scr. Mater. 50, 943–947. doi: 10.1016/j.scriptamat.2004.01.010

CrossRef Full Text | Google Scholar

Sumitomo, T., Veidt, M., and Ca, C. H. (2003). Pseudoelastic behaviour of cast magnesium AZ91 alloy under cyclic loading – unloading. Acta Mater. 51, 6211–6218. doi: 10.1016/S1359-6454(03)00444-0

CrossRef Full Text | Google Scholar

Sun, S. P., Yi, D. Q., Jiang, Y., Zang, B., Xu, C. H., and Li, Y. (2011). An improved atomic size factor used in miedema's model for binary transition metal systems. Chem. Phys. Lett. 513, 149–153. doi: 10.1016/j.cplett.2011.07.076

CrossRef Full Text | Google Scholar

Suzuki, A., Saddock, N. D., Jones, J. W., and Pollock, T. M. (2004). Structure and transition of eutectic (mg,al)2ca laves phase in a die-cast mg-al-ca base alloy. Scr. Mater. 51, 1005–1010. doi: 10.1016/j.scriptamat.2004.07.011

CrossRef Full Text | Google Scholar

Suzuki, A., Saddock, N. D., TerBush, J. R., Powell, B. R., Jones, J. W., and Pollock, T. M. (2008). Precipitation strengthening of a Mg-Al-Ca - based AXJ530 die-cast alloy. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 39, 696–702. doi: 10.1007/s11661-007-9455-4

CrossRef Full Text | Google Scholar

Suzuki, H. (1962). Segregation of solute atoms to stacking faults. J. Phys. Soc. Jpn. 17, 322–325. doi: 10.1143/JPSJ.17.322

PubMed Abstract | CrossRef Full Text | Google Scholar

Tane, M., Kimizuka, H., Hagihara, K., Suzuki, S., Mayama, T., Sekino, T., et al. (2015). Effects of stacking sequence and short-range ordering of solute atoms on elastic properties of Mg-Zn-Y alloys with long-period stacking ordered structures. Acta Mater. 96, 170–188. doi: 10.1016/j.actamat.2015.06.005

CrossRef Full Text | Google Scholar

Terada, Y., Ishimatsu, N., Mori, Y., and Sato, T. (2005). Eutectic phase investigation in a Ca-added AM50 magnesium alloy produced by die casting. Mater. Trans. 46, 145–147. doi: 10.2320/matertrans.46.145

CrossRef Full Text | Google Scholar

Tsuru, T., and Chrzan, D. C. (2015). Effect of solute atoms on dislocation motion in Mg: an electronic structure perspective. Sci. Rep. 5:8793. doi: 10.1038/srep08793

PubMed Abstract | CrossRef Full Text | Google Scholar

Uesugi, T., Kohyama, M., Kohzu, M., and Higashi, K. (2009). Generalized stacking fault energy and dislocation properties for various slip systems in magnesium: a first-principles study. Mater. Sci. Forum. 419–422, 225–230. doi: 10.4028/www.scientific.net/MSF.419-422.225

CrossRef Full Text | Google Scholar

van der Planken, J., and Deruyttere, A. (1969). Solution hardening of magnesium single crystals by tin at room temperature. Acta Metall. 17, 451–454. doi: 10.1016/0001-6160(69)90026-1

CrossRef Full Text | Google Scholar

Van Swygenhoven, H., Derlet, P. M., and Frøseth, A. G. (2004). Stacking fault energies and slip in nanocrystalline metals. Nat. Mater. 3, 399–403. doi: 10.1038/nmat1136

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitek, V. (1968). Intrinsic stacking faults in body-centered cubic. Acta Metall. Sinica 18, 773–786. doi: 10.1080/14786436808227500

CrossRef Full Text | Google Scholar

Waber, J. T., Gschneidner, K. Jr., Larson, A. C., and Prince, M. Y. (1963). Prediction of solid solubility in metallic alloys. Trans. Metal. Soc. AlME 227, 717–723.

Wang, C., Zhang, H. Y., Wang, H. Y., Liu, G. J., and Jiang, Q. C. (2013). Effects of doping atoms on the generalized stacking-fault energies of Mg alloys from first-principles calculations. Scr. Mater. 69, 445–448. doi: 10.1016/j.scriptamat.2013.05.026

CrossRef Full Text | Google Scholar

Wang, F., Sun, S. J., Yu, B., Zhang, F., Mao, P. L., and Liu, Z. (2016). First principles investigation of binary intermetallics in Mg-Al-Ca-Sn alloy: stability, electronic structures, elastic properties and thermodynamic properties. Trans. Nonferr. Metals Soc. China 26, 203–212. doi: 10.1016/S1003-6326(16)64107-9

CrossRef Full Text

Wang, H. Y., Zhang, N., Wang, C., and Jiang, Q. C. (2011). First-principles study of the generalized stacking fault energy in Mg-3Al-3Sn alloy. Scr. Mater. 65, 723–726. doi: 10.1016/j.scriptamat.2011.07.016

CrossRef Full Text | Google Scholar

Wang, J., Hirth, J. P., and Tomé, C. N. (2009). (1 0 1 2) Twinning nucleation mechanisms in hexagonal-close-packed crystals. Acta Mater. 57, 5521–5530. doi: 10.1016/j.actamat.2009.07.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Chen, J., Zhao, Z., and He, S. (2010). Microstructure and super high strength of cast Mg-8.5Gd-2.3Y-1.8Ag-0.4Zr alloy. Mater. Sci. Eng. A 528, 323–328. doi: 10.1016/j.msea.2010.09.004

CrossRef Full Text | Google Scholar

Wang, T., Jiang, L., Mishra, R. K., and Jonas, J. J. (2014). Effect of Ca addition on the intensity of the rare earth texture component in extruded magnesium alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 45, 4698–4709. doi: 10.1007/s11661-014-2371-5

CrossRef Full Text | Google Scholar

Wang, W. Y., Shang, S. L., Wang, Y., Darling, K. A., Mathaudhu, S. N., Hui, X. D., et al. (2012). Electron localization morphology of the stacking faults in Mg: a first-principles study. Chem. Phys. Lett. 551, 121–125. doi: 10.1016/j.cplett.2012.09.028

CrossRef Full Text | Google Scholar

Wang, W. Y., Shang, S. L., Wang, Y., Mei, Z. G., Darling, K. A., Kecskes, L. J. et al. (2014). Effects of alloying elements on stacking fault energies and electronic structures of binary Mg alloys: a first-principles study. Mater. Res. Lett. 2, 29–36. doi: 10.1080/21663831.2013.858085

CrossRef Full Text | Google Scholar

Wang, Y. F., Zhang, W. B., Wang, Z. Z., Deng, Y. H., Yu, N., Tang, B. Y., et al. (2007). First-principles study of structural stabilities and electronic characteristics of Mg-La intermetallic compounds. Comput. Mater. Sci. 41, 78–85. doi: 10.1016/j.commatsci.2007.03.003

CrossRef Full Text | Google Scholar

Weinert, N. C. M. (1997). Stacking fualts in magnesium. Phys. Rev. B 56, 844–851. doi: 10.1103/PhysRevB.56.10844

CrossRef Full Text | Google Scholar

Wen, L., Chen, P., Tong, Z. F., Tang, B. Y., Peng, L. M., and Ding, W. J. (2009). A systematic investigation of stacking faults in magnesium via first-principles calculation. Eur. Phys. J. B 72, 397–403. doi: 10.1140/epjb/e2009-00365-2

CrossRef Full Text | Google Scholar

Wiese, B., Mendis, C. L., Tolnai, D., Stark, A., Schell, N., Reichel, H. P., et al. (2015). CaO dissolution during melting and solidification of a Mg-10 wt.% CaO alloy detected with in situ synchrotron radiation diffraction. J. Alloys Compd. 618, 64–66. doi: 10.1016/j.jallcom.2014.08.151

CrossRef Full Text | Google Scholar

Witte, F. (2015). Reprint of: the history of biodegradable magnesium implants: a review. Acta Biomater. 23, S28–S40. doi: 10.1016/j.actbio.2015.07.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L., Jain, A., Brown, D. W., Stoica, G. M., Agnew, S. R., Clausen, B., et al. (2008). Twinning-detwinning behavior during the strain-controlled low-cycle fatigue testing of a wrought magnesium alloy, ZK60A. Acta Mater. 56, 688–695. doi: 10.1016/j.actamat.2007.10.030

CrossRef Full Text | Google Scholar

Wu, X. L., Youssef, K. M., Koch, C. C., Mathaudhu, S. N., Kecskés, L. J., and Zhu, Y. T. (2011). Deformation twinning in a nanocrystalline hcp Mg alloy. Scr. Mater. 64, 213–216. doi: 10.1016/j.scriptamat.2010.10.024

CrossRef Full Text | Google Scholar

Wu, Y. F., Li, S., Ding, Z. G., Liu, W., Zhao, Y. H., and Zhu, Y. T. (2016). Effect of charge redistribution factor on stacking-fault energies of Mg-based binary alloys. Scr. Mater. 112, 101–105. doi: 10.1016/j.scriptamat.2015.09.023

CrossRef Full Text | Google Scholar

Xu, C., Zheng, M. Y., Xu, S. W., Wu, K., Wang, E. D., Kamado, S., et al. (2012). Ultra high-strength Mg-Gd-Y-Zn-Zr alloy sheets processed by large-strain hot rolling and ageing. Mater. Sci. Eng. A 547, 93–98. doi: 10.1016/j.msea.2012.03.087

CrossRef Full Text | Google Scholar

Xu, D., Han, E. H., and Xu, Y. (2016). Effect of long-period stacking ordered phase on microstructure, mechanical property and corrosion resistance of Mg alloys: a review. Progr. Nat. Sci. Mater. Int. 26, 117–128. doi: 10.1016/j.pnsc.2016.03.006

CrossRef Full Text | Google Scholar

Yadav, T. P., and Mukhopadhyay, N. K. (2018). Quasicrystal: a low-frictional novel material. Curr. Opin. Chem. Eng. 19, 163–169. doi: 10.1016/j.coche.2018.03.005

CrossRef Full Text | Google Scholar

Yang, K. V., Cáceres, C. H., and Easton, M. A. (2014). Strengthening micromechanisms in cold-chamber high-pressure Die-Cast Mg-Al alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 45, 4117–4128. doi: 10.1007/s11661-014-2326-x

CrossRef Full Text | Google Scholar

Yasi, J. A., Hector, L. G., and Trinkle, D. R. (2010). First-principles data for solid-solution strengthening of magnesium: from geometry and chemistry to properties. Acta Mater. 58, 5704–5713. doi: 10.1016/j.actamat.2010.06.045

CrossRef Full Text | Google Scholar

Yasi, J. A., Hector, L. G., and Trinkle, D. R. (2011). Prediction of thermal cross-slip stress in magnesium alloys from direct first-principles data. Acta Mater. 59, 5652–5660. doi: 10.1016/j.actamat.2011.05.040

CrossRef Full Text | Google Scholar

Yin, B., Wu, Z., and Curtin, W. A. (2017). First-principles calculations of stacking fault energies in Mg-Y, Mg-Al and Mg-Zn alloys and implications for <c+a> activity. Acta Mater. 136, 249–261. doi: 10.1016/j.actamat.2017.06.062

CrossRef Full Text | Google Scholar

Yokobayashi, H., Kishida, K., Inui, H., Yamasaki, M., and Kawamura, Y. (2011a). Enrichment of Gd and Al atoms in the quadruple close packed planes and their in-plane long-range ordering in the long period stacking-ordered phase in the Mg-Al-Gd system. Acta Mater. 59, 7287–7299. doi: 10.1016/j.actamat.2011.08.011

CrossRef Full Text | Google Scholar

Yokobayashi, H., Kishida, K., Inui, H., Yamasaki, M., and Kawamura, Y. (2011b). Structure analysis of a long period stacking ordered phase in Mg-Al-Gd alloys. Mater. Res. Soc. Symp. Proc. 1295, 267–272. doi: 10.1557/opl.2011.36

CrossRef Full Text | Google Scholar

Yoo, M. H. (1981). Slip, twinning and fracture in hexagonal close-packed metals. Metall. Trans. A 12A, 409–418. doi: 10.1007/BF02648537

CrossRef Full Text | Google Scholar

Yoo, M. H., and Lee, J. K. (1991). Deformation twinning in h.c.p. metals and alloys. Phil. Mag. A 5, 987–1000. doi: 10.1080/01418619108213931

CrossRef Full Text | Google Scholar

You, B. S., Park, W. W., and Chung, I. S. (2000). Effect of calcium additions on the oxidation behavior in magnesium alloys. Scr. Mater. 42, 1089–1094. doi: 10.1016/S1359-6462(00)00344-4

CrossRef Full Text | Google Scholar

Yu, Q., Jiang, Y., and Wang, J. (2015). Cyclic deformation and fatigue damage in single-crystal magnesium under fully reversed strain-controlled tension-compression in the [1010] direction. Scr. Mater. 96, 41–44. doi: 10.1016/j.scriptamat.2014.10.020

CrossRef Full Text | Google Scholar

Yu, Q., Qi, L., Chen, K., Mishra, R. K., Li, J., and Minor, A. M. (2012). The nanostructured origin of deformation twinning. Nano Lett. 12, 887–892. doi: 10.1021/nl203937t

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Q., Zhang, J., and Jiang, Y. (2011). Direct observation of twinning-detwinning-retwinning on magnesium single crystal subjected to strain-controlled cyclic tension-compression in [0 0 0 1] direction. Philos. Mag. Lett. 91, 757–765. doi: 10.1080/09500839.2011.617713

CrossRef Full Text | Google Scholar

Yuasa, M., Miyazawa, N., Hayashi, M., Mabuchi, M., and Chino, Y. (2015). Effects of group II elements on the cold stretch formability of Mg-Zn alloys. Acta Mater. 83, 294–303. doi: 10.1016/j.actamat.2014.10.005

CrossRef Full Text | Google Scholar

Zhang, B., Gavras, S., Nagasekhar, A. V., Cáceres, C. H., and Easton, M. A. (2014). The strength of the spatially interconnected eutectic network in HPDC Mg-La, Mg-Nd, and Mg-La-Nd alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 45, 4386–4397. doi: 10.1007/s11661-014-2416-9

CrossRef Full Text | Google Scholar

Zhang, J., Dou, Y., and Dong, H. (2014a). Intrinsic ductility of Mg-based binary alloys: a first-principles study. Scr. Mater. 89, 13–16. doi: 10.1016/j.scriptamat.2014.06.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Dou, Y., and Zheng, Y. (2014b). Twin-boundary segregation energies and solute-diffusion activation enthalpies in Mg-based binary systems: a first-principles study. Scr. Mater. 80, 17–20. doi: 10.1016/j.scriptamat.2014.02.004

CrossRef Full Text | Google Scholar

Zhang, Q., Fu, L., Fan, T. W., Tang, B. Y., Peng, L. M., and Ding, W. J. (2013). Ab initio study of the effect of solute atoms Zn and y on stacking faults in Mg solid solution. Phys. B Condensed Matter 416, 39–44. doi: 10.1016/j.physb.2013.02.013

CrossRef Full Text | Google Scholar

Zhang, R. F., and Liu, B. X. (2002). Proposed model for calculating the standard formation enthalpy of binary transition-metal systems. Appl. Phys. Lett. 81, 1219–1221. doi: 10.1063/1.1499510

CrossRef Full Text | Google Scholar

Zhang, R. F., and Liu, B. X. (2005). Thermodynamic criterion for the formation of laves phases in binary transition-metal systems. Philos. Mag. Lett. 85, 283–287. doi: 10.1080/09500830500197385

CrossRef Full Text | Google Scholar

Zhang, Y., Yu, S., Zhu, X., and Luo, Y. (2008). Study on as-cast microstructures and solidification process of Mg-Zn-Y alloys. J. Non-Cryst. Solids 354, 1564–1568. doi: 10.1016/j.jnoncrysol.2007.08.049

CrossRef Full Text | Google Scholar

Zhao, Y. H., Zhu, Y. T., Liao, X. Z., Horita, Z., and Langdon, T. G. (2006). Tailoring stacking fault energy for high ductility and high strength in ultrafine grained Cu and its alloy. Appl. Phys. Lett. 89, 89–91. doi: 10.1063/1.2356310

CrossRef Full Text | Google Scholar

Zhao, Z., and Wang, W. (2016). Mg-based Quasicrystals. Intech Open. doi: 10.5772/57353

CrossRef Full Text | Google Scholar

Zhiping, L., Shaoqing, Z., Yali, T., and Dongshan, Z. (1994). Microstructures of Mg-Zn-Zr-RE alloys with high RE and low ZN contents. J. Alloys Compd. 209, 275–278. doi: 10.1016/0925-8388(94)91113-4

CrossRef Full Text | Google Scholar

Zhu, S., Easton, M. A., Abbott, T. B., Nie, J. F., Dargusch, M. S., Hort, N., et al. (2015). Evaluation of magnesium die-casting alloys for elevated temperature applications: microstructure, tensile properties, and creep resistance. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 46, 3543–3554. doi: 10.1007/s11661-015-2946-9

CrossRef Full Text | Google Scholar

Zhu, Y. M., Morton, A. J., and Nie, J. F. (2010a). The 18R and 14H long-period stacking ordered structures in Mg-Y-Zn alloys. Acta Mater. 58, 2936–2947. doi: 10.1016/j.actamat.2010.01.022

CrossRef Full Text | Google Scholar

Zhu, Y. M., Morton, A. J., and Nie, J. F. (2012). Growth and transformation mechanisms of 18R and 14H in Mg-Y-Zn alloys. Acta Mater. 60, 6562–6572. doi: 10.1016/j.actamat.2012.08.022

CrossRef Full Text | Google Scholar

Zhu, Y. M., Morton, A. J., Weyland, M., and Nie, J. F. (2010b). Characterization of planar features in Mg-Y-Zn alloys. Acta Mater. 58, 464–475. doi: 10.1016/j.actamat.2009.09.025

CrossRef Full Text | Google Scholar

Zhu, Y. M., Weyland, M., Morton, A. J., Oh-ishi, K., Hono, K., and Nie, J. F. (2009). The building block of long-period structures in Mg-RE-Zn alloys. Scr. Mater. 60, 980–983. doi: 10.1016/j.scriptamat.2009.02.029

CrossRef Full Text | Google Scholar

Zhu, Y. T., Liao, X. Z., and Wu, X. L. (2012). Deformation twinning in nanocrystalline materials. Progr. Mater. Sci. 57, 1–62. doi: 10.1016/j.pmatsci.2011.05.001

CrossRef Full Text | Google Scholar

Zubair, M., Sandlöbes, S., Wollenweber, M. A., Kusche, C. F., Hildebrandt, W., Broeckmann, C., et al. (2019). On the role of Laves phases on the mechanical properties of Mg-Al-Ca alloys. Mater. Sci. Eng. A 756, 272–283. doi: 10.1016/j.msea.2019.04.048

CrossRef Full Text | Google Scholar