- Materials Modelling Division, Institute of Materials Science, Technische Universität Darmstadt, Darmstadt, Germany
Using molecular dynamics simulations, we compare the creep properties of a homogeneous Cu64Zr36 metallic glass, a nanoglass with the same nominal composition, and a nanoglass-crystal composite, where the amorphous grain boundary phase has been reinforced with the high-temperature stable Cu2Zr Laves phase. While the nanoglass architecture is successful at preventing shear band formation, which typically results in a brittle failure mode at room temperature and conventional loading conditions, we find that the high fraction of glass-glass grain boundary phase therein is not beneficial to its creep properties. This can be amended by reinforcing the glass-glass interphase with a high-temperature stable crystalline substitute.
1. Introduction
Nanoglasses (NGs) are amorphous materials with microstructural features analogous to nanocrystalline materials; they consist of glassy grains connected by glass-glass interfaces (Jing et al., 1989; Fang et al., 2012). The interfaces are characterized by an excess volume (Jing et al., 1989; Şopu et al., 2009; Fang et al., 2012), a defective short range order (Ritter et al., 2011), and a different composition than the glassy grains (Adjaoud and Albe, 2016, 2018). NGs are typically synthesized by cold-compaction of glassy particles prepared through inert gas condensation (Jing et al., 1989; Fang et al., 2012) or by magnetron sputtering (Chen et al., 2011; Śniadecki et al., 2016).
NGs exhibit enhanced plasticity in comparison to their homogeneous metallic glass (MG) counterparts, which has been observed in in situ tensile tests of Sc75Fe25 in a transmission electron microscope (Wang et al., 2015). Moreover, molecular dynamics (MD) simulations have shown that the interfaces in NGs promote the nucleation of shear transformation (ST) zones (Argon, 1979; Falk and Langer, 1998; Schuh et al., 2007) and prevent strain localization (Albe et al., 2013; Adibi et al., 2015; Şopu and Albe, 2015). However, this enhanced plasticity usually comes at the expense of the glasses' strength. Both experiments and computer simulations confirmed that the yield strength of a conventional NG is significantly lower than that of MG with an identical chemical composition (Ritter et al., 2011; Şopu and Albe, 2015; Wang et al., 2015).
Several studies of nanolaminate NG-MG composites with planar glass-glass interfaces have shown that these architectures can be used to successfully increase the strength of NG-composites (Sha et al., 2014, 2017; Adibi et al., 2016). In a previous computer simulation study, we showed that instead of using planar interfaces, reinforcing a conventional Cu–Zr NG without the loss of ductility can be realized by strengthening the amorphous grain boundary phase. The latter has been replaced with the high-temperature stable crystalline Cu2Zr Laves phase. In comparison to the as–prepared NG, the reinforced NG-composite showed an increased yield strength under conventional tensile testing at room-temperature (Kalcher et al., 2017a). At higher temperatures, especially approaching the glass transition temperature, the influence of the high fraction of glass–crystal interfaces on the mechanical properties of these nanocomposites is, however, still unclear and shall be the focus of this study.
At elevated temperatures and elastostatic loading conditions MG typically show viscoplastic behavior and exhibit creep deformation (Castellero et al., 2008; Yoo et al., 2010; Kassner et al., 2015), carried by homogeneous nucleation of ST zones (Kalcher et al., 2017b). For homogeneous MG matrix composites with crystalline secondary phases, we found that the glass-crystal interfaces can cause severe deterioration of the creep resilience, depending on the shape and percolation of the secondary phase (Kalcher et al., 2017b). This is because weak glass-crystal interfaces exhibit a lower activation barrier for ST activity and act as preferred nucleation sites for the latter. Moreover, from creep simulations of a MG-crystal composite containing nanocrystalline Cu2Zr precipitates, we could conclude that the macroscopic creep rate is indeed a function of the relaxation state of the glass-crystal interfaces defined by their excess energy (Kalcher et al., 2019).
As opposed to the above described MG-composites, NGs feature an inverse microstructure, i.e., they consist of amorphous glassy grains embedded in a percolating amorphous grain boundary phase or crystalline phase in the case of the NG-composite. Thus, it is not expected that the creep behavior of NGs can be deduced from our previous studies of MG-crystal composites.
2. Materials and Methods
In the following section, MD simulations were used to investigate the creep behavior of a Cu64Zr36 MG, a NG with the same nominal composition and a grain-boundary reinforced NG composite. The simulation package LAMMPS (Plimpton, 1995) was chosen to perform the MD simulations in conjunction with the Finnis-Sinclair type Cu–Zr potential by Mendelev et al. (2009). A timestep of 2 fs was used in all simulations. In order to control the pressure and temperature a Nosé-Hoover thermostat and Parinello–Rahman barostat were applied. Moreover, periodic boundary conditions were applied in all dimensions.
Virtual synthesis of the three different glass model types, i.e., MG, NG, and NG-composite, required multiple steps: First, a homogeneous MG of composition Cu_64Zr_36 was quenched from the melt with a quenching rate of Ṫ = 0.01 K/ps and subsequently relaxed for 1 ns. To obtain a NG with the same nominal composition, spherical particles cut from this MG model were then used as precursors for simulations of the cold-compaction preparation route described in Adjaoud and Albe (2016): The average diameter of the precursor particles was 7 nm and they were annealed at Tg before a hydrostatic compaction pressure of 5 GPa was applied to consolidate the particles. Moreover, the surface atoms of the virtual precursors were marked before compaction. In the finished NG, these atoms form an amorphous grain-boundary phase with an average thickness of about 1 nm. This information was used to define the extent of the grain boundary phase, which allows us to differentiate between the glassy grains and the glassy interface phase that they are embedded in. Finally, this NG was used to generate the reinforced NG composite. The latter has been realized by replacing the grain-boundary interface phase of the as–prepared NG with single crystalline Laves phase C15 Cu2Zr as described in Kalcher et al. (2017a). More specifically, the replacement procedure has been performed as follows: The glassy grain structure derived from the as–prepared NG sample has been overlaid with a scaled-to-size Cu2Zr bulk single crystal and all crystal atoms that were found within a 3.6 Å cutoff range of the glass grains have been removed. The resulting composite model was equilibrated at zero pressure and 50 K for 1 ns to allow for relaxation of the artificially created glass–crystal interfaces.
During creep testing the samples were heated up to the target temperature and then a uniaxial load of 750 MPa was instantaneously applied and kept constant for 50 ns. Comparison creep rates were determined from linear fits of the evolution of the creep strain between t = 25 ns and t = 50 ns. For visualization and analysis of the simulation results, the software OVITO (Stukowski, 2010) was used, which included local deformation analysis using the atomic shear strain measure (Falk and Langer, 1998; Shimizu et al., 2007) and analysis of structural motifs via Voronoi polyhedron statistics (Brostow et al., 1998). A cutoff radius of 5 Å was chosen for computing the per-particle atomic deformation gradient tensor and subsequently the atomic von Mises strain.
3. Results
Figure 1 shows the spatial distribution of the most frequently occurring structural motif, i.e., the Cu-centered 〈0, 0, 12, 0〉 Voronoi polyhedra (VP), in the NG and the reinforced NG. An exemplary grain is marked in yellow in both NG samples. As for the pristine NG shown in Figure 1A, the 〈0, 0, 12, 0〉 VP are homogeneously distributed throughout the glassy grain and also in the interface phase and show the typical interconnection through face and edge sharing, as marked with a black circle in Figure 1B. Since the Cu atoms in the regular C15 Cu2Zr lattice also have a 〈0, 0, 12, 0〉 VP coordination, the Laves-type interface in the reinforce NG phase becomes visible in Figure 1B as regular arrangement of face-sharing 〈0, 0, 12, 0〉 VP strings. Under conventional loading conditions and low temperatures, this NG-composite type has already shown superior mechanical strength as compared to the conventional NG (Kalcher et al., 2017a). We are thus particularly interested in the high-temperature properties of this composite type.

Figure 1. Snapshots of a slice through the (A) conventional NG and (B) nanoglass-crystal composite, showing two amorphous grains embedded in amorphous interphase and crystalline Cu2Zr Laves phase, respectively. Copper atoms are depicted in red and zirconium atoms are depicted in blue. The outlines of the grains are indicated with yellow dashed circles. In addition to the atomic configuration, the 〈0, 0, 12, 0〉 Voronoi polyhedra present in this structure are shown in light blue. This allows for a distinction to be made between atoms in a glassy grain, and the crystalline interphase, where the Cu-centered 〈0, 0, 12, 0〉 polyhedra must form regular chains of face-sharing VP (marked with a black box). Within the glassy grain, the typical clustering into irregular shapes can be observed (marked with a black circle).
Creep simulations at different temperatures but constant stress have been realized with the above described Laves phase reinforced NG-composite. For comparison, a homogeneous Cu64Zr36 glass sample and the cold-compacted NG with the same nominal composition have been probed under the same conditions. Starting with a comparison of the creep behavior of the homogeneous glass and the conventional NG, presented in Figures 2A,B it becomes evident, that the NG microstructure promotes creep. Even at room temperature, the conventional NG exhibits viscoelastic creep behavior and reaches a total creep strain of more than 4% after 50 ns elastostatic loading at 750 MPa. Adjaoud and Albe have shown that the cold-compacted NG used in this study, features a defective short-range order in the interphase (Adjaoud and Albe, 2018). Obviously, the activation energy for creep is lowered within the interphase region resulting in an overall increased creep activity. This is also supported by Figures 3D,F that depict the local von Mises strain field in the homogeneous glass and the conventional NG after 40 ns of creep deformation. Compared to the homogeneous MG, there is clearly increased ST activity in the whole sample, but even more so in the amorphous grain boundary phase.
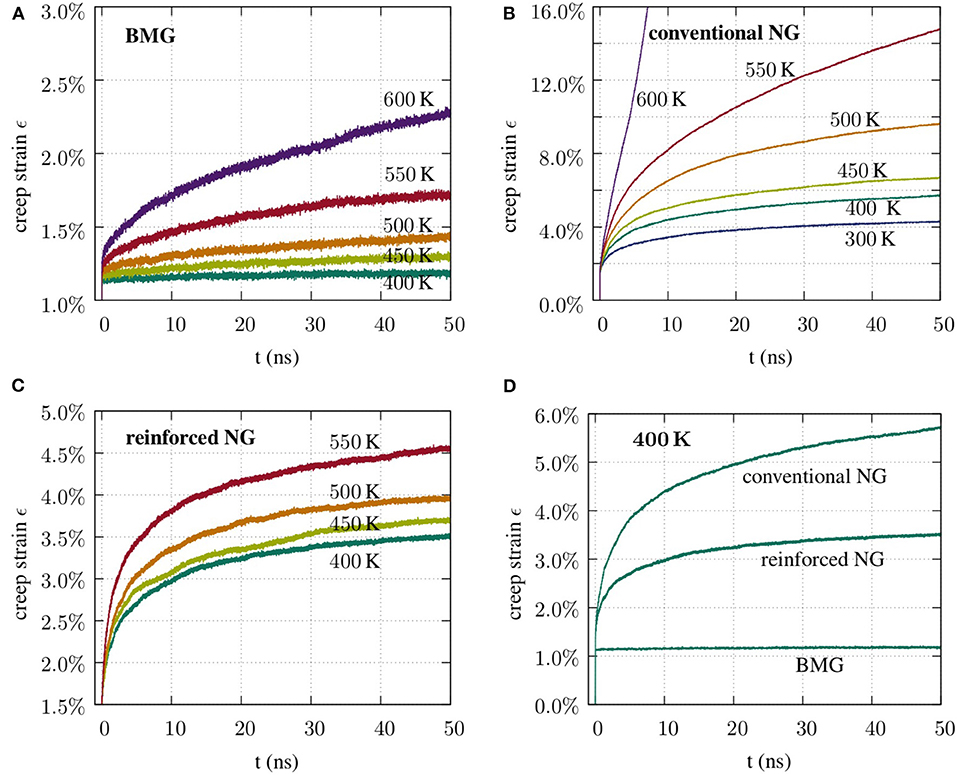
Figure 2. Creep curves under uniaxial elastostatic loading conditions at 750 MPa of (A) a homogeneous Cu64Zr36 MG, (B) a conventional NG with nominal composition Cu64Zr36, and (C) an interphase reinforced NG-composite. (D) For better comparison the 400 K creep curves of each sample type are shown in the same plot.
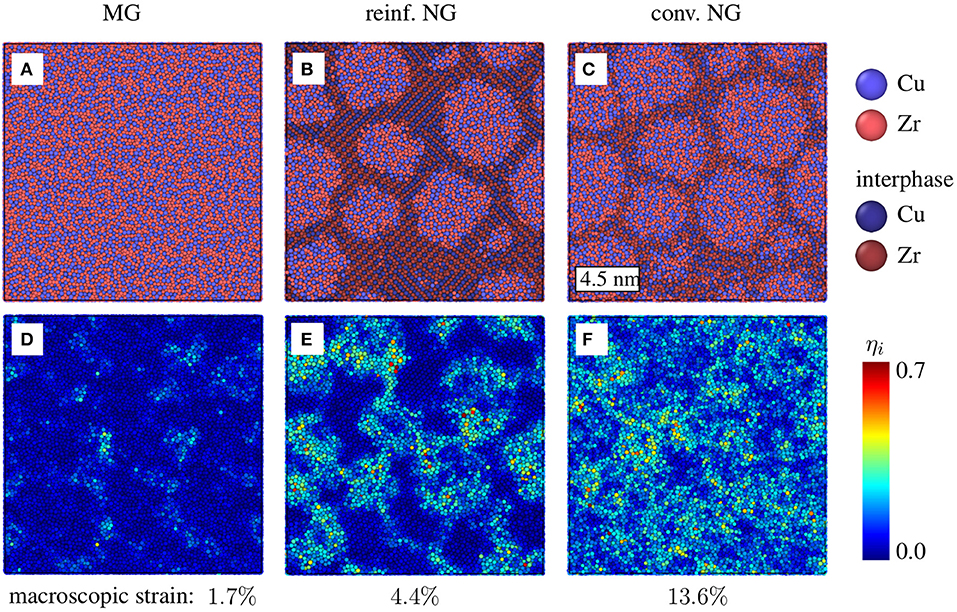
Figure 3. Snapshots of the atomic configurations of the (A,D) homogeneous glass, (B,E) reinforced NG, (C,F) conventional NG samples after 40 ns of creep at 550 K, color coded according to their particle type (top row) and according to the local von Mises strain (bottom row).
The creep compliance of the Laves phase reinforced NG ranges in between those of the homogeneous glass and the conventional NG (see Figures 2C,D). The total creep strain reached after 50 ns of creep at T = 500 K is 4%, which is less than half the creep strain the conventional NG did reach for that temperature and 2.6% more than observed for the homogeneous glass. The shape of the creep curves of the reinforced NG resemble more closely the shape of the creep curves of the conventional NG, since both feature high creep rates in the initial creep stage.
We performed linear fits to the creep data between t = 25 ns and t = 50 ns, for comparison of the creep rates in the three different glass types. The data is collected in Figure 4, that gives the temperature dependence of the creep rates at constant stress of 750 MPa. As a guide to the eye, a linear fit has been plotted for each data set. For the BMG and the NG, the slopes differ slightly. One reason is that the slope is defined not only by the activation energy for creep but also by the stress dependency. However, since the creep mechanisms, more precisely the ST zones in the NG and BMG, are the same, we can attribute the offset in the creep rates to the different densities of nucleation sites for ST zones in these two systems.
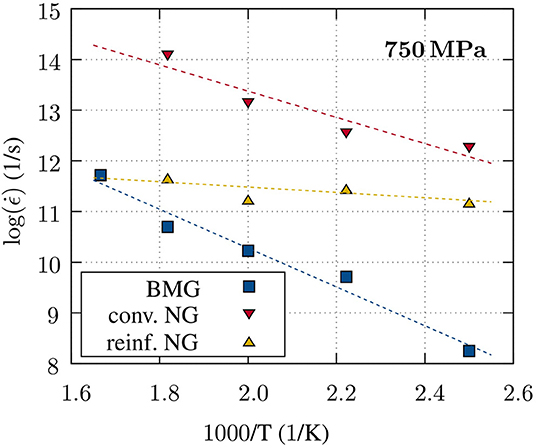
Figure 4. Comparison of the temperature dependence of the fitted creep rates for the three different glass types.
As for the NG composite, it is evident that the temperature dependence of the creep rates between t = 25 ns and t = 50 ns is not as pronounced as for the other two samples. Especially for higher temperatures, the rates approach those exhibited by the homogeneous glass. An explanation for this can be found in the von Mises strain field of the NG-composite after 40 ns of creep deformation, as shown in Figures 3B,E: During creep deformation of the NG-composite, most of the crystalline phase only responds elastically. But the glassy grains embedded therein start to flow. It seems that, at the temperature of 400 K ≤ T ≤ 550 K, the major fraction of glass phase already participates in the deformation. Thus, the creep rates exhibit a weaker temperature dependence within the testing temperature range. Moreover, at these elevated temperatures, further relaxation of the artificially created Cu2Zr–MG interfaces is expected. In line with previously presented results obtained for conventional loading conditions (Kalcher et al., 2017a), the reinforcing effect of the Laves phase still prevails under creep conditions at elevated temperatures.
4. Discussion
The behavior of the reinforced NG is not trivial to understand. This issue is rooted in the combination of several different effects. In this context the artificial synthesis procedure of the NG composite warrants further discussion. Assuming that the NG composite constitutes a single crystalline percolating network phase with glassy grains embedded therein, the expectation would be that the creep rates exhibited by such a composite should be lower than the ones observed in the bulk glass. In that case, the creep behavior will be determined by the glass phase, not the crystalline phase. More specifically, the Laves phase would be the load-bearing component, and at the applied stress, would only respond elastically. After this initial elastic response, plastic flow of the glass grains through the nucleation of ST zones should occur until a mechanical equilibrium between both phases is reached again. However, during initial relaxation of the NG composite, the initial percolating Laves network is partially damaged (Kalcher et al., 2017a). The partial amorphization of some ligaments of the crystalline network results in a different stress distribution in the composite, since the glass can also become a load-bearing component when probed under creep conditions. At the same time, there is an increased fraction of activation sites for ST zones with a lower activation energy than in the bulk glass. So creep deformation is also promoted by the presence of less well-relaxed interfaces. For a glass-composite with non-percolating Laves-type inclusions, we have shown that the creep rates significantly depend on the quality of the glass-crystal interfaces present in the composite (Kalcher et al., 2019). Another point to consider is that even though the remaining volume fraction of the intact Laves phase is still quite high (i.e., f≈30%) and a large fraction of the composite does therefore not participate in the plastic creep deformation (as visible in Figures 3D–F), this is compensated by the high ST activation volume fraction within the glass grains. Consequently, increasing the temperature can not cause a significantly increase in activated ST sites. This could explain the weak temperature dependence in the creep rates exhibited by the NG composite, shown in Figure 4.
In summary, by comparing the creep behavior of a Cu64Zr36 MG, a NG, and a NG-crystal composite, we showed that the glass-glass interfaces in the cold-compacted NG facilitate activation of ST zones and thus creep. The crystalline continuous Laves-phase network in the NG-composite, on the contrary, successfully reinforced the NG-composite against creep at higher temperatures.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
CK carried out the simulations, analyzed the data, and wrote the draft manuscript. OA contributed to the conception and design of this study and generated the nanoglass structures. KA supervised the work, reviewed, and edited the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge the financial support of the Deutsche Forschungsgemeinschaft (DFG) through SPP 1594 project 224504410-AL 578/15. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC). Computing time was also provided by Technische Universität Darmstadt on the Lichtenberg High Performance Computer.
References
Adibi, S., Branicio, P. S., and Ballarini, R. (2016). Compromising high strength and ductility in nanoglass–metallic glass nanolaminates. RSC Adv. 6, 13548–13553. doi: 10.1039/C5RA24715B
Adibi, S., Branicio, P. S., and Joshi, S. P. (2015). Suppression of shear banding and transition to necking and homogeneous flow in nanoglass nanopillars. Sci. Rep. 5:15611. doi: 10.1038/srep15611
Adjaoud, O., and Albe, K. (2016). Interfaces and interphases in nanoglasses: surface segregation effects and their implications on structural properties. Acta Mater. 113, 284–292. doi: 10.1016/j.actamat.2016.05.002
Adjaoud, O., and Albe, K. (2018). Microstructure formation of metallic nanoglasses: Insights from molecular dynamics simulations. Acta Mater. 145, 322–330. doi: 10.1016/j.actamat.2017.12.014
Albe, K., Ritter, Y., and Şopu, D. (2013). Enhancing the plasticity of metallic glasses: shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations. Mech. Mater. 67, 94–103. doi: 10.1016/j.mechmat.2013.06.004
Argon, A. (1979). Plastic deformation in metallic glasses. Acta Metall. 27, 47–58. doi: 10.1016/0001-6160(79)90055-5
Brostow, W., Chybicki, M., Laskowski, R., and Rybicki, J. (1998). Voronoi polyhedra and delaunay simplexes in the structural analysis of molecular-dynamics-simulated materials. Phys. Rev. B 57, 13448–13458. doi: 10.1103/PhysRevB.57.13448
Castellero, A., Moser, B., Uhlenhaut, D. I., Torre, F. H. D., and Loeffler, J. F. (2008). Room-temperature creep and structural relaxation of mg-cu-y metallic glasses. Acta Mater. 56, 3777–3785. doi: 10.1016/j.actamat.2008.04.021
Chen, N., Frank, R., Asao, N., Louzguine-Luzgin, D., Sharma, P., Wang, J., et al. (2011). Formation and properties of Au-based nanograined metallic glasses. Acta Mater. 59, 6433–6440. doi: 10.1016/j.actamat.2011.07.007
Falk, M. L., and Langer, J. S. (1998). Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192–7205. doi: 10.1103/PhysRevE.57.7192
Fang, J. X., Vainio, U., Puff, W., Würschum, R., Wang, X. L., Wang, D., et al. (2012). Atomic structure and structural stability of Sc75Fe25 nanoglasses. Nano Lett. 12, 458–463. doi: 10.1021/nl2038216
Jing, J., Krämer, A., Birringer, R., Gleiter, H., and Gonser, U. (1989). Modified atomic structure in a Pd-Fe-Si nanoglass. J. Non. Cryst. Solids 113, 167–170. doi: 10.1016/0022-3093(89)90007-0
Kalcher, C., Adjaoud, O., Rohrer, J., Stukowski, A., and Albe, K. (2017a). Reinforcement of nanoglasses by interface strengthening. Scripta Mater. 141, 115–119. doi: 10.1016/j.scriptamat.2017.08.004
Kalcher, C., Brink, T., Rohrer, J., Stukowski, A., and Albe, K. (2017b). Interface-controlled creep in metallic glass composites. Acta Mater. 141, 251–260. doi: 10.1016/j.actamat.2017.08.058
Kalcher, C., Brink, T., Rohrer, J., Stukowski, A., and Albe, K. (2019). Elastostatic loading of metallic glass-crystal nanocomposites: relationship of creep rate and interface energy. Phys. Rev. Mater. 3:093605. doi: 10.1103/PhysRevMaterials.3.093605
Kassner, M. E., Smith, K., and Eliasson, V. (2015). Creep in amorphous metals. J. Mater. Res. Technol. 4, 100–107. doi: 10.1016/j.jmrt.2014.11.003
Mendelev, M. I., Kramer, M. J., Ott, R. T., Sordelet, D. J., Yagodin, D., and Popel, P. (2009). Development of suitable interatomic potentials for simulation of liquid and amorphous Cu-Zr alloys. Philos. Mag. 89, 967–987. doi: 10.1080/14786430902832773
Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19. doi: 10.1006/jcph.1995.1039
Ritter, Y., Şopu, D., Gleiter, H., and Albe, K. (2011). Structure, stability and mechanical properties of internal interfaces in Cu64Zr36 nanoglasses studied by MD simulations. Acta Mater. 59, 6588–6593. doi: 10.1016/j.actamat.2011.07.013
Schuh, C. A., Hufnagel, T. C., and Ramamurty, U. (2007). Mechanical behavior of amorphous alloys. Acta Mater. 55, 4067–4109. doi: 10.1016/j.actamat.2007.01.052
Sha, Z., He, L., Pei, Q., Liu, Z., Zhang, Y., and Wang, T. (2014). The mechanical properties of a nanoglass/metallic glass/nanoglass sandwich structure. Scripta Mater. 83, 37–40. doi: 10.1016/j.scriptamat.2014.04.009
Sha, Z.-D., Branicio, P. S., Lee, H. P., and Tay, T. E. (2017). Strong and ductile nanolaminate composites combining metallic glasses and nanoglasses. Int. J. Plast. 90, 231–241. doi: 10.1016/j.ijplas.2017.01.010
Shimizu, F., Ogata, S., and Li, J. (2007). Theory of shear banding in metallic glasses and molecular dynamics calculations. Mater. Trans. 48, 2923–2927. doi: 10.2320/matertrans.MJ200769
Śniadecki, Z., Wang, D., Ivanisenko, Y., Chakravadhanula, V., Kübel, C., Hahn, H., et al. (2016). Nanoscale morphology of Ni50Ti45Cu5 nanoglass. Mater. Charact. 113, 26–33. doi: 10.1016/j.matchar.2015.12.025
Şopu, D., and Albe, K. (2015). Influence of grain size and composition, topology and excess free volume on the deformation behavior of Cu-Zr nanoglasses. Beilstein J. Nanotechnol. 6, 537–545. doi: 10.3762/bjnano.6.56
Şopu, D., Albe, K., Ritter, Y., and Gleiter, H. (2009). From nanoglasses to bulk massive glasses. Appl. Phys. Lett. 94:191911. doi: 10.1063/1.3130209
Stukowski, A. (2010). Visualization and analysis of atomistic simulation data with ovito- the open visualization tool. Modell. Simul. Mater. Sci. Eng. 18:015012. doi: 10.1088/0965-0393/18/1/015012
Wang, X. L., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2015). Plasticity of a scandium-based nanoglass. Scripta Mater. 98, 40–43. doi: 10.1016/j.scriptamat.2014.11.010
Keywords: metallic glass, grain interfaces, creep, molecular dynamics, nanoglass
Citation: Kalcher C, Adjaoud O and Albe K (2020) Creep Deformation of a Cu-Zr Nanoglass and Interface Reinforced Nanoglass-Composite Studied by Molecular Dynamics Simulations. Front. Mater. 7:223. doi: 10.3389/fmats.2020.00223
Received: 21 March 2020; Accepted: 19 June 2020;
Published: 28 August 2020.
Edited by:
Jürgen Horbach, Heinrich Heine University of Düsseldorf, GermanyReviewed by:
Paulo Sergio Branicio, University of Southern California, United StatesHaizheng Tao, Wuhan University of Technology, China
Copyright © 2020 Kalcher, Adjaoud and Albe. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Constanze Kalcher, a2FsY2hlckBtbS50dS1kYXJtc3RhZHQuZGU=
 Constanze Kalcher
Constanze Kalcher Omar Adjaoud
Omar Adjaoud Karsten Albe
Karsten Albe