Mechanical Cell-to-Cell Interactions as a Regulator of Topological Defects in Planar Cell Polarity Patterns in Epithelial Tissues

Introduction

Epithelial tissue is constituted by densely packed epithelium cells and has important structural and functional roles throughout embryonic development, morphogenesis, and adult life. The orderly packing and precise arrangement of epithelial cells are essential for separating biological compartments with different compositions by establishing selective permeability barriers between them (Nelson, 2009). Epithelial rearrangements are in general driven by forces that are transmitted via cytoskeletal elements and adhesion molecules within and between cells (Heisenberg and Bellaïche, 2013). At the level of single cells, the forces are modulated with changes of the subcellular actin–myosin flow, which is transmitted to other adjacent cells through cell–cell adhesion (Fernandez-Gonzalez et al., 2009; Heisenberg and Bellaïche, 2013). This force generating–transmitting motor is essential for the mechanical evolution of the multicellular system, which is, most importantly, governed by a surface energy minimization principle (Lecuit and Lenne, 2007; Yu and Fernandez-Gonzalez, 2017). Therefore, tissue pattern formation mechanisms are also associated with the development of specific packing geometries (Sugimura and Ishihara, 2013; Šiber and Ziherl, 2017). Optimized packing strategies were found essential for the functioning of different biological systems. For example, hexagonally packed hairs on the surface of the Drosophila wing enable a proper airflow during flight (Wootton, 1992). Similarly, a very regular crystalline-like distribution of cone photoreceptors in the retinal epithelium in adult zebrafish was found crucial for ensuring the optimal collection of light signal (Salbreux et al., 2012). In order to get a more precise understanding of the not well-known mechanisms of epithelial tissue formation, computational modeling approaches have recently been applied with considerable success in recapitulating properties of epithelial structure (Farhadifar et al., 2007; Fernandez-Gonzalez and Zallen, 2008; Hočevar and Ziherl, 2009; Salbreux et al., 2012; Fletcher et al., 2013; Osterfield et al., 2013; Kachalo et al., 2015; Chen et al., 2016; Ishihara et al., 2017; Ladan et al., 2019). The common point of all modeling endeavors is the implementation of the natural tendency of cells to adopt the most stable configuration with the lowest free energy (van Drongelen et al., 2018).

Nevertheless, the energy minimization principle alone cannot explain the diverse and complex organization of epithelial cytoarchitectures. In view of that, planar cell polarity (PCP) was recognized as an important feature that provides an additional ordering mechanisms needed to coordinate epithelium cell packing and orientation (Vladar et al., 2009; Sugimura and Ishihara, 2013; Butler and Wallingford, 2017; Fisher et al., 2017; Nissen et al., 2018; Axelrod, 2020). This plane polarity is a tissue-level phenomenon that is regulated by an anisotropic distribution of core PCP proteins involved in the PCP signaling pathway (Zallen, 2007; Marcinkevicius et al., 2009; Bosveld et al., 2012). Experimental studies performed on the wings of the Drosophila fly have shown that PCP of individual cells is established through the interplay between intracellular and intercellular communication accompanied by a global cue. Similarly, PCP-governed epithelium patterning mechanisms have also been reported for vertebrates (Goodrich and Strutt, 2011) and also for other types of tissues (Wang and Nathans, 2007). Moreover, it has been shown that in early developmental stages, the core PCP proteins are distributed symmetrically within the cells, whereas during development, the PCP proteins get increasingly more asymmetrically distributed, causing the cells to get more polarized (Strutt, 2001). As a result, the orientational order increases with age (Blankenship et al., 2006; Bayly and Axelrod, 2011; Markovič et al., 2014). For studying the complex spatio-temporal processes involved in PCP and the corresponding spatial arrangements, computational modeling has proven to be a very reliable approach (for review, see Axelrod and Tomlin, 2011; Wang et al., 2012), whereby some models implemented the PCP mechanisms in a phenomenological way (Burak and Shraiman, 2009; Hazelwood and Hancock, 2013; Zhu and Owen, 2013; Markovič et al., 2014; Shadkhoo and Mani, 2019), whereas other studies implemented and analyzed also biochemical details of the PCP pathways (Le Garrec et al., 2006).

Faults in PCP signaling caused by mutations in the intracellular signalization lead to an impaired organization of multicellular structures, which can impair normal physiological function and result in serious pathological conditions (Goodrich and Strutt, 2011; Butler and Wallingford, 2017; Markovič et al., 2017). Certain cells (so-called mutants) that lack the activity of particular transmembrane proteins provoke non-trivial and impaired polarity patterns by imposing a prescribed polarization in cells adjacent to the mutant cell boundary (Adler et al., 1997; Goodrich and Strutt, 2011; Hazelwood and Hancock, 2013). In particular, one type of mutant cells persuades neighboring cells to orient their polarity toward them, that is, attractive mutants (Gubb and García-Bellido, 1982; Vinson and Adler, 1987), whereas the other type causes the neighboring cells to orient their polarity away, that is, repulsive mutants (Taylor et al., 1998). In this way, mutant cells introduce cell polarity misorientations in their proximity, which can be regarded as topological defects that impair the normal functioning of the tissue (Hazelwood and Hancock, 2013; Markovič et al., 2014; Kim et al., 2016; Saw et al., 2017). Although mutants exhibit swirling patterns at the locus of the clone, a sufficiently strong global cue can retrieve the wild-type polarization (Ma et al., 2008; Shadkhoo and Mani, 2019). In addition, it has been shown that the polarity in mutants lacking graded global cues is susceptible to local geometric irregularities (Ma et al., 2008). Notably, local changes in the mechanical force balance within cells may, in turn, establish the regional variations in cell form and function that drive tissue patterning. It has been shown that the epithelial cells surrounding a mutant cell show a higher degree of variability in the length of contact lengths, which leads to a less efficient hexagonal repacking (Classen et al., 2005) and increased number of local defects (Kim et al., 2016). We argue that the remodeling of junctional components leading to variations in the strength of mechanical interactions between normal and mutant epithelium cells is a plausible regulatory mechanism that minimizes the distortion of the global orientational ordering caused by mutant cells. In the present study, we address this issue by developing a computational model that combines both features of epithelial pattern formation—the minimal free energy principle governing tissue morphogenesis and the PCP mechanisms. The combination of these two aspects enables us to analyze the impact of the interplay between localized mechanical energy balance and polarity patterns at different developmental stages and how the presence of mutant cells fabricates topological defects in epithelial tissues.

Materials and Methods

In this section, we describe the computational approaches used to study spatial arrangements of cells and polarity patterns in epithelial tissues. To this purpose, we combine two different models. The first model is based on the theoretical framework of Farhadifar et al. (2007), and we use it for simulating the tissue morphogenesis under different conditions. The model simulates cell proliferation and packing by taking into account cell compressibility and junctional forces arising from cortical contractility and adhesion, as specified in the continuation. For the generated epithelial structures, we then apply the second mathematical model proposed by Hazelwood and Hancock (2013) for analyzing the evolution of the PCP patterns. The PCP model provides a phenomenological description of the PCP patterns and includes the cell’s ability to maintain its intracellular polarization, the ability to interact with the polarity of adjoining cells, and the ability to sense and respond to a global cue, whereby detailed molecular interactions and processes have been integrated into a simple polarity measure. For both of the models, we utilize a Monte Carlo approach to find the ground state of the corresponding energy functions, as described in more detail in the next subsections.

Biomechanical Vertex Dynamics Model

During development of an organism, the shape of its organs and tissue structures is commonly governed by deformations of epithelial tissues. A common theoretical approach to generate in silico cellular structures of the epithelium is to consider the individual cells as 2D structures with a finite number of vertices connected into a polygon representing the cell membrane. Tissue development is then governed by reconfiguring the positions of vertices leading to intermediate mechanically stable states in which the system forces are in balance. To create a genuine epithelium structure, we make use of the vertex model described in detail in Farhadifar et al. (2007). In this model, the dynamics of the system is ruled with the following formulation of the total energy of the system:

$$E=\sum _{\mathrm{\alpha }}\frac{K_{\mathrm{\alpha }}}{2}{(A_{\mathrm{\alpha }}-A_0)}^2+\sum _{i,j}{\mathrm{\Lambda }}_{ij}{l}_{ij}+\sum _{\mathrm{\alpha }}\frac{{\mathrm{\Gamma }}_{\mathrm{\alpha }}}{2}{L}_{\mathrm{\alpha }}^2(1)$$

The total free energy function of the system E (Eq. 1) is governed by three terms. The first term refers to the compressibility of the cell, where K_α is the compressibility parameter, A_α is the actual area, and A₀ the preferred area of the cell α. In all simulations, the preferred area A₀ is considered to be equal to the surface of a hexagon with side lengths equal to l = 1, which leads to a value of $A_0=l3\sqrt{3}/2$. The second term accounts the line tensions at junctions between individual cells with the parameters Λ_ij and l_ij corresponding to the line-tension strengths and the lengths of the edge between vertex i and j, respectively. The last term considers cell contractility with the contractility coefficient Γ_α and the perimeter of the polygon around a cell (L_α). The contractility coefficient Γ_α reflects contractile forces generated by myosin contraction in the cell cortex (Koride et al., 2018; Staddon et al., 2018). Because actin–myosin contractility tends to reduce the perimeter of each cell and additionally affects the line tension, smaller perimeters, and smaller cell boundary lengths result in a state with lower free energy. The main parameters of Eq. (1) are schematically shown in Figure 1. In general, the following parameter values will be used in our simulations: K_α = 14, Λ_ij = 1, and Γ_α = 0.85, unless stated otherwise. Such a parameter set favors a hexagonal-like packing and thereby mimics well the circumstances in realistic epithelial tissues (Farhadifar et al., 2007). We are interested in alternations of global patterns of cells caused by variations in the strength of mechanical interaction among junctions between normal and mutant cells, as an abnormal polarity of junctional complexes around the edge of a mutant propagates to neighboring cells and affects cellular packing (Goodrich and Strutt, 2011; Kim et al., 2016). To this purpose, we numerically simulate the evolution (growth) of epithelial tissue around the mutant cell. The initial configuration of the simulation is a 2D lattice of 25 hexagonal cells, which have side lengths equal to 1. The cell in the center is defined as a mutant cell. In continuation, a non-mutant cell is selected, and its area is increased in a stepwise manner until its area is doubled. This is achieved by moving the vertices of the selected cell radially outward. The increment equals 1% of the distance between the corresponding vertex and the cell’s center of mass. After each increment of the cell’s area, we let the whole system relax toward its mechanically stable state with the lowest free energy defined by Eq. (1). When the area of a given cell is doubled in comparison with the initial area, the cell is divided. This is achieved by generating a line with a random slope through the center of the cell, which is determined as the center of mass of all its vertices. At the two intersection points of the line with the edges of the cell, two new vertices are created and connected with a new edge. This edge separates the two cells, which have been spawned from the initially selected cell. Finally, the system relaxes toward its mechanically stable state, as described by Sugimura and Ishihara (2013). The Metropolis Monte Carlo method is used to simulate the relaxation process. In each iteration step, individual vertices are randomly displaced within a circle centered around the selected vertex with a radius of 0.04. After each displacement, the total free energy of the system is computed and compared with the overall free energy of the system before the displacement. If the new energy (E_new) is lower the old energy (E_old), the rearrangement is accepted, and the processes are repeated. If, on the other hand, the old energy is lower than the new one, the change is accepted with a probability e^{−(E_new−E_old)/N}, where N equals the number of cells. If the average absolute change in the system’s total free energy after 1,000 successful Monte Carlo steps is less than 10^–8, the Metropolis Monte Carlo algorithm is stopped, and the current configuration of the system is regarded as the final state with the lowest free energy resembling a mechanically stable state. Following these steps, this process is repeated until there are 100 cells. In our simulations, open boundary conditions are considered. It should be noted that the shape of the mutant cell is allowed to adjust its shape and is involved in the energy minimization process but is never divided.

FIGURE 1

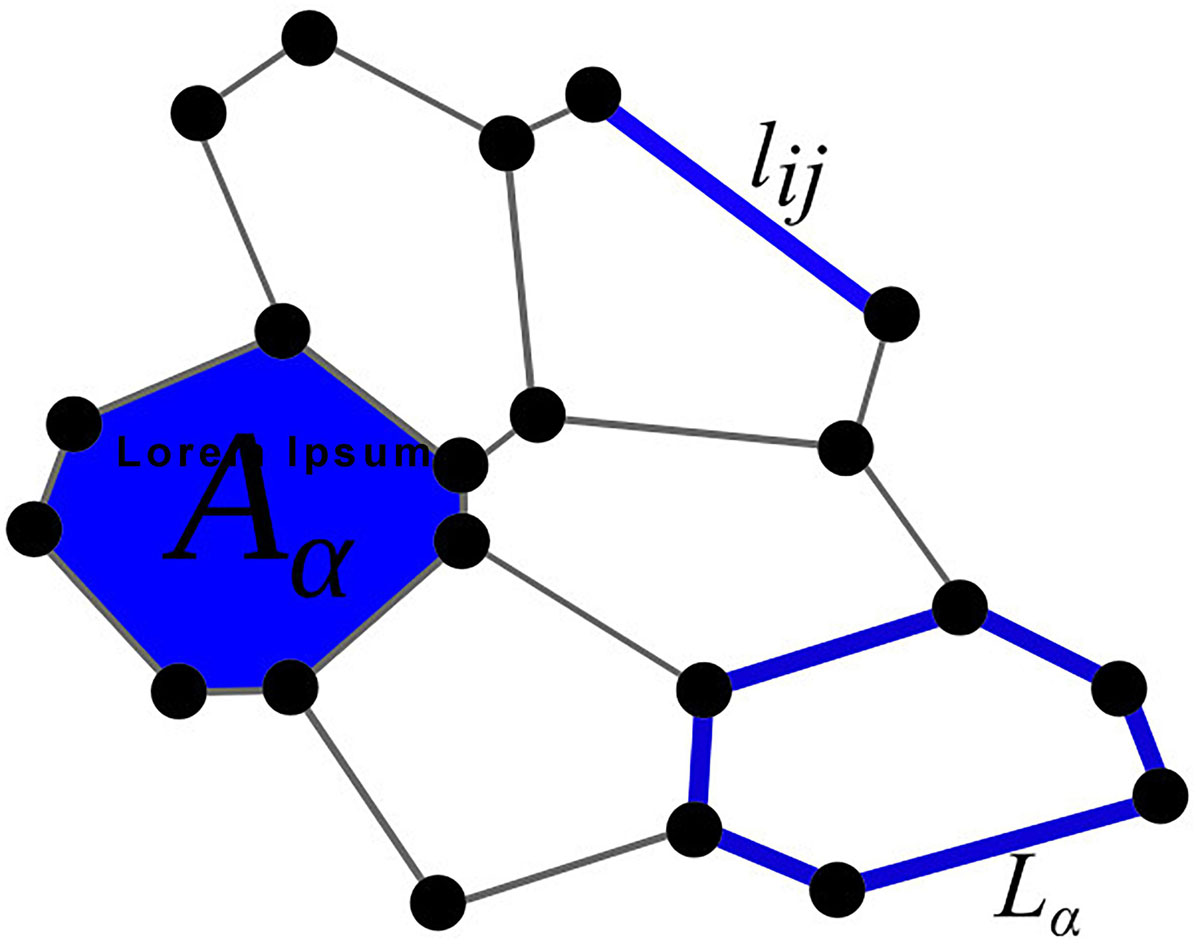
Figure 1. Graphical representation of the parameters used in the total energy function E [see Eq. (1)]: A_α is the area, l_ij the edge, and L_α the perimeter of a cell.

To visualize the impact of the line-tension paremeter Λ_mn on the spatial on the spatial packing of epithelium cells, we show illustrative calculations performed on a 2D grid of 25 cells, with the mutant cell located in the middle of the grid. The initial configuration of this simulation was a lattice with 25 hexagonal cells. All cells had equal side lengths l_ij = 1.0. To show the robustness of the Metropolis Monte Carlo algorithm, the initial configuration has been randomly disrupted. The line-tension strengths for edges between any non-mutant cell pair were set to Λ_ij = 1.0. In Figure 2, we present the resulting epithelium structures that have relaxed to their mechanically stable state for three different values of line-tension strengths Λ_mn. We can observe that an almost perfect hexagonal grid is attained when Λ_mn = 1 (all interactions in the tissue are the same), whereas the other two scenarios (Λ_mn = 0 and Λ_mn = 2) lead to accordingly adjusted cellular structures.

FIGURE 2

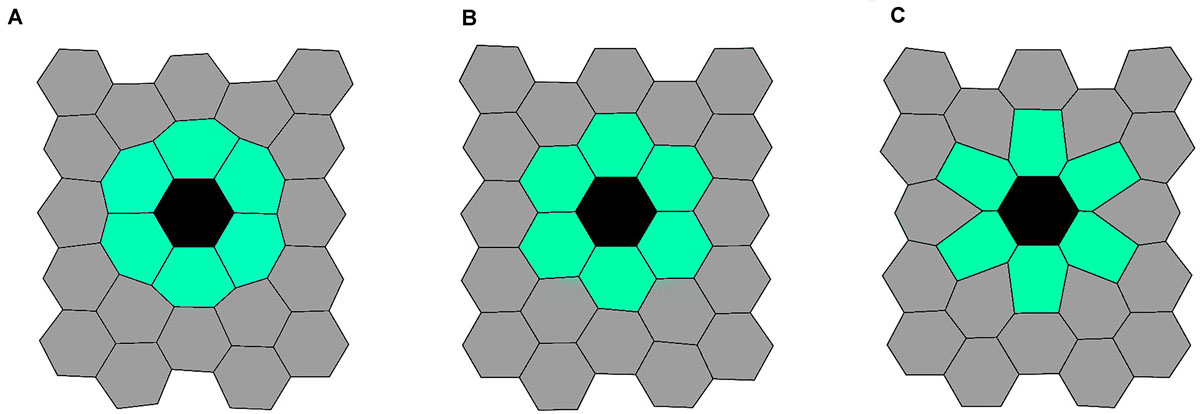
Figure 2. Three characteristic initial epithelium configurations. Generated structures for Λ_mn = 0.0 (left panel, A), Λ_mn = 1.0 (middle panel, B), and Λ_mn = 2.0 (right panel, C). The black colored cell corresponds to the mutant cell, the light green colored cells to mutant neighbors, and the gray colored cells’ to other cells in the tissue.

In all further simulations, where the PCP model was implemented on the top of tissue morphogenesis simulation, a lattice of 25 equal hexagonal cells was considered as our initial configuration. The cell in the center of this grid was assigned as a mutant cell. Tissue growth was then simulated as described above. We generate epithelium structures for different line-tension strengths (Λ_mn ∈ [0,2]). The obtained epithelial structures serve then as a basis for the study on how different scenarios of structural deviations, caused by the mutant cell, can affect the overall PCP pattern during tissue development.

Phenomenological Model of Planar Cell Polarity

In order to mathematically describe the asymmetric distribution of the six core PCP proteins, we use a phenomenological model introduced by Hazelwood and Hancock (2013), which implements the three-tiered mechanism for regulation of PCP (Tree et al., 2002). The model is based on the so-called Ginzburg–Landau method, commonly used to study ordering processes in condensed matter physics. As such, the model describes the system via a free energy function, which has the following form:

$$F_{\text{tot}}=F_c+F_e+F_f(2)$$

$$F_c=\sum _{i=1}^{N}B{\left({\left|{\overrightarrow{m}}_i\right|}^2-m_{A,i}^2\right)}^2(3)$$

$$F_e=\sum _{i=1}^N\sum _{j\in n_i}{K}_{ij}{\left({\overrightarrow{m}}_i-{\overrightarrow{m}}_j\right)}^2(4)$$

$$F_f=-C\sum _{i=1}^N{\overrightarrow{m}}_i\cdot \overrightarrow{G}.(5)$$

During the simulation, we update the polarization of individual cells, which is given by the vector ${\overrightarrow{m}}_i$, where the index i indicates that the polarity vector is assigned to the ith cell. The total free energy of the systems F_tot is composed of three parts. The first part, F_c, accounts for the ability of individual cells to maintain a certain degree of polarity, thereby mimicking the asymmetric distribution of proximal and distal proteins. Here, the preferred inherent polarization magnitude of an individual cell is given by m_A,i. The second part, F_e, captures intercellular physical interactions among adjacent cells, n_i, which try to impose a common direction of polarization. This reflects the maximization of intermolecular forces between cells due to ligand binding, as deviations from a uniform alignment lead to an increase in free energy. In this term, we additionally take into account that the orientation order among cells i and j, where j is an adjacent cell of cell i and is governed by the length of the junction between them, l_ij. Accordingly, K_ij is defined as follows:

$$K_{ij}=K\frac{l_{ij}}{{⟨l⟩}_i}(6)$$

where K represents the average interaction strength among adjacent cells and ⟨l⟩_i is the average junction length of the ith cell. The latter is computed by averaging the edge length of the polygon around the ith cell. Lastly, the third part, F_f, couples the polarization of individual cells with a global cue, $\overrightarrow{G}$. The contribution of the three individual terms to the total free energy F_tot is weighted with parameters B, K, and C, which reflect the contribution of intrinsic polarization, intercellular interactions, and interactions with the global cue, respectively. The main advantage of this model is that it is equipped with a small number of biologically relevant parameters thereby facilitating a qualitative assessment and comparison with experimental observations (Vu et al., 2019).

We consider two typical sets of parameters B, K, and C corresponding to the two different stages in the development of epithelium (Markovič et al., 2014). In the early developmental stage, the polarization shows a weak tendency of ordering and can be modeled by setting B = K = C. In a further developed stage, the global PCP patterns are found to be practically complete aligned with the direction of the global cue $\overrightarrow{G}$ (Bayly and Axelrod, 2011; Hazelwood and Hancock, 2013). In this case, we set the model parameters to B = K and C = 10 B, indicating a stronger contribution of global alignment to the total free energy of the system. We use this parameter set because in early developmental stages on a tissue level no uniform polarization of orientation is established. The latter embraces a lower contribution of the global cue signal compared with the terms B and K (Strutt, 2001). At the final stage of PCP development, the polarization direction of cells is very uniformly oriented in the same direction, which highlights that the energy term F_f is contributing more to the total free energy F_tot than the other two terms F_c and F_e. This in turn is considered by using larger values for the parameter C with regard to the parameters B and K (Strutt, 2001; Hazelwood and Hancock, 2013; Markovič et al., 2014). Therefore, the main two parameters, which determine if local or global ordering will be preferred, are the parameters K and C. If C < K, local interactions are considered to contribute more to the total free energy function compared with the contribution of global ordering. Consequently, local orientation is dominating the evolution of the system. On the other hand, if K < C, the contribution of the global ordering term is prescribed a higher weight in the energy function, and a more uniform polarization pattern is formed. The parameter, B, highlights the tendency of a cell to maintain a predefined inherent polarization. Lastly, it should be noted that only the relative relations of parameters B, K, and C are important, as they proportionally contribute to the free energy term F_tot and thereby determine which energy term is the main driving force in the system. In all calculations, the values of parameters B and K equal to 1.0, and only C was varied. In order to graphically represent how well an individual cell is aligned along with the global cue, we use a color code system as presented in Figure 3.

FIGURE 3

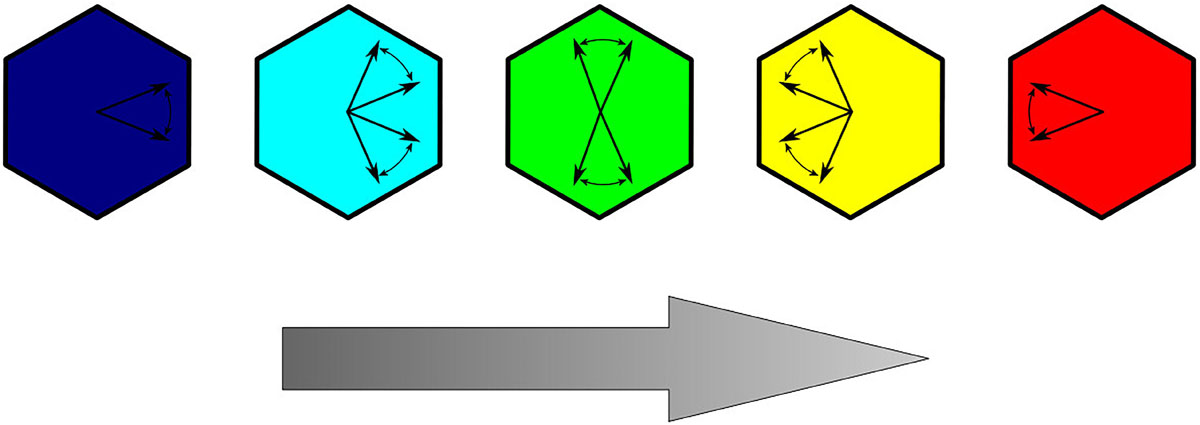
Figure 3. Color coding of cells representing the deviation of the polarization orientation relative to the direction of the global cue (represented with a gray arrow).

In all simulations, mutant cells are located in the middle of the tissue. We consider only attractive mutant cells, which means that the polarization of the neighboring cells always tends to be aligned radially inward with a magnitude equal to the cells preferred magnitude of polarization m_A,i. This mimics the lack of Fz in mutant cells, which induces neighboring cells to point their polarization toward the mutant (Goodrich and Strutt, 2011; Hazelwood and Hancock, 2013; Markovič et al., 2014). For all other cells, the initial orientation θ_i and the magnitude of polarization $\left|{\overrightarrow{m}}_i\right|$ are prescribed randomly. The random number interval used for the two variables is θ_i ∈ (−π/2,−π/2) and $\left|{\overrightarrow{m}}_i\right|$ ∈ (0.5,1.5). The preferred polarization magnitude of individual cells is set to m_A,i = 1. A generic Metropolis Monte Carlo simulation is then used to find the stationary state of the system, signified by the global minimum of the total free energy function given in Eq. (2). In each Monte Carlo step, one cell is randomly selected, and a new magnitude and orientation of polarization for the chosen cell are randomly generated. If the reformed configuration decreases the total free energy of the system F_tot, the change in ${\overrightarrow{m}}_i$ and θ_iis accepted. In order to avoid local minima, we implemented the Metropolis algorithm, which enables us to explore the energy landscape of the system and accept a given modification with a probability proportional to the corresponding Boltzmann weight. In turn, this allows us to move up or down on the energy landscape and to escape local minima in the space of arrangements (Frenkel, 2002). To enhance performance and prevent a bias in preferring only small or only large displacements, we used an adaptive step size for angle adjustments during this energy minimization protocol.

This process is repeated until the absolute average change in F_tot over 100 successful Monte Carlo steps exceed the values of 10^–8. Finally, we quantify the degree of global alignment of the tissue polarization with the order parameter ⟨r⟩ defined as,

$$⟨r⟩=\frac{1}{N}\sum _{i=1}^N\cos \left(\mathrm{\Delta }{\mathrm{\theta }}_i\right)(7)$$

where N equals the number of cells and Δθ_i is the angle of polarization of the ith cell relative to the symmetry breaking direction, specified by the global cue vector, $\overrightarrow{G}$ (Markovič et al., 2014).

Results

We investigate the impact of the strength of cell–cell adhesion, Λ_mn, between the mutant cell and its neighbors on the global polarity pattern. To this purpose, we generated several epithelial tissue architectures for different values of line-tension strengths around the mutant cell (Λ_mn ∈ [0,2]), as described in Biomechanical Vertex Dynamics Model. The interaction strength between all other cells was set to Λ_ij = 1. It should be noted that studying the role of the intercellular interaction strengths between normal and mutant cells and how they affect cellular arrangement was motivated by previous endeavors, which have suggested that intercellular contacts around mutants are modified (Goodrich and Strutt, 2011). Then, we used each of the generated epithelial structures to evaluate the impact of the defect incited by the mutant cell in the center of the global polarity pattern. Results presented in Figure 4 show six characteristic stationary polarity patterns for three values of Λ_mn and two different values of the global cue strength C. Different degrees of the global cue C correspond to different epithelium developmental stages. In the early developmental stages, the global polarization order is known to be lower (C=1) than in the late stage, where the polarity on the global scale is much more pronounced (C=10) (Markovič et al., 2014). It can be observed that the extent of the topological defect is lower for higher values of C. Modifications of the second parameter, Λ_mn, correspond to variations in strength of mechanical interactions between normal and mutant epithelium cells. For Λ_mn = 0, the cell-to-cell interactions do not contribute to the energy function [see Eq. (1)], and hence the constraint in the length of the cell boundary is not pronounced (see Figure 2). On the other hand, higher degrees of mechanical interactions (for example, Λ_mn = 2) provoke the opposite effect, thereby forcing the neighbors of the mutant cell to reduce their boundary lengths. Notably, it can be observed than for higher line-tension strengthΛ_mn values, the disruptions of the global polarity patterns are more pronounced than for lower values of Λ_mn. Apparently, a proper adjustment of the intercellular interactions along the junctional regions around the mutants can serve as a regulatory mechanism that reduces distortions of the orientational disorder provoked by the mutant cells.

FIGURE 4

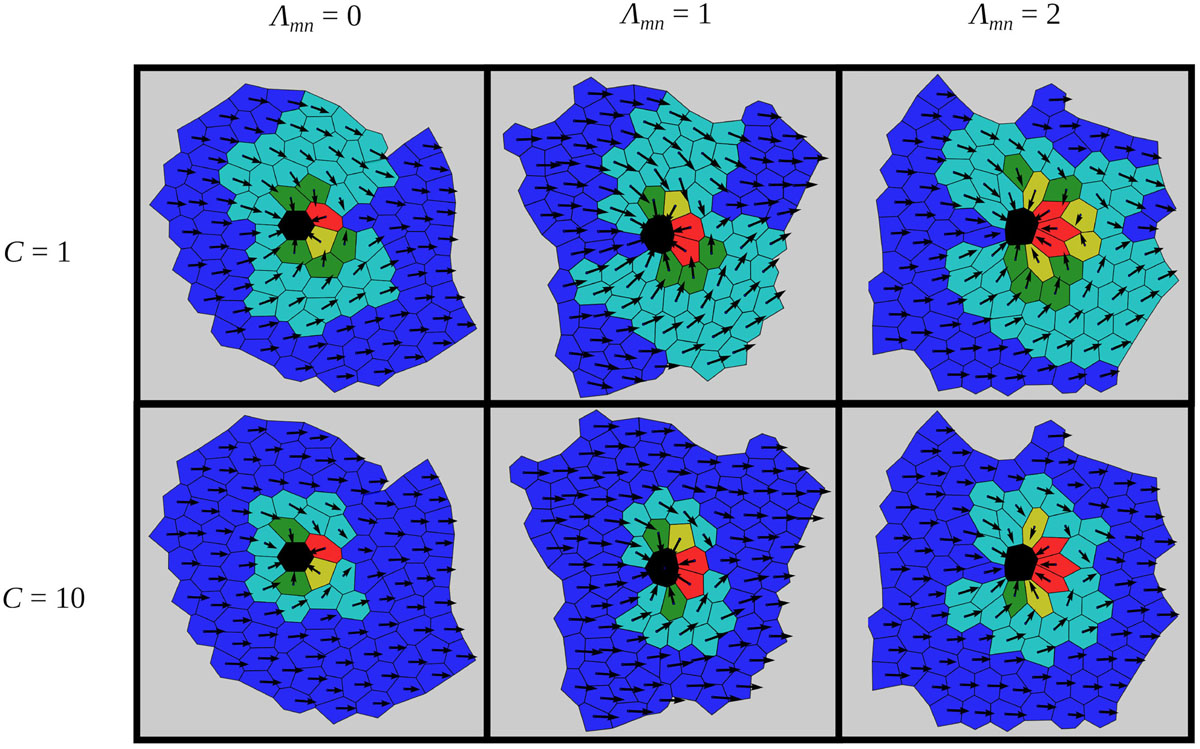
Figure 4. Characteristic epithelial structures for two values of the global signal strength C and for three different line-tension strengths around the mutant cell Λ_mn. The orientations of cell polarities are color coded as introduced in Figure 3. In all cases, the global cue is oriented in the positive direction of the x-axis: $\stackrel{\rightharpoonup }{G}$ = (1,0).

To quantify this visual assessment, we compute the average order parameter r as a function of the line-tension strength Λ_mn, for two different values of the global cue strength (C=1 and C=10). The results are presented in Figure 5A and were obtained by averaging over 100 realizations of the functional PCP model for individual line-tension strengths (see Biomechanical Vertex Dynamics Model) in order to ensure statistical accuracy. As expected, the overall degree of global alignment is higher for higher values of the global cue C, which is in agreement with previous studies (Axelrod and Tomlin, 2011; Hazelwood and Hancock, 2013; Markovič et al., 2014; Butler and Wallingford, 2017). Most importantly, for both values of C, the order parameter r is a decreasing function of the line-tension strength Λ_mn. This result confirms our abovementioned predictions, because reducing the costs for intercellular interactions on cell boundaries among cells that surround a mutant cell does indeed ensures a better global alignment of PCP.

FIGURE 5

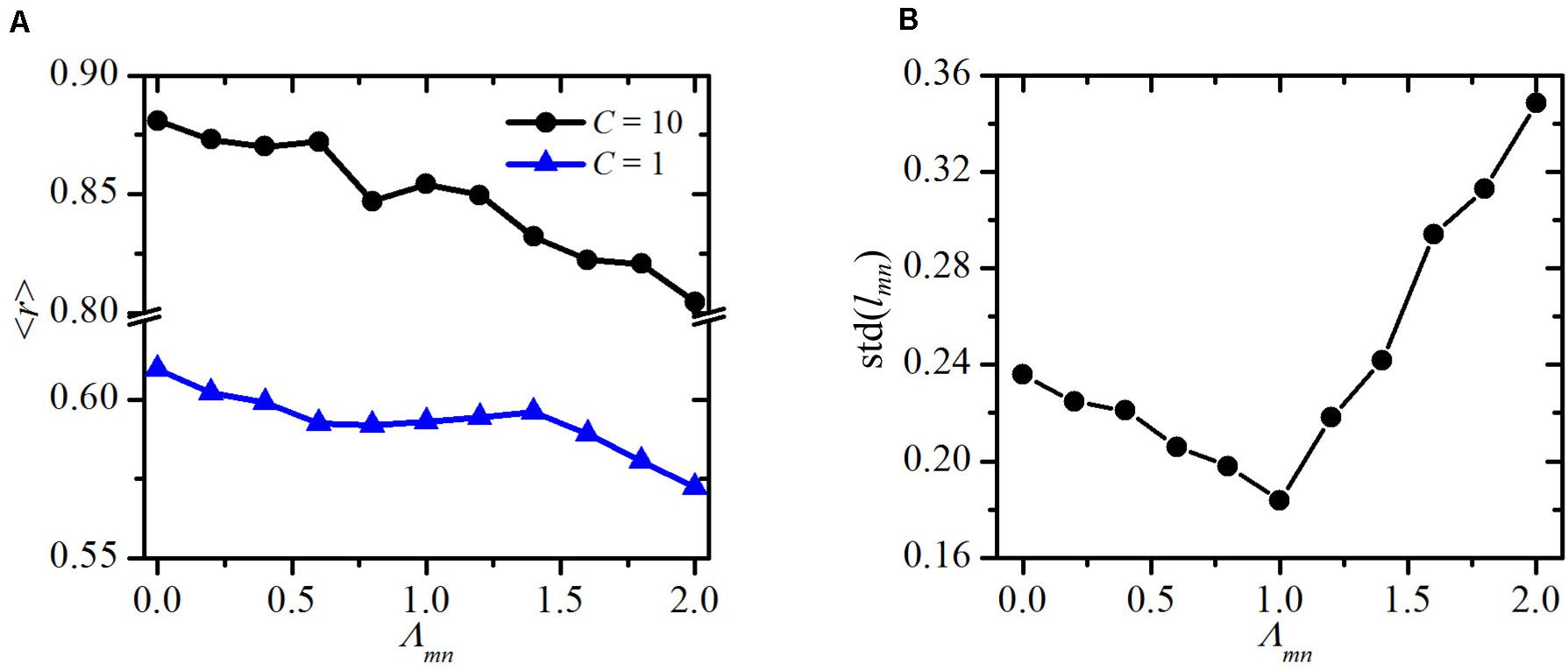
Figure 5. Quantitative assessment of variations of the structural and polarization. Global order parameter ⟨r⟩ as a function of the line-tensions strength around the mutant cell Λ_mn for an early developmental stage (C=1) and adult epithelium (C=10) (A) and standard deviation of cell site lengths std(l_mn) as a function of the line tensions strength Λ_mn around the mutant cell (B).

To further investigate the effect of altered mechanical interactions around the mutant cell, we calculate the standard deviation in the lengths of the cell boundaries of the mutant’s neighbors l_mn. In Figure 5B, we show this standard deviation values std(l_mn) as a function of the line tension Λ_mn. The results point out a non-trivial behavior. Minimal deviations of the lengths l_mn are attained when the cell-to-cell interaction in the whole system are homogeneous (Λ_mn = Λ_ij = 1). It should be noted that the simulated tissue growth process is governed by a stochastic step. As a result, the final packing geometries are characterized by different cell shapes, despite the fact that the initial configuration consisted of regular hexagons. Most importantly, such heterogeneous cellular architectures are also found in realistic epithelial tissues (Farhadifar et al., 2007). For that reason, the final value of std(l_mn) is not 0 even in the most homogeneous scenario, where Λ_mn = Λ_ij = 1. Either positive or negative variations of Λ_mn lead to higher variability in the boundary lengths. Notably, differences in intercellular interactions around mutants in comparison with other epithelial cells have also been observed experimentally (Classen et al., 2005), which supports our ideas on mechanical regulations of impaired polarity patterns.

By decreasing the line-tension strength Λ_mn, the neighbors of the mutant cell tend to magnify the lengths of cell boundaries among them and reduce the boundary lengths with other cells in their vicinity. This not only gives rise to the variations in lengths but also causes the formation of a kind of structural barrier, which tends to isolate the mutant cell from its environment (see Figures 2, 4). As a result, the impact of the mutant via PCP interactions on the whole epithelial tissue decreases [see Eq. (6)], and hence, the global polarity patterns become less impaired. On the other hand, an increase of the line tension strength Λ_mn causes the opposite effect, which in turn even more pronounces the topological defect provoked by the mutant cell.

Discussion

In this study, we have investigated how mutant cells affect the structural and functional organization of epithelial tissues. Because these mutant cells directly affect the orientation of polarization (Hazelwood and Hancock, 2013) and the structural properties (Classen et al., 2005) of its adjacent cells, the global properties of the developed epithelium depend on both effects. Therefore, we have combined two modeling approaches that independently one from another describe the mechanisms of mechanical development (Farhadifar et al., 2007) and the establishment of PCP in epithelial tissues (Hazelwood and Hancock, 2013). This enables us to study the interplay between mechanical interactions and the corresponding established global PCP patterns in growing cellular tissues, which is established by cell growth and cell division around a mutant cell. Special attention is given to the mutant cell-induced irregularities in polarized cytoarchitectures. Motivated by previous experimental findings, we have systematically investigated mechanical interactions at cell borders between healthy and mutant cells by varying the line-tension strength between these cells. Namely, previous studies have implied that intercellular contacts between normal and mutant cells are modified, thereby leading to local variations and structural disorder (Classen et al., 2005; Vladar et al., 2009; Salbreux et al., 2012; Heisenberg and Bellaïche, 2013; Kim et al., 2016; Butler and Wallingford, 2017). More precisely, mutant clones disturb the packing of adjacent wild-type cells, which are not able to assemble efficient boundaries with new neighbors and cannot regularize their packing geometry (Classen et al., 2005). In zebrafish mutants, adherens junctions are destabilized, and the apicobasal polarity of the retinal epithelium is destroyed (Salbreux et al., 2012). Removal of adherens junctions has also been shown to result in a substantial rounding of the cells caused by interfacial tension release (Brückner and Janshoff, 2018). It should be noted that even though the interplay between adherens junctions and PCP is incompletely understood, recent findings suggest that they are intimately linked (Tatin et al., 2013; Stocker and Chenn, 2015). In addition, in epithelial cell populations in the Drosophila wing, it has been shown that cells lacking Fz or Ds function cause trichomes proximal to the mutant to invert their polarity (Goodrich and Strutt, 2011). The functional PCP model (Hazelwood and Hancock, 2013) enabled us to investigate how a mutant cell affects global polarization in an early and final developmental stage (see Figure 4). At an earlier developmental stage, local interactions prevail (Strutt, 2001). In turn, this causes the defect in polarization initiated by the mutant cell to affect a wider area compared with the final developmental stage, where the global cue is more strongly expressed. The effect of the strength of the global cue has been shown to affect the extent of such swirling polarization patterns in such a way that increasing global cue values lower the degree of swirling (Ma et al., 2008; Burak and Shraiman, 2009; Shadkhoo and Mani, 2019).

Our findings are in agreement with the abovementioned phenomena. For example, by changing the relative contribution of the global cue strength in the PCP model, we mimic the effect of a stronger or weaker contribution of the global cue on the global polarization pattern (Ma et al., 2008; Burak and Shraiman, 2009; Shadkhoo and Mani, 2019). By adjusting the line-tension strength between the edges of a mutant and wild-type cell, we can further consider how changes in mechanical cell-to-cell interactions affect the cytoarchitecture of the numerically evolved epithelium and the corresponding PCP patterns. We have computed and analyzed several epithelial structures for different sets of model parameters (see Figure 4). Our results revealed that the line-tension strength between mutant and wild-type cells does not only affect the evolved global structure but additionally influences the established global PCP pattern. This link is predominately a consequence of the increasing number of wild-type cells around a mutant cell, with higher Λ_nm values. The latter is caused by the fact that with increasing values of Λ_nm, wild-type cells tend to minimize the cell boundary length common to the mutant cell and maximize the cell boundary length with adjacent wild-type cells. In turn, this leads to an accumulation of wild-type cells surrounding a mutant cell. The neighbors of those cells mediate the improper polarity pattern to a larger proportion of the tissue, causing a lower degree of global ordering. This tendency can be observed for weak and strong global cues strengths (see Figure 5A). Regarding the structural features of cells in the vicinity of a mutant cell, our results show that the variability in the lengths of the cell sites around the mutant cell increases as the line-tension strength is either decreased or increased from the reference value of Λ_nm = 1 (see Figure 5B). This finding is in agreement with the experimental observations, which indicate that the cells surrounding a mutant cell are characterized by higher variability in their cell site lengths than are the other cells in the tissue (Classen et al., 2005). Previous reports have also suggested that modifying local strain cues can accelerate the reorientation of cells with respect to some static strains (Rens and Merks, 2017). This is a promising result indicating possibilities for regulating defects in epithelial structures and might have important therapeutic applications. It can be imagined that the defects could be regulated by tuning the line tension strength between the cells. In particular, a pharmacologically induced decrease in the strength of mechanical interactions between normal and mutant epithelium cells could act as an efficient regulatory mechanism for diminishing the topological defects caused by mutant cells. Because the current understanding of the interplay between the mechanical properties of the epithelium structure and the inherent polarity of the single cells is still limited, additional experimental as well as theoretical studies are needed. Our phenomenological framework allows only for a qualitative assessment of the processes occurring during tissue morphogenesis and the development of PCP, whereas the details about the molecular processes and interactions, which drive polarity transmission or mediate the orientation with the global cue, remained unaddressed. Most importantly, as also suggested by others (Minc and Piel, 2012), we need to integrate the mechanical properties and the PCP of the epithelium as two developmental driving processes that mutually affect each other, leading to asymmetric growth and shape-dependent cellular orientations.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

RM, MG, and MM designed the study and wrote the manuscript. RM performed numerical simulations and analyses. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Slovenian Research Agency (research core funding, nos. P1-0055 and P3-0396, as well as research project no. I0-0029).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adler, P. N., Krasnow, R. E., and Liu, J. (1997). Tissue polarity points from cells that have higher Frizzled levels towards cells that have lower Frizzled levels. Curr. Biol. 7, 940–949. doi: 10.1016/S0960-9822(06)00413-411

CrossRef Full Text | Google Scholar

Axelrod, J. D. (2020). Planar cell polarity signaling in the development of left–right asymmetry. Curr. Opin. Cell Biol. 62, 61–69. doi: 10.1016/j.ceb.2019.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Axelrod, J. D., and Tomlin, C. J. (2011). Modeling the control of planar cell polarity. Wiley Interdiscip. Rev. Syst. Biol. Med. 3, 588–605. doi: 10.1002/wsbm.138

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayly, R., and Axelrod, J. D. (2011). Pointing in the right direction: new developments in the field of planar cell polarity. Nat. Rev. Genet. 12, 385–391. doi: 10.1038/nrg2956

PubMed Abstract | CrossRef Full Text | Google Scholar

Blankenship, J. T., Backovic, S. T., Sanny, J. S. P., Weitz, O., and Zallen, J. A. (2006). Multicellular rosette formation links planar cell polarity to tissue morphogenesis. Dev. Cell 11, 459–470. doi: 10.1016/j.devcel.2006.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Bosveld, F., Bonnet, I., Guirao, B., Tlili, S., Wang, Z., Petitalot, A., et al. (2012). Mechanical control of morphogenesis by fat/dachsous/four-jointed planar cell polarity pathway. Science 336, 724–727. doi: 10.1126/science.1221071

PubMed Abstract | CrossRef Full Text | Google Scholar

Brückner, B. R., and Janshoff, A. (2018). Importance of integrity of cell-cell junctions for the mechanics of confluent MDCK II cells. Sci. Rep. 8:14117. doi: 10.1038/s41598-018-32421-32422

CrossRef Full Text | Google Scholar

Burak, Y., and Shraiman, B. I. (2009). Order and stochastic dynamics in Drosophila planar cell polarity. PLoS Comput. Biol. 5:e1000628. doi: 10.1371/journal.pcbi.1000628

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler, M. T., and Wallingford, J. B. (2017). Planar cell polarity in development and disease. Nat. Rev. Mol. Cell Biol. 18, 375–388. doi: 10.1038/nrm.2017.11

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, D., Aw, W. Y., Devenport, D., and Torquato, S. (2016). Structural characterization and statistical-mechanical model of epidermal patterns. Biophys. J. 111, 2534–2545. doi: 10.1016/j.bpj.2016.10.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Classen, A.-K., Anderson, K. I., Marois, E., and Eaton, S. (2005). Hexagonal packing of Drosophila wing epithelial cells by the planar cell polarity pathway. Dev. Cell 9, 805–817. doi: 10.1016/j.devcel.2005.10.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Farhadifar, R., Röper, J.-C. C., Aigouy, B., Eaton, S., and Jülicher, F. (2007). The influence of cell mechanics. cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 17, 2095–2104. doi: 10.1016/j.cub.2007.11.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandez-Gonzalez, R., Simoes, S., de, M., Röper, J.-C., Eaton, S., and Zallen, J. A. (2009). Myosin II dynamics are regulated by tension in intercalating cells. Dev. Cell 17, 736–743. doi: 10.1016/j.devcel.2009.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandez-Gonzalez, R., and Zallen, J. A. (2008). Epithelial organization: may the force be with you. Curr. Biol. 18, R163–R165. doi: 10.1016/j.cub.2007.12.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher, K. H., Strutt, D., and Fletcher, A. G. (2017). Integrating planar polarity and tissue mechanics in computational models of epithelial morphogenesis. Curr. Opin. Syst. Biol. 5, 41–49. doi: 10.1016/j.coisb.2017.07.009

CrossRef Full Text | Google Scholar

Fletcher, A. G., Osborne, J. M., Maini, P. K., and Gavaghan, D. J. (2013). Implementing vertex dynamics models of cell populations in biology within a consistent computational framework. Prog. Biophys. Mol. Biol. 113, 299–326. doi: 10.1016/j.pbiomolbio.2013.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Frenkel, D. (2002). Understanding Molecular Simulation. Elsevier, doi: 10.1016/B978-0-12-267351-1.X5000-7

CrossRef Full Text | Google Scholar

Goodrich, L. V., and Strutt, D. (2011). Principles of planar polarity in animal development. Development 138, 1877–1892. doi: 10.1242/dev.054080

PubMed Abstract | CrossRef Full Text | Google Scholar

Gubb, D., and García-Bellido, A. (1982). A genetic analysis of the determination of cuticular polarity during development in Drosophila melanogaster. Development 68, 37–57.

Google Scholar

Hazelwood, L. D., and Hancock, J. M. (2013). Functional modelling of planar cell polarity: an approach for identifying molecular function. BMC Dev. Biol. 13:20. doi: 10.1186/1471-213X-13-20

PubMed Abstract | CrossRef Full Text | Google Scholar

Heisenberg, C.-P., and Bellaïche, Y. (2013). Forces in tissue morphogenesis and patterning. Cell 153, 948–962. doi: 10.1016/j.cell.2013.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Hočevar, A., and Ziherl, P. (2009). Degenerate polygonal tilings in simple animal tissues. Phys. Rev. E 80:011904. doi: 10.1103/PhysRevE.80.011904

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishihara, S., Marcq, P., and Sugimura, K. (2017). From cells to tissue: a continuum model of epithelial mechanics. Phys. Rev. E 96:022418. doi: 10.1103/PhysRevE.96.022418

PubMed Abstract | CrossRef Full Text | Google Scholar

Kachalo, S., Naveed, H., Cao, Y., Zhao, J., and Liang, J. (2015). Mechanical model of geometric cell and topological algorithm for cell dynamics from single-cell to formation of monolayered tissues with pattern. PLoS One 10:e0126484. doi: 10.1371/journal.pone.0126484

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Cassidy, J. J., Yang, B., Carthew, R. W., and Hilgenfeldt, S. (2016). Hexagonal patterning of the insect compound eye: facet area variation. defects, and disorder. Biophys. J. 111, 2735–2746. doi: 10.1016/j.bpj.2016.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Koride, S., Loza, A. J., and Sun, S. X. (2018). Epithelial vertex models with active biochemical regulation of contractility can explain organized collective cell motility. APL Bioeng. 2:031906. doi: 10.1063/1.5023410

CrossRef Full Text | Google Scholar

Ladan, M. K., Ziherl, P., and Šiber, A. (2019). Topology of dividing planar tilings: mitosis and order in epithelial tissues. Phys. Rev. E 100:012410. doi: 10.1103/PhysRevE.100.012410

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Garrec, J.-F., Lopez, P., and Kerszberg, M. (2006). Establishment and maintenance of planar epithelial cell polarity by asymmetric cadherin bridges: a computer model. Dev. Dyn. 235, 235–246. doi: 10.1002/dvdy.20617

PubMed Abstract | CrossRef Full Text | Google Scholar

Lecuit, T., and Lenne, P.-F. (2007). Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 8, 633–644. doi: 10.1038/nrm2222

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, D., Amonlirdviman, K., Raffard, R. L., Abate, A., Tomlin, C. J., and Axelrod, J. D. (2008). Cell packing influences planar cell polarity signaling. Proc. Natl. Acad. Sci. 105, 18800–18805. doi: 10.1073/pnas.0808868105

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcinkevicius, E., Fernandez-Gonzalez, R., and Zallen, J. A. (2009). Q&A: quantitative approaches to planar polarity and tissue organization. J. Biol. 8, 103. doi: 10.1186/jbiol191

PubMed Abstract | CrossRef Full Text | Google Scholar

Markovič, R., Gosak, M., Repnik, R., Kralj, S., and Marhl, M. (2014). Defects in planar cell polarity of epithelium. what can we learn from liquid crystals? Adv. Planar Lipid Bilayers Liposomes 20, 197–217.

Google Scholar

Markovič, R., Peltan, J., Gosak, M., Horvat, D., Žalik, B., Seguy, B., et al. (2017). Planar cell polarity genes frizzled4 and frizzled6 exert patterning influence on arterial vessel morphogenesis. PLoS One 12:e0171033. doi: 10.1371/journal pone.0171033

CrossRef Full Text | Google Scholar

Minc, N., and Piel, M. (2012). Predicting division plane position and orientation. Trends Cell Biol. 22, 193–200. doi: 10.1016/j.tcb.2012.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelson, W. J. (2009). Remodeling epithelial cell organization: transitions between front-rear and apical-basal polarity. Cold Spring Harb. Perspect. Biol. 1:a000513. doi: 10.1101/cshperspect.a000513

PubMed Abstract | CrossRef Full Text | Google Scholar

Nissen, S. B., Rønhild, S., Trusina, A., and Sneppen, K. (2018). Theoretical tool bridging cell polarities with development of robust morphologies. Elife 7:e38407. doi: 10.7554/eLife.38407

PubMed Abstract | CrossRef Full Text | Google Scholar

Osterfield, M., Du, X., Schüpbach, T., Wieschaus, E., and Shvartsman, S. Y. (2013). Three-dimensional epithelial morphogenesis in the developing Drosophila egg. Dev. Cell 24, 400–410. doi: 10.1016/j.devcel.2013.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Rens, E. G., and Merks, R. M. H. (2017). Cell contractility facilitates alignment of cells and tissues to static uniaxial stretch. Biophys. J. 112, 755–766. doi: 10.1016/j.bpj.2016.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Salbreux, G., Barthel, L. K., Raymond, P. A., and Lubensky, D. K. (2012). Coupling mechanical deformations and planar cell polarity to create regular patterns in the zebrafish retina. PLoS Comput. Biol. 8:e1002618. doi: 10.1371/journal.pcbi.1002618

PubMed Abstract | CrossRef Full Text | Google Scholar

Saw, T. B., Doostmohammadi, A., Nier, V., Kocgozlu, L., Thampi, S., Toyama, Y., et al. (2017). Topological defects in epithelia govern cell death and extrusion. Nature 544, 212–216. doi: 10.1038/nature21718

PubMed Abstract | CrossRef Full Text | Google Scholar

Shadkhoo, S., and Mani, M. (2019). The role of intracellular interactions in the collective polarization of tissues and its interplay with cellular geometry. PLoS Comput. Biol. 15:e1007454. doi: 10.1371/journal.pcbi.1007454

PubMed Abstract | CrossRef Full Text | Google Scholar

Šiber, A., and Ziherl, P. (2017). Cellular Patterns. Boca Rato, FLA: CRC Press, doi: 10.1201/9781351048675

CrossRef Full Text | Google Scholar

Staddon, M. F., Bi, D., Tabatabai, A. P., Ajeti, V., Murrell, M. P., and Banerjee, S. (2018). Cooperation of dual modes of cell motility promotes epithelial stress relaxation to accelerate wound healing. PLoS Comput. Biol. 14:e1006502. doi: 10.1371/journal.pcbi.1006502

PubMed Abstract | CrossRef Full Text | Google Scholar

Stocker, A. M., and Chenn, A. (2015). The role of adherens junctions in the developing neocortex. Cell Adh. Migr. 9, 167–174. doi: 10.1080/19336918.2015.1027478

PubMed Abstract | CrossRef Full Text | Google Scholar

Strutt, D. I. (2001). Asymmetric localization of frizzled and the establishment of cell polarity in the Drosophila wing. Mol. Cell 7, 367–375. doi: 10.1016/S1097-2765(01)00184-188

CrossRef Full Text | Google Scholar

Sugimura, K., and Ishihara, S. (2013). The mechanical anisotropy in a tissue promotes ordering in hexagonal cell packing. Development 140, 4091–4101. doi: 10.1242/dev.094060

PubMed Abstract | CrossRef Full Text | Google Scholar

Tatin, F., Taddei, A., Weston, A., Fuchs, E., Devenport, D., Tissir, F., et al. (2013). Planar cell polarity protein celsr1 regulates endothelial adherens junctions and directed cell rearrangements during valve morphogenesis. Dev. Cell 26, 31–44. doi: 10.1016/j.devcel.2013.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, J., Abramova, N., Charlton, J., and Adler, P. N. (1998). Van Gogh: a new Drosophila tissue polarity gene. Genetics 150, 199–210.

Google Scholar

Tree, D. R., Ma, D., and Axelrod, J. D. (2002). A three-tiered mechanism for regulation of planar cell polarity. Semin. Cell Dev. Biol. 13, 217–224. doi: 10.1016/S1084-9521(02)00042-43

CrossRef Full Text | Google Scholar

van Drongelen, R., Vazquez-Faci, T., Huijben, T. A. P. M., van der Zee, M., and Idema, T. (2018). Mechanics of epithelial tissue formation. J. Theor. Biol. 454, 182–189. doi: 10.1016/j.jtbi.2018.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinson, C. R., and Adler, P. N. (1987). Directional non-cell autonomy and the transmission of polarity information by the frizzled gene of Drosophila. Nature 329, 549–551. doi: 10.1038/329549a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Vladar, E. K., Antic, D., and Axelrod, J. D. (2009). Planar cell polarity signaling: the developing cell’s compass. Cold Spring Harb. Perspect. Biol. 1, a002964–a002964. doi: 10.1101/cshperspect.a002964

PubMed Abstract | CrossRef Full Text | Google Scholar

Vu, H. T.-K., Mansour, S., Kücken, M., Blasse, C., Basquin, C., Azimzadeh, J., et al. (2019). Dynamic polarization of the multiciliated planarian epidermis between body plan landmarks. Dev. Cell 51, 526–542.e6. doi: 10.1016/j.devcel.2019.10.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C.-C., Jamal, L., and Janes, K. A. (2012). Normal morphogenesis of epithelial tissues and progression of epithelial tumors. wiley interdiscip. Rev. Syst. Biol. Med. 4, 51–78. doi: 10.1002/wsbm.159

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., and Nathans, J. (2007). Tissue/planar cell polarity in vertebrates: new insights and new questions. Development 134, 647–658. doi: 10.1242/dev.02772

PubMed Abstract | CrossRef Full Text | Google Scholar

Wootton, R. J. (1992). Functional morphology of insect wings. Annu. Rev. Entomol. 37, 113–140. doi: 10.1146/annurev.en.37.010192.000553

CrossRef Full Text | Google Scholar

Yu, J. C., and Fernandez-Gonzalez, R. (2017). Quantitative modelling of epithelial morphogenesis: integrating cell mechanics and molecular dynamics. Semin. Cell Dev. Biol. 67, 153–160. doi: 10.1016/j.semcdb.2016.07.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Zallen, J. A. (2007). Planar polarity and tissue morphogenesis. Cell 129, 1051–1063. doi: 10.1016/j.cell.2007.05.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, H., and Owen, M. R. (2013). Damped propagation of cell polarization explains distinct PCP phenotypes of epithelial patterning. Sci. Rep. 3:2528. doi: 10.1038/srep02528

PubMed Abstract | CrossRef Full Text | Google Scholar