High-Throughput Calculations for High-Entropy Alloys: A Brief Review

High-entropy alloys (HEAs) open up new doors for their novel design principles and excellent properties. In order to explore the huge compositional and microstructural spaces more effectively, high-throughput calculation techniques are put forward, overcoming the time-consuming and laboriousness of traditional experiments. Here we present and discuss four different calculation methods that are usually applied to accelerate the development of novel HEA compositions, that is, empirical models, first-principles calculations, calculation of phase diagrams (CALPHAD), and machine learning. The empirical model and the machine learning are both based on summary and analysis, while the latter is more believable for the use of multiple algorithms. The first-principles calculations are based on quantum mechanics and several open source databases, and it can also provide the finer atomic information for the thermodynamic analysis of CALPHAD and machine learning. We illustrate the advantages, disadvantages, and application range of these techniques, and compare them with each other to provide some guidance for HEA study.

Introduction

High-entropy alloys (HEAs) have attracted significant interest in recent years owing to their novel alloy-design principles. Stemming from the entropy-stabilizing effect to solid-solution phases, they are originally defined as single-phase multicomponent alloys, which consist of five or more elements in equal or near-equal atomic ratios (Cantor et al., 2004; Yeh et al., 2004), but now the field expands to include intermetallics, nanoprecipitation, ceramic compounds, and non-equiatomic materials with as few as three principal elements (Senkov et al., 2010; Zhang et al., 2014; Liu et al., 2016; Yang M. et al., 2018). In pursuit of more promising mechanical behaviors, such as ultrahigh strength and good cryogenic toughness that have been reported in some of the HEAs (Gludovatz et al., 2014; Liang et al., 2018; Yang T. et al., 2018), the number of HEA compositions is increasing rapidly. However, their phase structures and properties are not as clearly related to the mixing entropy as originally designed. Therefore, a significant challenge is how to select the most suitable composition more effectively, in order to obtain the most desired phase structure and property.

An experiment was and remains one of the most effective methods in the search for novel alloys. To overcome the incompleteness and contingency of traditional “trial and error” methods and improve the alloy-development efficiency, the high-throughput preparation technique has been put forward, the core of which is to prepare a composition gradient to achieve a one-time characterization of a batch of compositions. The diffusion couples, supergravity field, and laser additive manufacturing can all contribute to the compositional-graded bulk alloys (Welk et al., 2013; Cao and Zhao, 2015; Li et al., 2017), and the multi-target co-sputtering is employed to prepare a compositional-graded film (Marshal et al., 2017). However, the experimental process is still limited by high costs and time-consuming synthesis procedures, especially the diffusion couples and laser additive manufacturing. Because of the high cooling rate, there is a gap between the properties of the film and those of the bulk materials, such as phase structures and the hardness. Moreover, the imperfectly-developed high-throughput measurement also makes the gradient materials still need to be tested one by one.

At the same time, theoretical and calculation research activities play an increasingly-important role in materials science. The combination of computer simulation and experimental data contributes to the better understand of the physical mechanism, which therefore enables the prediction of unknown data. In the present work, we present four methods and provide examples of their successful applications in the HEA development, including empirical models based on the Hume-Rothery rules and Pettifor map, first-principles “high-throughput” calculations, calculation of phase diagrams (CALPHAD) technique, and machine learning using different algorithms. Moreover, we illustrate the advantages, disadvantages, and application conditions of different high-throughput calculation techniques, in order to provide the guidance for HEA development.

Empirical Models

The empirical models are one of the most important means of the early composition design, which are developed by summarizing the relationship between phase structures and thermophysical properties of HEAs. There are two different methods in the empirical models, that is, the thermophysical-parameter calculation of an alloy and the phase structure reference of binary intermetallic.

The thermophysical parameter calculation is based on the “Hume-Rothery criterion.” Researchers extended this rule to the field of HEAs and proposed a variety of related parameters for predicting the phase formation, including the electronegativity difference (Δχ), atomic size difference (δ), mixing enthalpy (ΔH_mix), and the root-mean-square strain (ε_RMS) et al. All these empirical parameters are defined and summarized in Table 1. What they have in common is to minimize the differences in the thermodynamic and physical properties of the constituent elements, to obtain an atomic disordered solid solution, and vice versa to obtain intermetallics or amorphous structures. However, they have relatively poor accuracy due to the lack of phase diagram, especially for multiphase structures. For example, many alloys that contain two FCC phases or two BCC phases are counted as single-phase compositions, and the regions of multiphase solid solutions, intermetallics, and amorphous may overlap (Zhang et al., 2008). Therefore, only the formation range of single-phase solid solutions is emphasized here.

TABLE 1

Table 1. The thermo-physical parameters for HEAs’ phase selection.

Because entropy will compete with enthalpy during solidification, it does not always dominate in the Gibbs free energy, and the high mixing entropy (ΔS_mix > 1.5R) does not always result in the formation of a solid solution (Senkov et al., 2015). The S_corr/S_id criterion is also focus on the mixing entropy, which claims that the mixing entropy not only depends on the chemical composition but also on the nature of the constituent elements and the alloy’s melting temperature (He et al., 2017). The Δχ has little effect on the formation of the solid solution, while it affects the supercooled regions of the amorphous phase (Fang et al., 2003; Guo and Liu, 2011; Poletti and Battezzati, 2014). The simplest three criteria, δ, ΔH_mix, and Ω, appear to be very powerful in separating the single-phase solution and amorphous structure (Zhang et al., 2008; Yang and Zhang, 2012), while there is some overlap between single-phase and multiphase structures. The Φ parameter is then proposed by adding the excessive entropy, S_E, to the parameter, Ω (Ye et al., 2015), which means that the atomic packing, atom size, entropy, and enthalpy effects are all included. The effect of λ is to characterize the elemental segregation (Ye et al., 2016b). The combination of Φ and λ can effectively distinguish the single-phase, multi-phase, and the atom segregation in the alloy. φ and ${\mathrm{\kappa }}_1^{cr}$ are almost the two most complicated parameters. They both compare the Gibbs free energies of the solid solution phase and the intermetallics (King et al., 2016; Senkov and Miracle, 2016), and their accuracy is relatively higher because more influential factors are considered. Among all the empirical rules, the δ, γ, and ε_RMS values are similar and they all only consider atomic sizes (Wang et al., 2015; Ye et al., 2016a). On the other hand, although the valence electron concentration (VEC) criterion can effectively predict the structure type of solid solutions (Guo et al., 2011), including face-centered-cubic (FCC), body-centered-cubic (BCC), and hexagonal-close-packed (HCP) structures, it cannot be used to predict whether the solid solution phase can form.

Another method in empirical models is to consider the phase structure of binary intermetallics. Pettifor offered a radical new view of the structure of intermetallics by assigning one unique number to each element, which is called the Mendeleev number or the chemical scale, μ (Pettifor, 1986). In the Pettifor map, all the known binary compounds are written in the form of A_1–xB_x, the abscissa is the Mendeleev ordinal of A, and the ordinate is the Mendeleev ordinal of B. Different patterns represent the structures of different binary compounds. The Mendeleev number and the Pettifor map have emerged as the important parameter for choosing the promising alloys in the field of ferrous bulk metallic glasses (Takeuchi and Inoue, 2006), quasi-crystalline intermetallics (Ranganathan and Inoue, 2006), and binary metal hydrides (Matysik et al., 2014), and they also offer many advantages in searching HEAs (Takeuchi, 2016).

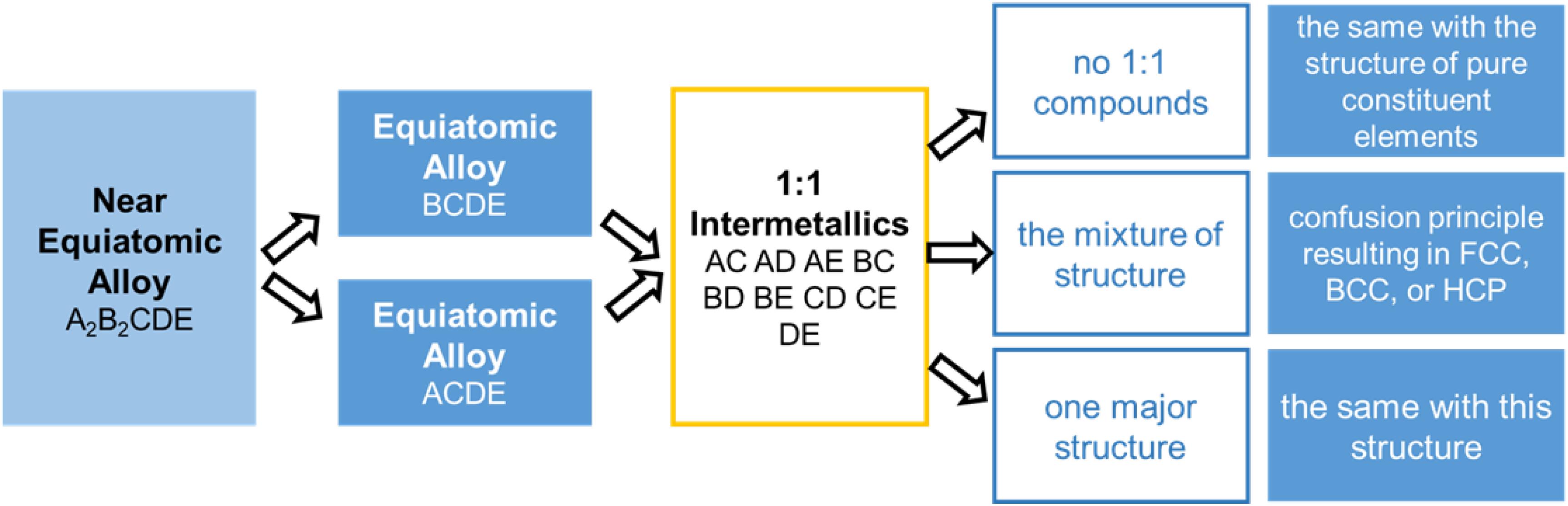
The phase structure is predicted by focusing on the majority of the crystallographic structure in the constituent binary systems in the HEAs. Takeuchi et al. (2015, 2017) utilized the crystallographic data of intermetallics with a binary stoichiometry of 1:1 in the Pettifor map, and they successfully predicted the structures of several equiatomic HEAs. Steps are shown in Figure 1. In ScYLaTiZrHf and NbTaTiZrHf, there are no 1:1 compounds in the constituent binary alloys. Hence, the microstructure of the alloys is affected by the pure elements. That is to say, since each constituent element in ScYLaTiZrHf exhibits an HCP structure, this alloy can be predicted as the same structure. Similarly, a BCC structure can be predicted in the NbTaTiZrHf alloy. On the other hand, the FCC-structured CoCrFeMnNi HEA possesses the intermetallics mixture at 1:1 binary constituent alloys, and this trend may contribute to a confusion principle. In another case of the Cu₂Ag₂GdTbDyY, the BCC structure is dominant in the constituent binary alloys of CuGdTbDyY and AgGdTbDyY, leading to the same BCC structure when alloyed. All these predictions have been confirmed to be correct by experiments, proving that the phase structure can be effectively predicted in the HEAs with equiatomic or near-equiatomic ratios using the Pettifor map.

FIGURE 1

Figure 1. Equiatomic or near-equiatomic HEAs phase selection using the Pettifor map.

These empirical models are actually not the refinement of scientific laws, while they provide a fast reference for predicting the unknown phase structures at the cost of reliability. They can be used without thresholds when there are no reliable phase diagrams or high performance computers. In terms of calculations based on the Hume-Rothery criterion, nearly every unknown composition can be predicted, because the required thermophysical parameters can be easily obtained. However, the prediction using the Pettifor map has a narrow application range and can only be used for equiatomic or near-equiatomic alloys.

Phase Diagram and CALPHAD

A phase diagram is the geometric description of the system under a thermal equilibrium, and it is the basis for the study of solidification, phase transformation, crystal growth, and solid-phase transformation. Takeuchi (2016) reported the YGdTbDyLu and TmGdTbDyLu HCP HEAs for the first time, using the binary phase diagram of lanthanide elements, which is supported by the fact that at the composition of A₅₀B₅₀ at.%, all the constituent binary systems in YGdTbDyLu and TmGdTbDyLu exhibit stable HCP structures.

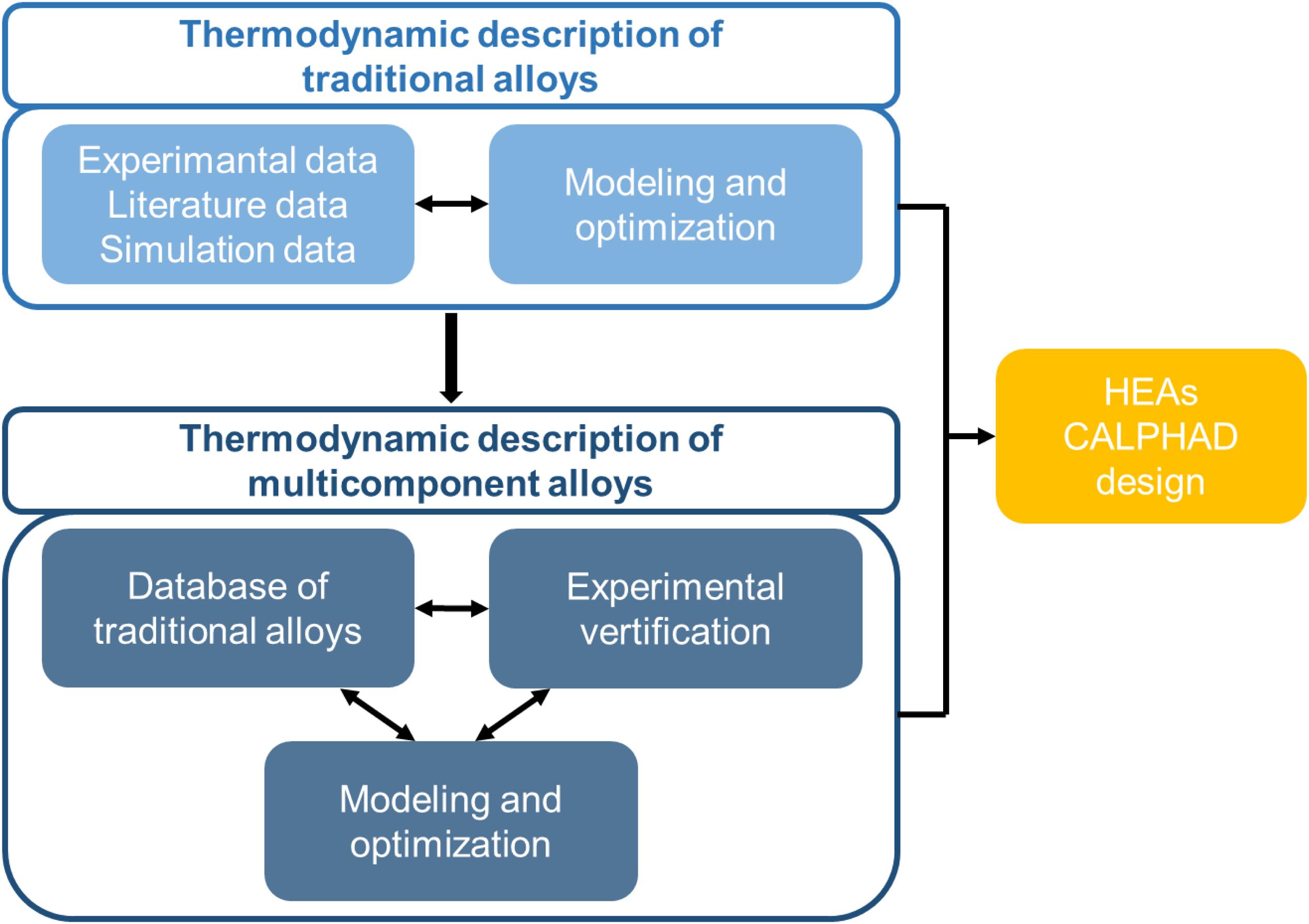
Since the 1970s, the calculation of phase diagrams based on thermodynamic theory has become a new trend, namely the CALPHAD technology. As shown in Figure 2, the steps of the HEAs design using CALPHAD are as follows. The current thermodynamic description of traditional alloys has been developed through the literature, experiment, or simulation. These suitable thermodynamic models can be directly used for HEAs, or new databases specifically for HEAs can be developed, based on them. After optimizing the parameters, the relevant thermodynamic information can be extracted, such as the composition of each phase, phase ratio, activity, and mixing enthalpy. Nowadays, the emergence of the first-principles calculation led CALPHAD into a new stage, which made up for the shortcomings of the lack of thermodynamic data of the new alloy systems.

FIGURE 2

Figure 2. The steps of HEAs compositional design using CALPHAD.

Obviously, the database selection is one of the most important matters in the calculation. Since the lack of the HEAs’ thermodynamic database, some other databases of traditional alloys, such as TCFE7, TCTI3, TCAL2, etc. are successfully used in the literature (Gurao and Biswas, 2017). Although those are specially designed for Fe, Ti, and Al based alloys, they do cover all the edge binaries of a specific HEA system. There are also some databases specifically designed for HEAs. Zhang et al. (2012) reported a sufficiently-large database for the reliable calculation of phase diagrams relating to the Al-Co-Cr-Cu-Fe-Ni HEA systems. They used the calculated primary solidified phases to explain the published experimental observations, and predicted the FCC/BCC phase transition in Al_xCoCrCuFeNi HEAs. Furthermore, Chen et al. (2018) established a TCHEA1 thermodynamic database especially for HEAs within a 15-element framework. TCHEA1 includes more than 100 binaries and more than 200 ternaries, and includes nearly all the stable solution phases and intermetallics in each of the alloy systems.

Gurao and Biswas (2017) proved that the CALPHAD method can significantly reduce the number of experimental trials and effectively find single-phase HEAs. As shown in Figure 3, they studied 1,287 equiatomic quinary alloy systems using both parametric and CALPHAD methods to find single-phase FCC and BCC HEAs. The fact is that the parametric method decreased the trials number to 124, and then the CALPHAD method further decreased the compositions number to 10. Based on the calculation, they only need to prepare two FCC alloys and seven BCC alloys, such as AlFeMnNbTi and AlCrMnTiV. After characterized by X-ray diffraction and scanning electron microscopy, the optimized composition can be quickly selected.

FIGURE 3

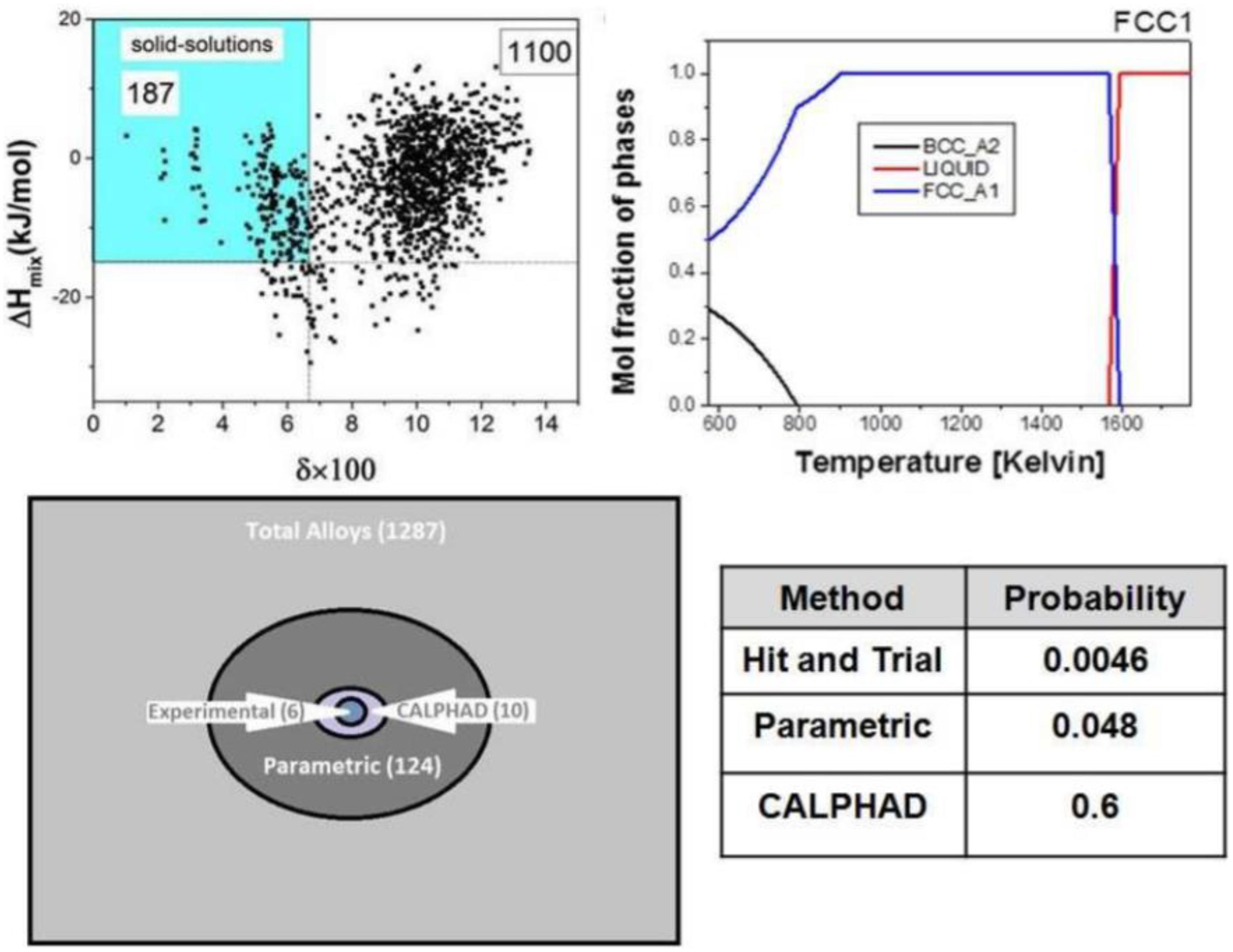
Figure 3. Thermodynamic serendipity in designing single-phase HEAs (Takeuchi et al., 2015).

Not only the single-phase solid-solution alloys, but also the eutectic HEAs can be developed with the aid of CALPHAD. The eutectic Al₁₉.₄Co₂₀.₆Cr₂₀.₆Ni₃₉.₄, Al₁₇.₄Co₂₁.₇Cr₂₁.₇Ni₃₉.₂, and Al₁₆.₀Co₃₈.₆Cr₂₂.₇Ni₂₂.₇ alloys are reported by Wu M. et al. (2020). In the present work, the quinary HEA is split into several pseudo-binary alloy systems. The CoCrNi-NiAl and CoCrNi-CoAl phase diagrams are built, where the CoCrNi is the FCC phase stabilizer and the CoAl or NiAl is an ordered B2 intermetallics provider. Similarly, a phase diagram of NiCo-Cr-NiAl is developed for further analysis. Then, the eutectic point, the eutectic temperature, and the eutectic reaction, etc. can be analyzed through the phase-diagram calculation. Besides the CALPHAD, the eutectic HEAs can also be designed by empirical rules and machine learning (Ding et al., 2017; Wu Q. et al., 2020). Ding et al. (2017) successfully used the empirical parameter S_corr/S_id for prediction, which contributes to single-phase solid solution formation when S_corr/S_id > 0.85. While in the eutectic HEAs, multiple phases are preferred, and the value of the parameter is supposed to be located in 0.7 < S_corr/S_id < 0.85. Transitional elements, such as Co, Cr, Cu, Fe, Ni, are usually act as high-entropy base elements, and a relatively small amount of Al, Nb, and Ti, as the eutectic transforming element. Having similar principles, Wu and colleagues trained an artificial neural network model by combining the literatures results and the CALPHAD calculations for Al-Co-Cr-Fe-Ni system. The use and summary of a large amount of data effectively improves the prediction accuracy. These three methods draw similar conclusions and complement each other to a certain extent.

CLAPHAD enables people to predict the phase diagram bypassing the difficulties of certain experiments (such as the high temperature and high pressure environment). The part that is easy to be calibrated by the experiment can be used to predict the component that is difficult to be calibrated by the experiment, so as to realize the rapid scientific design of materials. However, there are differences between the non-equilibrium solidification structures in experiments and the equilibrium CALPHAD calculations. Moreover, for HEAs, the extrapolation of CALPHAD is usually required, and the appropriate database selection is essential. The semi-empirical CALPHAD itself and the imperfect database may contribute to inaccuracy to some extent.

High-Throughput First-Principles Simulations

Based on the quantum mechanics, the first-principles calculation has capability of calculating the behavior of atoms and electrons in condensed states, and quantitatively describing the atomic bondings. Therefore, theoretically, the properties of any material can be reasonably predicted by first principles, only by solving the Schrodinger equation. However, in fact, there is a strong interaction between atoms and electrons, which will cause a certain degree of deviation when solving the Schrodinger equation. Approximate or hypothetical methods need to be introduced to modify the calculation results.

It has been mentioned that the multiphase structures are difficult to be predicted by the empirical rules, while these alloys may be more attractive due to their multiphase nature and useful properties. Cieslak et al. (2020) studied the effect of Al and Cu content on the different phase structures of Al_xCu_yFeCrNiCo multiphase alloys experimentally and theoretically (Matusiak et al., 2019). The phase stability is revealed by the Korringa-Kohn-Rostoker method with the coherent potential approximation (KKR-CPA) electronic structure calculations, and the reduction of total energy in the decomposition of this alloy is also clear. This calculation may concern any systems, even hypothetical ones that do not exist.

The high-throughput first-principles calculation method has higher accuracy and is more popular in predicting new materials. Curtarolo et al. (2005) calculated the total energy of 176 crystal structures of 80 binary alloys using the first-principles calculation. By comparing the calculation results and experimental data, it was found that 89 compounds have the same structure as the experimental data, confirming the high accuracy of ab initio methods. Then, they further develop a software framework for the high-throughput screening of crystal-structures of alloys, intermetallics, and inorganic compounds, namely AFLOW (Automatic Flow) (Curtarolo et al., 2012). Similar databases also include Open Quantum Materials Database (OQMD) and Materials Project (Behler, 2011; Kirklin et al., 2015). All these first-principles databases provide powerful tools for effective quantum computing material development.

These existing databases of binary phases support the first-principles design of HEAs. Considering the small enthalpic nature of multicomponent solid solutions and the small entropic nature of ordered compounds, only the entropy contributions for the solid-solution alloys and only the enthalpy of formation for the intermetallics can be utilized as a first approximation. To further simplify the calculation, only pairwise combinations can be considered, so that one can make use of the advantage that the structures of a large amount of binary phases have been exhibited in the above databases. It is sufficient to consider only binary systems, in part because alloy species diffuse slowly at typical annealing temperatures, which greatly reduces the possibility of forming more complex compounds.

Based on the above simplified assumptions, Troparevsky et al. (2015) proposed a model that predicts specific combinations of elements most likely to form single-phase HEAs, by setting the upper and lower limits of the enthalpy of formation of binary compounds. The lower limit of this range is set to -T_ann⋅ΔS_mix by the ideal mixing entropy, where T_ann is the annealing temperature used in the experimental setup, and the upper limit of the enthalpy range (37 meV) is selected to include all known single-phase alloys. As shown in Figure 4, alloys with binary formation enthalpy values within the set range can be predicted to form solid-solution structures.

FIGURE 4

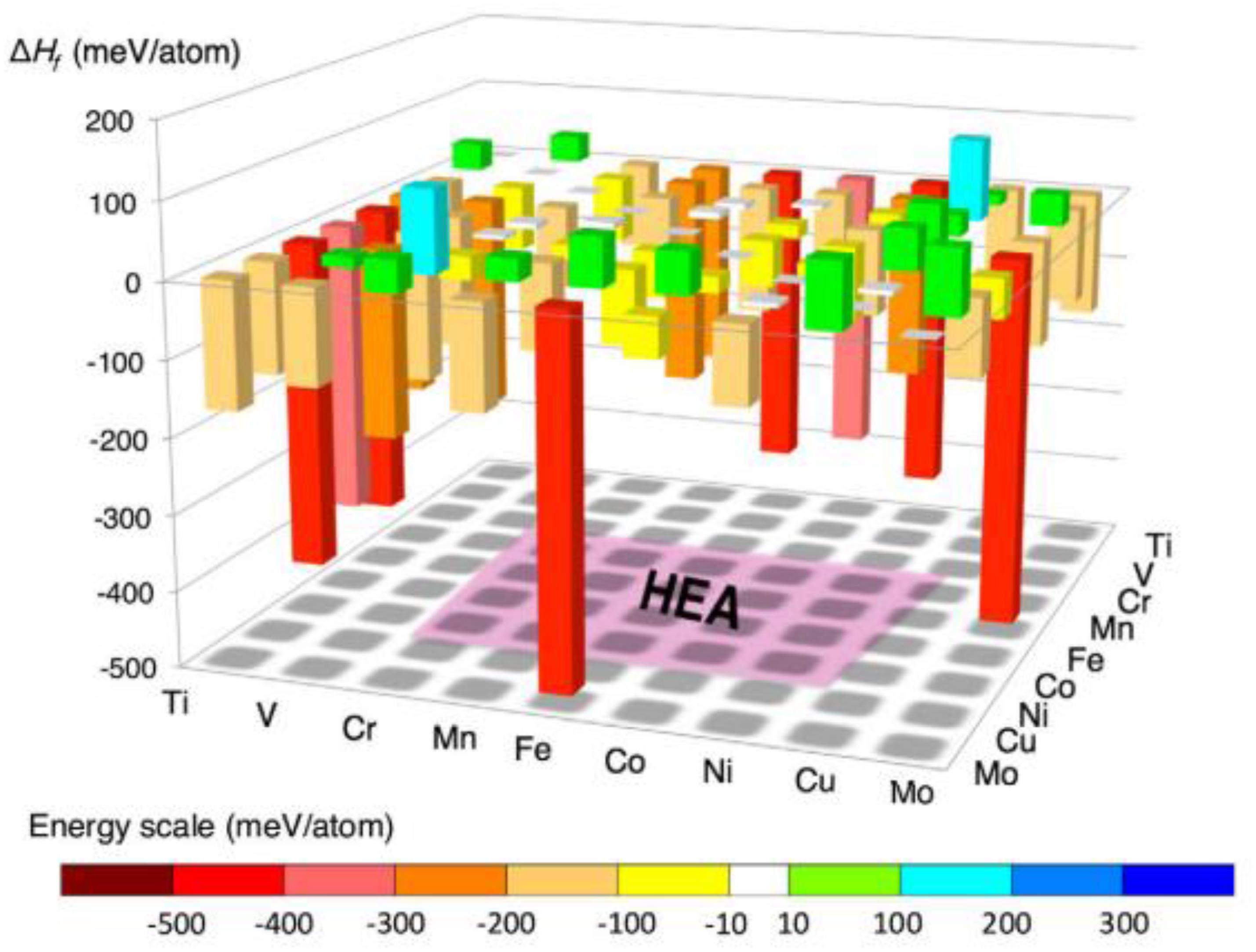
Figure 4. Graphical representation of high-throughput first-principles simulation method (Curtarolo et al., 2005).

Similarly, Tian et al. (2017) predicted four single BCC phases, CrMoW, CrMoWMn, CrMoWNi, and CrMoWCo HEAs by combining the empirical characteristics and the ab initio formation enthalpy. Then, the ab initio method is further employed to calculate the phase stability, elastic modulus, and ideal strength of the present HEAs. They concluded that the BCC structure is more stable than the FCC structure, and the late 3 days transitional elements reduce the mechanical properties of the BCC phase. The increase of the Ni content enhances the tensile plasticity and reduces the intrinsic strength of the CrMoW alloy. These results can guide the design of similar HEAs to a certain extent and reduce the amount of experimentation.

The combination of calculations and available experimental data establishes the connection between structures and properties. It provides the sufficient data information for the design of new materials, and eliminates the process of “trial” and “error,” especially the establishment of several high-throughput calculation databases. However, there are still some deficiencies. On the one hand, its core source code is not fully disclosed, and cannot be modified to meet specific application requirements. On the other hand, the binary alloy database focuses on ordered alloys, but is not completely applicable to disordered alloys.

Machine Learning

The Algorithms of Machine Learning

Machine learning is a state-of-the-art interdisciplinary field, which aims at giving computers the ability to learn automatically. Actually, it can be traced back to the least-square method and Markov chain in the 17th century. In recent years, machine learning has received extensive attention, and it has demonstrated excellent capabilities not only in production and life (Baskar and Kumar, 2018; Kahng, 2018; Ker et al., 2018) but also in materials science to develop new materials, such as Ti-alloy screening, assisted design of single-atom alloy catalysts, and exploration of aluminum-alloy corrosion inhibitors (Agnew et al., 2001; Wu et al., 2019; Dasgupta et al., 2020). The failed experimental data, (Raccuglia et al., 2016) successfully established a reaction model of the inorganic-organic hybrid materials’ crystallization, and predicted the formation of new compounds with an accuracy rate of 89% Raccuglia et al. (2016). This method of mining the valuable information behind large amounts of discarded (“failed”) experimental data promotes the prediction of new materials more efficiently.

The algorithms of machine learning can be generally divided into supervised learning, unsupervised learning, and reinforcement learning. Supervised learning is to compare the prediction results with the actual training data (input data) when building the model, and constantly adjust the parameter until the result reaches an expected accuracy. It is often used to deal with classification and regression. The unsupervised learning aims at finding the internal structure and relationship among data, while the reinforcement learning is often used in the control of dynamic systems and robots.

For the high-throughput screening and composition-property relationship determination of HEAs, supervised-learning algorithms are preferred, among which the support vector machine and artificial neural network are the most commonly used, as shown in Figure 5. The support vector machine is to use a classification hyperplane to divide the data in the high-dimensional space and maximize the interval between positive and negative samples. It can solve the small-sample problems perfectly, but it is only applicable to the classification of two types of tasks. Relatively speaking, artificial neural networks are more widely used in HEAs, which is composed of a large number of nodes (or neurons) connected to each other. Data from the outside world are transferred to the input layer, then extracted to the hidden layers to analyze the system, and finally received by the output layer to produce the result. A node in any layer represents the function: a_j = x_iW_ij + b_j, where W_ij are the weights associated with each input parameter x_i and b_j are the bias terms. The value of a_j is then passed through an activation function. The advantages are high accuracy, strong learning ability, and strong fault tolerance for noisy data, while there are too many parameters, and the learning process is relatively long.

FIGURE 5

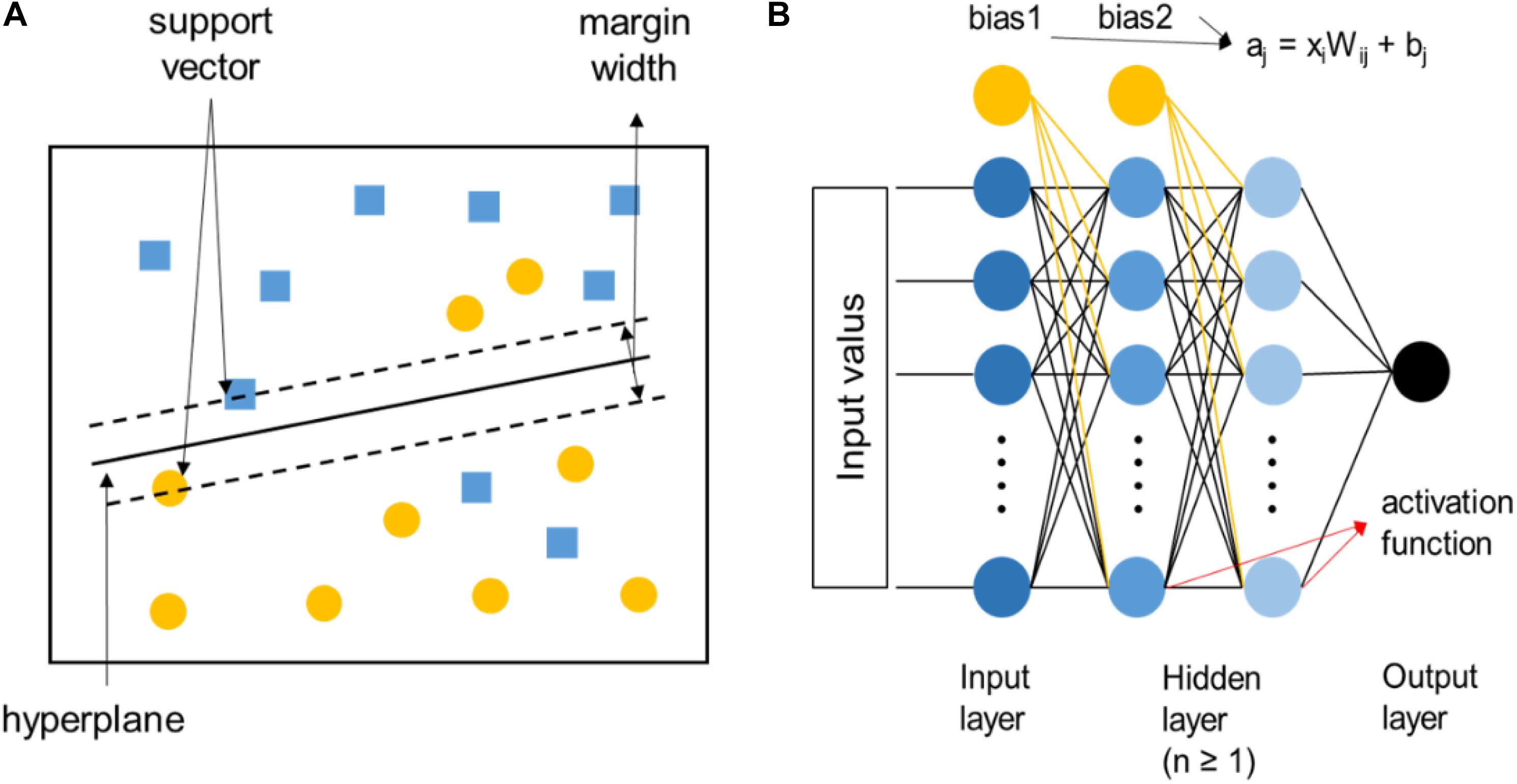
Figure 5. (A) The diagram of the linear support vector machine, where the two different symbols represent two various types of data samples, respectively. (B) The diagram of artificial neural networks.

Phase Selection

Islam et al. (2018) analyzed the correlations among VEC, Δχ, ΔH_mix, ΔS_mix, and δ (these five parameters are defined in Table 1 and see section “Empirical Models”), and trained a neural network model to classify the resulting phases according to the input features. Up to 99% high accuracy is reached in the learning of the full dataset, and the accuracy higher than 80% is obtained in the cross-validation training and testing datasets. On this basis, Huang et al. (2019) studied in depth the guiding role of these five empirical criteria for phase selection, that is more data, more different algorithms, and more hidden layers and neuron in the neural network. They applied three different algorithms to train the model, and found that the artificial neural network predicted the phase structure most accurately. By adopting different combinations of neurons in the hidden layers, the average testing accuracy in classifying the solid solution and intermetallics, the solid solution + intermetallics and intermetallics, and the solid solution and solid solution + intermetallics can reach 86.7, 94.3, and 78.9%, respectively. Both of the above two works claim that the VEC criterion is more important in the phase selection, while this is significantly different from the result of Guo et al. (2011), which claims that VEC can only be used to distinguish the FCC, BCC, and HCP structures.

Similarly based on the empirical rules, Zhou et al. (2019) explored the use of an extended set of new design parameters, including the mean value of atomic radius, melting point, mixing enthalpy, mixing entropy, VEC, electronegativity, and bulk modulus, as well as their corresponding standard deviation value. They extracted the standard deviation from the modeling to clarify the effect of each parameter, as shown in Figure 6. A positive standard deviation means that the phase structure is positively related to this parameter, and vice versa. For solid-solution phases, the atomic-size difference, mixing enthalpy and mixing entropy play the most important roles, while the intermetallics and amorphous phases are most affected by the standard deviation of the enthalpy of mixing, the average atomic radius, and the average melting point. This model predicts that in the selected HEA system, which has a chemical composition of (FeCrNi)_10–x(ZrCu)_x (x = 1, 2, …, 8), the phase will transit from solid solution, to solid solution + intermetallics, to intermetallics + amorphous, and finally to amorphous. They then fabricate the same HEAs through arc melting, vacuum melt spinning, and co-sputtering, and finally conclude that their prediction has cooling rate dependent.

FIGURE 6

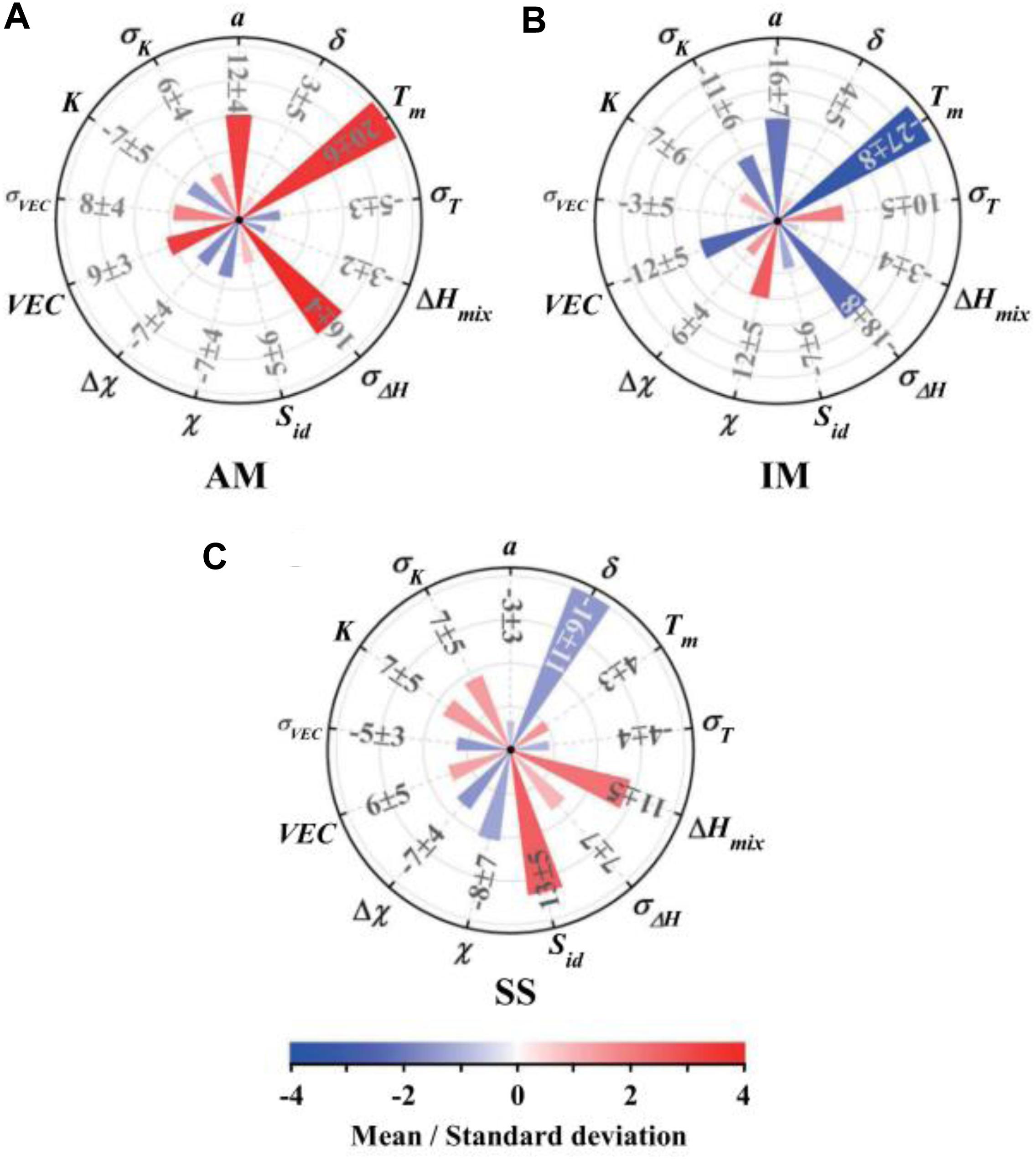
Figure 6. The sensitivity measures of the 13 parameters for (A) amorphous phase, (B) intermetallics, and (C) solid solution based on the result of the artificial neural network model. Here, a, T_m, ΔH_mix, χ, VEC, and K are the mean value of atomic radius, melting point, mixing enthalpy, electronegativity, valence electron concentration, and bulk modulus, respectively. δ, σ_T, σ_{Δ H}, Δχ, σ_VEC, and σ_K are their corresponding standard deviation value, respectively. S_id is the mixing entropy (Agnew et al., 2001).

Mechanical Properties

Molecular dynamics simulations can provide a property database under appropriate ensemble and periodic-boundary conditions. Hence, it is usually combined with machine learning to predict the mechanical properties of HEAs based on their elemental information. It should be noted that the dislocations, twinning, stacking faults, and other microstructural defects are not considered in the simulated properties. Sharma et al. (2017) developed a modified metaheuristic cuckoo search technique combined with molecular dynamics to optimize the composition for the desired high tensile strength. They employ the technique to examine the variation of mechanical strengths in binary Al-Fe, ternary Fe-Ni-Cr, and quinary Al-Cr-Co-Fe-Ni alloys. In the target Al-Cr-Co-Fe-Ni alloy, it is found that with decreasing the Al concentration from 10 to 1% and increasing Fe fraction, the strength of the alloy system increase linearly. However, this trend contradicts the increase of strengths with increasing Al contents in single-phase solid solutions.

Due to the above difference between simulation and experimental results, Zhang et al. (2020) obtained the property database from molecular dynamics and compared eight different machine-learning models, including a deep neural network, extreme learning machine, and support vector machine among others, as shown in Figure 7. The mechanical response database includes 900 single-crystal CuFeNiCrCo samples with different compositions, and the yield stress and Young’s modulus are set as output features of machine learning, which are classified into ‘Good’ and ‘Weak’ based on a benchmark value. By training, developing, and testing, the Kernel-based extreme learning machine model outperforms others for the prediction of mechanical properties. Finally, the accuracy of the optimized model is further verified by the large-sized polycrystal CuFeNiCrCo HEA samples. It was found that the yield stress and Young’s modulus of the equiatomic alloys were at a moderate level compared to non-equiatomic samples. The results are consistent with the predicted situation, that is to say, the effect of changing the element composition on the property is complicated, which may improve or reduce the mechanical properties of the polycrystalline HEA sample.

FIGURE 7

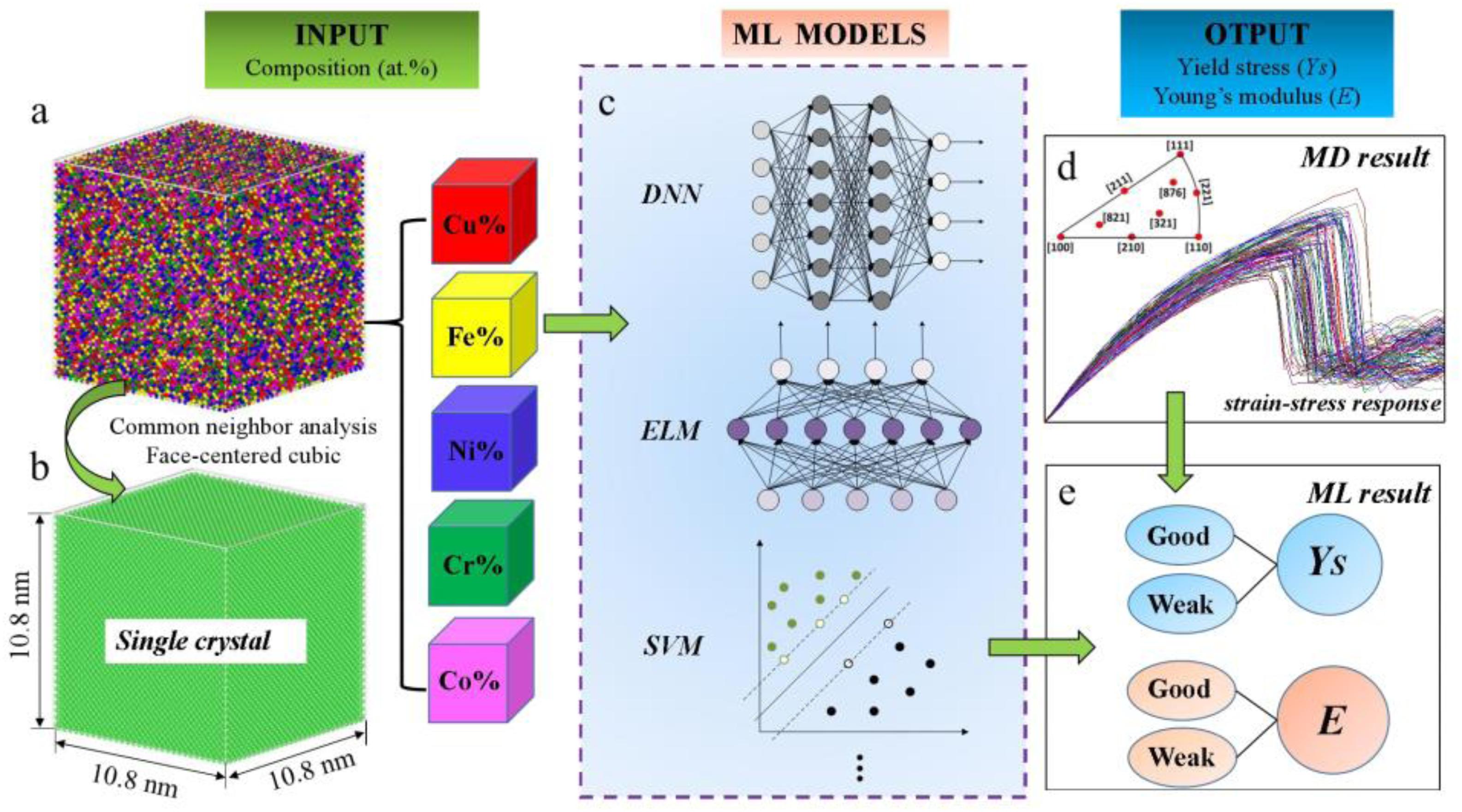
Figure 7. Schematic diagram of molecular dynamics simulation and machine learning methods (Islam et al., 2018). (a) Simulated CuFeNiCrCo single-crystal sample. (b) The CuFeNiCrCo single-crystal sample analyzed by neighbor analysis (CNA) method. (c) Schematic of some machine learning models. (d) Strain-stress curses of single-crystal CuFeNiCrCo samples. (e) Prediction of the mechanical properties by machine learning method.

Besides tensile properties, Wen et al. (2019) trained a surrogate model to learn the hardness-composition relationship of Al-Co-Cr-Cu-Fe-Ni alloys through two iteration loop. A utility function is employed during optimization to balance exploitation and exploration. In the optimized Al₄₃Co₂₂Cr₂₃Fe₇Ni₅ and Al₄₇Co₂₀Cr₁₈Cu₅Fe₅Ni₅, a mixture of BCC structures is revealed by the experiment, which is made up of a BCC solid solution and an ordered B2 structure, and the ordered phase is identified as Al and Ni rich. It is interesting to notice that phase structures of the Al-Co-Cr-Cu-Fe-Ni alloy system has been early studied in depth by the CALPHAD and empirical methods (Zhang et al., 2012). Different screening methods can complement each other, and ultimately achieve a comprehensive prediction of the alloy system.

Consequently, it is clear that machine learning, like the empirical models, is essentially an accumulation and summary. However, it makes visualization and analysis simple toward high-dimensional data space, and provides the possibility to analyze the relative importance of different phase formation rules. As long as a model is trained and updated in time, it can be used flexibly on similar problems. Unfortunately, algorithm selection, parameter adjustment, and training processes are still complicated and time-consuming. Moreover, data are often unusable for the data-driven research due to a lack of standardization at publication.

Prospects and Conclusion

We search 5,000 articles in the Web of Science from 2004 to 2020 on the theme of “high entropy alloys,” and analyze the changes of research keywords with the average appearance time, as shown in Figure 8. Obviously, in addition to mechanical properties, deformation and strengthening, the current field of HEAs has attracted increasing attention to alloy-design methods.

FIGURE 8

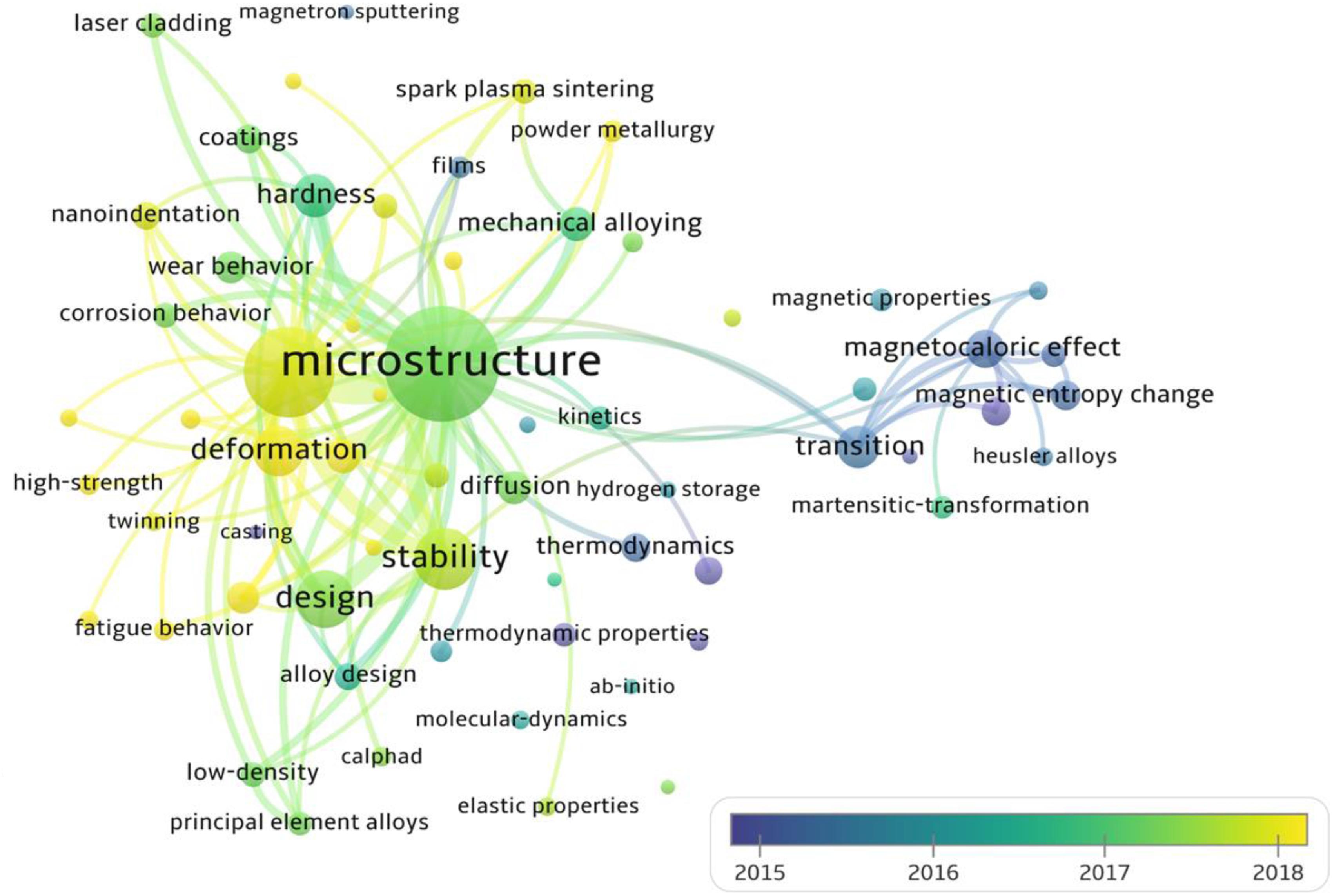
Figure 8. The changes of research keywords with the average time, reflecting the future development directions of HEAs. The search keyword is the “high entropy alloys,” and the total number of article analyses is 5000 from 2004 to 2020 in the Web of Science.

Here, we briefly introduce four different high-throughput calculation approaches, including empirical models based on the Hume-Rothery rules and Pettifor map, first-principles calculations, CALPHAD technique, and machine learning. Among these four methods, machine learning appears the latest, and the amount of research is still very small (Figure 8). The empirical models are developed, based on trying to minimize the differences in the thermodynamic and physical properties of each constituent element. The composition design utilizing the Pettifor map is to employ the structures of most binary constituent alloys to predict the structures of multicomponent alloys, while it has a narrow application range. The CALPHAD technique gives the geometric description of the system under the thermal equilibrium, and can be seemed as the most direct way for compositional design. As for the machine learning, it can solve almost all problems of the HEA design by reasonably selecting algorithms and optimizing parameters. First-principles calculations can provide much atomic information to the CALPHAD and the machine learning, and there are multiple databases creating significant convenience for alloy design. As shown in Table 2, we compare the advantages, disadvantages, and application conditions of these different high-throughput techniques, in order to provide guidance for the selection and design of specific HEA systems in the future.

TABLE 2

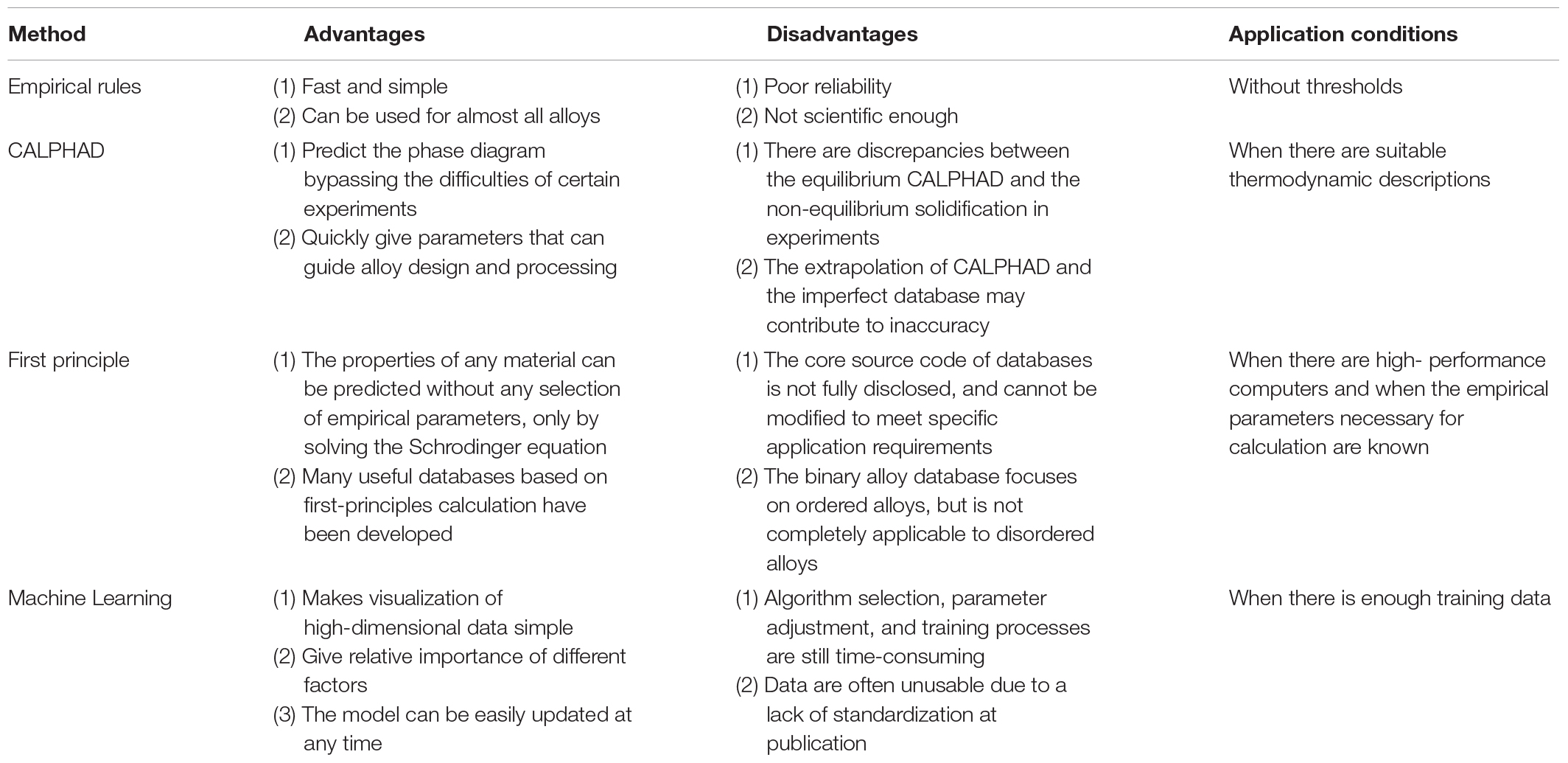
Table 2. Comparison of the advantages, disadvantages, and application conditions of the four different high-throughput calculation techniques for HEA screening.

Different methods can be used to predict the phase structure of the same alloy. For example, the eutectic HEAs can be predicted using the empirical method, CALPHAD, and the machine learning. Although the methods are different, they are all based on phase diagram thermodynamics and summaries, and complement each other, reaching comprehensive prediction of an alloy system. However, these calculation methods are still in the initial stage of exploration. Actually, they cannot fully screen the composition and microstructure space of HEAs, which are mainly due to the usage of empirical or semi-empirical parameters and the difference between experimental and simulation results. For instance, both of the works from Islam and Huang claim that the VEC is more important in the phase selection, while this is significantly different from the result of Guo et al. (2011), which claims that VEC can only be used to distinguish the FCC, BCC, and HCP structures. The former is obtained through machine learning, while the latter is one of the empirical models based on the Hume-Rothery rules. This gap can only be resolved by experiments. As a result, combining experimental results with theoretical guidance for specific target features is a necessary method for screening new HEAs with beneficial properties.

Author Contributions

RL wrote the manuscript with support from PL, LX, WW, and YZ. All authors contributed to the general discussion.

Funding

YZ would like to thank the financial support from National Natural Science Foundation of China (Grant Nos. 51471025 and 51671020), and the project of Al-Mg based medium entropy alloys with Dongguan Eontec company. PL very much appreciates the supports from (1) the National Science Foundation (DMR-1611180 and 1809640) with the program directors, Drs. J. Yang, J. G. Shiflet, and D. Farkas and (2) the U.S. Army Research Office Project (W911NF-13-1-0438 and W911NF-19-2-0049) with the program managers, Drs. M. P. Bakas, S. N. Mathaudhu, and D. M. Stepp. LX would like to thank the financial support from Joint Research Program of Ministry of Education (Grant No. 6141A02022242).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Agnew, S., Yoo, M., and Tome, C. (2001). Application of texture simulation to understanding mechanical behavior of Mg and solid solution alloys containing Li or Y. Acta Mater. 49, 4277–4289. doi: 10.1016/s1359-6454(01)00297-x

CrossRef Full Text | Google Scholar

Baskar, A., and Kumar, T. G. (2018). “Facial expression classification using machine learning approach: a review,” in Data Engineering and Intelligent Computing, eds S. Satapathy, V. Bhateja, K. Raju and B. Janakiramaiah (Berlin: Springer), 337–345. doi: 10.1007/978-981-10-3223-3_32

CrossRef Full Text | Google Scholar

Behler, J. (2011). Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 134:074106. doi: 10.1063/1.3553717

CrossRef Full Text | Google Scholar

Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 37, 213–218. doi: 10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Cao, S., and Zhao, J. C. (2015). Application of dual-anneal diffusion multiples to the effective study of phase diagrams and phase transformations in the Fe-Cr-Ni system. Acta Mater. 88, 196–206. doi: 10.1016/j.actamat.2014.12.027

CrossRef Full Text | Google Scholar

Chen, H. L., Mao, H., and Chen, Q. (2018). Database development and Calphad calculations for high entropy alloys: challenges, strategies, and tips. Mater. Chem. Phys. 210, 279–290. doi: 10.1016/j.matchemphys.2017.07.082

CrossRef Full Text | Google Scholar

Cieslak, J., Tobola, J., and Reissner, M. (2020). The effect of bcc/fcc phase preference on magnetic properties of AlCrFeCoNi high entropy alloys. Intermetallics 118, 12–24.

Google Scholar

Curtarolo, S., Morgan, D., and Ceder, G. (2005). Accuracy of ab initio methods in predicting the crystal structures of metals: a review of 80 binary alloys. Calphad 29, 163–211. doi: 10.1016/j.calphad.2005.01.002

CrossRef Full Text | Google Scholar

Curtarolo, S., Setyawan, W., Hart, G. L. W., Jahnatek, M., Chepulskii, R. V., Taylor, R. H., et al. (2012). AFLOW: an automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 58, 218–226. doi: 10.1016/j.commatsci.2012.02.005

CrossRef Full Text | Google Scholar

Dasgupta, A., Gao, Y., Broderick, S. R., Pitman, E. B., and Rajan, K. (2020). Machine learning aided identification of single atom alloy catalysts. J. Phys. Chem. C 10, 86–98.

Google Scholar

Ding, Z., He, Q., and Yang, Y. (2017). Exploring the design of eutectic or near-eutectic multicomponent alloys: from binary to high entropy alloys. Sci. China Technol. Sci. 61, 159–167. doi: 10.1007/s11431-017-9051-6

CrossRef Full Text | Google Scholar

Fang, S., Xiao, X., Xia, L., Li, W., and Dong, Y. (2003). Relationship between the widths of supercooled liquid regions and bond parameters of Mg-based bulk metallic glasses. J. Non-Cryst. Solids 321, 120–125. doi: 10.1016/s0022-3093(03)00155-8

CrossRef Full Text | Google Scholar

Gludovatz, B., Hohenwarter, A., Catoor, D., Chang, E. H., George, E. P., and Ritchie, R. O. (2014). A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158. doi: 10.1126/science.1254581

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, S., and Liu, C. T. (2011). Phase stability in high entropy alloys: formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 21, 433–446. doi: 10.1016/s1002-0071(12)60080-x

CrossRef Full Text | Google Scholar

Guo, S., Ng, C., Lu, J., and Liu, C. T. (2011). Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 109:103505. doi: 10.1063/1.3587228

CrossRef Full Text | Google Scholar

Gurao, N., and Biswas, K. (2017). In the quest of single phase multi-component multiprincipal high entropy alloys. J. Alloys Compd. 697, 434–442. doi: 10.1016/j.jallcom.2016.11.383

CrossRef Full Text | Google Scholar

He, Q. F., Ding, Z. Y., Ye, Y. F., and Yang, Y. (2017). Design of high-entropy alloy: a perspective from nonideal mixing. JOM 69, 2092–2098. doi: 10.1007/s11837-017-2452-1

CrossRef Full Text | Google Scholar

Huang, W., Martin, P., and Zhuang, H. L. (2019). Machine-learning phase prediction of high-entropy alloys. Acta Mater. 169, 225–236. doi: 10.1016/j.actamat.2019.03.012

CrossRef Full Text | Google Scholar

Islam, N., Huang, W., and Zhuang, H. L. (2018). Machine learning for phase selection in multi-principal element alloys. Comput. Mater. Sci. 150, 230–235. doi: 10.1016/j.commatsci.2018.04.003

CrossRef Full Text | Google Scholar

Kahng, A. B. (2018). “Machine learning applications in physical design,” in Proceedings of the 2018 International Symposium on Physical Design, Monterey, CA, 68–73.

Google Scholar

Ker, J., Wang, L., Rao, J., and Lim, T. (2018). Deep learning applications in medical image analysis. IEEE Access 6, 9375–9389.

Google Scholar

King, D. J. M., Middleburgh, S. C., McGregor, A. G., and Cortie, M. B. (2016). Predicting the formation and stability of single phase high-entropy alloys. Acta Mater. 104, 172–179. doi: 10.1016/j.actamat.2015.11.040

CrossRef Full Text | Google Scholar

Kirklin, S., Saal, J. E., Meredig, B., Thompson, A., Doak, J. W., Aykol, M., et al. (2015). The open quantum materials database (OQMD): assessing the accuracy of DFT formation energies. npj Computa. Mater. 1, 1–15.

Google Scholar

Li, R. X., Liaw, P. K., and Zhang, Y. (2017). Synthesis of AlxCoCrFeNi high-entropy alloys by high-gravity combustion from oxides. Mater. Sci. Eng. A 707, 668–673. doi: 10.1016/j.msea.2017.09.101

CrossRef Full Text | Google Scholar

Liang, Y. J., Wang, L., Wen, Y., Cheng, B., Wu, Q., Cao, T., et al. (2018). High-content ductile coherent nanoprecipitates achieve ultrastrong high-entropy alloys. Nat. Commun. 9:4063.

Google Scholar

Liu, W. H., Lu, Z. P., He, J. Y., Luan, J. H., Wang, Z. J., Liu, B., et al. (2016). Ductile CoCrFeNiMox high entropy alloys strengthened by hard intermetallic phases. Acta Mater. 116, 332–342. doi: 10.1016/j.actamat.2016.06.063

CrossRef Full Text | Google Scholar

Marshal, A., Pradeep, K. G., Music, D., Zaefferer, S., De, P. S., and Schneider, J. M. (2017). Combinatorial synthesis of high entropy alloys: introduction of a novel, single phase, body-centered-cubic FeMnCoCrAl solid solution. J. Alloys Compd. 691, 683–689. doi: 10.1016/j.jallcom.2016.08.326

CrossRef Full Text | Google Scholar

Matusiak, K., Berent, K., Marciszko, M., and Cieslak, J. (2019). The experimental and theoretical study on influence of Al and Cu contents on phase abundance changes in AlCuFeCrNiCo HEA system. J. Alloys Compd. 790, 837–846. doi: 10.1016/j.jallcom.2019.03.162

CrossRef Full Text | Google Scholar

Matysik, P., Czujko, T., and Varin, R. A. (2014). The application of Pettifor structure maps to binary metal hydrides. Int. J. Hydrogen Energy 39, 398–405. doi: 10.1016/j.ijhydene.2013.10.104

CrossRef Full Text | Google Scholar

Pettifor, G. D. (1986). The structures of binary compounds. J. Phys. C Solid State Phys. 19:285.

Google Scholar

Poletti, M. G., and Battezzati, L. (2014). Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems. Acta Mater. 75, 297–306. doi: 10.1016/j.actamat.2014.04.033

CrossRef Full Text | Google Scholar

Raccuglia, P., Elbert, K. C., Adler, P. D. F., Falk, C., Wenny, M. B., Mollo, A., et al. (2016). Machine-learning-assisted materials discovery using failed experiments. Nature 533, 73–76. doi: 10.1038/nature17439

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranganathan, S., and Inoue, A. (2006). An application of Pettifor structure maps for the identification of pseudo-binary quasicrystalline intermetallics. Acta Mater. 54, 3647–3656. doi: 10.1016/j.actamat.2006.01.041

CrossRef Full Text | Google Scholar

Senkov, O. N., Miller, J. D., Miracle, D. B., and Woodward, C. (2015). Accelerated exploration of multi-principal element alloys with solid solution phases. Nat. Commun. 6:6529.

Google Scholar

Senkov, O. N., and Miracle, D. B. (2016). A new thermodynamic parameter to predict formation of solid solution or intermetallic phases in high entropy alloys. J. Alloys Compd. 658, 603–607. doi: 10.1016/j.jallcom.2015.10.279

CrossRef Full Text | Google Scholar

Senkov, O. N., Wilks, G. B., Miracle, D. B., Chuang, C. P., and Liaw, P. K. (2010). Refractory high-entropy alloys. Intermetallics 18, 1758–1765.

Google Scholar

Sharma, A., Singh, R., Liaw, P. K., and Balasubramanian, G. (2017). Cuckoo searching optimal composition of multicomponent alloys by molecular simulations. Scr. Mater. 130, 292–296. doi: 10.1016/j.scriptamat.2016.12.022

CrossRef Full Text | Google Scholar

Takeuchi, A. (2016). Recent progress in alloy designs for high-entropy crystalline and glassy alloys. J. Jpn. Soc. Powder Powder Metall. 63, 209–216. doi: 10.2497/jjspm.63.209

CrossRef Full Text | Google Scholar

Takeuchi, A., Amiya, K., Wada, T., and Yubuta, K. (2015). Alloy design for high-entropy alloys based on Pettifor map for binary compounds with 1:1 stoichiometry. Intermetallics 66, 56–66. doi: 10.1016/j.intermet.2015.06.014

CrossRef Full Text | Google Scholar

Takeuchi, A., and Inoue, A. (2006). Analyses of characteristics of atomic pairs in ferrous bulk metallic glasses using classification of bulk metallic glasses and pettifor map. J. Optoelectron. Adv. Mater. 8, 1679–1684.

Google Scholar

Takeuchi, A., Wada, T., and Zhang, Y. (2017). MnFeNiCuPt and MnFeNiCuCo high-entropy alloys designed based on L10 structure in Pettifor map for binary compounds. Intermetallics 82, 107–115. doi: 10.1016/j.intermet.2016.12.002

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., and Vitos, L. (2017). Predicting single phase CrMoWX high entropy alloys from empirical relations in combination with first-principles calculations. Intermetallics 83, 9–16. doi: 10.1016/j.intermet.2016.12.007

CrossRef Full Text | Google Scholar

Troparevsky, M. C., Morris, J. R., Kent, P. R. C., Lupini, A. R., and Stocks, G. M. (2015). Criteria for predicting the formation of single-phase high-entropy alloys. Phys. Rev. X 5:11041.

Google Scholar

Wang, Z., Huang, Y., Yang, Y., Wang, J., and Liu, C. T. (2015). Atomic-size effect and solid solubility of multicomponent alloys. Scr. Mater. 94, 28–31. doi: 10.1016/j.scriptamat.2014.09.010

CrossRef Full Text | Google Scholar

Welk, B. A., Williams, R. E., Viswanathan, G. B., Gibson, M. A., Liaw, P. K., and Fraser, H. L. (2013). Nature of the interfaces between the constituent phases in the high entropy alloy CoCrCuFeNiAl. Ultramicroscopy 134, 193–199. doi: 10.1016/j.ultramic.2013.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, C., Zhang, Y., Wang, C., Xue, D., Bai, Y., Antonov, S., et al. (2019). Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 170, 109–117. doi: 10.1016/j.actamat.2019.03.010

CrossRef Full Text | Google Scholar

Wu, C. T., Chang, H. T., Wu, C. Y., Chen, S. W., Huang, S. Y., Huang, M., et al. (2019). Machine learning recommends affordable new Ti alloy with bone-like modulus. Mater. Today 34, 41–50. doi: 10.1016/j.mattod.2019.08.008

CrossRef Full Text | Google Scholar

Wu, M., Wang, S., Huang, H., Shu, D., and Sun, B. (2020). CALPHAD aided eutectic high-entropy alloy design. Mater. Lett. 262:127175. doi: 10.1016/j.matlet.2019.127175

CrossRef Full Text | Google Scholar

Wu, Q., Wang, Z., Hu, X., Zheng, T., Yang, Z., He, F., et al. (2020). Uncovering the eutectics design by machine learning in the Al–Co–Cr–Fe–Ni high entropy system. Acta Mater. 182, 278–286. doi: 10.1016/j.actamat.2019.10.043

CrossRef Full Text | Google Scholar

Yang, M., Yan, D., Yuan, F., Jiang, P., Ma, E., and Wu, X. (2018). Dynamically reinforced heterogeneous grain structure prolongs ductility in a medium-entropy alloy with gigapascal yield strength. Proc. Natl. Acad. Sci. U.S.A. 115, 7224–7229. doi: 10.1073/pnas.1807817115

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, T., Zhao, Y., Tong, Y., Jiao, Z., Wei, J., Cai, J., et al. (2018). Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys. Science 362, 933–937. doi: 10.1126/science.aas8815

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X., and Zhang, Y. (2012). Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 132, 233–238. doi: 10.1016/j.matchemphys.2011.11.021

CrossRef Full Text | Google Scholar

Ye, Y. F., Liu, X. D., Wang, S., Liu, C. T., and Yang, Y. (2016a). The general effect of atomic size misfit on glass formation in conventional and high-entropy alloys. Intermetallics 78, 30–41. doi: 10.1016/j.intermet.2016.08.005

CrossRef Full Text | Google Scholar

Ye, Y. F., Wang, Q., Zhao, Y. L., He, Q. F., Lu, J., and Yang, Y. (2016b). Elemental segregation in solid-solution high-entropy alloys: experiments and modeling. J. Alloys Compd. 681, 167–174. doi: 10.1016/j.jallcom.2016.04.239

CrossRef Full Text | Google Scholar

Ye, Y. F., Wang, Q., Lu, J., Liu, C. T., and Yang, Y. (2015). Design of high entropy alloys: a single-parameter thermodynamic rule. Scr. Mater. 104, 53–55. doi: 10.1016/j.scriptamat.2015.03.023

CrossRef Full Text | Google Scholar

Yeh, J. W., Chen, S. K., Lin, S. J., Gan, J. Y., Chin, T. S., Shun, T. T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303. doi: 10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Zhang, C., Zhang, F., Chen, S., and Cao, W. (2012). Computational thermodynamics aided high-entropy alloy design. JOM 64, 839–845. doi: 10.1007/s11837-012-0365-6

CrossRef Full Text | Google Scholar

Zhang, L., Qian, K., Schuller, B. W., Lu, C., Shibuta, Y., and Huang, X. (2020). Prediction of mechanical properties of non-equiatomic high-entropy alloy by atomistic simulation and machine learning. arXiv [Preprint] Avaliable online at: https://arxiv.org/ftp/arxiv/papers/2004/2004.04439.pdf

Google Scholar

Zhang, Y., Zhou, Y. J., Lin, J. P., Chen, G. L., and Liaw, P. K. (2008). Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 10, 534–538. doi: 10.1002/adem.200700240

CrossRef Full Text | Google Scholar

Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93.

Google Scholar

Zhou, Z., Zhou, Y., He, Q., Ding, Z., Li, F., and Yang, Y. (2019). Machine learning guided appraisal and exploration of phase design for high entropy alloys. npj Comput. Mater. 5:128.

Google Scholar