- 1Department of Physics, The University of Texas at Arlington, Arlington, TX, United States
- 2Department of Physics, Jazan University, Jazan, Saudi Arabia
- 3Department of Physics, University of Hafr Al Batin, Hafr Al Batin, Saudi Arabia
Silicon carbide (SiC) is a technologically significant material. A recent report on the abundance of C60 fullerenes in interstellar space, along with the presence of SiC precursors, sparked interest in potentially similar SiC nanostructures. C60 fullerene was found experimentally and is an exceptionally stable form of carbon. As Si and C have similar valence electron properties, it has been long envisioned that Si and SiC could also form similar fullerene-type structures. In this paper, Si30C30 fullerene-derived clusters were studied from the first principle, starting from an ideal Si60 fullerene template with various arrangements of silicon and carbon atoms and then relaxing them without any symmetry constraint. Hydrogen passivation was considered as well to model the effect of ligands that may be available during chemical synthesis processes. We have found that, after passivation, the relative stability of different configurations of Si30C30 clusters changed compared to the unpassivated structures, while some structures collapsed. We have also noticed several Si–Si and Si–C double bonds in the unpassivated structures. Upon relaxation, some Si atoms lost their hydrogen, while carbon atoms capture those hydrogen atoms. Finally, we tested the endohedral doping of a transition metal, tungsten atom, to stabilize and magnetize Si30C30. With hydrogen passivation, the magnetic moment on W atom was enhanced. Overall, the effects of passivation on these fullerene structures are not very straightforward.
Introduction
Due to the similar valence electronic structures of Si and C, there are reports on silicon fullerene being similar to C60 fullerene. However, it is well known that the hollow-cage-type clusters by Si are not energetically preferred configurations, as compact structures are usually preferred due to sp3 bonding. In some earlier studies, the Si60 clusters were simulated with the same symmetry as C60. The results showed significant distortions and that Si60 was not nearly as stable as C60 (Li et al., 2000; Menon, 2001; Sun et al., 2003; Wang et al., 2006; Bainglass et al., 2017). A recent study showed that, for Si60, a lower energy structure could be achieved by a triangular-shaped structure with three Si20 units at the vertices (Bainglass et al., 2017) rather than by a hollow cage structure. Cage-like clusters are desirable because the hollow of the cage can be used for endohedral doping. Several endohedral dopants in the Si cages were considered to stabilize fullerene-like structures and to produce materials with tailored properties (Hiura et al., 2001; Kumar and Kawazoe, 2001). Some of these endohedral transition-metal-doped nanostructures can exhibit magnetic properties as well. Besides that, it has been proposed that the spin property of the doped atoms inside the cage can be utilized in spintronics applications (Zhu and Khanna, 2012; Wang and Liu, 2016).
For similar reasons, as mentioned above, it is tempting to construct SiC fullerene structures. Silicon carbide is a technologically important material, for example, in power electronics (Gorai et al., 2019) and for device applications in extreme conditions (Cheung, 2006; Wijesundara and Azevedo, 2011). In addition, a recent astrophysical finding of the abundance of C60 fullerenes in interstellar space also sparked interest in SiC clusters. SiC nanoclusters formed near dead stars were proposed as the precursor for the formation of these interstellar C60 fullerenes under certain conditions (Candian, 2019). It is possible, for example, for some other intermediate “deformed fullerene” SimCn (m + n = 60) structures to be formed before turning into C60 or other carbon-based clusters.
Silicon carbide clusters were observed experimentally as well as studied theoretically (Flores and Largo-Cabrerizo, 1987; Nakajima et al., 1995; Fye and Jarrold, 1997; Pellarin et al., 1997, 1999; Yamamoto and Asaoka, 2001; Ray and Huda, 2006; Li et al., 2011; Huda and Ray, 2012; Song et al., 2013; Anafcheh and Ghafouri, 2014; Huda, 2014; Yong et al., 2014). The theoretical studies by Srinivasan et al. (2005, 2006) on Si60C2n (n = 1, 2), Si40C20, Si36C24, and Si60C20 showed that the SiC clusters were more stable than the bare Si60 cage and further reported that the stability of the cluster depended on the carbon atoms’ configurations inside or on the surface of the cages. It also reported that the Si–C interactions significantly affected the stability of the cages as compared to the C–C interactions. A similar conclusion was reached for these sizes of SiC clusters by Matsubara et al. (2006) by noting, in an alternate manner, that the higher number of Si atoms away from the Si–C interface increases the instability of the structure. On the other hand, studies on Si12C12 clusters showed that the stability of these structures was due to the maximizing strong C–C bonds in the segregated carbon region, minimizing the weaker Si–Si bonds in the segregated silicon regions and the Si–C bonds which are at the interface (Duan and Burggraf, 2015).
Smaller SiC cage-type structures were reported as well; for example, a highly stable SiC cluster consists of an eight-atom silicon cube with a carbon dimer inside it (Huda and Ray, 2004a). In another theoretical study, various stable isomers of Si20 cages were reported, where carbon atoms were put inside these cages; it was reported that ionic interactions play an important role in the stabilization and the symmetrization of these Si20Cn cages (Huda and Ray, 2004b). On the other hand, starting from a set of smaller C20 fullerene structures, Si atoms were put systematically on the C20 fullerene surfaces. These set of SimCn (m + n = 20) clusters were then studied computationally (Huda and Ray, 2008). It was found that, even though SiC fullerene could not be formed starting from C-fullerene, the process provided some interesting thermodynamically stable structural motifs. In fact, both studies provided several useful metastable cage structures.
It is worth noting that it is customary to identify the ground-state structure for a given size of cluster with the first principle density functional theory (DFT) calculations. However, metastable structures can be stabilized during synthesis via kinetic processes, such as stabilization by surface energy or by surface passivations. For example, even though diamond is the ground-state structure for the bulk Si, ultra-small Si nanocrystals can be stabilized in wurtzite form, especially by hydrogen passivation on its surface (Mayfield and Huda, 2013). One such example for Si30C30 clusters can be found in this work as well, where a less stable isomer becomes more stable due to passivation. On the other hand, the synthesis route can influence the favorability of one structure upon the other (Abreu et al., 2015). In addition, the relative thermodynamic stability of a structure obtained by DFT is at 0 K. In contrast, at a higher temperature, a highly stable structure can be dynamically unstable, and in comparison, a relatively less stable structure can become dynamically more stable (Scipioni et al., 2011).
In this paper, we have considered Si30C30 clusters with various arrangements of silicon and carbon atoms, starting from a Si60 fullerene structure with icosahedral symmetry and then relaxing those configurations without any symmetry constraint. These structures were relaxed without and with hydrogen passivation, where only Si atoms were passivated. The goal of this study is to understand the effect of hydrogen passivation on SiC fullerene’s stability. Note that the aim was not to predict the ground-state structure of the similar-sized SiC clusters. Previous studies (Wang et al., 2006) showed that Si60H60 is energetically stable with high symmetry due to the strong interaction between Si and H. On the other hand, it has also been demonstrated that Si60H60 is less stable than Si60 because the H atoms, while encouraging sp3 bonds with Si, take away the sp2-bond-like feature from the Si60 Si–Si bond network (Bainglass et al., 2017). In addition, the literature review above shows inconsistent reports regarding the relative importance of C–C, Si–C, and Si–Si bonds on the stability of the SiC cage-type structures. These questions will be addressed in this study, with emphasis on how passivation impacts these bonds. Finally, a representative transition metal, W, was incorporated in the most stable Si30C30 cluster to study its impact on cluster stability along with hydrogen passivation. Brief comments will be made regarding the magnetic properties of the Si30C30 structure within the scope of this study with the transition metal doped in it. For the transition metal, only the tungsten atom is considered. The rationale for selecting the W atom was that W has six valence electrons, and it has almost the same electronegativity as the Si atoms, with first ionization potential of about 8 eV. So, it is expected that the W atom will retain its spin moment inside the cage. In fact, this was also one of the first atoms that were encapsulated in Si cages experimentally (Hiura et al., 2001).
Computational Method
The DFT (Kohn et al., 1996), with B3LYP hybrid functional (Becke, 1993) as implemented in the Gaussian 09 suite of codes (McLean and Chandler, 1980), was employed to study the Si60, Si30C30, and Si30C30H30 fullerenes and fullerene-derived structures. The atomic wave functions were populated by the atomic centered all-electron 6-311G basis set. Binding energy (Eb), highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and several structural features were calculated. The binding energy (Eb) values were calculated with respect to the infinitely separated atomic limit, namely by:
where E(si), E(C), and E(SimCn) and are total energies of the Si and C atoms and the SimCn clusters in their respective ground-state spin multiplicities; m and n are the numbers of Si and C atoms in the SimCn clusters, and for this study, m = n = 30. A negative number will imply a thermodynamically stable configuration; the more negative a binding energy is, the more stable a structure is. For hydrogen-passivated structures, the modified formulas will be discussed in a later section. The basis set and hybrid functional used here have been used in several earlier studies, including in one of our studies (Bainglass et al., 2017), and yielded reasonable results. To test here, we have considered several dimers’ bond lengths. The computed bond lengths for Si–C, Si–Si, and C–C are 1.76, 2.38, and 1.32 Å, respectively, and the corresponding experimental values are 1.72, 2.35, and 1.34 Å (Bernath et al., 1988; Lide, 1990), respectively. Besides that, as we have computed the hydrogenated SimCn structures as well, we have calculated the relaxed SiH4 and CH4 molecules. The calculated Si–H and C–H bond lengths are 1.49 and 1.09 Å, whereas the corresponding experimental values are 1.49 and 1.08 Å (Chase et al., 1982; Park et al., 2006), respectively. These numbers show very good agreements between our calculated and experimental geometric features. Therefore, the relaxed structures in this study, both passivated and unpassivated, represent reliable configurations to study their structural and electronic properties.
Finally, for W-doped Si30C30, we used the LANL2DZ basis set (Chiodo et al., 2006) as available in Gaussian 09 package, keeping the B3LYP functional. Such a method for W is justified in previous publications (Sun et al., 2002). The binding energy was calculated in a similar approach as in Eq. (1):
here l is the number of W atoms inside the Si30C30 cluster; for the present study, we considered l = 1 and 2. Tungsten atomic energy, E(W), is in its lowest energy spin-state. For Si30C30Wl, we have only considered the lowest energy structure of Si30C30 obtained in this study and its passivated counterpart.
Results and Discussion
Si30C30 Fullerene
Structural Analysis
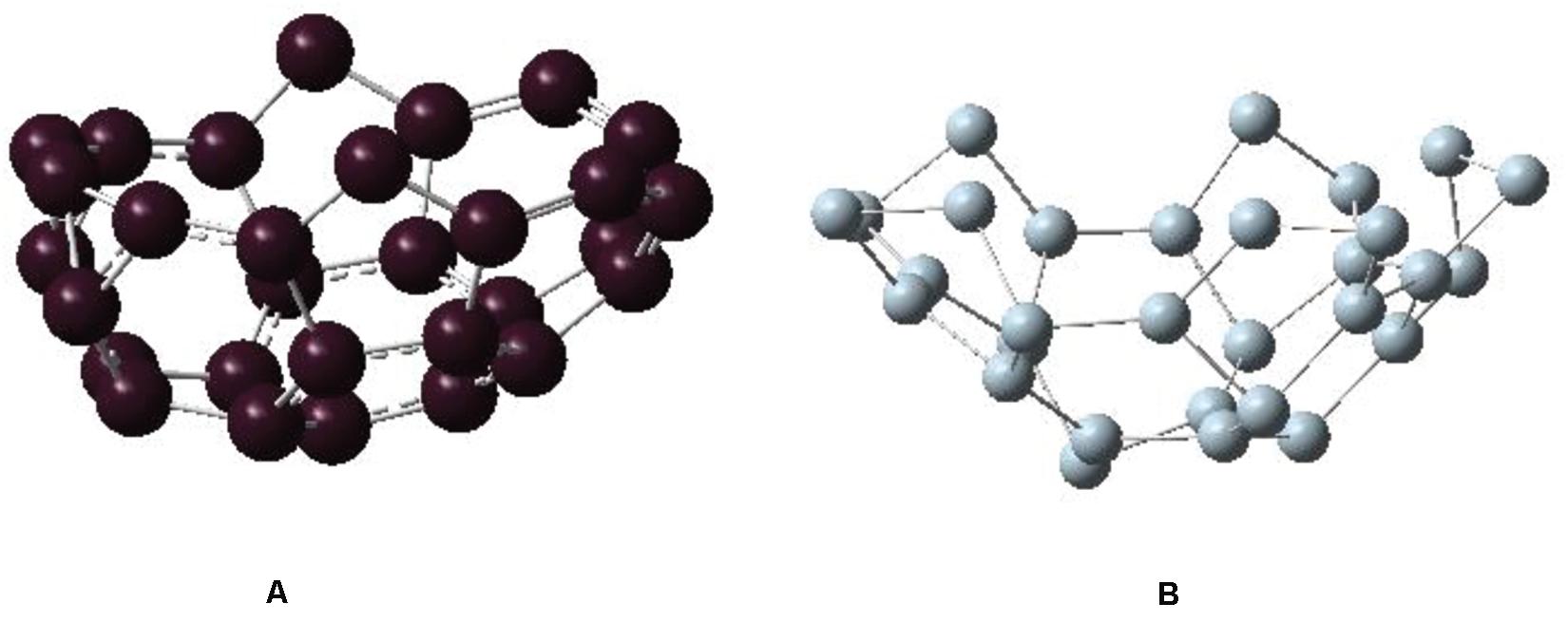
The well-known C60 fullerene cage has 20 hexagons and 12 pentagons with icosahedral symmetry. Figure 1 shows a relaxed Si60 structure with the same symmetry. This is the only structure in this study that was relaxed with symmetry constraints. As a result, the final structure remained a fullerene structure; in general, it has been reported that a fully relaxed structure of Si60 is usually a distorted one (Li et al., 2000; Menon, 2001; Wang et al., 2006). The average bond length of Si60 in Figure 1 is 2.03 Å. The purpose of symmetry-constrained relaxation was that the relaxed fullerene Si60 was used as a template to construct the Si30C30 structures to be studied in this paper.
Figure 1. Si60 fullerene relaxed with symmetry constraint. This structure was used as a template to construct the other Si30C30 configurations.
As mentioned in the introduction, earlier silicon carbide clusters based on Si60 fullerene resulted in highly distorted structures. Among those, some SiC structures maintained cage-like features. For the present study, to build Si30C30, the first step was to take the symmetry-restricted relaxed Si60 fullerene, and then 30 carbon atoms replaced 30 Si atoms at different possible configurations. Due to differences in the electronic properties of Si–Si and C–C bonds, SiC fullerene-like structures do not have high symmetry (Srinivasan et al., 2006; Huda et al., 2009). The relaxed Si30–C30 configurations that have been investigated in this study are shown in Figure 2. Note that all these Si30C30 structures, although started from an ideal Si60 fullerene structure, relaxed completely without any symmetry constraint. Table 1 shows the binding energies, HOMO–LUMO gaps, and bond lengths for these Si30C30 structures.
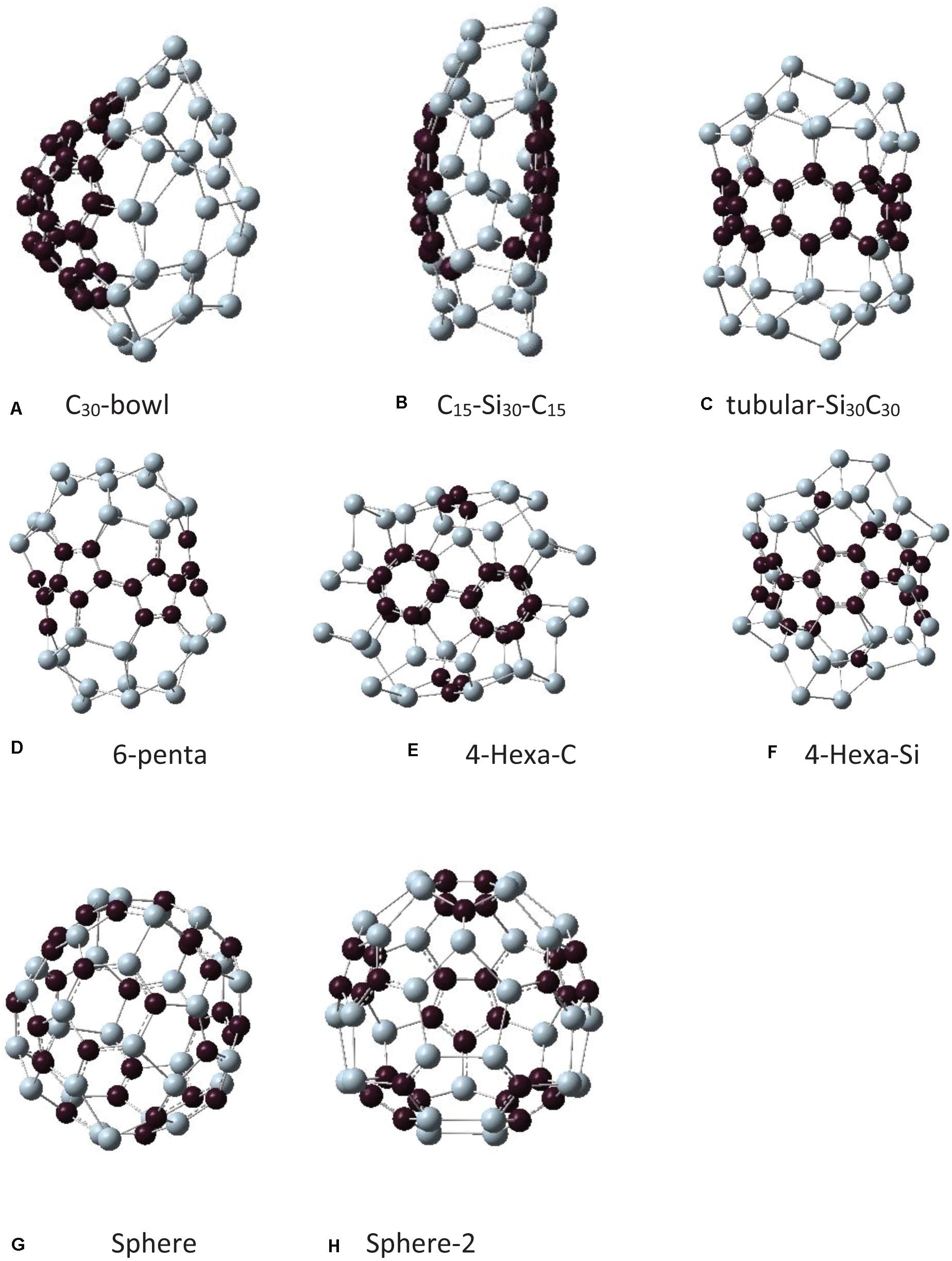
Figure 2. Different isomers of the Si30C30 structures obtained from Figure 1 and then relaxed completely without any symmetry constraint. The names of these structures are explained in the text. Structures are presented from panels (A–H) in order of their stability, most to least stable.
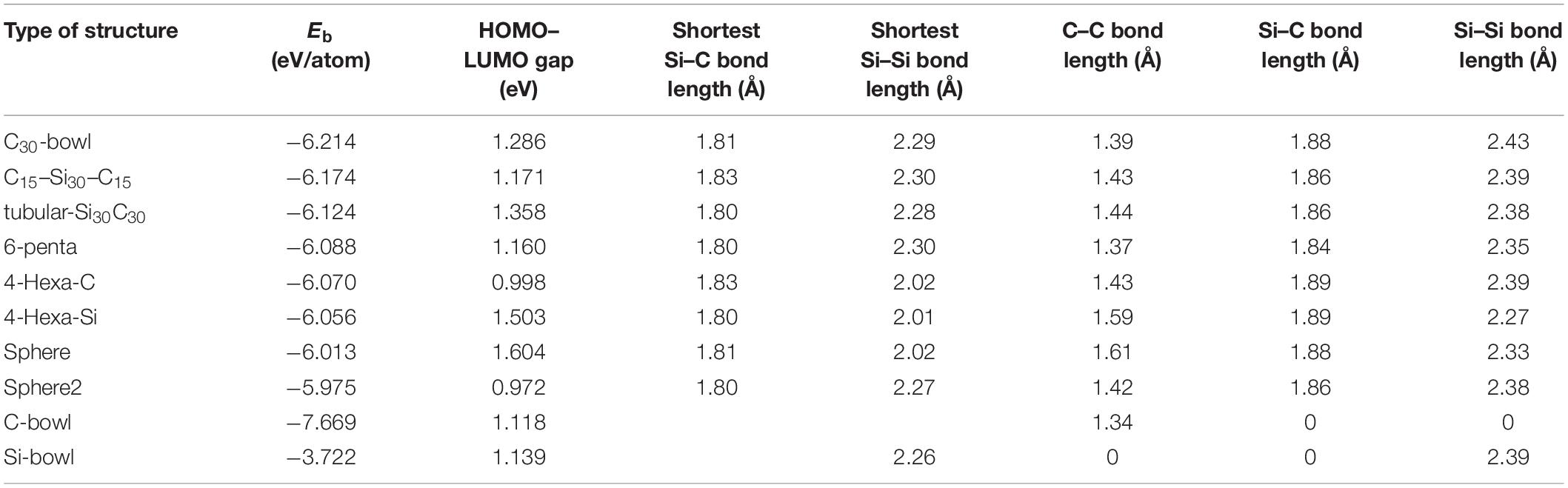
Table 1. The following table shows the binding energies (Eb), highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gaps, the shortest Si–Si, Si–C bond lengths, and the average bond lengths of Si–C, C–C, and Si–Si bonds for different configurations of Si30C30 structures.
As the initial geometry was a fullerene structure, in the structure the Si atoms will have unsaturated 3-fold coordinated bonds, where the Si atoms are supposed to make π-bonds and the bond lengths are too large to Si-p orbital’s side-wise overlap. To passivate these unsaturated bonds, hydrogen atoms were added to each Si atom in the unrelaxed Si30C30 fullerenes initially and then optimized completely (Si30C30H30); the initial set of structures was the same as for those in Figure 2, but here with passivating H atoms. The relaxed set of passivated structures is shown in Figure 3. After relaxation, in some structures, a few Si atoms lost passivating H atoms, and these H atoms then re-boned with nearby C atoms. Hence, these H atoms also act as an indicator to investigate the local bonding coordination and configurations. The binding energies, the HOMO–LUMO gaps, and the bond lengths for Si30C30H30 are given in Table 2.
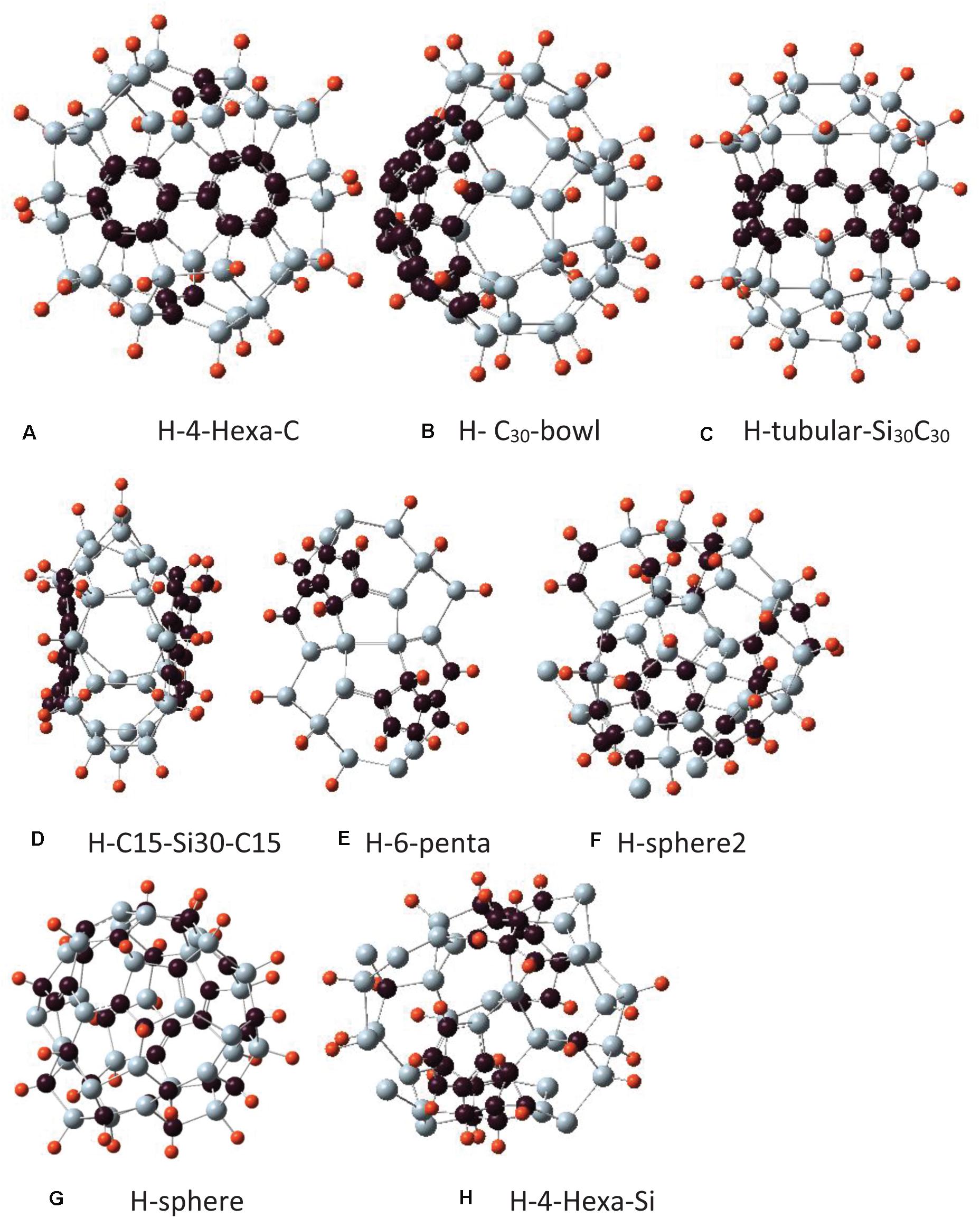
Figure 3. Different isomers of Si30C30 structures with hydrogen passivation, Si30C30H30, where hydrogen atoms bonded with the 3-fold coordinated Si atoms on the Si30 side of the surface. The Si30C30 configurations and the naming conventions are the same as in Figure 2. For hydrogen passivation, each cluster name has an H prefix. Structures are presented from panels (A–H) in order of their stability, most to least stable.
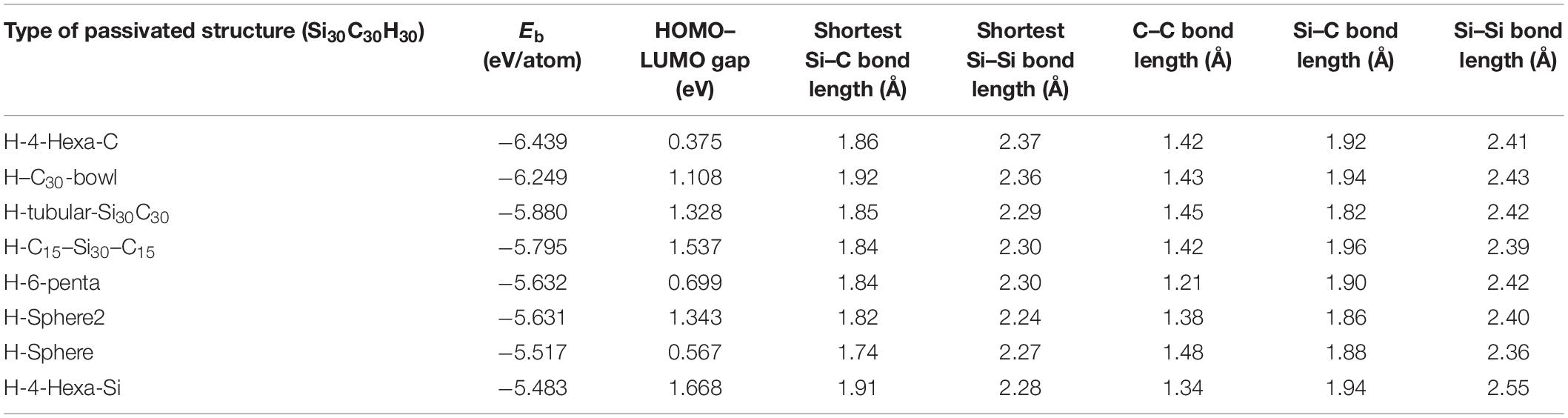
Table 2. The following table shows the binding energies (Eb), the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gaps, the shortest Si–Si, Si–C bond lengths, and average C–C, Si–C, and Si–Si bond lengths of the passivated structure Si30C30H30.
Nomenclature
In the following discussion, each structure in Figure 2 will be assigned a name to facilitate further discussions. In Figure 3, the initial structures were the same as in Figure 2, but with added H passivations, so the names in Figure 3 have an H prefix with each of them. The structures in Figures 2, 3 are arranged in order of their relative stability. In the remaining discussion of the paper, these names will be referred to when discussing these structures.
The first one in Figure 2A is the C30-bowl structure: the left side of this structure has 30 carbon atoms making a bowl-like configuration, and 30 Si atoms are on the right of it. The initial Si60 fullerene was segregated with 30 C and 30 Si atoms and then relaxed entirely without any symmetry constraints. The 30 carbon atoms relaxed into almost half of the C60 fullerene sphere. The C30-bowl structure has Si–C bonds only at the two segregated regions’ boundary. There are 10 Si–C bonds with an average of 1.88 Å.
In Figure 2B, the structure C15–Si30–C15 is presented, where 15 C atoms make caps in the left and the right ends of the fullerene cage and the 30 silicon atoms are in the middle. In Figure 2C, a similar model was constructed, but this time the 15 silicon atoms are located in the right and the left end, and the 30 atoms of carbons are in the middle of fullerene, Si15–C30–Si15. However, because of the shape of the relaxed structure, we named it as a tubular-Si30C30 structure. Both structures have 18 Si–C bonds with the same average bond lengths of 1.86 Å.
The next structure in Figure 2D is named as 6-penta, where C atoms substituted six pentagons in Si60, and the rest were Si atoms. In this structure, there are Si and C pentagons, and the others are Si–C hexagons. There are 18 Si–C bonds with an average bond length of 1.84 Å.
In Figure 2E, the structure is named 4-Hexa-C, where we select the four hexagon faces in the diagonally opposite sides of Si60 fullerene sphere (front and back in the viewing direction), replaced by carbon atoms, and three carbon atoms at the top and bottom in the pentagon faces of that fullerene. In Figure 2F, a complementary structure of Figure 2E was constructed, where the positions of Si and C were swapped. We call it 4-Hexa-Si. The final relaxed structures of these two configurations are significantly different, as seen in Figures 2E,F. However, the total Si–C bonds in these two structures are the same, 30, with equal average bond lengths of 1.89 Å.
In Figures 2G,H, we model the structures to minimize the number of C–C and Si–Si bonds and to maximize the number of Si–C bonds. In the structure, as shown in Figure 2G, the Si and the C atoms were placed alternately on Si60 fullerene as much as possible, however, there remained some Si–Si and C–C bonds in the structure. The relaxed structure was somewhat a spherical one; therefore, we named it as sphere. The total number of Si–C bonds is 56 for this structure with an average bond length of 1.88 Å. The last structure that we tried in this group is shown in Figure 2H, where the structure starts with a pentagon face by silicon atoms (the frontal pentagon). The next neighbor atoms were replaced by carbon atoms and, after that, the next neighbors were kept as silicon atoms and went on alternating until the structure ends with the pentagon face of carbon atoms (the back pentagon). So, in this structure, two diagonally opposite pentagons are made up of Si and C atoms, respectively. This structure also preserves its spherical nature, and we named it sphere-2. The total number of Si–C bonds in this structure is 60, the highest in all the Si30C30 configurations studied in this paper. The average Si–C bond length here is 1.86 Å.
The hydrogen-passivated structures are presented in Figure 3. They were constructed in the same way as described above, with added hydrogen on the Si atoms; hence, these passivated Si30C30H30 structures are named with an H-prefix.
Electronic Properties
The relaxed C30-bowl structure in Figure 2A shows the distortion in the Si30 side, as expected. The reason is the tendency for Si atoms to form sp3 bonds with each other, as compared to the favorability of sp2 in C–C bonds. On the C-side, the C30 bowl remained almost a part of the C60 fullerene, except at the boundary where the Si–C bonds formed. The average bond length of C–C is 1.39 Å, and the average Si–C bond length is 1.88 Å (presented in Table 1). The experimental value of the S = C double bond length was reported to be 1.77 Å (Bravo-Zhivotovskii et al., 2008), which is close to the shortest S–C bond length of 1.81 Å in this structure, as listed in Table 1. The bond length of this structure compares well with previously published values for a similar structure also calculated by DFT (Matsubara and Massobrio, 2005). The binding energy of this structure was −6.214 eV/atom, which is the most stable one in the unpassivated group of structures studied here. This structure is more stable than the previously studied similar Si and C segregated Si40C20 and Si36C24 fullerene-derived structures with binding energies of −4.748 and −4.977 eV/atom, respectively (Srinivasan et al., 2005). A trend that emerges from these three segregated silicon carbide structures is that, as C atoms are increasing in the carbon side, the clusters’ stabilities become higher. All these three structures have dipole moments of about 1.4 D, so the orbital charge distribution is not spherical, indicating a polar nature of the structure. A similar conclusion was reached by Matsubara and Massobrio (2006), where they also found this Si30C30 configuration as the one with the lowest energy.
Figure 2B shows the relaxed C15–Si30–C15 structure, where two groups of 15 carbon atoms are placed on the right and the left side of the fullerene. These two C15 caps consist of two hexagons and two pentagons, and they almost became flat upon relaxation, not like the C15 bowls. As a result, the 30 Si atoms are spread out almost in a bi-layer structure with two C15 caps in the middle of each layer, with a bi-layer separation distance of 4.55 Å for C–C distance and, around the edge, the shortest Si–Si distance was 2.38 Å. The shortest Si–C bond length is 1.80 Å; the average of the C–C bond length in a layer is also 1.44 Å. This structure is the second stable fullerene-derived structure with Eb of −6.174 eV/atom and HOMO–LUMO gap of 1.171 eV.
Due to the strong C–C bonds and weak Si–Si bonds in the tubular-Si30C30, the 30 carbon atoms tightened the fullerene around the middle, and the silicon atoms that located on the caps extended a little bit without breaking the Si–Si bond, and the structure looks like a closed tube. The Eb is −6.124 eV/atom, with −0.050 eV higher than C15Si30C15. However, the Si and the C atom distribution is more symmetric than the previous structures, as is evident by the lower dipole moment, with a reduction of about 50% and with a less polar structure.
The relaxed 6-penta is shown in Figure 2D, and it has a binding energy of −6.088 eV/atom. The average C–C bond length in this structure is 1.37 Å, the lowest among all Si30C30 structures considered in Table 1, whereas the average Si–C bond length was also lower at 1.84 Å. This structure has a similarity with the previous structure of Figure 2C tubular-Si30C30, the main difference being that 6-penta has 30 C atoms as pentagons around the middle. Although lower in stability, 6-penta is higher in symmetry and with a very low dipole moment of 0.13 D.
The 4-Hexa-C structure shows the distorted open structure because some Si–Si bonds broke while relaxing the structure (Figure 2E). The binding energy is 0.144 eV/atom higher than the most stable structure in Table 1, and it has a smaller value of the HOMO–LUMO gap of 0.998 eV. Its complementary structure is the 4-Hexa-Si structure shown in Figure 2F, where the Si atoms were switched with C atoms in 4-Hexa-C. The 4-Hexa-Si has a higher binding energy of −6.056 eV/atom; however, the binding energy difference between these two structures is only 0.014 eV/atom. It also has a higher HOMO–LUMO gap of 1.503 eV. It also does not show distorted open structure as was found in 4-Hexa-C structure with a smaller average Si–Si bond length of 2.27 Å, which is 0.12 Å lower than that of 4-Hexa-C. The average Si–C bond length for these two structures is the same, 1.89 Å; it is the largest Si–C bond length of all relaxed structures in Table 1. These two structures have zero dipole moments, implying that the effective negative and positive charge centers coincide at the center of these two cages. This also signifies an overall “spherical” nature of orbital charge distributions for these two structures.
The structure named sphere in Figure 2G is 12.060 eV higher in energy compared to that of the most stable C30-bowl, which agrees well with the total energy difference value between two similar structures obtained by Scipioni et al. (2011). In our calculation, this sphere structure has the largest HOMO–LUMO gaps of 1.605 eV. The last structure is shown in Figure 2H, sphere-2. It has the highest Eb of −5.975 eV/atom, hence the least stable and with the lowest HOMO–LUMO gap of 0.972 eV, as presented in Table 1. These last two almost spherical Si30C30 structures have a binding energy difference of 0.038 eV/atom. After relaxing these two configurations, we found that, even though the apparent spherical nature of fullerene was not significantly distorted like the other configurations in this study, the orbital charge distributions were significantly distorted. The dipole moments were 2.15 and 3.20 D, respectively, for sphere and sphere-2 structures.
All the structures discussed above have no higher spin state, that is, they have a spin multiplicity of one. The range of binding energy within the scope of this study is −6.089 ± 0.080 eV/atom, which implies that the fullerene-derived Si30C30 structures overall are very stable. The Si–C bond lengths remained consistent across the structures, with an average value of 1.868 ± 0.017 Å. In addition, the binding energy trend follows the increasing number of C–C bonds in the structures. Figure 4 represents such a plot, which shows that the stability of the structures increases as the number of C–C bond increases in the Si30C30 structures considered for this study. Except for the two least stable structures on the top-left corner of the plot, all the structures follow the trend. For these two structures, sphere and sphere-2, they have the least number of C–C bonds and the highest number of Si–C bonds; these are the most polar structures. A competition between the covalent and the ionic bonding changes the trend for these two structures.
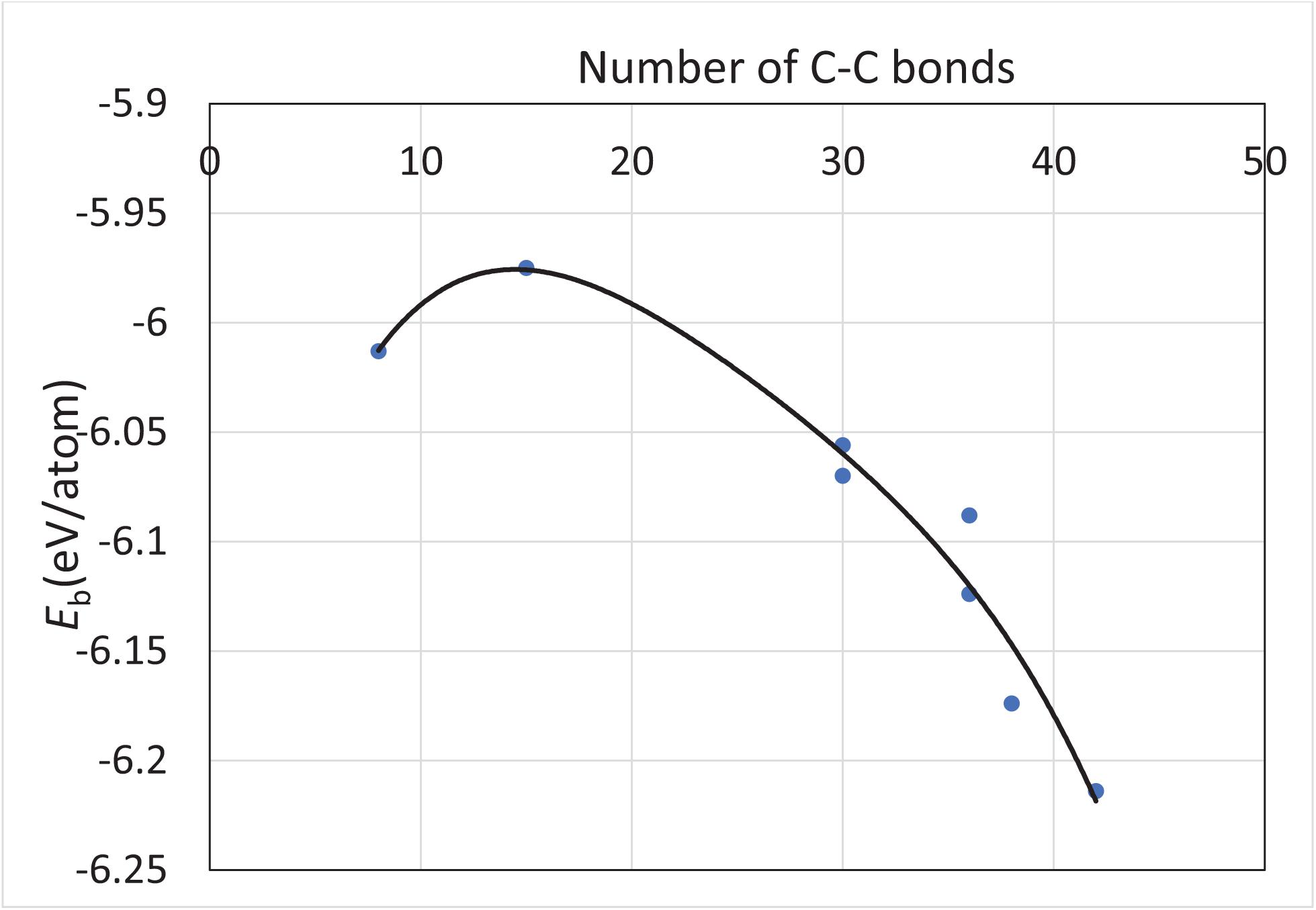
Figure 4. The trend of the binding energy of unpassivated structures with respect to the number of C–C bonds in the structures from Figure 2. The solid line is a polynomial fit of the calculated binding energies represented by the solid circular dots. Except for the two least stable structures on the top-left corner of the plot, all the structures follow the trend that the stability of a structure increases as the number of C–C bonds increases in that structure.
So far, we have found that C30-bowl configuration, with segregated Si and C atoms, is the most favorable one for Si30C30 cage structure within this study. We now ask the question on how the pre-relaxed input precursor structures impact the relative stability of this configuration. To investigate, we considered C30 and Si30 “half-fullerene” as two bowl structures separately, as shown in Figures 5A,B, respectively. The binding energy for C30 is −7.669 eV/atom, and it has HOMO–LUMO gap of 1.118 eV; the Si30 structure is relatively less stable with a higher binding energy of −3.722 eV/atom and with a slightly higher HOMO–LUMO gap of 1.139 eV, all of which are listed in Table 1. Then, we put these two Si30 and C30 half-fullerene at a distance of 5 Å apart, as shown in Figure 6. After full relaxation, these two “half-fullerenes” came together and made the bond between Si and C atoms at the periphery of these two bowl structures, with a final relaxed distorted Si30C30 configuration. This configuration, named as Si30–C30-bowl, has a binding energy of −6.130 eV/atom and HOMO–LUMO gap of 1.046 eV. The main difference between the Si30–C30-bowl and the C30-bowl structures in Figure 2A is the initial structure: before relaxation, the initial structure for C30-bowl was constructed from a relaxed Si60 fullerene. The C30-bowl has −0.084 eV/atom more stable than the Si30–C30-bowl structure. In Si30–C30-bowl, the carbon part of the structure is also more distorted than the C30-bowl. The two approaches for obtaining a similar segregated Si30C30 configuration shows that (i) due to different initial conditions, even the stronger part of the structure, here the C30 part, can be susceptible to distortions and (ii) initial conditions also determine the final stability of the clusters. Hence, in selecting the precursors while synthesizing these clusters, initial conditions need to be optimized.
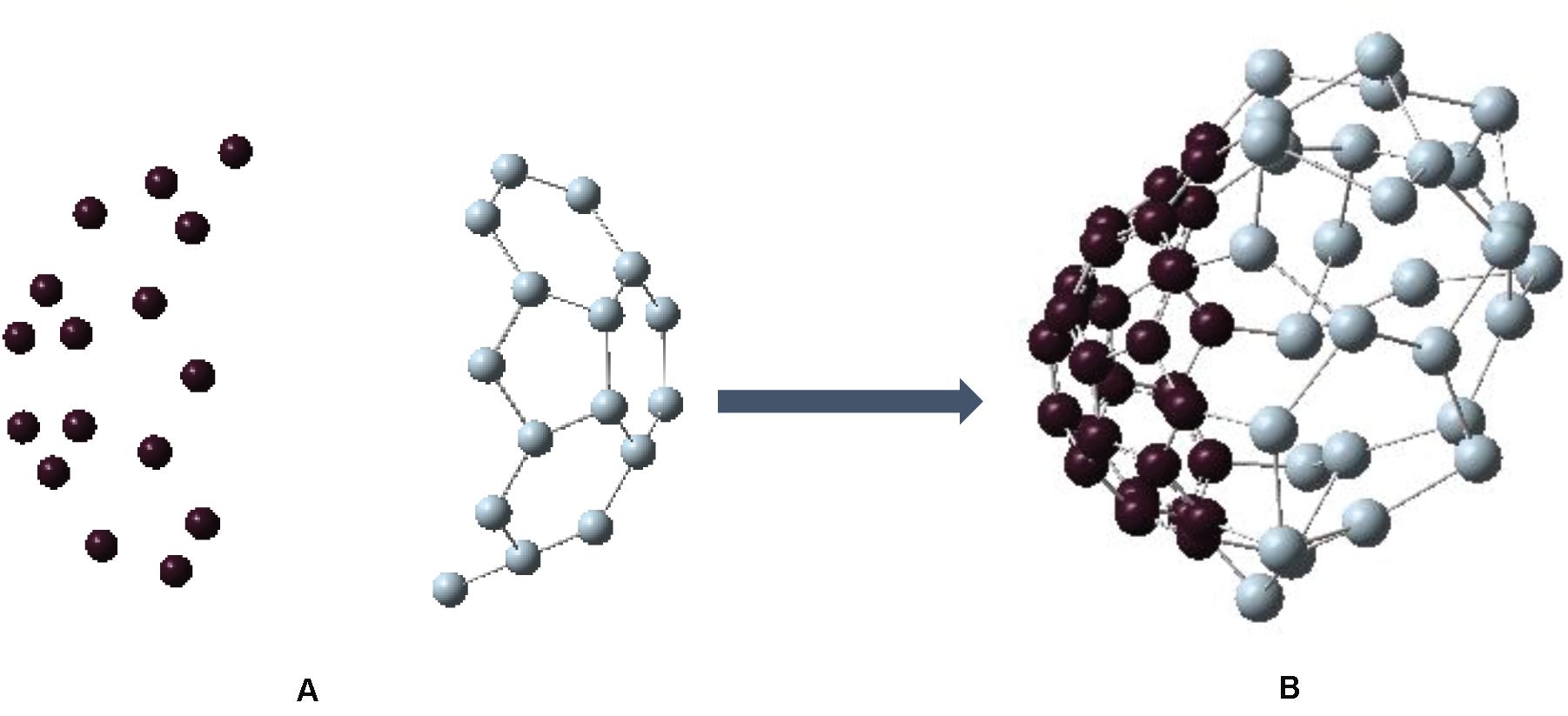
Figure 6. (A) Initial configuration of fullerene with a left bowl of carbon (C30) and a right bowl of silicon (Si30) with 5-Å distance between them. (B) The structure after geometry relaxation. This configuration is similar to Figure 1A. However, the carbon side looks more distorted due to the different initial conditions.
The Hydrogen-Passivated Fullerene
Under passivation, the fullerene structures relaxed differently compared to their unpassivated counterparts. We note here again that the initial structures were the same as for the unpassivated ones, as presented in Figure 2; the difference is that, for the passivated initial fullerene configuration, each Si atom was bonded with an additional hydrogen atom. Upon relaxation, some of the passivated structures have shown interesting behaviors, such as some hydrogen atoms breaking bonds with the Si atoms and then re-bonding with nearby C atoms. This phenomenon resulted in significant structural changes as compared to their unpassivated counterparts. Hence, the relative stability order of the structures changed due to H-passivation, as can be found from comparing the binding energies in Tables 1, 2.
To estimate the stabilities of the passivated structures, we calculated the binding energies of Si30C30H30 in the following way: First, we calculated the energy of the carbon–hydrogen bond [E(C−H)b] by removing a hydrogen atom from the surface of a passivated structure that was bonded with a carbon atom and calculating the energy of the remaining structure without relaxing. Then, this energy and the energy of a hydrogen atom was subtracted from the total energy of the passivated structure [E(Si30C30H30)] to provide the energy value of [E(C−H)b] (Eq. 3). Second, similarly, by removing a hydrogen atom bonded with a Si atom, we have calculated the term [E(Si−H)b] as in Eq. 4. If there are n number of C–H bonds and m number of Si–H bonds, [nE(−H)b + mE(Si−H)b] is the binding energy contributed by H-related bonding to the structures, and (n + m) = 30. The idea here is to take out the hydrogens’ contribution to the binding energy from the passivated Si30C30 clusters. Now, given that the total atomic energies of b and d numbers of Si and C atom, [bE(Si) + dE(C)], the binding energy of the Si30C30H30 structures is calculated by the following equations:
where E(…) refers to the total energy of the system indicated in parenthesis; also b = 30 and d = 30; hence, b + d = 60.
The results of Eb and HOMO–LUMO gaps of the relaxed passivated structures are listed in Table 2. The H-4-Hexa-C structure in Figure 3A shows the most stable structure with hydrogen passivation, with Eb of −6.439 eV/atom and with a significantly lower HOMO–LUMO gap of 0.375 eV. The higher stability is mainly because the hydrogen-passivated Si atoms have 4-fold coordination and created a favorable sp3-like bonding environment. Among all the hydrogen-passivated structures in this study, this is the one of the two structures where all the 30 Si atoms are 4-fold coordinated and the 30 C atoms are 3-fold coordinated. Hence, the two C hexagons on each side of the structure have adopted a flatter configuration due to C–C sp2 bonding, and hydrogenated silicon atoms occupy the curved edge sides with sp3 bonds. Therefore, the initial Si30C30 sphere became a squashed structure by carbon hexagons from both sides. The stability of H-4-Hexa-C increased significantly compared to its unpassivated counterpart 4-Hexa-C (Figure 2E). Even though stability increased by −0.369 eV/atom due to hydrogen passivation, the dipole moment increased by 0.16 D compared to its unpassivated structures.
The second most stable passivated structure was found to be the H–C30-bowl structure (Figure 3B), with a binding energy of −6.249 eV/atom. The passivation helped to reduce the distortion on the silicon side as compared to the unpassivated C30-bowl structure. The relaxed H–C30-bowl has four H atoms migrated to make C–H bonds. These four hydrogen atoms made bonds with the neighboring carbon atoms, and the Si–C–H bonds made a sp3 bonding environment. The value of the HOMO–LUMO gap of the H–C30 H–C30-bowl structure is 1.108 eV. Passivation for this structure also increased the dipole moment by 0.97 D, with a total dipole moment of 2.64 D. The higher dipole moment in a cluster usually implies a relatively higher contribution of ionic properties in overall bonding.
The H-tubular-Si30C30 structure (Figure 2C) shows that all H atoms are still bonded with Si atoms after relaxation, and the final structure looks like a dumbbell-shaped structure, as the 30 carbon atoms in the middle slightly tighten the structure. The binding energy is −5.880 eV/atom, and the HOMO–LUMO gap is 1.328 eV, with a significantly short Si–Si average bond length of 2.29 Å. In the following discussion, we will show, by analyzing the HOMO plots, that some of these bonds may qualify for Si–Si double bonds. In this structure, hydrogen passivation reduces the dipole moment by 0.10 D when compared to its unpassivated counterpart.
Figure 2D shows the H–C15–Si30–C15 structure, where the C15 units squeezed the structure from the right and the left sides of the fullerene. Some of the carbon atoms from these two C15-units has significant distortions after relaxation; as a result, 12 hydrogen atoms broke bonds with silicon atoms and created new bonds with unsaturated carbon atoms, with seven hydrogen atoms on one side and five on the other. Higher C–H bonds show here a higher order of distortions. The number of Si–C bonds in the unpassivated structure (Figure 2B) was 18; after the passivation, the number of Si–C bonds reduced to 14. This shows significant reconfigurations within the structure after hydrogen passivation; as a result, the passivated structure is less stable by 0.979 eV/atom as compared to the unpassivated one (C15–Si30–C15). The passivated structure has HOMO–LUMO gap of 1.537 eV, and the dipole moment of this structure is 3.81 D.
The H-6-penta structure in Figure 3E has an easily recognizable symmetry; there is a vertical mirror plane, and the two sides are then related by the mirror reflection and a 180° rotation, which results in an inversion symmetry. Due to the inversion symmetry, this is the only hydrogen-passivated structure with a dipole moment of 0.00 D. The silicon atoms around the middle tightened the passivated relaxed structure. The mid-section Si atoms lose their hydrogen atoms to the carbon atoms, as those Si atoms are 4-fold coordinated. Each side of the H-6-penta structure has three pentagon faces of carbon atoms, which bonded with three hydrogen atoms. This structure loses four Si–C bonds upon passivation, as does the previous structure. However, here some Si atoms, which lost hydrogen, bonded with each other to make the mid-section 4-fold coordination as seen in Figure 3E. This structure has binding energy of −5.632 eV/atom and HOMO–LUMO gap of 0.699 eV.
Figure 3F presents the H-sphere2 structure, which distorted significantly after relaxation; its distortions are quite evident from the fact that 19 hydrogen atoms rebounded with carbon atoms after relaxation. Therefore, the bonding features have been significantly changed as well throughout the surface of the structure. In addition, it has the highest dipole moment among all the Si30C30 structures considered here, about 6.00 D. Note that sphere2 (Figure 3H) has the highest dipole moment of 3.20 D in their respective unpassivated structure group as well. The H-sphere2 structure has binding energy of −5.631 eV/atom and HOMO–LUMO gap of 1.343 eV.
For H-sphere in Figure 3G, the stability decreased by 0.922 eV/atom, and the HOMO–LUMO gap increased by 0.192 eV compared to the most stable structure H-4-Hexa-C. No significant distortion was found in this structure after relaxing; in fact, it remained like a spherical cage. In addition, the average Si–C bond length, 1.74 Å, listed in Table 2, is smaller than the value of Si = C double bond length reported in earlier literature (Matsubara and Massobrio, 2005; Bravo-Zhivotovskii et al., 2008), which was 1.77 Å. Hence, the H-sphere structure has some Si = C double bonds in it. Even though 16 hydrogen atoms migrated to carbon atoms from Si atoms, the structure remains mostly spherical.
The least stable H-4-Hexa-Si structure is presented in Figure 3H; it is a distorted passivated structure. In this structure, 21 hydrogen atoms broke bonds with silicon atoms and re-bonded with carbon atoms. There were 30 Si–C bonds in 4-Hexa-Si structure, whereas H-4-Hexa-Si has 23 of them after passivation. The unpassivated 4-Hexa-Si also has zero dipole moment with inversion symmetry, while with passivation, it gained a moment of 5.42 D. These are indications of the extent of distortions. The binding energy is −5.483 eV/atom and the HOMO–LUMO gap is 1.668 eV. Its stability is the lowest and the gap is the highest among all the Si30C30 structures considered here.
A note regarding the migration of hydrogen atoms from the silicon atoms to the carbon atoms: The starting template of Si30C30 was Si60 fullerene, where all the Si atoms are 3-fold coordinated, and all bond lengths, involving both Si and C, are equal to Si60 fullerene’s Si–Si bond length. Silicon atoms do not prefer 3-fold coordinated bonds among themselves. So, to provide their favorable sp3 bonding environment, each Si atom in Si30C30 was passivated with one hydrogen atom. On the other hand, upon relaxation, the C30 part of Si30C30 remains 3-fold coordinated and creates almost a local environment of a half-fullerene of C60. Now, first, usually Si–Si and Si–C bonds are too large to allow for double bonds. However, due to the configurational effect in some structures, upon relaxation, some of the Si–C and Si–Si distances shorten enough to make double bonds. When a double bond is made involving a Si atom, that Si atom may not need the previously attached hydrogen atom. As a result, Si–H bonds became weaker during relaxation. Second, when a carbon atom near a Si atom favors sp3 bonds due to a local distortion in structure, it gets the hydrogen from the Si atom as a C–H bond is much favorable than a Si–H bond. In this case, a carbon atom with a hydrogen atom became 4-fold coordinated. In both scenarios, hydrogen detached from these Si and then reattached to a nearby sp3-like C atom. In general, these types of hydrogen-passivated Si30C30 structures are relatively more distorted from the ideal fullerene shape.
HOMO–LUMO Properties
In general, silicon prefers sp3 hybridization, and forcing it to form sp2 bonds leads to destabilization. The carbon can accommodate both sp3 as well as sp2 hybridization due to shorter C–C bond lengths (Huda and Ray, 2004a; Huda et al., 2009; De Padova et al., 2011). However, there were reports of sp2-like hybridization in silicon carbide, such as in SiC multi-wall nanotubes (Huda et al., 2009; De Padova et al., 2011). Due to local chemical configurations in Si30C30 fullerenes, the molecular orbital calculations may establish the sp2-like π bonds that we hypothesized in earlier sections. The orbital plots can verify such features. Figures 7, 8 show the HOMO and LUMO plots for all the structures, without and with hydrogen passivation, respectively. In the following paragraphs, we discuss a few selected HOMO and LUMO plots from the figures.

Figure 7. The left panel shows the highest occupied molecular orbital and the right panel shows the lowest unoccupied molecular orbital plots for unpassivated Si30C30 clusters. Structures are presented from panels (A–H) in order of their stability, most to least stable.
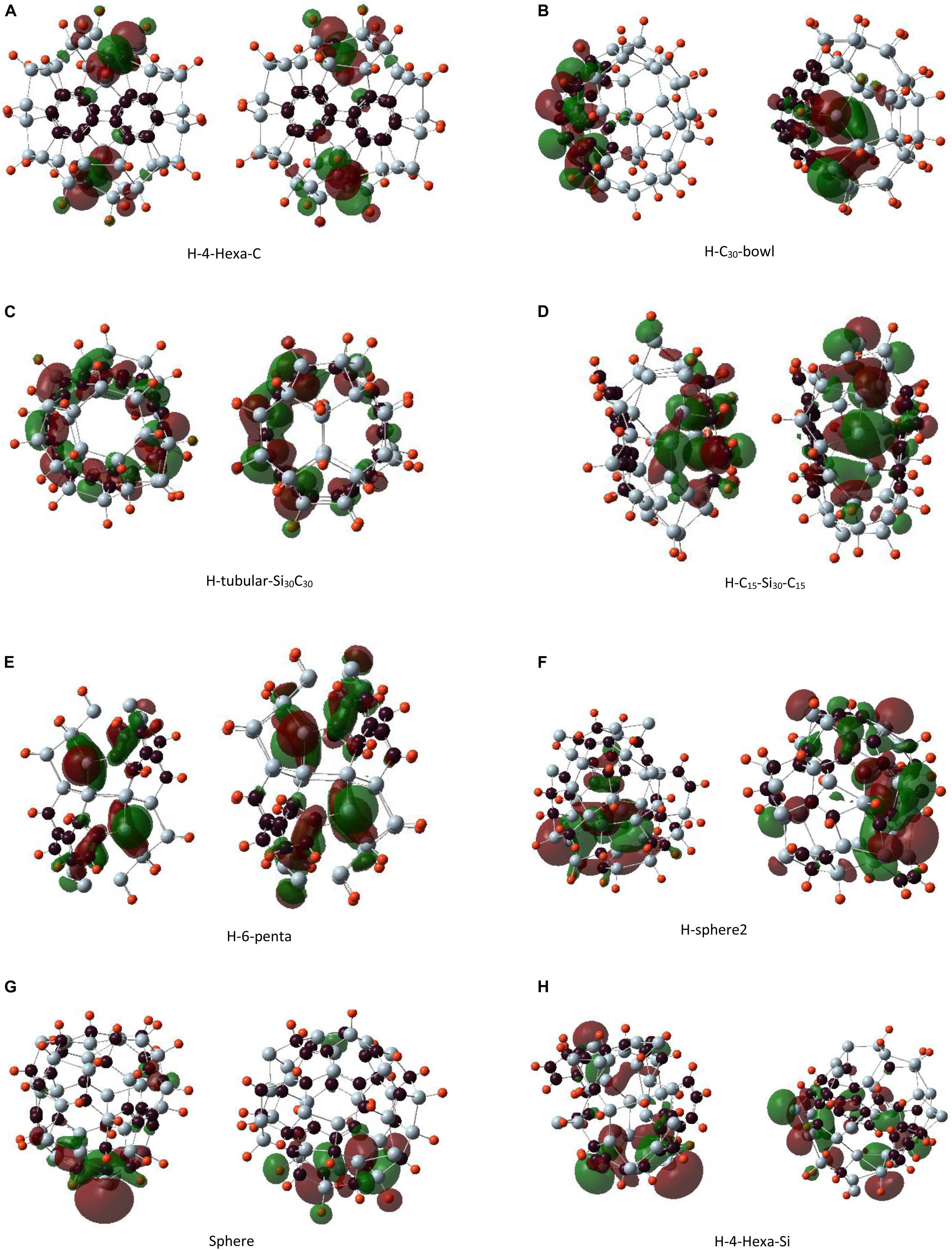
Figure 8. The left panel shows the highest occupied molecular orbital and the right panel shows the lowest unoccupied molecular orbital plots for hydrogen-passivated Si30C30H30 clusters. Structures are presented from panels (A–H) in order of their stability, most to least stable.
The HOMO plot of the C30-bowl structure in Figure 7A shows the π-bond-like feature on the silicon side at the left-most part of the figure where the Si–Si bond length is 2.31 Å. This bond length is comparable to the previously published Si–Si double bonds, which were in the range of 2.15 to 2.23 Å (Wang et al., 2008; Fischer and Power, 2010; Kira, 2012; Gau et al., 2016). On the other hand, for passivated H–C30-bowl structure in Figure 8B, there is no sp2 hybridization on the silicon side, as all Si atoms, except four Si atoms, are passivated with hydrogen and have 4-fold sp3-like coordination, however, the π bond does show up on the carbon side of the structure. In Figure 8C, for the H-tubular-Si30C30 structure, both the HOMO and the LUMO appear on the carbon atoms in the middle of the structure. Si atoms do contribute significantly to these frontier orbitals because the hydrogen-passivated silicon atoms created an almost perfect sp3-like bonding environment with bonding angles of about 104°, whereas the ideal sp3 bonding angles are 109.5°.
Figure 7B shows in the C15–Si30–C15 structure that HOMO is almost symmetrically distributed on both C15 units; except for a pair of carbon atoms on both faces, these two carbon atoms are doubly bonded on their respected faces. Most of the Si atoms are not contributing to HOMO. Si atoms from one of the most distorted sides of the structure dominate the LUMO. Interestingly, H–C15–Si30–C15 in Figure 8D shows the HOMO in only one of the C15 caps, particularly on the side where more hydrogen atoms are broken away from Si atoms and re-bonded with C-atoms. On the other hand, LUMO, as it is for its unpassivated counterpart, is on the side of the structure that is more distorted with Si atoms without hydrogen atoms. The highest contribution for LUMO came from a pair of Si and C atoms that are separated by 3.66 Å.
Highest occupied molecular orbital and LUMO are mainly distributed on the Si caps in the 6-penta structure in Figure 7D. Unlike some other structures, no π-bond-like feature was found on the HOMO plot. H-6-penta in Figure 8E has main contributions to HOMO and LUMO, which are from the Si atoms that are 3-fold coordinated and without hydrogen atoms and from a few carbon atoms. Therefore, bonding–antibonding splitting that created HOMO and LUMO occurs almost on the same set of atoms. The eight 4-fold coordinated Si atoms in the mid-section of the structure remained tightly bound, with no contribution to either HOMO or LUMO. H-sphere2 has the shortest Si–Si bond, 2.24 Å, which is significantly close to experimental Si–Si double bond length values, as quoted earlier (Wang et al., 2008; Fischer and Power, 2010; Kira, 2012; Gau et al., 2016). The HOMO plot in Figure 8F reflects the π bond between these two silicon atoms as well.
Regarding the double bonds, we make some remarks here: when a bond is well formed and saturated, the orbitals’ energy for that bond becomes lower in energy, and it may not contribute to HOMO. In the unpassivated Si30C30 structures, atoms that contribute to HOMO are from the part of the structure that is prone to distortion or are not still in their preferred bonding state. For example, in the C30-bowl structure, both HOMO and LUMO have major contributions from the unpassivated Si atoms. Once these Si atoms are hydrogenated, in the H–C30-bowl structure, the Si part of the structure does not contribute to these frontier orbitals anymore; these Si atoms tend to have sp3-like bonding with the help of passivating agents such as hydrogen. Therefore, some Si–Si double bonds showing up in HOMO in the unpassivated structures are prone to be reactive with chemical stimulations because, with passivation, these bonds are more likely oriented in standard sp3 hybridization. For example, in both the most stable C30-bowl and lest stable sphere-2 structures, there were indications for Si–Si double bonds from the HOMO plots; then, with hydrogen passivation, these double bond features were lost. In general, in any chemical synthesis of these structures, there will possibly be passivating ligands available in the synthesis environment, and hence the detection of Si–Si double bonds in these larger structures is unlikely.
W Doping in Si30C30
For the endohedral doping of tungsten atoms, the C30-bowl configuration is considered. The reason for selecting the C30-bowl is that, firstly, without passivation, it was the most stable Si30C30 configuration, and it kept a cage-type feature; secondly, its passivation increased its stability (by 0.035 eV/atom) and improved its overall cage feature. Figure 9A shows the relaxed W-C30-bowl structure. The initial structure was constructed by placing W atom at the C30-bowl sphere’s center, and then the structure was relaxed without any symmetry constraint. Figure 9B shows a similarly, obtained structure; this is a W-dimer inside the cage, W2-C30-bowl. The W2-C30-bowl was found to be magnetically not very interesting, as the W-dimer in the cage prefers not to retain spin as much magnetic moments as in W-C30-bowl-based structures. So, the following discussion is based on a single W atom in Si30C30, W-C30-bowl structure (Figure 9A).
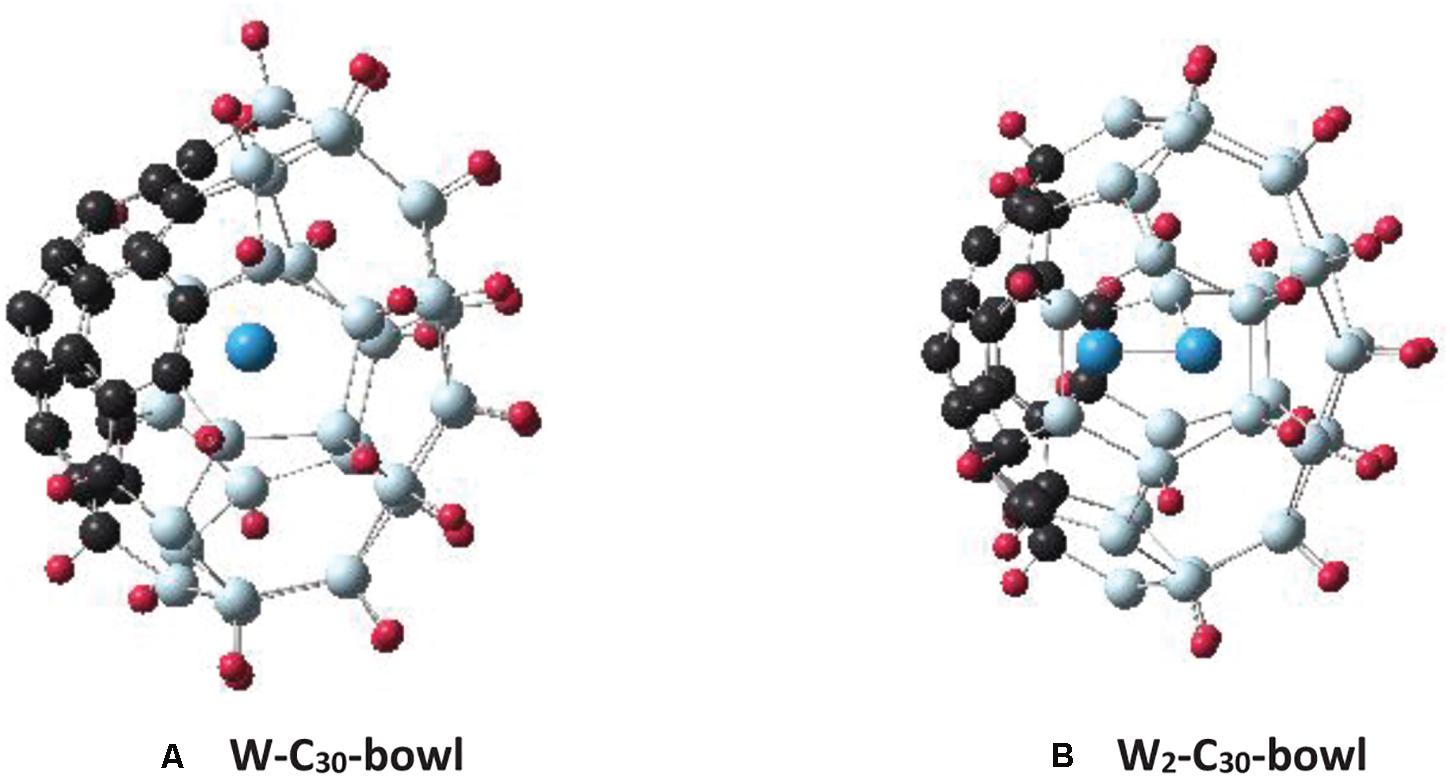
Figure 9. The figures show the C30-bowl structure (as in Figure 2A) with tungsten atom(s) in the center of the structures: (A) with one W atom, C30-bowl-W and (B) with two W atoms, W2-C30-bowl.
Several spin-multiplicities have been considered for the W-C30-bowl structure. From the binding energy calculations, the spin-triplet state was found to be 28 meV/atom more stable than the singlet state. In all spin-states considered, including the quintet state, after relaxation, the W atom moved toward the Si side. The C30 side remained almost unaffected with fullerene-like structure. In the triplet state, there is only one W–Si bond, with a bond length of 2.57 Å. On the other hand, in the singlet state, the W atom is 3-fold coordinated, with an average bond length of 2.53 Å. For the triplet spin state structure, the W atom does possess almost all the spin, namely, 1.85 mB, out of a total magnetic moment of 2 mB. In contrast, in the hydrogen-passivated H–W–C30-bowl triplet structure, where hydrogen atoms passivate Si atoms, the spin-magnetic moment on the W atom is 1.99 mB, and the W atom remains almost at the center of the cage without any bond. A similar effect was found for the structure with an even higher spin-multiplicity of five states; 3.99 mB was found on the W atom out of the total 4 mB and sitting at the center of the H–W–C30-bowl structure. Retention of spin-magnetic moment on the endohedral transition metal atom is much higher in Si30C30 cages than what was reported for smaller Si cages earlier (Guo et al., 2008).
In addition, the W atom increased the binding of the C30-bowl structure by 84 meV/atom and decreased the dipole moment by 59%; this implies that the stability of the overall structure improved by W atom doping. On the other hand, for the passivated H–C30-bowl structure, the HOMO–LUMO gap increased by 0.715 eV, implying increased electronic stability compared to the undoped structure. In short, two important findings with endohedral W atom doping in conjunction with hydrogen passivations are: (i) higher spin moment is retained at the W atom sitting at the center of the cage and (ii) the cage stability increases.
Conclusion
Starting from Si60 fullerene template, several configurations of Si30C30 clusters were studied first without any passivating agent. Then, all 3-fold coordinated 30 Si atoms were passivated by hydrogen atoms, and the effects of the passivation of the structures have been analyzed. The first noticeable effect of passivation is the change of the relative stability of the Si30C30 isomers; the order of relative stability of the unpassivated Si30C30 isomers changes when they are passivated. Second, the position of HOMO shifted significantly with H-passivation. Third, depending on the local chemical environment, such as coordination order, neighboring elements, and bond angles, some C–H bonds were found after relaxation, even though no carbon atom was bonded with H before relaxing the structures. Fourth, hydrogen passivation has significant effects on the endohedral metal dopant, such as it helps keep the metal atom almost at the center of the Si30C30 cage and retain a very high spin-magnetic moment on the dopant metal atom. So, inside the hydrogenated Si30C30 cage, the spin state of the W atom can be preserved from the outside chemical perturbations; this can have a potential application in spintronics applications.
Finally, enhancing the stability of SiC fullerene structures by surface passivation is not a very straightforward phenomenon. The integrity of the structure and the cohesion between the atoms within the structure upon passivation depend on the local chemical environment on the fullerene surface. Even though all Si atoms in both Si60 and Si30C30 are 3-fold coordinated, none of the hydrogenated Si30C30 structures could maintain their fullerene sphere as was in Si60H60, albeit among the Si30C30 structures considered here, a few isomers could maintain sufficiently large cage-type structures. Note that in the case of cage structures, there are no bulk atoms, and all are surface atoms. When bonding mismatch weakens the bonds on the surface atoms, even during passivations, distortions and even collapse of the cages are possible, as there is no support from inside; several of the Si30C30 structures showed the behavior in this study. In addition, having a prior knowledge for the need of passivation for a particular set of atoms for a large cage structure can be a daunting task. In this study, we have found that, in several cases, some hydrogen atoms that initially bonded with 3-fold Si atoms were later moved to carbon atoms due to structural relaxations. The migration of hydrogen atoms from silicon to carbon atoms causes significant distortions in the cage structures; the higher the number of hydrogen atoms moved to the carbon atoms, the higher distortions were found in the Si30C30 cages. The near-spherical one is the one where the sp3-type bonding was distributed almost equally over the structure, including the carbon part. For example, in the H-sphere structure in Figure 3G, even though it is one of the least stable isomers, it maintains a near-spherical form. A symmetrization of the bonding over the surface of the structure is needed to maintain a large fullerene-like spherical structure.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
HA performed the computations. HA and NA performed the analysis. HA and MH mainly wrote the manuscript. NA helped in organizing the references. MH planned the project and supervised the work. All authors contributed to the article and approved the submitted version.
Funding
MH was supported by the National Science Foundation (award no. 1609811). HA and NA acknowledge the support of the Saudi Arabian Cultural Mission via Jazan University and University of Hafr Al Batin, respectively.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledged the generous computation time at the High Performance Computing (HPC) Center of the University of Texas at Arlington.
References
Abreu, M. B., Reber, A. C., and Khanna, S. N. (2015). Making sense of the conflicting magic numbers in WSin clusters. J. Chem. Phys. 143, 1–9. doi: 10.1063/1.4928755
Anafcheh, M., and Ghafouri, R. (2014). Theoretical identification of the lowest energy structure of C70–n Si n, n = 1, 2, 6, 10, and 20 heterofullerenes. Struct. Chem. 25, 617–623. doi: 10.1007/s11224-013-0324-z
Bainglass, E., Mayfield, C. L., and Huda, M. N. (2017). Weakening of Si[sbnd]Si bonding in exohydrogenated Si60 nanoclusters. Chem. Phys. Lett. 684, 60–66. doi: 10.1016/j.cplett.2017.06.022
Becke, A. D. (1993). A new mixing of hartree-fock and local density-functional theories. J. Chem. Phys. 98, 1372–1377. doi: 10.1063/1.464304
Bernath, P. F., Rogers, S. A., O’Brien, L. C., Brazier, C. R., and McLean, A. D. (1988). Theoretical predictions and experimental detection of the SiC molecule. Phys. Rev. Lett. 60, 197–199. doi: 10.1103/PhysRevLett.60.197
Bravo-Zhivotovskii, D., Dobrovetsky, R., Nemirovsky, D., Molev, V., Bendikov, M., Molev, G., et al. (2008). The synthesis and isolation of a metal-substituted bis-silene. Angew. Chemie. Int. Ed. 47, 4343–4345. doi: 10.1002/anie.200800973
Chase, M. W., Curnutt, J. L., Downey, J. R., Mcdonald, R. A., Syverud, A. N., and Valenzuela, E. A. (1982). JANAF thermochemical tables, 1982 supplement. J. Phys. Chem. Ref. Data 11:695. doi: 10.1063/1.555666
Cheung, R. (2006). Silicon Carbide Microelectromechanical Systems for Harsh Environments. London: Imperial College Press.
Chiodo, S., Russo, N., and Sicilia, E. (2006). LANL2DZ basis sets recontracted in the framework of density functional theory. J. Chem. Phys. 125:104107. doi: 10.1063/1.2345197
De Padova, P., Quaresima, C., Olivieri, B., Perfetti, P., and Le Lay, G. (2011). Sp2-like hybridization of silicon valence orbitals in silicene nanoribbons. Appl. Phys. Lett. 98, 96–99. doi: 10.1063/1.3557073
Duan, X. F., and Burggraf, L. W. (2015). Theoretical investigation of stabilities and optical properties of Si12C12 clusters. J. Chem. Phys. 142:034303. doi: 10.1063/1.4905542
Fischer, R. C., and Power, P. P. (2010). π-Bonding and the lone pair effect in multiple bonds involving heavier main group elements: developments in the new millennium. Chem. Rev. 110, 3877–3923. doi: 10.1021/cr100133q
Flores, J. R., and Largo-Cabrerizo, J. (1987). A comparative ab initio study of the H2SiN+ and H2CN+. Chem. Phys. Lett. 142, 159–164. doi: 10.1016/0009-2614(87)80914-4
Fye, J. L., and Jarrold, M. F. (1997). Structures of silicon-doped carbon clusters. J. Phys. Chem. A 101, 1836–1840. doi: 10.1021/jp962759w
Gau, D., Nougué, R., Saffon-Merceron, N., Baceiredo, A., De Cózar, A., Cossío, F. P., et al. (2016). Donor-Stabilized 1,3-Disila-2,4-diazacyclobutadiene with a Nonbonded Si…Si distance compressed to a Si=Si double bond length. Angew. Chem. Int. Ed. 55, 14673–14677. doi: 10.1002/anie.201608416
Gorai, P., McKinney, R. W., Haegel, N. M., Zakutayev, A., and Stevanovic, V. (2019). A computational survey of semiconductors for power electronics. Energy Environ. Sci. 12, 3338–3347. doi: 10.1039/c9ee01529a
Guo, L. J., Zhao, G. F., Gu, Y. Z., Liu, X., and Zeng, Z. (2008). Density-functional investigation of metal-silicon cage clusters M Sin (M=Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn; n=8-16). Phys. Rev. B 77, 1–8. doi: 10.1103/PhysRevB.77.195417
Hiura, H., Miyazaki, T., and Kanayama, T. (2001). Formation of metal-encapsulating Si cage clusters. Phys. Rev. Lett. 86, 1733–1736. doi: 10.1103/PhysRevLett.86.1733
Huda, M. N. (2014). SiC nanostructures from a theoretical perspective. Rev. Nanosci. Nanotechnol. 3, 88–106. doi: 10.1166/rnn.2014.1046
Huda, M. N., and Ray, A. K. (2004a). Carbon dimer in silicon cage: a class of highly stable silicon carbide clusters. Phys. Rev. A At. Mol. Opt. Phys. 69, 112011–112014. doi: 10.1103/PhysRevA.69.011201
Huda, M. N., and Ray, A. K. (2004b). Novel silicon-carbon fullerene-like cages: a class of sp3 – sp2 covalent-ionic hybridized nanosystems. Eur. Phys. J. D 31, 63–68. doi: 10.1140/epjd/e2004-00128-9
Huda, M. N., and Ray, A. K. (2008). Evolution of SiC nanocluster from carbon fullerene: a density functional theoretic study. Chem. Phys. Lett. 457, 124–129. doi: 10.1016/j.cplett.2008.03.057
Huda, M. N., and Ray, A. K. (2012). Theoretical study of SiC nanostructures: current status and a new theoretical approach. J. Comput. Theor. Nanosci. 9, 1881–1905. doi: 10.1166/jctn.2012.2599
Huda, M. N., Yan, Y., and Al-Jassim, M. M. (2009). On the existence of Si-C double bonded graphene-like layers. Chem. Phys. Lett. 479, 255–258. doi: 10.1016/j.cplett.2009.08.028
Kira, M. (2012). Bonding and structure of disilenes and related unsaturated group-14 element compounds. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 88, 167–191. doi: 10.2183/pjab.88.167
Kohn, W., Becke, A. D., and Parr, R. G. (1996). Density functional theory of electronic structure. J. Phys. Chem. 100, 12974–12980. doi: 10.1021/jp960669l
Kumar, V., and Kawazoe, Y. (2001). Metal-encapsulated fullerenelike and cubic caged clusters of silicon. Phys. Rev. Lett. 87:45503. doi: 10.1103/PhysRevLett.87.045503
Li, B. X., Cao, P. L., and Que, D. L. (2000). Distorted icosahedral cage structure of clusters. Phys. Rev. B Condens Matter Mater Phys. 61, 1685–1687. doi: 10.1103/PhysRevB.61.1685
Li, Q. X., Lu, W. C., Zang, Q. J., Zhao, L. Z., Wang, C. Z., and Ho, K. M. (2011). Carbon-rich C9Sin (n = 1-5) clusters from ab initio calculations. Comput. Theor. Chem. 963, 439–447. doi: 10.1016/j.comptc.2010.11.010
Matsubara, M., Kortus, J., Parlebas, J. C., and Massobrio, C. (2006). Dynamical identification of a threshold instability in Si-doped heterofullerenes. Phys. Rev. Lett. 96, 1–4. doi: 10.1103/PhysRevLett.96.155502
Matsubara, M., and Massobrio, C. (2005). Stable highly doped C60–mSim heterofullerenes: a first principles study of C40Si20. C36Si24, and C30Si30. J Phys Chem A 109, 4415–4418. doi: 10.1021/jp058094s
Matsubara, M., and Massobrio, C. (2006). First principles study of extensive doping of C60 with silicon. Mater Sci. Eng. C 26, 1224–1227. doi: 10.1016/j.msec.2005.09.091
Mayfield, C. L., and Huda, M. N. (2013). The effect of hydrogen passivation on Si nanocrystals: surface and spin states. Comput. Theor. Chem. 1019, 125–131. doi: 10.1016/j.comptc.2013.06.036
McLean, A. D., and Chandler, G. S. (1980). Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11-18. J. Chem. Phys. 72, 5639–5648. doi: 10.1063/1.438980
Menon, M. (2001). Generalized tight-binding molecular dynamics scheme for heteroatomic systems: application to SimCn clusters. J. Chem. Phys. 114, 7731–7735. doi: 10.1063/1.1366697
Nakajima, A., Taguwa, T., Nakao, K., Gomei, M. G., and Kishi, R. (1995). Photoelectron spectroscopy of silicon – carbon cluster anions (Sin Cm –). J. Chem. Phys. 103, 2050–2057.
Park, J., Nam, G. J., Tokmakov, I. V., and Lin, M. C. (2006). Experimental and theoretical studies of the phenyl radical reaction with propene. J. Phys. Chem. A 110, 8729–8735. doi: 10.1021/jp062413d
Pellarin, M., Ray, C., Lermé, J., Vialle, J. L., Broyer, M., Blase, X., et al. (1999). Photolysis experiments on SiC mixed clusters: from silicon carbide clusters to silicon-doped fullerenes. J. Chem. Phys. 110, 6927–6938. doi: 10.1063/1.478598
Pellarin, M., Ray, C., Mélinon, P., Lermé, J., Vialle, J. L., Kéghélian, P., et al. (1997). Silicon-carbon mixed clusters. Chem. Phys. Lett. 277, 96–104. doi: 10.1016/S0009-2614(97)00869-5
Ray, A. K., and Huda, M. N. (2006). Silicon-carbide nano-clusters: a pathway to future nano-electronics. J. Comput. Theor. Nanosci. 3, 315–341. doi: 10.1166/jctn.2006.3014
Scipioni, R., Matsubara, M., Ruiz, E., Massobrio, C., and Boero, M. (2011). Thermal behavior of Si-doped fullerenes vs their structural stability at T = 0 K: a density functional study. Chem. Phys. Lett. 510, 14–17. doi: 10.1016/j.cplett.2011.05.019
Song, B., Song, X., and Liu, K. (2013). Density functional study of transition-metal-encapsulated Si10C10H20 cage-like clusters. Comput. Theor. Chem. 1021, 256–261. doi: 10.1016/j.comptc.2013.07.042
Srinivasan, A., Huda, M. N., and Ray, A. K. (2005). Silicon-carbon fullerenelike nanostructures: an ab initio study on the stability of Si60C2n (n=1,2) clusters. Phys. Rev. A At. Mol. Opt. Phys. 72, 1–10. doi: 10.1103/PhysRevA.72.063201
Srinivasan, A., Huda, M. N., and Ray, A. K. (2006). A density functional theoretic study of novel silicon-carbon fullerene-like nanostructures: Si40C20, Si60C20, Si36C24, and Si60C24. Eur. Phys. J. D 39, 227–236. doi: 10.1140/epjd/e2006-00104-5
Sun, Q., Wang, Q., Briere, T. M., and Kawazoe, Y. (2002). Dimer interactions of magic W@Si12 clusters. J. Phys. Condens Matter 14, 4503–4508. doi: 10.1088/0953-8984/14/17/320
Sun, Q., Wang, Q., Jena, P., Rao, B. K., and Kawazoe, Y. (2003). Stabilization of Si60 Cage Structure. Phys. Rev. Lett. 90:135503. doi: 10.1103/PhysRevLett.90.135503
Wang, J., and Liu, Y. (2016). Magnetic silicon fullerenes: experimental exploration and theoretical insight. J. Clust. Sci. 27, 861–873. doi: 10.1007/s10876-015-0959-6
Wang, L., Li, D., and Yang, D. (2006). Fully exohydrogenated Si60 fullerene cage. Mol. Simul. 32, 663–666. doi: 10.1080/08927020600880786
Wang, Y., Xie, Y., Wei, P., King, B., Schaefer, H., Schleyer, P. V. R., et al. (2008). Stable Silicon(0) compound with a Si = Si double bond. Science 321, 1069–1071. doi: 10.1126/science.1160768
Wijesundara, M., and Azevedo, R. (2011). Silicon Carbide Microsystems for Harsh Environments. New York, NY: Springer.
Yamamoto, H., and Asaoka, H. (2001). Formation of binary clusters by molecular ion irradiation. Appl. Surf. Sci. 169–170, 305–309. doi: 10.1016/S0169-4332(00)00680-2
Yong, Y., Song, B., and He, P. (2014). Theoretical prediction of novel ultrafine nanowires formed by Si 12C12 cage-like clusters. Eur. Phys. J. D 68:37. doi: 10.1140/epjd/e2013-40020-y
Keywords: silicon-carbide fullerene, hydrogen passivation, magnetic dopant, Si-C double bonds, DFT (B3LYP), spintronics application
Citation: Alathlawi HJ, Alkhaldi ND and Huda MN (2020) Effects of Hydrogen Passivation on Fullerene-Derived Si30C30 Clusters. Front. Mater. 7:525553. doi: 10.3389/fmats.2020.525553
Received: 09 January 2020; Accepted: 13 August 2020;
Published: 15 September 2020.
Edited by:
Dimitrios Gournis, University of Ioannina, GreeceReviewed by:
George E. Froudakis, University of Crete, GreeceEmmanuel Klontzas, National Hellenic Research Foundation, Greece
Copyright © 2020 Alathlawi, Alkhaldi and Huda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad N. Huda, aHVkYUB1dGEuZWR1
 Hussain J. Alathlawi
Hussain J. Alathlawi Noura D. Alkhaldi
Noura D. Alkhaldi Muhammad N. Huda
Muhammad N. Huda