Phononic Thermal Transport in Yttrium Hydrides Allotropes

Room-temperature superconductivity has been attracting increasing attention in recent years. Recent studies have proved the potential of compressed H-rich materials for achieving room-temperature superconductivity. In this paper, we study the phononic thermal transport in the rare earth yttrium hydrides allotropes under 0, 50, and 300 GPa by using Boltzmann transport equation. We find that the lattice thermal conductivity of yttrium hydrides increases with the pressure among different allotropes, which is attributed to the increase of bond strength and the decrease of phonon-phonon scattering due to structural compression. Yttrium hydrides structure at high pressure of 300 GPa is the superconducting phase, and has high thermal conductivity around 1,360 Wm⁻¹K⁻¹ at room temperature. Comparison of phonon properties with existing high thermal conductivity materials further uncovers the origin for the observed high thermal conductivity. For the zero pressure allotrope, a large number of optical flat bands mix with the low-frequency acoustic phonons, which significantly increases the phonon scattering channel and effectively suppresses the phonon lifetime. As for yttrium hydrides allotropes under 50 and 300 GPa, there are two obvious band gaps in the phonon dispersion relation, and the band gap of the structure at 300 GPa is significantly wider. The occurrence of the band gap effectively inhibits the absorption and emission process of the three-phonon interactions, leading to the decrease of phonon scattering and thus the increase of the phonon lifetime and thermal conductivity at high pressure. Our work reveals the physical mechanism of the thermal transport behaviors in yttrium hydrides structures under different pressures.

Introduction

Because of the fascinating electrical transport ability, the high transition temperature (Tc) superconductivity has attracted lots of research attention (Wigner and Huntington, 1935; Ashcroft, 1968). Previous studies demonstrated that the light element riched metallic solids at high pressure possess promising high-Tc phonon-mediated superconductivity due to the high Debye temperature and strong electron-phonon coupling, such as the H-riched materials (Kim et al., 2010; Errea et al., 2016; Zhong et al., 2016). H-rich materials have been considered as a potential superconductor at high pressure (Ashcroft, 2004; Wang H. et al., 2012) because they can become metallic and superconducting at much lower pressure than hydrogen due to “chemical compression” (Soroka et al., 2018). Extensive explorations of the superconducting high pressure phase diagrams of rare earth (Sc, Y, La, Ce, Pr, etc.) hydrides are revealed (Li and Peng, 2017; Liu et al., 2017; Peng et al., 2017), concentrating on H-rich materials by performing swarm intelligence algorithm based on Crystal structure Analysis by Particle Swarm Optimization structure searches (Wang et al., 2010; Wang Y. et al., 2012). For example, Peng et al. (2017) reported some high pressure phases of yttrium hydrides (YH₃) that are more likely to be superconducting materials.

On the other hand, the thermal transport property is crucial for the performance and reliability of various devices, which can have promising applications in both thermal management and thermoelectric devices (Shi et al., 2012; Alva et al., 2018; Hu et al., 2018; Xie et al., 2018; Zhang and Chen, 2018; Zhang et al., 2018; Ouyang et al., 2019; Zhu et al., 2019; Xu et al., 2020; Zhang et al., 2020a; Zhang et al., 2020b). Especially the materials with high thermal conductivity and excellent mechanical properties are of great importance in solving the heat dissipation problem of highly integrated electronic devices (Ghosh et al., 2008). Meanwhile, the thermal transport properties of superconductors have also been investigated (Li et al., 2015; Tanaka et al., 2017; Hummel et al., 2020). For example, Ito et al. (2005) found the thermal conductivity of the yttrium hydrides can reach about 80 W/mK, which is larger than that of metal and depends significantly on temperatures. Moreover, previous studies also demonstrated that lattice thermal conduction can be largely tuned by external pressure or strains (Chen et al., 2014; Ouyang and Hu, 2015; Liu et al., 2016). Remarkably, due to the change of the valence electronic state of Y atom under high pressure, there is more possibility of bonding between Y atom and H atom (Heil et al., 2019). Among these different yttrium hydrides, YH₃ allotropes provides a broad platform for the study of the structural behavior and pressure tunable thermal properties (Liu et al., 2017; Soroka et al., 2018; Grishakov et al., 2019). For example, YH₃ is insulating in nature at ambient pressure (0 GPa) (Jarosik et al., 2017), while the insulator to superconductor transition in YH₃ occurs at pressure around 20 GPa (Kim et al., 2009; Kim et al., 2010). More interestingly, with increasing external pressure, the system becomes normal metallic (i.e., not superconductivity) around 35 GPa, eventually, the superconducting phase re-emerges in YH₃ when pressure is greater than 50 GPa (Kim et al., 2010). As lots of new allotropes of YH₃ at different pressures have been proposed recently, it would be interesting to study the thermal conductivity of these new superconductors and also the effect of pressure on their thermal transport properties. Here, we focus on the effect of pressure on thermal conductivity of yttrium hydrides allotropes, so we choose the stable structures for YH₃ under different pressures (0, 50, and 300 GPa) as research objects.

In this work, based on the Boltzmann transport equation and ab initio calculations, we study the phononic thermal transport properties of yttrium hydrides allotropes at different pressures. We limit our discussion on the lattice thermal conductivity only, as the electron contribution and electron-phonon coupling are neglected. The simulation results indicate that the lattice thermal conductivity of yttrium hydrides is strongly dependent on the pressure. An unexpected high thermal conductivity, around 1,360 Wm⁻¹K⁻¹ at room temperature, is observed in the structure under high pressure (300 GPa). The underlying mechanisms are studied from the structural compressibility, group velocity phonon dispersion, and phonon lifetime. Our study uncovers thermal transport behaviors in yttrium hydrides, and also provides the perspective to achieve high lattice thermal conductivity via pressure.

Computational Method

The computational studies in this paper are based on the generalized gradient approximation by adopting the Perdew-Burke-Ernzerhof parametrization as the exchange-correlation for density functional theory. The projector augmented wave potentials are adopted for Y and H in Y-H system with the Vienna ab initio simulation package (Kresse and Furthmüller, 1996). Due to the application of high pressure phase hydrogen, the plane wave basis set is employed with the energy cutoff of 1,000 eV in calculations at 50 and 300 GPa, whereas the energy cutoff adopted in YH₃ at 0 GPa is 450 eV. Brillouin zone sampling is done with a 16 × 16 × 16 Monkhorst-Pack k-points mesh (Monkhorst and Pack, 1976) for the YH₃ structures. In order to ensure the accuracy of the results and decrease the calculation scale, the self-consistent convergence of the total energy is set to 10^–7 eV/atom. Combining the Vienna ab initio simulation package and PHONOPY package (Togo et al., 2008), the phonon dispersion relation and density of states are obtained for all structures.

The lattice thermal conductivity ($\kappa$) of YH₃ was calculated by using ShengBTE code (Omini and Sparavigna, 1995; Li et al., 2014), which implements a fully iterative solution of Peierls-Boltzmann transport equation (PBTE). Based on the solution of PBTE, the lattice thermal conductivity can be described as (Omini and Sparavigna, 1995; Li et al., 2014).

${\kappa }^{\alpha \beta }=\frac{1}{k_B{T}^2\text{Ω}N}{\displaystyle \sum }_{\lambda }{n}_0(n_0+1){\left(\hslash {\omega }_{\lambda }\right)}^2{\upsilon }_{\lambda }^{\alpha }{F}_{\lambda }^{\beta },(1)$

where $k_B$, $T$, $\text{Ω},$$\hslash$, and N are Boltzmann constant, temperature, the volume of the unit cell, the reduced Plank constant and the number of q-points, respectively. Here, $n_0$ is the distribution function, ${\omega }_{\lambda }$ is the phonon frequency of the phonon mode λ defined by the phonon branch, and the sum goes over all the phonon modes that are composed of wave vector and phonon branch. ${\upsilon }_{\lambda }^{\alpha }$ is the phonon group velocity in the $\alpha$-direction, and $F_{\lambda }^{\beta }$ can be expressed as (Omini and Sparavigna, 1995; Lindsay and Broido, 2008; Li et al., 2014)

$F_{\lambda }^{\beta }={\tau }_{\lambda }^0\left({\upsilon }_{\lambda }^{\beta }+{\text{Δ}}_{\lambda }\right),(2)$

where ${\tau }_{\lambda }^0$ is phonon lifetime of mode $\lambda$ which is obtained by relaxation time approximation (RTA), and ${\text{Δ}}_{\lambda }$ is a correction term obtained by fully iterative solution of PBTE that merges the inelastic three-phonon scattering processes (Li et al., 2014).

The anharmonic three-phonon scattering process is the dominating phonon scattering mechanism in pristine crystals, and the resulting phonon lifetime can be calculated based on the Fermi’s Golden Rule as the inversion of the intrinsic scattering rate (Li et al., 2012)

${\tau }_{\lambda }^{ph}=N{({\displaystyle \sum }_{{\lambda }^{\prime }{\lambda }^{\prime \prime }}{\text{Γ}}_{\lambda {\lambda }^{\prime }{\lambda }^{\prime \prime }}^{+}+\frac{1}{2}{\displaystyle \sum }_{{\lambda }^{\prime }{\lambda }^{\prime \prime }}{\text{Γ}}_{\lambda {\lambda }^{\prime }{\lambda }^{\prime \prime }}^{-})}^{-1},(3)$

where ${\lambda }^{\prime }$ and ${\lambda }^{\prime \prime }$ represent the second and third phonon mode scattering corresponding to the first phonon mode $\lambda$. ${\text{Γ}}_{\lambda {\lambda }^{\prime }{\lambda }^{\prime \prime }}^{+}$ and ${\text{Γ}}_{\lambda {\lambda }^{\prime }{\lambda }^{\prime \prime }}^{-}$ represent the absorbing ($\lambda +{\lambda }^{\prime }\to {\lambda }^{\prime \prime }$) and emitting ($\lambda \to {\lambda }^{\prime }+{\lambda }^{\prime \prime }$) three-phonon scattering processes, respectively. The linewidth ${\text{Γ}}_{\lambda {\lambda }^{\prime }{\lambda }^{\prime \prime }}^{\pm }$ can be obtained by Fermi's Golden Rule and the third-order force-constant matrix. Apart from the three-phonon scatterings, we have put the phonon-isotopic scattering into consideration in this work, and the scattering rate can be expressed as (Tamura, 1983; Kundu et al., 2011)

${\Gamma }_{\lambda {\lambda }^{\prime }}=\frac{\pi {\omega }^2}{2}{\displaystyle \sum }_{i\in u.c.}g\left(i\right){\left|{\mathit{e}}_{\lambda }^{\ast }\left(i\right)\cdot {\mathit{e}}_{{\lambda }^{\prime }}\left(i\right)\right|}^2\delta \left({\omega }_{\lambda }-{\omega }_{{\lambda }^{\prime }}\right),(4)$

where $g\left(i\right)={\displaystyle \sum }_s{f}_s\left(i\right){[1-M_s\left(i\right)/\overline{M}\left(i\right)]}^2$ is the Pearson deviation coefficient for the mass $M_s\left(i\right)$ of isotopes s for atom i (found with relative frequency $0<f_s\left(i\right)\le 1$) and $\overline{M}\left(i\right)={\displaystyle \sum }_s{f}_s\left(i\right)M_s\left(i\right)$ represents the average mass. The natural concentration of isotope in literature (Michael and Michael, 2011) is adopted in our work. Meanwhile, all scattering rates follow the Matthiessen rule (Feng et al., 2015).

The phase space of all possible three-phonon scattering processes that conserve both energy and quasi-lattice momentum based on phonon dispersions and Fermi's Golden Rule is determined. The allowed three-phonon scattering processes must conform to

${\omega }_{\lambda }\left(\overrightarrow{q}\right)\pm {\omega }_{{\lambda }^{\prime }}\left({\overrightarrow{q}}^{\prime }\right)={\omega }_{{\lambda }^{\prime \prime }}\left({\overrightarrow{q}}^{\prime \prime }\right);\overrightarrow{q}\pm {\overrightarrow{q}}^{\prime }={\overrightarrow{q}}^{\prime \prime }+\overrightarrow{G},(5)$

where $\overrightarrow{G}$ is the reciprocal lattice vector. $\overrightarrow{G}=0$ represents the normal (N) processes, while $\overrightarrow{G}\ne 0$ denotes the umklapp (U) processes. The parameter $W_{\lambda }^{\pm }$ denote the phase space corresponding to absorption and emission of the phonon mode $\lambda$, which are defined as the sum of frequency-dependent factors in the three-phonon transition probabilities expressions, as follows (Li and Mingo, 2015)

$W_{\lambda }^{\pm }=\frac{1}{2N}{\displaystyle \sum }_{{\lambda }^{\prime }{\lambda }^{\prime \prime }}\left\{\begin{array}{c}2\left(n_{{\lambda }^{\prime }}^0-n_{{\lambda }^{\prime \prime }}^0\right)\\ n_{{\lambda }^{\prime }}^0+n_{{\lambda }^{\prime \prime }}^0+1\end{array}\right\}\frac{\delta \left({\omega }_{\lambda }\pm {\omega }_{{\lambda }^{\prime }}-{\omega }_{{\lambda }^{\prime \prime }}\right)}{{\omega }_{\lambda }{\omega }_{{\lambda }^{\prime }}{\omega }_{{\lambda }^{\prime \prime }}}.(6)$

Results and Discussion

Phonon Dispersion and Group Velocity

The unit cells of YH₃ under different pressures are displayed in Figure 1. As reported by Peng et al. (2017), these crystals have strong thermal stability. The three types of YH₃ are all three-dimensional structures with different space groups and number of atoms in their unit cells (Peng et al., 2017). The optimized lattice constants and atomic position coordinates of YH₃ in our calculations are obtained from the work by Peng et al. (2017), as listed in Table 1. These different phases of YH₃ provide a valuable comparison for revealing the deep relationship among structures, electrical properties and thermal conductivities (Ashcroft, 1968; Ashcroft, 2004; Grishakov et al., 2019). Due to the same stoichiometry of YH₃ crystals, we denote these structures with different pressures for convenience in the following sections.

FIGURE 1

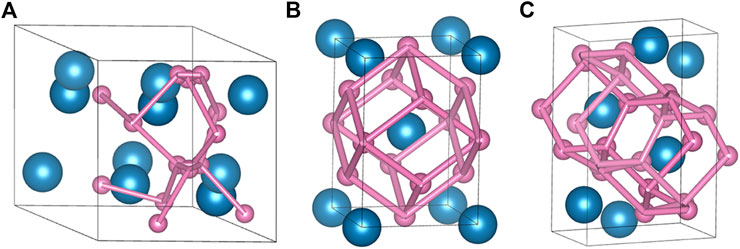
FIGURE 1. The unit cell of YH₃ crystals under different pressures. (A) YH₃ at 0 GPa, (B) YH₃ at 50 GPa, (C) YH₃ at 300 GPa. The pink ball is H, and the blue ball is rare earth yttrium (Y).

TABLE 1

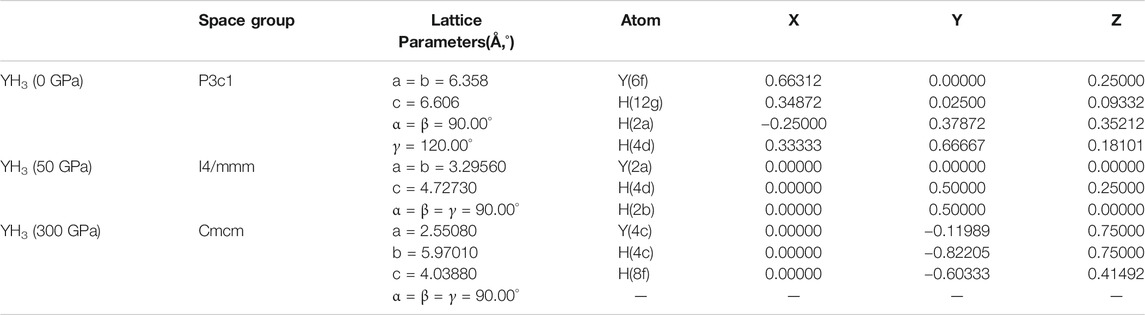
TABLE 1. Structural parameters of YH₃ for 0, 50 and 300 GPa, respectively, adapted from Ref. (Peng et al., 2017).

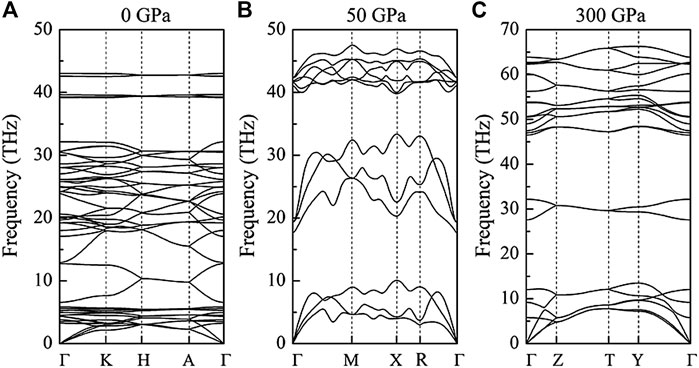
Figure 2 shows the phonon dispersions for YH₃ structures calculated based on the harmonic force constant matrix under different pressures. For the zero pressure structure, the phonon band below 6 THz is notably flattened, which provides more channels for phonon-phonon scattering. In contrast, the phonon dispersion of YH₃ at 50 and 300 GPa have two obvious band gaps. The first band gap is between acoustic and medium optical branches, and the second band gap is between medium optical and highest optical branches. With the increase of pressure, the first band gap becomes wider. For instance, the first band gap of YH₃ at 300 GPa is 12.5 THz, which is 42% wider than that of YH₃ at 50 GPa. The appearance of phonon band gap can effectively inhibit the absorption and emission three-phonons processes and further affect the thermal conductivity (Lindsay et al., 2013), which implies the high thermal conductivity of YH₃ under 300 GPa.

FIGURE 2

FIGURE 2. The phonon dispersion for YH₃ under different pressures.

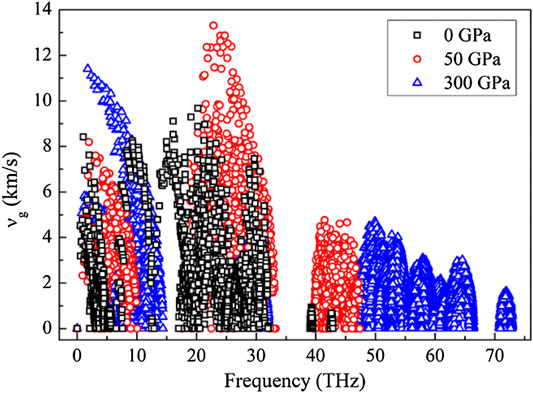
In addition, YH₃ structure becomes even harder with the increase of pressure, which is manifested by the increases of frequency for both acoustic and optical phonon branches. By comparing their lattice constants between these three YH₃ structures in Table 1, we can find that the unit cell volume is compressed by more than 70% when the pressure increases from 0 to 300 GPa. As the unit cell volume of YH₃ is compressed, all bond lengths in YH₃ decrease significantly, and the bond energy increases sharply, especially the H-H bonds with weak covalent interactions. The enhancement of band energy will increase the harmonic force constant, which will bring a vast improvement in phonon frequency and group velocity of YH₃. Consequently, as shown in Figure 3, this dependence leads to the increase of phonon group velocities with pressure, particularly for the substantial enhancement in group velocity for low frequency phonons (below 15 THz). The phonon group velocity of YH₃ at 300 GPa is the largest, which is significantly higher than the case at 0 GPa.

FIGURE 3

FIGURE 3. Phonon group velocity for YH₃ under different pressures.

Thermal Conductivity

Figure 4 shows the calculated temperature dependent thermal conductivities of YH₃ structures, which decreases significantly as temperature increases for all pressures. In our calculation, anharmonic phonon-phonon scattering acts as a major scattering mechanism in pristine crystals without defect or boundary scattering. At high temperature, more phonons are excited due to the enhanced phonon population with temperature. At the same time, the anharmonic effect is enhanced, which greatly increases the scattering rate and limits the phonon mean free path. Moreover, we find that thermal conductivities of YH₃ under different pressures follow the ĸ∼T⁻¹ law quite well at high temperatures, indicating the dominance of U-process in the three-phonon scattering process (Zhang et al., 2017a). More significantly, the enhancement of thermal conductivity is observed with increasing pressure. The room temperature thermal conductivity of YH₃ reaches 1,360 Wm⁻¹K⁻¹ at 300 GPa. Such high thermal conductivity is comparable to the superior thermal conductive materials, such as graphene (∼3,000 Wm⁻¹K⁻¹) (Balandin, 2011), boron arsenide (∼1,400 Wm⁻¹K⁻¹) (Feng et al., 2017; Kang et al., 2018; Li et al., 2018; Tian et al., 2018), boron phosphide (580 Wm⁻¹K⁻¹) (Zheng et al., 2018), BC₂N (1,200 Wm⁻¹K⁻¹) (Shafique and Shin, 2019). In addition, the room temperature thermal conductivities of YH₃ at 0 and 50 GPa are around 10 and 70 Wm⁻¹K⁻¹, respectively. Previous studies reveal that thermal conductivity in solids is positively associated with external pressure, and the relationship is almost linear when the lattice structure is not changed (Mann et al., 2016). In this work, the observed dependence of thermal conductivity in YH₃ on pressure is highly nonlinear, suggesting that the influences of phase transformation and structure variation are quite significant to the thermal conductivity of YH₃. For the whole temperature range, the thermal conductivity of YH₃ at 300 GPa is at least one order of magnitude higher than that at low pressure. However, it can be seen from Figure 3 that the phonon group velocities for three structures, although different, are still on the same order of magnitude. Obviously, the phonon group velocity is not the dominant factor responsible for the observed significantly different thermal conductivity.

FIGURE 4

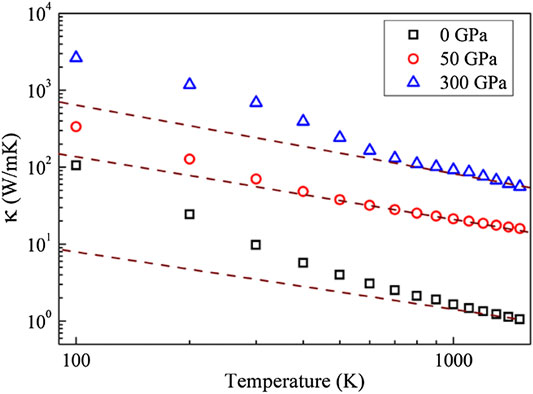
FIGURE 4. Temperature dependent lattice thermal conductivity of YH₃ under different pressures. The dashed lines indicate the κ∼T⁻¹ dependence.

To further explore the different thermal conductivity among three structures, the normalized accumulative thermal conductivities at 300 K vs. phonon frequency are presented in Figure 5. It is noteworthy that accumulative thermal conductivities in all YH₃ structures increase rapidly with frequency in the low-frequency acoustic region (<15 THz), indicating the dominant contributions from acoustic phonon branches. With the increased frequency of phonon, the accumulative thermal conductivity of YH₃ at 0 GPa converges after ∼4.8 THz, while the saturation frequency is ∼9.8 THz and ∼12.6 THz (vertical lines in Figure 5) for the 50 GPa structure and 300 GPa structure, respectively. This increase of saturation frequency with pressure among different structures is consistent with the lifting of phonon frequency upon pressure in the dispersion relation observed in Figure 2.

FIGURE 5

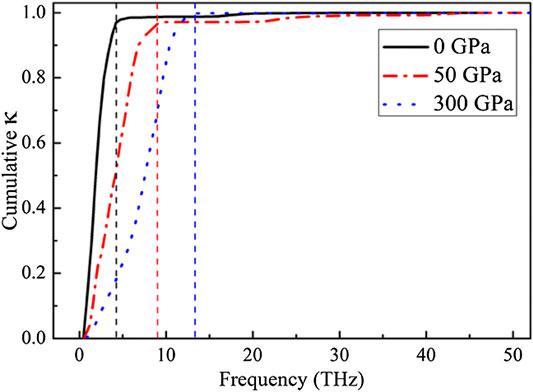
FIGURE 5. Normalized accumulative thermal conductivity for YH₃ under different pressures. The vertical dashed lines highlight the upper bound of acoustic branches for different YH₃ structures.

Phonon Lifetime and Phase Space

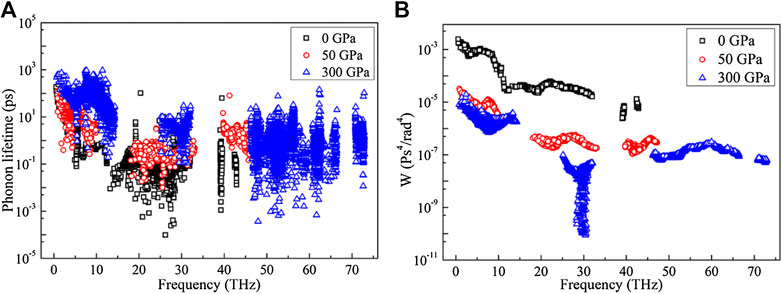
Considering that the harmonic property in terms of phonon group velocity is on the same order of magnitude among three YH₃ structures, the anharmonic phonon-phonon scatterings should have a significant impact on thermal transport in YH₃. In this regard, we further compare in Figure 6A the phonon lifetime of three YH₃ structures at 300 K. The phonon lifetime of YH₃ at 300 GPa is significantly higher than that in other two structures for the whole frequency range, while the phonon lifetime in the structure at 0 GPa is the smallest. Particularly for the low-frequency phonons below 15 THz, the phonon lifetime in the structure at 300 GPa is at least one order of magnitude higher than that in other two structures, which is consistent with the observed notable difference in thermal conductivity. This result further indicates that the large difference in thermal conductivities of structures under different pressures is mainly caused by anharmonic phonon-phonon scattering. Moreover, we found that the phonon relaxation time of YH₃ is on the same order of magnitude as that of the high thermal conductivity materials such as graphene (Zhang et al., 2017b). Therefore, the large phonon group velocity and relaxation time, especially in the low frequency region (<15 THz), eventually lead to the high thermal conductivity of YH₃ at 300 GPa.

FIGURE 6

FIGURE 6. The phonon lifetime (A) and phase space (B) of YH₃ under different pressures at 300 K.

The suppression of phonon lifetime should be originated from the detailed phonon-phonon scattering channels, which can be evaluated by the phase space parameter W in Eq. 6. The phase space parameter W essentially quantifies the existing scattering channels for various phonons, with a large value indicating frequent phonon-phonon scattering process thus a small phonon lifetime (Li and Mingo, 2014).

As shown in Figure 6B, the phase space of the structure at 0 GPa is the largest for the whole frequency range, followed by the structure at 50, and 300 GPa. This observation also agrees well with the obtained phonon lifetime in Figure 6A. As we mentioned before, there are two obvious band gaps in the phonon dispersion for the YH₃ structures at 50 and 300 GPa, which is absent in the structure at 0 GPa. Moreover, the band gap for the structure at 300 GPa is notably wider than that at 50 GPa. The existence of band gap makes the phonon absorption process ($\lambda +{\lambda }^{\prime }\to {\lambda }^{\prime \prime }$) and emission process ($\lambda \to {\lambda }^{\prime }+{\lambda }^{\prime \prime }$) more difficult (Lindsay et al., 2013). On the one hand, when the pressure varies from 0 to 300 GPa, YH₃ undergoes a phase transition from a hexagonal to a cubic crystal system. Table 1 reveals that the unit cell volume is compressed by more than 70% when the pressure increases from 0 to 300 GPa. As the unit cell volume of YH₃ is compressed, all bond lengths in YH₃ decrease significantly, and the bond energy increases sharply, especially the H-H bonds with weak covalent interactions. For crystalline materials, the enhancement of bond energy will increase the force constant matrix of lattice vibration, which makes the phonon frequency and group velocity increase rapidly (Ouyang and Hu, 2015; Hummel et al., 2020), especially for the acoustic phonon branch. Moreover, the increase of pressure can weaken the phonon-phonon scattering and increase the phonon relaxation time, thus enhancing the material’s thermal conductivity (Beldjoudi et al., 2019). As the number of three phonon-phonon scattering channels is greatly reduced at high pressure, the phonon lifetime of low-frequency acoustic phonons and further thermal conductivity is significantly enhanced. As the band gap is smaller in the structure at 50 GPa, the enhancement of phonon lifetime and thermal conductivity is suppressed. Moreover, because of the mixed acoustic and optical branches for the structure at 0 GPa, the pronounced phonon-phonon scattering processes are observed, manifested by the large phase space parameter. Thus, the suppressed phonon lifetime and thermal conductivity are observed in the structure at 0 GPa.

Conclusion

We have studied the lattice thermal conductivities of YH₃ structures under different pressures by using Boltzmann transport equation and first-principle calculations. It is found that thermal conductivity of YH₃ increases nonlinearly with pressure. Strikingly, the YH₃ structure at 300 GPa, which is the superconducting phase, has remarkably high thermal conductivity around 1,360 W m⁻¹K⁻¹ at room temperature. For the YH₃ structure at 0 GPa, a large number of flat bands appear at the low-frequency region in the phonon dispersion relation, and are mixed with the acoustic branches, which causes the strong phonon-phonon scattering and thus effectively suppresses the phonon lifetime and thermal conductivity. With increasing pressure, the unit cell volume of YH₃ is compressed by more than 70% and YH₃ structure changes from a hexagonal to a cubic crystal system. The increase of group velocity due to the enhancement of bond energy and the weakened phonon-phonon scattering are both responsible for the ultrahigh thermal conductivity of YH₃ at 300 GPa. Our study uncovers the phononic thermal transport properties of yttrium hydrides allotropes, and also provides a new opportunity to achieve high thermal dissipation ability with external pressure.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WR performed the calculations. JC supervised the project. All authors discussed the results and wrote the manuscript.

Funding

This project is supported in part by the grants from the National Natural Science Foundation of China (Grant Nos. 11890703 and 11775158), Science and Technology Commission of Shanghai Municipality (Grant Nos. 19ZR1478600 and 18JC1410900), the Fundamental Research Funds for the Central Universities (Grant No. 22120200069), and Open Fund of Hunan Provincial Key Laboratory of Advanced Materials for New Energy Storage and Conversion (Grant No. 2018TP1037_201901).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alva, G., Lin, Y., and Fang, G. (2018). An overview of thermal energy storage systems. Energy 144, 341–378. doi:10.1016/j.energy.2017.12.037

PubMed | CrossRef Full Text | Google Scholar

Ashcroft, N. W. (1968). Metallic hydrogen: a high-temperature superconductor?. Phys. Rev. Lett. 21, 1748–1749. doi:10.1103/physrevlett.21.1748

PubMed | CrossRef Full Text | Google Scholar

Ashcroft, N. W. (2004). Hydrogen dominant metallic alloys: high temperature superconductors?. Phys. Rev. Lett. 92, 187002. doi:10.1103/physrevlett.92.187002

PubMed | CrossRef Full Text | Google Scholar

Balandin, A. A. (2011). Thermal properties of graphene and nanostructured carbon materials. Nature Mater 10, 569–581. doi:10.1038/nmat3064

PubMed | CrossRef Full Text | Google Scholar

Beldjoudi, K., Sahraoui, F. A., and Bouhemadou, A. (2019). Pressure effect on the structural, elastic and thermodynamic properties of the BeP2N4 compound: first-principles investigation. Comput. Condens. Matter 21, e00408. doi:10.1016/j.cocom.2019.e00408

PubMed | CrossRef Full Text | Google Scholar

Chen, J., Walther, J. H., and Koumoutsakos, P. (2014). Strain engineering of kapitza resistance in few-layer graphene. Nano Lett. 14, 819–825. doi:10.1021/nl404182k

PubMed | CrossRef Full Text | Google Scholar

Errea, I., Calandra, M., Pickard, C. J., Nelson, J. R., Needs, R. J., Li, Y., et al. (2016). Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system. Nature 532, 81–84. doi:10.1038/nature17175

PubMed | CrossRef Full Text | Google Scholar

Feng, T., Lindsay, L., and Ruan, X. (2017). Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96, 161201. doi:10.1103/physrevb.96.161201

PubMed | CrossRef Full Text | Google Scholar

Feng, T., Qiu, B., and Ruan, X. (2015). Coupling between phonon-phonon and phonon-impurity scattering: a critical revisit of the spectral Matthiessen's rule, Phys. Rev. B 92, 235206. doi:10.1103/physrevb.92.235206

PubMed | CrossRef Full Text | Google Scholar

Ghosh, S., Calizo, I., Teweldebrhan, D., Pokatilov, E. P., Nika, D. L., Balandin, A. A., et al. (2008). Extremely high thermal conductivity of graphene: prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 92, 151911. doi:10.1063/1.2907977

PubMed | CrossRef Full Text | Google Scholar

Grishakov, K. S., Degtyarenko, N. N., and Mazur, E. A. (2019). Electron, phonon, and superconducting properties of yttrium and sulfur hydrides under high pressures. J. Exp. Theor. Phys. 128, 105–114. doi:10.1134/s1063776119010072

PubMed | CrossRef Full Text | Google Scholar

Heil, C., di Cataldo, S., Bachelet, G. B., and Boeri, L. (2019). Superconductivity in sodalite-like yttrium hydride clathrates, Phys. Rev. B 99, 220502. doi:10.1103/physrevb.99.220502

PubMed | CrossRef Full Text | Google Scholar

Hu, S., Zhang, Z., Jiang, P., Chen, J., Volz, S., Nomura, M., et al. (2018). Randomness-induced phonon localization in graphene heat conduction. J. Phys. Chem. Lett. 9, 3959–3968. doi:10.1021/acs.jpclett.8b01653

PubMed | CrossRef Full Text | Google Scholar

Hummel, P., Lechner, A. M., Herrmann, K., Biehl, P., Rössel, C., Wiedenhöft, L., et al. (2020). Thermal transport in ampholytic polymers: the role of hydrogen bonding and water uptake. Macromolecules 53, 5528–5537. doi:10.1021/acs.macromol.0c00596

PubMed | CrossRef Full Text | Google Scholar

Ito, M., Matsunaga, J., Setoyama, D., Muta, H., Kurosaki, K., Uno, M., et al. (2005). Thermal properties of yttrium hydride. J. Nucl. Mater. 344, 295–297. doi:10.1016/j.jnucmat.2005.04.058

PubMed | CrossRef Full Text | Google Scholar

Jarosik, M. W., Szczȩśniak, R., Wrona, I. A., and Kostrzewa, M. (2017). Non-BCS superconducting state in yttrium hydride at a record low value of the external pressure. Solid State Commun. 250, 5–8. doi:10.1016/j.ssc.2016.11.002

PubMed | CrossRef Full Text | Google Scholar

Kang, J. S., Li, M., Wu, H., Nguyen, H., and Hu, Y. (2018). Experimental observation of high thermal conductivity in boron arsenide. Science 361, 575–578. doi:10.1126/science.aat5522

PubMed | CrossRef Full Text | Google Scholar

Kim, D. Y., Scheicher, R. H., and Ahuja, R. (2009). Predicted high-temperature superconducting state in the hydrogen-dense transition-metal hydride YH3 at 40 K and 17.7 GPa. Phys. Rev. Lett. 103, 077002. doi:10.1103/physrevlett.103.077002

PubMed | CrossRef Full Text | Google Scholar

Kim, D. Y., Scheicher, R. H., Mao, H.-k., Kang, T. W., and Ahuja, R. (2010). General trend for pressurized superconducting hydrogen-dense materials. Proc. Natl. Acad. Sci. U. S. A. 107, 2793–2796. doi:10.1073/pnas.0914462107

PubMed | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

PubMed | CrossRef Full Text | Google Scholar

Kundu, A., Mingo, N., Broido, D. A., and Stewart, D. A. (2011). Role of light and heavy embedded nanoparticles on the thermal conductivity of SiGe alloys. Phys. Rev. B 84, 125426. doi:10.1103/physrevb.84.125426

PubMed | CrossRef Full Text | Google Scholar

Li, R., Cheng, X., Xie, Q., Sun, Y., Li, D., Li, Y., et al. (2015). Topological metal of NaBi with ultralow lattice thermal conductivity and electron-phonon superconductivity. Sci. Rep. 5, 8446. doi:10.1038/srep08446

PubMed | CrossRef Full Text | Google Scholar

Li, S., Zheng, Q., Lv, Y., Liu, X., Wang, X., Huang, P. Y., et al. (2018). High thermal conductivity in cubic boron arsenide crystals. Science 361, 579–581. doi:10.1126/science.aat8982

PubMed | CrossRef Full Text | Google Scholar

Li, W., Carrete, J., Katcho, N. A., and Mingo, N. (2014). ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

PubMed | CrossRef Full Text | Google Scholar

Li, W., Lindsay, L., Broido, D. A., Stewart, D. A., and Mingo, N. (2012). Thermal conductivity of bulk and nanowire Mg2SixSn1-x alloys from first principles. Phys. Rev. B 86, 174307. doi:10.1103/physrevb.86.174307

PubMed | CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2014). Thermal conductivity of fully filled skutterudites: role of the filler. Phys. Rev. B 89, 184304. doi:10.1103/physrevb.89.184304

PubMed | CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2015). Ultralow lattice thermal conductivity of the fully filled skutterudite YbFe4Sb12 due to the flat avoided-crossing filler modes. Phys. Rev. B 91, 144304. doi:10.1103/physrevb.91.144304

PubMed | CrossRef Full Text | Google Scholar

Li, X., and Peng, F. (2017). Superconductivity of pressure-stabilized vanadium hydrides. Inorg. Chem. 56, 13759–13765. doi:10.1021/acs.inorgchem.7b01686

PubMed | CrossRef Full Text | Google Scholar

Lindsay, L., and Broido, D. A. (2008). Three-phonon phase space and lattice thermal conductivity in semiconductors. J. Phys. Condens. Matter 20, 165209. doi:10.1088/0953-8984/20/16/165209

PubMed | CrossRef Full Text | Google Scholar

Lindsay, L., Broido, D. A., and Reinecke, T. L. (2013). First-Principles determination of ultrahigh thermal conductivity of boron arsenide: a competitor for diamond?. Phys. Rev. Lett. 111, 025901. doi:10.1103/physrevlett.111.025901

PubMed | CrossRef Full Text | Google Scholar

Liu, H., Naumov, I. I., Hoffmann, R., Ashcroft, N. W., and Hemley, R. J. (2017). Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. U. S. A. 114, 6990–6995. doi:10.1073/pnas.1704505114

PubMed | CrossRef Full Text | Google Scholar

Liu, H., Qin, G., Lin, Y., and Hu, M. (2016). Disparate strain dependent thermal conductivity of two-dimensional penta-structures. Nano Lett. 16, 3831–3842. doi:10.1021/acs.nanolett.6b01311

PubMed | CrossRef Full Text | Google Scholar

Liu, L.-L., Sun, H.-J., Wang, C. Z., and Lu, W.-C. (2017). High-pressure structures of yttrium hydrides. J. Phys. Condens. Matter 29, 325401. doi:10.1088/1361-648x/aa787d

PubMed | CrossRef Full Text | Google Scholar

Mann, S., Rani, P., Kumar, R., Dubey, G. S., and Jindal, V. K. (2016). Thermodynamic properties of pure and doped (B, N) graphene. RSC Adv. 6, 12158–12168. doi:10.1039/c5ra25239c

PubMed | CrossRef Full Text | Google Scholar

Michael, B., and Michael, E. W. (2011). Isotopic compositions of the elements 2009 (IUPAC technical report). Pure Appl. Chem. 83, 397–410. doi:10.1351/PAC-REP-10-06-02

PubMed | CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations Phys. Rev. B 13, 5188–5192. doi:10.1103/physrevb.13.5188

PubMed | CrossRef Full Text | Google Scholar

Omini, M., and Sparavigna, A. (1995). An iterative approach to the phonon Boltzmann equation in the theory of thermal conductivity. Phys. B Condens. Matter 212, 101–112. doi:10.1016/0921-4526(95)00016-3

PubMed | CrossRef Full Text | Google Scholar

Ouyang, T., and Hu, M. (2015). Competing mechanism driving diverse pressure dependence of thermal conductivity of XTe (X = Hg, Cd, and Zn). Phys. Rev. B 92, 235204. doi:10.1103/physrevb.92.235204

PubMed | CrossRef Full Text | Google Scholar

Ouyang, Y., Zhang, Z., Li, D., Chen, J., and Zhang, G. (2019). Emerging theory, materials, and screening methods: new opportunities for promoting thermoelectric performance. Ann. Phys. 531, 1800437. doi:10.1002/andp.201800437

PubMed | CrossRef Full Text | Google Scholar

Peng, F., Sun, Y., Pickard, C. J., Needs, R. J., Wu, Q., and Ma, Y. (2017). Hydrogen clathrate structures in rare earth hydrides at high pressures: possible route to room-temperature superconductivity. Phys. Rev. Lett. 119, 107001. doi:10.1103/physrevlett.119.107001

PubMed | CrossRef Full Text | Google Scholar

Shafique, A., and Shin, Y.-H. (2019). Ultrahigh and anisotropic thermal transport in the hybridized monolayer (BC2N) of boron nitride and graphene: a first-principles study. Phys. Chem. Chem. Phys. 21, 17306–17313. doi:10.1039/c9cp02068c

PubMed | CrossRef Full Text | Google Scholar

Shi, L., Chen, J., Zhang, G., and Li, B. (2012). Thermoelectric figure of merit in Ga-doped [0001] Z00nO nanowires. Phys. Lett. 376, 978–981. doi:10.1016/j.physleta.2011.12.040

PubMed | CrossRef Full Text | Google Scholar

Soroka, O., Sturm, J. M., van de Kruijs, R. W. E., Lee, C. J., and Bijkerk, F. (2018). Control of YH3 formation and stability via hydrogen surface adsorption and desorption, Appl. Surf. Sci. 455, 70–74. doi:10.1016/j.apsusc.2018.05.134

PubMed | CrossRef Full Text | Google Scholar

Tamura, S.-i. (1983). Isotope scattering of dispersive phonons in Ge. Phys. Rev. B 27, 858–866. doi:10.1103/physrevb.27.858

PubMed | CrossRef Full Text | Google Scholar

Tanaka, K., Tse, J. S., and Liu, H. (2017). Electron-phonon coupling mechanisms for hydrogen-rich metals at high pressure. Phys. Rev. B 96, 100502. doi:10.1103/physrevb.96.100502

PubMed | CrossRef Full Text | Google Scholar

Tian, F., Song, B., Chen, X., Ravichandran, N. K., Lv, Y., Chen, K., et al. (2018). Unusual high thermal conductivity in boron arsenide bulk crystals. Science 361, 582–585. doi:10.1126/science.aat7932

PubMed | CrossRef Full Text | Google Scholar

Togo, A., Oba, F., and Tanaka, I. (2008). First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-typeSiO2 at high pressures. Phys. Rev. B 78, 134106. doi:10.1103/physrevb.78.134106

PubMed | CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2010). Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116. doi:10.1103/physrevb.82.094116

PubMed | CrossRef Full Text | Google Scholar

Wang, H., Tse, J. S., Tanaka, K., Iitaka, T., and Ma, Y. (2012). Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. U. S. A. 109, 6463–6466. doi:10.1073/pnas.1118168109

PubMed | CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070. doi:10.1016/j.cpc.2012.05.008

PubMed | CrossRef Full Text | Google Scholar

Wigner, E., and Huntington, H. B. (1935). On the possibility of a metallic modification of hydrogen. J. Chem. Phys. 3, 764–770. doi:10.1063/1.1749590

PubMed | CrossRef Full Text | Google Scholar

Xie, G., Ju, Z., Zhou, K., Wei, X., Guo, Z., Cai, Y., et al. (2018). Ultra-low thermal conductivity of two-dimensional phononic crystals in the incoherent regime. Npj Comput. Mater. 4, 21. doi:10.1038/s41524-018-0076-9

PubMed | CrossRef Full Text | Google Scholar

Xu, X., Zhou, J., and Chen, J. (2020). Thermal transport in conductive polymer-based materials. Adv. Funct. Mater. 30, 1904704. doi:10.1002/adfm.201904704

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., and Chen, J. (2018). Thermal conductivity of nanowires. Chin. Phys. B 27, 035101. doi:10.1088/1674-1056/27/3/035101

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., Chen, J., and Li, B. (2017a). Negative Gaussian curvature induces significant suppression of thermal conduction in carbon crystals. Nanoscale 9, 14208–14214. doi:10.1039/c7nr04944g

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., Hu, S., Chen, J., and Li, B. (2017b). Hexagonal boron nitride: a promising substrate for graphene with high heat dissipation. Nanotechnology 28, 225704. doi:10.1088/1361-6528/aa6e49

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., Hu, S., Nakayama, T., Chen, J., and Li, B. (2018). Reducing lattice thermal conductivity in schwarzites via engineering the hybridized phonon modes. Carbon 139, 289–298. doi:10.1016/j.carbon.2018.06.057

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., Hu, S., Xi, Q., Nakayama, T., Volz, S., Chen, J., et al. (2020a). Tunable phonon nanocapacitor built by carbon schwarzite based host-guest system. Phys. Rev. B 101, 081402(R). doi:10.1103/physrevb.101.081402

PubMed | CrossRef Full Text | Google Scholar

Zhang, Z., Ouyang, Y., Cheng, Y., Chen, J., Li, N., and Zhang, G. (2020b). Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 860, 1–26. doi:10.1016/j.physrep.2020.03.001

PubMed | CrossRef Full Text | Google Scholar

Zheng, Q., Li, S., Li, C., Lv, Y., Liu, X., Huang, P. Y., et al. (2018). High thermal conductivity in isotopically enriched cubic boron phosphide. Adv. Funct. Mater. 28, 1805116. doi:10.1002/adfm.201805116

PubMed | CrossRef Full Text | Google Scholar

Zhong, X., Wang, H., Zhang, J., Liu, H., Zhang, S., Song, H.-F., et al. (2016). Tellurium hydrides at high pressures: high-temperature superconductors, Phys. Rev. Lett. 116, 057002. doi:10.1103/physrevlett.116.057002

PubMed | CrossRef Full Text | Google Scholar

Zhu, X.-L., Liu, P.-F., Zhang, J., Zhang, P., Zhou, W.-X., Xie, G., et al. (2019). Monolayer SnP3: an excellent p-type thermoelectric material. Nanoscale 11, 19923–19932. doi:10.1039/c9nr04726c

PubMed | CrossRef Full Text | Google Scholar