Analysis of the Influence of Temperature Field on the Dynamic Modulus of Rubber Asphalt Pavement

In this paper, asphalt mixture performance test is used to study the dynamic modulus of different types of rubber asphalt mixtures in the laboratory, based on the viscoelastic theory, in order to determine the actual dynamic modulus of different structural layers under the action of temperature field in the asphalt pavement. Based on the time-temperature equivalence principle and Sigmund model, the dynamic modulus main curve is established, and establish the correlation equation between temperature and dynamic modulus. The actual dynamic modulus of asphalt concrete at each pavement layer is calculated by referring to the test data of pavement temperature field in Shijiazhuang and Tangshan, and compare and analyze the design value and actual value of dynamic modulus. The results show that the influence of external factors such as temperature and frequency on the dynamic modulus of asphalt mixture is far greater than that of internal factors such as cement and gradation type. Affected by the temperature field, the dynamic modulus of concrete at different structural levels is dynamically changing. Taking the dynamic modulus at 20°C and 10 Hz as the limiting index for design data selection is inconsistent with reality and needs to be improved. This study not only provides the basis for dynamic modulus selection in asphalt pavement design, but also has certain reference value for improving the life of asphalt pavement.

Introduction

Waste tire rubber powder modified asphalt not only solves the environmental pollution of solid waste, but also realizes the reuse of waste resources. Many experts and scholars have studied rubber asphalt and mixture (Li et al., 2019; Fang et al., 2020; Xia et al., 2021), and proved that rubber asphalt mixture has excellent pavement performance. With the implementation of Highway Asphalt Pavement Design Code (JTG D50-2017), dynamic compression modulus is one of the important parameters in asphalt pavement design. The test and model estimation of dynamic compression modulus of asphalt mixture are still the research hotspots.

In order to determine the influencing factors of the dynamic modulus of asphalt mixture, 8 AC mixtures were selected in reference (Ali et al., 2016). Uniaxial dynamic moduli at various temperatures and frequencies were tested using asphalt mixture performance testers. The nonlinear regression model is established. The dynamic modulus is expressed as the test temperature and is loaded as a function of the frequency and volume parameters of the mixture. In reference (Wang et al., 2019), specimens with different asphalt content layers were prepared and Superpave Simple Performance Tester was used for dynamic modulus test. The results show that the dynamic modulus of asphalt mixture increases with the increase of loading frequency and decreases with the increase of test temperature.The study of the main dynamic modulus curve of asphalt mixture (Ruan et al., 2018; Su et al., 2018) facilitated the selection of dynamic modulus in a wide range. In the field of dynamic modulus prediction of asphalt mixtures, literature (Nemati and Dave, 2018) developed an asphalt mixture dynamic modulus and phase Angle prediction model based on the laboratory test results of more than 4,300 asphalt mixtures in New England, USA. Literature (Ghasemi et al., 2019) developed an accurate finite element (FE) model using a mixture of elastic modulus and asphalt binder performance prediction. This model has been verified in nine different pavement projects in five regions in the United States, which proves that ANN modeling can accurately predict dynamic modulus.

In literature (Rahman et al., 2019), the Witczak dynamic modulus prediction equation based on viscosity was modified, and the dynamic modulus of asphalt concrete under 21 different conditions was tested. The results showed that the Witczak model based on viscosity underestimates the dynamic modulus, and the modified Witczak model based on viscosity had a higher accuracy in determining the dynamic modulus. In terms of the impact of asphalt aging on dynamic modulus of asphalt mixture, three types of asphalt mixture with different aging states were used in literature (Wen and Wang, 2019) to study the change of the impact of aging on dynamic modulus of asphalt mixture. In the literature (Arefin et al., 2019), asphalt mixture was prepared with four bitumen binators and one aggregate. The prediction model 1-37A and NCHRP 1-40D and the Global Aging System integrated in MEPDG were used to predict the dynamic modulus of short-term and long-term Aging HMA and foaming WMA mixtures. The results showed that the NCHRP 1-37A model generally underestimates the dynamic modulus of HMA mixtures, but provides better adhesion quality for foaming WMA mixtures. The NCHRP 1-40D model usually results in higher dynamic modulus values. In terms of dynamic modulus prediction of pavement performance, literature (Hou et al., 2016) evaluated pavement performance by using the predicted dynamic modulus for model analysis. In literature (Robbins and Timm, 2011), binder and mixture were used to estimate various frequencies and dynamic moduli in combination with the application of dynamic moduli of asphalt mixtures in the southeastern United States.

In terms of the influence of temperature field on the performance of asphalt concrete, the literature (Qian et al., 2020) found that the rolling temperature and layer thickness affect the overall temperature field in the compaction process, and the wind speed and air temperature mainly affect the hot mixed asphalt. (HMA) The temperature field of the upper layer. The temperature change of the bottom layer mainly affects the temperature field at the bottom of the layer. Literature (Chen et al., 2017) uses the Green's function method, taking solar radiation, wind speed and temperature and other climate factors as input parameters to obtain an analytical solution for the temperature field in the multilayer pavement structure. Literature (Huang et al., 2016) uses the discrete element method to analyze the feasibility of the asphalt mixture temperature field. The test results show that the numerical simulation results are basically consistent with the experimental results. DEM may become a promising new method to study the temperature field distribution and other properties of asphalt mixtures. Literature (Sun et al., 2020) uses a multi-scale finite element method based on microstructure to study the influence of temperature field on the internal damage of asphalt pavement under traffic load, and recognize the importance of considering temperature field in pavement structure analysis.

Based on the above-mentioned documents, people have realized the influencing factors of the dynamic modulus of asphalt mixture, and carried out the dynamic modulus prediction model; the temperature field is an important factor affecting the damage of the asphalt pavement, and numerical simulations have been carried out. However, there are still some gaps in the impact of the temperature field on the dynamic modulus of asphalt concrete, the difference between the design dynamic modulus of asphalt pavement and the actual dynamic modulus, and the impact on the pavement performance.

In this paper, based on viscoelastic theory and asphalt mixture performance test (AMPT) method, the relationship between dynamic modulus of rubber asphalt mixture and temperature and loading frequency was determined by indoor AMPT test, and the main dynamic modulus curve was established. Based on the research results of temperature field of asphalt pavement in Hebei Province, the dynamic modulus of asphalt concrete in different layers was calculated, the influence of temperature field on dynamic modulus was analyzed, and the suggested indexes for dynamic modulus selection were put forward. This study not only determines the change rule and value range of the actual dynamic modulus of asphalt pavement, but also improves the pertinence of the selection of asphalt pavement design parameters, which has important research value and practical significance.

Theoretical Basis and Methods

Viscoelastic Theory

General mechanical analysis, model construction and failure mechanism research of asphalt mixture (Teixeira et al., 2014; Liu et al., 2018; Zhang et al., 2019) are mostly based on viscoelastic theory. When the stress is the input and the strain is the stress response, the mathematical description of the material input and response is called the constitutive relationship. When describing the constitutive equations of Hooke's elasticity, Newtonian viscosity and viscoelastic, the spring is used to represent Hooke's elasticity, the viscous flow is used to represent Newtonian viscous flow, and the combination of spring and viscoelastic element is used to represent viscoelastic element. According to the number and combination of spring and clay pot elements, the viscoelastic model can be divided into Kelvin element, Maxwell element, three-element model and four-element model.

The viscoelastic model of asphalt mixture can be constructed by means of integral equation, differential equation and complex equation. The viscoelastic model can be divided into static and dynamic load forms according to the loading time. The stress generated by vibration load is called periodic alternating stress. Cyclic alternating stress can better represent the effect of moving vehicle on asphalt pavement than static test stress. In recent years, it has become an important method to analyze the mechanical response of viscoelastic materials with alternating stress. The stress can be described by Eq. 1 (Zhang, 2006).

$\text{σ}\left(t\right)={\sigma }_0{e}^{i\omega t}={\sigma }_0\left(\cos \omega t+\sin \omega t\right)(1)$

where, ${\sigma }_0$ is the strain amplitude and ω is the angular frequency. The stress at a certain moment can be divided into real part ${\epsilon }_0\cos \omega t$and imaginary part ${\epsilon }_0\sin \omega t$.

The volume constitutive equation is:

$\frac{\sigma }{\eta }+\frac{\dot{\sigma }}{E}=\dot{\epsilon }(2)$

After substituting Eq. 1 into Eq. 2, it can be obtained:

$\dot{\epsilon }=\left(\frac{1}{\eta }+i\frac{\omega }{E}\right){\sigma }_0{e}^{i\omega t}(3)$

So,

$\text{ε}=\frac{{\sigma }_0}{i\omega }\left(\frac{1}{\eta }+i\frac{\omega }{E}\right)e^{i\omega t}=\frac{1}{E}\sqrt{1+\frac{1}{{\omega }^3{\tau }_r^3}}{\sigma }_0{e}^{\left(i\omega -\delta \right)}={\epsilon }_0{e}^{\left(i\omega -\delta \right)}\omega (4)$

where, $\text{δ}={\tan }^{-1}\frac{1}{\omega {\tau }_r}$ .

The above equation shows that when the alternating stress vibrates at angular frequency $\omega$, the strain response has the same vibration frequency. But there is $\text{δ}$ difference between the stress vector and the strain vector. The ratio of the stress vector to the strain vector is the complex modulus of elasticity, represented by $E^{\ast }$.

$E^{\ast }=\frac{\sigma }{\epsilon }=\frac{{\sigma }_0{e}^{i\omega t}}{\frac{1}{E}\left(1-i\frac{1}{\omega {\tau }_r}\right){\sigma }_0{e}^{i\omega t}}=E\frac{{\omega }^2{\tau }_r^2+i\omega {\tau }_r}{1+{\omega }^2{\tau }_r^2}(5)$

Let the real part be $E^{\prime }=E\frac{{\omega }^2{\tau }_r^2}{1+{\omega }^2{\tau }_r^2}$ , and the imaginary part be $E^{″}=E\frac{\omega {\tau }_r}{1+{\omega }^2{\tau }_r^2}$, then:

$E^{\ast }=E^{\prime }+i{E}^{″}=\left|E^{\ast }\right|\left(E^{\prime }\cos \delta +i{E}^{″}\sin \delta \right)(6)$

The modulus $\left|E^{\ast }\right|$ of the complex function is called the dynamic modulus, and $\delta$ is the phase Angle of stress and strain. $E^{\prime }$ represents the energy stored and released by the material under the action of alternating stress, which is called the storage modulus. $E^{″}$ represents the lost energy, which is called the loss modulus.

Since the mechanical behavior of viscoelastic materials is affected by the viscous component and the viscous flow deformation is a function of time, the mechanical behavior of viscoelastic materials is a function of time. Meanwhile, the flow characteristics of viscoelastic materials are also affected by temperature changes, as shown in Eq. 7.

$\text{E}\left(T_1\mathrm{，}t\right)=\text{E}\left(T_2\mathrm{，}t/a_T\right)(7)$

The above equation shows that there is a certain conversion relation between time factor and temperature factor. This conversion is called the time-temperature conversion rule.

Time-Temperature Equivalence Principle

At present, the time-temperature conversion calculation theory of asphalt mixture mainly adopts three methods (Rowe and Sharrock, 2011), Williams-Landel-Ferry (WLF) equation, Arrhenius equation and polynomial equation. Where, the WLF equation is shown in Eq. 8.

${\log }_{10}a\left(T\right)=\frac{-C_1\left(T-T_r\right)}{C_2+\left(T-T_r\right)}(8)$

where, $a\left(T\right)$ is the shift factor, $T$ is the temperature corresponding to the translation curve, $T_r$ is the reference temperature (the temperature field of the road at the site of the project), and $C_1$, $C_2$ are the regression coefficients.

Arrhenius equation is shown in Eq. 9.

${\log }_{10}a\left(T\right)=\frac{\Delta E_a}{19.14714}\left[\left(\frac{1}{T}\right)-\left(\frac{1}{T_r}\right)\right](9)$

where, $\Delta E_a$ is the activation energy, which is related to the asphalt material itself and can be obtained in the regression analysis.

Polynomial equation means to move a test curve towards a curve with known test results. The reference temperature is one of the curves in the cluster. The value of the shift factor was obtained by regression analysis, as shown in Eq. 10.

${\log }_{10}a\left(T\right)=a{T}^2+bT+c(10)$

where, $a$, $b$ and $c$ are regression coefficients. From the equation form, the value of the shift factor is a quadratic function of temperature.

Since WLF Eq. 8 is not well applied to low temperature, the polynomial equation cannot obtain the main curve at unknown temperature. Therefore, the Arrhenius equation was used as the calculation method of dynamic modulus shift factor in this paper.

Asphalt Mixture Samples

Based on the viscoelastic theory, the AMPT applied the load to the specimen in the form of input alternating stress. It can measure the mechanical behavior of concrete under different temperature and frequency and simulate the dynamic load response of asphalt pavement.

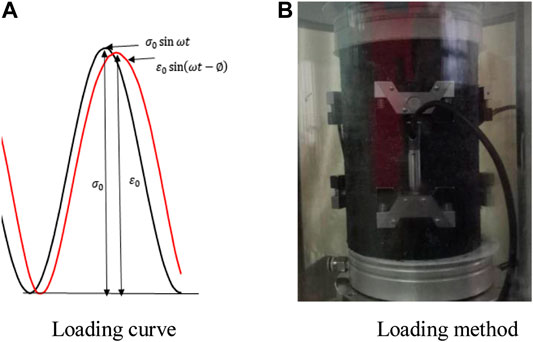
Figure 1A is the loading curve of the test dynamic modulus, and Figure 1B is the test equipment of the test dynamic modulus. The modulus loading curve is usually half sinusoidal. Dynamic modulus equipment can be applied at different temperatures, loads and frequencies.

FIGURE 1

FIGURE 1. Dynamic modulus test.

Four frequency - modulus curves were obtained by four temperature dynamic modulus tests in the laboratory. Six frequencies are measured at each temperature. Select the pavement temperature of the project site as the reference temperature. Translate each curve to the reference temperature according to the Anius time-temperature conversion principle. The least square fitting of an S-shaped curve results in a modulus curve with a wide range of frequencies.

Major curve fitting was performed by Using Sigmoidal function (Su et al., 2018), as shown in Eq. 11.

$\log \left|E^{\ast }\right|=\log \left(min\right)+\frac{\left(\log \left(Max\right)-\log \left(Min\right)\right)}{1+e^{\beta +\gamma \left\{\log \omega +\frac{\Delta E_a}{19.14714}\left[\left(\frac{1}{T}\right)-\left(\frac{1}{T_r}\right)\right]\right\}}}(11)$

where, |E*| is the dynamic modulus. ω is the loading frequency (Hz) at the test temperature. Max represents the limited maximum modulus (MPa). Min is the limited minimum modulus (MPa). β and γ are the fitting parameters. The maximum modulus is obtained from Eqs 12 and 13.

${\left|E^{\ast }\right|}_{max}=P_c\left[4 200 000\left(1-\frac{VMA}{100}\right)+435 000\left(\frac{VFA\times VMA}{10 000}\right)\right]+\frac{1-P_c}{\left[\frac{\left(1-\frac{VMA}{100}\right)}{4 200 000}+\frac{VMA}{435 000\left(VFA\right)}\right]}(12)$

$P_c=\frac{{\left(20+\frac{435 000\left(VFA\right)}{VMA}\right)}^{0.58}}{650+{\left(\frac{435 000\left(VFA\right)}{VMA}\right)}^{0.58}}(13)$

where, VFA is the saturation of asphalt mixture and VMA is the clearance rate of asphalt mixture ore.

Indoor Dynamic Modulus Test and Analysis of Asphalt Mixture

Test Materials

The test material is modified asphalt with 30% and 40% rubber powder. The performance indexes of rubber powder modified asphalt are shown in Table 1.

TABLE 1

TABLE 1. Performance index of rubber powder modified asphalt.

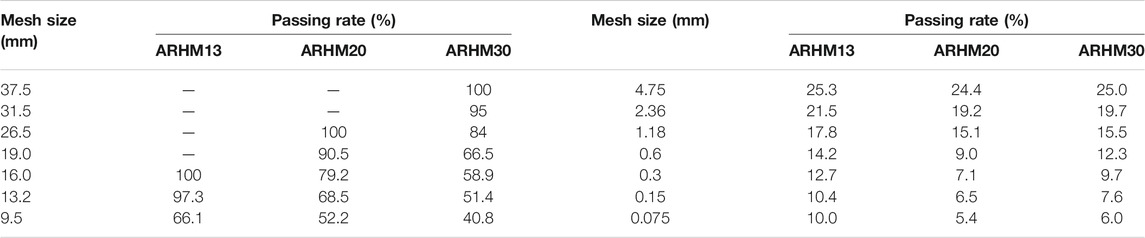
The ore material is five-grade stone material, whose performance conforms to the specification requirements. They are mechanism sand, filler, 5∼10, 10∼15, 10∼20 mm, respectively. According to the demand of the upper, middle and lower layers of pavement, the rubber asphalt mixture is of ARHM13, ARHM20 and ARHM30 respectively. The gradation of rubber asphalt mixture synthesis is shown in Table 2.

TABLE 2

TABLE 2. Types of rubber asphalt mixture.

Test Design

In order to determine the impact of asphalt binder on the dynamic modulus of rubber asphalt mixture, 30% and 40% rubber asphalt were used to prepare ARHM13 mixture for comparison test; ARHM20 and ARHM30 two mixtures used 40% rubber asphalt .

In the experiment, Marshall test method was used to determine the best whetstone ratio. The design void ratio was 4.0%, and the test process was not repeated. The optimum whetstone ratios of ARHM13, ARHM20 and ARHM30 were 6.4%, 4.5% and 4.0%, respectively. The dynamic modulus test piece was prepared on the rotating compacting instrument PCG, and the size test piece was φ 50 mm × H170 mm. Let cool at room temperature for 1 day. The specimen was processed into a size of 100 mm × 150 mm by means of drilling core and cutting, and its volume indexes were measured.

The test temperature is −10, 5, 20, 35°C, 50°C, respectively. The corresponding test frequency is 0.1, 0.5, 1, 5, 10, 25 Hz. An LVDT sensor was placed at 120° intervals along the circumference of the specimen. The dynamic modulus of asphalt mixture was measured after 5 h of heat preservation. The range of axial deformation of the specimen is 85–135 με.

Test Results

Analysis of Influencing Factors of ARHM13 Dynamic Modulus

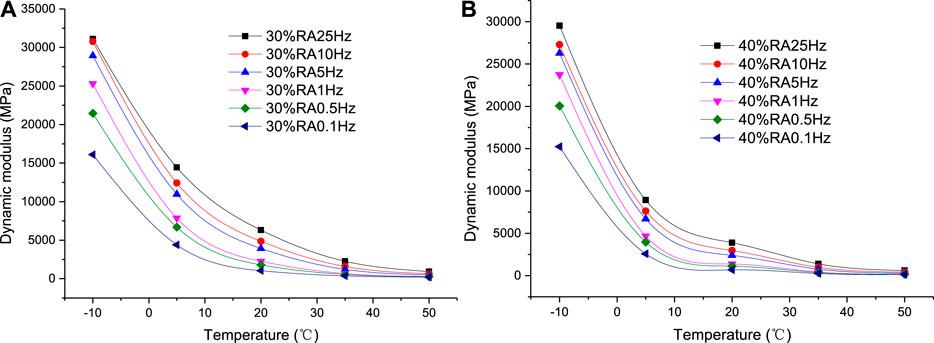
The dynamic modulus test results of ARHM13 mixtures with different binders are shown in Figure 2.

FIGURE 2

FIGURE 2. The effect of binder on the dynamic modulus of ARHM13.

Figure 2 shows that the dynamic modulus of different rubber asphalt mixtures has the same changing law, and is affected by temperature and loading frequency. With the increase of temperature, the dynamic modulus shows a decreasing trend; with the increase of loading frequency, the dynamic modulus is Increasing trend.

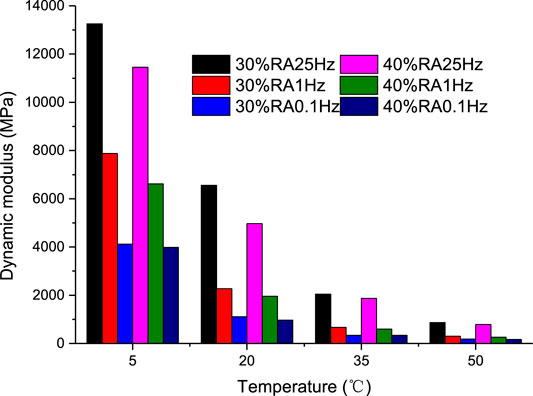
Select three frequencies and four temperatures to analyze the factors affecting the dynamic modulus of the rubber asphalt mixture, as shown in Figure 3.

FIGURE 3

FIGURE 3. Influencing factors of dynamic modulus of ARHM13 mixture.

It can be seen from Figure 3 that when the 30% RA mixture is at a frequency of 0.1 Hz, the dynamic modulus at 20, 35, and 50°C decreases by 73.0%, 91.7%, and 95.6%, compared to the dynamic modulus at 5°C; At 25 Hz, the dynamic modulus at 20, 35, and 50°C is relatively. The dynamic modulus decreased by 50.6%, 84.6% and 93.5% respectively at °C. The data shows that under the same loading frequency conditions, the dynamic modulus decreases with the increase of temperature; at the same temperature, the dynamic modulus increases with the increase of frequency. As the frequency increases, the dynamic modulus of asphalt mixture decreases gradually at 20°C relative to 5°C. Either increasing the temperature or reducing the frequency can achieve the purpose of reducing the dynamic modulus.

Comparing the dynamic modulus of the two rubber asphalt mixtures, it is found that under the conditions of 0.1 Hz and 5, 20, 35, 50°C, the dynamic modulus of 40%RA mixture relative to 30%RA mixture decreases by 3.1%, 12.79%, 0, 9.3%;under the conditions of 1 Hz and 5, 20, 35, 50°C, the dynamic modulus of 40%RA mixture relative to 30%RA mixture decreases by 8.8%, 16.9%, 2.3%, 6.5%; Under 25 Hz and 5, 20, 35, 50°C, the dynamic modulus of 40%RA mixture is reduced by 13.6%, 24.1%, 8.6%, 9.1, respectively %. It shows that the dynamic modulus of 30%RA mixture is higher than 40%RA under the same conditions.

Based on the above data, the influence of temperature and frequency on the dynamic modulus of the mixture is far greater than the influence of the cement on the dynamic modulus.

Effect of Mixture Type on Dynamic Modulus

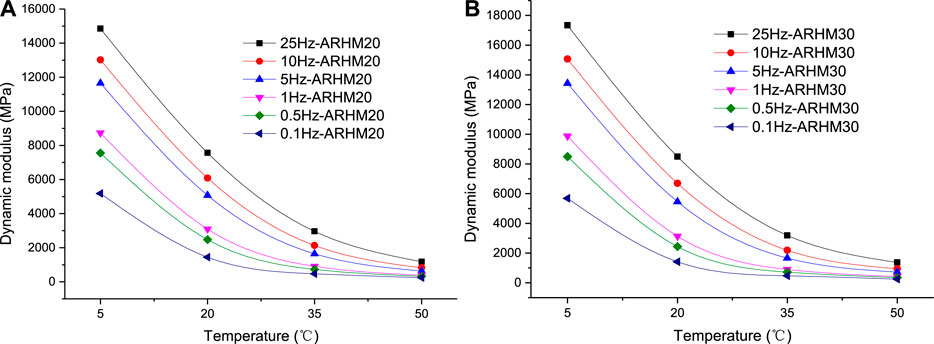
The test results of ARHM20 and ARHM30 asphalt mixtures are shown in Figure 4.

FIGURE 4

FIGURE 4. Dynamic modulus of different types of rubber asphalt mixture.

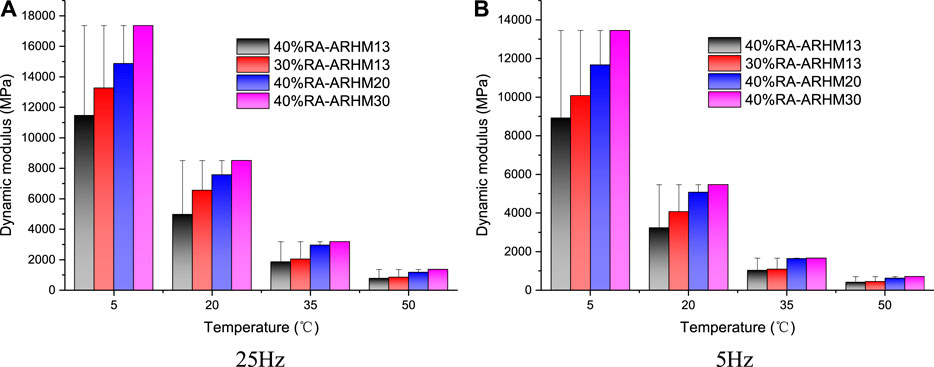
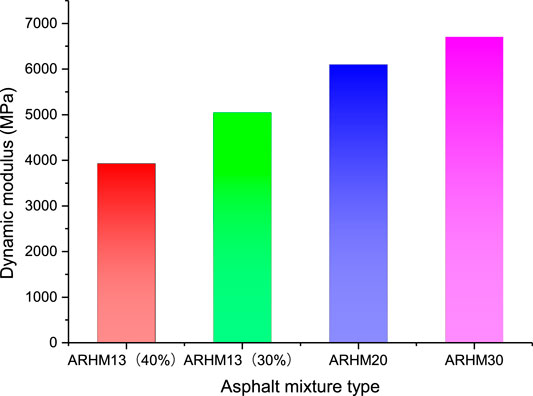
Figure 4 shows that although the gradation type and oil-stone ratio of the two asphalt mixtures have changed, the dynamic modulus changes are consistent with the ARHM13 mixture. In order to determine the influence of gradation type on the dynamic modulus of asphalt mixture, the test data of Figures 2 and 4 are combined. At 25 Hz and 5 Hz, the dynamic modulus of four asphalt mixtures is shown in Figure 5.

FIGURE 5

FIGURE 5. Dynamic modulus of different types of mixtures.

It can be seen from Figure 5 that under the same conditions, the order of the dynamic modulus of the asphalt mixture from large to small is ARHM30, ARHM20, 30% RA-ARHM13, 40% RA-ARHM13, which can be achieved by changing the asphalt binder or gradation type. To achieve the purpose of adjusting the dynamic modulus of the asphalt mixture.

Fitting the Relationship Between Dynamic Modulus and Temperature

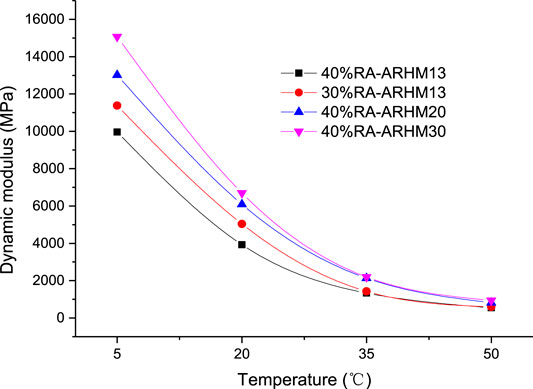
Considering that the asphalt pavement is in a temperature-changing environment, the test data at 10 Hz is selected to fit the dynamic modulus and temperature. The fitting curve is shown in Figure 6.

FIGURE 6

FIGURE 6. Dynamic modulus and temperature correlation curve.

According to the fitting curve in Figure 6, it is found that the dynamic modulus and temperature satisfy the exponential function model system, the dynamic modulus (y) is set as the dependent variable and the temperature (x) is the independent variable. The relationship between the two is $\text{y}=\text{a}{e}^{bx}$ , The model parameters are shown in Table 3.

TABLE 3

TABLE 3. Correlation equation model parameters.

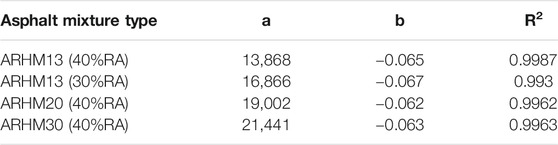
It can be seen from Table 3 that the dynamic modulus of asphalt mixture has a high correlation with temperature, which is above 0.993. The dynamic modulus of asphalt mixture at any temperature can be solved by this model.

Dynamic Modulus Master Curve

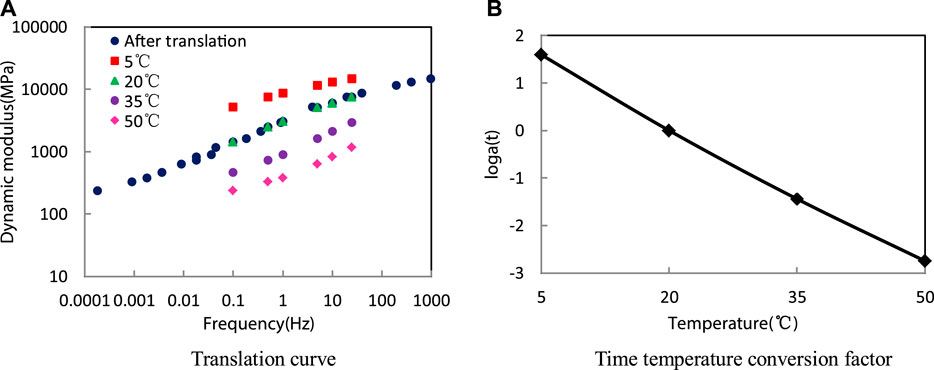
Taking ARHM20 mixture as an example, the dynamic modulus curve at different temperatures was translated to the reference temperature (20°C) in combination with the time-temperature equivalence principle. The translation curve and displacement factor are shown in Figure 7.

FIGURE7

FIGURE7. ARHM20 translation curve.

After the dynamic modulus is translated, the three-dimensional space composed of temperature, dynamic modulus and loading frequency is transformed into a two-dimensional coordinate system of dynamic modulus and frequency.

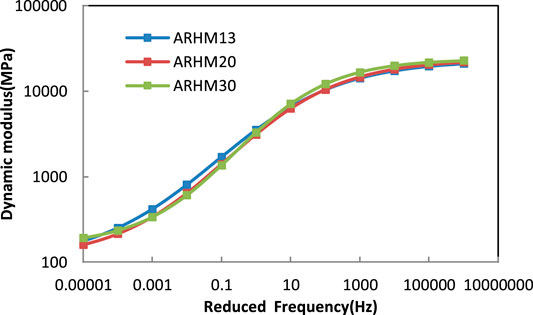
Using the above method and using 20°C as the reference temperature, the master curve of the dynamic modulus of the three asphalt mixtures was fitted, as shown in Figure 8.

FIGURE 8

FIGURE 8. Main curve of dynamic modulus.

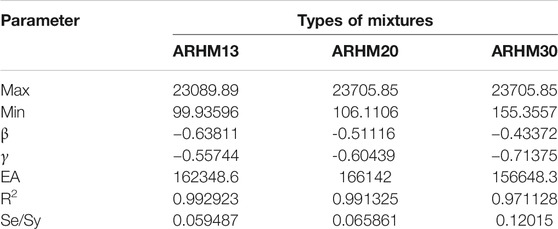
Figure 8 shows that the dynamic modulus of the three types of mixtures varies slightly at different frequencies. The effect of gradation type on dynamic modulus is much less than that of temperature and frequency. The main curve model parameters of the three asphalt mixtures are shown in Table 4.

TABLE 4

TABLE 4. Main curve model parameters of different types of mixtures.

The main curve models of dynamic modulus of the three types of asphalt mixtures have a high correlation, which are 0.993, 0.991 and 0.971, respectively. As the mixture type changes, the model parameters change accordingly. According to the main dynamic modulus curve, the dynamic modulus of asphalt mixture at any temperature or loading frequency can be solved. This curve is helpful to study the dynamic modulus of the mixture in the wide band or temperature range.

Dynamic modulus analysis of mixture in Different Asphalt Pavement

The thickness of the asphalt pavement above, in the middle and below shall be 4cm, 6cm and 8cm respectively. The pavement material is ARHM13, ARHM20 and ARHM30 mixture respectively. According to the main curve model of dynamic modulus and pavement temperature field data, the actual dynamic modulus of different pavement depths at 10 Hz can be solved and analyzed.

Design Value of Dynamic Modulus of Asphalt Mixture

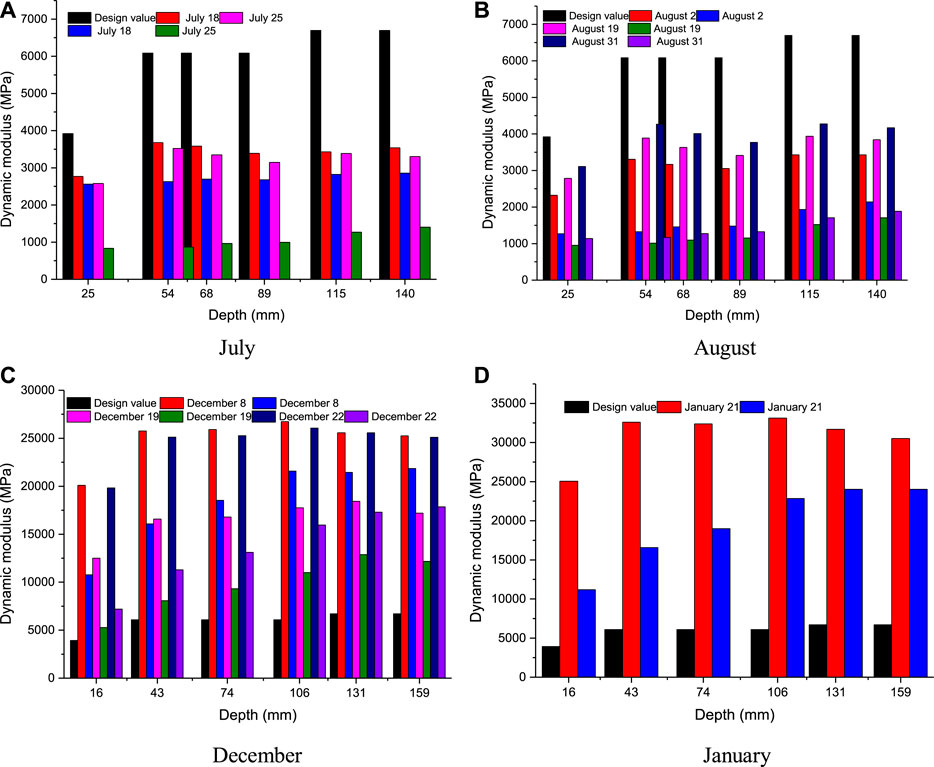
ARHM13, ARHM20 and ARHM30 mixtures are used for the surface layer, middle surface layer and lower layer, respectively. According to the test data of Figures 3 and 5 and the "Code for Design of Highway Asphalt Pavement,” the dynamic modulus of asphalt mixture at 20°C and 10 Hz is selected. It is the design value, as shown in Figure 9

FIGURE 9

FIGURE 9. Design value of dynamic modulus of asphalt mixture.

Figure 9 illustrates that the dynamic modulus of the three-layer asphalt mixture changes to a fixed value. The change takes into account the change of the temperature field and causes the change of the dynamic modulus of the asphalt concrete.

Distribution Law of Temperature Field of Asphalt Pavement

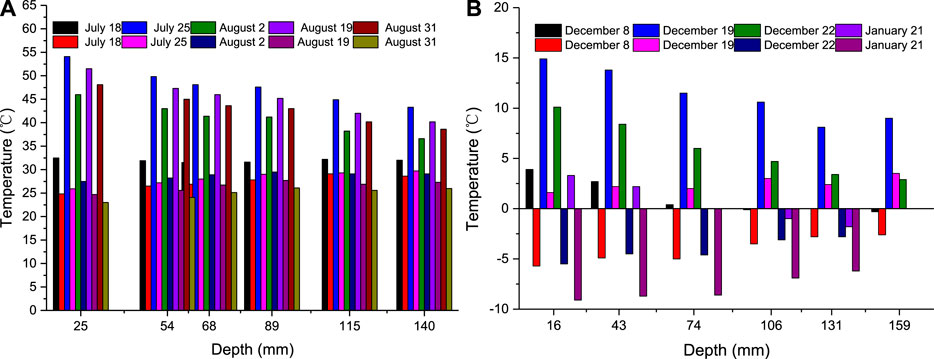
Combined with the results of previous research (Wang et al., 2014), the daily maximum and minimum temperatures at different depths of the road surface are shown in Figure 10.

FIGURE 10

FIGURE 10. Temperature distribution of asphalt pavement.

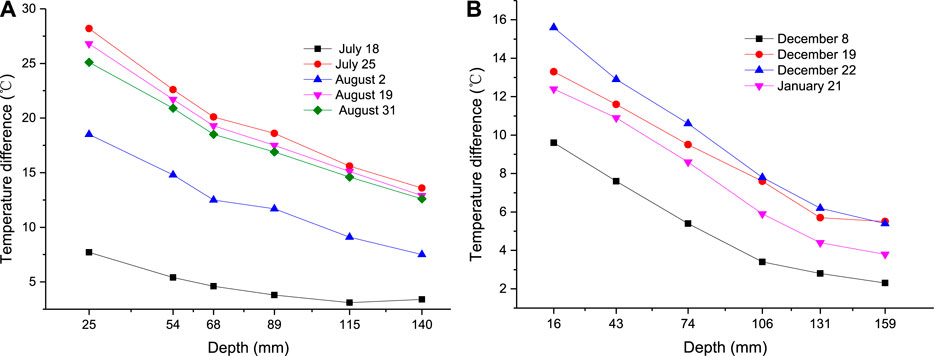
It can be seen from Figure 10 that the road temperature field varies with depth and seasons. Picture (a) the daily maximum temperature can reach 54.1°C and the lowest temperature is 23.1°C; figure (b) the daily maximum temperature can reach 14.9°C, the lowest temperature is −9.1°C, and the extreme temperatures are concentrated around 20 mm deep on the road surface. Through calculation, the difference between the highest and lowest daily temperature is shown in Figure 11.

FIGURE 11

FIGURE 11. Temperature distribution of asphalt pavement.

Figure 11 shows that the daily temperature difference is a dynamically changing value, and the surface layer pavement temperature difference is the largest. As the road depth increases, it gradually decreases and tends to stabilize.

Comparative Analysis of Dynamic Modulus of Pavement Structure Layers

Substitute the road temperature field data into the temperature and dynamic modulus correlation equation to solve the asphalt concrete dynamic modulus when the loading frequency is 10 Hz. In different months, the design and actual values of asphalt concrete are shown in Figure 12.

FIGURE 12

FIGURE 12. Comparative analysis of dynamic modulus of asphalt pavement.

It is found from Figure 12 that the actual dynamic modulus of pavement concrete is comprehensively affected by factors such as temperature, pavement depth, and asphalt mixture type. Among them, the change in dynamic modulus caused by the temperature difference between day and night is much greater than the impact of asphalt mixture type on dynamic modulus. In (A), the design values of the dynamic modulus of the surface layer, the middle layer and the lower layer are respectively 1.3 to 1.7 times, 1.4 to 2.0 times, and 1.6 to 2.0 times the actual dynamic modulus. In (B), the design values of the dynamic modulus of the surface layer, the middle layer and the lower layer are 1.5 to 4.7 times, 2.3 to 7 times, and 2.3 to 5.3 times of the actual dynamic modulus, respectively. The actual dynamic modulus is much smaller than the design value of the dynamic modulus, and there is a large gap between the actual stress state of the road surface and the design.

In (C), the design values of the dynamic modulus of the surface layer, middle layer and lower layer are respectively 15.6–31.4%, 18.7–36.7%, and 20.2–38.9% of the actual dynamic modulus; The design values of the dynamic modulus of the surface layer and the lower layer are respectively 25∼74.5%, 32∼75.4%, 27.9∼60.9% of the actual dynamic modulus. The actual dynamic modulus is much larger than the design value of the dynamic modulus, and the asphalt pavement is in an elastic state.

Conclusions

(1) The dynamic modulus of rubber asphalt mixture is comprehensively affected by factors such as binder, mixture type, temperature, and loading frequency. Among them, external factors such as temperature and loading frequency have a greater influence on the dynamic modulus of the mixture than the binder, mixture type, etc. Internal factors should pay attention to the influence of temperature on the dynamic modulus.

(2) Through laboratory research on the dynamic modulus of different types of rubber asphalt mixtures, the correlation equation between dynamic modulus and temperature is established, which lays the foundation for the next step to study the dynamic modulus of asphalt concrete through the temperature field.

(3) After analyzing the data of asphalt mixture design and actual dynamic modulus, it is found that the current asphalt pavement design specification uses 20°C and 10 Hz as the limiting conditions for the selection of dynamic modulus of all mixtures, which is far from the actual situation. The modulus data at the highest temperature of the structural layer is recommended as a design parameter.

Data Availability Statement

All datasets presented in this study are included in the article/supplementary material.

Author Contributions

GW: methodology, resources, supervision and writing-review. XW: conceptualization, experiments, methodology, writing-original draft, and editing. ZY: methodology and writing-review. LQ: investigation, visualization, formal analysis and writing-review. ZG: validation, experiments. All authors contributed to the article and approved the submitted version.

Conflict of Interest

LQ was employed by the company Hebei Transportation Investment Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ali, Y., Irfan, M., Ahmed, S., Khanzada, S., Mahmood, T., et al. (2016). Investigation of factors affecting dynamic modulus and phase angle of various asphalt concrete mixtures. Mater. Struct. 49 (3), 857–868. doi:10.1617/s11527-015-0544-3 CrossRef Full Text

Google Scholar

Arefin, M. S., Quasem, T., Nazzal, M., and Dessouky, S. (2019). Accuracy of MEPDG dynamic modulus predictions for short-term and long-term aged asphalt mixtures. J. Transp. Eng., Part B: Pavements 145 (3). doi:10.1061/jpeodx.0000125 CrossRef Full Text|

Google Scholar

Chen, J., Wang, H., and Zhu, H. (2017). Analytical approach for evaluating temperature field of thermal modified asphalt pavement and urban heat island effect. Appl. Therm. Eng. 113, 739–748.

CrossRef Full Text | Google Scholar

Fang, C., Guo, N., You, Z., and Tan, Y. (2020). Investigating fatigue life prediction of rubber asphalt mixture based on damage evolution using residual strain analysis approach. Constr. Build. Mater. 257, 119476. doi:10.1016/j.conbuildmat.2020.119476 CrossRef Full Text

Google Scholar

Ghasemi, P., Lin, S., Rollins, D., and Williams, R. (2019). Predicting dynamic modulus of asphalt mixture using data obtained from indirect tension mode of testing. Chem. Biol. Eng. Pub. 375. https://lib.dr.iastate.edu/cbe_pubs/375

Google Scholar

Hou, H., Wang, T., Wu, S., Xue, Y., Tan, R., Chen, J., and Zhou, M. (2016). Investigation on the pavement performance of asphalt mixture based on predicted dynamic modulus. Constr. Build. Mater. 106, 11–17. doi:10.1016/j.conbuildmat.2015.10.178 CrossRef Full Text

Google Scholar

Huang, K., Xu, T., Li, G., and Jiang, R. (2016). The feasibility of DEM to analyze the temperature field of asphalt mixture. Constr. Build. Mater. 106, 592–599.

Google Scholar

Li, H., Dong, B., Zhao, D., Guo, P., and Zhang, J. (2019). Physical, rheological and stability properties of desulfurized rubber asphalt and crumb rubber asphalt. Arabian J. Sci. Eng. 44, 5043–5056. doi:10.1007/s13369-018-3684-2 CrossRef Full Text

Google Scholar

Liu, H., Luo, R., and Lv, H. (2018). Establishing continuous relaxation spectrum based on complex modulus tests to construct relaxation modulus master curves in compliance with linear viscoelastic theory. Construct. Build. Mater. 165, 372–384.

Google Scholar

Nemati, R., and Dave, E. (2018). Nominal property based predictive models for asphalt mixture complex modulus (dynamic modulus and phase angle). Constr. Build. Mater. 158, 308–319. doi:10.1016/j.conbuildmat.2017.09.144 CrossRef Full Text

Google Scholar

Qian, G., He, Z., Yu, H., Gong, X., and Sun, J. (2020). Research on the affecting factors and characteristic of asphalt mixture temperature field during compaction. Constr. Build. Mater. 257, 119509. doi:10.1016/j.conbuildmat.2020.119509 CrossRef Full Text

Google Scholar

Rahman, A. S. M. A., Islam, M. R., and Tarefder, R. A. (2019). Dynamic modulus and phase angle models for New Mexico’s Superpave mixtures. Road Mater. Pavement Des. 20 (3), 740–753. doi:10.1080/14680629.2017.1422002 CrossRef Full Text

Google Scholar

Robbins, M., and Timm, D. H. (2011). Evaluation of dynamic modulus predictive equations for Southeastern United States asphalt mixtures. Transp. Res. Rec.: J. Transp. Res. Board. 2210, 122–129. doi:10.3141/2210-14 CrossRef Full Text

Google Scholar

Rowe, G. M., and Sharrock, M. J. (2011). Alternate shift factor relationship for describing temperature dependency of viscoelastic behavior of asphalt materials. Transp. Res. Rec. 2207 (1), 125–135. doi:10.3141/2207-16 CrossRef Full Text

Google Scholar

Ruan, L., Luo, R., Hu, X., and Pan, P. (2018). Effect of bell-shaped loading and haversine loading on the dynamic modulus and resilient modulus of asphalt mixtures. Constr. Build. Mater. 161, 124–131. doi:10.1016/j.conbuildmat.2017.11.038 CrossRef Full Text

Google Scholar

Su, N., Xiao, F., Wang, J., and Amirkhanian, S. (2018). Precision analysis of sigmoidal master curve model for dynamic modulus of asphalt mixtures. J. Mater. Civ. Eng. 30 (11), 04018290.1–04018290.11. doi:10.1061/(asce)mt.1943-5533.0002449 CrossRef Full Text

Google Scholar

Sun, Y., Du, C., Gong, H., Li, Y., and Chen, J. (2020). Effect of temperature field on damage initiation in asphalt pavement: A microstructure-based multiscale finite element method. Mech. Mater. 144, 103367.

Google Scholar

Teixeira, J. E. S. L., Kim, Y.-R., Souza, F. V., Allen, D. H., and Little, D. N. (2014). Multiscale model for asphalt mixtures subjected to cracking and viscoelastic deformation. Transp. Res. Rec. 2447 (1), 136–145. doi:10.3141/2447-15 CrossRef Full Text

Google Scholar

Wang, H., Zhan, S., and Liu, G. (2019). The effects of asphalt migration on the dynamic modulus of asphalt mixture. Appl. Sci. 9, 2747. doi:10.3390/app9132747 CrossRef Full Text

Google Scholar

Wang, G., Wang, Q., Liu, G., and Wang, L. (2014). Key technology of highway asphalt pavement [M]. Beijing, China: China Communications Press, 17-19 [in Chinese].

Google Scholar

Wen, Y., and Wang, Y. (2019). Effect of oxidative aging on dynamic modulus of hot-mix asphalt mixtures. J. Mater. Civ. Eng. 31 (1), 04018348. doi:10.1061/(asce)mt.1943-5533.0002547 CrossRef Full Text

Google Scholar

Xia, C., Lv, S., Cabrera, M. B., Wang, X., Zhang, C., and You, L. (2021). Unified characterizing fatigue performance of rubberized asphalt mixtures subjected to different loading modes. J. Clean. Prod. 279, 123740. doi:10.1016/j.jclepro.2020.123740 CrossRef Full Text

Google Scholar

Zhang, J., Li, Z., Chu, H., and Lu, J. (2019). A viscoelastic damage constitutive model for asphalt mixture under the cyclic loading. Constr. Build. Mater. 227, 116631.

Google Scholar

Zhang, X (2006). The principle and application of viscoelastic mechanics of asphalt and asphalt mixture [M]. Beijing, China: China Communications Press, 51–53 [in Chinese].

Google Scholar