- 1Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing,China
- 2Institute for Applied Physics, University of Science and Technology Beijing, Beijing,China
- 3CAEP Software Center for High Performance Numerical Simulation, Beijing,China
During the past two decades, the high-entropy alloy AlCoCrFeNi has attracted much attention due to its outstanding thermal and mechanical properties under ambient conditions. However, the exploration on the thermodynamic properties of this alloy under high temperatures and high pressures is relatively insufficient. Combining structural modeling with the similar atomic environment (SAE) method and first-principles simulations with the modified mean-field potential (MMFP) approach, we studied the lattice and magnetic structure as well as the thermodynamic properties of the body-centered-cubic AlCoCrFeNi, through supercell simulations. AlCoCrFeNi was found to display a strong local lattice distortion compared with typical 3d high-entropy alloys; the ferromagnetic structure stable at 0 K was predicted to transform to the paramagnetic structure at the Curie temperature TC = 279.75 K, in good agreement with previous calculations; the calculated equilibrium volumes, bulk modulus, and shock Hugoniot all agree well with available experimental data and other theoretical values. These results demonstrate the validity and reliability of our methods used to study the dynamic properties of AlCoCrFeNi, providing a promising scheme for accessing the dynamic properties of sophisticated high-entropy alloys.
Introduction
High-entropy alloys (HEAs) or multi-principle–element alloys represent a special group of solid solutions containing five or more elements, where the concentration He et al., 2018, Korchuganov, 2018, Li et al., 2018 of each element is between 5 and 35 at. % (Cantor et al., 2004; Yeh et al., 2004; Zhang et al., 2014). Because of tunable compositions and unique microstructures, HEAs possess superior mechanical properties such as high hardness, outstanding strength and excellent fracture toughness (Li et al., 2019; Miracle, 2019). Different from conventional alloys with only one or two principal components such as steels, HEAs pave a new way for the design of novel alloys. Thus, HEAs have promising potential for application in various industrial fields, and have attracted great attention during the past two decades.
Among all the HEAs studied so far, AlxCoCrFeN is one kind under intensive investigations, mostly because its properties can be fine-tuned by the concentration of the Al element (Miracle, 2019). The concentration of Al has strong effects on the phase structure of AlxCoCrFeNi, which consequently influences the mechanical, electronic, and magnetic properties of this alloy (Tong et al., 2005; Santodonato et al., 2015; Santodonato et al., 2018). According to Wang et al. (2012), when x < 0.5, AlxCoCrFeNi possesses the face-centered cubic (fcc) structure; when x > 0.9, AlxCoCrFeNi has the body-centered cubic (bcc) structure (with a chemically ordered B2 or disordered A2 structure); when 0.5 < x < 0.9, the crystal structure of AlxCoCrFeNi is a mixture of fcc and bcc (A2 or B2). These results indicate that the addition of the element Al tends to stabilize the bcc structure. With increasing concentration of Al, the hardness and strength of AlxCoCrFeNi increases accordingly (Zhang et al., 2012). It is worth noting that, CoCrFeNi (equivalently AlxCoCrFeNi with x = 0) is paramagnetic at ambient conditions, while Al2CoCrFeNi (AlxCoCrFeNi with x = 2) becomes paramagnetic at a higher Curie temperature of around 430 ± 3 K (Tian et al., 2013).
Though most experimental and theoretical reports on AlxCoCrFeNi have been focusing on its mechanic properties at quasi-static strain-rates under ambient conditions, its responses under strong shock compression have gradually attracted more attention from researchers. The mechanical properties of the fcc phase of AlxCoCrFeNi were investigated experimentally by Kumar et al. (2015), Li et al. (2017), Zhang et al. (2017), Gangireddy et al. (2018) and Meyers et al. (2018) using the split Hopkinson pressure bar. They found that these alloys show high resistance to adiabatic shear location, high strain rate sensitivity, and high strain hardening rate due to complex multiple hardening mechanisms (He et al. (2018), Korchuganov (2018), Li et al. (2018)). Recently, Jiang et al. (2016) found that the equal molar ratio AlCoCrFeNi HEA (with the bcc structure) exhibits high Hugoniot elastic limit (HEL). They measured the shock Hugoniot of AlCoCrFeNi using the normal plate impact technique, and the shock yield stress was estimated with the von Mises yield criterion (Meyer, 1994). However, this work only covers a fairly low pressure range of the shock equation of state (EOS), and the shock EOS at high pressures and high temperatures is still lacking.
The EOS of materials is indispensable to many scientific research and technological applications, such as those related to high-velocity impact, shock waves, explosions, and high-power lasers (Golosnoy et al., 1994). First-principle calculations have been found to predict accurately the EOS and thermodynamics properties of many metals at high temperatures and high pressures (Fortov et al., 1998; Song et al., 2007; Song and Liu, 2007; Liu et al., 2016; Söderlind and Young, 2018). As for first-principles calculations of HEAs, challenging obstacles originate from how to deal with three aspects (Tian, 2017; Ikeda et al., 2019): 1) the chemical disorder, 2) the magnetic disorder (Šebesta et al., 2019; Tian et al., 2019), and 3) the lattice vibrational contributions to the free energy. The quasi-harmonic approximation (QHA) models (Ma et al., 2015; Song et al., 2016) are applicable at low temperatures, while the computational cost and time are significant using frozen phonon method or first-principles molecular dynamics simulations (Körmann et al., 2017). Therefore, we need to seek other ways to calculate the free energy of HEAs that balance both the accuracy and the efficiency.
In this work, we combine structural modeling with the similar atomic environment (SAE) method (Tian et al., 2020) and first-principles calculations with the modified mean-field potential (MMFP) approach (Song and Liu, 2007) to predict the EOS and thermodynamic properties of the bcc AlCoCrFeNi HEA. We first use the SAE method to construct representative supercell structures to describe the chemical disorder of AlCoCrFeNi. Then both ferromagnetic and paramagnetic structures are characterized with randomly distributed magnetic elements in the SAE supercell, and the static EOS and ground-state structural properties are obtained by first-principles calculations with structural relaxations. The calculated equilibrium volume, bulk modulus, and Curie temperature are found to agree well with the experimental data in Tian et al. (2013) and Jiang et al. (2016). Next, within the MMFP approach, the static EOS is used to establish a mean-field potential (MFP), to estimate efficiently the lattice vibrational contributions to the Helmholtz free energy. Following the above steps, the thermal EOS is set up, and thermodynamic properties at high temperatures and high pressures are predicted for the bcc AlCoCrFeNi. Moreover, we calculated the shock Hugoniot, and our results are in good agreement with the experimental data in Jiang et al. (2016). This provides a persuasive verification for our modeling of the lattice structure with magnetism and the corresponding thermal EOS.
The rest of this article is arranged as follows. In Section II, the computational methods and details are introduced. In Section III, the ground-state properties of ferromagnetic and paramagnetic structures of AlxCoCrFeNi are investigated. In Section IV, the thermal EOS and thermodynamic properties AlxCoCrFeNi at high temperatures and high pressures are predicted. Concluding remarks are made in the last section.
Methodology
In this section, we introduce the computational methods for modeling solid-solution structures and magnetic structure, as well as for predicting the free energy.
Modeling Solid-Solution Structures
Since local lattice distortions can be strong in HEAs (Song et al., 2017), for the bcc AlCoCrFeNi, the supercell approach should be more appropriate than the conventional coherent potential approximation (CPA) (Gyorffy, 1972). Very recently, we proposed a supercell modeling approach for random alloys, that is, the similar atomic environment (SAE) method (Tian et al., 2020). The SAE method has been thoroughly cross-validated with the special quasi-random structure (SQS) method (Zunger et al., 1990) and applied to study the phase stability of AlCoCrFeNi (Guan et al., 2020). In the SAE method, the similarity function quantitatively describes the deviation of the current configuration from the corresponding fully disordered one in terms of clusters with different sizes. In practice, it suffices to consider both diatomic clusters and triatomic clusters (Liu et al., 2005).
We start from a
where
Modeling Magnetic Structure
To consider the temperature induced magnetic structural transition, we need to describe the ferromagnetic (FM) and paramagnetic (PM) states of the bcc AlCoCrFeNi. For the ferromagnetic state, we perform colinear calculations for the structural relaxation. The paramagnetic state above the Curie temperature is modeled with the disordered local moment (DLM) approximation (Gyorffy et al., 1985). That is, spin-up and spin-down atoms with equal atomic fraction for the same elements are treated as different atomic species distributed randomly in the SAE supercell. Theoretically, we could construct a larger SAE supercell with PM state containing nine components: (18Al) (9Cr↑9Cr↓) (9Fe↑9Fe↓) (9Co↑9Co↓) (9Ni↑9Ni↓). In practice, due to the random distribution of the magnetic moments, we can describe the magnetic disorder by randomly specifying spin-up and spin-down for the atomic sites of each magnetic element. Consequently, we have considered both the chemical and the magnetic disorder in a 90-atom SAE supercell. The validity of the DLM approximation will be demonstrated in Section 3.
First-Principles Computational Details
In the present ab initio calculations, we employed the Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b) based on the density functional theory (Hohenberg and Kohn, 1964; Kohn and Sham, 1965). The exchange-correlation functional was treated by the generalized gradient approximation of Perdew, Burkey, and Ernzerhof (Perdew et al., 1996). The electron-ion interaction was described by the projector augmented wave (PAW) method (Blochl, 1994). The plane-wave cutoff energy is 600 eV. The Brillouin zone is sampled with the special k-mesh generated by the Monkhorst-Pack scheme (Monkhorst and Pack, 1976) with a k-point spacing of 0.03 Å-1. The convergence tolerance is 10−4 eV for total energy and 0.03 eV/Å for the maximum force on each atom.
Free Energy and Thermal EOS Model
The key for the prediction of EOS and thermodynamic properties is to calculate the Helmholtz free-energy as a function of volume (or pressure) and temperature. For a solid alloy at temperature
where
and the magnetic entropy the evaluated as
where
The ground-state energy
To obtain the vibrational contribution, we employ the MMFP approach (Song and Liu, 2007), which is a generalization of the mean-field potential (MFP) approach proposed in Wang (2000) and Wang et al. (2000) for thermodynamics. By introducing additional freedoms associated with lattice parameters in MFP calculations, the MMFP method can be applied to more complicated systems (Song et al., 2007; Tian et al., 2015). The vibrational free energy
Lattice Distortion and Magnetic States
According to Kao et al. (2009), the addition of Al destabilizes the fcc CoCrFeNi, and the associated local lattice distortion leads to the structural transformation to bcc when x ≥ 0.9 for Al in AlxCoCrFeNi. Thus, local lattice distortion is an essential factor when studying HEAs (Song et al., 2017), and the supercell method is fully capable of evaluating it. We set the lattice parameters of the bcc (Wang et al., 2008; Wang et al., 2012) supercell according to experimental measurements (Kao et al., 2009). As shown in Figure 1A, the supercell contains 90 atoms with five elements randomly distributed.
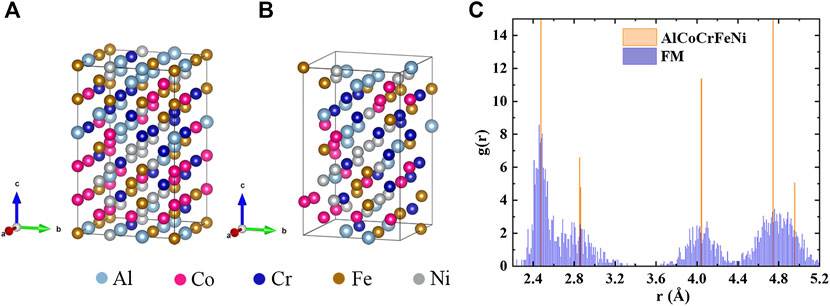
FIGURE 1. The supercell structure of AlCoCrFeNi before (A) and (B) after optimization with FM, and (C) the corresponding radial distribution function. The spreading peaks illustrate lattice distortion after structure relaxation with FM.
We also performed an FM static calculation with the unrelaxed FM structure, to compare with that of the relaxed FM one (Tian et al., 2013). The total energy for unrelaxed FM structure is -6.81 eV/atom, while that for the relaxed FM structure is -6.85 eV/atom. This indicates that the relaxed FM structure is energetically more stable. The relaxed FM structure is displayed in Figure 1B, where distinct local distortions can be observed, quite different from the case for the unrelaxed FM structure in Figure 1C. To see how strong the lattice distortion is, we first compare the radial distribution functions (RDF) between the FM structure and the unrelaxed structure in Figure 1C. The unrelaxed structure has sharp peaks which represent interatomic distances from the first-nearest-neighboring (1NN) to the 5NN, while the peaks are broader in the relaxed FM structure, indicating the presence of the lattice distortion in the relaxed FM structure. Furthermore, we calculated the coefficient,
to evaluate local lattice distortions of the relaxed structure relative to the unrelaxed one quantitatively. Here, with respect to the lattice basis of unit cell, (xi, yi, zi) and
To investigate the properties of AlCoCrFeNi under ambient conditions (Tian et al., 2013), we propose to describe the paramagnetic state based on the relaxed FM structure. First, according to the above analysis, we found that ion positions have larger effect on the total energy than the magnetic configuration. Thus, modeling the AlCoCrFeNi under FM relaxation is appropriate for PM studies. Second, we use an approximate model to describe the PM state by randomly specifying spin-up and spin-down in each element and restrict the total magnetic moment to be zero in the subsequent static calculation with collinear magnetism. The resulting total energy of the PM structure is -6.82 eV/atom, larger than the relaxed FM structure -6.85 eV/atom. This is in agreement with the trend that PM is the stable state under ambient conditions (Tian et al., 2013).
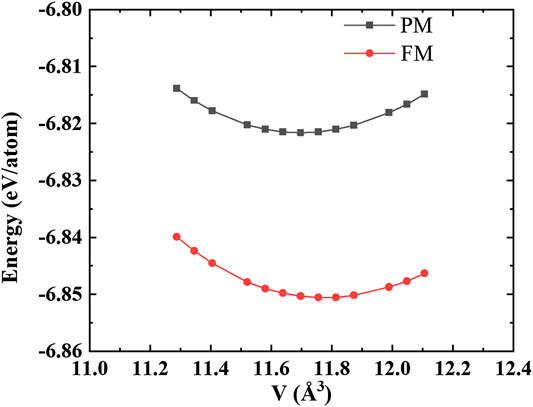
To further verify the model describing the PM state, we calculated the static E-V relation of the relaxed FM structure and PM structure under different volumes, and fit the E-V relation of the relaxed FM structure and PM structure, respectively, the results are shown in Figure 2. The ground-state volume of the PM structure is 11.67 Å3/atom and the relaxed FM structure is 11.77 Å3/atom, indicating that ferromagnetism leads to volume expansion. Moreover, the estimated ground-state energy for the PM structure is still larger than that of the relaxed FM structure. Besides, we calculated the Curie temperature TC of AlCoCrFeNi within the mean-field approximation (Ge et al., 2018). In this approximation, TC is expressed as follows:
where
Results for Ground-State Properties
First of all, we have calculated the equilibrium volume and bulk modulus at room temperature as listed in Table 1. The difference is 0.04 Å3/atom between the volume
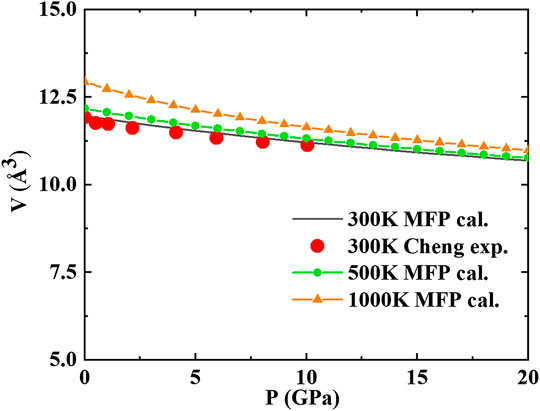
FIGURE 3.
In Figure 4, we plot the thermal EOS of bcc AlCoCrFeNi at temperatures between 300 and 1000 K. The figure shows that our results at 300 K are in good agreement with experimental values. The calculated thermal EOS exactly goes through the equilibrium state derived from the experimental relation between the shock velocity and the particle velocity from Jiang et al. (2016). Since the relation between the shock velocity and the particle velocity depends largely on
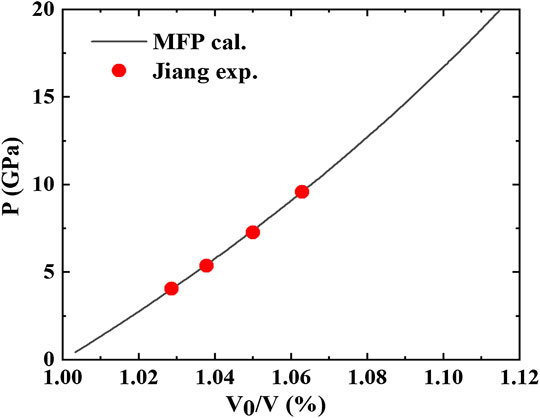
FIGURE 4.
Results for Thermodynamic Properties
An important source of information on the EOS at high compressions and high temperatures is the shock wave data. Shock wave experiments often provides data for the shock velocity
where
where
Then the shock wave data can be derived from the calculated Hugoniot states as follows:
which are plotted in Figure 5. The predicted
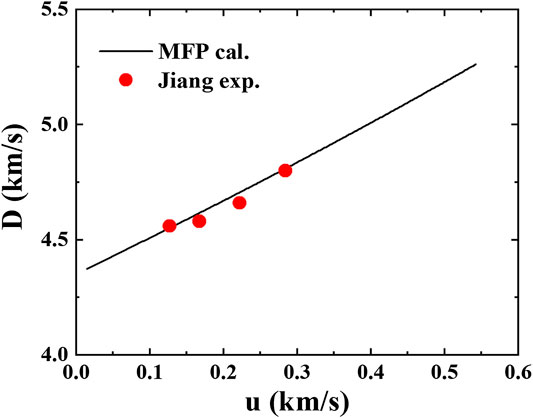
FIGURE 5.
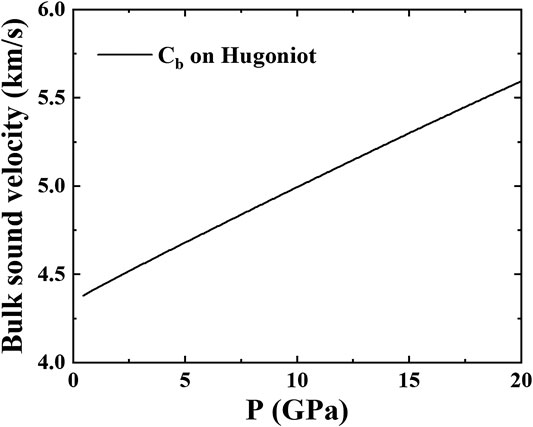
Sound velocity is often measured in shock compression experiments. At present, there are not too much data for AlCoCrFeNi under shock compression. We calculate the bulk sound velocity
Conclusion
In summary, three conclusions are made from our ab initio calculations.
(1) By constructing a supercell to study the local lattice distortion of AlCoCrFeNi, we found that the local lattice distortion has a strong effect on the structure of AlCoCrFeNi.
(2) On the basis of the relaxed ferromagnetic structure, we studied the paramagnetic state of AlCoCrFeNi, and showed that the Curie temperature is in line with previous estimated results and the E-V relation is in agreement with the experimental trend, suggesting the validity of the model to describe the paramagnetic structure.
(3) We calculate the equilibrium volumes, bulk modulus, and the shock Hugoniot equation of state of AlCoCrFeNi. Our results are in good agreement with the dynamic impact experiment. Our results show the validity and reliability of our methods to study the dynamic properties of AlCrFeCoNi, providing a promising scheme for investigating the thermodynamic properties of complicated high-entropy alloys.
Data Availability Statement
All datasets presented in this study are included in the article/ supplementary material.
Author Contributions
JW and ZY have the same contribution to this work. All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Fawei Zheng for the help with the calculations of paramagnetic structure. We thank Pro. Fuyang Tian for the help of supercell methods. We are grateful to Dr. Yu Liu and Dr. Dan Jian for calculations of elastic moduli and evaluation of lattice distortion. We acknowledge the support from the Science Challenge Project under Grant No. TZ2018002 and the National Key Research and Development Program of China under Grant No. 2016YFB0201204.
References
Blochl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953. doi:10.1103/physrevb.50.17953.
Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural development in equiatomic multicomponent alloys. Materials Science and Engineering: A. 375–377 213–218. doi:10.1016/j.msea.2003.10.257.
Cheng, B., Zhang, F., Lou, H., Chen, X., Liaw, P. K., Yan, J., and Zeng, Q. (2019). Pressure-induced phase transition in the AlCoCrFeNi high-entropy alloy. Scripta Materialia., 161, 88-92. doi:10.1016/j.scriptamat.2018.10.020.
Fortov, V. E., Khishchenko, K. V., Levashov, P. R., and Lomonosov, I. V. (1998). Nuclear instruments and methods in physics research section A: accelerators, spectrometers, detectors and associated equipment. Phys. Res. 415, 604–608. doi:10.1016/S0168-9002(98)00405-7.
Gangireddy, S., Gwalani, B., Liu, K., Banerjee, R., and Mishra, R. S. (2018). Microstructures with extraordinary dynamic work hardening and strain rate sensitivity in Al0.3CoCrFeNi high entropy alloy. Materials Science and Engineering: A. 734, 42–50. doi:10.1016/j.msea.2018.07.088.
Ge, H., Song, H., Shen, J., and Tian, F. (2018). Effect of alloying on the thermal-elastic properties of 3d high-entropy alloys, Mater. Chem. Phys. 210, 320-326. doi:10.1016/j.matchemphys.2017.10.046
Golosnoy, I. O., Kalitkin, N. N., and Volokitin, V. S. Wide-range equation of state of matter. I. Analysis of nonideality models, Russ. Phys. J. 37, 1029–1047 (1994).
Guan, H. Q., Huang, S. S., Ding, J. H., Tian, F. Y., Xu, Q., and Zhao, J. J. (2020). Chemical environment and magnetic moment effects on point defect formations in CoCrNi-based concentrated solid-solution alloys. Acta Materialia. 187, 122 doi:10.1016/j.actamat.2020.01.044.
Gyorffy, B. L. Coherent-potential approximation for a nonoverlapping-muffin-tin-potential model of random substitutional alloys. (1972). Phys. Rev. B. 5, 2382. doi:10.1103/PhysRevB.5.2382.
Gyorffy, B. L., Pindor, A. J., Staunton, J., Stocks, G. M., and Winter, H. (1985). A first-principles theory of ferromagnetic phase transitions in metals. J. Phys. F Met. Phys. 15, 1337. doi:10.1088/0305-4608/15/6/018.
He, J., Wang, Q., Zhang, H., Dai, L., Mukai, T., Wu, Y., et al. (2018). Dynamic deformation behavior of a face-centered cubic FeCoNiCrMn high-entropy alloy, Sci. Bull. 63 362–368. doi:10.1016/j.scib.2018.01.022.
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136(3B), B864. doi:10.1103/physrev.136.b864.
Ikeda, Y., Grabowski, B., and Körmann, F. (2019). Ab initio phase stabilities and mechanical properties of multicomponent alloys: a comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Char. 147 464–511. doi:10.1016/j.matchar.2018.06.019.
Jiang, Z. J., He, J. Y., Wang, H. Y., Zhang, H. S., Lu, Z. P., and Dai, L. H. (2016). Shock compression response of high entropy alloys. Mater. Res. Let. 4, 226–232. doi:10.1080/21663831.2016.1191554.
Kao, Y. F., Chen, S. K., Chen, T. J., Chu, P. C., Yeh, J. W., and Lin, S. J. (2011). Electrical, magnetic, and Hall properties of AlxCoCrFeNi high-entropy alloys, J. Alloys Compd. 509, 1607–1614. doi:10.1016/j.jallcom.2010.10.210
Kao, Y.-F., Chen, T.-J., Chen, S.-K., and Yeh, J. -W. (2009). Microstructure and mechanical property of as-cast, -homogenized, and -deformed AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. J. Alloys Compd. 488, 57–64. doi:10.1016/j.jallcom.2009.08.090
Kohn, W., and Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140(4A), A1133 (1965). doi:10.1103/physrev.140.a1133.
Korchuganov, A. V. (2018). Onset of plastic deformation in non-equiatomic fcc CoCrFeMnNi high-entropy alloys under high-rate loading. Letters on Materials. 8, 311–316. doi:10.22226/2410-3535-2018-3-311-316.
Körmann, F., Ikeda, Y., Grabowski, B., and Sluiter, M. H. F. (2017). Phonon broadening in high entropy alloys. Npj Computational Materials. 3, 36. doi:10.1038/s41524-017-0037-8.
Kresse, G., and Furthmüller, J. (1996a). Efficiency iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 54, 11169. doi:10.1103/PhysRevB.54.11169.
Kresse, G., and Furthmüller, J. (1996b). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Computiontal Materials Science. 6, 15. doi:10.1016/0927-0256(96)00008-0.
Kumar, N., Ying, Q., Nie, X., Mishra, R. S., Tang, Z., Liaw, P. K., et al. (2015). High strain-rate compressive deformation behavior of the Al0.1CrFeCoNi high entropy alloy. Mater. Des. 86, 598–602. doi:10.1016/j.matdes.2015.07.161.
Li, Z., Zhao, S., Alotaibi, S. M., Liu, Y., Wang, B., and Meyers, M. A. (2018). Adiabatic shear localization in the CrMnFeCoNi high-entropy alloy, Acta Materialia. 151, 424–431. doi:10.1016/j.actamat.2018.03.040.
Li, Z., Zhao, S., Diao, H., Liaw, P. K., and Meyers, M. A. (2017). High-velocity deformation of Al0.3CoCrFeNi high-entropy alloy: remarkable resistance to shear failure. Sci. Rep. 7, 42742. doi:10.1038/srep42742.
Li, Z., Zhao, S., Ritchie, R. O., and Meyers, M. A. (2019). Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys. Prog. Mater. Sci. 102, 296–345. doi:10.1016/j.pmatsci.2018.12.003.
Liu, H., Song, H., Zhang, Q., Zhang, G., and Zhao, Y. (2016). Validation for equation of state in wide regime: copper as prototype, Matter and Radiation at Extremes. 1, 123–131. doi:10.1016/j.mre.2016.03.002.
Liu, J. Z., Van De Walle, A., Ghosh, G., and Asta, M. (2005). Structure, energetics, and mechanical stability of Fe-Cu bcc alloys from first-principles calculations. Phys. Rev. B. 72, 144109. doi:10.1103/PhysRevB.72.144109.
Ma, D., Grabowski, B., Körmann, F., Neugebauer, J., and Raabe, D. (2015). Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: importance of entropy contributions beyond the configurational one. Acta Materialia. 100 90–97. doi:10.1016/j.actamat.2015.08.050.
Meyers, M. A., Li, Z., Zhao, S., Wang, B., Liu, Y., and Liaw, P. K. (2018). Shear localization of fcc high-entropy alloys, EPJ Web Conf. 183, 03028. doi:10.1051/epjconf/201818303028.
Miracle, D. B. (2019). High entropy alloys as a bold step forward in alloy development. Nat. Commun. 10. doi:10.1038/s41467-019-09700-1.
Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B. 16, 1748. doi:10.1103/physrevb.13.5188.
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865. doi:10.1103/physrevlett.77.3865.
Santodonato, L. J., Liaw, P. K., Unocic, R. R., Bei, H., and Morris, J. R. (2018). Predictive multiphase evolution in Al-containing high-entropy alloys. Nat. Commun. 9, 4520. doi:10.1038/s41467-018-06757-2.
Santodonato, L. J., Zhang, Y., Feygenson, M., Parish, C. M., Gao, M. C., Weber, R. J. K., et al. (2015). Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy, Nat. Commun. 6, 5964 doi:10.1038/ncomms6964.
Šebesta, J., Carva, K., and Legut, D. (2019). Role of magnetism in the stability of the high-entropy alloy CoCrFeMnNi and its derivatives. Phys. Rev. Mater. 3. doi:10.1103/PhysRevMaterials.3.124410.
Song, H.-F., and Liu, H.-F. (2007). Modified mean-field potential approach to thermodynamic properties of a low-symmetry crystal: beryllium as a prototype. Phys. Rev. B. 75. doi:10.1103/PhysRevB.75.245126.
Song, H.-F., Liu, H.-F., and Tian, E. (2007). Structural and thermodynamic properties of hexagonal BeO at high pressures and temperatures, J. Phys. Condens. Matter. 19 456209. doi:10.1088/0953-8984/19/45/456209.
Song, H., Tian, F., and Wang, D. (2016). Thermodynamic properties of refractory high entropy alloys, J. Alloys Compd. 682, 773–777. doi:10.1016/j.jallcom.2016.04.320.
Song, H. Q., Tian, F. Y., Hu, Q. M., Vitos, L., and Chen, N. X. (2017). Local lattice distortion in high-entropy alloys, Phys Rev Mater. 1, 023404. doi:10.1103/PhysRevMaterials.1.023404.
Söderlind, P., and Young, D. (2018). Assessing density-functional theory for equation-of-state. Computation. 6 13. doi:10.3390/computation6010013.
Tian, F. (2017). A review of solid-solution models of high-entropy alloys based on ab initio calculations. Frontiers in Materials. 4. doi:10.3389/fmats.2017.00036.
Tian, F., Delczeg, L., Chen, N., Varga, L. K., and Vitos, L. (2013). Structural stability of NiCoFeCrAlx high-entropy alloy from ab initio theory. Phys. Rev. B. 88, 085128. doi:10.1103/PhysRevB.88.085128.
Tian, F., Zhao, H., Wang, Y., and Chen, N. (2019). Investigating effect of ordering on magnetic-elastic property of FeNiCoCr medium-entropy alloy. Scripta Materialia. 166, 164–167. doi:10.1016/j.scriptamat.2019.03.023.
Tian, F. Y., Lin, D.-Y., Gao, X. Y., Zhao, Y.-F., and Song, H.-F. (2020). A structural modeling approach to solid solutions based on the similar atomic environment. J. Chem. Phys. 153, 034101. doi:10.1063/5.0014094.
Tian, M. F., Song, H. F., Liu, H. F., Wang, C., Fang, Z., and Dai, X. (2015). Thermodynamics of the α -γ transition in cerium studied by an LDA + Gutzwiller method. Phys. Rev. B. 91, 125148. doi:10.1103/PhysRevB.91.125148.
Tong, C.-J., Chen, Y.-L., Yeh, J.-W., Lin, S.-J., Chen, S.-K., Shun, T.-T., et al. (2005). Microstructure characterization of AlxCoCrCuFeNi high-entropy alloy system with multiprincipal elements. Metall. Mater. Trans. 36, 881–893. doi:10.1007/s11661-005-0283-0.
Wang, W.-R., Wang, W.-L., Wang, S.-C., Tsai, Y.-C., Lai, C.-H., and Yeh, J.-W. (2012). Effects of Al addition on the microstructure and mechanical property of AlxCoCrFeNi high-entropy alloys. Intermetallics. 26, 44-51. doi:10.1016/j.intermet.2012.03.005
Wang, Y. (2000). Classical mean-field approach for thermodynamics: ab initio thermophysical properties of cerium. Phys. Rev. B. 61, R11863. doi:10.1103/PhysRevB.61.R11863.
Wang, Y., Chen, D., and Zhang, X. (2000). Calculated equation of state of Al, Cu, Ta, Mo, and W to 1000 GPa, Phys. Rev. Lett. 84, 3220. doi:10.1103/PhysRevLett.84.3220.
Wang, Y.-P., Li, B.-S., Ren, M.-X., Yang, C., and Fu, H.-Z. (2008). Microstructure and compressive properties of AlCrFeCoNi high entropy alloy, Mater. Sci. Eng. 491 154–158. doi:10.1016/j.msea.2008.01.064
Yeh, J.-W., Chen, S.-K., Lin, S.-J., Gan, J.-Y., Chin, T.-S., Shun, T.-T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes, Adv. Eng. Mater. 6, 299–303. doi:10.1002/adem.200300567.
Zhang, C., Zhang, F., Chen, S., and Cao, W. (2012). Computational thermodynamics aided high-entropy alloy design. JOM. 64, 839–845. doi:10.1007/s11837-012-0365-6.
Zhang, T. W., Jiao, Z. M., Wang, Z. H., and Qiao, J. W., (2017). Dynamic deformation behaviors and constitutive relations of an AlCoCr1.5Fe1.5NiTi0.5 high-entropy alloy. Scripta Materialia. 136, 15–19. doi:10.1016/j.scriptamat.2017.03.039.
Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001.
Keywords: high-entropy alloy, ab initio calculations, thermodynamic properties, AlCoCrNiFe, lattice and magnetic structure
Citation: Wu J, Yang Z, Xian J, Gao X, Lin D and Song H (2020) Structural and Thermodynamic Properties of the High-Entropy Alloy AlCoCrFeNi Based on First-Principles Calculations. Front. Mater. 7:590143. doi: 10.3389/fmats.2020.590143
Received: 31 July 2020; Accepted: 21 October 2020;
Published: 23 November 2020.
Edited by:
Peter Liaw, The University of Tennessee, Knoxville, United StatesReviewed by:
Jijun Zhao, Dalian University of Technology, ChinaYiping Lu, Dalian University of Technology, China
Copyright © 2020 Wu, Yang, Xian, Gao, Lin and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xingyu Gao, Z2FvX3hpbmd5dUBpYXBjbS5hYy5jbg==; Deye Lin, bGluX2RleWVAaWFwY20uYWMuY24=; Haifeng Song c29uZ19oYWlmZW5nQGlhcGNtLmFjLmNu
†These authors have contributed equally to this work.
 Juefei Wu
Juefei Wu Zhen Yang1,2†
Zhen Yang1,2† Jiawei Xian
Jiawei Xian Xingyu Gao
Xingyu Gao Deye Lin
Deye Lin Haifeng Song
Haifeng Song