- 1Institute of Advanced Structure Technology, Beijing Institute of Technology, Beijing, China
- 2Beijing Key Laboratory of Lightweight Multi-functional Composite Materials and Structures, Beijing Institute of Technology, Beijing, China
The origami structure has caused a great interest in the field of engineering, and it has fantastic applications in the deployable and reconfigurable structures. Owing to the unique multi-stable states, here a typical hexagon-twist origami structure is fabricated via multi-material printing technology. The printed structure has multi-stable features and the stiffness of the deformable structure is dramatically reduced under thermal triggering. Such behavior causes an increase in the structural degree of freedom, allowing for self-deployment via releasing the prestored energy in the elastic crease. The response time and reaction time of the self-deployment process are also studied and illustrate the higher energy barrier of the folded state, the longer self-deployment time. Utilizing such unique features and design principles, a prototype of frequency reconfigurable origami antenna of nine diverse operating modes is subsequently designed and assembled with the hexagon-twist origami structure as the dielectric substrate. The antenna implements the cross-band from two different frequency bands, enabling to realize frequency reconfigurable under thermal condition.
Introduction
Origami is an ancient oriental art and an emerging frontier science. It is in the intersecting fields of mathematics, mechanics, mechanics, materials, control, biology, medicine and other basic disciplines, resulting in many scientific applications, such as solar panels design, airbag structure, and even the spatial folding of biological macro-molecules such as DNA and proteins (Xie, 2010; Leng et al., 2011; Fernandes and Gracias, 2012; Hu et al., 2012; Felton et al., 2014; Ge et al., 2014; Gladman et al., 2015; Zhao et al., 2015; Li et al., 2017; Zhao et al., 2017). Origami technology has always been regarded as a means of developing deployable and reconfigurable engineering systems because of its characteristics of easy bending and twisting (Anfinsen et al., 1973; Bromberg and Ron, 1998; Li and Lewis, 2003; Ahn et al., 2010; Lu et al., 2010b; Leng et al., 2011; Erb et al., 2012; Ge et al., 2012; Ge et al., 2013; Therien-Aubin et al., 2013; Tibbits, 2014; Breger et al., 2015; Gladman et al., 2015; Luo et al., 2015; Mu et al., 2015; Su et al., 2018). This technology can be used in designing large-scale planar structures such as building structures (Overvelde et al., 2016; Faber et al., 2018), and space antenna reflection surfaces, as well as the design of micro surgical instrument (Wong et al., 1994; Fernandes and Gracias, 2012; Breger et al., 2015).
As electromagnetic communication systems are more widely used in life, the demand for the number of antennas is also growing. In order to reduce electromagnetic coupling and system weight, the frequency reconfigurable antenna that can replace the function of multiple antennas with one antenna has become a research hotspot for engineers and scientists (Li et al., 2014; Song et al., 2017).
In this paper, a multi-material printed hexagon-twist origami structure was designed. When folded according to different crease pattern, the origami structure unit had three different folding stable states (Silverberg et al., 2015). Due to the property of the structural material, the folded stable state configuration could self-deploy under the influence of temperature, and the self-deployment temperature could be controlled by the geometric parameters of the structure. The dipole antenna is a hotspot in antenna research because of its simple principle, low cost, and ease of manufacturing. In our research, a hexagonal twist origami structure was used as the antenna substrate to design a dipole frequency reconfigurable antenna with simulation and experiment.
Materials and Methods
Fabrication of the Hexagon-Twist Origami Structure
All of the hexagon-twist origami structures in this work were fabricated using the multimaterial polyjet 3D printing technique after the structure designed with specific geometry parameter by the CAD software SOLIDWORKS. In the 3D printing process, two different mechanical properties materials VeroWhitePlusPlus (VW) and TangoBlackPlus (TG) used in the fabrication were all available from the multimaterial 3D printer (Object 350, Stratasys). For hexagon-twist origami structure, the crease and paper face material were adopted with TG and VW, respectively, which was determined by their material property (Figure 1). Of the two materials, TG is a soft elastomer that mainly consists of exo-1,7,7-trimethyl-bicyclo[2.2.1]hept-2-yl acrylate and photoinitiators, and VW is a rigid polymer mainly consisting of exo-1,7,7-trimethylbicyclo [2.2.1] hept-2-ylacrylate, tricyclodecane dimethanol diacrylate, titanium dioxide, and photoinitiators. Both TangoBlackPlus and VeroWhitePlus can be cured by ultraviolet light at room temperature. The corresponding uniaxial stretching mechanical testing results were shown in Figure 2A (adopted with INSTRON electronic universal testing machine LEGEND 2367). According to the stress-strain curve, the material TG in the crease area undergone large deformation when stretched under a small stress and the material VW in the paper face area is a high elastic modulus material (∼527 MPa) compared with the material TG (∼0.5 MPa). When the structure was folded, the crease area could withstand relatively large elastic deformation and the paper face area shown small strain. The folding stable state of the hexagon-twist origami structure could achieve self-deployment at high temperature. In order to explore the mechanical principle of self-deployment behavior, it was necessary to analyze the thermodynamic behavior of the TG and VW material via dynamic mechanical analysis (DMA). In the typical measurement, a preload of 1 mN was applied to the sample (dimensions of 12 × 5.0 × 0.5 mm) and the strain was oscillated at a frequency of 1 Hz with a peak-to-peak amplitude of 0.1%. In the process, the samples were firstly heated up to 150°C and stabilized for 10 min to reach thermal equilibrium. The temperature was then decreased from 150°C to -50°C at a rate of 2°C/min. The temperature dependence of the storage modulus and tanδ are shown in Figure 2B. The glass transition temperature (Tg) is identified as the temperature corresponding to the peak of the tanδ curve. The Tg values of the VeroWhitePlus and the TangoBlackPlus are ∼80 and ∼20°C, respectively. DMA tests were performed on a dynamic mechanical analyzer (Model Q800, TA Instruments, New Castle, DE, USA) in the uniaxial tension mode. When the folding stable state of the hexagon-twist origami structure is at a high temperature range (20–80°C), the storage modulus of the material VW decreased rapidly and the material TG remains essentially constant.
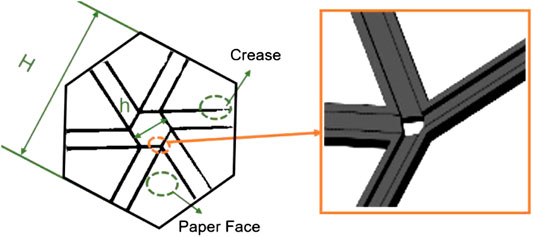
FIGURE 1. Fabrication of the hexagon-twist origami structure. The multimaterial 3D printed hexagon-twist origami structure with the specific design parameter. H denotes the height of outer hexagon. h denotes the height of inter hexagon. The design details about the vertex is shown in the illustration.
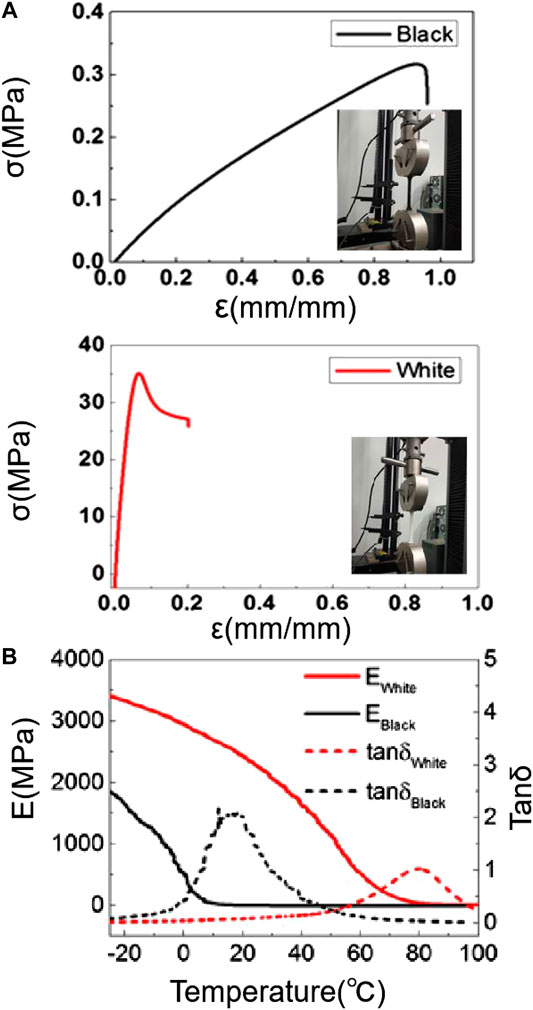
FIGURE 2. Basic mechanical test results of 3D printed materials VeroWhitePlus and TangoBlackPlus. (A) The uniaxial stretching mechanical and (B) the dynamic mechanical analysis testing results of the two materials.
Measurements of Hexagon-Twist Origami Structure Self-Deployment Temperature
The self-deployment temperatures were measured in a water bath. The heat source was from the magnetic heating stirrer that could set the final heated temperature. The thermocouple temperature sensor was used as a feedback for the real time water temperature. The square-twist origami structures with the transformation modes I and II stable state were put in a round beaker with a certain amount of water that was heated at a required temperature, according to the various experimental requirements. The heat rate was kept in a constant value while heating these structures. The self-deployment temperature was defined as the temperature when the structure was obviously converted to the flat state. When the stable state of the structure was altered, the temperature was recorded as one measurement. In this paper, two different methods were used to generate thermal stimulus for driving square-twist origami structures: water bath and infrared light. The first type was mainly based on heat conduction, while the second type was heat radiation. Considering the heat effects on the twist structures, the method of using uniform heat conduction was selected in the water bath. For practical application, a noncontact infrared radiation heating method was applied. The multi-material 3D printed square-twist origami structures were manipulated by temperature, triggering for self-deployment under heating.
Design and Fabrication of Frequency Reconfigurable Dipole Antenna
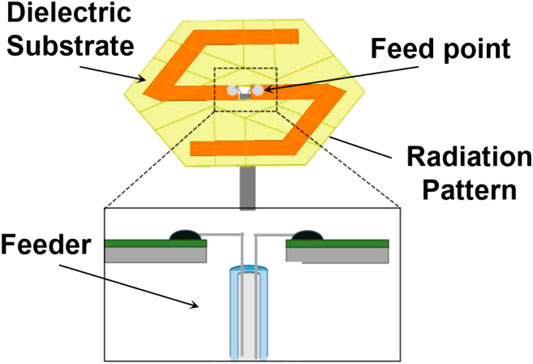
In this work, three design principles were obeyed for designing frequency reconfigurable dipole antennas. Primarily, the dipole antenna required center symmetry of the radiation pattern. Additionally, for pursuing large degree of short circuit, the radiation pattern should be designed across creases as much as possible. Finally, to maintain the foldability of hexagon-twist structure media board, the radiation pattern should avoid the vertices of the hexagon-twist structure as far as possible. Based on the above rules, a basic configuration design of dipole antenna is shown in Figure 3, and then the 3D electromagnetic simulation software HFSS was used to simulate the specific geometry size of the hexagon-twist frequency reconfigurable dipole antenna. The pattern of the antenna radiation patch were arranged along the distribution and arrangement of the folds for the antenna substrate. The material of the antenna arm was set ideal conductor. Since the dipole antenna had a symmetrical structure, the lumped port excitation method was used to feed the antenna, and the simulation frequency band was set to 1–6 GHz. According to the initial simulation results, the design parameters could be optimized by running loop variables for obtaining the optimal performance with the condition of impedance matching. For fabricating aspects of the frequency reconfigurable antenna, the origami dielectric substrate and the radiation patch were fabricated with multi-material 3D printing technology and copper tape, respectively. For the antenna arm of the dipole antenna, that is, the radiation patch, the sputtered copper foil was initially selected to be directly glued to the surface of the dielectric substrate. However, due to its small toughness during the folding and unfolding with the structure, it was easy to break and result antenna failure, so the double-sided conductive copper tape was selected as the radiation patch. Because of its good toughness, the reliability of the antenna was effectively improved during the folding and unfolding process. Coaxial feeder feeding method was adopted for the hexagon-twist frequency reconfigurable origami antenna (Figure 3).
Results and Discussion
Based on our previous work experience research on polygon-twist origami structure (Wang et al., 2019), the length and proportion of the inner and outer sides have an important role in the origami folding stability. In this work, the height of the inner and outer hexagons structure was selected as a key parameter for studying the stability of hexagon-twist origami. The varies size structure were described with h-H where h and H denotes the height of the inner and outer hexagon, respectively. According to the results in Figure 4A, the hexagon-twist structure with sizes 15–50, 15–60, 17–70 existed no stable state which meant “unfoldable” and were unsuitable for reconfigurable dielectric substrate. As for the size of 30–100, 30–120, 30–140, the hexagon-twist structure showed multi-stable state which meant “foldable”, and the specific folded stable state with size 30–100 were shown in Figure 4B. When all the outer panels were folded up counterclockwise around the center hexagon, this self-locking stable state was regarded as state A; When four outer panels and the other two outer panel were symmetrically folded up and down counterclockwise around the center hexagon, respectively, this stable state was named state B; When five outer panels and one outer panel were folded up and down counterclockwise around the center hexagon, this stable state was regarded as state C (Figure 4B). According to our previous work (Wang et al., 2020), because the elastic modulus of material VW decreased drastically as the temperature increased (Figure 2B), the stiffness ratio of the paper facet to the crease was varied (Tawk et al., 2010), thereby decreasing the energy barrier of the structure. The self-deployment of the multi-material 3D printed polygon-twist origami structure was driven by the energy stored in the crease material TG. The hexagon-twist 3D printed origami structure could also self-deploy under the higher temperature condition as shown in Figure 5 for state A, state B and state C. In order to further research the influence of the key geometric parameters of the origami structure on its self-deployment behavior, the self-deployment behavior of stable state A, state B, and state C with varies geometry size under the 65°C water bath condition was studied. To quantify the self-deployment process, the response time and reaction time required to be defined. Response time referred to the time from the beginning of excitation to the moment of observing apparent motion. The reaction time was defined as the subsequent time from the moment of observing apparent motion to the completion of deployment. As the outer contour of the hexagonal increased (H = 100,120, 140 mm) with the same central hexagon (h = 30 mm), the response time and reaction time of the stable state during self-deployment gradually increased (Figure 6). This was because the larger geometric size of the outer hexagon, the greater energy barrier of the structure, and the more energy that needed to be absorbed during self-deployment, so the time required increased. By comparing the self-deployment behavior time between different stable states, state C and state A required the shortest and the longest reaction time with the same geometric parameter ratio of the origami structure, respectively. According to the author’s previous work (Wang et al., 2020), the order of energy barriers of different states can be obtained based on their reaction time as state A > state B > state C. (Although the crease pattern of square-twist and hexagon-twist structure are different, they have the same self-deployment mechanism, and both them belong to the twist origami category).
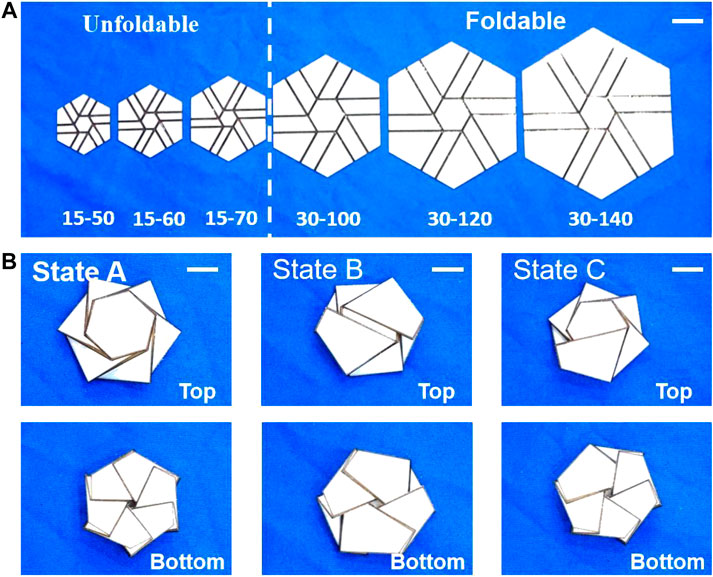
FIGURE 4. The multi-material 3D printed hexagon-twist origami structure. (A) Multi-stable research about hexagon-twist origami structure with different size ( h-H: h and H denotes the height of the inner and outer hexagon, respectively). Scale bar, 30 mm. (B) The multi-stable states of 3D printed hexagon-twist origami structure with size 30–100. Scale bar, 10 mm.
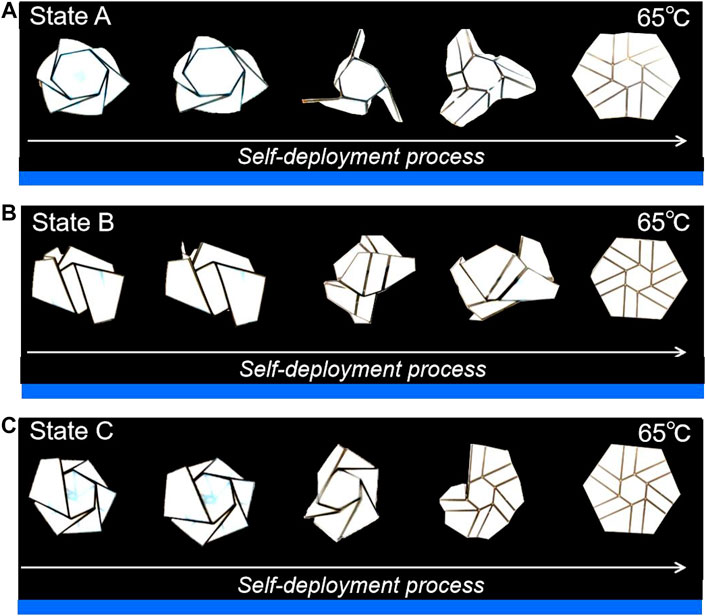
FIGURE 5. The self-deployment process of multi-material 3D printed hexagon-twist origami structure with (A) state A, (B) state B and (C) state C under 65°C water bath condition. Each image of the structure during the self-deployment process is scaled to ensure the overall picture effect.
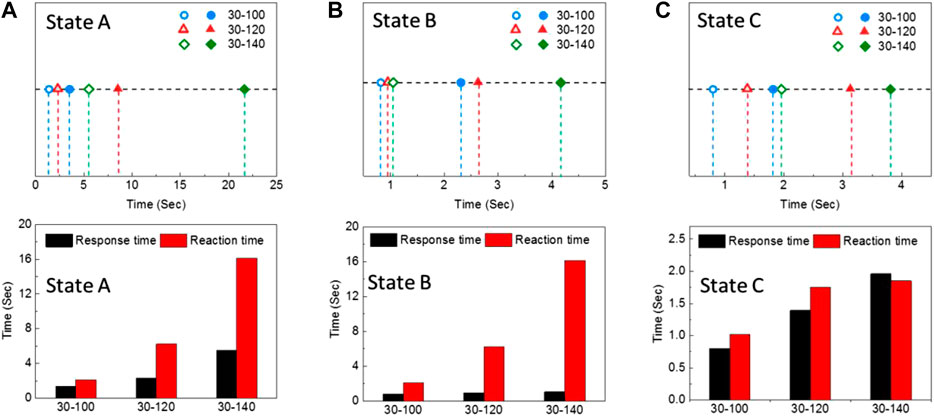
FIGURE 6. The self-deployment response and reaction time results of (A) state A, (B) state B and (C) state C with various size. In the top row of graphs, the response time is from zero to the hollow point, and the reaction time is from the hollow point to the solid point.
In the following content, a frequency reconfigurable dipole antenna was manufactured with the 3D multi-material printed hexagon-twist origami structure as the dielectric substrate. The thickness, the height of central hexagon and the outer hexagon of the hexagon-twist origami dielectric substrate were 0.5, 30, and 100 mm, respectively (Figure 3). The relative dielectric constant ε and the loss tangent angle tanδ for the structure were 2.8 and 0.0001, respectively. Keeping the dielectric substrate in a flat state, the dipole arms were not in contact with each other, which was the initial frequency state. When the dielectric substrate maintained various folded stable state, the antenna dipole arms were in contact with each other to produce a short circuit, which in turn reduced the electrical length of the dipole antenna, there by ultimately leading to an increase in the antenna frequency. It was worth noting that even if the dipole arms were not in contact with each other, the relative position of the antenna arm changes would also produce spatial resonance, which could make the antenna reconfigurable frequency. In order to shorten the design cycle and save costs, the simulation for antenna performance was carried out (Materials and Methods). The simulation results about the current distribution of the hexagon-twist frequency reconfigurable antenna clearly illustrated different state with various operating frequency (Figure 7). It should be noted here that pasting a radiation patch on one side of the dielectric substrate to form an antenna resulted in various electrical lengths of the dipole antenna with folded forward and backward in a stable state. Because of the position of the radiation patch fixed relative to the structure, even if various folding methods formed the same state, different electrical lengths would be generated, there by forming different operating frequencies for frequency reconfigurable antenna. Through the above illustration, the frequency reconfigurable antenna had nine antenna configurations (Flat state, State A, state B, and state C generated one, two, three and three antenna configurations, respectively.) with hexagon-twist origami substrate. In order to better design and manufacture frequency reconfigurable antenna, the influence of geometric parameters on the antenna frequency was discussed via finite element simulation (Figure 8). The frequency of the antenna was related to the geometric parameters of the substrate and the antenna arm. In this paper, the parameters I, w, d,and H which denoted the length, the width of the antenna arm, the thickness of the dielectric plate and the size of the outer contour, respectively, were selected as specific research factors. In order to study the influence of these parameters on the antenna resonance frequency, a standard model was chosen with I = 50 mm,w = 10 mm,d = 0.5 mm and H = 100 mm, maintaining 30 mm for the height of central hexagon. Considering the thickness d of the dielectric substrate with 0.5–2 mm, the antenna frequency decreased as the thickness of the dielectric substrate increased. The change of the overall hexagon-twist origami size H had little effect on the frequency. In the design of a general dipole antenna, the equivalent electrical length of the antenna is inversely proportional to the center resonance frequency. In Figure 8C, as the antenna arm I grows, the center resonance frequency did not show an obvious inverse law. Perhaps due to the error of the finite element model itself, the antenna arm growth did not increase the equivalent electrical length. The influence of the width of the antenna arm on the resonance frequency had no obvious linear law. According to the above study, the hexagon-twist origami structure exhibited self-deployment behavior due to the rapidly decrease in the storage modulus of the paper surface material under heating conditions. This kind of behavior was introduced into the antenna design, so that the antenna could realize deployment and frequency reconfigurable under the temperature field conditions. Figure 9 showed the self-deployment deformation of the dipole antenna in the initial folded state under infrared heating and the experiment conditions of light intensity and temperature were 3.96 mW/cm2 and approximately 75°C, respectively. The unfolding time principle of the antennas in different folded states is consistent with the unfolding law of the dielectric substrate studied in the high temperature field. The actual operating frequency of the antenna could be obtained by measuring the return loss S11 parameter. In this work, the S11 parameter was measured by the E5071C vector network analyzer that was produced by Keysight, whose test frequency range was from 0.5 to 6 GHz. The dual port of the vector network analyzer was calibrated with an electronic calibration component prior to testing, and then connected the coaxial line of the antenna to the test interface of the vector network analyzer port1. Finally, related parameters about the analyzer was adjusted to test the various states of their parameter S11 via changing the configuration of the hexagon-twist dielectric substrate. In Figure 10, the actual test results of the antenna were in agreement with the simulation results, although there existed a certain error. It could be seen from the test results that the return loss of each antenna’s operating frequency was below -10 db, which met the basic requirements for antenna operation. Maintaining the antenna in flat state, the center resonance frequency was 3.97 GHz. According to the actual measurement results, when the antenna was folded to the state 1, the center resonance frequency was 3.39 GHz. The antenna center resonance frequencies of folded state 2∼state 9 were 2.39, 2.41, 4.13, 3.67, 3.07, 2.77, and 2.66 GHz, respectively. The antenna realized nine kinds of center operating frequency changes with nine various stable states, and implemented multi-mode frequency reconfiguration.
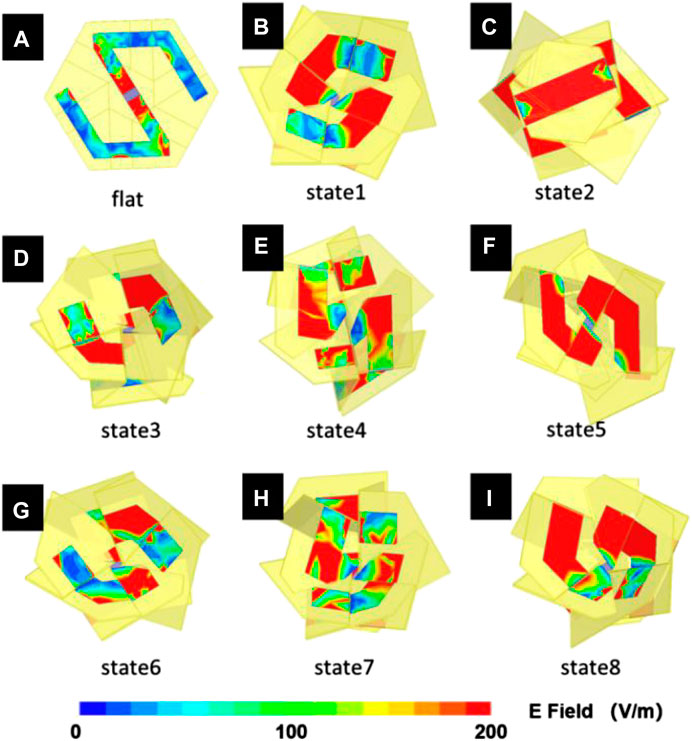
FIGURE 7. The current distribution finite element simulation results of the hexagon-twist origami structure stable (A) flat state and (B–I) state 1–8.
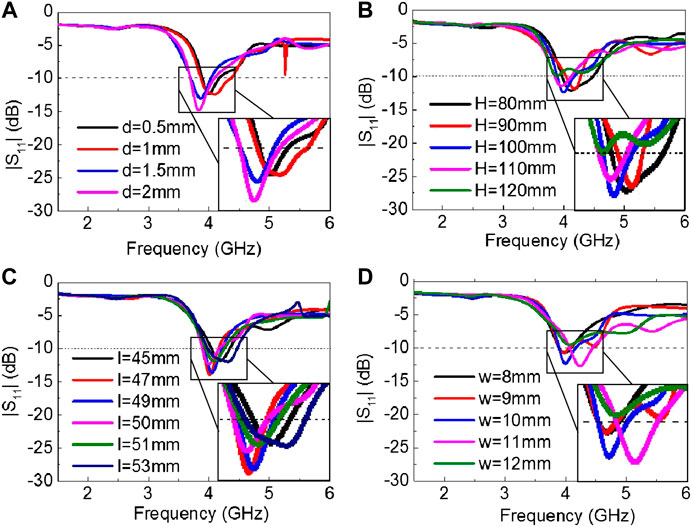
FIGURE 8. Geometric parameters (A) the thickness of the dielectric substrate-d, (B) the height of outer hexagon for the dielectric substrate-H, (C) the length of antenna arm-I, and (D) the width of antenna arm-w) effect on antenna frequency.
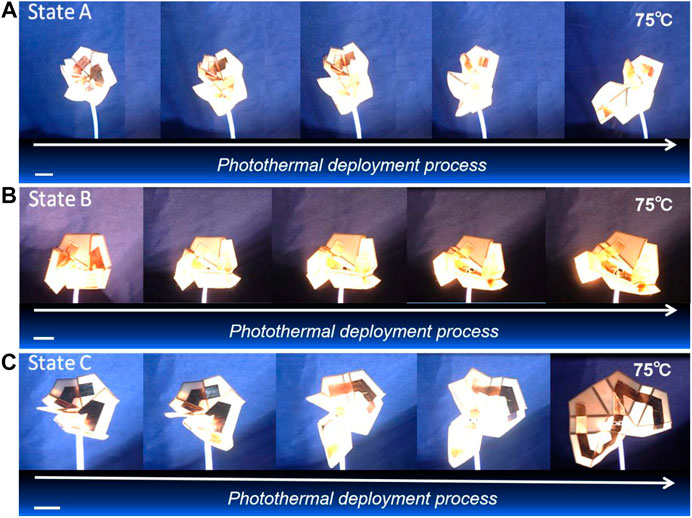
FIGURE 9. The self-deployment process of hexagon-twist frequency reconfigurable antenna with (A) state A, (B) state B and (C) state C under photothermal condition. Scale bar, 30 mm.
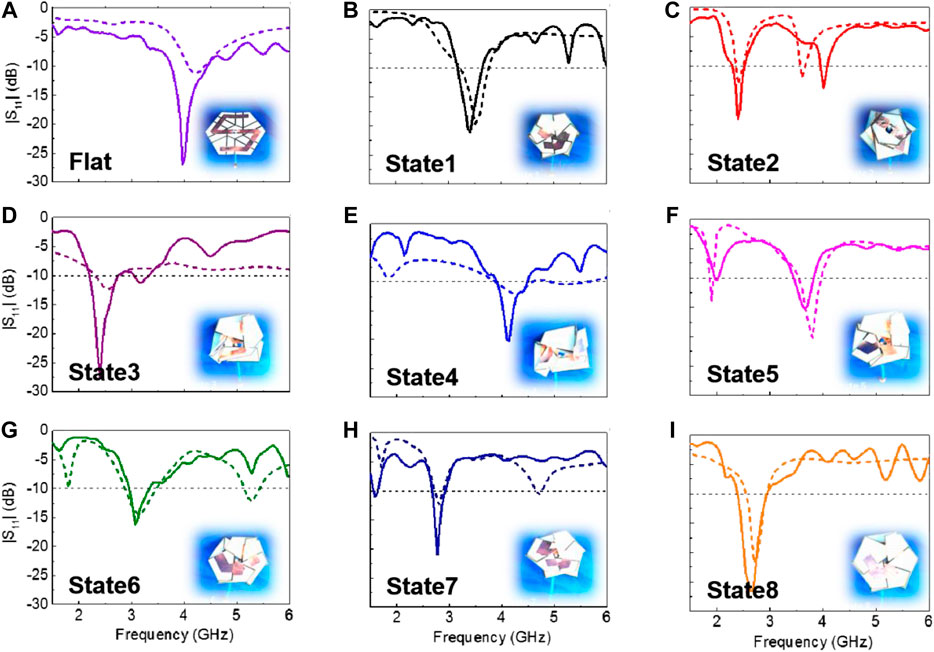
FIGURE 10. The results of hexagon-twist origami antenna return loss. (A–I) Comparison of measured and simulated results of antenna return loss in nine different stable state for hexagon-twist origami structure. The corresponding stable state configurations are shown in the illustration.
The traditional frequency reconfigurable antenna mainly used a switch to change the electrical length of the antenna to achieve antenna frequency reconfiguration. The on and off of the switch determined the antenna reconfigurable mode. Not only were there fewer reconfigurable modes, but also the external bias circuit affected the performance of the antenna and reduced the antenna efficiency. Compared with the work of other frequency reconfigurable antennas (Table 1), the dipole frequency reconfigurable antenna implemented in this paper used an origami structure to self-deploy at high temperature to achieve reconfigurable frequency without additional bias circuit affects. The antenna made in this paper was a dipole antenna, that was, an omnidirectional antenna. The radiation pattern was also tested using the microwave far-field darkroom (Figure 11). From the results of the radiation pattern, the H-plane graphic showed an omnidirectional antenna, but the E-plane graphic illustrated a non-omnidirectional antenna. This was because the electric field in the vertical plane tilted down due to the feeder, which affected the radiation characteristics in the horizontal direction. One thing to note was that state 2 had two operation frequency points, so the radiation pattern at the two frequency points were measured in state 2.
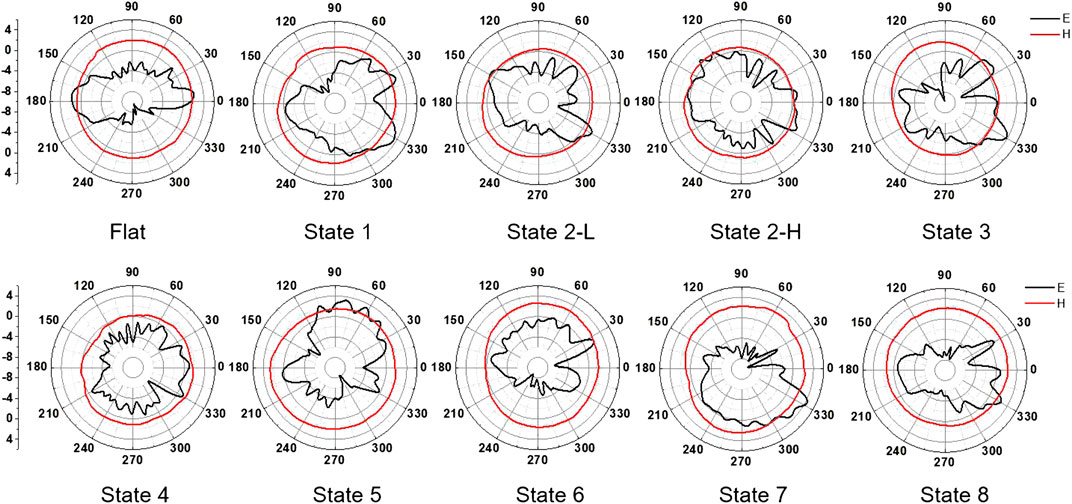
FIGURE 11. The radiation pattern test results of hexagon-twist frequency reconfigurable antenna with different stable state. E and H denotes the radiation pattern cut plane with parallel electric field direction and magnetic field direction, respectively.
In this paper, a self-deployment origami antenna was realized based on a multi-material 3D printed hexagon twist structure dielectric substrate, and the multi-material hexagon twist structure played an important part to realize the function. In the future, the following aspects will be further studied. In terms of the self-deployment mechanism of the structure, more attention will be paid to the influence of polymer swelling and relaxation time on the self-deployment behavior and deployment time of the structure (Lu et al., 2010a; Lu et al., 2010b; Lu and Du, 2014). In terms of driving methods, the photothermal driving method in this article will have shortcomings in practical applications, and more reliable electronic control methods may be used in subsequent work (Lu et al., 2011). In addition, the multi-stability of the hexagonal twist structure can also be applied in many aspects, such as a smart substrate with buckling-induced kirigami structure (Pang et al., 2020), making multi-stable mechanical metamaterials (Ma et al., 2016; Yan et al., 2020), or making flexible electronic devices (Ma and Zhang, 2016).
Conclusions
In this paper, a dipole cross-band frequency reconfigurable antenna based on a multi-material hexagon-twist origami structure was designed. The specific conclusion contents were as follows:
(1) The multi-stable state of the hexagon-twist origami structure was studied. The hexagon-twist origami structure was prepared via 3D multi-material printing, in which the paper face and the crease area were printed with resin-based materials VW and rubber-like materials TG, respectively. It was found that the folded stable state was related to the ratio and size of the inner and outer hexagons of the structure. The structure had three kinds of stable state called state A, state B and state C.
(2) The mechanism and law of self-deployment behavior with hexagonal twist origami structure at high temperature were studied. The self-deployment behavior in the folded state was because that the storage modulus of the material VW decreased rapidly at high temperature, causing a sharp reduction in stiffness, and thereby reducing the energy barrier of the structure to less than the elastic driving energy stored in the crease material TG. The various folded states had different self-deployment behavior. The higher the energy barrier of the structure, the longer the self-deployment time was required. In this paper, the self-deployment time was state A greater than state B and state B greater than state C.
(3) A dipole frequency reconfigurable antenna based on hexagon-twist origami structure was designed. The operating frequency and radiation pattern of the dipole antenna had been tested. The frequency reconfigurable antenna had nine operating modes according to different crease pattern, which implemented cross-band reconfigurable frequency from S to C band. The dielectric substrate could self-deploy from the folded state at high temperature. Therefore, the antenna could realize the function of deformation and frequency reconfiguration.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
W-LS, MC, and DF conceived the idea and experimental work; Y-JZ and L-CW led the experiments and simulation with assistance from W-LS and MC; W-LS and Y-JZ contributed to data analysis and interpretation and wrote the paper. All authors provided feedback.
Funding
Financial support from Beijing Natural Science Foundation (Grant No. 2182065) and National Natural Science Foundation of China (Grant No. 11872113) is gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ahn, B. Y., Shoji, D., Hansen, C. J., Hong, E., Dunand, D. C., and Lewis, J. A. (2010). Printed origami structures. Adv. Mater. 22, 2251–2254. doi:10.1002/adma.200904232
Ahyat, E. N., Kamarudin, M. R., Rahman, T. A., Jamlos, M. F., Hamid, M. R., Jamaluddin, M. H., et al. (2013). Frequency and pattern reconfiguable dipole-yagi antenna. Microw. Opt. Techn. Let. 55, 447–450. doi:10.1002/mop.27323
Anfinsen, C. B. (1973). Principles that govern the folding of protein chains. Science 181, 223–230. doi:10.1126/science.181.4096.223
Breger, J. C., Yoon, C., Xiao, R., Kwag, H. R., Wang, M. O., Fisher, J. P., et al. (2015). Self-folding thermomagnetically responsive soft microgrippers. ACS Appl. Mater. Interfaces 7, 3398–3405. doi:10.1021/am508621s
Bromberg, L., and Ron, E. S. (1998). Temperature-responsive gels and thermogelling polymer matrices for protein and peptide delivery. Adv. Drug Delivery Rev. 31, 197–221. doi:10.1016/S0169-409X(97)00121-X
Erb, R. M., Sander, J. S., Grisch, R., and Studart, A. R. (2012). Self-shaping composites with programmable bioinspired microstructures. Nat. Commun. 4, 1712. doi:10.1038/ncomms2666
Faber, J. A., Arrieta, A. F., and Studart, A. R. (2018). Bioinspired spring origami. Science 359, 1386–1391. doi:10.1126/science.aap7753
Felton, S., Tolley, M., Demaine, E., Rus, D., and Wood, R. (2014). A method for building self-folding machines. Science 345, 644–646. doi:10.1126/science.1252610
Fernandes, R., and Gracias, D. H. (2012). Self-folding polymeric containers for encapsulation and delivery of drugs. Adv. Drug Delivery Rev. 64, 1579–1589. doi:10.1016/j.addr.2012.02.012
Ge, Q., Dunn, C. K., Qi, H. J., and Dunn, M. L. (2014). Active origami by 4D printing. Smart Mater. Struct. 23, 094007. doi:10.1088/0964-1726/23/9/094007
Ge, Q., Luo, X., Rodriguez, E. D., Zhang, X., Mather, P. T., Dunn, M. L., et al. (2012). Thermomechanical behavior of shape memory elastomeric composites. J. Mech. Phys. Solids. 60, 67–83. doi:10.1016/j.jmps.2011.09.011
Ge, Q., Qi, H. J., and Dunn, M. L. (2013). Active materials by four-dimension printing. Appl. Phys. Lett. 103, 131901. doi:10.1063/1.4819837
Gladman, A. S., Matsumoto, E. A., Nuzzo, R. G., Mahadevan, L., and Lewis, J. A. (2015). Biomimetic 4D printing. Nat. Mater. 15, 413–418. doi:10.1038/NMAT4544
Guo, T. F., Leng, W., Wang, A. G., Li, J. J., and Zhang, Q. F. (2014). A novel planar parasitic array antenna with frequency and pattern-reconfigurable characteristics. IEEE Antenn. Wirel. Pr. 13, 1569–1572. doi:10.1109/LAWP.2012.2221073
Hu, J., Meng, H., Li, G., and Lbekwe, S. I. (2012). A review of stimuliresponsive polymers for smart textile applications. Smart Mater. Struct. 21, 053001. doi:10.1088/0964-1726/21/5/053001
Jamlos, M. F., Aziz, O. A., Rahman, T. A., Kamarudin, M. R., Saad, P., Ali, M. T., and Md Tan, M. N. (2010). A beam steering radial line slot array (RLSA) antenna with reconfigurable operating frequency. J. Electromagnet. Wave 24, 1079–1088. doi:10.1163/156939310791586034
Lee, W. W., and Cho, Y. S. (2015). A frequency reconfigurable MIMO antennas using RF tuning element for mobile handset. Microw. Opt. Techn. Let. 57, 1092–1096. doi:10.1002/mop.29023
Leng, J., Lan, X., Liu, Y., and Du, S. (2011). Shape-Memory polymers and their composites: stimulus methods and applications. Prog. Mater. Sci. 56, 1077–1135. doi:10.1016/j.msec.2018.12.054
Li, Q., and Lewis, J. A. (2003). Nanoparticle inks for directed assembly of three-dimensional periodic structures. Adv. Mater. 15, 1639–1643. doi:10.1002/adma.200305413
Li, T., Zhai, H. Q., Long, Li., and Liang, C. H. (2014). Frequency-reconfigurable bow-tie antenna with a wide tuning range frequency. IEEE Antenn. Wirel. Pr. 13, 1549–1552. doi:10.1109/LAWP.2014.2344676
Li, Y. C., Zhang, Y. S., Akpek, A., Shin, S. R., and Khademhosseini, A. (2017). 4D bioprinting: the next-generation technology for biofabrication enabled by stimuli-responsive materials. Biofabrication 9, 012001. doi:10.1088/1758-5090/9/1/012001
Lu, H. B., and Du, S. Y. (2014). A phenomenological thermodynamic model for the chemo-responsive shape memory effect in polymers based on Flory–Huggins solution theory. Polym. Chem. 5, 1155–1162. doi:10.1039/c3py01256e
Lu, H. B., Liang, F., and Gou, J. H. (2011). Nanopaper enabled shape-memory nanocomposite with vertically aligned nickel nanostrand: controlled synthesis and electrical actuation. Soft Matter 7, 7416. doi:10.1039/c1sm05765k
Lu, H. B., Liu, Y. J., Leng, J. S., and Du, S. Y. (2010a). Qualitative separation of the physical swelling effect on the recovery behavior of shape memory polymer. Eur. Polym. J. 46, 1908–1914. doi:10.1016/j.eurpolymj.2010.06.013
Lu, H., Liu, Y., Gou, J., Leng, J., and Du, S. (2010b). Electrical properties and shape-memory behavior of self-assembled carbon nanofiber nanopaper incorporated with shape-memory polymer. Smart Mater. Struct. 19, 075021. doi:10.1088/0964-1726/19/7/075021
Luo, R., Wu, J., Dinh, N. D., and Chen, C. H. (2015). Gradient porous elastic hydrogels with shape-memory property and anisotropic responses for programmable locomotion. Adv. Funct. Mater. 25, 7272−7279. doi:10.1002/adfm.201570299
Ma, Q., Cheng, H., Jang, K. I., Luan, H., Hwang, K. C., Rogers, J. A., et al. (2016). A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures. J. Mech. Phys. Solids 90, 179–202. doi:10.1016/j.jmps.2016.02.012
Ma, Q., and Zhang, Y. H. (2016). Mechanics of fractal-inspired horseshoe microstructures for applications in stretchable electronics. Int. J. Appl. Mech. 83, 111008. doi:10.1115/1.4034458
Majid, H. A., Kamal, M., Rahim, A., Hamid, M. R., and Ismail, M. F. (2012). A compact frequency-reconfigurable narrowband microstrip slot antenna. IEEE Antenn. Wirel. Pr. 11, 616–619. doi:10.1109/LAWP.2012.2202869
Mu, J., Hou, C., Wang, H., Li, Y., Zhang, Q., and Zhu, M. (2015). Origami inspired active graphene-based paper for programmable instant selffolding walking devices. Sci. Adv. 1, e1500533. doi:10.1126/sciadv.1500533
Overvelde, J. T. B., Jong, T. A., Shevchenko, Y., Becerra, S. A., Whitesides, G. M., Weaver, J. C., et al. (2016). A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929. doi:10.1038/ncomms10929
Pang, W., Cheng, X., Zhao, H., Guo, X., Ji, Z., Li, G., et al. (2020). Electro-mechanically controlled assembly of reconfigurable 3D mesostructures and electronic devices based on dielectric elastomer platforms. Natl. Sci. Rev. 7, 342–354. doi:10.1093/nsr/nwz164
Silverberg, J. L., Na, J. H., Evans, A. A., Liu, B., Hull, T. C., Santangelo, C. D., et al. (2015). Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater. 14, 389–393. doi:10.1038/nmat4275
Song, Y. X., Xu, Q. H., Tian, Y., Yang, J., Wu, Y. Q., Tang, X. H., et al. (2017). An on-chip frequency-reconfigurable antenna for q-band broadband applications. IEEE Antenn. Wirel. Pr. 16, 2232–2235. doi:10.1109/LAWP.2017.2709911
Su, J. W., Xie, T., Deng, H., Zhang, C., Jiang, S., Lin, Y., et al. (2018). 4D printing of a self-morphing polymer driven by a swellable guest medium. Soft Matter 14, 765–772. doi:10.1039/c7sm01796k
Tawk, Y., Albrecht, A. R., Hemmady, S., Balakrishnan, G., and hristodoulou, C. G. (2010). Optically pumped frequency reconfigurable antenna design. IEEE Antenn. Wirel. Pr. 9, 280–283. doi:10.1109/LAWP.2010.2047373
Tawk, Y., Costantine, J., Avery, K., and Christodoulou, C. G. (2011). Implementation of a cognitive radio front-end using rotatable controlled reconfigurable antennas. IEEE T. Antenn. Propag. 59, 1773–1778. doi:10.1109/TAP.2011.2122239
Therien-Aubin, H., Wu, Z. L., Nie, Z., and Kumacheva, E. (2013). Multiple shape transformations of composite hydrogel sheets. J. Am. Chem. Soc. 135, 4834–4839. doi:10.1021/ja400518c
Tibbits, S. (2014). 4D printing: multi-material shape change. Archit. Des. 84, 116–121. doi:10.1002/ad.1710
Wang, L. C., Song, W. L., and Fang, D. N. (2019). Twistable origami and kirigami: from structure-guided smartness to mechanical energy storage. ACS Appl. Mater. Interfaces 11, 3450–3458. doi:10.1021/acsami.8b17776
Wang, L. C., Song, W. L., Zhang, Y. J., Qu, M. J., Zhao, Z. A., Chen, M. J., et al. (2020). Active reconfigurable tristable square-twist origami. Adv. Funct. Mater. 30, 1909087. doi:10.1002/adfm.201909087
Wong, J. Y., Langer, R., and Ingber, D. E. (1994). Electrically conducting polymers can noninvasively control the shape and growth of mammalian cells. Proc. Natl. Acad. Sci. 91, 3201–3204. doi:10.1073/pnas.91.8.3201
Yan, D., Chang, J., Zhang, H., Liu, J., Song, H., Xue, Z., et al. (2020). Soft Three-dimensional network materials with rational bio-mimetic designs. Nat. Commun. 11, 1180. doi:10.1038/s41467-020-14996-5
Zhao, Q., Qi, H. J., and Xie, T. (2015). Recent progress in shape memory polymer: new behavior, enabling materials, and mechanistic understanding. Prog. Polym. Sci. 49−50, 79–120. doi:10.1016/j.progpolymsci.2015.04.001
Keywords: multi-material 4D printed, origami structures, reconfigurable antennas, hexagon-twist, self-deployment
Citation: Zhang Y-J, Wang L-C, Song W-L, Chen M and Fang D (2020) Hexagon-Twist Frequency Reconfigurable Antennas via Multi-Material Printed Thermo-Responsive Origami Structures. Front. Mater. 7:600863. doi: 10.3389/fmats.2020.600863
Received: 31 August 2020; Accepted: 03 November 2020;
Published: 23 November 2020.
Edited by:
Yusheng Shi, Huazhong University of Science and Technology, ChinaReviewed by:
Yu Wang, University of Science and Technology of China, ChinaHaibao Lu, Harbin Institute of Technology, China
Copyright © 2020 Zhang, Wang, Song, Chen and Fang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei-Li Song, d2VpbGlzQGJpdC5lZHUuY24=
†These authors have contributed equally to this work
 Ya-Jing Zhang1,2†
Ya-Jing Zhang1,2† Li-Chen Wang
Li-Chen Wang Wei-Li Song
Wei-Li Song