Demultiplexing Infrasound Phonons With Tunable Magnetic Lattices

Introduction

Infrasound waves are ubiquitous in nature, appearing in animal communications (von Muggenthaler et al., 2003; Barklow, 2004; Von Muggenthaler, 2013), natural phenomena such as earthquakes and volcanic eruptions (Garcés et al., 2003; Fee and Matoza, 2013; Nakano et al., 2018; Ripepe et al., 2018), and man made systems such as machinery and explosions. These waves can cause high volumes of damage to their surroundings, particularly when originating from natural phenomena (Le Pichon et al., 2010). Deciphering infrasound waves can lead to potential detection of various natural phenomena prior to their occurrences, offering a type of early warning system through their detection. Phononic crystals and acoustic metamaterials, defined as artificial arrangements of spatial patterns, can manipulate waves at different frequency ranges from a few Hertz to a few Terahertz (Deymier, 2013; Maldovan, 2013; Hussein et al., 2014; Khelif and Adibi, 2015). These phononic metamaterials usually consist of unit cells that repeat periodically. Phononic crystals have the ability to affect waves through Bragg scattering (Kushwaha et al., 1993), while metamaterials utilize resonances to affect waves (Liu et al., 2000). The wave controlling characteristics of phononic crystals and acoustic metamaterials have a variety of potential applications, including vibration and sound insulation (Yang et al., 2010; Mei et al., 2012; Ma et al., 2015), seismic wave protection (Kim and Das, 2012; Brûlé et al., 2014), wave guiding (Torres et al., 1999; Rupp et al., 2007), frequency filtering (Rupp et al., 2010), acoustic lenses, (Molerón et al., 2014), and sensors (Ke et al., 2011; Amoudache et al., 2014).

The presence of scattering in phononic crystals and resonances in metamaterials gives rise to specific frequency ranges where waves cannot propagate (i.e., band gaps). In a scattering-based band gap, the unit cell size has to be on the same order of the targeted frequency wavelength. This usually translates into a meter sized structure that affects waves at ultra-low frequencies (Brûlé et al., 2014). Resonance based metamaterials can open band gaps where the targeted frequency wavelength does not correlate with the unit cell size (i.e, subwavelength band gaps). However, opening band gaps at ultra-low frequencies could translate to a resonator with mass on the order of many kilograms (Palermo et al., 2016; Colombi et al., 2020) or coupling stiffness that is prone to fatigue. In addition, most phononic metamaterial realizations have fixed operational frequency. Once a sample is fabricated, its band gap frequency, for example, cannot change (Matar et al., 2013; Bergamini et al., 2014; Bilal et al., 2017a).

In this paper we utilize tunable lattices of repelling magnets to guide and sort infrasound waves into different channels based on their frequencies. We realize these lattices by confining meta-atoms (free-floating macroscopic disks with embedded magnets) within a magnetic boundary. We control the spacing between the meta-atoms by changing the magnetic potential of the confining boundary. The same meta-atoms with different lattice constants and coupling intensity can have different wave propagation characteristics by design. As a demonstration of principle, we experimentally realize an infrasound phonon demultiplexer (i.e., guiding ultra-low frequency waves into different channels based on their frequencies). By constructing channels with identical building blocks, yet different boundary potentials, we can demultiplex infrasound waves based on their frequencies. There exist multiple theoretical proposals for realizing phonon demultiplexers (Pennec et al., 2004; Hussein et al., 2005; Pennec et al., 2005; Vasseur et al., 2011; Rostami-Dogolsara et al., 2016; Zou et al., 2017; Moradi and Bahrami, 2019; Babaki and Nazari, 2020; Ben-Ali et al., 2020; Gharibi and Bahrami, 2020; Motaei and Bahrami, 2020) with few experimental demonstrations (Mohammadi and Adibi, 2011; Faiz et al., 2020; Bilal et al., 2020). However, demultiplexing infrasound phonons has not been observed.

Design Methodology

To design our infrasound phonon demultiplexer, we start by considering a unit cell composed of a disk with a concentrically embedded magnet, referred to as meta-atoms hereinafter. The meta-atoms are confined between two arrays of fixed, identical, permanent magnets (Figure 1A). The fixed magnets create a boundary potential to hold the meta-atoms in place. The fixed magnets are equally spaced by a length a. The two arrays of fixed magnets are separated by a distance b. Both a and b define the equilibrium position of the meta-atoms. The assembly of these meta-atoms for a given a and b gives rise to various band gaps within the frequency spectrum. By changing the values of a and b, we can change the relative position of pass bands and band gaps. Each one of these designs (with a given a and b) can work as a designated channel for specific frequency phonons, while rejecting the phonons within the band gap frequency ranges. We connect multiple channels composed of different configurations of a and b, allowing only certain frequencies to pass in each channel. As a demonstration of principle, we connect three channels in a T-shaped configuration to function as a demultiplexer for infrasound phonons (Figure 1D). The left and right junctions of the T-shaped waveguide have out-of-sync pass and stop bands, while the vertical junction has a pass band encompassing both pass band frequencies (Figure 1B). For example, when exciting the vertical junction at a frequency $f_1$ within the band gap of the right junction, the wave propagates only through the left channel (CH.1). Similarly, when exciting the vertical junction at a frequency $f_2$ within the band gap of the left junction, the wave propagates only through the right channel (CH.3) (Figure 1C).

FIGURE 1

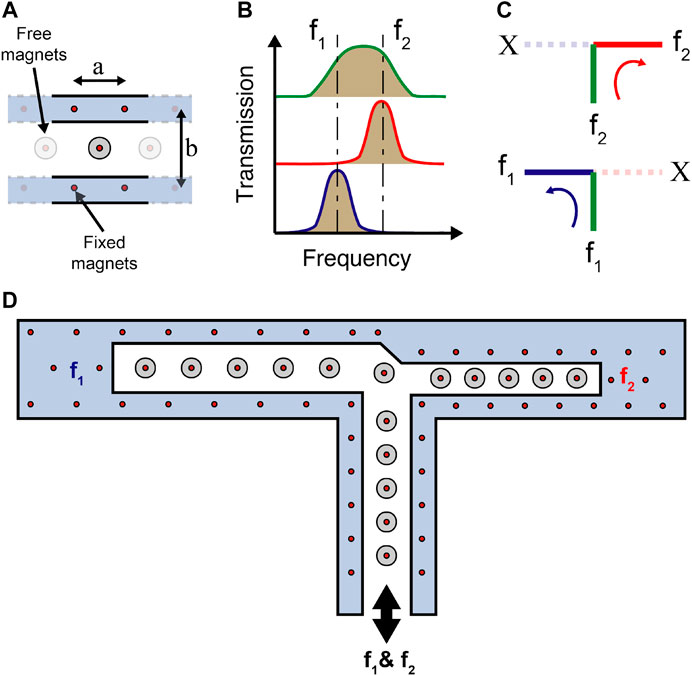
FIGURE 1. Design concept. (A) Schematic of a unit cell depicting the locations of a and b as well as the fixed and free magnets. (B) Transmission spectrum of channel 1 (blue), 2 (green), and 3 (red). (C) A visual representation of two different frequencies ($f_1$ and $f_2$) passing through the channels. (D) A full schematic of the t-shaped demultiplexer with $f_1$ and $f_2$ excited at the vertical channel (CH. 2) and sorted into their respective channels.

Results

To analyze our magnetic lattices, we first consider the basic building block of our structure, a single meta-atom and its coupling to the boundary. We use Bloch’s theorem to generate the dispersion curves of our magnetic lattice (Bloch, 1929). The dispersion analysis of our unit cell takes into account the nearest neighbor interaction between the meta-atoms (Figure 2 inset). Each meta-atom (i.e., the disk with the embedded concentric magnet) is coupled to four fixed boundary magnets and one other freely moving meta-atom on each side. Each meta-atom has two degrees of freedom (i.e., movement in x and y direction). The dispersion equation for our system can be written as:

$\left[-{\omega }^2\mathbf{M}+\mathbf{K}\left(\mathit{\kappa }\right)\right]\mathit{\varphi }=0,(1)$

where ω is the frequency, κ is the wavenumber, $\mathit{\varphi }={\left[uv\right]}^T$ is the Bloch displacement vector in x and y direction, $\mathit{M}=\left[\begin{array}{cc}m& 0\\ 0& m\end{array}\right]$ is the mass matrix and $\mathit{K}$ is the stiffness matrix (Jiao and Gonella, 2019):

$\mathbf{K}\left(\mathit{\kappa }\right)=2{\displaystyle \sum }_{i=1}^3\left\{f_{,d}\left(d_i\right){\mathit{e}}_{\mathit{i}}\otimes {\mathit{e}}_{\mathit{i}}\left[{\delta }_{i1}cos\left(\mathit{\kappa }\cdot {\mathit{R}}_{\mathit{i}}\right)-1\right]\right\}+2{\displaystyle \sum }_{i=1}^3\left\{\frac{f\left(d_i\right)}{d_i}\left(\mathit{I}-{\mathit{e}}_{\mathit{i}}\otimes {\mathit{e}}_{\mathit{i}}\right)\left[{\delta }_{i1}cos\left(\mathit{\kappa }\cdot {\mathit{R}}_{\mathit{i}}\right)-1\right]\right\},(2)$

where $d_1=d_a$ is the distance between the meta-atoms, $d_{\mathrm{2,3}}=d_b$ is the distance between the meta-atoms and the boundary, δ is the Kronecker delta function and $\otimes$ is the dyadic product. The stiffness matrix in Eq. 2 takes into account the repulsive forces between the magnetic particles following an inverse power law in the form $f\left(d\right)=A{d}^{\gamma }$ and $f_{,d}\left(d\right)$ as its first derivative. For a dipole-dipole interaction (Mehrem et al., 2017) $A=3\mu B^2/4\pi$, where μ is the permeability of air and B is the magnetic moment. ${\mathit{R}}_1=d_a{\mathit{e}}_1$, ${\mathit{R}}_2=d_b{\mathit{e}}_2$ and ${\mathit{R}}_3=d_b{\mathit{e}}_3$ are the lattice vectors and ${\mathit{e}}_1={\left[10\right]}^T$, ${\mathit{e}}_2={\left[d_a/2d_{b}b/2d_b\right]}^T$, and ${\mathit{e}}_3={\left[-d_a/2{\mathit{d}}_{b}b/2d_b\right]}^T$ are the unit vectors.

FIGURE 2

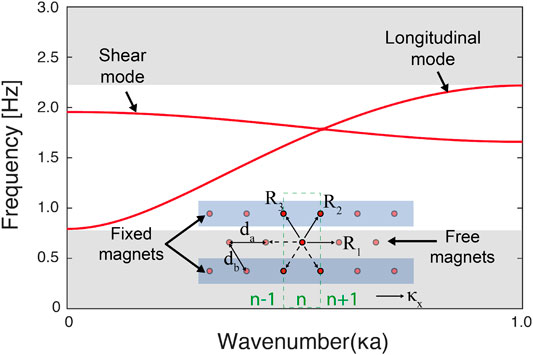
FIGURE 2. Dispersion curves. Numerical dispersion curves for both the shear and longitudinal modes for a lattice with $a=15.4\hspace{0.17em}\hspace{0.17em}mm$, $b=24.5\hspace{0.17em}\hspace{0.17em}mm$ and m = 0:118 g. The band gaps are shaded in gray. The inset shows a unit cell n along with its lattice vectors.

The dispersion curves for an example magnetic lattice with $a=15.4mm$, $b=24.5mm$, $\gamma =-4$, $m=0.118g$ and $A=1.0935\times {10}^{-12}$ shows a pass band sandwiched between two band gaps (Figure 2). The dispersion analysis considers both longitudinal and shear modes. The two branches within the dispersion curves correlate with the two degrees of freedom of the meta-atoms. Both branches correlate with pure modes, due to the diagonal nature of the eigenvalue problem. The pass band in Figure 2 shows both modes overlapping. The lower band gap is a result of the boundary coupling, while the top band gap is the cut off frequency for the lattice. The width of the lower band gap can be reduced to zero in the limit of a vanishing boundary coupling (e.g., large b). The width of the pass band and its position within the frequency spectrum is more sensitive to the inter-coupling between the meta-atoms than their coupling with the boundary (i.e., the lattice constant a). A larger influence of the lattice constant a stems from the fact that a change in a changes both $d_a$ and $d_b$ in Figure 2 inset), while a change in the value of b only changes $d_b$. In addition to the geometric parameters of the lattice, the position of the pass band can be dynamically tuned by nondestructive external factors such as an external magnetic field (Matar et al., 2013; Bilal et al., 2017a; Bilal et al., 2017b; Wang et al., 2018; Palermo et al., 2019; Wang et al., 2020).

The purpose of the demultiplexer is to allow for the propagation of waves through the input channel, while selectively attenuating waves based on their frequencies through the output channels. To achieve such functionality, we design an input channel with a pass band that encompasses all operational frequencies, while each output channel has a pass band in only one of the operational frequency ranges. Our demultiplexer channels are designed by utilizing identical meta-atoms with varying boundary coupling b and lattice spacing a. The modification of a and b allows for the control of the band gap position within the frequency spectrum. Three designs are created; design 1 with dimensions a and b, design 2 with $0.75a$ and b and design 3 with $0.75a$ and $0.75b$. The dispersion curves for each design are plotted with dashed red lines in (Figures 3A–C) based on Eq. 1.

FIGURE 3

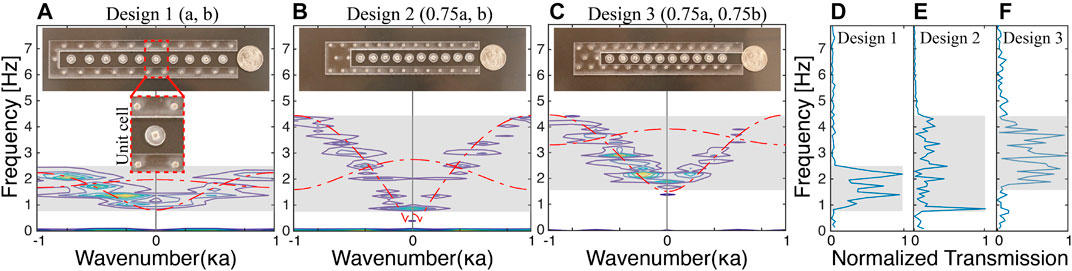
FIGURE 3. Characterization of individual channels. The experimentally measured dispersion curves plotted as contours with the numerical dispersion curves superimposed as dashed red lines for (A) design 1 with $a=15.4\mathit{m}m$, $b=24.5\mathit{mm}$(B) design 2, with $a=11.5\mathit{mm}$, $b=24.5\mathit{mm}$, and C) design 3, with $a=11.5\mathit{mm}$, $b=18.4\mathit{mm}$. The insets show the experimental samples used. The measured normalized transmission at the center of lattice for D) design 1, E) design 2, and F) design 3. The transmission bands are shaded in gray.

To experimentally verify the analytically computed dispersion curves, we fabricate three separate U-shaped boundaries with the parameters of designs one to three out of acrylic glass using a laser cutter (Full-spectrum 24 pro-series). The meta-atoms (i.e., disks) are identical across all three designs with a radius $r_{disk}=4$ mm. The meta-atoms are placed within the boundary and the magnets oriented with the north pole facing upwards. The fixed magnets inside the boundary are oriented in the same way. To minimize friction, we attach a glass slide at the bottom of each disk and float them on an air bearing (New way S1030002). Each design is excited separately with a chirp signal between 0.1 and 10 Hz at its open end with a mechanical shaker (Brüel and Kjær 4,180) and a function generator (Keysight Technologies 33512B). The motion of the disks is captured using a computer vision camera (Blackfly S USB3) and the resulting images are analyzed using the digital image correlation software (DICe).

The displacement profiles of all the meta-atoms in each design (characterized separately) are post-processed using 2D fast Fourier transform (2D-FFT). The resulting FFT corresponds to the longitudinal dispersion curve of each design, as we only consider the x-displacement in our analysis (Figure 3). For all three cases, the measured displacement signals through DICe show displacements in the y-direction on the same order as noise. The experimental dispersion curves for the three designs match well with the numerically calculated ones. In addition, we plot the measured transmission at a central meta-atom in each design. The pass band region within the transmission spectrum matches well with the dispersion curves for all three designs. Design 1 has a pass band between 0.8 and 2.5 Hz, while design 3 has a pass band between 1.6 and 4.5 Hz. Both designs have operational frequency ranges that do not overlap (e.g., below 1.6 Hz and above 2.5 Hz). Design 2 has a pass band between 0.8 and 4.5 Hz, which encompasses the pass bands of both design 1 and 3. This pass band range gives channel 2 the characteristic to act as an input channel for our demultiplexer.

To test our design principle we connect the three distinct channels made out of designs 1, 2 and 3. We note that the meta-atoms behave as a self-assembled fluidic material. Therefore, once the three designs are merged within a T-junction, the meta-atoms’ equilibrium positions are altered. To ensure that the position of the meta-atom within each unit cell is as close as possible to the equilibrium position as in the separate experiments, we add an extra meta-atom and a boundary magnet at the junction point. To verify the operational frequencies of the T-shaped assembly, we excite the input channel (design 2) with a chirp signal from 0.1 to 10 Hz. A fast Fourier transform is performed on the displacements of the central meta-atoms in each channel and repeated for a total of three trials (Figures 4A–C). The FFT of the three trials along with its average, for each channel, is plotted in log-scale (Figures 4D–F). The transmission of channel 1 is between 0.9 and 2.3 Hz, for channel 2 is between 0.8 and 3.4 Hz, and for channel 3 is between 1.7 and 2.7 Hz. The operational frequency of each channel is altered slightly. This may be due to the imbalance in the force potentials between the different channels which causes a shift in the equilibrium position of each meta-atom.

FIGURE 4

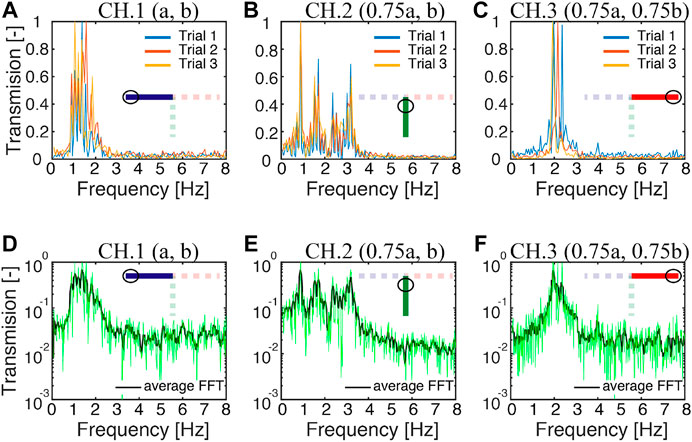
FIGURE 4. Chirp signal transmission through the demultiplexer. Fast Fourier transform of the displacement of the central meta-atom and their average over three trials for (A, D) channel 1, (B, E) channel 2, and (C, F) channel 3. The input channel is excited with a chirp signal between 0.1‒10 Hz. The inset shows the corresponding channel in the T-shaped demultiplexer.

To characterize the performance of the demultiplexer at a single operational frequency, we excite the input channel with two sine waves, separately, and measure the transmission at each output terminal (Figure 5A). The device is first excited at a frequency $f_1=1.1$ Hz, corresponding to an operational frequency for channel 1 (left). The FFT of the displacement of the central meta-atoms in each channel shows a clear transmission of the wave from CH.2 to CH.1, while the wave is attenuated at CH.3 (Figure 5B). When excited at a frequency $f_2=2.4$ Hz, the wave is transmitted through CH.3, while attenuated in CH.1 (Figure 5C). The ratio of transmission $\left(T\right)$ at $f_1$ is 0.88, calculated as $T_{CH1}/T_{CH2}$, and the ratio of transmission at $f_2$ is 0.59, calculated as $T_{CH3}/T_{CH2}$. The ratio of transmission for the attenuated signals at CH.1 and CH.3 are 7 and 1%, respectively. We attribute the relatively lower transmission ratio through channel 3 (in comparison to channel 2) to the coupling asymmetry at the junction point between the three channels. We note the existence of the second and the third harmonic of the excitation frequency in Figure 5B,C, due to the inherent nonlinearity in magnetic lattices. Such nonlinear response can be harnessed by increasing the amplitude of the excitation and introducing defects within the lattice (Boechler et al., 2011; Mehrem et al., 2017; Deng et al., 2018; Molerón et al., 2019; Chong et al., 2020; Jiao and Gonella, 2020).

FIGURE 5

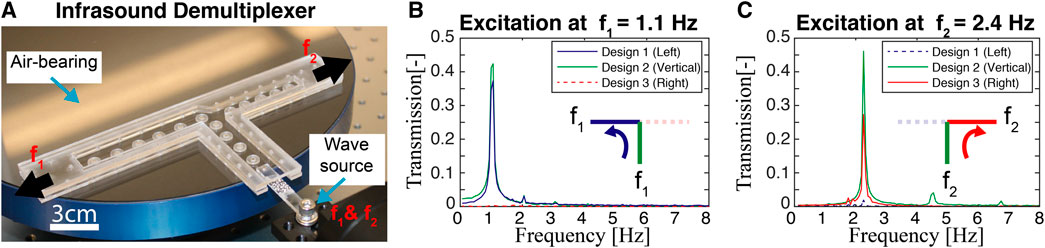
FIGURE 5. Infrasound demultiplexer. (A) The experimental setup for the T-shaped demultiplexer positioned on an air bearing. The demultiplexer is filled with identical meta-atoms confined between different magnetic boundaries. A mechanical shaker drives the input channel through an arm with an embedded magnet. The signal transmission at (B)$f_1=1.1$ Hz and C)$f_2=2.4$ Hz.

Conclusion

In conclusion, we utilize tunable magnetic lattices to control the propagation of infrasound waves. We tune the wave propagation characteristics of these lattices by changing their boundary couplings while using the same meta-atoms. Different designs are combined to create a T-shaped demultiplexer consisting of one input channel and two output channels. The device is characterized experimentally, validating both dispersion curves and transmission frequency spectrum. This platform can be utilized to manipulate ultra-low frequency waves, within a relatively small space. The inherent nonlinear potentials between the meta-atoms can be harnessed to demonstrate phenomena with no linear parallel such as amplitude dependent response, bifurcation, chaos and solitons (Porter et al., 2015; Mehrem et al., 2017; Amendola et al., 2018; Gendelman and Vakakis, 2018; Kim and Yang, 2019; Grinberg and Matlack, 2020; Ramakrishnan and Frazier, 2020). In addition, the self-assembly of the meta-atoms can be key in creating re-programmable materials with exceptional properties (Culha et al., 2020).

Data Availability Statement

All the data supporting the findings in this study are available in the article. Further data and methods are available from the corresponding author upon request.

Author Contributions

AW performed the research and wrote the manuscript. OB designed the research, performed the research and wrote the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Amendola, A., Krushynska, A., Daraio, C., Pugno, N. M., and Fraternali, F. (2018). Tuning frequency band gaps of tensegrity mass-spring chains with local and global prestress. Int. J. Solid Struct. 155, 47. doi:10.1016/j.ijsolstr.2018.07.002

CrossRef Full Text | Google Scholar

Amoudache, S., Pennec, Y., Djafari Rouhani, B., Khater, A., Lucklum, R., and Tigrine, R. (2014). Simultaneous sensing of light and sound velocities of fluids in a two-dimensional phoXonic crystal with defects. J. Appl. Phys. 115, 134503. doi:10.1063/1.4870861

CrossRef Full Text | Google Scholar

Babaki, J., and Nazari, F. (2020). Heterostructure based demultiplexer using solid-solid phononic crystal ring resonators. J. Phys. D Appl. Phys. 53, 375301. doi:10.1088/1361-6463/ab904b

CrossRef Full Text | Google Scholar

Barklow, W. E. (2004). Low‐frequency sounds and amphibious communication in Hippopotamus amphibious. J. Acoust. Soc. Am. 115, 2555. doi:10.1121/1.4783854

CrossRef Full Text | Google Scholar

Ben-Ali, Y., Ouariach, A., Khaled, A., and Bria, D. (2020). Double Frequency Filtering in One Dimensional Comb-Like Phononic Structure Containing a Segment Defect. Mater. Today 13–21. doi:10.1007/978-3-030-62199-5_2

CrossRef Full Text | Google Scholar

Bergamini, A., Delpero, T., Simoni, L. D., Lillo, L. D., Ruzzene, M., and Ermanni, P. (2014). Phononic crystal with adaptive connectivity. Adv. Mater. 26, 1343. doi:10.1002/adma.201305280

PubMed Abstract | CrossRef Full Text | Google Scholar

Bilal, O. R., Foehr, A., and Daraio, C. (2017b). Bistable metamaterial for switching and cascading elastic vibrations. Proc. Natl. Acad. Sci. U.S.A. 114, 4603. doi:10.1073/pnas.1618314114

PubMed Abstract | CrossRef Full Text | Google Scholar

Bilal, O. R., Foehr, A., and Daraio, C. (2017a). Reprogrammable phononic metasurfaces. Adv. Mater. 29, 1700628. doi:10.1002/adma.201700628

CrossRef Full Text | Google Scholar

Bilal, O. R., Hwee Yee, C., Rys, J., Schumacher, C., and Daraio, C. (2020). Experimental realization of phonon demultiplexing in three-dimensions. arXiv e-prints, [Preprint]. Avaialable at: https://arxiv.org/abs/2009.12025 (Accessed Sepetember 25, 2020).

Google Scholar

Bloch, F. (1929). Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 52, 555–600. doi:10.1007/bf01339455

CrossRef Full Text | Google Scholar

Boechler, N., Theocharis, G., and Daraio, C. (2011). Bifurcation-based acoustic switching and rectification. Nat. Mater. 10, 665–668. doi:10.1038/nmat3072

PubMed Abstract | CrossRef Full Text | Google Scholar

Brûlé, S., Javelaud, E., Enoch, S., and Guenneau, S. (2014). Experiments on seismic metamaterials: molding surface waves. Phys. Rev. Lett. 112, 133901. doi:10.1103/physrevlett.112.133901

PubMed Abstract | CrossRef Full Text | Google Scholar

Chong, C., Wang, Y., Marechal, D., Charalampidis, E., Moleron, M., Martinez, A. J., et al. (2020). Nonlinear localized modes in two-dimensional hexagonally-packed magnetic lattices. arXiv [Preprint]. Available at: https://arxiv.org/abs/2009.10300 (Accessed September 22, 2020).

Google Scholar

Colombi, A., Zaccherini, R., Aguzzi, G., Palermo, A., and Chatzi, E. (2020). Mitigation of seismic waves: metabarriers and metafoundations bench tested. J. Sound Vib. 485, 115537. doi:10.1016/j.jsv.2020.115537

CrossRef Full Text | Google Scholar

Culha, U., Davidson, Z. S., Mastrangeli, M., and Sitti, M. (2020). Statistical reprogramming of macroscopic self-assembly with dynamic boundaries. Proc. Natl. Acad. Sci. U.S.A. 117, 11306. doi:10.1073/pnas.2001272117

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, B., Wang, P., He, Q., Tournat, V., and Bertoldi, K. (2018). Nat. Commun. 9, 1. doi:10.1038/s41467-018-05908-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Deymier, P. A. (2013). Acoustic metamaterials and phononic crystals. Amsterdam, Netherlands: Springer Science & Business Media, Vol. 173.

Google Scholar

Faiz, M. S., Addouche, M., Zain, A. R. M., Siow, K. S., Chaalane, A., and Khelif, A. (2020). Experimental demonstration of a multichannel elastic wave filter in a phononic crystal slab. Appl. Sci. 10, 4594. doi:10.3390/app10134594

CrossRef Full Text | Google Scholar

Fee, D., and Matoza, R. S. (2013). An overview of volcano infrasound: from Hawaiian to plinian, local to global. J. Volcanol. Geotherm. Res. 249, 123–139. doi:10.1016/j.jvolgeores.2012.09.002

CrossRef Full Text | Google Scholar

Garcés, M., Hetzer, C., Merrifield, M., Willis, M., and Aucan, J. (2003). Observations of surf infrasound in Hawai‘i. Geophys. Res. Lett. 30, 2264. doi:10.1029/2003gl018614

CrossRef Full Text | Google Scholar

Gendelman, O. V., and Vakakis, A. F. (2018). Introduction to a topical issue “nonlinear energy transfer in dynamical and acoustical Systems”. Phil. Trans. R. Soc. A. 376, 20170129. doi:10.1098/rsta.2017.0129

PubMed Abstract | CrossRef Full Text | Google Scholar

Gharibi, H., and Bahrami, A. (2020). Phononic crystals for sensing FAMEs with demultiplexed frequencies. J. Mol. Liq. 305, 112841. doi:10.1016/j.molliq.2020.112841

CrossRef Full Text | Google Scholar

Grinberg, I., and Matlack, K. H. (2020). Nonlinear elastic wave propagation in a phononic material with periodic solid-solid contact interface. Wave Motion 93, 102466. doi:10.1016/j.wavemoti.2019.102466

CrossRef Full Text | Google Scholar

Hussein, M. I., Hulbert, G. M., and Scott, R. A. (2005). Hierarchical Design of Phononic Materials and Structures. ASME Int. Mech. Eng. Cong. Exp. 42258, 163–172.

Google Scholar

Hussein, M. I., Leamy, M. J., and Ruzzene, M. (2014). Closure to “Discussion of ‘Dynamics of Phononic Materials and Structures: Historical Origins, Recent Progress, and Future Outlook’”. Appl. Mech. Rev. 66, 046002. doi:10.1115/1.4027795

CrossRef Full Text | Google Scholar

Jiao, W., and Gonella, S. (2019). Nonlinear harmonic generation in two-dimensional lattices of repulsive magnets. arXiv [Preprint]. Available at: https://arxiv.org/pdf/1911.10410 (Accessed August 25, 2020).

Google Scholar

Jiao, W., and Gonella, S. (2020). Nonlinear harmonic generation in two-dimensional lattices of repulsive magnets. arXiv [Preprint]. Available at: https://arxiv.org/abs/2007.03855 (Accessed July 8, 2020).

Google Scholar

Ke, M., Zubtsov, M., and Lucklum, R. (2011). Sub-wavelength phononic crystal liquid sensor. J. Appl. Phys. 110, 026101. doi:10.1063/1.3610391

CrossRef Full Text | Google Scholar

Khelif, A., and Adibi, A. (2015). Phononic crystals. Springer.

Google Scholar

Kim, E., and Yang, J. (2019). Review: Wave propagation in granular metamaterials. Funct. Compos. Struct. 1, 012002. doi:10.1088/2631-6331/ab0c7e

CrossRef Full Text | Google Scholar

Kim, S.-H., and Das, M. P. (2012). Seismic waveguide of metamaterials. Mod. Phys. Lett. B 26, 1250105. doi:10.1142/s0217984912501059

CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 71, 2022. doi:10.1103/physrevlett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Pichon, A., Blanc, E., and Hauchecorne, A. (2010). Infrasound monitoring for atmospheric studies. Springer.

Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y., Yang, Z., Chan, C., et al. (2000). Locally resonant sonic materials. Science 289, 1734. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, F., Wu, J. H., Huang, M., Zhang, W., and Zhang, S. (2015). A purely flexible lightweight membrane-type acoustic metamaterial. J. Phys. D Appl. Phys. 48, 175105. doi:10.1088/0022-3727/48/17/175105

CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Sound and heat revolutions in phononics. Nature 503, 209. doi:10.1038/nature12608

PubMed Abstract | CrossRef Full Text | Google Scholar

Matar, O. B., Vasseur, J., and Deymier, P. A. (2013). Acoustic metamaterials and phononic crystals. Amsterdam, Netherlands: Springer, 253–280.

CrossRef Full Text | Google Scholar

Mehrem, A., Jimenez, N., Salmerón-Contreras, L., García-Andrés, X., García-Raffi, L., Picó, R., et al. (2017). Nonlinear dispersive waves in repulsive lattices. Phys. Rev. 96, 012208. doi:10.1103/physreve.96.012208

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, J., Ma, G., Yang, M., Yang, Z., Wen, W., and Sheng, P. (2012). Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 3, 756. doi:10.1038/ncomms1758

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, S., and Adibi, A. (2011). On chip complex signal processing devices using coupled phononic crystal slab resonators and waveguides. AIP Adv. 1, 041903. doi:10.1063/1.3676168

CrossRef Full Text | Google Scholar

Molerón, M., Chong, C., Martínez, A. J., Porter, M. A., Kevrekidis, P. G., and Daraio, C. (2019). Nonlinear excitations in magnetic lattices with long-range interactions. New J. Phys. 21, 063032. doi:10.1088/1367-2630/ab0118

CrossRef Full Text | Google Scholar

Molerón, M., Serra-Garcia, M., and Daraio, C. (2014). Acoustic Fresnel lenses with extraordinary transmission. Appl. Phys. Lett. 105, 114109. doi:10.1063/1.4896276

CrossRef Full Text | Google Scholar

Moradi, P., and Bahrami, A. (2019). Three channel GHz-ranged demultiplexer in solid-solid phononic crystals. Chin. J. Phys. 59, 291. doi:10.1016/j.cjph.2019.03.005

CrossRef Full Text | Google Scholar

Motaei, F., and Bahrami, A. (2020). Eight-channel acoustic demultiplexer based on solid-fluid phononic crystals with hollow cylinders. Photonics Nanostruct. Fundam. Appl. 39, 100765. doi:10.1016/j.photonics.2020.100765

CrossRef Full Text | Google Scholar

Nakano, M., Hori, T., Araki, E., Kodaira, S., and Ide, S. (2018). Shallow very-low-frequency earthquakes accompany slow slip events in the Nankai subduction zone. Nat. Commun. 9, 1. doi:10.1038/s41467-018-03431-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Palermo, A., Krödel, S., Marzani, A., and Daraio, C. (2016). Engineered metabarrier as shield from seismic surface waves. Sci. Rep. 6, 39356. doi:10.1038/srep39356

PubMed Abstract | CrossRef Full Text | Google Scholar

Palermo, A., Wang, Y., Celli, P., and Daraio, C. (2019). Tuning of surface-acoustic-wave dispersion via magnetically modulated contact resonances. Physical Review Applied 11, 044057. doi:10.1103/physrevapplied.11.044057

CrossRef Full Text | Google Scholar

Pennec, Y., Djafari-Rouhani, B., Vasseur, J., Khelif, A., and Deymier, P. A. (2004). Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. 69, 046608. doi:10.1103/physreve.69.046608

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennec, Y., Djafari-Rouhani, B., Vasseur, J., Larabi, H., Khelif, A., Choujaa, A., et al. (2005). “Channel drop pro-cess of elastic wave in a two dimensional phononic crystal,” in IEEE Ultrasonics Symposium 2005, Rotterdam, Netherlands, September 18–21, 2005 (IEEE), Vol. 1, 69–72.

Google Scholar

Porter, M. A., Kevrekidis, P. G., and Daraio, C. (2015). Granular crystals: Nonlinear dynamics meets materials engineering. Phys. Today 68, 44. doi:10.1063/pt.3.2981

CrossRef Full Text | Google Scholar

Ramakrishnan, V., and Frazier, M. J. (2020). Transition waves in multi-stable metamaterials with space-time modulated potentials. Appl. Phys. Lett. 117, 151901. doi:10.1063/5.0023472

CrossRef Full Text | Google Scholar

Ripepe, M., Marchetti, E., Delle Donne, D., Genco, R., Innocenti, L., Lacanna, G., et al. (2018). Infrasonic early warning system for explosive eruptions. J. Geophys. Res. Solid Earth 123, 9570. doi:10.1029/2018jb015561

CrossRef Full Text | Google Scholar

Rostami-Dogolsara, B., Moravvej-Farshi, M. K., and Nazari, F. (2016). Designing switchable phononic crystal-based acoustic demultiplexer. IEEE Trans. Ultrason. Ferroelectrics Freq. Contr. 63, 1468. doi:10.1109/tuffc.2016.2586489

CrossRef Full Text | Google Scholar

Rupp, C. J., Dunn, M. L., and Maute, K. (2010). Switchable phononic wave filtering, guiding, harvesting, and actuating in polarization-patterned piezoelectric solids. Appl. Phys. Lett. 96, 111902. doi:10.1063/1.3341197

CrossRef Full Text | Google Scholar

Rupp, C. J., Evgrafov, A., Maute, K., and Dunn, M. L. (2007). Design of phononic materials/structures for surface wave devices using topology optimization. Struct. Multidiscip. Optim. 34, 111. doi:10.1007/s00158-006-0076-0

CrossRef Full Text | Google Scholar

Torres, M., Montero de Espinosa, F. R., García-Pablos, D., and García, N. (1999). Sonic band gaps in finite elastic media: surface states and localization phenomena in linear and point defects. Phys. Rev. Lett. 82, 3054. doi:10.1103/physrevlett.82.3054

CrossRef Full Text | Google Scholar

Vasseur, J., Matar, O. B., Robillard, J., Hladky-Hennion, A.-C., and Deymier, P. A. (2011). Band structures tunability of bulk 2D phononic crystals made of magneto-elastic materials. AIP Adv. 1, 041904. doi:10.1063/1.3676172

CrossRef Full Text | Google Scholar

Von Muggenthaler, E. (2013). Proceedings of meetings on acoustics ICA2013. Acoustical Society of America, Vol. 19, 010012.

Google Scholar

von Muggenthaler, E., Reinhart, P., Lympany, B., and Craft, R. B. (2003). Songlike vocalizations from the sumatran rhinoceros (dicerorhinus sumatrensis). Acoust Res. Lett. Online 4, 83. doi:10.1121/1.1588271

CrossRef Full Text | Google Scholar

Wang, Y.-F., Wang, Y.-Z., Wu, B., Chen, W., and Wang, Y.-S. (2020). Tunable and Active Phononic Crystals and Metamaterials. Appl. Mech. Rev. 72, 35. doi:10.1115/1.4046222

CrossRef Full Text | Google Scholar

Wang, Y., Yousefzadeh, B., Chen, H., Nassar, H., Huang, G., and Daraio, C. (2018). Observation of Nonreciprocal Wave Propagation in a Dynamic Phononic Lattice. Phys. Rev. Lett. 121, 194301. doi:10.1103/physrevlett.121.194301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Dai, H., Chan, N., Ma, G., and Sheng, P. (2010). Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 96, 041906. doi:10.1063/1.3299007

CrossRef Full Text | Google Scholar

Zou, Q., Liu, W., Yu, T., Liu, N., Wang, T., and Liao, Q. (2017). Decoupling of multiple coupled phononic crystal waveguides: application to acoustic demultiplexing. J. Phys. D Appl. Phys. 50, 125102. doi:10.1088/1361-6463/aa5873

CrossRef Full Text | Google Scholar