Multi-Physics of Dynamic Elastic Metamaterials and Earthquake Systems

Microstructured materials, namely metamaterials, are one of the most relevant topics of the recent period due to their interdisciplinary nature. Driven by their wide range of applications, we provide an overview of a class of elastic solids which embed dynamic microstructures capable of trapping energy when subject to dynamic loads. Based on the recently developed modeling approaches, we show several applications related to wave cloaking, filtering and also multi-structured surfaces, often referred to as meta-surfaces. These culminate in the analysis of a practical example, based on a real-life recent seismic event induced by a hydrofracture exploration. The latter shows the viability of the vibration analysis in the assessment of the seismic response, and also the role of meta-surfaces as localisers of vibrations, e.g. suggesting non-periodic earthquake tolerant design strategies of housing estates.

1 Introduction

The Nature is known to be the best Mathematician who creates amazing patterns in rocks and natural crystals. Also, the global geological structure of Tectonic plates is linked to several processes including waves phenomena. For a geological system, the micro-structure of rocks and geological interfaces is often present, and during seismic events a localised damage may lead to a dynamic failure, often referred to as a crack/fault or an interfacial wave. Such waves were considered by Galin and Cherepanov (1966), Grigoryan (1967), Slepyan (1968), Slepyan (1977), Slepyan and Troyankina (1969), Slepyan and Troyankina (1984), with the phase transition waves being the main focus of the study, and an interface condition at the wavefront was analyzed.

On the other hand, the theory of Floquet-Bloch waves has proved to be especially useful in identifying special regimes of dispersion associated with strong dynamic anisotropy, standing waves or wave blockages (stop band frequency regimes); as discussed, for example, in Kittel (1954), such problems are set in infinite periodic structures. The connection between Floquet-Bloch waveforms and solutions of the transmission problems for finite width interfaces is discussed in the classical work by Lekner (1987) and in the more recent work on flexural waves by Evans and Porter (2007), Movchan et al. (2011), Haslinger et al. (2012). For infinite structures, which include interfaces separating two semi-infinite regions, analytical approaches have been developed to reduce the formulation to functional equations of the Weiener-Hopf type (see, for example, Mishuris et al., 2009; Brun et al., 2012; Nieves et al., 2013). As explained by Mishuris et al. (2009), the kernel function of the Wiener-Hopf equation is directly linked to the corresponding Green’s function describing waves in an infinite periodic structure, and thus the dispersion properties of Floquet-Bloch waves contribute to the reflection-transmission properties of semi-infinite interfaces.

Metamaterials are multi-scale systems, which are designed to perform in a desired, sometimes unusual, way: examples include negative refraction, wave cloaking, imaging on flat interfaces, wave filtering and localisation (see, for example Craster and Guenneau, 2013). Often, such a pre-designed material involves periodic systems of resonators to achieve the required dynamic response to external loads. Multi-scale resonators may have different design, and of course some of interesting ideas come from nature. Spider web-inspired acoustic metamaterials have been modeled by Miniaci et al. (2016a), where the periodic metamaterial structure had a web-like macro-cell, and its dynamic response and wave attenuation mechanisms were studied. The ideas generated by this work are used in the design of lightweight structures for tunable vibration damping and impact protection. Metamaterials were analyzed in the context of seismic protection by Miniaci et al. (2016b), as smart foundations, built of resonators embedded into the ground. This work has led to a design of passive isolation for seismic waves interacting with large-scale mechanical metamaterials, as well as realistic engineering structures. Three-dimensional metamaterials are of special interest in the context of engineering applications and manufacturing. The new study of labyrinthine acoustic metamaterials with space-coiling channels was conducted by Krushynska et al. (2018a) to control low frequency acoustic waves. The authors of this study have identified the special stop band frequency regimes when the sound waves cannot propagate through the structure, and have demonstrated that labyrinthine metamaterials have potential applications for reflection and filtering of low-frequency airborne sound. Three-dimensional hybrid metamaterials combining pentamode lattices and phononic plates were analyzed by Krushynska et al. (2018b): in this work alternating phononic plates and pentamode units were combined in a periodic system to produce complete bandgaps for elastic waves. Three-dimensional mechanical metamaterials, whose design incorporates a geometrical chirality, were manufactured and studied by Frenzel et al. (2017).

In modeling of earthquakes, full three-dimensional transient computations can be applied to a geoblock. In some cases, simpler models based on the elastic plate theory can be applicable. Analysis of waves in elastic plates, with specially designed micro-structures or systems of embedded resonators, and in particular with chiral resonators, has been published by Haslinger et al. (2016) and by Carta et al. (2020). In particular, we distinguish between dispersion of flexural waves in periodically micro-structured plates, which can be designed to achieve special dynamic anisotropy as well as stop band regimes, and the interaction between incident waves and finite micro-structured systems. The latter class also includes wave cloaks, understood as systems which reduce scattering cross-section (for comparison of membrane and flexural waves and reduction of scattering, see, for example Jones et al., 2015). The idea of geometrical transformations, which lead to cloaking designs for time-harmonic waves, goes back more than 50 years, when it was introduced by Dolin (1961) and was explored in the last 20 years (see, for example, Nicorovici et al., 1993; Nicorovici et al., 1994; Greenleaf et al., 2003a; Greenleaf et al., 2003b; Leonhardt, 2006a; Leonhardt, 2006b; Milton et al., 2006; Pendry et al., 2006; Norris and Shuvalov, 2011) extensively in order to design and construct devices, which reduce scattering for acoustic, electromagnetic and elastic waves from finite objects. Cloaks can be active or passive, as discussed in Vasquez et al. (2011): for passive cloaks the micro-structure, which forms the cloak, remains the same at any instant of time, and it does not produce any energy input, whereas for active cloaks the extra energy input is produced via external sources. The cloaking approaches are so well developed that an impression may be made that passive cloak can always be achieved. Such an impression is not correct, and counterexamples related to “uncloakable scatterers” for flexural waves are discussed by Jones et al. (2015), with the emphasis on the boundary conditions, imposed at the boundary of the scatterer, and in particular, the case of flexural waves.

Without a doubt, the area of metamaterials and control of waves is one of the most fascinating in terms of theory and numerical simulations. For elastic waves, there is also an important area of applications—analysis of the dynamic response of structures to seismic waves. In particular, waves in structured plates deserve a special attention. Structured cloaks for elastic plates were designed and implemented by Misseroni et al. (2016), Misseroni et al. (2019). The challenge is to combine the geophysical predictions with the wave analysis in the context of seismic response. Here, we use the methods of Movchan and Yakovleva (2017), Movchan and Yakovleva (2020) and Egorov et al. (2018) to assess a seismic response of a geological systems combined with meta-surfaces of elastic resonators (see Colombi et al., 2016; Carta et al., 2016; Haslinger et al., 2016; Skelton et al., 2018).

The structure of the paper is as follows. In Section 2 we describe examples of dispersive flexural waves, with the emphasis on micro-structures, as well phase transition waves and failure waves. Section 2.3 addresses wave cloaking and the concept of flexural metamaterials. The case study, which shows the vibration analysis and effects of metasurfaces in dynamic events induced by earthquakes, is discussed in Section 4, followed by concluding remarks.

2 Elementary Examples for Dispersive Flexural Waves: Micro-structures and Interfaces

Some seismic events can be modeled through the analysis of a dynamic response of a geoblock, which possesses given elastic properties, subject to appropriate boundary conditions. Although it is impossible to replicate an exact physical configuration, analysis of Floquet-Bloch waves in media characterised by a repeated pattern, or studies of the eigenvalue problems in regions, where vibrations are observed to be localised, may be helpful. Furthermore such data can be used as an auxiliary material complementing experimental measurements and observations.

2.1 Elastic Continuum and Interfacial Waves

If a model of a flexural plate or a beam is used to describe the transverse displacement w then it is also common to assume that the remaining substrate is modeled via “springs” often referred to as the Winkler foundation. In the simplest case of one spatial dimension (the beam model), the flexural displacement $w\left(x,t\right)$ satisfies the fourth-order partial differential equation

$D\frac{{\partial }^{4}w\left(x,t\right)}{\partial x^4}+\rho h\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+\kappa *w\left(x,t\right)-\rho gh=0,(1)$

where x and t are spatial and temporal variables, respectively; the coefficient D is the flexural rigidity, ρ is the mass density and h is the beam thickness, g is the gravity acceleration, and κ* is the Winkler foundation stiffness coefficient per unit area. If the coefficients in the above Eq. 1 are constant, the dispersion of time-harmonic flexural waves for such a system is very well-known, and the group velocity increases monotonically with frequency. However, the dynamic phenomenon associated with the variable, time-dependent κ* brings interesting observations linked to the interfacial waves associated with earthquakes. Such interfacial elastic waves may propagate in the subsonic, intersonic and supersonic range, and for continuous beam systems the solutions were derived in the closed analytical form and analyzed by Brun et al. (2013a). In particular, when the front of the interfacial wave separates two semi-infinite regions, the approach based on the analysis of functional equations of the Wiener-Hopf type has proved to be especially effective.

2.2 Discretely Structured Systems

The wave phenomena become more interesting if a discrete structure is added to the elastic beam, as the interaction between discretely positioned inertial elements brings additional features into the wave dispersion, including formation of stop bands and standing waves. Examples of such systems can be found often, when a long slender elastic structure, like a bridge, has a repeated pattern of supporting piers of stiffness κ at $x=nd,n\in \mathbf{Z}$, with d being the positive distance between neighboring supports, accompanied by an inertial junction region of mass M connecting neighboring sections of the bridge itself.

In this case, the transverse displacement $w\left(x,t\right)$ can be described via the partial differential equation with the delta function terms representing point loads, or alternatively, an equivalent description can be viewed as follows

$D\frac{{\partial }^{4}w\left(x,t\right)}{\partial x^4}+\rho h\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}-\rho gh=0,x/d\in \mathbf{R}\mathrm{\setminus }\mathbf{Z},(2)$

$M\frac{{\partial }^{2}w}{\partial t^2}\left(nd,t\right)+\kappa w\left(nd,t\right)-{\mathrm{ℱ}}_n^{+}+{\mathrm{ℱ}}_n^{-}-Mg=0,{\mathrm{ℳ}}^{+}-{\mathrm{ℳ}}^{-}=0.(3)$

Here the first Eq. 2 represents the flexural motion of an elastic section between the neighbouring pillars; the second Eq. 3 characterises the dynamic response of the inertial junction at $x=nd$, with the transverse forces ${\mathrm{ℱ}}_n^{\pm }$ and the bending moments ${\mathrm{ℳ}}_n^{\pm }$ representing the load on the inertial junction at $x=nd$. The superscripts ^± in Eq. 3 correspond to the right-side and the left-side limit, respectively.

The interfacial wave in this configuration can be described based on the ideas introduced by Slepyan (2002), which would be adequate for modeling of failure of a bridge, where the stiffness of pillars supporting the inertial junctions changes its magnitude across the front of the wave. Examples of reduction of the formulation to a functional equation of the Wiener-Hopf type and the analysis of its solution are presented by Brun et al. (2013a).

2.3 Applications to Bridge Dynamics

The models based on the mathematical studies of flexural waves in beams with discretely positioned supports and inertial junctions have been used to describe the dynamic response of real-life bridges. Examples include S’Adde bridge, Millau viaduct, San Saba bridge and the Volga bridge, with the dynamic simulations being published by Brun et al. (2012), Brun et al. (2013b) and Magalhães et al. (2012).

The question, raised sometimes by industrial scientists, is about the link between the dynamic response of finite span slender bridges and mathematical models, which refer to infinite (or semi-infinite) structured waveguides. On the one hand, for a finite span bridge the boundary conditions at the end regions of the bridge are indeed important in the assessment of the dynamic response of the overall structure. On the other hand, when a wave propagates from the one end of the bridge to the other end, it shows, in the middle section, the dispersion properties similar to those observed in the infinite waveguide.

The formulation for an infinite periodic waveguide, in the time-harmonic regime, is based on the Floquet-Bloch theory and has the form

$\mathrm{ℒ}\left(D_x\right)U\left(x\right)+{\omega }^{2}MU\left(x\right)=0,x\in Q_d,(4)$

$U\left(x+d\right)=U\left(x\right)e^{ikd},(5)$

where (Eq. 4) is the governing equations of motion, which is set on the elementary cell $Q_d$ of the periodic structure, with the period d. The relation (Eq. 5) is known as the Floquet-Bloch condition (which is also referred to as the condition of “quasi-periodicity”). The differential operator $\mathrm{ℒ}\left(D_x\right)$ characterises the elastic response of the structure, and M is the operator of inertia; the spectral parameter ω represents the radian frequency; in Eq. 5, the quantity k is referred to as the Floquet-Bloch parameter or the wave number. Non-trivial solutions of Eqs. 4, 5 are called Floquet-Bloch waves. The dispersion of Floquet-Bloch waves is represented by the dispersion equation $\omega =\omega \left(k\right)$, with the right-hand side being periodic in k. The intervals of values of ω, where the dispersion equation has real roots k, are referred to as the pass-band frequency intervals. The study of the problem Eqs. 4, 5 on a finite elementary cell $Q_d$ of the periodic structure is relatively straightforward, and on many instances the analysis of Floquet-Bloch waves can be done in a closed analytical form. It has also been demonstrated in Brun et al. (2012) that the results for such an analysis provide bounds for the eigenvalues of an elongated finite structure with a periodic pattern. In particular, at low frequencies, the eigenmodes of the finite span bridge, which has a repeated pattern in its supporting structure, are expected to be associated with the pass-band frequency intervals identified for the infinite periodic waveguide.

In addition, if the bridge is failing and an interfacial failure wave propagates along then the corresponding Wiener-Hopf formulations capturekey features of the interfacial wave itself. Examples of such major events include the failure of the San Saba railway bridge in 2013 in Texas and the very sad event of 1879 known at the Tay Bridge Disaster in Scotland (see Brun et al. (2013b); Brun et al. (2014)). In particular, in the paper by Brun et al. (2013a), the evaluation of the critical displacement, under which a failure of the supporting pylons can propagate along the bridge, has been carried out in conjunction with the analysis of the Wiener-Hopf functional equation describing the interfacial wave. The failure wave was associated with a reduction of the stiffness of the supporting structure and of the total mass. The models, based on the governing equation associated with flexural waves, capture dispersion properties and the properties of the dynamic phase transitions, which are absent in the conventional scalar two-dimensional lattice crack models.

3 Review of Wave Cloaking and Flexural Metamaterials

The classical idea of “cloaking geometrical transformation” is old and goes back to Dolin (1961) who presented a formal derivation, which used a singular coordinate transformation $\mathbf{x}\to x^{\prime }$, such that

${\text{x}}^{\prime }=A\mathbf{x}+B\mathbf{x}/\left|\mathbf{x}\right|,(6)$

with A and B being appropriately chosen real constants, leading to a radially symmetric design of a wave cloak made of an inhomogeneous anisotropic material. Although the work by Dolin has not been cited as much as it deserves, it has brought a new thought that has evolved into a powerful stream of research linked to the theory of metamaterials, control of wave scattering and design of new physical devices. In 2003 and 2006, similar cloaking algorithms were analyzed by Greenleaf et al. (2003) for conductivity and acoustics and by Leonhardt (2006a), Leonhardt (2006b) and Pendry et al. (2006) for electromagnetism.

The work by Nicorovici et al. (1993) has addressed the transport properties of three phase composite materials in the context of the method of images, which has brought an analytical insight into the effects of ghost images and anomalous resonance. The latter were essential in the explanation of the mechanism of superresolution, and “opaque perfect lenses” as described by Milton et al. (2007). The wave cloaking transition layer may have a non-radial shape, and in contrast with (Eq. 6) an effective design of a square cloak, based on a piece-wise smooth “push-out” transformation, was introduced by Rahm et al. (2008). An analytical ray-tracing algorithm for square cloaks, followed by an extension to lattice systems, were developed by Colquitt et al. (2013). Technological advance in multi-scale manufacturing, 3D printing, combined with the theoretical work published by Pendry et al. (2006) on modeling of metamaterials and wave cloaking has brought attention of physicists and industrial sponsors to this exciting area of wave control.

With the smooth and rapid development of the cloaking theory in mind, there was a catch: the cloaking transformation applied well to the problems of electromagnetism and acoustics, where the waves in the original un-transformed medium were governed by the Helmholtz equations or by the system of Maxwell’s equations. Equations of elasticity, in general, were not covered by this theory, with the exception of scalar problems of antiplane shear.

3.1 Cloaking in Elasticity

Although it may appear to be intuitively sensible to suggest that if cloaking of waves works in electromagnetism then it should work for elastic waves in a similar way, it is not that simple. Even for isotropic linearly elastic materials, the pressure and shear waves propagate with different speeds. If an elastic solid is not homogeneous, say it has inclusions, voids, then the boundary conditions and interface conditions will lead to the pressure and shear waves being coupled. The cloaking geometrical transformation, which works so well for problems of acoustics, will not work in the same way for vector equations of linear elasticity. Even for the case of isotropic linear elasticity, there are two types of waves (shear waves and dilatational waves) which propagate at different speeds, and which couple through the boundary conditions or interface conditions for multi-phase media. When the standard cloaking coordinate transformation is applied to the Lamé system, it is straightforward to deduce that the transformed equations have the form, which is different from equations of classical anisotropic elasticity. This does not mean that there is no way forward though—it is just a different way. The papers by Milton et al. (2006), and Milton and Willis (2007) analyze the dynamics of elastic cloaking and note that the coordinate transformation

$\mathbf{x}\to {\mathbf{x}}^{\prime }\left(\mathbf{x}\right)(7)$

should be considered together with the displacement field $\mathbf{u}\left(\mathbf{x}\right)$ before the transformation and the displacement field ${\mathbf{u}}^{\prime }\left({\mathbf{x}}^{\prime }\right)$ after the geometrical mapping has been completed

$\mathbf{u}\left(\mathbf{x}\right)\to {\mathbf{u}}^{\prime }\left({\mathbf{x}}^{\prime }\right).(8)$

Importantly, with the mapping Eqs. 7, 8 in hand, the governing equations for the dynamic displacements are written in the transformation invariant form. The subtlety is that it is not sufficient any longer to characterise the inertia of the medium by a scalar mass density. The cloaking algorithm requires a tensor description of the inertia.

An alternative approach was described by Brun et al. (2009) where the elastic properties of a cylindrical cloak for in-plane coupled shear and pressure waves are derived, and the cloak is characterised by a rank 4 elasticity tensor with spatially varying entries, which are deduced from a geometric transform. However, in the approach of Brun et al. (2009) the symmetries are not preserved in the constitutive equations characterising the cloak. Although, a theoretical approach to cloaking for vector elastic waves is in place and numerically realisable, the question of practical implementation of a vector elastic cloak remains open.

3.2 Flexural Waves and Approximate Cloaking

The work by Misseroni et al. (2016) has delivered a full implementation, both experimental and numerical, of approximate cloaking of flexural vibrations in a structured elastic plate.

Flexural waves are elastic waves in thin plates or beams. Mathematically, they are scalar fields governed by the fourth-order partial differential equations, and cloaking (or approximate cloaking) for flexural waves can be modeled and implemented in a more straightforward way, compared to the general vector case of elastic waves governed by the dynamic Lamé system. If $w\left(\mathbf{x}\right)$ stands for the displacement amplitude of flexural vibrations of radian frequency ω in a homogeneous elastic plate of flexural rigidity D, mass density ρ and thickness h then

${\text{Δ}}_{\mathbf{x}}^{2}w\left(\mathbf{x}\right)-\frac{{\omega }^2}{{\mathcal{C}}^4}w\left(\mathbf{x}\right)=0,(9)$

where $\mathcal{C}=[D/{\left(\rho h\right)]}^{1/4}$, and the first term represents the bi-harmonic operator applied to the field $w\left(\mathbf{x}\right).$ Following the appropriately chosen mapping $\mathbf{x}\to {\mathbf{x}}^{\prime }\left(\mathbf{x}\right)$ with the non-degenerate Jacobi matrix $\mathbf{F}={\nabla }_{\mathbf{x}}{\mathbf{x}}^{\prime }\left(\mathbf{x}\right)$, and $\mathrm{}=\text{det}\mathbf{F}$, the transformed form of the governing Eq. 9 becomes

$\nabla \cdot {\mathrm{}}^{-1}\mathbf{F}{\mathbf{F}}^T\nabla \mathrm{}\nabla \cdot {\mathrm{}}^{-1}\mathbf{F}{\mathbf{F}}^T\nabla w\left({\mathbf{x}}^{\prime }\right)-\frac{{\omega }^2}{\mathrm{}{\mathcal{C}}^4}w\left({\mathbf{x}}^{\prime }\right)=0.(10)$

As the physical interpretation of this equation is concerned, it represents a dynamic time-harmonic response of a heterogeneous anisotropic plate subjected to pre-stress. This theoretical set-up was analyzed in detail in Colquitt et al. (2014).

If the effects of pre-stress are small, and an approximate factorisation of the transformed differential operator is implemented, an approximate cloaking can be designed and implemented. In Stenger et al. (2012) an approximation based on the classical radial cloaking transformation was used for flexural waves in a uniform elastic plate. In that configuration, the membrane waves governed by the second-order partial differential equations were dominant and the contribution from evanescent wave appeared to be insignificant within a certain frequency range.

Exact implementation of an elastic cloak has never been done in an experimental set-up. In the vector elasticity, this challenge is connected to the necessity of introducing a locally micro-polar solid or having a tensorial inertia term in the equations of motion. On the other hand, cloaking approximations for elastic plates appears to be feasible, as demonstrated in Stenger et al. (2012), where the radially symmetric coordinate transformation, leading to (Eq. 10), was employed.

Highly anisotropic plates can be approximated by elastic flexural lattices. The cloak does not have to be radially symmetric, especially if the plate has a non-radial micro-structure, and hence the Eq. 10 will employ the Jacobi matrix F, which is different from the one corresponding to the classical radially symmetric transform. Misseroni et al. (2016) have used the “square cloak” for an elastic plate, which has a square background structure, as shown in Figures 1A,B, and hence there is an excellent geometrical match between the cloak itself and the ambient structure. Non-circular cloaks were studied in earlier papers by Rahm et al. (2008) and by Farhat et al. (2008). The paper by Colquitt et al. (2013) has developed the concept of the square cloak to a new level, where the square push-out transformation was combined with the regularisation that takes into account the boundary conditions at the interior contour of the cloak itself. This was followed by the ray analysis based on the derivation of the ray equations. The regularised square cloak design was especially effective for the physical fabrication, and a discrete lattice cloak was made for the first time by Misseroni et al. (2016) to approximate the regularised continuum cloak, and it has been demonstrated that the lattice structure acts as an effective cloak for flexural waves in a wide range of frequencies. This paper has also been the first micro-structured elastic cloak ever implemented in the real life experimental set up, and has demonstrated the viability of the approximate cloaking design for flexural elastic waves.

FIGURE 1

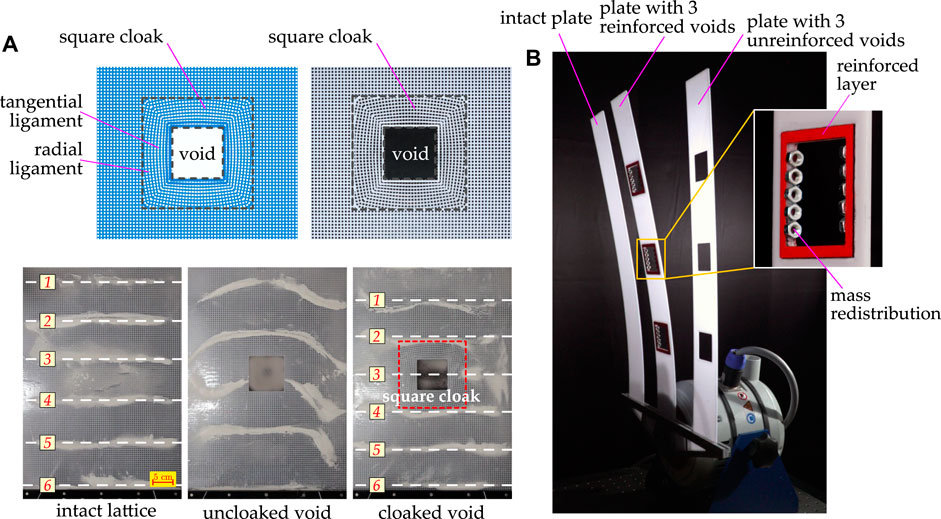
FIGURE 1. (A) Experimental implementation of a square cloak embedded in a square lattice (Misseroni et al., 2016). (top) Geometrical model implemented in Abaqus and its comparison with physical model realized by milling a Polycarbonate plate. (bottom) Dynamic response for an applied frequency of 120 Hz. The nodal lines (white/dashed lines) of the intact lattice and the lattice with the cloaked void almost coincide and differs from those of the lattice with the uncloaked void. (B) Cloaking system based on the reinforcement of the boundary and the redistribution of the mass (Misseroni et al. 2019). A sinusoidal displacement is applied at the base of the plates. The dynamic response of the intact plate and the plate with the reinforced voids is the same and it is different from that of the plate with the unreinforced voids.

The extensive study Misseroni et al. (2016) was followed by a new radical and very effective idea of elastic cloaking for elastic plates containing voids published by Misseroni et al. (2019). A new method of Misseroni et al. (2019) does not involve a geometrical cloaking transform, and it is based on the algorithm of reinforcement, through anisotropic elastic stiffening along the boundary of voids, combined with the appropriate redistribution of inertia, also along the boundary of voids, as shown in Figure 1B. This effective technique delivered a significant reduction in scattering by randomly distributed voids for omnidirectional flexural waves within a broad range of frequencies. The new design was also complemented by the eignevalue analysis for finite plates containing voids to demonstrate that the perturbation of eigenvalues and the eigenmodes is reduced significantly due to the inertial cloaking layer. The proposed design has been implemented in the real life experiment. Its applicability covers mechanical problems ranging from the micro-scale elastic systems to the macro-scale of civil engineering structures. This is especially important in the engineering designs in seismic regions: the results by Misseroni et al. (2019) show a constructive way to design a perforated load-bearing building wall, vibrating during an earthquake exactly as the same wall, but unperforated, which is a radical and highly effective way of seismic protection.

4 Vibration Analysis for a Region Affected by an Earthquake

Often analysis of earthquake protection systems is conducted via model simulations, subjected to required modeling assumptions. On the contrary, this section refers to a real life recent seismic event, for which the predictions made by exploration company were not observed, and an alternative explanation is offered in the context of vibration of metasurfaces and vibration analysis of non-uniform Mindlin’s plates.

We discuss in this section the case study based on the actual recent seismic events of 2019 linked to the process of hydrofracture exploration in the South East of Blackpool in the United Kingdom.

Although every earthquake is a highly complex three-dimensional and transient process, it is often associated with formation of surface waves or waves propagating along the interfaces (Rayleigh, Love or Stoneley waves). When such waves meet an obstacle or an array of obstacles on the surface or at an interface separating two elastic media, they scatter and convert some of their energy into the S and P volume waves. The process is so complex that a full three-dimensional transient simulation is literally impossible, but nevertheless there are effective ways to describe the effects of wave dynamic and localization in certain types of Earth crust systems. A special attention is given to resonance phenomena and localisation of earthquake-induced waveforms.

4.1 Metasurfaces Versus Seismic Waves

The term “metasurface” is used for the boundary of a solid containing patterns of surface resonators. Special features of elastic metasurfaces include standing waves and localised waveforms.

As for a good example of ground surface waves, we refer to recent experimental studies of filtering and dispersion of surface elastic waves by a periodic array of scatterers, published by Colombi et al. (2016). In this study, the source of vibrations was positioned on the ground surface, and a repeated pattern of scatterers was introduced ahead of the front of a propagating surface wave. A unique opportunity was chosen to use a doubly periodic pre-planted pine tree forest, in the Bordeaux region of France, as an array of surface scatterers, which influenced the dispersion properties of the surface waves. This is also an example of scatterers, which are elastic resonators and hence can also be characterised by their own eigenfrequencies.

Furthermore, theoretical concepts of metasurfaces, in the context of structured arrays of elastic resonators attached to the boundaries of large or semi-infinite solids, were analyzed by Carta et al. (2016) and by Skelton et al. (2018). The work of Carta et al. (2016) presented a mathematical model for an industry-inspired problem of vibration isolation applied to a periodic array of elastic fluid-filled containers, which also incorporated the effect of dynamic fluid-solid interaction. Numerical simulations of this paper also included the vibration patterns linked to several major earthquakes. The work of Skelton et al. (2018) has presented the concept of metawedges, as the wave trapping devices, which can also be used for mode coversion of elastic surface waves.

In this context, a housing estate, incorporating repeated patterns of terraced houses or small closely located detached dwellings, represents a metasurface, i.e. surface arrays of low frequency resonators. Although the results of the spectral analysis would different for different structures, the interval of frequencies of (0, 2 Hz) is of special interest. Examples of such metasurfaces can be found in the North of England, and in particular, in the County of Lancashire. The area affected by the seismic event, discussed here, includes Blackpool region and Preston.

4.2 The Seismic Case Study

The geographical region is shown in Figure 2. This case is special, as the eigenvalue problem can be set and analyzed to extract the relevant data for the given combination of the geometry and the geological structure of the test region.

FIGURE 2

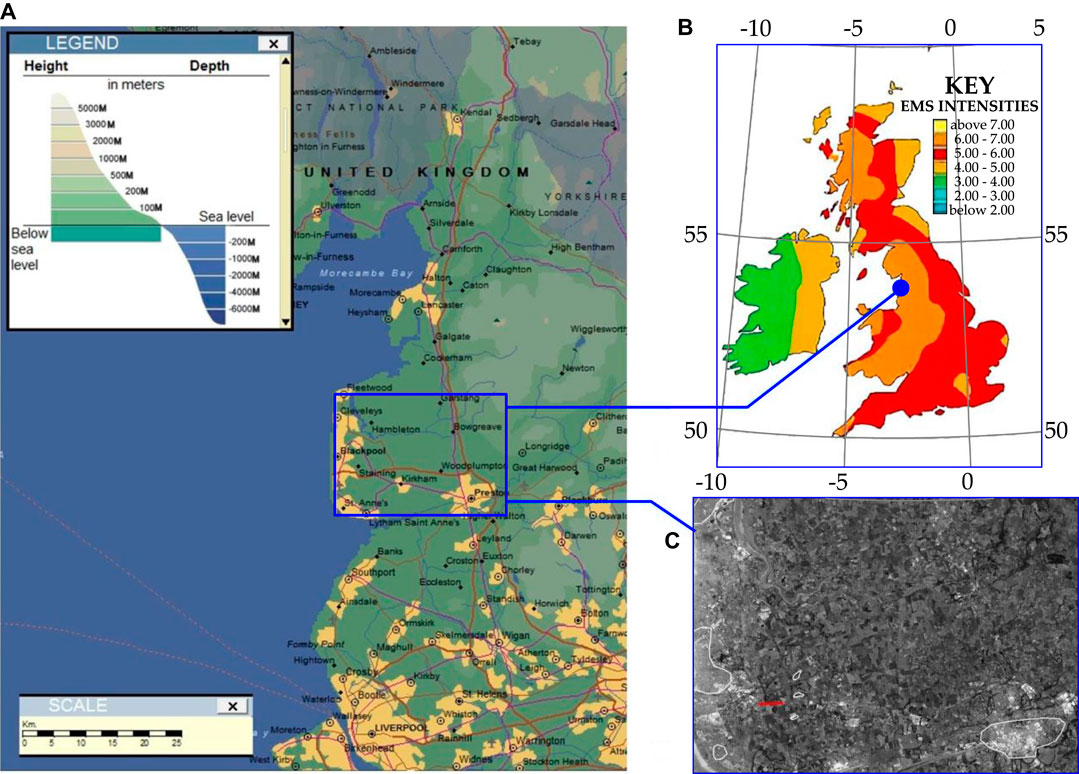
FIGURE 2. Location of the seismic area: (A) the geographical location of the region and the relief (the region of interest is marked by the white rectangle); (B) the same region (blue rectangle) on the larger seismic zoning scheme (see British Geological Survey, 2020); (C) the areal image of the Blackpool region: white contours indicate the areas of significant seismic measurements within residential areas; red marker shows the location of the horizontal well extension, along which the hydraulic fracturing is carried out.

The Blackpool peninsula is bounded on the West by the Irish Sea, on the North by Morecambe Bay and the River Wyre, and by the River Ribble on the South. High grounds of Bowland can be observed on the East, adjacent to a major M6 motorway, heading South-North parallel to the shore line. One of the characteristic features is the interface between different bedrock structures, running across the Blackpool peninsula (see [British Geological Survey, 2020] for Lancashire). The hydrofracture site is positioned West from this geological bedrock interface, at the Preston New Road Site, near the village of Little Plumpton, South East of Blackpool. The surface coordinates of the drilling stations are (Lat. ${53}^{\circ }{47}^{\prime }14.2827"N,$ Long. ${02}^{\circ }{57}^{\prime }04.0278"W$) and (Lat. ${53}^{\circ }{47}^{\prime }14.3712"N,$ Long. ${02}^{\circ }{57}^{\prime }03.7984"W$); the Cuadrilla’s Preston New Road Hydraulic Fracture Plan is outlined in Cuadrilla Hydraulic Fracture Plan (2018). The detailed Cuadrilla Bowland Ltd. (2019) report also noted a sequence of 38,383 micro-seismic events within the redline permit boundary at Preston New Road, and nine local seismic events that were reported to regulators as part of the “Traffic Light Mitigation System,” none of the local seismic magntidutes exceeded the level of 1.5 ML.

On the other hand, the publications by Tsai and Rice (2012), Viesca and Rice (2012), and the recent study of the 2019 Ridgecrest Earthquake by Chen et al. (2020) emphasised on the non-local nature of the dynamics induced by high-pressure fluid saturation in seismic phenomena. Of course, the specific features attributed to geological structures, as well as the wave dynamics associated with the hydrofracture, play an important role.

Despite the prediction of insignificant seismicity made in the report Cuadrilla Bowland Ltd., 2019, in August 2019 earthquakes of magnitude 2.1 and 2.9 had been observed in the wider Blackpool region. A series of hydrofracture-induced seismic events were registered in 2019 in the areas of Central Blackpool, Staining, Lytham, St Annes, Ansdell, which are positioned West and South of the drilling site, as shown in Figure 2C and Figures 3A, B (also see Blackpool earthquake, 2019). There was also a follow-up seismic wave registered in Fleetwood, North of Blackpool (see https://twnews.co.uk/gb-news/earthquake-sends-desks-sliding-across-office-in-fleetwood-but-it-wasn-t-fracking).

FIGURE 3

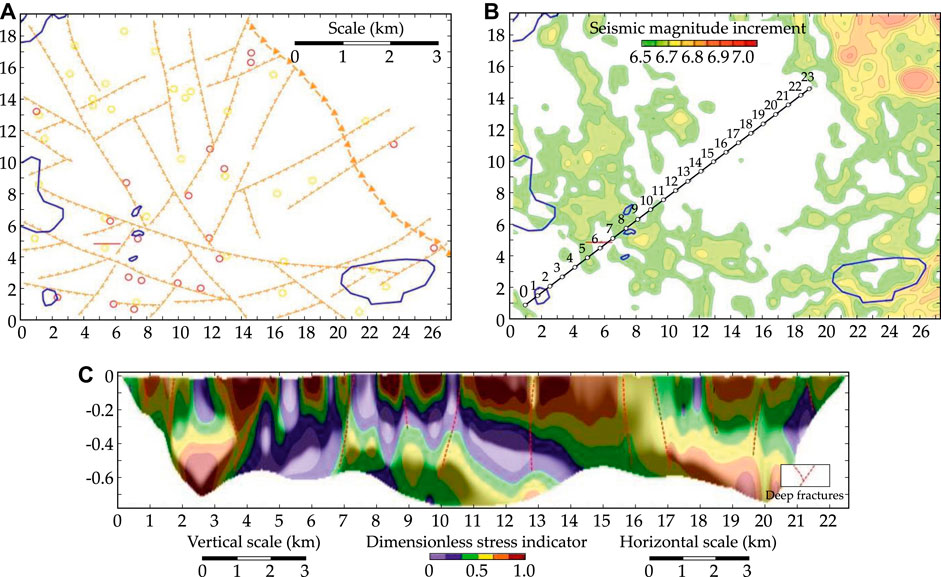
FIGURE 3. Reconstruction and ranging of geodynamic zones: (A) the zone imaging: 1—strip-shaped GDH; 2—zone of hypothetical looming; 3—geostructural anomalies; (B) the seismic profile; (EMS intensities) (C) a cross-sectional map representing log of the normalised modulus of the gradient of the height of the Earth’s surface. Blue contours represent the regions of the registered seismic damage, horizontal red segment shows the horizontal shaft in the hydraulic fracturing area.

4.3 Geodynamics Mapping and Simulation of Vibrations

An independent geophysical analysis has been carried for the test region, based on the methodology developed by Movchan and Yakovleva (2017), Movchan and Yakovleva (2020).

For the present case, geodynamic zones extend as strip shapes, and contain most of all geostructural anomalies. The hydraulic fracturing area lies directly on one of the discordant structures. Seismic micro-zoning and the approximation of the dependence between seismic intensities have been determined through Open Access geological and geophysical data available for the Blackpool peninsula.

Figure 3 presents reconstruction and ranging of geodynamic zones, which includes geostructural anomalies, the seismic mapping, and a cross-sectional map representing $\text{log}$ of the normalised modulus of the gradient of the height of the Earth’s surface. The latter is considered to be one of the key characteristics of seismicity in addition to the other parameters used by geophysicists in the method of acoustic rigidities. In Figure 3, the areas bounded by blue contours represent the regions of registered seismic events, the horizontal red segment represents the horizontal shaft of the hydraulic fracture at the New Preston Road drilling site.

The geophysical analysis, outlined in Figure 3, has been complemented by the mathematical modeling of vibrations of a finite elastic solid, whose shape and the thickness profile were chosen according to the geophysical data, as shown in Figure 4A.

FIGURE 4

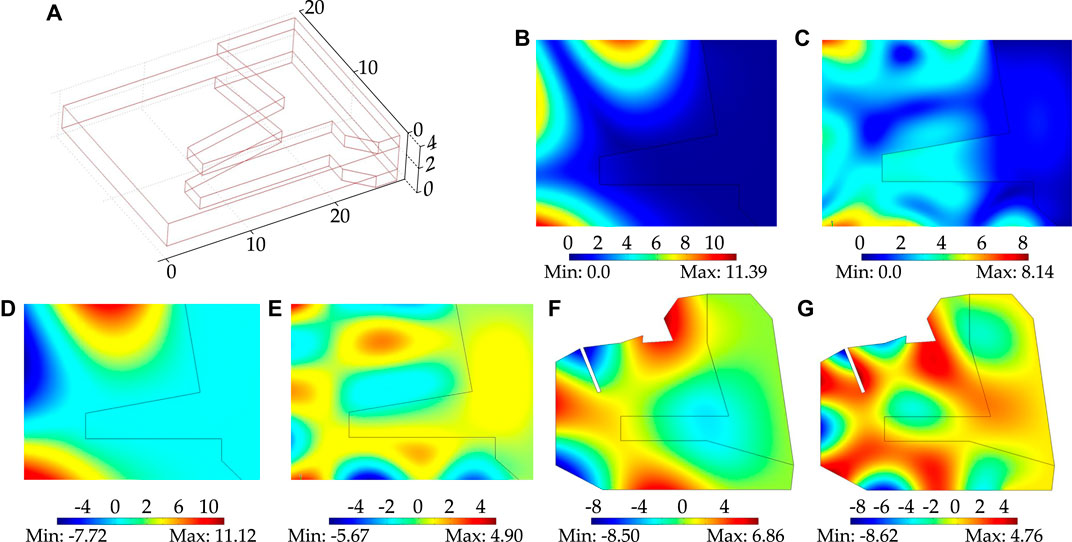
FIGURE 4. Vibrations pattern obtained via numerical simulations of a finite elastic solid having variable thickness. The thickness of the solid is comparable to the variable depth of the sedimentary cover commensurate with the geoblock that accommodates the test seismic region. (A) details of the shape and the thickness profile used in the simulations and chosen according to the geophysical data; 3D simulation of the dynamics of a solid of variable thickness in the rectangular computational window; (B-E)—3D simulation of the dynamics of a solid of variable thickness in the rectangular computational window, (B–C)—modulus of the longitudinal displacement, (D–E) the vertical displacement; (F,G) Mindlin plate approximation, with the accurate morphology of the geoblock, the map of the vertical displacement is shown for these eigenmodes. Illustrations are given for: (B-E) a low frequency vibration (mode No. 3, at 0.32 Hz), (C-D) a higher frequency (mode No. 22 at a frequency of 1.5 Hz), (F) mode No. 8 at 0.7 Hz and (G) mode No. 18 at 1.5 Hz. In the Figure, all magnitudes are shown in the normalised form. Additional explanations are in the text.

The thickness of the solid is comparable to the variable depth of the sedimentary cover (from 2 to 4 km), with the average mass density of 2.3 g/cm³. The boundary conditions on the periphery of the plate include the Dirichlet boundary condition on the right Eastern side of the block (high ground mountain ridge is present in the geological profile), and the Neumann boundary conditions on the remaining part of the boundary (shore line or proximity to the river networks in the geological profile).

The result of calculating of the natural oscillations takes into account the real size of the test region—about 23 × 25 km. The vibration patterns shown in Figure 4 are consistent with the seismic micro-zoning of the geophysical analysis. The three-dimensional elasticity simulation and the Mindlin plate approximations were used in the model.

The full three-dimensional simulations, shown in the parts (A)-(E) of Figure 4, are related to a rectangular computational domain. The Mindlin plate simulation, shown in the parts (F) and (G) of Figure 4, uses the refined geometrical profile, which takes into account the shape of the shore line and the boundary with the mountain ridge. The modeling of the Mindlin’s plate is a possible alternative to a full 3D simulation, as it provides the results for transverse and longitudinal displacements, with the relative simplicity of the model itself.

Illustrations are given for a low frequency vibration (mode No. 3, at 0.32 Hz) and for a higher frequency (mode No. 22 at a frequency of 1.5 Hz) shown in Figures 4B,E and Figures 4C,D, respectively. Parts (B) and (C) of Figure 4 show the modulus of the horizontal displacement, while parts (D) and (E) of this figure display the vertical displacement. The indicative structure of the Northwest stretch corresponds to the Western part of the zone at the lower mode of its natural vibrations at the frequency below 1 Hz (Figure 4B). For the higher modes of natural vibrations, the computations show characteristic sub-expansion stretch in the Southern part of the zone (Figure 4C—mode No. 22 at the natural frequency of 1.5 Hz). Figures 4D,E show the vertical displacement field (Figure 4D—mode No. 3, at 0.32 Hz, Figure 4E—mode No. 22 at a frequency of 1.5 Hz).

Additional modeling of the Mindlin’s plate natural oscillations has been carried out for the computational domain of the refined shape, which takes into account geographical features such as the shore line, river contours and mountain boundaries. The vertical displacement profiles are shown in Figures 4F,G for the Mindlin plate of variable thickness, with the assumption of the average ratio of the diameter to the thickness of the plate as 10:1. The actual size of the test zone has been used in the simulations. The results of the computations are shown in Figures 4F,G: part (F)—mode No. 8 at 0.7 Hz, and part (G)—mode No. 18 at 1.5 Hz.

Some experts in geotectonics would rely on the statistical analysis and the results of field measurements over a long period of time, and of course the short-time seismic events, induced by the industrial hydrofracture, in the Blackpool region would not be included in the range of their interests. These experts may also consider the spectral analysis of a “geoblock” as unconventional, in a similar way to that of structural engineers who would be reluctant, a decade ago, to use the Floquet-Bloch theory to analyze standing waves within elongated periodically structured elastic systems. As time has passed, and the effectiveness of the analytical approach has become apparent, the Floquet-Bloch theory is now a tool used across the engineering community for studying the dynamics of structured elastic systems. The Figure 4 also demonstrates that the spectral analysis applied for the geoblock delivers an invaluable information about the expected vibration patterns. Although setting up the model requires certain expertise that may be absent in the community of structural geology and geotectonics, the data required to set up the model is readily available. In particular, for the Blackpool region and the surrounding areas, British Geological Survey, 2020 provides the detailed information about the geological stratified structure, as well as the material properties of rocks and other geological components. Identification of the shape of the geoblock and setting up the boundary conditions depends on the particular case study. For the present problem, we used the special location of the Blackpool region, with the high ground (Dirichlet boundary conditions) on the East, and the coastal line (Neumann boundary conditions) in the North, West and South. The thickness for the computational model was also chosen according to the geological profile (British Geological Survey, 2020). There are different ways to approach such a problem. Figure 4 provides an illustration of two of such approaches:

• Full three-dimensional computation for a rectangular geoblock; Figures 4B,C represent the normalised magnitude of the longitudinal displacement at 0.32 and 1.5 Hz, whereas Figures 4D,E represent the normalised vertical displacement field at 0.32 and 1.5 Hz.

• The Mindlin’s plate model, which takes into account the refined geometry of the coastal boundary of the Blackpool region; Figures 4F,G show the normalised vertical displacement field at frequencies of 0.7 and 1.5 Hz.

The formulations of the computational models can be refined to a great depth, but the main message, given by the results in Figure 4, is that the problem is non-local, and after the vibrations have been triggered, the vibration pattern at low frequencies shows ripples along the entire coastal region. This non-locality was observed during the Blackpool’s seismic events of 2019.

Moreover, some remote residential areas were affected to a greater extent than the industrial regions (Blackpool airport and RAF Warton), which were in the closer proximity to the hydrofracture drilling site. The notion of an elastic metasurface provides a possible explanation of wave localisation in the populated areas, which include certain patterns of buildings and structures, as discussed in the section below.

4.4 Metasurfaces and Wave Localisation

The work by Skelton et al. (2018) analyzed surface and bulk waves in elastic solids with the boundaries, which incorporate multi-scale elastic resonators, known as Metasurfaces were also studied experimentally by Colombi et al. (2016). It was concluded that arrays of surface resonators “absorb vibrations” from the incident waves and in resonant regimes may act as polarisers of elastic waves.

For the present case study, related to seismic events of 2019 in the Blackpool-Preston region in the United Kingdom, the observers noted a significant structural damage in several densely populated areas of the region, although the magnitude of earthquakes did not exceed the level 3 on the Richter scale. Surprisingly, no damage was reported at two aerodromes (Blackpool airport and RAF Warton), which were in the close proximity of the hydrofracture drilling site. The concept of dynamic metasurfaces may provide an explanation. While the areas of aerodromes is reinforced with concrete and steel, the populated areas with housing estates include repeated patterns of terraced houses or closely positioned detached dwellings. They act as low frequency elastic resonators and form metasurfaces when a combined dynamic response is considered. Metasurfaces may develop a significant displacement amplitude for individual resonators even when the overall level of the earthquake is not excessive.

5 Concluding Remarks

The paper has given a review of several theoretical concepts of waves in structured elastic media, with the focus on metamaterials, phase transition waves, elastic cloaking and anomalous resonances. The idea of metasurfaces brings a link between the bulk and surface waves in elastic solids, and it has a direct connection with dynamic phenomena observed during earthquakes. A seismic event of 2019 has been considered as the case study, and vibration analysis was supplied in addition to the geophysical seismic mapping. It is also noted that the earthquakes considered here followed a hydrofracture and hence a dynamic crack propagation. The latter is a non-local phenomenon: the crack may propagate a vast distance, and crack dynamics is always associated with elastic waves emanated from the crack edge. As hydrofracture also incorporates diffusion type processes, which may occur over some period of time, a seismic event may be observed several days, weeks or even months after the hydrofracture drilling has taken place. Even though the magnitude of the earthquake may appear sufficiently low, densely populated areas, where repeated patterns of housing estates act as elastic resonators, represent dynamic metasurfaces, which may support standing waveforms.

The approaches, discussed in this paper, can be used in a wide range of applications for seismic assessments and dynamic problems in geophysics and mining engineering. Optimisation of seismic zoning and analysis of a dynamic response of curved underground tunnels were considered in Movchan and Yakovleva (2019), Gospodarikov and Chi (2019). In realistic geological scenarios, fluid-solid interaction and the effects of fluid saturation may need to be taken into account, as discussed in Lalomov et al. (2019), Petrakov et al. (2020). Mathematical modeling benefits strongly from the information, provided for a three-dimensional geological structure, including defects, such as cavities, mine shafts and interfaces (see, for example, Danilev and Danileva, 2018; Mazurov et al., 2019; Danilev and Danileva, 2020); the modeling of the dynamic response of a multi-physics system may focus on the wave localisation around the defects, which have been identified. The idea of computational models to take into account the coastal boundaries along large water reservoirs may require an additional study of vertical geological profiles (see for example, Egorov et al., 2016; Ageev and Egorov, 2019). Seismic and geological monitoring represents a highly developed area (examples are in Gorelik et al., 2019; Pashkevich and Petrova, 2019), but metasurfaces may provide an extremely efficient and highly sensitive new tool for monitoring and designing of dynamic responses and seismic waves, for the ground surfaces, as well as underground tunnels.

Author Contributions

All authors contributed to writing the text of the paper. IM and AY have produced the simulations for seismic analysis and finite element simulations and made the main contribution to the section on seismic zoning and analysis. AM has written the article, with the focus on metamaterials and metasurfaces. DM has produced the work on flexural cloaking reflected in Figure 1 and has contributed to the sections on metamaterials and seismic analysis. NP and AM have worked on the text by emphasising the connection between metamaterials and seismic effects discussed in the paper.

Funding

DM and NP are supported by the European Commission under the FET Open (Boheme) grant No. 863179. Some of the work, reviewed in Sections 3.2, 4.1 and 4.4, was supported through the UK Engineering and Physical Sciences Research Council Programme Grant EP/L024926/1, and ERC Advanced Grant ’Instabilities and nonlocal multiscale modelling of materials’ ERC-2013-ADG-340561-INSTABILITIES.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ageev, A. S., and Egorov, A. S. (2019). “Deep structure of the Baikal-Stanovaya shear zone: results of geological-geophysical data interpretation,” in Topical issues of rational use of natural resources. Editor V. Litvinenko (London, United Kingdom: CRC Press, Francis Taylor Group), 3–8.

Google Scholar

Blackpool earthquake (2019). Blackpool earthquake. Available at: https://www.express.co.uk/news/uk/1170146/Blackpool-earthquake-huge-tremor-fylde-lancashire-twitter.

Google Scholar

British Geological Survey (2020). Earthquake seismology. UK Seismic Hazard, Available at: https://earthquakes.bgs.ac.uk/hazard/UKhazard.html.

Google Scholar

Brun, M., Giaccu, G. F., Movchan, A. B., and Movchan, N. V. (2012). Asymptotics of eigenfrequencies in the dynamic response of elongated multi-structures. Proc. R. Soc. A. 468, 378–394. doi:10.1098/rspa.2011.0415

CrossRef Full Text | Google Scholar

Brun, M., Giaccu, G. F., Movchan, A. B., and Slepyan, L. I. (2014). Transition wave in the collapse of the san Saba bridge. Front. Mater. 1, 12. doi:10.3389/fmats.2014.00012

CrossRef Full Text | Google Scholar

Brun, M., Guenneau, S., and Movchan, A. B. (2009). Achieving control of in-plane elastic waves. Appl. Phys. Lett. 94, 061903. doi:10.1063/1.3068491

CrossRef Full Text | Google Scholar

Brun, M., Movchan, A. B., and Slepyan, L. I. (2013a). Transition wave in a supported heavy beam. J. Mech. Phys. Solid. 61, 2067–2085. doi:10.1016/j.jmps.2013.05.004

CrossRef Full Text | Google Scholar

Brun, M., Movchan, A., Jones, I., and McPhedran, R. (2013b). Bypassing shake, rattle and roll. Phys. World 26, 32–36. doi:10.1088/2058-7058/26/05/34

CrossRef Full Text | Google Scholar

Carta, G., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2020). Chiral flexural waves in structured plates: directional localisation and control. J. Mech. Phys. Solid. 137, 103866. doi:10.1016/j.jmps.2020.103866

CrossRef Full Text | Google Scholar

Carta, G., Movchan, A. B., Argani, L. P., and Bursi, O. S. (2016). Quasi-periodicity and multi-scale resonators for the reduction of seismic vibrations in fluid-solid systems. Int. J. Eng. Sci. 109, 216–239. doi:10.1016/j.ijengsci.2016.09.010

CrossRef Full Text | Google Scholar

Chen, K., Avouac, J. P., Aati, S., Milliner, C., Zheng, F., and Shi, C. (2020). Cascading and pulse-like ruptures during the 2019 ridgecrest earthquakes in the Eastern California shear zone. Nat. Commun. 11, 22. doi:10.1038/s41467-019-13750-w |

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Roux, P., Guenneau, S., Gueguen, P., and Craster, R. V. (2016). Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 6, 19238. doi:10.1038/srep19238 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Colquitt, D. J., Jones, I. S., Movchan, N. V., Movchan, A. B., Brun, M., and McPhedran, R. C. (2013). Making waves round a structured cloak: lattices, negative refraction and fringes. Proc. Math. Phys. Eng. Sci. 469, 20130218. doi:10.1098/rspa.2013.0218 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Colquitt, D. J., Brun, M., Gei, M., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2014). Transformation elastodynamics and cloaking for flexural waves. J. Mech. Phys. Solid. 72, 131–143. doi:10.1016/j.jmps.2014.07.014

CrossRef Full Text | Google Scholar

Craster, R. V., and Guenneau, S. (2013). Acoustic metamaterials: negative refraction, imaging, lensing and cloaking. Berlin, Germany: Springer.

Cuadrilla Bowland Ltd (2019). Preston new road-1z: LJ/06-09(z) HFP report. Available at: https://www.ogauthority.co.uk/media/5845/pnr-1z-hfp-report.pdf.

Google Scholar

Cuadrilla Hydraulic Fracture Plan (2018). Preston New Road. Available at: https://consult.environment-agency.gov.uk/onshore-oil-and-gas/information-on-cuadrillaspreston-new-road-site/supporting20documents/Preston202020New202020Road202020HFP.pdf, and https://consult.environment-agency.gov.uk/onshore-oil-and-gas/information-on-cuadrillaspreston-new-road-site/useruploads/hydraulic-fracture-plan-preston-new-road-2–v2.0.

Google Scholar

Danilev, S. M., and Danileva, N. A. (2018). “Characteristics electromagnetic waves of GPR data for study of hidden cavities in the engineering objects,” in Conference proceedings engineering and mining geophysics, Almaty, Kazakhstan, April 2018 (Engineering and Mining Geophysics), 1–4. doi:10.3997/2214-4609.201800540

CrossRef Full Text | Google Scholar

Danilev, S. M., and Danileva, N. A. (2020). Investigation destruction zones of mine workings by GPR data,” in Conference proceedings engineering and mining geophysics, Perm, Russia, September 2020 (Engineering and Mining Geophysics), 1–7. doi:10.3997/2214-4609.202051097

CrossRef Full Text | Google Scholar

Dolin, L. S. (1961). To the possibility of comparison of three-dimensional electromagnetic systems with non-uniform anisotropic filling. Izvestiya Vysshikh Uchebnykh Zavedenii. Radiofizika 4 (5), 964–967.

Google Scholar

Egorov, A. S., Vinokurov, I. Y., Kalenich, A. P., Belevskaya, E. S., and Ageev, A. S. (2016). “Deep structure of the Barents-Kara region according to geophysical investigations along 1-AR and 2-AR geotravers,” in Conference proceedings 7th EAGE Saint Petersburg international conference and exhibition, Saint Petersburg, Russia, April 2016. doi:10.3997/2214-4609.201600173

CrossRef Full Text | Google Scholar

Egorov, A. S., Vinokurov, I. Yu., and Telegin, A. N. (2018). Scientific and methodical approaches to increase prospecting efficiency of the Russian Arctic shelf state geological mapping. J. Mini. Insti. (Zapiski Gornogo Instituta). 233, 447–458. doi:10.31897/PMI.2018.5.447

CrossRef Full Text | Google Scholar

Evans, D. V., and Porter, R. (2007). Penetration of flexural waves through a periodically constrained thin elastic plate in vacuo and floating on water. J. Eng. Math. 58 (1–4), 317–337. doi:10.1007/s10665-006-9128-0

CrossRef Full Text | Google Scholar

Farhat, M., Guenneau, S., Enoch, S., Movchan, A., Zolla, F., and Nicolet, A. (2008). A homogenization route towards square cylindrical acoustic cloaks. New J. Phys. 10, 115030. doi:10.1088/1367-2630/10/11/115030

CrossRef Full Text | Google Scholar

Frenzel, T., Kadic, M., and Wegener, M. (2017). Three-dimensional mechanical metamaterials with a twist. Science 358 (6366), 1072–1074. doi:10.1126/science.aao4640 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Galin, L. A., and Cherepanov, G. P. (1966). Self-sustaining failure of a stressed brittle body. Sov. Phys. Dokl. 11, 367–369.

Google Scholar

Gorelik, G. D., Budanov, L. M., Ryabchuk, D., Zhamoida, V., and Neevin, I. (2019). Application of CDP seismic reflection method in buried paleo-valley study,” in Conference proceedings, engineering and mining geophysics 2019 15th conference and exhibition, Gelendzhik, Russia, April 2019. doi:10.3997/2214-4609.201901777

CrossRef Full Text | Google Scholar

Gospodarikov, A. P., and Chi, T. N. (2019). The impact of earthquakes on the tunnel from Hanoi metro system when the tunnel has a horseshoe shape cross-section. Int. J. Civ. Eng. Technol. 10 (2), 79–86.

Google Scholar

Greenleaf, A., Lassas, M., and Uhlmann, G. (2003b). Anisotropic conductivities that cannot be detected by EIT. Physiol. Meas 24, 413–419. doi:10.1088/0967-3334/24/2/353

CrossRef Full Text | Google Scholar

Greenleaf, A., Lassas, M., and Uhlmann, G. (2003a). On nonuniqueness for Calderón’s inverse problem. Math. Res. Lett. 10, 685–693. doi:10.4310/mrl.2003.v10.n5.a11

CrossRef Full Text | Google Scholar

Grigoryan, S. S. (1967). Some problems of the mathematical theory of deformation and fracture of hard rocks. Appl. Math. Mech. 31, 667–686.

Google Scholar

Haslinger, S. G., Craster, R. V., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2016). Dynamic interfacial trapping of flexural waves in structured plates. Proc. Math. Phys. Eng. Sci 472 (2186), 20150658. doi:10.1098/rspa.2015.0658 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Haslinger, S. G., Movchan, N. V., Movchan, A. B., and McPhedran, R. C. (2012). Transmission, trapping and filtering of waves in periodically constrained elastic plates. Proc. R. Soc. A. 468, 76–93. doi:10.1098/rspa.2011.0318

CrossRef Full Text | Google Scholar

Jones, I. S., Brun, M., Movchan, N. V., and Movchan, A. B. (2015). Singular perturbations and cloaking illusions for elastic waves in membranes and Kirchhoff plates. Int. J. Solid Struct. 69–70 (70), 498–506. doi:10.1016/j.ijsolstr.2015.05.001 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kittel, C. (1954). Introduction to solid state physics. Hoboken, NJ: John Wiley & Sons Inc.

Krushynska, A. O., Bosia, F., and Pugno, N. M. (2018a). Labyrinthine acoustic metamaterials with space-coiling channels for low-frequency sound control. Acta Acustica United Acustica 104 (2), 200–210. doi:10.3813/aaa.919161

CrossRef Full Text | Google Scholar

Krushynska, A. O., Galich, P., Bosia, F., Pugno, N. M., and Rudykh, S. (2018b). Hybrid metamaterials combining pentamode lattices and phononic plates. Appl. Phys. Lett. 113, 201901. doi:10.1063/1.5052161

CrossRef Full Text | Google Scholar

Lalomov, D., Glazunov, V., Tatarskiy, A., Burlutsky, S., and Efimova, N. (2019). “Methodical features of studying the geological structure of the coastal part of the sea of Okhotsk based on the integration of continuous aquatic electrical sounding and seismoacoustics data,” in 25th European meeting of environmental and engineering geophysics, near surface geoscience conference and exhibition 2019, The Hague, The Netherlands, September 8–12, 2019 (Nippon Suisan Gakkaish). doi:10.3997/2214-4609.201903466

CrossRef Full Text | Google Scholar

Lekner, J. (1987). Theory of reflection of electromagnetic and particle waves. Heidelberg, Germany: Springer-Verlag.

CrossRef Full Text

Leonhardt, U. (2006a). Optical conformal mapping. Science 312, 1777–1780. doi:10.1126/science.1126493

CrossRef Full Text | Google Scholar

Leonhardt, U. (2006b). Notes on conformal invisibility devices. New J. Phys. 8, 118. doi:10.1088/1367-2630/8/7/118

CrossRef Full Text | Google Scholar

Magalhães, F., Caetano, E., Cunha, Á., Flamand, O., and Grillaud, G. (2012). Ambient and free vibration tests of the Millau Viaduct: evaluation of alternative processing strategies. Eng. Struct 45, 372–384. doi:10.1016/j.engstruct.2012.06.038

CrossRef Full Text | Google Scholar

Mazurov, B. T., Mustafin, M. G., and Panzhin, A. A. (2019). Estimation method for vector field divergence of Earth crust deformations in the precess of Mineral deposits development. J. Min. Inst. (Zapiski Gornogo Instituta) 238 (4), 376–383. doi:10.31897/pmi.2019.4.376

CrossRef Full Text | Google Scholar

Milton, G. W., Briane, M., and Willis, J. R. (2006). On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 8, 248. doi:10.1088/1367-2630/8/10/248

CrossRef Full Text | Google Scholar

Milton, G. W., Nicorovici, N.-A. P., and McPhedran, R. C. (2007). Opaque perfect lenses. Phys. B Condens. Matter 394 (2), 171–175. doi:10.1016/j.physb.2006.12.010

CrossRef Full Text | Google Scholar

Milton, G. W., and Willis, J. R. (2007). On modifications of Newton’s second law and linear continuum elastodynamics. Proc. R. Soc. A. 463, 855–880. doi:10.1098/rspa.2006.1795

CrossRef Full Text | Google Scholar

Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016b). Large scale mechanical metamaterials as seismic shields. New J. Phys 18, 083041. doi:10.1088/1367-2630/18/8/083041

CrossRef Full Text | Google Scholar

Miniaci, M., Krushynska, A., Movchan, A. B., Bosia, F., and Pugno, N. M. (2016a). Spider web-inspired acoustic metamaterials. Appl. Phys. Lett. 109, 071905. doi:10.1063/1.4961307

CrossRef Full Text | Google Scholar

Mishuris, G. S., Movchan, A. B., and Slepyan, L. I. (2009). Localised knife waves in a structured interface. J. Mech. Phys. Solid. 57, 1958–1979. doi:10.1016/j.jmps.2009.08.004

CrossRef Full Text | Google Scholar

Misseroni, D., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2016). Cymatics for the cloaking of flexural vibrations in a structured plate. Sci. Rep. 6, 23929. doi:10.1038/srep23929 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Misseroni, D., Movchan, A. B., and Bigoni, D. (2019). Omnidirectional flexural invisibility of multiple interacting voids in vibrating elastic plates. Proc. Math. Phys. Eng. Sci. 475, 20190283. doi:10.1098/rspa.2019.0283 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Movchan, I. B., and Yakovleva, A. A. (2017). Experience of qualitative and quantitative interpretation of non-potential geofields with surface and deep morphostructural reconstructions on the example of unica ore province (Kareljya, Russia). Int. J. Mech. Eng. Technol. 8 (12), 926–932.

Google Scholar

Movchan, I. B., and Yakovleva, A. A. (2019). Refined assessment of seismic microzonation with a priori data optimization. J. Mini. Inst. (Zapiski gornogo instituta) 236, 133–141. doi:10.31897/pmi.2019.2.133

CrossRef Full Text | Google Scholar

Movchan, I. B., and Yakovleva, A. A. (2020). Wave analogies in the quantitative interpretation of potential fields. Ijatcse 9 (2), 1793–1799. doi:10.30534/ijatcse/2020/136922020

CrossRef Full Text | Google Scholar

Movchan, N. V., McPhedran, R. C., and Movchan, A. B. (2011). Flexural waves in structured elastic plates: mindlin versus bi-harmonic models. Proc. R. Soc. A. 467, 869–880. doi:10.1098/rspa.2010.0375

CrossRef Full Text | Google Scholar

Nicorovici, N. A., McPhedran, R. C., and Milton, G. W. (1994). Optical and dielectric properties of partially resonant composites. Phys. Rev. B Condens. Matter 49 (12), 8479–8482. doi:10.1103/physrevb.49.8479 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicorovici, N. A., McPhedran, R. C., and Milton, G. W. (1993). Transport properties of a three-phase composite material: the square array of coated cylinders. Proc. R. Soc. A. 442, 599–620. doi:10.1098/rspa.1993.0124

CrossRef Full Text | Google Scholar

Nieves, M. J., Movchan, A. B., Jones, I. S., and Mishuris, G. S. (2013). Propagation of Slepyan’s crack in a non-uniform elastic lattice. J. Mech. Phys. Solid. 61, 1464–1488. doi:10.1016/j.jmps.2012.12.006

CrossRef Full Text | Google Scholar

Norris, A. N., and Shuvalov, A. L. (2011). Elastic cloaking theory. Wave Motion 48, 525–538. doi:10.1016/j.wavemoti.2011.03.002

CrossRef Full Text | Google Scholar

Pashkevich, M. A., and Petrova, T. A. (2019). Development of an operational environmental monitoring system for hazardous industrial facilities of Gazprom Dobycha. Urengoy/J. Phys. Conf. 2019 (1384), 012940. doi:10.1088/1742-6596/1384/1/012040

CrossRef Full Text | Google Scholar

Pendry, J. B., Schurig, D., and Smith, D. R. (2006). Controlling electromagnetic fields. Science 312, 1780–1782. doi:10.1126/science.1125907 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrakov, D. G., Kupavykh, K., and Kupavykh, A. (2020). The effect of fluid saturation on the elastic-plastic properties of oil reservoir rocks. Curved Layer. Struct. 7, 29–34. doi:10.1515/cls-2020-0003

CrossRef Full Text | Google Scholar

Rahm, M., Schurig, D., Roberts, D. A., Cummer, S. A., Smith, D. R., and Pendry, J. B. (2008). Design of electromagnetic cloaks and concentrators using form-invariant coordinate transformations of Maxwell’s equations. Photo.Nano.–Fund. App. 6, 87–95. doi:10.1016/j.photonics.2007.07.013

CrossRef Full Text | Google Scholar

Skelton, E., Craster, R. V., Colombi, A., and Colquitt, D. (2018). The multi-physics metawedge: graded arrays on fluid-loaded elastic plates and the mechanical analogues of rainbow trapping and mode conversion. New J. Phys. 20, 053017. doi:10.1088/1367-2630/aabecf

CrossRef Full Text | Google Scholar

Slepyan, L. I. (1968). Brittle failure waves. Mech. Solid 3, 202–204.

Google Scholar

Slepyan, L. I. (2002). “Models and phenomena in fracture,” in Mechanics. Berlin, Germany: Springer.

Google Scholar

Slepyan, L. I. (1977). Models in the theory of brittle fracture waves. Mech. Solid 12, 170–175.

Google Scholar

Slepyan, L. I., and Troyankina, L. V. (1984). Fracture wave in a chain structure. J. Appl. Mech. Tech. Phys. 25, 921–927. doi:10.1007/bf00911671

CrossRef Full Text | Google Scholar

Slepyan, L. I., and Troyankina, L. V. (1969). The failure of brittle bar under longitudinal impact. Mech. Solid 4, 57–64.

Google Scholar

Stenger, N., Wilhelm, M., and Wegener, M. (2012). Experiments on elastic cloaking in thin plates. Phys. Rev. Lett. 108, 014301. doi:10.1103/PhysRevLett.108.014301 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, V. C., and Rice, J. R. (2012). Modeling turbulent hydraulic fracture near a free surface. J. Appl. Mech 79 (3), 031003. doi:10.1115/1.4005879

CrossRef Full Text | Google Scholar

Vasquez, F. G., Milton, G. W., and Onofrei, D. (2011). Exterior cloaking with active sources in two dimensional acoustics. Wave Motion 46 (6), 515–524. doi:10.1016/j.wavemoti.2011.03.005

CrossRef Full Text | Google Scholar

Viesca, R. C., and Rice, J. R. (2012). Nucleation of slip-weakening rupture instability in landslides by localized increase of pore pressure. J. Geophys. Res.: Solid Earth. 117 (B3), B03104. doi:10.1029/2011JB008866

CrossRef Full Text | Google Scholar