Magnetic Hyperthermia in the 400–1,100 kHz Frequency Range Using MIONs of Condensed Colloidal Nanocrystal Clusters

Introduction

The application of nanotechnology in the field of medicine promises to revolutionize the treatment of malignant diseases such as cancer. This has led to the development of multifunctional nano-assemblies termed as theranostics (Xie et al., 2010; Hu et al., 2020; Misra et al., 2020; Shakeri et al., 2020) for their combined diagnostic and therapeutic action. Hybrid magnetic nanostructures (in particular, iron oxides) are among the most interesting classes of nano-theranostics and have been the topic of extensive research interest over the past decade (Yoo et al., 2011; Revia and Zhang, 2016; Lorkowski et al., 2021). Their excellent biocompatibility and inherent multifunctional nature of their magnetic core mark them suitable for a diverse set of biomedical applications, mainly including MRI (Zhou et al., 2014), physical tumor targeting through magnetic manipulation (Feng et al., 2017), and magnetic fluid hyperthermia (MHF) (Kozissnik et al., 2013; Deatsch and Evans, 2014; Das et al., 2019). The magnetic properties of magnetic iron oxide nanoparticles (MIONs) are strongly dependent on their physical characteristics. When the size of magnetic nanoparticles (MNPs) decreases below a certain limit (~20 nm for MIONs), then the nanoparticles exhibit a single magnetic domain and the total magnetic moment of all unpaired electrons will have a preferred orientation (Krishnan et al., 2006). Further reduction in the size of nanoparticles results in a reduction in the energy barrier required to rotate this magnetic moment, until ultimately the thermal energy is sufficient to force the moment to random directions, a phenomenon known as “super-paramagnetism.” In the absence of an external magnetic field, superparamagnetic particles do not exhibit magnetization phenomena, a property critical for their colloidal stability. However, under the application of an external magnetic field, the magnetic moments of the nanoparticles align along the direction of the field and the saturation magnetization can be achieved at relatively low fields. Another important physical parameter in work related to MNPs is the relaxation time τ which is an inherent characteristic time of the MNPs as a response to the alternating magnetic field (AMF), describing different rotational modes. Two such modes are usually present, namely the Néel rotation according to which the magnetization of the MNPs is rotating with the particle remaining fixed and the Brownian rotation where the magnetization of the MNPs is locked at some crystal axis and thus in an effort to follow the field, it forces the particle to rotate as well. MNPs have the potential to generate heat through the application of external AMF, property that can be exploited for in-vivo induction of hyperthermia (Fortin et al., 2007; Ortega and Pankhurst, 2012) aiming to the destruction of the cancerous tumors. The heating performance of different MNPs for the applications of magnetic fluid hyperthermia (MFH) is often quantified by the “specific loss power” (SLP) parameter (also known as “specific absorption rate” [SAR]), which is defined as the power diffused by a MNP per unit mass (Rosensweig, 2002). The unit of SLP is mW/g. Usually, the MNPs are suspended in aqueous solutions (ferrofluids) and this important property is determined experimentally by the simple formula (Sudame et al., 2020):

$\begin{array}{ll}SLP=\frac{c}{\mu }\frac{\Delta T}{\Delta t}& (1)\end{array}$

where c is the ferrofluid-specific heat (of the carrier fluid in J/g·K), μ = m_n/m is the mass fraction of the MNPs mass m_n to the total solution mass m, ΔT is the temperature rise of the ferrofluid, and Δt is the duration of the heating. As the T(t) curve is not linear but has an exponential rise–saturation behavior, the quantity ΔT/Δt is implied as the largest slope in Equation 1 which happens at the initial time t = 0 of the application of the AC field. The physical meaning of SLP is that the higher it is, the more heat is produced by the MNPs. Different experimental setups have been developed for the assessment of the heating efficiency of MNPs (Andreu and Natividad, 2013). These mainly include calorimetry experiments conducted in an adiabatic or non-adiabatic way (Rajan and Sahu, 2020; Boekelheide et al., 2021) as well as AC magnetometry experiments, where the dynamic magnetic hysteresis loops M(H) are measured with a pickup coil technology (Connord et al., 2014; Garaio et al., 2014; Salas et al., 2014). Nevertheless, the widely different experimental conditions (i.e., oscillating frequency, AMF amplitude, sample volume, etc.) employed by different groups, have led to the introduction of another parameter called “intrinsic loss power” (ILP) which is defined as

$\begin{array}{ll}ILP=\frac{SLP}{H^{2}f}& (2)\end{array}$

where H is the magnitude of the applied external field and f is the excitation frequency. ILP has been proposed as a “normalized SLP parameter” as the magnetic excitation power is proportional to H² and the frequency f. ILP aims to be an independent parameter of AMF strength and frequency, eliminating the effect of different experimental conditions, thus enabling a direct comparison of the heating efficiency of MNPs (Kallumadil et al., 2009). However, the advantages of the concept of ILP are still under debate as SLP rarely appears as quadratic in field intensity (Périgo et al., 2015). In addition, the resonance phenomena due to the aforementioned relaxation times can also change this linear dependence of the measured signal to f. The theoretical models (Rosensweig, 2002) have also been employed for the prediction of power dissipation from the MNPs. These models are based on the intrinsic properties of MNPs, with the most commonly used being the linear response theory (LRT) model by Rosenweig (Rosensweig, 2002). In this study, it can be seen that the power loss [(Rosensweig, 2002), Equation 14 therein] has a frequency dependence on the form f²/(1 + (2πfτ)²) which is quadratic at low f, leads to saturation at high f, and has roughly a linear increase at values somewhat lower than 2πfτ = 1. Nevertheless, this model refers to non-interacting particles, neglecting the interparticle interactions developed in concentrated samples (De La Presa et al., 2012), multicore systems (Yoon et al., 2011; Serantes et al., 2014), or condensed–clustered nanoparticles (Puntes et al., 2004; Zoppellaro et al., 2014) which can strongly affect the heating performance of MNPs (Deatsch and Evans, 2014; Salas et al., 2014). Condensed clustering of MIONs refers to a specific structural motif of colloidal nanocrystal clusters (CNCs) in which individual magnetic nanocrystallites are densely packed in such a fashion that their crystal planes adopt the same crystallographic orientation through the epitaxial aggregation during their crystal growth (Zoppellaro et al., 2014; Coral et al., 2018). This can result in large crystallites of ~50–300 nm size to show a single-crystal-like structure throughout the large areas of their volume and yet behave like the ensembles of smaller independent (5–15 nm) nanocrystallites (i.e., superparamagnetic behavior). This internal organization of MNPs can significantly enhance their magnetic properties due to the collective phenomena exhibiting high magnetic moment, high contrast with MRI applications (Xu et al., 2012), and improved hyperthermic performance (Lartigue et al., 2012). In these systems, the developed dipolar interparticle interactions are particularly strong due to the very close proximity of the magnetic nanocrystals. Such strong interactions may lead to increased magnetic anisotropy in the system which in turn could result in enhanced heating efficiency. Nonetheless, this is not always the case as more complex phenomena arising in such systems [e.g., surface spin disordering due to defected nanoparticle surface coordination and spin glass features (Kostopoulou et al., 2014)] could either favor or hinder the heating performance of clustered systems (Landi, 2014; Blanco-Andujar et al., 2015).

In this context, the experimental evaluation of hyperthermia agents remains the most valid route for the extraction of SLP and related hyperthermia parameters, especially for strongly interacting systems with a high interest for the applications of magnetic hyperthermia, such as the condensed–clustered MIONs.

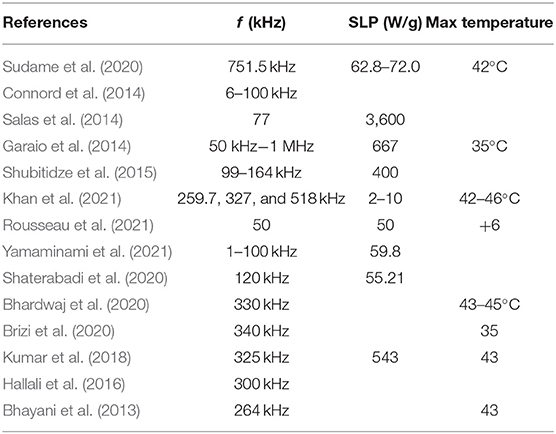
This article aims to study the effects of frequency on the hyperthermia power, for a condensed–clustered MION-based system developed by Zoppellaro et al. (2014). The frequency range was 400 kHz to 1.1 MHz, (a) which covers almost all of the width of the fixed frequencies reported previously in the literature [see Table 1 that summarizes a quick outline of the parameters used in references (Bhayani et al., 2013; Hallali et al., 2016; Kumar et al., 2018; Bhardwaj et al., 2020; Brizi et al., 2020; Shaterabadi et al., 2020; Sudame et al., 2020; Khan et al., 2021; Rousseau et al., 2021; Yamaminami et al., 2021)] and (b) it is in agreement with the medically accepted range, as described in Khan et al. (2021), quoted here: “The choice of frequency must be appropriate for the site location of magnetic Hyperthermia applications in clinical trials like, preferably > 50 kHz to avoid skeletal muscles' stimulations and lower than 2 MHz (2, 000 kHz) for penetration depth inside the tissues.” In addition, other reports state that frequencies <10 MHz are not attenuated by tissue and thus penetrate deep into the body (Attaluri et al., 2020). Furthermore, for in-vivo applications, safety limits regarding the strength of the magnetic field should also be considered to ensure that patients will not experience any discomfort during therapy sessions, caused by non-specific tissue heating due to eddy currents. To ensure that, a widespread limit known as “Brezovich criterion” (Atkinson et al., 1984) has been introduced, where the product of the applied magnetic field and oscillating frequency should be H f < 4.85 × 10⁸ A/ms. Nevertheless, it is estimated that for exposure of adequate small body regions this strict limit can be exceeded up to 10 times, thus becoming H f ≤ 5 × 10⁹ A/ms, as proposed by Hergt and Dutz (Hergt and Dutz, 2007). In the present study, all experiments were performed fulfilling the above Hf condition with the highest frequency tested to be Hf = 2.58 × 10⁹ A/ms and therefore suitable for biomedical applications. Even though Néel relaxation times could result in resonance frequencies (Yamaminami et al., 2021) within our range, no such resonance was observed in our case and the measured temperature was proportional to the applied frequency. This could be explained by the increased interparticle interactions of the condensed magnetic clusters, as discussed later.

TABLE 1

Table 1. Typical parameters used in hyperthermia experiments.

Experimental Details

Materials

Iron(II) sulfate heptahydrate (Fe₂SO₄ × 7H₂O, assay >99%, Chem Lab NV, Zedelgem, Belgium), sodium alginate (Na-alginate, Sigma-Aldrich, viscosity of 2% solution at 25°C: ~250 cps), HCl (37% Carlo Erba, Barcelona), ammonium hydroxide (NH₄OH, 30% for analysis, Carlo Erba), and ultrapure water (conductivity of ~1 μS/cm) prepared with an SG ultrapure water system were used for the synthesis of the MNPs.

Synthesis of Condensed–Clustered MIONs

For the synthesis of the MIONs, we followed the protocol presented in our earlier study (Zoppellaro et al., 2014), which is quoted here for the convenience of the reader: Briefly, alkaline precipitation of MIONs was performed from a single ferrous precursor of Fe₂SO₄ × 7H₂O in the presence of sodium alginate at 50°C. 300 mg of alginate was dissolved in deionized H₂O (60 mL). Then NH₃ (4 mL, 30%) was added to the solution followed by 1,440 mg of FeSO₄ × 7H₂O (in 20 mL of H₂O containing 60 μL of 37% HCl). The mixture was heated at 50°C under magnetic stirring for 80 min. The final product (denoted as MagAlg) was purified and fractionated by centrifugation. The resulting solution used for the measurements had a concentration of 2.5 mg/mL in Fe₂O₃.

Physicochemical Characterization of MIONs

The morphology of the synthesized nanoparticles was investigated by transmission electron microscopy (TEM), wherein samples were prepared by casting a droplet of a dilute aqueous suspension of nanoparticles (0.01% w/v in Fe2O3) on copper grids coated by a Formvar carbon film. The images were obtained by a JEOL, JEM-2100 instrument operating at 200 kV. The determination of the hydrodynamic diameter (D_h) of nanoparticles dispersed in deionized H₂O was performed with a ZetaSizer Nano series Nano-ZS (Malvern Instruments Ltd., Malvern, UK) equipped with a He–Ne laser beam at a wavelength of 633 nm and a fixed backscattering angle of 173°. The concentration of the measured colloids was 0.0125% w/v (g/100 mL) in Fe₂O₃. The zeta potential of the nanoparticles was assessed with the same instrument as the average of 100 runs with the phase analysis light scattering (PALS) mode, after equilibration at 25°C.

Hyperthermia Experimental Setup

Figure 1 shows our setup used for hyperthermia experiments which are composed of the following devices:

I. A custom-designed High Frequency Resonator Unit (KEL, S. Roudis Company, Greece).

II. Matching ceramic capacitors of high voltage.

III. Air-cooled copper excitation coil.

IV. TDS 1002 Oscilloscope (Tektronix, 60 MHz-1 GS/s).

V. Alcohol thermometers, one with 20–120°F range (H-B Durac Plus Pocket Liquid-in-Glass Thermometer) and another with 20–100°C range.

VI. MNPs solution inside a glass vial (our sample).

VII. Detection coil.

FIGURE 1

Figure 1. Experimental setup. (A) Schematic and (B) photograph showing the whole setup and (C) photograph showing the sample surrounded by the detection coil and two thermometers.

The Resonator Unit was connected to the RLC circuit which was formed by the resistance and the inductance of the excitation coil together with the capacitance of the capacitor. The circuit was brought to resonance to get the maximum current to the coil and thus a maximum magnetic field. To achieve a broad range of resonance frequencies, the matching capacitor had the following preset values as summarized in Table 2, which when they were combined with the inductance 3.27 ± 0.04 μH of the excitation coil, resulted in the resonance frequencies in the range of 400 to 1075 kHz. The excitation coil of length 3.9 cm was composed of 8 turns each with a diameter of 4.2 cm and it was made of copper wire of 1.05 mm diameter integrated with a cooling fin in order to be easily air-cooled by a nearby fan. In all experiments, the voltage of the resonator was adjusted so as to have a constant magnetic field of 3.0 ± 0.1 mT, which was measured indirectly by the induced voltage of a single-turn detection coil, since the high frequencies produce enough high voltages to be recorded on the oscilloscope.

TABLE 2

Table 2. Capacitance preset values.

Two different alcohol thermometers were used for the temperature measurements, one of which was directly immersed in the sample solution to record hyperthermia phenomena and the other to record the air temperature inside the detection coil, in order to ensure that temperature rises in the first coil were emerging from the solution itself and not the coil self-heating. The presence of high-frequency magnetic fields inside the detection coil makes it impossible to use conventional thermometers such as thermocouples or resistance temperature detectors, since they contain metals that will develop induced voltages with corresponding reading errors. Thus, the traditional alcohol thermometers were used and their values were read with the help of a magnifier in order to get more precise readings.

Experimental Procedure

The aim of this study was to record temperature rises in the MNP solutions at different frequencies and at different exposure times, in order to observe the effect of the exciting field frequency on the hyperthermia phenomenon. In order to achieve this task, we followed the steps below:

Initial steps

• The sample, which has the form of a solution in a sealed glass vial, was removed from the refrigerator where it was kept at a low temperature of 5°C so as to be chemically inert.

• The sealed vial was placed in an ultrasonic bath to homogenize and eliminate the agglomerations which were sometimes created during measurements. Magnetic particles tended to accumulate together due to their mutual magnetic attraction to each other.

• Following the ultrasonication, the vial was placed at the center of the excitation coil and one of the thermometers was brought into contact with the solution through a snag hole on the vial lid.

• The second thermometer was held by a clamp so as to have its measuring tip inside the excitation coil but not in contact with the glass vial.

Repeating steps

• The matching capacitance was set to an appropriate value so as to achieve the desired frequency.

• Enough time was given to the sample (30 min) with no AC field present, to be brought to a thermal equilibrium with its environment. At this point, its initial temperature θ₀ was recorded.

• The resonator was then turned on and its output voltage was adjusted so as to have a value of an AC magnetic field equal to 3.0±0.1 mT, according to the oscilloscope reading. This happened when the timer was set to zero.

• The temperatures θ and θ_air of the two thermometers (sample and air correspondingly) were recorded every minute for a total period of 10 min.

• The resonator was then turned off at t = 10 min and the vial was shaken by hand, without removing the thermometer, to avoid agglomeration and to have a homogeneous solution without precipitations.

• The last five steps were repeated with a new frequency.

Results and Discussion

The MNPs used herein (coded as MagAlg) have been studied and characterized in a previous study, where their physicochemical and magnetic properties are described in detail (Zoppellaro et al., 2014). The basic physicochemical characterization was conducted for the present study, on new and freshly synthesized MagAlg samples. As shown in Figures 2a,d, the TEM micrographs revealed the morphology of the densely packed MNPs, in which the individual magnetic nanocrystals, having dimensions in the range of 8–13 nm, aggregate together in a way to form larger clusters. Figure 2b shows the selected area electron diffraction (SAED) pattern recorded for the MagAlg assembly. The diffraction rings are consistent with the Miller indexes known for the g-Fe₂O₃ phase (inverse spinel, PDF chart 00-039-1346), falling at [220] (2.95 Å), [311] (2.52 Å), [400] (2.09 Å), [422] (1.70 Å), [511] (1.61 Å), and [440] (1.48 Å). In addition, the high-resolution TEM images (HR-TEM) of MagAlg (Figures 2c,e) show the appearance of crystalline fringes in the condensed cluster nanoparticles (Figure 2c, the arrows indicate the spacing corresponding to the [311] plane, d = 2.52 Å). Furthermore, the large areas of the clustered magnetic material form crystallographically aligned nanocrystals. The results from Dynamic Light Scattering (DLS) and electrokinetic measurements are given in Figures 2f,g. The MagAlg nanoparticles exhibit an average size (D_h) of 93 nm and the zeta potential value of −40 mV, confirming the absence of much larger aggregates when dispersed in deionized H₂O and ensuring colloidal stability of this system during the magnetic hyperthermia measurements. The magnetic behavior of MagAlg, in powder form, at 300 K is given in Figure 2h, which describes the variation of the magnetic susceptibility (M_s) vs. strength of the applied external field (B). The M_s value reaches 71.11 Am²kg⁻¹ at 7.5 T, fully consistent with the previous results (Zoppellaro et al., 2014). At a much lower field (B = 0.3 T), the M_s value remains large (63.06 Am²kg⁻¹) without the appearance of a coercive field. Taken together, these results translate into the possible implementation of the MagAlg system in hyperthermia treatments. It is recognized, however, that thorough in-vitro and in-vivo studies are required to establish the biocompatibility/safety of the MagAlg nanoparticles for any potential biomedical applications.

FIGURE 2

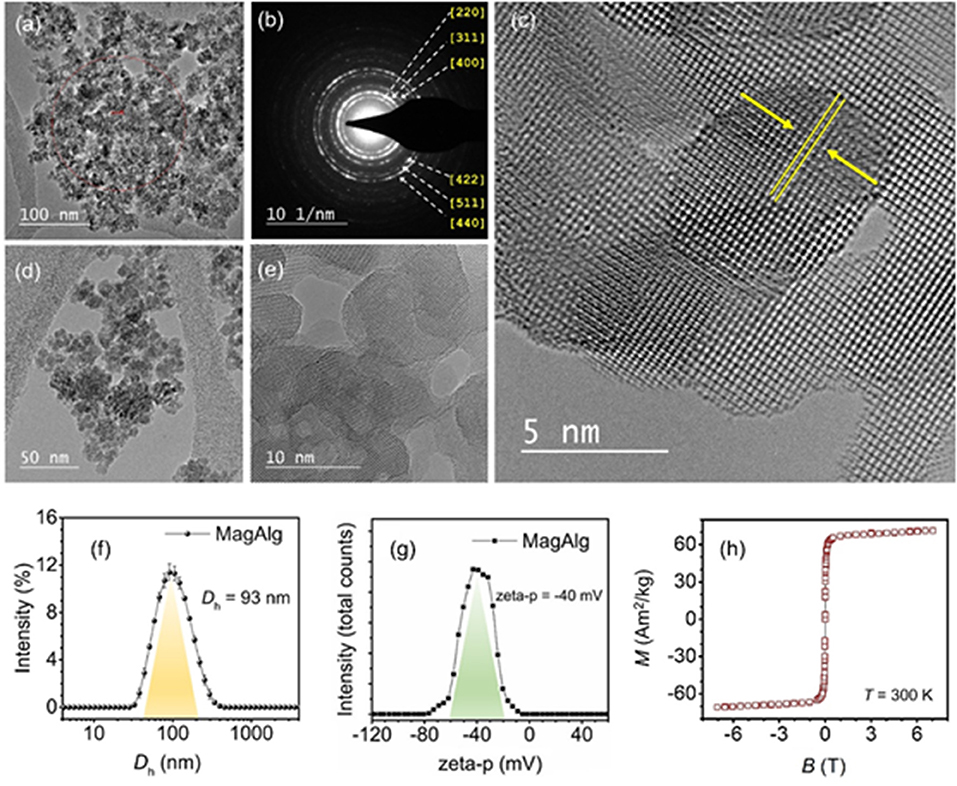
Figure 2. (a–e) HR-TEM micrographs of the MagAlg MNPs. (b) shows the SAED pattern, with diffraction rings indexed for inverse spinel iron oxide (maghemite phase). (c) the crystalline planes, [311], are highlighted by arrows. (f) shows the intensity distributions of the mean hydrodynamic diameter and (g) the zeta potential in water of the MagAlg nanoparticles. (h) shows the saturation magnetization (Ms) vs. applied field (B) for MagAlg recorded at T = 300 K.

Concerning the calorimetric measurements of this study, Figure 3 shows the Δθ₁₀ = θ(10) − θ(0) data, where θ(10) is the final and θ(0) is the initial temperature for the 10-min interval, for the range of frequencies of 400 to 1075 kHz that our resonator was able to cover. The strength of the magnetic field was kept fixed at 3 mT (2.4 kA/m). The top data correspond to the MIONs solution temperature and the bottom to the air temperature inside the coil. It is noted from this graph that Δθ₁₀ for MNPs increases roughly linearly with the frequency, while the air temperature is practically constant. In fact, the Δθ₁₀ data are fitted better to a second-degree polynomial with an intercept at zero frequency equal to 1.4°C which is within the error range in the graph so it can be assumed as zero, as expected for a zero frequency field (DC field). Upon judging the air data, it is concluded that the high-frequency AC current does not heat up the coil and subsequently the air inside it (remember that the coil is air-cooled externally by the help of its fins) and that any significant rise in the temperature in the graph is entirely due to the hyperthermia of the MIONs solution. Similar experiments performed in our lab with water replacing the MIONs solution (data not shown) confirm this conclusion as there were no temperature changes recorded by both thermometers.

FIGURE 3

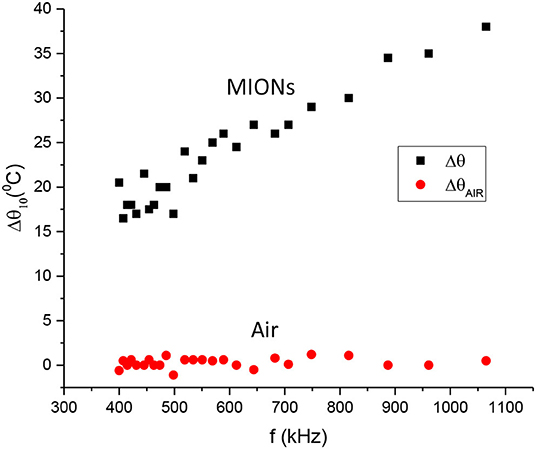
Figure 3. Temperature change. Δθ₁₀ = θ(10) − θ(0) between the final and the initial temperatures for the 10-min interval vs. frequency. Top dataset: MIONs solution. Bottom dataset: Air inside the coil.

To examine the time dependence of the hyperthermia effect, we plotted in Figure 4 the Δθ = θ(t) − θ(0) data vs. time for different frequencies in the range of 400 to 1075 kHz. It is obvious from this graph that Δθ increases with both time and frequency. In particular, Δθ seems to achieve saturation during the time interval of 10 min in our experiment. This is typical with heating experiments in which the system always reaches a time-standing condition where the temperature no longer changes with time. It will be shown in the next subsection that the Δθ(t) curve has an exponential dependence from which the important parameters of the solution, such as the heat power and the saturation temperature, can be extracted.

FIGURE 4

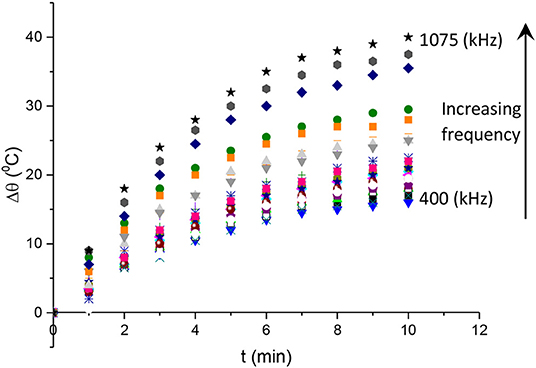
Figure 4. Changes in the sample temperatu vs. time with respect to the initial temperature at t = 0min.

Analysis

Let the MNP sample solution have mass m, specific heat c, and a temperature θ which is assumed to be a function of time t. According to Newton's law of cooling, the solution loses heat at a rate of hA(θ − θ₀), where h is the heat transfer coefficient, A the surface area through which the transfer takes place, and θ₀ is the surrounding temperature. Additionally, let a heat source (the hyperthermia) supplying the solution with a heat rate $\stackrel{\bullet }{Q_H}$ (heat per time). Even though this is an internal heat source, it can be assumed as an external source in order to better understand the thermal physics of the system. In this fashion, let the solution exchange an amount dQ of total heat with its surrounding (cooling plus warming) within a time interval dt. Then its heat rate $\frac{dQ}{dt}$ will be equal to the sum of the above two rates, one being negative as it describes heat loss and the other being positive as it describes heat gain:

$\begin{array}{ll}\frac{dQ}{dt}=-hA(\theta -{\theta }_0)+\stackrel{\bullet }{Q_H}& (3)\end{array}$

From the definition of the specific heat c, we have dQ = mcdθ, where dθ is an incremental change of θ upon an incremental exchange of heat dQ. Substituting this expression in Equation 3, it results in a first-order linear differential equation (DE) on θ(t):

$\begin{array}{ll}mc\frac{d\theta }{dt}=-hA(\theta -{\theta }_0)+\stackrel{\bullet }{Q_H}& (4)\end{array}$

This DE can be easily solved for Δθ(t) = θ(t) − θ₀ as

$\begin{array}{ll}\Delta \theta (t)=\Delta {\theta }_s\left(1-e^{-kt}\right)& (5)\end{array}$

where

$\begin{array}{ll}\Delta {\theta }_s=\stackrel{\bullet }{Q_H}/hA& (6)\end{array}$

and

$\begin{array}{ll}k=hA/mc& (7)\end{array}$

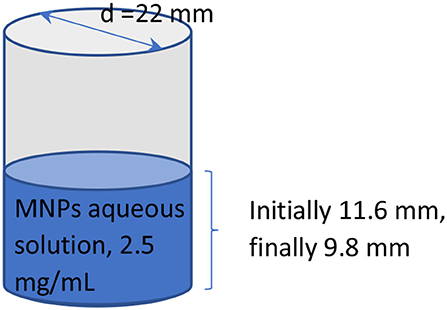
Equation 5 has a classic exponential increase-saturation behavior, like the curves formed by the data shown in Figure 4 and it is an excellent fit for them [the corresponding fit function in Mathematics is known as the empirical Box–Lucas mode, also used in a study by Kumar et al. (2018)]. The fits are shown in Figure 5, where only selected curves for specific frequencies are plotted for clarity. The results for the fitted parameters Δθ_s and k are shown in Table 3 and a plot of k vs. the excitation frequency is presented in Figure 6. From Equation 7, we expected k to be a constant, independent of frequency. Indeed, it seems from Figure 6 that either this parameter is constant with a relatively large error, or it is partially constant, exhibiting a steplike behavior, with the lower frequency values being accumulated around the value $k_1=0.20mi{n}^{-1}$ while the higher frequency values being around $k_2=0.25mi{n}^{-1}$. A possible explanation for this behavior is perhaps the loss of mass that we observed in our experiments, which is shown schematically in Figure 7. Even though our glass vial was sealed during the whole experiment with only a tight hole on its lid for the thermometer to be placed snag through it, we observed that the solution level dropped from the initial height of 11.6 mm to a final height of 9.8 mm. The origin of this loss is not understood, which could be possibly due to a partial evaporation. But even if this is true, it looks strange to have happened only at the narrow frequency range of 620–650 kHz. Anyhow, whatever the source of the mass loss is, it is quite clear from Equation 7 that it directly affects the value of k because it is inversely proportional to the mass m. In fact, the proportion 11.6/9.8 = 1.18 of the aforementioned levels is quite close to the ratio k₂/k₁ = 1.25 of the two-step k values in Figure 6. In the rest of this study, it will be assumed that there are two different solution masses, the initial mass m₁ corresponding to k₁ and the final mass m₂ corresponding to k₂. As our aqueous solution of 2.5 mg/mL is quite dilute, it can be safely assumed that its density is close to the water density of 1.0 g/mL and from it, we can calculate the two masses using the solution volumes as m₁ = 4.4 g and m₂ = 3.7g.

FIGURE 5

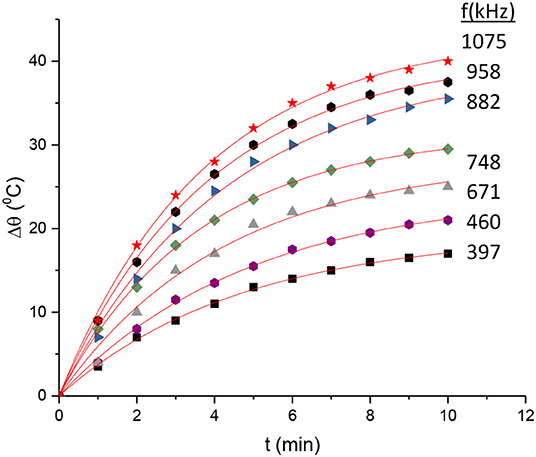
Figure 5. Fitting of Equation 3 in the data of Figure 3.

TABLE 3

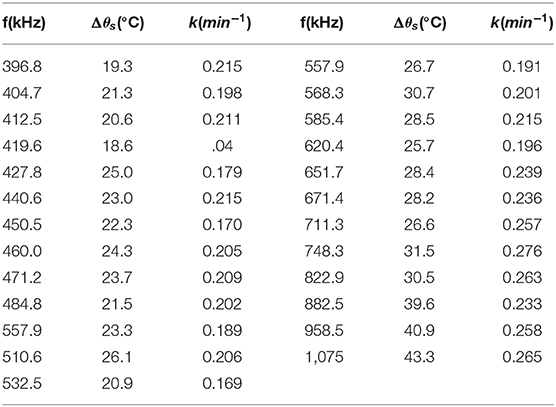
Table 3. Results of the fit of Equation 3 in the data of Figure 3.

FIGURE 6

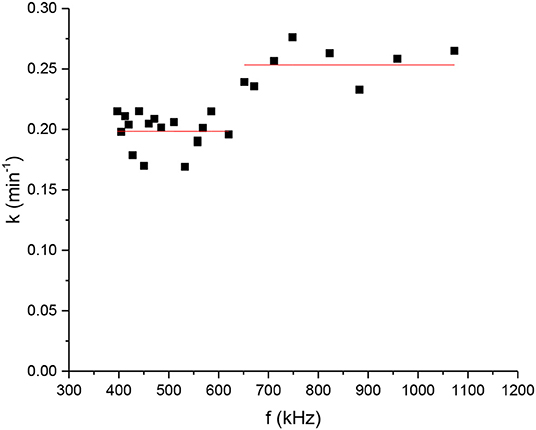
Figure 6. Fitting parameter. of Equation 3n the data of Figure 3 vs. frequency.

FIGURE 7

Figure 7. Schematic of the sample solution.

Equations 6 and 7 can be combined to get the hyperthermia heat produced per unit time $\stackrel{\bullet }{Q_H}$ as follows:

$\begin{array}{ll}\stackrel{\bullet }{Q_H}=\Delta {\theta }_{s}kmc& (8)\end{array}$

Note that from Equation 5 it can be easily seen that the initial slope is equal to kΔθ_s. Thus, Equation 8 is in agreement with Equation 1 above. The only thing missing to convert $\stackrel{\bullet }{Q_H}$ to SLP is to convert the total solution mass m to the mass fraction μ = m_n/m. This is easily done by using the water density ρ = 1.0 g/mL by denoting μ = m_n/ρv = x/ρ where x is our MNP concentration of 2.5 mg/mL and v is the solution volume. Thus

$\begin{array}{ll}SLP=\frac{\rho }{x}c\Delta {\theta }_{s}k& (9)\end{array}$

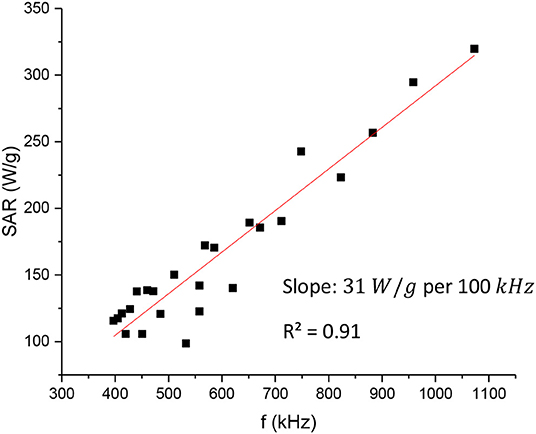
For the specific heat c, the assumption is similar to that we did for the mass calculation, i.e., the dilute solution basically behaves like pure water, and we can take as c the value of the water c = 4.18 J/gK. Our SLP values were calculated with the help of Equation 9 and Table 3 at different frequencies and are shown in Figure 8 in Watts/g units (the minutes in our calculations have been converted to seconds). We concluded that the data of Figure 3 fit better to a quadratic function of the frequency rather than a linear one. However, the difference is rather small and for the purpose of simplicity and calibration, it can be assumed that the data points of Figure 8 are approximately lying on a straight line (the R² value is close to 0.91, indicating a fair linear fit), and get for the slope a value of 0.31 W/g · kHz, i.e., an SLP increase of 31 W/g per 100 kHz. Additionally, a power law fit leads to a power exponent of 1.1, and it is not a better fit (R² = 0.85) compared with the linear one. This observed linearity of SLP with frequency is in agreement with the previous studies of the clustered systems at low AMF field strength (Shubitidze et al., 2015) and could be possibly attributed to the inherent strong interparticle interactions in such ensembles. Such strong dipolar interparticle interactions can result in a coupling of Brownian and Néel processes leading to an increasing “effective” relaxation time of the system, as it has been proposed by computational studies (Ilg and Kröger, 2020), thus shifting the resonance of the condensed–clustered systems to lower frequencies (Shubitidze et al., 2015). As summarized in Table 1, the obtained SLP values are within the range of values found in the literature, wherever they are reported. In particular, our SLP increase shown in Figure 8 of about 200W/g in the range of 400 - 1,000 kHz is in agreement with Garaio et al. (2014), Table 1 therein for the low field regime. However, in the study by Garaio et al., the SLP values were derived at higher magnetic fields (~4 times higher) and with more concentrated samples (an order of magnitude higher), highlighting the superior performance of condensed–clustered MIONs employed for the present study compared with non-clustered systems.

FIGURE 8

Figure 8. Hyperthermia heat produced per unit te vs. the excitation frequency.

Conclusions

In the current study, we evaluated the hyperthermia efficiency of condensed–clustered MIONs in a wide frequency range. According to this study, there is a direct relationship the power produced by the condensed–clustered MIONs on. f In particular, the SLP parameter, which is the ratio of the heat power in Watts produced per MNP grams, is linear to a good degree to the frequency with an increase of roughly 30W/g per 100kHz. This linearity can be interpreted in the frame of the inherent strong interparticle interactions in such ensembles, resulting in the coupling of the Brownian and Néel processes, thus shifting the resonance of the condensed–clustered MIONs to lower frequencies away from the ones usually employed for in-vivo magnetic hyperthermia. The recorded SLP values were in the 100 to 300 W/g range of which is in agreement with the previous reports. Nevertheless, the lower magnetic field employed in the present study highlights the enhanced heating efficiency of condensed–clustered MIONs. The produced heat rate ${\stackrel{\bullet }{Q}}_H$ was extracted by a simple thermodynamic analysis where the fit parameters are related to different physical quantities. The temperature vs. time curves show a simple exponential rise–saturation behavior. For the majority of studies reported in the literature, the AC frequency f is usually fixed, as it is hard to produce high magnetic fields at these frequencies. In the present study, we were able to use a 3mT field (2.4kA/m) over a frequency scan of 400 kHz to 1.1 MHz being always within the safety limits as proposed by the Hergt and Dutz criterion of H.f ≤ 5 × 10⁹A/ms for the clinical application of magnetic hyperthermia. Evaluating the heating performance of condensed–clustered MIONs at higher frequencies and low magnetic field amplitudes can provide invaluable information for their potential use as magnetic hyperthermic agents in cases where low magnetic fields or low nanoparticle doses are required for safety reasons.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

DK: experiment design and theoretical model. GS: experiment design and hyperthermia measurements. AK-N: synthesis of nanoparticles and hyperthermia measurements. GZ: synthesis of nanoparticles and characterization of nanoparticles. KS: hyperthermia measurements. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

GZ acknowledges the support from the ERDF project Development of pre-applied research in nanotechnology and biotechnology (No. CZ.02.1.01/0.0/0.0/17_048/0007323). AK-N acknowledges the support from Alexander S. Onassis Public Benefit Foundation (Grant No. GZ 037-1/2015-2016), as well as from the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), under the HFRI PhD Fellowship grant (GA. No. 33, MIS 80198). In addition, DK would like to thank Stelios Roudis and K.E.L. Company for the custom design and construction of the RF resonator according to our needs.

References

Andreu, I., and Natividad, E. (2013). Accuracy of available methods for quantifying the heat power generation of nanoparticles for magnetic hyperthermia. Int. J. Hyperther. 29, 739–751. doi: 10.3109/02656736.2013.826825

PubMed Abstract | CrossRef Full Text | Google Scholar

Atkinson, W. J., Brezovich, I. A., and Chakraborty, D. P. (1984). Usable frequencies in hyperthermia with thermal seeds. IEEE Trans. Biomed. Eng. 31, 70–75. doi: 10.1109/TBME.1984.325372

PubMed Abstract | CrossRef Full Text | Google Scholar

Attaluri, A., Kandala, S. K., Zhou, H., Wabler, M., DeWeese, T. L., and Ivkov, R. (2020). Magnetic nanoparticle hyperthermia for treating locally advanced unresectable and borderline resectable pancreatic cancers: the role of tumor size and eddy-current heating. Int. J. Hyperther. 37, 108–119. doi: 10.1080/02656736.2020.1798514

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhardwaj, A., Parekh, K., and Jain, N. (2020). In vitro hyperthermic effect of magnetic fluid on cervical and breast cancer cells. Sci. Rep. 10, 1–13. doi: 10.1038/s41598-020-71552-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhayani, K. R., Rajwade, J. M., and Paknikar, K. M. (2013). Radio frequency induced hyperthermia mediated by dextran stabilized LSMO nanoparticles: in vitro evaluation of heat shock protein response. Nanotechnology 24:015102. doi: 10.1088/0957-4484/24/1/015102

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanco-Andujar, C., Ortega, D., Southern, P., Pankhurst, Q. A., and Thanh, N. T. (2015). High performance multi-core iron oxide nanoparticles for magnetic hyperthermia: microwave synthesis, and the role of core-to-core interactions. Nanoscale 7, 1768–1775. doi: 10.1039/C4NR06239F

PubMed Abstract | CrossRef Full Text | Google Scholar

Boekelheide, Z., Hunagund, S., Hussein, Z. A., Miller, J. T., El-Gendy, A. A., and Hadimani, R. L. (2021). Particle size-dependent magnetic hyperthermia in gadolinium silicide micro- and nano-particles from calorimetry and AC magnetometry. J. Magn. Magnet. Mater. 519:167441. doi: 10.1016/j.jmmm.2020.167441

CrossRef Full Text | Google Scholar

Brizi, D., Fontana, N., Giovannetti, G., Menichetti, L., Cappiello, L., Doumett, S., et al. (2020). A radiating system for low-frequency highly focused hyperthermia with magnetic nanoparticles. IEEE J. Electromagn. RF Microwaves Med. Biol. 4, 109–116. doi: 10.1109/JERM.2019.2945833

CrossRef Full Text | Google Scholar

Connord, V., Mehdaoui, B., Tan, R. P., Carrey, J., and Respaud, M. (2014). An air-cooled Litz wire coil for measuring the high frequency hysteresis loops of magnetic samples - a useful setup for magnetic hyperthermia applications. Rev. Sci. Instrum. 85:093904. doi: 10.1063/1.4895656

PubMed Abstract | CrossRef Full Text | Google Scholar

Coral, D. F., Soto, P. A., Blank, V., Veiga, A., Spinelli, E., Gonzalez, S., et al. (2018). Nanoclusters of crystallographically aligned nanoparticles for magnetic thermotherapy: aqueous ferrofluid, agarose phantoms and: ex vivo melanoma tumour assessment. Nanoscale 10, 21262–21274. doi: 10.1039/C8NR07453D

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, P., Colombo, M., and Prosperi, D. (2019). Recent advances in magnetic fluid hyperthermia for cancer therapy. Colloids Surf B: Biointerf. 174, 42–55. doi: 10.1016/j.colsurfb.2018.10.051

PubMed Abstract | CrossRef Full Text | Google Scholar

De La Presa, P., Luengo, Y., Multigner, M., Costo, R., Morales, M. P., Rivero, G., et al. (2012). Study of heating efficiency as a function of concentration, size, and applied field in γ-Fe2O3 nanoparticles. J. Phys. Chem. C 116, 25602–25610. doi: 10.1021/jp310771p

CrossRef Full Text | Google Scholar

Deatsch, A. E., and Evans, B. A. (2014). Heating efficiency in magnetic nanoparticle hyperthermia. J. Magn. Magnet. Mater. 354, 163–172. doi: 10.1016/j.jmmm.2013.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, Q., Zhang, Y., Zhang, W., Hao, Y., Wang, Y., Zhang, H., et al. (2017). Programmed near-infrared light-responsive drug delivery system for combined magnetic tumor-targeting magnetic resonance imaging and chemo-phototherapy. Acta Biomater. 49, 402–413. doi: 10.1016/j.actbio.2016.11.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortin, J. P., Wilhelm, C., Servais, J., Ménager, C., Bacri, J. C., and Gazeau, F. (2007). Size-sorted anionic iron oxide nanomagnets as colloidal mediators for magnetic hyperthermia. J. Am. Chem. Soc. 129, 2628–2635. doi: 10.1021/ja067457e

PubMed Abstract | CrossRef Full Text | Google Scholar

Garaio, E., Collantes, J. M., Garcia, J. A., Plazaola, F., Mornet, S., Couillaud, F., et al. (2014). Journal of magnetism and magnetic materials a wide-frequency range AC magnetometer to measure the specific absorption rate in nanoparticles for magnetic hyperthermia. J. Magn. Magn. Mater. 368, 432–437. doi: 10.1016/j.jmmm.2013.11.021

CrossRef Full Text | Google Scholar

Hallali, N., Clerc, P., Fourmy, D., Gigoux, V., and Carrey, J. (2016). Influence on cell death of high frequency motion of magnetic nanoparticles during magnetic hyperthermia experiments. Appl. Phys. Lett. 109:032402. doi: 10.1063/1.4958989

CrossRef Full Text | Google Scholar

Hergt, R., and Dutz, S. (2007). Magnetic particle hyperthermia-biophysical limitations of a visionary tumour therapy. J. Magnet. Magnet. Mater. 311, 187–192. doi: 10.1016/j.jmmm.2006.10.1156

CrossRef Full Text | Google Scholar

Hu, X.-L., Kwon, N., Yan, K.-C., Sedgwick, A. C., Chen, G.-R., He, X.-P., et al. (2020). Bio-conjugated advanced materials for targeted disease theranostics. Adv. Funct. Mater. 30:13. doi: 10.1002/adfm.201907906

CrossRef Full Text | Google Scholar

Ilg, P., and Kröger, M. (2020). Dynamics of interacting magnetic nanoparticles: effective behavior from competition between Brownian and Néel relaxation. Phys. Chem. Chem. Phys. 22, 22244–22259. doi: 10.1039/D0CP04377J

PubMed Abstract | CrossRef Full Text | Google Scholar

Kallumadil, M., Tada, M., Nakagawa, T., Abe, M., Southern, P., and Pankhurst, Q. A. (2009). Suitability of commercial colloids for magnetic hyperthermia. J. Magn. Magn. Mater. 321, 1509–1513. doi: 10.1016/j.jmmm.2009.02.075

CrossRef Full Text | Google Scholar

Khan, A. S., Nasir, M. F., Khan, M. T., Murtaza, A., and Hamayun, M. A. (2021). Study of structural, magnetic and radio frequency heating aptitudes of pure and (Fe-III) doped manganite (La1-x SrxMnO3) and their incorporation with Sodium Poly-Styrene Sulfonate (PSS) for magnetic hyperthermia applications. Phys. B Condens. Matter. 600:412627. doi: 10.1016/j.physb.2020.412627

CrossRef Full Text | Google Scholar

Kostopoulou, A., Brintakis, K., Vasilakaki, M., Trohidou, K. N., Douvalis, A. P., Lascialfari, A., et al. (2014). Assembly-mediated interplay of dipolar interactions and surface spin disorder in colloidal maghemite nanoclusters. Nanoscale 6, 3764–3776. doi: 10.1039/C3NR06103E

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozissnik, B., Bohorquez, A. C., Dobson, J., and Rinaldi, C. (2013). Magnetic fluid hyperthermia: advances, challenges, and opportunity. Int. J. Hyperther. 29, 706–714. doi: 10.3109/02656736.2013.837200

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnan, K. M., Pakhomov, A. B., Bao, Y., Blomqvist, P., Chun, Y., Gonzales, M., et al. (2006). Nanomagnetism and spin electronics: materials, microstructure and novel properties. J. Mater. Sci. 41, 793–815. doi: 10.1007/s10853-006-6564-1

CrossRef Full Text | Google Scholar

Kumar, R., Chauhan, A., Jha, S. K., and Kuanr, B. K. (2018). Localized cancer treatment by radio-frequency hyperthermia using magnetic nanoparticles immobilized on graphene oxide: from novel synthesis to in vitro studies. J. Mater. Chem. B 6, 5385–5399. doi: 10.1039/C8TB01365A

PubMed Abstract | CrossRef Full Text | Google Scholar

Landi, G. T. (2014). Role of dipolar interaction in magnetic hyperthermia. Phys. Rev. B Conden Matter Mater. Phys. 89:014403. doi: 10.1103/PhysRevB.89.014403

CrossRef Full Text | Google Scholar

Lartigue, L., Hugounenq, P., Alloyeau, D., Clarke, S. P., Lévy, M., Bacri, J. C., et al. (2012). Cooperative organization in iron oxide multi-core nanoparticles potentiates their efficiency as heating mediators and MRI contrast agents. ACS Nano 6, 10935–10949. doi: 10.1021/nn304477s

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorkowski, M. E., Atukorale, P. U., Ghaghada, K. B., and Karathanasis, E. (2021). Stimuli-responsive iron oxide nanotheranostics: a versatile and powerful approach for cancer therapy. Adv. Healthcare Mater. 10:e2001044. doi: 10.1002/adhm.202001044

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, R., Kandoi, S., Varadaraj, S., Vijayalakshmi, S., Nanda, A., and Verma, R. S. (2020). Nanotheranostics: a tactic for cancer stem cells prognosis and management. J. Drug Del. Sci. Technol. 55:101457. doi: 10.1016/j.jddst.2019.101457

CrossRef Full Text | Google Scholar

Ortega, D., and Pankhurst, Q. A. (2012). Magnetic hyperthermia. Nanoscience 1, 60–88. doi: 10.1039/9781849734844-00060

CrossRef Full Text | Google Scholar

Périgo, E. A., Hemery, G., Sandre, O., Ortega, D., Garaio, E., Plazaola, F., et al. (2015). Fundamentals and advances in magnetic hyperthermia. Appl. Phys. Rev. 2:041302. doi: 10.1063/1.4935688

CrossRef Full Text | Google Scholar

Puntes, V. F., Gorostiza, P., Aruguete, D. M., Bastus, N. G., and Alivisatos, A. P. (2004). Collective behaviour in two-dimensional cobalt nanoparticle assemblies observed by magnetic force microscopy. Nat. Mater. 3, 263–268. doi: 10.1038/nmat1094

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajan, S., and Sahu, N. K. (2020). Inductive calorimetric assessment of iron oxide nano-octahedrons for magnetic fluid hyperthermia. Colloids Surf. A Physicochem. Eng. Asp. 603:125210. doi: 10.1016/j.colsurfa.2020.125210

CrossRef Full Text | Google Scholar

Revia, R. A., and Zhang, M. (2016). Magnetite nanoparticles for cancer diagnosis, treatment, and treatment monitoring: recent advances. Mater. Today 19, 157–168. doi: 10.1016/j.mattod.2015.08.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosensweig, R. E. (2002). Heating magnetic fluid with alternating magnetic field. J. Magn. Magnet. Mater. 252, 370–374. doi: 10.1016/S0304-8853(02)00706-0

CrossRef Full Text | Google Scholar

Rousseau, A., Tellier, M., Marin, L., Garrow, M., Madelaine, C., Hallali, N., et al. (2021). Influence of medium viscosity on the heating power and the high-frequency magnetic properties of nanobeads containing magnetic nanoparticles. J. Magn. Magn. Mater. 518:167403. doi: 10.1016/j.jmmm.2020.167403

CrossRef Full Text | Google Scholar

Salas, G., Camarero, J., Cabrera, D., Takacs, H., Varela, M., Ludwig, R., et al. (2014). Modulation of magnetic heating via dipolar magnetic interactions in monodisperse and crystalline iron oxide nanoparticles. J. Phys. Chem. C 118, 19985–19994. doi: 10.1021/jp5041234

CrossRef Full Text | Google Scholar

Serantes, D., Simeonidis, K., Angelakeris, M., Chubykalo-Fesenko, O., Marciello, M., del Puerto Morales, M., et al. (2014). Multiplying magnetic hyperthermia response by nanoparticle assembling. J. Phys. Chem. C 118, 5927–5934. doi: 10.1021/jp410717m

CrossRef Full Text | Google Scholar

Shakeri, S., Ashrafizadeh, M., Zarrabi, A., Roghanian, R., Afshar, E. G., Pardakhty, A., et al. (2020). Multifunctional polymeric nanoplatforms for brain diseases diagnosis, therapy and theranostics. Biomedicines 8:13. doi: 10.3390/biomedicines8010013

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaterabadi, Z., Nabiyouni, G., and Soleymani, M. (2020). Correlation between effects of the particle size and magnetic field strength on the magnetic hyperthermia efficiency of dextran-coated magnetite nanoparticles. Mater. Sci. Eng. C 117:111274. doi: 10.1016/j.msec.2020.111274

PubMed Abstract | CrossRef Full Text | Google Scholar

Shubitidze, F., Kekalo, K., Stigliano, R., and Baker, I. (2015). Magnetic nanoparticles with high specific absorption rate of electromagnetic energy at low field strength for hyperthermia therapy. J. Appl. Phys. 117, 1–12. doi: 10.1063/1.4907915

PubMed Abstract | CrossRef Full Text | Google Scholar

Sudame, A., Kandasamy, G., Singh, D. V., Tomy, C., and Maity, D. (2020). Symbiotic thermo-chemotherapy for enhanced HepG2 cancer treatment via magneto-drugs encapsulated polymeric nanocarriers. Colloids Surf. A Physicochem. Eng. Asp. 606:125355. doi: 10.1016/j.colsurfa.2020.125355

CrossRef Full Text | Google Scholar

Xie, J., Lee, S., and Chen, X. (2010). Nanoparticle-based theranostic agents. Adv. Drug Deliv. Rev. 62, 1064–1079. doi: 10.1016/j.addr.2010.07.009

CrossRef Full Text | Google Scholar

Xu, F., Cheng, C., Chen, D. X., and Gu, H. (2012). Magnetite nanocrystal clusters with ultra-high sensitivity in magnetic resonance imaging. ChemPhysChem 13, 336–341. doi: 10.1002/cphc.201100548

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamaminami, T., Ota, S., Trisnanto, S. B., Ishikawa, M., Yamada, T., Yoshida, T., et al. (2021). Power dissipation in magnetic nanoparticles evaluated using the AC susceptibility of their linear and nonlinear responses. J. Magn. Magn. Mater. 517:167401. doi: 10.1016/j.jmmm.2020.167401

CrossRef Full Text | Google Scholar

Yoo, D., Lee, J.-H., Shin, T.-H., and Cheon, J. (2011). Theranostic magnetic nanoparticles. Acc. Chem. Res. 44, 863–874. doi: 10.1021/ar200085c

CrossRef Full Text | Google Scholar

Yoon, T. J., Lee, H., Shao, H., Hilderbrand, S. A., and Weissleder, R. (2011). Multicore assemblies potentiate magnetic properties of biomagnetic nanoparticles. Adv. Mater. 23, 4793–4797. doi: 10.1002/adma.201102948

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Sun, Y., Shen, J., Wei, J., Yu, C., Kong, B., et al. (2014). Iron/iron oxide core/shell nanoparticles for magnetic targeting MRI and near-infrared photothermal therapy. Biomaterials 35, 7470–7478. doi: 10.1016/j.biomaterials.2014.04.063

PubMed Abstract | CrossRef Full Text | Google Scholar

Zoppellaro, G., Kolokithas-Ntoukas, A., Polakova, K., Tucek, J., Zboril, R., Loudos, G., et al. (2014). Theranostics of epitaxially condensed colloidal nanocrystal clusters, through a soft biomineralization route. Chem. Mater. 26, 2062–2074. doi: 10.1021/cm503591z

CrossRef Full Text | Google Scholar