Low-Cycle Fatigue Life Prediction of 10CrNi3MoV Steel and Undermatched Welds by Damage Mechanics Approach

Welding of steel is a technique frequently used in practical engineering applications; however, their mechanical performance is strongly dependent on the physical metallurgical status of the weldments. In the present study, fully reversed, strain-controlled low-cycle fatigue (LCF) tests were conducted on 10CrNi3MoV steel and its undermatched weldments with strain amplitudes varying from Δε = ±0.5 to ±1.2%. Both base metal and weldments exhibited softening behavior at the beginning of the cyclic stage. Numerical investigations of cyclic stress–strain evolutions of the materials have been studied by the cyclic plastic model considering nonlinear hardening. The continuous damage mechanics (CDM) theory based on the experimental hysteresis stress–strain energy concept was employed to illustrate LCF failure, including damage initiation and deterioration. The damage mechanics approach calibrates the material parameters from the measured fatigue life for initiation and growth stages. Afterward, the combination of material cyclic plastic parameters and damage parameters was implemented to predict the LCF life. Good agreement can be observed between the experimental results and the FE results based on the CDM approach. Finally, the damage evolution of the materials under different strain amplitudes by this approach was assessed.

Introduction

High/ultrahigh-strength steel has become an increasing choice for the manufacturing industries of machinery, marine structures, offshore structures, bridge structures, and other engineering facilities with excellent strength-to-self weight ratios and mechanical properties (Miki et al., 2002; Feng and Qian, 2018b; Ahola et al., 2019b; Chung et al., 2020). The integrity of these structures experiencing service cyclic loading under different environmental actions (e.g., wave, heavy traffic, wind, current, and seismic loadings) is directly dependent on the material fatigue properties and structural designs of local details. High-strength steel and its corresponding welded structures undergoing LCF are subjected to large cyclic stresses and strains, which results in local plastic deformation and final fatigue failure, respectively. The elastic–plastic material behavior under LCF conditions is more complicated than that under monotonic loading. Hence, the reliable estimation of the cycle numbers under fatigue loading becomes critical and essential for the design and structural integrity assessment of welded engineering components.

Numerous investigations on the fatigue capability of high-strength steel welded components have been conducted considering different essential thermal and mechanical effects, such as ambient temperature (Feng and Qian, 2018b), welding heat input energy (Chung et al., 2020), and cyclic softening behavior (Tang et al., 2020). For instance, the high-temperature creep rupture life of P92 heat-resistant steel is affected due to the improvement of the microstructure and mechanical properties by the thermomechanical treatment (Li et al., 2013). Meanwhile, the high-temperature strength mechanism of P92 steel transforms from lath and dislocation hardening at the initial service stage into the lath and precipitate hardening with service time increasing (Jin et al., 2020). While the following literature survey has been carried out to assess the fatigue properties of high-strength steel by experimental and numerical simulation approaches for different engineering fields, a series of strain-controlled LCF experiments of high-strength steel S550 under different strains were analyzed based on cyclic plastic theory and CDM (Feng and Qian, 2018a). Zarandi et al. (Zarandi and Skallerud, 2020) investigated the fatigue properties and cyclic plasticity behavior of mooring chain steel grade R4 to assess the plastic dissipation at the pit sites on a corroded mooring chain link. The progress of crack initiation from an existing corrosion pit is further predicted. Considering the combined effect between welding residual stress and ultrasonic impact treatment (UIT) processing of welded joints, the numerical simulations of the residual stress distributions and fatigue crack propagation are conducted to evaluate the fatigue performance of 304 L stainless steel T-welded joints based on fracture mechanics theory (Tang et al., 2020). Some investigations have been conducted for the fatigue properties, and loading capacities of undermatched welded joints, some related assessment criteria for LCF, and high cycle fatigue (HCF) are also established according to notch mechanics theory (Hanji et al., 2011; Saiprasertkit et al., 2012; Hanji et al., 2014). It should be noted that the tensile residual stress is only effective in the loading range of HCF for welded components. However, when fatigue loading is above this range, either during constant amplitude loading within the finite life and LCF range or during variable amplitude loading, thermal stress relief can be dropped, as cyclic plastic deformation will have already eliminated the tensile residual stresses (Sonsino, 2009).

Different sophisticated models based on the stress, strain, energy, or other fatigue failure criteria were proposed to improve the fatigue life prediction accuracy of specimens and components for HCF and LCF. For some typically welded joints or some industries complicated welded components under uniaxial or multiaxial cyclic loading (Lazzarin et al., 2008), the fatigue life assessments based on the elastic mechanics for HCF regime have been investigated by th hotspot stress approach (Hobbacher, 2008), effective notch stress approach, effective traction structural stress approach (Xing et al., 2017), notch stress intensity factor (NSIF) approach (Radaj et al., 2006) and its extended strain energy density (SED) method (Lazzarin et al., 2008), or peak stress method, etc., while fatigue crack readily initiates due to the existence of notches or weld root nonpenetration in welded joints. Thus, the life for welded joints and components is dominated by fatigue crack growth. Further, it illustrates the reliability and popularity of fatigue strength and fatigue life assessments for different failure modes in welded joints (Zhang et al., 2018; Ahola et al., 2019a; Chapetti and Steimbreger, 2019; Liu et al., 2020). The contribution of either fatigue crack initiation or propagation onto the fatigue life is strongly influenced by the material properties and loading conditions. In terms of the LCF regime of material and components, related fatigue indicators are generally focused on the strain and energy fatigue characteristics due to the local plastic deformation. These parameters cannot demonstrate fatigue damage’s evolution with the increases of loading cycles by static mechanical analysis. It is necessary to estimate the LCF life by simulating the plastic response of the material. The famous plastic cyclic model proposed by Armstrong and Frederick is often recommended to calculate strain materials or components to exhibit the multiaxial Bauschinger effect (Armstrong and Frederick, 1966). Further, Chaboche and his coworkers extended this model, considering the nonlinear kinematic hardening rule (Chaboche, 1989). It also effectively expresses three critical parts of a stable hysteresis curve. The model has been widely applied for the fatigue characteristic of plastic deformation under large cyclic loading for different welded joints or components (Song et al., 2018a; Chatziioannou et al., 2019; Ji et al., 2019; Hanji et al., 2020; Hemmesi et al., 2020; Yonezawa et al., 2020).

Material failure of high-strength steel experiences three different stages: softening, stabilization, and damage. The first two stages occur in the first few cycles from the experimental data. With a combination of the cyclic plastic model in the Finite Element (FE) method, CDM has been utilized successfully to estimate the fatigue initiation and the fatigue crack propagation considering the fundamental thermodynamics principles and the progressive damage (Bhattacharya and Ellingwood, 1998; Murakami, 2012; Zarandi and Skallerud, 2020). These CDM approach applications enable us to realize the damage and fracture behavior simulations based on crack nuclear of local microcracks and structural failure. Regarding the CDM theory, Hormozi et al. (Hormozi et al., 2014) conducted the sensitivity analysis of the damage parameters for 9Cr steel at room and elevated temperature to predict fatigue life by nonlinear kinematic softening criterion and the Chaboche constitutive equation. Even though the Chaboche model is widely used in fatigue behaviors of traffic or civil steel welded joints and structures, their applicability in marine structures remains unclear, considering the material strength mismatch by the CDM approach.

The article aims to conduct a fatigue assessment approach capable of considering the yield stress effect and cyclic plasticity effect, of determining the difference of fatigue life for different materials in welded joints by both experimental investigation and numerical analysis. The CDM approach combining the cyclic plasticity model is utilized to evaluate the LCF life for 10CrNi3MoV steel and its undermatched weldments directly. It is determined based on the criteria utilizing physical quantities by stress, strain, and energy definitions. The stress vs. mechanical strain hysteresis loops of the first cycle and stabilized state, the evolution of the maximum and minimum stress cycle, and the accumulated inelastic strain energy density per cycle at different stress ratios are extracted. Furthermore, cyclic plasticity characterizations of base metal and weldments for fatigue damage assessment are calibrated by extracted experimental data. A directed cyclic analysis based on the accumulated inelastic hysteretic strain energy per cycle is conducted to calculate the damage accumulation from the initiation stage and evolution stage under the combination of cyclic plasticity variation. According to the fatigue damage calculation, the LCF life for base metal and undermatched weldments is estimated. Finally, the experimental LCF data can calibrate fatigue life prediction accuracy by the verified damage material parameters.

Experimental

Material and Fatigue Test

The material used in this study was 10CrNi3MoV high-strength steel, which was received in the quenched and tempered condition. Butt-welded joints with a V-groove were fabricated by Single Pulsed Gas Metal Arc Welding (SP-GMAW) processing for evenmatched configuration using corresponding wire (wire diameter Φ 1.2 mm). In contrast, Gas Metal Arc Welding (GMAW) processing was performed for undermatched welded joints by lower strength filler metal (wire diameter Φ 1.2 mm). The chemical compositions of the evenmatched and undermatched filler material are presented in Table 1.

TABLE 1

TABLE 1. Nominal chemical composition of the base metal and the undermatched weldments.

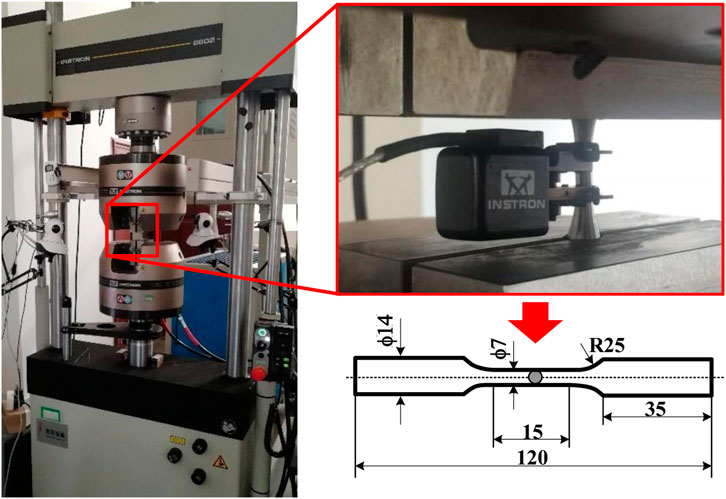
The LCF tests were performed using the Instron-8802 hydraulic servo system machine, presented in Figure 1. The fatigue specimens are cut by wire cutting machine and manufactured by general mechanical equipment, and the detailed dimensions were given in Figure 1. It should be noticed that the strain gauge system kept running and collecting data throughout the cycling tests. To eliminate the potential residual stress in welded specimens, all of the samples, including the base metal specimens, were subjected to heat treatment at 550°C for 4 h and cooling in the furnace. Figure 2 presents the electron backscattered diffraction (EBSD) maps, including normal direction–inverse pole figure (IPF-Z) maps, grain orientation spread (GOS, 0–6°) maps, and kernel average misorientation (KAM, 0–5°) maps, of the as-received base metal and its undermatched weldments. The GOS and KAM values can be used to indicate the local residual plastic deformation (higher GOS and KAM values indicate higher strain level) as they count the local crystallographic misorientation in the grains. Therefore, these EBSD maps can visualize strain distribution in the scanned area (Liu et al., 2019). The base metal shows a dominating martensitic structure with a large number of laths and a relatively higher residual strain level, while the weldment has a more equiaxed grain shape and a relatively lower level of deformation. The small micron-sized blue grains in Figure 2E show a misorientation-free (deformation-free) structure, as can also be read from Figure 2F, which might be the embryos for recrystallization during the welding procedure.

FIGURE 1

FIGURE 1. Overview of the Instron-8802 fatigue test system and detailed specimen sizes.

FIGURE 2

FIGURE 2. EBSD maps of the 10CrNi3MoV steel and its undermatched weldment: (A–C) as-received base metal and (D–F) undermatched weldment. (A and D) IPF-Z maps, and (B and E) GOS maps, and (C and F) KAM maps. The black lines indicate high-angle grain boundaries (>15°). The blue lines indicate the low-angle grain boundaries (2–15°) (digital version in color).

Mechanical Properties and Fatigue Data

The basic mechanical properties have been given by Song et al. (2018b). Figure 3 shows the monotonic (blue dash lines) and uniaxial cyclic (red solid lines) stress–strain curves under symmetrical strain-controlled cycling conditions. It can be seen that the ratio of 0.2% offset yield strength to ultimate tensile strength is higher than 0.9 for 10CrNi3MoV steel and the undermatched welds. From the stress–strain comparison of monotonic and cyclic loadings, both of them display cyclic softening behavior. For the base metal, it exhibits prominent softening characteristics under each strain ratio. While the undermatched welds reveal significant softening behavior below 0.8% strain amplitudes, in over 0.8% strain amplitudes, the monotonic and uniaxial cyclic stress–strain values seem to be consistent. Therefore, the monotonic and cyclic mechanical match ratios of base metal and weldments exist discrepancy. Table 2 summarized the cyclic strain components and stress results of fatigue tests carried out with smooth specimens for both materials under strain-controlled conditions (Song et al., 2018b).

FIGURE 3

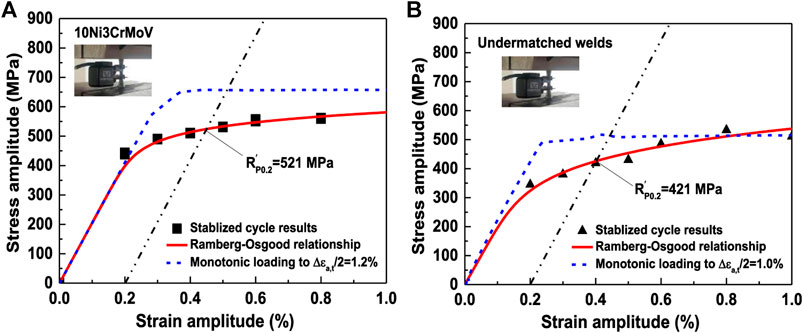
FIGURE 3. Comparison between monotonic stress–strain curves and cyclic R–O relationship curves in the middle of fatigue life. (A) 10CrNi3MoV steel and (B) undermatched weldments.

TABLE 2

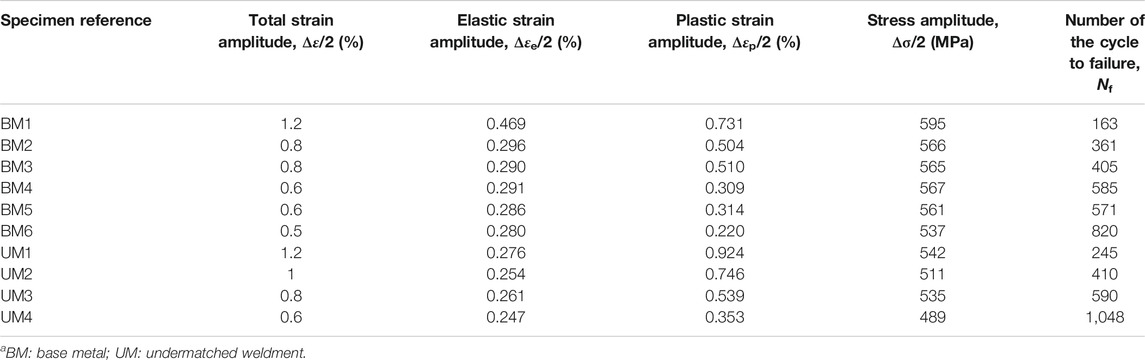
TABLE 2. Summary of LCF test results (Song et al., 2018b).

Theoretical Background

Nonlinear Kinematic Hardening Models

The Lemaitre-Chaboche model (Chaboche, 1989) is often used to characterize the nonlinear mixed kinematic hardening behavior. As implemented in the ABAQUS FE code, the isotropic and nonlinear kinematic parts of a cyclic hardening model describe the yield surface’s translation in the stress space by the backstress tensor α. The function of the yield surface can be expressed as follows:

$f\left(\sigma -\alpha \right)={\sigma }^0,(1)$

where σ is the stress tensor, σ⁰ is the radius of the yield surface, and $f\left(\sigma -\alpha \right)$ can be shown as follows:

$f\left(\sigma -\alpha \right)=\sqrt{\frac{3}{2}\left(S-{\alpha }^{dev}\right):\left(S-{\alpha }^{dev}\right)},(2)$

here α^dev strands for the deviatoric part of the back stress tensor and S is the deviatoric stress tensor.

On the other hand, the kinematic hardening components can be defined by combining a purely kinematic term and a relaxation term, which is shown as the following equation:

$\alpha ={\displaystyle {\sum }_i\left[C_i\frac{1}{{\sigma }^0}{\left(\sigma -\alpha \right)}^{{\epsilon }^p}-{\gamma }_i{\alpha }^{{\epsilon }^p}\right]},(3)$

where C_i and γ_i are the material constants obtained from the cyclic experimental data, C_i presents the initial kinematic hardening modulus, and γ_i determines the variation rate of kinematic hardening modulus with the increasing plastic deformation. ε^p is the equivalent plastic strain rate. The deviatoric term α expresses the deviatoric part depending on the material hardening behavior. i is the number of decomposed A-F rules utilized, which is set to five in this study. The effective cumulative plastic strain ε^p can define the isotropic hardening components:

${\sigma }_0=\sigma {|}_0+Q_{\inf }\left(1-\exp \left(-b\cdot {\epsilon }^p\right)\right),(4)$

where $\sigma {|}_0$ is the yield stress at the zero plastic strain, $Q_{\inf }$ denotes the maximum change in the size of the yield surface, and b refers to the rate at which the size of the yield surface changes as plastic straining evolution. These two material parameters well describe the nonuniformity of the isotropic hardening through loading cycles of the material. The Bauschinger effect, which is demonstrated with the yield surface transition, can be illustrated by the backstress tensor under cyclic loading.

According to the kinematic hardening theory, the corresponding parameters are fitted from the cyclic stress–strain curves of base metal and undermatched welds from the initial cycle to the 0.5N_f cycle, which is given in Table 2. It should be noted that these plastic parameters can be used to characterize the different strain amplitudes in the range of strain amplitudes from 0.2 to 1.2%. This model has robust advantages of calculating the cyclic material behavior by the fitting parameters, which can be derived from uniaxial cyclic test data. However, some limitations of the kinematic hardening model have been mentioned for the residual stress simulation (Smith et al., 2019).

Although the isotropic hardening parameters Q_inf and b are fitted from a single stress–strain curve, they are applied for all strain ranges. There are no significant cyclic hardening variations with the changing of strain ranges for structural steels; however, it can simulate the cyclic plastic behavior representing the real strain ranges. On the other hand, the kinematic parameters C_i and γ_i are obtained from a single cyclic response of the material presented in Table 3. It cannot characterize the monotonic and cyclic response simultaneously. Thus, these parameters can only be used to fit the cyclic mechanical behaviors of the materials.

TABLE 3

TABLE 3. Chaboche nonlinear kinematic hardening model parameters of BM and UM.

Damage Accumulation

For LCF, the damage development initiates once the incubation period has been reached. It means the materials will be subjected to cyclic plastic strain when the nominal loading levels exceed the yield stress. However, it is difficult to measure the material damage under cyclic tests by nondestructive direct measurements. From the perspective of phenomenological observation, the damage measurement technology proposed by Lemaitre and Desmorat (Lemaitre, 1985; Lemaitre and Desmorat, 2005) can be employed to quantify the isotropic damage based on the relationship between elasticity, plasticity, and damage, which is expressed in an inverse form as follows:

$D_i=1-\frac{E_i}{E^{\prime }},(5)$

$D_i=1-\frac{{\sigma }_i}{{\sigma }^{\prime }}.(6)$

These equations can be demonstrated by Eq. 5, 6 in Figure 4. The damage evolution of material under cyclic loading is measured by Young’s modulus variation. Thus, the D_i represents the ith cycle, the E′ is the initial Young’s modulus, and E_i is the apparent Young’s modulus of the ith cycle. Considering the damage from the effective stress, the σ is the damaged stress tensor, and the σ′ strands for the initial stress tensor from the stabilized cycle. In our study, the damage expresses are based on Young’s modulus evolution.

FIGURE 4

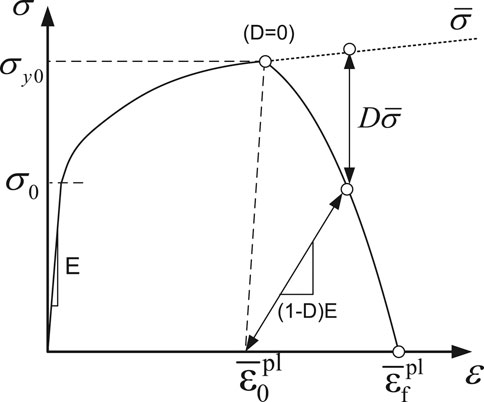
FIGURE 4. Damage evolution during material failure (Hormozi et al., 2014).

Regarding the determination of fatigue damage by strain energy density parameter, the material energy at any moment during the strain-controlled cycling period can be expressed as follows, which is similar to Eq. 5, 6:

$D_i=1-\frac{\Delta w_i}{\Delta w_0},(7)$

where Δw₀ is the hysteresis energy density after cyclic softening and Δw_i is the apparent hysteresis energy density of the ith cycle.

Damage Initiation

The damage initiation for ductile materials under LCF loading is calculated by the cyclic hysteresis energy, which is shown as follows:

$N_0=c_1\cdot \Delta w_0^{c_2},(8)$

where N₀ refers to the number of cycles of the damage initiation and Δw₀ is the hysteresis energy density of the stabilized cycle. c₁ and c₂ represent the material constants, which are fitted from the experimental tests. The following equation can express the log relationship between energy density and fatigue life.

$Log\left(N_0\right)=Log\left(c_1\cdot \Delta w_0^{c_2}\right)=c_{2}Log\left(\Delta w\right)+Log\left(c_1\right).(9)$

The linear expression between the accumulated inelastic hysteresis energy density and damage initiation for each cycle is given in Eq. 9. N₀ stands for the numbers of the cycle before hysteresis loop stabilization according to experimental data. For the continuous cyclic softening materials, the fatigue damage initiation life is challenging to determine. However, the final failure criteria can be identified by the maximum load drop of 10%, according to BS7279:2006. The 5% drop of the maximum load during the fatigue test is defined as the fatigue initiation life N₀. The values of N₀ used to derive c₁, c₂ will not affect the damage prediction for the different strain ranges as the derivation of Δw is based on the values of stabilized cycles specified.

Damage Evolution

Damage evolution based on the plastic hysteresis energy density of the stabilized cycle is determined with accommodating material degradation after the stage of damage initiation. The rate of the damage, D of one cycle, can be defined as

$\frac{dD}{dN}=\frac{c_3\cdot \Delta w^{c_4}}{L},(10)$

where Δw is the average of the plastic hysteresis energy density of the stabilized cycle, c_3, and c₄ represent the material constants, and L is the characteristic length associated with an integration point. Like the fatigue damage initiation, the log rule is suitable for determining the material damage parameters c₃ and c₄ from experimental data, as follows. The results can be used to compare the damage accumulation during the element degradation.

$Log\left(N_e\right)=-c_{4}Log\left(\Delta w\right)+Log\left(\frac{L}{c_3}\Delta D\right).(11)$

The determination of parameters c₃ and c₄ will be provided from the fitting curves between damage evolution and the accumulated inelastic hysteresis energy for each cycle (∆N vs. ∆w). Therefore, the final fatigue life can be demonstrated by the following:

$N_f=N_i+N_e=c_1\cdot \Delta w_0^{c_2}+\frac{L}{c_3\cdot \Delta w^{c_4}}\cdot \frac{1}{1-c_4}.(12)$

Equation 12 can be used to estimate the total fatigue life when the material parameters are given by the combination of fatigue damage initiation and evolution. These four damage-related parameters can be fitted from experimental data under different stress ratios.

FE Results and Discussion

The Geometry of the FE Model

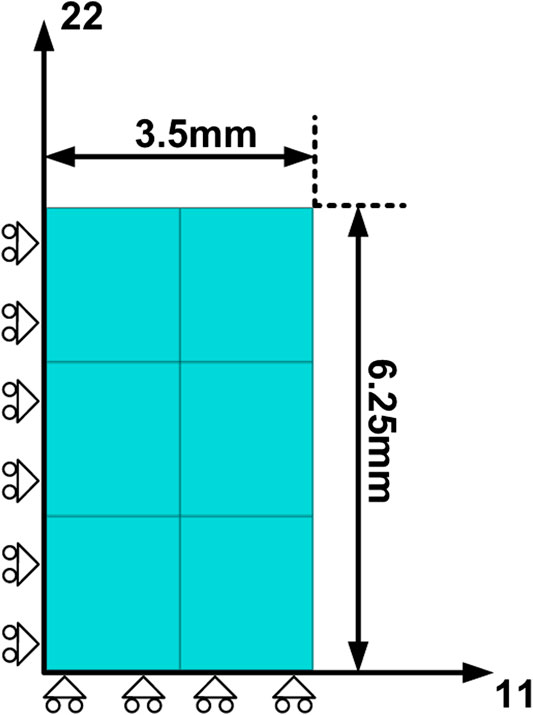
To predict the material total fatigue life, we adopt the continuum mechanics theory proposed by Darveau (Darveau, 2002) and Lau et al. (Lau et al., 2002) for the LCF calculation in ABAQUS. The FE model of a cyclic tensile bar is established in this software. The direct cyclic analysis setting in the software is used to realize the cycle-by-cycle iteration. A 2D axisymmetric model with a 3.5 mm radius and 6.25 mm height was meshed using CAX4R elements to calculate damage results, which is shown in Figure 5. The displacement-controlled loading boundary is applied to the top part of the model corresponding to the mechanical strain range. The asymmetrical boundary of the one-quarter model is also shown in Figure 5.

FIGURE 5

FIGURE 5. FE model for damage imitation and evolution in ABAQUS.

Cyclic Hardening and Stabilization

The plasticity parameters for base metal and undermatched weldments are obtained by the least square method in Table 3. These parameters are validated in terms of hysteresis loops at the first cycle. Figure 6 shows the comparison between experimental data and simulation results of fully reversed strain cyclic tests for base metal and undermatched welds under uniaxial fatigue loading. The calculation results of the first hysteresis cyclic stress–strain curves and the peak stress evolution curves at the strain amplitudes of 0.6 and 0.8% agree with the experimental results perfectly. It indicates that the Chaboche plastic model has an excellent prediction capability for the cyclic hardening behavior for uniaxial fatigue loading. Furthermore, the experimental data and calculation results of maximum/minimum stress relaxation curves for the first 100 cycles are given in Figure 6. It can be seen that a good agreement between the experiments and the simulations has been achieved. The maximum stress drops slowly and keeps stable during stress relaxation, which demonstrates stable cyclic softening behavior.

FIGURE 6

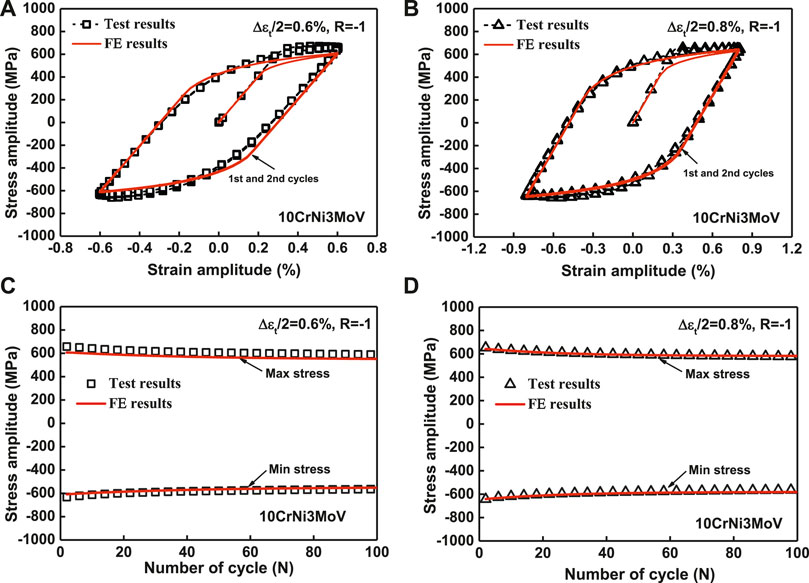
FIGURE 6. Experimental and simulation comparisons of the first and second cyclic hysteresis loops and max–min stress evolution for 10CrNi3MoV steel. (A) Hysteresis loops under ∆ε_t/2 = 0.6%, (B) hysteresis loops under ∆ε_t/2 = 0.8%, (C) max–min stress evolution under ∆ε_t/2 = 0.6%, and (D) max–min stress evolution under ∆ε_t/2 = 0.8%.

Similarly, the comparison results between experimental data and simulation results regarding hysteresis cyclic stress–strain curves and stress relaxation curves for undermatched welds demonstrate good agreements under 0.6 and 0.8% strain ratios in Figure 7.

FIGURE 7

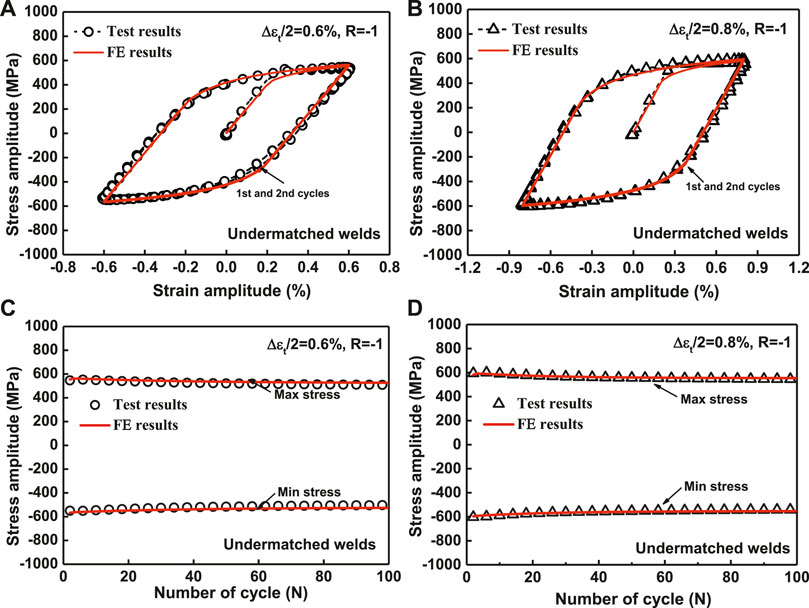
FIGURE 7. Experimental and simulation comparisons of the first and second cyclic hysteresis loops and max–min stress evolution for undermatched welds. (A) Hysteresis loops under ∆ε_t/2 = 0.6%, (B) hysteresis loops under ∆ε_t/2 = 0.8%, (C) max–min stress evolution under ∆ε_t/2 = 0.6%, and (D) max–min stress evolution under ∆ε_t/2 = 0.8%.

For a more explicit illustration of the accuracy of simulation results, the comparison is made between the calculation results and experimental data by stable hysteresis loop at half-life cycle from the strain range from 0.6 to 1.2% for base metal and weldments. The comparison of simulation and experimental results of hysteresis stress–strain curves of base metal and undermatched welds in the stabilization stage is given in Figure 8A,B, respectively. The calculation results exhibit good prediction at different strain amplitudes. Therefore, these plasticity parameters used in the research are calibrated reasonably.

FIGURE 8

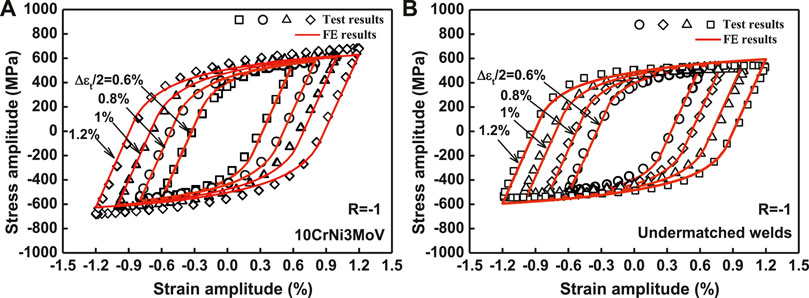
FIGURE 8. Experimental data and simulation results of hysteresis loops at the half-life cycle for specimens. (A) 10CrNi3MoV steel and (B) undermatched welds.

Damage Initiation and Evolution Parameters

The cyclic number of damage initiation and final failure should be defined to predict the LCF life based on the CDM approach. However, the number of cycles for the damage initiation and stabilization cannot be determined in a procedural standard. According to previous references, a quotient curve method was used to estimate the number of cycles for the stage of damage initiation and rupture (Rao et al., 1988). Hormozi et al. chose the strain energy density to obtain the damage parameters in cyclic stress–strain curves (Hormozi et al., 2014; Hormozi et al., 2015).

From the analysis of the material, the evolution of stress amplitudes for each cycle demonstrates different patterns. Therefore, various materials may provide different stress evolution response and further give dissimilar stabilized plateau. Before the stabilized cycle, the damage initiation could be estimated by the inelastic strain energy density per cycle (i.e., ∆w vs. N). The parameter ∆w is widely used to describe the damage initiation (Hormozi et al., 2014) and crack propagation (Korsunsky et al., 2007) in strain-controlled LCF investigation. The following equation can define the inelastic strain density (plastic strain energy density):

$\Delta w={\displaystyle {\int }_{{\epsilon }_{ie1}}^{{\epsilon }_{ie2}}{\sigma }_{ij}}d{\epsilon }_{ifie},(13)$

where ${\sigma }_{ij}$ is the stress tensor, ${\epsilon }_{ifie}$ is the inelastic strain tensor, ${\epsilon }_{ie1}$ is the inelastic strain tensor at the beginning of the cycle, and ${\epsilon }_{ie2}$ is the inelastic strain tensor at the end of the cycle. It should be noted that Eq. 13 could be employed to derive the inelastic strain by subtracting the strain results from the LCF experimental data. The inelastic strain is equivalent to the plastic strain for the LCF tests if other strains (i.e., creep strain) are not considered. Thus, the relationship of inelastic strain and plastic strain can be expressed as follows:

${\epsilon }_{ie}={\epsilon }_p.(14)$

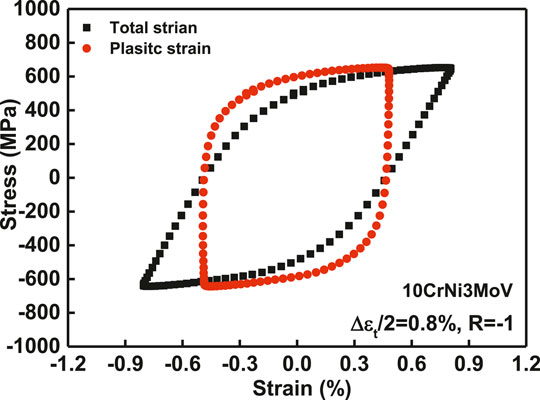
The inelastic strain energy density is equivalent to the plastic strain energy density in this study. The relationships among cyclic stress, total strain, and plastic strain in the stabilized cyclic state can be demonstrated typically under 0.8% total strain amplitudes in Figure 9. Finally, the value of ∆w is equivalent to the critical area of the hysteresis loop by the red circle.

FIGURE 9

FIGURE 9. Stabilized hysteresis loops for the LCF test under 0.8% total strain amplitude.

The evolution of plastic strain energy density with per cycle (denoted as ∆w₀) of LCF tests under 0.6% strain amplitudes is illustrated in Figure 10A. It can be seen that the plastic strain energy density per cycle seems to be the same pattern as the stress response evolution plots. In Figure 10, the ∆w₀ line can be divided into three stages according to the material behavior. The first is the initial cycle stage that the ∆w₀ decreases with the increase of cycle due to the cyclic softening behavior. After the initial stage, the plastic strain energy density values reach a stable response since the energy dissipated per cycle keeps constant. In the last stage, the ∆w₀ starts falling once the damage is initiated. No detailed rules or standards define the exact number of the cycle when the damage initiates. In a previous study (Hormozi et al., 2015), the start number of cycles after the noticeable cyclic softening performance is defined as stabilized points (N_s). Simultaneously, a 0.5% drop of the ∆w from the maximum value of plastic strain energy density is considered a reliable value at which the damage was initiated (N_i). Similarly, a 10% drop of stabilized ∆w value from the initial damage point is defined as the final fatigue fracture.

FIGURE 10

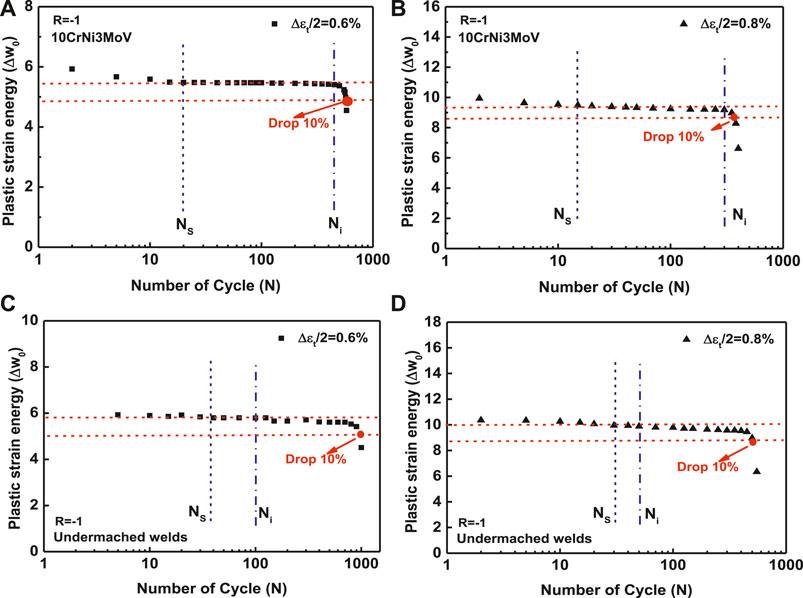
FIGURE 10. The evolution of plastic strain energy density ∆w₀ with cycles. (A) ∆ε_t/2 = 0.6% for 10CrNi3MoV steel, (B) ∆ε_t/2 = 0.8% for 10CrNi3MoV steel, (C) ∆ε_t/2 = 0.6% for undermatched welds, and (D) ∆ε_t/2 = 0.8% for undermatched welds.

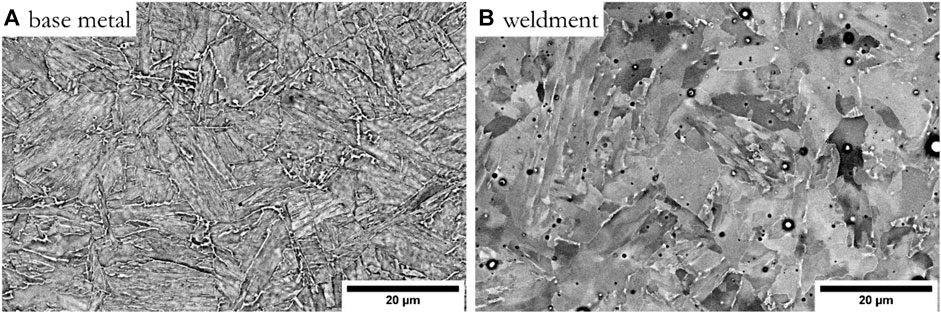
Figure 10B is the evolution of ∆w₀ with per cycle under 0.8% strain amplitudes for the base metal. It can be seen that the values of ∆w₀ in different stages are higher than the results of 0.6% strain amplitudes. In contrast to the undermatched welds results, the ∆w₀ degradation under 0.6 and 0.8% strain amplitudes are depicted in Figure 10C,D. Comparing the ∆w₀ of base metal and undermatched welds, the percentage of initial stage in the whole stage of weldments seems to be shorter than that of base metal. It implied that the weldments demonstrate a higher possibility for fatigue damage initiation. Afterward, the damage accumulation stage of undermatched welds shows more cycles than the base metal. It can be proved that the material degradation grows slower than the base metal. If we remove the fatigue damage standard of an initial 0.5% drop and the final 10% drop, the damage deterioration of base metal exhibits higher stability than the weldment. According to the SEM micrographs of the base metal and undermatched welds shown in Figure 11A, the inner base metal does not have significant defects and shows a generally homogeneous microstructure before welding. In contrast, the formation of some micron-sized precipitated particles in the undermatched welds is visible in Figure 11B. These small defects lead to the formation and propagation of microcrack and resulting in damage failure. Furthermore, according to the EBSD characterizations in Figure 2, the undermatched weldment has some micron-sized recrystallization nuclei. The local residual deformation in these nuclei (almost zero) is significantly different from the grain matrix (higher deformation level and thus higher strength due to work-hardening), leading to an intense strength difference between them. The stress and strain incompatibility between the recrystallized cells and the matrix grains with higher deformation levels can contribute to the local stress concentration and initiating microcracks. As the loading continues, the recrystallized small deformation-free grains in the weldment have a higher chance of being work hardened, consuming more plastic strain energy and slowing down the damage accumulation procedure. It can be the reason that the weldment shows more cycles than the base metal.

FIGURE 11

FIGURE 11. SEM comparison of (A) base metal and (B) weldment.

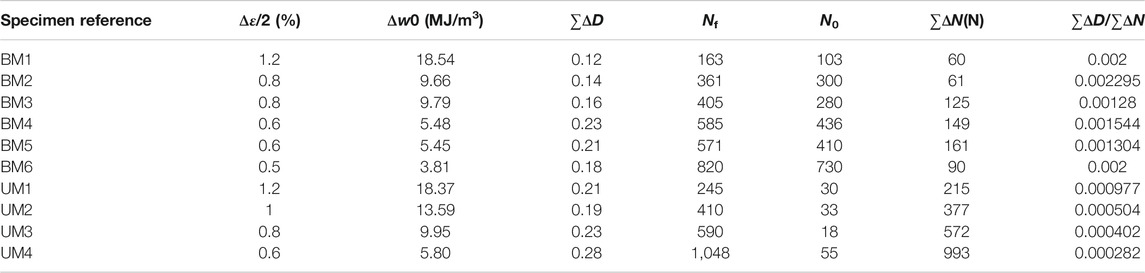
The values obtained for ∆w, ∑ΔD, N_f, N_0, and ∑ΔD/∑ΔN from the LCF experimental tests are summarized in Table 4. It should be noted that the damage accumulations (∑ΔD) are acquired by stabilization and the evolution of plastic strain energy density magnitudes.

TABLE 4

TABLE 4. Fatigue damage values under each cycle from the experimental data.

Linear log–log relationships between the plastic strain energy density and fatigue life in the initial stage for base metal and undermatched welds are shown in Figure 12. The related equations are given as follows:

$\{\begin{array}{l}{N}_0=3162.3\cdot {\left(\Delta w\right)}^{-1.126},\text{for base metal,}\\ N_0=135.8\cdot {\left(\Delta w\right)}^{-0.53},\text{for undermatched welds}\text{.}\end{array}(15)$

FIGURE 12

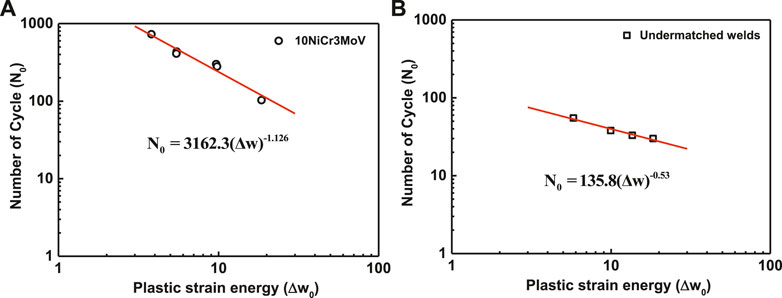
FIGURE 12. The log–log relationship between ∆w₀ and fatigue life in the initial stage. (A) 10CrNi3MoV steel and (B) undermatched welds.

Furthermore, the linear relationships of ∆w and damage value per cycle for two materials are shown in Figure 13, and the fitting equations are depicted as follows:

$\{\begin{array}{l}\Delta D/\Delta N=1.39E-3\cdot {\left(\Delta w\right)}^{-0.095}\text{,}\text{for base metal,}\\ \Delta D/\Delta N=4.35E-5\cdot {\left(\Delta w\right)}^{1.01},\text{for undermatched welds}\text{.}\end{array}(16)$

FIGURE 13

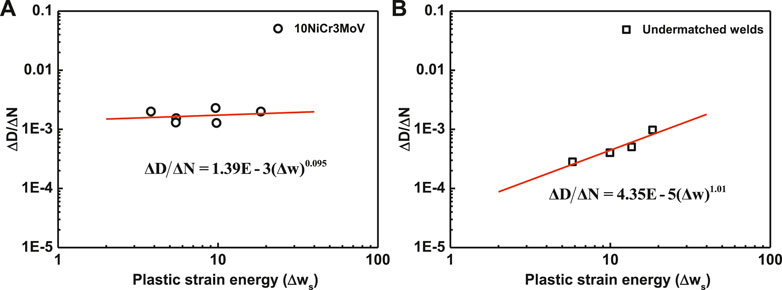
FIGURE 13. The log–log relationship of ∆w₀ and damage values in the degradation stage. (A) 10CrNi3MoV steel and (B) undermatched welds.

It should be noted that the c₃ parameter should be calculated by the characteristic length L, which is associated with the adjacent distance between integration points. The L is set as 1.75 mm in fine mesh portion by ABAQUS. Finally, the damage parameters for LCF are summarized in Table 5.

TABLE 5

TABLE 5. Determination of fatigue damage parameters.

FE and Experimental Results

The direct cyclic FE analysis is conducted in ABAQUS under different loading conditions by combining the Chaboche cyclic plastic parameters with CDM parameters of base metal and undermatched weldments. Figure 14 illustrates the LCF damage evolution at the critical material point in the specimen for base metal and undermatched welds under 0.6 and 0.8% symmetrical strain amplitudes. FE hysteresis damage growth under 0.6% strain amplitude, as shown in Figure 14A, is overestimated compared with the experimental data of base metal. Due to the intermediate processing of damage parameters, the deviation of total experimental damages leads to the overestimated FE damage. Figure 14C,D compare the fatigue damage of experimental data and computation results by the LCF damage model for undermatched welds in ABAQUS. The excellent agreement of experimental and FE results in damage initiation and degradation stages validates the damage model’s accuracy in ABAQUS. Despite the minor deviations in the FE results, it can be concluded that the FE damage model is capable of accurately predicting the damage magnitude based on energy damage evolution. It implies that the damage laws are feasible, and the effect of damage on the fatigue initiation and degradation of FE material characteristics can demonstrate the experimental observations accurately.

FIGURE 14

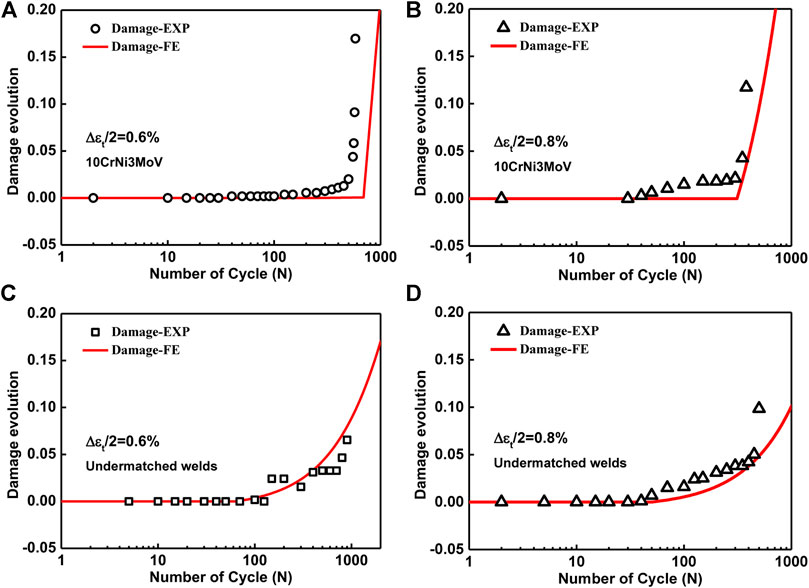
FIGURE 14. Damage evolution for base metal and undermatched welds. (A) ∆ε_t/2 = 0.6% for 10CrNi3MoV steel, (B) ∆ε_t/2 = 0.8% for 10CrNi3MoV steel, (C) ∆ε_t/2 = 0.6% for undermatched welds, and (D) ∆ε_t/2 = 0.8% for undermatched welds.

Based on validated fatigue damage parameters proposed from the experimental data, the LCF damage predictions of different strain amplitudes from 0.6 to 1.2% are given in Figure 15. As can be observed from Figure 15A, the damage initiation life for base metal decreases with the increase of strain amplitude. Regarding damage degradation after the damage initiation, it overgrows with the decrease of strain amplitude. However, Figure 15B shows the same damage initiation state for undermatched welds; the speed of damage degradation seems to be faster with the increase of strain amplitudes. As defined by the actual damage boundary of material rupture, the calculation damage limitation is also set to 0.1. Thus, we can obtain the predicted fatigue life based on the damage simulation results.

FIGURE 15

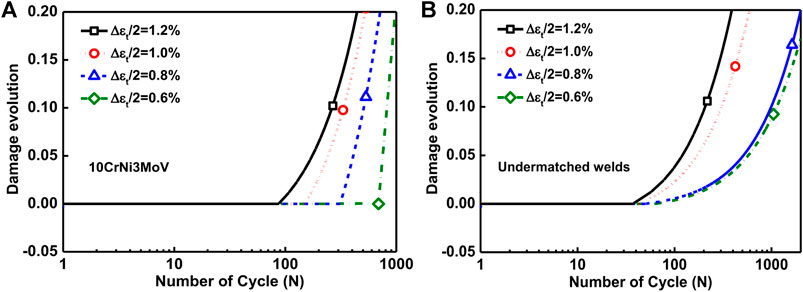
FIGURE 15. Simulation damage evolution under different strain amplitudes. (A) Base metal and (B) undermatched welds.

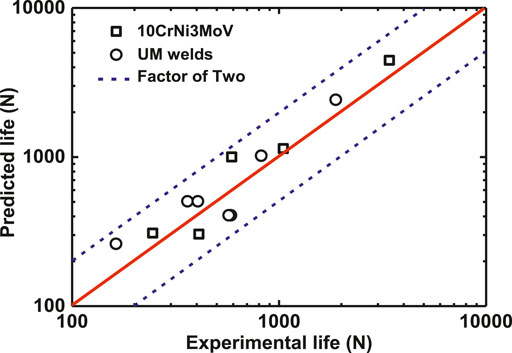
Figure 16 plots the predicted fatigue life based on the CDM approach against the experimental values for base metal and undermatched welds. It can be seen that all data points of the predicted results fall within the factor of two lines. For the undermatched welds, most of the predicted fatigue lives from the damage model are nonconservative. Therefore, the calibrated damage material parameters can be further applied to assess the fatigue life for more complicated structures.

FIGURE 16

FIGURE 16. Fatigue life prediction of different materials.

Conclusion

The present study investigated the LCF behavior of 10CrNi3MoV steel and its undermatched welds using a combined experimental and numerical investigation by the CDM approach. The methodology uses an elastic–plastic FE framework to compute valid damage parameters based on the plastic strain energy density of critical material points. At the same time, the damage evolution and fatigue life were accessed by the comparison of experimental data and calculation results. The following conclusions can be drawn from the present work:

1) The cyclic stress–strain curves of base metal and undermatched welds demonstrate the softening behavior at the beginning of the cyclic period, which is proficiently characterized by the Chaboche nonlinear kinematic hardening and the cyclic plastic model. The model material parameters are accurately calibrated by the first cycle, and stabilized stress–strain hysteresis loops on the strain amplitude range from 0.6 to 1.2%.

2) The article employs the CDM approach to predict LCF life successfully. A damage evolution law based on the damage approach into the FE method allows for the simulation of material damage processing. The damage laws are valid, and the effect of damage on the fatigue initiation and degradation of FE material characteristics can illustrate the experimental observations accurately.

3) This developed approach enables the calculation to display the whole fatigue damage process, including the damage initiation and propagation stages. Various damage initiation life states of base metal are captured by the damage criterion with the increase of strain amplitudes, and the damage deterioration accelerates with the decrease of strain amplitudes, while the damage initiation of undermatched welds is unchanged with modification of strain amplitudes, and the damage growth stage is dependent on the strain conditions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WS and XL together proposed this methodology. WS did finite element analysis and calculations. JX and YF helped to develop the finite element models. DS and XX helped to write part of this manuscript. FY polished and contributed to the final version of the manuscript. DW and FB supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.

Funding

The research project is supported by the Natural Science Foundation of Jiangsu Province (grant no. BK20200174) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (grant no. 20KJB430008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahola, A., Björk, T., and Barsoum, Z. (2019a). Fatigue strength capacity of load-carrying fillet welds on ultra-high-strength steel plates subjected to out-of-plane bending. Eng. Structures 196, 109282. doi:10.1016/j.engstruct.2019.109282

CrossRef Full Text | Google Scholar

Ahola, A., Skriko, T., and Björk, T. (2019b). Fatigue strength assessment of ultra-high-strength steel fillet weld joints using 4R method. J. Constructional Steel Res. 167, 105861. doi:10.1016/j.jcsr.2019.105861

CrossRef Full Text | Google Scholar

Armstrong, P. J., and Frederick, C. O. (1966). A mathematical representation of the multiaxial Bauschinger effect. Mater. at High Temp. 24, 1–26. doi:10.1179/096034007X207589

CrossRef Full Text | Google Scholar

Bhattacharya, B., and Ellingwood, B. (1998). Continuum damage mechanics analysis of fatigue crack initiation. Int. J. Fatigue 20, 631–639. doi:10.1016/s0142-1123(98)00032-2

CrossRef Full Text | Google Scholar

Chaboche, J. L. (1989). Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plasticity 5, 247–302. doi:10.1016/0749-6419(89)90015-6

CrossRef Full Text | Google Scholar

Chapetti, M. D., and Steimbreger, C. (2019). A simple fracture mechanics estimation of the fatigue endurance of welded joints. Int. J. Fatigue 125, 23–34. doi:10.1016/j.ijfatigue.2019.03.021

CrossRef Full Text | Google Scholar

Chatziioannou, K., Karamanos, S. A., and Huang, Y. (2019). Ultra low-cycle fatigue performance of S420 and S700 steel welded tubular X-joints. Int. J. Fatigue 129, 105221. doi:10.1016/j.ijfatigue.2019.105221

CrossRef Full Text | Google Scholar

Chung, K.-F., Ho, H.-C., Hu, Y.-F., Wang, K., Liu, X., Xiao, M., et al. (2020). Experimental evidence on structural adequacy of high strength S690 steel welded joints with different heat input energy. Eng. Structures 204, 110051. doi:10.1016/j.engstruct.2019.110051

CrossRef Full Text | Google Scholar

Darveau, R. (2002). Effect of simulation methodolofy on solder joint crack growth correlation and fatigue life prediction. J. Electron. Packag 124, 147–154.

Google Scholar

Feng, L., and Qian, X. (2018a). Low cycle fatigue test and enhanced lifetime estimation of high-strength steel S550 under different strain ratios. Mar. Structures 61, 343–360. doi:10.1016/j.marstruc.2018.06.011

CrossRef Full Text | Google Scholar

Feng, L., and Qian, X. (2018b). Size effect and life estimation for welded plate joints under low cycle actions at room and low ambient temperatures. Thin-Walled Structures 132, 195–207. doi:10.1016/j.tws.2018.08.017

CrossRef Full Text | Google Scholar

Hanji, T., Park, J.-E., and Tateishi, K. (2014). Low cycle fatigue assessments of corner welded joints based on local strain approach. Int. J. Steel Struct. 14, 579–587. doi:10.1007/s13296-014-3015-8

CrossRef Full Text | Google Scholar

Hanji, T., Saiprasertkit, K., and Miki, C. (2011). Low- and high-cycle fatigue behavior of load-carrying cruciform joints with incomplete penetration and strength under-match. Int. J. Steel Struct. 11, 409–425. doi:10.1007/s13296-011-4002-y

CrossRef Full Text | Google Scholar

Hanji, T., Tateishi, K., Ohashi, Y., and Shimizu, M. (2020). Effect of weld penetration on low-cycle fatigue strength of load-carrying cruciform joints. Weld World 64, 327–334. doi:10.1007/s40194-019-00834-w

CrossRef Full Text | Google Scholar

Hemmesi, K., Mallet, P., and Farajian, M. (2020). Numerical evaluation of surface welding residual stress behavior under multiaxial mechanical loading and experimental validations. Int. J. Mech. Sci. 168, 105127. doi:10.1016/j.ijmecsci.2019.105127

CrossRef Full Text | Google Scholar

Hobbacher, A. (2008). Recommendations for fatigue design of welded joints and components. IIW Doc. IIW-1823-07.

Hormozi, R., Biglari, F., and Nikbin, K. (2015). Experimental and numerical creep-fatigue study of Type 316 stainless steel failure under high temperature LCF loading condition with different hold time. Eng. Fracture Mech. 141, 19–43. doi:10.1016/j.engfracmech.2015.05.007

CrossRef Full Text | Google Scholar

Hormozi, R., Biglari, F., and Nikbin, K. (2014). Taguchi sensitivity analysis of damage parameters for predicting the damage mechanism of 9Cr steel under low-cycle fatigue test. Fatigue Fract. Engng. Mater. Struct. 37, 1211–1222. doi:10.1111/ffe.12200

CrossRef Full Text | Google Scholar

Ji, X., Cheng, Y., Leong, T., and Cui, Y. (2019). Seismic behavior and strength capacity of steel coupling beam-to-SRC wall joints. Eng. Structures, 201, 109820. doi:10.1016/j.engstruct.2019.109820

CrossRef Full Text | Google Scholar

Jin, X., Zhu, B., Li, Y., Zhao, Y., Xue, F., and Zhang, G. (2020). Effect of the microstructure evolution on the high-temperature strength of P92 heat-resistant steel for different service times. Int. J. Press. Vessels Piping 186, 104131. doi:10.1016/j.ijpvp.2020.104131

CrossRef Full Text | Google Scholar

Korsunsky, A., Dini, D., Dunne, F., and Walsh, M. (2007). Comparative assessment of dissipated energy and other fatigue criteria☆. Int. J. Fatigue 29, 1990–1995. doi:10.1016/j.ijfatigue.2007.01.007

CrossRef Full Text | Google Scholar

Lau, J. H., Pan, S. H., and Chang, C. (2002). A new thermal-fatigue life prediction model for wafer level chip scale package (WLCSP) solder joints. J. Electron. Packag 124, 212–220. doi:10.1115/1.1462625

CrossRef Full Text | Google Scholar

Lazzarin, P., Livieri, P., Berto, F., and Zappalorto, M. (2008). Local strain energy density and fatigue strength of welded joints under uniaxial and multiaxial loading. Eng. Fracture Mech. 75, 1875–1889. doi:10.1016/j.engfracmech.2006.10.019

CrossRef Full Text | Google Scholar

Lemaitre, J. (1985). A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. Trans. ASME 107, 83–89. doi:10.1115/1.3225775

CrossRef Full Text | Google Scholar

Lemaitre, J., and Desmorat, R. (2005). Engineering damage mechanics: ductile, creep, fatigue and brittle failures, Berlin, Germany: Springer.

Li, S., Eliniyaz, Z., Sun, F., Shen, Y., Zhang, L., and Shan, A. (2013). Effect of thermo-mechanical treatment on microstructure and mechanical properties of P92 heat resistant steel. Mater. Sci. Eng. A 559, 882–888. doi:10.1016/j.msea.2012.09.040

CrossRef Full Text | Google Scholar

Liu, S.-D., Zhu, M.-L., Zhou, H.-B., Wan, D., and Xuan, F.-Z. (2019). Strain visualization of growing short fatigue cracks in the heat-affected zone of a Ni-Cr-Mo-V steel welded joint: intergranular cracking and crack closure. Int. J. Press. Vessels Piping 178, 103992. doi:10.1016/j.ijpvp.2019.103992

CrossRef Full Text | Google Scholar

Liu, Y., Tsang, K. S., Hoh, H. J., Shi, X., and Pang, J. H. L. (2020). Structural fatigue investigation of transverse surface crack growth in rail steels and thermite welds subjected to in-plane and out-of-plane loading. Eng. Structures, 204, 110076. doi:10.1016/j.engstruct.2019.110076

CrossRef Full Text | Google Scholar

Miki, C., Homma, K., and Tominaga, T. (2002). High strength and high performance steels and their use in bridge structures. J. Constructional Steel Res. 58, 3–20. doi:10.1016/s0143-974x(01)00028-1

CrossRef Full Text | Google Scholar

Murakami, S. (2012). Continuum damage mechanics-A continuum mechanics approach to the analysis of damage and fracture, Berlin, Germany: Springer.

Radaj, D., Sonsino, C. M., and Fricke, W. (2006). Fatigue assessment of welded joints by local approaches. 2nd Edn, Amsterdam, Netherlands: Elsevier.

Rao, K. B. S., Schiffers, H., and Nickel, H. H. (1988). Influence of time and temperature dependent processes on strain controlled low cycle fatigue behavior of alloy 617. Mta 19, 359–371. doi:10.1007/bf02652546

CrossRef Full Text | Google Scholar

Saiprasertkit, K., Hanji, T., and Miki, C. (2012). Fatigue strength assessment of load-carrying cruciform joints with material mismatching in low- and high-cycle fatigue regions based on the effective notch concept. Int. J. Fatigue 40, 120–128. doi:10.1016/j.ijfatigue.2011.12.016

CrossRef Full Text | Google Scholar

Smith, M. C., Muránsky, O., Xiong, Q., Bouchard, P. J., Mathew, J., and Austin, C. (2019). Validated prediction of weld residual stresses in austenitic steel pipe girth welds before and after thermal ageing, part 1: mock-up manufacture, residual stress measurements, and materials characterisation. Int. J. Press. Vessels Piping 172, 233–250. doi:10.1016/j.ijpvp.2019.01.004

CrossRef Full Text | Google Scholar

Song, W., Liu, X., Berto, F., and Razavi, S. M. J. (2018a). Energy-based low cycle fatigue indicator prediction of non-load-carrying cruciform welded joints. Theor. Appl. Fracture Mech. 96, 247–261. doi:10.1016/j.tafmec.2018.05.005

CrossRef Full Text | Google Scholar

Song, W., Liu, X., Berto, F., and Razavi, S. M. J. (2018b). Low-cycle fatigue behavior of 10CrNi3MoV high strength steel and its undermatched welds. Materials 11. doi:10.3390/ma11050661

CrossRef Full Text | Google Scholar

Sonsino, C. (2009). Effect of residual stresses on the fatigue behaviour of welded joints depending on loading conditions and weld geometry. Int. J. Fatigue 31, 88–101. doi:10.1016/j.ijfatigue.2008.02.015

CrossRef Full Text | Google Scholar

Tang, L., Ince, A., and Zheng, J. (2020). Numerical modeling of residual stresses and fatigue damage assessment of ultrasonic impact treated 304L stainless steel welded joints. Eng. Fail. Anal. 108, 104277. doi:10.1016/j.engfailanal.2019.104277

CrossRef Full Text | Google Scholar

Xing, S., Dong, P., and Wang, P. (2017). A quantitative weld sizing criterion for fatigue design of load-carrying fillet-welded connections. Int. J. Fatigue 101, 448–458. doi:10.1016/j.ijfatigue.2017.01.003

CrossRef Full Text | Google Scholar

Yonezawa, T., Shimanuki, H., and Mori, T. (2020). Influence of cyclic loading on the relaxation behavior of compressive residual stress induced by UIT. Weld World 64, 171–178. doi:10.1007/s40194-019-00821-1

CrossRef Full Text | Google Scholar

Zarandi, E. P., and Skallerud, B. H. (2020). Cyclic behavior and strain energy-based fatigue damage analysis of mooring chains high strength steel. Mar. Structures 70, 102703. doi:10.1016/j.marstruc.2019.102703

CrossRef Full Text | Google Scholar

Zhang, X., Gao, H., and Huang, H.-Z. (2018). Total fatigue life prediction for welded joints based on initial and equivalent crack size determination. Int. J. Damage Mech. 27, 1084–1104. doi:10.1177/1056789517723171

CrossRef Full Text | Google Scholar