Field–Frequency-Dependent Non-linear Rheological Behavior of Magnetorheological Grease Under Large Amplitude Oscillatory Shear

Introduction

Magnetorheological (MR) grease is a kind of magneto-induced smart material that is normally prepared by dispersing magnetic particles in grease matrix. With the utilization of viscoelastic continuous phases, i.e., grease matrix, MR grease can effectively avoid the sedimentation problem of magnetic particles, which often occurred in conventional MR fluid. So far, MR grease has been used in the application of many MR devices, namely MR damper (Shiraishi et al., 2011; Sakurai and Morishita, 2017), MR clutch (Kavlicoglu et al., 2015), MR brake (Sukhwani and Hirani, 2008), and MR engine mount (Sarkar et al., 2015). By comparing conventional MR devices using MR fluid, the MR grease device can maintain good settlement stability for a long period of time. In addition, considering the lubricating properties of the grease matrix, it can reduce the wear and tear of the moving parts of the devices and increase life, which eventually will reduce the maintenance cost in the long run. In the operation of MR devices, the internal MR grease usually works in the shear mode, which mainly includes steady shear and oscillatory shear (Zhang et al., 2019, 2020; Li et al., 2020). Therefore, it is necessary to conduct investigations on the rheological properties of MR grease under steady shear and oscillatory shear, which can provide insight and understanding for the design and application of MR grease devices.

To date, the rheology of MR grease under steady shear and oscillatory shear was studied by a number of researchers. For steady shear, researchers mainly focused on the dependence of rheological parameters, namely viscosity, yield stress, the magnetic field, shear rate, and temperature. Sahin et al. (2007) studied the yield stress and viscosity of MR grease under steady shear and compared them with the results obtained using conventional silicon-based MR fluid. They found that the yield stress of MR grease is higher than that of the traditional MR fluid, which is at the expense of increased off-state viscosity of MR grease (Sahin et al., 2007). Park et al. investigated the flow curve responses of MR grease with different external magnetic fields under steady shear. They indicated that MR grease presents the properties of Bingham fluid under the application of the magnetic field (Park et al., 2011). Mohamad et al. (2018) examined the field-dependent rheology of MR grease with platelike particles. They found that the platelike carbonyl iron (CI)-based MR grease can provide higher yield stress than spherical particle-based MR grease at a low magnetic field with a low weight fraction of particles (Mohamad et al., 2018). Wang et al. (2019a,b,c) investigated the temperature-dependent rheology of MR grease under steady shear. They demonstrated that the influence of temperature on the rheological properties of MR grease decreased with the magnetic field (Wang et al., 2019a,b,c). For oscillatory shear, the main focus is the influence of the magnetic field, oscillatory shear strain, and frequency on the dynamic parameters, such as storage/loss modulus and loss factor. Rankin et al. (1999) tested the storage modulus of MR grease under a series of the strain sweep tests. They found that the storage modulus of MR grease under the small strain amplitude is time-dependent (Rankin et al., 1999). Park et al. (2011) studied the influence of oscillatory frequency on storage and loss moduli under different magnetic fields. They found that the storage and loss moduli are all independent of frequency at a fixed magnetic field (Park et al., 2011). Mohamad et al. (2016) tested the relationship between dynamic parameters and oscillatory shear strain under different magnetic fields. They concluded that the linear viscoelastic (LVE) range (storage modulus independent of shear strain) of MR grease is smaller compared with the MR gel, and the relative MR effect of MR grease is larger than that of the MR fluid (Mohamad et al., 2016). In addition, Mohamad et al. (2019a,b) also investigated the field-dependent viscoelastic and transient response of MR grease with different particle shapes. They found that the shape of the CI particles (CIPs) has a significant effect on the field-dependent behaviors of MR grease, e.g., the bidisperse MR grease with platelike CI particles exhibits an increase in the initial apparent viscosity and the stiffness property compared with MR grease with spherical particles only (Mohamad et al., 2019a,b).

Although a lot of research was conducted on the rheological properties of MR grease under steady shear and oscillatory shear, the rheological study of MR grease under oscillatory shear, especially large amplitude oscillatory shear (LAOS), is yet to be fully explored. The reason is that the storage and loss moduli, which are normally acquired from rheometer and used to characterize the rheology of MR grease under oscillatory shear, may not be sufficient to characterize the rheology of MR grease under LAOS. As shown in a previous research, under LAOS, the shear strain amplitude that was applied on MR grease enters into the non-linear range (Hyun et al., 2011). The response stress wave deviates from the sine wave and contains higher harmonics. The output moduli from the commercial rheometer, namely storage modulus (G’) and loss modulus (G”), are the first harmonic moduli of the Fourier transform of the response data (Wilhelm, 2002). This method that ignores the contribution of higher modulus but only considers the first harmonic modulus will inevitably result in the loss of rich information when characterizing the rheology of MR grease under LAOS.

Recently, we introduced a non-linear characterization method, namely Fourier transform (FT)-Chebyshev analysis (Wilhelm, 2002; Cho et al., 2005), which could detect the higher harmonics triggered by LAOS. Compared with commonly used approaches, namely elastic Lissajous curves, storage/loss modulus, and FT analysis, we found that the FT-Chebyshev analysis could provide more insight on non-linear viscoelastic (NLVE) behavior of MR materials under LAOS. Subsequently, we also utilized the FT-Chebyshev analysis to quantitatively analyze the non-linearity of MR grease under different strain amplitudes at a fixed frequency (Wang et al., 2020). In addition to the oscillatory strain amplitude, frequency is an important factor that affects the non-linear rheological properties of MR grease. Exploring the influence of the frequency on the non-linear behavior of MR grease is the basis for the development of efficient control algorithms in practical MR grease device applications. Thus, in this article, we investigate the field-dependent non-linearity of MR grease under LAOS at different driving frequencies. First, MR grease with a 70% weight percentage of CIPs (MRG-70) is prepared, and the LAOS test with different driving frequencies is conducted on MR grease at four different magnetic fields. Then, the storage and loss moduli at different frequencies are compared. Later, the influence of the frequency on the non-linear rheology is qualitatively analyzed by the three-dimensional (3D) Lissajous curves and the stress decomposed method. Finally, the elastic and viscous measures containing higher harmonics from the FT-Chebyshev analysis under different frequencies are calculated to further characterize the field-dependent non-linear rheology under LAOS at different driving frequencies.

Materials and Methods

Preparation of MR Grease

For this research, MR grease is composed of lithium-based commercial grease and CIPs. The lithium-based commercial grease (Gadus S2 V220, Shell Ltd., Zhuhai, China) has an NLGI grade of 0, which presents the appearance of brown mustard. The CIPs are obtained from BASF Ltd. (Ludwigshafen, Germany) and have an average diameter of 6 μm. We prepared MRG-70 in this study. The preparation processes are as follows: first, 140 g of CIPs and 60 g of commercial grease were weighed and put into two different vials. Then, the commercial grease was stirred at 500 rpm for 10 min at the temperature of 80°C. Finally, the prepared CIPs were dispersed into the commercial grease with a mechanical stirrer at 800 rpm until the grease and the CIPs form a stable and homogeneous product.

Experiment Methods

Fibrous Structure Observation

Magnetorheological (MR) grease has almost no sedimentation problem because of the fibrous structure of the grease matrix. The microstructures of the grease matrix and MRG-70 were observed with a scanning electron microscopy (SEM) (FEI, Quanta 250 FEG). As indicated in a previous study, lubricating greases are highly structured colloidal dispersions consisting of a thickener dispersed in the base oil (Wang et al., 2019a). Due to the influence of the base oil, it is difficult to see the fibrous structures of the untreated MR grease through SEM. Delgado et al. reported the solvent infiltration method to extract the base (Delgado et al., 2006). However, we found this method to be effective only for the grease with a higher NLGI grade. In this article, we used ultrasonic centrifugation to extract the base oil, which mainly consists of three parts: (1) adding a small amount of sample into the hexane and stirring it with a glass rod for 30 s; (2) using ultrasonic dispersion for 5 min; and (3) centrifuging for 2 min at 10,000 rpm and discarding the centrifugal fluid. Repeating the above steps three times can provide the sample without the base oil.

Rheological Test

The rheological tests of MR grease under LAOS were all carried out using the MCR 302 rheometer (Anton Paar instrument, Graz, Austria) in parallel-plate geometry with a diameter of 20 mm. In the experiment, 0.4 ml of MRG-70 was injected into the gap between the upper parallel plate and the base. The gap was kept constant at 1 mm throughout the test. The temperature was always controlled at 25°C. In each LAOS test, a series of sinusoidal strain waves with different strain amplitudes and frequencies were performed at a fixed magnetic field. The strain amplitude varies from 0.01 to 100%, and the frequency is set as 0.1 and 1.0 Hz, respectively. Two different magnetic fields, i.e., 0 and 391 kA/m, were selected for this study. To obtain a homogeneous reproducible test, the sample was pre-sheared under 1/s for 1 min and stalled for 30 s before formal testing. LAOS experiments are tested for at least 30 cycles to ensure the response stress at a steady state.

Rheological Analysis of LAOS Data

To obtain the elastic and viscous measures, the LAOS data analysis processes are performed as follows: first, the real-time response stress was analyzed by the FT-Chebyshev analysis, and then, the n-th order elastic and viscous moduli, i.e., G′ n and G′′ n, were calculated (Wilhelm, 2002). Second, according to the analysis of the results provided by Ewoldt et al. (2008), the elastic and viscous Chebyshev coefficients, i.e., e_n and v_n, can be calculated as follows:

$\begin{array}{c}{e}_n={\sum }_{\begin{array}{c}n=1\hfill \\ nodd\hfill \end{array}}{G}_n^{\prime }{(-1)}^{(n-1)/2}\hfill \\ v_n={\sum }_{\begin{array}{c}n=1\hfill \\ nodd\hfill \end{array}}{G}_n^{{}^{″}}/\mathrm{\omega }\hfill \end{array}(1)$

where n = 1, 3, 5… and ω is the angular frequency of LAOS.

Then, the newly defined elastic and viscous measures can be represented as:

$S=\frac{4e_3-4e_5+8e_7+\mathrm{\cdots }}{e_1+e_3+e_5+e_7+\mathrm{\cdots }}(2)$

$T=\frac{4v_3-4v_5+8v_7+\mathrm{\cdots }}{v_1+v_3+v_5+v_7+\mathrm{\cdots }}(3)$

where S is the strain-stiffening ratio and T is the shear-thickening ratio.

Results and Discussion

Microstructure of MRG-70 and CIPs

Figure 1 shows the microstructures of the fresh MR grease product, i.e., MRG-70, and its matrix, i.e., commercial grease. Figure 1a shows the microstructure of the lithium-based grease matrix Figure 1b shows the microstructure of MRG-70, and the white point in the figure is the CIPs and the dark background is the grease matrix. From Figures 1a,b, it is difficult to observe the fibrous structure due to the influence of the base oil in grease. Figures 1c,d show the microstructures of the grease and MRG-70 with the extracted base oil, respectively. From Figure 1c, the obvious 3D fibrous structures can be observed. Due to the function of that entangled fibrous structures, the CIPs in MR grease are trapped when the external magnetic field is not applied, which can effectively avoid the sedimentation problem of conventional MR fluid. In Figure 1d, the red arrow represents the CIP, and the green arrow represents the entangled fibrous structures. The CIP entangled by the fibrous structures can be observed.

FIGURE 1

Figure 1. SEM images of (a) grease matrix and (b) MRG-70 without magnetic field. (c) and (d) microstructures of the grease and MRG-70 with the extracted base oil, respectively. The red arrow shows the CIP, and the green arrow shows the entangled fibrous structures.

Oscillatory Strain Sweep Under Different Frequencies and Magnetic Fields

The oscillatory strain sweep is widely utilized to detect the viscoelastic rheological behavior of MR materials. Based on whether the storage and loss moduli response depends on the input strain amplitude, the oscillatory strain sweep can be divided into LVE and NLVE ranges (Upadhyay et al., 2013; Agirre-Olabide et al., 2014). In the NLVE range, the stress response normally contains higher harmonics than the input frequency. The LVE moduli, i.e., G’ and G”, are actually the real and imaginary coefficients of the first harmonics (Wilhelm et al., 2000). Figure 2 shows the field-dependent storage and loss moduli which vary with shear strain amplitude under different frequencies, i.e., 0.1, 0.5, 1, and 5 Hz. Figures 2A,B show that, irrespective of the frequency, the LVE range without the magnetic field is wider than that with the magnetic field, e.g., the critical strain amplitude between LVE and NLVE is around 0.2% without the magnetic field. When the magnetic field is applied, the critical strain amplitude decreases to about 0.08%. This is because the stronger CIP chain and cluster structures are formed in the direction of the magnetic field. In addition, in the NLVE range, for MRG-70 with the magnetic field at the fixed frequency of 0.1 Hz (see Figure 2A), both storage and loss moduli monotonically decrease with the strain amplitude, indicating the intercycle shear thinning behavior. When the oscillatory frequency is higher than 0.1 Hz, i.e., 0.5, 1, and 5 Hz (see Figures 2B–D), the storage modulus of MRG-70 with the magnetic field still exhibits a monotonic decrease, while the loss modulus presents a typical overshoot at the onset of the non-linear, and this phenomenon is more pronounced at the higher magnetic field, e.g., 391 kA/m. The reason for the above feature may relate to the shear rate-dependent viscoelastic relaxation and thixotropy of the CIPs chain structures induced by the external magnetic field (Ghosh et al., 2019). Through the earlier analysis, it can be seen that, when the frequency rises from 0.1to 5 Hz, MRG-70 mainly exhibits two viscoelastic characteristics, namely strain thinning in which G’ and G” decrease in the NLVE range at 0.1 Hz and weak strain overshoot in which G’ decreases but G” increases, followed by a decrease in the NLVE range at the frequencies of 0.5, 1, and 5 Hz. Thus, the following part of the paper will focus on the behavior of MR grease at 0.1 and 1 Hz to characterize the above frequency-dependent viscoelasticity under LAOS with different magnetic fields. In summary, the viscoelastic behavior of MRG-70 under the oscillatory shear can be divided into three parts: the LVE part, the onset of the NLVE part, and the post NLVE part. In the LVE part, the storage modulus was maintained constantly due to the elastic deformation of the CIPs structures. As the shear strain amplitude approached the yield point, i.e., the onset of the NLVE part, the CIPs chain or cluster structures start to rupture, resulting in the overshot behavior of loss modulus which is closely related to the frequency and the magnetic field. With the further increase in the strain amplitude, loss modulus exceeds the storage modulus, indicating that MRG-70 entered into the viscous flow that prevents viscous dominant. At this time, the destruction of CIPs chain structures caused by shear and rearrangement of CIPs induced the magnetic field to reach an equilibrium state.

FIGURE 2

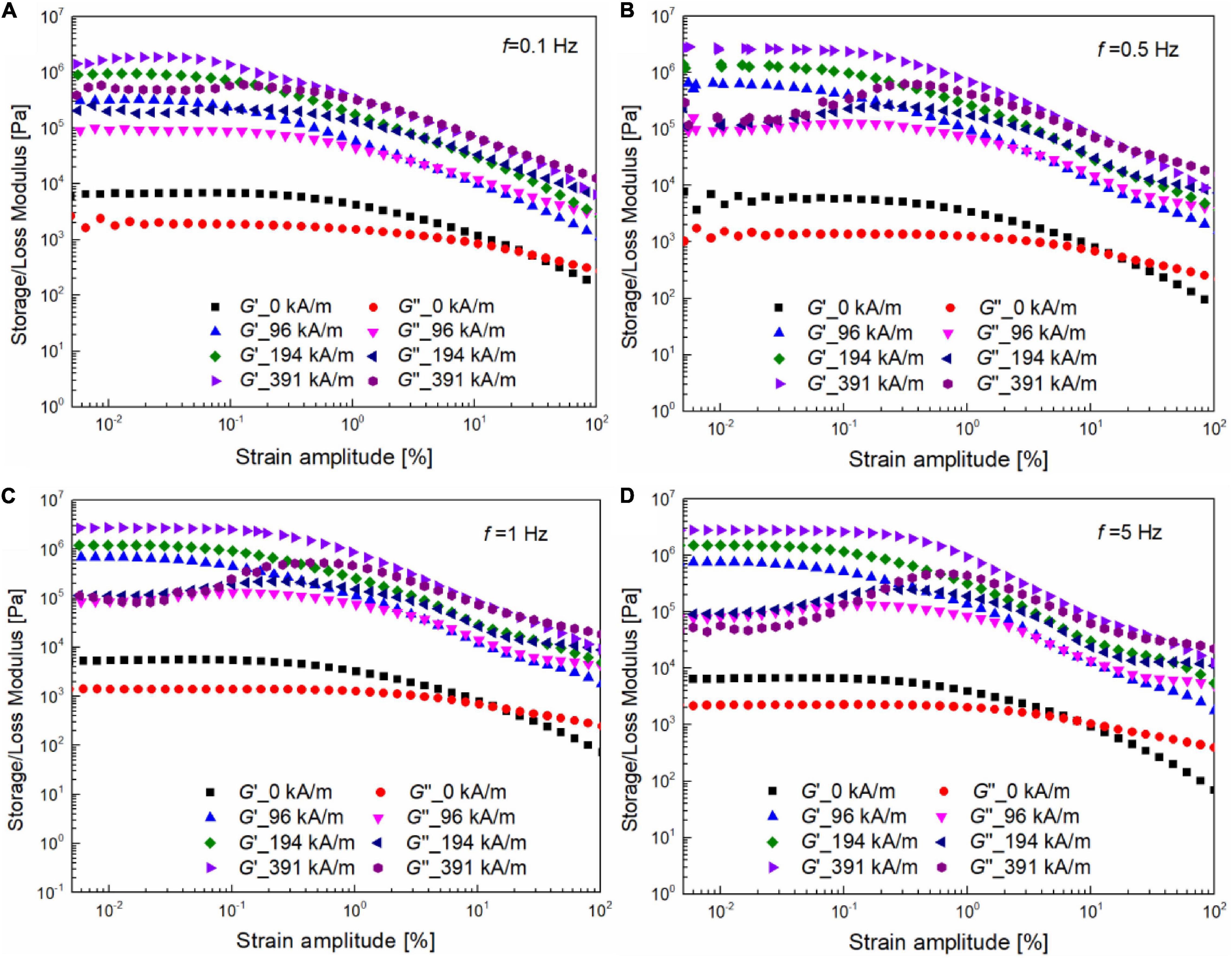
Figure 2. Oscillatory strain sweeps were conducted under different magnetic fields, i.e., 0, 96, 194, and 391 kA/m, at the fixed frequencies of (A) 0.1, (B) 0.5, (C) 1, and (D) 5 Hz.

Field-Dependent Elastic and Viscous Lissajous Curves

It is well known that the storage/loss modulus obtained from the oscillatory strain sweep demonstrates the average viscoelastic properties over different oscillation cycles, i.e., intercycle rheology. However, it is difficult to characterize the viscoelastic properties within an oscillation cycle, especially when the shear strain enters the non-linear regime, i.e., intracycle non-linear rheology (Hyun et al., 2011). To characterize the intracycle non-linear properties of MRG-70 under the LAOS test, the dependence of the response stress on time, shear strain, and shear rate within one cycle for two different strain amplitudes at a fixed frequency of 1 Hz is depicted in Figure 3. Figures 3A–D show the stress response and the FT-Chebyhev analysis of MRG-70 under the oscillatory shear with the strain amplitude in the linear regime, i.e., 0.1%. In this study, the response stress of MRG-70 remained in a standard sinusoidal waveform (Figure 3A). The elastic Lissajous curve shown in Figure 3B presented an elliptical shape where the tangent slope at zero strain is equal to the storage modulus, i.e., G’, and the area of the curve is proportional to the loss modulus, i.e., G”. The above linear response can also be confirmed by the results of FT-Chebyshev analysis where the relative intensity from higher harmonics (n ≥ 3) is equal to 0 (Figure 3D). However, when the shear strain amplitude increased into the non-linear regime, e.g., 10%, as shown in Figures 3E–H, the time–history curve of the response stress shown in Figure 3E deviated from the sinusoidal waveform. In the present study, the elastic and viscous Lissajous curves were all distorted, indicating the intracycle non-linearities of strain stiffening and shear thinning, respectively. In this case, the contribution from higher-order harmonics was detected by the FT-Chebyshev analysis (Figure 3H). By comparing the stress response of MRG-70 under different shear strain amplitudes, i.e., 0.1 and 10%, it can be concluded that the non-linearity of MRG-70 was strongly dependent on the strain amplitude. In the following section, the strain dependence of the non-linearity for MRG-70 under different frequencies is discussed.

FIGURE 3

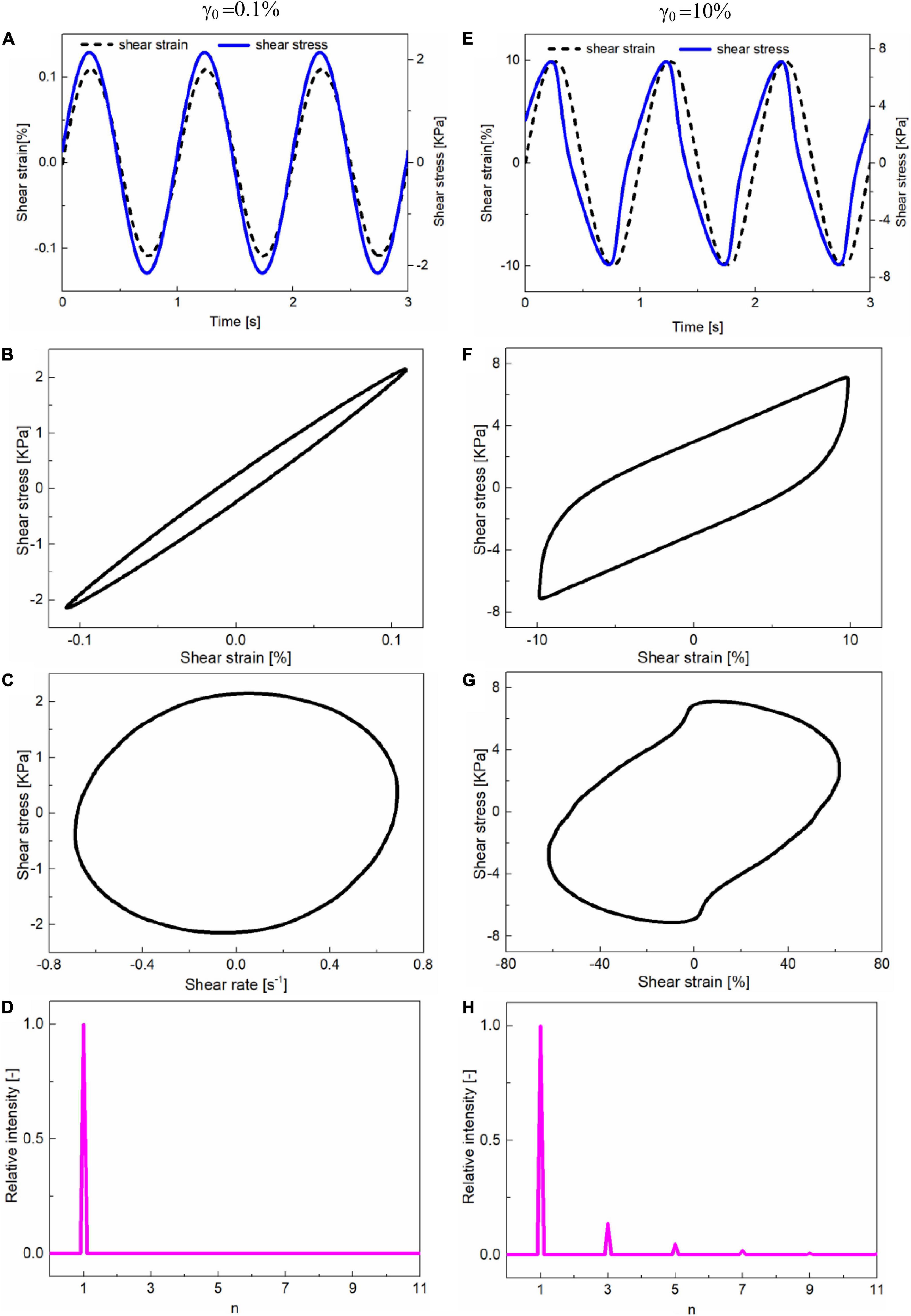
Figure 3. (A,E) represent the dependence of input strain and response stress on time. (B,F) show the Lissajous curves of the shear stress that varies with the shear strain (elastic Lissajous curves). (C,G) show the Lissajous curves of the shear stress that varies with the shear rate (viscous Lissajous curves). (D,H) show the results from FT-Chebyshev analysis. The data used in (A–D) were obtained from the LAOS test with γ = 0.1% and f = 1 Hz. The data used in (E–H) were obtained from the LAOS test with γ = 10% and f = 1 Hz. All these tests were conducted on the magnetic field of 391 kA/m.

In the 3D Lissajous curve at a fixed shear strain amplitude, the maximum instantaneous shear strain corresponds to the minimum instantaneous shear rate, e.g., when γ (t) = γ₀, the shear rate is equal to 0. Similarly, when γ (t) = 0, the instantaneous shear rate reaches the maximum, i.e., ± γ₀ω. As the shear strain amplitude varies, the intracycle stress at the maximum instantaneous shear strain (shear rate), which is shown in the shear strain (shear rate) domain, i.e., elastic and viscous Lissajous curves, changes, and its location, can be used to characterize the elastic and viscous contribution (Goudoulas and Germann, 2019a,b). Figure 4 depicts the comparison of the 3D Lissajous curves under different shear strain amplitudes, i.e., 0.01, 1, 10, and 100% at a fixed frequency of 1 Hz. At sufficient small strain amplitude shown in Figure 4A, i.e., 0.01%, the area of the elastic Lissajous (curve the green line in Figure 4A) tends to be very small, and MRG-70 has the maximum intracycle stress at γ₀. On the other hand, the intracycle stress at the maximum shear rate, i.e., ± γ₀ω, in the approaches of the corresponding viscous Lissajous (curves the blue line in Figure 3A) was 0. This demonstrates that, at sufficient small strain amplitude, the viscous contribution is 0, and MRG-70 only presents elasticity during the oscillatory shear. With the further increase in shear strain amplitude, i.e., 1 and 10% (Figures 4B,C), the area of the elastic Lissajous curves rapidly increases and the intracycle stress at the maximum shear rate increases between 0 and maximum stress, indicating the emergence of the viscous contribution. Thus, MRG-70 at the medium shear strain amplitude showed the viscoelastic behavior composed of elastic deformation and viscous dissipation. When the shear strain amplitude increased to a large value, i.e., 100%, the elastic Lissajous curves showed a shape of quadrilateral that represents the typical flow-induced structure of MRG-70 under oscillatory shear with 100% strain (Goudoulas and Germann, 2019a). Besides, the intracycle stress at the maximum shear rate in the approaches of the corresponding viscous Lissajous curves increased to the maximum value, indicating that the non-linearity of MRG-70 at 100% comes mainly from the viscous flow. In summary, the contribution of the viscous part to the non-linearity of MRG-70 was highly strain amplitude-dependent.

FIGURE 4

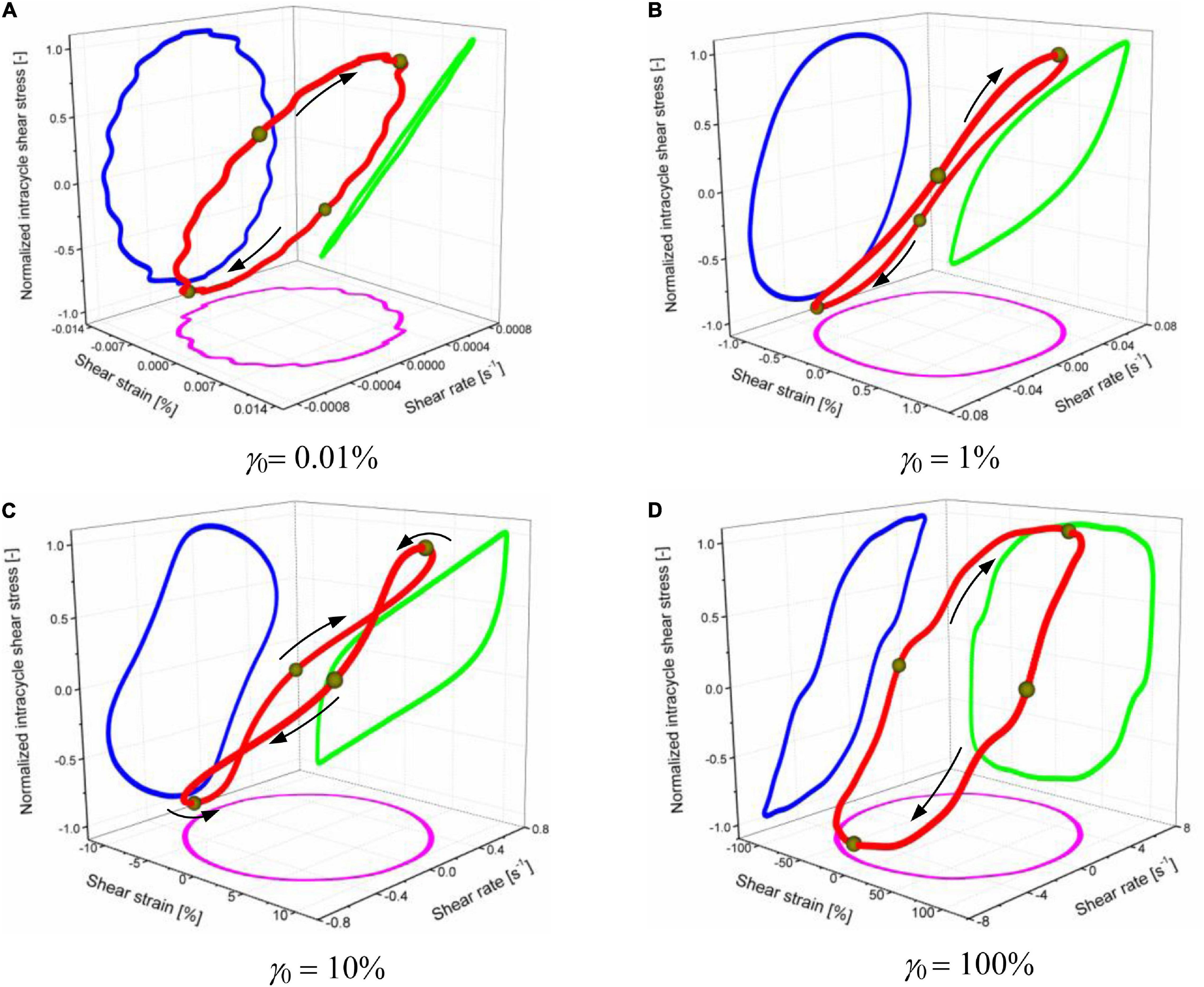
Figure 4. Three-dimensional normalized intracycle stress response of MRG-70 under different shear strain amplitudes, i.e., (A) 0.01%, (B) 1%, (C) 10%, and (D) 100%. The frequency f was always kept at 1 Hz. The external magnetic field was set as 391 kA/m.

To provide a further qualitative analysis on the effect of frequency and the magnetic field on the non-linear rheology of MRG-70 under LAOS, the field-dependent elastic and viscous Lissajous curves under LAOS with two typical driving frequencies are shown in Figures 5–8. The left and right columns in Figures 5–8 represent the elastic and viscous Lissajous curves, respectively, in which the red dash lines represent the corresponding decomposed shear stress, i.e., the intracycle elastic and viscous stress. From Figure 5, without the magnetic field, the Lissajous curves under the oscillatory frequency of 0.1 Hz maintained linear behavior up to 4% shear strain. This is further validated by the decomposed elastic and viscous stress that linearly increased with instantaneous intracycle shear strain and rate, respectively. However, as the oscillatory frequency increases to 1 Hz, the critical shear strain from linearity to non-linearity was decreased, i.e., around 1%, which demonstrated that the onset of the non-linear behavior was frequency-dependent. On the other hand, when the shear strain amplitude increased into the non-linear regime, the non-linearities seem to be less affected by the frequency, i.e., at frequencies of 0.1 and 1 Hz, and the non-linearities of MRG-70 show the combination of strain stiffening of elastic stress and shear thinning for energy dissipation, which is confirmed by the upturn of the decomposed elastic stress and the downturn of the decomposed viscous stress. In addition, as the shear strain amplitude increased to a large value, e.g., 100%, the contribution of the elastic stress to the non-linearity was kept constant over a wide range of the oscillatory shear. For example, from the elastic Lissajous curves at 100% shear strain amplitude shown in Figure 5, the decomposed elastic stress linearly changed with the instantaneous intracycle shear strain between − 90 and 90%. When the instantaneous intracycle shear strain approached the maximum value, i.e., 100%, the decomposed elastic stress presented a sharp increase. However, the similar behavior was not appeared in the decomposed viscous stress, in which the slope of that curve slowly changed over the whole oscillatory shear.

FIGURE 5

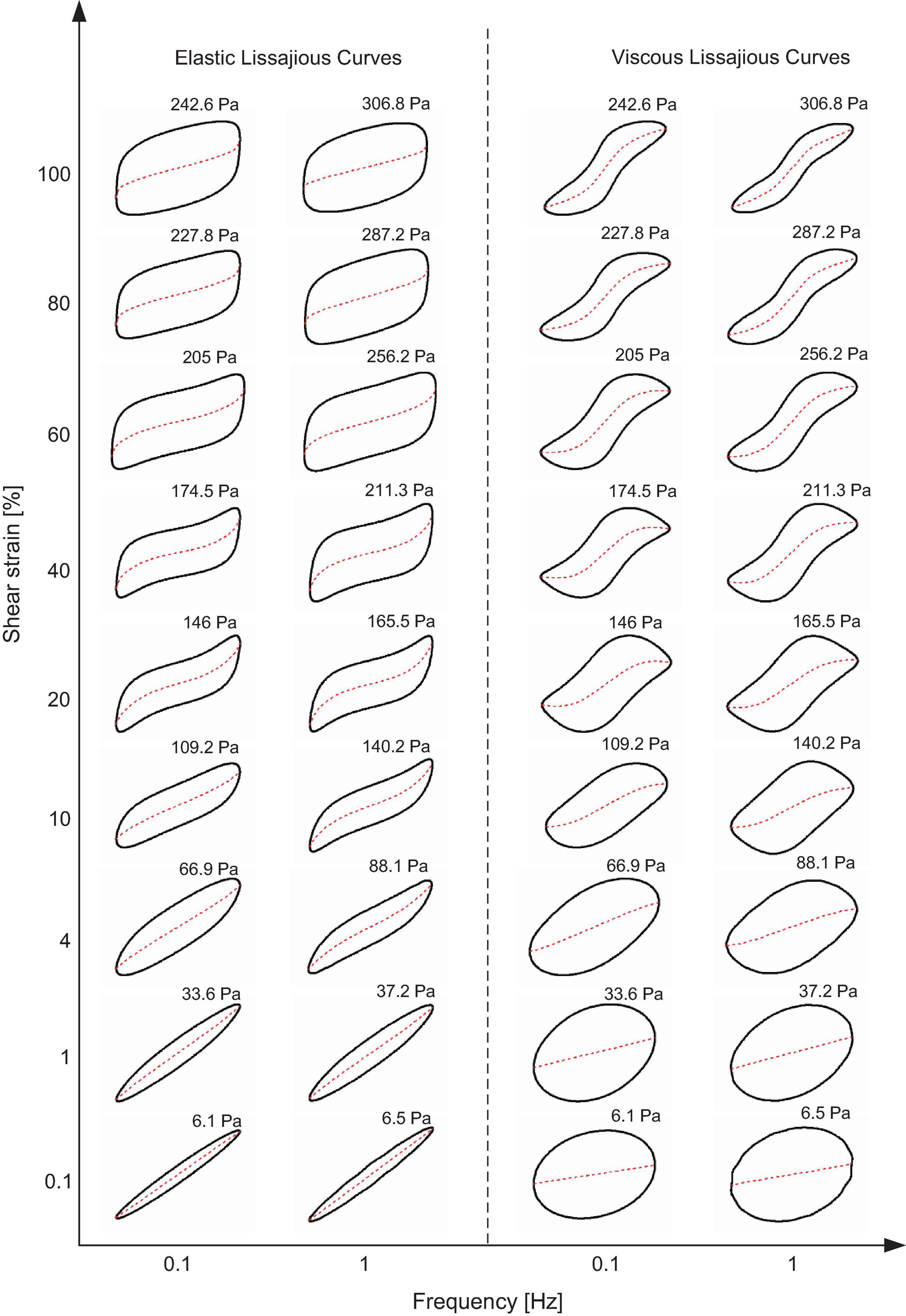
Figure 5. Elastic and viscous Lissajous curves of MRG-70 generated from the strain-controlled oscillatory shear under the magnetic field of 0 kA/m. Each curve is positioned according to the imposed value of shear strain and frequency. The red dash line represents the corresponding decomposed elastic and viscous stress, respectively. The value above each curve is the maximum shear stress τ_max.

FIGURE 6

Figure 6. Elastic and viscous Lissajous curves of MRG-70 generated from the strain-controlled oscillatory shear under the magnetic field of 96 kA/m. Each curve is positioned according to the imposed value of shear strain and frequency. The red dash line represents the corresponding decomposed elastic and viscous stress. The value above each curve is the maximum shear stress τ_max.

FIGURE 7

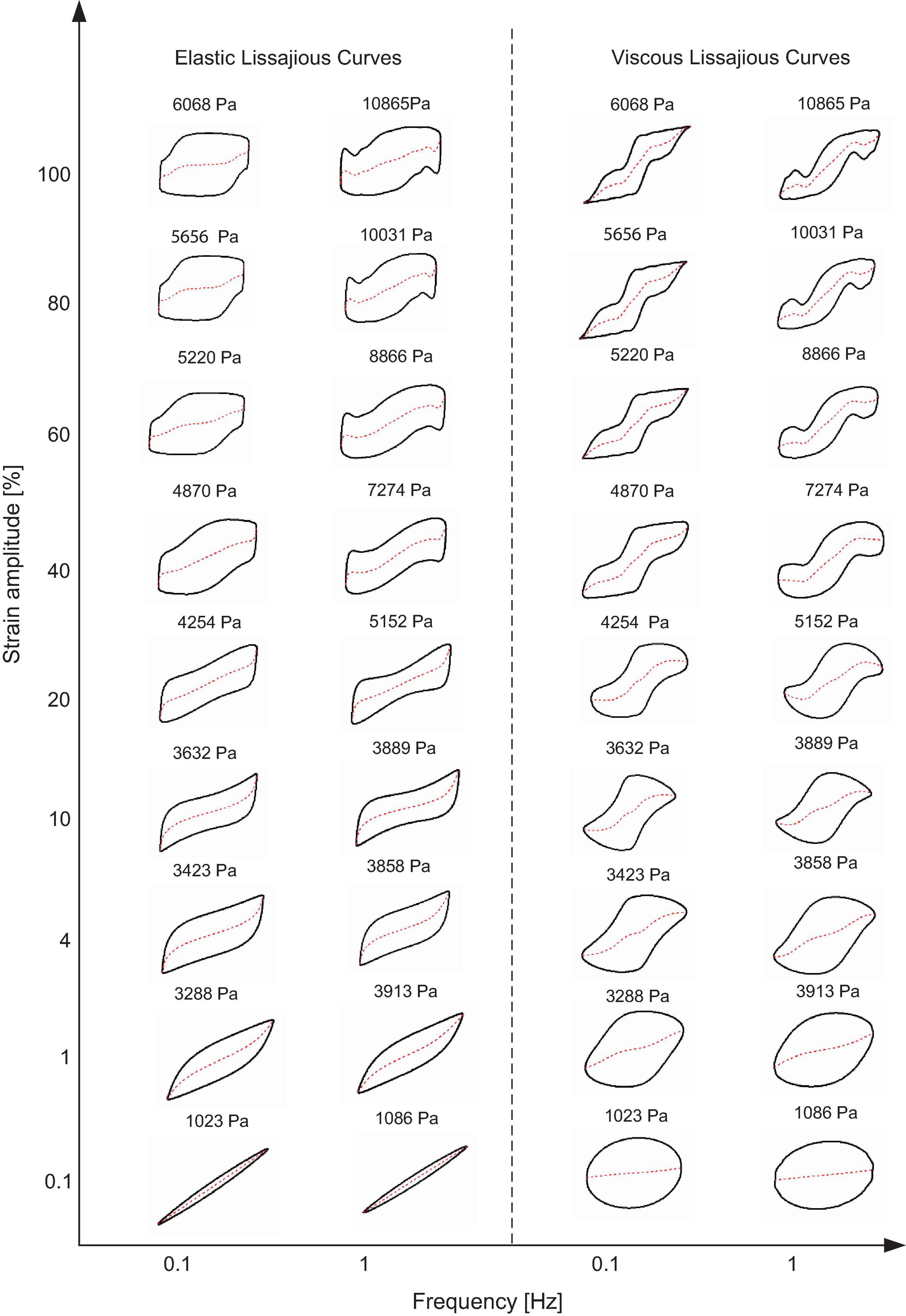
Figure 7. Elastic and viscous Lissajous curves of MRG-70 generated from the strain-controlled oscillatory shear under the magnetic field of 194 kA/m. Each curve is positioned according to the imposed value of shear strain and frequency. The red dash line represents the corresponding decomposed elastic and viscous stress. The value above each curve is the maximum shear stress τ_max.

FIGURE 8

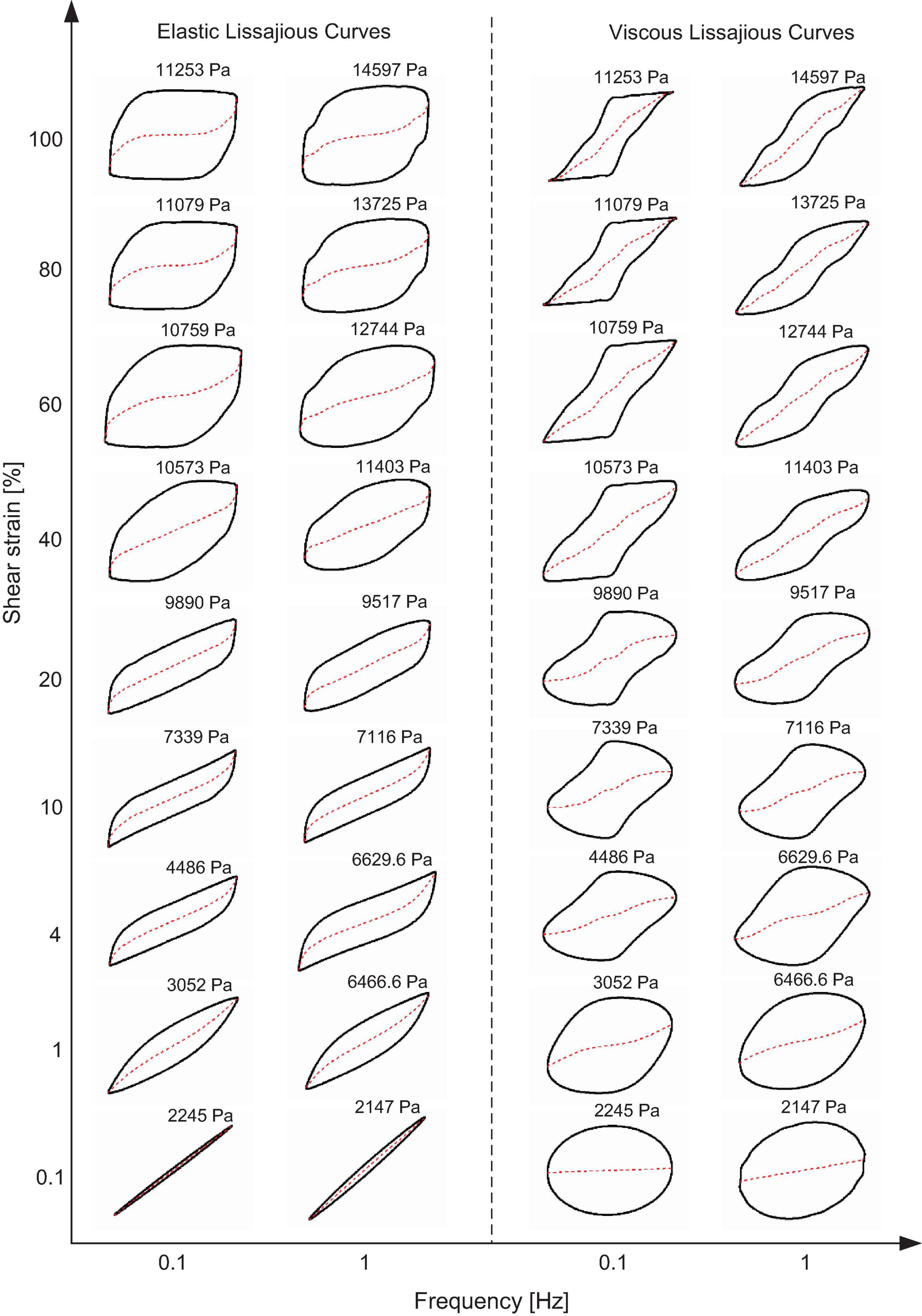
Figure 8. Elastic and viscous Lissajous curves of MRG-70 generated from the strain-controlled oscillatory shear under the magnetic field of 391 kA/m. Each curve is positioned according to the imposed value of shear strain and frequency. The red dash line represents the corresponding decomposed elastic and viscous stress. The value above each curve is the maximum shear stress τ_max.

Figures 6, 7 show the frequency-dependent elastic and viscous Lissajous curves under the small and medium magnetic fields, i.e., 96 and 194 kA/m, respectively. Different from MRG-70 without the magnetic field, when the magnetic field, i.e., 96 or 194 kA/m, is applied, the elastic Lissajous curves of MRG-70 deviated from the elliptical shape at the strain amplitude of 1% due to the arrangement of the CIPs along the direction of the magnetic field, indicating that the LVE range was magnetic field-dependent. Moreover, in the NLVE range, the elastic and viscous Lissajous curves were observed to be less affected by the frequency when the shear strain amplitude increased from 1 to 10%. With the further increase in the strain amplitude, the shape of the elastic and Lissajous curves exhibited a strong frequency dependency. For example, at the shear strain amplitude of 60% under 0.1 Hz, as shown in Figures 6, 7, the elastic Lissajous curves presented a plateau after the shear strain changed the direction. However, a typical overshoot behavior was observed under the frequency of 1 Hz. Such behavior was further strengthened as the shear strain amplitude increased to 100%. The reason for the above characteristics can be attributed to the frequency-dependent relaxation of the CIPs chain or cluster structures. On the other hand, from the decomposed elastic and viscous stress, as shown in Figures 5–7, at two frequencies, i.e., 0.1 and 1 Hz, the elastic non-linearity of MRG-70 under the magnetic fields of 0, 96, and 194 kA/m always showed strain stiffening. However, the viscous non-linearity contains two types, namely shear thickening and then shear thinning, as the magnetic field increases from 96 to 194 kA/m. This is different from MRG-70 that only exhibits viscous non-linearity of shear thickening under zero magnetic field.

Figure 8 depicts the elastic and viscous Lissajous curves under the application of the large magnetic field, i.e., 391 kA/m. In Figure 8, the LVE response, represented by the elliptical shape of the Lissajous curves, can be observed at sufficient small shear strain amplitude, i.e., 0.1%. When the shear strain increased from 0.1 to 100%, it was observed that the non-linear behavior of MRG-70 under the magnetic field of 391 kA/m was almost independent of the oscillatory frequency, and the typical overshoot behavior was disappeared, which is different from that under the small and medium magnetic fields, i.e., 96 and 194 kA/m, as shown in Figures 6, 7. In the NLVE range, the non-linearity of MRG-70 with the magnetic field of 391 kA/m, shown in the elastic domain, was similar to that under the magnetic field of 194 kA/m, i.e., strain stiffening, and the viscous non-linearity of MRG-70 first presented an obvious shear thickening, followed by shear thinning. By comparing Figures 5–8, as the magnetic field increased from 0 to 391 kA/m, the decomposed elastic stress curve under 0.1% strain amplitude approaches coincided with the elastic Lissajous curves, and the slope of the corresponding decomposed viscous stress curve tended to be zero, and this feature was less affected by the frequency. Therefore, we can conclude that MRG-70 at the large magnetic field, i.e., 391 kA/m, under sufficient small strain amplitude almost exhibits purely elastic materials, which is attributed to the fact that the stronger chain or cluster structures are formed. Moreover, in the NLVE range with a large strain amplitude, as the increase of the magnetic field, the elastic curves of MRG-70 gradually formed a quadrilateral shape, indicating that the apparent flow-induced structure was dominated by viscosity. This was also validated by the decomposed elastic and viscous stress. Another interesting phenomenon that can be found from Figures 6–8 is that, as the magnetic field increases, the decomposed elastic stress at the higher shear strain amplitude was zero during the instantaneous intracycle shear strain. For example, under the magnetic field of 391 kA/m at 100% strain amplitude, the decomposed elastic stress of MRG-70 would be zero during the instantaneous intracycle shear strain between − 45 and 45%. This implies that the contribution of the intracycle elastic stress to the non-linearity within that range is almost zero. In summary, by comparing Figures 5–8, it can be concluded that the external magnetic field has a large impact on the non-linearity rheology of MRG-70, especially the viscous contribution to the non-linearity at large shear strain amplitude, and the effect of the oscillatory frequency on the non-linearity was also magnetic field-dependent. For instance, due to the formation of the stronger CIPs chain or cluster structures under the large magnetic field, i.e., 391 kA/m, MRG-70 exhibited purely elastic material behavior at sufficient small strain, e.g., 0.1%, but fluidlike structure was dominated by viscous dissipation at large shear strain, e.g., 100%.

Elastic and Viscous Measures of MRG-70

The elastic and viscous measures, i.e., Chebyshev coefficients ratios, strain-stiffening, and shear-thickening ratios, corresponding to Figures 5–8, were used to quantitatively analyze the field-dependent non-linearities of MRG-70 at two different frequencies. In this study, we used the different orders of elastic (viscous) Chebyshev coefficients, i.e., e₁ (v₁), e₃ (v₃), e₅ (v₅), etc., to calculate the strain-stiffening (shear-thickening) ratios since they can better reconstruct the decomposed elastic (viscous) stress. Figure 9 shows the elastic measures, i.e., third-order elastic Chebyshev coefficient, e₃/e₁, and strain-stiffening ratio, S, as a function of the shear strain amplitude under different oscillatory frequencies, i.e., 0.1 and 1 Hz, and magnetic fields, i.e., 0, 96, 194, and 391 kA/m. As mentioned in the “Introduction” section, S and e₃/e₁ have the same sign and can be used to interpolate the intracycle non-linearities of elastic, i.e., S and e₃/e₁ > 0 represent strain stiffening and S and e₃/e₁ < 0 represent strain softening (Ewoldt et al., 2008). From Figure 9, S and e₃/e₁ all tended to zero at low shear strain amplitude, i.e., 0.4, 0.06, 0.1, and 0.4% for 0, 96, 194, and 391 kA/m, indicating the LVE response. The critical shear strain obtained in this study was little different from that shown in Figures 5–7. The reason is that, for detecting the transition from linearity to non-linearity, higher-order Chebyshev coefficient were more accurate than the elastic and viscous Lissajous curves (Renou et al., 2010). After entering into the non-linear range, S and e₃/e₁ had the same trend and are positive at two different oscillatory frequencies under the magnetic fields of 0 and 391 kA/m, indicating the intracycle strain-stiffening behavior. However, under the small and medium magnetic fields, i.e., 96 and 194 kA/m, S or e₃/e₁ changes to be negative and shows the frequency dependency, suggesting the strain-softening behavior which is different from the results shown in Figures 6, 7. The reason is that the decomposed elastic stress curves are interfered by the yield behavior. Moreover, from Figures 9A–D, the dependence of the elastic non-linearity on shear strain amplitude was less affected by the oscillatory frequency but had a close relationship with the external magnetic field. For example, S and e₃/e₁ almost exhibited the same trend with the strain amplitude at two different frequencies. However, under large shear strain amplitude (>40%), S and e₃/e₁ decreased with the shear strain at 0 kA/m but increased with the shear strain amplitude when the magnetic field was applied. This shows that the non-linear elastic contribution at large shear strain amplitude (>40%) was enhanced when the magnetic field was applied. The possible reason is that MRG-70 undergoes the interaction between the breaking and reorganization of the CIPs chain structures under the combination of oscillatory shear and magnetic field.

FIGURE 9

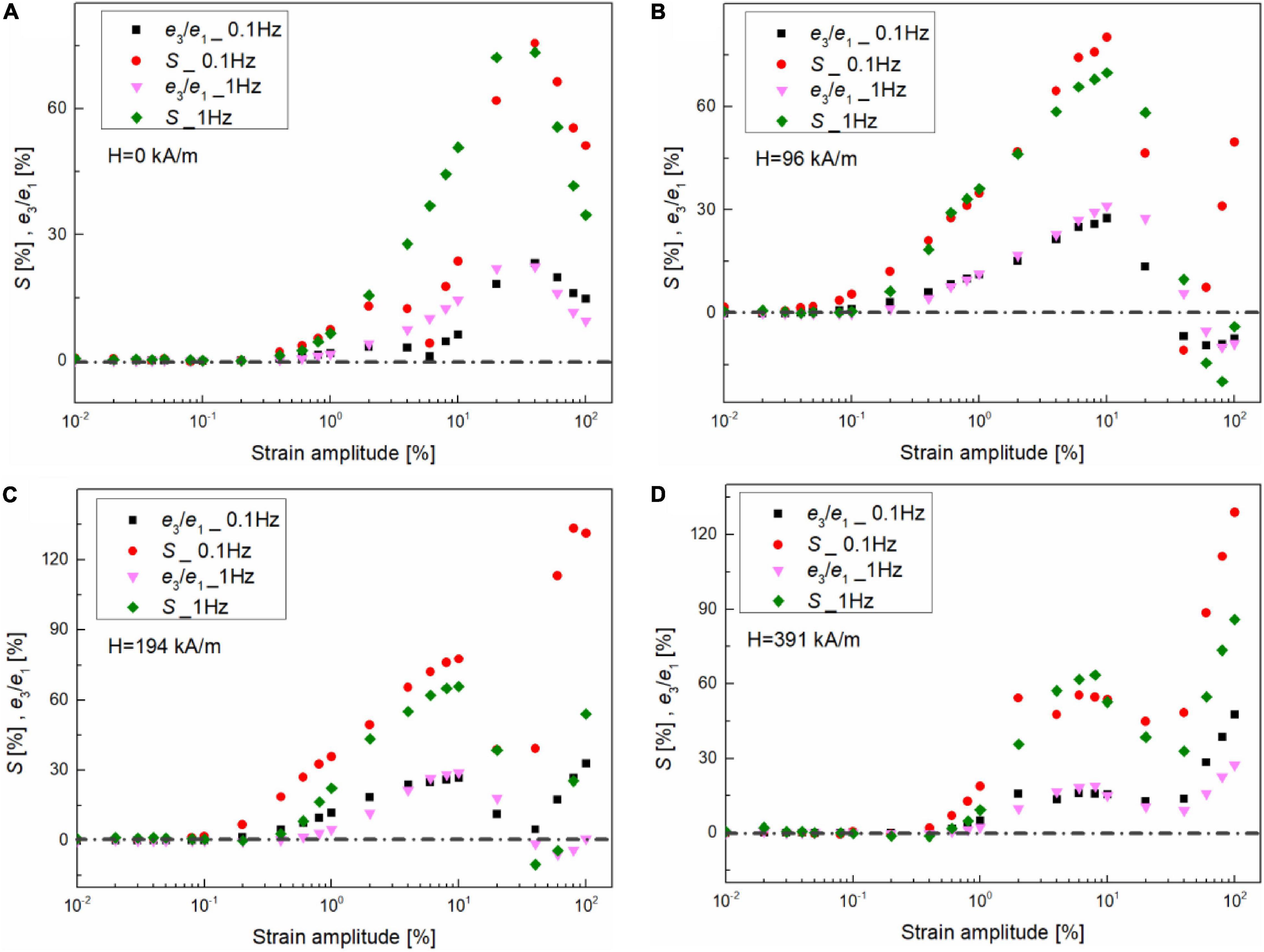
Figure 9. Strain dependence of third-order elastic Chebyshev coefficient, i.e., e₃/e₁, and strain-stiffening ratio, S, for MRG-70 under different oscillatory frequencies, i.e., 0.1 and 1 Hz. The LAOS test was conducted on four different magnetic fields, such as (A) 0, (B) 96, (C) 194, and (D) 391 kA/m. The dashed lines indicate the value of zero.

Figure 10 shows the shear strain amplitude-dependent viscous measures, i.e., third-order viscous Chebyshev coefficient, v₃/v₁, and shear-thickening ratio, T, at two different oscillatory frequencies, i.e., 0.1 and 1 Hz, and magnetic fields, i.e., 0, 96, 194, and 391 kA/m. Similarly, T and v₃/v₁ can be used to interpolate the intracycle non-linearities of viscous, i.e., T and v₃/v₁ > 0 representing shear thickening, and T and v₃/v₁ < 0 representing shear thinning (Ewoldt et al., 2008). From Figures 10A–D, T and v₃/v₁ fluctuate and suffer from more residual noise than the elastic measures within the linear regime at a large magnetic field, i.e., 0–0.07% for 391 kA/m. The reason is that the viscous contribution to the total stress response at this stage was too small, which is also verified in Figure 8. Moreover, when the magnetic field is not applied, an identical intracycle non-linear behavior, i.e., shear thinning, was observed throughout the non-linear regime, as indicated by the negative of T and v₃/v₁ (Figure 10A). However, when the magnetic field is applied (Figures 10B–D), MRG-70 exhibits two different viscous non-linear behaviors in the non-linear regime from 0.1 to 100%, i.e., shear thickening first, followed by shear thinning, which complies with the qualitative analysis shown in Figures 6, 7. Moreover, the critical strain amplitude between shear thickening and shear thinning is frequency- and magnetic field-dependent. For instance, the critical strain amplitude under 0.1 Hz was always smaller than that of under 1 Hz for different magnetic fields, e.g., 15% for 0.1 Hz and 40% for 1 Hz under the magnetic field of 96 kA/m. Comparing Figure 10 with Figure 9, we can conclude that the intracycle non-linearity of viscous seems to be more sensitive to the magnetic field in comparison with the non-linearity of elasticity.

FIGURE 10

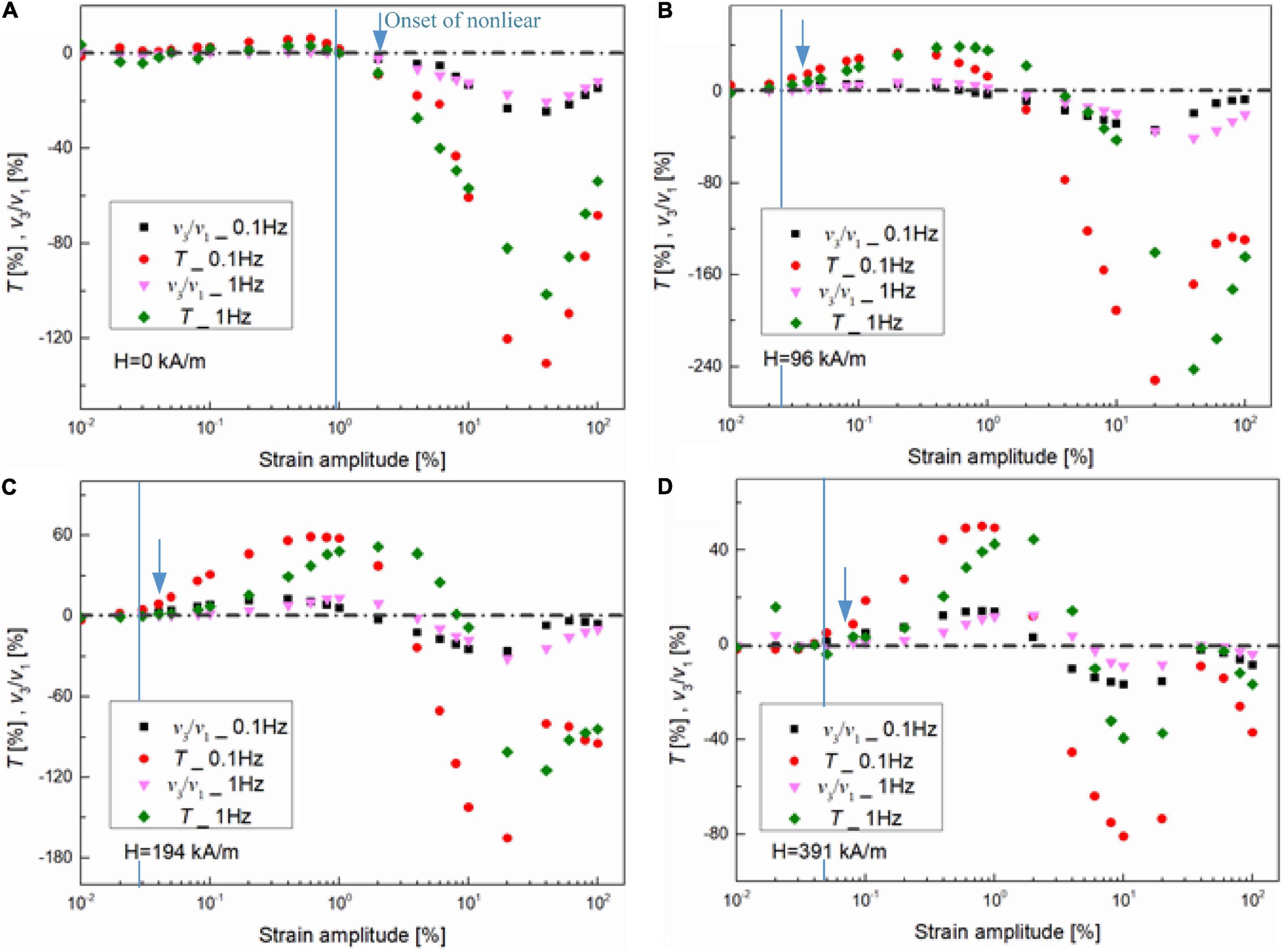
Figure 10. Strain dependence of viscous Chebyshev coefficients ratios, i.e., v₃/v₁, and shear-thickening ratio, T, for MRG-70 under different oscillatory frequency, i.e., 0.1 and 1 Hz. The LAOS test was conducted on four different magnetic fields, such as (A) 0, (B) 96, (C) 194, and (D) 391 kA/m. The dashed lines indicate the value of zero. The blue solid line is the boundary between linear and non-linear viscoelastic regimes. The blue arrow indicates the appearance of non-linearity.

To characterize the frequency-dependent composition of the non-linearity for MRG-70 under different oscillatory strain amplitudes and magnetic fields, the comparison between S and T as a function of strain amplitude is shown in Figure 11. It can be seen that, in the LVE range, the elastic and viscous contributions are equal to 0. Along with the increasing shear strain amplitude, the NLVE appeared. From Figure 11A, the appearance of the non-linearity without the magnetic field seems to be slightly affected by the magnetic field. However, under the application of the magnetic field shown in Figures 10B–D, the onset of the non-linearity is frequency-dependent, i.e., the appearance of the NLVE under 0.1 Hz is always fast than that of under 1 Hz. On the other hand, in the NVLE range, the non-linearity of MRG-70 under the magnetic field of 0 kA/m was portrayed as the combination of strain stiffening (S > 0) and shear thinning (T < 0) through the non-linear range. However, when the magnetic field is applied, MRG-70 shows a substantial variation with the non-linear strain amplitude. For example, at the magnetic field of 391 kA/m, as shown in Figure 11D, MRG-70 only showed shear thickening (T > 0) at the onset of the non-linearity, i.e., 0.04 to 0.4%. Then, in the shear range from 0.4 to 2%, the non-linearity consisted of strain stiffening (S > 0) and shear thickening (T > 0). Above 2% strain, the non-linearity showed the combination of strain stiffening (S > 0) and shear thinning (T < 0). Interestingly, the similar behavior was also observed for MRG-70 at the oscillatory frequency of 1 Hz (Figures 11B–D). Combining the study on the strain dependence storage and loss modulus shown in Figure 2, we found that, in the shear strain range of S > 0 and T < 0, e.g., about 4–100% under 96 kA/m, 8–100% under 194 kA/m, and 5–100% under 391 kA/m, the corresponding storage and loss moduli always decreased with the shear strain. This phenomenon indicates that, in the post-yield range, the non-linearity of MRG-70 with the magnetic field exhibited the strain stiffening for the elastic stress and predominant shear thinning of the energy dissipation. Finally, the above analysis points out that the non-linear rheology of MRG-70 had little relationship with the oscillatory frequency but was highly affected by the shear strain amplitude and external magnetic field, which is composed of different elastic and viscous intracycle physical mechanisms.

FIGURE 11

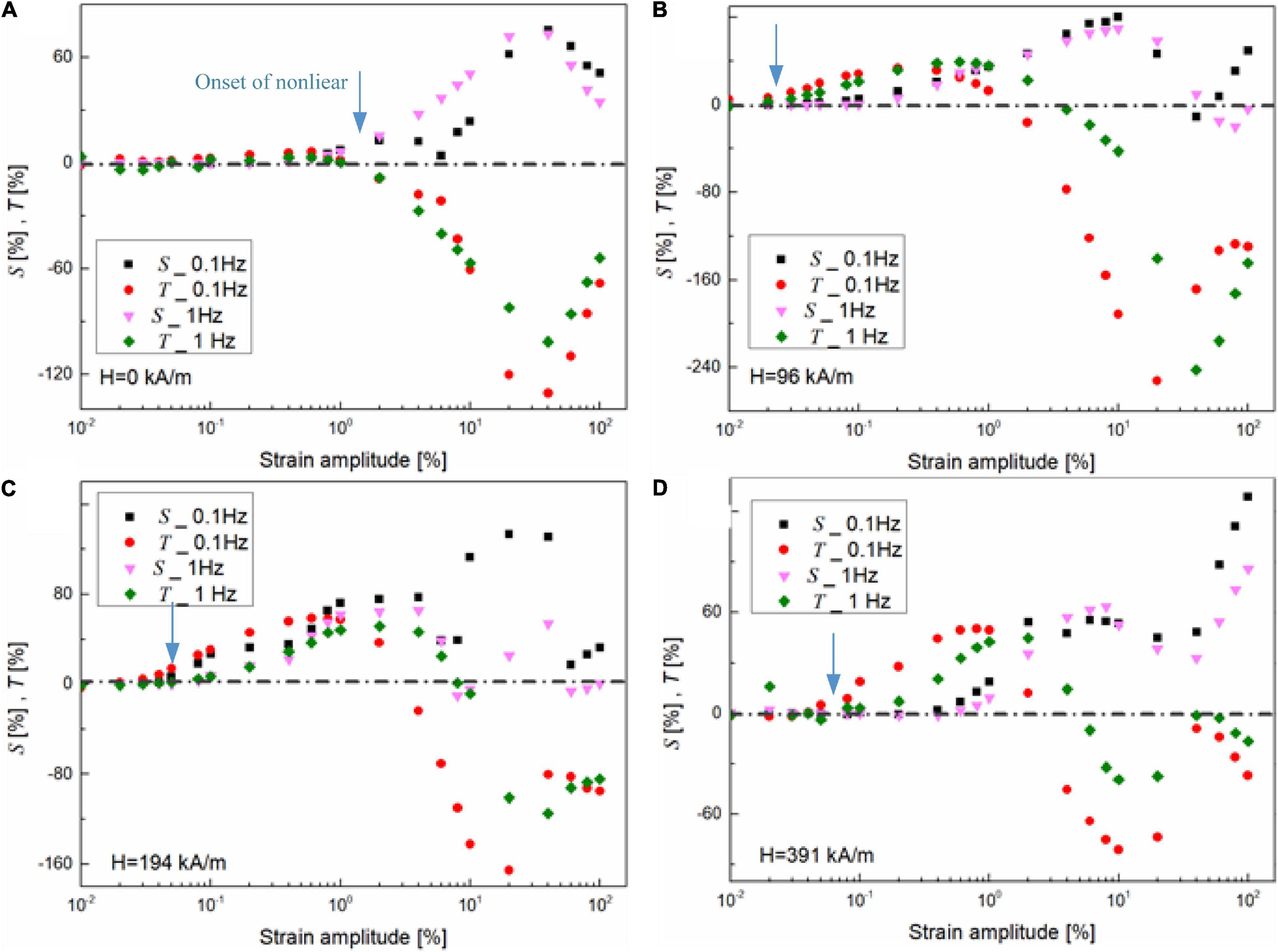
Figure 11. Strain dependence of strain-stiffening ratio and shear-thickening ratio, i.e., S and T, for MRG-70 under different oscillatory frequencies, i.e., 0.1 and 1 Hz. The LAOS test was conducted on four different magnetic fields, such as (A) 0, (B) 96, (C) 194, and (D) 391 kA/m. The dashed lines indicate the value of zero. The blue arrow indicates the appearance of non-linearity.

Conclusion

We studied the field-dependent non-linear rheology of MRG-70 under LAOS at different driving frequencies. First, the storage and loss moduli under the frequencies of 0.1, 0.5, 1, and 5 Hz were compared, and the results showed that, when the frequency rose from 0.1 to 5 Hz, MRG-70 mainly exhibits two viscoelastic characteristics, i.e., strain thinning in which G’ and G” decrease in the NLVE range at 0.1 Hz, weak strain overshoot in which G’ decreases but G” increases, followed by a decrease in the NLVE range at frequencies of 0.5, 1, and 5 Hz. Moreover, the viscoelastic behavior of MRG-70 under oscillatory shear can be divided into three parts: linear region, the onset of the non-linear region, and the post-yield region. Second, the 3D Lissajous curves and the decomposed elastic and viscous stress curves were presented and utilized to qualitatively analyze the field-dependent non-linear rheology of MRG-70 at two typical frequencies. It was found that, irrespective of the frequency, MRG-70 always has elasticity during the oscillatory shear at the sufficient small strain amplitude. When the strain amplitude increased to a large value, the elastic Lissajous curves presented with the shape of quadrilateral, and the maximum stress in viscous Lissajous curves was located at the maximum shear strain of ± γ₀ω, indicating that the non-linearity of MRG-70 at 100% mainly comes from viscous flow, and the above behavior has highly dependent on the external magnetic field. Finally, the elastic and viscous measures, i.e., Chebyshev coefficient ratios (e₃/e₁ and v₃/v₁), strain-stiffening ratio (S), and shear-thickening ratio (T), were used to conduct the quantitative analysis to characterize the non-linear rheology of MRG-70. It was demonstrated that the onset of the non-linear behavior of MR grease was frequency-dependent when the magnetic field was applied. However, in the post-yield region, the field-dependent non-linear rheology of MRG-70 had little relationship with the oscillatory frequency but was highly affected by the shear strain amplitude.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

HW: formal analysis, investigation, methodology, writing—original draft. GZ, TC, and SL: resources. YL and JW: supervision. JW: writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work has been supported by the National Natural Science Foundation of China (NSFC) grant funded by the Chinese government (Nos. 51675280, 51705467, and 51805209). It has also been supported by the Postgraduate Scientific Innovation Research Foundation of Jiangsu Province (No. KYCX18_0391).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the financial support obtained from China Scholarship Council (CSC) in the exchange program at the University of Technology Sydney, Australia.

References

Agirre-Olabide, I., Berasategui, J., Elejabarrieta, M. J., and Bou-Ali, M. M. (2014). Characterization of the linear viscoelastic region of magnetorheological elastomers. J. Intellig. Mater. Syst. Struct. 25, 2074–2081. doi: 10.1177/1045389x13517310

CrossRef Full Text | Google Scholar

Cho, K. S., Hyun, K., Ahn, K. H., and Lee, S. J. (2005). A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 49, 747–758. doi: 10.1122/1.1895801

CrossRef Full Text | Google Scholar

Delgado, M., Valencia, C., Sánchez, M., Franco, J., and Gallegos, C. (2006). Influence of soap concentration and oil viscosity on the rheology and microstructure of lubricating greases. Indust. Eng. Chem. Res. 45, 1902–1910. doi: 10.1021/ie050826f

CrossRef Full Text | Google Scholar

Ewoldt, R. H., Hosoi, A., and McKinley, G. H. (2008). New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J. Rheol. 52, 1427–1458. doi: 10.1122/1.2970095

CrossRef Full Text | Google Scholar

Ghosh, A., Chaudhary, G., Kang, J. G., Braun, P. V., Ewoldt, R. H., and Schweizer, K. S. (2019). Linear and nonlinear rheology and structural relaxation in dense glassy and jammed soft repulsive pNIPAM microgel suspensions. Soft Matter. 15, 1038–1052. doi: 10.1039/c8sm02014k

PubMed Abstract | CrossRef Full Text | Google Scholar

Goudoulas, T. B., and Germann, N. (2019a). Nonlinear rheological behavior of gelatin gels: in situ gels and individual gel layers filled with hard particles. J. Coll. Interf. Sci. 556, 1–11. doi: 10.1016/j.jcis.2019.08.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Goudoulas, T. B., and Germann, N. (2019b). Nonlinear rheological behavior of gelatin gels: in situ gels and individual layers. J. Coll. Interf. Sci. 553, 746–757. doi: 10.1016/j.jcis.2019.06.060

PubMed Abstract | CrossRef Full Text | Google Scholar

Hyun, K., Wilhelm, M., Klein, C. O., Cho, K. S., Nam, J. G., Ahn, K. H., et al. (2011). A review of nonlinear oscillatory shear tests: analysis and application of large amplitude oscillatory shear (LAOS). Prog. Poly. Sci. 36, 1697–1753. doi: 10.1016/j.progpolymsci.2011.02.002

CrossRef Full Text | Google Scholar

Kavlicoglu, B. M., Gordaninejad, F., and Wang, X. (2015). Study of a magnetorheological grease clutch. Smart Mater. Struct. 22:125030. doi: 10.1088/0964-1726/22/12/125030

CrossRef Full Text | Google Scholar

Li, S., Tian, T., Wang, H., Li, Y., Li, J., Zhou, Y., et al. (2020). Development of a four-parameter phenomenological model for the nonlinear viscoelastic behaviour of magnetorheological gels. Mater. Design 194:108935. doi: 10.1016/j.matdes.2020.108935

CrossRef Full Text | Google Scholar

Mohamad, N., Mazlan, S. A., Choi, S.-B., Aziz, A., Aishah, S., and Sugimoto, M. (2019a). The effect of particle shapes on the field-dependent rheological properties of magnetorheological greases. Intern. J. Mol. Sci. 20:1525. doi: 10.3390/ijms20071525

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohamad, N., Mazlan, S. A., Ubaidillah, Choi, S.-B., Imaduddin, F., and Abdul Aziz, S. A. (2019b). The field-dependent viscoelastic and transient responses of plate-like carbonyl iron particle based magnetorheological greases. J. Intellig. Mater. Syst. Struct. 30, 788–797. doi: 10.1177/1045389x19828504

CrossRef Full Text | Google Scholar

Mohamad, N., Mazlan, S. A., Ubaidillah, S.-B., Choi, M., and Nordin, F. M. (2016). The field-dependent rheological properties of magnetorheological grease based on carbonyl-iron-particles. Smart Mater. Struct. 25:095043. doi: 10.1088/0964-1726/25/9/095043

CrossRef Full Text | Google Scholar

Mohamad, N., Ubaidillah, S., Imaduddin, F., Choi, S.-B., and Yazid, I. (2018). A comparative work on the magnetic field-dependent properties of plate-like and spherical iron particle-based magnetorheological grease. PLoS One 13:e0191795. doi: 10.1371/journal.pone.0191795

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, B. O., Park, B. J., Hato, M. J., and Choi, H. J. (2011). Soft magnetic carbonyl iron microsphere dispersed in grease and its rheological characteristics under magnetic field. Colloid Polym. Sci. 289, 381–386. doi: 10.1007/s00396-010-2363-y

CrossRef Full Text | Google Scholar

Rankin, P. J., Horvath, A. T., and Klingenberg, D. J. (1999). Magnetorheology in viscoplastic media. Rheol. Acta 38, 471–477. doi: 10.1007/s003970050198

CrossRef Full Text | Google Scholar

Renou, F., Stellbrink, J., and Petekidis, G. (2010). Yielding processes in a colloidal glass of soft star-like micelles under large amplitude oscillatory shear (LAOS). J. Rheol. 54, 1219–1242. doi: 10.1122/1.3483610

CrossRef Full Text | Google Scholar

Sahin, H., Gordaninejad, F., Wang, X., and Fuchs, A. (2007). “Rheological behavior of magneto-rheological grease (MRG),” in Proceedings of the Active & Passive Smart Structures & Integrated Systems, San Diego, CA.

Google Scholar

Sakurai, T., and Morishita, S. (2017). Seismic response reduction of a three-story building by an MR grease damper. Front. Mechan. Eng. 12, 224–233. doi: 10.1007/s11465-017-0413-6

CrossRef Full Text | Google Scholar

Sarkar, C., Hirani, H., and Sasane, A. (2015). Magnetorheological smart automotive engine mount. Intern. J. Curr. Eng. Technol. 5, 419–428.

Google Scholar

Shiraishi, T., Miida, Y., Sugiyama, S., and Morishita, S. (2011). Typical characteristics of magnetorheological grease and its application to a controllable damper. Mechan. Eng. J. 77, 2193–2200. doi: 10.1299/kikaic.77.2193

PubMed Abstract | CrossRef Full Text | Google Scholar

Sukhwani, V. K., and Hirani, H. (2008). A comparative study of magnetorheological-fluid-brake and magnetorheological-grease-brake. Tribology 3, 31–35. doi: 10.2474/trol.3.31

CrossRef Full Text | Google Scholar

Upadhyay, R., Laherisheth, Z., and Shah, K. (2013). Rheological properties of soft magnetic flake shaped iron particle based magnetorheological fluid in dynamic mode. Smart Mater. Struct. 23:015002. doi: 10.1088/0964-1726/23/1/015002

CrossRef Full Text | Google Scholar

Wang, H., Chang, T., Li, Y., Li, S., Zhang, G., Wang, J., et al. (2020). Characterization of nonlinear viscoelasticity of magnetorheological grease under large oscillatory shear by using Fourier transform-Chebyshev analysis. J. Intellig. Mater. Syst. Struct. 32, 614–631.

Google Scholar

Wang, H., Li, Y., Zhang, G., and Wang, J. (2019a). Effect of temperature on rheological properties of lithium-based magnetorheological grease. Smart Mater. Struct. 28:e035002-13.

Google Scholar

Wang, H., Zhang, G., and Wang, J. (2019b). Normal force of lithium-based magnetorheological grease under quasi-static shear with large deformation. RSC Adv. 9, 27167–27175. doi: 10.1039/c9ra04987h

CrossRef Full Text | Google Scholar

Wang, H., Zhang, G., and Wang, J. (2019c). Quasi-static rheological properties of lithium-based magnetorheological grease under large deformation. Materials 12:2431. doi: 10.3390/ma12152431

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilhelm, M. (2002). Fourier-transform rheology. Macromolecul. Mater. Eng. 287, 83–105.

Google Scholar

Wilhelm, M., Reinheimer, P., Ortseifer, M., Neidhöfer, T., and Spiess, H.-W. (2000). The crossover between linear and non-linear mechanical behaviour in polymer solutions as detected by Fourier-transform rheology. Rheol. Acta 39, 241–246. doi: 10.1007/s003970000084

CrossRef Full Text | Google Scholar

Zhang, G., Li, Y., Wang, H., and Wang, J. (2019). Rheological properties of polyurethane-based magnetorheological gels. Front. Mater. 6:56. doi: 10.3389/fmats.2019.00056

CrossRef Full Text | Google Scholar

Zhang, G., Li, Y., Yu, Y., Wang, H., and Wang, J. (2020). Modeling the nonlinear rheological behavior of magnetorheological gel using a computationally efficient model. Smart Mater. Struct. 29: aba809.

Google Scholar