Magneto-Induced Normal Stress of Magnetorheological Gel Under Quasi-Statically Monotonic and Periodically Cyclic Loading

Introduction

Magnetorheological (MR) gel is a sort of intelligent material whose rheological properties could be changed expeditiously and reversibly by controlling the excited magnetic field (Xu et al., 2017; Meharthaj et al., 2019). MR gel (MRG), an analog of MR fluid and MR elastomer, is typically fabricated by dispersing soft magnetic particles into the cross-linked polymer matrix. Due to the existence of the viscoelastic polymeric matrix, MRG could overcome many defects occurred in MR fluid (Ashtiani et al., 2015) to some extent, such as sedimentation problem and sealing problem. Also, magnetic particles in MR elastomer could not move easily owing to the constraint of the rigid rubber matrix, which means that the MR effect of MR elastomer is highly weaker than that of MRG (Xu et al., 2011). Therefore, it is promising for MRG to be employed in engineering devices, such as MR dampers (Rahman et al., 2017; Rossi et al., 2018), MR isolators (Li et al., 2013; Ahamed et al., 2018), and MR actuators (Khazoom et al., 2020).

Up to date, publications on MRG paid attention to the shear response behavior (Auernhammer, 2019; de Sousa et al., 2019; Zhang et al., 2019), such as shear yield stress, damping performance, and shear modulus. In contrast, the investigations on normal stress behavior of MRG are relatively infrequent. However, normal stress of MR material has a strong effect on the performance of some engineering devices, such as MR damper (Yazid et al., 2016) and MR finishing (Lambropoulos et al., 2010). Moreover, the normal stress behavior is also significant for understanding the mechanism of the MR effect and the evolution of particle microstructures. Gong et al. (2012) investigated the normal force behavior of MR fluid under the steady and oscillatory shear condition by employing a commercial rheometer with parallel-plate geometry. They proposed a dynamic simulation method to predict the normal force of MR fluid. Lopez-Lopez et al. (2010) conducted a series of experiments to validate the accuracy of their proposed theoretical model used to calculate the normal force of MR suspensions (Lopez-Lopez et al., 2010). The proposed model comprised the viscoelastic response of MR fluid and the influence of Maxwell stress and can help us better understand the normal force of MR fluid. See et al. observed that the normal force pushed apart the plate with the increase of the magnetic field when no deformation was applied to the MR suspension (See and Tanner, 2003). However, the normal force decreased firstly and then plateaued with the shear strain when continuous shearing was applied to MR suspension. The normal force of MRG under steady and oscillatory shear condition was firstly investigated by Ju et al. (2013). They systematically analyzed the influence of various excited factors (temperature, time history and frequency, etc.) on the normal force of MRG. The results revealed that the normal force of MRG is highly dependent on the magnetic field. Gong et al. (2012) discussed the non-linear behavior of normal stress of MR polymer gel under large amplitude oscillatory shear condition (Pang et al., 2018). They found that the alteration of normal stress was mainly influenced by two factors, Poynting effect and excited magnetic field, which are both relevant to the interior microstructures of MR polymer gel. The experimental results in the literature of Yang et al. (2017) revealed that the loss factor of MRG witnessed a reduction with the increase of CIP content. This is possibly because the molecular chain of polyurethane (PU) matrix becomes shorter and the particle chains keep thickening due to the increment of CIP content. Wang et al. (2016) used a modified split Hopkinson pressure bar (SHPB) instrument to study the strain-rate compressing behavior of a kind of new smart material, magnetically responsive shear-stiffening gel (MSTG). They found that the elastic modulus of MSTG with 45% CIP content could be as high as 126.6 MPa, nearly 791,250 times larger than that at normal state. Zhang et al. proposed a new phenomenon model for predicting the non-linear mechanical behavior of MRG, and the model is more computationally efficient than the previous models (Zhang and Wang, 2020).

As mentioned above, the current research on normal stress of MR materials is investigated mostly under the static shear and dynamic shear. However, it is worthwhile to note that many engineering devices work under the quasi-statically monotonic shear and periodically cyclic shear condition (Liu et al., 2014), such as high building and vehicle suspension system. In general, the loadings that are exerted on MR devices are divided into three kinds—static loading, dynamic loading, and quasi-static loading—which are distinguished by shear rate (Kuwano et al., 2013; Perez et al., 2016; Wang et al., 2019). The shear rate of quasi-static loading ranges from 10^–4 to 10^–1 s^–1, which works as a “bridge” between static loading and dynamic loading. The performance of MR device usually has a close correlation to the normal stress behavior of MR material in the process of quasi-static loading. On the other hand, MRG exhibits the feature of magneto-stimuli and magnetostriction due to the existence of polymeric matrix and magnetic particles. The prolongation of MRG is large in the presence of a magnetic field, resulting from the stretching and twining of soft segments in polymeric matrix and the particle-assembled chain structures. However, the microstructures of MRG, such as particle chains and soft segments, will be sheared ceaselessly under the application of large deformation. Simultaneously, the microstructures are tended resist the shearing and to recover continuously due to the quite low shear rate. This complex evolutive process of internal microstructures leads to the special normal stress behavior of MRG. However, up to now, publications on the normal stress of MRG under quasi-static loading condition are relatively rare. Thus, to better employ MRG in engineering devices, it is a necessity to close this gap, and this is also the motivation of this work.

This work intends to study the normal stress of MRG under quasi-statically monotonic loading and periodically cyclic loading condition. Firstly, MRG with different carbonyl iron powder (CIP) contents, i.e., 40%, 60%, and 70%, was fabricated. Then, the influence of the magnetic field, shear rate, and CIP content on the normal stress of MRG was systematically investigated under monotonic loading condition. Finally, influence of shear strain amplitude on the normal stress of MRG was analyzed under cyclic loading condition. The relevant microscopic mechanisms were proposed to explain the corresponding macroscopic phenomena.

Experiment

Fabrication of Magnetorheological Gel

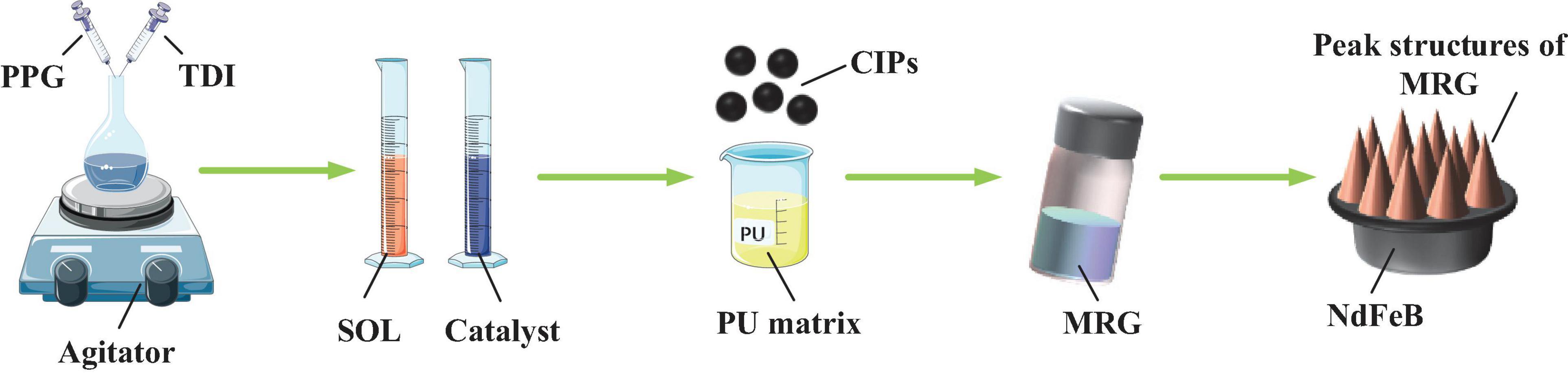
Figure 1 shows briefly the process of fabrication of MRG sample. Polypropylene glycol [PPG-2000, M_n = 2,000, Sigma-Aldrich (Shanghai) Trading Co., Ltd., China] and toluene diisocyanate (TDI; 2,4- ≈ 80%, 2,6- ≈ 20%, Tokyo Chemical Industry Co., Ltd., Japan) are the two main reactants. They were stirred vigorously in a flask, and the reaction was conducted at 80°C. Two hours later, dipropylene glycol [SOL; Sigma-Aldrich (Shanghai) Trading Co., Ltd., China], a chain extender, was added to the flask, and the temperature was controlled at 60°C. Then, moderate stannous octoate (Sinopharm Chemical Reagent Co., Ltd., China) was selected as a catalyst and added to the reaction. The preparation of PU matrix was completed until the viscosity of the mixture increased considerably. Finally, the MRG samples with different CIP contents were fabricated after blending CIP with PU matrix evenly and named as MRG-40, MRG-60, and MRG-70. More details about the synthesized procedure could be seen in our previous work (Mao et al., 2020).

FIGURE 1

Figure 1. Schematic diagram of the fabrication process for magnetorheological gel (MRG).

Testing for Normal Stress

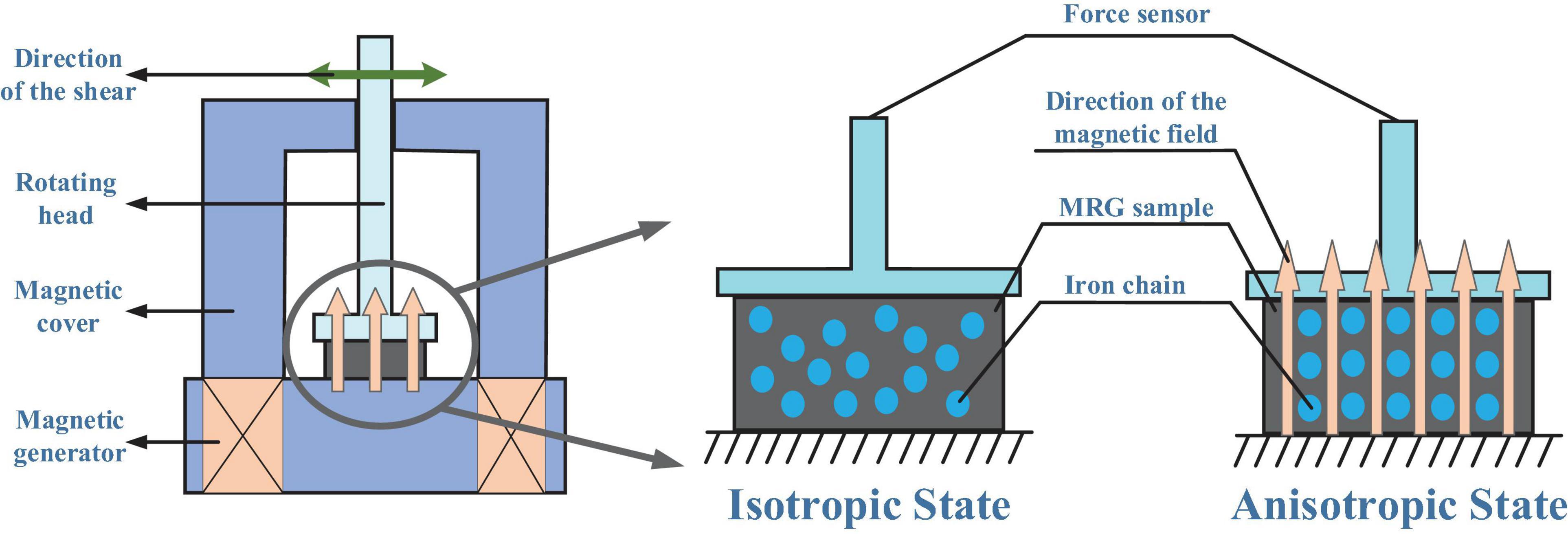
A commercial rheometer (Type MCR 302, Anton Paar Co., Graz, Austria) with a plate–plate geometry was adopted to test the normal stress of MRG, and its schematic diagram is presented in Figure 2. MRG samples were placed between the upper and lower plates. The diameter of the two plates is both 20 mm, and the gap distance between them is 1 mm. In this work, the directions parallel to the magnetic field and vertical to the magnetic field are defined as the normal direction and the lateral direction, respectively. The normal stress and the lateral stress (i.e., shear stress) are simultaneously collected during the testing process. Moreover, according to Laun and Tian, the normal stress (N_d) of MRG could be calculated on the basis of the following equation (Laun et al., 2008; Jiang et al., 2011): N_d = N₁−N₂ = 2F_n/πR², where N₁ is the primary normal stress, N₂ is the secondary normal stress, F_n is the measured normal force by rheometer, and R is the radius of the plate (i.e., 10 mm). The measurable range of normal force F_n is from −50 to 50 N with an accuracy of 0.03 N.

FIGURE 2

Figure 2. Schematic diagram of the MCR 302 commercial rheometer.

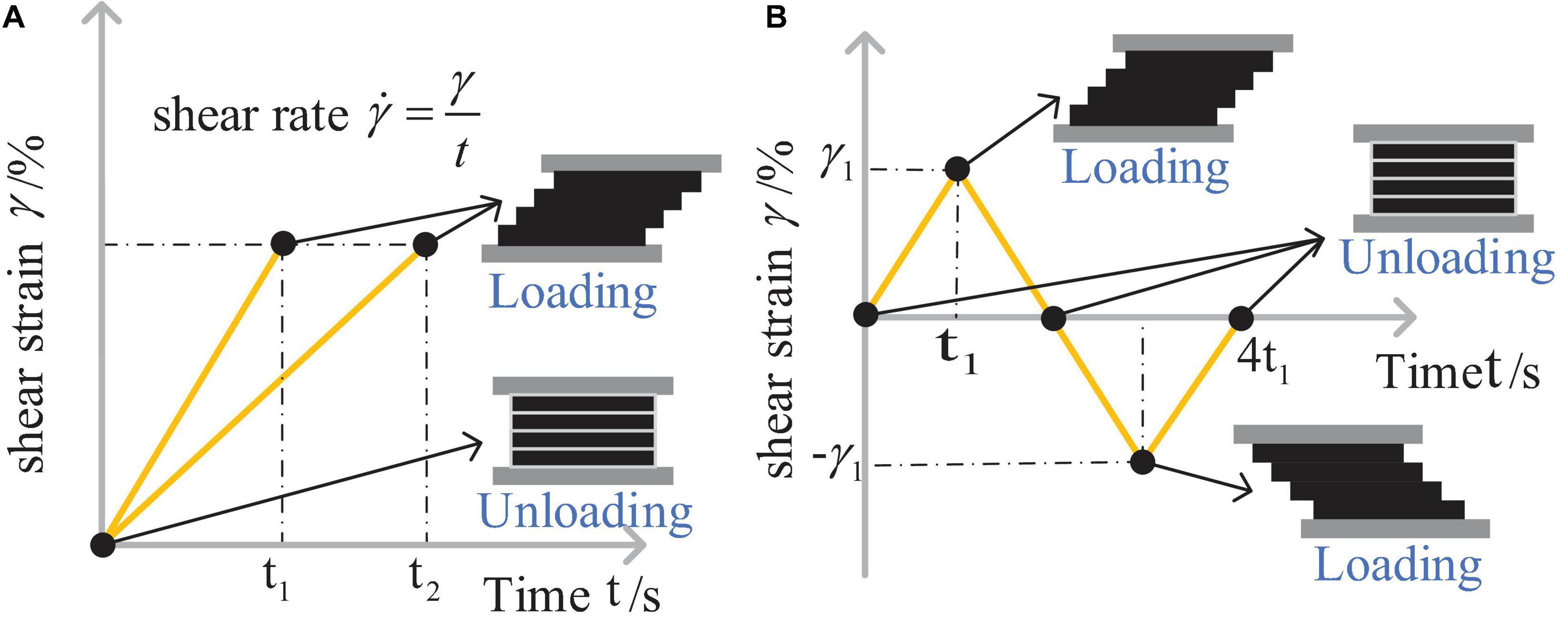
On the other hand, the quasi-static loading comprises two types of loading mode (Mao et al., 2020)—monotonic loading mode and cyclic loading mode—as shown in Figure 3. In the monotonic loading mode, the shear strain applied on the samples increases linearly from 0 to 100% in four different times (i.e., 200, 50, 25, and 12 s). The shear rates could be calculated as $\stackrel{.}{\mathrm{\gamma }}=\mathrm{\gamma }/t$, and thus the shear rates are 0.005, 0.02, 0.04, and 0.083 s^–1, respectively. In the cyclic loading mode, the shear strain increases firstly from 0 to 100%, and then from 100 to −100%, and finally from −100 to 0%. Furthermore, all the tests were undertaken at 25°C.

FIGURE 3

Figure 3. Testing principles of quasi-static monotonic loading (A) and cyclic loading (B).

Results and Discussion

The influencing factors on MRG include the magnetic field, CIP content, shear rate, and shear strain. The purpose of investigating the rheological properties of MRG is to apply it into practical engineering devices, such as dynamic vibration absorber (DVA). In practice, the magnitudes of shear rate and shear strain amplitude depend on the external working conditions, and therefore, the investigation about the influence of stain rate and strain amplitude on normal stress behavior is necessary. In addition, the MRG itself is also a kind of magnetic responsive material. Thus, except for the exterior operating conditions, it is imperative to know that the magnetic field and the quantities of magnetic particles (i.e., CIP content) could influence the normal stress behavior of MRG to a certain degree.

Normal Stress Behavior of Magnetorheological Gel Under Quasi-Statically Monotonic Loading Condition

Influence of Magnetic Field on the Normal Stress Behavior

Figure 4 shows the photographs and microstructures of MRG with and without magnetic fields. MRG presents a semi-fluid-like state, and the magnetic particles disperse randomly in PU matrix when the external magnetic field is not applied. It is because the occurrence of a normal attracting effect (Guo et al., 2012) of MRG makes the plates be attracted to each other. In the presence of a magnetic field, MRG experiences a phase change from a semi-fluid-like state to a semi-solid-like state. Correspondingly, the particles form chain-like microstructures along the direction of the magnetic field, resulting in the occurrence of macroscopic peak structures (Yao et al., 2016). These peak structures will act to push apart the plate of rheometer, and this normal pushing effect will overcome the normal attracting effect. Therefore, the normal stress of MRG is measured. Also, it can be seen from Figures 4B,C that the larger the magnetic field strength, the more the peak structures. Therefore, one can conclude that the effect of the magnetic field will increase the attractive force between particles, resulting in the generation of normal stress. Simultaneously, the peak structures are highly dependent on the microscopic transformation of particle-chain structures (Yao et al., 2015). On the other hand, the evolution of microstructures could be significantly controlled by the external magnetic field. Thus, the normal stress behavior of MRG is hugely relevant to the excited magnetic field.

FIGURE 4

Figure 4. Photographs of magnetorheological gel (MRG) with and without a magnetic field: 0 kA/m (A), 293 kA/m (B), and 740 kA/m (C). Microstructures of MRG (D). The white points represent magnetic particles.

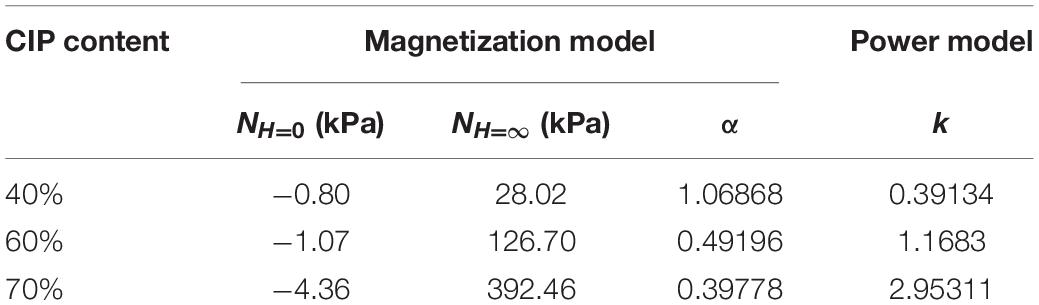
Then, a magnetic field sweep mode was applied to investigate the normal stress behavior of MRG with different CIP contents under quasi-static shear (as shown in Figure 5). The normal stress increases with the increase of magnetic field strength and CIP content. The experimental data in Figure 5 are consistent with the morphology changes of MRG presented in Figure 4. The higher the magnetic field strength is, the stronger the magnetic attractive force between iron particles is, and the larger the normal stress is (as directly displayed in Figures 4B,C). Moreover, compared with MRG-40 and MRG-60, MRG-70 possesses more magnetic particles, leading to the more column-like or cluster-like particle chains under constant magnetic field strength. Therefore, MRG with a higher CIP content will achieve larger normal stress under higher magnetic field strength. Under a dynamic shear mode, the normal stress behavior of MRG could be estimated by the power model (Ju et al., 2013): N_d = kH², where k is the coefficient and H is the magnetic field strength. The fitting results are displayed as black lines in Figure 6, and the magnitudes of coefficient k are presented in Table 1. However, it can be seen from Figure 6 that the power model could not perfectly characterize the normal stress behavior of MRG under the quasi-static shear mode. This is possibly due to the special sigmoid shapes of the N_d–H curves. The increasing speed of normal stress (i.e., the slopes of N_d–H curves) firstly appears a fast growth and then slows down after the magnetic field strength exceeds a critical value (Mao et al., 2020). Thus, a modified magnetization model (Zubieta et al., 2009) was used to describe the variation of normal stress with magnetic field strength under the quasi-static shear mode. The expression of magnetization model is N_d = N_{H = ∞} + (N_{H = 0}−N_{H = ∞})2(e^−αH−0.5e^−2αH), where N_{H    =0} is the field-off normal stress, N_{H    =∞} is the saturation value of normal stress, and α is saturation moment of index of normal stress (Guo et al., 2012). It can be seen from Figure 6 that the magnetization model, compared with the power model, could fit the experimental results better because the magnetization model takes the influence of magnetic saturation into account. Thus, magnetization model is more appropriate to characterize the normal stress behavior of MRG under the quasi-static shear mode, while the power model could estimate the normal stress of MRG under a dynamic shear mode.

TABLE 1

Table 1. Magnitudes of the fitting parameters.

FIGURE 5

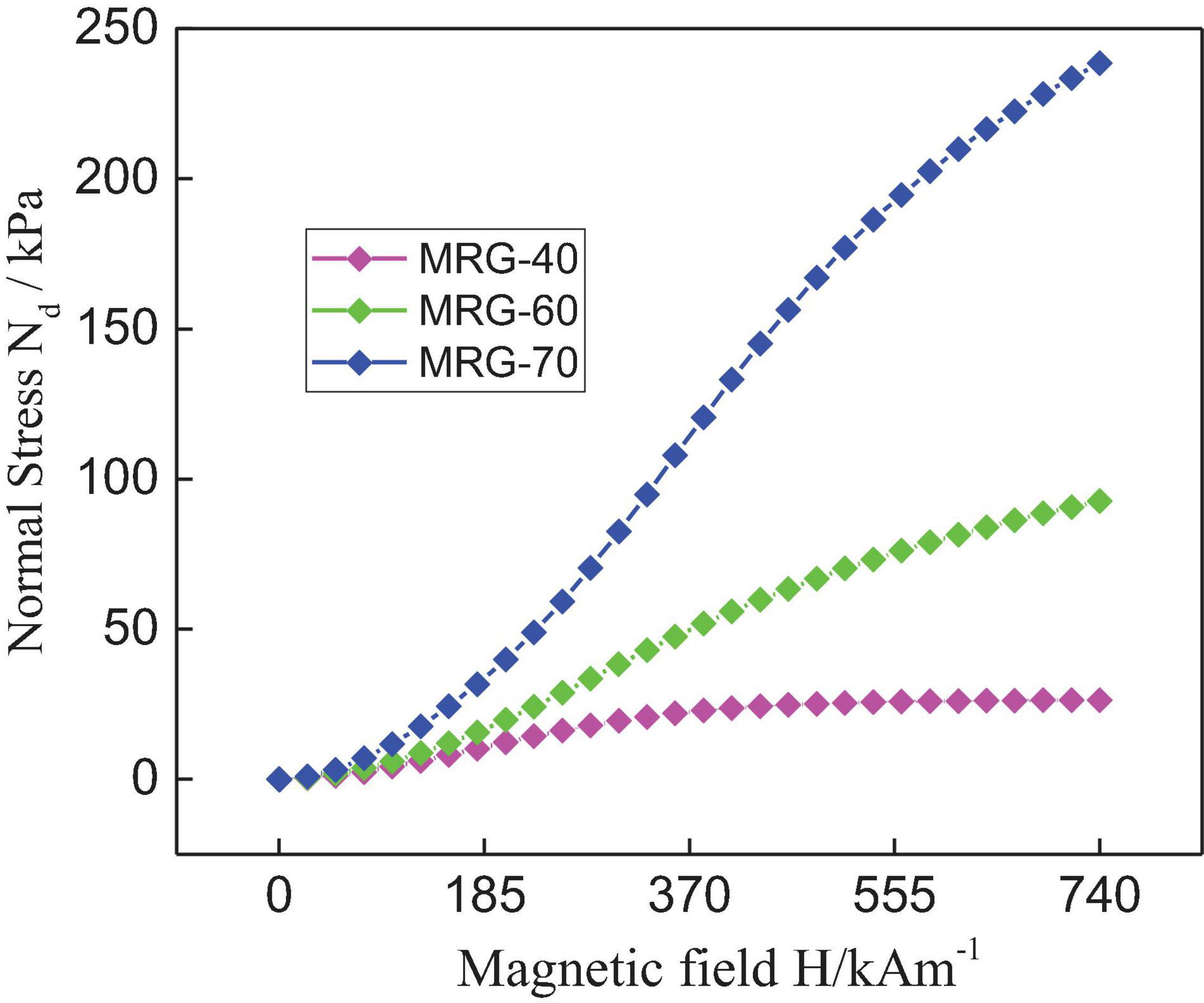
Figure 5. Normal stress of magnetorheological gel (MRG) with different carbonyl iron powder (CIP) contents under magnetic field sweep (quasi-static shear with a shear rate of 0.04 s^–1).

FIGURE 6

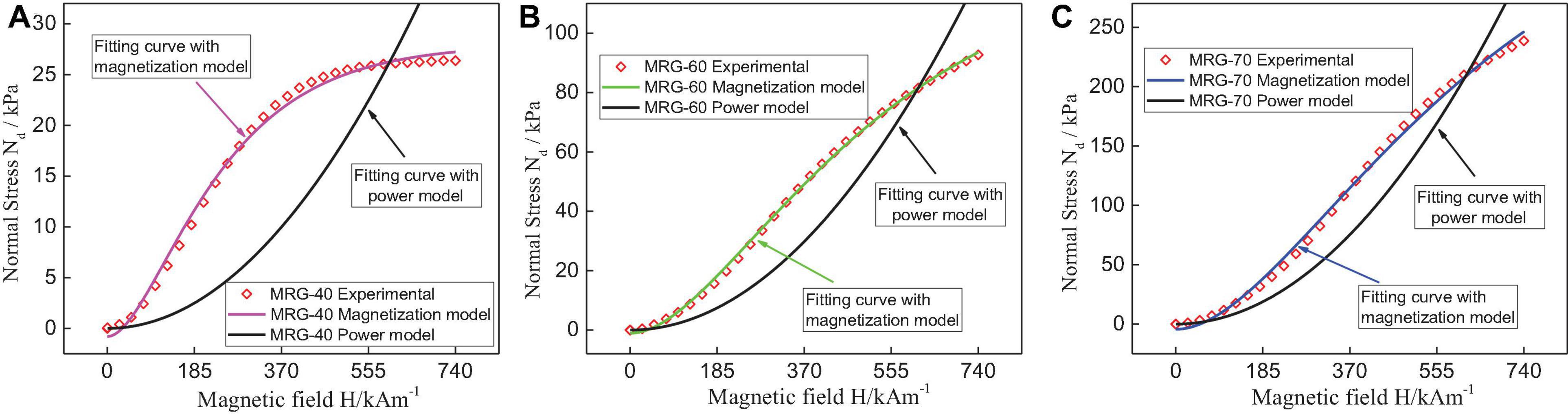
Figure 6. The experimental results and fitting cures with the power model and magnetization model for MRG-40 (A), MRG-60 (B), and MRG-70 (C).

To further understand the mechanism of filed-dependent normal stress behavior of MRG, the normal stress of MRG-60 versus shear strain under four different magnetic fields and constant shear rates of 0.04 s⁻¹ is displayed in Figure 7. The normal stress of MRG is nearly zero and negligible in the absence of a magnetic field while significant in the presence of a magnetic field, corresponding to the change of morphological structures displayed in Figures 4A–C. When the external magnetic field is not applied, the magnetic particles disperse evenly without forming chain-like structures, and thus, no peak structures appear due to the surface tension of MRG and the gravity of magnetic particles (Yao et al., 2015). Thus, normal stress of MRG is almost constant and negligible with the increase of shear strain. This phenomenon indirectly implies that the effect of shear deformation on normal stress behavior is much weaker than that of the magnetic field. When a magnetic field is applied, normal stress of MRG firstly appears an abrupt increase (stage 1), then decreases rapidly with the increase of shear strain (stage 2), and finally reaches a plateau after the shear strain exceeds a critical value (stage 3) (Wang et al., 2019). Besides, larger normal stress will be achieved at larger magnetic field strength. Transformation of normal stress from stage 1 to stage 2 and then to stage 3 could be explained with a microstructure theory (Lopez-Lopez et al., 2010; Wang et al., 2019), as shown in Figure 8. The randomly dispersed magnetic particles (Figure 8A) will aggregate to vertical chain-like structures (Figure 8B) within milliseconds as soon as a magnetic field is applied, resulting in the magnetic interaction and attractive force between the magnetic particles. Thus, the normal stress of MRG appears a sudden increment firstly (stage 1), which indicates that MRG changes from a viscous flow state (Figure 4A) to a semi-solid state (Figures 4B,C). Then, the perpendicular long particle chains tilt into angles (Figure 8C) and break into unstable short chains with the increase of shear strain. This process leads to the rapid reduction of the normal stress of MRG (stage 2). Finally, the unstable short chains are inclined to aggregate together to form stable long chains due to the existence of the magnetic attractive force between magnetic particles. Simultaneously, the fracture of the long chains is still in process with the increase of shear strain. Therefore, a dynamic balance will eventually occur between the fracture and reconstruction of particle chains (Figure 8D), which gives rise to the gradual stability of the normal stress (stage 3).

FIGURE 7

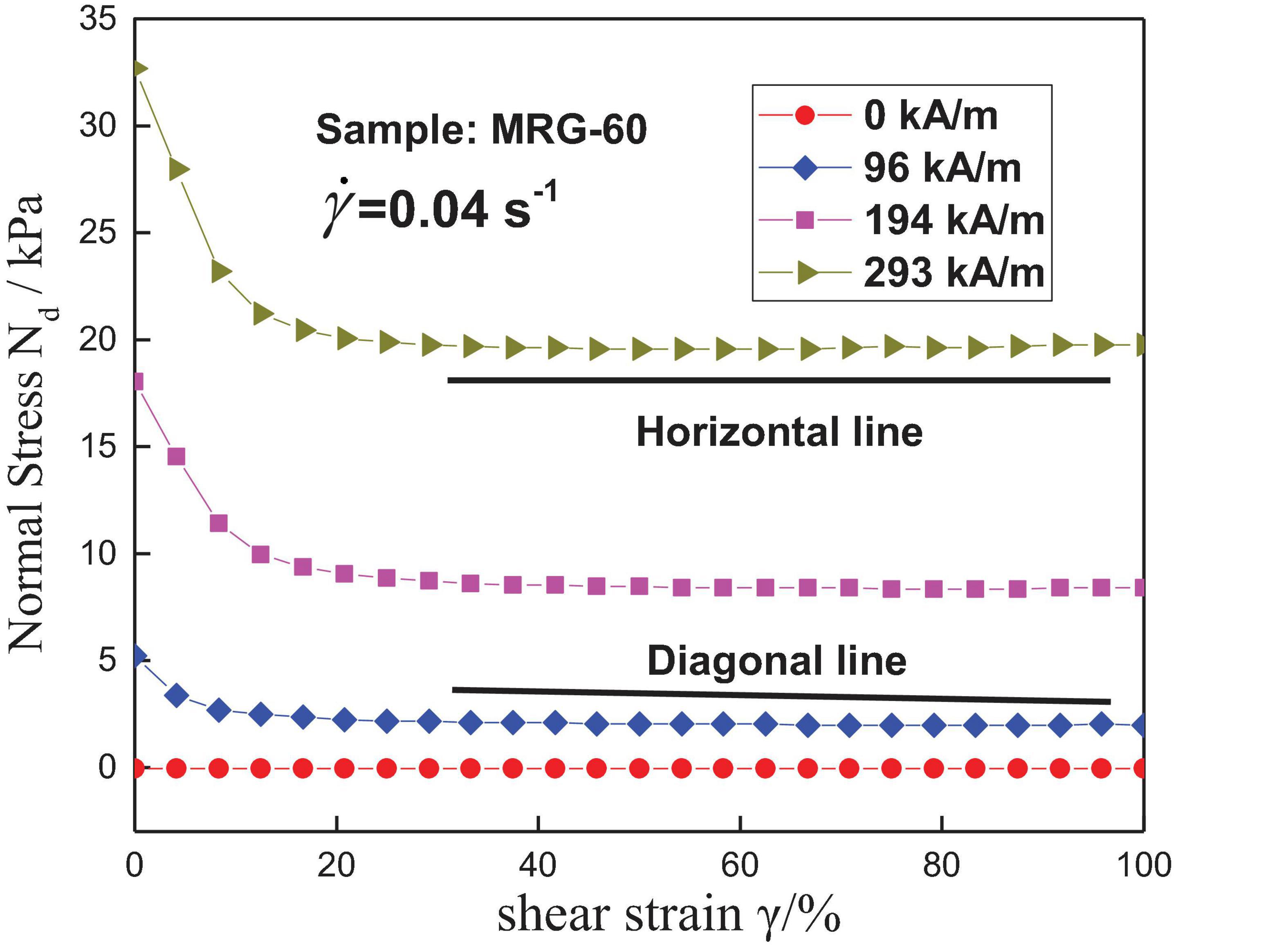
Figure 7. Variation of the normal stress with shear strain for MRG-60 under four different magnetic fields and constant shear rate.

FIGURE 8

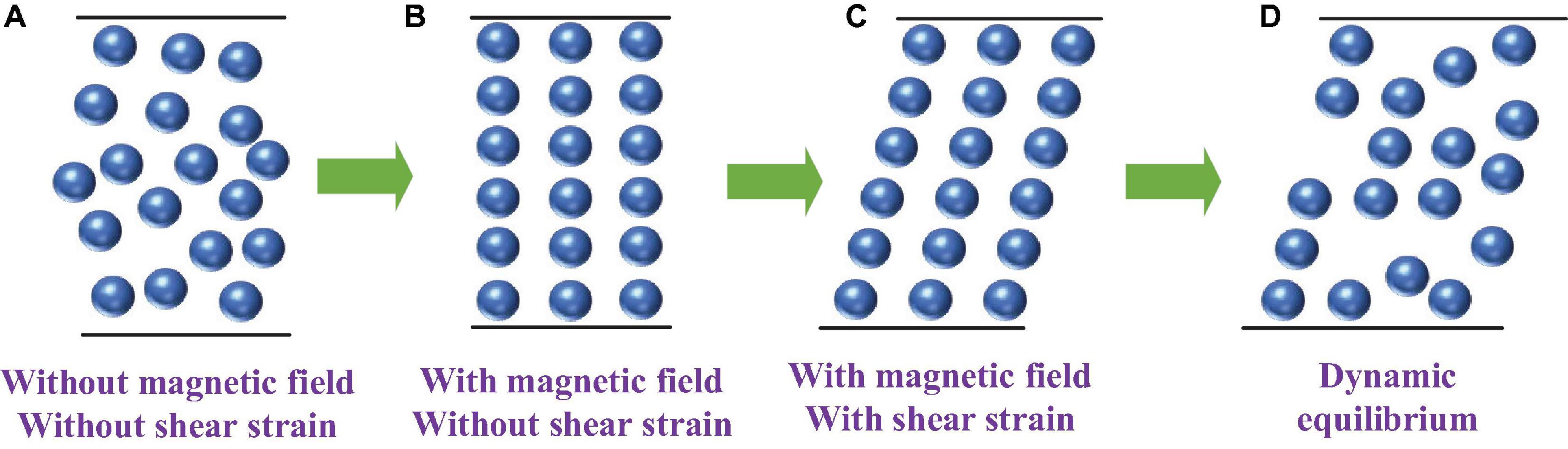
Figure 8. The microstructure of magnetorheological gel (MRG): randomly dispersed particles (A), magnetic field-induced perpendicular particle chains (B), shear strain-induced tilted particle chains (C), and dynamic equilibrium between the fracture and rebuilding of particle chains (D).

Interestingly, another notable phenomenon is that the normal stress will still decrease slightly and obscurely after getting into stage 3, which is similar with the MR fluid (Guo et al., 2012). For example, the normal stress decreases to a certain extent at 96 kA/m of magnetic field strength when the shear strain exceeds the critical value (corresponding to the diagonal line shown in Figure 7). However, this phenomenon will progressively disappear with the increase of the excited magnetic field. This could be interpreted with the following theory. The contribution of shear strain to the fracture of particle chains is constant no matter how large the magnetic field strength is. However, the larger the magnetic field strength, the stronger the magnetic interaction between the particles, and the greater the contribution of the magnetic field to the reconstruction of long particle chains. Thus, the effect of reconstruction on particle chains is weaker than that of fracture when the magnetic strength is relatively small, which leads to the above-mentioned phenomenon.

The MR effect, the most important rheological properties of MR materials, generally results from the magnetic interaction between the polarized magnetic particles. Since both the normal stress and shear stress are also highly relevant to the magneto-induced particle chain microstructures, an investigation on the correlation between the normal stress and shear stress is of great benefit to better understand the mechanism of the MR effect and guide the design of MR device (Jiang et al., 2011). It can be seen from Figure 9A that the stress behavior of MRG could be segmented into pre-yield region and post-yield region, which depends on whether the shear strain exceeds the critical value, γ_c, or not (Wang and Liao, 2011). The shear stress of MRG increases rapidly and then tends to level off with the increase of shear strain, whereas the normal stress appears on an opposite trend in the pre-yield region. Also, similar to MR fluid, MRG could be regarded as a kind of linear viscoelastic material in the pre-yield region, where the stress nearly increases (or decreases) linearly with the shear strain. Moreover, the saturations of normal stress and shear stress in the post-yield region arise from the magnetic saturations in MRG. On the other hand, since the MR effect could be simply expressed as the ratio of field-on shear stress to field-off shear stress (Chen et al., 2013) (i.e., MR effect = $\frac{{\mathrm{\tau }}_{H\ne 0}}{{\mathrm{\tau }}_{H=0}}$), MRG with high shear tress is of great benefit to design precise devices. Thus, it is necessary to study the factors influencing shear stress. According to the research of Li and Chen, the shear stress is mainly influenced by two factors: magnetic force and friction force. The shear stress could be predicted as follows (Li and Zhang, 2008; Chen et al., 2013): τ = τ_f + τ_m = μ⋅N_d + γ⋅N_d, where τ_f and τ_m represent friction-induced stress and magnetic-induced stress, respectively, and μ is the friction coefficient. From the equations, one could conclude that shear stress is strongly relevant to the normal stress, particle–particle friction coefficient, and shear strain. Thus, the ratio of shear stress to normal stress is proposed here and may be helpful for better investigating the mechanism of the magneto-responsive behavior of MRG from a new perspective. The ratio of shear stress to normal stress as a function of shear strain is displayed in Figure 9B. Although the ratio of shear stress to normal stress, r, is $r=\frac{\mathrm{\tau }}{N_d}=\mathrm{\gamma }+\mathrm{\mu }$, the ratio under different magnetic fields does not increase linearly with the increase of shear strain. The variation of ratio with shear strain could also be divided into two regions: pre-yield and post-yield regions. The ratio appears as a rapid growth firstly (i.e., the pre-yield region) and then reaches saturation (i.e., the post-yield region) with the increase of shear strain. In the pre-yield region, unordered particle structures gradually evolve into cluster-like microstructures or complex network-like structures (Liu et al., 2013) under constant magnetic field strength, which gives rise to the increase of friction coefficient. Thus, the ratio of shear stress to normal stress grows in the pre-yield region. In addition, the ratio reaches saturation in the post-yield region for the reason that the shear stress and normal stress are both nearly constant in that region (shown in Figure 9A). On the other hand, larger ratio happens at smaller magnetic field strength, which is similar with the results of MR fluid (Chen et al., 2013). This is because the normal stress and shear stress increase at different levels with the increase of magnetic fields. Taking the normal stress and shear stress at 194 and 293 kA/m of magnetic field, for example, the increment of shear stress is 3.4 kPa (from 3.2 kPa under 194 kA/m to 5.6 kPa under 293 kA/m), while that of normal stress is 11.3 kPa (from 8.4 kPa under 194 kA/m to 19.7 kPa under 293 kA/m). Because normal stress was much larger than shear stress, with normal stress being the denominator ($r=\frac{\mathrm{\tau }}{N_d}$), higher ratio happens under small magnetic fields.

FIGURE 9

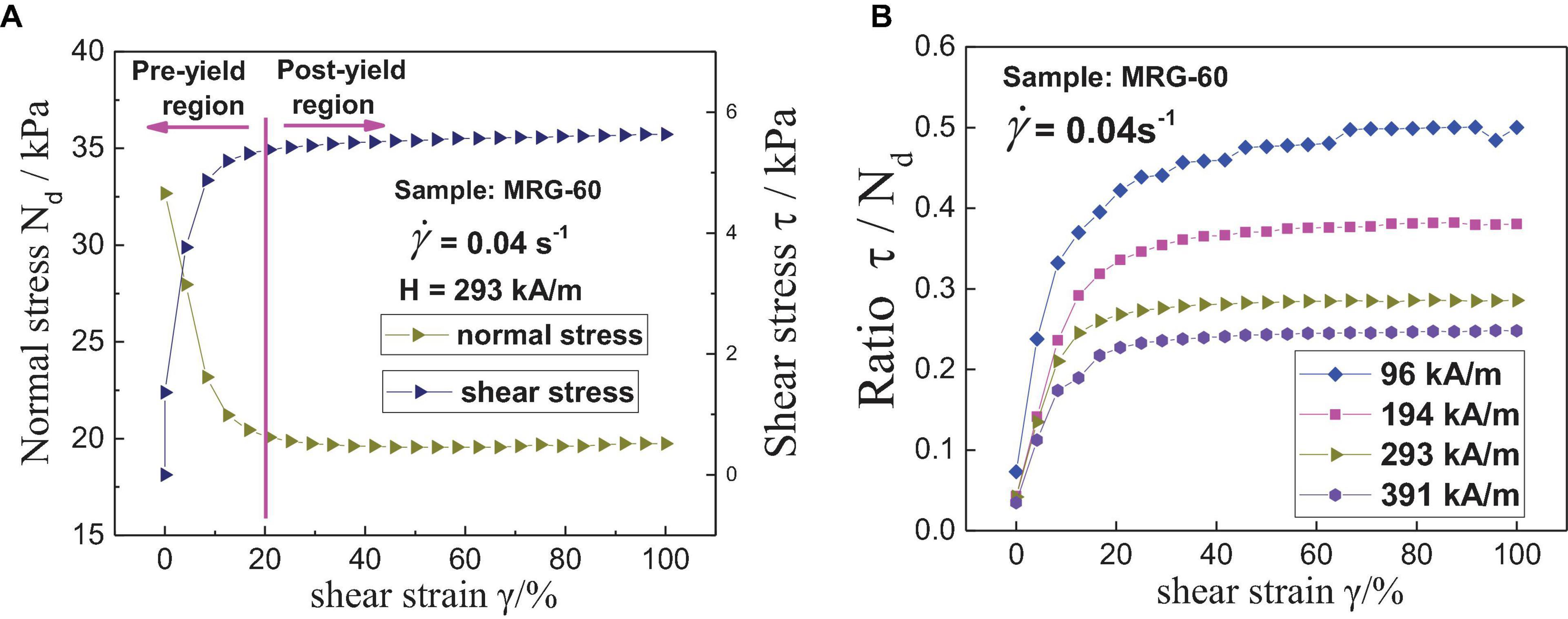
Figure 9. The normal stress (N_d) and shear stress (τ) of magnetorheological gel (MRG) as a function of shear strain (A); the ratio of shear stress to normal stress (τ/N_d) as a function of shear strain (B).

It is worth noting here that the total shear stress could be divided into two parts: the magnetic-induced elastic shear stress and the friction-induced shear stress. Thus, to quantitatively analyze the contribution of friction to shear stress, the shear stress (Figure 10A) and storage modulus (Figure 10B) of MRG-60 were tested under quasi-static loading and under oscillatory loading, respectively. It can be seen from Figure 10A that the shear stress increases rapidly at small shear strain, whereas it almost behaves independently from shear strain at high shear strain. However, Figure 10A cannot show the information about the specific contributions of magnetic force or friction force to shear stress. Therefore, the oscillatory experiments with low frequency were conducted, and the results are displayed in Figure 10B. The storage modulus, G′, of viscoelastic material could represent an elastic part or magnetic force contribution because the energy stored in the material could be recovered after the shear is removed (Li and Zhang, 2008). The elastic shear stress, τ_E (i.e., magnetic force contribution), could be calculated using the equation τ_E = G′γ, and the results are displayed in Figure 10C. The stress difference between the results presented in Figures 10A,C indirectly demonstrates the contribution of friction to the total shear stress (i.e., friction-induced shear stress, τ_F = τ−τ_E). Taking MRG-60 at 391 kA/m of magnetic field strength for example, the total shear stress is 7,554 Pa, and the elastic shear stress is 4,672.1 Pa. Thus, the contribution of friction force to shear stress is 2,881.9 Pa (approximately 38.2% to the total shear stress). It implies that the friction contribution plays a significant role in the total shear stress. Furthermore, these discoveries may provide a great method to fabricate high-efficiency MRG from a new aspect, such as increasing the friction coefficient of magnetic particles.

FIGURE 10

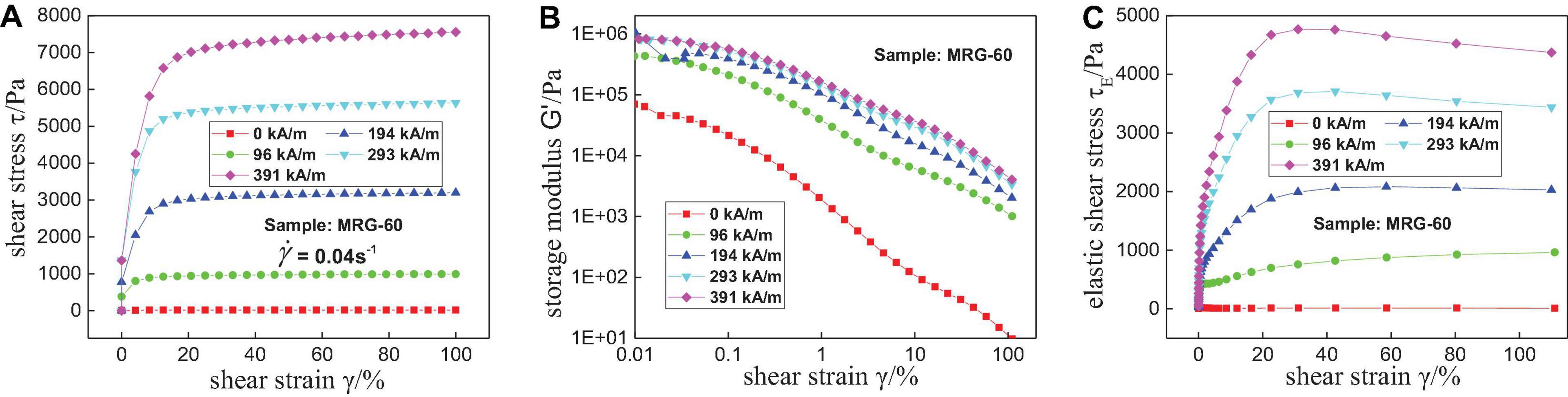
Figure 10. The variation of total shear stress (A), storage modulus (B), and elastic shear stress (C) with shear strain under magnetic field sweep. The oscillatory frequency is 0.5 Hz.

Influence of Shear Rate on the Normal Stress Behavior

To investigate the influence of the shear rate on the normal stress behavior of MRG, Figure 11 shows the normal stress of MRG-60 as a function of shear strain under four different shear rates and constant magnetic fields. In the absence of a magnetic field, the normal stress of MRG-60 is almost zero (Figure 11A). The reason for this has been discussed in the former section and for brevity will not be repeated here. The normal stress of MRG-60 decreases dramatically in the first place and then gradually goes into a stable state with the increase of shear strain. It can be seen from Figure 11B that the normal stress of MRG is higher under lower shear rate, which is opposite to the findings of Ju et al. (2013). The experiments were conducted three times, and the results did not change. Theoretically speaking, according to the previous findings in Ju et al. (2013), MRG is a kind of shear thinning material, which means that the apparent viscosity of MRG decreases with the increase of shear rate (Ju et al., 2013). Thus, the magnetic particles need to overcome the stronger restrictions to form chain-like microstructures under lower shear rate, resulting in the growth of normal stress with the increase of shear rate. However, the results shown in Figure 11B do not agree with that theory and its corresponding phenomenon. The results displayed in Figure 11B could be explained with the following hypothesis (Liu et al., 2014; Mao et al., 2020). The macroscopic normal stress behavior of MRG is primarily dependent on the evolution of particle chain microstructure. The excited magnetic field and shear strain are the two main aspects driving the transformation of the interior particle chain structure. The contribution of the magnetic field to the formation of stable long chains or dense network structures is positive, whereas shear strain tends to demolish the long chains or columnar aggregates. For a higher shear rate (i.e., 0.083 s⁻¹), the apparent viscosity is smaller, and thus the resistance to the formation of particle chain is weaker in comparison with the lower shear rate. However, smaller apparent viscosity also means weaker resistance to the shear strain. Thus, the demolishing effect of shear strain on long chains is more considerable under a higher shear rate. Besides, MRG is given less time (i.e., 12 s) to complete the shearing under a shear rate of 0.083 s⁻¹. In this case, the smaller excited magnetic field, i.e., 96 kA/m, could barely drive the transformation of the interior chain structure. Contrarily, for a lower shear rate (i.e., 0.005 s⁻¹), there is enough time (i.e., 200 s) for MRG to thoroughly complete the reconstruction of the long chains or dense network structures after being destroyed by shear deformation. Thus, larger normal stress achieves a smaller shear rate. This implies that the normal stress behavior of MRG under quasi-static loading (i.e., particularly small shear rate) is opposite to that under dynamic loading when the external magnetic field is small.

FIGURE 11

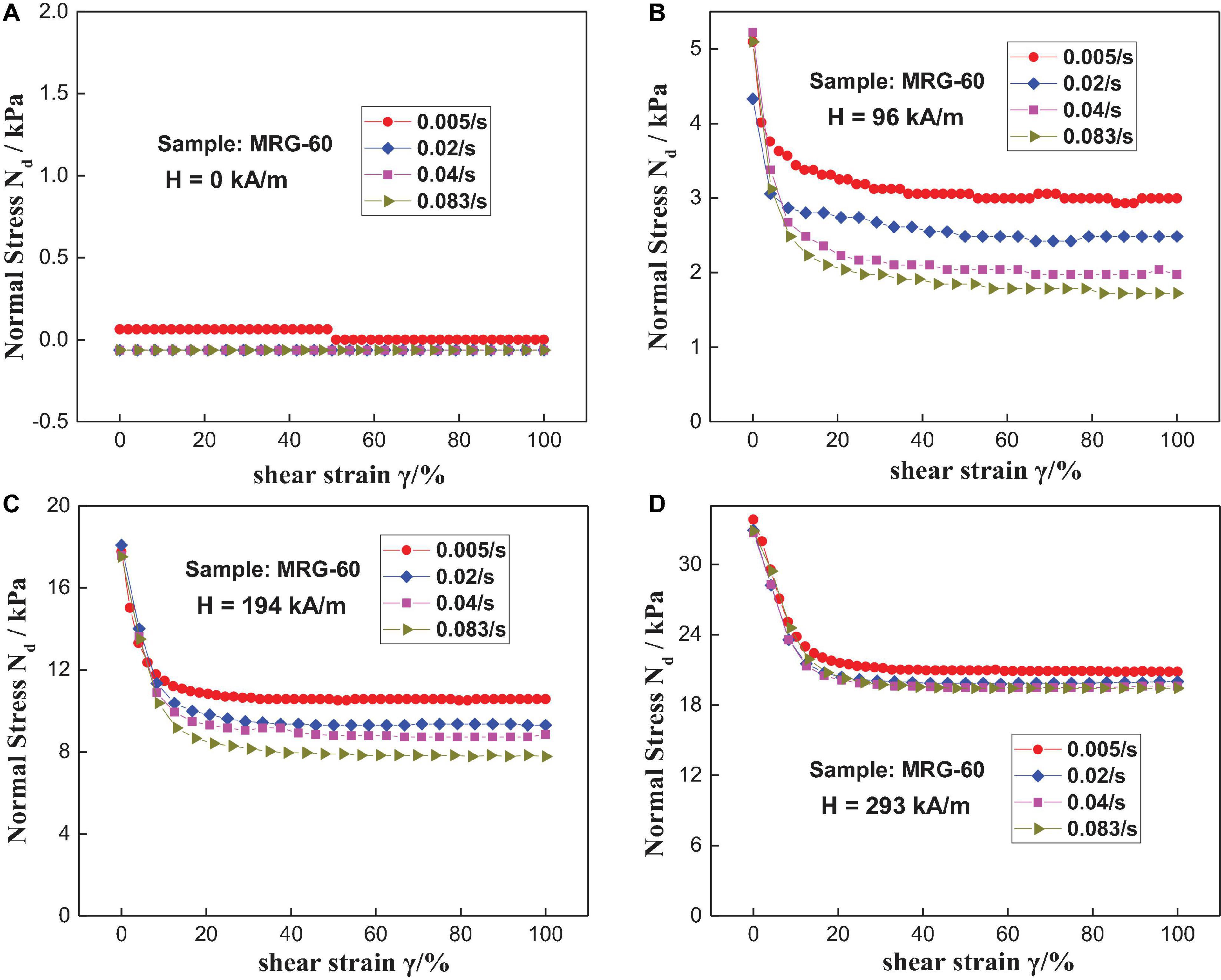
Figure 11. Variation of normal stress with shear strain for MRG-60 under different shear rates and constant magnetic fields: 0 kA/m (A), 96 kA/m (B), 194 kA/m (C), and 293 kA/m (D).

Furthermore, the steady-state value of normal stress decreases with the increase of the shear rate when the magnetic field strength is small (such as 96 kA/m). That is to say, the shear rate is influential on the normal stress behavior of MRG to a certain extent. However, it is worthwhile to mention that the influence of the shear rate on the normal stress behavior gradually becomes insignificant with the growth of the excited magnetic field strength. In other words, differences between the steady-state value of normal stress still exist at 96 kA/m of magnetic field strength while it nearly disappears in 293 kA/m of magnetic field strength (as can be intuitively seen from Figures 11B–D). It is because the magnetic interaction between particles is powerful enough to drive the particle chains to behave stably and robustly when the excited magnetic field strength is large (e.g., 293 kA/m). Although the time for reconstruction of the broken particle chains is less at a higher shear rate, the particle–particle magnetic attractive force is strong enough to complete the rebuilding of chains due to the presence of a higher magnetic field (i.e., 293 kA/m). Also, the effect of the magnetic field on the normal stress is much more considerable than that of shear strain, as discussed in “Influence of Magnetic Field on the Normal Stress Behavior” section. Therefore, the shear rate has little effect on the normal stress of MRG in steady state under high magnetic field strength (as shown in Figure 11D).

Influence of Carbonyl Iron Powder Content on the Normal Stress Behavior

Figures 12A–C present the normal stress of MRG with three different CIP contents as a function of shear strain under constant magnetic fields and shear rate of 0.04 s⁻¹. The normal stress of MRG with various CIP contents is nearly negligible for the lack of an excited magnetic field. The results and reason are similar to those discussed in “Influence of Magnetic Field on the Normal Stress Behavior” and “Influence of Shear Rate on the Normal Stress Behavior” sections and not displayed here for simplicity. The curves presented in Figures 12A–C indicate that the normal stress of MRG exhibits a rapid drop and then a plateau with the increase of shear strain, which is also similar with the changing regularity of normal stress–strain curve displayed in Figure 7. Moreover, a higher CIP content will contribute to larger normal stress under constant magnetic field strength. This is because the more the magnetic particles, the more the long chains, and the more the peak structures acing to push apart the rheometer plate (Yao et al., 2015). Figures 12D–F display the ratio of shear stress to normal stress of MRG with different CIP contents under different magnetic fields. Most notably, the ratio of MRG-60 is higher than that of MRG-40 and MRG-70 at the magnetic field strength of 293 kA/m while lower than that of MRG-70 at the magnetic field strength of 391 kA/m. Precisely speaking, the magnetic attractive force between particles is dependent on the effective magnetic field (Lemaire and Bossis, 1991) (H_eff) rather than the applied magnetic field (H_app). The effective magnetic field could be represented as H_eff = H_app−4πM. The magnetic magnetization M = χH_eff, where χ is magnetic susceptibility. Thus, $H_{eff}=\frac{H_{app}}{{\mathrm{\mu }}_{H_{eff}}}$, where the permeability μH_eff = 1 + 4πχH_eff. The permeability grows with the increase of CIP content, resulting in the decrease of magnetic force. However, a larger quantity of chains will generate due to the increase of CIP content, leading to the increase of magnetic force. Thus, there exists a competition between the CIP content and permeability. It implies that the stress behavior and ratio are highly dependent on the CIP content of MRG and the excited magnetic field (Guo et al., 2012). Actually, the research on magnetic powders also concluded similar results (Chen et al., 2013); i.e., the variation of ratio with the CIP content is irregular and unpredictable under a constant magnetic field. From the changing regularity of ratio, one can also conclude that under a constant magnetic field, the rapid increase of ratio means the interior structures of MRG evolve from isotropic state with evenly dispersed particles to anisotropic state with long particle chains or dense network microstructures. Moreover, according to the equation r = γ + μ, the reduction of ratio represents decline of the friction between the iron particles when the magnetic field and shear strain are constant. MRG with a moderate CIP content possibly possesses a regular particle chain microstructure, while that with a large quantity of magnetic particles might form an irregular chain structure that induces the decline of friction (Chen et al., 2013). However, the contribution of friction to shear stress is considerably fundamental. Therefore, except for magnetic field and CIP content, the ratio and normal stress should both be taken into consideration when achieving a high MR effect or high field-on shear stress. Further investigations on the mechanism of this phenomenon are needed.

FIGURE 12

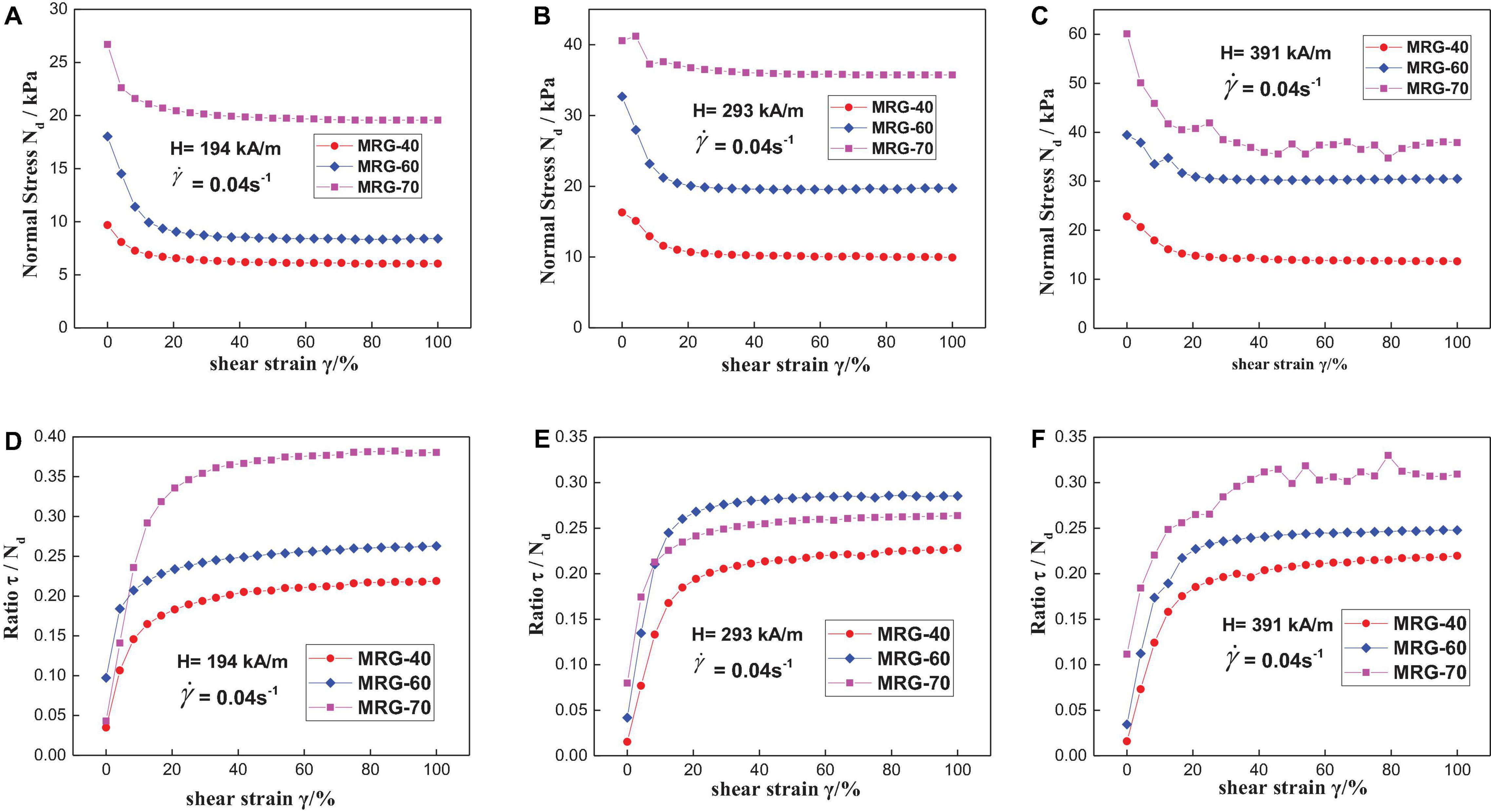
Figure 12. The normal stress as a function of shear strain for magnetorheological gel (MRG) with different carbonyl iron powder (CIP) contents under different magnetic fields: 194 kA/m (A), 293 kA/m (B), and 391 kA/m (C). The ratio of shear stress to normal stress (τ/N_d) as a function of shear strain for MRG with different CIP contents under different magnetic fields: 194 kA/m (D), 293 kA/m (E), and 391 kA/m (F).

Normal Stress Behavior of Magnetorheological Gel Under Periodically Cyclic Loading Condition

Influence of Shear Strain Amplitude on the Normal Stress Behavior

In this section, MRG-60 was selected as an experimental sample to investigate the normal stress under periodically cyclic loading condition. The shear strain increases linearly from 0 to 100% (or 20%, etc.) and then decreases linearly to 0% under a constant shear rate. Subsequently, the shear strain reversely processes from 0 to −100% and then from −100 to 0%. Figure 13A presents the variation of normal stress with different shear strain amplitudes, and Figures 13B–F present the enlarged view of normal stress–strain curves under various shear strain amplitudes, i.e., 20%, 40%, 60%, 80%, and 100%. Taking normal stress–strain curve under 100% strain amplitude, for example, the black arrows represent the changing process of the magneto-induced normal stress. The normal stress appears as an abrupt increment immediately due to the application of 194 kA/m of magnetic field strength. This results from the magnetic interaction between the particles. After that, the magneto-induced normal stress decreases rapidly due to the negative contribution of tilted particle chains to normal stress. Then, the dynamic balance between the strain-induced rupture and magneto-induced rebuilding of particle chains occurs with the continuous application of shear strain, which results in the minimum value of normal stress (i.e., 8.73 kPa). When the shear strain returns to 0% after it arrives at 100%, the tilted and elongated chains start to constrict, and the gaps between the magnetic particles begin to squeeze to some extent. These effects are coupled together and contribute to the sudden rise of normal stress. Therefore, a peak of normal stress (i.e., 27.01 kPa) emerges. However, the effect of the rebuilding and fracture of particle chains on normal stress is opposite. When the effect of the fracture of particle chains is stronger than that of rebuilding, the normal stress will descend again with the continuous application of shear strain and magnetic field. Thus, the normal stress could be adjusted in a large scale from 8.73 to 27.01 kPa under cyclic loading. In addition, the changing trend of normal stress at the other side will not be discussed here due to the symmetry of normal stress–strain curve.

FIGURE 13

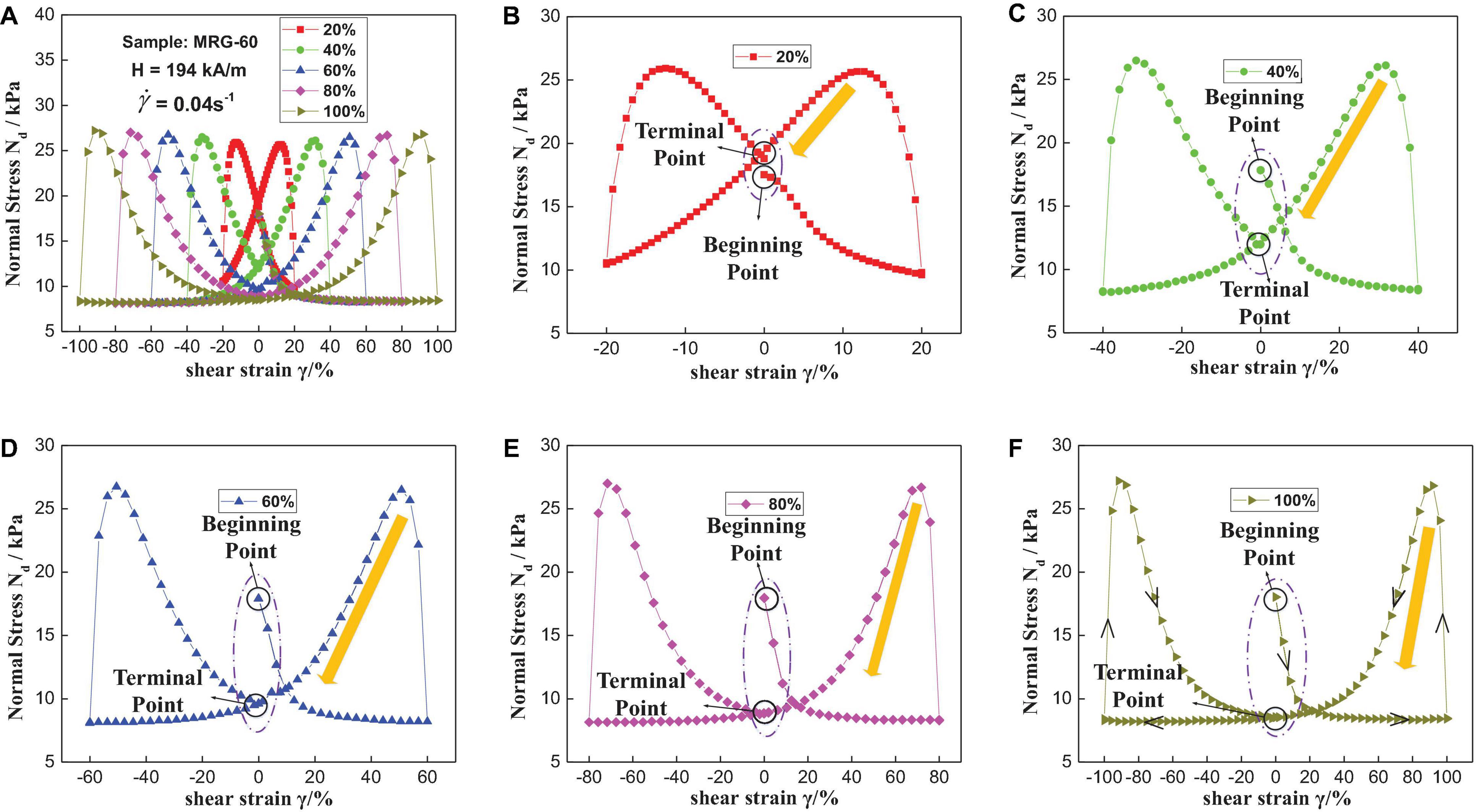
Figure 13. Variation of normal stress with shear strain for MRG-60 under five different shear strain amplitudes (A), i.e., 20% (B), 40% (C), 60% (D), 80% (E), and 100% (F). The black arrows in (F) represent the changing trend of normal stress.

It can be seen from Figures 13B–F that the shapes enclosed by normal stress–strain curves change from a “butterfly-like” shape (Figure 13A) to a “tooth-like” shape (Figures 13C–F). Moreover, the distances between the beginning point and the terminal point increase progressively with the increase of shear strain amplitudes, which can be intuitively seen from the purple dotted lines in Figures 13B–F. In other words, the terminal points of normal stress gradually tend to the steady-state value (i.e., minimum value) with the increase of shear strain amplitudes. For example, the terminal point is 18.79 kPa, and the steady-state value is 9.62 kPa when the shear strain amplitude is 20%. However, the terminal point of normal stress is 8.56 kPa, which is close to the steady-state value (i.e., 8.34 kPa) at the shear strain amplitude of 100%. Another interesting phenomenon is that the “slopes” of normal stress–strain curves at the unloading stage (e.g., shear strain changes from 100 to 0%) become steeper with the increase of shear strain amplitudes, which are shown as yellow arrows in Figures 13B–F. These phenomena indicate that normal stress of MRG changes sharply under higher shear strain amplitudes while gently under lower shear strain amplitudes. The results are significantly beneficial for the design of MR devices because the shear strain amplitude is limited by the structure of the devices.

Conclusion

This work focuses on the normal stress behavior of MRG under quasi-statically monotonic loading and periodically cyclic loading. The influence of magnetic field, shear rate, CIP content, and shear strain on the normal stress was systematically analyzed. The normal stress is nearly negligible due to the absence of dense particle aggregates when the excited magnetic field is not applied. In the presence of a magnetic field, the normal stress appears in three various stages—a dramatic increase, then a rapid decrease, and finally a steady-state value—corresponding to the three various microstructures (i.e., stable chains along the direction of external magnetic field firstly, then titled long chains under the application of shear and the eventual dynamic equilibrium between the fraction and rebuilding of chains, respectively). The magnetization model, compared with the power model, could better characterize the normal stress behavior of MRG under magnetic field sweeping. Moreover, the normal stress is higher at a smaller shear rate under quasi-static loading, whereas it behaves in an opposite trend under dynamic loading. It also found that the normal stress of MRG decreases with the increase of the shear rate under smaller magnetic field strength. However, the influence of the shear rate on the normal stress almost disappears under higher magnetic field strength because MRG is a highly magnetic field-dependent material. Besides, the larger the CIP content of MRG, the larger the normal stress. The normal stress of MRG-60 could be adjusted from 8.73 to 27.01 kPa at 194 kA/m of magnetic field strength under periodically cyclic loading. The shear strain amplitudes have a strong effect on the changing regularity of normal stress while a weak effect on the magnitude of normal stress. Furthermore, the ratio of shear stress to normal stress, an analog of friction coefficient, was proposed to understand the rheological effect of MRG from a novel perspective. The results demonstrate that the ratio has a great correlation with the excited magnetic field and CIP content. Larger magnetic field strength usually gives rise to the smaller ratio. To achieve a high MR effect or high field-on shear stress, the ratio and normal stress should both be taken into consideration. This is because the increase of normal stress is beneficial for the increase of friction-induced stress. However, the mechanism on how the CIP content influences the ratio still needs to be investigated.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

RM: formal analysis, investigation, and writing – original draft. RM and HW: methodology. GZ: resources. JW: supervision and writing – review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 51805209, 51705467, and 51675280).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahamed, R., Choi, S. B., and Ferdaus, M. M. (2018). A state of art on magneto-rheological materials and their potential applications. J. Intel. Mater. Syst. Struct. 29, 2051–2095. doi: 10.1177/1045389x18754350

CrossRef Full Text | Google Scholar

Ashtiani, M., Hashemabadi, S. H., and Ghaffari, A. (2015). A review on the magnetorheological fluid preparation and stabilization. J. Magn. Magn. Mater 374, 716–730. doi: 10.1016/j.jmmm.2014.09.020

CrossRef Full Text | Google Scholar

Auernhammer, G. K. (2019). Magnetorheological gels in two and three dimensions: understanding the interplay between single particle motion, internal deformations, and matrix properties. Arch. Appl. Mech. 89, 153–165. doi: 10.1007/s00419-018-1479-2

CrossRef Full Text | Google Scholar

Chen, K. K., Tian, Y., Shan, L., Zhang, X. J., and Meng, Y. G. (2013). The rheological properties of magnetic field excited magnetic powders sheared between two parallel plates. Smart Mater. Struct. 22:115036. doi: 10.1088/0964-1726/22/11/115036

CrossRef Full Text | Google Scholar

de Sousa, S. R. G., dos Santos, M. P., and Bombard, A. J. F. (2019). Magnetorheological gel based on mineral oil and polystyrene-b-poly(ethene-co-butadiene)-b-polystyrene. Smart Mater. Struct. 28:105016. doi: 10.1088/1361-665x/ab3600

CrossRef Full Text | Google Scholar

Gong, X. L., Guo, C. Y., Xuan, S. H., Liu, T. X., Zong, L. H., and Peng, C. (2012). Oscillatory normal forces of magnetorheological fluids. Soft. Matter. 8, 5256–5261. doi: 10.1039/c2sm25341k

CrossRef Full Text | Google Scholar

Guo, C. Y., Gong, X. L., Xuan, S. H., Zhang, Y. L., and Jiang, W. Q. (2012). An experimental investigation on the normal force behavior of magnetorheological suspensions. Korea Aust. Rheol. J. 24, 171–180. doi: 10.1007/s13367-012-0021-2

CrossRef Full Text | Google Scholar

Jiang, J. L., Tian, Y., Ren, D. X., and Meng, Y. G. (2011). An experimental study on the normal stress of magnetorheological fluids. Smart Mater. Struct. 20:085012. doi: 10.1088/0964-1726/20/8/085012

CrossRef Full Text | Google Scholar

Ju, B. X., Yu, M., Fu, J., Zheng, X., and Liu, S. Z. (2013). Magnetic field-dependent normal force of magnetorheological gel. Ind. Eng. Chem. Res. 52, 11583–11589. doi: 10.1021/ie4013419

CrossRef Full Text | Google Scholar

Khazoom, C., Caillouette, P., Girard, A., and Plante, J. S. (2020). A supernumerary robotic leg powered by magnetorheological actuators to assist human locomotion. IEEE Robot. Autom. Lett. 5, 5143–5150. doi: 10.1109/lra.2020.3005629

CrossRef Full Text | Google Scholar

Kuwano, O., Ando, R., and Hatano, T. (2013). “Granular friction in a wide range of shear rates,” in Proceedings of the Powders and Grains 2013 7th International Conference on Micromechanics of Granular Media: AIP Conference Proceedings, Sydney, Vol. 1542, 32–37.

Google Scholar

Lambropoulos, J. C., Miao, C., and Jacobs, S. D. (2010). Magnetic field effects on shear and normal stresses in magnetorheological finishing. Opt. Express 18, 19713–19723. doi: 10.1364/oe.18.019713

PubMed Abstract | CrossRef Full Text | Google Scholar

Laun, H. M., Gabriel, C., and Schmidt, G. (2008). Primary and secondary normal stress differences of a magnetorheological fluid (MRF) up to magnetic flux densities of 1 T. J. Non Newton Fluid 148, 47–56. doi: 10.1016/j.jnnfm.2007.04.019

CrossRef Full Text | Google Scholar

Lemaire, E., and Bossis, G. (1991). Yield stress and wall effects in magnetic colloidal suspensions. J. Phys. D 24, 1473–1477. doi: 10.1088/0022-3727/24/8/037

CrossRef Full Text | Google Scholar

Li, W. H., and Zhang, X. Z. (2008). The effect of friction on magnetorheological fluids. Korea Aust. Rheol. J. 20, 45–50.

Google Scholar

Li, Y. C., Li, J. C., Li, W. H., and Samali, B. (2013). Development and characterization of a magnetorheological elastomer based adaptive seismic isolator. Smart Mater. Struct. 22:035005. doi: 10.1088/0964-1726/22/3/035005

CrossRef Full Text | Google Scholar

Liu, T. X., Gong, X. L., Xu, Y. G., Pang, H. M., and Xuan, S. H. (2014). Magneto-induced large deformation and high-damping performance of a magnetorheological plastomer. Smart Mater. Struct. 23:105028. doi: 10.1088/0964-1726/23/10/105028

CrossRef Full Text | Google Scholar

Liu, T. X., Xu, Y. G., Gong, X. L., Pang, H. M., and Xuan, S. H. (2013). Magneto-induced normal stress of magnetorheological plastomer. AIP Adv. 3:082122. doi: 10.1063/1.4819462

CrossRef Full Text | Google Scholar

Lopez-Lopez, M. T., Kuzhir, P., Duran, J. D. G., and Bossis, G. (2010). Normal stresses in a shear flow of magnetorheological suspensions: viscoelastic versus Maxwell stresses. J. Rheol. 54, 1119–1136. doi: 10.1122/1.3479043

CrossRef Full Text | Google Scholar

Mao, R. S., Wang, H. X., Zhang, G., Ye, X. D., and Wang, J. (2020). Magneto-induced rheological properties of magnetorheological gel under quasi-static shear with large deformation. RSC Adv. 10, 31691–31704. doi: 10.1039/d0ra05843b

CrossRef Full Text | Google Scholar

Meharthaj, H., Sivakumar, S. M., and Arockiarajan, A. (2019). Significance of particle size on the improved performance of magnetorheological gels. J. Magn. Magn. Mater. 490:165483. doi: 10.1016/j.jmmm.2019.165483

CrossRef Full Text | Google Scholar

Pang, H. M., Pei, L., Sun, C. L., and Gong, X. L. (2018). Normal stress in magnetorheological polymer gel under large amplitude oscillatory shear. J. Rheol. 62, 1409–1418. doi: 10.1122/1.5030952

CrossRef Full Text | Google Scholar

Perez, J. C. L., Kwok, C. Y., O’Sullivan, C., Huang, X., and Hanley, K. J. (2016). Assessing the quasi-static conditions for shearing in granular media within the critical state soil mechanics framework. Soils Found 56, 152–159. doi: 10.1016/j.sandf.2016.01.013

CrossRef Full Text | Google Scholar

Rahman, M., Ong, Z. C., Julai, S., Ferdaus, M. M., and Ahamed, R. (2017). A review of advances in magnetorheological dampers: their design optimization and applications. J. Zhejiang Univ. Sci. A 18, 991–1010. doi: 10.1631/jzus.a1600721

CrossRef Full Text | Google Scholar

Rossi, A., Orsini, F., Scorza, A., Botta, F., Belfiore, N. P., and Sciuto, S. A. (2018). A review on parametric dynamic models of magnetorheological dampers and their characterization methods. Actuators 7:16. doi: 10.3390/act7020016

CrossRef Full Text | Google Scholar

See, H., and Tanner, R. (2003). Shear rate dependence of the normal force of a magnetorheological suspension. Rheol. ACTA 42, 166–170. doi: 10.1007/s00397-002-0268-5

CrossRef Full Text | Google Scholar

Wang, D. H., and Liao, W. H. (2011). Magnetorheological fluid dampers: a review of parametric modelling. Smart Mater. Struct. 20:023001. doi: 10.1088/0964-1726/20/2/023001

CrossRef Full Text | Google Scholar

Wang, H. X., Zhang, G., and Wang, J. (2019). Normal force of lithium-based magnetorheological grease under quasi-static shear with large deformation. RSC Adv. 9, 27167–27175. doi: 10.1039/c9ra04987h

CrossRef Full Text | Google Scholar

Wang, Y., Wang, S., Xu, C., Xuan, S., Jiang, W., and Gong, X. (2016). Dynamic behavior of magnetically responsive shear-stiffening gel under high strain rate. Compos. Sci. Technol. 127, 169–176. doi: 10.1016/j.compscitech.2016.03.009

CrossRef Full Text | Google Scholar

Xu, Y. G., Gong, X. L., Xuan, S. H., Zhang, W., and Fan, Y. C. (2011). A high-performance magnetorheological material: preparation, characterization and magnetic-mechanic coupling properties. Soft. Matter. 7, 5246–5254. doi: 10.1039/c1sm05301a

CrossRef Full Text | Google Scholar

Xu, Y. G., Liu, T. X., Liao, G. J., and Lubineau, G. (2017). Magneto-dependent stress relaxation of magnetorheological gels. Smart Mater. Struct. 26:115005. doi: 10.1088/1361-665x/aa89ac

CrossRef Full Text | Google Scholar

Yang, P., Yu, M., Fu, J., Liu, S., Qi, S., and Zhu, M. (2017). The damping behavior of magnetorheological gel based on polyurethane matrix. Polym. Compos. 38, 1248–1258. doi: 10.1002/pc.23689

CrossRef Full Text | Google Scholar

Yao, X. Y., Liu, C. W., Liang, H., Qin, H. F., Yu, Q. B., and Li, C. (2016). Normal force of magnetorheological fluids with foam metal under oscillatory shear modes. J. Magn. Magn. Mater. 403, 161–166. doi: 10.1016/j.jmmm.2015.12.014

CrossRef Full Text | Google Scholar

Yao, X. Y., Yu, M., and Fu, J. (2015). Magnetic-enhanced normal force of magnetorheological fluids. Smart Mater. Struct. 24:035001. doi: 10.1088/0964-1726/24/3/035001

CrossRef Full Text | Google Scholar

Yazid, I. I. M., Mazlan, S. A., Imaduddin, F., Zamzuri, H., Choi, S. B., and Kikuchi, T. (2016). An investigation on the mitigation of end-stop impacts in a magnetorheological damper operated by the mixed mode. Smart Mater. Struct. 25:125005. doi: 10.1088/0964-1726/25/12/125005

CrossRef Full Text | Google Scholar

Zhang, G., Li, Y. C., Wang, H. X., and Wang, J. (2019). Rheological properties of polyurethane-based magnetorheological gels. Front. Mater. 6:56. doi: 10.3389/fmats.2019.00056

CrossRef Full Text | Google Scholar

Zhang, G., and Wang, J. (2020). A novel phenomenological model for predicting the nonlinear hysteresis response of magnetorheological gel. Mater. Des. 196:109074. doi: 10.1016/j.matdes.2020.109074

CrossRef Full Text | Google Scholar

Zubieta, M., Eceolaza, S., Elejabarrieta, M. J., and Bou-Ali, M. M. (2009). Magnetorheological fluids: characterization and modeling of magnetization. Smart Mater. Struct. 18:095019. doi: 10.1088/0964-1726/18/9/095019

CrossRef Full Text | Google Scholar