Nonlinear Magneto-Electro-Mechanical Response of Physical Cross-Linked Magneto-Electric Polymer Gel

Introduction

Magnetorheological (MR) gel is a kind of magneto-controllable soft gel that acts by dispersing the magnetic particles into a low cross-linking density gel matrix (Wang et al., 2014; Zhang et al., 2019). Under external magnetic fields, magnetic particles could overcome the constraint of the matrix and form a chain-like structure. In contrast to MR fluid, the MR gel is more stable and can offer more favorable and convenient conditions for engineering applications. Therefore, with its excellent performance in magnetorheology, the MR gel is expected to be used as a new alternative material for intelligent devices, such as magneto-dampers, energy absorbers, and vibration isolations (Lin et al., 2018; O’Driscoll et al., 2018; Petare and Jain, 2018).

To further improve the mechanical properties, shearing stiffening gel (SSG) has been adopted as the polymer matrix of the MRG (Gurgen and Yildiz, 2020; Hapipi et al., 2020; Zheng et al., 2020). SSG is a kind of soft and viscous boron-siloxane polymer gel with dynamic boron-oxygen (B-O) weak cross-linking bonds, of which the storage modulus, elastic modulus, and viscosity would significantly increase under the external high rate excitation (Xu et al., 2020). Owing to the non-covalent, physical cross-link characteristic of the B-O bonds, SSG can exhibit a typical strain-rate dependence by transforming the gel, rubber, and glassy states under different external loading rates. Moreover, due to the reversibility of the B-O bond, SSG has the capacity for restoration and self-healing even under high speed loading (Wang et al., 2016; Wang et al., 2018). The magnetic additives render the SSG with special magnetically responsive behaviors. The storage modulus of magneto-sensitive SSG will increase under the external magnetic field stimulation (Xu et al., 2018; Liu et al., 2020). The dual hardening mechanism of the mechanics and magnetic field provides a new method for engineering equipment such as vibration isolators and energy absorbers.

Because of the additives of conductive magnetic fillers, the electrical properties of MR materials also change under an external magnetic field (Xu et al., 2013; Puente-Cordova et al., 2018). Magnetic CIPs can be easily moved from isotropic status to anisotropic status by the stimulus of the magnetic field. The CIPs are aligned along the direction of the magnetic field, which forms effective conductive paths (ECPs). The transient time of the alignment progress was studied via the change of storage modulus (An et al., 2012). Meanwhile, owing to the microstructure variations induced by ECPs, the electrical conductivity properties of the magneto-sensitive SSG show synchronous behaviors with the mechanical behaviors when the external magnetic field is varied (Wang et al., 2015; Cvek et al., 2020; Yun et al., 2020). The alignment of the CIPs can be monitored by conductivity. However, even if the anisotropic chain-like structure of CIPs is formed, the resistance of the magneto-sensitive SSG is still very high due to the obstacle of the polymer gel matrix, which hinders the potential application in the field of magnetic sensing sensors for intelligent devices (Xu et al., 2013). To improve the conductivity of MR composite, (Mietta et al., 2012) modified the CIPs with silver and obtained the anisotropic effects in magnetic properties and piezoelectric. (Pang et al., 2015) blended carbon black into an MR plastomer and studied the relationship between electrical conductivity vs. magnetic flux density. (Yun et al., 2019) mixed liquid metal into MRE and obtained a self-sensing material with anisotropic and unconventional piezo-conductivity. These studies reveal that anisotropic electricity is highly dependent on the alignment of CIP clusters. Past research was generally conducted under quasi-static and cyclic loading with low frequency. However, the application of engineering materials under high frequency is also often encountered. More work should be done to study the conductive sensitivity and the magneto-sensitivity of SSG under dynamic stimulus.

In this study, a novel magneto-electric polymer composite was fabricated by introducing the CNTs and CIPs into SSG. Rheological experiments, which studied the magneto-rheological properties and shear stiffening characteristic of e-SSG. The compressive tests showed the enhancement of the magnetic field on self-sensing capacity and durability. A drop weight machine was adopted to test its electrical responses under low-velocity impact. It was found that with the application of the magnetic field, enhancement of mechanical behaviors, electrical sensitivity, and stability were shown by this material. In summary, due to its excellent dual response mechanism of strain and magnetic field, this material has the potential for intelligent vibration control.

Experiment Materials

Boric acid and benzoyl peroxide (BPO) were purchased from Sinopharn Chemical Reagent Co. Ltd., Shanghai, China. Hydroxyl silicone oil was purchased from Jining Huakai Resin Co. Ltd. Multi-walled CNTs with 3–5 nm in diameter and 8–13 μm in length were purchased from Conductive Materials of Luelida Co. Ltd., Xinxiang City, Henan Province, China. Carbonyl iron particles were purchased from BASF Germany. All the reagents were analytically pure and were adopted without additional purification.

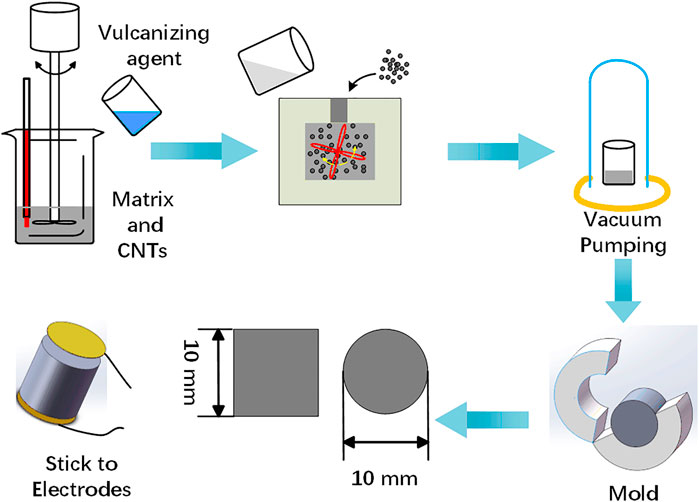
The fabrication progress is illustrated in Figure 1. First, the boric acid and hydroxyl silicone oil were mixed with the mass ratio of 1:15 and heated in the oven at 180°C for 2 h. During the heating progress, CNTs and BPO were added into the matrix in turn and the mass fractions were 1 and 0.4%. 5 μL caprylic acid was added to every 100 g composite and mixed uniformly. Here, caprylic acid was cross-linking agent and plasticizer in the polymer matrix, which helped improve the roughness and the shear stiffening behaviors. After one hour of heating, the SSG matrix was obtained. The CIPs were mixed into the matrix homogeneously through a rubber mill (Taihu Rubber Machinery Factory, China, Model XK-160). According to our previous work (Fan et al., 2019), the electrical conductivity and sensing capacity of the composite achieved their highest values when the mass fraction of CIPs was 50%. Subsequently, the composite was vacuumed to remove air bubbles for 2 h and the conductive self-sensing composite, e-SSG, was obtained. The composite was molded into a cylinder shape with a 5 mm radius and 10 mm height. Finally, copper electrodes with 0.01 mm in thickness and 5 mm in radius were stuck to the specimen.

FIGURE 1

FIGURE 1. Schematic of the material progress.

Characterization

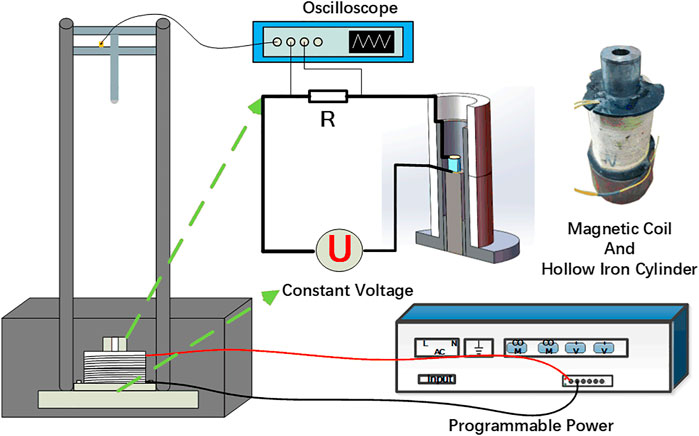
The rheological behaviors of SSG were tested by a commercial rheometer (Physical MCR 302, Anton Paar Co., Austria). Plane to plane with 19 mm in diameter rheological test system was adopted and the height of specimen was set as 1 mm. Compressive tests were conducted by a universal testing machine (MTS criterion 43, MTS System Co., America). The dynamic mechanical behaviors of the specimen were tested by a drop tower testing machine (Mode ZCJ1302-A, MTS Industrial Systems, China). The drop hammer weighed 500 g and the impact head was a round surface with 25 mm diameter. A piezo-electrical acceleration sensor was used to record the velocity change of the drop hammer. The data acquisition system was composed of a charge amplifier (Mode YE5853, Jiangsu Sinocera Piezotronics, INC., China) and an oscilloscope (Mode DPO 2012B, Tektronix INC., United States). A programmable power supply (ITECH Electronic C. Ltd., China) was used to excite the magnetic field. All tests were conducted at room temperature.

Rheology Characterization of e-SSG

The rheology behaviors were tested under oscillatory shear mode. The shear amplitude was set to be 0.1%. As shown in Figure 2A, the storage modulus of the SSG increased from 45 Pa to 0.53 MPa when the shear frequency increased from 0.1 to 100 Hz. At 20 Hz, the loss modulus achieved its peak value, 0.30 MPa. The damping factor, which is defined as the ratio of the loss modulus to the storage modulus, can usually be adopted to illustrate the state of the composite materials. According to the work of (Boland et al., 2016) and (Sun et al., 2019), when the damping factor is larger than 1, the viscous components play a dominant role in material deformation. Herein, with the external frequency increasing from 0.1 to 100 Hz, the damping factor decreased from 74.46 to 0.31, indicating the polymer composite translated from a viscous state (or plastic state) to a rubbery state. Inherited from the SSG matrix, the e-SSG also showed typical rate-dependent behaviors. Compared to SSG, the primary and peak modulus of e-SSG were much higher. Simultaneously, the damping factor was smaller. With test frequencies increasing from 0.1 to 100 Hz, the storage modulus increased from 0.26 to 1.15 MPa. The loss modulus increased from 0.11 to 0.33 MPa at 2 Hz. Then, the loss modulus decreased down to 0.05 MPa when the shear frequency reached 100 Hz.

FIGURE 2

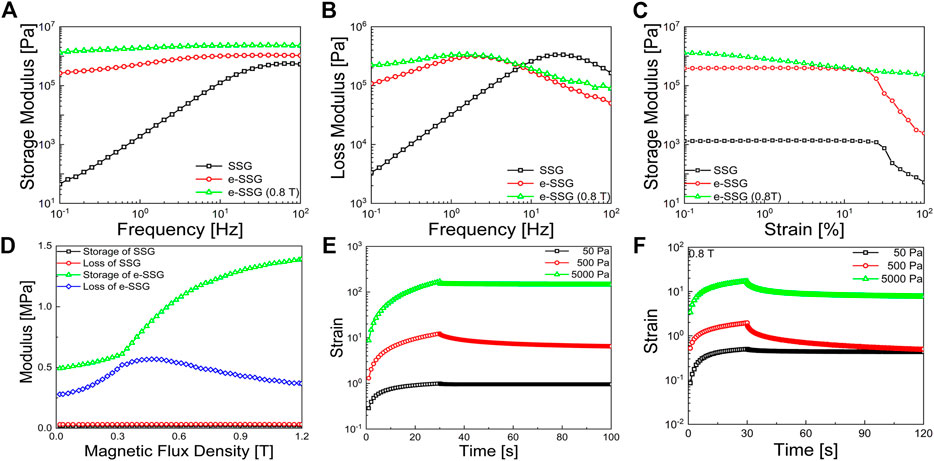
FIGURE 2. The rheology behaviors of the SSG. (A,B) The shear stiffening behaviors of SSG and e-SSG. (C) The storage modulus under different shear strain. (D) The magnetorheological effect of SSG and e-SSG. The creep and recovery behaviors of the e-SSG under different shear stress and with the absence (E) and presence (F) of the magnetic field.

The strain-dependent and magnetorheological behaviors of the e-SSG were tested as well Figure 2C. When the shear strain reached 0.18, a drastic decrease was observed in the storage modulus of SSG and e-SSG, which indicated failure to emerge in composites. The influence of the magnetic field was remarkable. Increasing strain led to the decrease of storage, known as the Payne effect. However, no failure happened to the e-SSG when the magnetic field was applied. To investigate the MR effect, a shear strain with an amplitude of 0.1% and frequency of 1 Hz was applied. When the magnetic flux density increased from 0 to 1.2 T, the storage modulus of e-SSG increased from 0.49 to 1.39 MPa Figure 2D. The loss modulus increased from 0.28 to 0.57 MPa when the magnetic flux density increased to 0.44 T and finally decreased to 0.37 MPa with 1.2 T. Furthermore, the shear stiffening behaviors under magnetic field were also investigated. The green lines in Figures 2A,B illustrated the shear stiffening behavior of e-SSG under 0.8 T. The storage modulus increased from 1.1 to 2.3 MPa when the shear frequency increased from 0.1 to 100 Hz. Higher storage modulus and lower damping factors helped the composite materials hold shapes and recover from external stress loading.

The creep and recovery behaviors of the e-SSG were shown in Figures 2E,F. The creep compliance was dependent on the external stress, which showed a typical nonlinear material characteristic. Generally, the creep strain, γ_t, consisted of instantaneous strain, γ_e, delayed elastic strain, γ_d, and residual strain, γ_r. The function could be expressed as follows (Xu et al., 2012).

${\gamma }_t={\gamma }_e+{\gamma }_d+{\gamma }_r=J\left(t\right){\tau }_0(1)$

where τ₀ indicates the cnstant stress. The constant stresses were set at 50, 500 and 5,000 Pa. Figure 2E shows the creep behaviors with different magnetic fields. When the shear stress was 50 Pa, γ_e was negligible and the composite showed plastic characteristics. With the shear stress increasing to 5 kPa, γ_e increased to 0.19 and the instantaneous creep compliance changed to 1.75 × 10⁻⁵ Pa⁻¹. With the presence of a magnetic field, the creep compliance was further diminished and the recovery behaviors were more remarkable. The instantaneous creep compliance of e-SSG under the magnetic flux density of 0.8 T was 6.83 × 10⁻⁶ and 4.68 × 10⁻⁶ Pa⁻¹ when the shear stress was 0.5 and 5 kPa, respectively. The viscous flow component became smaller with the increase of shear stress and magnetic flux density. This dual hardening mechanism provided a favorable condition to absorb external stimuli and hold linear mechanical properties.

Piezo-Resistive Response Under Quasi-Static Loading

The piezo-resistive response under quasi-static state was investigated via MTS. The initial electrical conductivity of e-SSG was 25 Ω·m. The measurement method is illustrated in Figures 3A,B. The test rate was set at 0.010, 0.015, and 0.020 s⁻¹. The compress stress was recorded at the same time. In series circuits with constant electromotive force, the voltages of different components were proportional to resistance. The electrical resistance was calculated by the following function:

$R_x=\frac{E-U}{U}R(2)$

where the E, U, and R represented the electromotive force of the constant voltage source, the voltage of the constant resistance, and the resistor.

FIGURE 3

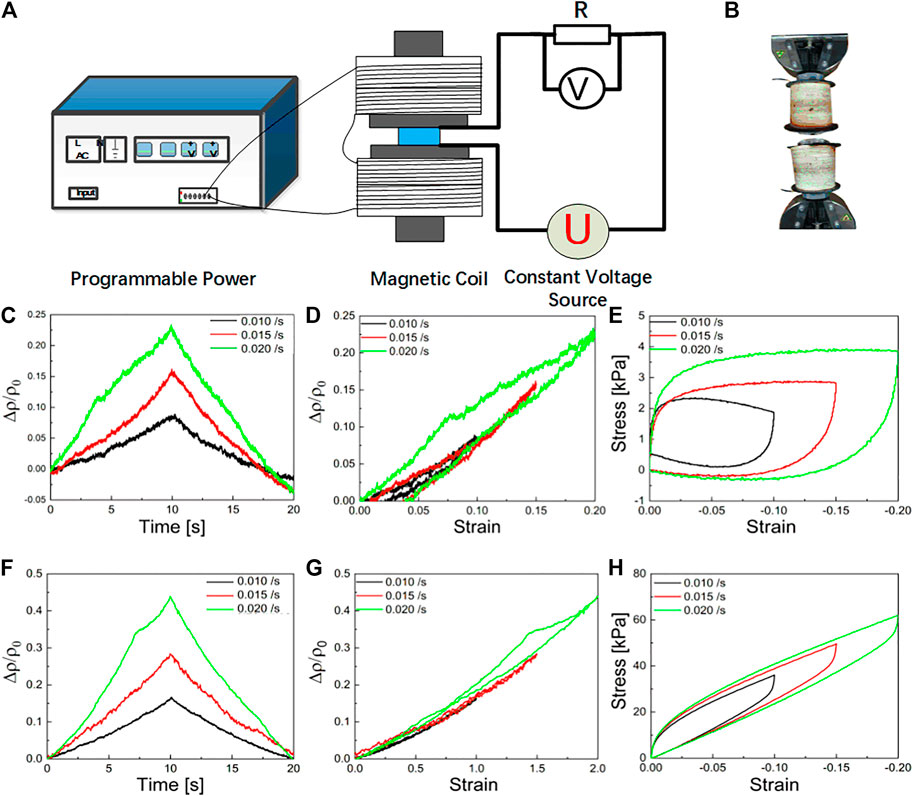
FIGURE 3. (A) Schematic of the test equipment and the measuring method. (B) The testing equipment. (C–E) The electrical resistivity behaviors vs. time and compressive strain, the stress-strain without magnetic field. (F–H) illustrated the behaviors under a magnetic flux density of 0.3 T.

Electrical conductivity showed a negative relationship to the compressive strain. With the increase of compressive speed, the sensitivity of the electrical conductivity was also improved. Here, gauge factor was defined as,

$GF=\frac{\Delta \rho }{{\rho }_0}/\Delta \text{ε}(3)$

when it came to 10 s, the changes of $\frac{\Delta \rho }{{\rho }_0}$ achieved peak values and came to be 0.088, 0.162, and 0.233 with a compressive strain rate of 0.010, 0.015, and 0.020 s⁻¹, respectively, Figure 3D shows the relationship between the compressive strain and resistivity. The resistivity increased with compressive strain. The final resistivity was lower than the initial value. According to Zhang (Zhang et al., 2000), a possible reason for this phenomenon could be attributed to the time dependence characteristic of the electrical threshold. The GFs were 0.88, 1.08, and 1.065. With the enhancement of the magnetic field, the sensitivity was improved and the time effect was negligible. The electrical response held nearly linearly Figure 3G and GFs increased to 1.01, 1.89, and 2.19. The presence of a magnetic field increased the linear response and helped to hold the stable electrical properties. To provide an insight into the influence of the magnetic field, the stress-strain curves are shown in Figures 3E,H.

Typical rate-dependent behaviors could be observed in Figures 3C,H. With the increase of compressive speed, the compress modulus and yield stress increased rapidly. When the compressive strain came to 0.54% with the compressive rate of 0.010 s⁻¹, the compressive stress started to decrease. Plastic flow deformation came to dominate. When the compressive rate was 0.020 s⁻¹, the yield strain increased to 0.64%. The stress-strain hysteresis areas are shown in Figure 3H. With the presence of a magnetic field, the elasticity of the e-SSG was highly improved. The compressive modulus could be calculated at 0.22, 0.23, and 0.24 MPa, corresponding to the compressive rates of 0.010, 0.015, and 0.020 s⁻¹. The magnetic field improved the strain sensitivity of e-SSG. Furthermore, we should attach more importance to the fact that the magnetic field improved mechanical behaviors. The linear elastic scope of the e-SSG was greatly extended. The unloading progress was also linear. The dynamic response was then investigated to ensure the role of the magnetic field.

Piezo-Resistive Response Under Low-Velocity Impact

The dynamic mechanical and electrical responses were investigated via a drop weight machine. The acceleration data and voltage were recorded by one oscilloscope to ensure the synchronization of mechanical and electrical responses. Regarding the impact duration within several microseconds, the data sampling rate was set at 50 MHz. A constant voltage source was adopted to excite the coils to generate a magnetic field. To achieve a uniform magnetic field, the specimen was fixed upon an aluminum cylinder and placed at the center of an iron hollow cylinder as seen in the schematic in Figure 4. When the exciting current was 3A, the magnetic flux density reached 0.3 T.

FIGURE 4

FIGURE 4. Schematic of the test equipment and measuring method.

Figures 5A–C showed the dynamic responses of the e-SSG to drop weight without a magnetic field.Figures 5D–F illustrates the results with the magnetic field. With the increase of drop height, the impact duration was shortened, which indicated hardening progress corresponding to the higher impact energy (Figure 5A). The force-displacement curves are shown in Figure 5B. With an increase in drop height, the stiffness was improved. Herein, the peak stiffness of the composites was illustrated by the secant slope. With the drop height increasing from 0.2 to 0.7 m, the peak stiffness shifted from 0.56 × 10⁶ to 0.94 × 10⁶ N/m. When the compressive progress was finished, e-SSG became soft. The electrical behaviors recorded this progress in Figure 5C. During the compressive progress, the electrical resistance of e-SSG increased rapidly and then stayed nearly constant. The peak values of $\Delta R/R_0$ depended on the drop height. With higher drop height, the $\Delta R/R_0$ achieved higher values. However, the rise progress was not linear and could be divided into three stages, which were the fast rise stage, the slow rise stage, and the secondary fast rise stage. The values and duration of the three stages are shown in Table 1. With the increase of drop height, the slow rise stage was gradually eliminated and the response of electrical resistance came to be linear.

FIGURE 5

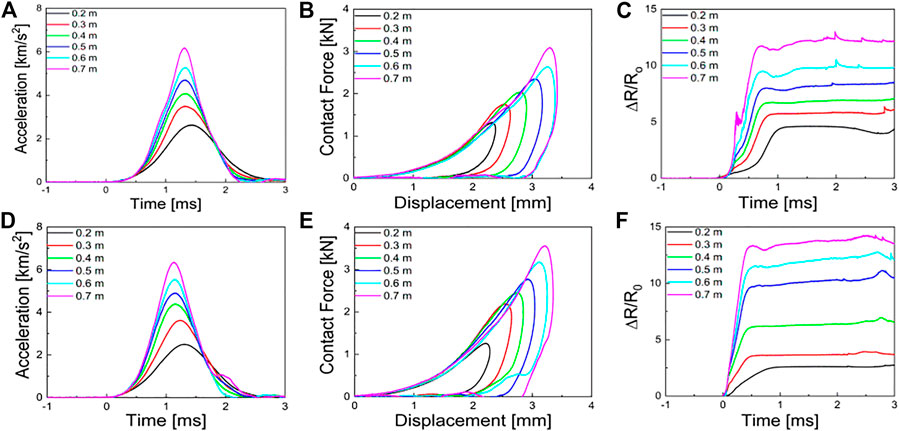
FIGURE 5. (A) The acceleration data vs. time, (B) the contact force vs. displacement curves, (C) the changes of electrical resistance under different drop heights without magnetic field. (D–F) illustrated response behaviors with the magnetic flux density of 0.3 T.

TABLE 1

TABLE 1. The stage value and duration time of the results in Figure 5C.

The enhancement of the magnetic field was remarkable. Compared to the results with the absence of a magnetic field, the impact duration was further shortened under the same drop weight (Figure 5D). The peak values of the $\Delta R/R_0$ of different drop heights also increased. When the drop height ranged from 0.2 to 0.7 m, the $\Delta R/R_0$ were 2.52, 4.05, 6.16, 9.69, 11.47, and 13.31. As seen from the results of MTS, the magnetic field enhanced the linear elastic scope of the e-SSG and the electrical resistance showed continuous rise progress.

According to the theory of Boland et al. (Boland et al., 2016),

$\frac{\Delta R}{R_0}\mathrm{=}\frac{n_{\epsilon }}{W}{\left(\frac{2E_{mgh}}{{\epsilon }_c^{2}E{y}_0}\right)}^m\mathrm{=}a{\left(\frac{h}{k}\right)}^m(4)$

where $n_{\epsilon }$, W and y₀ were the electrical constants and the geometric parameters. ${\epsilon }_c$ was the yield strain. k was the stiffness of the specimen, E was Young’s modulus, $k=\frac{ES}{h}$. In Figure 6, the relation between $\frac{\Delta R}{R_0}$ and $\frac{h}{k}$ was plotted. With the absence of a magnetic field, m₀ = 1.06 and a₀ = 13.28. With the presence of a magnetic field, m₁ = 2.19 and a₁ = 4.81. The parameter “a” in Eq. 4 was negatively corrected with the yield strain of the e-SSG. Its changes indicated the improvement of the stiffness of composites. With the presence of a magnetic field, the CIP clusters aligned in a specific direction. The anisotropy micro-structure helped improve the electrical sensitivity of e-SSG.

FIGURE 6

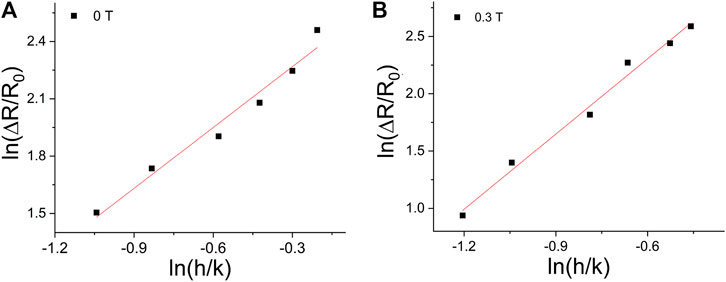
FIGURE 6. The peak values of $\Delta R/R_0$ with different drop height in the absence (A) and presence (B) of the magnetic field. The lines showed fitting results.

To obtain detailed information on the electrical response, the relationship between resistance and resistivity vs. compressive strain is shown in Figure 7. The three stages could be observed in Figure 7A. With the increase of drop height, the sensitivity of e-SSG to strain was improved. When the compressive strain was larger than a critical point, the resistance kept stable. However, the resistivity kept increasing. The increase of resistivity and the deformation of the compression came to balance and the resistance of e-SSG kept nearly constant (Figures 7A,C). The response of e-SSG under the magnetic field showed continuous upward progress (Figure 7B,D). The magnetic field improved the elastic behaviors and kept the electrical response continuous.

FIGURE 7

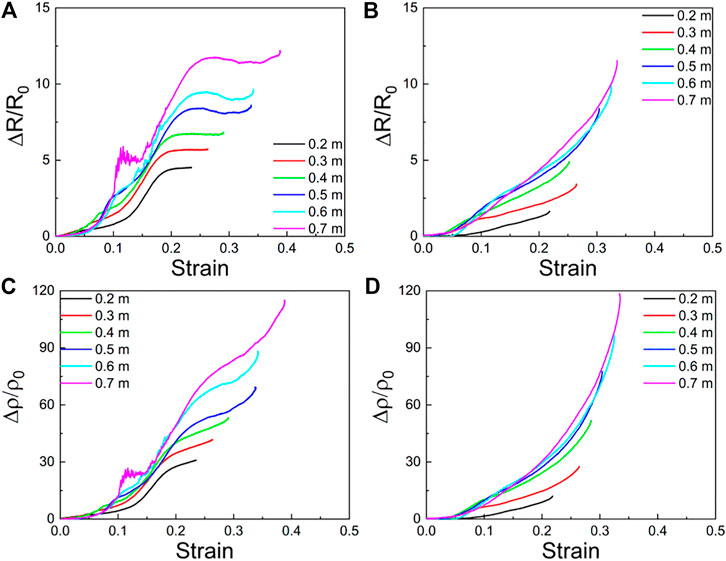
FIGURE 7. Response of (A) resistance and (C) resistivity to compressive strain. (B,D) illustrated the results with a magnetic flux density of 0.3 T.

To illustrate the rate-dependent behaviors, a phenomenological function was adopted. According to the tunneling effect theory (Wang and Cheng, 2014), the conductivity of the composite depends on the effective conductive paths (ECPs). The aggregation and alignment of the conductive fillers are the key factors that determine the numbers of ECPs. The initial state of the composite was homogeneous and isotropic. During the compressive progress, the lateral extension led by the Poisson effect made the CNTs move from their initial position and rotate to a specific direction (Figure 8A). The rearrangement of the CNTs destroyed the original ECPs. Since the restriction of the matrix to the CNTs depended on the mechanical properties of SSG (Zimmerman et al., 2009; de Vicente et al., 2011; Bastola et al., 2020), it was assumed that the sensitivity of the e-SSG was related to the strain rate of external stimulus and the elastic modulus of the specimen. Based on the theory of Boland (Boland et al., 2016), the resistivity of composites depended on the total number of ECPs per volume,

$\rho ={\rho }_0{\left\{{\left[1+{\left(\epsilon \right)}^m\right]}^{-1}\mathrm{+}\frac{\epsilon }{{\epsilon }_t}\right\}}^n(5)$

where the first term in Eq. 5 represented the strain term and the second represented the time dependence. Parameter “n” was a constant related to the microstructure of ECPs. Since the impact duration was short, the time dependence was ignored. Considering that the electrical sensitivity showed remarkable dependence on the strain rate, strain rate, $\dot{\epsilon }$, was adopted to describe the resistivity behaviors. k was the stiffness of the specimen. With the drop height varied from 0.2 to 0.7 m, k was 0.67 × 10⁶, 0.80 × 10⁶, 0.88 × 10⁶, 0.92 × 10⁶, 1.00 × 10⁶, and 1.01 × 10⁶ N/m. Then, the function could be given:

$\frac{\rho }{{\rho }_0}={\left[1+{\left(\epsilon \right)}^m\right]}^{\frac{n\dot{\epsilon }}{k}}(6)$

The curves in Figures 8B,C plot the experiment data and fitting results of function 6. The relationship between electrical resistivity and strain could be expressed as:

$\frac{\rho }{{\rho }_0}={\left[1+{\left(\epsilon \right)}^{1.06}\right]}^{6.5\times {10}^4\frac{\dot{\epsilon }}{k}}(7)$

This phenomenological model illustrated the relationship between strain, strain rate, and the equivalent stiffness of the specimen. The shear stiffening behaviors weakened the effect of impact. This expression could be adopted in engineering applications to monitor external stimulus.

FIGURE 8

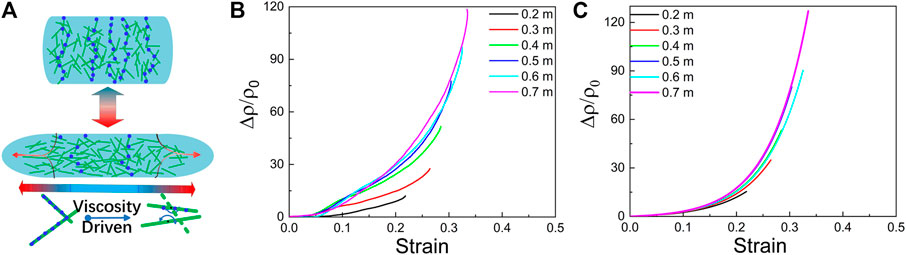
FIGURE 8. (A) The illustration of the negative behaviors of the piezo-resistance. (B) The experiment results and (C) the fitting results of Eq. 6.

The recovery behaviors of the electrical properties under different drop heights and the strength of the external magnetic field were investigated (Figure 9). The impact response was finished in several microseconds, but the recovery progress lasted for seconds. With higher drop heights, the electrical conductivity recovers sooner. To characterize the recovery behaviors, the Prony series with one order was adopted (Belyaeva et al., 2016; Wen et al., 2018).

$\frac{\Delta R}{R_0}\left(t\right)=A_0-{{\displaystyle \sum }}^{\text{}}{A}_n{e}^{-\frac{t}{{\tau }_n}}(8)$

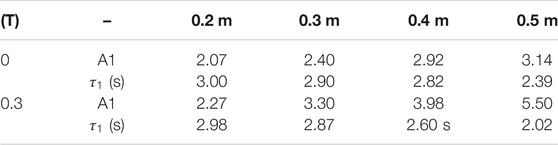
The fitting results are shown in Table 2. Herein, symbols A₁ and τ₁ represent the amplitude and the characteristic time of the decay time, respectively. With an increase of the drop height, the decay amplitude increased from 2.07 to 3.14, and the characteristic time decreased from 3.00 to 2.39 s. The magnetic field further enlarged the amplitude and shortened the characteristic time. The recovery progress was related to the viscoelasticity behaviors of e-SSG. Generally, the relaxation behaviors of the polymer composite depended on the ratio of viscosity to elasticity. High drop height led to the shear stiffening behaviors and the elastic recovery became more remarkable. Meanwhile, the magnetic field improved the elastic modulus and enhanced the recovery progress.

FIGURE 9

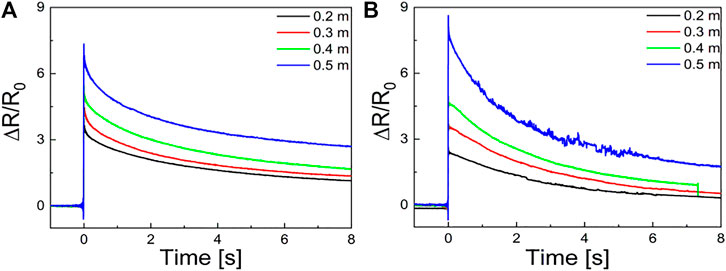
FIGURE 9. The recovery behaviors of the electrical properties under drop weight impact with the strength of the external magnetic field are zero (A) and the strength of the external magnetic field is 0.3 T (B).

TABLE 2

TABLE 2. The fitting results of Prony function.

To demonstrate the durability of the e-SSG, a cyclic drop test was conducted (Figure 10). The drop heights varied from 0.2 to 0.5 m. The magnetic flux density was 0.3 T. With the increase of test number, the response accumulated. Regarding the initial resistance of every impact, $\mathrm{\Delta }R/R_0$ kept stable. After the impact, the conductivity of the composite could recover to its initial state.

FIGURE 10

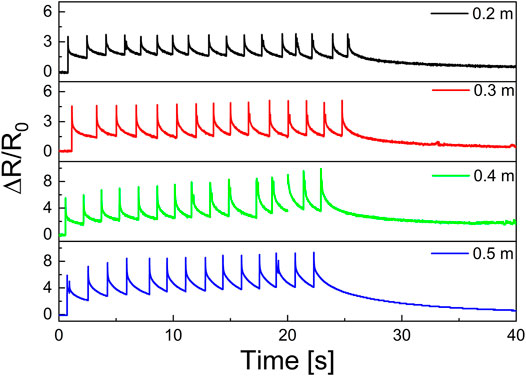
FIGURE 10. The electrical resistance response to cyclic drop weight test with the drop heights of 0.2, 0.3, 0.4, and 0.5 m.

Conclusion

In summary, we developed a novel soft sensor with high sensitivity to strain under quasi-static and low-velocity impact. Inherited from the SSG matrix, this soft sensor could harden itself to burden external stimuli. Magnetic-dependent characteristics further improved the stiffness of the smart material. Quasi-static tests and drop weight experiments were conducted to investigate the electrical and mechanical behaviors. The relationship between resistivity and strain rate was revealed.

Based on these results, this study came to the below conclusions.

(1) The mechanical and electrical behaviors of e-SSG depend on the strain rate and the magnetic field. A higher strain rate led to an increase in yield stress and enhanced the recovery progress of the e-SSG.Due to the magneto-rheological effect, the electrical response of e-SSG to strain was higher and linear under a uniform magnetic field.

(2) The response of the e-SSG to dynamic loading with large amplitude was nonlinear. Magnetic field improved the sensitivity and stability. The shear stiffening behaviors and magneto-rheology behaviors could improve the recovery capacity.

(3) e-SSG could be utilized to monitor the quasi-static deformation and low-velocity impact. Within an appropriate range, the e-SSG could hold stable mechanical and electrical properties and respond regularly to external stimuli.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XF conducted all the experiments and wrote the draft of the article. YW, BW, LS, JL, ZX, SW, and XG revised and discussed the article.

Funding

The authors acknowledge financial supports from the National Natural Science Foundation of China (Grant No. 11972337, 11772320, 11972343), the National Key R&D Program of China (Grant No. 2018YFB1201703) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB2204002) are gratefully acknowledged.

Conflict of Interest

Author JL was employed by the company Anhui Weiwei Rubber Parts Group Co.Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

An, H.-N., Sun, B., Picken, S. J., and Mendes, E. (2012). Long Time Response of Soft Magnetorheological Gels. J. Phys. Chem. B 116, 4702–4711. doi:10.1021/jp301482a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bastola, A. K., Paudel, M., Li, L., and Li, W. (2020). Recent Progress of Magnetorheological Elastomers: a Review. Smart Mater. Struct. 29, 123002. doi:10.1088/1361-665X/abbc77

CrossRef Full Text | Google Scholar

Belyaeva, I. A., Kramarenko, E. Y., Stepanov, G. V., Sorokin, V. V., Stadler, D., and Shamonin, M. (2016). Transient Magnetorheological Response of Magnetoactive Elastomers to Step and Pyramid Excitations. Soft Matter 12, 2901–2913. doi:10.1039/c5sm02690c

PubMed Abstract | CrossRef Full Text | Google Scholar

Boland, C. S., Khan, U., Ryan, G., Barwich, S., Charifou, R., Harvey, A., et al. (2016). Sensitive Electromechanical Sensors Using Viscoelastic Graphene-Polymer Nanocomposites. Science 354, 1257–1260. doi:10.1126/science.aag2879

PubMed Abstract | CrossRef Full Text | Google Scholar

Cvek, M., Kutalkova, E., Moucka, R., Urbanek, P., and Sedlacik, M. (2020). Lightweight, Transparent Piezoresistive Sensors Conceptualized as Anisotropic Magnetorheological Elastomers: A Durability Study. Int. J. Mech. Sci. 183, 105816. doi:10.1016/j.ijmecsci.2020.105816

CrossRef Full Text | Google Scholar

De Vicente, J., Klingenberg, D. J., and Hidalgo-Alvarez, R. (2011). Magnetorheological Fluids: a Review. Soft Matter 7, 3701. doi:10.1039/c0sm01221a

CrossRef Full Text | Google Scholar

Fan, X., Wang, S., Zhang, S., Wang, Y., and Gong, X. (2019). Magnetically Sensitive Nanocomposites Based on the Conductive Shear-Stiffening Gel. J. Mater. Sci. 54, 6971–6981. doi:10.1007/s10853-019-03360-8

CrossRef Full Text | Google Scholar

Gürgen, S., and Yıldız, T. (2020). Stab Resistance of Smart Polymer Coated Textiles Reinforced with Particle Additives. Compos. Structures 235, 111812. doi:10.1016/j.compstruct.2019.111812

CrossRef Full Text | Google Scholar

Hapipi, N. M., Mazlan, S. A., Ubaidillah, U., Abdul Aziz, S. A., Ahmad Khairi, M. H., Nordin, N. A., et al. (2020). Solvent Dependence of the Rheological Properties in Hydrogel Magnetorheological Plastomer. Ijms 21, 1793. doi:10.3390/ijms21051793

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, X.-G., Guo, F., Du, C.-B., and Yu, G.-J. (2018). The Mechanical Properties of a Novel STMR Damper Based on Magnetorheological Silly Putty. Adv. Mater. Sci. Eng. 2018, 1–15. doi:10.1155/2018/2681461

CrossRef Full Text | Google Scholar

Liu, B., Du, C., Yu, G., and Fu, Y. (2020). Shear Thickening Effect of a Multifunctional Magnetorheological Gel: the Influence of Cross-Linked Bonds and Solid Particles. Smart Mater. Struct. 29, 015004. doi:10.1088/1361-665X/ab5243

CrossRef Full Text | Google Scholar

Mietta, J. L., Ruiz, M. M., Antonel, P. S., Perez, O. E., Butera, A., Jorge, G., et al. (2012). Anisotropic Magnetoresistance and Piezoresistivity in Structured Fe3O4-Silver Particles in PDMS Elastomers at Room Temperature. Langmuir 28, 6985–6996. doi:10.1021/la204823k

PubMed Abstract | CrossRef Full Text | Google Scholar

O'driscoll, D. P., Vega-Mayoral, V., Harley, I., Boland, C. S., and Coleman, J. N. (2018). Optimising Composite Viscosity Leads to High Sensitivity Electromechancial Sensors. 2d Mater. 5 (3). doi:10.1088/2053-1583/aacba6

CrossRef Full Text | Google Scholar

Pang, H., Xuan, S., Liu, T., and Gong, X. (2015). Magnetic Field Dependent Electro-Conductivity of the Graphite Doped Magnetorheological Plastomers. Soft Matter 11, 6893–6902. doi:10.1039/c5sm00984g

PubMed Abstract | CrossRef Full Text | Google Scholar

Petare, A. C., and Jain, N. K. (2018). Improving spur Gear Microgeometry and Surface Finish by AFF Process. Mater. Manufacturing Process. 33, 923–934. doi:10.1080/10426914.2017.1376074

CrossRef Full Text | Google Scholar

Puente-Córdova, J., Reyes-Melo, M., Palacios-Pineda, L., Martínez-Perales, I., Martínez-Romero, O., and Elías-Zúñiga, A. (2018). Fabrication and Characterization of Isotropic and Anisotropic Magnetorheological Elastomers, Based on Silicone Rubber and Carbonyl Iron Microparticles. Polymers 10, 1343. doi:10.3390/polym10121343

CrossRef Full Text | Google Scholar

Sun, C., Jia, H., Lei, K., Zhu, D., Gao, Y., Zheng, Z., et al. (2019). Self-healing Hydrogels with Stimuli Responsiveness Based on Acylhydrazone Bonds. Polymer 160, 246–253. doi:10.1016/j.polymer.2018.11.051

CrossRef Full Text | Google Scholar

Wang, L., and Cheng, L. (2014). Piezoresistive Effect of a Carbon Nanotube Silicone-Matrix Composite. Carbon 71, 319–331. doi:10.1016/j.carbon.2014.01.058

CrossRef Full Text | Google Scholar

Wang, S., Jiang, W., Jiang, W., Ye, F., Mao, Y., Xuan, S., et al. (2014). Multifunctional Polymer Composite with Excellent Shear Stiffening Performance and Magnetorheological Effect. J. Mater. Chem. C 2, 7133–7140. doi:10.1039/c4tc00903g

CrossRef Full Text | Google Scholar

Wang, S., Xuan, S., Jiang, W., Jiang, W., Yan, L., Mao, Y., et al. (2015). Rate-dependent and Self-Healing Conductive Shear Stiffening Nanocomposite: a Novel Safe-Guarding Material with Force Sensitivity. J. Mater. Chem. A. 3, 19790–19799. doi:10.1039/c5ta06169e

CrossRef Full Text | Google Scholar

Wang, Y., Ding, L., Zhao, C., Wang, S., Xuan, S., Jiang, H., et al. (2018). A Novel Magnetorheological Shear-Stiffening Elastomer with Self-Healing Ability. Composites Sci. Tech. 168, 303–311. doi:10.1016/j.compscitech.2018.10.019

CrossRef Full Text | Google Scholar

Wang, Y., Wang, S., Xu, C., Xuan, S., Jiang, W., and Gong, X. (2016). Dynamic Behavior of Magnetically Responsive Shear-Stiffening Gel under High Strain Rate. Composites Sci. Tech. 127, 169–176. doi:10.1016/j.compscitech.2016.03.009

CrossRef Full Text | Google Scholar

Wen, Q., Wang, Y., Feng, J., and Gong, X. (2018). Transient Response of Magnetorheological Elastomers to Step Magnetic Field. Appl. Phys. Lett. 113, 081902. doi:10.1063/1.5048368

CrossRef Full Text | Google Scholar

Xu, J., Wang, P., Pang, H., Wang, Y., Wu, J., Xuan, S., et al. (2018). The Dynamic Mechanical Properties of Magnetorheological Plastomers under High Strain Rate. Composites Sci. Tech. 159, 50–58. doi:10.1016/j.compscitech.2018.02.030

CrossRef Full Text | Google Scholar

Xu, Y., Gong, X., Liu, T., and Xuan, S. (2013). Magneto-induced Microstructure Characterization of Magnetorheological Plastomers Using Impedance Spectroscopy. Soft Matter 9, 7701. doi:10.1039/c3sm51072g

CrossRef Full Text | Google Scholar

Xu, Y., Gong, X., Xuan, S., Li, X., Qin, L., and Jiang, W. (2012). Creep and Recovery Behaviors of Magnetorheological Plastomer and its Magnetic-dependent Properties. Soft Matter 8, 8483. doi:10.1039/c2sm25998b

CrossRef Full Text | Google Scholar

Xu, Y., Lubineau, G., Liao, G., He, Q., and Xing, T. (2020). Rate-dependent Viscoelasticity of an Impact-Hardening Polymer under Oscillatory Shear. Mater. Res. Express 7, 075701. doi:10.1088/2053-1591/ab9fbc

CrossRef Full Text | Google Scholar

Yun, G., Tang, S.-Y., Sun, S., Yuan, D., Zhao, Q., Deng, L., et al. (2019). Liquid Metal-Filled Magnetorheological Elastomer with Positive Piezoconductivity. Nat. Commun. 10, 1300. doi:10.1038/s41467-019-09325-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, G., Tang, S.-Y., Zhao, Q., Zhang, Y., Lu, H., Yuan, D., et al. (2020). Liquid Metal Composites with Anisotropic and Unconventional Piezoconductivity. Matter 3, 824–841. doi:10.1016/j.matt.2020.05.022

CrossRef Full Text | Google Scholar

Zhang, G., Li, Y., Wang, H., and Wang, J. (2019). Rheological Properties of Polyurethane-Based Magnetorheological Gels. Front. Mater. 6, 56. doi:10.3389/fmats.2019.00056

CrossRef Full Text | Google Scholar

Zhang, X.-W., Pan, Y., Zheng, Q., and Yi, X.-S. (2000). Time Dependence of Piezoresistance for the Conductor-Filled Polymer Composites. J. Polym. Sci. B Polym. Phys. 38, 2739–2749. doi:10.1002/1099-0488(20001101)38:21<2739::Aid-Polb40>3.0.Co;2-O

CrossRef Full Text | Google Scholar

Zheng, J., He, X., Li, Y., Zhao, B., Ye, F., Gao, C., et al. (2020). Viscoelastic and Magnetically Aligned Flaky Fe-Based Magnetorheological Elastomer Film for Wide-Bandwidth Electromagnetic Wave Absorption. Ind. Eng. Chem. Res. 59, 3425–3437. doi:10.1021/acs.iecr.9b06143

CrossRef Full Text | Google Scholar

Zimmerman, D. T., Bell, R. C., Filer, J. A., Karli, J. O., and Wereley, N. M. (2009). Elastic Percolation Transition in Nanowire-Based Magnetorheological Fluids. Appl. Phys. Lett. 95, 014102. doi:10.1063/1.3167815

CrossRef Full Text | Google Scholar