Molecular Dynamics Simulation of Zener Pinning by Differently Shaped and Oriented Particles

Zener pinning between a curved Cu grain boundary (GB) and a differently shaped and oriented Ag particle has been simulated via molecular dynamics. The computed magnitudes of the maximum pinning force agreed with theoretical predictions only when the force was small. As the force increased, discrepancy became obvious. Through careful inspection of the structures of the Cu–Ag interfaces, detailed interaction processes, and variation of the Cu GB during the interaction, the discrepancy is found to correlate with GB faceting, which very likely reduces the maximum pinning force and facilitates boundary passage. GB anisotropy and/or interface characteristics are also found to slightly contribute to the discrepancy. These findings suggest that the assumption of an isotropic GB with constant energy utilized in previous theoretical studies for deriving the maximum pinning force might be inappropriate and that an accurate maximum pinning force could not be predicted without knowing the effects of GB evolution together with detailed properties of both GBs and interfaces.

Introduction

Zener pinning (Smith, 1948; Zener, 1949), i.e., grain boundary (GB) migration hindered by second-phase particles, has been widely exploited for refining grain sizes (Gladman et al., 1999; Cao et al., 2005; St John et al., 2005), as well as stabilizing nanostructures (Koch et al., 2013). The Zener equation, predicting that a limiting mean grain size D_lim is a function of particle radius, r, and particle volume fraction, f, reads.

$\begin{array}{ll}{D}_{lim}=K\frac{r}{f^m}& (1)\end{array}$

This equation was initially proposed in theoretical works and later partly verified by a number of experiments (Manohar et al., 1998). Nevertheless, magnitudes of the two factors, K and m, obtained from experiments frequently differed from the ones from the theories. The discrepancies were usually ascribed to the great complexities occurring in experiments, e.g., irregular distribution of the particles with various shapes, but not to the correctness of the assumptions made during the theoretical derivation.

In the theoretical studies, the maximum pinning force of one particle acting on one moving GB was derived as the first key step in obtaining Equation 1. This derivation step was performed based on either GB energy/shape evolution (Gladman, 1966; Hellman and Hillert, 1975) or mechanics of surface tensions with respect to the GB and the GB–particle interface (Smith, 1948; Ashby et al., 1969; Ryum et al., 1983; Nes et al., 1985; Ringer et al., 1989; Li and Easterling, 1990). All the studies, however, commonly assumed that, during GB–particle interaction, (I) equilibrium between the surface tensions is maintained at intersection position; thus, for an incoherent particle, a GB meets a particle at 90°; (II) a GB is isotropic and assumes constant energy/mobility; and (III) the intersection line is of a rather regular shape, e.g., a spherical particle makes a planar hole on an initially flat GB.

With the three assumptions, which have never been assessed for their influences on the maximum pinning force, the effects of particle shape, particle orientation, and coherency of the interface had been investigated. The initial version of the maximum pinning force F for an incoherent spherical particle was proposed by Zener (1949) and Smith (1948) as

$\begin{array}{ll}F=\pi r\gamma & (2)\end{array}$

where γ is GB energy. Ashby et al. (1969) considered a coherent spherical particle and suggested

$\begin{array}{ll}F=2\pi r\gamma & (3)\end{array}$

Nes et al. (1985) and Ryum et al. (1983) studied an incoherent ellipsoidal particle with a–a–b axes interacting with a GB migrating along either the normal of the a–a plane (case 1) or the one of the a–b plane (case 2) and derived.

$\begin{array}{ll}F=F_S\frac{2}{(1+ϵ){ϵ}^{1/3}}& (4)\end{array}$

$\begin{array}{l}F=\frac{F_S}{\pi }\frac{(1+2.14ϵ)}{{ϵ}^{1/2}} ϵ\ge 1\\ F=F_s·{ϵ}^{0.47}ϵ\ge 1& (5)\end{array}$

where ϵ = b/a is the aspect ratio (AR) and F_S is the F from an equivalent volume spherical particle. Li and Easterling (1990) and Ringer et al. (1989) further explored the effects of both particle orientation and interface coherency on F for an ellipsoidal and a cubic particle, respectively.

Equations 2–5, however, have never been directly verified by experiments (due to experimental difficulties). In simulation, F had been evaluated mainly via phase field (PF) and molecular dynamics (MD) methods. With the PF method, Chang and Chen (2012) simulated the GB–particle interaction for differently shaped and differently oriented incoherent particles. The evaluated F magnitudes were found to agree with Equation 4 for an ellipsoidal particle in case 1 but obviously disagree with either Equation 5 for an ellipsoidal particle in case 2 or the theoretical predictions for a cubic particle (Ringer et al., 1989). Generally, the PF method is unable to provide detailed interaction mechanisms at atomic scale, and more significantly, it made use of the same assumptions (e.g., assumptions I and II) as the ones in theoretical studies.

Compared with the PF method, no such assumptions were enforced in the MD method developed by Zhou et al. (2016, 2017, 2018) and Li et al. (2020). In these studies, a curved Cu GB driven by a capillary driving force migrated toward a spherical Ag/Ni particle, and the GB–particle interaction, during which the GB, the interface, and the contact curve were all free to evolve without any restrictions, proceeded spontaneously. There are many interesting findings, including (1) different GBs exhibit distinct ability to move past a second-phase particle of the same size, resulting in misorientation dependence of GB migration velocity becoming more obvious than the cases without the pinning process (Zhou et al., 2016, 2017); (2) nano-sized particles can reorient to keep coherency with matrix grains via various atomistic mechanisms, e.g., cutting, rotation, and migration of newly nucleated GB inside the particle (Zhou et al., 2017); (3) the MD method is able to accurately predict the F magnitudes via a boundary–energy–evolution approach (Zhou et al., 2018; Li et al., 2020); (4) boundary faceting, as a form of GB evolution products, broadly occurs and is dependent on GB types (Li et al., 2020). Overall, the MD method has been proved to be a powerful tool for studying Zener pinning both qualitatively and quantitatively.

To this end, we further applied the MD method to study the effects of differently shaped and differently orientated particles on F. Special efforts were taken to inspect the correctness of the assumptions I–III. The results eventually demonstrated that these assumptions, in some cases, are inappropriate and that boundary faceting, GB anisotropy, and interface characteristics had been considered for rationalizing the evaluated F values.

Methodology

The simulations were performed exploiting a coherent Ag second-phase particle embedded in a half-loop Cu bicrystal, as employed in previous studies (Zhou et al., 2016, 2017, 2018; Li et al., 2020) and illustrated in Figure 1. The two Cu grains shared a common <111> axis, set to be parallel to the Z-axis, and were disorientated by an angle of 21.79°. In such a way, we obtained a <111> tilt 21.79° GB, which was chosen since no significant faceting was found during both its free motion and its initial interaction with the Ag particle (Zhou et al., 2017, 2018; Li et al., 2020). The dimensions of the half-loop are given in Figure 1 and the crystallographic planes of the two grains along the X-, Y-, and Z-axes are (231), (451), and (111), respectively.

FIGURE 1

Figure 1. Illustration of simulation configuration with an ellipsoidal/cubic Ag particle embedded in a Cu bicrystal. The dimensions (in nm) of the simulation cell and the half-loop Cu grain boundary (GB) are denoted.

The Ag particles were set to be either ellipsoidal or cubic (Ag particle shape is nearly spherical in reality, while shape variation only aims to study its effect on the pinning). In the former case, the ellipsoid was of a constant volume equivalent to a 5 nm diameter sphere but with a varying AR b/a (b and a are shown in Figure 1, and the particle turns to be more plate- or needle-shaped as b/a becomes smaller or larger than unity, respectively). The principal axis b of the particle was further changed to lie along the X-, Y-, and Z-axes, respectively. Combining with seven different values of the AR given in Table 1, there are, in total, 21 different samples studied (there are actually only 19 different samples since the three ones of b/a = 1 are virtually identical). In the latter case, the cubic particle only possessed one orientation, with one of its faces parallel to the X–Z plane, but a varying volume equivalent to a sphere in diameter ranging from 4 to 7 nm.

TABLE 1

Table 1. Cutting extent for various ellipsoidal particles during the particle–GB interaction.

The atomistic interactions of the Cu–Ag alloy were described by an embedded atom method (EAM) potential (Williams et al., 2006), which was demonstrated to reproduce mechanical properties and even phase diagram of the alloy. For example, stacking fault energies (SFEs) of Cu and Ag were computed to be 44.4 (Williams et al., 2006) and 17.8 (Mishin et al., 2001) mJ/m², respectively, which are in good agreement with experimental values of 45 and 16 mJ/m², respectively.

The MD simulations were run by LAMMPS (Plimpton, 1995), and the resulting configurations were visualized via OVITO (Stukowski, 2010). Periodic boundary conditions were enforced along all the three directions, while atoms with their Y-coordinates smaller than 1 nm were fixed to prevent motion of the boundary segments present there. Initially, the as-built sample was relaxed at 10 K for 200 ps in order to minimize system enthalpy. The relaxed sample was then gradually heated to 800 K during another 200 ps, and this temperature was maintained in the following: For calculating system energy evolution, resulting configurations with an interval of 10 ps were quenched to 1 K during 3 ps. This period was found to be sufficient to achieve enthalpy convergence of the system.

To evaluate the F of the differently shaped particle acting on the half-loop GB, the approach proposed in a previous study (Zhou et al., 2018) was utilized. This approach compares system energy evolution between free GB migration and boundary migration affected by GB–particle interaction and calculates F as the largest derivative of the energy difference with respect to boundary position. The approach has been verified for many GBs as well as differently sized spherical particles (Zhou et al., 2018; Li et al., 2020). In this study, the free boundary migration is largely omitted, since corresponding results with the same settings as this study have been reported in a previous study (Zhou et al., 2018).

Simulation Results

Ellipsoidal Particles

We begin by inspecting configurations right after the relaxation treatment. It was found that many defects of misfit dislocations and stacking faults/twin boundaries (SFs/TBs) formed at the Cu–Ag interface and in the Ag particles, respectively, which can be seen in Figure 2 as clusters of disorder atoms and layers of hcp atoms, respectively. The non-fcc atoms, i.e., the disorder and hcp ones, are quantified for three consecutive configurations (with the interval of 10 ps) just after the relaxation, and average numbers are plotted as a function of AR in Figure 3. Generally, as AR deviated from unity, i.e., the particles became more needle- or plate-shaped, and more defects were formed.

FIGURE 2

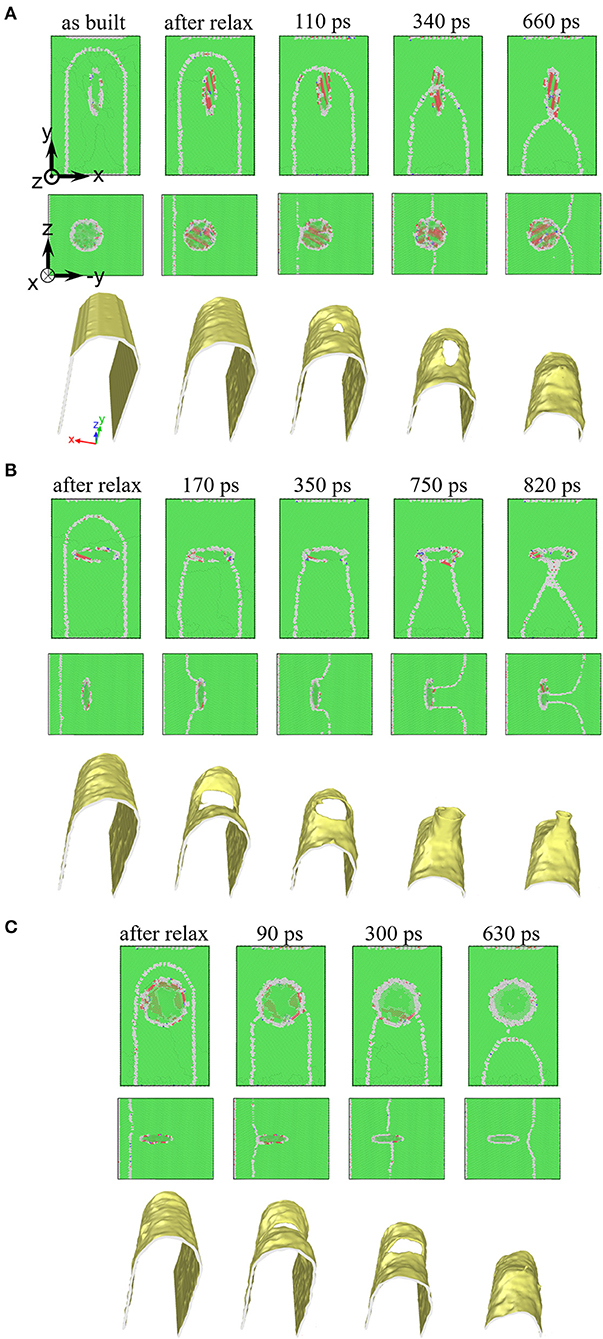
Figure 2. Snapshots and boundary configurations during the GB–particle interaction. (A) Full cutting of the ellipsoidal particle with b // X and aspect ratio (AR) = 0.25; (B) partial cutting of the particle with b // Y and AR = 0.25; (C) no cutting of the particle with b // Z and AR = 0.25. The colors of the atoms are assigned based on their local environments: green, gray, and red for fcc, disorder, and hcp, respectively (for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article).

FIGURE 3

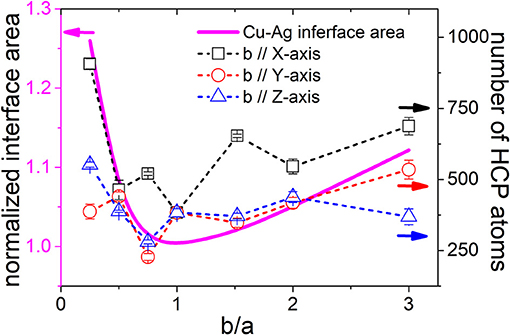
Figure 3. Number of non-fcc atoms vs. AR for the differently shaped ellipsoidal particles after the relaxation process. Cu–Ag interface area normalized by the one of the spherical particle is also given for comparison.

After the relaxation, for all the samples containing the ellipsoidal particles, four stages, i.e., initial free boundary migration, attraction of the boundary to the particle, retardment of boundary motion by the particle, and at last detachment from the particle, were observed, which had also been found in a previous studies on spherical particles (Zhou et al., 2016, 2017, 2018; Li et al., 2020). As the particle shape changed, the samples, however, exhibited very dissimilar behaviors in terms of boundary passage modes and also boundary shape evolution.

First, some ellipsoidal particles were cut by the boundary during the passage. Based on cutting extent, three types, named henceforth as full cutting, partial cutting, and no cutting, have been determined and summarized in Table 1. In the full cutting case, as shown in Figure 2A, a curved Ag GB formed inside the particle, and the GB appeared to migrate together with the Cu GB, causing the Ag particle to reorient and become thoroughly coherent with the growing grain. This type of cutting was only observed in the case of b // X and AR = 0.25. Differing from the full cutting, partial cutting partly cuts the particle and it occurred in many cases when the particle shape largely deviates from a sphere. Figure 2B presents such an example, which shows that cutting stopped inside the particle, while the Cu GB continued to pass the particle, resulting in both coherent and incoherent interfaces after the passage. The last cutting type is no cutting, which is mainly observed for particle shape close to a sphere. In this case, the particle did not experience cutting (see Figure 2C), thus there was no reorientation and the particle became totally incoherent with the growing grain.

Second, the boundaries underwent considerably complex shape evolution during the interaction. As seen in Figure 2, GB segments, especially the ones adjacent to the GB–particle intersection curve, continuously varied during the attraction, retardment, and detachment stages, and this variation largely differed among the cases of the distinct particle shapes. As a result, the hole shape made by the particle changed continuously, so did the GB–particle contact angle, which even assumed dissimilar degrees along the intersection curve. Furthermore, boundary faceting was extensively observed [facets in the Y–Z views of Figures 2, 4 are 21.79° <111> twist GBs, as discussed in detail in Zhou et al. (2016)]. In some cases, the faceting started to take place at the beginning of the retardment stage and became more obvious till the detachment (see, e.g., b // Y and AR = 0.25 at 350 ps and right before detachment, as shown in Figures 2B, 4, respectively). In others, e.g., b // X and AR = 0.25 in Figure 4, no significant faceting occurred. Based on the configurations right before detachment summarized in Figure 4, faceting extent differed from case to case, and it monotonically increased/decreased with AR when b lied along the three axes.

FIGURE 4

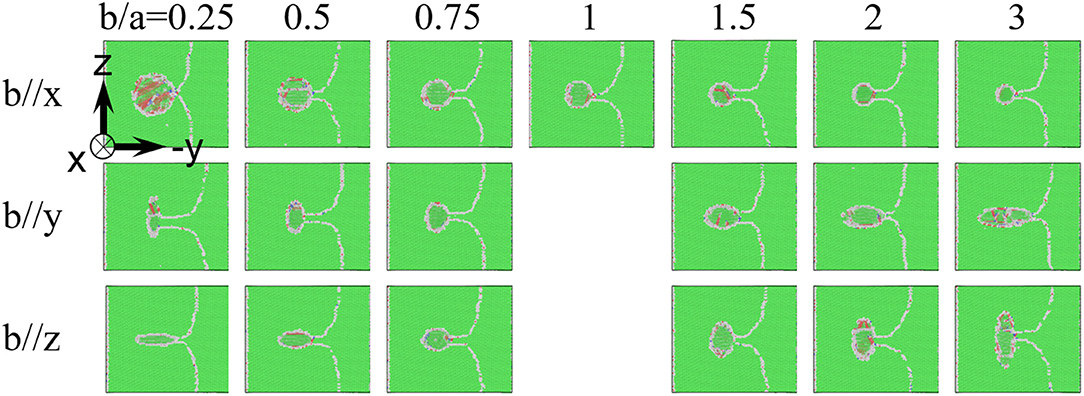
Figure 4. Configurations right before the detachment of the boundaries from the particles (See online article for color version of this figure).

We turn next to the key findings regarding F. As proposed in Zhou et al. (2018) and briefly introduced in the methodology section, the system energy difference between the free GB migration and the retarded migration was evaluated against GB position, so that energy evolution exclusively due to the GB-particle interaction could be obtained. Typical curves are plotted in Figures 5A–C, which displays that, as the position increases, the energy commonly first oscillates around zero, quickly drops to a minimum, slowly increases to a maximum, and finally decreases again. These four behaviors exactly correspond to the four interaction stages mentioned above, i.e., the free motion, attachment, retardment, and detachment, respectively.

FIGURE 5

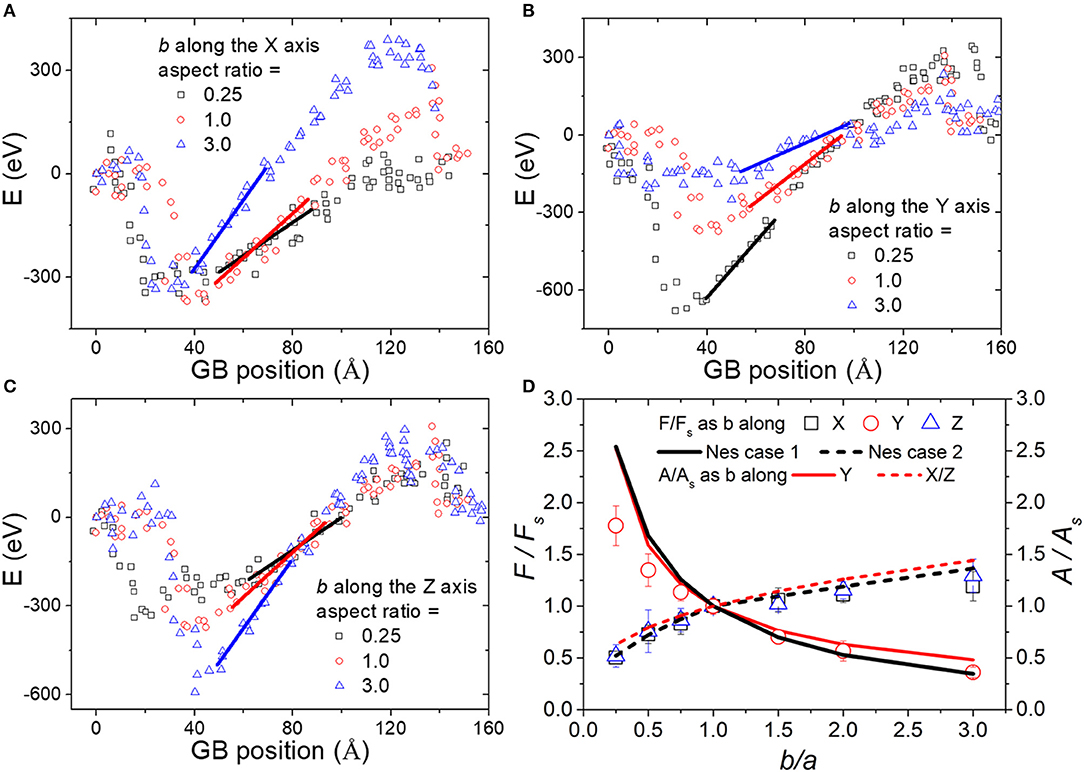
Figure 5. Energy evolution as a function of GB position during the GB–particle interaction for the ellipsoidal particles of different AR values when b is parallel to the (A) X-, (B) Y-, and (c) Z-axes, respectively. In (A–C), the maximum slope of each curve, corresponding to the maximum pinning force is marked. (D) Maximum pinning force vs. AR for the ellipsoidal particles. Theoretical predictions by Nes et al. (1985) together with the projection area of the particles to the plane normal to the boundary migration direction, i.e., the Y direction, are given for comparison. The maximum pinning force, F, and the area, A, are normalized by the F_s and A_s of the spherical particle case, respectively.

Focusing on the retardment stage, the largest slope, which yields F, always occurred at the beginning of the stage. By plotting the measured F as a function of AR for the differently shaped and/or oriented particles in Figure 5D, in which the theoretical values predicted by Nes et al. (1985) are given for comparison, it was found that our simulation results generally agree with the theoretical ones, i.e., pinning effect becomes pronounced when the plate normal of the plate-shaped particle or the long edge of the needle-shaped particle turn to be parallel or perpendicular to the boundary migration direction, respectively. Nevertheless, it seems that discrepancies turn to be increasingly evident for large Fs, and the simulated values of b lying along the X- and Z-axes are not exactly the same.

Cubic Particles

In addition to the ellipsoidal particles, the cubic ones with fixed orientation and several sizes (with volumes equal to 4–7 nm diameter spheres) have also been investigated. The relaxed Ag particles also contained the defects, i.e., misfit dislocations and SFs/TBs, as exemplified in Figure 6. Amounts of the defects quantified with the same approach for the ellipsoidal particles are shown in Figure 7, from which it was observed that the defects increase with the particle size. During the GB–particle interaction, in any case, cutting was not found and the variation in the boundary shape was complicated. It is noticeable that the facets of 21.79° <111> twist boundary at the retardment stage always formed for all the samples with the cubic particles. One example is shown in Figure 6, which displays that facets increasingly formed between 530 ps and the detachment moment.

FIGURE 6

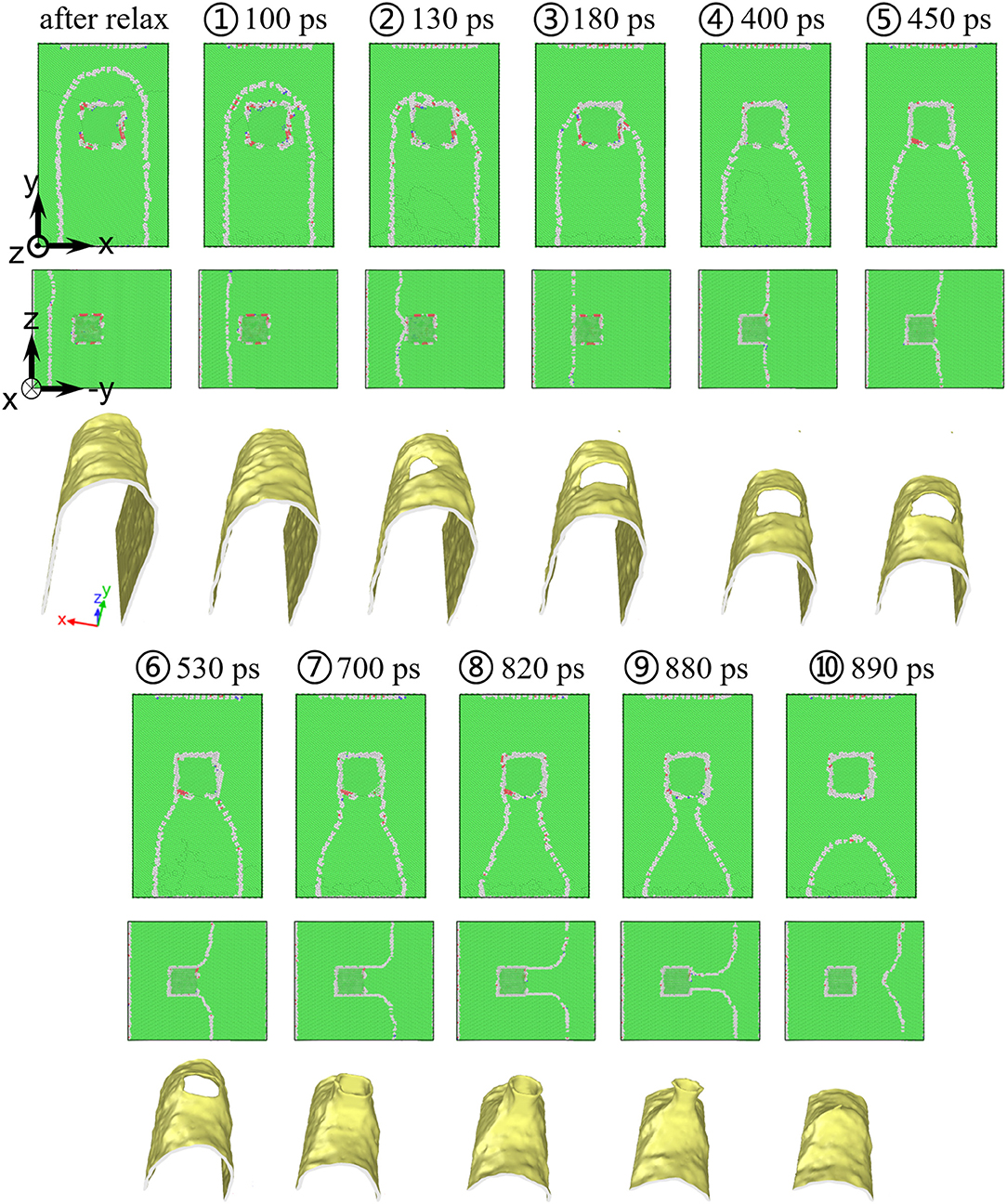
Figure 6. Snapshots and boundary configurations during the GB–particle interaction for the cubic particle with its volume identical to a spherical particle of 6 nm diameter. The atoms are colored based on their local environments: green, gray, and red for fcc, disorder, and hcp, respectively (for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article).

FIGURE 7

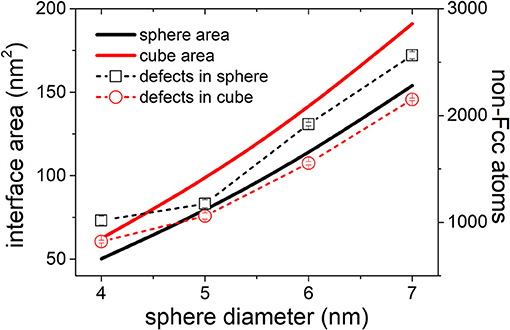
Figure 7. Number of non-fcc atoms vs. sphere diameter for both spherical and cubic particles after the relaxation process. The cubic particles are of the same volumes as the spherical ones. Cu–Ag interface areas are also given for comparison.

Regarding the energy–position curves shown in Figure 8, except the four stages found in the cases of the ellipsoidal particles, one new stage featured in nearly invariable boundary shape and roughly constant energy evolution (see e.g., moments between 180 and 400 ps in Figures 6, 8C) was determined between the attachment and the retardment stages for all the cubic particle cases. F was always at the beginning of the retardment stage, and the force increased with the particle size (see Figure 8A), as found in the cases of spherical particles (Zhou et al., 2018; Li et al., 2020). Nevertheless, according to Figures 8B–E, Fs of equal-volume cube and sphere are rather similar, both are equal to ~2πrγ. These forces arising from the cubic particles are much smaller than theoretical values (Ringer et al., 1989) or phase field results (Chang and Chen, 2012).

FIGURE 8

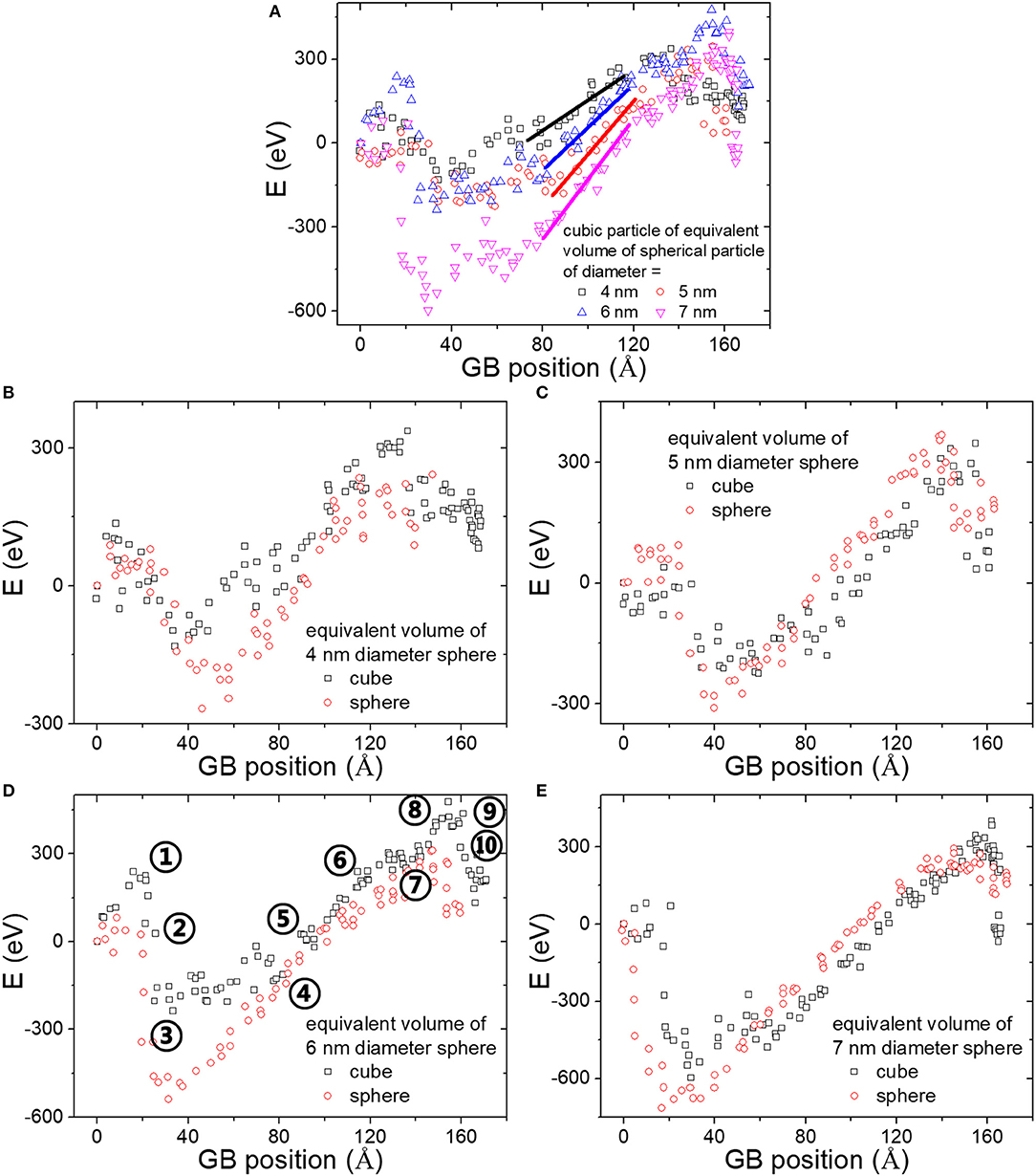
Figure 8. (A) Energy vs. boundary position for the cubic particles. (B–E) Comparisons of the energy–position curves between the cubic and spherical particles. Indexes in (D) correspond to the ones given in Figure 6.

Discussion

This study examined Zener pinning of one differently shaped Ag particle on a half-loop Cu GB. It was noticed that, without the pinning, the curved 21.79° <111> tilt GB driven by a very large capillary driving force of 274 MPa migrated at a high velocity of 22.3 m/s, as measured in Li et al. (2020). With the pinning, the interaction time (from attachment to detachment) for the distinct cases was found to be always <1 ns. Within such a short period, the tension equilibrium between the Cu GB and the Cu–Ag interface might not be established.

It is also noticeable that the interface coherency was reported to greatly affect the pinning force (Ashby et al., 1969). By definition, since the Cu matrix and the Ag particle owned the same lattice type and orientation, a coherent interface is expected form. Nevertheless, semi-coherent interfaces were frequently observed after the relaxation, as shown in Figures 2, 6. This can be ascribed to a large misfit of 13.1% calculated by the lattice constants of the applied EAM potential. In addition, the coherency from the GB–particle interaction point of view, was defined in Ringer et al. (1989) as

$\begin{array}{ll}cos\beta =\frac{{\gamma }_{1p}-{\gamma }_{2p}}{{\gamma }_{GB}}& (6)\end{array}$

where γ_1p and γ_2p are energies of interfaces after and before the boundary passage, respectively, γ_GB is GB energy, and β is contact angle. In this definition, β decreases from 90° to 0°, as a completely incoherent interface changes to be a fully coherent one. In this study, the complexly changing boundaries during the interactions, mentioned above, however, render that it is almost impossible to measure the contact angle. Therefore, we checked the coherency by setting sufficiently large (23 × 23 nm) immobile flat boundaries interacting with a spherical particle. Through the same relaxation process mentioned in the section “Methodology” and a further relaxation at 800 K for as long as 1 ns, equilibrium configurations were obtained and displayed in Figure 9. It is surprising to see that the coherency changed with GB type and that the GB employed in this study, i.e., the 21.79° GB yielded a nearly incoherent interface. To this end, the interfaces in this study are recognized to be structurally semi-coherent and energetically incoherent. The latter is true, at least, for the spherical particles.

FIGURE 9

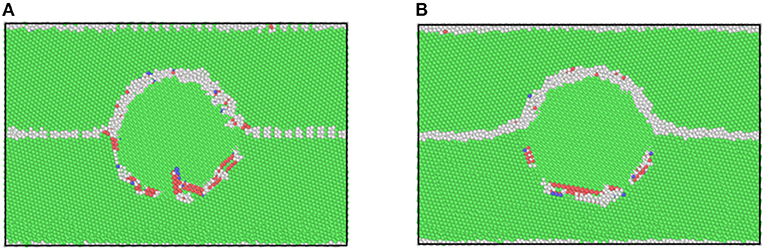
Figure 9. Equilibrium configurations of flat (A) 21.79° and (B) 38.21° <111> tilt Cu GBs connecting to an 8 nm diameter Ag particle. The particle and the lower grain own a cube-on-cube orientation relationship.

After clarifying interaction conditions with respect to the interaction time and the interface type, we move forward to the interaction stages and more importantly to the pinning effects with regard to F. Considering the configurations (Figures 2, 6) together with the energy–position curves (Figures 5, 8), it demonstrates that, for both the ellipsoidal and cubic particles, the three stages of attachment, retardment, and detachment occurred during the interaction, and F was always determined at the beginning of the retardment stage, which is consistent with previous findings with regard to the spherical particles (Zhou et al., 2018; Li et al., 2020). The additional stage existing between the attachment and detachment stages is specific to the cubic particles with their special orientation.

Comparing the evaluated F magnitudes with theoretical predictions (Nes et al., 1985; Ringer et al., 1989), there are agreements and disagreements. In the case of the ellipsoidal particles, the trend of the F changing with the three orientations and AR generally agrees with the theoretical result predicted by Nes et al. (1985) (see Figure 5D) for incoherent particles (the interface in this study is virtually incoherent as discussed above), although the corresponding theoretical model was developed based on tension equilibrium. In fact, rough agreement is also determined when comparisons are made between the Fs and projection area of the particles to the plane perpendicular to the GB migration direction, which is also plotted in Figure 5D.

Referring to specific F values, it appears that the F gradually deviated from the theoretical value as the F became larger than the one of the spherical particle and the Fs for the cases of b // X- and Z- axes slightly differed. The latter possibly stems from anisotropic nature of the GB and/or the different interfaces. For example, with small ARs, the interface approaches (231) and (111) when b // X and Z, respectively. In case of the cubic particles, the evaluated Fs are much lower than theoretical values by Ringer et al. (1989). The authors predicted that the F of a cube is about two times larger than the one of an equivalent volume spherical particle when interface is totally incoherent, while almost identical Fs are found in this study.

By examining possible correlations between the unmatched simulated Fs (lower than theoretical magnitudes) and the other simulation observations (relaxed configurations, cutting extent, and boundary faceting), we found that the unmatched low Fs are very likely due to the faceting. Consider the relaxed configurations first. The defects of misfit dislocations and SFs/TBs were merely found at the structurally semi-coherent Cu–Ag interface and inside the Ag particle, respectively. The SFs/TBs are expected to occur due to dissociation of the misfit dislocations together with following glide of partial dislocations. All of these are reasonable since Ag possesses a much lower SFE than Cu (SFEs have been given in the section “Methodology”). The amounts of the defects for the spherical and cubic particles are further found to roughly correlate with corresponding interface area, although discrepancies exist, as shown in Figures 3, 7. The discrepancies again are ascribed to the different interfaces. The relaxed configurations, however, are not the reason for the unmatched Fs. For example, as shown in Figures 3, 5D, with the same AR = 0.25, the relaxed configurations of b // Y and Z owned approximately same amount of defects, but only the case of b // Y yielded the unmatched F; the relaxed configurations of b // X and Z owned very distinct defect amounts, but both cases were of predicted Fs.

The cutting of the particles by the GB is next considered. This phenomenon had been reported in both experiment (Randle and Ralph, 1986) and MD simulation (Zhou et al., 2017). In the study of Zhou et al. (2017), which concerned Zener pinning of a Cu–Ni system (4−8 nm diameter spherical Ni particles interacting with 11 different <111> tilt Cu GBs), cutting was found to occur more readily for small particles, and its extent differed with the different GBs and the Ni particles were much easier to be cut than the Ag ones due to low misfit of the Cu–Ni system (2.7%). In this study, cutting took place only for a part of ellipsoidal particles with ARs largely deviating from unity, and its extent was drastically distinct for the three particle orientations (see Table 1). The cutting always initiated at interface segments associated with large interface curvature (see e.g., Figures 2A,B), which rationalizes the finding of no occurrence of cutting for the cubic particles as most interface segments of these particles are of infinitely small curvature and the ones at corners are still of smaller curvatures than the ellipsoidal cases. Overall, cutting is found to be affected by multiple factors, including misfit degree, boundary types, and again interface types.

Like the relaxed configurations, the cutting is not related to the unmatched Fs either. For instances, according to Table 1; Figure 5d, the particle of AR = 0.25 and b // Y resulted in an F much lower than the theoretical value, but there is no cutting at all. In contrast, the particle of AR = 0.25 and b // X gave rise to a perfectly matched F, while this particle was fully cut during the interaction. It is surprising to find that the Fs were not affected by the cutting, which can cause two boundaries and two interfaces to meet together and therefore fundamentally alter tension equilibrium (if existing) when compared with the cases without the cutting. This, in turn, might indicate that tension equilibrium is not a key point to determine pinning effects.

Instead of the relaxed microstructure and the cutting phenomenon, the boundary faceting, which can develop within a rather short time period (<1 ns as discussed above) at the retardment stage to form low-energy 21.79° <111> twist boundary facets (Zhou et al., 2018), correlates well with the unmatched Fs. Through comparing the results of both the ellipsoidal and cubic particles (e.g., Figures 4, 5D for the ellipsoidal ones), it can be clearly seen that more faceting led to larger deviation of F, and these two phenomena became more pronounced as F increased. The latter suggests that a large pinning force is able to trigger localized boundary variation to low-energy segments, which in turn lowers the pinning force and favors boundary passage.

Faceting has been broadly observed in both experiments (Straumal et al., 2006; Kirch et al., 2007, 2008) and MD simulations (Brown and Mishin, 2007; Li et al., 2020), which commonly indicate that ability of faceting is highly related to GB types. In a recent study on 86 GBs interacting with one spherical particle (Li et al., 2020), faceting was found to possibly occur at the free migration and/or the retardment stages, and <111> tilt GBs, including the one studied in the present study, faceted at the retardment stage. Since the occurrence of faceting tends to lower the pinning force, it is assumed that <111> tilt GBs are easier to pass second-phase particles than other GBs. Additional research on this point is called for in the future.

Finally, we address whether the assumptions employed in the theoretical derivations of F are feasible. First, we believe that tension equilibrium of the pinning process is practically impossible to be directly and accurately inspected by any research methods, since a moving GB at atomic scale has to migrate in a segment-by-segment way, yielding non-constant shapes. The equilibrium might be even harder to reach for small size systems, as applied in this study. In spite of this, the Fs computed based on the boundary–energy–evolution method in many cases agree with theoretical predictions obtained on the basis of tension equilibrium. Second, the assumption of an isotropic GB with a constant energy/mobility is inappropriate, especially when faceting prevails for some GBs, which can lower the pinning force. In fact, GB—particle interfaces its own different natures, which was largely ignored in previous studies. The different characteristics can also affect the pinning force, although not as effective as the faceting based on the findings in this study. Third, shape of the hole made by the interaction is not constant and regular, but rather it is changing and in many cases irregular.

Conclusions

In this study, Zener pinning with regard to a curved 21.79° <111> tilt Cu GB and a differently shaped (ellipsoidal and cubic) and oriented (only for the ellipsoidal cases) Ag particle has been investigated via MD simulations. Conclusions are drawn as follows.

1.In spite of a cube-on-cube orientation relationship, the Cu–Ag interfaces of both the ellipsoidal and the cubic particles are structurally semi-coherent and energetically incoherent.

2.For ellipsoidal particles, the evaluated magnitudes of F agree well with theoretical values predicted by Nes et al. (1985), only when F is small. As the force increases to be larger than the one resulting from an equivalent volume spherical particle, the evaluated forces turn to deviate away from the predictions (Nes et al., 1985; Ringer et al., 1989) for both the ellipsoidal and the cubic particles.

3.The deviation is mainly ascribed to the boundary faceting occurring at the retardment stage during the GB–particle interaction. The faceting, as a type of localized boundary variation in shape and energy, can reduce F and facilitate boundary passage. The GB anisotropy and/or the distinct interfaces of the differently shaped and differently oriented particles might also contribute to the deviation.

4.The equilibrium particles after relaxation possess different amounts of defects (misfit dislocations and SFs/TBs) and are cut during the interaction by the migrating GB to different extents. Both the amounts and the extents are also attributed to the distinct interfaces.

5.The results found in this study suggest that the assumption of an isotropic GB with constant energy/mobility utilized in previous theoretical studies for deriving F is inappropriate, especially when a GB (e.g., <111> tilt GBs) is prone to faceting. The results also indicate that tension equilibrium might not be established in the case of quick GB migration of nano-sized grains and that the contact curve is frequently of an irregular shape.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ and QZ provided guidance and revised the manuscript. All the authors performed the simulations, analyzed the results, and wrote the manuscript.

Funding

The authors are grateful for the financial support from the Natural Science Foundation of China (Grant Nos. 51874204, 51901148), the Fundamental Research Program of Shenzhen (Grant No. JCYJ20170412153039309), and the state Key Laboratory of Solidification Processing in Northwestern Polytechnical University, China (Grant No. SKLSP202006).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ashby, M., Harper, J., and Lewis, J. (1969). Interaction of crystal boundaries with second-phase particles. Trans. Met. Soc. AIME 245, 413–420.

PubMed Abstract | Google Scholar

Brown, J. A., and Mishin, Y. (2007). Dissociation and faceting of asymmetrical tilt grain boundaries: molecular dynamics simulations of copper. Phys. Rev. B 76:134118. doi: 10.1103/PhysRevB.76.134118

CrossRef Full Text | Google Scholar

Cao, P., Qian, M., and St John, D. H. (2005). Native grain refinement of magnesium alloys. Scripta Mater. 53, 841–844. doi: 10.1016/j.scriptamat.2005.06.010

CrossRef Full Text | Google Scholar

Chang, K., and Chen, L. Q. (2012). Quantitative evaluation of particle pinning force on a grain boundary using the phase-field method. Model. Simul. Mater. Sci. Eng. 20:055004. doi: 10.1088/0965-0393/20/5/055004

CrossRef Full Text | Google Scholar

Gladman, T. (1966). On theory of effect of precipitate particles on grain growth in metals. P. Roy. Soc. Lond. A-Math. Phys. Sci. 294, 298–309. doi: 10.1098/rspa.1966.0208

CrossRef Full Text | Google Scholar

Gladman, T., Fourlaris, G., and Talafi-Noghani, M. (1999). Grain refinement of steel by oxidic second phase particles. Mater. Sci. Technol. 15, 1414–1424. doi: 10.1179/026708399101505400

CrossRef Full Text | Google Scholar

Hellman, P., and Hillert, M. (1975). On the effect of second-phase particles on grain growth. Scand. J. Metall. 4, 211–219.

Google Scholar

Kirch, D. M., Jannot, E., Barrales-Mora, L. A., Molodov, D. A., and Gottstein, G. (2008). Inclination dependence of grain boundary energy and its impact on the faceting and kinetics of tilt grain boundaries in aluminum. Acta Mater. 56, 4998–5011. doi: 10.1016/j.actamat.2008.06.017

CrossRef Full Text | Google Scholar

Kirch, D. M., Zhao, B., Molodov, D. A., and Gottstein, G. (2007). Faceting of low-angle <100> tilt grain boundaries in aluminum. Scripta Mater. 56, 939–942. doi: 10.1016/j.scriptamat.2007.02.010

CrossRef Full Text | Google Scholar

Koch, C. C., Scattergood, R. O., Saber, M., and Kotan, H. (2013). High temperature stabilization of nanocrystalline grain size: thermodynamic versus kinetic strategies. J. Mater. Res. 28, 1785–1791. doi: 10.1557/jmr.2012.429

CrossRef Full Text | Google Scholar

Li, R. J., Zhou, J., Li, Y., Liu, Y. H., Zhao, B. B., and Ren, F. Z. (2020). Grain boundary migration and Zener pinning in a nanocrystalline Cu–Ag alloy. Modelling Simul. Mater. Sci. Eng. 28:065017. doi: 10.1088/1361-651X/aba737

CrossRef Full Text | Google Scholar

Li, W. B., and Easterling, K. E. (1990). The influence of particle-shape on Zener drag. Acta Metall. Mater. 38, 1045–1052. doi: 10.1016/0956-7151(90)90177-I

CrossRef Full Text | Google Scholar

Manohar, P. A., Ferry, M., and Chandra, T. (1998). Five decades of the Zener equation. ISIJ Int. 38, 913–924. doi: 10.2355/isijinternational.38.913

CrossRef Full Text | Google Scholar

Mishin, Y., Mehl, M. J., Papaconstantopoulos, D. A., Voter, A. F., and Kress, J. D. (2001). Structural stability and lattice defects in copper: ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 63:16. doi: 10.1103/PhysRevB.63.224106

CrossRef Full Text | Google Scholar

Nes, E., Ryum, N., and Hunderi, O. (1985). On the zener drag. Acta Metall. 33, 11–22. doi: 10.1016/0001-6160(85)90214-7

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 117, 1–19. doi: 10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Randle, V., and Ralph, B. (1986). Interactions of grain-boundaries with coherent precipitates during grain-growth. Acta Metall. 34, 891–898. doi: 10.1016/0001-6160(86)90062-3

CrossRef Full Text | Google Scholar

Ringer, S. P., Li, W. B., and Easterling, K. E. (1989). On the interaction and pinning of grain-boundaries by cubic shaped precipitate particles. Acta Metall. 37, 831–841. doi: 10.1016/0001-6160(89)90010-2

CrossRef Full Text | Google Scholar

Ryum, N., Hunderi, O., and Nes, E. (1983). On grain boundary drag from second phase particles. Scripta Metall. 17, 1281–1283. doi: 10.1016/0036-9748(83)90216-8

CrossRef Full Text | Google Scholar

Smith, C. S. (1948). Grains, phases, and interfaces - an interpretation of microstructure. Trans. Am. Inst. Min. Metall. Engrs. 175, 15–51.

Google Scholar

St John, D. H., Qian, M., Easton, M. A., Cao, P., and Hildebrand, Z. (2005). Grain refinement of magnesium alloys. Metall. Mater. Trans. A. 36A, 1669–1679. doi: 10.1007/s11661-005-0030-6

CrossRef Full Text | Google Scholar

Straumal, B. B., Polyakov, S. A., and Mittemeijer, E. J. (2006). Temperature influence on the faceting of Sigma 3 and Sigma 9 grain boundaries in Cu. Acta Mater. 54, 167–172. doi: 10.1016/j.actamat.2005.08.037

CrossRef Full Text | Google Scholar

Stukowski, A. (2010). Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Modelling Simul. Mater. Sci. Eng. 18, 1–7. doi: 10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Williams, P. L., Mishin, Y., and Hamilton, J. C. (2006). An embedded-atom potential for the Cu-Ag system. Modelling Simul. Mater. Sci. Eng. 14, 817–833. doi: 10.1088/0965-0393/14/5/002

CrossRef Full Text | Google Scholar

Zener, C. (1949). Theory of growth of spherical precipitates from solid solution. J. Appl. Phys. 20, 950–953. doi: 10.1063/1.1698258

CrossRef Full Text | Google Scholar

Zhou, J., Li, C., Guan, M., Ren, F. Z., Wang, X. N., Zhang, S. H., et al. (2017). Zener pinning by coherent particles: pinning efficiency and particle reorientation mechanisms. Modelling Simul. Mater. Sci. Eng. 25:065008. doi: 10.1088/1361-651X/aa6cfb

CrossRef Full Text | Google Scholar

Zhou, J., Li, W., Zhao, B. B., and Ren, F. Z. (2018). Direct measurement of the maximum pinning force during particle-grain boundary interaction via molecular dynamics simulations. Acta Mater. 148, 1–8. doi: 10.1016/j.actamat.2018.01.057

CrossRef Full Text | Google Scholar

Zhou, J., Zhang, S. H., Wang, X. N., Zhao, B. B., Dong, X. P., and Zhang, L. T. (2016). Interaction between coherent second-phase particles and migrating boundaries: boundary effect and particle reorientation. Scripta Mater. 116, 100–103. doi: 10.1016/j.scriptamat.2016.02.010

CrossRef Full Text | Google Scholar