Gradient Nonlocal Enhanced Microprestress-Solidification Theory and Its Finite Element Implementation

Time-dependent responses of cracked concrete structures are complex, due to the intertwined effects between creep, shrinkage, and cracking. There still lacks an effective numerical model to accurately predict their nonlinear long-term deflections. To this end, a computational framework is constructed, of which the aforementioned intertwined effects are properly treated. The model inherits merits of gradient-enhanced damage (GED) model and microprestress-solidification (MPS) theory. By incorporating higher order deformation gradient, the proposed GED-MPS model circumvents damage localization and mesh-sensitive problems encountered in classical continuum damage theory. Moreover, the model reflects creep and shrinkage of concrete with respect to underlying moisture transport and heat transfer. Residing on the Kelvin chain model, rate-type creep formulation works fully compatible with the gradient nonlocal damage model. 1-D illustration of the model reveals that the model could regularize mesh-sensitivity of nonlinear concrete creep affected by cracking. Furthermore, the model depicts long-term deflections and cracking evolutions of simply-supported reinforced concrete beams in an agreed manner. It is noteworthy that the gradient nonlocal enhanced microprestress-solidification theory is implemented in the general finite element software Abaqus/Standard with the implicit solver, which renders the model suitable for large-scale creep-sensitive structures.

Introduction

Concrete creep is the deformation phenomenon developing over time under the load action (Bažant and Li 2008). The current mechanical models are suitable for describing serviceability limit states (Schlappal et al., 2020). Concrete creep deformation in the early stage mainly comes from the viscoelasticity deformation (Mei and Wang 2020). Meanwhile, the long-term creep behavior can affect the safety and serviceability limit state of concrete structures. Concrete creep, intertwined with damage or cracking, gradually leads to damage evolution and stress redistribution of structural components. One notorious engineering example is the continuously vertical deflections of large-span prestressed concrete bridges (Yu et al., 2012; Tong et al. 2016). Massive concrete cracks at box-shape segments′ bottom slabs and webs appear phenomenally together, which indicates complex interactions between concrete creep and cracking (Tong et al. 2016).

As for concrete creep, microprestress-solidification (MPS) theory successfully describes concrete creep considering the processes of moisture transport and heat transfer (Boumakis et al., 2018). With the MPS theory, the solidification theory assumes the concrete aging as the volume growth of gels related to a hydration degree (Rahimi-Aghdam et al., 2019), and the microprestress theory assumes the relaxation of self-equilibrated stresses in the solid nanostructure of cement gels governing the long-term creep, drying creep (Pickett effect), and transitional thermal creep (Bažant et al., 1997a; Bažant et al., 1997b). The MPS theory supersede empirical formulas in specifications (i.e., ACI, B3/B4, and CEB-FIP models) in terms of the multiphysics approach, which effectively accounts for moisture transport and heat transfer. Consequently, the effects of varying temperature or humidity on concrete creep can be captured.

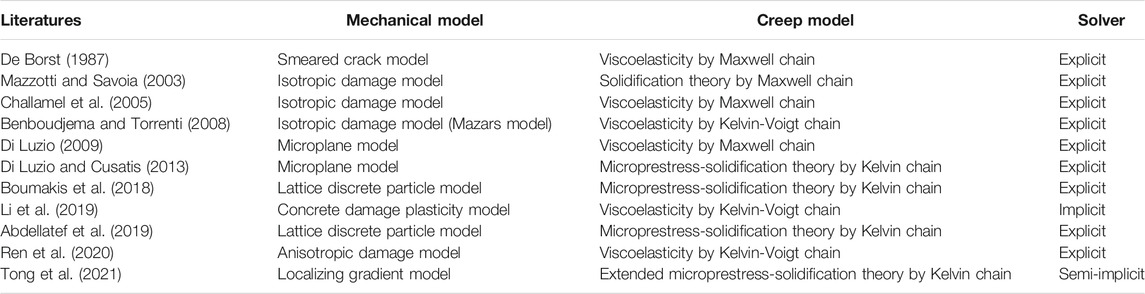
Accurate prediction of time-dependent responses of these concrete structures necessitates a detailed analysis of interactions between concrete creep and cracking. Some contributions are made to take these interactions in numerical analyses and they are comparatively presented in Table 1. To name a few, the smeared crack approach was combined with the viscoelastic behaviors for concrete in De Borst (1987). Concrete creep subject to uniaxial compression was modeled in Mazzotti and Savoia (2003) and Challamel et al. (2005) with an isotropic damage law being taken into account. Moreover, the viscoelastic behaviors of concrete, realized through a Maxwell chain, were coupled to a microplane constitutive model in Di Luzio, (2009). They further elaborated the concrete creep modeling with the microprestress-solidification theory realized through Kelvin chain (Di Luzio and Cusatis 2013). Recently, Luzio′s continuum method was replaced with a discrete element model in the work by Boumakis et al. (2018). Similar work was also found in Abdellatef et al. (2019). Although exhibiting sufficient accuracy, the lattice discrete particle model adopted in Boumakis et al. and Abdellatef et al. (2019) essentially is not a continuum model and is not suitable for structural analysis. Li et al. (2019) realized the nonlinear time-dependent analysis of prestressed concrete bridges considering cracking, creep, and shrinkage within the framework of Abaqus/Standard. The implicit solver was adopted in their study through viscous regularization provided by Abaqus/Standard. More recently, the coupled effects between creep, damage, and plasticity for concrete were taken into account in Ren et al. (2020). Unfortunately, the concrete damage plasticity model in Li et al. (2019) and anisotropic damage model in Ren et al. (2020) is still a local constitutive law without considering nonlocal effect. Tong et al. (2021) tentatively coupled the localizing gradient damage model to the extended microprestress-solidification theory. The semi-implicit algorithm was adopted and four-field evolutions made this method difficult to be implemented within FE framework.

TABLE 1

TABLE 1. Existing researches for the time-dependent damage analyses of concrete structures.

Although exhibiting apparent advantages, the above literatures still have limitation in the numerical analyses, as follows:

• Most of the above analyses are implemented with explicit finite element (FE) solver, and the computational cost is prohibitively high for long-term analyses of large-scale structures.

• The softening behavior of concrete is not properly regularized, and, therewith, it would lead to unrealistic results due to mesh-sensitivity problem (Peerlings et al. 1996).

• Most of creep models in the above analyses adopt empirical formulas in specifications and cannot reflect the real environmental conditions, of which varying temperature or humidity cannot be ignored.

It is acknowledged that the continuum-based constitutive law is easy to implement and is appropriate for large-scale concrete structures, especially with implicit finite element (FE) solver (Tong et al., 2016). Nevertheless, coupling concrete cracking with time-dependent behaviors is a nontrivial task. Strain softening in quasibrittle materials is the dilemma that has to been properly treated (Peerlings et al., 1996), which leads to loss of ellipticity of the differential equations and also the so-called mesh-dependent solutions upon element size. A series of regularization methods are continuously proposed targeting for mesh-objective simulations, i.e., the introduction of nonlocality in the constitutive model in either integral forms (Bažant et al., 1984), or gradient-enhanced damage (GED) forms (Schreyer and Chen, 1986; Peerlings et al., 1998; Poh and Sun, 2017), and the so-called phase-field approach (Kou et al., 2019; Li et al., 2020), although the integral-type forms are the most straightforward to implement the nonlocal theory in the FE model. The difficulty in deriving the tangent modulus at the element level prohibits the implicit FE solver and can only rely on the explicit FE solver (Bažant et al., 1984). Among them, the phase-field approach to the progressive events of brittle and quasibrittle fracture is proven to capture all stages of fracture, such as crack nucleation, initiation, propagation, and coalescence (Tanne et al., 2017). However, the computational cost of the phase field approach is prohibitively high and is not suitable for structural analyses hitherto. In this study, the GED model incorporating the high-order deformation terms is utilized. It is admitted that many efforts are made continuously to improve the original one proposed by Peerlings et al. (1996), i.e., the localizing GED model (Poh and Sun 2017) and stress-based GED model (Vandoren and Simone 2018). These improvements effectively overcome the spurious damage growth of the original GED model at large tensile strain. However, the selection of GED models is out of the scope of this study. We deliberatively select the original GED model in Peerlings et al. (1996) as its FE implementation is more easy compared to other GED models.

The proposed framework (termed as “GED-MPS” model hereafter) integrates the GED model for concrete′s mechanical behaviors with the MPS theory describing concrete’s creep behaviors. The model is implemented within the general FE software Abaqus/Standard with the implicit solver. In detail, Sect-2 introduces the theoretical background and computational framework of the GED-MPS model. Sect-3 illustrates the FE implementation of the model within Abaqus/Standard with implicit solver. Sect-4 reveals that the model can obtain mesh-objective solutions, not only for mechanical responses but creep deformations intertwined with concrete damage and cracking. Sect-5 validates the proposed model with the experiments by Gilbert and Nejadi (2004), who recorded the long-term deflections and cracking of a series of simply-supported reinforced concrete beams. Finally, conclusions are derived in Sect-6. To facilitate potential researchers and users, parts of the code and the input file are released at https://github.com/TengTongSEU/Coupled-creep-damage.

Constitutive Modeling Frameworks

Thermo-Hydro-Mechanical Coupling for Concrete

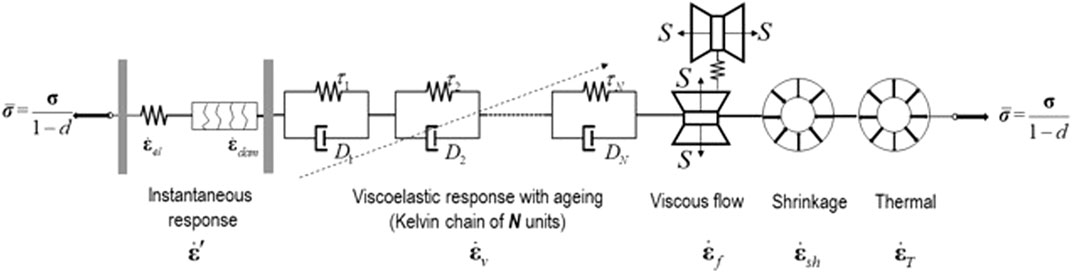
The GED-MPS model takes an engineering approach to the coupled time-dependent and mechanical behaviors of concrete, aiming to describe the most important aspects with sufficient accuracy at an affordable computational cost. Complete constitutive law of the GED-MPS model follows a rheological representation, as shown in Figure 1, which consists of

• a nonaging spring unit representing instantaneous elastic strain tensor ${\mathit{\epsilon }}_{el}$;

• a damage unit with the strain tensor ${\mathit{\epsilon }}_{dam}$;

• a solidifying kelvin chain unit with typically more than ten elements in series representing the viscoelastic response with aging effect ${\mathit{\epsilon }}_v$;

• a dashpot unit with viscosity dependent on microprestress $S$ for the long-term creep strain tensor ${\mathit{\epsilon }}_f$;

• a shrinkage unit for strain tensor ${\mathit{\epsilon }}_{sh}$; and

• a thermal unit for strain tensor ${\mathit{\epsilon }}_T$.

FIGURE 1

FIGURE 1. Rheological model for coupling in the GED-MPS model.

These units are connected in series, with the identical stress tensor $\mathit{\sigma }$ being transmitted (Yu et al., 2012; Tong et al., 2016). In the absence of significant plastic and viscoelastic strains that may arise at very high confining pressures, the total strain rate ${\dot{\mathit{\epsilon }}}_{tot}$ is the sum of individual strain rates (Figure 1), as

${\dot{\mathit{\epsilon }}}_{tot}={\dot{\mathit{\epsilon }}}_{el}+{\dot{\mathit{\epsilon }}}_{dam}+{\dot{\mathit{\epsilon }}}_v+{\dot{\mathit{\epsilon }}}_f+{\dot{\mathit{\epsilon }}}_{sh}+{\dot{\mathit{\epsilon }}}_T.(1)$

Concrete is interpreted as a composite material in which the coarse aggregates are embedded as inclusions in cement paste. Aging creep occurs exclusively in cement paste, whereas aggregates behave elastically. To capture the mesoscale behaviors of concrete creep in a more realistic manner, multiscale approaches and more sophisticated micromechanical models are necessary, which require more parameters and detailed information on the individual phases (Pichler et al., 2007; Scheiner and Hellmich 2009).

Theoretically, time-dependent evolutions of all relevant material properties should be taken into account to achieve an accurate damage process, i.e., creep and mechanical properties. Nevertheless, the loading of concrete structures at a very early-stage is not the focus of this study. Therewith, the mechanical properties of mature concrete are assumed to be constant, i.e., tensile strength or fracture energy. Their changes with concrete aging are ignored in this work. The multidecade prediction will provide conservative estimations as the slight increase in the mature concrete’s mechanical properties is not considered. The local age-dependent fracture properties should be enriched for the framework for concrete structures subject to early-age loadings.

Creep Evaluation by Microprestress-Solidification Theory

To predict creep deformations, semiempirical models are generally adopted by the engineering community, i.e., ACI, B3/B4, and CEB-FIP models. Numerous material properties act as input variables for these models, i.e., compressive strength, water to cement ratio, cement content, temperature, humidity, etc. Afterward, these engineering creep models predict the time-dependent deformation on a cross-sectional level in accumulated form (Boumakis et al., 2018).

Concrete creep can be mainly categorized into the aging of concrete, drying creep (Pickett effect), and transitional thermal creep (Bažant and Jirásek 2018). Bažant et al. (1997a,b) and assume that the continuous formation of C-S-H gels is responsible for the aging of concrete, including short-term chemical aging and long-term nonchemical aging. The first two creep sources, namely concrete aging and drying creep, can be formulated in the B4 model (Hubler et al., 2015), as the compliance function $J\left(t,t\mathrm{\prime }\right)$:

$J\left(t,t\mathrm{\prime }\right)=q_1+J_b\left(t,t\mathrm{\prime }\right)+J_d\left(t,t\mathrm{\prime }\right),(2)$

where $t$ is the current time in days, $t\mathrm{\prime }$ is the age in days when the sustained stress is exerted, $J_b\left(t,t\mathrm{\prime }\right)$ is the basic compliance function, $J_d\left(t,t\mathrm{\prime }\right)$ is the compliance function for drying creep, and $q_1$ is the instantaneous compliance function ($q_1=0.4/E_{28}=1/E_0$, $E_0$ is the instantaneous elastic modulus without any creep effect, and $E_{28}$ is the 28-day Young’s modulus).

Note that all the empirical models often yield the predictions far away from the measured responses, which can be attributed to the intrinsic heterogeneity of concrete and the variability in mix designs and environmental conditions. On the other hand, these engineering models lack the capacity to accurately predict the local point-wise response at varying stress/strain, local temperature, moisture content, and curing degree. To this end, the MPS theory is employed to describe the concrete’s time-dependent behaviors.

Solidification Theory for Aging Viscoelasticity in a Rate-Type Formulation

Concrete creep is found to follow the rules of aging linear viscoelasticity (Bažant et al., 2012a; Bažant et al.,2012b), within the service stress range ($\mathit{\sigma }\le 0.4f{\mathrm{\prime }}_{\mathrm{c}}$, and $f{\mathrm{\prime }}_{\mathrm{c}}$ is the compressive strength of concrete). As a consequence, Volterra integral equation can be utilized to evaluate creep deformation under a general stress history $\mathit{\sigma }\left(t\right)$. Unfortunately, the compliance function, which is not of a convolution type due to the phenomenon of concrete aging, requires the history variables in all previous time steps to be stored for the current time step analysis. The computation is prohibitively expensive to predict the long-term performance of large-scale structures. Alongside, it is difficult to couple these memory-dependent variables with other memory-independent phenomena, e.g., concrete cracking, corrosion, and steel relaxation (Teng et al., 2017).

A rate-type formulation can overcome these obstacles. In the rate-type approach, the previous history can be fully represented by internal variables only in the last time step (Yu et al., 2012). Rheological model is popularly adopted for rate-type concrete creep (Jirásek and Havlásek 2014; Yu et al., 2012). To this end, A K chain is employed herein, consisting of more than 10 K units, of distinctive modulus $D_u$ ($\mu =\mathrm{1,2},\cdots ,N$) and retardation time ${\tau }_u$ ($\mu =\mathrm{1,2},\cdots ,N$); see Figure 1 for details. If the ${\tau }_{\mu }$ is arranged to own an infinitely close spacing, the continuous retardation spectrum forms (Bažant and Xi 1995). Widder proposed an approximate inversion formula to uniquely identify the continuous retardation spectrum (Widder 1971). The analytical solution for a given compliance function yields

$L\left({\tau }_u\right)=-\underset{k\to \infty }{\lim }\frac{{\left(-k{\tau }_u\right)}^k}{\left(k-1\right)!}{C}^{\left(k\right)}\left(k{\tau }_u\right),(3)$

where $C^{\left(k\right)}$ is the $k$-th order derivative on time $t$ of the creep part of the compliance function. In this work $C\left(t,t\mathrm{\prime }\right)$ is chosen as

$C\left(t,t\mathrm{\prime }\right)=J_b\left(t,t\mathrm{\prime }\right)=q_{2}Q\left(t,t\mathrm{\prime }\right)+q_3\mathrm{In}\left[\mathrm{1}+{\left(t,t\mathrm{\prime }\right)}^n\right],(4)$

with $q_2$ and $q_3$ as the adjustable parameters for the viscoelasticity based on the solidification theory, $Q\left(t,t\mathrm{\prime }\right)$ is a function that can be referred to the B4 mode, $n=0.1$ is the fixed exponent, and $t-t\mathrm{\prime }$ is the duration since the load application $t\mathrm{\prime }$ and is replaced with $k{\tau }_u$ in Eq. 3. In the current application, the limit in Eq. 3 needs not to be realized and it suffices to use $k$ = 3 (Yu et al., 2012). A discrete approximation of continuous spectrum gives the discrete spectrum:

$A_{\mu }=L\left({\tau }_u\right)\mathrm{In}10,(5)$

which corresponds to a discrete Kelvin chain and is required for numerical computations. The exponential algorithm is generally adopted to quantify the time increment $\Delta t$, which would effectively avoid the numerical instability problem frequently occurring in the central or backward difference method or Runge-Kutta method.

Utilizing the Kelvin units, one can express the effective incremental modulus $E\mathrm{″}$ of concrete at the current time step $t_n$, as

$\frac{1}{E^{″}}=\frac{1}{E_0}+{\displaystyle \sum _{\mu =1}^N{D}_{\mu }^{-1}}=\frac{1}{E_0}+{\displaystyle \sum _{\mu =1}^N{A}_{\mu }\left(1-{\lambda }_{\mu }\right)},(6)$

where $E_0$ is the instantaneous modulus, $N$ is the total number of Kelvin units (see Figure 1), and ${\lambda }_{\mu }$ is determined by the time increment $\Delta t$ and the retardation time ${\tau }_u$, as

${\lambda }_u={\tau }_u\left(1-e^{-\Delta t/{\tau }_u}\right)\text{/}\Delta t.(7)$

Finally, the solidifying Kelvin chain gives the short-term creep strain tensor rate $\Delta {\mathrm{\epsilon }}_v$ at the current time step $t_{\mathrm{n}}$, as

$\Delta {\mathit{\epsilon }}_v={\displaystyle \sum _{\mu =1}^N\left(1-e^{-\Delta t/{\tau }_{\mu }}\right){\mathit{\gamma }}_{\mu }^{\left(n-1\right)}},(8)$

where ${\mathrm{\gamma }}_{\mu }^{\left(n-1\right)}$ is a state variable at the last time step and it should be updated for each Kelvin chain unit at the end of the current time step for each integration point, as

${\mathit{\gamma }}_{\mu }^{\left(n\right)}={\lambda }_u\Delta \mathit{\sigma }{D}_{\mu }^{-1}+e^{-\Delta t/{\tau }_u}{\mathit{\gamma }}_{\mu }^{\left(n-1\right)},(9)$

with the rate-type formulation at hand, the values of ${\mathit{\gamma }}_{\mathit{u}}$, $\mathit{\sigma }$, and ${\mathit{\epsilon }}_v$ in all the previous time steps (from 1 to n−1) need not be stored, which are required in the conventional integral-type creep analysis. These history variables can now be represented only by the state variable ${\mathit{\gamma }}_{\mu }^{\left(n\right)}$ in the current time step. The continuous spectrum method and exponential algorithm enable the implementation of the rate-type formulations for creep analysis; for more details, refer to Yu et al. (2012).

Microprestress Theory for Viscous Flow

The rate of viscous strain tensor ${\dot{\mathit{\epsilon }}}_f$ originates in the slippage between adsorbed water layers at the microscale level and can be described by the microprestress theory. Effects of temperature and humidity on the microstructure can be described by introducing three transformed time variables: the equivalent age $t_e$ describing the degree of hydration, the reduced time $t_r$ characterizing the changes in the rate of bond breakages and restoration on the microstructural level, and the reduced microprestress time $t_s$.

Under standard conditions (i.e., room temperature and sealed specimens), all the three time scales, namely $t_e$, $t_r$, and $t_s$, are equal to the actual age of concrete $t$. For the general condition, the rates of the transformed time are defined as the product of two functions, which respectively characterizes the effects of temperature and humidity histories. The derivatives of the three transformation times with respect to the actual age of concrete $t$ are (Jirásek and Havlásek 2014)

$\frac{\mathrm{d}{t}_e}{\mathrm{d}t}=\exp \left[\frac{Q_e}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right]\cdot \frac{1}{1+{\left[{\alpha }_e\left(1-h\right)\right]}^4},(10)$

$\frac{\mathrm{d}{t}_r}{\mathrm{d}t}=\exp \left[\frac{Q_r}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right]\cdot \left[{\alpha }_r+\left(1-{\alpha }_r\right)h^2\right],(11)$

$\frac{\mathrm{d}{t}_s}{\mathrm{d}t}=\exp \left[\frac{Q_s}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right]\cdot \left[{\alpha }_s+\left(1-{\alpha }_s\right)h^2\right],(12)$

where $T$ is the absolute temperature, $h$ is the humidity, $R$ is the universal gas constant, and $Q_e$, $Q_r$, and $Q_s$ are active energies for the hydration, viscous process, and microprestress relaxation, respectively.

The bonds across the slip plane representing the nanopore filled with hindered adsorbed water are subject to two stresses: the macroscopic applied stress $\mathit{\sigma }$ causing shear slip and the tensile microprestress. The rate of flow strain tensor ${\dot{\mathit{\epsilon }}}_f$ is

${\dot{\mathit{\epsilon }}}_f=\frac{\mathrm{d}{t}_r}{\mathrm{d}t}\frac{1}{\eta \left(S\right)}\mathit{\sigma },(13)$

where the effective viscosity $\eta$ is a decreasing function of $S$.

The source of ${\dot{\mathit{\epsilon }}}_f$ lies in the relaxation of disjoining pressure and the rupture of atomic bonds and is formulated by microprestress $S$. The concept of microprestress is useful for the theoretical justification of evolving viscosity $\eta$. With the temperature $T$ and humidity $h$ being taken into account, the drying creep effect and transitional thermal creep can be reflected in the viscous flow strain rate ${\dot{\mathit{\epsilon }}}_f$. However, the microprestress cannot be directly measured and the calibration of microprestress relaxation is difficult. To this end, by some manipulations and rearrangements, Jirásek and Havlásek (2014) obtain the evolution of the viscous dashpot, as

$\dot{\eta }+\frac{1}{{\mu }_S{T}_0}\left|T\frac{\dot{h}}{h}-{\kappa }_T\dot{T}\right|{\left({\mu }_S\eta \right)}^{p/\left(p-1\right)}=\frac{\mathrm{d}{t}_s}{\mathrm{d}t}\frac{1}{q_4},(14)$

with

${\mu }_S=c_0{T}_0^{P-1}{k}_1^{P-1}{q}_4{\left(p-1\right)}^p(15)$

in which $c_0$ and $k_1$ are the constant parameters and $P$ is an exponent usually set equal to 2. The internal variable ${\kappa }_T$ was introduced to keep track of the previously obtained maximum temperature and to adjust the temperature variation on creep and is defined as

${\kappa }_T=\{\begin{array}{l}{\kappa }_{Tm}\mathrm{if}T=T_{\max }\mathrm{and}\Delta T>0\\ {\kappa }_{Tc}\mathrm{if}T<T_{\max }\mathrm{or}\Delta T>0\end{array},(16)$

where ${\kappa }_{Tm}$ and ${\kappa }_{Tc}$ are material parameters and ${\kappa }_{Tm}$ = 0.017 and ${\kappa }_{Tc}$ = 0.001 are recommended in Jirásek and Havlásek (2014). For a standard choice $p=2$, the above equations are simplified to

$\dot{\eta }+\frac{1}{{\mu }_S{T}_0}\left|\dot{T}\mathrm{In}\left(h\right)-{\kappa }_T\dot{T}\right|{\left({\mu }_S\eta \right)}^2=\frac{{\psi }_s}{q_4},(17)$

${\mu }_S=c_0{T}_0{k}_1{q}_4.(18)$

By assuming that the evolution of viscosity should be the same as in model B4, the initial condition for differential Eq. 17 can be simply postulated as

$\eta \left(t_0\right)=\frac{t_0}{q_4},(19)$

where $q_4$ is the variable governing the long-term creep in the B4 model.

Damage Evaluation by Gradient-Enhanced Damage Model

Local Damage Model

With the assistance of the effective stress concept (Rokhgireh and Nayebi 2019), the stress-strain relation of quasibrittle materials can be expressed as

$\mathit{\sigma }=\left(\mathrm{1}-d\right){\mathit{D}}^e:\mathit{\epsilon }\mathrm{\prime },(20)$

where $\mathit{\sigma }$ is the second-order Cauchy stress tensor, $d$ is the scalar damage variable ($0\le d\le 1$), ${\mathit{D}}^e$ is the fourth-order elastic stiffness tensor, and $\mathit{\epsilon }\mathrm{\prime }$ is the second-order elastodamage strain tensor. The $\mathit{\epsilon }\mathrm{\prime }$ is the sum of the elastic strain tensor ${\mathit{\epsilon }}_{el}$ and damage strain tensor ${\mathit{\epsilon }}_{dam}$. It can be written in the rate form as

$\dot{\mathit{\epsilon }}\mathrm{\prime }={\dot{\mathit{\epsilon }}}_{el}+{\dot{\mathit{\epsilon }}}_{dam}={\dot{\mathit{\epsilon }}}_{tot}-{\dot{\mathit{\epsilon }}}_v-{\dot{\mathit{\epsilon }}}_f-{\dot{\mathit{\epsilon }}}_{sh}-{\dot{\mathit{\epsilon }}}_T.(21)$

To describe the damage evolution, the local scalar-valued equivalent strain $\tilde{\epsilon }$ is adopted to evaluate the elastodamage strain tensor $\mathit{\epsilon }\mathrm{\prime }$. The details expression of $\tilde{\epsilon }\left(\mathit{\epsilon }\mathrm{\prime }\right)$ would be given in Eq. 29. For strain-based damage models, a history variable $\kappa$ is defined as the maximum $\tilde{\epsilon }$ ever obtained in the previous time steps to guarantee the damage irreversibility as

$\kappa \left(t\right)=\max \left\{\tilde{\epsilon }\left(\tau \right)|0\le \tau \le t\right\}.(22)$

The loading function $f\left(\tilde{\epsilon },\kappa \right)$ is introduced to complement the stress-strain relation in Eq. 20, as

$f(\overline{\epsilon },\kappa )=\overline{\epsilon }-\kappa .(23)$

The loading function $f(\tilde{\epsilon },\kappa )$ and the rate of the history variable, $\Delta \kappa$, have to satisfy the discrete Kuhn-Tucker loading-unloading conditions:

$f\le 0\Delta \kappa \ge 0\Delta \kappa \cdot f=0.(24)$

The history variable $\kappa$ describes the damage variable $d\left(\kappa \right)$ and damage irreversibility is automatically satisfied. The $\kappa$ starts at a damage threshold level ${\kappa }_{\text{0}}$ and is updated by the requirement during the damage growth $f=0$ (De Borst and Verhoosel, 2016).

Nonlocal Gradient-Enhanced Formulations

In a conventional local damage model, $\kappa$ is related to the local scalar measure of the strain tensor $\tilde{\epsilon }$. Nevertheless, in a nonlocal generalization, the (local) equivalent scalar strain $\tilde{\epsilon }$ is replaced by a spatially averaged (nonlocal) equivalent strain $\overline{\epsilon }$, which is computed in each material point approximately by the differential form (Peerlings et al., 1996):

$\overline{\epsilon }-c{\nabla }^2\overline{\epsilon }=\tilde{\epsilon },(25)$

where ${\nabla }^2$ denotes the Laplacian operator and $c$ is a positive gradient parameter of the dimension length squared. The parameter $c$ follows a specific form of the weight function and averaging volume and provides the internal length scale which is needed to regularize the damage localization. Hereafter this parameter is treated as an intrinsic material property and should be carefully calibrated to characterize the material’s meso- or microstructure.

By integrating the averaging partial differential equation Eq. 25 over the entire domain and adopting Gauss’ divergence theorem on the term $c{\displaystyle {\int }_{\mathit{\Omega }}{\nabla }^2\overline{\epsilon }\mathrm{d}\mathit{\Omega }}$, we can obtain

${\displaystyle {\int }_{\mathit{\Omega }}\overline{\epsilon }\mathrm{d}}\mathit{\Omega }-c{\displaystyle {\int }_{\mathit{\Gamma }}\nabla \overline{\epsilon }\cdot \mathit{n}\mathrm{d}\mathit{\Gamma }}={\displaystyle {\int }_{\mathit{\Omega }}\tilde{\epsilon }\mathrm{d}\mathit{\Omega }},(26)$

where $\mathit{n}$ is the unit directional vector perpendicular to the boundary.

To guarantee that the average of $\overline{\epsilon }$ over the entire domain equals that of $\tilde{\epsilon }$, the natural boundary condition

$\nabla \overline{\epsilon }\cdot \mathit{n}=0(27)$

is adopted, resulting in the vanishment of the second term in the left-hand side of Eq. 26.

Damage Evolution

Two relations should be well defined to characterize the macroscopic stress-strain behavior: the evolution law of damage $d\left(\kappa \right)$ and the local equivalent strain $\tilde{\epsilon }$. The evolution of the damage variable $d\left(\kappa \right)$ is critical to govern the postpeak softening behavior and the degree of brittleness. The damage law proposed in Peerlings et al. (1996) is adopted for simplicity:

$d\left(\kappa \right)=\{\begin{array}{l}0\kappa \le {\kappa }_0\\ 1-\frac{{\kappa }_0}{\kappa }\left[\left(1-\alpha \right)+\alpha \exp \left(-\beta \left(\kappa -{\kappa }_0\right)\right)\right]\kappa >{\kappa }_0\end{array},(28)$

where ${\kappa }_0$ is the threshold to initiate the damage and $\alpha$ and $\beta$ are material constants governing the softening behavior.

The local equivalent strain $\tilde{\epsilon }$ adopts the modified von Mises equivalent strain, which originates from plasticity models for polymers and proposed (Vogler et al., 2013), resulting in

$\tilde{\epsilon }\left(\mathit{\epsilon }\mathrm{\prime }\right)=\frac{k-1}{2k\left(1-2v\right)}{I}_1+\frac{1}{2k}\sqrt{\frac{{\left(\mathrm{k}-1\right)}^2}{{\left(1-2v\right)}^2}{I}_1^2+\frac{2k}{{\left(1+v\right)}^2}{J}_2},(29)$

where $\mathit{\epsilon }\mathrm{\prime }$ represent the summation of elastic and damage strain tensors in Eq. 21, $I_1$ is the first invariant of strain tensor $\mathit{\epsilon }\mathrm{\prime }$, $J_2$ is the second invariant of deviatoric strain tensor $\mathit{\epsilon }\mathrm{\prime }$, and $v$ is the Poisson’s ratio. An important feature of this definition of local equivalent scalar strain is the parameter $k$ which is defined as the ratio of the compressive strength $f_c$ to the tensile strength $f_t$ of the material, $k$ = $f_c$/$f_t$. Compressive failure would vanish as $k$ goes to infinity.

Coupling Damage and Creep

To describe the nonlinear concrete time-dependent behavior, a stress-strain law based on the rate independent isotropic damage model is formulated in Eq. 20, which can be interpreted as Hooke’s law linking the strain to the effective stress tensor $\overline{\mathit{\sigma }}$(Bažant and Jirásek 2018):

$\overline{\mathit{\sigma }}=\frac{\mathit{\sigma }}{1-d}.(30)$

The above equation indicates the stress transmitted by the undamaged continuous solid material, which would be $\overline{\mathit{\sigma }}$, rather than $\mathit{\sigma }$ with defects being excluded. Considering that the creep stress is much lower than the cracking threshold, this nonlinear creep model is only suitable for the undamaged concrete, not for a cracked body. Thus, the creep strain calculation, similar to the plastic strain, is based on the effective stress tensor $\overline{\mathit{\sigma }}$, rather than the nominal stress tensor $\mathit{\sigma }$. As a consequence, the short-term creep strain tensor ${\mathit{\epsilon }}_v$ and the long-term creep strain tensor ${\mathit{\epsilon }}_f$, obtained in sections Solidification Theory for Aging Viscoelasticity in a Rate-Type Formulation and Microprestress Theory for Viscous Flow based on nominal stress tensor $\mathit{\sigma }$, should be amplified by the factor $1/(1-d)$.

Finite Element Formulation

Governing Equations and FE Discretization

The model presented in this work is discretized using a Galerkin FE approach. Strong forms of governing equations for the GED-MPS model for quasistatic problems are

$\nabla \cdot \mathit{\sigma }+\mathit{b}=\mathrm{0}\mathrm{in }\Omega ,(31)$

$\overline{\epsilon }-c{\nabla }^2\overline{\epsilon }=\tilde{\epsilon }\mathrm{in }\Omega ,(32)$

where $\mathit{b}$ represents an external load vector. The two unknown fields to be calculated are the displacement field $\mathit{u}\left(\mathit{x,t}\right)$ and the so-called nonlocal equivalent strain field $\overline{\epsilon }\left(\mathit{x,t}\right)$.

These equations are supplemented by the following Neumann and Dirichlet boundary conditions:

$\mathit{\sigma }\cdot \mathit{n}={\mathit{t}}^{\text{*}}\nabla \overline{\epsilon }\cdot \mathit{n}=0\mathrm{on}\partial {\mathit{\Omega }}_t\mathit{u}\left(\mathit{x},t\right)={\mathit{u}}^{\ast }\mathrm{on}\partial {\mathit{\Omega }}_u,(33)$

where ${\mathit{t}}^{\text{*}}$ and ${\mathit{u}}^{\ast }$ are prescribed force and displacement at the boundary. Integrating Eqs 31, 32 over the domain $\Omega$ and weighting with ${\mathit{w}}_{\mathit{u}}$ and ${\mathit{w}}_{\overline{\epsilon }}$ respectively yields the weak form after applying the divergence theorem and the boundary conditions:

${\displaystyle {\int }_{\mathit{\Omega }}\nabla {\mathit{w}}_u^T\mathit{\sigma }\mathrm{d}\mathit{\Omega }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{w}}_u^T\mathit{b}\mathrm{d}\mathit{\Omega }}+{\displaystyle {\int }_{\mathit{\Gamma }}{\mathit{w}}_u^T{\mathit{t}}^{\text{*}}\mathrm{d}\mathit{\Gamma }},(34)$

${\displaystyle {\int }_{\mathit{\Omega }}{\mathit{w}}_{\overline{\epsilon }}^T\overline{\epsilon }\mathrm{d}\mathit{\Omega }}+{\displaystyle {\int }_{\mathit{\Omega }}\nabla {\mathit{w}}_{\overline{\epsilon }}^{T}c\nabla \overline{\epsilon }\mathrm{d}\mathit{\Omega }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{w}}_{\overline{\epsilon }}^T\tilde{\epsilon }\mathrm{d}\mathit{\Omega }}(35)$

In the FE implementation, the displacement field $\mathit{u}$ and nonlocal equivalent strain field $\overline{\epsilon }$ at an arbitrary point is interpolated by their nodal values (Sarkar et al., 2019):

$\mathrm{u}={\mathit{N}}_{\mathit{u}}\underset{˜}{u}\mathrm{and}\overline{\epsilon }={\mathit{N}}_{\overline{\epsilon }}\underset{˜}{\overline{\epsilon }}(36)$

$\epsilon ={\mathit{B}}_{\mathit{u}}\underset{˜}{u}\mathrm{and}\nabla \overline{\epsilon }={\mathit{B}}_{\overline{\epsilon }}\underset{˜}{\overline{\epsilon }},(37)$

with ṵ and $\underset{˜}{\overline{\epsilon }}$ being the nodal degrees of freedom, ${\mathit{N}}_{\mathit{u}}$ and ${\mathit{N}}_{\overline{\epsilon }}$ represent the shape functions, and ${\mathit{B}}_{\mathit{u}}$ and ${\mathit{B}}_{\overline{\epsilon }}$ are their partial derivatives with respect to the spatial coordinates. According to the Bubnov-Galerkin method, the corresponding weight functions ${\mathit{w}}_{\mathit{u}}$ and ${\mathit{w}}_{\overline{\epsilon }}$ can be discretized analogously. Consequently, the discretized equilibrium equations of Eqs 34, 35 reduce to

${\displaystyle {\int }_{\mathit{\Omega }}{\mathit{B}}_u^T\mathit{\sigma }\mathrm{d}\mathit{\Omega }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{N}}_u^T\mathit{b}\mathrm{d}\mathit{\Omega }}+{\displaystyle {\int }_{\mathit{\Gamma }}{\mathit{N}}_u^T{\mathit{t}}^{\text{*}}\mathrm{d}\mathit{\Gamma }},(38)$

${\displaystyle {\int }_{\mathit{\Omega }}\left({\mathit{N}}_{\overline{\epsilon }}^T{\mathit{N}}_{\overline{\epsilon }}+{\mathit{B}}_{\overline{\epsilon }}^{T}c{\mathit{B}}_{\overline{\epsilon }}\right)\overline{\epsilon }\mathrm{d}\mathit{\Omega }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{N}}_{\overline{\epsilon }}^T\tilde{\epsilon }\mathrm{d}\mathit{\Omega }}.(39)$

To construct a consistent incremental-iterative Newton-Raphson solution procedure, Eqs 38, 39 have to be linearized. The linearization at iteration $i$ with respect to the previous iteration $i-1$ is outlined as

$\left[\begin{array}{cc}{\mathit{K}}_{i-1}^{uu}& {\mathit{K}}_{i-1}^{u\overline{\epsilon }}\\ {\mathit{K}}_{i-1}^{\overline{\epsilon }u}& {\mathit{K}}_{i-1}^{\overline{\epsilon }\overline{\epsilon }}\end{array}\right]\left\{\begin{array}{l}\mathrm{d}\underset{\mathrm{\sim }}{\mathrm{u}}\\ \mathrm{d}\underset{˜}{\overline{\epsilon }}\end{array}\right\}=\left[\begin{array}{l}{\mathit{f}}_{\mathrm{ext}}^u\\ {\mathit{f}}_{\mathrm{ext}}^{\overline{\epsilon }}\end{array}\right]-\left[\begin{array}{l}{\mathit{f}}_{\mathrm{int}\text{,}\mathit{i}-\mathrm{1}}^u\\ {\mathit{f}}_{\mathrm{int}\text{,}\mathit{i}-\mathrm{1}}^{\overline{\epsilon }}\end{array}\right].(40)$

Of special attention is that the components in the stiffness matrix and the right-hand side vector depend on the $\mathit{\epsilon }\prime$ in Eq. 21. The submatrices are defined as

${\mathit{K}}_{i-1}^{uu}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{B}}_u^T(1-d_{i-1}){\mathrm{D}}^e{\mathit{B}}_{\mathit{u}}\mathrm{d}\mathit{\Omega }},(41)$

${\mathit{K}}_{i-1}^{\overline{\epsilon }\overline{\epsilon }}={\displaystyle {\int }_{\mathit{\Omega }}\left({\mathit{N}}_{\overline{\epsilon }}^T{\mathit{N}}_{\overline{\epsilon }}+{\mathit{B}}_{\overline{\epsilon }}^{T}c{\mathit{B}}_{\overline{\epsilon }}\right)\mathrm{d}\mathit{\Omega }},(42)$

${\mathit{K}}_{i-1}^{u\overline{\epsilon }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{B}}_u^T\frac{\partial d}{\partial \kappa }{\mathit{D}}^e\mathit{\epsilon }{\mathrm{\prime }}_{\mathrm{i-1}}{\mathit{N}}_{\overline{\epsilon }}\mathrm{d}\mathit{\Omega }},(43)$

${\mathit{K}}_{i-1}^{\overline{\epsilon }u}=-{\displaystyle {\int }_{\mathit{\Omega }}{\mathit{N}}_{\overline{\epsilon }}^T{\left(\frac{\partial \tilde{\epsilon }}{\partial \mathit{\epsilon }\mathrm{\prime }}\right)}_{i-1}{\mathit{B}}_{\mathit{u}}{\mathit{D}}^e\mathrm{d}\mathit{\Omega }},(44)$

and the subvectors in the right-hand sides are defined as

${\mathit{f}}_{\mathrm{ext}}^u={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{N}}_u^T\mathit{b}\mathrm{d}\mathit{\Omega }}+{\displaystyle {\int }_{\mathit{\Gamma }}{\mathit{N}}_u^T{\mathit{t}}^{\text{*}}\mathrm{d}\mathit{\Gamma }},(45)$

${\mathit{f}}_{\mathrm{int,}\mathit{i}-\mathrm{1}}^{\overline{\epsilon }}={\displaystyle {\int }_{\mathit{\Omega }}{\mathit{B}}_u^T}{\sigma }_{i-1}d\Omega ,(46)$

${\mathit{f}}_{\mathrm{ext}}^{\overline{\epsilon }}=\mathrm{0},(47)$

${\mathit{f}}_{\mathrm{int,}\mathit{i}-\mathrm{1}}^{\overline{\epsilon }}={\displaystyle {\int }_{\mathit{\Omega }}\left[\left({\mathit{N}}_{\overline{\epsilon }}^T{\mathit{N}}_{\overline{\epsilon }}+{\mathit{B}}_{\overline{\epsilon }}^{T}c{\mathit{B}}_{\overline{\epsilon }}\right){\overline{\epsilon }}_{i-1}-{\mathit{N}}_{\overline{\epsilon }}^T\mathit{\epsilon }{\mathrm{\prime }}_{\mathit{i-1}}\right]\mathrm{d}\mathit{\Omega }}.(48)$

Note that the element stiffness matrix becomes nonsymmetric since ${\mathit{K}}_{i-1}^{u\overline{\epsilon }}$ is not equal to the transpose of ${\mathit{K}}_{i-1}^{\overline{\epsilon }u}$. The implicit solver with Newton-Raphson algorithm could guarantee the quadratic rate of convergence, even if the nonsymmetric tangential stiffness matrix in Eq. 40 is utilized (Peerlings et al., 1996).

Creep Strain Tensors

The key parameter in implementing the GED-MPS model is to obtain the local equivalent strain field $\tilde{\epsilon }\left(\mathit{\epsilon }\mathrm{\prime }\right)$, which is a function of the strain tensor $\mathit{\epsilon }\mathrm{\prime }$. To this end, now we turn our attention to the numerical treatments of increments of creep strain tensors, namely the aging viscoelasticity $\Delta {\mathit{\epsilon }}_v$ and the viscous flow $\Delta {\mathit{\epsilon }}_f$.

The aforementioned rate-type formulation can be used for the basic creep compliance $J_b\left(t,t\mathrm{\prime }\right)$, as presented in Eq. 4. Taking derivative of $J_b\left(t,t\mathrm{\prime }\right)$ with respect to time gives

${\dot{J}}_b\left(t,t\mathrm{\prime }\right)=\frac{1}{v\left[t_e\left(t\right)\right]}\Phi \left[t_r\left(t\right)-t{\mathrm{\prime }}_r\left(t\right)\right],(49)$

where reduced time $t_e\left(t\right)$ and $t_r\left(t\right)$ are introduced to account for general temperature and humidity conditions, $v\left(t\right)$ describes the volume growth function with the solidification process, and $\Phi \left(t,t\mathrm{\prime }\right)$ is the strain in nonaging solidified matter whose material properties are assumed to be invariable with time. The $v\left(t\right)$ and $\Phi \left(t,t\mathrm{\prime }\right)$ are defined as

$\frac{1}{v\left(t\right)}=\sqrt{\frac{1}{t}}+\frac{q_3}{q_2},(50)$

$\Phi \left(t-t\mathrm{\prime }\right)=q_2\frac{n{\left(t-t\mathrm{\prime }\right)}^{n-1}}{\mathrm{1}+{\left(t-t\mathrm{\prime }\right)}^n}.(51)$

As a consequence, the exponential algorithm following the procedures can be implemented to obtain the increment of aging viscoelasticity $\Delta {\mathit{\epsilon }}_v$:

1) At $t=t_0$, where $t_0$ indicates the time with the external load being applied, initialize the internal variables ${\mathit{\gamma }}_{\mu }^{\left(0\right)}$. Select ${\tau }_u={10}^{-7+u}$, with $u$ = 1, 2, 3,…, 14.

2) Let $\xi =t-t^{\prime }$, and the continuous spectrum is calculated as

$L\left({\tau }_u\right)=q_2\frac{{\left(3{\tau }_u\right)}^3}{\mathrm{2}}\cdot \frac{{\mathrm{d}}^3\Phi }{\mathrm{d}{\xi }^3},(52)$

with

$\frac{{\mathrm{d}}^3\Phi }{\mathrm{d}{\xi }^3}=\frac{2n^3{\xi }^{3n-3}}{{\left(1+{\xi }^n\right)}^3}-\frac{3n^2\left(n-1\right){\xi }^{2n-3}}{{\left(1+{\xi }^n\right)}^2}+\frac{n\left(n-1\right)\left(n-2\right){\xi }^{n-3}}{\left(1+{\xi }^n\right)}.(53)$

3) Discretize the spectrum using

$A\left({\tau }_u\right)=\left(\sqrt{\frac{1}{t_{n-1/2}}}+\frac{q_3}{q_2}\right)L\left({\tau }_u\right)\mathrm{In}10.(54)$

4) Calculate ${\lambda }_u$ according to Eq. 7, and calculate $E″$ according to Eq. 6.

5) Obtain increment of aging viscoelasticity $\Delta {\mathit{\epsilon }}_v$, according to Eq. 8.

6) After retrieving the stress increment $\Delta \mathit{\sigma }$ by the GED model, update the internal variable ${\mathit{\gamma }}_{\mu }^{\left(\mathrm{n}\right)}$; refer to Eq. 9.

7) Begin the next time step.

Now we turn to the increment of viscous flow $\Delta {\mathit{\epsilon }}_f$, which needs the viscosity Eq. 17 with initial condition Eq. 19. Suppose that the value of viscosity ${\eta }_{n-1}$ at time $t_{n-1}$ is known from the previous time step or from the initial condition, we wish to obtain the value of viscosity ${\eta }_n={\eta }_{n-1}+\Delta \eta$ at time $t_n=t_{n-1}+\Delta t$. The exponential algorithm (Bažant 1971) following the procedures is implemented to obtain the increment of viscous flow $\Delta {\mathit{\epsilon }}_f$.

1) The temperature and humidity of the previous time step $T_{n-1}$ and $h_{n-1}$ are known, as well as their increments $\Delta T$ and $\Delta h$, from the external heat transfer and moisture transport analyses. The viscosity ${\eta }_n$ at the current time step is explicitly evaluated as for arbitrary large $\Delta t$, as

${\eta }_n=\frac{B}{A}\cdot \frac{B\left(1-\tilde{e}\right)+A{\eta }_{n-1}\left(1-\tilde{e}\right)}{B\left(1+\tilde{e}\right)+A{\eta }_{n-1}\left(1-\tilde{e}\right)},(55)$

with

$A=\sqrt{\frac{{\mu }_S\left|\Delta \left(T\mathrm{In}h\right)\right|}{T_0\Delta t}},(56)$

$B=\frac{{\psi }_s}{q_4},(57)$

$\tilde{e}=e^{-2AB\Delta t}.(58)$

2) Suppose $\left|\Delta \tilde{\eta }\right|\ll {\tilde{\eta }}_n$, the increment of viscous flow $\Delta {\mathit{\epsilon }}_f$ is evaluated as

$\Delta {\mathit{\epsilon }}_f=\frac{\Delta \mathit{t}}{{\tilde{\eta }}_n}\left[{\mathit{\sigma }}_{n-1}\left(1-\frac{\Delta \tilde{\eta }}{2{\tilde{\eta }}_{n-1}}\right)+\Delta \mathit{\sigma }\left(\frac{1}{2}-\frac{\Delta \tilde{\eta }}{3{\tilde{\eta }}_{n-1}}\right)\right].(59)$

For the creep deformation coupled with concrete damage or cracking, the nominal stress tensor $\mathit{\sigma }$ or its increment $\Delta \mathit{\sigma }$ should be replaced by their effective counterparts $\overline{\mathit{\sigma }}$ and $\Delta \overline{\mathit{\sigma }}$, respectively, to evaluate $\Delta {\mathit{\epsilon }}_v$ and $\Delta {\mathit{\epsilon }}_f$. Afterwards, the increment of strain tensor $\Delta \mathit{\epsilon }\mathrm{\prime }$ can be obtained by subtracting $\Delta {\mathit{\epsilon }}_v$ and $\Delta {\mathit{\epsilon }}_f$ from the increment of total strain tensor $\Delta {\mathit{\epsilon }}_{tot}$, as well as the increments of hygral and thermal strain tensors ($\Delta {\mathit{\epsilon }}_{sh}$ and $\Delta {\mathit{\epsilon }}_T$). The $\Delta \mathit{\epsilon }\mathrm{\prime }$ is subsequently adopted to obtain the stress tensor ${\mathit{\sigma }}_n$ and damage indicator $d_n$ at the current step time $t_n$.

Implementation Aspects in Abaqus

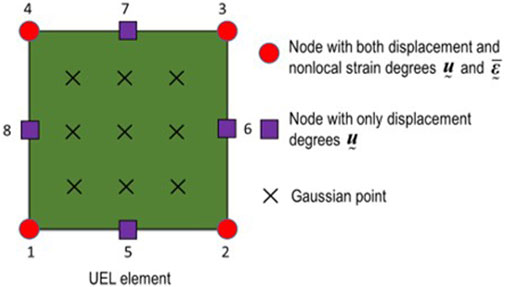
The system of equations above is highly nonlinear. To implement the model with implicit FE solver, the general FE software Abaqus/Standard is selected for its built-in implicit incremental-iterative Newton-Raphson algorithm and automatic time-step-ping schemes. The user-defined element (UEL) subroutine enables us to define the element, of which computation of element tangent stiffness and nodal force vectors is realized.

Plane stress is taken into account in the following simulations. To guarantee the consistency requirements, the shape functions and their derivatives for the displacement field $\mathit{u}\left(\mathrm{x},t\right)$ are defined over 2D quadrilateral element of eight nodes, whereas these terms are defined over 2D quadrilateral element of four nodes for nonlocal equivalent strain field $\overline{\epsilon }\left(\mathrm{x},t\right)$ (Sarkar et al., 2019). These two element types share the same nodes at the four corners; see Figure 2 for details. Consequently, the nodal displacement vector $\underset{\mathrm{\sim }}{u}$ and nodal nonlocal equivalent strain vector $\underset{\mathrm{\sim }}{\overline{\epsilon }}$ are expressed as

$\begin{array}{l}\underset{\mathrm{\sim }}{\mathit{u}}={\left[u_1^1,u_2^1,u_1^2,u_2^2,\mathrm{...}{u}_1^8,u_2^8\right]}^T\\ \underset{\mathrm{\sim }}{\overline{\epsilon }}={\left[{\overline{\epsilon }}^1,{\overline{\epsilon }}^2,{\overline{\epsilon }}^3,{\overline{\epsilon }}^4\right]}^T\end{array}.(60)$

FIGURE 2

FIGURE 2. Degrees of freedom of 2D element for the GED-MPS model.

The corresponding shape functions and their derivatives are

${\mathit{N}}_{\mathit{u}}=\left[\begin{array}{ccccc}{N}_1& 0& \mathrm{...}& N_8& 0\\ 0& N_1& \mathrm{...}& 0& N_8\end{array}\right]{\mathit{N}}_{\overline{\epsilon }}=\left[\begin{array}{cccc}{N}_1& N_2& N_3& N_4\end{array}\right](61)$

and

${\mathit{B}}_{\mathit{u}}=\left[\begin{array}{ccccc}\frac{\partial N_1}{\partial x}& 0& \mathrm{...}& \frac{\partial N_8}{\partial x}& 0\\ 0& \frac{\partial N_1}{\partial y}& \mathrm{...}& 0& \frac{\partial N_8}{\partial y}\\ \frac{\partial N_1}{\partial y}& \frac{\partial N_1}{\partial x}& \mathrm{...}& \frac{\partial N_8}{\partial y}& \frac{\partial N_8}{\partial x}\end{array}\right]\hspace{0.17em}{\mathit{B}}_{\overline{\epsilon }}=\left[\begin{array}{ccc}\frac{\partial N_1}{\partial x}& \mathrm{...}& \frac{\partial N_4}{\partial x}\\ \frac{\partial N_1}{\partial y}& \mathrm{...}& \frac{\partial N_4}{\partial y}\end{array}\right].(62)$

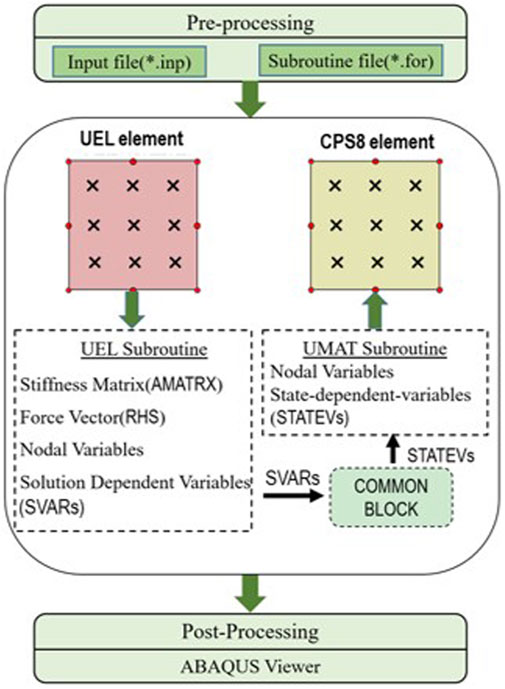
It is noteworthy that the analysis with UEL subroutine is inconvenient in the postprocessing and visualization of the results. Because shape functions are defined by users in the UEL subroutine, the Abaqus cannot extrapolate variables from Gauss points to the element nodes, automatically. To this end, an auxiliary dummy mesh is adopted, consisting of standard Abaqus elements that resemble the UEL elements in terms of number of nodes and integration points. The material response at each integration point in the auxiliary mesh is defined using a user material subroutine (UMAT), which enables the user to define the constitutive matrix and stresses from the strain values.

In this auxiliary mesh, the stress components are deliberatively set as zero so as not to influence the global solution. The data from the UEL for each time increment we want to observe in Abaqus/Viewer is stored as built-in array SVARS, which allows transferring to the UMAT subroutine by the built-in array STATEV for each corresponding element and integration point. Transferring of values from SVARS array to STATEV array is accomplished by making use of the common statement (Msekh et al., 2015). Figure 3 shows the technique to implement the visualization of the analyses with the UEL subroutines.

FIGURE 3

FIGURE 3. Layered system of the FE elements and data flow in Abaqus with UEL and UMAT.

Illustration of GED-MPS Model

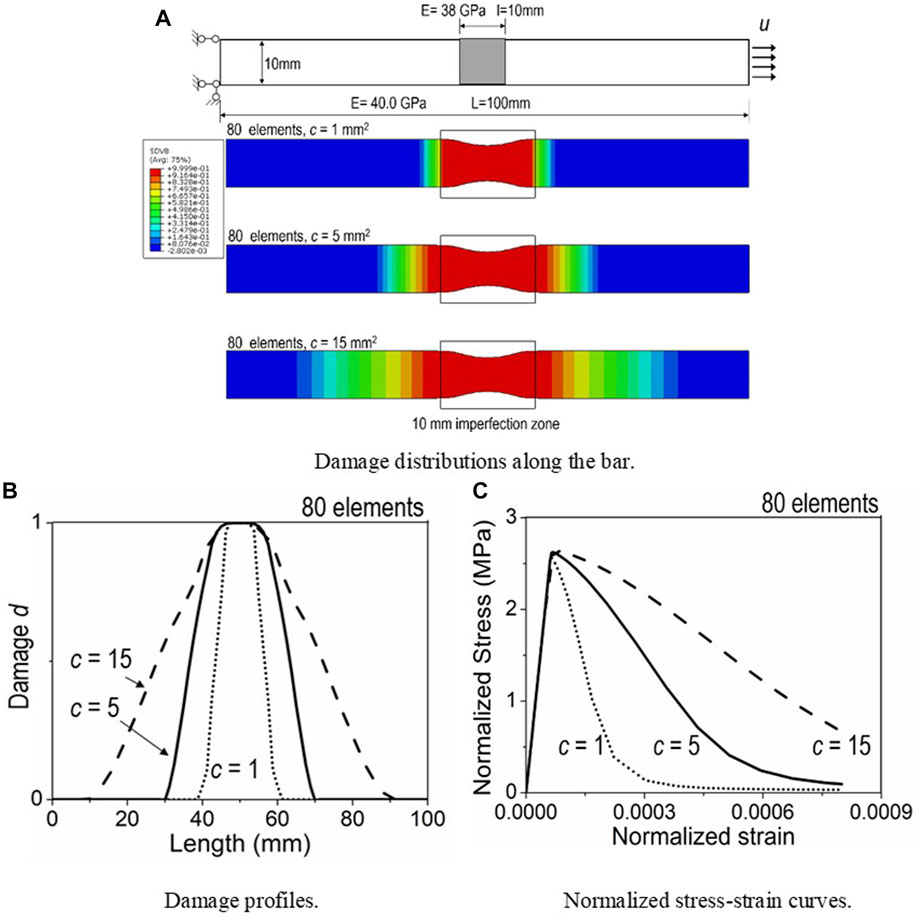
A 100 mm long bar is taken for an illustration, which is subject to uniaxial tensile loading. The Young’s modulus is deliberatively reduced by 5% in a 10 mm wide zone in the middle of the bar to trigger localization of deformation. The following mechanical parameters are set for this illustration, with $E_{28}$ = 40 GPa, $v$ = 0.2, ${\kappa }_0$ = 0.000075, $\beta$ = 300, $\alpha$ = 0.99, and $k$= 10. The bar is discretized with 40, 80, and 160 elements, respectively. Moreover, three different values of gradient parameter $c$ are selected, with $c$ = 1, 5, and 15 mm², respectively.

The first group of analyses embraces the bar discretized with 80 elements, but with three different values of gradient parameter $c$. Profiles of the damage indicator $d$ corresponding to different $c$ are depicted in Figures 4A,B. For the case with $c$ = 1 mm², a clear narrowing of the localization zone is observed, in terms of $d$. This indicates that the case with $c$ = 1 mm² is very close to the local damage model, which is effective for brittle materials, but quasibrittle materials. On the other hand, profiles of damage indicator $d$ are different for the other two cases with $c$ = 1 and 5 mm², as nonlocality is clearly depicted as the damage overflowing the 10 mm imperfection zone. The value of gradient parameters $c$ clearly affects the width of damage zone in the middle of the bar. Alongside, the effects of gradient parameters $c$ on the force-displacement relations of the bar are also revealed as the normalized stress-strain curves in Figure 4C. Obviously, with the increase of $c$, the bar behaves more ductile and the load-carrying capacity also increases slightly.

FIGURE 4

FIGURE 4. Damage and normalized stress-strain curves for the simulations of different c.

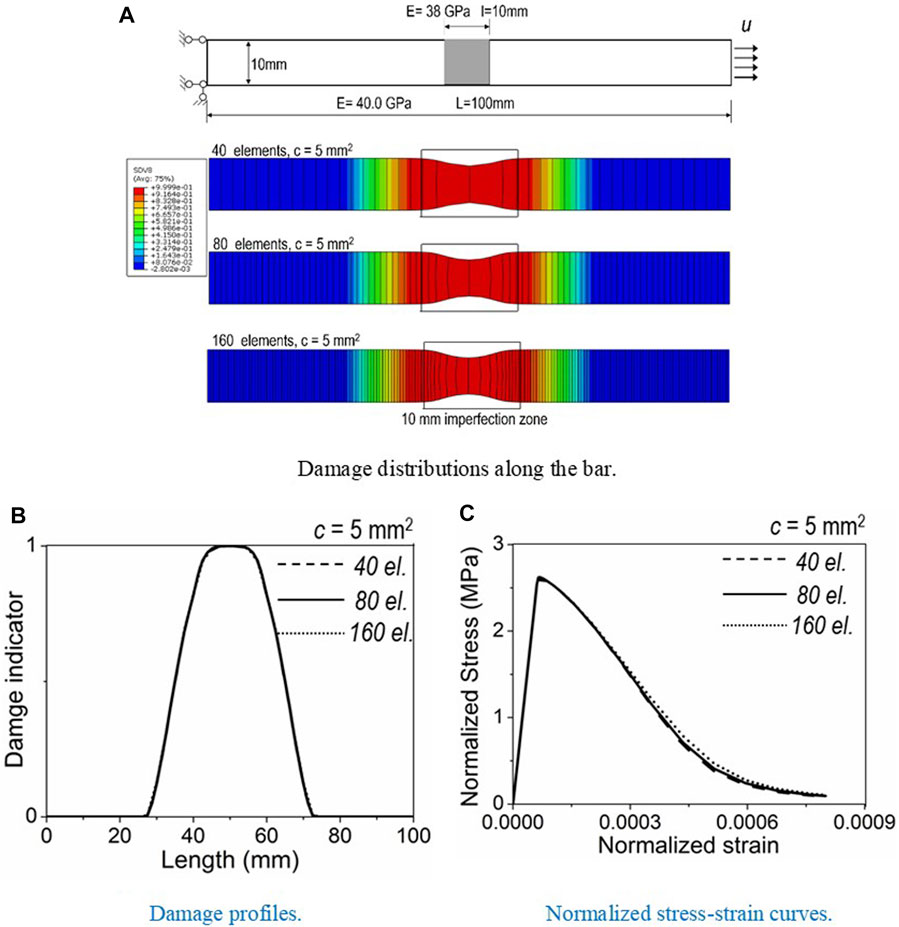
The second group of analyses embraces the bar discretized with different element size, but with identical gradient parameter $c$ = 5 mm². Profiles of the damage indicator $d$ corresponding to different element size are depicted in Figures 5A,B. Clearly, although with different element size, all the three cases converge to an identical result, indicating that the GED model satisfactorily eliminates the mesh-sensitive problem frequently encountered in the softening region of quasibrittle materials. Nonlocality is clearly demonstrated with nearly the same three damage zones with the width bigger than the 10 mm imperfection zone. Alongside, effects of element size on the force-displacement relations of the bar are also revealed as the normalized stress-strain curves in Figure 5C. Only a slight difference is observed for the three cases.

FIGURE 5

FIGURE 5. Damage and normalized stress-strain curves for the simulations of different element size.

Figure 5 clearly shows that mesh-dependent solutions of mechanical responses of quasibrittle materials are regularized by the GED model, without creep deformation. However, limited literatures report the mesh-sensitivity problem in the time-dependent analyses of quasibrittle materials, especially when coupled with cracking, according to the authors’ knowledge. Intuitively, mesh-sensitivity solution is a concern, as the creep depends on the stress tensor and the damage state at each material point.

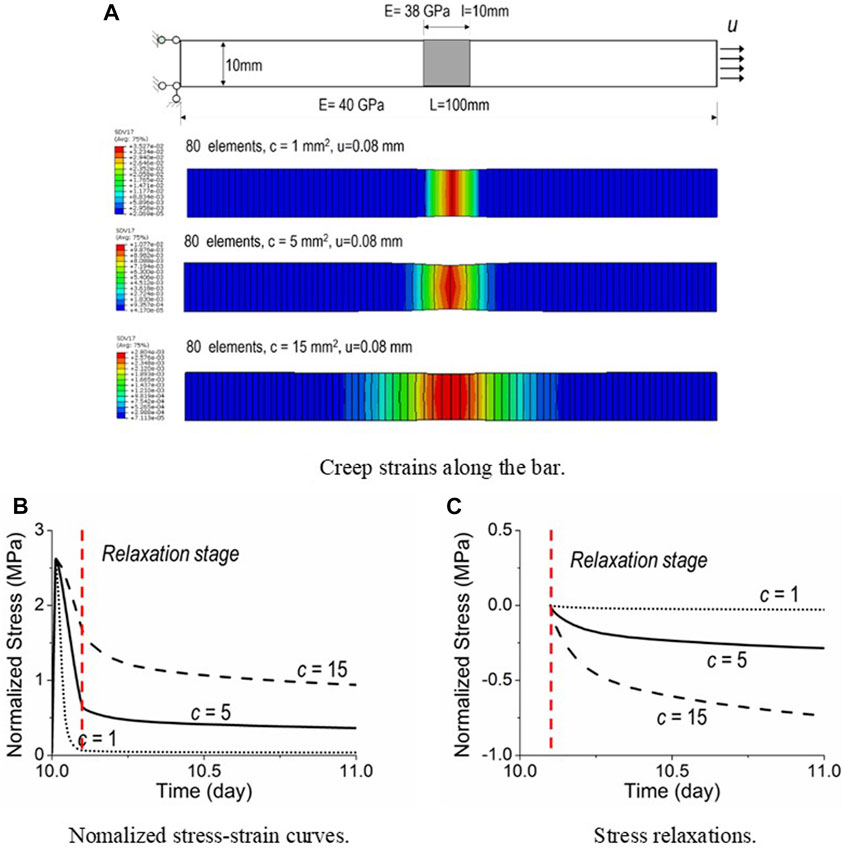
To this end, the proposed GED-MPS model is applied to the same bar. The external loading is applied at the bar’s right end at the day of $t^{\prime }$ = 10. The external displacement is set as 0.08 m and the loading is finished within 0.01 day, and it is kept constant for another 1 day. Loading rate effect, aging effect, shrinkage, and thermal strains are not considered for simplicity. The following parameters are selected: $q_1$ = 25 × 10^–6 MPa⁻¹, $q_2$ = 200 × 10^–6 MPa⁻¹, $q_3$ = 20 × 10^–6 MPa⁻¹, $q_4$ = 0 MPa⁻¹, $T$ = 293 K, and $h$ = 1.

Similarly, the first group of analyses embraces the bar discretized with identical 80 elements, but with different gradient parameters as $c$ = 1, 5 and 15 mm². Profiles of creep strain $\epsilon \prime$ in the horizontal direction for the three cases are illustrated in Figure 6A, with effects of damage being involved. For the case with $c$ = 1 mm² which approaches local damage analysis, the localized creep-induced strain, with peak value of $\epsilon \prime$ = 3.53 × 10^–2 is observed. For the other two cases, with $c$ = 5 and 15 mm², nonlocality is clearly captured for the creep strain $\epsilon \prime$, which overflows the 10 mm imperfection zone. Nevertheless, the peak value of $\epsilon \prime$ decreases to 1.08 × 10^–2 for the case with $c$ = 5 mm² and 0.28 × 10^–2 for the case with $c$ = 15 mm², respectively.

FIGURE 6

FIGURE 6. Simulations of creep behaviors intertwined with damage with different c.

Alongside, effects of gradient parameters $c$ on the relationship between time and normalized stress are revealed in Figure 6B. The time from day 10.0 to day 10.1is the loading time and various strain-softening responses are captured, with analogy to the phenomenon revealed in Figure 4C. Moreover, relaxations of normalized stresses are illustrated from day 10.1 to day 11.1 in Figure 6C, with effects of $c$. Interestingly, apparent mesh-sensitivity is witnessed for the three cases. Although with the peak value of creep strain $\epsilon \prime$ = 3.53 × 10^–2, the relaxation of normalized stress is not significant for the case with $c$ = 1 mm². It looks like that the localization of creep strain does not significantly affect the relaxation of normalized stress. On the other hand, the loss of normalized stress approaches 0.29 MPa for the case with $c$ = 5 mm² and 0.75 MPa for the case with $c$ = 5 mm²; see Figure 6C. Obviously, the gradient parameter $c$ smears the damage into the neighboring zone, so as for the creep strain intertwined with damage or cracking.

Calibration With Tests of Simply-Supported Concrete Beams

Engineering community concerns more about long-term deflections of reinforced concrete or prestressed concrete structures, coupled to concrete cracking. In this section, the capability of the GED-MPS model is further extended to the reinforced concrete structures. Long-term tests of simply-supported reinforced concrete beams in Gilbert and Nejadi (2004) are simulated.

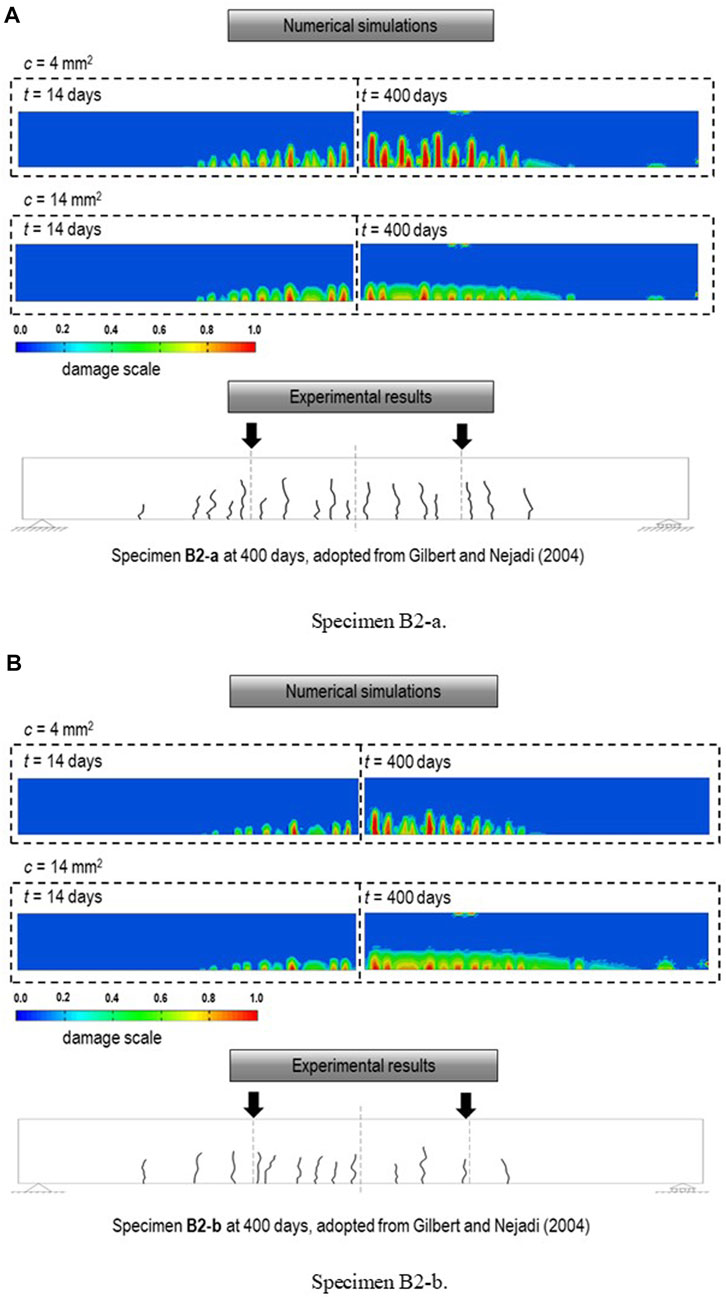
Although totally 6 beams and 6 slabs were reported, this paper selected two typical specimens for simulations, namely specimens B2-a and B2-b. These two specimens owned a 250 × 340 rectangular cross-section and 3,500 mm in length. The concrete cover thickness is 25 mm. Two 16 mm diameter rebars were arranged as the flexural reinforcement. During the test, these two specimens were loaded to 50% (specimen B2-a) and 30% (specimen B2-b) of their flexural strengths, respectively. A constant external loading was applied on the concrete specimens. This loading test began at 14 days and lasted for around 400 days. Concrete properties were measured at different ages and they are summarized in Table 2.

TABLE 2

TABLE 2. Concrete properties at different ages.

Creep Calibrations

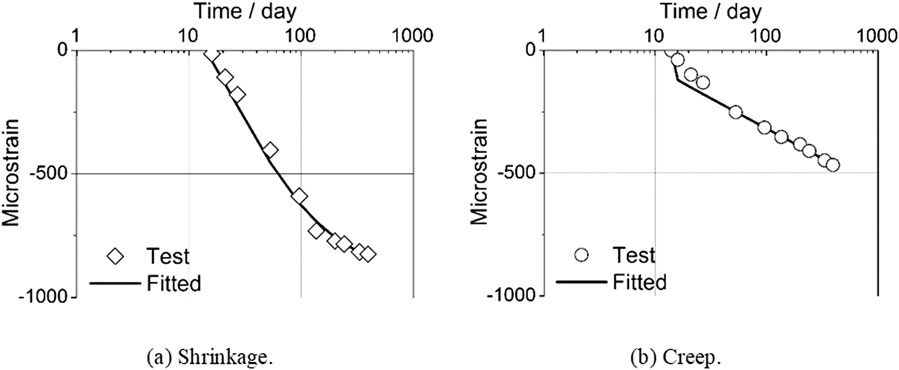
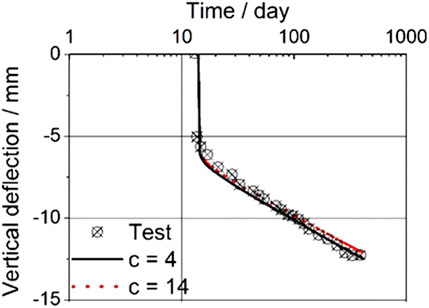
The concrete creep and shrinkage tests were provided in Gilbert and Nejadi (2004), which begun at the 14-day concrete age. No data is provided regarding temperature and humidity, and they are set as $T$ = 293 K and $h$ = 0.6, respectively. The values are appropriate since they fit the measured shrinkage strain in an agreed manner (see Figure 7A), with the employment of the shrinkage model in ACI code (ACI 2009).

FIGURE 7

FIGURE 7. Experimental data and numerical fitting for concrete shrinkage and creep.

With respect to parameters for concrete creep, the following creep parameters are selected to fit the experimental creep data, with $q_1$ = 47.4 × 10^–6 MPa⁻¹, $q_2$ = 200 × 10^–6 MPa⁻¹, $q_3$ = 20 × 10^–6 MPa⁻¹, and$q_4$ = 46 × 10^–6 MPa⁻¹; see Figure 7B. In addition, the following fracture parameters are adopted according to Table 2, with $E_{28}$ = 22.8 GPa, $v$ = 0.18, ${\kappa }_0$ = 0.000122 ($f_t$ = 2.8 MPa), $\beta$ = 300, $\alpha$= 0.99, and $k$ = 24.8/2.8 = 8.5. The $E_0$ is the Young’s modulus at concrete age of 14 days, and it would rise according to data in Table 2 concerning concrete aging effect.

Long-Term Deflections and Cracking Distributions

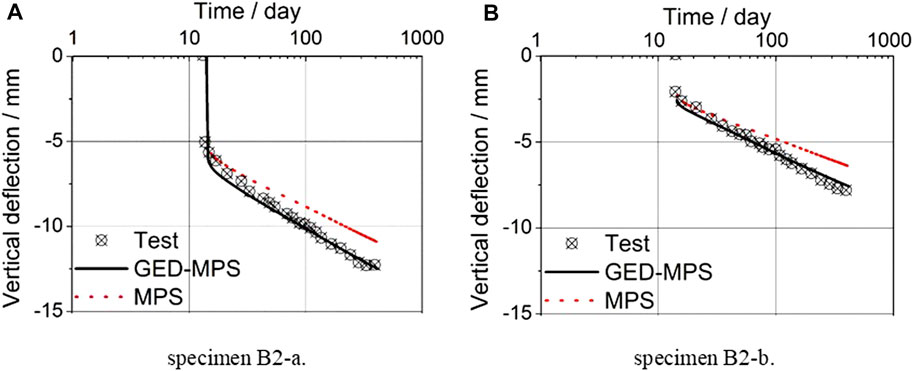
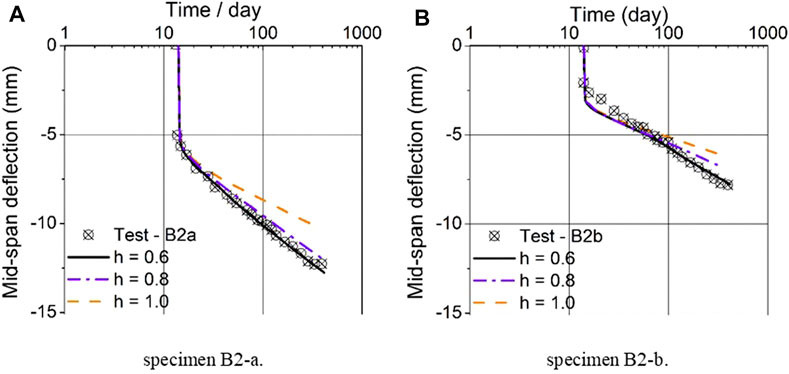
The GED-MPS model is verified with experimental data of specimens B2-a and B2-b, which were subject to external loading of 18.6 and 11.7 kN, respectively. The identical calibrated parameters listed in Sect-5.1 are utilized without any modification. Some artificial defects were deliberatively introduced at the bottoms of FE models to trigger the cracks.

ffects of different gradient parameter $c$ = 4 and 14 mm² on the long-term behaviors are investigated with the other parameters being the same. Comparisons of FE and experimental crack profiles for specimens B2-a and B-2b are illustrated in Figures 8A,B, respectively. For the FE results with $c$ = 4 mm², crack patterns correspond well with the test in height, region, and spacing of cracks. On the other hand, cracking profile for the case with $c$ = 14 mm² yields less accurate prediction in the cracking height. Absent data are provided in the report regarding the cracking profiles at the commencement of the test.

FIGURE 8

FIGURE 8. Experimental and numerical crack profiles.

Long-term vertical deflections of Specimen B2-a with different $c$ are compared with experimental data in Figure 9. Both simulation results yield satisfactory agreements. Interestingly, little difference is observed for the deflections with different $c$. Possible reasons are attributed to the following two reasons. Shrinkage deformation plays a dominant role over creep deformation for the specimen, as merely 50% peak strength is applied and the stress level is low. Another possible reason is that although higher $c$ reduces the damage height, it broadens the damage zone with respect to the case with lower $c$.

FIGURE 9

FIGURE 9. Experimental and numerical deflections of specimen B2-a with different c.

Furthermore, conventional linear viscoelastic analysis considering only creep and shrinkage deformations, without intertwined effect with concrete damage and cracking (termed as MPS in Figure 10), is compared to the GED-MPS model in Figure 10A for specimens B2-a and Figure 10B for specimen B2-b. Clearly, conventional linear viscoelastic analysis underestimates their long-term vertical deflections, which can be satisfactorily remedied by the GED-MPS model.

FIGURE 10

FIGURE 10. Experimental and numerical deflections w/wo concrete cracking.

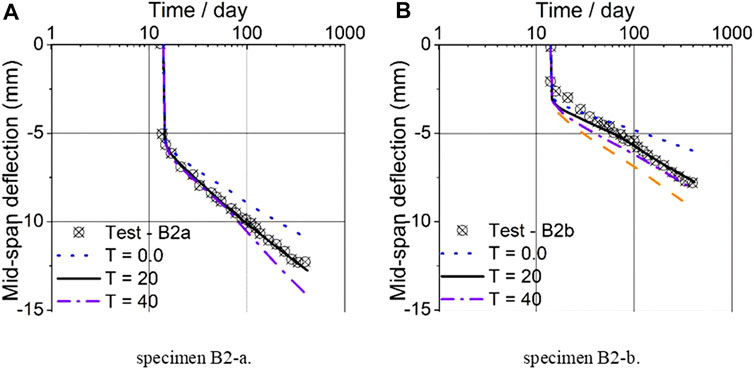
Considering the effect of different temperatures on the long-term deflection of these specimens, four different temperatures are selected, and they are $T$ = 0.1°C (273.1 K), 20°C (293.1 K), 40°C (313.1 K), and 60°C (333.1 K). The long-term deflections subject to different temperatures of specimens B2-a and B2-b are presented in Figure 11, while all the other parameters are kept constant.

FIGURE 11

FIGURE 11. Mid-span deflection curves at various temperatures.

The effects of different humidity on long-term deflection of specimens B2-a and B2-b are further revealed in Figure 12, with different humidity of $h$ = 0.6, 0.8, and 1.0, whilst all other parameters are fixed. It is noteworthy that $h$ = 1.0 illustrates the effect of creep on the long-term deflection only, without shrinkage effect.

FIGURE 12

FIGURE 12. Mid-span deflection curves at various humidity.

Conclusion

The GED-MPS model is proposed and implemented with implicit FE software Abaqus/Standard. The model integrates the GED model capable of circumventing the mesh-sensitivity in the conventional mechanical analyses for quasibrittle materials exhibiting strain softening behaviors, and the MPS theory capable of predicting point-wise creep responses.

The GED-MPS model anchors at the rate-type formulation, and, therefore, is capable of incorporating other memory-dependent processes. After being enriched with continuous spectrum method and exponential algorithm, the model is efficient and stable for large-scale structural analysis. The model successfully regularizes the mesh-sensitivity problem, which is already concerned with mechanical analyses of materials exhibiting softening, but less with the nonlinear creep intertwined with cracking. The GED-MPS model is applied to simply supported reinforced concrete beams. It is proven that the proposed model is capable of capturing not only the long-term vertical deflection trends, but also the time-dependent cracking propagations affected by creep and shrinkage.

Further improvements to polish the model could be conducted, i.e., implementing more accurate anisotropic constitutive model for concrete, instead of the isotropic one, replacing the current GED model with stress-based GED model to address the issue of spurious damage growth. With the GED-MPS model being implemented in the implicit FE algorithm, authors are expected to extend this model to accurately predict long-term behaviors of real large-scale creep-sensitive structures.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation. To facilitate potential researchers and users, parts of the code and the input file are released at https://github.com/TengTongSEU/Coupled-creepdamage.

Author Contributions

TT: Conceptualization, Methodology, Writing-Original draft preparation. CD: Conceptualization, Supervision. XL: Methodology, Writing- Reviewing and Editing. SY: Conceptualization, Supervision, Writing- Reviewing and Editing. ZL: Supervision, Writing- Reviewing and Editing.

Funding

This research is supported by the National Key Research and Development Program of China (2019YFE0119800), the National Natural Science Foundation for Young Scientists of China (51808113), the National Natural Science Foundation for Young Scientists of Jiangsu Province (BK20180389), and the Zhishan Youth Scholar Program of SEU.

Conflict of Interest

CD and XL were employed by the company State Gird Jiangsu Electric Power Engineering Consulting Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdellatef, M., Boumakis, I., Wan-Wendner, R., and Alnaggar, M. (2019). Lattice Discrete Particle Modeling of Concrete Coupled Creep and Shrinkage Behavior: A Comprehensive Calibration and Validation Study. Construction Building Mater. 211, 629–645. doi:10.1016/j.conbuildmat.2019.03.176

CrossRef Full Text | Google Scholar

ACI Committee 209 (2008). Guide for Modeling and Calculating Shrinkage and Creep in Hardened concrete. ACI. 209, 2.R-08

Google Scholar

Bažant, Z. P. (1971). Numerically Stable Algorithm with Increasing Time Steps for Integral-type Aging Creep. Proc. 1st Int. Conf. Struct. Mech. Reactor Tech.

Google Scholar

Bažant, Z. P., and Li, G. H. (2008). Comprehensive Database on Concrete Creep and Shrinkage. ACI Mater. J. 105 (6), 635–637.

CrossRef Full Text | Google Scholar

Bažant, Z. P., Belytschko, T. B., and Chang, T. P. (1984). Continuum Theory for Strain-Softening. J. Eng. Mech-asce. 110 (12), 1666–1692. doi:10.1061/(ASCE)0733-9399(1984)110:12(1666)

Google Scholar

Bažant, Z. P., Hauggaard, A. B., Baweja, S., and Ulm, F. J. (1997a). Microprestress-Solidification Theory for concrete Creep. I: Aging and Drying Effects. J. Eng. Mech-asce. 123 (11), 1188–1194. doi:10.1061/(ASCE)0733-9399(1997)123:11(1188)

Google Scholar

Bažant, Z. P., Hauggaard, A. B., and Baweja, S. (1997b). Microprestress-Solidification Theory for Concrete Creep. II: Algorithm and Verification. J. Eng. Mech-asce. 123 (11), 1195–1201. doi:10.1061/(ASCE)0733-9399(1997)123:11(1195)

Google Scholar

Bažant, Z. P., and Jirásek, M. (2018). Creep and Hygrothermal Effects in concrete Structures. Basingstoke, UK: Springer, Vol. 225

Bažant, Z. P., and Xi, Y. (1995). Continuous Retardation Spectrum for Solidification Theory of Concrete Creep. J. Eng. Mech-asce. 121 (2), 281–288. doi:10.1061/(ASCE)0733-9399(1995)121:2(281)

CrossRef Full Text | Google Scholar

Bažant, Z. P., Yu, Q., and Li, G. H. (2012a). Excessive Long-Time Deflections of Prestressed Box Girders. I: Record-Span Bridge in Palau and Other Paradigms. J. Struct. Eng-asce. 138 (6), 676–686. doi:10.1061/(ASCE)ST.1943-541X.0000487

Google Scholar

Bažant, Z. P., Yu, Q., and Li, G. H. (2012b). Excessive Long-Time Deflections of Prestressed Box Girders. II: Numerical Analysis and Lessons Learned. J. Eng. Mech-asce. 138 (6), 687–696. doi:10.1061/(ASCE)ST.1943-541X.0000375

Google Scholar

Benboudjema, F., and Torrenti, J. M. (2008). Early-age Behaviour of Concrete Nuclear Containments. Nucl. Eng. Des. 238 (10), 2495–2506. doi:10.1016/j.nucengdes.2008.04.009

CrossRef Full Text | Google Scholar

Boumakis, I., Di Luzio, G., Marcon, M., Vorel, J., and Wan-Wendner, R. (2018). Discrete Element Framework for Modeling Tertiary Creep of Concrete in Tension and Compression. Eng. Fracture Mech. 200, 263–282. doi:10.1016/j.engfracmech.2018.07.006

CrossRef Full Text | Google Scholar

Challamel, N., Lanos, C., and Casandjian, C. (2005). Creep Damage Modelling for Quasi-Brittle Materials. Eur. J. Mech. A - Solids. 24 (4), 593–613. doi:10.1016/j.euromechsol.2005.05.003

CrossRef Full Text | Google Scholar

De Borst, R. (1987). Smeared Cracking, Plasticity, Creep, and thermal Loading-A Unified Approach. Computer Methods Appl. Mech. Eng. 62 (1), 89–110. doi:10.1016/0045-7825(87)90091-0

CrossRef Full Text | Google Scholar

De Borst, R., and Verhoosel, C. V. (2016). Gradient Damage vs Phase-Field Approaches for Fracture: Similarities and Differences. Computer Methods Appl. Mech. Eng. 312, 78–94. doi:10.1016/j.cma.2016.05.015

CrossRef Full Text | Google Scholar

Di Luzio, G., and Cusatis, G. (2013). Solidification-Microprestress-Microplane (SMM) Theory for concrete at Early Age: Theory, Validation and Application. Int. J. Sol. Structures. 50 (6), 957–975. doi:10.1016/j.ijsolstr.2012.11.022

CrossRef Full Text | Google Scholar

Di Luzio, G. (2009). Numerical Model for Time-Dependent Fracturing of concrete. J. Eng. Mech. 135 (7), 632–640. doi:10.1061/(asce)0733-9399(2009)135:7(632)

CrossRef Full Text | Google Scholar

Gilbert, R. I., and Nejadi, S. (2004). An Experimental Study of Flexural Cracking in Reinforced concrete Members under Short Term Loads. Sydney, NSW, Australia: School of Civil and Environmental Engineering. University of New South Wales.

Hubler, M. H., Wendner, R., and Bažant, Z. P. (2015). Statistical Justification of Model B4 for Drying and Autogenous Shrinkage of Concrete and Comparisons to Other Models. Mater. Struct. 48 (4), 797–814. doi:10.1617/s11527-014-0516-z

CrossRef Full Text | Google Scholar

Jirásek, M., and Havlásek, P. (2014). Microprestress-Solidification Theory of Concrete Creep: Reformulation and Improvement. Cement Concrete Res. 60, 51–62. doi:10.1016/j.cemconres.2014.03.008

CrossRef Full Text | Google Scholar

Kou, M. M., Lian, Y. J., and Wang, Y. T. (2019). Numerical Investigations on Crack Propagation and Crack Branching in Brittle Solids under Dynamic Loading Using Bond-Particle Model. Eng. Fracture Mech. 212, 41–56. doi:10.1016/j.engfracmech.2019.03.012

CrossRef Full Text | Google Scholar

Li, G., Yin, B. B., Zhang, L. W., and Liew, K. M. (2020). Modeling Microfracture Evolution in Heterogeneous Composites: A Coupled Cohesive Phase-Field Model. J. Mech. Phys. Sol. 142, 103968. doi:10.1016/j.jmps.2020.103968

CrossRef Full Text | Google Scholar

Li, S., Yang, Y., Pu, Q., Yang, D., Sun, B., and Li, X. (2019). Three‐dimensional Nonlinear Creep and Shrinkage Effects of a Long‐Span Prestressed concrete Box Girder Bridge. Struct. Concrete. 20 (2), 638–649. doi:10.1002/suco.201800148

CrossRef Full Text | Google Scholar

Mazzotti, C., and Savoia, M. (2003). Nonlinear Creep Damage Model for Concrete Under Uniaxial Compression. J. Eng. Mech. 129 (9), 1065–1075. doi:10.1061/(asce)0733-9399(2003)129:9(1065)

CrossRef Full Text | Google Scholar

Mei, S., and Wang, Y. (2020). Viscoelasticity: A New Perspective on Correlation Between Concrete Creep and Damping. Construction Building Mater. 265, 120557. doi:10.1016/j.conbuildmat.2020.120557

CrossRef Full Text | Google Scholar

Msekh, M. A., Sargado, J. M., Jamshidian, M., Areias, P. M., and Rabczuk, T. (2015). Abaqus Implementation of Phase-Field Model for Brittle Fracture. Comput. Mater. Sci. 96, 472–484. doi:10.1016/j.commatsci.2014.05.071

CrossRef Full Text | Google Scholar

Peerlings, R. H. J., De Borst, R., Brekelmans, W. A. M., and De Vree, J. H. P. (1996). Gradient Enhanced Damage for Quasi-Brittle Materials. Int. J. Numer. Meth. Engng. 39 (19), 3391–3403. doi:10.1002/(sici)1097-0207(19961015)39:19<3391::aid-nme7>3.0.co;2-d

CrossRef Full Text | Google Scholar

Peerlings, R. H. J., De Borst, R., Brekelmans, W. A. M., and Geers, M. G. D. (1998). Gradient-Enhanced Damage Modelling of concrete Fracture. Mech. Cohes.-Frict. Mater. 3 (4), 323–342. doi:10.1002/(sici)1099-1484(1998100)3:4<323::aid-cfm51>3.0.co;2-z

CrossRef Full Text | Google Scholar

Pichler, C., Lackner, R., and Mang, H. A. (2007). A Multiscale Micromechanics Model for the Autogenous-Shrinkage Deformation of Early-Age Cement-Based Materials. Eng. Fract. Mech. 74 (1-2), 34–58. doi:10.1016/j.engfracmech.2006.01.034

CrossRef Full Text | Google Scholar

Poh, L. H., and Sun, G. (2017). Localizing Gradient Damage Model With Decreasing Interactions. Int. J. Numer. Meth. Engng. 110 (6), 503–522. doi:10.1002/nme.5364

CrossRef Full Text | Google Scholar

Rahimi-Aghdam, S., Bažant, Z. P., and Cusatis, G. (2019). Extended Microprestress-Solidification Theory for Long-Term Creep With Diffusion Size Effect in Concrete at Variable Environment. J. Eng. Mech. 145 (2), 04018131. doi:10.1061/(asce)em.1943-7889.0001559

CrossRef Full Text | Google Scholar

Ren, J., Wang, J., Li, X., Wei, K., Li, H., and Deng, S. (2020). Influence of Cement Asphalt Mortar Debonding on the Damage Distribution and Mechanical Responses of CRTS I Prefabricated Slab. Construction Building Mater. 230, 116995. doi:10.1016/j.conbuildmat.2019.116995

CrossRef Full Text | Google Scholar

Rokhgireh, H., and Nayebi, A. (2019). Non-proportional Stress and Stress-Strain Controlled Paths Cyclic Loading Modeling by Using Anisotropic Continuum Damage Model. Theor. Appl. Fracture Mech. 103, 102311. doi:10.1016/j.tafmec.2019.102311

CrossRef Full Text | Google Scholar

Sarkar, S., Singh, I. V., Mishra, B. K., Shedbale, A. S., and Poh, L. H. (2019). A Comparative Study and ABAQUS Implementation of Conventional and Localizing Gradient Enhanced Damage Models. Finite Elem. Anal. Des. 160, 1–31. doi:10.1016/j.finel.2019.04.001

CrossRef Full Text | Google Scholar

Scheiner, S., and Hellmich, C. (2009). Continuum Microviscoelasticity Model for Aging Basic Creep of Early-Age concrete. J. Eng. Mech. 135 (4), 307–323. doi:10.1061/(asce)0733-9399(2009)135:4(307)

CrossRef Full Text | Google Scholar

Schlappal, T., Kalliauer, J., Vill, M., Gmainer, S., Mang, H. A., Eberhardsteiner, J., et al. (2020). Serviceability Limits of Reinforced Concrete Hinges. Eng. Structures. 208, 109861. doi:10.1016/j.engstruct.2019.109861

CrossRef Full Text | Google Scholar

Schreyer, H. L., and Chen, Z. (1986). One-dimensional Softening with Localization. J. Appl. Mech. 53 (4), 791–797. doi:10.1115/1.3171860

CrossRef Full Text | Google Scholar

Tanne, E., Li, T., and Bourdin, B. (2017). Crack Nucleation in Variational Phase-Field Models of Brittle Fracture. J. Mech. Phys. Sol. 110, 80–99. doi:10.1016/j.jmps.2017.09.006

Google Scholar

Tong, T., Hua, G., Liu, Z., Liu, X., and Xu, T. (2021). Localizing Gradient Damage Model Coupled to Extended Microprestress-Solidification Theory for Long-Term Nonlinear Time-dependent Behaviors of Concrete Structures. Mech. Mater. 154, 103713. doi:10.1016/j.mechmat.2020.103713

CrossRef Full Text | Google Scholar

Tong, T., Liu, Z., Zhang, J., and Yu, Q. (2016). Long-Term Performance of Prestressed Concrete Bridges Under the Intertwined Effects of concrete Damage, Static Creep and Traffic-Induced Cyclic Creep. Eng. Structures. 127, 510–524. doi:10.1016/j.engstruct.2016.09.004

CrossRef Full Text | Google Scholar

Vandoren, B., and Simone, A. (2018). Modeling and Simulation of Quasi-Brittle Failure With Continuous Anisotropic Stress-Based Gradient-Enhanced Damage Models. Computer Methods Appl. Mech. Eng. 332, 644–685. doi:10.1016/j.cma.2017.12.027

CrossRef Full Text | Google Scholar

Vogler, M., Rolfes, R., and Camanho, P. P. (2013). Modeling the Inelastic Deformation and Fracture of Polymer Composites - Part I: Plasticity Model. Mech. Mater. 59, 50–64. doi:10.1016/j.mechmat.2012.12.002

CrossRef Full Text | Google Scholar

Widder, D. V. (1971). An Introduction to Transform. Cambridge, Massachusetts: Academic Press, Vol. 42

Yu, Q., Bažant, Z. P., and Wendner, R. (2012). Improved Algorithm for Efficient and Realistic Creep Analysis of Large Creep-Sensitive concrete Structures. ACI Struct. J. 109 (5), 665.

CrossRef Full Text | Google Scholar

Nomenclature

${\mathit{D}}^e$: Elastic stiffness tensor (fourth-order)

$\mathit{\sigma }$: Cauchy stress tensor

$\overline{\mathit{\sigma }}$: Effective stress tensor

${\mathit{\epsilon }}_{tot}$: Total strain tensor

${\mathit{\epsilon }}_{el}$: Elastic strain tensor

${\mathit{\epsilon }}_{dam}$: Damage strain tensor

${\mathit{\epsilon }}_v$: Short-term viscoelastic strain tensor

${\mathit{\epsilon }}_{\mathit{f}}$: Long-term viscous creep strain tensor

${\mathit{\epsilon }}_{sh}$: Shrinkage strain tensor

${\mathit{\epsilon }}_T$: Thermal strain tensor

$\mathit{\epsilon }\mathrm{’}$: Elastodamage strain tensor

$\alpha$, $\beta$: Material constants governing the softening behavior

$c$: Gradient parameter

$d$: Scalar damage variable

$D_u$: Distinctive modulus of $u$-th Kelvin unit

${\tau }_u$: Retardation time of $u$-th Kelvin unit

$L\left({\tau }_u\right)$: Continuous spectrum of $u$-th Kelvin unit

${\mathit{\gamma }}_{\mathit{u}}$: State variable of $u$-th Kelvin unit

$N$: Total number of Kelvin units

$C^{\left(k\right)}$: k-th order derivative on time $t$ of the creep compliance function

$\tilde{\epsilon }$: Local scalar equivalent strain

$\overline{\epsilon }$: Nonlocal scalar equivalent strain

$E_0$: Instantaneous elastic modulus without any creep effect

$E_{28}$: 28-day Young’s modulus

$E″$: The effective incremental modulus of concrete at the current time step

$v$: Poisson’s ratio

$t$: Current time in days

$t\prime$: The concrete age in days when the sustained stress is exerted

$t_e$: Equivalent age describing degree of hydration

$t_r$: Reduced time characterizing changes in rate of bond breakages and restoration on microstructural level

$t_s$: Reduced microprestress time

$t_{\mathrm{n}}$: The current time step in FE analysis

$\Delta t$: Time increment in FE analysis

$Q_e$,$Q_r$,$Q_s$: Active energies for hydration, viscous process, and microprestress relaxation

$f{\prime }_c$: Compressive strength

$f_t$: Tensile strength

$J\left(t,t\prime \right)$: Creep compliance function

$J_b\left(t,t\prime \right)$: Basic creep compliance function

$J_d\left(t,t\prime \right)$: Drying creep compliance function

$\eta$: Effective viscosity

$f\left(\tilde{\epsilon },\kappa \right)$: Loading function

$q_1$,$q_2$,$q_3$,$q_4$: Creep coefficient in the B4 model

$R$: Universal gas constant

$S$: Microprestress

$T$: Absolute temperature

$h$: Humidity

${\nabla }^2$: Laplacian operator

${\kappa }_0$: The threshold to initiate the damage

$\kappa$: The maximum $\tilde{\epsilon }$ ever obtained in the previous time

$v\left(t\right)$: Volume growth function with solidification process.