- 1Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, School of Aeronautics and Astronautics, Institute of Applied Mechanics, Zhejiang University, Hangzhou, China
- 2State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace Engineering, Xi’an Jiaotong University, Xi’an, China
In this work, without introducing mass-in-mass units or inertial amplification mechanisms, we show that two Bragg atomic chains can form an acoustic metamaterial that possesses different types of bandgaps other than Bragg ones, including local resonance and inertial amplification-like bandgaps. Specifically, by coupling masses of one monatomic chain to the same masses of a diatomic or triatomic chain, hybrid bandgaps can be generated and further be switched through the adjustment of the structural parameters. To provide a tuning guidance for the hybrid bandgaps, we derived an analytical transition parameter (p-value) for the mass-coupled monatomic/diatomic chain and analytical discriminants for the mass-coupled monatomic/triatomic chain. In our proposed mass-coupled monatomic/triatomic chain system, each set of analytical discriminants determines a hybrid bandgap state and a detailed examination reveals 14 different bandgap states. In addition to bandgap switching, the analytical p-value and discriminants can also be used as a guide for designing the coupled-chain acoustic metamaterials. The relations between the mass-coupled monatomic/triatomic chain system and a three-degree-of-freedom (DOF) inertial amplification system further indicate that the band structure of the former is equivalent to that of the latter through coupling masses by negative dynamic stiffness springs.
Introduction
Being classic textbook models that can explain lattice vibrations in solid state physics, one-dimensional atomic chains can capture the most fundamental properties of phononic crystals (PCs) (Kittel et al., 1996; Hofmann, 2015), which are known for having Bragg bandgaps that can suppress the propagation of mechanical waves (Deymier, 2013; Khelif and Adibi, 2015). Over the past decade, based on PCs that contain the simplest spring-mass systems in a unit cell, some important advances in the domains of nonlinear wave guides (Narisetti et al., 2010; Porubov and Andrianov, 2013; Ganesh and Gonella, 2015; Fang et al., 2016), topological edge states (Pal et al., 2018; Al Ba'ba'a et al., 2019), and diode-like acoustic structures (Vila et al., 2017; Attarzadeh et al., 2018) have been achieved. The atomic chains have also been used to explain nonlocal interactions of the panels of origami metamaterials (Pratapa et al., 2018). Despite being an idealized spring-mass lattice system, the simplest atomic chains can capture the bandgap phenomenon of PCs and to which other bandgap-generation mechanisms can be introduced.
Since the properties of the Bragg bandgaps depend heavily on the lattice constant, it is difficult to achieve low-frequency bandgaps if not increasing the size of the periodic cell. By introducing mass-in-mass units to a monatomic lattice system, acoustic metamaterials exhibiting local resonance (LR) bandgaps independent of the spatial periodicity can be obtained (Huang et al., 2009). Acoustic metamaterials have attracted significant interest due to their unusual mechanical properties such as subwavelength bandgaps, negative effective mass density, or negative effective modulus (Liu et al., 2000; Li and Chan, 2004; Fang et al., 2006; Lazarov and Jensen, 2007; Yao et al., 2008; Huang and Sun, 2010; Huang and Sun, 2012). The concept of infinite mass-in-mass atomic chains have been extended to the design of continuum structures such as elastic metamaterial rods (i.e., through the homogenization method), beams, plates or pillared metamaterial (i.e., surfaces that consist of pillars or branching substructures) in which longitudinal, lateral or flexural vibrations can be suppressed (Yu et al., 2006; Kundu et al., 2014; Zhu et al., 2014; Liu et al., 2015; MuhammadLim, 2019; Jin et al., 2021). Although LR bandgaps are low-frequency ones compared to Bragg bandgaps, several researchers have attempted to further push the bandgaps to lower frequencies without adding extra masses. By introducing internal couplings to mass-in-mass lattices through negative stiffness springs, Hu et al. recently showed that multiple bandgaps and ultra-low resonance bandgaps can be achieved without adding extra masses (Hu et al., 2017; Hu et al., 2019). In addition to mass-in-mass units, inertial amplification mechanisms have also been introduced to mass-spring chains to generate wide and deep low-frequency bandgaps (Yilmaz et al., 2007; Yilmaz and Hulbert, 2010; Taniker and Yilmaz, 2013; Yilmaz et al., 2017). Frandsen et al. investigated an elastic rod with a periodically attached inertial amplification mechanism and found the characteristic double-peak phenomenon in bandgap regions (Frandsen et al., 2016). Through deriving the effective mass of a modified monatomic chain with a lightweight attached mass-link system, Bennetts et al. obtained its low-frequency vibration-isolation properties (Bennetts et al., 2019). Recently, Li and Zhou proposed a periodic mass-spring-truss chain based on a scissor-like structure and inertial amplification to achieve low-frequency vibration attenuation (Li and Zhou, 2021). One interesting question arises: Can we generate local resonance or inertial amplification bandgaps in the band structures of atomic chains without mass-in-mass units or inertial amplification mechanisms?
To solve the above question, we introduce mass coupling to two Bragg atomic chains at certain masses. Specifically, as illustrated in Figure 1A, considering a fundamental configuration of a mass-coupled atomic chain, where a diatomic chain is coupled to a monatomic chain. It is well known that, depending on the existence of certain springs, the mass-coupled atomic chain can be degenerated to a local resonant (LR) acoustic metamaterial with mass-in-mass units (seeFigure 1B) or an alternating mass-spring Bragg system (i.e., also known as phononic crystal) showed in Figure 1C. What we are going to demonstrate is that the local resonance, as well as the inertial amplification-like (IA-like) bandgaps can be opened through adjusting parameters without altering system configuration (i.e., without performing mechanical cutting of certain springs or arranging the inertial amplification mechanisms).
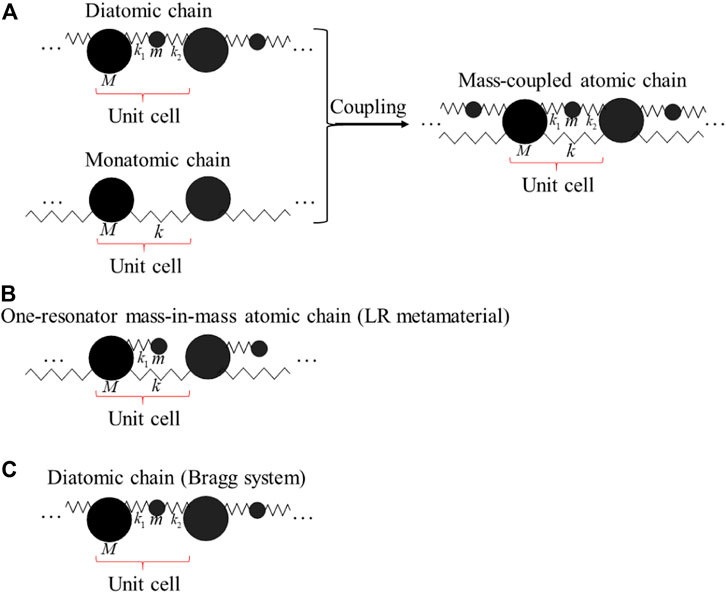
FIGURE 1. (A) The mass-coupled atomic chain coupled by a diatomic chain and a monatomic chain. (B) One-resonator mass-in-mass atomic chain. (C) Diatomic chain.
In this work, we first obtain the governing equations of the mass-coupled atomic chain with n-degree-of-freedom (DOF) by analytical mechanics. Then, the analytical expressions of band structures, anti-resonant frequencies, and edge frequencies of passbands are deduced. In Section 3.1, through discussions about mass-coupled monatomic/diatomic chain, we show that LR bandgaps can be generated simply by performing parametric switching, which is characterized by an inherent transition parameter (p-value). The different bandgap behaviors of mass-coupled monatomic/triatomic chain are classified by different sets of discriminants in Section 3.2. Finally, the relations between the mass-coupled monatomic/triatomic chain system and a 3-DOF inertial amplification system are further discussed in Section 3.3.
Model Descriptions and Transition Conditions of Hybrid Bandgaps
The mass-coupled atomic chain, as illustrated in Figure 1A, can be generalized as a model shown in Figure 2A, where a polyatomic chain is coupled to a monatomic chain. There are arbitrary
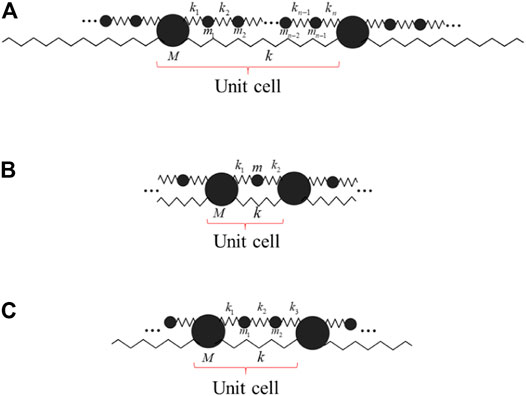
FIGURE 2. (A) The mass-coupled atomic chain with
The band structures of this infinite mass-coupled atomic chain can be deduced as follows. First, we list all expressions about kinetic and potential energies related to the displacements:
And
According to the Lagrange equation for conservative systems, i.e.,
Where
Then the band structures can be obtained by solving the following eigenvalue problem according to Bloch theorem (Huang et al., 2009; Hu et al., 2017; Hu et al., 2019):
Where
The coefficient polynomial of Eq. 7 can be expressed as
Where
And the analytical formulas of
It is worth noting that in band structures any single curve of passbands is continuous when
There is a LR bandgap around a root if the root of Eq. 11 is between the adjacent two solutions of
Based on the above inference, by comparing distributions of solutions corresponding to Eqs 11, 12, we can derive an analytical parameter (p-value) or analytical discriminants describing the transition conditions between the LR bandgaps and Bragg bandgaps. The bandgap transition p-value will be defined and its analytical expression will be given in the next section (Section 3.1). The discriminants for a monatomic/triatomic chain will also be given in the next section (Section 3.2).
Results and Discussion
P-value in Mass-coupled Monatomic/Diatomic Chain
Let’s first discuss the simplest 2-DOF case where a monatomic chain is coupled to a diatomic chain as illustrated in Figure 2B. According to theories in Section 2 and Eq. (A3) in Appendix A, the transition condition from the LR bandgap to Bragg bandgap can be written as
i.e.,
Where
The expression of
Where
In classical acoustic metamaterials with local resonators, as shown in Figure 1B, the value of
Figure 3 shows the transition process from LR bandgap to Bragg bandgap with respect to the change of p-value. If
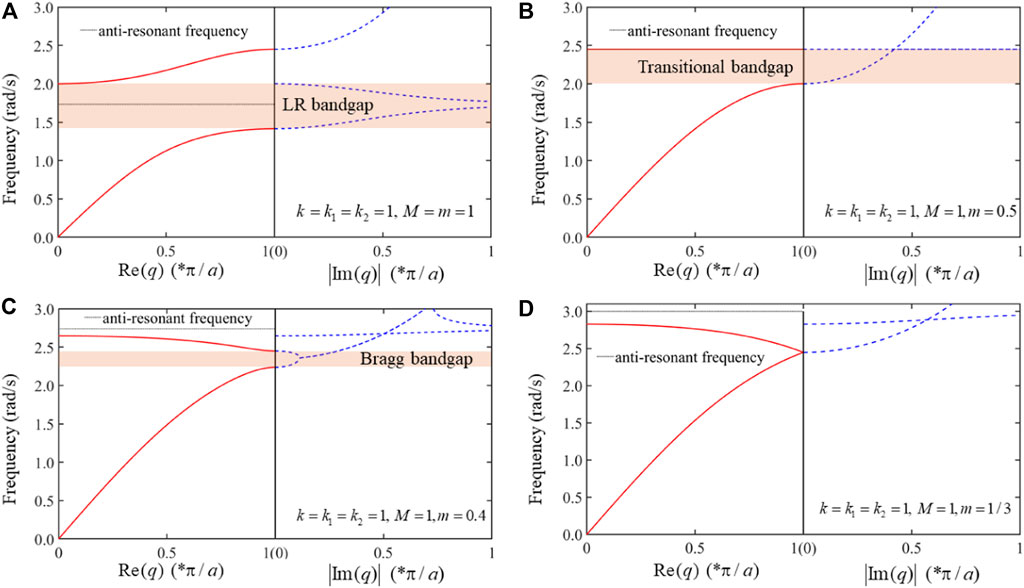
FIGURE 3. Band structures of the mass-coupled monatomic/diatomic chain (2-DOF). (A) The anti-resonant frequency is between the adjacent frequencies at
In addition, when there is a LR bandgap, the ratio of the width of bandgap region to the maximum frequency of passbands in band structure can be calculated by
But for Bragg bandgap, the ratio becomes
Noting that Eq. 17 or Eq. 18 can be expressed by three independent variables,
So Eqs 17, 18 can be rewritten as
The discriminant of Eq. 16 turns to
Hence the bandgap transition condition is separated by a hyperbolic paraboloid. The isosurfaces of ratios for LR bandgap and Bragg bandgap are plotted in Figure 4 respectively. One can construct a wide bandgap at low frequency through changing the material parameters according to the isosurfaces.
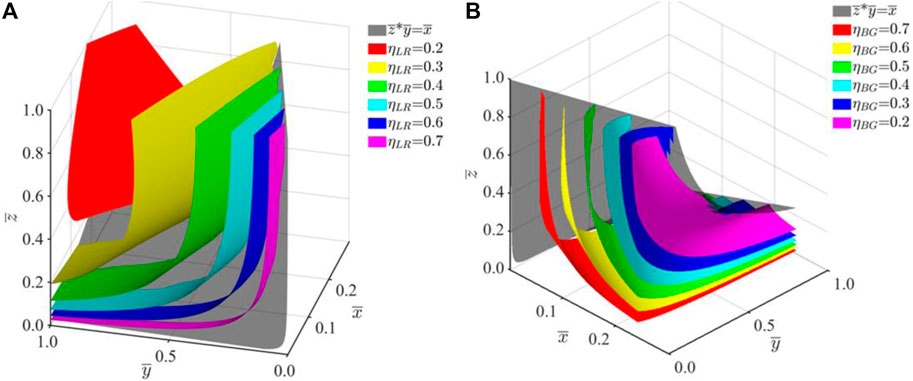
FIGURE 4. Isosurfaces of the ratios of the width of bandgap region to the maximum frequency of passbands for (A) LR bandgap, and (B) Bragg bandgap.
Bandgap States of Mass-coupled Monatomic/triatomic Chain Classified by Discriminants
In this section, we study the 3-DOF mass-coupled monatomic/triatomic chain as shown in Figure 2C. Here the transition parameter p-value will turn to several sets of discriminants determining the transition conditions between LR bandgaps and Bragg bandgaps. We note that as the number of degrees of freedom further increases, the complexity of the problem sharply arises despite the number of material parameters only increase by two compared to the 2-DOF system.
According to Eqs 9, 11, 12 and Eq. (A4), the equations about nonzero edge frequencies of passbands can be obtained,
And anti-resonant frequencies can be acquired by
The distribution of solutions of these equations are discussed in detail in Appendix B. There are total 14 different bandgap behaviors, referred to as bandgap states, in our mass-coupled monatomic/triatomic chain according to Eq. (B16). For the sake of convenience, we use “L,” “B,” and “P” to represent the normal LR bandgap, the Bragg bandgap, and the passband, respectively. When the values of anti-resonant frequencies solved by Eq. 24 are conjugate imaginary numbers (i.e., anti-resonant frequencies don’t actually exist), there are four different states as shown in Figure 5. The states from (a) to (d) correspond to sets of discriminants from (1) to (4) in Eq. (B16), respectively. Obviously, there are no LR bandgaps due to non-existence of anti-resonant frequencies.
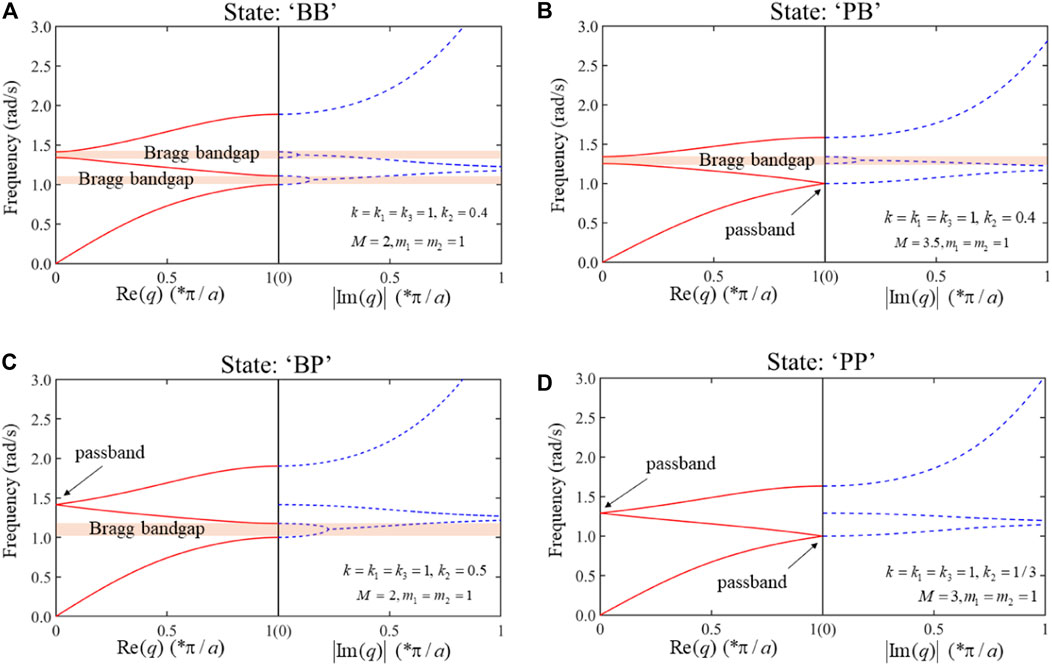
FIGURE 5. Different bandgap states when anti-resonant frequencies are absent in the mass-coupled monatomic/triatomic chain system. (A) State “BB”: the first and second bandgaps are Bragg bandgaps. (B) State “PB”: the first Bragg bandgap closes. (C) State “BP”: the second Bragg bandgap closes. (D) State “PP”: both first and second bandgaps disappear.
Figure 6 shows five bandgap states, corresponding to sets of discriminants from (5) to (9) in Eq. (B16), where there is only one anti-resonant frequency. In Figure 6A, the anti-resonant frequency lies between edge frequencies of passbands, which leads to the formation of LR bandgap. The second bandgap can turn into LR bandgap with tuning of parameters as shown in Figures 6C,D. A widened LR bandgap is generated in Figure 6E due to coincidence of the anti-resonant frequency line and a dispersion curve.
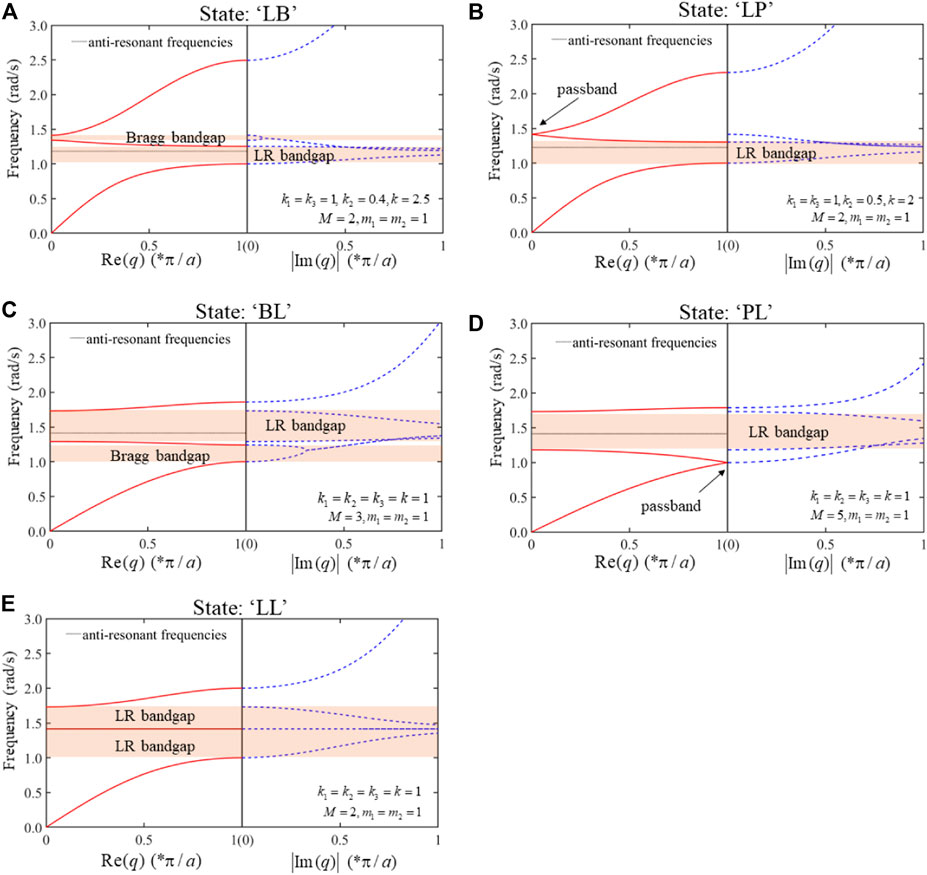
FIGURE 6. Different bandgap states when there is only one anti-resonant frequency in the mass-coupled monatomic/triatomic chain system. (A) State “LB”: the first bandgap is LR bandgap and second one is Bragg bandgap. (B) State “LP”: the second Bragg bandgap disappears. (C) State “BL”: the first bandgap is Bragg bandgap and second one is LR bandgap. (D) State “PL”: the first Bragg bandgap has vanished and only the LR bandgap is left. (E) State “LL”: the anti-resonant frequency line coincides with a curve of passband, which generates an enlarged LR bandgap.
When there are two anti-resonant frequencies, other five bandgap states arise as shown in Figure 7, corresponding to sets of discriminants from (10) to (14) in Eq. (B16). A LR bandgap with double anti-resonant peaks is observed in Figures 7A–D. In order to distinguish the LR bandgap with double anti-resonant peaks from the normal LR bandgap, which is labeled as “L,” the former is represented by the symbol “
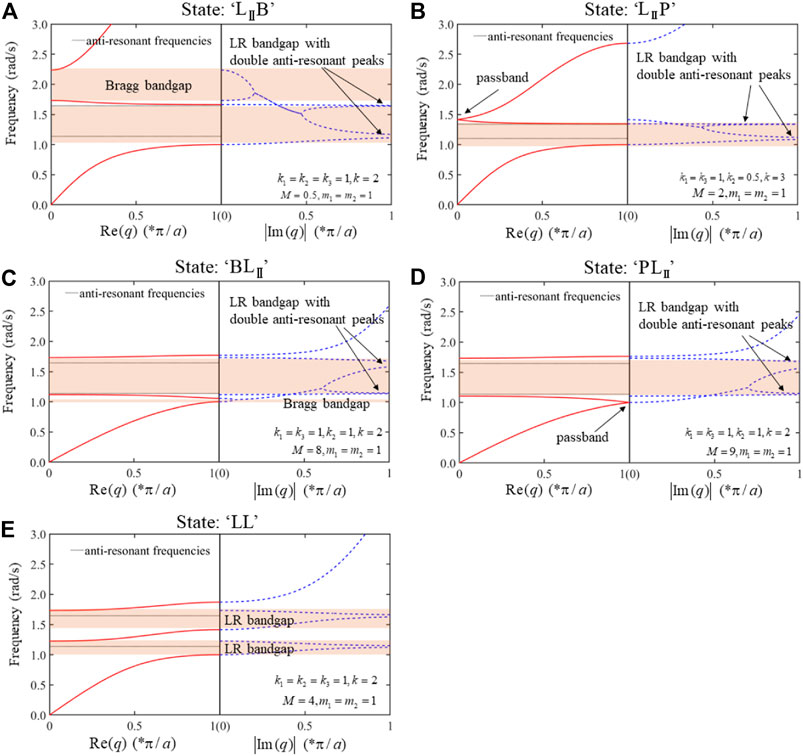
FIGURE 7. Different bandgap states when there are two anti-resonant frequencies in the mass-coupled monatomic/triatomic chain system. (A) State “
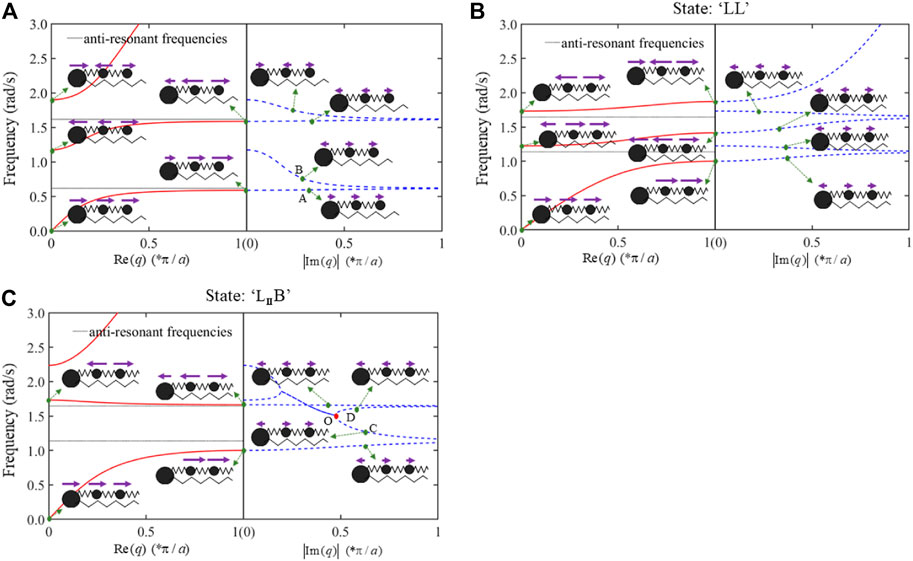
FIGURE 8. Vibration modes of a unit cell at certain points in band structures for the (A) LR acoustic metamaterial with two resonators in series (
In addition, the weak coupling phenomenon, known as veering that occurs when branches of the dispersion curves interact in coupled periodic waveguide system, is also observed in band structures in Figure 9 (Mace and Manconi, 2012). As shown in Figure 9, two dispersion curves ab and cd come close together as frequency increases then the curves veer apart, which results in an extremely narrow LR bandgap.
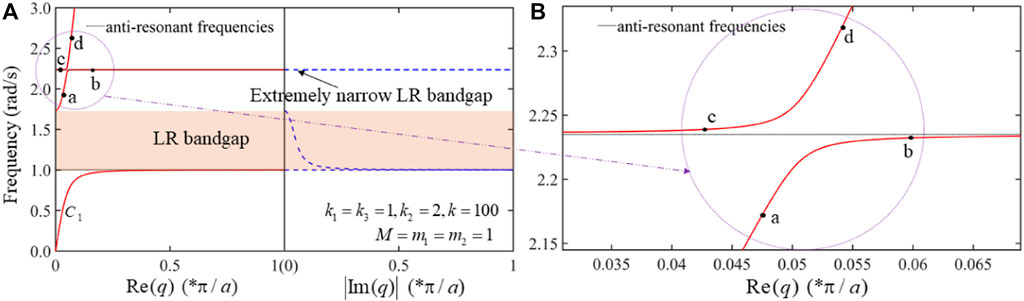
FIGURE 9. State “LL”: (A) the dispersion curves ab and cd veer apart in dotted circle region. (B) Enlarged view of the veering region.
Relations Between the Mass-coupled Monatomic/triatomic Chain and Inertial Amplification System
In the previous section, we find that under certain parameters there is a double anti-resonant peak in the LR bandgap region of the mass-coupled monatomic/triatomic chain, which is also a representative characteristic of the bandgap behaviors possessed in a periodic structure with inertial amplification mechanisms (Frandsen et al., 2016). Next, we will show that IA-like bandgaps can exist in band structures of mass-coupled monatomic/triatomic chain.
As shown in Figure 10B, in a classical 3-DOF inertial amplification system (Yilmaz et al., 2017), an added mass
Which can be rewritten as
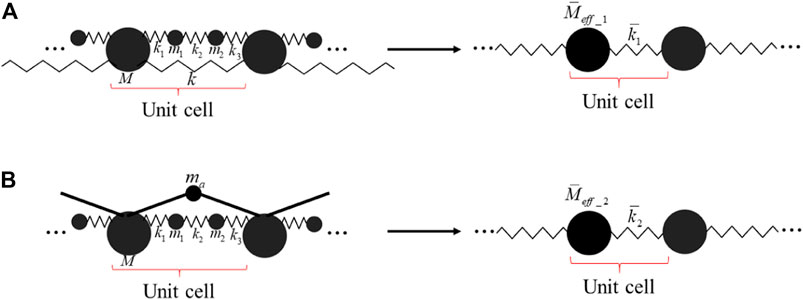
FIGURE 10. Schematic diagrams of the effective monatomic chains for (A) the mass-coupled monatomic/triatomic chain (3-DOF), and (B) the inertial amplification system of 3-DOF.
The mass-coupled atomic chain and the inertial amplification system can be simplified as effective monatomic chains. The effective stiffness and mass for the mass-coupled atomic chain are listed as
And
For the inertial amplification system. The dimensionless dynamic effective masses are
Besides double anti-resonant peaks, the mass-coupled atomic chain can also offer high attenuation in the bandgap regions and similar width of bandgaps compared to the inertial amplification system by adjusting material parameters (seeFigure 11A). As shown in Figures 11A,B, a wide bandgap in low frequency can also be opened in mass-coupled atomic chain.
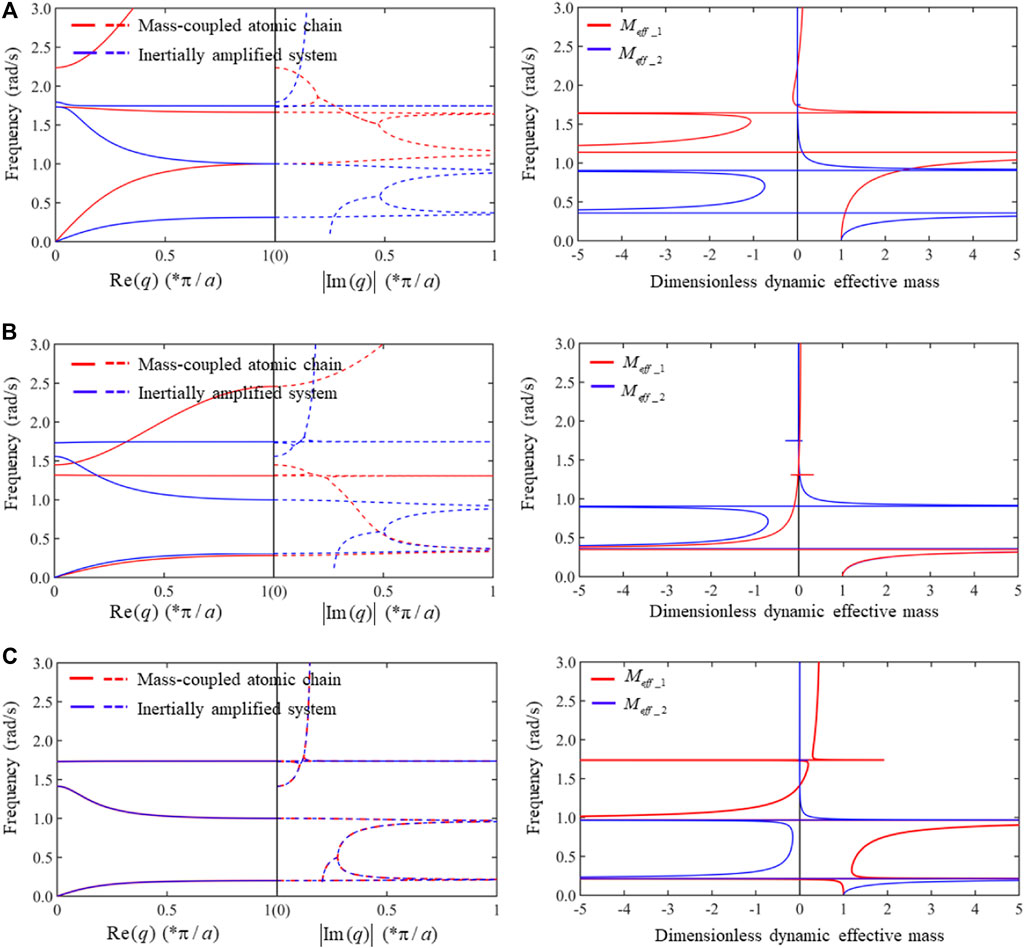
FIGURE 11. Band structures of the mass-coupled monatomic/triatomic chains and inertial amplification systems of 3-DOF and their corresponding dimensionless dynamic effective masses. The parameters are listed as follows: (A)
In fact, the band structures of the mass-coupled atomic chain can be exactly the same as that of an inertial amplification system through introducing a negative dynamic stiffness
As seen in Figure 11C, the band structures are identical for these two atomic chains. The effective dynamic masses are not exactly the same because the effective stiffnesses are different when these two systems are simplified to monatomic chains according to Eqs 27, 28. Thus far, we have shown that IA-like bandgaps can exist in band structures of mass-coupled monatomic/triatomic chain.
Conclusion
In this work, we propose an acoustic metamaterial formed by two coupled Bragg atomic chains that can possess various bandgap behaviors through the adjustment of parameters. The transition condition between LR bandgaps and Bragg bandgaps in the mass-coupled monatomic/diatomic chain can be characterized by an analytical transition parameter, referred to as p-value. If
The transition p-value turns to several sets of discriminants when considering bandgap states for mass-coupled monatomic/triatomic chain due to the increase of the degrees of freedom. After careful classification, we find that there are 14 different sets of discriminants, which correspond to 14 possible bandgap states. In addition, the weak coupling phenomenon termed veering which occurs in coupled periodic elastic systems is observed in the band structures. The veering phenomenon can be used to construct an extremely narrow LR bandgap. IA-like bandgaps can be opened by adjusting parameters without requirement of changing structural topological properties. Moreover, through coupling masses by a negative dynamic stiffness spring, the band structure of mass-coupled monatomic/triatomic chain system is equivalent to that of the 3-DOF inertial-amplification periodic system.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SX and K-CC conceived and designed the main ideas together; SX, ZX, and K-CC performed theoretical analysis; SX and K-CC wrote the paper draft. All authors conducted subsequent improvements to the manuscript.
Funding
Financial support from the National Natural Science Foundation of China (No. 11972318) and the Opening Project of State Key Laboratory for Strength and Vibration of Mechanical Structures (No. SV2020-KF-16), Xi’an Jiaotong University is gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al Ba'ba'a, H., Nouh, M., and Singh, T. (2019). Dispersion and Topological Characteristics of Permutative Polyatomic Phononic Crystals. Proc. R. Soc. A: Math. Phys. Eng. Sci. 475 2226. doi:10.1098/rspa.2019.0022
Attarzadeh, M. A., Al Ba’ba’a, H., and Nouh, M. (2018). On the Wave Dispersion and Non-reciprocal Power Flow in Space-Time Traveling Acoustic Metamaterials. Appl. Acoust. 133, 210–214. doi:10.1016/j.apacoust.2017.12.028
Bennetts, L. G., Peter, M. A., Dylejko, P., and Skvortsov, A. (2019). Effective Properties of Acoustic Metamaterial Chains with Low-Frequency Bandgaps Controlled by the Geometry of Lightweight Mass-Link Attachments. J. Sound Vibration 456, 1–12. doi:10.1016/j.jsv.2019.05.022
Deymier, P. A. (2013). Acoustic Metamaterials and Phononic Crystals. Berlin: Springer Science and Business Media.
Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C., et al. (2006). Ultrasonic Metamaterials with Negative Modulus. Nat. Mater 5 (6), 452–456. doi:10.1038/nmat1644
Fang, X., Wen, J., Yin, J., and Yu, D. (2016). Wave Propagation in Nonlinear Metamaterial Multi-Atomic Chains Based on Homotopy Method. AIP Adv. 6 (12),121706. doi:10.1063/1.4971761
Frandsen, N. M. M., Bilal, O. R., Jensen, J. S., and Hussein, M. I. (2016). Inertial Amplification of Continuous Structures: Large Band Gaps from Small Masses. J. Appl. Phys. 119 (12), 124902. doi:10.1063/1.4944429
Ganesh, R., and Gonella, S. (2015). From Modal Mixing to Tunable Functional Switches in Nonlinear Phononic Crystals. Phys. Rev. Lett. 114 (5), 054302. doi:10.1103/PhysRevLett.114.054302
Hu, G., Tang, L., Das, R., Gao, S., and Liu, H. (2017). Acoustic Metamaterials with Coupled Local Resonators for Broadband Vibration Suppression. AIP Adv. 7, 2. doi:10.1063/1.4977559
Hu, G., Tang, L., Xu, J., Lan, C., and Das, R. (2019). Metamaterial with Local Resonators Coupled by Negative Stiffness Springs for Enhanced Vibration Suppression. J. Appl. Mech. 86, 8. doi:10.1115/1.4043827
Huang, G. L., and Sun, C. T. (2010). Band Gaps in a Multiresonator Acoustic Metamaterial. J. Vibration Acoust. 132, 3. doi:10.1115/1.4000784
Huang, H. H., and Sun, C. T. (2012). Anomalous Wave Propagation in a One-Dimensional Acoustic Metamaterial Having Simultaneously Negative Mass Density and Young's Modulus. The J. Acoust. Soc. America 132 (4), 2887–2895. doi:10.1121/1.4744977
Huang, H. H., Sun, C. T., and Huang, G. L. (2009). On the Negative Effective Mass Density in Acoustic Metamaterials. Int. J. Eng. Sci. 47 (4), 610–617. doi:10.1016/j.ijengsci.2008.12.007
Jin, Y., Pennec, Y., Bonello, B., Honarvar, H., Dobrzynski, L., Djafari-Rouhani, B., et al. (2021). Physics of Surface Vibrational Resonances: Pillared Phononic Crystals, Metamaterials, and Metasurfaces. Rep. Prog. Phys. 84, 8. doi:10.1088/1361-6633/abdab8
Kittel, C., McEuen, P., and McEuen, P. (1996). Introduction to Solid State Physics. New York, NY: Wiley.
Kundu, T., Nouh, M., Aldraihem, O., and Baz, A. (2014). Metamaterial Structures with Periodic Local Resonances. San Diego, CA: Health Monitoring of Structural and Biological Systems.
Lazarov, B. S., and Jensen, J. S. (2007). Low-frequency Band Gaps in Chains with Attached Non-linear Oscillators. Int. J. Non-Linear Mech. 42 (10), 1186–1193. doi:10.1016/j.ijnonlinmec.2007.09.007
Li, J., and Chan, C. T. (2004). Double-negative Acoustic Metamaterial. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 70 (5 Pt 2), 055602. doi:10.1103/PhysRevE.70.055602
Li, Y., and Zhou, W. (2021). Bandgap and Vibration Transfer Characteristics of Scissor-like Periodic Metamaterials. J. Appl. Phys. 130 (2). doi:10.1063/5.0047119
Liu, Y., Su, X., and Sun, C. T. (2015). Broadband Elastic Metamaterial with Single Negativity by Mimicking Lattice Systems. J. Mech. Phys. Sol. 74, 158–174. doi:10.1016/j.jmps.2014.09.011
Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289 (5485), 1734–1736. doi:10.1126/science.289.5485.1734
Mace, B. R., and Manconi, E. (2012). Wave Motion and Dispersion Phenomena: Veering, Locking and strong Coupling Effects. J. Acoust. Soc. America 131 (2), 1015–1028. doi:10.1121/1.3672647
Muhammad, , and Lim, C. W. (2019). Elastic Waves Propagation in Thin Plate Metamaterials and Evidence of Low Frequency Pseudo and Local Resonance Bandgaps. Phys. Lett. A 383 (23), 2789–2796. doi:10.1016/j.physleta.2019.05.039
Narisetti, R. K., Leamy, M. J., and Ruzzene, M. (2010). A Perturbation Approach for Predicting Wave Propagation in One-Dimensional Nonlinear Periodic Structures. J. Vibration Acoust. 132 (3). doi:10.1115/1.4000775
Pal, R. K., Vila, J., Leamy, M., and Ruzzene, M. (2018). Amplitude-dependent Topological Edge States in Nonlinear Phononic Lattices. Phys. Rev. E 97 (3-1), 032209. doi:10.1103/PhysRevE.97.032209
Porubov, A. V., and Andrianov, I. V. (2013). Nonlinear Waves in Diatomic Crystals. Wave Motion 50 (7), 1153–1160. doi:10.1016/j.wavemoti.2013.03.009
Pratapa, P. P., Suryanarayana, P., and Paulino, G. H. (2018). Bloch Wave Framework for Structures with Nonlocal Interactions: Application to the Design of Origami Acoustic Metamaterials. J. Mech. Phys. Sol. 118, 115–132. doi:10.1016/j.jmps.2018.05.012
Taniker, S., and Yilmaz, C. (2013). Phononic Gaps Induced by Inertial Amplification in BCC and FCC Lattices. Phys. Lett. A 377 (31-33), 1930–1936. doi:10.1016/j.physleta.2013.05.022
Vila, J., Pal, R. K., Ruzzene, M., and Trainiti, G. (2017). A Bloch-Based Procedure for Dispersion Analysis of Lattices with Periodic Time-Varying Properties. J. Sound Vibration 406, 363–377. doi:10.1016/j.jsv.2017.06.011
Yao, S., Zhou, X., and Hu, G. (2008). Experimental Study on Negative Effective Mass in a 1D Mass–spring System. New J. Phys. 10, 4. doi:10.1088/1367-2630/10/4/043020
Yilmaz, C., and Hulbert, G. M. (2017). “Dynamics of Locally Resonant and Inertially Amplified Lattice Materials,” in Dynamics of Lattice Materials. Editors A. S. Phani, and M. I. Hussein, 233–258. doi:10.1002/9781118729588.ch11
Yilmaz, C., Hulbert, G. M., and Kikuchi, N. (2007). Phononic Band Gaps Induced by Inertial Amplification in Periodic media. Phys. Rev. B 76, 5. doi:10.1103/physrevb.76.054309
Yilmaz, C., and Hulbert, G. M. (2010). Theory of Phononic Gaps Induced by Inertial Amplification in Finite Structures. Phys. Lett. A 374 (34), 3576–3584. doi:10.1016/j.physleta.2010.07.001
Yu, D., Liu, Y., Wang, G., Zhao, H., and Qiu, J. (2006). Flexural Vibration Band Gaps in Timoshenko Beams with Locally Resonant Structures. J. Appl. Phys. 100, 12. doi:10.1063/1.2400803
Zhu, R., Liu, X. N., Hu, G. K., Sun, C. T., and Huang, G. L. (2014). A Chiral Elastic Metamaterial Beam for Broadband Vibration Suppression. J. Sound Vibration 333 (10), 2759–2773. doi:10.1016/j.jsv.2014.01.009
Zucker, I. J. (2016). 92.34 The Cubic Equation - A New Look at the Irreducible Case. Math. Gaz. 92 (524), 264–268. doi:10.1017/s0025557200183135
Appendix A
(Note: All material parameters discussed in Appendix A and B are positive by default.)
The analytical formulas of
where
noting that value range of
Some concrete expressions are as follows:
When
when
Appendix B
We will solve Eq. 22 as well as Eq. 24 and make a thorough classified discussion to obtain the discriminants about bandgap transitions.
The criterion on existence of solutions of Eq. 22 is:
and for Eq. 24 it becomes
First, we will confirm that Eq. (B1) is always greater than or equal to zero, i.e.,
The Eq. (B1) can be written as function of
then the criterion on roots of this quadratic function is
Therefore, Eq. (B3) has been proven to be correct for all situations.
Next, we will discuss the following six situations:
The equivalent formulas below can be derived:
and
Solutions of Eq. 22 can be expressed as
and those of Eq. 24 are
For every situation in Eq. (B6), the classified discussions are carried forward by comparing the distribution between solutions of Eq. 22 and that of Eq. 24. Several sets of discriminants, which are used to distinguish different bandgap behaviors, of all possible results of discussions are listed below,
where
The above results have not included the influence of frequencies of passbands at another edge (i.e.,
where
Adopting similar approaches on proving Eq. (B3), one can ascertain the following inequalities
are true for any material parameters. It means that Eq. (B13) has three distinct real roots or has a double real root as well as a single real root. The Bragg bandgaps at
The final sets of discriminants are as follows after above discussion:
where each set of discriminants corresponds to a bandgap behavior in the mass-coupled monatomic/triatomic chain system.
Keywords: metamaterials, atomic chains, bandgaps, local resonance, inertial amplification, phononic crystal
Citation: Xu S-F, Xu Z-L and Chuang K-C (2021) Hybrid Bandgaps in Mass-coupled Bragg Atomic Chains: Generation and Switching. Front. Mater. 8:774612. doi: 10.3389/fmats.2021.774612
Received: 12 September 2021; Accepted: 27 September 2021;
Published: 30 November 2021.
Edited by:
Yan-Feng Wang, Tianjin University, ChinaCopyright © 2021 Xu, Xu and Chuang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kuo-Chih Chuang, Y2h1YW5na2NAemp1LmVkdS5jbg==
 Shao-Feng Xu
Shao-Feng Xu Zhu-Long Xu
Zhu-Long Xu Kuo-Chih Chuang
Kuo-Chih Chuang