- School of Mechanical, Electrical and Information Engineering, Shandong University, Weihai, China
The local structures of U-Co melts have been studied by first-principle calculations. Two sub-peaks are observed in the first peaks of U-U pair distribution functions. The Voronoi polyhedral analyses also show two separate core-shell U-U distances. Therefore, the calculated results propose that U atoms will play dual roles, “chemical” and “topological”, in the local structures of U-Co melts. In addition, the chemical effect of U atoms will be strengthened when containing more U atoms. The interaction of Co and U atoms is slightly affected by the compositions. The Co-centered clusters are mostly prism-like or antiprism-like polyhedral, which can be predicted by the solute-solvent model. The distribution of the coordinated numbers of Co atoms is much narrower than that of U atoms, showing relatively stable Co-centered clusters. The chemical and topological roles of U atoms are intuitively observed in the electron density of U-Co melts, which presents both metallic and covalent bonding characteristics for U-U bonds. In the end, we conclude that the partial localization of U 5f-electron is responsible for the dual roles of U atoms. The present results provide a theoretical understanding of the origin of the local structures of U-Co melts.
Introduction
Uranium-based materials have been used in energy power, aerospace, biomedical instrument, and military weapons due to their high hardness and radioactivity. However, the corrosion resistance and process ability of the pure U metals are poor to limit their applications. Alloying is one of the effective methods to improve the properties of U metals. For example, U-Mo alloys firstly studied by Argonne National Laboratory present a good radiation resistance (Wiencek and Prokofiev, 2000; Hofman et al., 2003). Small amounts of Ti can improve the mechanical properties and the corrosion resistance of U-Ti alloys, which are considered as substitutes for W alloys (Zurek, 1994; Zurek, 1999; Shi et al., 2015; Li et al., 2020). U-Nb alloys with moderate Nb contents keep a high density compared to the pure U metals and show a good corrosion resistance (Manner et al., 1999; Orlov, 2002). Furthermore, Huang et. al. exploited U-Co-Al and U-Co-B metallic glasses (MGs) by melt-spin quenching method, in which the corrosion resistance is better than that in crystal alloys (Huang et al., 2016; Xu et al., 2018). The better performance can be contributed to homogeneity and no grain boundaries of the amorphous alloys.
However, the glass-forming ability (GFA) of U-based alloys is poor and the design of alloy compositions is still confusing. U-M (M = Co, Fe, Ni, Cr) MGs were prepared by Hammer-and-Anvil technique (HA) (Giessen and Elliott, 1978; Elliott et al., 1980; Elliott et al., 1981; Elliott and Giessen, 1982) and melt-spinning technique (MS) (Drehman, 1985; Drehman and Poon, 1985; Poon et al., 1985), which are mostly amorphous ribbons rather than bulk MGs. Elliott et. al. prepared U-Fe MGs by liquid quenching and irradiation techniques, but there were some crystal phases in materials (Elliott et al., 1980). Previously, Dreham’s work noted that the U-Co alloy’s composition with the best GAF was U72Co48 based on the differential scanning calorimeter analysis (Drehman and Poon, 1985; Poon et al., 1985). Huang et. al. noted that the amorphous phase was most readily formed in the vicinity of U66.7Co33.3 composition (Huang et al., 2020). It is well known that the GFA of alloys is related to the structural properties of melts because most MGs are prepared by supercooling melts. Therefore, the understanding of local structures of U-based melts is in favor of designing alloy composition to get better U-based MGs. Theoretical researches have been used to analyze the local structures of U-based alloy or MGs. Xiang et. al. calculated the occupied positions of Nb in γ-U crystal, which related the structural stability to the charges distribution (Xiang et al., 2008). Recently, Zhang et. al. have studied the atomic structure of U-Fe MGs based on reverse Monte Carlo simulations (Zhang et al., 2012). The work revealed the topological and chemical local structures of U-centered and Fe-centered clusters, and noted the structural complexity of these MGs. However, the relevant studies of local structures of U-based melts are still scarce, and there is an urgent need for theoretical work.
In the present work, the local structures of U-Co melts (U50Co50, U67Co33, and U86Co14) are studied by first-principle dynamics calculations. Several structural indicators, such as pair distribution function, Voronoi polyhedra, and coordination number, are used to correlate the structural characteristics with melt compositions. At last, we try to reveal the origin of the special structures in the U-Co melts by studying the atomic bonding characteristic. The present work will provide a theoretical view to understand the local structures of U-Co melts.
Materials and Methods
The first-principle dynamics calculations were performed by Vienna Ab-initio Simulation Package (VASP) (Kresse and Furthmüller, 1996). The projector augmented wave method (PAW) was used to treat the core electrons (Blöchl, 1994; Kresse and Joubert, 1999). The valence electronic configurations of U and Co atoms were 5f36s26p66d17s2 and 3s84p1, respectively. The exchange and correlation interactions were dealt with the GGA-PBE functional (Perdew et al., 1996). The plane wave cut-off energy was 350 eV. Cubic supercells containing 200 atoms with periodic boundary conditions were constructed by a random distribution of U and Co atoms, which were used to act as the original structures for the subsequent dynamic process. The densities of the cubic supercells are determined by Drehman’s experiment (Drehman and Poon, 1985), which are 14.66, 16.27, and 17.49 g/cm3 for U50Co50, U67Co33, and U86Co14. Then the densities of the different U-Co systems were adjusted by the zero external pressure method. Only the Γ point was used to sample the supercell Brillouin zone. The canonical ensemble (NVT) was used to perform the dynamic calculations. The temperature was controlled through a Nosé thermostat (Nosé, 1984). To achieve liquid U-Co systems, the supercells were firstly well equilibrated for 45 ps with 3 fs time step at 2000K. Then the temperature of the systems was reduced to 1,500, 1,200, and 1500 K for U50Co50, U67Co33, and U86Co14, which are about 200 K higher than the melting points based on the U-Co phase diagram (Massalski et al., 1990). At the temperature, the structures were also equilibrated for 45 ps with the time step of 3 fs, and the last 5,000 dynamic configurations were employed to analyze the structural characteristic.
Results
Pair Distribution Function
The structures of U-Co melts are described by the total and partial pair distribution function (PDF). As shown in Figure 1, the PDFs, gTotal(r), gU-U(r), gU-Co(r), and gCo-Co(r), show a liquid structural characteristic. Generally, the first peaks of PDFs correspond to the short-range orders (SROs). It can be seen from Figure 1A that the positions of the first peaks of the total PDFs are at about 2.63, 2.66, and 2.73 Å for U50Co50, U67Co33, and U86Co14, respectively. The right-shifts of the peaks are also observed for the second peaks at about 4.92, 5.07, and 5.19 Å for U50Co50, U67Co33, and U86Co14 melts, respectively. This is in agreement with the larger atomic radii of about 1.56 Å of U atoms than 1.25 Å of Co atoms (Porterfield, 1984; Kaye and Laby, 1993), which may present larger and more open short-range configurations. Importantly, with increasing U concentrations, the heights of the first peaks become smaller, while the shoulder peaks at about 3.1–3.2 Å are more significant. The phenomenon implies the complexity of the SROs of U-Co melts.
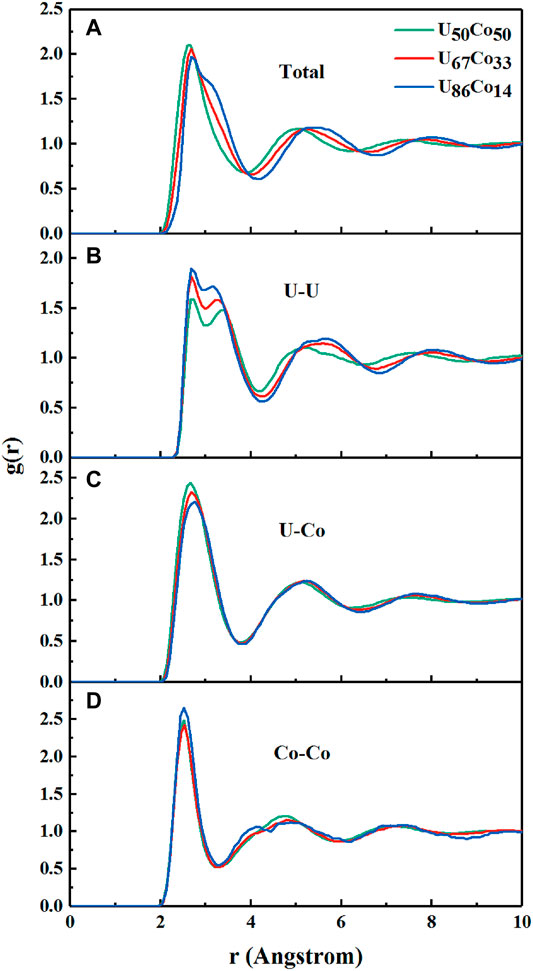
FIGURE 1. The pair distribution functions of (A) Total, (B) U-U, (C) U-Co, and (D) Co-Co for U50Co50, U67Co33, and U86Co14 melts.
As shown in Figure 1B, the first peaks of the three U-U PDFs are splitting into two sub-peaks. Hereinto, the positions of the first sub-peaks (U-U)1 are hardly affected by the compositions, which are all localized at about 2.74 Å. The value is much smaller than 3.12 Å used in the hard spheres model, while it is close to the U-U bond length of about 2.77 Å measured by Bowen (Bowen and Sutton, 1958). The second sub-peaks (U-U)2 are at about 3.21, 3.13, and 3.08 Å for U50Co50, U67Co33, and U86Co14 melts, respectively. These positions are close to the results of the hard spheres model and are in agreement with the shoulder peaks of the total PDFs. Therefore, we conclude that the splitting of the first peaks originates from the double-shell U-centered clusters with separate U-U bond lengths. The splitting peaks are also observed in the liquid uranium (del Rio et al., 2020) and the Ce-Ce peaks of the high-density Ce-Al alloy (Sheng et al., 2007), and are similar to the asymmetric shape of the peak in Cu-Zr alloy (Ding et al., 2014). It should be emphasized that the (U-U)1 distance of 2.74 Å is even shorter than the U-U bond lengths (2.8–3.2 Å) in U/Co metals and intermetallic compounds (Baenziger et al., 1950). Namely, some U atoms show a strong chemical effect. Therefore, in U-Co melts, the U atoms play two roles: one is the “chemical sphere” while another is the “topological sphere”, which will markedly influence the SROs of U-Co melts. The chemical effect is also observed between U and Co atoms. As shown in Figure 1C, the positions of the first peaks of U-Co PDFs are at about 2.64–2.76 Å, which are smaller than 2.81 Å based on the hard spheres model and 2.78–2.90 Å in U/Co intermetallic compounds (Baenziger et al., 1950). Therefore, the effect of Co atoms in the U-Co melts is similar to the Fe atoms in U-Fe alloy, which play a certain chemical role (Zhang et al., 2012). However, the positions of the first peaks of Co-Co PDFs are fixed at about 2.50 Å as shown in Figure 1D, which are equal to the result of the hard spheres model. The results suggest that both the chemical and the topological factors play an important role in the SROs of U-Co melts.
Voronoi Polyhedra
The Voronoi polyhedral analyses are employed to further illuminate the topological characteritics of the SROs in different melts. As shown in Figure 2, only the polyhedra with more than 2% distributions are listed with different Voronoi indexs. Figure 2A gives the total distributions, where the top five polyhedra are <0,2,8,1>, <0,3,6,1>, <0,4,4,3>, <0,3,6,2>, and <0,3,6,4> for U50Co50, <0,3,6,4>, <0,2,8,1>, <0,3,6,3>, <0,3,6,1>, and <0,2,8,2> for U67Co33, and <0,3,6,4>, <0,3,6,3>, <0,2,8,2>, <0,2,8,1>, and <0,2,8,4> for U86Co14, respectively. With increasing U atoms, the quantities of large clusters such as <0,2,8,2>, <0,4,4,4>, <0,3,6,3>, <0,3,6,4>, <0,1,10,2>, <0,2,8,4> increase, while the quantities of small clusters such as <0,3,6,1>, <0,4,4,2>, <0,2,8,0>, <0,2,8,1>, <0,4,4,3>, <0,3,6,2> decrease. The result is agreement with the larger U atomic radius. As shown in Figures 2B,C, for all melts, the ideal “icosahedral ordering” <0,0,12,0> in both U- and Co-centered polyhedra are much less than 1%, which influence to the SROs is slight. In the U-centered polyhedra, the icosahedra-like clusters such as Voronoi indexs <0,3,6,4>, <0,1,10,2>, <0,3,6,3>, <0,2,8,3>, <0,2,8,2>, <0,4,4,5>, <0,4,4,4>, <0,2,8,1>, and <0,4,4,3> observably increase for the higher U concentrations. Conversely, the Frank-Kasper polyhedra such as <0,2,8,4>, <0,3,6,5>, <0,4,5,4,1>, <0,3,7,4,1>, <0,2,8,5>, and <0,3,6,6> decrease for the higher U concentrations. The Co-centered <0,2,8,1> polyhedra are canonical Kasper polyhedra, which also can be classified as defected icosahedra-like clusters. The polyhedra with indexs <0,3,6,2> and <0,4,4,3> are based on the <0,2,8,1> polyhedra with increasing defects in polytetrahedral packing. Interestingly, as shown in Figure 2C, the prism-like or antiprism-like packing polyhedra such as <0,3,6,0> (tri-capped trigonal prism, TTP), <0,2,8,0> (bi-capped square archimedean antiprism, BSAP), <0,4,4,1>, and <0,3,6,1> (distorted TTP and BSAP) gradually increase and become dominant from U50Co50, U67Co33, to U86Co14 melts, while the numbers of icosahedra clusters decrease.
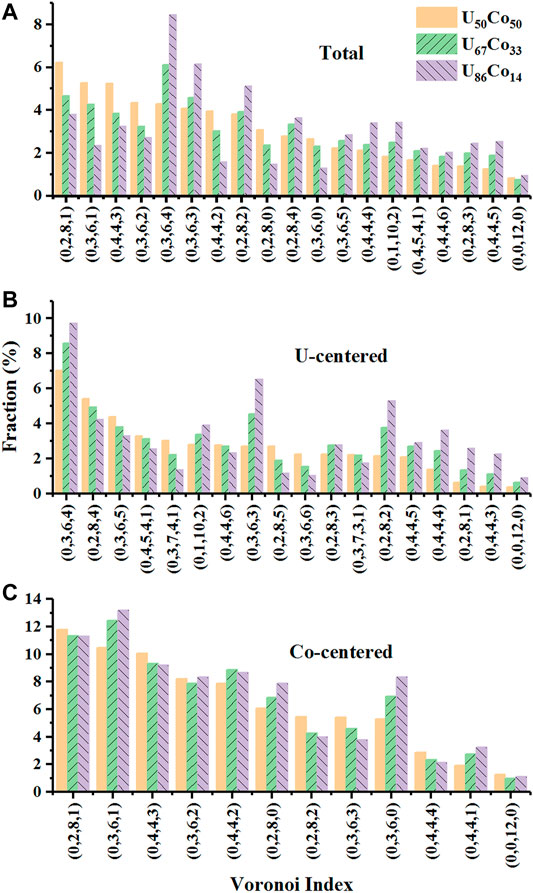
FIGURE 2. The distributions of (A) total, (B) U-centered, and (C) Co-centered Voronoi polyhedron for U50Co50, U67Co33, and U86Co14.
In the previous Miracle’s work (Miracle, 2004; Miracle, 2006), the radius ratios R (the solute atom radius normalized by the solvent atom radius) of the U-Co alloy should be 0.81 (atomic radius 0.158 for U and 0.128 for Co). Therefore, the predicted Co concentration for the better glass-forming ability of U-Co binary alloy is less than 20% according to the Ma and Xu’s idealized atomic packing model (Shi et al., 2008). However, the work by Egami and Waseda (Egami and Waseda, 1984) noted that the U-Co alloy might contain at least 21.8% Co to form metallic glasses by liquid quenching method. As mentioned above, the Co-centered polyhedra are mainly dense packing local structures, which types are slightly influenced by compositions. However, the U-centered polyhedra are mainly larger open Frank-Kasper polyhedra due to the larger U atomic radius. This is the reason for keeping high Co concentrations in the experiments. Therefore, the decreasing of Co atoms will be disadvantage for the glass-forming ability of U-Co alloys. On the other hand, the icosahedra-like U-centered polyhedra observably increase for the higher U concentrations due to the enhanced chemical role of U atoms. Namely, there is an equilibrium point of the quantity of the dense packing local structures when the U concentration is increasing. Thus, the present work concludes the U67Co33 alloy may possess a better glass-forming ability, which is agreement with Huang’s experiments (Huang et al., 2015; Huang et al., 2016; Xu et al., 2018; Xu et al., 2018).
Sheng et. al. (Sheng et al., 2006) presented the dependence of the local packing on atomic size ratio (R*) based on the solute-solvent model (Miracle, 2004; Miracle, 2006). The method was used to analyze the dependence of the Co- centered clusters on atomic size ratio R*. Sheng’s calculations gave the icosahedral type polyhedron with R* around 1.2–0.902, the BSAP type polyhedron with R* around 0.902–0.835, and the TTP type polyhedron with R* around 0.835–0.732. The actual sizes of atoms in a material depend upon the local chemistry and structure. In the present work, the chemical effect is introduced to correct the atomic sizes. For Co-centered clusters (Co solute and U solvent), a half of the position of the first peak in gCo-Co(r) is considered as the Co atomic size (RCo), while the U atomic size (RU) is calculated by subtracting RCo from the position of the first peak in gU-Co(r). Table 1 lists the calculated atomic size ratio
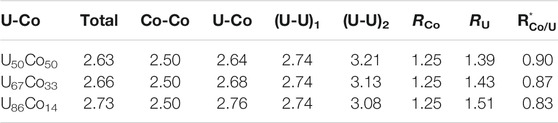
TABLE 1. The positions of the first peaks of PDFs (Å), the positions of the two sub-peaks in U-U PDFs (Å), and the calculated atomic radii (Å) are listed for U50Co50, U67Co33, and U86Co14 melts.
We also try to trace the origin of the SROs of the U-centered clusters. Figure 3 gives the core-shell U-U distances in the top ten Voronoi polyhedra. It can be seen that two separate peaks are present at about 2.70 and 3.34 Å for U50Co50, 2.70 and 3.28 Å for U67Co33, and 2.70 and 3.24 Å for U86Co14, respectively, which are in keeping with the PDFs’ results. For the icosahedral type polyhedron, there are more peaks with shorter U-U distances (2.50–3.00 Å). For the Frank-Kasper polyhedron, the peaks with shorter U-U distances are less. For example, the ratio of the shorter U-U distances is 33.3% in the icosahedral type polyhedron <0,3,6,3>, while the ratio of the shorter U-U distances is only 14.3% in the Frank-Kasper polyhedron <0,2,8,4>. In summary, the polyhedral analyses again indicate that two effects of U atoms in U-Co melts are responsible for the special atomic local packing.
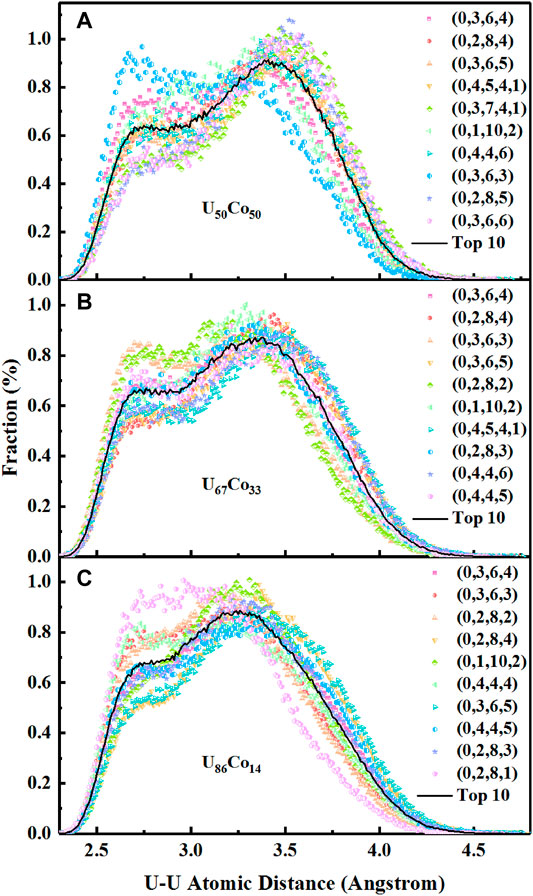
FIGURE 3. The U-U distances in the top ten Voronoi polyhedra of (A) U50Co50, (B) U67Co33, and (C) U86Co14 melts.
Coordination Number
The NN coordination numbers (CNs) and the componential proportions of U and Co atoms in partial CNs can be achieved from the PDFs using the first hollow as cutoff values for U50Co50, U67Co33, and U86Co14, respectively, which are listed in Table 2. The calculated CNs of U atoms are 14.1 (7.3U + 6.8 Co), 13.5 (9.6U + 3.9 Co), and 13.0 (11.6U + 1.4 Co) for U50Co50, U67Co33, and U86Co14, respectively. The calculated CNs of Co atoms are 10.8 (6.8U + 4.0 Co), 10.6 (8.2U + 2.4 Co), and 10.5 (9.5U + 1.0 Co) for U50Co50, U67Co33, and U86Co14, respectively. The larger partial CNs of U atoms agree with the Voronoi polyhedral analyses, which gives larger U-centered clusters (Frank-Kasper type) than the Co-centered clusters (BSAP and TTP type). Around U and Co atoms, the componential proportions of U atoms are 52.2 and 63.3% (U50Co50), 71.1 and 77.1% (U67Co33), and 88.6 and 90.4% (U86Co14), which are all larger than the nominal proportions. The componential segregation can be contributed to the chemical effect between U and U/Co atoms. Moreover, more U atoms are around the Co atom than those around the U atom, suggesting that stronger U-Co bonding than U-U bonding. For higher U contents, the difference of U-U and U-Co bonding is weakened as a result of the participation of more U atoms in the chemical bonding.
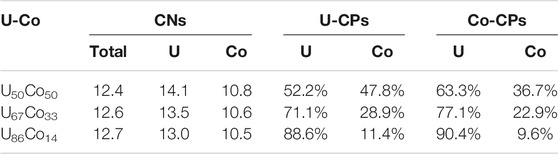
TABLE 2. The NN coordination numbers (CNs), and the componential proportions around U and Co atoms (U-CPs and Co-CPs) in U-Co melts are listed for U50Co50, U67Co33, and U86Co14.
Instead of the CNs results from PDFs, the CNs can be calculated by the statistics of the different Voronoi polyhedra. As shown in Figure 4, the method will give the distribution of the integral CNs. Unlike the crystal, each atom in the liquid/melt has its own CN. Therefore, the most probable CN represents the average structure and the favored SRO, whereas higher or lower CNs represent inevitable packing fluctuations (Egami, 2011). For U50Co50, the U-centered CNs mainly focus on 14, while the Co-centered CNs mostly center on 11. However, for U67Co33 and U86Co14, the proportions of the high CNs (≥14 for U-centered, and ≥11 for Co-centered) decrease while the proportions of the low CNs (≤13 for U-centered, and ≤10 for Co-centered) increase, which should be contributed to the changes of the atomic packing type as discussed in Voronoi polyhedra. It should be emphasized that the packing around the smaller Co atoms has a narrower distribution of CNs (8–13), while the distribution around the larger U atoms is wide (10–17). The CNs’ distribution of the U-Co melts is similar to the r-MC results of the U-Fe metallic glasses (Zhang et al., 2012), which also show larger U-centered structures. The observation can be contributed to two perspectives based on the previous work (Cheng et al., 2013). One originates from the limited possibilities in the topological SROs of smaller atoms. A missing or extra neighbor will introduce an obvious deviation from the efficient packing scenario and thus higher energy costs (Miracle et al., 2003). The other is due to the stronger chemical effect between U and Co atoms. The formation of U-Co bonds will be more energetic. The results suggest that Co-centered clusters are relatively more ordered and regular, which can be treated as building blocks in U-Co melts.
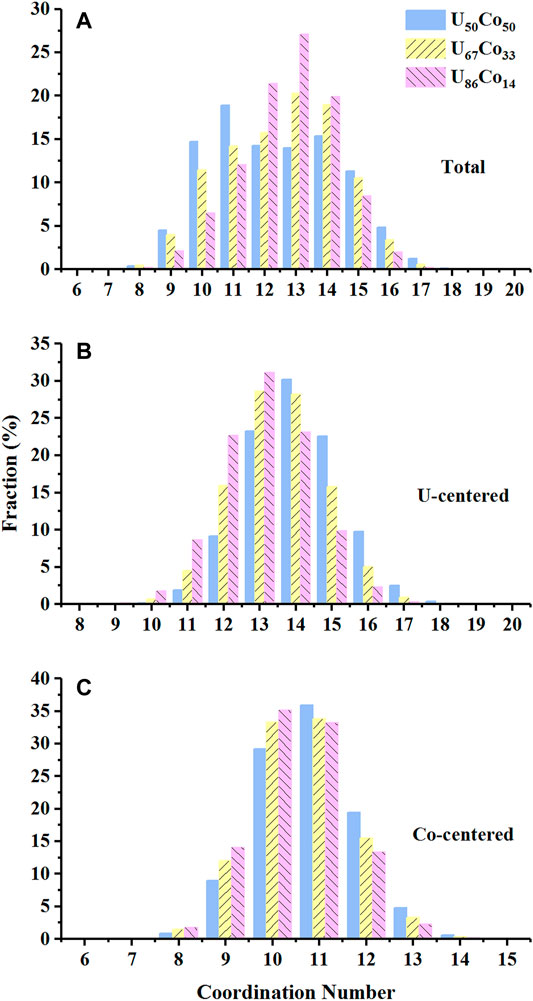
FIGURE 4. The coordination numbers calculated by the statistics of (A) Total, (B) U-centered, and (C) Co-centered Voronoi polyhedra.
Distribution of Electron Density
As mentioned above results of structural indicators, two roles of U atoms, “chemical” and “topological”, may be present in U-Co melts. To intuitively exhibit the roles of U atoms, the electron density of U-Co melts is calculated. As shown in Figure 5, the electron density map also shows the SROs of U-Co melts consist of both longer U-U bonds and shorter U-U bonds, which is in agreement with the polyhedral analyses in Figure 3. The longer U-U bonds are mainly metallic bonding characteristics. The shorter U-U bonds are connected by overlapping electron clouds, which are covalent bonding characteristics. It should be emphasized that although there are many dynamic configurations of U-Co melts, the configuration used to calculate the electron density is representative. Therefore, both the chemical and the topological effect of U atoms are commonly present in U-Co melts. In some Ln-alloys/metals, a high-pressure condition will promote the delocalization of 4f-electron and the chemical effect of Ln-Ln, which induces the evolution of the atomic long or short-range order (Errandonea et al., 2000). However, for light Ans (Th ∼ Pu), the localization of 5f-electron is weaker than that of 4f-electron. The partial localization of 5f-electron was observed for the high-temperature behavior of γ-U (Yoo et al., 1998) and thermal expansion of δ-Pu (Gouder et al., 2002). Namely, the partial localization of U 5f-electron is responsible for the dual roles of U atoms in U-Co melts, which are also the origin of the special SROs of U-Co melts.
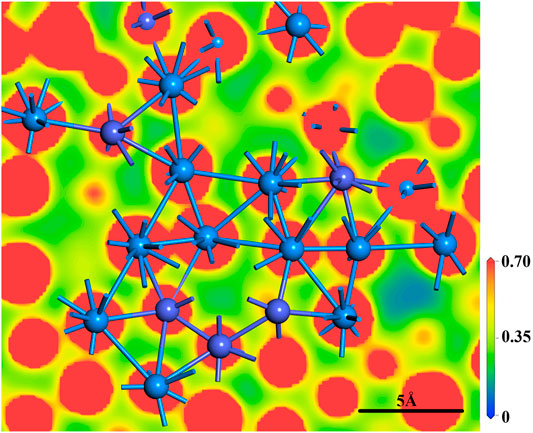
FIGURE 5. The slice map of electron density of U-Co melts. Some U and Co atoms on the slice are shown in the figure. The cyan balls are U atoms, and the purple balls are Co atoms. The unit of the scale plate is |e|/Å3.
Discussions
In the present calculations, several structural indicators of U-Co melts are shown to discuss the special short-range orders. The first peaks of U-U PDFs consist of two sub-peaks, which deviate from the predictions of the hard spheres model. The deviation suggests that U atoms play dual roles, “chemical” and “topological” effects, to affect the SROs of U-Co melts. The dual roles are also confirmed by the Voronoi polyhedral analyses, which show two separate core-shell U-U distances. The behaviors of Co-centered clusters can be predicted by the solute-solvent model. Combined with the CNs results, we note that Co-centered clusters are the foundation of U-Co melts. By the electron density of U-Co melts, both metallic and covalent bonding characteristics are observed for U-U bonds. Finally, the dual roles of U atoms in U-Co melts are contributed to the partial localization of U 5f-electron. The result of the present work gives a theoretical view to analyze the origin of the SROs of Uranium alloys.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was funded by the National Natural Science Foundation of China (51871132), and Shandong Provincial Natural Foundation, China (ZR2019MB008).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Baenziger, N. C., Rundle, R. E., Snow, A. I., and Wilson, A. S. (1950). Compounds of Uranium with the Transition Metals of the First Long Period. Acta Cryst. 3, 34–40. doi:10.1107/S0365110X50000082
Blöchl, P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953
Bowen, H. J. M., and Sutton, L. E. (1958). Tables of Interatomic Distances and Configuration in Molecules and Ions. London, UK: The Chemical Soc.
Cheng, Y. Q., Ding, J., and Ma, E. (2013). Local Topology vs. Atomic-Level Stresses as a Measure of Disorder: Correlating Structural Indicators for Metallic Glasses. Mater. Res. Lett. 1, 3–12. doi:10.1080/21663831.2012.722759
del Rio, B. G., González, L. E., and González, D. J. (2020). First Principles Study of Liquid Uranium at Temperatures up to 2050 K. J. Phys. Condens. Matter 32 (13), 304001. doi:10.1088/1361-648X/ab7f6f
Ding, J., Xu, M., Guan, P. F., Deng, S. W., Cheng, Y. Q., and Ma, E. (2014). Temperature Effects on Atomic Pair Distribution Functions of Melts. J. Chem. Phys. 140 (8), 064501. doi:10.1063/1.4864106
Drehman, A. J. (1985). “Density and Packing in Uranium Based Metallic Glasses,” in Phase transitions in condensed systems-Experiments and Theory (Boston, USA: Cambridge University Press). doi:10.1557/proc-57-283
Drehman, A. J., and Poon, S. J. (1985). Anomalous Glass-Forming Ability of Uranium-Based Alloys. J. Non-Cryst. Sol. 76, 321–332. doi:10.1016/0022-3093(85)90008-0
Egami, T. (2011). Atomic Level Stresses. Prog. Mater. Sci. 56, 637–653. doi:10.1016/j.pmatsci.2011.01.004
Egami, T., and Waseda, Y. (1984). Atomic Size Effect on the Formability of Metallic Glasses. J. Non-Cryst. Sol. 64, 113–134. doi:10.1016/0022-3093(84)90210-2
Elliott, R. O., and Giessen, B. C. (1982). On the Formation of Metallic Glasses Based on U, Np or Pu. Acta Metall. 30 (4), 785–789. doi:10.1016/0001-6160(82)90076-1
Elliott, R. O., Koss, D. A., and Giessen, B. C. (1980). On the Characteristics of Amorphous U-Fe Alloys Formed by Liquid Quenching vs. Irradiation Techniques. Scr. Metall. 14, 1061–1065. doi:10.1016/0036-9748(80)90206-9
Elliott, R. O., Smith, J. L., Finocchiaro, R. S., and Koss, D. A. (1981). Influence of Structure on the Properties of an Amorphous U-Fe alloy. Mater. Sci. Eng. 49, 65–69. doi:10.1016/0025-5416(81)90134-8
Errandonea, D., Boehler, R., and Ross, M. (2000). Melting of the Rare Earth Metals Andf-Electron Delocalization. Phys. Rev. Lett. 85, 3444–3447. doi:10.1103/PhysRevLett.85.3444
Ganesh, P., and Widom, M. (2008). Ab Initiosimulations of Geometrical Frustration in Supercooled Liquid Fe and Fe-Based Metallic Glass. Phys. Rev. B 77 (10), 014205. doi:10.1103/PhysRevB.77.014205
Giessen, B. C., and Elliott, R. O. (1978). “Properties of Metallic Glasses Containing Actinide Metals. I. Thermal Properties of U-M Glasses (M = V, Cr, Mn, Fe, Co, and Ni),” in Conference on Rapid Quenching, Brighton, UK, 3 July, 1978.
Gouder, T., Havela, L., Wastin, F., and Rebizant, J. (2002). 5f Localization in Ultrathin Pu Layers. J. Nucl. Sci. Tech. 39, 49–55. doi:10.1080/00223131.2002.10875407
Hofman, G. L., Kim, Y. S., Finlay, M. R., Snelgrove, J. L., Hayes, S. L., Meyer, M. K., et al. (2003). “Recent Observations at the Postirradiation Examination of Low-Enriched U-Mo Miniplates Irradiated to High Burnup,” in 25th International Meeting on Reduced Enrichment for Research and Test Reactors, Munich, Germany, 21-24 March 2004. (Chicago, USA: IAEA).
Huang, H. G., Zhang, P. G., Zhang, P., and Wang, Q. G. (2020). Comparison of Glass Forming Ability between U-Co and U-Fe Base Systems. Acta Metall. Sin. 56, 849–854. doi:10.11900/0412.1961.2019.00349
Huang, H. G., Ke, H. B., Wang, Y. M., Pu, Z., Zhang, P., Zhang, P. G., et al. (2016). Stable U-Based Metallic Glasses. J. Alloys Comp. 684, 75–83. doi:10.1016/j.jallcom.2016.05.124
Huang, H. G., Wang, Y. M., Chen, L., Pu, Z., Zhang, P. G., and Liu, T. W. (2015). Study on Formation and Corrosion Resistance of Amorphous alloy in U-Co System. Acta Metall. Sin. 51, 623–630. doi:10.11900/0412.1961.2014.00580
Kaye, G. W. C., and Laby, T. H. (1993). Table of Physical and Chemical Constants. 15th edition. London, UK: Longman.
Kresse, G., and Furthmüller, J. (1996). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Li, F. F., Lu, L., Meng, X. D., Xiao, H., Ji, H. F., Zeng, R. G., et al. (2020). An Enhanced Hydrogen Corrosion by the Ti(C,N) Inclusions in U-0.79 wt%Ti alloy. J. Alloys Comp. 820, 153124. doi:10.1016/j.jallcom.2019.153124
Manner, W. L., Lloyd, J. A., Hanrahan, R. J., and Paffett, M. T. (1999). An Examination of the Initial Oxidation of a Uranium-Base alloy (U-14.1 at.% Nb) by O2 and D2O Using Surface-Sensitive Techniques. Appl. Surf. Sci. 150, 73–88. doi:10.1016/S0169-4332(99)00225-1
Massalski, T. B., Okamoto, H., Subramanian, P. R., and Kacprzak, L. (1990). Binary Alloy Phase Diagrams. Ohio, USA: ASM International.
Miracle, D. B. (2004). A Structural Model for Metallic Glasses. Nat. Mater. 3, 697–702. doi:10.1038/nmat1219
Miracle, D. B., Sanders, W. S., and Senkov, O. N. (2003). The Influence of Efficient Atomic Packing on the Constitution of Metallic Glasses. Phil. Mag. 83, 2409–2428. doi:10.1080/1478643031000098828
Miracle, D. B. (2006). The Efficient Cluster Packing Model - an Atomic Structural Model for Metallic Glasses. Acta Mater. 54, 4317–4336. doi:10.1016/j.actamat.2006.06.002
Nosé, S. (1984). A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 81, 511–519. doi:10.1063/1.447334
Orlov, V. K. (2002). Fundamentals of the Physical Metallurgy of Uranium, Plutonium, and Their Alloys. Metal Sci. Heat Treat. 44, 11–12. doi:10.1023/1022596403845
Pan, S., Feng, S., Qiao, J., Dong, B., and Qin, J. (2015). The Atomic Structure of Liquid Fe-C Alloys. J. Alloys Comp. 648, 178–183. doi:10.1016/j.jallcom.2015.06.252
Pan, S. P., Qin, J. Y., Gu, T. K., Yang, L., and Bian, X. F. (2009). Correlation between Local Structure of Melts and Glass Forming Ability for Fe78M9B13 (M=Nb, Si, and Zr) Alloys. J. Appl. Phys. 105 (4), 013531. doi:10.1063/1.3041473
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Poon, S. J., Drehman, A. J., Wong, K. M., and Clegg, A. W. (1985). Superconductivity in Amorphous Actinide Alloys. Phys. Rev. B 31, 3100–3103. doi:10.1103/PhysRevB.31.3100
Porterfield, W. W. (1984). Inorginic Chemistry, a Unified Approach. Reading Masschusetts, USA: Addison Wesley Publishing Co.
Sheng, H. W., Liu, H. Z., Cheng, Y. Q., Wen, J., Lee, P. L., Luo, W. K., et al. (2007). Polyamorphism in a Metallic Glass. Nat. Mater 6, 192–197. doi:10.1038/nmat1839
Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M., and Ma, E. (2006). Atomic Packing and Short-To-Medium-Range Order in Metallic Glasses. Nature 439, 419–425. doi:10.1038/nature04421
Shi, L.-L., Xu, J., and Ma, E. (2008). Alloy Compositions of Metallic Glasses and Eutectics from an Idealized Structural Model. Acta Material. 56, 3613–3621. doi:10.1016/j.actamat.2008.04.002
Shi, P., Li, F., Wu, Y., Ji, H., Li, R., and Wang, X. (2015). Effect of Alloyed Ti on the Microstructure and Corrosion Characteristics of a U-Ti alloy in a Hydrogen Environment. Corrosion Sci. 93, 58–62. doi:10.1016/j.corsci.2015.01.005
Watson, R. E., and Bennett, L. H. (1991). Crystalline and Glassy Phases of Transition-Metal-Metalloid Systems. Phys. Rev. B 43, 11642–11652. doi:10.1103/PhysRevB.43.11642
Wiencek, T. C., and Prokofiev, I. G. (2000). “Low-enriched Uranium-Molybdenum Fuel Plate Development,” in International Meeting on Reduced Enrichment for Research and Test Reactors, Las Vegas, NV, USA, 1-6 October 2000. (Las Vegas, NV, USA: RERTR).
Xiang, S., Huang, H., and Hsiung, L. M. (2008). Quantum Mechanical Calculations of Uranium Phases and Niobium Defects in γ-uranium. J. Nucl. Mater. 375, 113–119. doi:10.1016/j.jnucmat.2007.11.003
Xu, H., Ke, H., Huang, H., Zhang, P., Pu, Z., Zhang, P., et al. (2018). U-based Metallic Glasses with superior Glass Forming Ability. J. Nucl. Mater. 499, 372–376. doi:10.1016/j.jnucmat.2017.11.043
Yoo, C.-S., Cynn, H., and Söderlind, P. (1998). Phase Diagram of Uranium at High Pressures and Temperatures. Phys. Rev. B 57, 10359–10362. doi:10.1103/PhysRevB.57.10359
Zhang, Y., Mattern, N., Liang, T. X., Huang, Q., and Eckert, J. (2012). Atomic Packing and Short to Medium Range Order in a U-Fe Metallic Glass. Appl. Phys. Lett. 101, 021909. doi:10.1063/1.4736563
Zurek, A. K. (1999). Preshock-induced Phase Transition in Spalled U-0.75 wt.% Ti. J. Nucl. Mater. 264, 155–160. doi:10.1016/S0022-3115(98)00462-0
Keywords: U-Co melt, local structure, first-principle, SROs, bonding
Citation: Zhang H, Sun H, Li Q and Wang L (2022) Origin of Local Structures of U-Co Melts: A First-Principles Study. Front. Mater. 8:821306. doi: 10.3389/fmats.2021.821306
Received: 24 November 2021; Accepted: 23 December 2021;
Published: 13 January 2022.
Edited by:
Ran Li, Beihang University, ChinaCopyright © 2022 Zhang, Sun, Li and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Honggang Sun, c3VuaGdAc2R1LmVkdS5jbg==; Li Wang, d2FuZ2xpaHhmQHNkdS5lZHUuY24=
 Huanqing Zhang
Huanqing Zhang Honggang Sun
Honggang Sun