- 1School of Material Science and Engineering, Nanjing University of Science and Technology, Nanjing, China
- 2School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, China
The grain size effect on the shaped charge jet (SCJ) stretching process was analytically formulated and experimentally verified by penetration tests. The present analytical model predicts an optimum grain size for the SCJ performance, deduced from the concurrent effect of grain size on flow stress, strain rate sensitivity, and surface roughness. Specifically, reducing the grain size will improve the initial surface roughness and decrease the initial perturbation amplitude, favoring the SCJ stretching. On the other hand, the strain rate sensitivity and flow stress for copper increase with the decrease of grain size, facilitating the perturbation growth and leading to a premature breakup. Thus, the present analytical model predicts that the optimum grain size of the SCJ is about 1–5 μm. The penetration test verified that the shaped charge liner with an average grain size of about 3.6 ± 2.5 μm exhibited the largest penetration depth. The consistent results from the analytical model and the penetration experiments certify the feasibility of the present analytical model on the SCJ performance.
Introduction
A shaped charge liner (SCL) is one of the key parts of a shaped charge warhead. After the explosive charge is detonated, the SCL material lined on its hollow cavity is accelerated under the high detonation pressure (200–300 kbar) of the explosive at a very high strain rate (104∼7 s−1) (Shekhar, 2012). As a consequence, the SCL material collapses, and the shaped charge jet (SCJ) is squeezed out with a possible jet tip velocity of 9–12 km/s, while the rearward tail, namely, a slug, can attain a velocity up to a maximum of 2 km/s (Bai et al., 2012). The velocity gradient along the length of the SCJ leads to stretching and ultimately fracture.
In conventional views, greater penetration depth
The SCJ stretching is an extremely complicated process, which relates to material deformation at an extremely high strain rate, high strain, and high temperature. Mott (1947) proposed the first classical dynamic fragmentation model, assuming the fragmentation as a process of random fractures, and concluded that the resulting fragment sizes were controlled by the momentum diffusion (Mott model) from each crack. Based on the Mott model, the fragmentation process and its fragmentation size distribution have been extensively investigated and described based on the geometrical/mathematical random statistical distribution functions, such as logarithmico-normal (lognormal) distribution (Epstein, 1947), Linenau distribution (Lienau, 1936), and Weibull distribution (Brown and Wohletz, 1995). These statistical distribution analyses described the experimental results very well. However, none of them could illustrate the physical mechanism of the fragmentation process since the framework of the Mott model did not concern the mechanical properties of materials, such as strain hardening, strain rate sensitivity, fracture energy, and toughness.
To establish a basic physical model to evaluate the shaped charge jet performance, Kipp and Grady (1985) considered the dynamic fragmentation as a process of energy dissipation during the cohesive fracture rather than an instantaneous event and introduced the fracture energy and strain rate to modify the Mott model. Chou and Carleone (1977) presented the perturbation model to describe the evolution of the necking and fragmentation processes of the SCJ stretching. Further work conducted by Walsh (1984) predicted that a critical wavelength corresponding to a maximum perturbation growth rate should be responsible for the comparable fragment size observed in experiments. The detailed work conducted by Fressengeas and Molinari (Fressengeas and Molinari, 1985; Fressengeas and Molinari, 1987; Fressengeas and Molinari, 1994) proved the critical wavelength existed in a 1D visco-plastic bar and a 2D visco-plastic sheet. Numerical simulations conducted by Shenoy and Freund (1999) and Guduru and Freund (2002) found the dynamic stretching process in strain rate-independent materials can also be well explained by the identical model. Zhou et al. (2006) investigated the strain rate-dependent dominant necking pattern during dynamic expanding using a constitutive relationship for thermo-visco-plastic material based on the linear perturbation analysis. They found the number of ductile fragments was much less than (about 1/3–1/4) the number of necks, while the distance between the necking was approximately equal to the critical wavelength. Interestingly, their numerical solutions gave an identical conclusion that the fragment size was still controlled by the unloading Mott wave propagation in the ultimate fragmentation stage (Zhou et al., 2006). In comparison, experimental research studies showed that the dynamic stretching and perturbation were seriously affected by the macroscopic machining accuracy and microstructure homogeneity. Typically, the effect of microstructure refinement on the perturbation and fragmentation of shaped charge jet needs to be recognized as an important factor to predict the performance of SCL (Petit et al., 2006). However, the fundamental mechanism of interaction between microstructure and SCL performance is still pending, and research on this topic is almost blank. Furthermore, the development of fabrication of ultra-fine grained (UFG) and nano-crystalline (NC) metals makes it possible to extend the SCL grain size to the UFG and NC range. Thus, another key task of this work is to experimentally extend the grain size effect on SCJ stretching as well as the subsequent shaped charge penetration performance at such fine grain size.
In the present work, the grain size effect on the SCJ stretching process is analytically formulated by citing the grain size effect on material performance in solving the basic equations of motion under boundary conditions of SCJ. The influence of grain size is introduced by establishing its effect on flow stress, strain rate sensitivity, and surface roughness of the SCJ described as the inertia terms and the surface perturbation amplitude. To validate the analytical model developed in the present work and to experimentally extend the grain size effect of SCJ performance to UFG, a penetration test was conducted using SCLs made of pure Cu with different grain sizes, ranging from UFG to tens of micrometers.
Theoretical model
Figure 1 gives a configuration showing the dynamic stretching process of an SCJ with an axial velocity gradient. For the ideal state, the SCJ was expected to stretch uniformly and infinitely without necking or fragmentation, as shown by the green dashed lines in Figure 1. However, the experimental observations in flash X-ray pictures (Held, 2003) demonstrated the truth that the SCJ would fragment into pieces, the length of which was measured to be approximately the same. This conclusion was consistent with other reports in literature studies (Chou et al., 1977; Fressengeas and Molinari, 1994). These results indicated that the SCJ stretching process might be under the control of a periodic perturbation, the wavelength of which is correlated with the fragment size, shown as black solid lines in Figure 1.
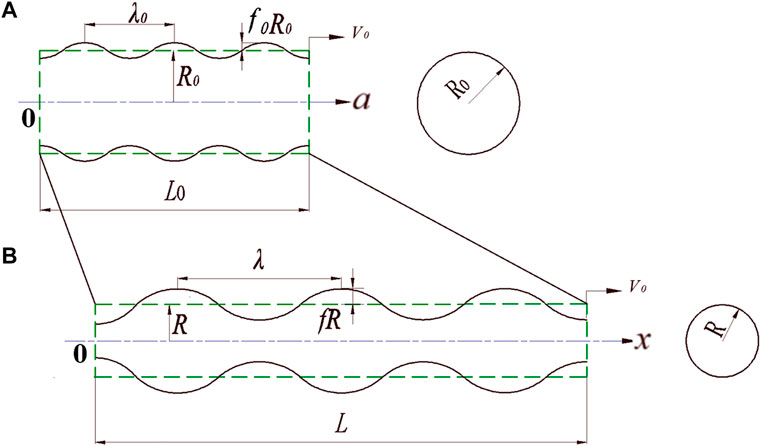
FIGURE 1. Configuration of the stretching and necking processes for a shaped charge jet with a velocity gradient in the Lagrange
The stretching of an SCJ can be approximated as a slender bar (of initial length,
1) The stretching of SCJ occurs at tens to hundreds of micro-seconds, and the velocity degrading or motion energy consumption is ignored, that is, the axial velocity difference between the jet tip and slug is regarded as a constant of
2) The SCJ length is far longer than the jet radius, and thus the stretching of SCJ could be simplified as a uniaxial elongation process under uniform axial inertial stress, ignoring the stress distributions along the radius and tangential direction.
3) Similar to assumption 2, only the velocity variation along the axial direction is considered, which is believed to be initially gradient and the velocity gradient is uniform throughout the bar. Then, the initial strain rate of SCJ stretching can be estimated as
4) The SCJ is incompressible; its density
Based on the abovementioned simplifications and assumptions, the SCJ stretching process can be considered as a set of equations on the dynamics of plastically stretching slender bars. For Lagrange coordinate, the axial location of cross section
Governing equations
Based on the abovementioned simplification and assumptions, an ideal physical model is first simplified as a stretching bar with a uniform velocity gradient and uniform diameter. In this physical model, the velocity of the jet tip relative to its rear end, set at the tip location or jet length
Considering the stretching process of the SCJ in motion, the law of conservation of mass leads to the relationship between the Lagrange coordinate
According to the incompressibility condition of assumption 4,
Furthermore, the momentum balance in the axial direction is described as follows:
In Eq. 4, the
where
By substituting Eq. 5 in Eq. 4 and retaining only the first order components, a fundamental equation for the one-dimensional dynamic stretching of the SCJ can be obtained as follows:
The combination of Eqs. 2–6 with the initial and boundary conditions for an SCJ under uniform stretching deformation and constant axial velocity gradient.
These constitute the governing equations for an unperturbed SCJ stretching process.
From Eq. 6, we can infer that
1) The axial velocity gradient should be high enough to introduce high acceleration
2) The converse side also applies that the material with high flow stress and high strain rate sensitivity requires a high critical axial velocity gradient to realize the shaped charge stretching; otherwise, the SCJ could be considered stable within the elastic deformation regime.
Surface perturbation and breakup criterion of jet
There exist ideal homogenous solutions for Eqs. 2–7, corresponding to the SCJ, which could be infinite uniformly stretched if all assumptions could be fulfilled. Unfortunately, the SCJ stretching process was not always uniform. Instead, the X-ray diffraction observations illustrated that the SCJ stretched, necked, and fragmented into pieces as solid-state metals (Chou et al., 1977; Fressengeas and Molinari, 1994). Furthermore, these fragmented particles are frequently of approximately the same length or their size distribution follows a random distribution function, suggesting the existence of a periodic surface perturbation (Grady, 1982; Curtis, 1987; Zhou et al., 2006). These periodic surface perturbations can be represented as a sum of harmonically related sinusoids and cosinusoids according to the Fourier transformation (Carslaw, 1921). The simultaneous radius of the SCJ could be written as follows:
In the formula of the Fourier series, the Fourier coefficients
where the time
At the same time, the number of wavelengths is constant and the wavelength increases monotonically with the SCJ stretching, which is proportional to the length of SCJ; thus,
Substitution of Eq. 8 into the governing equation Eq. 3 gives the general motion equation about cross-section area and coordinate system for the SCJ under cosinusoidal perturbation:
After partial differentiation of the position function and sectional area function of Eq. 10, the basic motion governing Eq. 6 will be substituted and modified, and the perturbation growth equation is finally written as:
The nature of solutions of Eq. 11 is discussed now. Eq. 11 is a second-order ordinary differential equation about the perturbation amplitude
where
For Eq. 12a, since all parameters on the right side of the equations are positive, it gives that
Taking the derivative of
Clearly, the value of
In the following sections, we focused on the effect of material microstructure on shaped jet performance and discussed their fundamental mechanism based on the grain size effect on flow stress, wavelength, and perturbation growth rate.
Microstructure effect
Generally, in dealing with the microstructure effect on mechanical properties, the Hall–Petch equation has been extensively applied to relate grain size with yield strength and the flow stress during plastic deformation (Gourdin and Lassila, 1991; Meyers et al., 1995).
where
It is very important to mention that the yield stress
In line with the dislocation motion as the domain deformation mechanism, the grain size-related self-affine behavior (Zaiser et al., 2004) was introduced to assess surface roughness and the magnitude of perturbation. This has been long known to metallurgists who observed pronounced surface traces (“slip lines”) resulting from the collective motion of many dislocations. By monitoring the evolution of surface features, it is, therefore, possible to study collective behavior in surface roughness (
Mahmudi and Mehdizadeh (1998) found that at any given grain size, the roughness increment of the copper alloy was linearly related to the equivalent strain. Thus, the self-affine behavior implies a function of surface roughness with grain size as (Mahmudi and Mehdizadeh, 1998)
The constant
Analytical results and experimental verification
Prediction results of analytical model
From the typical X-ray experiment results for the SCJ described in reference (Cai et al., 2022), the following parameter values were selected:
The evolutions of perturbation amplitude during SCJ stretching with time for SCJ with some different grain sizes are calculated and plotted in Figure 2 from the combination of governing equations of Eqs. 5–7 and analytical model Eqs. 12–14 by applying the material parameters, Typically, flow stress and roughness are determined through Eqs. 15 and 17, respectively. It is obvious that the perturbation amplitude increases non-linearly with the SCJ stretching, which is suitable for all present SCJs with a wide grain size range. It reflects the complex influence of material microstructure on the shaped charge stretching process. First of all, at t = 0, the initial perturbation amplitude is different depending on the surface roughness and the self-affine behavior related to grain size (Mahmudi and Mehdizadeh, 1998). The deformation mechanism of the SCJ stretching is believed to be still under the control of the dislocation-based thermal activated plastic deformation mechanism. As a consequence of dislocation gliding to the free surface, some steps will be formed and the crystals are forced to rotate. Therefore, the height of the macro-emboss was the direct reason for the deformation-induced roughness. Thus, the larger the initial grain size, the higher the surface roughness and the larger the perturbation amplitude, and the shorter the jet stretching time will be expected.
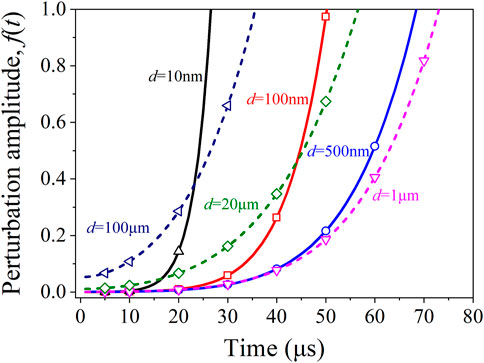
FIGURE 2. Calculated perturbation amplitude evolutions as a function of stretching time for copper SCJs with different grain sizes. In order to distinguish them from each other, the curves for SCJ with a grain size above 1 μm are solid lines, while the dashed lines correspond to curves for SCJ with a grain size below 1 μm.
The increasing surface roughness with the increasing plastic strain during SCJ stretching can also partly explain the non-linear increasing perturbation amplitude. From this point, the coarser microstructure should result in earlier fragmentation of the SCJ. Unfortunately, the curves in Figure 2 show that the breakup time does not monotonically increase with the decrease of grain size. The breakup time increases with the decrease of grain size to about 1 μm. The further decrease in grain size induces the growth rate of perturbation amplitude to increase rapidly because the flow stress increases significantly with grain size reduction, which surpasses the advantage of the declining surface roughness. The high flow stress that favors the growth of perturbation is consistent with the trend stated by Chou and Carleone (1977) and Chou et al. (1977) that the perturbation growth rate increases with increasing flow stress and the ratio of flow stress and the jet density. As a result, the present analytical model predicts that there is an optimum grain size of around 1 μm for the copper SCJ.
Experimental results of Cu shaped charge jet penetration
In order to verify the feasibility of the present model, a series of penetration tests were conducted. The penetration tests used a standard 64-mm shaped charge design, loaded with JH-2 high explosive, incorporating precision initiation and copper shaped charge liners with a Ф56 mm conical liner of 60° cone angle and constant thickness (Figure 3). Finally, the effect of grain size on SCL performance and SCJ stretching behavior was characterized as a function of penetration depth against homogeneous 45# steel targets based on the linear relationship between penetration depth and SCJ length (Birkhoff et al., 1948).
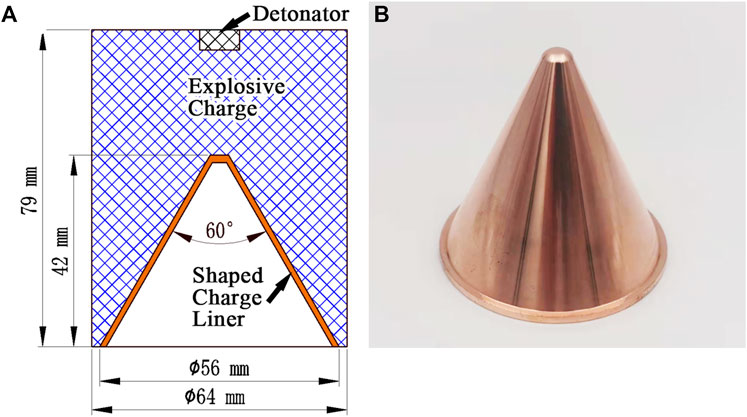
FIGURE 3. Structure of the shaped charge (A) and product of the Ф56 mm shaped charge liner of copper (B).
The commercial coarse-grained pure copper billets (99.9%) were processed by the combination process of equal channel angular processing (ECAP) and room temperature rolling to fabricate Cu sheets with ultra-fine grained (Jiang et al., 2016). Since the typical mechanical property of UFG Cu exhibits a trade-off relation, high strength, and low uniform tensile elongation, the spinning forming process was utilized to fabricate the UFG copper SCLs. The subsequent annealing treatment at different temperatures for various durations was applied to introduce recrystallization and grain growth to obtain SCLs with different average grain sizes, and the influence of annealing treatment on microstructure could be found in our previous work (Jiang et al., 2021). Figure 4 shows the microstructure of the copper SCL with UFG and coarse-grained microstructure. The average grain size estimation from the EBSD data based on the ASTM E2627 standard gave average grain sizes of d = 0.5 ± 0.3, 1.7 ± 1.2, 3.6 ± 2.5, and 20.2 ± 7.8 μm after spinning forming and the subsequent annealing treatments, respectively.
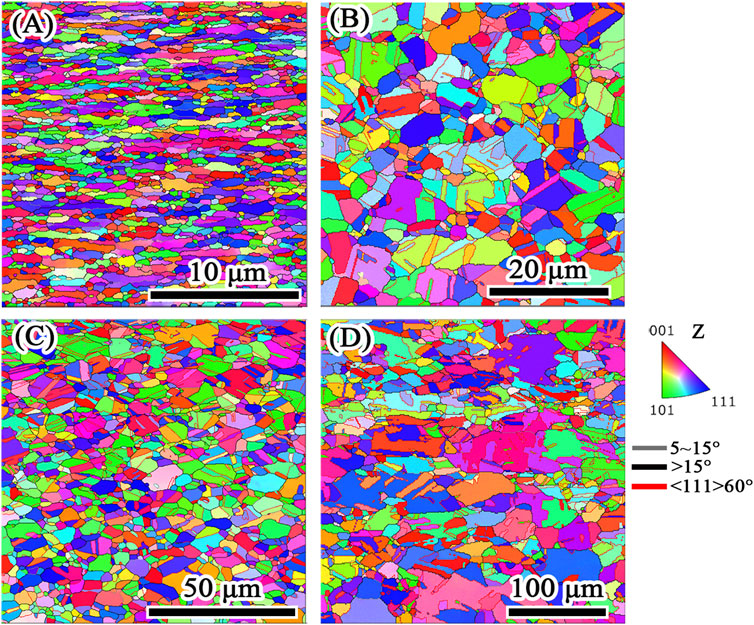
FIGURE 4. EBSD images for the microstructures of SCLs with different grain sizes: (A) d = 0.5 ± 0.3 μm, (B) d = 1.7 ± 1.2 μm, (C) d = 3.6 ± 2.5 μm, and (D) d = 20.2 ± 7.8 μm. It is to be noted that different image scale bars for each EBSD microscopy should be used. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article).
In the penetration experiments, the penetration depth of the crater was measured to evaluate the breakup time of the SCJ based on their linear relationship as stated by Birkhoff et al. (1948). The penetration tests were performed at a stand-off of 160 mm. Combining the variation of perturbation amplitude (Figure 2) with stretching time and the SCJ breakup criterion (Eq. 13), the breakup time is determined and plotted as a function of grain size in Figure 5. The breakup time was calculated to increase from ∼57 μs to ∼73 μs, by almost 28.1%, as the grain size of SCJ decreases from 20 μm to 1 μm. This trend is fairly consistent with our original expectation and the prediction in literature studies (Petit et al., 2005; Petit et al., 2006) that reducing grain size should favor the stretching of SCJ and significantly increase the breakup time. The paradox is that the present analytical model predicts the breakup time of SCJ will monotonically decrease if the grain size is further decreased to the UFG and NC regimes. The investigation conducted by Petit et al. (2005) and co-workers analyzed the effect of grain size reduction on SCJ stability in the regime of an average grain size from 20 μm to about 45 μm. Their analytical model found that such a fluctuation of grain size from 45 to 20 μm leads to only 5 MPa variations in the flow stress for Cu at elevated temperatures. The significant increase in the SCJ stability gained from reducing the grain size was believed to originate primarily in the improvement of surface roughness since such a small fluctuation of flow stress yields virtually the experimental uncertainty (Petit et al., 2005). Ascribe to the rapid development in the field of severe plastic deformation (SPD), the preparation of bulk UFG materials makes it possible to fabricate and investigate the performance of SCL with an ultra-fine microstructure. The primary experimental research on the dynamic mechanical behavior of Cu at elevated temperatures conducted by Suo et al. (2013) showed the effect of grain size reduction on flow stress cannot be ignored anymore if it is refined to the UFG regime. The measured flow stress of UFG Cu (d ∼ 300 nm) increased up to about 440 MPa at the homologous temperature of ∼0.4
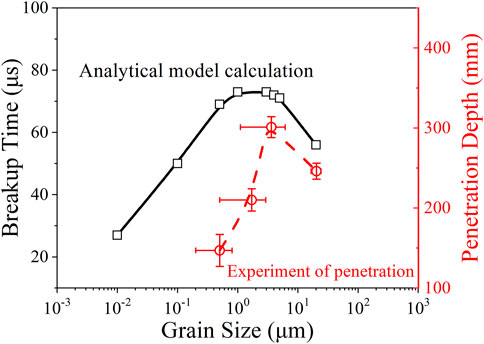
FIGURE 5. Relations of shaped charge jet performance with grain size, solid line, and dashed line correspond to the function of calculated breakup time from the present analytical model and measured experimental penetration depths from penetration tests with grain size, respectively.
The experimental results of penetration tests present a consistent and realistic description of the grain size effect on SCJ breakup. The largest penetration depth appears as the average grain size of the SCL is about 3.6 ± 2.5 μm, the value of which is about 23.6% larger than that of the SCL with an average grain size of 20.2 ± 7.8 μm. This trend is very consistent with the increasing breakup time (28.1%) with grain size reduction predicted by the analytical model. However, it is worth mentioning that the grain size dependence of SCJ breakup time predicted in this work is somewhat different from the experimental work, especially in the UFG and NC regimes. First, the penetration test illustrates that the SCL with an average grain size of about 3.6 ± 2.5 μm exhibits the largest penetration depth rather than the predicted value of about 1 μm, that is, the SCL with an average grain size of 1.7 ± 1.2 μm should be the optimum one. Exactly, the analytically predicted breakup time difference among the SCJ with an average grain size that varies from 1 to 5 μm is tiny, that is, 73–71 μs. From this point, the penetration results can be identified as fully consistent with the analytical prediction since the average grain size (3.6 ± 2.5 μm) of the SCL with the largest penetration depth is still located in this interval (1–5 μm). Essentially, there must be some other factors corresponding to the observed deviation between analytical prediction and experiment results, as well as the deterioration as the grain size is further reduced. Typically, why does the penetration depth decrease rapidly as the average grain size of the SCL reduces to 1.7 ± 1.2 μm?
One possible reason is that the dynamic performance may not correspond to the initial, as-prepared SCL structure but rather to the structure developed by the combined temperature and strain history prior to and during the SCJ formation and stretching. However, recovering the SCJ and eliminating the influence of aging, cooling, and deformation for microstructure characterization to reveal its simultaneous grain size is still a challenge. Chokshi and Meyers (1990) analyzed the SCJ stretching behavior under the concept of material superplasticity and deduced that the initial coarse grains had to be seriously refined to a sub-micron microstructure (<100 nm) through dynamic recrystallization. The microstructure observations of the recovered SCJ fragment and its slug usually demonstrated grain growth and annealing during the cooling cycle (Chokshi and Meyers, 1990; Murr et al., 1997).
On the other hand, the advantage of microstructure refinement to decrease the surface roughness through the “self-affine” effect might be suppressed by the negative influence of limited machining accuracy, including the geometrical dimension, surface finish, symmetry, and coaxiality. Schwartz and Baker (1999) conducted experimental observations to examine the influence on the SCJ stretching of the surface finish. Their results found that the coarse surface finish (9.5 μm) enhanced local fracture and even induced quite brittle behavior, that is, the copper jet particles were shorter and wider (Schwartz and Baker, 1999), although copper was known as a typical ductile fracture material in common sense. Quantitatively, the average breakup time for coarse-grained SCL was determined to decrease by 18.4% as its surface finish increased from 1.1 to 9.5 μm, very similar to the present grain size effect (as shown in Figure 5). Their consistent results demonstrate that the surface finish of SCL also determines the evolution of surface roughness and the perturbation amplitude of the SCJ. If the present perturbation theory was still applicable and the surface finish of SCL was applied as a factor of initial perturbation of the SCJ, the parameter of initial surface roughness
Conclusion
The grain size effect on the shaped charge jet stretching process was analytically formulated by correlating the evolution of SCJ perturbation with grain size-dependent material factors, such as flow stress, strain rate sensitivity, and surface roughness. Moreover, experimental verification by penetration test was carried out by fabricating shaped charge liners with different average grain sizes, ranging from tens of micrometers down to ultra-fine-grained size. The consistent results from the analytical model and experimental test lead to the following conclusions:
1. The analytical model demonstrates that the concurrent effect of microstructure on flow stress, strain rate sensitivity, and roughness is the key reason for the grain size effect on SCJ stretching. Specifically, reducing the grain size will improve the initial surface roughness and decrease the initial perturbation amplitude, favoring the SCJ stretching. On the other hand, the strain rate sensitivity and flow stress for copper increase with the decrease of grain size, facilitating the perturbation growth and leading to a premature breakup.
2. An optimum grain size for SCJ stretching, about 1–5 μm, is obtained from the comprehensive effect of the abovementioned concurrent influences against each other. The penetration test verifies the shaped charge liner with an average grain size of about 3.6 ± 2.5 μm exhibited the largest penetration depth.
3. The consistent results between the predicted breakup time from the analytical model and the penetration depth from penetration tests indicate the feasibility of the present analytical model on the SCJ performance.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
Methodology, YJ, JW, and Z-XH; experiments and characterizations, YJ and RG; analysis and validation, YJ, JW, Q-QX, and Z-XH; writing—original draft, YJ; writing—review and editing, YJ, JW, Q-QX, and Z-XH. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant nos. 52074160 and 52150410424).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bai, X., Liu, J. X., Li, S. K., Lv, C. C., Guo, W. Q., and Wu, T. T. (2012). Effect of interaction mechanism between jet and target on penetration performance of shaped charge liner. Mat. Sci. Eng. A 553, 142–148.
Birkhoff, G., MacDougall, D. P., Pugh, E. M., and Taylor, S. G. (1948). Explosives with lined Cavities. J. Appl. Phys. 19 (6), 563–582. doi:10.1063/1.1698173
Brown, W. K., and Wohletz, K. H. (1995). Derivation of the Weibull distribution based on physical principles and its connection to the Rosin–Rammler and lognormal distributions. J. Appl. Phys. 78 (4), 2758–2763. doi:10.1063/1.360073
Cai, Y. E., Huang, Z. X., Tan, Y. P., Zu, X. D., Shen, X. J., and Jia, X. (2022). Influence of strongly-constrained liquid-filled composite armor on stability of incoming shaped charge jet during eccentric penetration. Lat. Am. J. solids Struct. 19. doi:10.1590/1679-78257098
Carslaw, H. S. (1921). Introduction to the theory of Fourier's series and integrals. London: Macmillan.
Chokshi, A. H., and Meyers, M. A. (1990). The prospects for superplasticity at high strain rates: Preliminary considerations and an example. Scripta Metallurgica Materialia 24, 605–610. doi:10.1016/0956-716x(90)90209-y
Chou, P. C., and Carleone, J. (1977). The stability of shaped-charge jets. J. Appl. Phys. 48 (10), 4187–4195. doi:10.1063/1.323456
Chou, P. C., Tanzio, C. A., Carleone, J., and Cicarelli, R. D. (1977). Shaped charge jet break up studies using radiograph measurement and surface instability calculations, shaped charge jet break up studies using radiograph measuirement and surface instability calculations. Wynnewood: USA Ballistic Research Laboratory, 91.
Cowan, K. G., and Bourne, B. (2001). Analytical code and hydracode modelling and experimental characterisation of shaped charges containing conical molybdenum liners, 19th International Symposium of Ballistics. Switzerland: Interlaken, 763–771.
Curtis, J. P. (1987). Axisymmetric instability model for shaped charge jets. J. Appl. Phys. 61 (11), 4978–4985. doi:10.1063/1.338317
Epstein, B. (1947). The mathematical description of certain breakage mechanisms leading to the logarithmico-normal distribution. J. Frankl. Inst. 244 (6), 471–477. doi:10.1016/0016-0032(47)90465-1
Fressengeas, C., and Molinari, A. (1994). Fragmentation of rapidly stretching sheets. Eur. J. Mech. Solids. 13 (2), 251–268.
Fressengeas, C., and Molinari, A. (1985). Inertia and thermal effects on the localization of plastic flow. Acta Metall. 33 (3), 387–396. doi:10.1016/0001-6160(85)90081-1
Fressengeas, C., and Molinari, A. (1987). Instability and localization of plastic flow in shear at high strain rates. J. Mech. Phys. Solids 35 (2), 185–211. doi:10.1016/0022-5096(87)90035-4
Golaski, S. K., and Duffy, M. L. (1987). Effect of grain size on shaped charge jet performance and characteristics, Effect of grain size on shaped charge jet performance and characteristics. U.S. ARMY BALLISTIC RESEARCH LAB, BRL-TR-2800.
Gourdin, W. H., and Lassila, D. H. (1991). Flow stress of OFE copper at strain rates from 10−3 to 104s−1: Grain-size effects and comparison to the mechanical threshold stress model. Acta Metallurgica Materialia 39 (10), 2337–2348. doi:10.1016/0956-7151(91)90015-s
Grady, D. E. (1982). Local inertial effects in dynamic fragmentation. J. Appl. Phys. 53 (1), 322–325. doi:10.1063/1.329934
Guduru, P. R., and Freund, L. B. (2002). The dynamics of multiple neck formation and fragmentation in high rate extension of ductile materials. Int. J. Solids Struct. 39 (21), 5615–5632. doi:10.1016/s0020-7683(02)00367-0
Held, M. (2003). Optical diagnostic of shaped-charge jets, 25th international Congress on high-Speed Photography and Photonics. GERMANY: SCHROBENHAUSEN, 476–489.
Jiang, Y., Gu, R. C., Peterlechner, M., Liu, Y. W., Wang, J. T., and Wilde, G. (2021). Impurity effect on recrystallization and grain growth in severe plastically deformed copper. Mater. Sci. Eng. A 824. doi:10.1016/j.msea.2021.141786doi:141786
Jiang, Y., Hu, J., Jiang, Z., Lian, J., and Wen, C. (2018). Strain rate dependence of tensile strength and ductility of nano and ultrafine grained coppers. Mater. Sci. Eng. A 712, 341–349. doi:10.1016/j.msea.2017.11.083
Jiang, Y., Zhu, R., Wang, J. T., and You, Z. S. (2016). An investigation on rolling texture transition in copper preprocessed by equal channel angular pressing. J. Mat. Sci. 51 (12), 5609–5624. doi:10.1007/s10853-016-9862-2
Kipp, M. E., and Grady, D. E. (1985). Dynamic fracture growth and interaction in one dimension. J. Mech. Phys. Solids 33 (4), 399–415. doi:10.1016/0022-5096(85)90036-5
Kumar, A., and Kumble, R. G. (1969). Viscous drag on dislocations at high strain rates in copper. J. Appl. Phys. 40 (9), 3475–3480. doi:10.1063/1.1658222
Lienau, C. C. (1936). Random fracture of a brittle solid. J. Frankl. Inst. 221 (4), 769–787. doi:10.1016/s0016-0032(36)90526-4
Mahmudi, R., and Mehdizadeh, M. (1998). Surface roughening during uniaxial and equi-biaxial stretching of 70-30 brass sheets. J. Mat. Process. Technol. 81 (0), 707–712. doi:10.1016/s0924-0136(98)00099-5
Mao, Z. N., An, X. H., Liao, X. Z., and Wang, J. T. (2018). Opposite grain size dependence of strain rate sensitivity of copper at low vs high strain rates. Mater. Sci. Eng. A 738, 430–438. doi:10.1016/j.msea.2018.09.018
Meyers, M., Andrade, U., and Chokshi, A. (1995). The effect of grain size on the high-strain, high-strain-rate behavior of copper. Metall. Mat. Trans. A 26 (11), 2881–2893. doi:10.1007/bf02669646
Mott, N. F. (1947). Fragmentation of shell cases. Proc. R. Soc. Lond. A Math. Phys. Sci. 189 (1018), 300–308. doi:10.1098/rspa.1947.0042
Murr, L. E., Niou, C. S., Garcia, E. P., Ferreyra, E., Rivas, T. J. M., and Sanchez, J. C. (1997). Comparison of jetting-related microstructures associated with hypervelocity impact crater formation in copper targets and copper shaped charges. Mater. Sci. Eng. A 222 (2), 118–132. doi:10.1016/s0921-5093(96)10518-9
Petit, J., Jeanclaude, V., and Fressengeas, C. (2005). Breakup of Copper shaped-charge jets: Experiment, numerical simulations, and analytical modeling. J. Appl. Phys. 98 (12), 123521. doi:10.1063/1.2141647
Petit, J., Jeanclaude, V., and Fressengeas, C. (2006). Effects of liner grain size on shaped – charge jet performance: A combined experimental/numerical/analytical approach. J. Phys. IV Fr. 134 (1), 379–384. doi:10.1051/jp4:2006134058
Schwartz, A. J., and Baker, E. L. (1999). Effect of interior surface finish on the break-up of commercial shaped charge liners, 18th International Symposium on Ballistics. San Antonio, TX (US): Lawrence Livermore National Laboratory.
Shekhar, H. (2012). Theoretical Modelling of shaped charges in the Last Two Decades (1990-2010): A review. Central Eur. J. Energetic Mater. 9 (2), 155–185.
Shenoy, V. B., and Freund, L. B. (1999). Necking bifurcations during high strain rate extension. J. Mech. Phys. Solids 47 (11), 2209–2233. doi:10.1016/s0022-5096(99)00031-9
Suo, T., Li, Y., Zhao, F., Fan, X., and Guo, W. (2013). Compressive behavior and rate-controlling mechanisms of ultrafine grained copper over wide temperature and strain rate ranges. Mech. Mat. 61, 1–10. doi:10.1016/j.mechmat.2013.02.003
Walsh, J. M. (1984). Plastic instability and particulation in stretching metal jets. J. Appl. Phys. 56 (7), 1997–2006. doi:10.1063/1.334234
Wang, C. T., and Langdon, T. G. (2021). An examination of strain weakening and self-annealing in a Bi-Sn alloy processed by high-pressure torsion. Mater. Lett. 301. doi:10.1016/j.matlet.2021.130321doi:130321
Wei, Q., and Kecskes, L. J. (2008). Effect of low-temperature rolling on the tensile behavior of commercially pure tungsten. Mater. Sci. Eng. A 491 (1–2), 62–69. doi:10.1016/j.msea.2008.01.013
Wei, Q. (2007). Strain rate effects in the ultrafine grain and nanocrystalline regimes—Influence on some constitutive responses. J. Mat. Sci. 42 (5), 1709–1727. doi:10.1007/s10853-006-0700-9
Zaiser, M., Grasset, F. M., Koutsos, V., and Aifantis, E. C. (2004). Self-affine surface Morphology of plastically deformed metals. Phys. Rev. Lett. 93 (19). doi:10.1103/physrevlett.93.195507doi:195507
Keywords: grain size effect, shaped charge jet, analytical model, dynamic stretching, copper
Citation: Jiang Y, Gu RC, Wang JT, Xiao Q-Q and Huang Z-X (2022) Investigation on the grain size effect on the copper shaped charge jet stretching behavior. Front. Mater. 9:1017629. doi: 10.3389/fmats.2022.1017629
Received: 12 August 2022; Accepted: 13 September 2022;
Published: 04 October 2022.
Edited by:
Jianghua Shen, Northwestern Polytechnical University, ChinaCopyright © 2022 Jiang, Gu, Wang, Xiao and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yao Jiang, amlhbmd5YW9Abmp1c3QuZWR1LmNu; Jing Tao Wang, anR3YW5nQG5qdXN0LmVkdS5jbg==
 Yao Jiang
Yao Jiang Rui Cong Gu1
Rui Cong Gu1