- 1School of Flight Technology, Civil Aviation Flight University of China, Guanghan, China
- 2Guanghan Branch, Civil Aviation Flight University of China, Guanghan, China
- 3School of Aviation Engineering, Civil Aviation Flight University of China, Guanghan, China
- 4College of Aviation, Kunming University of Science and Technology, Kunming, China
The modified uncoupled lower-order beam theory (LBT) based on the third-order shear deformation model was established for functionally graded (FG) beams with circular cross-section in this paper. Based on the shear stress free condition on the boundary of the circular cross-section, the bidirectional warping function of the axial displacement is mathematically derived for the first time. The power-law form in the radial direction is adopted to describe continuous variation of material properties. Generalized stresses are defined through the orthogonal form of the axial displacement and then expressed in the decoupling form, in which the shear correction factor and three relatively small coefficients are involved. The frame independent uncoupled equilibrium equations and the corresponding boundary conditions are obtained via the asymptotic principle of virtual work. The present LBT is validated through the pure bending of a Clamped-Clamped FG beam by comparing the obtained deflections with the published results. Accordingly, the effects of shear, warping and stress mitigation acting on the cross-section influenced by the power-law exponent have been described graphically and discussed.
1 Introduction
Functionally graded (FG) materials are a class of composites, the properties of which vary continuously and smoothly from one surface to another. Typically, these materials are made from a mixture of ceramic and metal or from a combination of materials. The ceramic constituent provides high-temperature resistance due to its low thermal conductivity. Beams with solid or hollow circular cross-section are widely used in macro and micro fields, such as the steel ropes of bridges and the landing gears of aircrafts, the cylindrical beams for building support, oil pipelines in the transportation field, carbon nanotubes and microtubules in the fields of medicine, biotechnology and smart material (Kapuria et al., 2008; Şimşek, 2010; El Meiche et al., 2011; Shi and Voyiadjis, 2011; Neves et al., 2013; Belabed et al., 2014; Pradhan and Chakraverty, 2014). When the beams with circular cross-section are made of FG materials, the mechanical properties will be significantly improved.
Theories for FG beams or plates have been proposed successively. In the early stage, in order to take the shear effect on the cross-section into account, it is very common to use Timoshenko beam theory (TBT) to study the FG beam problems (Timoshenko, 1921; Popescu and Hodges, 2000; Yu et al., 2002; Li, 2008; Dong et al., 2010). Due to the linear variation of the normal strain on the cross-section, the TBT can be regarded as the first-order shear deformation theory with the shear coefficient KT. The shear coefficient KT is introduced to improve the calculation accuracy, that has been studied in detail by many scholars (Cowper, 1966; Hutchinson, 2001; Dong et al., 2010). According to the results of Cowper’s (Cowper, 1966) study on homogeneous beams, the shear coefficient is close to 5/6 for rectangular cross-section and is close to 6/7 for circular cross-section. However, it is difficult to determine the value of shear coefficient for FG beams because of different cross-section shapes and material distribution. In addition, the shear stress free condition on the boundary of cross-section is not satisfied in TBT.
In order to overcome the disadvantages of TBT, Levinson (Levinson, 1981) first proposed the beam theory based on the third-order shear deformation model that has received the most attention. In the higher-order shear deformation (HSD) model, the warping effect on the cross-section is taken into consideration and the shear stress free condition is satisfied. Since then, a variety of theories based on HSD models have been proposed by many scholars (Reddy et al., 2001; Aydogdu, 2009; Şimşek, 2010; El Meiche et al., 2011; Shi and Voyiadjis, 2011; Huang et al., 2013; Belabed et al., 2014; Pradhan and Chakraverty, 2014; Duan and Li, 2016a; Duan and Li, 2016b; Geng et al., 2017; Pei et al., 2018; Pei et al., 2019; Huang, 2020; Ma et al., 2021), and can be divided into two types according to the differential order of the governing equations, i.e., the higher-order beam theory (HBT) and the lower-order beam theory (LBT).
The proposal of HBT is mainly inspired by Reddy’s (Reddy et al., 2001) idea of deriving the governing equations through the variational principle. Based on different HSD models, the sixth-order differential governing equation of the deflection is obtained in HBT, that results in high computational accuracy. Meanwhile, the boundary layer effect near concentrated load and fixed support constraints is revealed by HBT (Shi and Voyiadjis, 2011; Duan and Li, 2016c). This has since become a common way of deriving the governing equations (Reddy et al., 2001; Aydogdu and Taskin, 2007; Şimşek, 2010; El Meiche et al., 2011; Shi and Voyiadjis, 2011), even ignoring the difficulty of solving the equations analytically or numerically.
Compared with HBT, the fourth-order differential governing equation of the deflection is obtained in HBT or TBT. Although the calculation accuracy of LBT is not as high as that of HBT, LBT is more convenient to solve and can be widely used in engineering with sufficient calculation accuracy like TBT. In view of this, the governing equations of TBT should be derived by reasonable approximation of the variational principle, which depends on the proper definition of the generalized stresses to decompose the higher order small quantities of the energy functional (Duan and Li, 2016a; Pei et al., 2018). However, some LBTs are established by the differential equilibrium relationship of the forces (Huang et al., 2013; Huang, 2020), that are often questioned.
Compared with FG beams with rectangular cross-sections, there are a few studies on FG beams with circular cross-sections. The LBT for FG beams with circular-section based on the third-order HSD model was proposed by Huang (Huang et al., 2013; Huang, 2020) through the differential equilibrium relationship of forces, in which the axial displacement can be considered to be obtained by trial and error. Ma (Ma et al., 2021) also proposed the LBT to study the buckling and vibration behavior of axially-loaded hollow cylindrical FG pipes. Li (Li et al., 2019) investigated the vibration control and analysis of a rotating FG beam with a lumped mass and bonded piezoelectric films in temperature field. Dong (Dong et al., 2019) studied the dynamic modeling and free vibrations of rotating FG tapered cantilever beams with hollow circular cross-section. The significant effects of extensional–coupling bending are studied for the tapered beam–column with FG cross-sections (Rezaiee-Pajand and Masoodi, 2019).
For FG beams, due to the inappropriate selection of coordinate system and the definitions of basic variables, the coupling between bending and stretch which does not exist for the uniform beam appears unexpectedly. For example, there are coupled expressions of bending and stretch in (Aydogdu and Taskin, 2007; Thai and Vo, 2012; Huang, 2020). For the uncoupled beam theory (Geng et al., 2017; Pei et al., 2019), the bending content is decoupled with the stretching content in the constitutive relations, and hence, the governing equations are greatly simplified.
Motivated by the great importance to overcome disadvantages, this paper begins with the fundamentals of beam problems to develop the modified uncoupled LBT for FG beams with circular cross-section. To this end, this paper is organized as follows. In Section 2, the FG beam with circular cross-section is described and the bidirectional warping function of axial displacement is mathematically derived. In Section 3, the generalized strains and stresses are defined, then the constitutive relations are expressed in the decoupling form, and the rigidity coefficients are calculated. In Section 4, the equilibrium equations and the corresponding boundary conditions are derived based on the principle of virtual work, which ignores the virtual work generated by the higher-order moment. In Section 5, the pure bending problems of the radial graded material beam with circular cross-section are analytically solved and compared with the published results. The concluding remarks are finally made in Section 6.
2 Kinematics of FG beam with circular cross-sections
2.1 Description of the FG beam with circular cross-sections
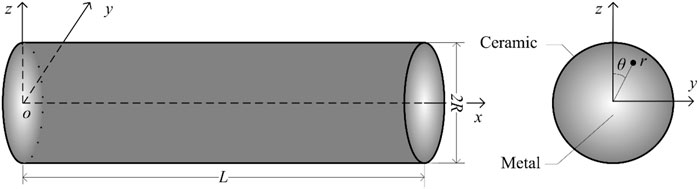
To focus our attention on the FG beam, a straight beam structure with circular cross-section is taken into consideration, as shown in Figure 1. For convenience, the origin o is chosen as the central point of the circular cross-section on the left end, the x-axis is the centroid line of cross-sections, and the Cartesian coordinate system (x, y, z) is established. Meanwhile, the cylindrical coordinate system (x, r, θ) (see Figure 1) is introduced as well, which have the same origin o and the same x-axis described before. R is the radius of the circular cross-section. So, the coordinate transformation relationships are
To exclude the coupling of bending and torsion it will be assumed that the applied loads are symmetric about the x-z plane.
It is assumed that the material properties of FG beam vary along the radial direction. For simplicity, the power-law variation of Young’s modulus can be expressed as
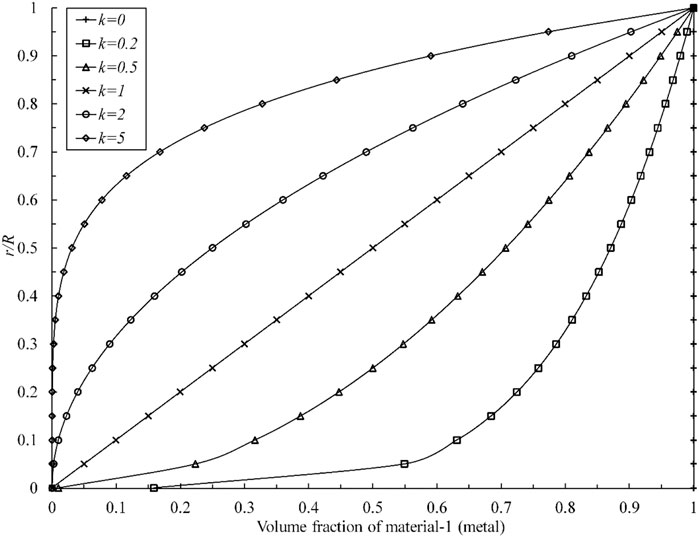
where E1 and E2 denote the Young’s modulus of the metal (material-1) and ceramic (material-2) constituents of the FG beam respectively, k is the non-negative variable parameter (power-law exponent). Poisson’s ratio is assumed to be a constant, and this can be found in the relevant references (Pradhan and Chakraverty, 2014; Pei et al., 2019). Thus, the Young’s modulus of metal with respect to r/R is depicted for various k, as shown in Figure 2.
It can be seen from Figure 2 that k = 0 represents the homogeneous material, k = 1 represents the linearly distributed material and k = 5 represents the exponential distribution material which changes rapidly in r-direction.
2.2 Assumptions and definitions for FG beam problem
Firstly, in order to facilitate theoretical derivation, the basic assumptions and definitions of beam problem are introduced.
Assumption 1: stress assumption.
Based on the elasticity theory for bending of a column, it is reasonable to assume that the following stress components vanish (Huang et al., 2013)
The Assumption 1 adopted for columns is totally different from the plane stress assumption (Aydogdu, 2009; Şimşek, 2010; Pei et al., 2018) for beams with rectangular cross-section.
Assumption 2: displacement field assumption.
Based on Assumption 1, the displacement field of the column can be assumed in a general form as
where fc(x), f1(x) and fR(x) are three unknown functions to be determined, g (y,z) is called the bidirectional warping function in (Geng et al., 2017) with two properties
It should be pointed out that, the displacement field assumption Eq. 4 in the present work is different from the displacement field in the theory for beams with rectangular cross-section (Geng et al., 2017; Pei et al., 2019) due to the bidirectional warping function g (y,z).
In the first of Eq. 4, zc is the neutral point defined in Definition 1.
Definition 1: the definition of neutral point. (Pei et al., 2018)
where A is the area of cross-section and
is the tensile rigidity. Unlike homogeneous material beams, the neutral axis of FG beam is often inconsistent with the centroid axis, except for some special distribution of material, such as the radial FG distribution.
In addition, based on the displacement field Eq. 4, the definition of basic variables in the beam theory is also introduced.
Definition 2: the definition of generalized displacement.
Based on Eq. 4, the variables in beam theory are defined as
where
is the flexural rigidity.
2.3 Derivation of g (y,z) for circular cross-section
In order to derive the explicit expression of axial displacement, the shear stress free condition on the outer lateral surface is introduced as well which requires
where S is the outer boundary
According to Eq. 4, the radial shear strain γxr which can be expressed by
where ny and nz are the cosines of outward normal on boundary S which are expressed
Substituting Eq. 13 into Eq. 12, the shear stress free condition is re-expressed as
In order to make Eq. 14 be satisfied, considering a simple case, the partial differential equation is given by
It is worth mentioning that the right term of Eq. 15 can also be selected as sinusoidal function, exponential function, logarithmic function and other forms with respect to S (y, z), which will derive a variety of HSD models.
On the one hand, by solving partial differential equation Eq. 15, the explicit expression of g (y,z) can be derived as
and the third-order HSD model is obtained.
On the other hand, Eq. 14 is further recast as
Based on Definition 1 Eq. 8 and making use of Eq. 17, the axial displacement of the FG beam can be represented by generalized displacements and arranged in the following orthogonal form
with
In addition, we have following three properties to guarantee decoupling of the three terms in Eq. 18
It will be seen later that the orthogonal decomposition form of the axial displacement Eq. 18 is conducive to the complete decoupling of stretching, bending and warping of the FG beam, which lays a foundation for the simplification of the theoretical expression in this paper.
3 Constitutive relations of FG beam with circular cross-sections
3.1 Definition of generalized strains and generalized stresses
According to Eq. 18 and the last two of Eq. 4, the strains of the FG beam are further cast as
Based on the first of Eq. 21, the normal strain of present LBT can be decomposed into 3 parts, i.e., the uniform stretching, the linear normal strain and the warping strain. The linear normal strain (zϕ’) is the same as that obtained by the first-order model or TBT, while the warping strain a high-order deformation determined by bidirectional warping function g (y,z).
And the stresses are expressed as
Similarly, the normal stress of present LBT can be decomposed into 3 parts corresponding to the three strains, which are the uniform stretching, the first-order normal stress and the warping stress, respectively.
According to the expression of Eq. 21, the generalized strains of FG beam can be defined as
And the generalized stresses (also called stress resultants) for the FG beam problem are defined as
where N, M and
3.2 Constitutive relations
Substituting Eq. 22 into Eq. 24 and making use of Eq. 20, the uncoupled constitutive relations of the FG beam expressed by generalized stresses and strains are
with
and
where Bs is the shear rigidity, Kz, η, ξz and ξy are the four non-dimensional rigidity coefficients, and Ks is like the shear coefficient KT in TBT. It is interesting to see that, the four of Eq. 25 are respectively related to stretching, bending, shearing and higher-order bending which are in the decoupling form (Pei et al., 2018). Besides, these four coefficients will vary with the shape of the cross-section and the power-law exponent k.
3.3 Calculation of the non-dimensional rigidity coefficients
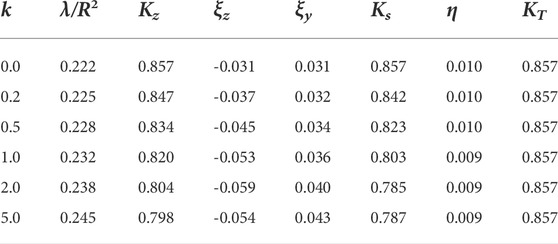
By the way, the higher-order non-dimensional rigidity coefficients η, ξz and ξy are relatively small which have been proved in the theory for FG beams with rectangular cross-section (Pei et al., 2018; Pei et al., 2019), and this property still need to be verified in the present work.
Since the explicit expression of g (y,z) have already been obtained in Eq. 16, the non-dimensional rigidity coefficients in Eq. 27 are derived in the following form
with the following integral
For comparative purpose, aluminum is chosen as the material-1 and zirconia is the material-2, of which the material properties are listed in Table 1.
The non-dimensional rigidity coefficients in Eq. 28 are calculated and listed in Table 2. It is very interesting to notice the fact that the three higher-order rigidity coefficients (i.e. ξx, ξy and η) in Table 3 are indeed small quantities for the FG beam with the third-order HSD mode, which are usually ignored in traditional LBT (Huang et al., 2013; Huang, 2020). As for the shear coefficients Kz and Ks, we know that Kz is the shear coefficients in traditional LBT (Huang et al., 2013; Huang, 2020) and Ks is the shear coefficient corrected by the algebraic sum of ξx and ξy. For the homogeneous beam (when k = 0) with circular cross-section, there is no difference between the shear coefficient in the present LBT and KT = 6/7 ˜ 0.857 in TBT. It is worth mentioning that, according to the change of material distribution, the shear coefficients Kz and Ks in LBT can be adjusted automatically, but the shear coefficient KT in TBT cannot.
4 The lower-order uncoupled theory for FG beam
4.1 Principle of virtual work
In the theory of elasticity, the principle of virtual work for elastic body can be written as
where
On the other hand, according to the generalized strains and stresses of the FG beam, the principle of virtual work for FG beams can be written as
Noticing Eqs. 21–24 and making use of the orthogonal properties Eq. 20, it is easy to prove the equivalence of Eq. 30 and Eq.(31). That is to say that the principle of virtual work of FG beam is variationally consistent with the one of elastic body which will lead to the HBT.
However, considering the characteristic of the small parameter η in Table 2 and ignoring the virtual deformation energy caused by high-order bending moment P, Eq. 31 will degenerate into an approximate form which is
4.2 Modified uncoupled LBT for FG beam
Via integration by parts, Eq. 32 yields
From Eq. 33, the equilibrium equations are obtained as
And the corresponding BCs (e.g. at the end of x = x0) are
It can be seen from Eq. 34 that, equilibrium equations are frame independent, and the stretching, bending, higher-order bending are reciprocally uncoupled in the present framework with the help of the definitions of neutral point and generalized displacements, i.e., Eq. 6 and Eq. 8. In contrast, due to the coupled constitutive relations, the equilibrium equations will inevitably be coupled between bending and tension for the higher-order theories in (Aydogdu and Taskin, 2007; Thai and Vo, 2012).
Making use of Eq. 23 and Eq. 25, in terms of the generalized displacements, the governing equations of the variationally approximated lower-order theory are
As we can see, the first of Eq. 36 is the separately governing equation for stretch. Using the second of Eq. 36 to eliminate ϕ, in terms of w, the third of Eq. 36 yields the governing equation for deflection as
After manipulations, it is not difficult to obtain the rotation as
Eq. 35 provides three pairs of different boundary conditions for Eq. 34. Among them, the first pair (2 in total) is also individually responsible for stretch governed by the first of Eq. 36 -a second-order ODE, while the last two pairs (4 in total) are individually for bending governed by Eq. 37 -a fourth-order ODE. Different from the coupled governing equations in (Huang, 2020), the present theory has concise mathematical form and clear physical meaning. Noticing that Eq. 34 and Eq. 35 are derived from the approximate principle of virtual work Eq. 32, compared with the variationally consistent HBT (Pei et al., 2018), the present LBT will bring great convenience to the calculation due to the reduction of the differential order of the governing equation.
5 Theoretical results and comparison
5.1 Solutions of a Clamped-Clamped FG beam by present LBT
In this section, the static bending problem of the FG beam will be studied to demonstrated the validity and accuracy of the present LBT. Considering the Clamped-Clamped (C-C) supported FG beam subjected to uniformly distributed load (q(x) = q0), based on Eq. 35, the C-C BCs can be expressed by
Since Eqs. 37, 38 are in the same form as the governing equations of lower-order theory for homogeneous beams (Duan and Li, 2016b), it is convenient to obtain the theoretical solutions expressed as
with
5.2 Comparison of the transverse deflections
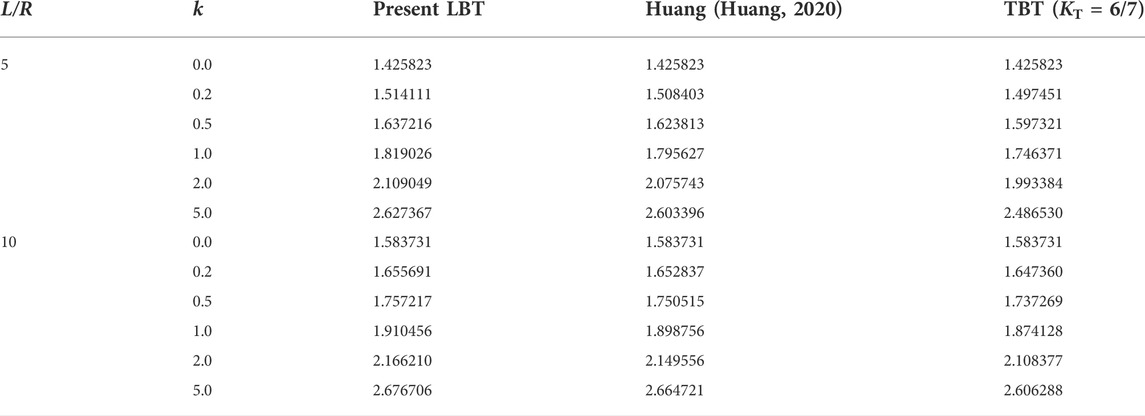
In order to illustrate the correctness of the calculation results in this paper, the comparison of dimensionless maximum transverse deflections w (0)*100E1R3/q0L3 by present LBT, by Huang (Huang, 2020) and by TBT with KT = 6/7 are listed in Table 3.
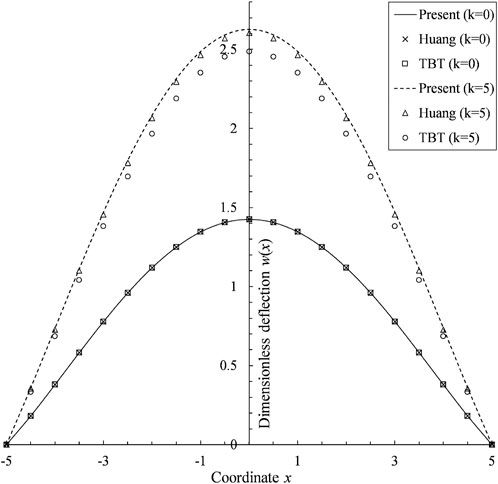
In addition, for the case when L/R = 5 and k = 0 or 5, the dimensionless transverse deflections w(x)* 100E1R3/q0L3 are compared, as shown in Figure 3.
It can be seen from Figure 3 that the results are the same for a homogeneous beam (i.e., k = 0). For the FG beam when k = 5, the deflection obtained by the present LBT is slightly larger than that obtained by Huang, and is also larger than that obtained by TBT.
5.3 Comparison of the normal strains and stresses
The fact is that the bidirectional warping effect on the cross-section can be described based on the present LBT which is not taken into consideration in TBT because of the rigid cross-section hypothesis and can only be described in z-direction for beams with rectangular cross-section because of the one-variate warping function g(z). In view of this, it is very interesting to study the warping effect on the circular cross-section through the bidirectional warping function g (y, z).
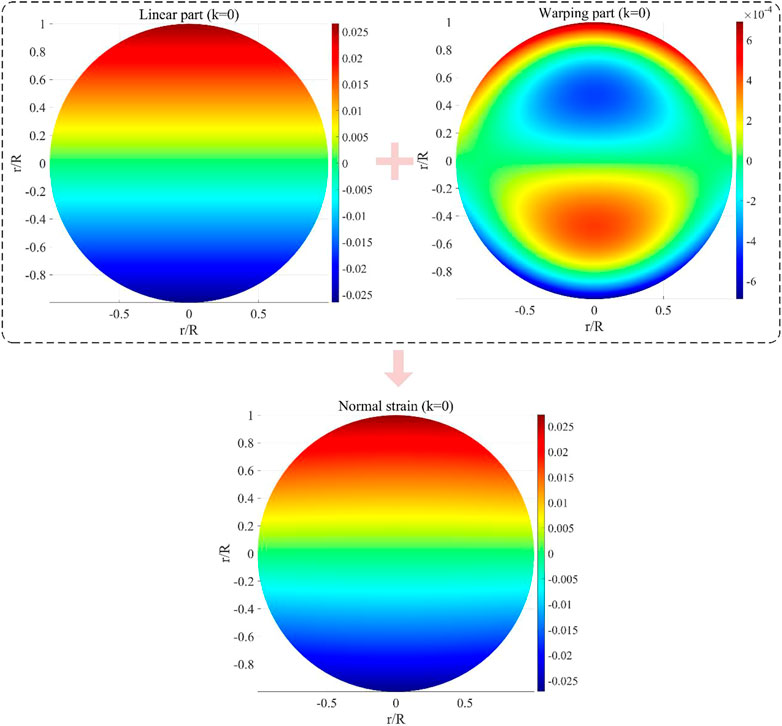
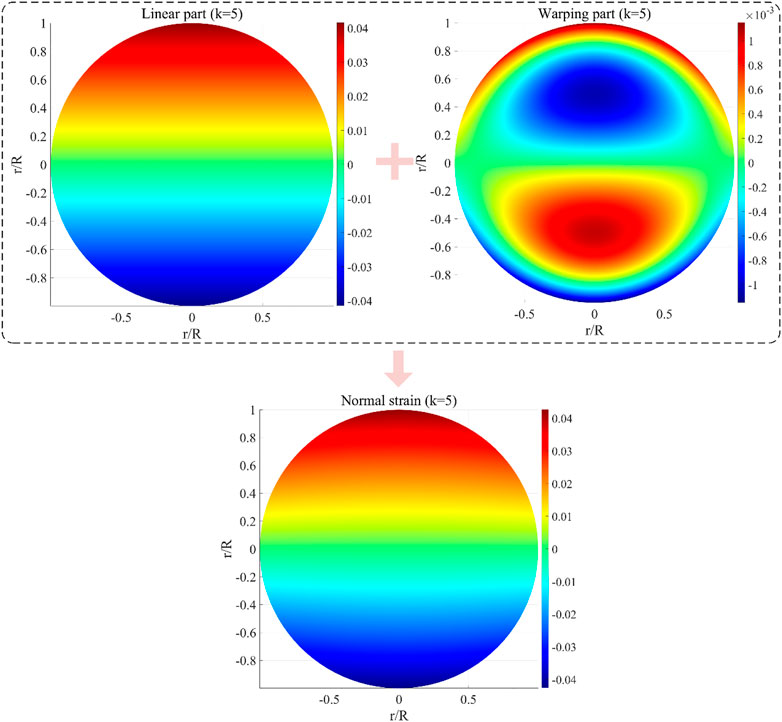
Considering the cross-section of the FG beam with L/R = 10 at x = 0, the normal strains are described by the present LBT for k = 0 and k = 5 are shown in Figure 4 and Figure 5, respectively.
It can be seen from Figure 4 and Figure 5 that the normal strains are both symmetric about the z-axis and anti-symmetric about the y-axis, and this characteristic can also be found in radial shear strain and stresses (or in Figure 8 and Figure 9). It can be found from Eq. 21 that, in the pure bending problem, the normal strains are composed of two parts, i.e., the linear part and the warping part. Because the warping part is much smaller than the linear part, the normal strains are mainly determined by the linear part. The warping part obeys the variation law of cubic function in z-direction, and is significantly affected by the power-law exponent k. By comparing Figure 4 and Figure 5, it can be seen that there is an obvious transition area of material properties on the cross-section when k = 5, which leads to a more obvious difference between tensile and compressive deformation in the warping part of the normal strain.
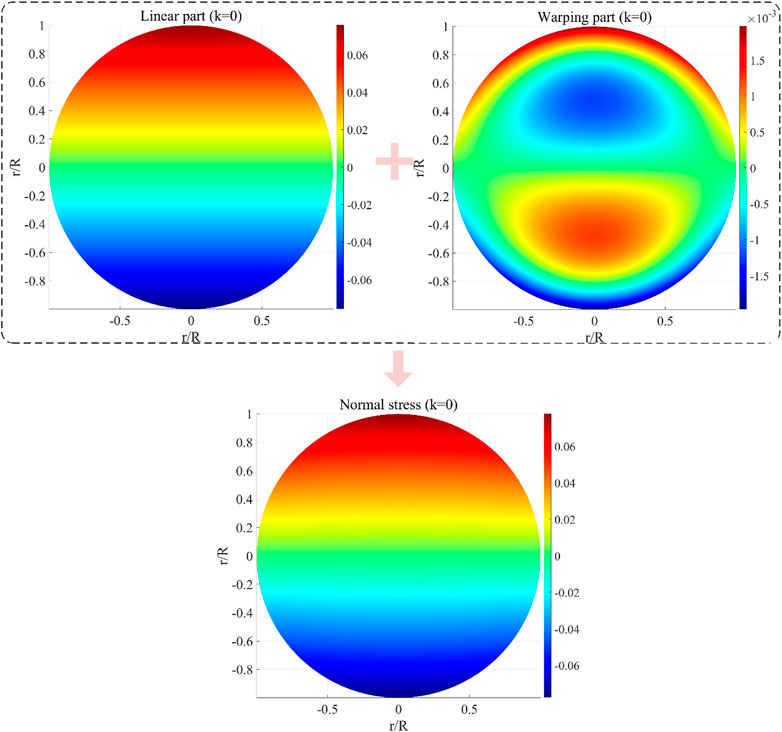
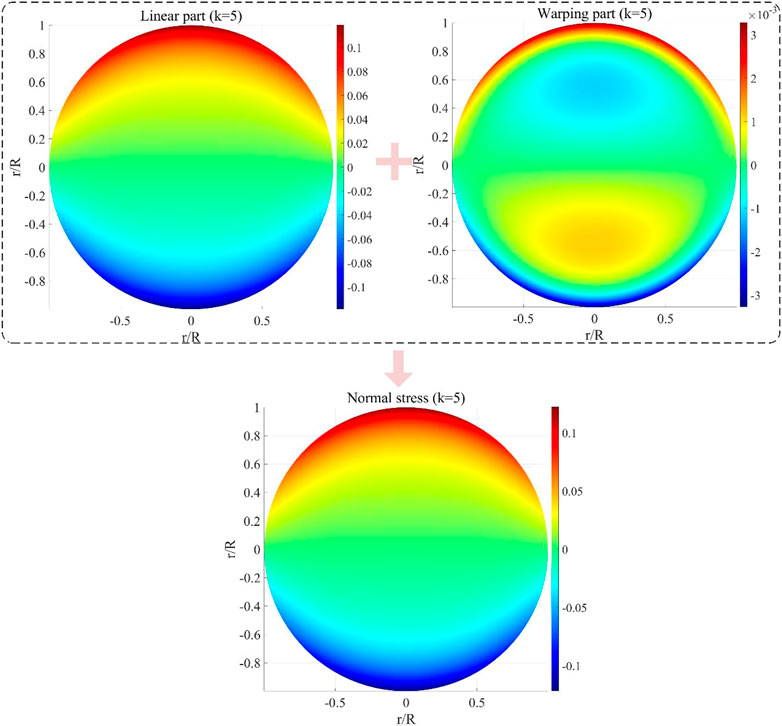
Meanwhile, the normal stresses are described by the present LBT for k = 0 and k = 5 are shown in Figure 6 and Figure 7, respectively.
It can be seen from Figure 6 and Figure 7 that the stress distribution is obviously affected by the power-law exponent k. Compared with the results for k = 0, when k = 5 the normal stress is obviously eased, and the transition regions of tensile and compressive stresses move to the upper and lower boundaries respectively. Meanwhile, the warping parts of normal stresses have little effect on the normal stress distribution, and the warping part is also eased for k = 5.
5.4 Comparison of the radial shear strains and stresses
Since the shear stress free condition on the outer lateral surface is adopted in the HSD model, the radial shear strain and stress state on the cross-section need to be discussed.
Based on Eq. 12, the non-dimensional radial shear strain and stress can be expressed as
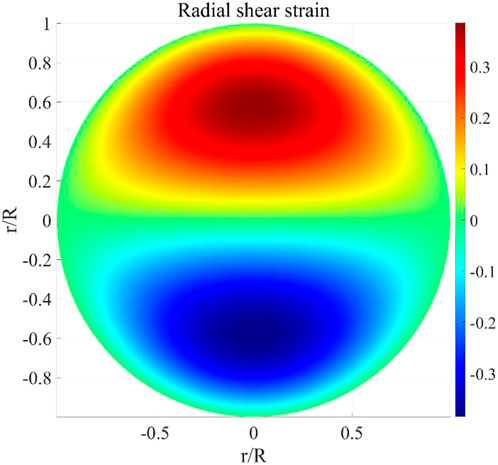
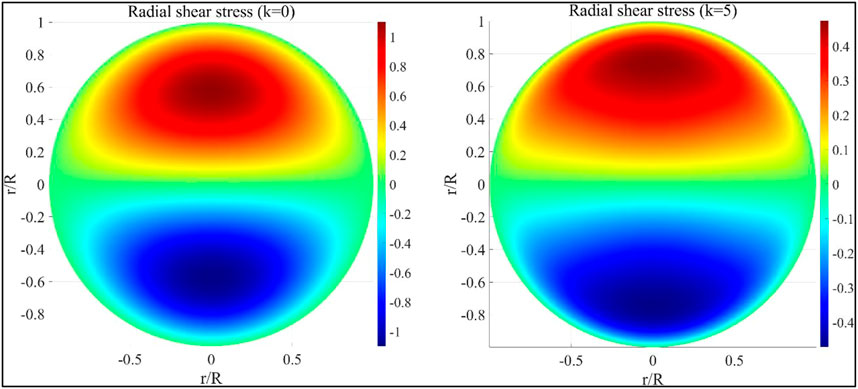
Obviously, according to the first of Eq. 42, the non-dimensional radial shear strain on cross-section of FG beam is independent of k, which is shown in Figure 8. The peaks of the radial shear strain appear near the centroid of the upper and lower semi-circles. In addition, the non-dimensional radial shear stresses on cross-section of FG beam for k = 0 and 5 are shown in Figure 9.
It can be seen from Figure 8 and Figure 9 that the radial shear strain and stresses are free on the boundary of the cross-section. This further verifies the rationality of the HSD model. In Figure 9, compared with radial shear stress for k = 0, the peaks of the radial shear stress move to the upper and lower boundaries for k = 5, respectively.
6 Conclusion
In this paper, the modified uncoupled LBT based on the third-order HSD model has been established for FG beams with circular cross-section via the asymptotic principle of virtual work. The pure bending problem of the C-C FG beam has been studied, and the accuracy and effectiveness of the present uncoupled LBT can be confirmed by comparing the results with those calculated by the TBT and the coupled LBT.
There are three main outcomes of the investigation listed as follows:
1) The nonphysical coupling between bending and stretch has been removed in the present theory.
2) The bidirectional warping function of the third-order HSD model that satisfied the shear stress free condition on the boundary of circular cross-section has been derived.
3) The effects of shear, warping and stress mitigation acting on the cross-section have been described graphically.
The current idea can be extended to the uncoupled lower-order and higher-order theories for FG beams with elliptic or thin-walled cross-section. The study on these topics will be reported elsewhere.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
TD: Theoretical derivation and writing draft paper. XL: writing—reviewing and supervision. YX: numerical calculation and writing. LZ: writing—reviewing and supervision. CC: paper editing. ZL: Material scheme design.
Funding
This work was supported by the Fundamental Research Funds for the Central Universities (Nos. J2020-001, ZJ2021-08) and the National Natural Science Foundation of China (Grant Nos. U2033213, 51864026). The authors are grateful for their financial support.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aydogdu, M. (2009). A new shear deformation theory for laminated composite plates. Compos. Struct. 89, 94–101. doi:10.1016/j.compstruct.2008.07.008
Aydogdu, M., and Taskin, V. (2007). Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 28, 1651–1656. doi:10.1016/j.matdes.2006.02.007
Belabed, Z., Ahmed Houari, M. S., Tounsi, A., Mahmoud, S. R., and Anwar Bég, O. (2014). An efficient and simple higher order shear and normal deformation theory for functionally graded material (FGM) plates. Compos. Part B Eng. 60, 274–283. doi:10.1016/j.compositesb.2013.12.057
Cowper, G. R. (1966). The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 33, 335–340. doi:10.1115/1.3625046
Dong, S. B., Alpdogan, C., and Taciroglu, E. (2010). Much ado about shear correction factors in Timoshenko beam theory. Int. J. Solids Struct. 47, 1651–1665. doi:10.1016/j.ijsolstr.2010.02.018
Dong, S., Li, L., and Zhang, D. (2019). Vibration analysis of rotating functionally graded tapered beams with hollow circular cross-section. Aerosp. Sci. Technol. 95, 105476. doi:10.1016/j.ast.2019.105476
Duan, T. C., and Li, L. X. (2016). Discussion: “A sixth-order theory of shear deformable beams with variational consistent boundary conditions” (Shi, G., and Voyiadjis, G. Z., 2011, ASME J. Appl. Mech., 78(021019), pp. 1-11). J. Appl. Mech. 83, 025501.
Duan, T. C., and Li, L. X. (2016). Study on higher-order shear deformation theories of Thick-plate. Chin. J. Theor. Appl. Mech. 48, 1096–1113.
Duan, T. C., and Li, L. X. (2016). The unified solution for a beam of rectangular cross-section with different higher-order shear deformation models. Lat. Am. J. solids Struct. 13, 1716–1737. doi:10.1590/1679-78252732
El Meiche, N., Tounsi, A., Ziane, N., Mechab, I., and Bedia, E. A. (2011). A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. Int. J. Mech. Sci. 53, 237–247. doi:10.1016/j.ijmecsci.2011.01.004
Geng, P. S., Duan, T. C., and Li, L. X. (2017). An uncoupled higher-order beam theory and its finite element implementation. Int. J. Mech. Sci. 134, 525–531. doi:10.1016/j.ijmecsci.2017.10.041
Huang, Y. (2020). Bending and free vibrational analysis of bi-directional functionally graded beams with circular cross-section. Appl. Math. Mech. 41, 1497–1516. doi:10.1007/s10483-020-2670-6
Huang, Y., Wu, J. X., Li, X. F., and Yang, L. E. (2013). Higher-order theory for bending and vibration of beams with circular cross section. J. Eng. Math. 80, 91–104. doi:10.1007/s10665-013-9620-2
Hutchinson, J. R. (2001). Shear coefficients for timoshenko beam theory. J. Appl. Mech. 68, 87–92. doi:10.1115/1.1349417
Kapuria, S., Bhattacharyya, M., and Kumar, A. N. (2008). Bending and free vibration response of layered functionally graded beams: A theoretical model and its experimental validation. Compos. Struct. 82, 390–402. doi:10.1016/j.compstruct.2007.01.019
Levinson, M. (1981). A new rectangular beam theory. J. Sound Vib. 74, 81–87. doi:10.1016/0022-460x(81)90493-4
Li, L., Liao, W.-H., Zhang, D., and Zhang, Y. (2019). Vibration control and analysis of a rotating flexible FGM beam with a lumped mass in temperature field. Compos. Struct. 208, 244–260. doi:10.1016/j.compstruct.2018.09.070
Li, X. F. (2008). A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler–Bernoulli beams. J. Sound Vib. 318, 1210–1229. doi:10.1016/j.jsv.2008.04.056
Ma, W. L., Cheng, C., Chen, X., and Li, X. F. (2021). Free vibration of radially graded hollow cylinders subject to axial force via a higher-order shear deformation beam theory. Compos. Struct. 255, 112957. doi:10.1016/j.compstruct.2020.112957
Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Cinefra, M., Roque, C. M. C., Jorge, R. M. N., et al. (2013). Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Compos. Part B Eng. 44, 657–674. doi:10.1016/j.compositesb.2012.01.089
Pei, Y. L., Geng, P. S., and Li, L. X. (2018). A modified higher-order theory for FG beams. Eur. J. Mech. - A/Solids 72, 186–197. doi:10.1016/j.euromechsol.2018.05.008
Pei, Y. L., Geng, P. S., and Li, L. X. (2019). A modified uncoupled lower-order theory for FG beams. Arch. Appl. Mech. 89, 755–768. doi:10.1007/s00419-018-1494-3
Popescu, B., and Hodges, D. H. (2000). On asymptotically correct Timoshenko-like anisotropic beam theory. Int. J. Solids Struct. 37, 535–558. doi:10.1016/s0020-7683(99)00020-7
Pradhan, K. K., and Chakraverty, S. (2014). Effects of different shear deformation theories on free vibration of functionally graded beams. Int. J. Mech. Sci. 82, 149–160. doi:10.1016/j.ijmecsci.2014.03.014
Reddy, J. N., Wang, C. M., Lim, G. T., and Ng, K. H. (2001). Bending solutions of Levinson beams and plates in terms of the classical theories. Int. J. Solids Struct. 38, 4701–4720. doi:10.1016/s0020-7683(00)00298-5
Rezaiee-Pajand, M., and Masoodi, A. R. (2019). Stability analysis of frame having FG tapered beam–column. Int. J. Steel Struct. 19, 446–468. doi:10.1007/s13296-018-0133-8
Shi, G., and Voyiadjis, G. Z. (2011). A sixth-order theory of shear deformable beams with variational consistent boundary conditions. J. Appl. Mech. 78, 021019. doi:10.1115/1.4002594
Şimşek, M. (2010). Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl. Eng. Des. 240, 697–705. doi:10.1016/j.nucengdes.2009.12.013
Thai, H.-T., and Vo, T. P. (2012). Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 62, 57–66. doi:10.1016/j.ijmecsci.2012.05.014
Timoshenko, S. P. (1921). LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 41, 744–746. doi:10.1080/14786442108636264
Keywords: functionally graded beam, circular cross-section, bidirectional warping effect, principle of virtual work, uncoupled lower-order theory
Citation: Duan TC, Li XY, Xiao Y, Zhang L, Chen C and Li ZJ (2022) A modified lower-order theory for FG beam with circular cross-section. Front. Mater. 9:1020820. doi: 10.3389/fmats.2022.1020820
Received: 16 August 2022; Accepted: 27 September 2022;
Published: 10 October 2022.
Edited by:
Patrizia Trovalusci, Sapienza University of Rome, ItalyReviewed by:
Michele Bacciocchi, University of the Republic of San Marino, San MarinoAmir R. Masoodi, Ferdowsi University of Mashhad, Iran
Copyright © 2022 Duan, Li, Xiao, Zhang, Chen and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: X. Y. Li, bGl4aXV5aTY2OTBAMTYzLmNvbQ==
 T. C. Duan
T. C. Duan X. Y. Li
X. Y. Li Y. Xiao
Y. Xiao L. Zhang1
L. Zhang1