Optimal design of topological waveguides by machine learning

Topological insulators supply robust edge states and can be used to compose novel waveguides to protect energy propagation against various defects. For practical applications, topological waveguides with a large working bandwidth and highly localized interface mode are desired. In the present work, mechanical valley Hall insulators are described by explicit geometry parameters using the moving morphable component method first. From the geometry parameters, artificial neural networks (ANN) are then well-trained to predict the topological property and the bounds of nontrivial bandgaps. Incorporating those ANN models, mathematical formulation for designing optimal mechanical topological waveguides can be solved efficiently, with an acceleration of more than 10,000 times than the traditional topology optimization approach.

1 Introduction

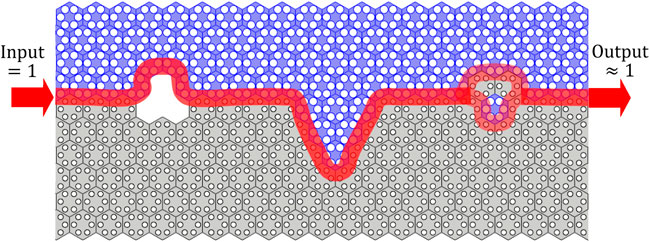
Utilizing the topologically protected edge states, topological waveguides surpass the classical waveguides from the following aspects: backscattering free, immunity to cavities, disorders and sharp corners, and a theoretically perfect transmission rate (Figure 1). The underlying principle is the well-known bulk-edge correspondence, which declares that the topological edge states are determined and protected by the difference of topological invariants for both sides of the waveguide (Hasan and Kane, 2010; Qi and Zhang, 2011; Asbóth et al., 2016). As a result, topological materials open a new avenue for the efficient manipulation of waves, and there has been a great interest in developing topological insulators in different physical systems (Huber, 2016; Ma et al., 2019; Ozawa et al., 2019; Tokura et al., 2019; He et al., 2022a; Breunig and Ando, 2022; Xue et al., 2022).

FIGURE 1

FIGURE 1. An illustration of a topological waveguide.

Besides the success of classic topological insulator models in photonic and phononic systems (He et al., 2016; Huber, 2016; Ma and Shvets, 2016; Dong et al., 2017; Pal and Ruzzene, 2017; Chen et al., 2018; Liu and Semperlotti, 2018; Lu et al., 2018; Chen et al., 2019a; Chen et al., 2019b; Fan et al., 2019; Ma et al., 2019; Ozawa et al., 2019; Zhou et al., 2020; Xue et al., 2022), topology optimization has been used for the inverse design of topological insulators with optimized performance, e.g., a wider topological band gap. Christiansen and his collaborators obtained acoustic and photonic spin-Hall insulators by realizing the novel wave propagation path in a well-designed waveguide (Christiansen et al., 2019a; Christiansen et al., 2019b). Nanthakumar et al. (2019) and Chen et al. (2019c) used topology optimization methods to rationally obtain band structures with Dirac cones. Based on that, first-order photonic topological insulators with extra-wide bandgaps and second-order topological insulators are successfully obtained (Chen et al., 2019c; Chen et al., 2020). Dong et al. (2021) customized Dirac cones with various symmetries and degeneracies, and further constructed novel broadband acoustic topological insulators in square lattices by topology optimization. To consider the topological requirement during the optimization process, Du et al. (2020) proposed a quantitative measure of band inversion and adopted the explicit topology optimization method to describe continuum unit cells (UCs). Mathematical formulations for quantum valley Hall insulators and spin Hall insulators were given in (Du et al., 2020; Luo et al., 2021a). Recently, multi-class and multi-functional topological crystalline insulators have been systematically designed by combining the moving morphable component method and symmetry indicator method (Luo et al., 2021b). A comprehensive review of the inverse design of topological insulators is referred to (Chen et al., 2022).

Although remarkable progress has been achieved in the above work, computational efficiency is still a bottleneck for the inverse design of topological insulators. In particular, in the solution process of the topology optimization method, tens to hundreds (or even thousands) of times of analyzing intermediate designs are necessary to obtain the final optimized design, especially when intelligent algorithms are used. Even though alternative physical requirements have been developed to escape from the expensive calculation of topological invariants, for continuum UCs, solving the mathematical formulations for optimal topological insulators with genetic algorithm (GA) is still a time-consuming task (Du et al., 2020; Luo et al., 2021a; Luo et al., 2021b). It is worth noting that machine learning techniques have been recently used for the classification of topological insulators (Long et al., 2020), prediction of topological transitions (Wu et al., 2020), summarization of the phase diagram of disordered higher-order topological insulators (Araki et al., 2019), and inverse design of photonic topological insulators (Long et al., 2019). Additionally, topological metaplates for flexural waves and phononic beams with nontrivial topological properties have been obtained by machine learning (He et al., 2021; He et al., 2022b). And a recent review of the intelligent on-demand design of phononic metamaterials is available (Jin et al., 2022).

In the present work, focused on continuum-type unit cells, based on the design method of optimal valley Hall insulators in (Luo et al., 2021a), artificial neural networks are constructed to predict the topological property and bounds of nontrivial bandgap first, and this can accelerate the computational efficiency by four orders of magnitude. Then alternative mathematical formulations for the inverse design of topological waveguide are presented and solved by the machine learning-assisted procedure. Finally, the present design paradigm obtains an optimal topological waveguide with a highly concentrated transmission path.

The rest of the paper is organized as follows: an explicit description of continuum valley Hall insulators using the moving morphable component (MMC) method is introduced in Section 2. The numerical analysis of band structure and topological property of valley Hall insulators is then sketched in Section 3. After training artificial neural networks for predicting the qualitative topological property and quantitative performance in Section 4, the optimal design of the topological waveguide assisted by machine learning is presented in Section 5. Finally, Section 6 summarizes some concluding remarks.

2 Valley Hall insulators described by moving morphable components

2.1 The MMC method

In the present work, the MMC method is used to describe the valley Hall insulators. In particular, moving morphable components determined by their geometric parameters are set as the basic building blocks to compose the optimal topological insulators (Guo et al., 2014; Zhang et al., 2017; Du et al., 2022). By optimizing those geometry parameters, the configurations of UCs are updated through the moving, morphing, or merging of MMCs. Since the number of design variables is reduced substantially as compared to the traditional implicit topology optimization method, gradient-free algorithms can be used for the inverse design of valley Hall insulators with reasonable time costs. Besides, the intermediate designs with crisp boundaries can be directly modeled in commercial software.

2.2 C3-symmetric unit cells described by MMCs

For the considered $C_3$-symmetric hexagonal lattice made of base medium Al and scattering medium Fe illustrated in Figure 2A, only the material distribution of the diamond region boxed by yellow dashed lines needs to be determined. As shown by Figure 2B, each MMC (representing the scatter) adopted here includes these geometry parameters: the center coordinate $\left(x_0,y_0\right)$, the length ${\rho }_i$ of each control line ${\mathrm{O}\mathrm{P}}_i$ and the inclined angle $\varphi$ of line $\mathrm{O}{\mathrm{P}}_1$. So the design variable of the $\alpha$-th component is denoted as ${\mathit{D}}_{\alpha }={\left(x_0^{\alpha },y_0^{\alpha },{\left\{{\rho }_i^{\alpha }\right\}}_{i=1,\dots ,4},{\varphi }^{\alpha }\right)}^{\top }$. To make the boundary smoother, 3 interpolation points are introduced between the adjacent control points (Luo et al., 2021a). The first irreducible Brillouin zone boundary of the hexagonal UC is illustrated in Figure 2C and will be used to obtain the band structures in the subsequent sections.

FIGURE 2

FIGURE 2. (A) The $C_3$-symmetric hexagonal UC described by the MMCs, (B) the design variables of each MMC and (C) the first irreducible Brillouin zone boundary of the hexagonal UC.

3 Valley Hall insulator classified by its band structure and topological property

As a typical topological matter, valley Hall insulators can hold protected edge states which are robust to various defects (Ma and Shvets, 2016; Dong et al., 2017; Pal and Ruzzene, 2017; Chen et al., 2018; Liu and Semperlotti, 2018; Lu et al., 2018; Chen et al., 2019a). Instead of calculating the expensive valley Chern numbers, it is to trace the gapped Dirac cone through the objective bandgap and phase vortexes for the identification of valley Hall insulators in this work (Luo et al., 2021a).

3.1 Band structures of valley Hall insulators

To illustrate the valley Hall insulators, a $C_3$-symmetric hexagonal unit cell with six inserted circles of radii $R_1$ and $R_2$ is presented in Figure 3. The harmonic elastic out-of-plane wave is governed by the following equations

$\begin{array}{c}\begin{array}{c}\mu {\nabla }^2{u}_z={\omega }^2\rho u_z\\ u_z\left(\mathit{r}+\mathit{R}\right)=e^{i\mathit{k}\bullet \mathit{R}}{u}_z\left(\mathit{r}\right)\end{array}\end{array}(1)$

where $\rho$ and $\mu$ are the mass density and Lame’s parameter; $\mathit{k}$, $\mathit{R}$ and $u_z$ are the wavevector, lattice vector and harmonic out-of-plane displacement field, respectively.

FIGURE 3

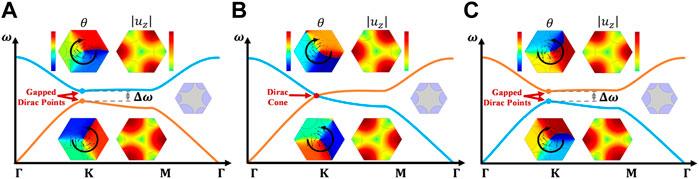
FIGURE 3. The band structures of C3-symmetric hexagonal UCs with setting (A) $R_1=0.3A,R_2=0.2A$, (B) $R_1=R_2=0.25A$ and (C) $R_1=0.2A,R_2=0.3A$ ($A$ denoting the lattice constant). The corresponding UCs, the out-of-plane displacement fields, and phase fields at the (gapped) Dirac points are inserted as well.

Thanks to the explicit geometry description, the UCs described by the MMC method are modeled in COMSOL 5.6 and analyzed with body-fitted mesh. By solving Eq. 1 for each wavevector $\mathit{k}$, band structures are present in Figure 3. The lattice constant is $A=1\mathrm{m}$, and the material parameters are set as: the base medium with elastic modulus $E_0=70\mathrm{G}\mathrm{P}\mathrm{a}$, Poisson’s ratio ${\nu }_0=0.35$ and mass density ${\rho }_0=2700\mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3}$, the scattering medium with elastic modulus $E=200\mathrm{G}\mathrm{P}\mathrm{a}$, Poisson’s ratio $\nu =0.3$ and mass density $\rho =7800\mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{-3}$. For the case $R_1=R_2$, a Dirac cone exists in the band structure of Figure 3B. By breaking the symmetry of the UC along different directions, i.e., $R_1>R_2$ and $R_1<R_2$, gaps would be introduced between the Dirac points and the eigenmodes at the gapped Dirac points will be reordered, as shown in Figures 3A,C. The UCs in Figures 3A,C are both valley Hall insulators and can be used for generating topological waveguides. Therefore, how to obtain a pair of valley Hall insulators with different topological properties and a common nontrivial bandgap is crucial for designing topological waveguides (Luo et al., 2021a).

3.2 Vortex of valley Hall insulators

Guaranteed by the bulk-edge correspondence (Hasan and Kane, 2010; Qi and Zhang, 2011; Asbóth et al., 2016), a pair of UCs with different topological invariants is sufficient to create a gapless edge band. For continuum UCs, however, the numerical calculation of topological invariants, e.g., valley Chern number, are very expensive. Therefore, an effective and rapid identification method is necessary.

By noticing the fact that, for the gapped Dirac points, their phase fields of valley Hall insulators present two opposed vortexes (clockwise or anticlockwise), as shown in Figures 3A,C. Luo et al. (2021a) suggested using the opposite phase vortexes as a measure to classify the topological property. Furthermore, the vortex index of the $n$ th eigenmode of the $i$ th unit cell at $\mathrm{K}$ point is defined as the following double integration of unit phase gradient along the tangent vector (positive in anticlockwise)

$\begin{array}{c}{\tau }_n^{\left(i\right)}=\frac{1}{\left|\Omega \right|}{\iint }_{\Omega }\frac{\nabla {\theta }_n^{\left(i\right)}\bullet {\mathit{e}}_{\tau }}{\left|\nabla {\theta }_n^{\left(i\right)}\right|}dS,{\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathit{e}}_{\tau }=\frac{1}{\sqrt{x^2+y^2}}\left(-y,x\right)\end{array}(2)$

In principle, a perfect vortex index is a quantized value of $-1$, $0$, or $+1$, and the topological phase transition can be effectively identified from the sign of the unvarnished vortex quantity. As pointed out in (Luo et al., 2021a), in numerical implementations, setting a relatively large threshold for the vortex index would be effective.

4 Artificial neural networks for mechanical valley Hall insulators

4.1 Dataset generation

To construct the dataset, one MMC is randomly generated in the primitive diamond region of a C3-symmetric hexagonal UC with lattice constant $A=1\mathrm{m}$ and its $y$-coordinate of the center is fixed as $A/2$. As a result, the UC can be determined only by 6 design variables, and the input vector denotes $\mathit{X}={\left(x_0,{\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,\varphi \right)}^{\top }$.

From the application aspect of topological waveguides, a wider common bandgap of the valley Hall insulators is beneficial for a larger working bandwidth and a more localized edge mode. Therefore, both the bounds of objective (nontrivial) bandgap and the vortex indexes are necessary information. For each UC, we set the normalized upper and lower bounds of the objective bandgap (denoted as $\mathit{Y}={\left({\overline{\omega }}_1,{\overline{\omega }}_2\right)}^{\top }$) (with ${\overline{\omega }}_1=A\underset{\mathit{k}}{\max }{\omega }_1\left(\mathit{k}\right)/\left(2\pi c_0\right)$ and ${\overline{\omega }}_2=A\underset{\mathit{k}}{\min }{\omega }_2\left(\mathit{k}\right)/\left(2\pi c_0\right)$) and the two vortex indexes (denoted as $\mathit{Y}={\left({\tau }_1,{\tau }_2\right)}^{\top }$) of the gapped Dirac points as the outputs.

By generating 100, 000 samples by random sampling about the input, the outputs are obtained using COMSOL 5.6. Normalization is adopted to the whole dataset to improve the accuracy of training tasks. The training, validation and test sets take 80%, 10% and 10% of the dataset, respectively.

4.2 Deep neural networks for mechanical valley Hall insulators

Since the bounds of the objective bandgap are continuous values, while their vortex indexes are in discrete type, two artificial neural networks are used for predicting them from the input respectively. All the training process is implemented by using the deep learning toolbox in Matlab 2019b.

4.2.1 Regression model predicting the bounds of objective bandgap

We first build a regression neural network to predict the bounds of the normalized objective bandgap of the MMC-described UCs, with the input vector of $\mathit{X}={\left(x_0,{\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,\varphi \right)}^{\top }$ and the output is $\mathit{Y}={\left({\overline{\omega }}_1,{\overline{\omega }}_2\right)}^{\top }$. As illustrated in Figure 4A, four fully connected layers are used to connect the input and output layers, with the number of neurons being 256, 128, 64, and 16 in order. For the $i\mathrm{t}\mathrm{h}$ fully connected layer, the relationship between the input vector ${\mathit{P}}_i$ and the output vector ${\mathit{Q}}_i$ can be expressed as ${\mathit{Q}}_i={\mathbf{W}}_i\times {\mathit{P}}_i+{\mathit{b}}_i$, where ${\mathit{W}}_i$ is the weight matrix and ${\mathit{b}}_i$ is the bias vector. For each hidden layer, the LeakyRelu activation function is used to introduce nonlinear factors into the neural network. The root-mean-square error (RMSE) is used to measure the difference between the predicted and the actual upper and lower bounds of the normalized objective bandgap, and the expression is:

$RMSE=\sqrt{\frac{{\sum }_{i=1}^N{\left({\stackrel{\sim }{\omega }}_1^i-{\overline{\omega }}_1^i\right)}^2+{\left({\stackrel{\sim }{\omega }}_2^i-{\overline{\omega }}_2^i\right)}^2}{N}}(3)$

where ${\left({\stackrel{\sim }{\omega }}_1^i,{\stackrel{\sim }{\omega }}_2^i\right)}^{\top }$ are the actual normalized bounds of the objective bandgap, and $N$ is the number of samples. The minibatch size and max epoch are set as 5120 and 3000, respectively. As an improvement of the Adagrad algorithm, the RMSprop algorithm is adopted to accelerate the learning process with an initial learning rate of $\alpha =0.01$, which is specifically updated to half of the previous value after every 1000 epochs.

FIGURE 4

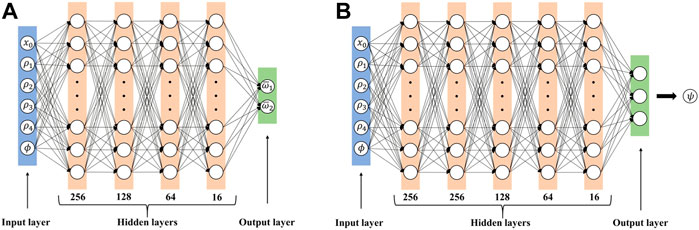
FIGURE 4. (A) The regression neural network for predicting the normalized bounds of the objective bandgap, and (B) the classification neural network for predicting the vortex indexes.

4.2.2 Classification model identifying vortex

Additionally, a classification neural network with the same input $\mathit{X}={\left(x_0,{\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,\varphi \right)}^{\top }$ is also trained to determine the topological properties of the MMC-described unit cells. The topological property of the UCs is further labeled as: $+1$ for the case $-1\le {\tau }_1\le -0.6$ and $0.6\le {\tau }_2\le 1$, $-1$ for the case $0.6\le {\tau }_1\le 1$ and $-1\le {\tau }_2\le -0.6$, and 0 for the rest. Obviously, UCs with a label $+1$ or $-1$ are valley Hall insulators, while trivial materials are labeled by 0. And this label is denoted as $\psi$ and set as the output of the classification model.

As shown in Figure 4B, for this triple classification problem, five fully connected layers with 256, 256, 128, 64, and 16 neurons are used to connect the input and output layers, respectively. The LeakyRelu activation function is used for each hidden layer while the softmax activation function is used for the output layer to generate the classification probability. The classification takes the probability values and assigns each input to one of three mutually exclusive categories using the cross-entropy loss function, which is defined as:

$\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}=-\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^M{w}_j{t}_{ij}\ln y_{ij}(4)$

where $N$ is the number of samples, $M$ is the number of categories, $w_j$ is the weight of the $j$ th category, and $t_{ij}$ is the indicator of the $i\mathrm{t}\mathrm{h}$ sample belonging to the $j$ th category. Specifically, when the $i\mathrm{t}\mathrm{h}$ sample is matched to the $j\mathrm{t}\mathrm{h}$ category, the $t_{ij}=1$; otherwise $t_{ij}=0$. As the output of the above softmax layer, $y_{ij}$ is the predicted probability for the case that the $i\mathrm{t}\mathrm{h}$ sample belongs to the $j\mathrm{t}\mathrm{h}$ category. For the classification neural network, satisfactory training efficiency and accuracy can be achieved by setting the minibatch size and max epoch as 1024 and 120, respectively. Similar as the regression model, the Rmsprop algorithm is again used with an initial learning rate of $\alpha =0.01$. The learning rate is set to decay to half of the previous value after every 20 epochs.

4.3 Training of the artificial neural networks

The convergence histories of the loss function values of both the regression and classification neural networks are shown in Figure 5. The difference between the validation and training losses is slight, and therefore no significant overfitting nor underfitting is observed in both models. In order to further verify the reliability of the regression neural network, comparisons between the predicted and actual values of the lower bounds and upper bounds of the normalized objective bandgaps are presented in Figures 6A,B. It can be found that, for both the normalized upper and lower bounds of the objective bandgap, the predicted values and actual values are quite close, i.e., besides only a few outliers, most points are quite close to the line $y=x$. Quantitatively, for the test set, the corresponding root-mean-square error is $RMSE=0.0590$, which guarantees the accuracy of the trained regression model.

FIGURE 5

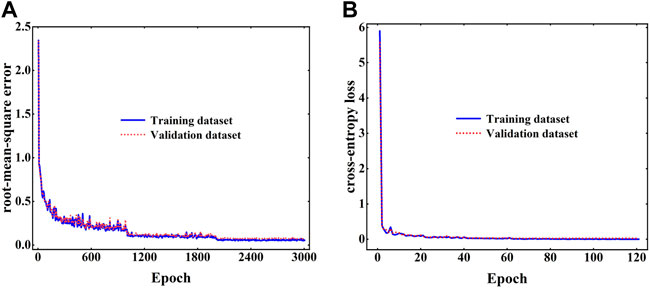
FIGURE 5. The convergence history of (A) the root-mean-square error of the regression neural network and (B) the cross-entropy loss of the classification neural network.

FIGURE 6

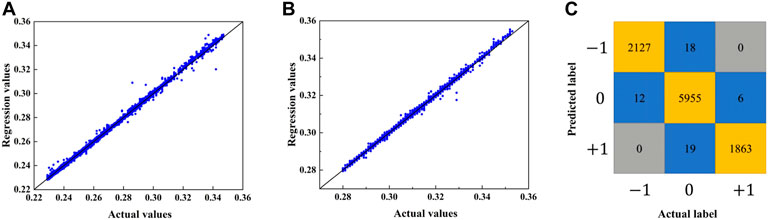
FIGURE 6. Comparisons between the predicted and actual values of (A) the lower bounds, and (B) the upper bounds of the normalized objective bandgap. (C) Confusion matrix of the test set of the classification neural network.

For the classification neural network, the classification accuracy of the test set is 99.45%. From the confusion matrix of the test set presented in Figure 6C, besides the high accuracy, it is worth noting that the nontrivial topological property is never classified oppositely, e.g., $-1$ to $+1$ or $+1$ to $-1$. And the fewer incorrect classification only happens for the cases when the vortex index is marginal, e.g., 0 to $\pm 1$ or $\pm 1$ to 0. And this will not happen when the nontrivial bandgap is not too narrow (please see the designs in Section 5.2 and Section 5.3). All these facts validate the accuracy of the trained classification model.

To summarize, we trained reliable regression and classification neural networks for the subsequent inverse design of the topological waveguide. The motivation and the greatest advantage of this work is the significant improvement in the solution efficiency. We randomly generated 100 pairs of UCs and calculated their bounds of the objective bandgap and vortex indexes of gapped Dirac points using COMSOL 5.6 and the trained neural networks, respectively. The results obtained by exact analysis took a total of 13310.0542 s, with an average time of 133.1005 s, while the latter took only 0.7963 s, with an average time of 0.0080 s, which is about 16, 000 times more efficient than the former¹. The above calculations are implemented on a desktop computer equipped with an Intel(R) Core(TM) aTctMTE3MDBLQDMuNjBHSHo= 3.60 GHz CPU, 32.0 GB of RAM, and Matlab 2019b under Windows 10.

5 Optimal design of valley Hall insulators by machine learning

5.1 Mathematical formulation

Since a pair of UCs with inverse topological labels and a common objective bandgap could compose a topological waveguide, the mathematical formulation of designing a topological waveguide described by the MMC method can be written as:

$\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{d}\mathit{d}={\left({{\mathit{d}}^{\left(1\right)}}^{\top },{{\mathit{d}}^{\left(2\right)}}^{\top }\right)}^{\top }$

$\min {\left({\psi }^{\left(1\right)}+1\right)}^2+{\left({\psi }^{\left(2\right)}-1\right)}^2+{\left(\min \left({\overline{\omega }}_2^{\left(1\right)},{\overline{\omega }}_2^{\left(2\right)}\right)-\max \left({\overline{\omega }}_1^{\left(1\right)},{\overline{\omega }}_1^{\left(2\right)}\right)-{\overline{\omega }}_{\mathrm{g}\mathrm{a}\mathrm{p}}\right)}^2$

$\mathrm{s}.\mathrm{t}.{\psi }^{\left(i\right)}={\mathcal{F}}_{\mathrm{c}}\left({\mathit{d}}^{\left(i\right)}\right),i=\mathrm{1,2}{\left({\overline{\omega }}_1^{\left(i\right)},{\overline{\omega }}_2^{\left(i\right)}\right)}^{\top }={\mathcal{F}}_{\mathrm{r}}\left({\mathit{d}}^{\left(i\right)}\right),i=\mathrm{1,2},{\mathit{d}}^{\left(i\right)}\in {\mathcal{U}}^{\mathit{d}},i=\mathrm{1,2}(5)$

where ${\mathit{d}}^{\left(i\right)}={\left(x_0^{\left(i\right)},{\rho }_1^{\left(i\right)},{\rho }_2^{\left(i\right)},{\rho }_3^{\left(i\right)},{\rho }_4^{\left(i\right)},{\varphi }^{\left(i\right)}\right)}^{\top }$ is the design variables of the $i$ th unit cell and their admissible set is denoted as ${\mathcal{U}}^{\mathit{d}}=\left\{{\left(x_1,\dots ,x_6\right)}^{\top }|x_1\in \left\{-1/2\sqrt{3}\mathrm{m},1/2\sqrt{3}\mathrm{m}\right\};0.05\mathrm{m}\le x_i\le 0.5\mathrm{m},i=2,\dots ,5;\pi /20\le x_6\le \pi /2\right\}$. By minimizing the objective function, the topological labels of the two UCs are $-1$ and $+1$, and the normalized width of their common objective bandgap is ${\overline{\omega }}_{\mathrm{g}\mathrm{a}\mathrm{p}}$. A critical point of this formulation is that the topological labels and the bounds of objective bandgap are predicted by the well-trained classification and regression neural networks, which guarantee the solution efficiency of this design formulation.

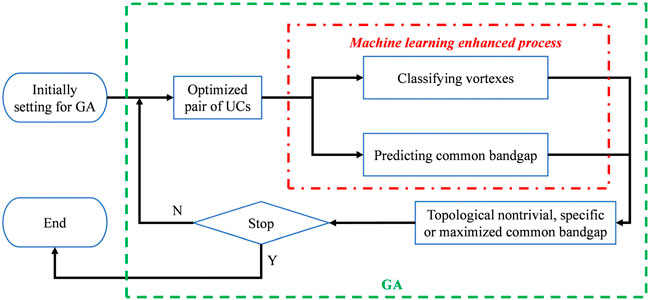
As illustrated in Figure 7, the design Eq. 5 is solved with the help of GA by setting the following parameters: the population size of $40$, the crossover fraction of $0.8$, the elite count of $2$, the stall generation limit of $15$ and the fitness function tolerance of ${10}^{-8}$.

FIGURE 7

FIGURE 7. Flowchart of the design procedure of optimal design of valley Hall insulators.

5.2 Design of valley Hall insulators with a target common bandgap

By setting the target normalized common objective bandgap as 0.04 and 0.07, two pairs of valley Hall insulators are obtained by solving the mathematical programming (Eq. 5). The corresponding design variables are: ${\mathit{d}}_{0.04}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\left(-1/2\sqrt{3},0.470,0.061,0.464,0.081,1.476,1/2\sqrt{3},0.180,0.477,0.082,0.125,0.208\right)}^{\top }$ and ${\mathit{d}}_{0.07}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\left(-1/2\sqrt{3},0.183,0.484,0.318,0.246,1.046,1/2\sqrt{3},0.471,0.149,0.433,0.275,0.251\right)}^{\top }$. Both designs are converged in 35 generations and the corresponding iteration histories are given in Figure 8.

FIGURE 8

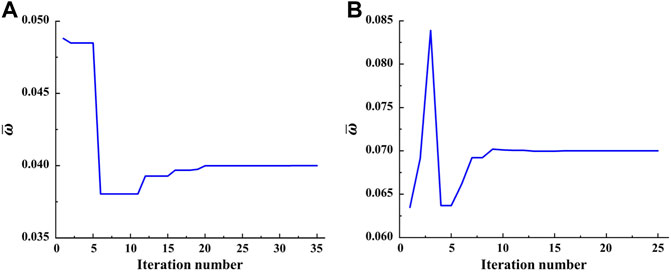
FIGURE 8. Iteration histories of the width of the normalized common bandgap for target values of (A) 0.04 and (B) 0.07.

Tables 1, 2 show the geometries of each pair of UCs and their band structures with the objective bandgap marked. Besides, the topological properties of the UCs are verified by plotting the phase distribution $\theta$ of the gapped Dirac points and the arrows indicate the phase gradient $\nabla \theta$. The widths of the normalized common bandgap are set as $0.04$ and $0.07$, while these values are actually $0.040$ (0.257-0.297) and $0.069$ (0.243-0.312), respectively, and the relative errors are both smaller than 1.5%. Furthermore, the vortexes are clockwise (the upper gapped Dirac point) and anticlockwise (the lower gapped Dirac point) in both first UCs, and this implies the corresponding topological labels are $-1$. Oppositely, the actual topological labels of both second UCs are $+1$. All these facts demonstrate the effectiveness of the proposed ML-assistant design framework for topological waveguides.

TABLE 1

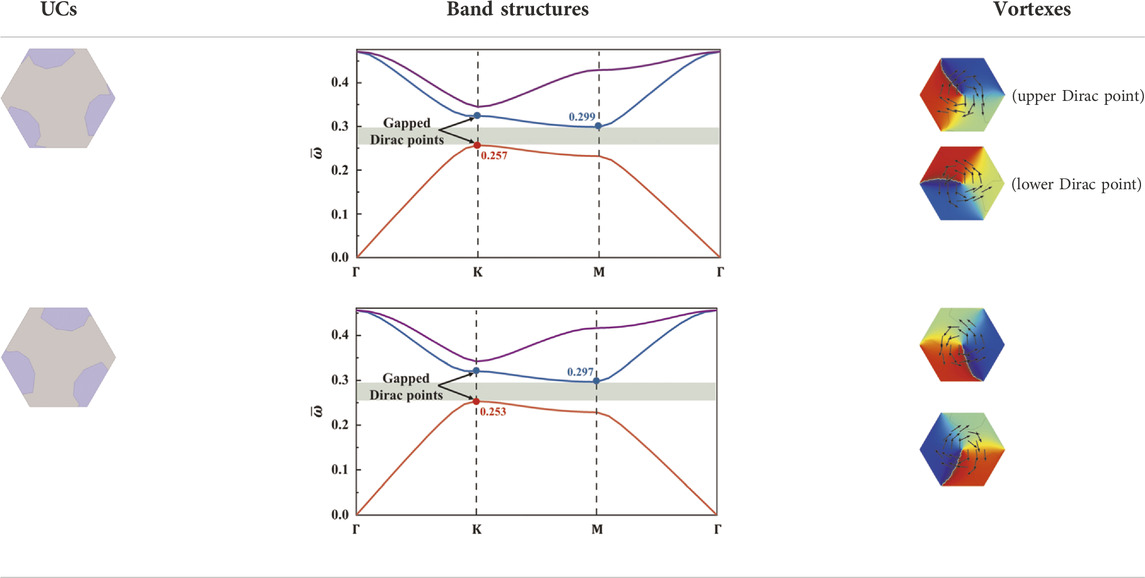
TABLE 1. The optimized topological insulators with a normalized common bandgap of 0.04, their band structures and the energy vortexes of the gapped Dirac points.

TABLE 2

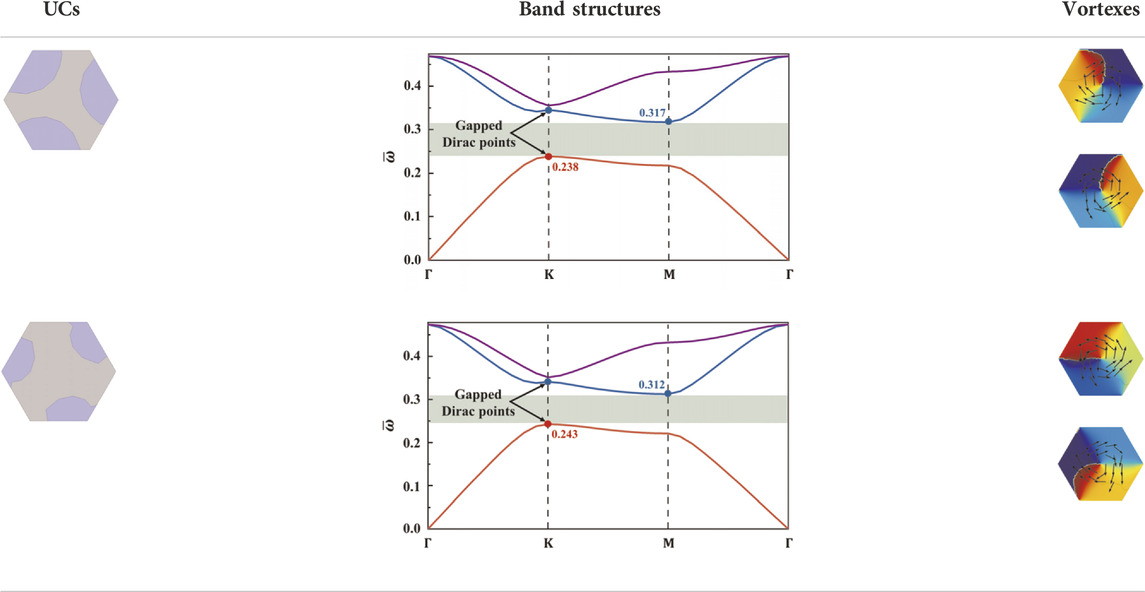
TABLE 2. The optimized topological insulators with a normalized common bandgap of 0.07, their band structures and their energy vortexes of the gapped Dirac points.

5.3 Design of valley Hall insulators with maximized working frequencies

The waveguide made of a pair of valley Hall insulators with different topological properties and a wider common bandgap, usually has a larger operating bandwidth and more concentrated edge states. Therefore, for real applications, a topological waveguide with better performance can be obtained by modifying the objective function of Eq. 5 as

$\min {\left({\psi }^{\left(1\right)}+1\right)}^2+{\left({\psi }^{\left(2\right)}-1\right)}^2-{\left(\min \left({\overline{\omega }}_2^{\left(1\right)},{\overline{\omega }}_2^{\left(2\right)}\right)-\max \left({\overline{\omega }}_1^{\left(1\right)},{\overline{\omega }}_1^{\left(2\right)}\right)\right)}^2(6)$

Solving the updated formulation, the common bandgap width of optimized UCs can reach 0.106, and the corresponding design variable is ${\mathit{d}}_{\max }^{\mathrm{o}\mathrm{p}\mathrm{t}}={\left(-1/2\sqrt{3},0.290,0.373,0.311,0.325,0.401,1/2\sqrt{3},0.359,0.317,0.315,0.453,0.202\right)}^{\top }$.

The optimized UCs, their band structures and the corresponding energy vortexes are presented in Table 3. It can be found that, the actual width of the normalized common bandgap is $0.105$ (0.229-0.334), and the relative error is about 1.0%. And the topological properties of the two UCs are also consistent with classified labels. This also validates the effectiveness of the proposed paradigm for designing topological insulators with a maximized width of the common bandgap.

TABLE 3

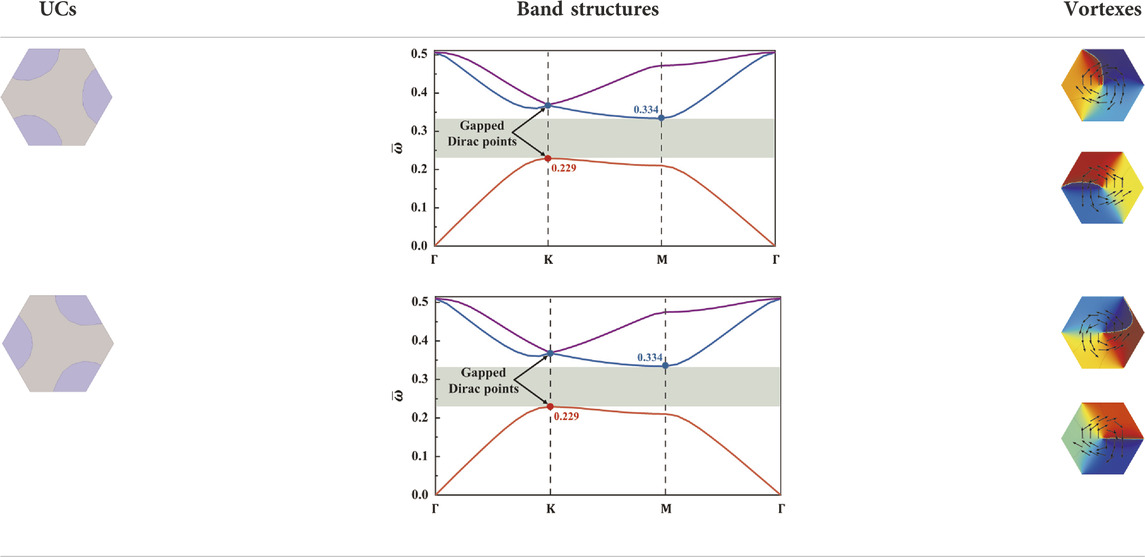
TABLE 3. The optimized topological insulators with a maximized normalized common bandgap, their band structures and their energy vortexes of the gapped Dirac points.

5.4 Validation and evaluation of the optimized topological waveguides

To validate the proposed design paradigm for designing topological waveguide, each pair of optimized UCs in Section 5.2 and Section 5.3 is assembled into a finite supercell structure respectively, as shown in Figure 9. In their band structures, the bulk bands are depicted as black curves, and the interface bands depicted by the red curve appear in the objective bandgap and are responsible for the topologically protected wave propagation. As some interface bands are blurred by their adjacent bulk bands, the applicable operating frequency ranges are highlighted in light green, and the corresponding widths are marked as well. To be specific, the operating bandwidths are 140.4 Hz and 246.3 Hz in Figures 9A,B, corresponding to the cases in which the normalized common bandgap is set as 0.04 and 0.07, respectively. And this value is increased to 382.0 Hz in Figure 9C, corresponding to the design with a maximized width of the common bandgap. Notably, there is almost no intersections nor gap between the interface band and the bulk bands, which is a critical band structure (Du et al., 2020). Compared to the former two groups of designs, the operating bandwidth of optimized waveguides is increased by 172.1% and 55.1%, respectively. Besides, it is also shown that, as the operating bandwidth (and the width of common bandgap) increases, the energy of interface mode gets more concentrated at the interface (Figure 9C). This clearly shows the significance of the optimal design of topological insulators.

FIGURE 9

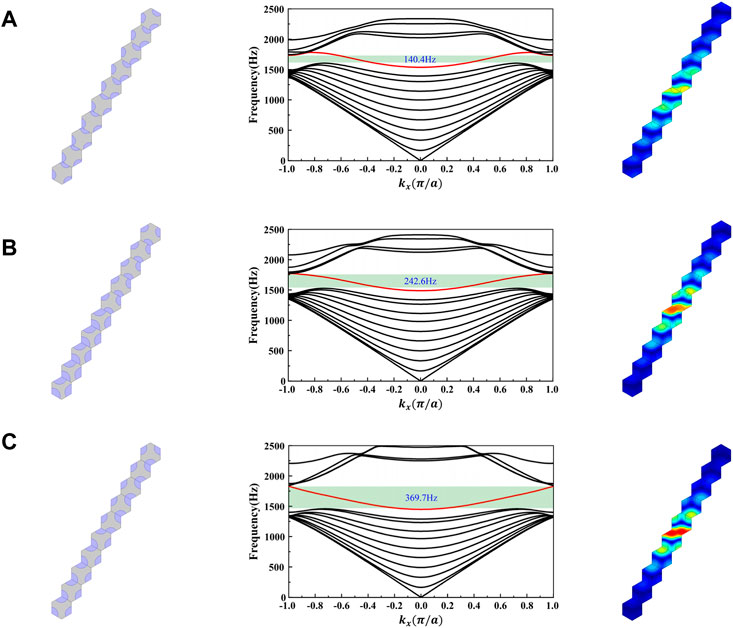
FIGURE 9. Optimized supercells, their band structures and the corresponding interface modes at $k_x=0.5\pi /A$ with the width of common bandgap as (A) 0.04 (B) 0.07 (C) 0.105.

To further verify the performance of the above designs, their waveguides were modeled in COMSOL 5.6 by imposing absorption boundary conditions. Each waveguide model consists of $40\times 40$ optimized UCs and contains a straight interface or a Z-shaped interface. A unit monopole point source is applied at the point with a distance of $4A$ from the left side along the interface. Referring to the operating bandwidth of each finite supercell described above, representative elastic wave propagation modes of the three optimized waveguides are shown in Figure 10. Obviously, elastic waves can robustly pass through all the interfaces, including the sharp corners of the Z-shaped interface, and this indicates that the valley Hall insulators-based waveguides enjoy the topological protection property. Furthermore, it is obvious that the energy propagation is more concentrated for a waveguide consisting of a pair of UCs with a wider common bandgap width. In particular, the energy transport in the optimized waveguide composed of UCs with maximized common bandgap is most concentrated, occupying only a 4-UC-width region.

FIGURE 10

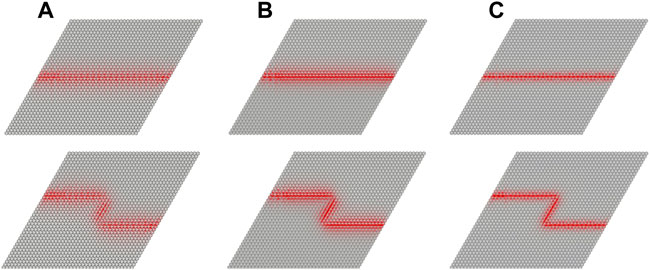
FIGURE 10. Topologically protected elastic wave propagation modes along optimized straight and Z-shaped waveguides with a width of the normalized common bandgap as (A) 0.04 (B) 0.07 (C) 0.105.

6 Concluding remarks

In the present work, describing the valley Hall insulators by the moving morphable component method, two artificial neural networks are trained to predict the discrete topological property and the continuous bounds of the objective bandgap. From the application point of view, mathematical formulations are proposed for the inverse design of optimal topological waveguides to achieve a target or maximized working bandwidth. Numerical examples illustrate that, taking advantage of machine learning, the solution efficiency can be accelerated by more than 10,000 times. The obtained optimized mechanical topological waveguide robustly concentrates the energy transmission in a 4-UC-width interface region. The proposed design paradigm can be easily generalized for the artificial intelligence (AI)-assisted design of 3D topological materials, and topological materials in multi-physics systems, with a more pronounced improvement than the traditional inverse design method.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZD: Conceptualization, methodology, and writing; XD: Modeling, coding, and writing; JL and XG: Methodology and writing; others: Discussions and editing.

Funding

The financial supports from the National Natural Science Foundation (11821202, 11732004, 12002073, 12002077, 12272075, 11922204, and 11872141), the National Key Research and Development Plan (2020YFB1709401), Dalian Talent Innovation Program (2020RQ099), the Fundamental Research Funds for the Central Universities (DUT20RC (3)020, DUT21RC (3)076), and 111 Project (B14013) are gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹There is no doubt that, those specific time values may vary with different implementations; however, the orders of efficiency improvement, which is essential for the subsequent optimization, can always be achieved by using the proposed machine learning enhanced process.

References

Araki, H., Mizoguchi, T., and Hatsugai, Y. (2019). Phase diagram of a disordered higher-order topological insulator: A machine learning study. Phys. Rev. B 99 (8), 085406. doi:10.1103/physrevb.99.085406

CrossRef Full Text | Google Scholar

Asbóth, J. K., Oroszlány, L., and Pályi, A. (2016). A short course on topological insulators. Lect. notes Phys. 919, 166. doi:10.1007/978-3-319-25607-8

CrossRef Full Text | Google Scholar

Breunig, O., and Ando, Y. (2022). Opportunities in topological insulator devices. Nat. Rev. Phys. 4 (3), 184–193. doi:10.1038/s42254-021-00402-6

CrossRef Full Text | Google Scholar

Chen, H., Nassar, H., and Huang, G. L. (2018). A study of topological effects in 1D and 2D mechanical lattices. J. Mech. Phys. Solids 117, 22–36. doi:10.1016/j.jmps.2018.04.013

CrossRef Full Text | Google Scholar

Chen, H., Yao, L. Y., Nassar, H., and Huang, G. L. (2019). Mechanical quantum Hall effect in time-modulated elastic materials. Phys. Rev. Appl. 11 (4), 044029. doi:10.1103/physrevapplied.11.044029

CrossRef Full Text | Google Scholar

Chen, Y., Lan, Z., Su, Z., and Zhu, J. (2022). Inverse design of photonic and phononic topological insulators: A review. Nanophotonics 11 (19), 4347–4362. doi:10.1515/nanoph-2022-0309

CrossRef Full Text | Google Scholar

Chen, Y., Liu, X., and Hu, G. (2019). Topological phase transition in mechanical honeycomb lattice. J. Mech. Phys. Solids 122, 54–68. doi:10.1016/j.jmps.2018.08.021

CrossRef Full Text | Google Scholar

Chen, Y., Meng, F., Jia, B., Li, G., and Huang, X. (2019). Inverse design of photonic topological insulators with extra-wide bandgaps. Phys. Status Solidi RRL. 13 (9), 1900175. doi:10.1002/pssr.201900175

CrossRef Full Text | Google Scholar

Chen, Y., Meng, F., Kivshar, Y., Jia, B., and Huang, X. (2020). Inverse design of higher-order photonic topological insulators. Phys. Rev. Res. 2 (2), 023115. doi:10.1103/physrevresearch.2.023115

CrossRef Full Text | Google Scholar

Christiansen, R. E., Wang, F., Sigmund, O., and Stobbe, S. (2019). Designing photonic topological insulators with quantum-spin-Hall edge states using topology optimization. Nanophotonics 8 (8), 1363–1369. doi:10.1515/nanoph-2019-0057

CrossRef Full Text | Google Scholar

Christiansen, R. E., Wang, F., and Sigmund, O. (2019). Topological insulators by topology optimization. Phys. Rev. Lett. 122 (23), 234502. doi:10.1103/physrevlett.122.234502

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, H. W., Zhao, S. D., Zhu, R., Wang, Y. S., Cheng, L., and Zhang, C. (2021). Customizing acoustic Dirac cones and topological insulators in square lattices by topology optimization. J. Sound Vib. 493, 115687. doi:10.1016/j.jsv.2020.115687

CrossRef Full Text | Google Scholar

Dong, J. W., Chen, X. D., Zhu, H., Wang, Y., and Zhang, X. (2017). Valley photonic crystals for control of spin and topology. Nat. Mat. 16 (3), 298–302. doi:10.1038/nmat4807

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, Z., Chen, H., and Huang, G. (2020). Optimal quantum valley Hall insulators by rationally engineering Berry curvature and band structure. J. Mech. Phys. Solids 135, 103784. doi:10.1016/j.jmps.2019.103784

CrossRef Full Text | Google Scholar

Du, Z., Cui, T., Liu, C., Zhang, W., Guo, Y., and Guo, X. (2022). An efficient and easy-to-extend Matlab code of the Moving Morphable Component (MMC) method for three-dimensional topology optimization. Struct. Multidiscipl. Optim. 65 (5), 158. doi:10.1007/s00158-022-03239-4

CrossRef Full Text | Google Scholar

Fan, H., Xia, B., Tong, L., Zheng, S., and Yu, D. (2019). Elastic higher-order topological insulator with topologically protected corner states. Phys. Rev. Lett. 122 (20), 204301. doi:10.1103/physrevlett.122.204301

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, X., Zhang, W., and Zhong, W. (2014). Doing topology optimization explicitly and geometrically—A new moving morphable components based framework. J. Appl. Mech. 81 (8), 081009. doi:10.1115/1.4027609

CrossRef Full Text | Google Scholar

Hasan, M. Z., and Kane, C. L. (2010). Colloquium: Topological insulators. Rev. Mod. Phys. 82 (4), 3045–3067. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

He, C., Ni, X., Ge, H., Sun, X. C., Chen, Y. B., Lu, M. H., et al. (2016). Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12 (12), 1124–1129. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

He, L., Guo, H., Jin, Y., Zhuang, X., Rabczuk, T., and Li, Y. (2022). Machine-learning-driven on-demand design of phononic beams. Sci. China Phys. Mech. Astron. 65, 214612. doi:10.1007/s11433-021-1787-x

CrossRef Full Text | Google Scholar

He, L., Wen, Z., Jin, Y., Torrent, D., Zhuang, X., and Rabczuk, T. (2021). Inverse design of topological metaplates for flexural waves with machine learning. Mater. Des. 199, 109390. doi:10.1016/j.matdes.2020.109390

CrossRef Full Text | Google Scholar

He, Q. L., Hughes, T. L., Armitage, N. P., Tokura, Y., and Wang, K. L. (2022). Topological spintronics and magnetoelectronics. Nat. Mat. 21 (1), 15–23. doi:10.1038/s41563-021-01138-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, S. D. (2016). Topological mechanics. Nat. Phys. 12 (7), 621–623. doi:10.1038/nphys3801

CrossRef Full Text | Google Scholar

Jin, Y., He, L., Wen, Z., Mortazavi, B., Guo, H., Torrent, D., et al. (2022). Intelligent on-demand design of phononic metamaterials. Nanophotonics 11 (3), 439–460. doi:10.1515/nanoph-2021-0639

CrossRef Full Text | Google Scholar

Liu, T. W., and Semperlotti, F. (2018). Tunable acoustic valley–Hall edge states in reconfigurable phononic elastic waveguides. Phys. Rev. Appl. 9 (1), 014001. doi:10.1103/physrevapplied.9.014001

CrossRef Full Text | Google Scholar

Long, Y., Ren, J., and Chen, H. (2020). Unsupervised manifold clustering of topological phononics. Phys. Rev. Lett. 124 (18), 185501. doi:10.1103/physrevlett.124.185501

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Y., Ren, J., Li, Y., and Chen, H. (2019). Inverse design of photonic topological state via machine learning. Appl. Phys. Lett. 114 (18), 181105. doi:10.1063/1.5094838

CrossRef Full Text | Google Scholar

Lu, J., Qiu, C., Deng, W., Huang, X., Li, F., Zhang, F., et al. (2018). Valley topological phases in bilayer sonic crystals. Phys. Rev. Lett. 120 (11), 116802. doi:10.1103/physrevlett.120.116802

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, J., Du, Z., Guo, Y., Liu, C., Zhang, W., and Guo, X. (2021). Multi-class, multi-functional design of photonic topological insulators by rational symmetry-indicators engineering. Nanophotonics 10 (18), 4523–4531. doi:10.1515/nanoph-2021-0433

CrossRef Full Text | Google Scholar

Luo, J., Du, Z., Liu, C., Mei, Y., Zhang, W., and Guo, X. (2021). Moving Morphable Components-based inverse design formulation for quantum valley/spin Hall insulators. Extreme Mech. Lett. 45, 101276. doi:10.1016/j.eml.2021.101276

CrossRef Full Text | Google Scholar

Ma, G., Xiao, M., and Chan, C. T. (2019). Topological phases in acoustic and mechanical systems. Nat. Rev. Phys. 1 (4), 281–294. doi:10.1038/s42254-019-0030-x

CrossRef Full Text | Google Scholar

Ma, T., and Shvets, G. (2016). All-Si valley-Hall photonic topological insulator. New J. Phys. 18 (2), 025012. doi:10.1088/1367-2630/18/2/025012

CrossRef Full Text | Google Scholar

Nanthakumar, S. S., Zhuang, X., Park, H. S., Nguyen, C., Chen, Y., and Rabczuk, T. (2019). Inverse design of quantum spin Hall-based phononic topological insulators. J. Mech. Phys. Solids 125, 550–571. doi:10.1016/j.jmps.2019.01.009

CrossRef Full Text | Google Scholar

Ozawa, T., Price, H. M., Amo, A., Goldman, N., Hafezi, M., Lu, L., et al. (2019). Topological photonics. Rev. Mod. Phys. 91 (1), 015006. doi:10.1103/revmodphys.91.015006

CrossRef Full Text | Google Scholar

Pal, R. K., and Ruzzene, M. (2017). Edge waves in plates with resonators: An elastic analogue of the quantum valley Hall effect. New J. Phys. 19 (2), 025001. doi:10.1088/1367-2630/aa56a2

CrossRef Full Text | Google Scholar

Qi, X. L., and Zhang, S. C. (2011). Topological insulators and superconductors. Rev. Mod. Phys. 83 (4), 1057–1110. doi:10.1103/revmodphys.83.1057

CrossRef Full Text | Google Scholar

Tokura, Y., Yasuda, K., and Tsukazaki, A. (2019). Magnetic topological insulators. Nat. Rev. Phys. 1 (2), 126–143. doi:10.1038/s42254-018-0011-5

CrossRef Full Text | Google Scholar

Wu, B., Ding, K., Chan, C. T., and Chen, Y. (2020). Machine prediction of topological transitions in photonic crystals. Phys. Rev. Appl. 14 (4), 044032. doi:10.1103/physrevapplied.14.044032

CrossRef Full Text | Google Scholar

Xue, H., Yang, Y., and Zhang, B. (2022). Topological acoustics. Nat. Rev. Mat., 1–17. doi:10.1038/s41578-022-00465-6

CrossRef Full Text | Google Scholar

Zhang, W., Yang, W., Zhou, J., Li, D., and Guo, X. (2017). Structural topology optimization through explicit boundary evolution. J. Appl. Mech. 84 (1), 011011. doi:10.1115/1.4034972

CrossRef Full Text | Google Scholar

Zhou, W., Wu, B., Chen, Z., Chen, W., Lim, C. W., and Reddy, J. N. (2020). Actively controllable topological phase transition in homogeneous piezoelectric rod system. J. Mech. Phys. Solids 137, 103824. doi:10.1016/j.jmps.2019.103824

CrossRef Full Text | Google Scholar