- 1Materials Science and Engineering Department, Texas A&M University, College Station, TX, United States
- 2Materials Science and Engineering, The Ohio State University, Columbus, OH, United States
- 3J. Mike Walker ’66 Department of Mechanical Engineering, Texas A&M University, College Station, TX, United States
- 4Air Force Research Laboratory, Wright-Patterson AFB, Materials and Manufacturing Directorate, Dayton, OH, United States
In computational materials research, uncertainty analysis (more specifically, uncertainty propagation, UP) in the outcomes of model predictions is essential in order to establish confidence in the models as well as to validate them against the ground truth (experiments or higher fidelity simulations). Unfortunately, conventional UP models relying on exhaustive sampling from the distributions of input parameters may be impractical, particularly when the models are computationally expensive. In these cases, investigators must sacrifice accuracy in the propagated uncertainty by down-sampling the input distribution. Recently, a method was developed to correct for these inaccuracies by re-weighing the input distributions to create more statistically representative samples. In this work, the method is applied to computational models for the response of materials under high strain rates. The method is shown to effectively approximate converged output distributions at a lower cost than using conventional sampling approaches.
1 Introduction
1.1 Uncertainty quantification and material performance
The central paradigm in materials science rests on the existence of process-structure-property-performance (PSPP) relationships, which constitute the foundation to materials design Smith (1982). Although PSPP linkages depend mainly on experimental observations, simulation-based approaches to design and analysis can be used when experiments are too costly to run, mediated by data analytics techniques to provide a statistically-valid surrogate to costly experiments Shi et al. (2015); DeCost et al. (2017).
Even in simulation-focused approaches, a limited number of experiments are necessary in order to properly parameterize the (hopefully predictive) models. In the case of materials behavior under quasi-static loading conditions, uncertainty tends to arise from the stochastic nature of materials microstructure. This uncertainty is somewhat controllable and bounded by the stochastic nature of the microstructure of the material being investigated. In the case of polycrystalline metals, the spread in the mechanical response when comparing separate experimental runs is not significant, provided the materials are nominally the same–i.e. they have a very similar distribution in chemical and microstructural attributes.
Under high-strain rate conditions, however, extreme sensitivity of experimental conditions can lead to dramatic variance in the observed materials response. Such uncertainties can be quite significant, even when comparing the response of nominally identical materials under virtually indistinguishable experimental conditions. This makes prediction of properties and performance of metals subject to high strain rate deformation difficult. Thus, constitutive equations designed to predict the state of stress under dynamic loading conditions are less reliable for prediction of the mechanical response of a material Johnson and Cook (1985); Zerilli and Armstrong (1987); Allison (2011). To account for uncertainties in experiments, techniques such as Markov Chain Monte Carlo (MCMC) can be used to sample the parameter space in the constitutive equations based on a small set of experimental data Robert and Casella (2013).
In the context of materials design, uncertainty quantification (UQ) and uncertainty propagation (UP) play important roles Panchal et al. (2013); McDowell and Kalidindi (2016); Arroyave et al. (2018). Under nearly every experimental condition, uncertainty in the measured value can stem from slight variations in material microstructure (aleatory) and/or the physics associated with a ground truth realization that are not accounted for in a model (epistemic). Such uncertainties are difficult or impossible to account for directly Chen et al. (2004); Chernatynskiy et al. (2013); Ghoreishi and Allaire (2017); Allaire and Willcox (2014), and are the subject of UQ. We note that these sources of uncertainty exist not only in physical experimentation, but also in computational experiments. In either case, it is important to account for these variations in measured results so that they can be propagated accurately and proper calibration and validation and verification (V&V) of the models is carried out.
Once this information is gathered, it can be used to define distributions of probable parameters of a model that predicts a quantity of interest (QoI). Subsequently, the model can be run multiple times with different parameter values taken from these distributions. This creates a distribution on the output which can serve as an estimate of material performance, which is the outcome of uncertainty propagation Lee and Chen (2009); Li and Allaire (2016); Amaral et al. (2014). Ultimately, data on performance ranges for a material’s behavior can determine an intended application and also provide a factor of safety for a minimum or maximum performance expectation. Furthermore, when high fidelity simulations are available, this information can be determined before a part is ever manufactured.
More often than not, UP is carried out using Markov Chain Monte Carlo integration or the MCMC approach Robert and Casella (2013), which can generate parameter values for models based on any experimental realizations available to the investigator. Other approaches include local expansion, functional expansion, and numerical integration-based methods Sanghvi et al. (2019). These techniques often require hundreds of thousands (or more) of samples from the input space in order to achieve proper convergence in the predicted propagated uncertainties.
Returning to the general problem of simulating the response of a material under high strain rates, each parameter set can be used to inform a unique simulation to predict how a material will perform in certain loading conditions and what properties it is expected to have. Such loading configurations include the Taylor-Anvil and spall plate impact configurations, which can be modeled with a suitable hydrocode. The present work investigates the Taylor-Anvil configuration as a validation of the constitutive models fit to intermediate strain rate
1.2 The cost of sampling high fidelity simulations
High-fidelity hydrocode simulations accounting for material response may be computationally expensive. In such situations, one can only probe a limited number of samples from the input space. This makes the propagation of parameters obtained by MCMC-based approaches impractical. Rather than carrying out an extensive parameter sampling, a solution would be instead to extract sub-samples out of the total number of observations that can be drawn from the parameter distribution space. While propagating this sub-sampled distribution does reduce computation time, it can consequently misrepresent the output distribution depending on whether the sub-sample is weighted and the sampling method used. If the sub-sampled data does not accurately reflect the ground truth parameter distribution, there cannot be proper propagation of uncertainty. Different methods of sampling exist, such as k-medoids Kaufman and Rousseeuw (1987), Latin-Hypercube McKay et al. (2000), or simply random selection–we note that such misrepresentation will occur with any sampling method that does not properly account for the importance of a given sample relative to the full, ground truth distribution.
Overall, the sheer volume of possible input values to try can pose a problem if the subsequent simulations are expensive to run. In such situations, an investigator must down-select values from the UQ-generated pool to input into a simulation, and therefore risk missing the “true” output distribution since all possible inputs to the models were not propagated. Noting the challenge in appropriately down-selecting UQ-generated input values, the present effort investigates the effect of applying the Probability Law Optimized importance Weights (PLOW) method to the output distribution generated by the propagation of a sub-sample of input values across a simulation chain1.
In the current work, the output distribution obtained from the down-selected inputs will be referred to as the proposal distribution. This distribution with probability law optimized weights applied will be referred to as the weighted proposal distribution and the output distribution that comes from running all of the available inputs will be referred to as the true distribution or target distribution. Depending on the number of down-selected inputs, the proposal distribution can deviate substantially from the true distribution. The data used in the study is based on predicting the high-strain-rate response of a low alloy, high performance steel, AF9628 Neel et al. (2020); Gibbons et al. (2018); Abrahams (2017b), which shows a similar mechanical response to a related armament steel–Eglin Steel Dilmore (2003).
In general, the PLOW method can be used to improve the fidelity of input samples for uncertainty quantification with respect to a desired, target input distribution. This capability has many uses, including allowing for the offline evaluation of expensive model chains prior to having complete information about the input distributions that should be propagated through the chain. In this case, the PLOW method is used to weight the output distribution so as to simulate appropriately the desired target distribution without any addition model chain evaluations. Another capability of the PLOW method, explored here for the first time, is the use of the method to weight samples from an MCMC estimation of model parameters. In this scenario, MCMC is used to produce a large set of samples representative of a desired target distribution, albeit in empirical form. It is usually not possible to execute all of the MCMC samples in forward model chain runs. Thus, a sub-sample of the MCMC run (this can be done randomly or intelligently, e.g., using k-medoids) is usually used for forward evaluations (a brief explanation of the k-medoids algorithm is provided in Section 3). Using PLOW, we can ensure that this sub-sample accurately reflects the MCMC target distribution by weighting the sub-samples so as to match the empirical MCMC distribution.
The PLOW procedure has been shown to work well in models of up to 10 dimensions Sanghvi et al. (2019). However, it has not yet been applied across a high-fidelity simulation that is often used for material property estimation. The shape of the distributions of the sub-samples and the full data set will be compared using the Kolmogorov-Smirnov (KS) statistic, or distance-value (D-value) Jr. (1951). Specifically, the predicted density of a material after a simulated Taylor-Anvil test is studied. Additionally, a constitutive model will be used to compare the effects of the PLOW weighting method on a larger data set than can be captured in the hydrocode simulations, given the resource allotment for this work. It is expected that the D-value between the weighted proposal distribution and the target distribution will be smaller than the D-value between the proposal distribution and the target distribution.
Figure 1 shows an overview of the steps taken in the present work to perform the analysis. In the remainder of the paper, we first discuss the methodology behind the PLOW approach. We then carry out an MCMC-based calibration, or UQ, of the Zerilli-Armstrong (ZA) constitutive model based on limited experimental data. This is followed by a demonstration of the PLOW method on propagated uncertainty distributions across the ZA model, due to its inexpensive nature. We then apply PLOW on the outputs obtained from uncertainty propagation across high fidelity Taylor-Anvil (TA) simulations. Lastly, a discussion of the results is presented, followed by conclusions on the work overall.
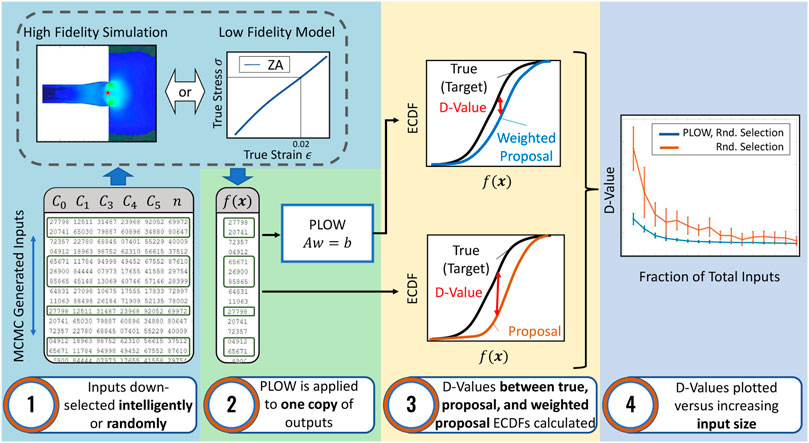
FIGURE 1. Process used to analyze the effect of the PLOW method on the high fidelity Taylor-Anvil simulation and at scale using the Zerilli-Armstrong model. In step 1, a distribution of possible parameter values is generated and down-selected. In step 2, PLOW is applied to one copy of outputs obtained by propagating the down-selected inputs. The term f(x) in step 2 represents the output from the simulation or model evaluations. In step 3 the full output distribution, non-weighted, down-selected distribution, and the PLOW weighted, down-selected distribution are compared. Here, f(x) is the random variable on the axis of abscissas. The D-value, or distance value, is the metric used to determine how similar two empirical distributions are. In step 4, the D-values are plotted as a function of the number of down-selected inputs in step 1.
2 Probability law optimized importance weights approach
The Probability Law Optimized importance Weighting (PLOW) approach, first proposed by Sanghvi et al. Sanghvi et al. (2019), employs a least squares formulation to determine a set of empirical importance weights to achieve a change of probability measure. The notion of using importance weights to simulate the moving of a probability distribution has its roots in optimal transport and the concept of the Earth mover’s or Wasserstein metric Villani (2009). The objective of the PLOW approach is to estimate statistics from a target distribution of interest, by using random samples generated from a different proposal distribution for which samples are more easily attained. The approach taken here works directly with the probability law of the proposal and target random variables (which may be vector-valued), from which only samples from each are needed. For completeness, we note that the probability law of a random variable x is a mapping,
The PLOW approach described here enables weighting to be applied to the output distribution of model chains Amaral et al. (2014); Ghoreishi and Allaire (2017); Amaral et al. (2012); Amaral et al. (2017a). Model chains refer to frameworks that employ multiple models sequentially, where the outputs of one model become the inputs of the next model. PLOW utilizes decomposition-based approaches to calculate weights, which allows it to be used across model chains without losing accuracy in the target distribution prediction. Because of this, investigators can use UP more reliably. The approach is based on the change of probability measure. The general idea is that for the propagation of uncertainty, there is a desired input distribution we wish to propagate through a model. We refer to this distribution as the target distribution Robert and Casella (2013). In many cases however, the target distribution of an upstream model is not known, or was sampled without knowing the underlying distribution of the model’s parameters, which can negatively affect the following model. PLOW can be used to estimate the target distribution of such upstream models, given an already existing set of function evaluations composing a proposal distribution.
To obtain the target distribution, it is common to use traditional importance weighting methods such as density ratio estimation (e.g., importance sampling), typically determined using kernel density estimation Billingsley (2008) or in approximate form using approaches based on minimizing an L2-norm between the proposal and target distributions. Amaral et al. (2017b). With PLOW, the importance weights are calculated using only the samples of the proposal distribution or (if available) target distribution information. This approach enables the user to determine the regions in the input space over which to calculate importance weights. This leads to excellent scalability of the PLOW method in comparison to current weighting methods that are subject to numerical ill-conditioning at high dimensions.
Similar to the procedure described by Sanghvi et al., the first step is to build a probability space
To determine the weights needed to adjust the proposal distribution, we first calculate the empirical measure of each hyper-sphere using
Here
The objective is to determine the weights that would adjust the proposal distribution such that the proposal measures approach the target measures as shown in Eq. 2
Computing the importance weights, w = {w1, w2, … , wn}, is an optimization between the proposal and target measures in the L2-norm sense. The weights are calculated via the solution to a linear system of equations that can be written as
The construction of the A, w, and b is described in the following paragraphs. Once constructed, the solution of Eq. 3 can be calculated via least squares using the normal equations noted below.
The matrix A and the vector b of Eq. 3 are determined using specified regions within the domain of the random variables whose measure we seek to change. Here, A represents the presence, or absence, of each measured input sample point with respect to each hypersphere. The vector b represents the joint probability of points contained within a specific hypersphere. A graphical depiction of this region selection procedure is shown in Figure 2. A distribution space that represents the input values (black dots) available for each parameter of the model in question is shown in the left portion of the figure. In this case, the model would have two input parameters, represented by the two axes making up the base of the graph. Here, the points are normally distributed for both parameters, although this is generally not known or necessary prior to applying PLOW. This illustration can also represent the distribution of points that make up the proposal distribution, or model output space. The difference being that there would be less points on the proposal distribution space due to the experimenter’s inability to run all input conditions through their model. For simplicity of describing the generation of the matrices only four points and four regions are considered.

FIGURE 2. Illustration of the process to construct a measure matrix, like A in Eq. 3. In (A), a bivariate distribution space is displayed corresponding to a model with two parameters for simplicity. In the case of inputs, the dots on the surface represent the co-variance of points the investigator is able to run. The borders show each parameter’s individual distribution. In (B), circles Sj (hyper-spheres in higher dimensions) are drawn over the space to populate the measure matrix.
The regions, S1, S2, S3, S4 shown on the right side of Figure 2 are deterministically-generated to capture every point in the space. In the present case, the regions are in the shape of circles. However, in higher dimensions, they would be hyperspheres. Their size and location are determined based on the samples in the space alone. The process of generating these regions involves growing a hypersphere around each proposal point so that all points are within at least one region. This ensures that the process is scalable with respect to problem dimensionality, which is essential for higher dimensional problems where hyper-spheres do a poor job of space filling. We note that because each point has a hyper-sphere associated with it, we ensure each point is represented in the matrix A. In very high dimensional problems (e.g.,
In our approach, we grow the regions until the union of the regions covers the entire space. In practice, this typically yields a matrix A with dependent columns, leading to a non-unique solution to the least squares problem. To recover dependent columns, we identify non-unique rows in the matrix A, which identify those points that are currently indistinguishable from one another. For these rows, we reduce the radius of the respective hyper-spheres until the rows are unique. We then add a region that covers the entire space to ensure the weights are associated with a probability measures (that is, the probability of the entire input space is still unity). This approach leads to independent columns and the matrix A has more rows than columns. Thus, the normal equations of Eq. 3 shown below, have a unique solution. It is a topic of future work to explore that non-unique solution case that can occur when sample points are nearby one-another. It is expected that this could lead to a capability to delete input samples and potentially lead to enhanced computational efficiency.
In the example of Figure 2, for clarity, there are five proposal points shown as Xi, where i ∈ {1, 2, … , 5}. The hypersphere, S1, contains only X1 among the proposal samples. This region, S1, and its proposal sample contents are captured as a row vector within a matrix Aij by populating a 1 in entry [j, i] if proposal sample i is in hypersphere j (in this case, j ∈ {1, 2, … , 4}. Therefore, we have entry A11 = 1, since sample 1 is in region 1. The remaining random sample points, X2, X3, X4, and X5 are equal to 0 for S1. This gives A1 = [1, 0, 0, 0] for the first row of the A matrix.
Filling in data according to the example in Figure 2 for the remaining points and hyper-spheres, the following matrix would be generated:
The b vector is created to contain the probability of a random sample landing in region Sj under the target distribution as the jth element of the vector. This can be computed via target samples or via a known target distribution with traditional integration. For the example, the b vector is
3 Methodology
3.1 Generating inputs and down selection
To obtain the intermediate rate stress-strain response for AF9628, five Split-Hopkinson Pressure Bar (SHPB) Kolsky (1949) experiments were performed using an indirect tension configuration Brar et al. (2009) at a temperature of 300°C, performed with identical input conditions targeting a strain rate of 1500 s−1. The AF9628 material was heat treated from the as-received condition using the patented heat treatment schedule Abrahams (2017a); Sinha et al. (2017); Sinha et al. (2020). Five subscale E8 tension specimens of AF9628 were carefully machined with tight tolerances, and a low stress grinding (LSG) process was used to reduce the sample geometry and surface finish variability across all specimens. The five tests were controlled, as much as possible, for all input variables including material composition, microstructure, geometry, and impact bar velocity, among others. This was to ensure that any variability in the stress-strain response came from aleatoric sources in the experimental apparatus and not from neglecting known effects. The resulting measured strain rates for the 5 experiments were 1440, 1400, 1430, 1350, and 1440 s−1. The stress-strain data were fit to a Zerilli-Armstrong (ZA) constitutive model using a minimization routine that combined sequential quadratic programming and MCMC, assuming an average strain rate of 1412 s−1 for the parameterization.
The Body Centered Cubic (BCC) ZA constitutive model shown in Eq. 4 is used for predicting the plastic stress-strain response of AF9628 at high strain rates:
Here, C1, C3, C4, C5, and n are material constants determined by calibrating the model to experimental data. T, ϵp, and
For the MCMC run, a uniform prior distribution was set for each of the parameter values. Also, the likelihood distribution was assumed to be normally distributed and a Metropolis-Hastings selection criteria was used for the selection of new points. (MCMC was implemented via the MCMC toolbox for Matlab package Laine (2022)). The process was carried out for the ZA parameter fitting for one million iterations, enough to assume adequate convergence. The result of the MCMC fitting is a matrix of values with one million rows and six columns. Each row is an estimated value for the six parameters in the ZA model shown in Eq. 4. In the current work, the word “points” is used to describe a single six column row in the matrix. Each one of these points is a potential input to the TA simulation via the ZA model. Afterwards, an inferred burn-in region of 200,000 points was removed from this data set, leaving 800,000 possible parameters for each constant.
Of the 800,000 value sets, however, a large amount of them were identical. To obtain a target data set of unique values, the replicate data was removed, leaving nearly 260,000 parameter sets. The means and standard deviations of each parameter are shown in Table 1. Furthermore, after applying the PLOW method on an increasing number of sub-sample distributions, there came a point where increasing the number of values in the sub-sample resulted in a negligible change in shape compared to the target distribution. At this point, the sub-sample and the target distribution shapes were essentially the same. The threshold sub-sample size of 15,000 points was therefore selected for the target distribution size. This set of parameter values would serve as the “bank” of input values that could be propagated into a ZA model or a CTH simulation of a Taylor Anvil test.

TABLE 1. Mean and standard deviations of 259,035 Zerilli-Armstrong model constants after calibrating to experimental data using MCMC.
The down-selection method, k-medoids, is used throughout the work to reduce the input data sets generated by the MCMC process. Essentially, the k-medoids algorithm first partitions the data set into k different groups. A single value from each partition is then selected to represent the group of points in that partition. Furthermore, the algorithm ensures that the selected value is within the original data set. K-medoids works even if each data point is represented by a set of values i.e. multi-dimensional.
3.2 Constitutive model
For the large scale test that would utilize the entire data set of 15,000 points, a less computationally expensive model than a full Taylor-Anvil simulation in CTH was needed. The constitutive model was selected to be the Zerilli-Armstrong stress-strain function itself
To obtain the output stress distribution first one set, of the possible 15,000 parameterizations, were substituted into ZA model, Eq. 4. Next, a value of 0.02 was input as the strain level and the corresponding stress was obtained and saved. The process was repeated until all of the input parameter values were propagated into the model.
The distribution of 15,000 output points would serve as the known, true distribution because it includes all of the input data points. Once this distribution was obtained, its shape would be compared to that of varying subset sizes of this data set. Consequently, in order to show the effectiveness of the PLOW method, the method would need to be applied to incrementally sized sub-sampled distributions of the full 15,000 points up to 15,000.
3.3 Taylor-Anvil simulation
The Taylor Anvil test was simulated in the multi-material Eulerian hydrocode CTH (Version 12.0, Sandia National Laboratory) McGlaun et al. (1990). The Taylor Anvil impact simulation models an AF9628 rod impacting a Vascomax 250 anvil, as shown in Figure 3 where the pressure was output at the final frame of the simulation. Relevant time-histories of thermodynamic and mechanical field variables (e.g. Pressure, stress, temperature, density, etc.) can be obtained from each CTH simulation over the length of the AF9628 Taylor rod impacting a Vascomax 250 anvil. The center point at the impact face of the rod was selected for monitoring all field variable data. The AF9628 Taylor rod was modeled with a Mie-Grüneisen equation of state (EOS) with parameters obtained from Neel et al. Neel et al. (2020), and the anvil was modeled with a Mie-Grr̈uneisen EOS with parameters obtained from the Los Alamos Shock Compendium Marsh (1980). The simulations were conducted at an impact velocity of 200 m/s and ran for 20 μ s. An automatic mesh refinement (AMR) algorithm was employed with a final mesh size of 100 μ m at the smallest element. Fracture was not modeled in the present work.
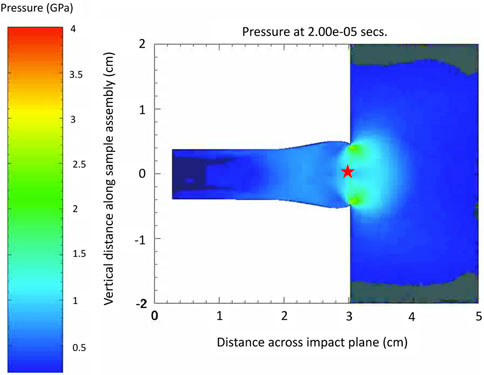
FIGURE 3. Representative Taylor Anvil simulation of an AF9628 rod impacting a Vascomax 250 anvil. Pressure contours are superimposed onto the model geometries. The simulation is one of 499 total, in alignment with the number of ZA parameter sets obtained via MCMC. Each simulation is informed by the ZA model with a different set of parameter values. The red star shows the location on the rod where the density data was obtained.
Simulations were run on a 48 core high performance computing system with Intel Xeon Platinum 8168 cores. Exact wall time was not recorded per simulation, however the estimated run time for a single simulation was 15 min. Even with run time scaling linearly with total number of simulations, the run time can quickly become impractical for larger numbers of runs. For instance, at just 500 simulations, the total wall time can exceed 125 h.
Due to limits on computational time, only a subset of the original 15,000 points generated could be run, since a separate, computationally expensive simulation would need to be run for each parameter set 500 points was chosen as a reasonable number of simulations that could fit within the high performance computing time allotment constraints for this work. To reduce the data set to 500 parameter sets either random selection or k-medoids, the previously discussed method for sub-sampling data, was used. This set of 500 data points was used to inform 500 different Taylor Anvil simulations. In each simulation, only the ZA constants changed while all other input conditions were held constant. Notably, one simulation did not finish, leaving 499 simulations to analyze. Although it is unclear what precisely caused the run not to finish, the most likely reason could be that the simulation simply didn’t finish within the HPC hours allotted to this project.
Properties that can be extracted from this simulation include density, particle (material) velocity, final specimen length, and final specimen width, among many others. With the 499 tests, a distribution of the predictions for a given property could be plotted. For this work, the density of the material at a tracer particle located at the center of the impact surface was chosen as the single property of interest to be analyzed (cf. Figure 3). Density was selected due to its relatively low sensitivity to changes in constitutive parameters. This would permit a good assessment of the down-selection methodology employed in the present work.
3.4 Application of PLOW
Once the outputs from the sub-sampled inputs are calculated, one copy of the data set is created. For the original outputs, there are no weights applied to the data points. For the copy, the probability law optimized weights are applied to the outputs. In addition to the original and the copy, the output data set calculated by running all of the available inputs is obtained. In Figure 1, the original output distribution is illustrated by the orange ECDF labeled “Proposal”, the weighted output distribution is illustrated by the blue ECDF labeled “Weighted Proposal”, and the full output distribution is illustrated by the black ECDF labeled “True”.
The original output serves as a baseline distribution to compare with the performance of the distribution obtained after the weights have been applied. The performance of a sub-sampled distribution, weighted or not, is measured by how close that distribution is to the true distribution. Each step described here is applied in the same way, despite the technique used to obtain the sub-sample (random or intelligent) or the model used to calculate the outputs (low fidelity model or high fidelity simulation). The only change for a given iteration is the size of the sub-sample.
3.5 Calculating and plotting the D-Value
The 2-sample Kolmogorov-Smirnov (KS) test statistic was used to compare the shape of the target data sets to the smaller subset distributions. This test was used because it does not require the distributions to have a certain shape or standard deviation, i.e., it is a non-parametric test. For this test, the distributions to be compared are first converted to empirical Cumulative Distribution Functions (ECDFs). The vertical distance between the two ECDFs are measured across each point on the horizontal axis and the maximum value among these is selected. This maximum distance is referred to as the D-value. An example of this distance value is shown in Figure 4. Normally, this value serves as the KS-Statistic which is tested against the null hypothesis that the two models are sampled from the same distribution.
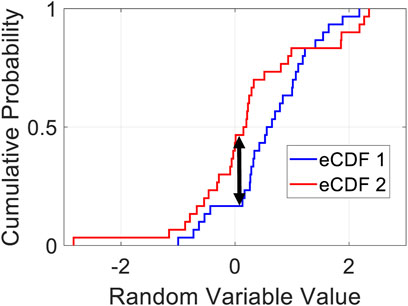
FIGURE 4. Illustration of the Kolmogorov–Smirnov statistic. The red and blue lines are the two CDFs being compared, while the black arrow is a measurement of the largest distance between the two distributions. It is commonly known as the K-S statistic Massey (1951), but is also referred to as the D-value (distance value) in the present work.
For this work, however, the distance value is used as a measure of convergence of the weighted proposal distribution to the target distribution. That is, the smaller the KS-Statistic, the closer the distribution in question (our proposal distribution or weighted proposal distribution) is to the distribution being tested against (the target distribution). This follows from the Glivenko-Cantelli theorem, which demonstrates that the KS-Statistic converges to zero with probability one when the distributions are the same and the number of samples tends to infinity. Thus, as the KS-statistic reduces, the two distributions in question are closer (in distribution), hence the use of the KS-Statistic as a convergence measure.
To measure the effect of the PLOW method, the D-values between the target distribution and four different proposal distributions were calculated. The four different approaches to creating the proposal distributions included: 1) random selection of inputs with no weighting on the outputs, 2) k-medoid selection of inputs with no weighting on outputs, 3) random selection of inputs with weighting on the outputs, and 4) k-medoid selection of inputs with weighting on the outputs. For the large scale case of 15,000 points, only two approaches were used to create the proposal distributions. These cases included random selection of inputs with no weighting on the outputs and random selection of inputs with weighting on the outputs.
In each case described above, the size of the sub-sample was increased incrementally to study the effect of sub-sample size on PLOW’s ability to more accurately weight the proposal distribution towards the target distribution. For each sub-sample size, 100 different iterations were complete. Doing so would allow a mean and standard deviation to be calculated. The means and standard deviations of the D-values are plotted versus the sub-sample size. An example of a D-value versus sub-sample size plot is shown in step 4 of Figure 1.
4 Results
4.1 Uncertainty propagation of constitutive model
For one D-value comparison of the constitutive model, shown in Figure 5, a random selection method of the sub-samples was used to generate proposal distributions to compare with the 15,000 target sample size. For this case, the sub-sample sizes began at 450 points, and incremented by fractions of roughly 0.07 of the full target data set. To compare the performance of PLOW on k-medoids for the constitutive model, shown in Figure 6, a target data set of 500 was selected from the full 15,000 points. The sub-sample sizes here started at 50 and incremented by fractions of 0.1 of 500 points up to 450. From here, the increment was changed to 0.02. This continued until the sub-sample size reached 500. Overall, the weighted k-medoid sampled data shows a better convergence than the random sampled inputs.
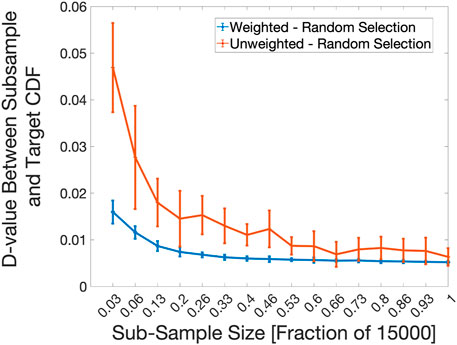
FIGURE 5. D-value versus sub-sample size trend for constitutive model. A comparison between a random sub-sample selection with PLOW applied after the selection (Weighted) and one without PLOW applied (Unweighted) is shown. At each X-axis interval, 100 2-Sample K-S statistic values (D-values) were calculated between the target distribution and a proposal distribution constructed using a different drawing of points from the pool of 15,000 total input points. The average and standard deviation of 100 D-values is plotted at each sub-sample size value.
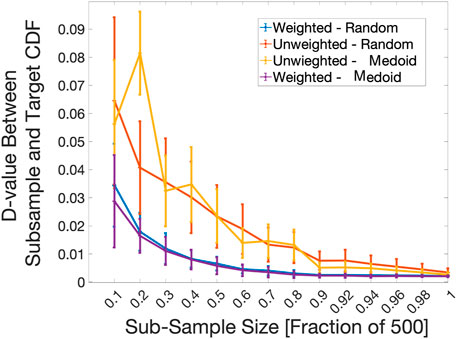
FIGURE 6. D-value versus sub-sample size trends for the constitutive model. A comparison of the convergence to the target distribution between random sub-sample selection with PLOW applied (Weighted-Random), random sub-sample selection without PLOW (Unweighted-Random), k-medoids sub-sample selection with PLOW applied (Weighted - Medoid), and k-medoids sub-sample selection without PLOW (Unweighted - Medoid) are shown. The sub-sample size represents the number of input points used to construct the proposal distribution. At each X-axis interval, 100 2-Sample K-S statistic values (D-values) were calculated between the target distribution and a proposal distribution constructed using a different drawing of points from the pool of 500 total input points. The average and standard deviation of the 100 D-values is plotted.
After applying the PLOW method proved effective in more accurately representing the target distribution generated by the cheap constitutive model, it was of high interest to apply the method to a model of higher fidelity. Doing so could also demonstrate the method’s effectiveness across a model chain, as the ZA constitutive equation serves as a direct input into the high fidelity simulation software. Unlike with the constitutive model, less parameter sets from the MCMC calibration could be used and tested because querying the TA simulation is much more time and computationally intensive than evaluating a constitutive model.
4.2 Uncertainty propagation of Taylor-Anvil simulations
The CTH simulations of the Taylor Anvil impact test provided field variable histories throughout the AF9628 rod. The equilibrium density was calculated and noted to converge to a stable value by the end of each simulation. Density distributions were plotted for the 499 Taylor Anvil simulations as shown in Figure 7 in the form of a solid, dark blue line. Each of the 499 simulations were informed by a unique set of ZA parameter values.
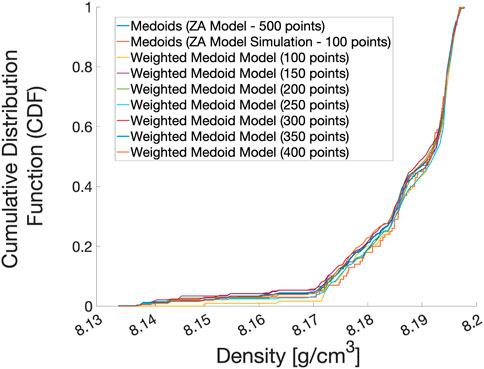
FIGURE 7. Cumulative distribution of material density values predicted by the Taylor Anvil simulation. Each line, except one, represents a proposal distribution determined by an input sub-sample size as indicated in the legend. One line represents the target distribution. Naturally, as the size of sub-sampled input points used to construct the proposal distribution approaches 500, the closer the proposal distribution will be to the target distribution.
From this dataset of density values, we can select subsets of values and apply the PLOW method to the subset to compare to other distribution subsets. Figure 7 shows how the subset distributions of density values begin to match the full set as the number of values in the sub-set approaches the total dataset size of 499 values. Although the convergence with increasing sub-sample size is an intended outcome, it is not easily seen when viewed as CDF distributions. Additionally, the distributions are not symmetric across the mean or mode. Therefore, comparing such distributions to each other would require a non-parametric testing method. To do this comparison, the testing parameter of the Komolgorov Smirnov test (KS-Test) Massey (1951) was used, as mentioned previously.
As shown in Figure 8, sub-samples of the original 499 sample distribution were taken in sizes of 100, 150, 200, 250, 300, 350, 400, 450, 460, 470, 480, and 490. At each sub-sample size, the k-medoid distribution either had PLOW applied or was left unmodified. The two were then compared to the known 499 sample distribution. Figure 8 shows the results of the KS-Statistic versus sample size calculations. The sub-samples that did not have the PLOW method applied to them were labeled Unweighted, while the samples that did were labeled Weighted.
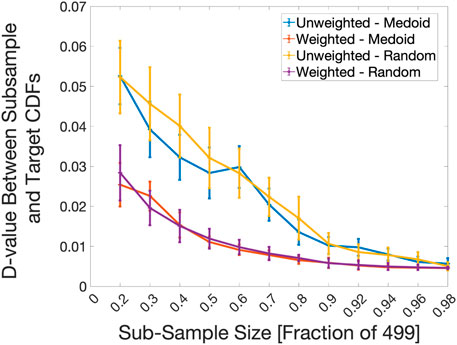
FIGURE 8. D-value versus sub-sample size trend for the Taylor-Anvil simulations. A comparison of the convergence to the target distribution between random sub-sample selection with PLOW applied (Weighted-Random), random sub-sample selection without PLOW (Unweighted-Random), k-medoids sub-sample selection with PLOW applied (Weighted - Medoid), and k-medoids sub-sample selection without PLOW (Unweighted - Medoid) are shown. The sub-sample size represents the number of input points used to construct the proposal distribution. At each X-axis interval, 100 2-Sample K-S statistic values (D-values) were calculated between the target distribution and a proposal distribution constructed using a different drawing of points from the pool of 499 total input points. The average and standard deviation of the 100 D-values is plotted.
5 Discussion
Overall, the method shows promise in fine-tuning distributions generated using a sub-selection of inputs and outputs, even if the model to determine the outputs is complex with no explicit function to map inputs to outputs. In every case of the D-value vs. sub-sample size plots, applying the PLOW method weights the outputs such that the distribution is closer in shape to the target distribution than without PLOW applied, on average. Additionally, in both the CTH simulation and constitutive model cases, the biggest difference between the two methods occurs in the smallest sub-sample size. This is where applying the PLOW method has the biggest impact on altering the distribution shape. The results also show that PLOW works across the CTH simulation, which is a more complex model than prior applications of the PLOW method.
In the case of the constitutive model with only the random sub-sample selection shown (Figure 5), the PLOW method creates proposal distributions similar in shape to the known, target distribution, even in small sub-sample sizes. For example, even when just 3% of the total data set is used as a sub-sample, the average D-value is roughly 0.017 for the weighted data, which is much lower than the average D-value of about 0.046 of the unweighted data set. Keep in mind that the lower the D-value, the closer the sub-sampled distribution is to the known output. The standard deviations (vertical lines at each sub-sample size fraction) are also very narrow compared to the unweighted case, highlighting the precision of the PLOW method.
The plots of the random and k-medoid selection methods with and without PLOW applied (Figure 8) show that increased accuracy can be achieved even after intelligently down-selecting inputs that best represent the population of available inputs. Furthermore, for nearly every sub-sample size, weighting the distribution changes its shape towards that of the target distribution enough that the standard deviations associated with weighting and not weighting do not overlap. For example, at a sub-sample size fraction of 0.5, the vertical bars representing standard deviation for the Weighted - Medoid and Weighted - Random D-values are between roughly 0.01 and 0.015. On the other hand, the vertical bars for the Unweighted - Medoid and Unweighted - Random are between 0.02 and 0.04.
Another takeaway from Figure 8 is that when k-medoids is used alone, it has the ability to select input points that bring the output distribution shape closer to the known, target distribution reasonably well compared to a purely random selection. This can be observed by comparing the mean D-value of the blue line (Unweighted-Medoid) to that of the yellow line (Unweighted-Random) for sub-sample fraction sizes of 0.3 through 0.5, and 0.7 to 0.8. Such gains in accuracy are very small between the random vs. medoid selection processes when PLOW has been applied. The average D-values nearly overlap for all sub-sample fraction sizes between the two lines in Figure 8 (purple vs. orange lines). The result signifies that PLOW has the ability to find a similar “optimum” shape regardless of the sub-sampling process used.
For both the constitutive model and CTH cases, the mean D-value decreases significantly with constant increases in sub-sample size. Such a trend can be used to define an optimum amount of sub-samples to run when computational resources are limited. For example, if a decrease in the average D-value is less than a pre-determined range with an incremental increase in sub-sample size, the final sub-sample size would be optimal. It is unclear whether this same trend remains at smaller sample sizes. For instance, if a trend turns out to be linear when the target distribution is less than 499 samples, the optimal fraction of sub-samples to run would be the most that the investigator could afford. Figure 5 shows that the exponentially decreasing behavior holds for target distributions of up to 150,000 points, given the ZA model. Generally, however, the smaller the proposal distribution size, the greater the difference PLOW makes on the distribution.
Additionally, as shown in Figures 5, 6, 8, as the sub-sample size increases, the shapes of the distributions becoming more and more similar until they are almost exact. Overall, the weighted data set consistently performs better than the unweighted one in essentially every ratio value. The only exceptions are the few ratios where the standard deviation of the unweighted plot reaches below the mean of the weighted plot. Overall, the weighted distribution tends to converge faster towards the ground truth distribution, thus saving computing resources.
Each D-value versus sub-sample size trend (Figures 5, 6, 8) also shows a reduction in computational cost on account of applying PLOW. For example, in Figure 8, the mean D-value between the target distribution and the Weighted-Random curve at a sub-sample fraction size of 0.3 is roughly 0.02. The fraction size equates to about 150 Taylor-Anvil simulations. To achieve a similar level of accuracy without weighting the proposal distribution, nearly 80% of the total 499 inputs would need to be run; a total of about 400 Taylor-Anvil simulations. In this example alone, it is shown that if PLOW was used to weight the proposal distribution, one would save 250 simulation evaluations. This equates to a times savings of 3,750 min, given the amount of time it takes to execute one Taylor-Anvil simulation. The calculation is under the assumption that the execution time scales linearly with the number of evaluations.
The results point toward the use of the PLOW method to obtain the most accurate distribution of a random variable when the number of possible inputs exceed the computational resources to sample the entire distribution. Such situations are prevalent in material design exploration where the possible input values for parameters like composition and annealing temperature in heat treatment studies are continuous (i.e. can take an infinite number of values), which can lead to very different bulk properties Khatamsaz et al. (2021); Ranaiefar et al. (2022); Johnson et al. (2019). Finally, although the PLOW method creates a more identical shape to the target distribution than without it, this difference is rather small. To strengthen its credibility, a test of the effectiveness of PLOW on sub-sample data selected from a more disparate target distribution would be required.
6 Conclusion
In this work, a method for predicting the true output distribution of a quantity of interest from only a limited number of inputs is presented. The PLOW method has been applied to a simple constitutive function and a more sophisticated hydrodynamic simulation to demonstrate its flexibility in different applications. Such a method has the potential to reduce the number of input samples needed to best represent the output distribution of interest, especially considering the cost of high fidelity simulations. Major findings include 1) the ability of PLOW to better predict a QoI distribution across a high fidelity simulation and 2) The PLOW method’s ability to predict the distribution of a QoI with improved accuracy, even when a selection algorithm is used to obtain a representative subset of inputs. Additionally, the gains in prediction accuracy were most prevalent in cases where computational resources limit calculations to only a small set of inputs. Here, the effectiveness of the method has been demonstrated on a problem where material performance is the quantity of interest. However, the approach is general enough that it can be applied to problems across essentially any discipline and has been shown to be effective at propagating uncertainty under resource constraints.
Data availability statement
The datasets presented in this article are not readily available because the data is available at the discretion of the Air Force Research Lab for national security purposes. Requests to access the datasets should be directed to Jaylen James, amF5bGVuLmphbWVzQGxpdmUuY29t.
Author contributions
JJ and MS performed the analysis. DA and RA developed the initial concept. AG and MG provided the input simulation data. JJ wrote the first draft of the manuscript. RA and DA provided feedback on subsequent edits. All authors revised and edited the manuscript.
Funding
The authors acknowledge the Air Force Research Laboratory core funding in supporting data collection for this study. RA and DA also acknowledge the National Science Foundation through Grant Nos. DMR-2001333 and CMMI-1663130. JJ also acknowledges the support from NSG through Grant No. DGE-1545403 as well as the AFRL-Minority Leadership Program (AFRL-MLP) under Sub-contract 165852-19F5830-19-02-C1. MG gratefully acknowledges support from the Air Force Office of Scientific Research Lab task no. 18RXCOR042 (Dr. Martin Schmidt, Program Officer). This work was supported in part by high-performance computer time and resources from the DoD High Performance Computing Modernization Program.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1The name is partially inspired by the soil-themed Earth Mover’s Distance metric analogy, which is a measure of distance between two distributions Rubner et al. (2000).
References
Abrahams, R. (2017b). “The science of cost-effective materials design-a study in the development of a high strength, impact resistant steel,” in APS Shock compression of condensed matter meeting abstracts. APS Topical Conference on the Shock Compression of Matter. O7–005.
Allaire, D., and Willcox, K. (2014). A mathematical and computational framework for multifidelity design and analysis with computer models. Int. J. Uncertain. Quantif. 4, 1–20. doi:10.1615/int.j.uncertaintyquantification.2013004121
Allison, J. (2011). Integrated computational materials engineering: A perspective on progress and future steps. JOM 63, 15–18. doi:10.1007/s11837-011-0053-y
Amaral, S., Allaire, D., and Willcox, K. (2012). “A decomposition approach to uncertainty analysis of multidisciplinary systems,” in 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, Indiana, 17 September 2012 - 19 September 2012, 5563.
Amaral, S., Allaire, D., Blanco, E. D. L. R., and Willcox, K. E. (2017a). A decomposition-based uncertainty quantification approach for environmental impacts of aviation technology and operation. Artif. Intell. Eng. Des. Anal. Manuf. 31, 251–264. doi:10.1017/s0890060417000154
Amaral, S., Allaire, D., and Willcox, K. (2014). A decomposition-based approach to uncertainty analysis of feed-forward multicomponent systems. Int. J. Numer. Methods Eng. 100, 982–1005. doi:10.1002/nme.4779
Amaral, S., Allaire, D., and Willcox, K. (2017b). Optimal $$L_2$$-norm empirical importance weights for the change of probability measure. Stat. Comput. 27, 625–643. doi:10.1007/s11222-016-9644-3
Arroyave, R., Shields, S., Chang, C.-N., Fowler, D., Malak, R., and Allaire, D. (2018). Interdisciplinary research on designing engineering material systems: Results from a National Science Foundation workshop. J. Mech. Des. 140, 110801. doi:10.1115/1.4041177
Brar, N., Joshi, V., and Harris, B. (2009). “Constitutive model constants for al7075-t651 and al7075-t6,” in Shock compression of condensed matter - 2009. Editors M. Elert, W. Buttler, M. Furnish, W. Anderson, and W. Proud (Melville, NY: American Institute of Physics), 945–948.
Chen, W., Baghdasaryan, L., Buranathiti, T., and Cao, J. (2004). Model validation via uncertainty propagation and data transformations. AIAA J. 42, 1406–1415. doi:10.2514/1.491
Chernatynskiy, A., Phillpot, S. R., and LeSar, R. (2013). Uncertainty quantification in multiscale simulation of materials: A prospective. Annu. Rev. Mat. Res. 43, 157–182. doi:10.1146/annurev-matsci-071312-121708
DeCost, B. L., Hecht, M. D., Francis, T., Webler, B. A., Picard, Y. N., and Holm, E. A. (2017). Uhcsdb: UltraHigh carbon steel micrograph DataBase: Tools for exploring large heterogeneous microstructure datasets. Integr. Mat. Manuf. Innov. 6, 197–205. doi:10.1007/s40192-017-0097-0
Dilmore, M. (2003). Eglin steel: Researchers developed a new high-strength, high-performance, low-cost steel. AFRL Technol. Horizons 4, 48–49.
Ghoreishi, S., and Allaire, D. (2017). Adaptive uncertainty propagation for coupled multidisciplinary systems. AIAA J. 55, 3940–3950. doi:10.2514/1.j055893
Gibbons, S., Abrahams, R., Vaughan, M., Barber, R., Harris, R., Arroyave, R., et al. (2018). Microstructural refinement in an ultra-high strength martensitic steel via equal channel angular pressing. Mater. Sci. Eng. A 725, 57–64. doi:10.1016/j.msea.2018.04.005
Johnson, G. R., and Cook, W. H. (1985). Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 21, 31–48. doi:10.1016/0013-7944(85)90052-9
Johnson, L., Mahmoudi, M., Zhang, B., Seede, R., Huang, X., Maier, J. T., et al. (2019). Assessing printability maps in additive manufacturing of metal alloys. Acta Mater. 176, 199–210. doi:10.1016/j.actamat.2019.07.005
Kaufman, L., and Rousseeuw, P. J. (1987). Clustering by means of medoids. Neuchatel, Switzerland: Proceedings of the Statistical Data Analysis Based on the L1 Norm conference.
Khatamsaz, D., Molkeri, A., Couperthwaite, R., James, J., Arróyave, R., Allaire, D., et al. (2021). Efficiently exploiting process-structure-property relationships in material design by multi-information source fusion. Acta Mater. 206, 116619. doi:10.1016/j.actamat.2020.116619
Kolsky, H. (1949). An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 62, 676–700. doi:10.1088/0370-1301/62/11/302
Lee, S. H., and Chen, W. (2009). A comparative study of uncertainty propagation methods for black-box-type problems. Struct. Multidiscipl. Optim. 37, 239–253. doi:10.1007/s00158-008-0234-7
Li, K., and Allaire, D. (2016). “A compressed sensing approach to uncertainty propagation for approximately additive functions,” in ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, North Carolina, USA, August 21–24, 2016 (Charlotte, North Carolina: American Society of Mechanical Engineers (ASME)), V01AT02A027.
Massey, F. J. (1951). The Kolmogorov-smirnov test for goodness of fit. J. Am. Stat. Assoc. 46, 68–78. doi:10.1080/01621459.1951.10500769
McDowell, D. L., and Kalidindi, S. R. (2016). The materials innovation ecosystem: A key enabler for the materials genome initiative. MRS Bull. 41, 326–337. doi:10.1557/mrs.2016.61
McGlaun, J., Thompson, S., and Elrick, M. (1990). Cth: A three-dimensional shock wave physics code. Int. J. Impact Eng. 10, 351–360. doi:10.1016/0734-743X(90)90071-3
McKay, M. D., Beckman, R. J., and Conover, W. J. (2000). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 42, 55–61. doi:10.1080/00401706.2000.10485979
Neel, C., Gibbons, S., Abrahams, R., and House, J. (2020). Shock and spall in the low-alloy steel af9628. J. Dyn. Behav. Mat. 6, 64–77. doi:10.1007/s40870-019-00228-5
Panchal, J. H., Kalidindi, S. R., and McDowell, D. L. (2013). Key computational modeling issues in integrated computational materials engineering. Computer-Aided Des. 45, 4–25. doi:10.1016/j.cad.2012.06.006
Ranaiefar, M., Honarmandi, P., Xue, L., Zhang, C., Elwany, A., Karaman, I., et al. (2022). A differential evaporation model to predict chemistry change of additively manufactured metals. Mater. Des. 213, 110328. doi:10.1016/j.matdes.2021.110328
Robert, C., and Casella, G. (2013). Monte Carlo statistical methods. New York, New York: Springer Science & Business Media.
Rubner, Y., Tomasi, C., and Guibas, L. J. (2000). The Earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vis. 40, 99–121. doi:10.1023/A:1026543900054
Sanghvi, M., Honarmandi, P., Attari, V., Duong, T., Arroyave, R., and Allaire, D. L. (2019). “Uncertainty propagation via probability measure optimized importance weights with application to parametric materials models,” in AIAA scitech 2019 forum (San Diego, California: American Institute of Aeronautics and Astronautics). doi:10.2514/6.2019-0967
Shi, X., Zeng, W., Sun, Y., Han, Y., Zhao, Y., and Guo, P. (2015). Microstructure-tensile properties correlation for the ti-6al-4v titanium alloy. J. Mat. Eng. Perform. 24, 1754–1762. doi:10.1007/s11665-015-1437-x
Sinha, V., Gonzales, M., Abrahams, R., Song, B., and Payton, E. (2020). Correlative microscopy for quantification of prior austenite grain size in AF9628 steel. Mat. Charact. 159, 109835. doi:10.1016/j.matchar.2019.109835
Sinha, V., Payton, E. J., Gonzales, M., Abrahams, R. A., and Song, B. S. (2017). Delineation of prior austenite grain boundaries in a low-alloy high-performance steel. Metallogr. Microstruct. Anal. 6, 610–618. doi:10.1007/s13632-017-0403-4
Smith, C. S. (1982). A search for structure. Selected essays on science, art and history. J. Aesthet. Art Crit..
Keywords: uncertainty quantification, uncertainty propagation, optimization, taylor anvil simulation, importance weights, change of measure
Citation: James JR, Sanghvi M, Gerlt ARC, Allaire D, Arroyave R and Gonzales M (2022) Optimized uncertainty propagation across high fidelity taylor anvil simulation. Front. Mater. 9:932574. doi: 10.3389/fmats.2022.932574
Received: 29 April 2022; Accepted: 31 August 2022;
Published: 20 September 2022.
Edited by:
Pinar Acar, Virginia Tech, United StatesReviewed by:
Pavlo Maruschak, Ternopil Ivan Pului National Technical University, UkraineAnh Tran, Sandia National Laboratories, United States
Copyright © 2022 James, Sanghvi, Gerlt, Allaire, Arroyave and Gonzales. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jaylen R. James, amF5bGVuX2phbWVzQHRhbXUuZWR1
 Jaylen R. James
Jaylen R. James Meet Sanghvi1
Meet Sanghvi1 Raymundo Arroyave
Raymundo Arroyave