Programmable metasurface RCS prediction under obstacles based on DNN

Programmable metasurfaces have attracted significant attention in various applications such as radar and 6G communications, owing to their ability freely shape the far-field pattern. However, complex calculations and simulations are always required when designing specific far-field patterns, especially when irregular obstacles are outside the metasurface. In this article, we propose a method using a four-layer artificial neural network to realize the far-field radar cross section (RCS) prediction of programmable metasurfaces in an environment with obstacles, and the prediction value agreed with the simulation data reasonably well. Results show that the proposed prediction model is characterized by better learning and generalization capacity. Our work has broad application prospects and value in complex environment signal transmission, metasurface inverse design, etc.

Introduction

Metamaterials are arrays of sub-wavelength structures that can interact with the electromagnetic (EM) wave in a way, which widely used in beam splitters (Ma et al., 2014), focusing lenses (Pendry, 2000; Smith et al., 2004), etc. However, these devices are complicated to fabricate. The metasurface is an unconventional method for controlling the phase, amplitude, and polarization of EM waves based on the generalized Snell’s law (Yu et al., 2011; Lin et al., 2014; Xie et al., 2020; Hu et al., 2021a). The subwavelength structure, ultra-thin thickness, and low cost make it widely used in various fields, such as broad diffusion (Wang et al., 2014; Gao et al., 2015a), beam steering (Zhang et al., 2018), polarization conversion (Cheng et al., 2014), cloaking (Tan et al., 2022) and focusing (Cai et al., 2020; Hao et al., 2021; Lu et al., 2021). The processed traditional metasurface has a single far-field mode and a fixed function, which limits its multifunctional applications (Chen et al., 2016; Liu et al., 2016). The emergence of programmable metasurfaces may solve this problem. They can realize more flexible regulation of EM waves through different pressure differences and have made outstanding progress in imaging, communication, beam steering, and other fields (Cui et al., 2014; Della and Engheta, 2014; Giovampaola and Engheta, 2014; Gao et al., 2015b; Liang et al., 2015; Cui, 2017; Wu et al., 2021), which make it possible to achieve free control of far-field patterns (Xie et al., 2017; Xiao et al., 2020).

Far-field patterns can reflect the scattering characteristics of objects and play an essential role in the field of communication or radar. In these fields, it is common for the signal to be blocked by obstacles, as shown in Figure 1A. When EM waves encounter obstacles, they will be diffusely reflected, scattering irregular beams in all directions. Thus, the signal the user receives will be weakened if there is an obstacle between the signal source and users. Metasurfaces can solve this problem by allowing signals to bypass obstacles, as shown in Figure 1B. However, using only tunable metasurfaces for pattern design require complex simulations and calculations, and the corresponding phase and amplitude information have to be recalculated once the direction map is changed. Furthermore, when the shape of the obstacle is complex, it is almost impossible to obtain the corresponding far-field radar cross section (RCS) by calculation. Therefore, predicting the RCS under this condition is highly important. In recent years, the combination of deep learning and metasurfaces has made breakthroughs in intelligent stealth, intelligent imaging, etc. (Cui et al., 2019; Qiu et al., 2019; Sensong et al., 2019; Chen et al., 2020; Huang et al., 2022), and also provides the possibility to solve this problem.

FIGURE 1

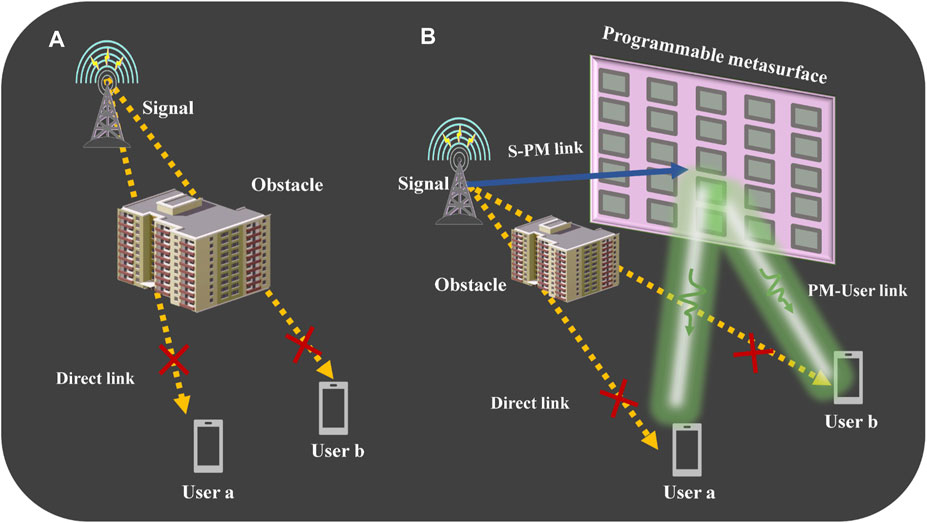
FIGURE 1. Schematic diagram of communication scenario. (A). Obstacles block user communication. (B). The direct link between the signal source and users is blocked by obstacles. Signals can be propagated to User a and User b when establishing an “S-PM” link between the signal source and metasurface.

In this letter, we propose a method to train an artificial neural network (DNN) to make a fast prediction to the far-field RCS for various programmable metasurface distributions with objects. As a demonstration, we design a programmable metasurface with an array of 41 units and verify it in simulation. We set up a metal cylinder in front of the metasurface to simulate the presence of obstacles. When the distribution of metasurface structures is known, the far-field RCS pattern formed by electromagnetic waves bypassing obstacles can be accurately predicted. The results show that the mean square error (MSE) error of the network prediction and simulation data is only 0.0336, and the cosine accuracy is as high as 90%, which shows the correctness and feasibility of the network. We believe this design will be helpful in various applications and could be an innovative attempt to solve communication problems in complex environments such as multiple obstacles and limited space.

Principle and methods

To meet the conditions for constructing a programmable metasurface, it is necessary to design a unit cell with wide phase coverage. Figure 2A shows that the unit cell we designed consists of a $9\times 9{\mathrm{m}\mathrm{m}}^2$ substrate (${\epsilon }_r=2.65$) with 2 mm thickness, a fully reflective metal patch attached to the back, and a specially designed metal structure with a varactor diode. The varactor diode model is ma46h120, whose capacitance can be tuned between 0.14 and 1.1 pF with a parasitic resistance of about 2 Ω. The equivalent circuit diagram is shown in Figure 2B. The RC model is used as an equivalent diode so that adjusting the value of the capacitance can equivalently change the working state of the diode. The metal sheet attached to the front is a center-symmetrical figure, and the diode is placed in the center.

FIGURE 2

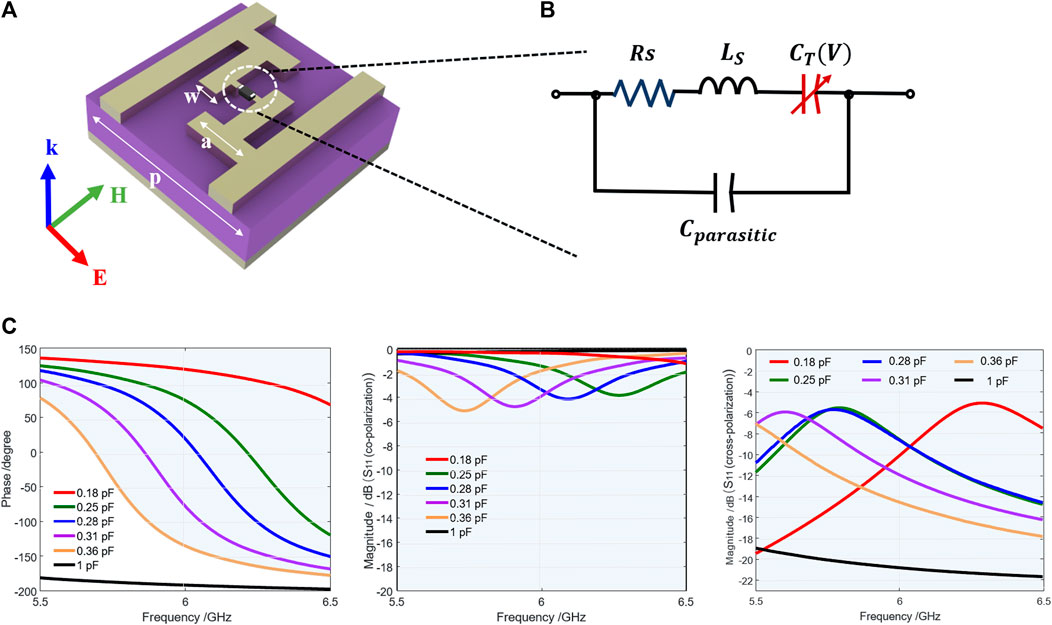
FIGURE 2. The unit cell and S-parameters. (A) 3D view of the designed unit cell. $p=\mathit{9}mm,a=\mathit{4}mm,w=\mathit{2}mm,b=\mathit{5}mm.$(B) Equivalent circuit diagram of the diode ma46h120, diode characteristics could be changed by adjusting the value of the capacitance. (C) The reflection phase of co-polarization, the amplitude of co-polarization and cross-polarization at different capacitance.

The commercial software CST is used to simulation and the exciting electrical field is along the gap direction. The result of S-parameters is shown in Figure 2C. Observing the co-polarization related parameter at 6 GHz, the reflection phase reaches 320°, and the amplitude is greater than −4 dB. Meanwhile the cross-polarization reflections are at least 4 dB less than the co-polarization reflection, which shows the cross-polarization has little effect on the final results. Six kinds of capacitors (corresponding to six phases) are selected as characteristic units, and the capacitance values are 0.18, 0.25, 0.28, 0.31, 0.36, and 1 pF, respectively. For the convenience of representation, the six types of feature units we defined are marked as unit one to unit 6.

The flat reflective metasurface arrangement comprises a group of unit cells of various capacitance, as shown in Figure 3. The proposed flat reflective metasurface dimensions contain 41 unit cells along the $x$-direction, and they all share the same voltage in the $y$-direction. During simulation, a cylinder with a bottom diameter of about one wavelength is used to simulate the obstacle, which is placed at the position three wavelengths away from the center of the metasurface. The boundary conditions in simulation for $x$ and $z$ directions are open, for the $y$-direction is periodic. Thus the whole metasurface above forms an infinite plane. For each unit cell, the reflected phase could be different by adjusting its diode capacitance when it works at the same frequency, and these randomly selected capacitance values form the input to the network.

FIGURE 3

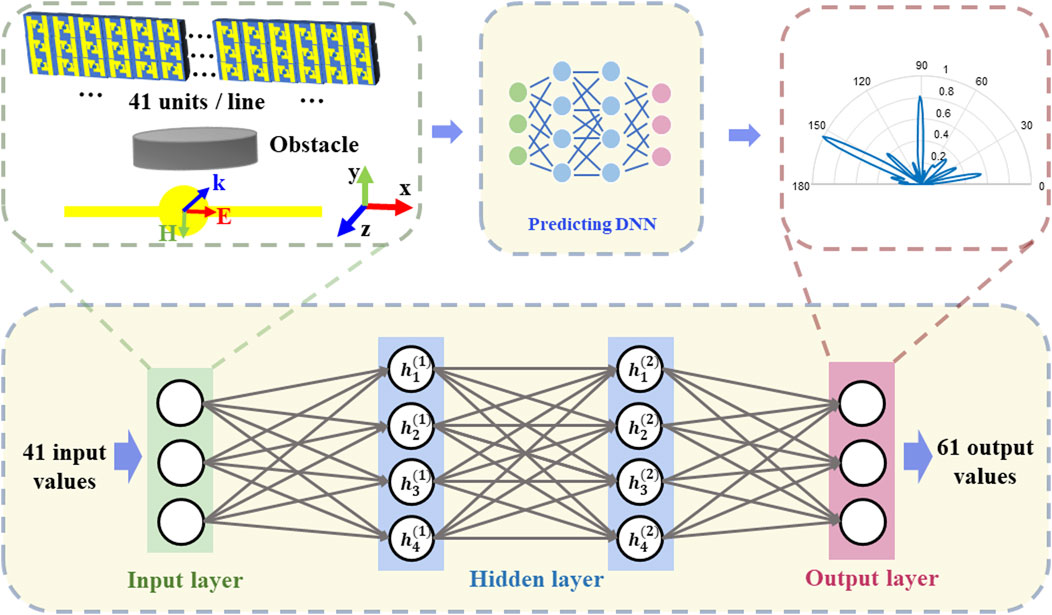
FIGURE 3. The four-layer artificial neural network. Network input: 1$\times$41 (corresponding to 41-unit-cell states). Network output: 1$\times$61 (corresponding to the far-field RCS).

Each unit cell has six states, which means the state space for network training is ${\mathit{6}}^{\mathit{41}}$. Using MATLAB combined with CST co-simulation, 10,000 sets of training data are randomly generated in the form of:

$\left[{Cap}_{\mathrm{1}},{Cap}_{\mathrm{2}}...{Cap}_{\mathrm{41}}\right]\sim \left[{RCS}_{\mathrm{1}},{RCS}_{\mathrm{2}}...{RCS}_{\mathrm{61}}\right](1)$

Figure 3 shows a random example. Among them, RCS has been normalized. In this data set, the maximum value of the far-field RCS appears in the directions around 90° and 150°, and the RCS in the remaining directions is relatively random.

A four-layer fully connected network (DNN) is designed for forwarding prediction, as shown in Figure 3. The input layer has 41 cells, which are the capacitance values of the 41-unit cells in each data set. The hidden layers consist of 200 and 150 cells, updating parameters constantly during training. The output layer consists of 61 cells, corresponding to the result of selecting a value for every 3° of the output 180° far field. The far-field results during training are normalized before being fed into the network to remove the effects of different orders of magnitude on the network’s predictions. The capacitance variables are encapsulated into a $1\times 41$one-dimensional linear tensor and input to the DNN, and a $1\times 61$ one-dimensional linear tensor is output. The loss function of the network is defined as the MSE as follows:

$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{R}\mathrm{C}\mathrm{S}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}-{\mathrm{R}\mathrm{C}\mathrm{S}}_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\right)}^2(2)$

Meanwhile, we define cosine similarity as the measure of accuracy to ensure the result’s performance on direction prediction as follows:

$\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}=\frac{{\sum }_{i=1}^N\left({RCS}_{predictioni}\times {RCS}_{simulationi}\right)}{\sqrt{{\sum }_{i=1}^N{\left({RCS}_{predictioni}\right)}^2}\times \sqrt{{\sum }_{j=1}^N{\left({RCS}_{simulationj}\right)}^2}}(3)$

DNN training adopts the stochastic gradient descent method, and the learning rate is set to be 0.002.

Results and discussion

80% of the saved 10,000 data are used as training data, and the rest 20% are testing data. Figure 4 shows that the training loss decreases and the cosine accuracy increases during the training process. After training, the MSE of the test dataset is 0.0336, and the cosine accuracy is about 90%. Results show the effectiveness of our proposed method. To visualize our results more intuitively, several predictions are randomly selected from the testing dataset, as shown in Figure 5. Interpolation is performed for both the simulated and predicted 61 values. In these data sets, the maximum values appear in different directions of 30°, 90°, and 150°, representing various possibilities for the generation of far-field RCS. In either case, we surprisingly find that these examples demonstrate the remarkable agreement between the DNN’s output (red curve) and simulation results (blue curve).

FIGURE 4

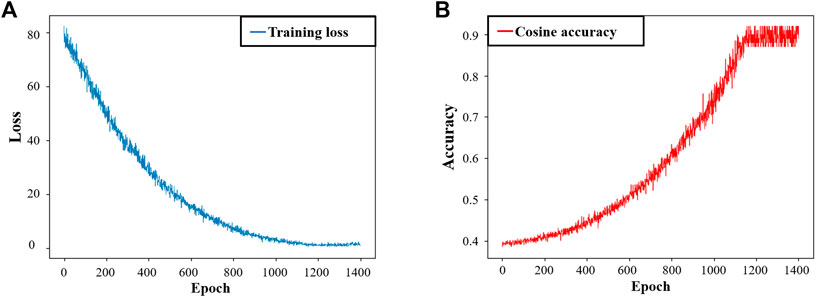
FIGURE 4. Training results. (A) The loss function decreases with the increase of training epochs. (B) With the increase in training times, the accuracy rate increased and tended to be stable when the epoch was about 1100.

FIGURE 5

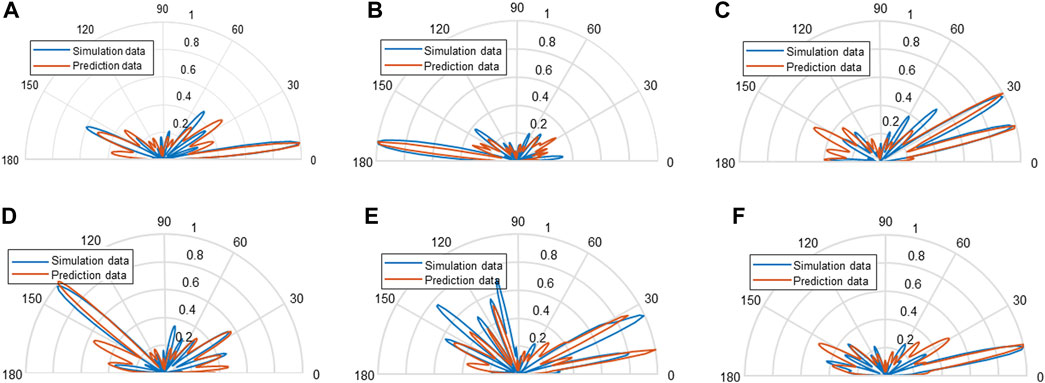
FIGURE 5. Far-field prediction results. (A). MSE = 0.0142; Accuracy = 91.26%. (B). MSE = 0.0201; Accuracy = 88.40%. (C). MSE = 0.0222; Accuracy = 88.74%. (D). MSE = 0.0265; Accuracy = 90.14%. (E). MSE = 0.0392; Accuracy = 89.54%. (F). MSE = 0.0161; Accuracy = 87.32%.

Although most of the predicted data, especially the maximum value prediction, is relatively accurate, there is still a certain prediction bias in the small value part of the RCS. It could be found that in the sixth graph of the examples, although the actual RCS is small in some directions, which is approximately 0.2 after normalization, the network predicts a value of around 0.4. It is mainly because that our loss function is the MSE of all data we input during network training. If most of the other data have a large value of RCS in this direction, the influence of individual data with a small value of RCS in this direction will little affect the results. Generating more training data, increasing the training dataset’s randomness, or switching to other networks for training are suitable methods to solve this problem. It should be noted that, although we only use a cylindrical object and target on single polarization, this method can be applied to other objects and more complex cases where we could also use dual-polarized metasurfaces or tunable omni-metasurfaces (Hu et al., 2021b; Hu et al., 2022).

Conclusion

We propose a novel approach for far-field RCS prediction of programmable metasurfaces with the presence of obstacles. A high reflectivity programmable metasurface is designed and far-field RCS predictions are performed in the presence of a cylindrical obstacle ahead. The capacitance values are fed into a four-layer DNN network to predict the RCS values, and prediction results show that the four-layer DNN we used can achieve almost accurate prediction and has an excellent performance in both value and direction. Our work creates a novel path for far-field prediction in obstacle-blocking situations without using complex computation and simulation, enabling various future applications, such as solving interference problems in communications.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

BZ and YJ conceived the idea and supervised the research. BZ and HL guided the theory and simulations. YJ designed the algorithm framework. RZ performed the simulations verifications. YJ, BZ, RZ, BY, TC, and HL analysed the data. YJ and RZ co-wrote the paper. All authors discussed the results and commented on the manuscript.

Funding

The work at Zhejiang University was sponsored by the National Natural Science Foundation of China (NNSFC) under Grant No. 62071423, Natural Science Foundation of Zhejiang Province under Grant No. LQ21F05002, and the Fundamental Research Funds for the Central Universities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, T., Tang, S., Zheng, B., Wang, G., Ji, W., Qian, C., et al. (2020). Ultrawideband chromatic aberration-free meta-mirrors. Adv. Photonics 3, 016001. doi:10.1117/1.ap.3.1.016001

CrossRef Full Text | Google Scholar

Chen, H., Taylor, A., and Yu, N. (2016). A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 79, 076401. doi:10.1088/0034-4885/79/7/076401

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Wei, Z., Li, M., and Rocca, P. (2020). A review of deep learning approaches for inverse scattering problems. Prog. Electromagn. Res. 167, 67–81. doi:10.2528/pier20030705

CrossRef Full Text | Google Scholar

Cheng, Y., Withayachumnankul, W., Upadhyay, A., Headland, D., Nie, Y., Gong, R. Z., et al. (2014). Ultrabroadband reflective polarization convertor for terahertz waves. Appl. Phys. Lett. 105, 181111. doi:10.1063/1.4901272

CrossRef Full Text | Google Scholar

Cui, T., Liu, S., Bai, G., and Ma, Q. (2019). Direct transmission of digital message via programmable coding metasurface. Research 2019, 1–12. doi:10.1155/2019/2584509

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, T. (2017). Microwave metamaterials—From passive to digital and programmable controls of electromagnetic waves. J. Opt. 19, 084004. doi:10.1088/2040-8986/aa7009

CrossRef Full Text | Google Scholar

Cui, T., Qi, Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding metamaterials, digital metamaterials and programmable metamaterials. Light. Sci. Appl. 3, e218. doi:10.1038/lsa.2014.99

CrossRef Full Text | Google Scholar

Della, G., and Engheta, N. (2014). Digital metasurfaces. Nat. Mater. 13, 1115–1121. doi:10.1038/nmat4082

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, L., Cheng, Q., Yang, J., Ma, S. J., Zhao, J., Liu, S., et al. (2015). Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light. Sci. Appl. 4, e324. doi:10.1038/lsa.2015.97

CrossRef Full Text | Google Scholar

Gao, L., Cheng, Q., Yang, J., Ma, S. J., Zhao, J., Liu, S., et al. (2015). Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light. Sci. Appl. 4, e324. doi:10.1038/lsa.2015.97

CrossRef Full Text | Google Scholar

Giovampaola, C., and Engheta, N. (2014). Digital metamaterials. Nat. Mat. 13, 1115–1121. doi:10.1038/nmat4082

CrossRef Full Text | Google Scholar

Hao, H., Ran, X., Tang, Y., Zheng, S., and Ruan, W. (2021). A single-layer focusing metasurface based on induced magnetism. Prog. Electromagn. Res. 172, 77–88. doi:10.2528/pier21111601

CrossRef Full Text | Google Scholar

Hu, Q., Zhao, J., Chen, K., Qu, K., Yang, W., Zhao, J., et al. (2022). An intelligent programmable omni-metasurface. Laser & Photonics Rev. 16, 2100718. doi:10.1002/lpor.202100718

CrossRef Full Text | Google Scholar

Hu, Q., Chen, K., Zhang, N., Zhao, J., Jiang, T., Zhao, J., et al. (2021). Arbitrary and dynamic poincaré sphere polarization converter with a time-varying metasurface. Adv. Opt. Mater. 10, 2101915. doi:10.1002/adom.202101915

CrossRef Full Text | Google Scholar

Hu, Z., He, N., Sun, Y., Jin, Y., and He, S. (2021). Wideband high-reflection chiral dielectric metasurface. Prog. Electromagn. Res. 172, 51–60. doi:10.2528/pier21121903

CrossRef Full Text | Google Scholar

Huang, M., Zheng, B., Cai, T., Li, X., Liu, J., Qian, C., et al. (2022). Machine learning-enabled metasurface for direction of arrival estimation. Nanophotonics 11, 2001–2010. doi:10.1515/nanoph-2021-0663

CrossRef Full Text | Google Scholar

Liang, L., Qi, M., Yang, J., Shen, X., Zhai, J., Xu, W., et al. (2015). Metamaterials: Anomalous terahertz reflection and scattering by flexible and conformal coding metamaterials (advanced optical materials 10/2015). Adv. Opt. Mater. 3, 1373. doi:10.1002/adom.201570062

CrossRef Full Text | Google Scholar

Lin, D., Fan, P., Hasman, E., and Brongersma, M. (2014). Dielectric gradient metasurface optical elements. Science 345, 298–302. doi:10.1126/science.1253213

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Cui, T., Zhang, L., Xu, Q., Wang, Q., Wan, X., et al. (2016). Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 3, 1600156. doi:10.1002/advs.201600156

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, H., Zheng, B., Cai, T., Qian, C., Yang, Y., Wang, Z., et al. (2021). Frequency-controlled focusing using achromatic metasurface. Adv. Opt. Mat. 9, 2001311. doi:10.1002/adom.202001311

CrossRef Full Text | Google Scholar

Ma, H., Wang, G., Jiang, W., and Cui, T. (2014). Independent control of differently-polarized waves using anisotropic gradient-index metamaterials. Sci. Rep. 4, 6337. doi:10.1038/srep06337

PubMed Abstract | CrossRef Full Text | Google Scholar

Pendry, J. (2000). Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969. doi:10.1103/physrevlett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, T., Shi, X., Wang, J., Li, Y., Qu, S., Cheng, Q., et al. (2019). Deep learning: A rapid and efficient route to automatic metasurface design. Adv. Sci. (Weinh). 6, 1900128. doi:10.1002/advs.201900128

PubMed Abstract | CrossRef Full Text | Google Scholar

Sensong, A., Fowler, C., Zheng, B., Shalaginov, M. Y., Tang, H., Li, H., et al. (2019). A deep learning approach for objective-driven all-dielectric metasurface design. ACS Photonics 6, 3196–3207. doi:10.1021/acsphotonics.9b00966

CrossRef Full Text | Google Scholar

Smith, D., Pendry, J., and Wiltshire, M. (2004). Metamaterials and negative refractive index. Science 305, 788–792. doi:10.1126/science.1096796

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, Q., Zheng, B., Cai, T., Qian, C., Zhu, R., Li, X., et al. (2022). Broadband spin‐locked metasurface retroreflector. Adv. Sci. 9, 2201397. doi:10.1002/advs.202201397

CrossRef Full Text | Google Scholar

Wang, K., Zhao, J., Cheng, Q., Dong, D., and Cui, T. (2014). Broadband and broad-angle low-scattering metasurface based on hybrid optimization algorithm. Sci. Rep. 4, 5935. doi:10.1038/srep05935

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, N., Zhang, Y., Ma, H., Chen, H., and Qian, H. (2021). Tunable high-Q plasmonic metasurface with multiple surface lattice resonances. Prog. Electromagn. Res. 172, 23–32. doi:10.2528/pier21112006

CrossRef Full Text | Google Scholar

Xiao, B., Zhang, Y., Tong, S., Yu, J., and Xiao, L. (2020). Novel tunable graphene-encoded metasurfaces on an uneven substrate for beam-steering in far-field at the terahertz frequencies. Opt. Express 28, 7125–7138. doi:10.1364/oe.386697

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, B., Tang, K., Cheng, H., Liu, Z., Chen, S., and Tian, J. (2017). Coding acoustic metasurfaces. Adv. Mat. 29, 27921327. doi:10.1002/adma.201603507

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, P., Wang, G., Li, H., Wang, Y., and Zong, B. (2020). Wideband RCS reduction of high gain fabry-perot antenna employing a receiver-transmitter metasurface. Prog. Electromagn. Res. 169, 103–115. doi:10.2528/pier20062703

CrossRef Full Text | Google Scholar

Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J. P., Capasso, F., et al. (2011). Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 334, 333–337. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Chen, X. Q., Liu, S., Zhang, Q., Zhao, J., Dai, J. Y., et al. (2018). Space-time-coding digital metasurfaces. Nat. Commun. 9, 4334. doi:10.1038/s41467-018-06802-0

PubMed Abstract | CrossRef Full Text | Google Scholar