Intelligent methods for optimization design of lightweight fiber-reinforced composite structures: A review and the-state-of-the-art

Chen, Yonglin; Zhang, Junming; Li, Zefu; Zhang, Huliang; Chen, Jiping; Yang, Weidong; Yu, Tao; Liu, Weiping; Li, Yan

doi:10.3389/fmats.2023.1125328

REVIEW article

Front. Mater., 31 March 2023

Sec. Polymeric and Composite Materials

Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1125328

This article is part of the Research Topic Fiber-Reinforced Composites: Design, Characterization, Analysis, and Application View all 6 articles

Intelligent methods for optimization design of lightweight fiber-reinforced composite structures: A review and the-state-of-the-art

Yonglin Chen¹

Junming Zhang¹

Zefu Li¹

Huliang Zhang¹

Jiping Chen^1,2

Weidong Yang¹*

Tao Yu¹

Weiping Liu²

Yan Li¹*

¹School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai, China
²COMAC Shanghai Aircraft Manufacturing Co., Ltd., Shanghai, China

As the application of lightweight fiber-reinforced composite structures reaches an unprecedented scale in industry, design technology for composite structures becomes crucial for enhancing performance, improving productivity, and reducing cost. In recent years, the rapid development of intelligent technology, such as big data, deep learning, and machine learning, has promoted the development of design technology. However, the current situation and intellectualization of the design technology is not well summarized. This paper reviews the advance in design technologies for fiber-reinforced composite structures, including prediction and optimization methods for composite properties. Then, their intellectualization development is overviewed. Finally, the development trend of intelligent design technologies and intelligent composite structures are discussed. This work can provide a reference for researchers in the related field.

1 Introduction

Lightweight fiber-reinforced polymer (FRP) composite has been widely used in aerospace industry due to its high strength-weight ratio, high temperature resistance, outstanding designability to meet different requirements and the ability to integrate large-scale integral structures (Zhao et al., 2016; Sun et al., 2020; Wang et al., 2021a; Wang et al., 2021b). As shown in Figure 1A, the application of lightweight FRP composite in aircraft has been increasing rapidly since the end of 20th century. The composite structure weights of Boeing 787 (Figure 1B (DOCSLIB, 2022)) and Airbus A350, most advanced commercial aircraft in the world, are over 50%. The application of FRP not only enhances their safety and energy-efficient significantly, but also is environment-friend (Van Grootel et al., 2020). Because of the benefits, the usage of FRP composite in aerospace industry will increase continuously.

FIGURE 1

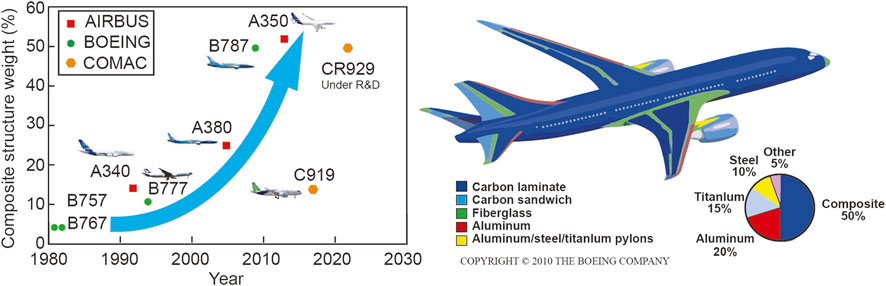
FIGURE 1. Composite application in aircraft (A) Percentage of total structural weight attributed to composites, (B) FRP composite in Boeing 787.

The mechanical properties of FRP composite in aircraft, such as engine and wing, mainly depend on both the design and manufacturing technologies (Figure 2). Design of FRP composite include the material selection, the determination of material content, the internal structure of composites and so on, which pursuits to figure out the relationship between their mechanical properties and these parameters. Manufacturing process of composites is complicated and primarily determines whether the final performance of the composites can reach the designed value. In this review, we emphasize on the development of design technology.

FIGURE 2

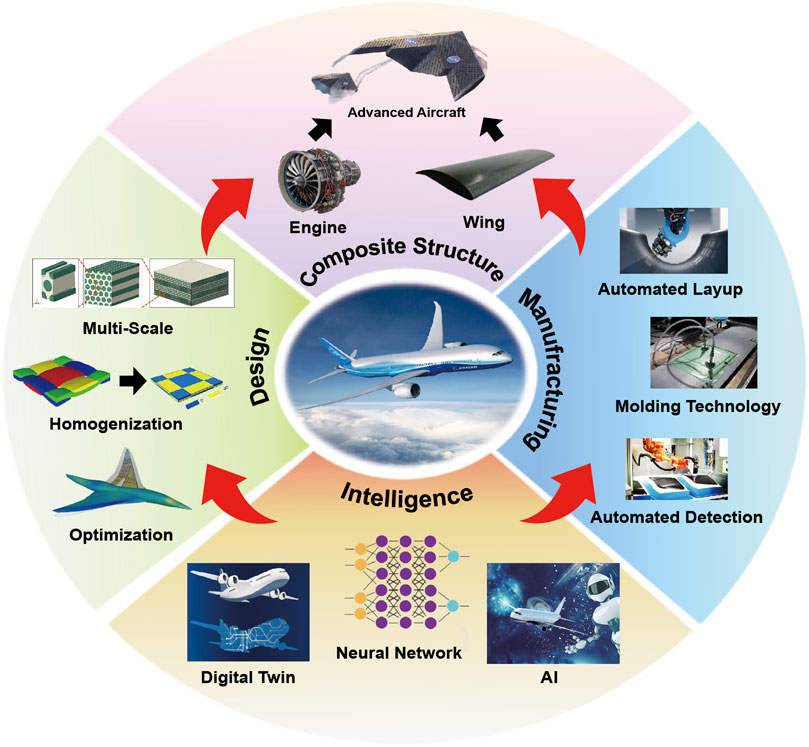
FIGURE 2. Development of design and manufacturing technologies of composite structures with intelligence.

Analytical methods are the early primary approaches to predict macro properties of simple composites, for example, laminated plates. However, due to the complex internal structure of composites, analytical methods are unable to elucidate micro- or meso-scale mechanical mechanism. In micro scale, a fiber tow consists of hundreds of unidirectional fibers in random arrangement, which are adhesive with polymer resin. A small defect in fibers, resin or the interface between fibers and resin may cause failure of composites under external forces. To illustrate the interdependence between macro properties and micro internal structure, some multi-scale methods from the view of micro- or meso-structure of composites are proposed such as method of cells (Aboudi, 1981; Aboudi, 1982; Aboudi, 1988; Aboudi, 1989; Aboudi, 1991).

Furthermore, multi-scale methods generally combined with finite element (FE) method have established to construct the relationship between the design parameters and mechanical properties of composites. However, it is still difficult to achieve high-throughput prediction because of the excessive time consumption in simulation process by FE method. To improve the prediction efficiency, artificial intelligent methods, e.g., neural network and machine learning, have been developed (Xu et al., 2015; Wagner et al., 2019; Wanigasekara et al., 2020; Wanigasekara et al., 2021; Parmar et al., 2022; Thomas et al., 2022). As well-know, one of the purposes of composite design is to improve the mechanical properties by optimizing design parameters. For this purpose, parameter analysis through experiment and FE method is a main conventional approach, but this approach is time-cost and global optimal solutions are not obtained all the time. The pursuit of rapid prediction and optimization of composites has driven the research into the combination of intelligent algorithm and artificial intelligence with the conventional experiment methods and FE method.

With the rapid development of intelligent technology, the digital and intelligent design has been the inevitable development trend. Researchers have made much progress in the application of intelligent technologies on many industrial fields. For instance, artificial neural network (ANN) has been used to predict the enhanced oil recovery using fluid injection (Abbassi et al., 2023), to identify parameters of a mechanical ductile damage in sheet metal forming (Abbassi et al., 2013), to monitor and assess environmental quality (Franceschi et al., 2018), etc. However, an overall review upon the intellectualization advance of design technology for FRP composites is still absent. This review dedicates design technologies for continuous fiber-reinforced polymer composites. In the first section, prediction methods for composite performance are presented, including multi-scale methods and intelligent prediction methods. Then the development of intelligence in the optimization of composite properties is introduced in detail. The research focusing on the difficult issues of the processes are introduced and discussed. Finally, the intellectualization development trend of composite design technologies is predicted.

2 Prediction of mechanical properties

Composite structures have the advantage of strong designability, and the designable parameters include the fiber and matrix type, the volume percent of fibers, the direction of the laminate, etc. If designers lack a clear understanding of the influence of design parameters on the composite properties, it will lead to a useless design and cause a waste of resources and time (Gooneie et al., 2017). The aim of predicting properties of composite structures is quantitatively figuring out the relationship between design parameters and mechanical properties, which can guide the design direction and is helpful for designing high-performance composite structures efficiently. The multi-scale and intelligent methods are two main approaches.

2.1 Multi-scale prediction method

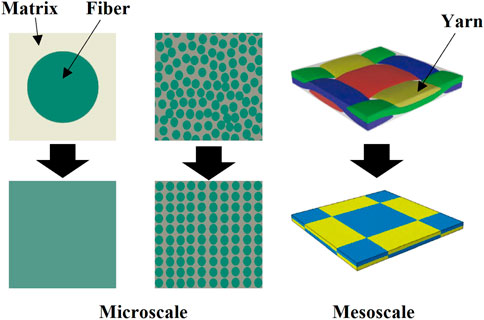
The prior prediction method for the mechanical properties of composites is macro-scale method, which is mainly to describe the overall mechanical behavior of a composite. Hence, this method is mostly based on phenomenological theory and experimental data, and classical finite element. It is well-know that various meso- or micro-damage in composite material, such as yarn or fiber breakage and matrix crack, could lead to macroscopic structural fracture. However, the macro-scale method is unable to accurately describe the complex damage process and failure mechanism of composites due to the neglect of the details inside them. In recent decades, meso- and micro-scale methods have been developed to solve many problems separately.

Nevertheless, for a FRP composite structure, its overall mechanical properties (structure level) are intimately linked with the meso-structure of yarns (yarn level). The yarn behavior depends on the arrangement of fibers and the interaction between fibers (fiber level), and the relative motion of fibers within a yarn is the main reason for the change of yarn cross-section shape (Miao et al., 2008). Recently, some researchers also use the molecular dynamics (MD) method to further study the interface properties between fibers and resin at nano-scale (Sun et al., 2018; Sun et al., 2021). This fact indicates that a single-scale method is insufficient for predicting mechanical properties of composites, especial the failure process from initial defects to structure damage. Besides, with the wide application of fiber-reinforced composites in aerospace, the size of target components is increasing, and the requirement of analysis accuracy is also improving. Therefore, the research on the approaches for predicting mechanical properties of composites has gradually developed from the traditional single-scale method to multi-scale method.

In multi-scale method, two different analysis strategies are proposed: sequential and concurrent multi-scale approach. The sequential approach divides the analysis objectives into multiple levels (for instance, from molecular to structure level) and selects appropriate parameters to realize the information transmission between different levels (Figure 3). Micro-scale, meso-scale and macro-scale models are adopted in sequence to study a composite structure. Different from the sequential approach where analysis is conducted in one scale model a time, multiple different scale models are analyzed simultaneously in a concurrent multi-scale model. The concurrent approach connects different regions through some sort of a handshaking procedure and multi-scale parallel computing (Broughton et al., 1999; Rudd and Broughton, 2000; Nakano et al., 2001).

FIGURE 3

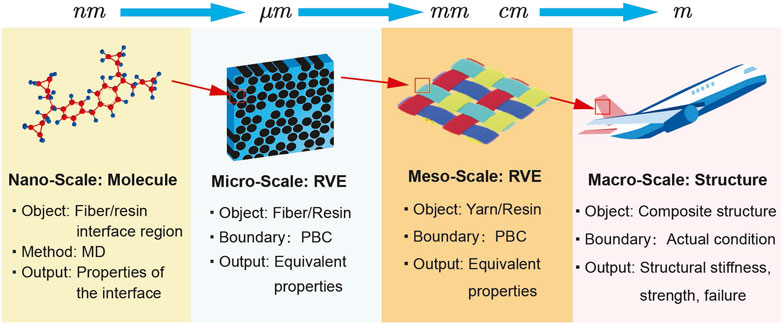
FIGURE 3. Sequential approach with the multi-scale modeling from nanoscale (molecule) to macro-Scale (structure).

2.1.1 Sequential approach

The sequential multi-scale approach mainly includes analytical and FE simulation method. The analytical method is mainly derived from the inclusion theory, including self-consistent method (Budiansky, 1965; Hill, 1965), Mori-Tanaka method (Benveniste, 1987), differential method (Roscoe, 1952), etc. This method can quickly predict the linear elastic properties of composites with simple microstructure, but it cannot solve the non-linear behavior and local field details of composites. The combination between analytical method and FE simulation method is a useful approach.

• Method of cells

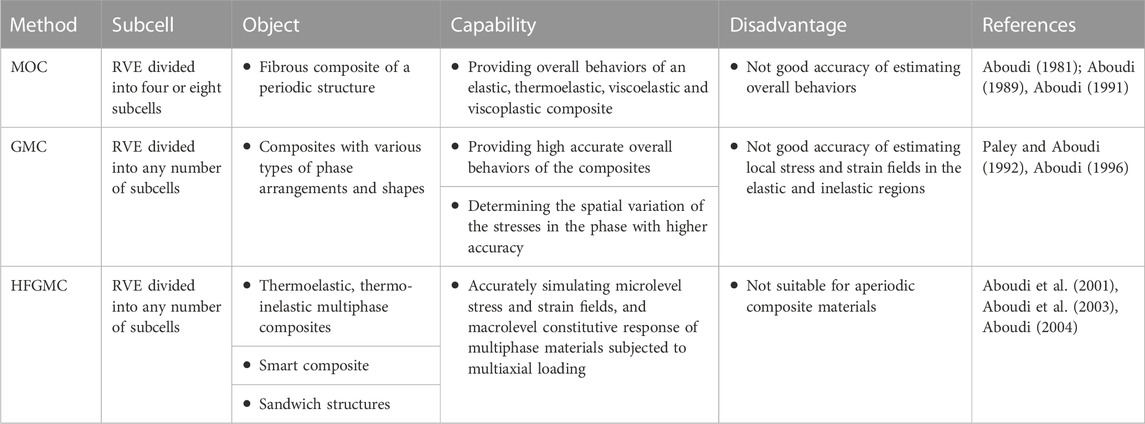
Method of Cells (MOC) is a typical multi-scale method proposed by Aboudi (Aboudi, 1981; Aboudi, 1982; Aboudi, 1988; Aboudi, 1989; Aboudi, 1991), which can provide the macro-behavior, such as yield surfaces, strength envelops and fatigue failure, of periodic multiphase materials of various types, also FRP composites by further divided RVE into four simpler subcells. At the cost of losing a little calculation accuracy of the local stress and strain field, this method can gain the fast solution of equilibrium equations and equivalent parameters.

From method of cells, the generalized method of cells (GMC) is obtained, which defines a repeating unit cell (RUC) in a periodic structure and divides it into an arbitrary number of orthogonal subcells rather than four or eight subcells in MOC (Paley and Aboudi, 1992; Aboudi, 1996). GMC, therefore, can achieve higher accurate overall behaviors of composites and model composites with various types of phase arrangements and shapes effectively. GMC has been widely used to study fiber reinforced composites and braided composites used in aviation engineering. For instance, Li et al. (Li and Zhang, 2015) developed a viscoelastic constitutive model of fiber reinforced composites based on GMC, in which the matrix is viscoelastic and the fiber is transversely isotropic.

Despite of this, the method’s accuracy of estimating local stress and strain fields is not as good as its macro-predictive capability both in the elastic and inelastic regions (Aboudi, 2004). Afterwards, Aboudi et al. (Aboudi et al., 2003) eliminated the drawback through a higher-order theory that has been developed to analyze functionally graded materials and the elements of the homogenization technique. This new model is referred to as high-fidelity generalized method of cells (HFGMC) and exhibits the ability to accurately simulate of microlevel stress and strain fields and macrolevel constitutive response of multiphase materials subjected to multiaxial loading.

The HFGMC method has already been applied on inelastic, smart composites, finite strain analysis, sandwich structures, etc. By employing the HFGMC model, Bednarcyk et al. have figured out the effects of fiber misalignment (Bednarcyk et al., 2014) and clustering (Bednarcyk et al., 2015), and the damping properties of unidirectional, laminated, and woven composites (Bednarcyk et al., 2016). The HFGMC was also successfully used for the mechanical property prediction of reinforced carbon nanotubes by David et al. (David et al., 2014). Surprisingly, the HFGMC has also been implemented to predict the behavior of smart composites, such as piezoresistive composites and magnetostrictive materials. Thus, piezoresistive composites, of which the electrical resistance changes with the application of mechanical deformation, have been analyzed by Haj-Ali et al. (Haj-Ali et al., 2014) by employing the HFGMC micromechanics model. Further, the HFGMC analysis has been formulated for the analysis of magnetostrictive composites, of which elastic strain can be generated by the application of magnetic field (Aboudi et al., 2014). In the HFGMC model, one of the phases behaves as a magnetostrictive material whose constitutive response is non-linear. Additionally, it has been found that HFGMC can be applied in sandwich structures. Kheyabani et al. (Kheyabani et al., 2022) presented a robust and computationally efficient multiscale analysis approach for linear elastic structural analysis of thick sandwich structures by coupling of the parametric HFGMC and the refined zigzag theory (RZT) based isogeometric analysis (IGA) plate formulation. The present method was computational efficiency, high accuracy, and low cost for sandwich structures. These methods are summarized and compared in Table 1.

TABLE 1

TABLE 1. Comparison of MOC, GMC and HFGMC.

Recently, Aboudi et al. (Aboudi and Gilat, 2021; Aboudi and Gilat, 2022a; Aboudi and Gilat, 2022b) applied the HFGMC method to predict the microbuckling of various types of viscoelastic composites containing several randomly located fiber waviness of spatially varying amplitudes under compression. They verified the applications of HFGMC for the prediction of the microbuckling stresses of bi-layered, continuously reinforced, and aligned short-fiber viscoplastic composites. For now, the HFGMC micromechanical method has the potential to address more mechanical problems regarding to various types of composites.

• computational homogenization

The homogenization method (Sánchez-Palencia, 1980; Oleïnik et al., 2009) is essentially a mathematical method, aiming to study the relevant physical parameters of composites at different scales, expand each physical parameter with the ratio of the two scales as a small parameter (Figure 4), and establish the relationship between the expansion parameters according to the geometric equations, physical equations and equilibrium equations. Then the periodicity and boundary value conditions of the RVE are used to solve the expansion quantities and macroscopic physical fields. The computational homogenization method can solve the corresponding equivalent mechanical properties, thermal properties, damage criteria and so on.

FIGURE 4

FIGURE 4. Homogenization of composites in microscale and mesoscale.

Based on the computational homogenization method, many researchers have carried out a lot of work on the elastic mechanical response, elastic property analysis and prediction of composite materials. They realize the leap from unidirectional composite materials to three-dimensional braided composite materials, and from simple boundary conditions to complex boundary conditions. For example, Balasubramani et al. (Balasubramani et al., 2022) proposed a RVE modeling method for unidirectional composites, which is closer to the real fiber layout, and successfully predicted the equivalent mechanical properties of composites through homogenization method. Zhou et al. (Zhou et al., 2016) considered the uncertainties associated with the material properties, and obtained the corresponding elastic properties of composites by using the computational homogenization method.

In addition to the elastic properties, homogenization method can also be used to study the damage of composites, such as the interface problem and impact problem of composite materials. Ullah et al. (Ullah et al., 2017) established a three-dimensional multi-scale computational homogenization framework to investigate the fiber-matrix debonding of composites, and modeled them using uncorrelated pressure-dependent paraboloid yield criterion and cohesive interface element respectively. Additionally, Sun et al. (Sun et al., 2018; Sun et al., 2021) combined the homogenization method with MD analysis to determine the elastic-plastic-damage constitutive law of the composite, and then obtained the properties of the interface between fiber and resin. They realized the high-precision simulation of the multi-scale failure strength and damage behavior of the composite. Furthermore, by adopting the homogenization multi-scale method, Canal et al. (Canal et al., 2017) successfully predicted the specimen thickness scaling effect in fiber bridging fracture under the consideration of the physical processes of interlaminar damage initiation, propagation and fiber bridging of composites. As the impact problem, Zhao et al. (Zhao et al., 2018) simulated the multi-scale failure behavior of triaxial braided composites during impact depending on homogenization method, and Yuta et al. (Yamazaki et al., 2018) used the homogenization method to predict the dynamic matrix dominant failure behavior of carbon fiber reinforced polymer (CFRP) composite structures under impact loading, where the strain rate effect of resin matrix was considered.

To illustrate the actual service state of composite structures more accurately, its viscoelastic behavior is also considered in a multi-scale model. An example is that the influence of matrix viscoelasticity and yarn geometry on the mechanical properties of composite structures were considered in the multi-scale modeling with homogenization method (Hofer et al., 2020). This research obtained the equivalent mechanical properties of composites and verified the proposed multi-scale model through the compression creep test of braided reinforced pipe. The viscoelastic behavior of three-dimensional braided composites was also concerned by Zhai et al. (Zhai et al., 2020). They used the asymptotic expansion homogenization (AEH) method and multi-phase finite element (MFE) to simulate the viscoelastic behavior from the micro-scale (fiber/resin), meso-scale (yarn/resin) and macro-scale (homogeneous composite). For the purpose of further improving the calculation efficiency of the dynamic response of composite structures, Hachemi et al. (El Hachemi et al., 2016) homogenized the composite through multi-scale finite element analysis, and obtained the viscoelastic properties of the composite structure, such as its storage modulus, loss modulus and mechanical impedance, as well as the overall dynamic response.

Furthermore, homogenization method has been used to research the irreversible curing deformation of thermosetting composite structures. The influence of the curing deformation on the geometry and mechanical properties of components in the actual manufacturing process should also be fully considered to prevent the design components from failing to meet the requirement on mechanical properties and geometric dimensions. Due to this fact, Peter et al. (Lenz and Mahnken, 2021) established a micro-meso-macro scale framework for thermal, mechanical and chemical homogenization of composites, and successfully took heat conduction, elastic properties, chemical reaction kinetics and curing kinetics into account in the homogenization process. Through micro and macro homogenization, Anton et al. (Trofimov et al., 2021a; Trofimov et al., 2021b) developed a multi-scale thermos-chemo-mechanical simulation method of composites, obtained the coefficients related to thermal expansion and chemical shrinkage of composites, and successfully predicted the distortion of 3D woven composites after RTM process.

• Multi-scale analysis considering the randomness of practical structures

In the above-mentioned methods, composite structures are generally regarded as the periodic arrangement of RVE, but the randomness of practical structures is not considered, like the random arrangement of fibers or yarns in Figure 4. Therefore, there is still a certain error between the simulation results and the practical response of composite structures. Andy et al. (Vanaerschot et al., 2016) considered the spatial randomness of fibers in textile composites for modeling and proposed a multi-scale modeling method approaching real textile composites.

For braided composites with more complex internal structure, the mechanical properties are greatly affected by the internal local properties of materials. Therefore, it is difficult to meet the requirements of accurate analysis by using the idealized periodic arrangement model rather than the accurate model of the internal fiber braiding structure. Bassam et al. (El Said et al., 2016) considered the changes of internal yarn geometry of 3D braided composites in different part configurations, proposed a multi-scale modeling method based on Voronoi subdivision in 3D space, and created an intermediate length scale suitable for homogenization to deal with the aperiodicity of the final material. This method considers the influence of material aperiodicity on properties and damage, and the results is in good agreement with the corresponding experimental data.

Woven composites with complex architecture and a certain feature of mutually orthogonal reinforcement arise particular interest for aerospace structural groups. Multiscale analysis is suitable for modelling woven composites. Focusing the multiscale modeling problem of woven composite, Gherissi et al. (Gherissi et al., 2013) created an anisotropic multiscale model method under Abaqus and Matlab software after resolving several difficulties, including modelling the mechanical behavior of yarns, discretizing geometric model of yarns, and so on. They claimed that this study contributes to solving the complex problem of woven composites at the mesoscale and the implementation of multi-scale procedure. Based on realistic geometry parameters and material property of an 8-harness satin woven composite, Yang et al. (Yang and Yan, 2020) established multiscale finite element models. The effective properties of fiber bundles can be obtained by the micro-scale model and then used in the meso-scale model, which is used to predict the global failure behavior of the woven composite. Recently, Liu et al. (Liu et al., 2023) developed a multiscale modeling approach to predict the force–displacement curve, elastic modulus and tensile strength of 3D braided CFRP composites. The results reveal that the fiber breakage, matrix cracking and debonding are the dominant failure modes.

2.1.2 Concurrent approach

In sequential approaches, the models in different scales are separated and the information are transferred between the models. Specifically, for example, elements in a single FE model are constructed in a single scale. However, critical regions, such as stress concentration, crack initiation and propagation, and other critical physical phenomena may occur in composites, which the sequential approach is unable to model accurately. Consequently, concurrent multiscale method was established, which divide the entire solution domain into non-critical far field and several critical sub-regions. The macroscopic analysis using bottom-up homogenization in the non-critical far field enhances the efficiency of the computational analysis. On the other hand, microscopic analysis using the top-down localization process in critical sub-regions is necessary for achieving sufficient accuracy. In a word, concurrent multiscale method implements sub-structuring and concurrently solves different models at regions with different resolutions or scales.

Qiao et al. (Qiao et al., 2023) developed a macro-mesoscale coupled model for evaluating the progressive damage behavior of notched 3D woven composites subjected to the tensile loading (Figure 5A). Instead of applying macroscopic phenomenological failure criterion, mesoscale continuum damage model was used in this model. Consequently, this model is capable of predicting stress–strain responses and simulating the propagation process of macro-meso coupled damage nearby the hole-edge. He et al. (He et al., 2021) pointed out two challenges in conducting a concurrent multiscale simulation for composites: How to solve the RVE fast and accurately and capture the non-linear behavior of 3D braided composites. To solve the challenges, they proposed a concurrent multiscale framework from microscale to mesoscale (Figure 5B) based on the data-driven self-consistent clustering analysis, an effective reduced order model. They further proposed a concurrent three-scale scheme FE-SCA² (SCA is short for self-consistent clustering analysis) for predicting the macroscopic non-linear behavior of braided composites associated with the microscopic plastic and damage of the constituents (He et al., 2022). The proposed approach can simultaneously capture the microscale, mesoscale, and macroscale non-linear behavior of braided composites, which would be difficult for experimental methods. Based on the approach, Gao et al. (Gao et al., 2022) adopted a data-driven concurrent n-scale modeling approach (FExSCAⁿ⁻¹) for woven composites. This framework provides an accurate prediction for the structural performance (e.g., non-linear structural behavior under tensile load), as well as the physics field evolution of woven and unidirectional composites (Figure 5C). Besides the abovementioned concurrent models, the molecular dynamics-coupled concurrent model has been developed. Nevertheless, the model is usually applied on nanocomposites rather than FRP composites (Li et al., 2018).

FIGURE 5

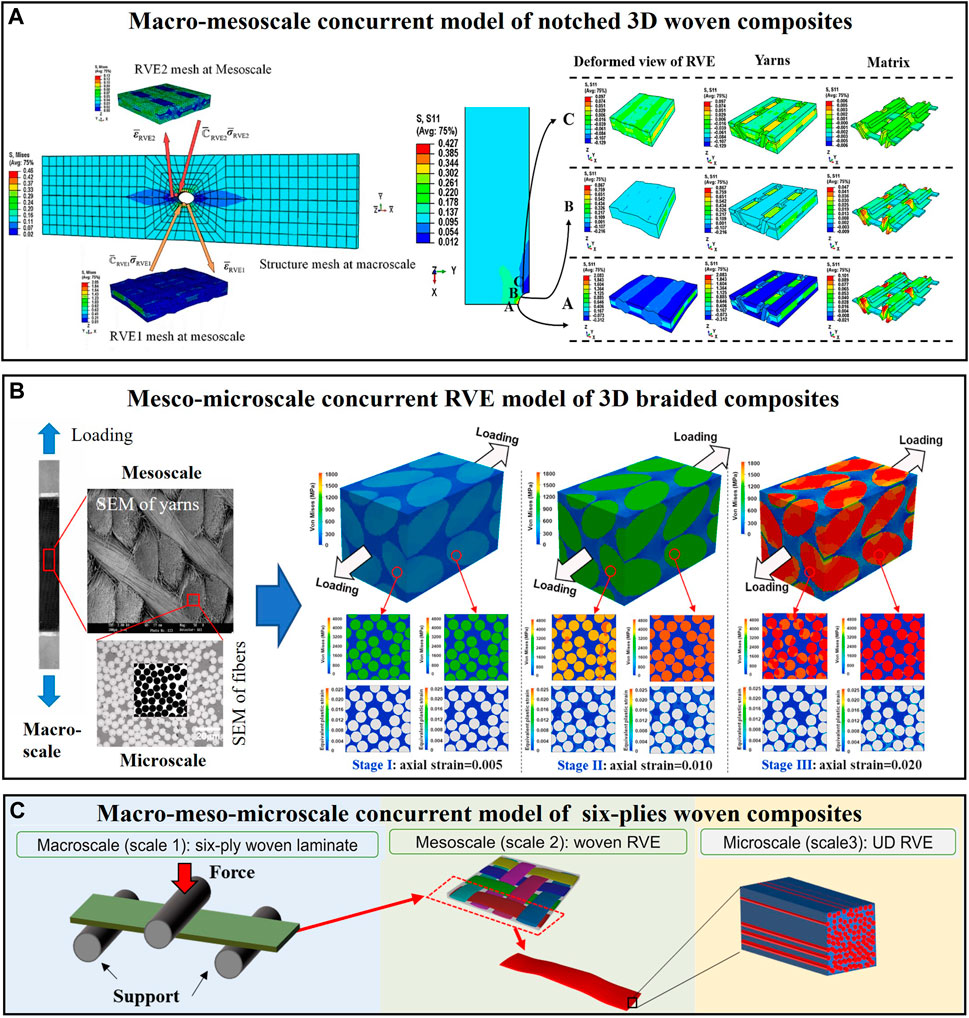
FIGURE 5. Concurrent multiscale models of composites (A) Macro-mesoscale (Qiao et al., 2023), (B) Meso-microscale (He et al., 2021), (C) Macro-meso-microscale (Gao et al., 2022).

Additionally, concurrent multiscale model can be combined with machine learning. Based on mechanistic homogenization theory of RVE and advanced machine learning techniques, a data-driven multiscale material modeling method is developed by Liu et al. (Liu et al., 2019). They believed that this intelligent material model can efficiently simulate a large-scale heterogeneous structure by a high-fidelity concurrent model (Liu et al., 2019). Afterwards, they proposed the transfer learning strategy of this model for structure–property predictions. The efficiency enables the generation of a large output space for a multi-objective materials design problem.

2.2 Intelligent prediction method

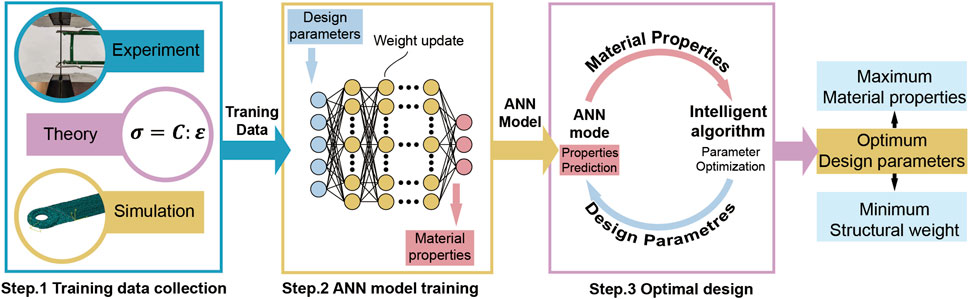
The microscopic structure and macroscopic design parameters of composites can directly determine their mechanical properties. Therefore, many researchers use artificial intelligent method to bridge the microstructure and macro design parameters-mechanical properties, and drive the rapid development of multi-scale mechanics of FRP composites. Specifically, this method depends on data to mine the internal relationship between design parameters and basic mechanical properties, fatigue properties, impact properties, or even establish constitutive laws of composites. Artificial neural network (ANN) is the most representative and common intelligent method for predicting mechanical properties of FRP composites. A well-trained ANN model (Figure 6A) can realize the non-linear mapping between the design parameters and mechanical properties of composites (Figure 6B), and shows good accuracy and efficiency in the prediction of composite properties. Owing to these features, ANN has attracted more and more attention. Besides, convolutional neural network (CNN) and deep neural network (DNN) have also been used for the prediction of some properties of FRP composites.

FIGURE 6

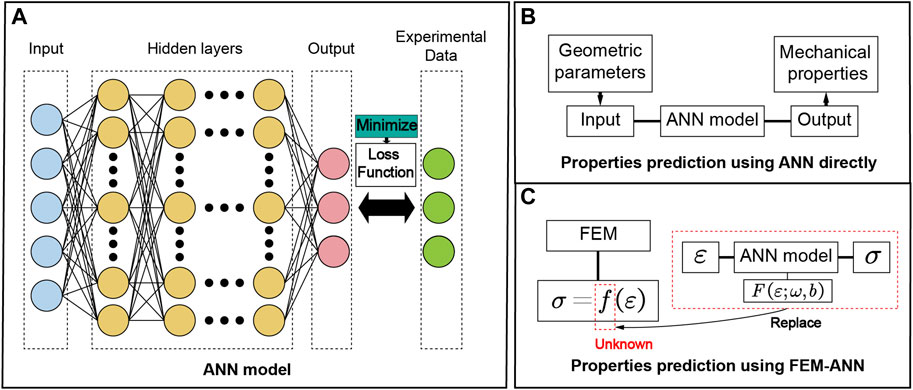
FIGURE 6. Prediction of properties of composites by ANN. (A) ANN model, (B) Predicting the properties of composite materials using ANN directly, (C) Predicting the properties of composite materials by combining ANN and finite element method.

2.2.1 Fundamental properties

Xu et al. (Xu et al., 2015) extracted the key geometric parameters of fiber scale and tow scale according to the microstructure of 3D braided composites, and then used ANN to construct the non-linear mapping relationship between microstructure parameters and tensile modulus. Bezerra et al. (Bezerra et al., 2007) used ANN to predict the shear mechanical properties of carbon fiber reinforced epoxy composites and glass fiber reinforced epoxy composites under different stacking sequences. By inputting the number of layers, the types of fiber and matrix into a trained ANN, Khan et al. (Khan et al., 2019) completed the prediction of the flexural modulus, hardness, impact and transverse rupture strength of four types of carbon/glass fiber reinforced composite materials. The average absolute error was less than 5%, proving that the ANN can still maintain good prediction stability under complex variables. The calculation speed of ANN can reach hundreds of times larger than that of the finite element method, which greatly improves the efficiency of evaluating the structural bearing capacity in the design of composite stiffened plates (Mallela and Upadhyay, 2016). Fan et al. (Fan et al., 2023) proposed an efficient prediction method to elucidate the process induced deformation (PID) contours of composites with different stacking sequences by combining the FE method and a convolutional neural network (CNN). Firstly, FE simulation was experimentally verified using rectangular laminates with 12 types of stacking sequences. Then, this deep learning method was employed to study the PID contours and gives a high accurate and fast assessment of a tail rudder structure after training.

ANN has been widely used to predict properties of sandwich structures because ANN models can capture the non-linear effects and requires lesser computational demand compared to the FE analysis. Fadlallah et al. (Fadlallah et al., 2021) offered a simulation–optimization model for behaviour prediction and structural optimization of lightweight honeycomb sandwich composite heliostats utilizing ANN technique and particle swarm optimization (PSO) algorithm. By utilizing the proposed integrated ANN-PSO approach, the structural performance of honeycomb sandwich composite-based heliostats was predicted and optimized to meet desired different requirements. Besides, the prediction of vibration response of sandwich structures by ANN is studied by Kallannavar et al. (Kallannavar et al., 2021) and Pham et al. (Pham et al., 2022). The ANN model can predict the natural frequency of sandwich structures and the effects of geometrical and material properties on vibration response. Garg et al. (Garg et al., 2017) focused on the application of ANN in predicting sound insulation performance of multi-layered sandwich gypsum partition panels and developed a multilayer feed-forward approach comprising of 13 input parameters, which shows an accurate prediction.

2.2.2 Constitutive relationship

With the increasingly complex composition and structure of composites, their non-linear mechanical behavior and failure mechanisms become more complex. However, the existing mechanical models are unable to reflect the conjoint action of these mechanisms simultaneously. In artificial intelligence method, the design parameters and measured stress-strain curves of composite materials can be directly used as data to construct the relationship between stress and strain under different material parameters. The complex internal mechanism of composite materials is unnecessary, contributing to avoiding the error caused by empirical modeling. Pidapart and Palakal (Pidaparti and Palakal, 1993) trained the ANN with fiber angles of orientation, initial stress and stress increment as input and total strain as output, and successfully constructed the stress-strain curve of unidirectional laminates under different layer angles. Ghaboussi et al. (Ghaboussi et al., 1998) proposed an ANN training method of automatic progressive training, which predicted the stress response of composites under different strains and further improved the accuracy of prediction. Additionally, Zobeiry et al. (Zobeiry et al., 2020) constructed the progressive damage model of quasi-isotropic composite laminates based on the multi-level connected ANN, and obtained the Load-POD (Pin Opening Displacement) curves highly coincident with the experimental results. As shown in Figure 6C, Guo and his co-works (Yang et al., 2019; Yang et al., 2020) use neural networks to replace the unknown function in finite element analysis and give the corresponding stress-strain relationship, which has broad application potential in the future multi-scale constitutive modeling of aerospace composites.

To ensure the reasonability of the prediction, Yu and his co-works (Tao et al., 2021) established Abaqus-DNN mechanics system, which consisting of deep neural network (DNN) model and FE code Abaqus, to learn constitutive laws based on structural level data of FRP composites. Consequently, the learned result automatically satisfies the equilibrium and kinematics equations, which avoids inaccuracies associated with the presumed functions in the constitutive laws and guaranteed the learned constitutive law following the laws of physics. Afterwards, they developed the system to discover the constitutive law of composites lamina. The blind prediction performance of the developed system was finally verified by a blind prediction test.

2.2.3 Impact property

In addition, artificial intelligence methods are also gradually developed to solve impact problems in aeronautical advanced composites. Addona et al. (D’addona et al., 2012) used ANN to predict the residual tensile strength of glass fiber reinforced composite laminates after bearing different degrees of low-speed impact damage according to the experimental data. Laban et al. (Laban et al., 2020) applied ANN to predict the quasi-static compression capacity of composite cubes under low-speed impact load through initial peak force, mean load and crush force efficiency, and successfully modeled the highly non-linear behavior of impact with mean square deviation of only 0.19 N.

Fernández et al. (Fernández-Fdz et al., 2008) combined experiment, finite element method and ANN to predict whether the composite will be penetrated under different impact angles and velocities, and the damaged area in the case of non-penetration and the residual angle and residual velocity in the case of penetration. The results show that the error between the ANN prediction results and the actual data is within 7%. Based on the paradigm of “experiment-FE analysis-ANN”, Artero-Guerrero et al. (Artero-Guerrero et al., 2018) predicted the ballistic limit of composites under different stacking sequences. The error of ANN in training set and test set is 3.7% and 7%, respectively. Based on the well-trained ANN, they found that the placement of 0° and 90° layers on the impacted side of the composite is helpful to improve the ballistic limit of the composite laminate and realize the guidance of composite design.

Ballistic performance of honeycomb-core sandwich panels subject to hypervelocity impact was studied by Carriere et al. (Carriere and Cherniaev, 2022). ANN and a dedicated ballistic limit equation were trained to predict the ballistic limit by using a database composed of results from experiments and simulations. This approach can accurately estimate the influence of the cell size and foil thickness of the honeycomb core, as well as the material of the core, on the ballistic performance of sandwich panels.

3 Intelligent optimization design of composite structures

After accurately predicting the properties of composite materials, design parameters of composite materials can be optimized to reduce the weight and cost of composite structural parts, while maintaining the bearing capacity of composite structures. The optimization of composite design is mainly divided into two aspects: the topology optimization in geometry and the stacking sequence parameter optimization of composite laminates. Due to the large amount of calculation and many coupling factors, the topology optimization of composite materials is less applied in the aviation industry at present. Therefore, this section mainly summarizes the stacking sequence optimization of composite structures.

3.1 Expert system

In the 1990 s, researchers introduced the expert system into the field of composite materials and carried out a series of studies on the material selection and design of composites (Choi and Lee, 1995; Lee and Liebowitz, 1995; Jeon and Song, 2002). But the expert system can only consider a limited range. Poor learning ability and dependence on prior knowledge of domain experts limit the further development of expert system. At the same time, the research on intelligent computing methods, such as genetic algorithm, simulated annealing and particle swarm optimization, is becoming more and more mature, and has become an effective method to solve complex problems. Based on certain design rules, researchers solved the stacking sequence optimization problem of composite laminates under simple load by using intelligent calculation method, which proves that this method is more accurate and efficient than manual design (Ball et al., 1993; Sargent et al., 1995). Kim J-s et al. (Kim et al., 2005; Kim, 2007) combined expert system with genetic algorithm to develop a stacking sequence optimization system for composite laminates under complex constraints, which improved the efficiency of expert system learning and design. With the continuous development of finite element method, the ability to solve complex problems is gradually enhanced.

3.2 Finite element method and intelligent algorithm

The combination of finite element method and intelligent algorithm makes it possible to optimize composite materials with complex geometric configurations and loading conditions. For example, Herencia et al. (Herencia et al., 2007) optimized the stacking sequence of T-stiffened plate with strength and buckling load as constraints. Lopes et al. (Lopes et al., 2009a; Lopes et al., 2009b) optimized a laminated plate under impact load with dispersed stacking sequence. The common intelligent algorithms include genetic algorithm, evolutionary algorithm, etc.

Genetic optimization algorithm combining with FE model is potential approach in the optimization of composite structure, especially for mass reduction, one of the important objectives of optimisation. Wang et al. (Wang et al., 2016) applied this method to optimize a wind turbine composite blade with 17.4% weight reduction under the consideration of stress constraint, deformation constraint, buckling constraint, stacking sequence constraint and manufacturability. The application of the method on an metal offshore wind turbine support structure also give 19.8% reduction in the global mass (Gentils et al., 2017). Furthermore, by combining evolutionary and topology optimization schemes and integrating the inverse FE method, Albanesi et al. (Albanesi et al., 2020) presented a novel methodology to reach up to 23% mass saving of a 28.5 m composite blade. Kim et al. (Kim et al., 1999) developed a patchwise optimal layup design method by integration of an expert system shell, genetic algorithm (GA) and finite element method to minimize the weight of a tapered composite laminates under strength constraint. The results show that the optimized layup can considerably reduce total weight of the composite laminates compared with the uniform thickness laminates.

Enhancing mechanical properties is another vital purpose of composite optimisation. Lee et al. (Lee et al., 2013) aimed to increase the design load of composite sandwich cylinders under external hydrostatic pressure by using FE analysis and micro-genetic algorithm. Based on the optimization, as the thickness of the sandwich increases, the buckling load becomes larger than the material failure. Consequently, the optimum point is determined by material failure. Generally, the optimisation of mechanical properties is multi-objective. Evolutionary algorithm has been confirmed owning the ability of dealing with two or more contradictory objective. Ratle et al. (Ratle et al., 2004) applied a multi-objective evolutionary algorithm to optimize the design of a composite helical spring, aiming to maximize the spring stiffness and minimize the mass. Seeger et al. (Seeger and Wolf, 2011) presented a design methodology integrated evolutionary algorithms with FE model to optimize complex composite aircraft structures such as composite test panels and CFRP composite fuselage tail sections for the minimum-weight design with the smallest possible cut-out deformation (Figure 7).

FIGURE 7

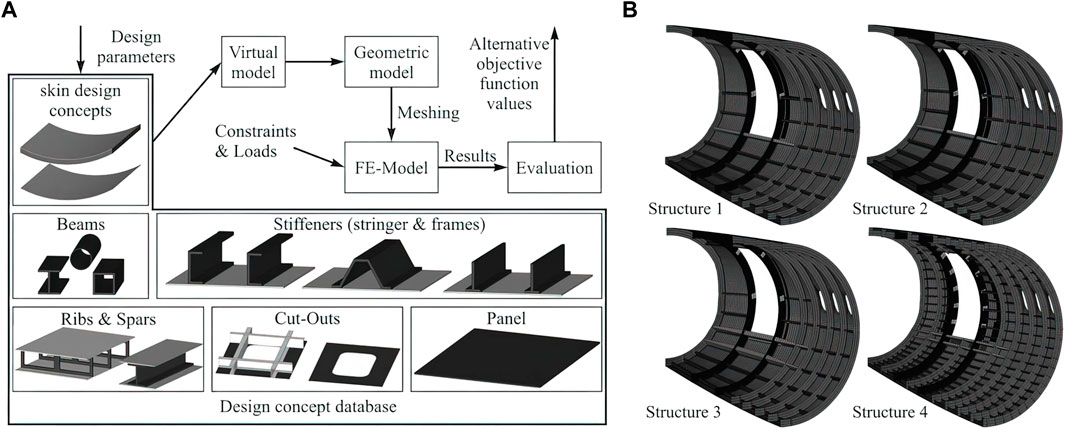
FIGURE 7. (A) Flowchart of the simulation model including the design concept database, (B) the optimization of CFRP composite fuselage tail sections (Seeger and Wolf, 2011).

3.3 Analytic solution and intelligent algorithm

The combination of finite element method and intelligent calculation method realizes the independent exploration of composite design space by computer. However, compared with the rapid response of intelligent computing methods, finite element method usually takes a lot of calculation time, which limits the further improvement of the speed of computer independent design. For some classical mechanical problems, theoretical calculation rather than finite element method can be used to save calculation time. For example, the combination of classical laminated plate theory and intelligent calculation method can realize rapid multi-objective optimization for composite strengths and reduce their weight and manufacturing cost (Omkar et al., 2011; António, 2014). Pelaez et al. (Pelaez et al., 2017) used the cultural gene algorithm to select fiber and matrix types, and optimize the stacking sequence based on the analytical solution of the strength problem of composite laminates under biaxial tensile load. Kamarian et al. (Kamarian et al., 2018) used the Mori-Tanaka method and the generalized differential quadrature method to calculate the natural frequencies of eight symmetric ply rectangular laminate, and further combined them with the firefly algorithm to optimize the stacking sequence. The optimization results show that although the firefly algorithm will lose a small amount of calculation accuracy, the design efficiency can be improved hundreds of times. Wagner et al. (Wagner et al., 2019) trained the decision tree model to get general design suggestions based on the data obtained from the analysis of single boundary perturbation method under ideal/non-ideal buckling loading, and optimized the stacking sequence of laminate. Compared with the laminates obtained by the traditional optimization method, the laminates designed by this method have higher buckling load and lower defect sensitivity.

3.4 Artificial intelligence and intelligent algorithm

The above studies are carried out for composite structures under simple loading or simple geometry, so the theoretical calculation has achieved good results. However, these methods is unable to obtain theoretical solutions of complex composite structures, especially under complex load. Inspired by the application of neural network in the prediction of composite properties, some researchers base on some successfully trained neural network, and gradually form an optimization design method combining neural network and intelligent computing as shown in Figure 8, which greatly improves the calculation efficiency of optimization problems. Jayatheertha et al. (Jayatheertha et al., 1996) trained an ANN instead of finite element method and combined it with a simulated annealing algorithm to optimize the stacking sequence of composite laminates under stiffness and strength constraints. Zhang et al. (Zhang et al., 2008) predicted the strength characteristics of composites from the maximum stress of composites through ANN, further optimized the wrapped fiber density and filled fiber density of 2.5D braided composites using genetic algorithm, and successfully realized the weight reduction design of composites. Szklarek et al. (Szklarek and Gajewski, 2020) used the combination of ANN and genetic algorithm to optimize the lamination stacking sequence of composite U-shaped plates and improve the critical buckling loading. Bisagni et al. (Bisagni and Lanzi, 2002) trained the ANN to replace the non-linear finite element analysis for the post buckling optimization of composite stiffened panel. The genetic algorithm was used to optimize the four design variables of composite plates: the stacking sequence of the skin, the stacking sequence of stiffeners, the number of stiffeners and the shape of stiffeners. The weight of composite stiffened plates was reduced by about 18%. In addition, they also optimized the post buckling of composite cylindrical shells and 3D braided composite stiffened plates, which improved the maximum buckling loading and stiffness of the structure (Fu et al., 2015; Pitton et al., 2019).

FIGURE 8

FIGURE 8. Combination of ANN and intelligent algorithm for optimal design.

4 Summary

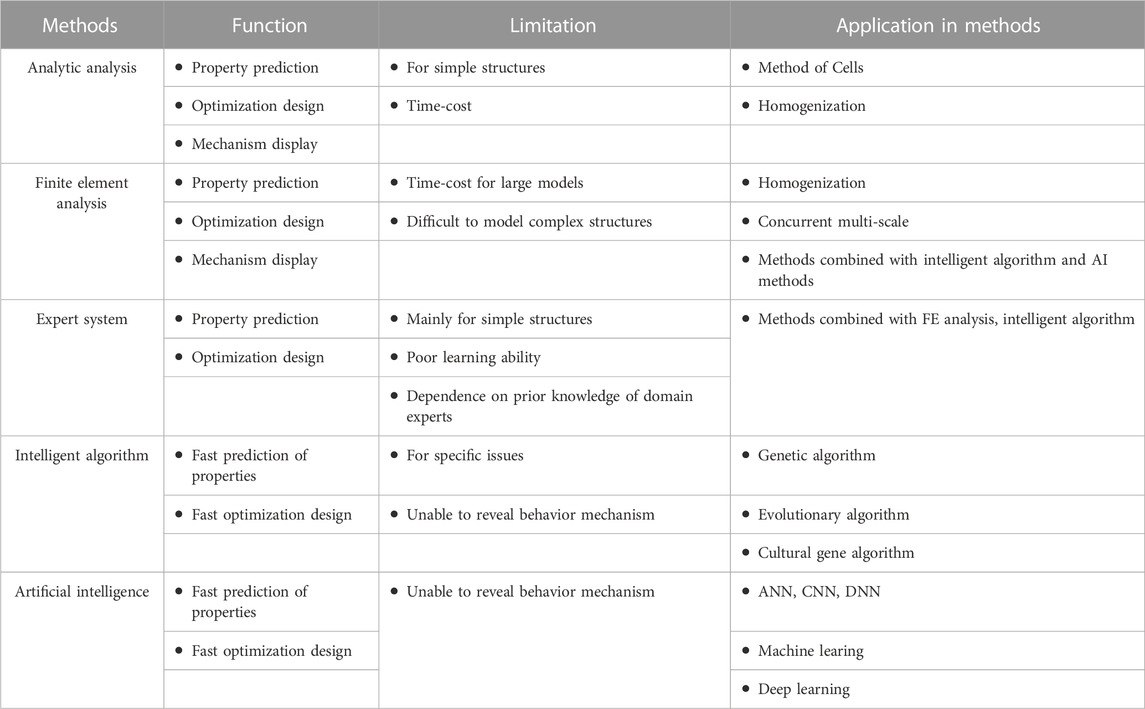
Lightweight fiber-reinforced composite structures have been widely used in various industries and create great value. The design technology for them has a significant development in recent decades. Currently, research in design focuses on the combination of multi-scale method, intelligent algorithm, and artificial intelligence to design composite structures efficiently, accurately, and intelligently for optimizing or developing novel composite structures. The main traditional and intelligent methods are compared in Table 2. Generally, the intelligent method exhibits the capability of much faster property prediction and optimization design for composites; whereas the analytic analysis and finite element analysis show the ability to reveal the mechanism of composite behaviors. The methods combining them has the potential to achieve fast and realistic prediction and optimization design of composite structures.

TABLE 2

TABLE 2. Comparison of the traditional and intelligent methods for design of FRP composites.

Although these techniques have many advantages and gradually enter the realm of aerospace, there still are many disadvantages and challenges, which will be overcome hopefully by using intelligent technology soon.

With the development of intelligent technology, there are two main foreseeable important trends in design and manufacture of composite structures.

Integrated and intelligent development of design process and manufacturing process

Design technology for intelligent composite structures.

An intelligent platform integrating of design and manufacturing technologies of composites based on big data, interpretable machine learning, digital twin, and industrial Internet of Things, will be developed gradually. This platform will provide the integrated technology including design, manufacturing, monitoring, self-optimization, and self-healing during the full life cycle of composites. Depending on the platform, the total research and development time of composite structures can be reduced significantly, their cost will be much lower, and the performance of production will be enhanced. In a word, intelligence technology has the potential to accelerate the development of design and manufacturing processes of composite structures.

Additionally, many concepts about new advanced aircraft have been proposed recently, for example, smart morphing aircraft. The smart aircraft can sense the external environment information and change shape or posture, which is an important development trend. Their smart functions depend on the development of intelligent composite structures which have the ability of self-perception, self-healing and other smart functions. Therefore, the design and manufacturing technologies integrating sensors and smart materials on the composite structures need to be developed and is one of development trend of advanced composite structures. Besides, many countries are accelerating the exploration of outer space, for example, the exploration of Mars. The success of the exploration depends on the high-performance materials for spaceships. Composite has the potential to satisfy the requirement due to its flexible designability. With the application extension of composites, the design and manufacturing technologies will also evolve to fabricate more intelligent composite structures with higher performance.

Author contributions

YC leading the writing of the review, writing the initial draft, and reviewing and editing the draft. JZ analyzing reference, preparation the figures, and writing the initial draft. ZL collection and analysis of literature on the prediction of composite properties. HZ collection and analysis of literature on the intelligent optimization design of composite structures. JC reviewing and editing the draft. WY, in charge of the project and guiding the writing of the review. TY critical review and commentary. WL conceptualization. YL supervising and leading the writing of the review.

Funding

This artical was funded by [The National Key R&D Program of China] grant number [2020YFB0311500]; [The National Natural Science Foundation of China] grant number [12002238]; [The National Natural Science Founda-tion of China] grant number [12202312]. And The APC is funded by [The National Key R&D Program of China] grant number [2020YFB0311500].

Conflict of interest

Authors JC and WL were Employed by the Company COMAC Shanghai Aircraft Manufacturing Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbassi, F., Belhadj, T., Mistou, S., and Zghal, A. (2013). Parameter identification of a mechanical ductile damage using Artificial Neural Networks in sheet metal forming. Mater. Des. 45, 605–615. doi:10.1016/j.matdes.2012.09.032