Analysis of the electrically conducting magnetohydrodynamic hybrid nanofluid flow past a convectively heated stretching surface with suction/injection and non-linear thermal radiation

Fluid flow through a porous media has many industrial applications such as water flowing through rocks and soil and purification of gas and oil mixed in rocks. Also, heat transfer enhancement has been introduced in various thermal and mechanical systems by improving the thermal conductance of base fluids. In this article, the flow of an electrically conducting water-based hybrid nanofluid comprising GO and Fe₃O₄ nanoparticles over an extending sheet using a porous medium has been investigated. The space-dependent heat source, Joule heating, Brownian motion, thermophoresis, thermal radiation, chemical reaction, and activation energy impacts are taken into account. For the solution of the modeled equations, the homotopy analysis method is considered. The homotopic convergence is shown with the help of a figure. This analysis is contrasted with previous outcomes and has found a great agreement. The impacts of embedded factors on different flow characteristics, skin friction coefficient, and Nusselt and Sherwood numbers are displayed using figures and tables. The outcomes of the present analysis show that the increasing magnetic and suction factors have reduced the fluid motion while amplifying the thermal profiles. Additionally, the suction factor has a reducing impact on both temperature and concentration profiles. The thermal profiles have increased with the increasing thermal Biot number, Eckert number, thermophoresis, and Brownian motion factors. The Nusselt numbers have increased with the increasing thermal Biot number and stretching factor but reduced with the increasing thermal radiation and temperature difference factors.

1 Introduction

The selection of the coolant of different devices/equipment at the industrial level and for various engineering applications is one of the most challenging tasks. Recently, thermal flow enhancement has been introduced in various thermal and mechanical systems by improving the thermal conductance of base fluids. Different fluids which are considered as pure base fluids are engine/kerosene oil, water, ethylene glycol, etc. The suspension of non-size particles in a pure fluid has been familiarized by Choi and Eastman (1995) first to expand the thermal flow characteristics of the base fluid. Acharya et al. (2022) discussed the fluid flow and thermal phenomenon for a time-based MHD nanoliquid on a spinning surface and explored that the thermal properties of the nanofluid were enhanced by 84.61% in comparison to the normal fluid. Shah et al. (2020) mixed gold particles in blood to enhance its thermal properties by incorporating radiation and rotational effects in the flow system. Khan et al. (2021) introduced radiative effects in the revolving motion of an MHD nanofluid on a spinning cylinder and noticed a difference in temperature growth at the wall as well as on the surface of the cylinder. Bhatti et al. (2022) explored a bioconvective MHD Williamson nanofluid flowing amid two spinning circular surfaces placed in a penetrable medium. Hussain et al. (2022) solved numerically the radiative EMHD Williamson fluid flow on a stretching surface. Rasheed et al. (2022) discussed the Brownian three-dimensional motion of a thin-film nanofluid past a stretched and rotary sheet and found that the Nusselt number augmented with growth in magnetic and Brownian factors and the concentration of nanoparticles. Akbar et al. (2022) scrutinized the exact solution of an unsteady thermal conductive pressure on peristaltic transport with temperature nanofluid viscosity. Carbon nanotubes (CNTs) are grasped as nanoparticles in an irregular channel. Akram et al. (2022) investigated the electroosmotic flow of peristaltic transport of a nanofluid over a curved microchannel.

It has further been noticed experimentally that the thermal conductance of a base fluid can be additionally enhanced by suspending two unlike natures of nanoparticles in it and is characterized as a hybrid nanofluid. Chu et al. (2022) examined the impact of different nanoparticle shapes for unsteady hybrid nanofluid flow amid two plates of infinite length and determined that velocity weakened whereas the temperature of the fluid upsurged with augmentation in the number of hybrid nanoparticles. Zhang et al. (2022) examined the effects of magnetic field on hybrid nanoparticle flow over an elastic sheet and noticed that motion of the fluid propagated faster with progression in tantalum nanoparticles and the Darcy number while the temperature of the fluid declined with an upsurge in nickel and tantalum nanoparticle concentration. Guedri et al. (2022) discussed the trihybrid radiative nanofluid motion over a non-linear extended sheet using the impression of the Darcy–Forchheimer model and noticed that the heat of the fluid amplified with growth in Brownian, temperature ratio, and thermophoretic parameters. Salahuddin et al. (2022) examined flow and thermal behavior for a highly magnetized wavy heated cylinder on which hybrid nanofluids flow. Alrabaiah et al. (2022) estimated the bioconvective hybrid nanoparticles’ flow in the cavity of a cone/disk using the influences of dissipation and microorganisms. Lone et al. (2022) explored MHD micro-rotational hybrid nanoparticles’ flow past a flat plate using thermally radiated effects and mixed convection. Khan et al. (2022a) examined hybrid dissipative nanofluid flow on a heated revolving needle using microorganisms and Hall current effects. Maraj et al. (2017) studied the closed-form solution of mixed convective MHD carbon nanotube nanofluid flow in a rotating channel. In this study, one can see that temperature is the enhancing function against the improving estimations of the volume fraction parameter. Habib and Akbar (2021) proposed the incorporation of novel nanofluids in clinical isolates to battle Staphylococcus aureus. Akram et al. (2021) reported water-based hybrid (Ag–Au) nanofluids electroosmotically pumped through an inclined asymmetric microfluidic channel in a porous setting. With the help of the Debye–Hückel and lubrication linearization principles, the governing equations of the current model are linearized.

The study of electrically conducted fluids associated with magnetic effects such as salty water and plasma is called magnetohydrodynamics (MHD). Such fluids are crucial in many engineering and industrial applications, for instance, design of nuclear reactors, MHD generators, and flow meters. Asjad et al. (2022) explored the impact of activated energy and magnetic effects on a Williamson fluid using bioconvective effects on an exponentially stretched surface. Bejawada et al. (2022) inspected radiated MHD fluid motion on a non-linear inclined sheet using a permeable Forchheimer surface and concluded that the motion of liquid degenerated while temperature expanded with progression in the magnetic factor. Kodi and Mopuri (2022) discussed MHD time-based oscillatory fluid flow on an inclined surface using chemically reactive effects and thermal absorption. Usman et al. (2021) explored the impact of EMHD couple stress on a thin film hybrid nanoliquid flow on a gyratory surface and established that thermal conductance is better in case of hybrid nanoparticles. Venkata Ramudu et al. (2022) explored the impact of convective diffusion conditions on Casson MHD fluid motion on a stretched sheet and noticed that the Sherwood number upsurged while the Nusselt number declined with an escalation in the non-linear radiative factor. Sharma et al. (2022) deliberated theoretically on convection MHD liquid flow past a rotary extended disk and recognized that the Nusselt number augmented with progression in the magnetic factor at the lower disk. Same ideas can be seen in Waseem et al. (2021); Mahabaleshwar et al. (2022); Nagendramma et al. (2022); and Nazeer et al. (2022).

The experimental and theoretical investigations of fluid flow under the impact of Joule heating have been handled frequently in the literature. It plays a pivotal role in controlling the thermal flow effects. Shamshuddin and Eid (2022) discussed a higher-order reactive nanofluid in a convective extending sheet under the impact of Joule heating and mixed convection and proved that the Eckert number supported the fluid motion and thermal characteristics, whereas growth in the magnetic factor declined the velocity and upsurged the Nusselt number. Wahid et al. (2022) examined an MHD nanofluid at the stagnant point of a shrinking surface with viscously dissipative Joule heating effects and noticed that 25% growth in melting effects augmented skin friction by 5%, whereas the flow phenomenon can be sustained as laminar by taking alumina nanoparticles as 2% instead of 1%. Xuan (2022) reviewed non-linear electro-kinetic fluid flow taking the effects of induced charge to Joule heating. Abbas et al. (2022) debated on the influence of the Darcy–Forchheimer model on dissipative MHD fluid flow using Joule heating effects on a porous sheet and explored that with progression in the thermal diffusion factor, the temperature, concentration, and velocity characteristics augmented. Khan et al. (2022b) examined the production of irreversibility for hydro-magnetic fluid flow using the Darcy–Forchheimer model and Joule heating effects and explained the thermal flow phenomenon both for prescribed thermal flux and surface temperatures. Waqas et al. (2022) deliberated on MHD nanoliquid flow on a radiated stretched surface using Joule heating as well as dissipative effects and noticed that the density of microbes degenerated with growth in the Peclet number. Saleem et al. (2022) discussed the bio-mathematical model for the flow of blood through an artery using Joule heating. Kumar et al. (2022) discussed numerically the chemically reactive MHD fluid slip flow with Joule heating on an exponentially extended sheet and explored that fluid motion weakened while the Nusselt number, as well as skin friction, amplified with an upsurge in magnetic effects. Xie et al. (2023a) designed experimental and numerical evaluations of a novel bearing’s fluid–structure interaction lubricating abilities. Xie et al. (2023b) demonstrated the fluid–structure–acoustic coupling dynamics of a new water-lubricated bearing being studied theoretically and experimentally.

Thermal radiation is another main factor that plays a significant role in thermal flow analysis. Rehman et al. (2022) thermally inspected the radiated MHD Jeffery fluid flow with a comparative analysis upon plan/cylindrical surfaces and deduced that fluid flow on cylindrical surfaces has better thermal flow properties than on plain surfaces. For instance, the Nusselt number has greater values in case of cylindrical surfaces. Shaw et al. (2022) inspected MHD cross-liquid motion with effects of linear as well as non-linear heat radiations using an arbitrary Prandtl number and highlighted the thermal flow characteristics for Prandtl numbers within the interval ${10}^{-4}\le \mathrm{Pr}\le {10}^4$ in case of the linear as well as non-linear thermal radiation factor. Bilal et al. (2022) explored the impact of heat radiation on liquid motion over a linear stretched surface and explained that with elevation in porosity and radiation factors, there is a growth in skin friction. Adnan (2022) discussed numerically the effects of radiative and convective thermal conduction on nanoliquid flow on a non-linear extended sheet and determined that fluid motion weakened with growth in the radiation factor, which, on the other hand, augmented both the Nusselt number and skin friction. Yaseen et al. (2022) discussed motion of hybrid nanoparticles amid two plates placed in parallel direction with the influence of the Darcy permeable medium and heat radiations effects and concluded that the Nusselt number augmented with progression in radiation and porosity factors. Ibrahim et al. (2022) debated on time-based viscously affected fluid flow using thermal radiations on a stretched plate. Ramesh et al. (2022) discussed CNT nanofluid flow on a gyratory sphere by employing the thermal radiation and thermophoretic effects.

Recently, thermal flow enhancement has been introduced in various thermal and mechanical systems by improving the thermal conductance of base fluids. Different fluids which are considered as base fluids are pure engine/kerosene oil, water, ethylene glycol, etc. This work investigates the flow of an electrically conducting hybrid nanofluid over an extending surface using a porous medium. The space-dependent heat source, Joule heating, Brownian motion, thermophoresis, thermal radiation, and chemically reactive activation energy impacts are taken into consideration. Section 2 comprises the main body of the study. Section 3 shows the homotopic solution of the model. The homotopic convergence is shown in Section 4. Section 5 shows the results and discussion part of the work. The final remarks are listed in Section 6.

2 Formulation of the problem

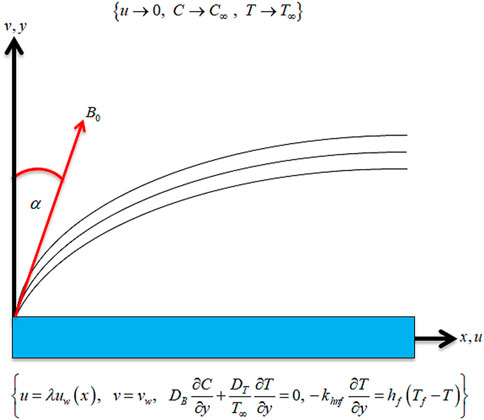
We consider the two-dimensional flow of an MHD hybrid nanofluid containing $GO$ and $F{e}_3{O}_4$ nanoparticles past a stretching sheet using porous media. A magnetic field of strength $B_0$ with an acute angle $\gamma$ is employed for the hybrid nanofluid flow. The stretching velocity of the sheet is depicted by $u_w\left(x\right)=ax$. The surface of the sheet is kept with a constant temperature and concentration, $T_w\left(\text{such}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t}{T}_w<T_f\right)$ and $C_w$, respectively, while the corresponding ambient temperature and concentration are $T_{\infty }$ and $C_{\infty }$, respectively. Here, $T_f$ is the reference temperature. A geometrical representation of the flow problem is shown in Figure 1. Additionally, the space-dependent heat source, Joule heating, Brownian motion, thermal radiation, thermophoresis, chemical reaction, and activation energy impacts are taken into consideration. The leading equations are (Reddy et al., 2020; Dawar et al., 2022a)

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{1}{K_p}u-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}_0^{2}u{\sin }^2\left(\alpha \right),(2)$

$\begin{array}{l}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_{hnf}}\left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right]\\ +\frac{{\sigma }_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{B}_0^2{u}^2{\sin }^2\left(\alpha \right)-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q_r}{\partial y}+\frac{Q}{{\left(\rho C_p\right)}_{hnf}}\left(T_f-T_{\infty }\right)\exp \left(-my\sqrt{\frac{a}{{\nu }_f}}\right),\end{array}(3)$

$v\frac{\partial C}{\partial y}+u\frac{\partial C}{\partial x}=\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}+D_B\frac{{\partial }^{2}C}{\partial y^2}-K_r^2{\left(\frac{T}{T_{\infty }}\right)}^n\left(C-C_{\infty }\right)\exp \left(-\frac{E_a}{\kappa T}\right),(4)$

subject to the following boundary conditions (Dawar et al., 2022b):

$\left\{\begin{array}{l}u=u_w\left(x\right)\lambda ,v=v_w,D_B\frac{\partial C}{\partial y}+\frac{\partial T}{\partial y}\frac{D_T}{T_{\infty }}=0,-\frac{\partial T}{\partial y}{k}_{hnf}=\left(T_f-T\right)h_f,y=0\\ u\to 0,C\to C_{\infty },T\to T_{\infty }\text{as}y\to \infty \end{array}\right\},(5)$

where $q_r$ is given as

$q_r=-\frac{16{\sigma }^{*}}{3K^{*}}\left(T^3\frac{\partial T}{\partial y}\right).(6)$

FIGURE 1

FIGURE 1. Flow geometry.

This can be reduced as

$\frac{\partial q_r}{\partial \widehat{y}}=-\frac{16{\sigma }^{*}}{3K^{*}}\left(3T^2{\left(\frac{\partial T}{\partial y}\right)}^2+T^3\frac{{\partial }^{2}T}{\partial y^2}\right).(7)$

So, Equation 3 can be written as

$\begin{array}{l}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_{hnf}}\left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{{\sigma }_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{B}_0^2{u}^2{\sin }^2\left(\alpha \right)\\ +\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{16{\sigma }^{*}}{3K^{*}}\left(3T^2{\left(\frac{\partial T}{\partial y}\right)}^2+T^3\frac{{\partial }^{2}T}{\partial y^2}\right)+\frac{Q}{{\left(\rho C_p\right)}_{hnf}}\left(T_f-T_{\infty }\right)\exp \left(-my\sqrt{\frac{a}{{\nu }_f}}\right).\end{array}(8)$

The thermophysical properties are defined as

$\left\{\begin{array}{l}\frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\nabla }_1-{\nabla }_2\right)}^{2.5}},\frac{{\rho }_{hnf}}{{\rho }_f}=\left(1-{\nabla }_2-{\nabla }_1\right)+\frac{{\rho }_{p2}{\nabla }_2+{\rho }_p{\nabla }_1}{{\rho }_f},\\ \frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}=\left(1-{\nabla }_1-{\nabla }_2\right)+\frac{{\left(\rho C_p\right)}_{p1}{\nabla }_1+{\left(\rho C_p\right)}_{p2}{\nabla }_2}{{\left(\rho C_p\right)}_f},\\ \frac{{\sigma }_{hnf}}{{\sigma }_f}=1+\frac{3\left(\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{{\sigma }_f}-\left({\nabla }_2+{\nabla }_1\right)\right)}{2+\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{\left({\nabla }_2+{\nabla }_1\right){\sigma }_f}-\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{{\sigma }_f}+\left({\nabla }_2+{\nabla }_1\right)},\\ \frac{k_{hnf}}{k_f}=\frac{\frac{\left({\nabla }_2{k}_{p2}+{\nabla }_1{k}_{p1}\right)}{\left({\nabla }_2+{\nabla }_1\right)}+2k_f+2\left({\nabla }_2{k}_{p2}+{\nabla }_1{k}_{p1}\right)-2\left({\nabla }_2+{\nabla }_1\right)k_f}{\frac{\left({\nabla }_2{k}_{p2}+{\nabla }_1{k}_{p1}\right)}{\left({\nabla }_2+{\nabla }_1\right)}+2k_f-\left({\nabla }_2{k}_{p2}+{\nabla }_1{k}_{p1}\right)+\left({\nabla }_2+{\nabla }_1\right)k_f}.\end{array}\right\}(9)$

For the aboveproposed model, the similarity variables are defined as

$u=a{f}^{\prime }\left(\eta \right)x,v=-f\left(\eta \right)\sqrt{a{\nu }_f},\phi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},\eta =\sqrt{\frac{a}{{\nu }_f}}y.(10)$

Using Equation 10, the leading equations are reduced as

$\frac{A_1}{A_2}{f}^{‴}\left(\eta \right)-{\left(f^{\prime }\left(\eta \right)\right)}^2+f^{″}\left(\eta \right)f\left(\eta \right)-\frac{A_3}{A_2}M{\sin }^2\left(\alpha \right)f^{\prime }\left(\eta \right)-f^{\prime }\left(\eta \right)\frac{A_1}{A_2}\gamma =0,(11)$

$\begin{array}{l}{A}_4{\theta }^{″}\left(\eta \right)+\left(Rd{\left(\theta \left(\eta \right)\left({\theta }_w-1\right)+1\right)}^2\left(3{\left({\theta }^{\prime }\left(\eta \right)\right)}^2\left({\theta }_w-1\right)+\left(\theta \left(\eta \right)\left({\theta }_w-1\right)+1\right){\theta }^{″}\left(\eta \right)\right)\right)+A_5\mathrm{Pr}f\left(\eta \right){\theta }^{\prime }\left(\eta \right)\\ +A_3\mathrm{Pr}EcM{\left(f^{\prime }\left(\eta \right)\right)}^2{\sin }^2\left(\alpha \right)+Nb\mathrm{Pr}{\phi }^{\prime }\left(\eta \right){\theta }^{\prime }\left(\eta \right)+Nt\mathrm{Pr}{\left({\theta }^{\prime }\left(\eta \right)\right)}^2+\mathrm{Pr}{Q}_e\exp \left(-m\eta \right)=0,\end{array}(12)$

${\phi }^{″}\left(\eta \right)+\frac{Nt}{Nb}{\theta }^{″}\left(\eta \right)+Scf\left(\eta \right){\phi }^{\prime }\left(\eta \right)-ScKr{\left(1+\delta \theta \left(\eta \right)\right)}^n\exp \left(-\frac{E}{\left(1+\delta \theta \left(\eta \right)\right)}\right)\phi \left(\eta \right)=0,(13)$

$\left\{\begin{array}{l}{f}^{\prime }\left(\eta \right)=\lambda ,f\left(\eta \right)=S,\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(\eta \right)=B{i}_T\left(\theta \left(\eta \right)-1\right),Nt{\theta }^{\prime }\left(\eta \right)+Nb{\phi }^{\prime }\left(\eta \right)=0at\eta =0\\ f^{\prime }\left(\eta \right)=0,\phi \left(\eta \right)=0,\theta \left(\eta \right)=0\text{as}\eta \to \infty \end{array}\right\}.(14)$

In the abovementioned equations, the embedded factors are defined as

$\left\{\begin{array}{l}\mathrm{Pr}=\frac{{\left(\mu C_p\right)}_f}{k_f},Rd=\frac{16{\sigma }^{*}{T_{\infty }}^3}{3k_f{K}^{*}},Nb=\frac{{\left(\rho C_p\right)}_p{D}_B\left(C_w-C_{\infty }\right)}{{\left(\rho C_p\right)}_f{\nu }_f},B{i}_T=\frac{h_f}{k_f}\sqrt{\frac{{\nu }_f}{a}},\\ Kr=\frac{K_r}{a},Nt=\frac{{\left(\rho C_p\right)}_p{D}_T\left(T_f-T_{\infty }\right)}{{\left(\rho C_p\right)}_f{\nu }_f{T}_{\infty }},\gamma =\frac{{\mu }_f}{a{K}_p{\rho }_f},Sc=\frac{{\nu }_f}{D_B},{\theta }_w=\frac{T_f}{T_{\infty }},\delta =\frac{T_w-T_{\infty }}{T_{\infty }},\\ M=\frac{{\sigma }_f{B}_0^2}{{\rho }_{f}a},Q_e=\frac{Q}{a{\left(\rho C_p\right)}_f},Ec=\frac{a^2{x}^2}{{\left(C_p\right)}_f\left(T_f-T_{\infty }\right)},S=-\frac{v_w}{\sqrt{a{\nu }_f}},E=\frac{E_a}{\kappa T_{\infty }}.\end{array}\right\}(15)$

In the abovementioned equations, $Rd$ is the thermal radiation factor, $Nb$ is the Brownian motion parameter, $\mathrm{Pr}$ is the Prandtl number, $Kr$ is the chemical factor, $Nt$ is the thermophoretic factor, $\gamma$ is the porosity factor, $Sc$ is the Schmidt number, $B{i}_T$ is the thermal Biot number, $Ec$ is the Eckert number, $Q_e$ is the heat source factor, $M$ is the magnetic parameter, $S$ is the suction/injection factor, $E$ is the activation energy factor, and $\delta$ is the temperature difference parameter. Furthermore, $A_1$, $A_2$, $A_3$, $A_4$, and $A_5$ are defined as

$\left\{\begin{array}{l}{A}_1=\left[\frac{1}{{\left(1-{\nabla }_1-{\nabla }_2\right)}^{2.5}}\right],A_2=\left[\left(1-{\nabla }_1-{\nabla }_2\right)+\frac{{\rho }_p{\nabla }_1+{\rho }_{p2}{\nabla }_2}{{\rho }_f}\right],\\ A_5=\left[\left(1-{\nabla }_1-{\nabla }_2\right)+\frac{{\left(\rho C_p\right)}_{p1}{\nabla }_1+{\left(\rho C_p\right)}_{p2}{\nabla }_2}{{\left(\rho C_p\right)}_f}\right],\\ A_3=\left[1+\frac{3\left(\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{{\sigma }_f}-\left({\nabla }_2+{\nabla }_1\right)\right)}{2+\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{\left({\nabla }_1+{\nabla }_2\right){\sigma }_f}-\frac{\left({\nabla }_2{\sigma }_{p2}+{\nabla }_1{\sigma }_{p1}\right)}{{\sigma }_f}+\left({\nabla }_2+{\nabla }_1\right)}\right],\\ A_4=\left[\frac{\frac{k_{p1}{\nabla }_1+k_{p2}{\nabla }_2}{{\nabla }_1+{\nabla }_2}+2k_f+2\left(k_{p1}{\nabla }_1+k_{p2}{\nabla }_2\right)-2\left({\nabla }_1+{\nabla }_2\right)k_f}{\frac{k_{p1}{\nabla }_1+k_{p2}{\nabla }_2}{{\nabla }_1+{\nabla }_2}+2k_f-\left(k_{p1}{\nabla }_1+k_{p2}{\nabla }_2\right)+\left({\nabla }_1+{\nabla }_2\right)k_f}\right].\end{array}\right\}(16)$

The quantities of interest such as $C_{fx}$, $N{u}_x$, and $S{h}_x$ are defined as

$C_{fx}=\frac{{\tau }_w}{{\rho }_f{\left(u_w\left(x\right)\right)}^2},N{u}_x=\frac{x{q}_w}{k_f\left(T_f-T_{\infty }\right)},S{h}_x=\frac{x{q}_m}{D_B\left(C_f-C_{\infty }\right)}.(17)$

Here,

${\tau }_w\left(={\left.{\mu }_{hnf}\frac{\partial u}{\partial y}\right|}_{y=0}\right),q_w\left(={\left.-k_{hnf}\frac{\partial T}{\partial y}\right|}_{y=0}\right)+{\left.q_r\right|}_{y=0},q_m\left(={\left.-D_B\frac{\partial C}{\partial y}\right|}_{y=0}\right).(18)$

Eq. 18 is reduced as

$C_{fx}\sqrt{{\mathrm{R}\mathrm{e}}_x}=A_1{f}^{″}\left(0\right),\frac{N{u}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-A_4\left(1+Rd{\theta }_w^3\right){\theta }^{\prime }\left(0\right),\frac{S{h}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-{\phi }^{\prime }\left(0\right).(19)$

Here, ${\mathrm{R}\mathrm{e}}_x=\frac{{\widehat{u}}_w\left(\widehat{x}\right)\widehat{x}}{{\widehat{\nu }}_{bf}}$ is the local Reynolds number.

3 Solution by HAM

The initial guesses are described as

$\left\{\begin{array}{l}{f}_0\left(\eta \right)=\left(S+\lambda \right)-\lambda \exp \left(-\eta \right)\\ {\theta }_0\left(\eta \right)=\frac{B{i}_T}{\left(k_{hnf}/k_f\right)+B{i}_T}\exp \left(-\eta \right)\\ {\phi }_0\left(\eta \right)=-\frac{Nt}{Nb}{\theta }_0\left(\eta \right)\end{array}\right\}.(20)$

The linear operators are defined as

$\left\{\begin{array}{l}{L}_f\left(\eta \right)=f\left(\eta \right)+f^{‴}\left(\eta \right)\\ L_{\theta }\left(\eta \right)={\theta }^{″}\left(\eta \right)+\theta \left(\eta \right)\\ L_{\phi }\left(\eta \right)={\phi }^{″}\left(\eta \right)+\phi \left(\eta \right)\end{array}\right\},(21)$

with the following properties:

$\left\{\begin{array}{l}{L}_f\left(Z_1+Z_2{e}^{-\eta }+Z_3{e}^{\eta }\right)=0\\ L_{\theta }\left(Z_4{e}^{-\eta }+Z_5{e}^{-\eta }\right)=0\\ L_{\phi }\left(Z_6{e}^{-\eta }+Z_7{e}^{-\eta }\right)=0\end{array}\right\},(22)$

where $Z_1-Z_7$ are the arbitrary constants. The chart shown in Figure 2 explains the procedure of the homotopy analysis method (Liao, 1999; Liao, 2010).

FIGURE 2

FIGURE 2. Flow chart of HAM.

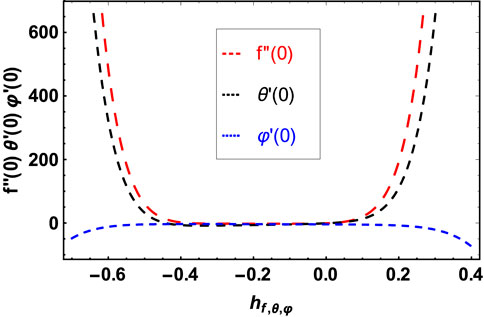
4 HAM convergence

We are assured of the convergence of the series solution by the homotopy analysis approach. Our series solutions’ convergence area is controlled and adjusted by the significant auxiliary parameter $\mathrm{\hslash }$. Because of this, we have displayed the $\mathrm{\hslash }-$curves in Figure 3. The acceptable value for the velocity profile is $-0.4\le {\mathrm{\hslash }}_f\le 0.1$, the temperature profile is $-0.41\le {\mathrm{\hslash }}_{\theta }\le 0.12$, and the concentration profile is $-0.65\le {\mathrm{\hslash }}_{\phi }\le 0.2$.

FIGURE 3

FIGURE 3. $\mathrm{\hslash }-$curves of $f^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right)$, and ${\phi }^{\prime }\left(0\right)$.

5 Results and discussion

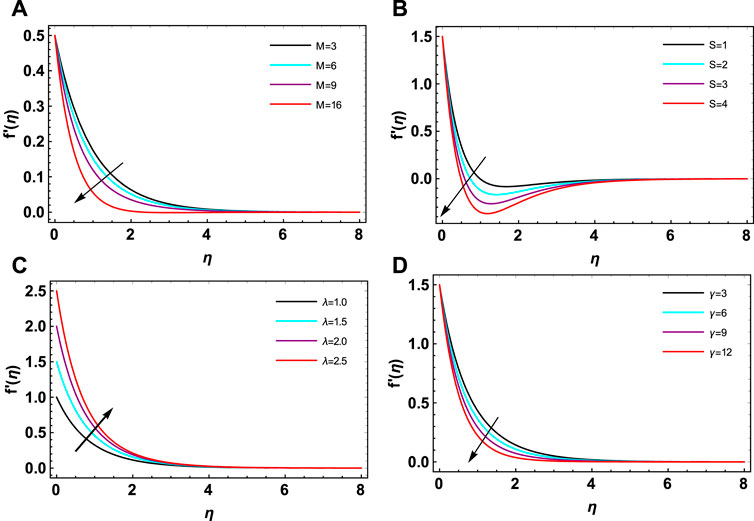
This section presents the discussion on the impacts of different embedded factors on the flow profiles of an electrically conducting hybrid nanofluid over an extending surface using a porous medium. The space-dependent heat source, Joule heating, Brownian motion, thermophoresis, thermal radiation, chemical reaction, and activation energy impacts are taken into consideration. Figure 4A shows the influence of the magnetic parameter $M$ on the velocity profile ($f^{\prime }\left(\eta \right)$). It is observed that the increasing $M$ reduces $f^{\prime }\left(\eta \right)$ significantly. Physically, when we increase $M$, an opposing force in the direction of fluid is created. This force is actually the Lorentz force, which resists the fluid particles’ motion. This force slows down the motion of the flow particles and, thus, $f^{\prime }\left(\eta \right)$ reduces. So, the velocity profile reduces with the increasing $M$. The effect of the suction/injection factor $S$ on the velocity profile $f^{\prime }\left(\eta \right)$ is depicted in Figure 4B. When $S>0$, $f^{\prime }\left(\eta \right)$ decreases. The heated fluid is physically forced away from the surface by the increased blowing factor, which causes the viscosity to drop and the fluid to accelerate. The momentum boundary layer is, however, thinned by the wall suction $S>0$, which imposes a drag force near the surface. The impact of $\lambda$ on the velocity profile $f^{\prime }\left(\eta \right)$ is shown in Figure 4C. $f^{\prime }\left(\eta \right)$ shows increasing conduct via $\lambda$. This is due to the fact that increasing $\lambda$ decreases the viscous influence on the flow. As a result, rising $\lambda$ reduces the thickness of the momentum boundary layer, and hence, $f^{\prime }\left(\eta \right)$ increases. The effect of the porosity factor $\gamma$ on $f^{\prime }\left(\eta \right)$ is shown in Figure 4D. It has been seen that $f^{\prime }\left(\eta \right)$ reduces with the upsurge in $\gamma$. This causes the motion of the fluid to reduce, which consequently reduces the thickness of the velocity boundary layer. So, $f^{\prime }\left(\eta \right)$ declines with the inclement in $\gamma$. The consequence of $M$ over the temperature profile $\theta \left(\eta \right)$ is shown in Figure 5A. According to this figure, the impact of the magnetic parameter results in the rise of $\theta \left(\eta \right)$ as $M$ increases. It is also important to note that the application of $M$ has a positive impact on the thickness of thermal boundary layers because the thickness increases in the presence of $M$. Figure 5B depicts how the injection/suction factor $S$ affects the temperature profile $\theta \left(\eta \right)$. It is understandable that when $S$ increases, the thickness of the thermal boundary layer decreases. In addition, the rate of deformation from the wall towards the fluid accelerates with the increasing $S$. The effect of the Brownian motion factor $Nb$ on $\theta \left(\eta \right)$ is displayed in Figure 5C. Increasing $Nb$ improves $\theta \left(\eta \right)$. Additionally, $Nb$ has an increasing effect on the thermal boundary layer. According to the definition, when $Nb$ grows, $\theta \left(\eta \right)$ rises because the fluid particles have more kinetic energy. The influence of $Nt$ on $\theta \left(\eta \right)$ is shown in Figure 5D. From Figure 5D, we can see that $\theta \left(\eta \right)$ increases due to the rising $Nt$. Figure 5E displays the variation in the temperature profile $\theta \left(\eta \right)$ due to $Ec$. It is seen that $\theta \left(\eta \right)$ rises as $Ec$ increases. To understand the thermal performance of fluid flow, $Ec$ is important. By raising $Ec$, the rising intermolecular interaction will increase the kinetic energy, which will increase $\theta \left(\eta \right)$ and allow $Ec$ to be utilized as a hot agent. Figure 5F and Figure 5G show how the radiation factor $Rd$ and the temperature ratio factor ${\theta }_w$ affect the temperature profile $\theta \left(\eta \right)$. By increasing ${\theta }_w$ and $Rd$, the fluid temperature rises significantly. Physically, the fluid particles are supported and activated by the rise in ${\theta }_w$ and $Rd$ as a result of obtaining thermal energy. The temperature of the boundary layer rises as a result of this. Increasing the thermal diffusion and thermal distribution, in turn, causes the boundary layer thickness to grow and its temperature to rise. Figure 5H shows how the temperature profile $\theta \left(\eta \right)$ is influenced by the space-dependent heat source parameter $Q_e$. $\theta \left(\eta \right)$ increases when we raise $Q_e$. Physically, when$Q_e>0$, the thermal boundary layer produces energy which causes augmentation in $\theta \left(\eta \right)$. Figure 5I illustrates the influence of the thermal Biot number $B{i}_T$ on the temperature profile $\theta \left(\eta \right)$. When $B{i}_T$ increases, $\theta \left(\eta \right)$ also increases. Physically, an enhancement in $B{i}_T$ results in more supported convection, which causes the increasing conduct in $\theta \left(\eta \right)$. Therefore, higher values of $B{i}_T$ increase the thermal boundary layer thickness, which, in turn, results in higher $\theta \left(\eta \right)$. The influence of $Nb$ on the concentration profile $\phi \left(\eta \right)$ is shown in Figure 6A. $\phi \left(\eta \right)$ significantly decreases with higher values of $Nb$. Physically, the increasing $Nb$ produces the random movement of the nanoparticles in fluid; as a result, $\phi \left(\eta \right)$ reduces. Figure 6B portrays the impact of the thermophoresis factor $Nt$ on $\phi \left(\eta \right)$. It is observed that the increasing $Nt$ increases $\phi \left(\eta \right)$. Physically, a rise in $Nt$ is followed by an upsurge in the thermal energy, which promotes the liquid’s temperature. As a result, the kinetic energy increases, and more collisions happen, which is enough to make the distribution of the concentration of nanoparticles large under the influence of $Nt$. The effect of activation energy $E$ on the concentration profile $\phi \left(\eta \right)$ is seen in Figure 6C. $\phi \left(\eta \right)$ increases when $E$ increases. Increasing values of $E$ diverge from the modified Arrhenius function, which increases the rate of generative chemical reactions. The concentration is increased as a result. The impact of the Schmidt number $Sc$ on the concentration profile $\phi \left(\eta \right)$ is exhibited in Figure 6D. $\phi \left(\eta \right)$ decreases as $Sc$ increases. The concentration boundary layer gets thinner because higher values of $Sc$ result in a faster mass transfer rate. So, $\phi \left(\eta \right)$ shows a decreasing impact against $Sc$. Figure 6E shows how the chemical reaction factor $Kr$ affects the concentration profile $\phi \left(\eta \right)$. It is obvious that $\phi \left(\eta \right)$ decreases as $Kr$ increases. The effect of the temperature difference parameter $\delta$ on the concentration profile $\phi \left(\eta \right)$ is seen in Figure 6F. $\phi \left(\eta \right)$ shows diminishing behavior when the temperature difference values are increased. Physically, a greater $\delta$ causes a decrease in molecular diffusivity, which lowers $\phi \left(\eta \right)$. Table 1 shows the thermophysical properties of the base fluid and nanoparticles. The comparison of the present results with published results are shown in Table 2. The values of $C_{fx}$ are shown in Table 3 for different stretching ratio parameters $\lambda$ and magnetic field parameters $M$. We determined the negative values for $C_{fx}$. When friction force is negative, it indicates that the sheet is causing the fluid to move more slowly. In terms of quality, the effects of $\lambda$ and $M$ on $C_{fx}$ caused by the flow are equivalent. In other words, $C_{fx}$ is the decreasing function of $M$ and $\lambda$. The numerical values of the Nusselt number $N{u}_x$ and Sherwood number $S{h}_x$ are shown in Tables 4 and Table 5 for various values of $Rd$, ${\theta }_w$, $B{i}_T$, $M$, and $\lambda$. $N{u}_x$, in this case, increases for high values of $B{i}_T$ and $\lambda$ while decreasing for larger values of $Rd$, ${\theta }_w$, and $M$. $S{h}_x$ is the increasing function of $B{i}_T$, and $M$ is a decreasing function of $Rd$, ${\theta }_w$, and $\lambda$.

FIGURE 4

FIGURE 4. Impact of $M$ on $f^{\prime }\left(\eta \right)$. Impact of $S$ on $f^{\prime }\left(\eta \right)$. Impact of $\lambda$ on $f^{\prime }\left(\eta \right)$. Impact of $\gamma$ on $f^{\prime }\left(\eta \right)$.

FIGURE 5

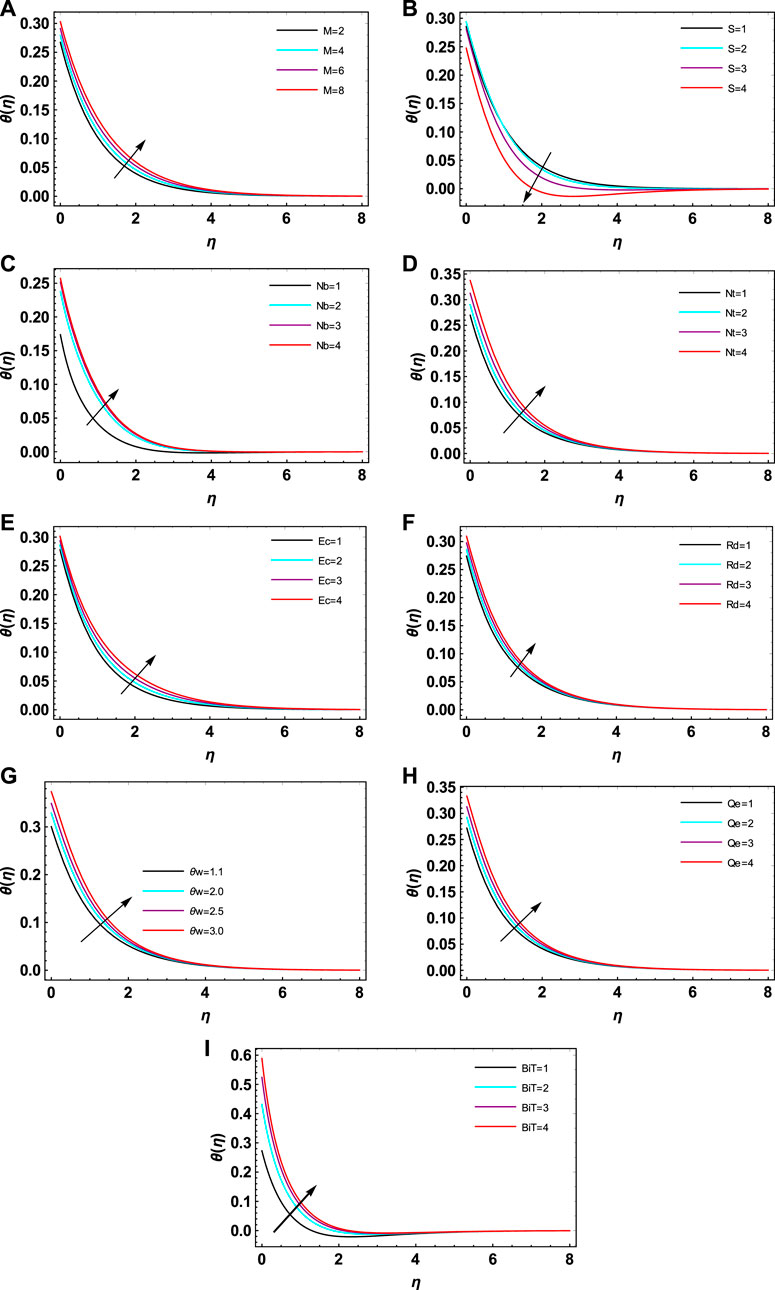
FIGURE 5. (A) Impact of M on θ(η). (B) Impact of S on θ(η). (C) Impact of Nb on θ(η). (D) Impact of Nt on θ(η). (E) Impact of Ec on θ(η). (F) Impact of Rd on θ(η). (G) Impact of θ_w on θ(η). (H) Impact of Q_e on θ(η). (I) Impact of Bi_T on θ(η).(a)(b)

FIGURE 6

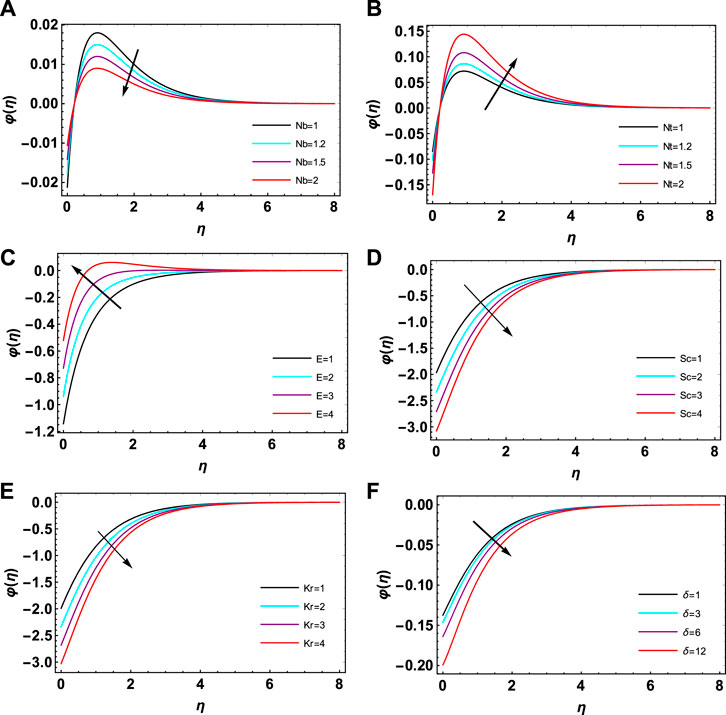
FIGURE 6. (A) Impact of $Nb$ on $\phi \left(\eta \right)$. (B) Impact of $Nt$ on $\phi \left(\eta \right)$. (C) Impact of $E$ on $\phi \left(\eta \right)$. (D) Impact of $Sc$ on $\phi \left(\eta \right)$. (E) Impact of $Kr$ on $\phi \left(\eta \right)$. (F) Impact of $\delta$ on $\phi \left(\eta \right)$.

TABLE 1

TABLE 1. Thermophysical properties of the base fluid and nanoparticles (Acharya, 2021).

TABLE 2

TABLE 2. Numerical comparison of the present results of $-{\theta }^{\prime }\left(0\right)$ with published results for different values of $\mathrm{Pr}$.

TABLE 3

TABLE 3. Numerical values of skin friction for different values of $M$ and $\lambda$.

TABLE 4

TABLE 4. Numerical value of the Nusselt number for different values of $Rd$, ${\theta }_w$, $B{i}_T$, $M$, and $\lambda$.

TABLE 5

TABLE 5. Numerical value of the Sherwood number for different values of $Rd$, ${\theta }_w$, $B{i}_T$, $M$, and $\lambda$.

6 Conclusion

In this article, the authors have presented an electrically conducting hybrid nanofluid flow over an extending surface using a porous medium. The homotopic approach is tackled for the solution of the modeled equations. The space-dependent heat source, Joule heating, Brownian motion, thermophoresis, thermal radiation, and chemically reactive activated energy impacts are used. The following are the concluding points of this study:

• The growing magnetic and suction factors reduced the velocity profiles, while they enlarged the thermal profiles by magnetic factor. Additionally, the suction factor has a reducing impression on the thermal profile.

• Motion of the fluid reduced with the increasing porosity factor, while it increased with the increasing stretching factor.

• The thermal profiles increased with the increasing thermal Biot number, Eckert number, thermophoresis, space-based heat source, Brownian motion, and non-linear thermal radiation factors.

• The concentration profiles reduced with the increasing Brownian motion, chemical reaction, and temperature difference factors, while they were increased by the activation energy factor.

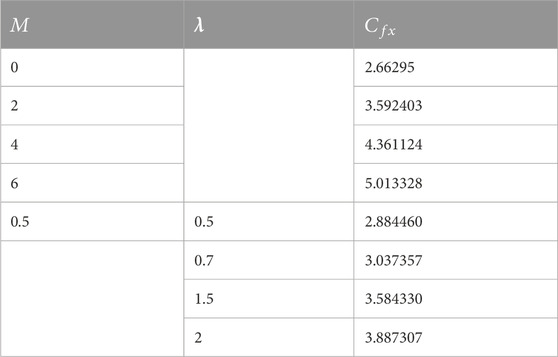
• The magnetic and stretching factors augmented the surface drag coefficient.

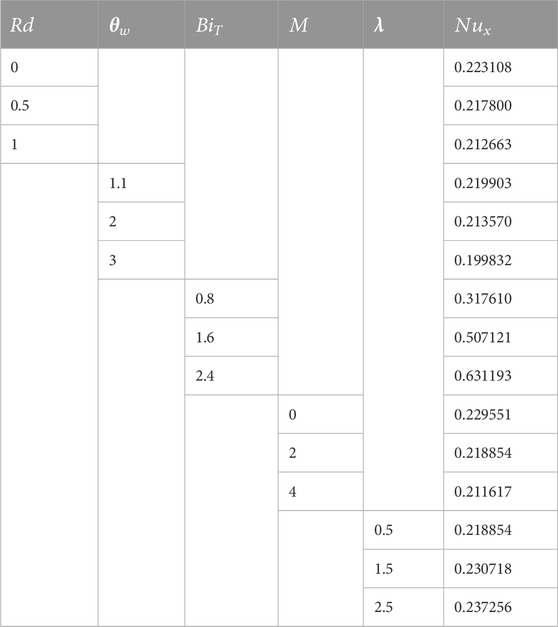
• The Nusselt numbers increased with the increasing thermal Biot number and stretching factor, while they reduced with the increasing thermal radiation and temperature difference factors.

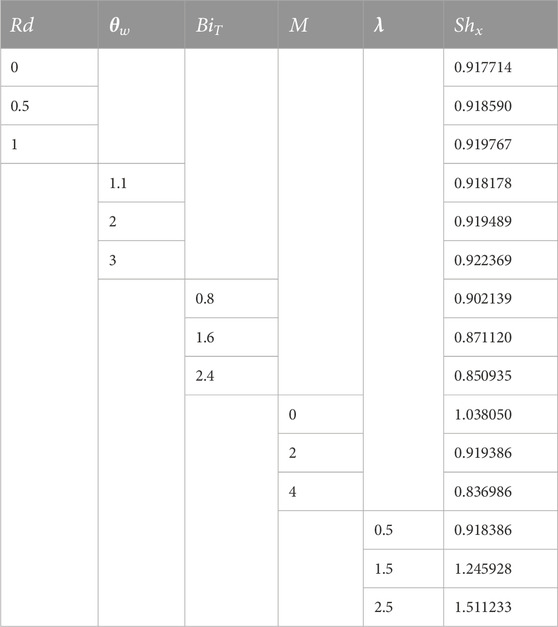
• The Sherwood numbers increased with the thermal Biot number and magnetic factor, while they reduced with the increasing thermal radiation, temperature difference, and stretching factors.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

EA and SL: conceptualization, methodology, software reviewing, and editing. ZR: data curation and writing—original draft preparation. SE: visualization and investigation. AS: software, validation, and supervision. AG: writing—reviewing and editing.

Acknowledgments

The author ZR extends her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number RGP.1/334/43.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, A., Jeelani, M. B., and Alharthi, N. H. (2022). Darcy–Forchheimer relation influence on MHD dissipative third-grade fluid flow and heat transfer in porous medium with joule heating effects: A numerical approach. Processes 10, 906. doi:10.3390/pr10050906

CrossRef Full Text | Google Scholar

Acharya, N., Mabood, F., Shahzad, S. A., and Badruddin, I. A. (2022). Hydrothermal variations of radiative nanofluid flow by the influence of nanoparticles diameter and nanolayer. Int. Commun. Heat. Mass Transf. 130, 105781. doi:10.1016/J.ICHEATMASSTRANSFER.2021.105781

CrossRef Full Text | Google Scholar

Acharya, N. (2021). Spectral quasi linearization simulation on the hydrothermal behavior of hybrid nanofluid spraying on an inclined spinning disk. Partial Differ. Equations Appl. Math. 4, 100094. doi:10.1016/J.PADIFF.2021.100094

CrossRef Full Text | Google Scholar

Adnan, W. Ashraf (2022). Numerical thermal featuring in γAl2O3-C2H6O2 nanofluid under the influence of thermal radiation and convective heat condition by inducing novel effects of effective Prandtl number model (EPNM). Adv. Mech. Eng. 14, 168781322211065. doi:10.1177/16878132221106577

CrossRef Full Text | Google Scholar

Alrabaiah, H., Bilal, M., Khan, M. A., Muhammad, T., and Legas, E. Y. (2022). Parametric estimation of gyrotactic microorganism hybrid nanofluid flow between the conical gap of spinning disk-cone apparatus. Sci. Rep. 12, 59–14. doi:10.1038/s41598-021-03077-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Akbar, N. S., Maraj, E. N., Noor, N. F. M., and Habib, M. B. (2022). Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud. Therm. Eng. 35, 102124. doi:10.1016/j.csite.2022.102124

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., and Tripathi, D. (2021). A theoretical investigation on the heat transfer ability of water-based hybrid (Ag–Au) nanofluids and Ag nanofluids flow driven by electroosmotic pumping through a microchannel. Arab. J. Sci. Eng. 46, 2911–2927. doi:10.1007/s13369-020-05265-0

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., Alansari, M., and Tripathi, D. (2022). Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Int. Commun. Heat. Mass Transf. 136, 106208. doi:10.1016/j.icheatmasstransfer.2022.106208

CrossRef Full Text | Google Scholar

Asjad, M. I., Zahid, M., Inc, M., Baleanu, D., and Almohsen, B. (2022). Impact of activation energy and MHD on Williamson fluid flow in the presence of bioconvection. Alex. Eng. J. 61, 8715–8727. doi:10.1016/j.aej.2022.02.013

CrossRef Full Text | Google Scholar

Bejawada, S. G., Reddy, Y. D., Jamshed, W., Nisar, K. S., Alharbi, A. N., and Chouikh, R. (2022). Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex. Eng. J. 61, 8207–8220. doi:10.1016/j.aej.2022.01.043

CrossRef Full Text | Google Scholar

Bhatti, M. M., Arain, M. B., Zeeshan, A., Ellahi, R., and Doranehgard, M. H. (2022). Swimming of Gyrotactic Microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage. 45, 103511. doi:10.1016/j.est.2021.103511

CrossRef Full Text | Google Scholar

Bilal, M., Saeed, A., Gul, T., Kumam, W., Mukhtar, S., and Kumam, P. (2022). Parametric simulation of micropolar fluid with thermal radiation across a porous stretching surface. Sci. Rep. 12, 2542–2611. doi:10.1038/s41598-022-06458-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in Proceedings of the Int. Mech. Eng. Congr. Exhib, San Fr. CA, United States, 12-17 Nov 1995.

Google Scholar

Chu, Y., Bashir, S., Ramzan, M., and Malik, M. Y. (2022). Model-based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. 22, 8234. doi:10.1002/mma.8234

CrossRef Full Text | Google Scholar

Dawar, A., Islam, S., Shah, Z., Mahmuod, S. R., and Lone, S. A. (2022). Dynamics of inter-particle spacing, nanoparticle radius, inclined magnetic field and nonlinear thermal radiation on the water-based copper nanofluid flow past a convectively heated stretching surface with mass flux condition: A strong suction case. Int. Commun. Heat. Mass Transf. 137, 106286. doi:10.1016/j.icheatmasstransfer.2022.106286

CrossRef Full Text | Google Scholar

Dawar, A., Said, N. M., Islam, S., Shah, Z., Mahmuod, S. R., and Wakif, A. (2022). A semi-analytical passive strategy to examine a magnetized heterogeneous mixture having sodium alginate liquid with alumina and copper nanomaterials near a convectively heated surface of a stretching curved geometry. Int. Commun. Heat. Mass Transf. 139, 106452. doi:10.1016/j.icheatmasstransfer.2022.106452

CrossRef Full Text | Google Scholar

Guedri, K., Khan, A., Sene, N., Raizah, Z., Saeed, A., and Galal, A. M. (2022). Thermal flow for radiative ternary hybrid nanofluid over nonlinear stretching sheet subject to Darcy–forchheimer phenomenon. Math. Probl. Eng. 2022, 1–14. doi:10.1155/2022/3429439

CrossRef Full Text | Google Scholar

Hamad, M. A. A. (2011). Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat. Mass Transf. 38, 487–492. doi:10.1016/j.icheatmasstransfer.2010.12.042

CrossRef Full Text | Google Scholar

Habib, M. B., and Akbar, N. S. (2021). New trends of nanofluids to combat Staphylococcus aureus in clinical isolates. J. Therm. Anal. Calorim. 143, 1893–1899. doi:10.1007/s10973-020-09502-4

CrossRef Full Text | Google Scholar

Hussain, S. M., Jamshed, W., Pasha, A. A., Adil, M., and Akram, M. (2022). Galerkin finite element solution for electromagnetic radiative impact on viscid Williamson two-phase nanofluid flow via extendable surface. Int. Commun. Heat. Mass Transf. 137, 106243. doi:10.1016/j.icheatmasstransfer.2022.106243

CrossRef Full Text | Google Scholar

Ibrahim, M., Saeed, T., and Zeb, S. (2022). Numerical simulation of time-dependent two-dimensional viscous fluid flow with thermal radiation. Eur. Phys. J. Plus. 137, 609. doi:10.1140/epjp/s13360-022-02813-5

CrossRef Full Text | Google Scholar

Khan, A., Saeed, A., Gul, T., Mukhtar, S., Ali, I., and Jawad, M. (2021). Radiative swirl motion of hydromagnetic Casson nanofluid flow over rotary cylinder using Joule dissipation impact. Phys. Scr. 96, 045206. doi:10.1088/1402-4896/abdf83

CrossRef Full Text | Google Scholar

Khan, A., Hassan, B., Ashraf, E. E., and Shah, S. Y. A. (2022). Thermally dissipative micropolar hybrid nanofluid flow over a spinning needle influenced by Hall current and gyrotactic microorganisms. Heat. Transf. 51, 1170–1192. doi:10.1002/htj.22347

CrossRef Full Text | Google Scholar

Khan, S. A., Khan, M. I., Alsallami, S. A. M., Alhazmi, S. E., Alharbi, F. M., and El-Zahar, E. R. (2022). Irreversibility analysis in hydromagnetic flow of Newtonian fluid with joule heating: Darcy-forchheimer model. J. Pet. Sci. Eng. 212, 110206. doi:10.1016/j.petrol.2022.110206

CrossRef Full Text | Google Scholar

Kodi, R., and Mopuri, O. (2022). Unsteady MHD oscillatory Casson fluid flow past an inclined vertical porous plate in the presence of chemical reaction with heat absorption and Soret effects. Heat. Transf. 51, 733–752. doi:10.1002/htj.22327

CrossRef Full Text | Google Scholar

Kumar, D., Sinha, S., Sharma, A., Agrawal, P., and Kumar Dadheech, P. (2022). Numerical study of chemical reaction and heat transfer of MHD slip flow with Joule heating and Soret–Dufour effect over an exponentially stretching sheet. Heat. Transf. 51, 1939–1963. doi:10.1002/htj.22382

CrossRef Full Text | Google Scholar

Liao, S.-J. (1999). An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non. Linear. Mech. 34, 759–778. doi:10.1016/s0020-7462(98)00056-0

CrossRef Full Text | Google Scholar

Lone, S. A., Alyami, M. A., Saeed, A., Dawar, A., Kumam, P., and Kumam, W. (2022). MHD micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal radiation. Sci. Rep. 12, 17283–17314. doi:10.1038/s41598-022-21255-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, S. (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 15, 2003–2016. doi:10.1016/J.CNSNS.2009.09.002

CrossRef Full Text | Google Scholar

Mahabaleshwar, U. S., Vishalakshi, A. B., and Hatami, M. (2022). MHD micropolar fluid flow over a stretching/shrinking sheet with dissipation of energy and stress work considering mass transpiration and thermal radiation. Int. Commun. Heat. Mass Transf. 133, 105966. doi:10.1016/j.icheatmasstransfer.2022.105966

CrossRef Full Text | Google Scholar

Maraj, E. N., Akbar, N. S., Iqbal, Z., and Azhar, E. (2017). Framing the MHD mixed convective performance of CNTs in rotating vertical channel inspired by thermal deposition: Closed form solutions. J. Mol. Liq. 233, 334–343. doi:10.1016/j.molliq.2017.03.041

CrossRef Full Text | Google Scholar

Nagendramma, V., Durgaprasad, P., Sivakumar, N., Rao, B. M., Raju, C. S. K., Shah, N. A., et al. (2022). Dynamics of triple diffusive free convective MHD fluid flow: Lie Group transformation. Mathematics 10, 2456. doi:10.3390/math10142456

CrossRef Full Text | Google Scholar

Nazeer, M., Hussain, F., Khan, M. I., El-Zahar, E. R., Chu, Y.-M., Malik, M. Y., et al. (2022). Retracted: Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 420, 126868. doi:10.1016/j.amc.2021.126868

CrossRef Full Text | Google Scholar

Ramesh, G. K., Madhukesh, J. K., Shah, N. A., and Yook, S.-J. (2022). Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alex. Eng. J. 64, 969–979. doi:10.1016/j.aej.2022.09.026

CrossRef Full Text | Google Scholar

Rasheed, H. U., Khan, W., Khan, I., Alshammari, N., and Hamadneh, N. (2022). Numerical computation of 3D Brownian motion of thin film nanofluid flow of convective heat transfer over a stretchable rotating surface. Sci. Rep. 12, 1–14.

PubMed Abstract | Google Scholar

Rehman, K. U., Shatanawi, W., and Al-Mdallal, Q. M. (2022). A comparative remark on heat transfer in thermally stratified MHD Jeffrey fluid flow with thermal radiations subject to cylindrical/plane surfaces. Case Stud. Therm. Eng. 32, 101913. doi:10.1016/j.csite.2022.101913

CrossRef Full Text | Google Scholar

Reddy Gorla, R. S., and Sidawi, I. (1994). Free convection on a vertical stretching surface with suction and blowing. Appl. Sci. Res. 52, 247–257. doi:10.1007/bf00853952

CrossRef Full Text | Google Scholar

Reddy, S. R. R., Reddy, P. B. A., and Chamkha, A. J. (2020). Heat transfer analysis OFMHD CNTS nanofluid flow over a stretching sheet. Spec. Top. Rev. Porous Media Int. J. 11, 133–147. doi:10.1615/specialtopicsrevporousmedia.2020030647

CrossRef Full Text | Google Scholar

Salahuddin, T., Siddique, N., Khan, M., and Chu, Y. (2022). A hybrid nanofluid flow near a highly magnetized heated wavy cylinder. Alex. Eng. J. 61, 1297–1308. doi:10.1016/j.aej.2021.06.014

CrossRef Full Text | Google Scholar

Saleem, A., Akhtar, S., and Nadeem, S. (2022). Bio-mathematical analysis of electro-osmotically modulated hemodynamic blood flow inside a symmetric and nonsymmetric stenosed artery with joule heating. Int. J. Biomath. 15, 2150071. doi:10.1142/s1793524521500716

CrossRef Full Text | Google Scholar

Shah, Z., Khan, A., Khan, W., Alam, M. K., Islam, S., Kumam, P., et al. (2020). Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Comput. Methods Programs Biomed. 186, 105197. doi:10.1016/j.cmpb.2019.105197

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaw, S., Samantaray, S., Misra, A., Nayak, M. K., and Makinde, O. D. (2022). Hydromagnetic flow and thermal interpretations of Cross hybrid nanofluid influenced by linear, nonlinear and quadratic thermal radiations for any Prandtl number. Int. Communiction Heat Mass Transf. 130, 105816. doi:10.1016/j.icheatmasstransfer.2021.105816

CrossRef Full Text | Google Scholar

Shamshuddin, M. D., and Eid, M. R. (2022). Nth order reactive nanoliquid through convective elongated sheet under mixed convection flow with joule heating effects. J. Therm. Anal. Calorim. 147, 3853–3867. doi:10.1007/s10973-021-10816-0

CrossRef Full Text | Google Scholar

Sharma, K., Kumar, S., Narwal, A., Mebarek-Oudina, F., and Animasaun, I. L. (2022). Convective MHD fluid flow over stretchable rotating disks with dufour and Soret effects. Int. J. Appl. Comput. Math. 8, 159–212. doi:10.1007/s40819-022-01357-7

CrossRef Full Text | Google Scholar

Usman, M., Gul, T., Khan, A., Alsubie, A., and Ullah, M. Z. (2021). Electromagnetic couple stress film flow of hybrid nanofluid over an unsteady rotating disc. Int. Commun. Heat. Mass Transf. 127, 105562. doi:10.1016/j.icheatmasstransfer.2021.105562

CrossRef Full Text | Google Scholar

Venkata Ramudu, A. C., Anantha Kumar, K., Sugunamma, V., and Sandeep, N. (2022). Impact of Soret and Dufour on MHD Casson fluid flow past a stretching surface with convective–diffusive conditions. J. Therm. Anal. Calorim. 147, 2653–2663. doi:10.1007/s10973-021-10569-w

CrossRef Full Text | Google Scholar

Wahid, N. S., Arifin, N. M., Pop, I., Bachok, N., and Hafidzuddin, M. E. H. (2022). MHD stagnation-point flow of nanofluid due to a shrinking sheet with melting, viscous dissipation and Joule heating effects. Alex. Eng. J. 61, 12661–12672. doi:10.1016/j.aej.2022.06.041

CrossRef Full Text | Google Scholar

Waqas, M., Sadiq, M. A., and Bahaidarah, H. M. S. (2022). Gyrotactic bioconvection stratified flow of magnetized micropolar nanoliquid configured by stretchable radiating surface with Joule heating and viscous dissipation. Int. Commun. Heat. Mass Transf. 138, 106229. doi:10.1016/j.icheatmasstransfer.2022.106229

CrossRef Full Text | Google Scholar

Waseem, M., Gul, T., Khan, I., Khan, A., Saeed, A., Ali, I., et al. (2021). Gravity-driven hydromagnetic flow of couple stress hybrid nanofluid with homogenous-heterogeneous reactions. Sci. Rep. 11, 17498–17512. doi:10.1038/s41598-021-97045-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Z., Jiao, J., and Yang, K. (2023). Theoretical and experimental study on the fluid-structure-acoustic coupling dynamics of a new water lubricated bearing. Tribol. Int. 177, 107982. doi:10.1016/j.triboint.2022.107982

CrossRef Full Text | Google Scholar

Xie, Z., Jiao, J., and Wrona, S. (2023). The fluid-structure interaction lubrication performances of a novel bearing: Experimental and numerical study. Tribol. Int. 179, 108151. doi:10.1016/j.triboint.2022.108151

CrossRef Full Text | Google Scholar

Xuan, X. (2022). Review of nonlinear electrokinetic flows in insulator-based dielectrophoresis: From induced charge to Joule heating effects. Electrophoresis 43, 167–189. doi:10.1002/elps.202100090

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., Shafiq, A., Kumar, M., and Nonlaopon, K. (2022). Analysis of heat transfer of mono and hybrid nanofluid flow between two parallel plates in a Darcy porous medium with thermal radiation and heat generation/absorption. Symmetry (Basel) 14, 1943. doi:10.3390/sym14091943

CrossRef Full Text | Google Scholar

Zhang, L., Bhatti, M. M., Michaelides, E. E., Marin, M., and Ellahi, R. (2022). Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 231, 521–533. doi:10.1140/epjs/s11734-021-00409-1

CrossRef Full Text | Google Scholar

Nomenclature

$a$ Constant

$B_0$ Magnetic field strength

${\left(C_p\right)}_f$, ${\left(C_p\right)}_{hnf}$ Specific heat for the base fluid and hybrid nanofluid

$D_B$, $D_T$ Brownian and thermophoresis diffusion coefficients

$h_f$ Thermal transmission coefficient

$k_p$, $k_f$, $k_{hnf}$ Thermal conductivities of the nanoparticles, base fluid, and hybrid nanofluid

$K_p$ Permeability of the porous medium

$Q$ Heat source coefficient

$q_m$ Mass flux at the surface

$q_w$, $q_r$ Surface and radiative heat fluxes

$T_f$, $T_w$, $T_{\infty }$ Reference, wall, and ambient temperatures

$u,v$ Velocity component

$x,y$ Coordinates

${\tau }_w$ Shear stress

$\lambda$ Stretching parameter

${\left(\rho C_p\right)}_p$, ${\left(\rho C_p\right)}_f$, ${\left(\rho C_p\right)}_{hnf}$ Heat capacitance of the nanoparticles, base fluid, and hybrid nanofluid

${\mu }_p$, ${\mu }_f$, ${\mu }_{hnf}$ Dynamic viscosities of the nanoparticles, base fluid, and hybrid nanofluid

${\rho }_p$, ${\rho }_f$, ${\rho }_{hnf}$ Densities of the nanoparticles, base fluid, and hybrid nanofluid

${\sigma }_p$, ${\sigma }_f$, ${\sigma }_{hnf}$ Electrical conductivities of the nanoparticles, base fluid, and hybrid nanofluid

$\alpha$ Angle of inclination

${\nabla }_1$, ${\nabla }_2$ Volumetric fraction of the first and second nanoparticle

$\mathrm{Pr}$ Prandtl number

$Rd$ Radiation factor

$Nb$ Brownian motion factor

$Nt$ Thermophoretic factor

$Kr$ Chemical factor

$\gamma$ Porosity factor

$Sc$ Schmidt number

$B{i}_T$ Thermal Biot number

$M$ Magnetic factor

$Q_e$ Exponential heating factor

$Ec$ Eckert number

${\theta }_w$ Thermal difference factor

$E$ Activation energy factor

$\delta$ Temperature difference parameter