Chemically reactive hybrid nanofluid flow past a Riga plate with nonlinear thermal radiation and a variable heat source/sink

The suspension of nanoparticles in base liquids has found extensive applications in various industrial processes like nanomedicines, microsystem cooling, and energy conversion. Owing to its important applications, this article investigates the hybrid nanofluid flow over a three-dimensional stretching surface. The fluid is influenced by thermal radiation, chemical reaction, and a variable thermal source/sink. The set of equations that administer the fluid behavior has been transformed to dimensionless form by a suitable set of similarity transformations that are further solved by the homotopy analysis method. It was found that as the ratio parameter increased, the velocity of hybrid nanofluid velocity decreased along the primary direction and increased along the secondary direction. The temperature characteristic was augmented with greater values of nonlinear thermal radiation and source/sink factors. Growth in the chemically reactive factor and Schmidt number has an adverse effect on the concentration profile of the hybrid nanofluid flow. A comparative analysis of the current results and those established in the literature was conducted. A close agreement with those published results was found. It was noted that temperature and concentration increase more quickly for the $Mo{S}_2+MgO/H_{2}O$ hybrid nanofluid than the $Mo{S}_2/H_{2}O,MgO/H_{2}O$ nanofluids.

1 Introduction

The heating and cooling of fluids is quite useful in industrial applications like power manufacturing and power transportation processes. Typical fluids have lower thermal conductivities because of their lower thermal flow characteristics. In contrast, the thermal conductivity of metals is higher. So, to create fluids with a desired level of thermal conductivity, solid nanoparticles are mixed with conventional fluids, as proposed by Choi (Choi and Eastman, 1995). Shah et al. (2020) mixed gold nanoparticles in blood, discussed the behavior of that fluid, and concluded that the thermal characteristics were enhanced with improvements in the radiation factor and number of solid nanoparticles. Bhatti et al. (2022) studied the swimming behavior of microorganisms in a Williamson MHD nanofluid flow over rotating plates embedded in a permeable region and concluded that an increase in magnetic factor and nanoparticle volume fraction increased the temperature characteristics and decreased fluid velocity. Acharya et al. (2022) inspected the variations in hydrothermal nanofluid flow influenced by the diameters of nanoparticles and a nanolayer and showed that the nanolayer enhanced the thermal flow by 84.61%. Shahid et al. (2022) presented a numerical examination of nanofluid flow over a permeable surface using the influences of activation energy and bioconvection.

Mixing two different types of nanoparticles in a base fluid will enhance its thermal conductivities. This is called a hybrid nanofluid. Manzoor et al. (2021) studied the improvement of thermal transmission of a magnetized hybrid nanofluid flow over a stretching sheet and concluded that the temperature distributions were augmented with enhancements in volume fractions and magnetic factors. Khan et al. (2022a) examined the flow of a hybrid nanoliquid on a moving heated needle placed horizontally in the fluid and found that the thermal transmission was enlarged with an increase in Brownian motion, Eckert number, and volume fractions of nanoparticles. Waseem et al. (2021) examined the couple stress hybrid nanofluid flow over a vertically placed heated plate using heterogeneous and homogeneous reactions. They concluded that the skin friction increased with the increase in buoyance forces. Eid and Nafe (2022) examined the thermal conductivity and heat generation influences on MHD hybrid nanoliquid flow over a stretching surface with slip conditions. Zhang et al. (2022) analyzed the flow of hybrid nanoliquid past a stretching surface and concluded that the fluid moved faster with higher values of the Darcy number, while the motion of fluid was retarded with an increase in the magnetic factor. Ojjela (2022) investigated the thermal transportation of hybrid nanofluid using alumina and silica nanoparticles and compared the results with established studies. The related analyses can be seen in Zabihi et al. (2020a), Zabihi et al. (2020b), Wahid et al. (2020), Alhowaity et al. (2022), Khan et al. (2022b), and Zabihi et al. (2022).

Fluids that conduct electrically, like liquid metals, plasmas, and electrolytes, can be organized using magnetic fields. These flows have many applications in earthquakes, astrophysics, geophysics, and sensors. In such phenomena, magnetic and electric fields are used to control and direct the flow of fluids; these are called EMHD flow. Fluids flowing in electrically weak conducted fluids can be organized and controlled by applying an external electric field using a Riga plate, which is an electromagnetic surface with alternatively assembled electrodes. Such an arrangement produces hydrodynamic and electromagnetic behavior within the fluid flow on a surface. Lielausis (1961) constructed a Riga plate to control the fluid flow by producing a Lorentz effect along a wall. Shafiq et al. (2021) studied double stratification at the stagnant point in a Walters-B nanofluid past a radiative Riga plate. They observed that intensive retardation in thermal flow and concentration was found for double stratification, while stronger radiation values corresponded to a significant rise in temperature. Asogwa et al. (2022) compared two different nanofluid characteristics regarding the thermal, skin friction, and concentration past an exponentially accelerated Riga plate. They found that in the case of increased radiation, a CuO-based nanofluid behaved much better than a $A{l}_2{O}_3$-based nanofluid. Gangadhar et al. (2021) investigated the flow of a radiative EMHD fluid on a Riga plate due to heat convection using the modified Buongiorno model. Rahman et al. (2022) examined the effects of suction and magnetic factors on a nanofluid flow containing copper oxide, metal, alumina, and titanium dioxide nanoparticles over a spinning disc. Anuar et al. (2020) analyzed the magnetohydrodynamic effect on a nanofluid flow over a nonlinear extending surface. Kumar et al. (2017) investigated the influence of chemical reactions on the MHD three-dimensional nanofluid flow over a Riga plate.

Thermal radiation plays a fundamental role in the heat transport phenomenon. Many investigations have been made on the nanofluid flow with thermal radiation effects. Hayat et al. (2013) investigated the Jeffery liquid flow past a stretching sheet with the impact of thermal radiation and found that the skin friction and Sherwood number were amplified due to the higher radiation factor. Sabir et al. (2021) examined the Sutterby fluid flow with the influence of thermal radiation and concluded that higher strength of magnetic and radiation factors augmented the thermal characteristic and skin friction. Ijaz et al. (2021) simulated the effects of a thermal radiation magnetic field on a nanofluid flow containing gyrotactic microorganisms and concluded that the temperature- and space-based heat absorptions were more appropriate for cooling. Ali et al. (2021) inspected the influences of thermal radiation and magnetic field effects on the Darcy flow and observed that with an increase in the diameter of copper nanoparticles, the temperature distribution was increased. Saeed et al. (2021) investigated the Darcy–Forchheimer nanoliquid flow with thermal radiation and determined that the velocity profile reduced with the higher Darcy number, and temperature was increased with growth in the radiation factor. The impacts of thermal radiation, chemical reaction, and heat absorption/generation on MHD Maxwell nanofluid flow were examined by Tlili et al. (2020).

In many investigations, there may be reasonable thermal differences between the ambient fluid and the surface on which the fluid flows. This idea necessitates deliberation in the presence of thermal heat or a thermal sink that strongly affects the thermal flow rate of a fluid flow system. This idea is gaining more attention because of its expanding uses in production engineering problems where the heat transportation is substantial to enhance the quality of the final product. Khader and Sharma (2021) evaluated the time-based MHD liquid flow over a shrinking/stretching sheet using thermal radiation and a heat source and found that temperature declined with an expansion in the steadiness factor and the thermal buoyancy parameter, whereas it increased with higher values of the heat source. Tarakaramu et al. (2022) discussed the three-dimensional couple stress fluid flow past a stretching surface with nonlinear thermal radiation and heat source impacts. Ram et al. (2022) examined the mixed convection thermal and mass transportations in a magnetized fluid flow at a stagnant point of a stretching surface with a heat source. Haq et al. (2022) examined the mixed convective nanofluid flow past an irregular inclined sheet with a chemical reaction and heat source impact and found that velocity rises with the increases in the angle of inclination. Sharma et al. (2022) explored the effect of a thermal source on EMHD nanofluid flow over an extending surface. Saleh et al. (2022) analyzed the influence of the heat source on nanoliquid flow past a stretching surface and found that thermal distribution increased as the temperature-based heat source and space factors increased. Li et al. (2022) discussed the double diffusion nanofluid flow with the influence of activation energy, a nonlinear heat source/sink, and convective conditions. Many similar studies can be seen in Alharbi et al. (2018), Alwawi et al. (2020), Hamarsheh et al. (2020), Sravanthi (2020), El-Zahar et al. (2021), Khan et al. (2021), Shamshuddin et al. (2021), El-Zahar et al. (2022), Thumma et al. (2022), Ullah et al. (2022), and Waini et al. (2022).

Apart from the aforementioned analyses, there is less work on the hybrid nanoliquid flow over a stretching surface. The surface of the plate is kept at a constant temperature and concentration. The nonlinear thermal radiation, variable heat source/sink, thermophoresis, Brownian motion, and chemical reaction impacts are considered to make this model novel. The mathematical formulation of the flow is presented in Section 2. Section 3 provides a semi-analytical solution to the flow problem. The validation of current results with published results is presented in Section 4. The discussion of the present results is presented in Section 5. Concluding remarks are presented in Section 6.

2 Problem formulation

Consider the flow of a hybrid nanofluid on a three-dimensional extending surface. The surface stretches along the $x$ axis with a velocity $u_w\left(x\right)=ax$ and along the $y$ axis with velocity $v_w\left(y\right)=by$, where $a$ and $b$ are positive fixed values. The flow in the system is induced by a Riga plate with $M=M_0\left(x\right)$ along the $z$ direction. At the surface of the Riga plate, $T_w$ is temperature and $C_w$ is concentration, whereas, at the free surface, these quantities are given as $T_{\infty }$ and $C_{\infty }$. Nonlinear thermal radiation, the variable heat source/sink, thermophoresis, and chemical reaction effects are also considered. Using these assumptions, the leading equations can be written as follows (Ahmad et al., 2016; Muhammad et al., 2021; Alqarni, 2022; Shah et al., 2022):

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial z^2}+\frac{1}{{\rho }_{hnf}}\frac{\pi j_{0}M}{8}\exp \left(-\frac{\pi }{{\alpha }_{0}z}\right),(2)$

$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}v}{\partial z^2},(3)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial z^2}-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q_r}{\partial z}+\frac{1}{{\left(\rho C_p\right)}_{hnf}}q,(4)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}=D_B\frac{{\partial }^{2}C}{\partial z^2}-K^{*}\left(C-C_{\infty }\right),(5)$

with boundary conditions:

$\left\{\begin{array}{l}u=u_w\left(x\right)=ax,\hspace{1em}v=v_w\left(y\right)=by,\hspace{1em}T=T_w,\hspace{1em}C=C_{w}atz=0\\ u\to 0,\hspace{1em}v\to 0,\hspace{1em}T\to T_{\infty }\hspace{1em},C\to C_{\infty }asz\to \infty \end{array}\right\}(6)$

As mentioned previously, $u,v,\mathrm{a}\mathrm{n}\mathrm{d}w$ are the velocity components along the coordinate axes, $M$ is the magnetic property of the plate surface due to the permanent magnet, and $j_0$ is the electrode current density.

The $q_r$ (radiative heat flux) is defined as follows (Alqarni, 2022):

$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial z}=-\frac{16{\sigma }^{*}}{3k^{*}}\frac{\partial }{\partial z}\left(T^3\frac{\partial T}{\partial z}\right).(7)$

The variable heat source/sink term $q$ is defined as follows (Khan et al., 2022c; Rawia et al., 2022):

$q=\frac{u_w\left(x\right)k_{hnf}}{{\nu }_{hnf}x}\left(S_p\left(T_w-T_{\infty }\right)f^{\prime }+H_s\left(T-T_{\infty }\right)\right).(8)$

In the aforementioned equation, $S_p$ is the space factor and $H_s$ is the heat sink/source factor.

Substituting Eqs 7, 8 in Eq. 4, we have

$\begin{array}{l}u\frac{\partial T}{\partial x}+w\frac{\partial T}{\partial z}+v\frac{\partial T}{\partial y}=\frac{1}{{\left(\rho C_p\right)}_{hnf}}\left(k_{hnf}\frac{{\partial }^{2}T}{\partial z^2}+\frac{16{\sigma }^{*}}{3k^{*}}\frac{\partial }{\partial z}\left(T^3\frac{\partial T}{\partial z}\right)\right)\\ +\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{u_w\left(x\right)k_{hnf}}{{\nu }_{hnf}x}\left(S_p\left(T_w-T_{\infty }\right)f^{\prime }+H_s\left(T-T_{\infty }\right)\right).\end{array}(9)$

The thermophoresis models for a nanofluid and hybrid nanofluid are appended as follows (Acharya et al., 2020), while their numerical values are assumed in Table 1.

$\left\{\begin{array}{l}\frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-\varphi \right)}^{2.5}},\hspace{0.17em}\hspace{0.17em}\frac{{\rho }_{nf}}{{\rho }_f}=\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f},\hspace{0.17em}\hspace{0.17em}\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f}=\left(1-\varphi \right)+\varphi \frac{{\left(\rho C_p\right)}_s}{{\left(\rho C_p\right)}_f},\\ \frac{k_{nf}}{k_f}=\frac{\left(k_s+2k_f\right)-2\varphi \left(k_f-k_s\right)}{\left(k_s+2k_f\right)+\varphi \left(k_f-k_s\right)},\hspace{1em}\frac{{\sigma }_{nf}}{{\sigma }_f}=1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(2+\frac{{\sigma }_s}{{\sigma }_f}\right)+\left(1-\frac{{\sigma }_s}{{\sigma }_f}\right)\varphi }.\end{array}\right\}(10)$

$\left\{\begin{array}{l}\frac{{\sigma }_{hnf}}{{\sigma }_f}=1+\frac{3\left(\frac{{\varphi }_1{\sigma }_{s1}+{\varphi }_2{\sigma }_{s2}}{{\sigma }_f}\right)-3\left({\varphi }_1+{\varphi }_2\right)}{2+\left(\frac{{\varphi }_1{\sigma }_{s1}+{\varphi }_2{\sigma }_{s2}}{\left({\varphi }_1+{\varphi }_2\right){\sigma }_f}\right)-\left(\frac{{\varphi }_1{\sigma }_{s1}+{\varphi }_2{\sigma }_{s2}}{{\sigma }_f}-\left({\varphi }_1+{\varphi }_2\right)\right)},\\ \frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{2.5}},\hspace{0.17em}\frac{{\rho }_{hnf}}{{\rho }_f}=\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\frac{{\rho }_{s1}}{{\rho }_f}+{\varphi }_2\frac{{\rho }_{s2}}{{\rho }_f},\\ \frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}=\left(1-{\varphi }_1-{\varphi }_2\right)+{\varphi }_1\frac{{\left(\rho C_p\right)}_{s1}}{{\rho }_f}+{\varphi }_2\frac{{\left(\rho C_p\right)}_{s2}}{{\rho }_f},\\ \frac{k_{hnf}}{k_f}=\frac{\frac{k_{s1}{\varphi }_1+k_{s2}{\varphi }_2}{{\varphi }_1+{\varphi }_2}+2k_f+2\left(k_{s1}{\varphi }_1+k_{s2}{\varphi }_2\right)-2\left({\varphi }_1+{\varphi }_2\right)k_f}{\frac{k_{s1}{\varphi }_1+k_{s2}{\varphi }_2}{{\varphi }_1+{\varphi }_2}+2k_f-2\left(k_{s1}{\varphi }_1+k_{s2}{\varphi }_2\right)+\left({\varphi }_1+{\varphi }_2\right)k_f}.\end{array}\right\}(11)$

TABLE 1

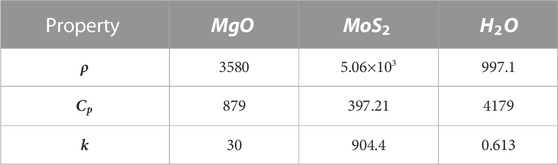
TABLE 1. Thermophysical characteristics of base fluid and nanoparticles (Mishra and Upreti, 2022).

The similarity variables are given as follows:

$\left\{\begin{array}{l}u=ax{f}^{\prime }\left(\xi \right),v=ay{g}^{\prime }\left(\xi \right),\hspace{1em}w=-\sqrt{a{\nu }_f}\left(g\left(\xi \right)+f\left(\xi \right)\right),\\ \phi \left(\xi \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\hspace{1em}\theta \left(\xi \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\hspace{1em}\xi =z\sqrt{\frac{a}{{\nu }_f}}.\end{array}\right\}(12)$

Employing Eq. 12, the governing equations are reduced as follows:

$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{f}^{‴}\left(\xi \right)+\left(g\left(\xi \right)+f\left(\xi \right)\right)f^{″}\left(\xi \right)-{\left(f^{\prime }\left(\xi \right)\right)}^2+\frac{H}{{\rho }_{hnf}/{\rho }_f}\exp \left(-\xi \alpha \right)=0,(13)$

$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{g}^{‴}\left(\xi \right)-{\left(g^{\prime }\left(\xi \right)\right)}^2+\left(g\left(\xi \right)+f\left(\xi \right)\right)g^{″}\left(\xi \right)=0,(14)$

$\begin{array}{l}\left(\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}+\frac{N}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{\left\{\left(1+\left({\theta }_w-1\right)\theta \left(\xi \right)\right)\theta \left(\xi \right)\right\}}^3\right){\theta }^{″}\left(\xi \right)+\\ \mathrm{Pr}\left(f\left(\xi \right)+g\left(\xi \right)\right){\theta }^{\prime }\left(\xi \right)+\frac{\left(k_{hnf}/k_f\right)\left({\rho }_{hnf}/{\rho }_f\right)}{\left({\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f\right)\left(\left({\mu }_{hnf}/{\mu }_f\right)\right)}\left(S_p{f}^{\prime }\left(\xi \right)+H_s\theta \left(\xi \right)\right)=0,\end{array}(15)$

$\frac{1}{Sc}{\phi }^{″}\left(\xi \right)+\left(f\left(\xi \right)+g\left(\xi \right)\right){\phi }^{\prime }\left(\xi \right)-\gamma \phi \left(\xi \right)=0,(16)$

with boundary conditions

$\left\{\begin{array}{l}f\left(\xi =0\right)=0,\hspace{1em}{f}^{\prime }\left(\xi =0\right)=1,\hspace{1em}{f}^{\prime }\left(\xi \to \infty \right)=0,\\ g\left(\xi =0\right)=0,\hspace{1em}{g}^{\prime }\left(\xi =0\right)=S,\hspace{1em}{g}^{\prime }\left(\xi \to \infty \right)=0,\\ \theta \left(\xi =0\right)=1,\hspace{1em}\theta \left(\xi \to \infty \right)=0,\\ \phi \left(\xi =0\right)=1,\hspace{1em}\phi \left(\xi \to \infty \right)=0.\end{array}\right\}(17)$

In the aforementioned equations, $\alpha \left(=\frac{\pi }{{\alpha }_0}\sqrt{\frac{{\nu }_f}{a}}\right)$ is the EMHD material parameter, $H\left(=\frac{\mu j_0{M}_0}{8a^2{\rho }_f}\right)$ is the modified Hartmann number, $S\left(=\frac{b}{a}\right)$ is the ratio parameter, $Sc\left(=\frac{{\nu }_f}{D_B}\right)$ is the Schmidt number, $\mathrm{Pr}\left(=\frac{{\left(\rho C_p\right)}_f{\nu }_f}{k_f}\right)$ is the Prandtl number, $N\left(=\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{k}_f}\right)$ is the thermal radiation factor, ${\theta }_w\left(=\frac{T_w}{T_{\infty }}\right)$ is the temperature ratio factor, and $\gamma \left(=\frac{K^{*}}{a}\right)$ is the chemical reaction factor.

2.1 Quantities of interest

The main engineering quantities of interest, skin friction ($C_{fx}$; $C_{fy}$), Nusselt number ($N{u}_x$), and Sherwood number ($S{h}_x$), are specified as follows:

$C_{fx}=\frac{{\tau }_{wx}}{{\rho }_f{\left(u_w\left(x\right)\right)}^2},\hspace{1em}{C}_{fy}=\frac{{\tau }_{wy}}{{\rho }_f{\left(v_w\left(y\right)\right)}^2},\hspace{1em}N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)},\hspace{1em}S{h}_x=\frac{x{q}_m}{D_B\left(C_w-C_{\infty }\right)},(18)$

such that

${\tau }_{wx}={\left.{\mu }_{hnf}\frac{\partial u}{\partial z}\right|}_{z=0},{\tau }_{wy}={\mu }_{hnf}{\left.\frac{\partial v}{\partial z}\right|}_{z=0},q_w=-k_{hnf}{\left.\frac{\partial T}{\partial z}\right|}_{z=0}+{\left.q_r\right|}_{z=0},q_m=-D_B{\left.\frac{\partial C}{\partial z}\right|}_{z=0}.(19)$

Using Eq. 12, we have

$\left\{\begin{array}{l}\sqrt{{\mathrm{R}\mathrm{e}}_x}{C}_{fx}=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),\sqrt{{\mathrm{R}\mathrm{e}}_y}{C}_{fy}=\frac{{\mu }_{hnf}}{{\mu }_f}{g}^{″}\left(0\right),\\ \frac{N{u}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-\left(\frac{k_{hnf}}{k_f}+N{\left(1+\left({\theta }_w-1\right)\theta \left(0\right)\right)}^3\right){\theta }^{\prime }\left(0\right),\frac{S{h}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-{\phi }^{\prime }\left(0\right).\end{array}\right\}(20)$

where ${\mathrm{R}\mathrm{e}}_x\left(=\frac{u_w\left(x\right)x}{{\nu }_f}\right)$ and ${\mathrm{R}\mathrm{e}}_y\left(=\frac{v_w\left(y\right)y}{{\nu }_f}\right)$ are the local Reynolds numbers.

3 Method of solution

To solve Eqs 13–16 with Eq. 17, we use the homotopy analysis approach (HAM) presented by Liao (1999) and Liao (2010). It is a semi-analytical approach used to find the solution of extremely nonlinear differential equations in the form of series solutions. It is a fast convergent approach for the solution of fluid problems. The initial guesses for this approach are given as follows:

$f_0\left(\xi \right)=1-\mathit{Exp}\left[-\xi \right],\hspace{1em}{g}_0\left(\xi \right)=S\left(1-\mathit{Exp}\left[-\xi \right]\right),\hspace{1em}{\theta }_0\left(\xi \right)=\mathit{Exp}\left[-\xi \right],\hspace{1em}{\phi }_0\left(\xi \right)=\mathit{Exp}\left[-\xi \right].(21)$

The linear operators are specified as follows:

$L_f\left(\xi \right)=\frac{{\partial }^{3}f}{\partial {\xi }^3}-\frac{\partial f}{\partial \xi },\hspace{1em}{L}_g\left(\xi \right)=\frac{{\partial }^{3}g}{\partial {\xi }^3}-\frac{\partial g}{\partial \xi },\hspace{1em}{L}_{\theta }\left(\xi \right)=\frac{{\partial }^2\theta }{\partial {\xi }^2}-\theta ,\hspace{1em}{L}_{\phi }\left(\xi \right)=\frac{{\partial }^2\phi }{\partial {\xi }^2}-\phi ,(22)$

with properties

$\left\{\begin{array}{l}{L}_f\left({\zeta }_1+{\zeta }_2\mathit{Exp}\left[-\xi \right]+{\zeta }_3\mathit{Exp}\left[\xi \right]\right)=0,\hspace{1em}{L}_g\left({\zeta }_4+{\zeta }_5\mathit{Exp}\left[-\xi \right]+{\zeta }_6\mathit{Exp}\left[\xi \right]\right)=0,\\ L_{\theta }\left({\zeta }_7\mathit{Exp}\left[-\xi \right]+{\zeta }_8\mathit{Exp}\left[\xi \right]\right)=0,\hspace{1em}{L}_{\phi }\left({\zeta }_9\mathit{Exp}\left[-\xi \right]+{\zeta }_{10}\mathit{Exp}\left[\xi \right]\right)=0,\end{array}\right\}(23)$

where ${\zeta }_1-{\zeta }_{10}$ are the constants in general solution.

These are zeroth-order problems:

$\left(1-\mathrm{{\rm H}}\right)L_f\left(f\left(\xi ;\mathrm{{\rm H}}\right)-f_0\left(\xi \right)\right)=\mathrm{{\rm H}}\mathit{\hslash }{N}_f\left(f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right),(24)$

$\left(1-\mathrm{{\rm H}}\right)L_g\left(g\left(\xi ;\mathrm{{\rm H}}\right)-g_0\left(\xi \right)\right)=\mathrm{{\rm H}}\mathit{\hslash }{N}_g\left(g\left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right)\right),(25)$

$\left(1-\mathrm{{\rm H}}\right)L_{\theta }\left(\theta \left(\xi ;\mathrm{{\rm H}}\right)-{\theta }_0\left(\xi \right)\right)=\mathrm{{\rm H}}\mathit{\hslash }{N}_{\theta }\left(\theta \left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right),(26)$

$\left(1-\mathrm{{\rm H}}\right)L_{\phi }\left(\phi \left(\xi ;\mathrm{{\rm H}}\right)-{\phi }_0\left(\xi \right)\right)=\mathrm{{\rm H}}\mathit{\hslash }{N}_{\phi }\left(\phi \left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right),(27)$

$\left\{\begin{array}{l}f\left(0;\mathrm{{\rm H}}\right)=0,\hspace{1em}{f}^{\prime }\left(0;\mathrm{{\rm H}}\right)=1,\hspace{1em}{f}^{\prime }\left(\infty ;\mathrm{{\rm H}}\right)=0,\\ g\left(0;\mathrm{{\rm H}}\right)=0,\hspace{1em}{g}^{\prime }\left(0;\mathrm{{\rm H}}\right)=S,\hspace{1em}{g}^{\prime }\left(\infty ;\mathrm{{\rm H}}\right)=0,\\ \theta \left(0;\mathrm{{\rm H}}\right)=1,\hspace{1em}\theta \left(\infty ;\mathrm{{\rm H}}\right)=0,\\ \phi \left(0;\mathrm{{\rm H}}\right)=1,\hspace{1em}\phi \left(\infty ;\mathrm{{\rm H}}\right)=0,\end{array}\right\}(28)$

where $\mathrm{{\rm H}}\in \left[01\right]$ is the embedding parameter and $\mathit{\hslash }$ is the non-zero auxiliary factor. The nonlinear operators can be written as follows:

$\begin{array}{l}{N}_f\left(f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right)=\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}f\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^3}\\ +\left(g\left(\xi ;\mathrm{{\rm H}}\right)+f\left(\xi ;\mathrm{{\rm H}}\right)\right)\frac{{\partial }^{2}f\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^2}-{\left(\frac{\partial f\left(\xi ;\mathrm{{\rm H}}\right)}{\partial \xi }\right)}^2+\frac{H}{{\rho }_{hnf}/{\rho }_f}\exp \left(-\xi \alpha \right),\end{array}(29)$

$N_g\left(g\left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right)\right)=\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}g\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^3}-{\left(\frac{\partial g\left(\xi ;\mathrm{{\rm H}}\right)}{\partial \xi }\right)}^2+\left(g\left(\xi ;\mathrm{{\rm H}}\right)+f\left(\xi ;\mathrm{{\rm H}}\right)\right)\frac{{\partial }^{2}g\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^2},(30)$

$\begin{array}{l}{N}_{\theta }\left(\theta \left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right)=\left(\begin{array}{l}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}+\frac{N}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\\ {\left\{\left(1+\left({\theta }_w-1\right)\theta \left(\xi ;\mathrm{{\rm H}}\right)\right)\theta \left(\xi ;\mathrm{{\rm H}}\right)\right\}}^3\end{array}\right)\frac{{\partial }^2\theta \left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^2}\\ +\mathrm{Pr}\left(f\left(\xi ;\mathrm{{\rm H}}\right)+g\left(\xi ;\mathrm{{\rm H}}\right)\right)\frac{\partial \theta \left(\xi ;\mathrm{{\rm H}}\right)}{\partial \xi }+\frac{\left(k_{hnf}/k_f\right)\left({\rho }_{hnf}/{\rho }_f\right)}{\left({\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f\right)\left(\left({\mu }_{hnf}/{\mu }_f\right)\right)}\left(S_p\frac{\partial f\left(\xi ;\mathrm{{\rm H}}\right)}{\partial \xi }+H_s\theta \left(\xi ;\mathrm{{\rm H}}\right)\right),\end{array}(31)$

$N_{\phi }\left(\phi \left(\xi ;\mathrm{{\rm H}}\right),f\left(\xi ;\mathrm{{\rm H}}\right),g\left(\xi ;\mathrm{{\rm H}}\right)\right)=\frac{1}{Sc}\frac{{\partial }^2\phi \left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^2}+\left(f\left(\xi ;\mathrm{{\rm H}}\right)+g\left(\xi ;\mathrm{{\rm H}}\right)\right)\frac{\partial \phi \left(\xi ;\mathrm{{\rm H}}\right)}{\partial \xi }-\gamma \phi \left(\xi ;\mathrm{{\rm H}}\right).(32)$

For $\mathrm{{\rm H}}=0$ and $\mathrm{{\rm H}}=1$, we have

$\left\{\begin{array}{l}f\left(\xi ;0\right)=f_0\left(\xi \right),\hspace{1em}f\left(\xi ;1\right)=f\left(\xi \right),\\ g\left(\xi ;0\right)=g_0\left(\xi \right),\hspace{1em}g\left(\xi ;1\right)=g\left(\xi \right),\\ \theta \left(\xi ;0\right)={\theta }_0\left(\xi \right),\hspace{1em}\theta \left(\xi ;1\right)=\theta \left(\xi \right),\\ \phi \left(\xi ;0\right)={\phi }_0\left(\xi \right),\hspace{1em}\phi \left(\xi ;1\right)=\phi \left(\xi \right).\end{array}\right\}(33)$

Using a Taylor series expansion with respect to $\mathrm{{\rm H}}$, we have

$\left\{\begin{array}{l}f\left(\xi ;\mathrm{{\rm H}}\right)=f_0\left(\xi \right)+{\displaystyle \sum }_{m=1}^{\infty }{f}_m\left(\xi \right){\mathrm{{\rm H}}}^m,\hspace{1em}{f}_m\left(\xi \right)=\frac{1}{m!}\frac{{\partial }^{m}f\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^m}\\ g\left(\xi ;\mathrm{{\rm H}}\right)=g_0\left(\xi \right)+{\displaystyle \sum }_{m=1}^{\infty }{g}_m\left(\xi \right){\mathrm{{\rm H}}}^m,\hspace{1em}{g}_m\left(\xi \right)=\frac{1}{m!}\frac{{\partial }^{m}g\left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^m}\\ \theta \left(\xi ;\mathrm{{\rm H}}\right)={\theta }_0\left(\xi \right)+{\displaystyle \sum }_{m=1}^{\infty }{\theta }_m\left(\xi \right){\mathrm{{\rm H}}}^m,\hspace{1em}{\theta }_m\left(\xi \right)=\frac{1}{m!}\frac{{\partial }^m\theta \left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^m}\\ \phi \left(\xi ;\mathrm{{\rm H}}\right)={\phi }_0\left(\xi \right)+{\displaystyle \sum }_{m=1}^{\infty }{\phi }_m\left(\xi \right){\mathrm{{\rm H}}}^m,\hspace{1em}{\phi }_m\left(\xi \right)=\frac{1}{m!}\frac{{\partial }^m\phi \left(\xi ;\mathrm{{\rm H}}\right)}{\partial {\xi }^m}\end{array}\right\}.(34)$

These are mth-order deformation problems:

$L_f\left(f_m\left(\xi \right)-{\chi }_m{f}_{m-1}\left(\xi \right)\right)=\mathit{\hslash }{R}_m^f\left(\xi \right),(35)$

$L_g\left(g_m\left(\xi \right)-{\chi }_m{g}_{m-1}\left(\xi \right)\right)=\mathit{\hslash }{R}_m^g\left(\xi \right),(36)$

$L_{\theta }\left({\theta }_m\left(\xi \right)-{\chi }_m{\theta }_{m-1}\left(\xi \right)\right)=\mathit{\hslash }{R}_m^{\theta }\left(\xi \right),(37)$

$L_{\phi }\left({\phi }_m\left(\xi \right)-{\chi }_m{\phi }_{m-1}\left(\xi \right)\right)=\mathit{\hslash }{R}_m^{\phi }\left(\xi \right),(38)$

$\left\{\begin{array}{l}{f}_m\left(0\right)=f_m^{\prime }\left(0\right)=f_m^{\prime }\left(\infty \right)=0\\ g_m\left(0\right)=g_m^{\prime }\left(0\right)=g_m^{\prime }\left(\infty \right)=0\\ {\theta }_m\left(0\right)={\theta }_m\left(\infty \right)=0\\ {\phi }_m\left(0\right)={\phi }_m\left(\infty \right)=0\end{array}\right\},(39)$

$R_m^f\left(\xi \right)=\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{f}_{m-1}^{‴}+{\displaystyle \sum }_{n=0}^{m-1}{g}_{m-1-n}{f}_m^{″}+{\displaystyle \sum }_{n=0}^{m-1}{f}_{m-1-n}{f}_m^{″}-{(f_{m-1}^{\prime })}^2+\frac{H}{{\rho }_{hnf}/{\rho }_f}\exp \left(-\xi \alpha \right),(40)$

$R_m^g\left(\xi \right)=\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{g}_{m-1}^{‴}-{(g_{m-1}^{\prime })}^2+{\displaystyle \sum }_{n=0}^{m-1}{g}_{m-1-n}{g}_m^{″}+{\displaystyle \sum }_{n=0}^{m-1}{f}_{m-1-n}{g}_m^{″},(41)$

$\begin{array}{l}{R}_m^{\theta }\left(\xi \right)=\left(\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}+\frac{N}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{\left\{\left(1+\left({\theta }_w-1\right){\theta }_{m-1}\right){\theta }_{m-1}\right\}}^3\right){\theta }_{m-1}^{″}\\ +{\displaystyle \sum }_{n=0}^{m-1}{f}_{m-1-n}{\theta }_m^{\prime }+{\displaystyle \sum }_{n=0}^{m-1}{g}_{m-1-n}{\theta }_m^{\prime }+\frac{\left(k_{hnf}/k_f\right)\left({\rho }_{hnf}/{\rho }_f\right)}{\left({\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f\right)\left(\left({\mu }_{hnf}/{\mu }_f\right)\right)}\left(S_p{f}_{m-1}^{″}+H_s{\theta }_{m-1}\right),\end{array}(42)$

$R_m^{\phi }\left(\xi \right)=\frac{1}{Sc}{\phi }_{m-1}^{″}+{\displaystyle \sum }_{n=0}^{m-1}{g}_{m-1-n}{\phi }_m^{\prime }+{\displaystyle \sum }_{n=0}^{m-1}{f}_{m-1-n}{\phi }_m^{\prime }-\gamma {\phi }_{m-1},(43)$

where

${\chi }_m=\left\{\begin{array}{l}0,\hspace{1em}m\le 1\\ 1,\hspace{1em}m>1\end{array}\right..(44)$

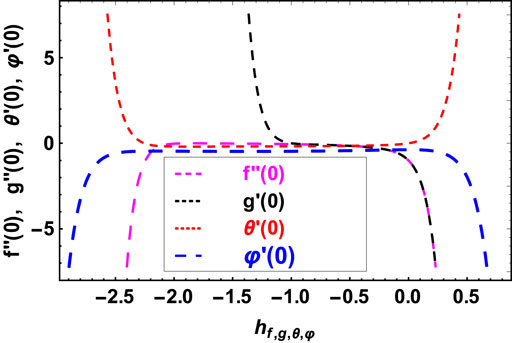
3.1 HAM convergence

HAM ensures the convergence of our series solution of the modeled equations. The auxiliary factor $\mathit{\hslash }$ plays a key role in adjusting and controlling the convergence region of the flow problem. To examine the convergence of our present model, we have plotted Figure 1. The convergence region of $f^{″}\left(0\right)$ is $-2.0\le {\mathit{\hslash }}_f\le 0.0$, $g^{″}\left(0\right)$ is $-1.0\le {\mathit{\hslash }}_g\le 0.0$, ${\theta }^{\prime }\left(0\right)$ is $-2.3\le {\mathit{\hslash }}_{\theta }\le 0.3,$ and ${\phi }^{\prime }\left(0\right)$ is $-2.5\le {\mathit{\hslash }}_{\phi }\le 0.5$.

FIGURE 1

FIGURE 1. $\mathit{\hslash }-$ curves for $f^{″}\left(0\right)$, $g^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right),$ and ${\phi }^{\prime }\left(0\right)$.

4 Validation

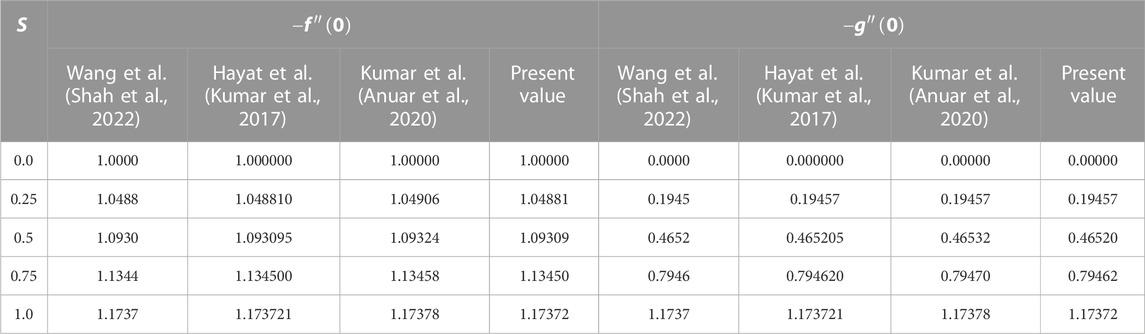
A comparative analysis was carried out, as shown in in Table 2, between the current results and the results given in Kumar et al. (2017), Anuar et al. (2020), and Shah et al. (2022). The current results have a close relationship with results previously published in the literature.

TABLE 2

TABLE 2. Comparative analysis of common factors among current and previous results for ${\varphi }_1={\varphi }_2=0$.

5 Results and discussion

This article investigates the EMHD flow of a hybrid nanofluid past a bi-directional extending surface. The fluid is influenced by nonlinear thermal radiation, chemical reactions, and a variable heat source. The set of equations that administered the fluid behavior has been transformed to dimensionless form by applying appropriate similarity variables. The impacts of various substantial parameters on the flow profiles are discussed in the following paragraphs.

Figure 2 depicts the influences of the Hartmann number on fluid velocity. It is observed that the higher values of $H$ increase the velocity profile. The higher $H$ intensity of the electric field enhances the parallel Lorentz force, and, as a result, the velocity of the hybrid nanofluid flow enhances. This shows that along the x-direction, the velocity gets support from the parallel Lorentz force. Therefore, the velocity profile of the hybrid nanofluid flow enhances with the greater $H$.

FIGURE 2

FIGURE 2. Impact of $H$ on $f^{\prime }\left(\xi \right)$.

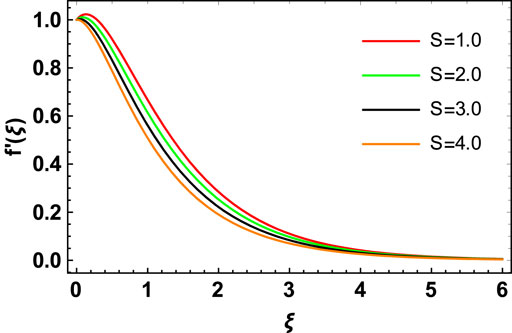
Figures 3, 4 show the impact of $S$ on $f^{\prime }\left(\xi \right)$ and $g^{\prime }\left(\xi \right)$. It is observed that $S$ is a retarding function of $f^{\prime }\left(\xi \right)$ and an augmenting function of $g^{\prime }\left(\xi \right)$. Physically, the increasing values of $S$ support the skin friction at the surface of the Riga plate by extending more friction to the fluid motion in its opposite direction at the surface. The reason for this is that the ratio parameter $S$ is in a direct relationship with the fluid velocity in the y-direction and in a reverse relationship in the x-direction. Hence, a retarding impact was noted in $f^{\prime }\left(\xi \right),$ and an augmenting effect was observed in $g^{\prime }\left(\xi \right)$.

FIGURE 3

FIGURE 3. Impact of $S$ on $f^{\prime }\left(\xi \right)$.

FIGURE 4

FIGURE 4. Impact of $S$ on $g^{\prime }\left(\xi \right)$.

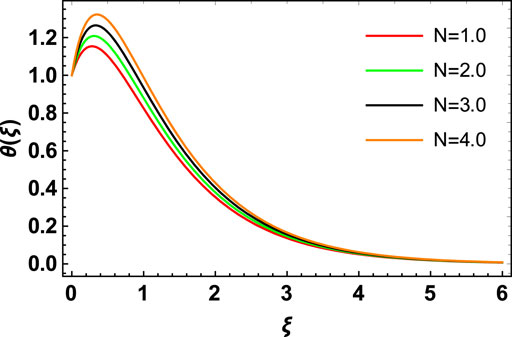
The behavior of temperature flow due to the increase in the nonlinear thermal radiation factor $N$ is depicted in Figure 5. We see that with the increase in $N$, the thermal profile increases. With growing values of $N$, maximum thermal diffusions occur at the surface of the Riga plate due to the electrical and magnetic characteristics at the surface. Hence, an increase in $N$ results in an expansion in the thermal distribution, as depicted in Figure 5.

FIGURE 5

FIGURE 5. Impact of $N$ on $\theta \left(\xi \right)$.

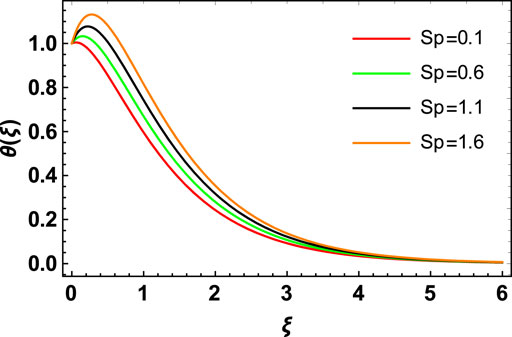
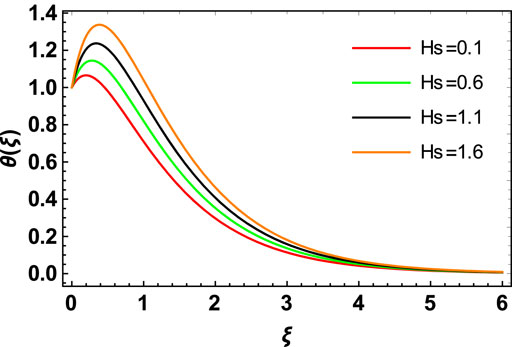
The influence of the space factor $S_p$ and the heat source/sink factor $H_S$ on temperature distribution is depicted in Figures 6, 7. Note that for the positive values of $S_p$ and $H_S$, both behave as a heat generation source. Furthermore, the presence of a heat source factor discharges the energy to the fluid flow system. This released energy augments the temperature boundary layer, and consequently, the temperature distribution increases.

FIGURE 6

FIGURE 6. Impact of $S_p$ on $\theta \left(\xi \right)$.

FIGURE 7

FIGURE 7. Impact of $H_S$ on $\theta \left(\xi \right)$.

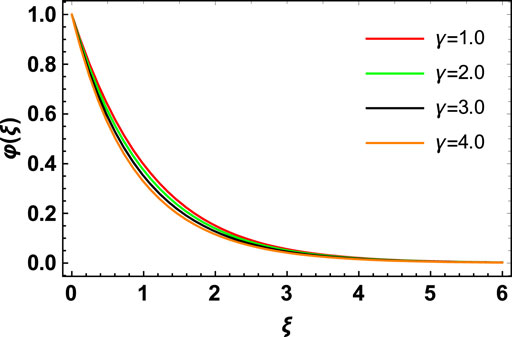
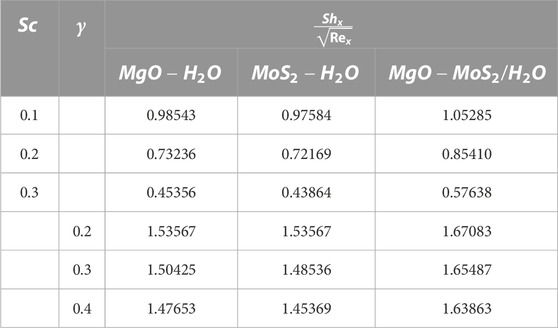
The effect of the chemical reactant factor $\gamma$ on the concentration profile is shown in Figure 8. The higher chemical reaction factor reduces the concentration profile of the hybrid nanofluid flow.

FIGURE 8

FIGURE 8. Impact of $\gamma$ on $\phi \left(\xi \right)$.

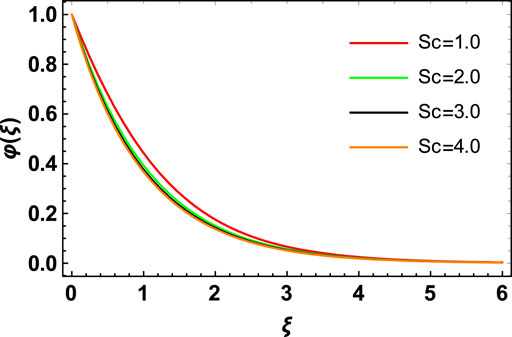
The behavior of concentration characteristic in response to the variation in Schmidt number $Sc$ is shown in Figure 9, which shows that the concentration profile reduces with the higher values of $Sc$. Note that $Sc$ has an adverse impact upon the concentration characteristics. Physically, with higher values of $Sc$, the mass diffusivity reduces, while the kinetic viscosity of fluid enhances, causing the declination in the mass profile. The fluid particles at the surface of the Riga plate with greater values of $Sc$ defuse less, due to which less mass transmission occurs. As a result, the concentration characteristic diminishes gradually, as portrayed in Figure 9.

FIGURE 9

FIGURE 9. Impact of $Sc$ on $\phi \left(\xi \right)$.

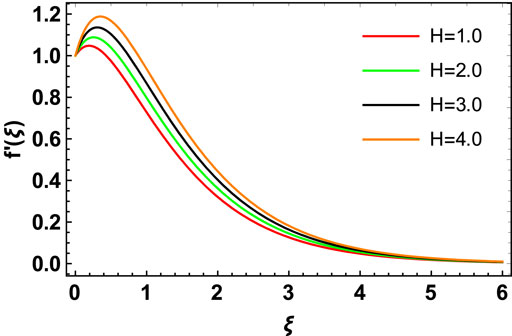
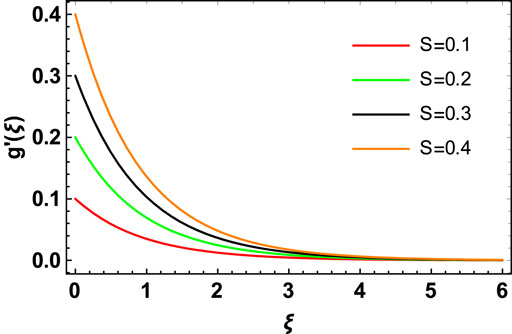
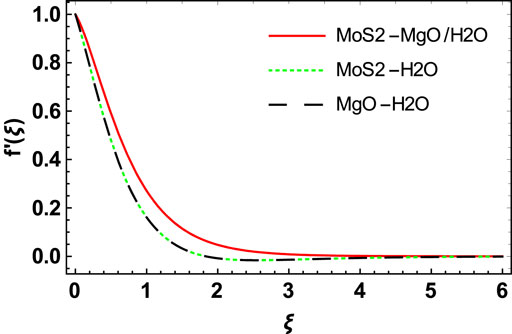
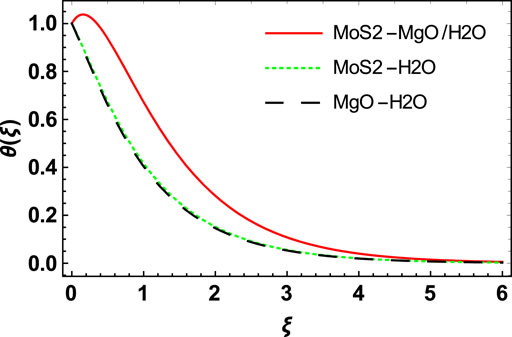
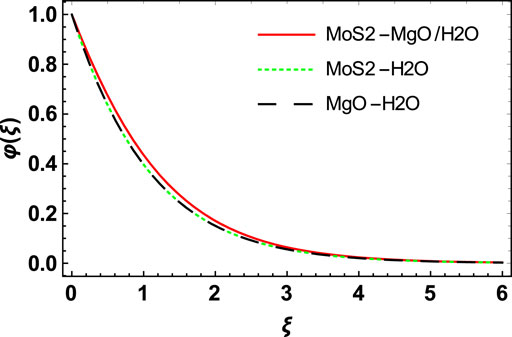
Figures 10, 11 depict the behavior of velocity profiles of the $MgO-H_{2}O$ nanofluid, the $Mo{S}_2-H_{2}O$ nanofluid, and the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid. In the case of the $MgO-H_{2}O$ and $Mo{S}_2-H_{2}O$ nanofluids, there are the same variations in velocity characteristics at the surface of the Riga plate. However, in the case of the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid, the behavior is different. Fluid motion is higher for the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid flow than the $Mo{S}_2-H_{2}O$ and $MgO-H_{2}O$ nanofluid flows, as depicted in Figures 10, 11.

FIGURE 10

FIGURE 10. Velocity profile ($f^{\prime }\left(\xi \right)$) for the comparison of $Mo{S}_2-MgO/H_{2}O$, $Mo{S}_2-H_{2}O$, and $MgO-H_{2}O$.

FIGURE 11

FIGURE 11. Velocity profile ($g^{\prime }\left(\xi \right)$) for the comparison of $Mo{S}_2-MgO/H_{2}O$, $Mo{S}_2-H_{2}O$, and $MgO-H_{2}O$.

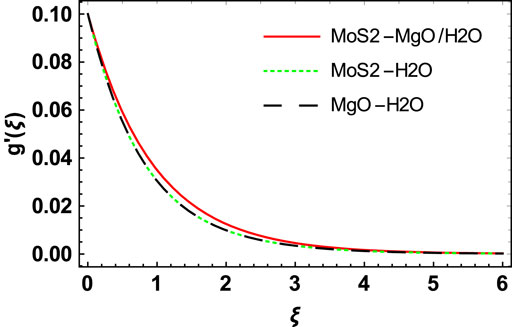
Similarly, from Figures 12, 13, we see that the behavior of temperature and concentration profiles for the $MgO-H_{2}O$, $Mo{S}_2-H_{2}O$,and $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluids are quite different. For the $MgO-H_{2}O$ and the $Mo{S}_2-H_{2}O$ nanofluids, there are some variations in temperature and concentration characteristics at the surface of the Riga plate. However, in the case of the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid flow, more heat transfer is offered to flow particles. Hence, the temperature is increased more in the case of the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid flow, as depicted in Figure 12. The reason is that the hybrid nanofluid flow has greater thermal conductivity than the two other nanofluids. Similarly, the concentration boundary layer thickness is largest in the case of the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid flow when compared to the $MgO-H_{2}O$ and $Mo{S}_2-H_{2}O$ nanofluids. Hence, the concentration profile is higher in the case of the $Mo{S}_2-MgO/H_{2}O$ hybrid nanofluid flow. The reason is that the hybrid nanofluid flow has more mass transfer rate than the other two nanofluids, as shown in Figure 13.

FIGURE 12

FIGURE 12. Temperature profile (${\theta }^{\prime }\left(\xi \right)$) for the comparison of $Mo{S}_2-MgO/H_{2}O$, $Mo{S}_2-H_{2}O$, and $MgO-H_{2}O$.

FIGURE 13

FIGURE 13. Concentration profile (${\phi }^{\prime }\left(\xi \right)$) for the comparison of $Mo{S}_2-MgO/H_{2}O$, $Mo{S}_2-H_{2}O$, and $MgO-H_{2}O$.

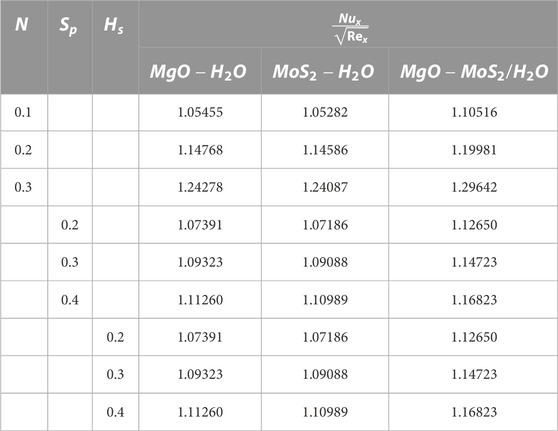
Table 1 portrays the numerical values of different thermophysical characteristics. Table 3 depicts the influences of nonlinear thermal radiation $N$, space factor $S_p,$ and a heat source/sink factor $H_S$ on the Nusselt number in the case of the $MgO-H_{2}O$ nanofluid, the $Mo{S}_2-H_{2}O$ nanofluid, and the $MgO-Mo{S}_2/H_{2}O$ hybrid nanofluid. With growing values of $N$, the maximum thermal diffusions occur at the surface of the Riga plate due to the electric and magnetic characteristics at the surface. Hence, amplification in the values of $N$ results in an increase in the Nusselt number. Similarly, an increase in the space factor $S_p$ and heat source/sink factor $H_S$ causes an increase in the Nusselt number. Growth in the Nusselt number in the case of the $MgO-Mo{S}_2/H_{2}O$ hybrid nanofluid is greater than in the $MgO-H_{2}O$ and $Mo{S}_2-H_{2}O$ nanofluids. In Table 4, the impacts of the chemical reactant factor $\gamma$ and the Schmidt number $Sc$ are shown on the Sherwood number. With the increase in $\gamma$, the solutal molecules grow and cause mass diffusions. Hence, growth in $\gamma$ causes a decline in the values of the Sherwood number. Similarly, with higher values of $Sc$, less mass transmission occurs; as a result, the Sherwood number decreases gradually.

TABLE 3

TABLE 3. Impacts of different physical factors on the Nusselt number.

TABLE 4

TABLE 4. Influence of $\gamma$ and $Sc$ on the Sherwood number.

6 Conclusion

This work investigates hybrid nanofluid flow past a bi-directional stretching surface. The hybrid nanofluid flow is affected by thermal radiation, chemical reactions, and a variable thermal source/sink. The set of equations that administer the hybrid nanofluid flow behavior was transformed to a dimensionless form by suitable similarity transformations. After a comprehensive analysis, the following points are noted.

a) Because the increase in the Hartmann number augments the strength of the electrical field externally, the behavior of the wall Lorentz force increases the decrease in the velocity of the fluid.

b) The ratio parameter has a direct relationship with the hybrid nanofluid flow velocity in the y-direction and a reverse relationship in the x-direction. Hence, a retarding impact was noted on the primary velocity, and an augmenting effect was observed on the secondary velocity.

c) With growing values of the nonlinear thermal radiation factor, the maximum thermal diffusions occur at the surface of the Riga plate. Hence, augmentation of the radiation factor results in an increase in the thermal distribution.

d) The space factor and heat source/sink factor behave as a heat generator and a heat absorption point, respectively, in the flow system; hence, an increase in these factors increases the temperature of hybrid nanofluid flow.

e) Increases in the chemical reaction factor and the Schmidt number have an opposing effect on the concentration distribution of the hybrid nanofluid flow.

f) Temperature and concentration increase more rapidly for the hybrid nanofluid than the other two nanofluids.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

EA and SL: conceptualization, methodology, software, reviewing and editing. ZR: data curation and writing—original draft preparation. SE: visualization and investigation. AS: software, validation, and supervision. AG: writing—reviewing and editing.

Acknowledgments

The author (ZR) extends her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP.1/334/43).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acharya, N., Bag, R., and Kundu, P. K. (2020). On the impact of nonlinear thermal radiation on magnetized hybrid condensed nanofluid flow over a permeable texture. Appl. Nanosci. 10, 1679–1691. doi:10.1007/s13204-019-01224-w

CrossRef Full Text | Google Scholar

Acharya, N., Mabood, F., Shahzad, S. A., and Badruddin, I. A. (2022). Hydrothermal variations of radiative nanofluid flow by the influence of nanoparticles diameter and nanolayer. Int. Commun. Heat. Mass Transf. 130, 105781. doi:10.1016/J.ICHEATMASSTRANSFER.2021.105781

CrossRef Full Text | Google Scholar

Ahmad, A., Asghar, S., and Afzal, S. (2016). Flow of nanofluid past a Riga plate. J. Magn. Magn. Mat. 402, 44–48. doi:10.1016/j.jmmm.2015.11.043

CrossRef Full Text | Google Scholar

Alharbi, S. O., Dawar, A., Shah, Z., Khan, W., Idrees, M., Islam, S., et al. (2018). Entropy generation in MHD eyring-powell fluid flow over an unsteady oscillatory porous stretching surface under the impact of thermal radiation and heat source/sink. Appl. Sci. 2, 2588. doi:10.3390/app8122588

CrossRef Full Text | Google Scholar

Alhowaity, A., Bilal, M., Hamam, H., Alqarni, M. M., Mukdasai, K., and Ali, A. (2022). Non-Fourier energy transmission in power-law hybrid nanofluid flow over a moving sheet. Sci. Rep. 12, 10406. doi:10.1038/s41598-022-14720-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, L., Wang, Y., Ali, B., Liu, X., Din, A., and Al Mdallal, Q. (2021). The function of nanoparticle’s diameter and Darcy-Forchheimer flow over a cylinder with effect of magnetic field and thermal radiation. Case Stud. Therm. Eng. 28, 101392. doi:10.1016/j.csite.2021.101392

CrossRef Full Text | Google Scholar

. Alqarni, M. S. (2022). Thermo-bioconvection flow of Walter’s B nanofluid over a Riga plate involving swimming motile microorganisms. Aimspress. Com. 7, 16231–16248. doi:10.3934/math.2022886

CrossRef Full Text | Google Scholar

Alwawi, F., Alkasasbeh, H., Rashad, A., and Idris, R. (2020). MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. Results Phys. 16, 102818. doi:10.1016/j.rinp.2019.102818

CrossRef Full Text | Google Scholar

Anuar, N. S., Bachok, N., Turkyilmazoglu, M., Arifin, N. M., and Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alex. Eng. J. 59, 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Asogwa, K. K., Mebarek-Oudina, F., and Animasaun, I. L. (2022). Comparative investigation of water-based Al₂O₃ nanoparticles through water-based CuO nanoparticles over an exponentially accelerated radiative Riga plate surface via heat transport. Arab. J. Sci. Eng. 47, 8721–8738. doi:10.1007/s13369-021-06355-3

CrossRef Full Text | Google Scholar

Bhatti, M. M., Arain, M. B., Zeeshan, A., Ellahi, R., and Doranehgard, M. H. (2022). Swimming of Gyrotactic Microorganism in MHD Williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage. 45, 103511. doi:10.1016/j.est.2021.103511

CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in Int. Mech. Eng. Congr. Exhib. San Fr, CA United States, 12-17 Nov 1995.

Google Scholar

Eid, M. R., and Nafe, M. A. (2022). Thermal conductivity variation and heat generation effects on magneto-hybrid nanofluid flow in a porous medium with slip condition. Waves Random Complex Media 32, 1103–1127. doi:10.1080/17455030.2020.1810365

CrossRef Full Text | Google Scholar

El-Zahar, E. R., El Nasser Mahdy, A., Rashad, A. M., Saad, W., and Seddek, L. F. (2021). Unsteady MHD mixed convection flow of Non-Newtonian Casson hybrid nanofluid in the stagnation zone of sphere spinning impulsively. Fluids 6, 197. doi:10.3390/fluids6060197

CrossRef Full Text | Google Scholar

El-Zahar, E., Rashad, A., Rashad, A. M., and Al-Juaydi, H. S. (2022). Studying massive suction impact on magneto-flow of a hybridized casson nanofluid on a porous continuous moving or fixed surface. Symmetry 14, 627. doi:10.3390/sym14030627

CrossRef Full Text | Google Scholar

Gangadhar, K., Kumari, M. A., and Chamkha, A. J. (2021). EMHD flow of radiative second-grade nanofluid over a Riga plate due to convective heating: Revised buongiorno’s nanofluid model. Arab. J. Sci. Eng. 47, 8093–8103. doi:10.1007/s13369-021-06092-7

CrossRef Full Text | Google Scholar

Hamarsheh, A., Alwawi, F., Alkasasbeh, H. T., and Rashad, A. M. (2020). Heat transfer improvement in MHD natural convection flow of graphite oxide/carbon nanotubes-methanol based casson nanofluids past a horizontal circular cylinder. Processes 8, 1444. doi:10.3390/pr8111444

CrossRef Full Text | Google Scholar

Haq, I., Bilal, M., Ahammad, N. A., Ghoneim, M. E., Ali, A., and Weera, W. (2022). Mixed convection nanofluid flow with heat source and chemical reaction over an inclined irregular surface. ACS Omega 7, 30477–30485. doi:10.1021/acsomega.2c03919

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayat, T., Shehzad, S. A., and Alsaedi, A. (2013). Three-dimensional stretched flow of Jeffrey fluid with variable thermal conductivity and thermal radiation. Appl. Math. Mech. 34, 823–832. doi:10.1007/s10483-013-1710-7

CrossRef Full Text | Google Scholar

Ijaz, M., Nadeem, S., Ayub, M., and Mansoor, S. (2021). Simulation of magnetic dipole on gyrotactic ferromagnetic fluid flow with nonlinear thermal radiation. J. Therm. Anal. Calorim. 143, 2053–2067. doi:10.1007/s10973-020-09856-9

CrossRef Full Text | Google Scholar

Khader, M. M., and Sharma, R. P. (2021). Evaluating the unsteady MHD micropolar fluid flow past stretching/shirking sheet with heat source and thermal radiation: Implementing fourth order predictor–corrector FDM. Math. Comput. Simul. 181, 333–350. doi:10.1016/j.matcom.2020.09.014

CrossRef Full Text | Google Scholar

Khan, A., Hassan, B., Ashraf, E. E., and Shah, S. Y. A. (2022). Thermally dissipative micropolar hybrid nanofluid flow over a spinning needle influenced by Hall current and gyrotactic microorganisms. Heat. Transf. 51, 1170–1192. doi:10.1002/htj.22347

CrossRef Full Text | Google Scholar

Khan, U., Ishak, A., and Zaib, A. (2021). Hybrid nanofluid flow containing single-wall and multi-wall CNTs induced by a slender stretchable sheet. Chin. J. Phys. 74, 350–364. doi:10.1016/j.cjph.2021.10.009

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Abu Bakar, S., Animasaun, I. L., and Yook, S-J. (2022). Insights into the dynamics of blood conveying gold nanoparticles on a curved surface when suction, thermal radiation, and Lorentz force are significant: The case of of Non-Newtonian Williamson fluid. Math. Comput. Simul. 193, 250–268. doi:10.1016/j.matcom.2021.10.014

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Sherif, E.-S. M., Waini, I., Chu, Y.-M., et al. (2022). Radiative mixed convective flow induced by hybrid nanofluid over a porous vertical cylinder in a porous media with irregular heat sink/source. Case Stud. Therm. Eng. 30, 101711. doi:10.1016/j.csite.2021.101711

CrossRef Full Text | Google Scholar

Kumar, K. G., Rudraswamy, N. G., and Gireesha, B. J. (2017). Effects of mass transfer on MHD three dimensional flow of a Prandtl liquid over a flat plate in the presence of chemical reaction. Results Phys. 7, 3465–3471. doi:10.1016/j.rinp.2017.08.060

CrossRef Full Text | Google Scholar

Li, Y.-X., Alqsair, U. F., Ramesh, K., Khan, S. U., and Khan, M. I. (2022). Nonlinear heat source/sink and activation energy assessment in double diffusion flow of micropolar (non-Newtonian) nanofluid with convective conditions. Arab. J. Sci. Eng. 47, 859–866. doi:10.1007/s13369-021-05692-7

CrossRef Full Text | Google Scholar

Liao, S. (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 15, 2003–2016. doi:10.1016/j.cnsns.2009.09.002

CrossRef Full Text | Google Scholar

Liao, S.-J. (1999). An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non. Linear. Mech. 34, 759–778. doi:10.1016/s0020-7462(98)00056-0

CrossRef Full Text | Google Scholar

Lielausis, O. (1961). On a possibility to reduce the hydrodynamic resistance of a plate in an electrolyte. Appl. Magnetohydrodyn. 12, 143–146.

Google Scholar

Manzoor, U., Imran, M., Muhammad, T., Waqas, H., and Alghamdi, M. (2021). Heat transfer improvement in hybrid nanofluid flow over a moving sheet with magnetic dipole. Waves Random Complex Media, 1–15. doi:10.1080/17455030.2021.1991602

CrossRef Full Text | Google Scholar

Mishra, A., and Upreti, H. (2022). A comparative study of Ag–MgO/water and Fe3O4–CoFe2O4/EG–water hybrid nanofluid flow over a curved surface with chemical reaction using Buongiorno model. Partial Differ. Equations Appl. Math. 5, 100322. doi:10.1016/j.padiff.2022.100322

CrossRef Full Text | Google Scholar

Muhammad, T., Waqas, H., Khan, S. A., Ellahi, R., and Sait, S. M. (2021). Significance of nonlinear thermal radiation in 3D Eyring–Powell nanofluid flow with Arrhenius activation energy. J. Therm. Anal. Calorim. 143, 929–944. doi:10.1007/s10973-020-09459-4

CrossRef Full Text | Google Scholar

Ojjela, O. (2022). Numerical investigation of heat transport in Alumina–Silica hybrid nanofluid flow with modeling and simulation. Math. Comput. Simul. 193, 100–122. doi:10.1016/j.matcom.2021.09.022

CrossRef Full Text | Google Scholar

Rahman, M., Sharif, F., Turkyilmazoglu, M., and Siddiqui, M. S. (2022). Unsteady three-dimensional magnetohydrodynamics flow of nanofluids over a decelerated rotating disk with uniform suction. Pramana 96, 170. doi:10.1007/s12043-022-02404-0

CrossRef Full Text | Google Scholar

Ram, M. S., Spandana, K., Shamshuddin, M., and Salawu, S. O. (2022). Mixed convective heat and mass transfer in magnetized micropolar fluid flow toward stagnation point on a porous stretching sheet with heat source/sink and variable species reaction. Int. J. Model. Simul., 1–13. doi:10.1080/02286203.2022.2112008

CrossRef Full Text | Google Scholar

Rawia, N. A., Alib, A., Rubaa’ic, A. F. A., and Shafied, S. (2022). The effect of non-uniform heat source/sink on mixed convection flow of hybrid nanofluid over A stretching sheet. Proceeding Sci. Math. 7, 56.

Google Scholar

Sabir, Z., Imran, A., Umar, M., Zeb, M., Shoaib, M., and Raja, M. A. Z. (2021). A numerical approach for 2-D Sutterby fluid-flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm. Sci. 25, 1975–1987.

Google Scholar

Saeed, A., Jawad, M., Alghamdi, W., Nasir, S., Gul, T., and Kumam, P. (2021). Hybrid nanofluid flow through a spinning Darcy–Forchheimer porous space with thermal radiation. Sci. Rep. 11, 16708. doi:10.1038/s41598-021-95989-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Saleh, B., Madhukesh, J. K., Varun Kumar, R. S., Afzal, A., Abdelrhman, Y., Aly, A. A., et al. (2022). Aspects of magnetic dipole and heat source/sink on the Maxwell hybrid nanofluid flow over a stretching sheet. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng., 09544089211056243.

CrossRef Full Text | Google Scholar

Shafiq, A., Mebarek-Oudina, F., Sindhu, T. N., and Abidi, A. (2021). A study of dual stratification on stagnation point Walters’ B nanofluid flow via radiative Riga plate: A statistical approach. Eur. Phys. J. Plus. 136, 407–424. doi:10.1140/epjp/s13360-021-01394-z

CrossRef Full Text | Google Scholar

Shah, N. A., Wakif, A., El-Zahar, E. R., Ahmad, S., and Yook, S.-J. (2022). Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG),(40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 35, 102046. doi:10.1016/j.csite.2022.102046

CrossRef Full Text | Google Scholar

Shah, Z., Khan, A., Khan, W., Alam, M. K., Islam, S., Kumam, P., et al. (2020). Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Comput. Methods Programs Biomed. 186, 105197. doi:10.1016/j.cmpb.2019.105197

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahid, A., Bhatti, M. M., Ellahi, R., and Mekheimer, K. S. (2022). Numerical experiment to examine activation energy and bi-convection Carreau nanofluid flow on an upper paraboloid porous surface: Application in solar energy. Sustain. Energy Technol. Assessments. 52, 102029. doi:10.1016/j.seta.2022.102029

CrossRef Full Text | Google Scholar

Shamshuddin, M. D., Mabood, F., and Bég, O. A. (2021). Thermomagnetic reactive ethylene glycol-metallic nanofluid transport from a convectively heated porous surface with Ohmic dissipation, heat source, thermophoresis and Brownian motion effects. Int. J. Model. Simul., 1–15.

CrossRef Full Text | Google Scholar

Sharma, B. K., Kumar, A., Gandhi, R., and Bhatti, M. M. (2022). Exponential space and thermal-dependent heat source effects on electro-magneto-hydrodynamic Jeffrey fluid flow over a vertical stretching surface. Int. J. Mod. Phys. B 36, 2250220. doi:10.1142/s0217979222502204

CrossRef Full Text | Google Scholar

Sravanthi, C. S. (2020). Second order velocity slip and thermal jump of Cu–water nanofluid over a cone in the presence of nonlinear radiation and nonuniform heat source/sink using homotopy analysis method. Heat. Transf. - Asian Res. 49, 86–102. doi:10.1002/HTJ.21600

CrossRef Full Text | Google Scholar

Tarakaramu, N., Satya Narayana, P. V., Sivajothi, R., Bhagya Lakshmi, K., Harish Babu, D., and Venkateswarlu, B. (2022). Three-dimensional non-Newtonian couple stress fluid flow over a permeable stretching surface with nonlinear thermal radiation and heat source effects. Heat. Transf. 51, 5348–5367. doi:10.1002/htj.22550

CrossRef Full Text | Google Scholar

Thumma, T., Mishra, S., Abbas, A. M., and Bhatti, M. M. (2022). Three-dimensional nanofluid stirring with non-uniform heat source/sink through an elongated sheet. Appl. Math. Comput. 421, 126927. doi:10.1016/j.amc.2022.126927

CrossRef Full Text | Google Scholar

Tlili, I., Naseer, S., Ramzan, M., Kadry, S., and Nam, Y. (2020). Effects of chemical species and nonlinear thermal radiation with 3D Maxwell nanofluid flow with double stratification—An analytical solution. Entropy 22, 453. doi:10.3390/e22040453

PubMed Abstract | CrossRef Full Text | Google Scholar

Ullah, I., Alajlani, Y., Pasha, A. A., Adil, M., and Weera, W. (2022). Theoretical investigation of hybrid nanomaterials transient flow through variable feature of Darcy–Forchheimer space with exponential heat source and slip condition. Sci. Rep. 12, 15085. doi:10.1038/s41598-022-17988-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahid, N. S., Arifin, N. M., Turkyilmazoglu, M., Hafidzuddin, M. E. H., and Abd Rahmin, N. A. (2020). “MHD hybrid Cu-Al₂O₃/water nanofluid flow with thermal radiation and partial slip past a permeable stretching surface: Analytical solution,” in J. Nano res. (Switzerland: Trans Tech Publ).

Google Scholar

Waini, I., Khan, U., Zaib, A., Ishak, A., and Pop, I. (2022). Inspection of TiO₂-CoFe₂O₄ nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J. Mol. Liq. 361, 119615. doi:10.1016/J.MOLLIQ.2022.119615

CrossRef Full Text | Google Scholar

Wang, C. Y. (1984). The three-dimensional flow due to a stretching flat surface. Phys. Fluids. 27, 1915–1917. doi:10.1063/1.864868

CrossRef Full Text | Google Scholar

Waseem, M., Gul, T., Khan, I., Khan, A., Saeed, A., Ali, I., et al. (2021). Gravity-driven hydromagnetic flow of couple stress hybrid nanofluid with homogenous-heterogeneous reactions. Sci. Rep. 11, 17498–17512. doi:10.1038/s41598-021-97045-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zabihi, A., Akinshilo, A. T., Rezazadeh, H., Ansari, R., Sobamowo, M. G., and Tunç, C. (2022). Application of variation of parameter’s method for hydrothermal analysis on MHD squeezing nanofluid flow in parallel plates. Comput. Methods Differ. Equations. 10, 580–594.

Google Scholar

Zabihi, A., Ansari, R., Hosseini, K., Samadani, F., and Torabi, J. (2020). Nonlinear pull-in instability of rectangular nanoplates based on the positive and negative second-order strain gradient theories with various edge supports. Z. Für Naturforsch. A 75, 317–331. doi:10.1515/zna-2019-0356

CrossRef Full Text | Google Scholar

Zabihi, A., Torabi, J., and Ansari, R. (2020). Effects of geometric nonlinearity on the pull-in instability of circular microplates based on modified strain gradient theory. Phys. Scr. 95, 115204. doi:10.1088/1402-4896/abba4e

CrossRef Full Text | Google Scholar

Zhang, L., Bhatti, M. M., Michaelides, E. E., Marin, M., and Ellahi, R. (2022). Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 231, 521–533. doi:10.1140/epjs/s11734-021-00409-1

CrossRef Full Text | Google Scholar

Nomenclature

${\mathit{T}}_{\mathit{w}}$ surface temperature

${\mathit{u}}_{\mathit{w}}$ stretching velocity

M magnetic factor

${\mathit{q}}_{\mathit{r}}$ radiative heat flux

$\mathit{q}$ variable heat source/sink

${\mathit{S}}_{\mathit{p}}\mathbf{a}\mathbf{n}\mathbf{d}{\mathit{H}}_{\mathit{s}}$ space and heat factors

${\mathit{k}}^{*}$ Stefan–Boltzmann constant

Sc Schmidt number

N nonlinear thermal radiation

$\mathit{\gamma }$ chemical reaction

${\mathit{C}}_{\mathit{p}}$ specific heat

MgO magnesium oxide

$\mathit{M}\mathit{o}{\mathit{S}}_{\mathbf{2}}$ molybdenum disulfide

(${\mathit{C}}_{\mathit{f}\mathit{x}}$; ${\mathit{C}}_{\mathit{f}\mathit{y}}$) skin frictions

${\mathit{\nu }}_{\mathit{f}}$ kinematic viscosity

$\mathit{\theta }\left(\mathit{\xi }\right)$ temperature profile

${\mathit{C}}_{\mathit{w}}$ surface concentration

${\mathit{E}}_{\mathit{I}\mathit{J}}$ rate of deformation

${\mathit{j}}_{\mathbf{0}}$ electrode current density

$\mathit{\rho }$ density

${\mathit{\sigma }}^{*}$ mean absorption coefficient

$\mathit{\alpha }$ EMHD factor

H modified Hartmann number

S ratio parameter

Pr Prandtl number

${\mathit{\theta }}_{\mathit{w}}$ temperature ratio parameter

$\mathit{k}$ thermal diffusivity

${\mathit{H}}_{\mathbf{2}}\mathit{O}$ water

$\mathit{N}{\mathit{u}}_{\mathit{x}}$ Nusselt number

$\mathit{S}{\mathit{h}}_{\mathit{x}}$ Sherwood number

Re Reynold number

${\mathit{f}}^{\prime }\left(\mathit{\zeta }\right)$ velocity profile