Numerical computation for dual stratification of slip flow of sutterby nanofluids with heat generation features

The current communication, manifest mathematical modelling and numerical computations of Sutterby nanofluids with radiant heat assessment subject to heat generation/absorption. The thermophoresis and Brownian motion effects are incorporated via the Buongiorno model in flow governing equations. Moreover, the present analysis reveals the impacts of thermal stratification, velocity slip, and a magnetic field on flow phenomena. The non-Newtonian nature is modelled using Sutterby fluid. The proposed model is formulated mathematically through basic partial differential equations relating mass, momentum, energy, and nanoparticle concentration conservations using boundary layer theory. We adapted the generated governed equations to ordinary differential equations utilizing similarity variables mechanism. Numerical treatment for the reduced system of ordinary differential equations is performed using the built-in MATLAB code bvp4c. The impacts of distinct characterizing parameters on velocity, temperature, and concentration profiles are determined and analyzed via graphs. The existence of velocity slip parameter, fluid flow is significantly dwindle, while the surface friction growth is sophisticated. Brownian and thermophoresis mechanisms degrade the heat transmission rate and escalate the mass flux. The thermal and solutal stratification exhibits opposite conduct for thermal and concentration of the nanoparticles.

1 Introduction

In the era of ever-increasing high demand for the improved thermal capabilities of ordinary fluids, like water, glycol, ethylene, etc., nanotechnology is an opening gate for a revolutionary modernized world. Nanofluids are a new generation of heat enhancement fluids with tiny metallic particles (1–100 nm) mixed in the ordinary fluids, thereby enhancing their thermal characteristics significantly. These particles consist of different metals (copper, gold, silver, titanium, etc.) or their oxides. They have novel implications in biomedical and engineering sciences, along with other industrial processes where heat transfer enhancement is prominent. The nanofluids have a wide range of uses in transportation, nuclear reactors, vehicle thermal applications, solar-based science, imaging and sensing applications, food packaging, etc. Choi (Choi, 1995) was the first to describe this type of fluid, which he dubbed “nanofluids”. Xuan and Li (Xuan and Li, 2000) developed preparatory techniques for multiple sampling nanoparticles, and their thermophysical properties, such as, shape, amount, attributes, and dimensions were investigated. Buongiorno (Buongiorno, 2006) discussed the significance of a heterogeneous scientific mixture of nanomaterial processing stimulus and heat transport limits. Later, Kuznetsov an d Nield (Kuznetsov and Nield, 2010) conducted an analytic study for natural convective flow of viscous nanofluids across a vertical flat surface. Makinde and Aziz (Makinde and Aziz, 2011) discussed the convective heat transport for boundary layer flow of nanofluid generated by a linearly stretched surface. In another study, Mustafa et al. (Mostafa et al., 2011) reported an analytic investigation for stagnation-point flow of nanofluid using Buongiorno model. After that, Ibrahim et al. (Ibrahim et al., 2013) gave numerical solutions for MHD stagnation point flow generated by stretching surface in the presence of nanoparticles. The comprehensive analysis of literature in the framework of nanofluids flow and heat transport characteristics can be found in the works of (Hamad and Ferdows (Hamad and Ferdows, 2012), Kalidas Das (Das, 2012), Bachok et al. (Bachok et al., 2012), Turkyilamzoglu (Turkyilmazoglu, 2012), and Alsaedi et also (Effect of heat generation, 2012), etc.).

The fundamental manifestation of Navier-Stoke’s theory of fluid dynamics is the no-slip boundary condition. However, there seem to be cases when this scenario is inappropriate. Specifically, for several non-Newtonian fluids and nanofluids, the no-slip boundary condition is inadequate, as certain polymer melts frequently exhibit microscopic wall slip, which is governed in general by a non-linear and monotone relationship between slip velocity and traction. Micro electromechanical systems (MEMS) have developed numerous microfluidic devices in the medical, physical, biological, chemical, engineering, and energy domains in recent years. The physical aspects of microscale flow and heat transmission, which may differ from macroscale flow, must be thoroughly understood to meet the technical needs. In an earlier studies, Andersson (Andersson, 2002) conducted the investigations that considered the slip boundary condition during the flow over a stretching sheet. He gave the exact solutions for modelled flow equations. Wang (Wang, 2002) gave the exact similarity solution for flow equations driven by a stretching geometry with partial slip condition. Again, Wang (Wang, 2006) researched at stagnation slip flow and heat transfer on a moving plate. Later, Wu (Wu, 2008) suggested a new second-order slip model based on the linear Boltzmann equation’s. Similarly, Fang et al. (Fang et al., 2009) used mathematical methods to study slip magnetohydrodynamics viscous flow over a stretching sheet. Some notable research works showcasing the innovative properties of velocity slip during fluid flows can found in the references (Sutterby, 1965; Sutterby, 1966; Aziz, 2010; Fang et al., 2010; Hayat et al., 2011; Mahantesh et al., 2012).

The stratification phenomenon in fluids has recently attracted a lot of attention in heat and mass transport assessment, and it is a mechanism that occurs as a result of temperature, concentration, and density fluctuations in various fluids. In fact, due to its prevalence in geophysical flows such as oceans, rivers, ponds, solar ponds, and thermal energy storage technologies, evaluating the flow through a double stratified media is an essential fluid topic. Hayat et al. (Hayat et al., 2015) evaluate a dual stratified radiative flow of reactive species Oldroyd-B fluid in the presence of mixed convection. Hayat et al. (Hayat et al., 2017) report an assessment of chemical reactions in mixed convective squeezing fluid flows with thermal radiation. Muhammad et al. (Rehman et al., 2016) demonstrate a dual stratified flow of squeezed viscous fluid utilizing modified Fick’s and Fourier’s theories. The stagnation point Magnetohydrodynamic flowing of reactive chemical Powell-Eyring nano-fluid through dual stratified substrate with thermal radiation was established by Ramzan et al. (Ramzan et al., 2017). Some applications of thermal radiation and chemical reaction of various stratified flows in physiology and industry can be seen in literature (Mahanthesh et al., 2016; Rehman et al., 2016; Daniel et al., 2017; Muhammad et al., 2017; Bég et al., 2020; Lin and Ghaffari, 2021; Rehman et al., 2021; Unyong et al., 2021; Nandi et al., 2022). However Rashid et al. studied the unsteady slip flow amicroplor nanofluid over an impulsively stretched vertical surface see (El-Hakiem and Rashad, 2007; El-Kabeir et al., 2007; El-Kabeir et al., 2010; Chamkha et al., 2011; Tlili et al., 2019; Reddy et al., 2020; Nabwey et al., 2022). Furthermore, Tripathi et al. investigated the peristaltic pumping of hybrid nanofluids throught an asymmetric microchannel in the presence of electromagnetic field see (Akram et al., 2020a; Akram et al., 2020b; Prakash et al., 2020; Tripathi et al., 2020; Akram et al., 2021; Tripathi et al., 2021; Akram et al., 2022; Prakash et al., 2022; Saleem et al., 2022).

In any of the aforementioned analyses, the Sutterby fluid model was never used in conjunction with thermal radiation and a heat generating or absorbing source. The constitutive equations of Sutterby fluid are used in mathematical modelling to achieve this goal. The Sutterby fluid framework illustrates diluted polymer solutions and is one of the non-Newtonian fluid models used to study the rheological properties of various materials. As a result, the current effort is to investigate the heat-producing/absorbing Sutterby fluid flow across horizontal geometry with thermal radiation, as well as double stratification near thermal radiation. As an outcome, the influence of different flow, heat, and mass transport attributes is reported. Nusselt and Sherwood values, as well as drag force (skin friction coefficient), are visually assessed versus numerous emerging parameters.

2 Model development

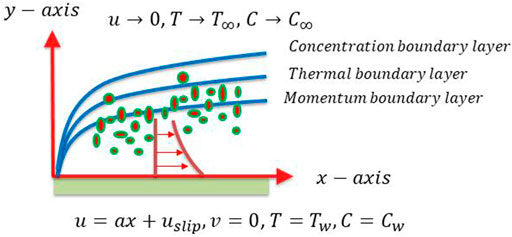
As shown in Figure 1, an incompressible two-dimensional flow of non-Newtonian Sutterby fluid with heat and mass transport past an infinite flat surface is deliberated. The stretching surface has the linear velocity u_w(x)=ax, where a is constant. Non-linearly varying thermal radiation, velocity slip, heat generation/absorption are also incorporated in this analysis. The thermal stratification mechanism is studied by considering the surface temperature T_w(x)=T₀+m₁x and ambient temperature T_∞(x)=T₀+m₂x, respectively. Similarly, the surface concentration C_w (x)=C₀+m₁x and free stream concentration C_∞(x)=C₀+m₂x, is taken to discuss the solutal stratification. A magnetic force of intensity B₀ is applied parallel to the plate's y-axis, which is perpendicular to it. The induced magnetic field created by the velocity of an electrically conducting fluid is supposed to be insignificant in this case. The fluid is supposed to be grayish, generating, and absorbent but quasi medium, and the optically thick radiating limit is taken into account in this study, where the radiant heat flux term can be reduced using the Rosselant estimation. The use of Cartesian coordinates (x,y) to study the flow under discussion is acceptable because the x-axis runs parallel to the stretched sheet and the y-axis runs perpendicular to it. The following are the rheological equations that characterize the incompressible flow of Sutterby fluid:

2.1 Sutterby fluid model

The Cauchy stress tensor for Sutterby fluid (Sutterby, 1965; Sutterby, 1966) is expressed as

$\tau =-pI+\mu S(1)$

where extra stress tensor has the form

$S={\mu }_0\left(\frac{{\sinh }^{-}1\left(\beta {\gamma }^{.}\right)}{\beta {\gamma }^{.}}\right)A_1(2)$

The shear rate can be defined as:

${\gamma }^{.}=\sqrt{\left(\frac{1}{2}tr{\left(A_1\right)}^2\right)}(3)$

where μ₀ is dynamic viscosity, B is the fluid parameter, n denoted the power-law index and “tr” means trace. For Sinh⁻¹ function, the second order approximation is considered as:

${\sinh }^{-}1\left(\beta {\gamma }^{.}\right)\approx \beta {\gamma }^{.}-\frac{{\left(\beta {\gamma }^{.}\right)}^3}{6}(4)$

As a result, the stress tensor takes the form:

$S={\mu }_0{\left[1-\frac{{\left(\beta {\gamma }^{.}\right)}^2}{6}\right]}^n{A}_1(5)$

For two-dimensional steady flow, we take the velocity field of the form

$V=\left(u\left(x,y\right),v\left(x,y\right),0\right](6)$

In view of Eq. 4, the shear rate takes the form.

The extra stress components are expressed as below

${\gamma }^{.}={\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2+2{\left(\frac{\partial u}{\partial x}\right)}^2\right]}^{\frac{1}{2}}(7)$

The extra stress components are expressed as below

$S_{xx}=-P+2{\mu }_0{\left(1-\frac{{\left(\beta {\gamma }^{.}\right)}^2}{6}\right)}^n\frac{\partial u}{\partial y}(8)$

$S_{xy}={\mu }_0{\left(1-\frac{{\left(\beta {\gamma }^{.}\right)}^2}{6}\right)}^n\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)(9)$

$S_{yy}=-P+2{\mu }_0{\left(1-\frac{{\left(\beta {\gamma }^{.}\right)}^2}{6}\right)}^n\frac{\partial v}{\partial y}(10)$

Based on the above restrictions and involving boundary layer approximations, the prevailing equations for Sutterby nanofluids using the Buongiorno model are given as

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0(11)$

$\begin{array}{ll}\hfill u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=& v{\left(1-\frac{{\beta }^2}{6}{\frac{\partial u}{\partial y}}^2\right)}^n\frac{{\partial }^{2}u}{\partial y^2}-\frac{nv{\beta }^2}{6}\left(1-\frac{{\beta }^2}{6}\right)\hfill \\ \hfill & \times \left({\frac{\partial u}{\partial y}}^n-1\right)\left({\frac{\partial u}{\partial y}}^2\right)\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B{0}^{2}u}{\rho },\hfill \end{array}(12)$

$\begin{array}{ll}\hfill u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=& \alpha \frac{{\partial }^{2}T}{\partial y^2}+{\tau }_{np}\left(D_B\frac{\partial C}{\partial y}\right)\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\hfill \\ \hfill & -\frac{1}{\rho C_p}\left(\frac{16{\sigma }^{*}{T}_{\infty }}{3k{k}^{*}}\right)\frac{{\partial }^{2}T}{\partial y^2}+Q_1\left(T-T_{\infty }\right),\hfill \end{array}(13)$

$u\frac{\partial T}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}c}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2},(14)$

The associated boundary conditions

$\begin{array}{ll}\hfill u=& u_w+L{\left[1-\frac{B^2}{6}{\left(\frac{\partial u}{\partial y}\right)}^2\right]}^2\left(\frac{\partial u}{\partial y}\right),v=0,T=T_w,\hfill \\ \hfill C=& C_{w}aty=0\hfill \end{array}(15)$

$u\to U_{\infty },T\to T_{\infty },C\to \infty asy\to \infty (16)$

2.2 Transformations

The dimensionless form of the modelled problem is obtained by utilizing the following dimensionless variables:

$\psi =\sqrt{av}xf\left(\eta \right),\eta =y\sqrt{\frac{a}{v}},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T{T}_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }}.(17)$

Here, f′(η), θ(η),and ϕ(η) represents the dimensionless stream function, dimensionless temperature and concentration. Making use of non-dimensional transformation, the leading Eqs. (4.12)–(4.14) reduced to

$\begin{array}{ll}\hfill & {\left(1-\frac{1}{6}DeRe{f}^{\prime \prime 2}\right)}^{n}f\prime \prime \prime -\frac{nDeRe}{3}{\left(1-\frac{1}{6}DeRe{f}^{\prime \prime 2}\right)}^{n-1}\hfill \\ \hfill & f\prime \prime \prime f^{\prime \prime 2}+f{f}^{\prime }-f^{\prime 2}-M{f}^{\prime }=0\hfill \end{array}(18)$

$\begin{array}{ll}\hfill & \left(1+\frac{4}{3}R\right){\theta }^{″}+\mathrm{Pr}\left(f{\theta }^{\prime }-f^{\prime }\theta \right)+\mathrm{Pr}\left(N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{\theta }^{\prime 2}\right)\hfill \\ \hfill & -\mathrm{Pr}{s}_t{f}^{\prime }+\mathrm{Pr}Q\theta =0,\hfill \end{array}(19)$

$h^{″}+Lef{\varphi }^{\prime }-Le\varphi f^{\prime }+\frac{N_b}{N_t}{\theta }^{″}-Le{S}_c{f}^{\prime }=0(20)$

$\begin{array}{ll}\hfill f\left(0\right)& =1,f^{\prime }\left(0\right)=1+A{f}^{\prime }\left(0\right){\left[1-\frac{1}{6}DeRe{f}^{\prime \prime 2}\left(0\right)\right]}^n,\hfill \\ \hfill \theta \left(0\right)& =1-S_t,\varphi \left(0\right)=1-S_c,at\eta =0,\hfill \end{array}(21)$

$f^{\prime }\left(\infty \right)=0,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0as\eta \to \infty (22)$

where η is the similarity variables and the prime denotes differentiation with respect toη. The dimensionless parameters in the above equations are the Deborah number De, heat generation/absorption parameter Q, thermal stratification parameter s_t and solutal stratification parameter s_c, given as $De=a^2{B}^2,Q=\frac{Q_1}{\rho C_{p}a},S_t=\frac{m_2}{m_1},S_t=\frac{m_4}{m_3}$

$\begin{array}{ll}\hfill C_f\sqrt{Rex}=& {\left[1-\frac{1}{6}DeRe{f}^{″}\left(0\right)\right]}^2{f}^{″}\left(0\right),\hfill \\ \hfill & N{u}_x\sqrt{Rex}=\left(\frac{1}{1-s_1}\right)Q^{\prime }\left(1\right),\hfill \\ \hfill & S{h}_x\sqrt{Rex}=-\left(\frac{1}{1-S_2}\right){\varphi }^{\prime }\left(1\right).\hfill \end{array}(23)$

$f=Z_1,f^{\prime }=Z_2,f^{″}=Z_3,\theta =Z_4,{\theta }^{\prime }=Z_5,{\varphi }^{\prime }=Z_7.(24)$

$\begin{array}{cc}\hfill & Z_1^{\prime }=Z_2,Z_2^{\prime }=Z_3,Z_3^{\prime }=\frac{Z_2^2-Z_1{z}_2+\mu Z_2}{A_1-\frac{nDeRe}{3}{A}_2},\hfill \\ \hfill & Z_5^{\prime }=\frac{\mathrm{Pr}\left(N_b{Z}_5{Z}_7-N_t{Z}_5^2+Z_1{Z}_5-Z_2{Z}_4-Z_{2}Z{S}_{t}Q{Z}_4\right)}{\left(1+\frac{4}{3}R\right)},\hfill \\ \hfill & Z_7^{\prime }=-Le{Z}_1{z}_7+Le{Z}_2{Z}_6+Le{Z}_2{S}_c-\frac{N_b}{N_t}{Z}_5^{\prime }\hfill \end{array}(25)$

along with boundary conditions

$\begin{array}{ll}\hfill & Z_1\left(0\right)=0,Z_2\left(0\right)=1+A{Z}_3\left(0\right){\left[1-\frac{1}{6}DeRe{Z}_3^2\left(0\right)\right]}^n,\hfill \\ \hfill & Z_4\left(0\right)=1-S_t,Z_6\left(0\right)=1-S_c\hfill \end{array}(26)$

$Z_2\left(\infty \right)\to 0,Z_4\left(\infty \right)\to 0,Z_6\left(\infty \right)\to 0.(27)$

The above set of seven first-order ODEs Eq. 25 with boundary conditions Eqs 26 and 27 is numerically integrated by exercising the MATLAB routine bvp4c which is a finite difference code that uses the collocation method to execute the three - stage Labatto IIIa formula. The numerical analysis is performed by selecting a suitable finite value (η_∞ = 10) to fulfill the for field boundary conditions. The error tolerance of 10⁻⁶is set for computational purpose. The RFK45 procedure is adaptive because it modifies the number and location of grid points throughout each iteration, keeping the local error within acceptable ranges. The asymptotic boundary conditions in Eq. 27 are supplemented in the existing situation by a predefined limit in the range 10–15, based on the parameter values. To assure that all numerical results approach the asymptotic values accurately, infinity is desired. The choice of an appropriately large number for infinity is essential for maintaining desirable reliability in boundary layer flows, and it is a common blunder seen in many investigations. The stepped equations used to estimate Eq. 25, employing fifth–fourth-order Runge-Kutta-Fehlberg procedures under conditions Eqs 26 and 27 are listed below (Bég et al., 2020; Bég et al., 2022).K₀ = f (x₀, y₀).$K_1=f\left(x_0+\frac{1}{4}h,y_0+\frac{1}{4}{K}_{0}h\right)$$K_2=f\left(x_0+\frac{3}{8}h,y_0+\left(\frac{3}{32}{K}_0+\frac{9}{32}{k}_1\right)\right)$$K_3=f\left(x_0+\frac{12}{13}h,y_0+\left(\frac{1932}{2197}{k}_0-\frac{7200}{2197}{K}_1+\frac{7296}{2197}{k}_2\right)h\right)$$K_4=f\left(x_0+h,y_0+\left(\frac{439}{216}{K}_0-8K_1+\frac{3860}{513}{K}_2-\frac{845}{4104}{K}_3\right)h\right)$$K_5=f\left(x_0+\frac{1}{2}h,y_0+\left(\frac{8}{27}{k}_0+2K_1-\frac{3544}{2565}{K}_2-\frac{1859}{4104}{K}_3-\frac{11}{40}{K}_4\right)h\right)$$y_{i+1}+\left(\frac{25}{216}{K}_0+\frac{1408}{2565}{K}_2+\frac{2197}{4104}{K}_3-\frac{11}{5}{K}_4\right)h$$Z_{i+1}=Z_i+\left(\frac{16}{135}{K}_0+\frac{6656}{12825}{K}_2+\frac{28561}{56430}{K}_3-\frac{9}{40}{K}_4+\frac{2}{55}{K}_5\right)h$The fourth-order Runge-Kutta component is denoted by y, and the fifth-order Runge-Kutta stage is denoted by Z. By subtracting the two values obtained, an estimate of the error can be obtained. The findings can be redone with a reduced step size if the deviation reaches a certain threshold. The following is an example of how to determine the new step size:

$h_{\mathit{new}}=h_{\mathit{old}}{\left[\frac{ϵh_{\mathit{old}}}{2\left(Z_{i+1}-y_{i+1}\right)}\right]}^{\frac{1}{4}}(28)$

2.3 Results and discussion

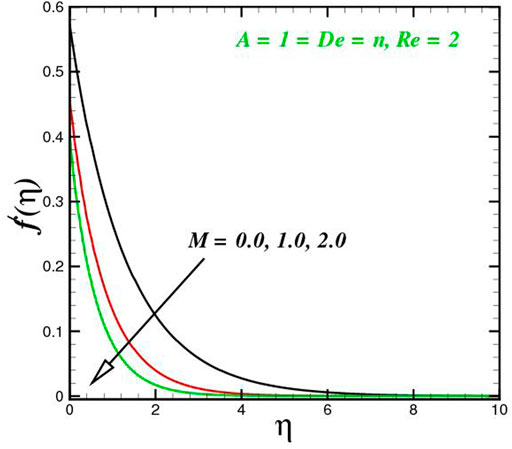
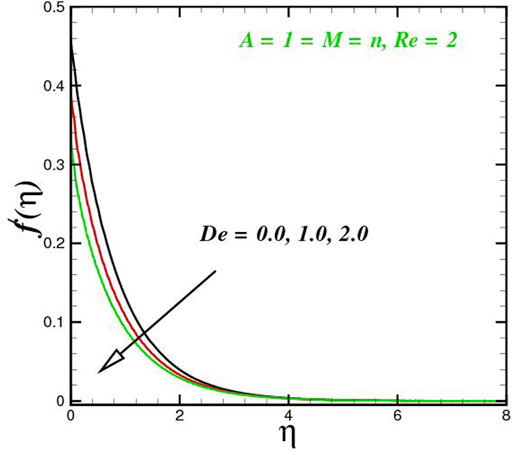
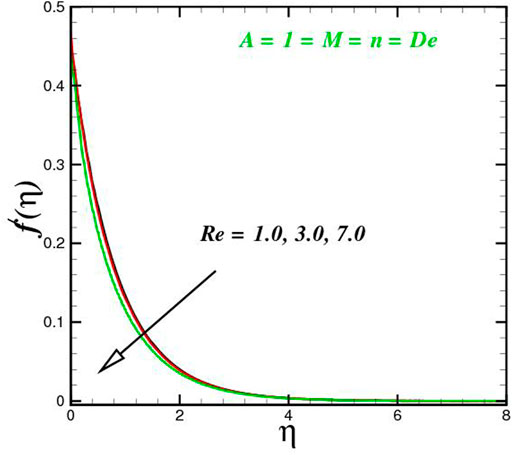
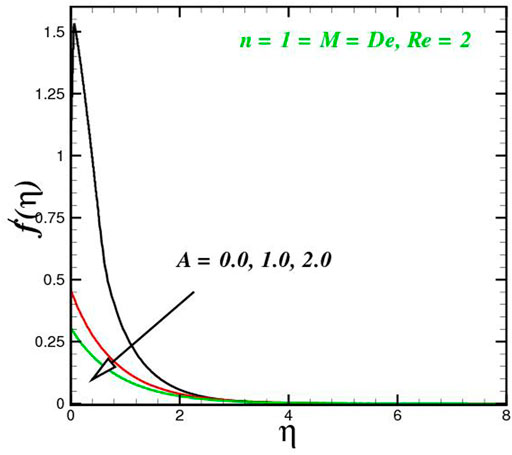
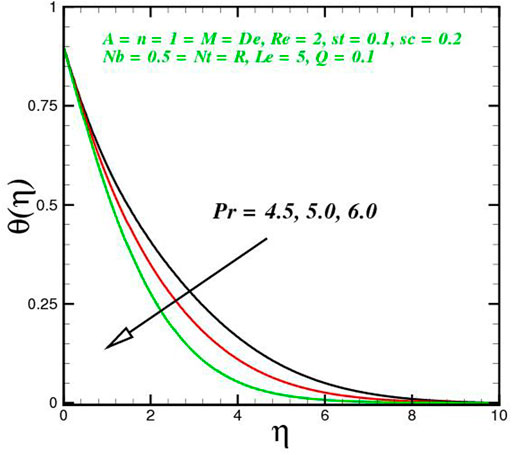
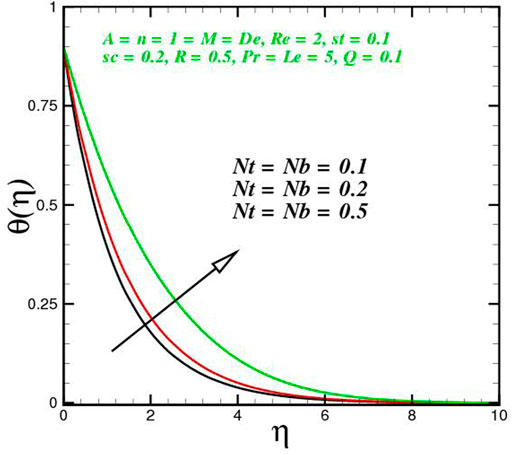
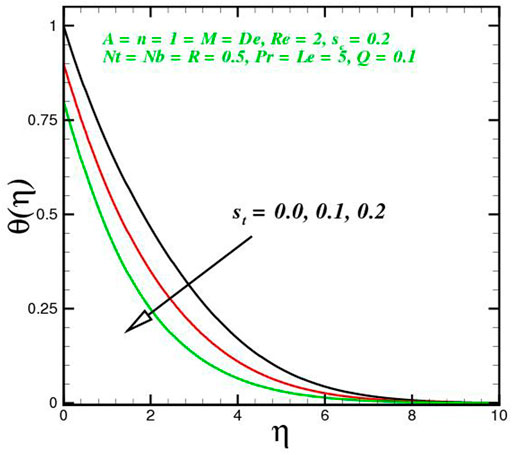
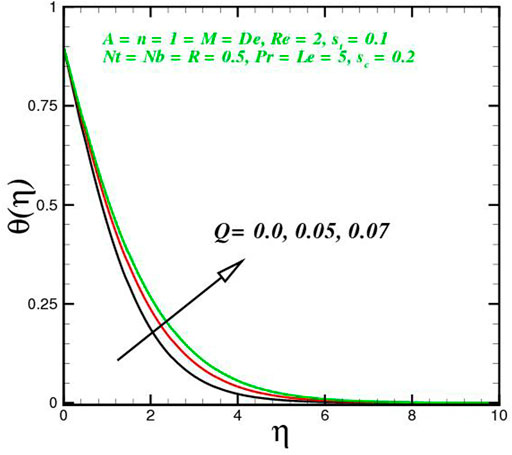
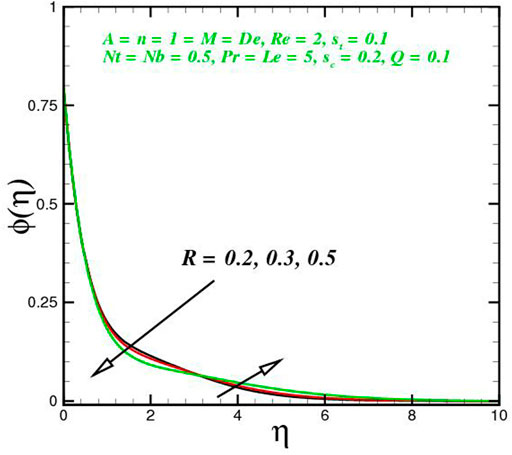
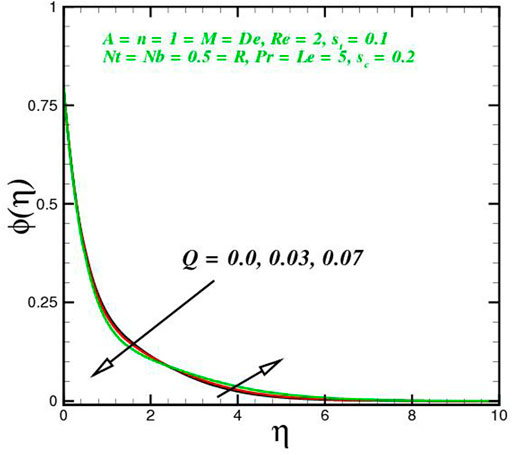
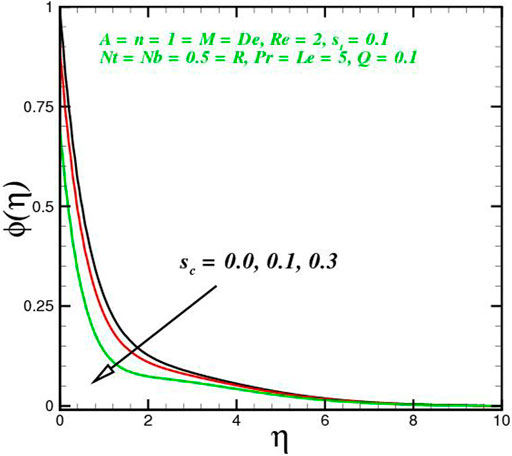
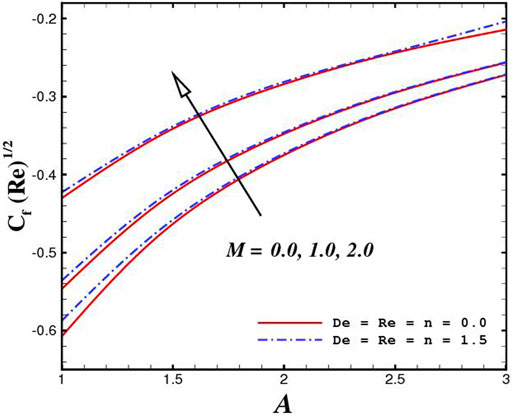
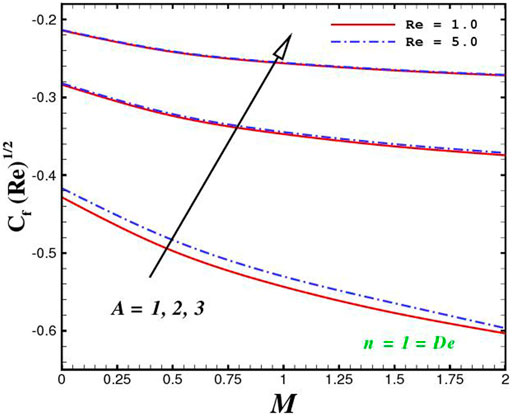
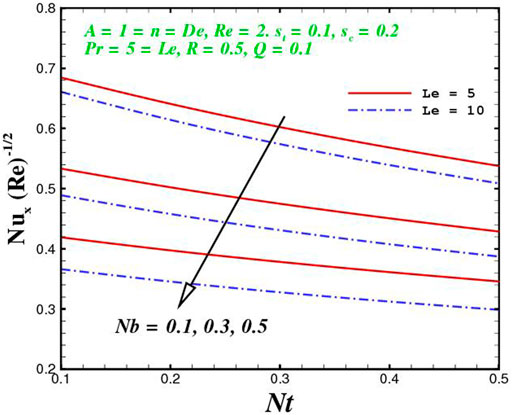
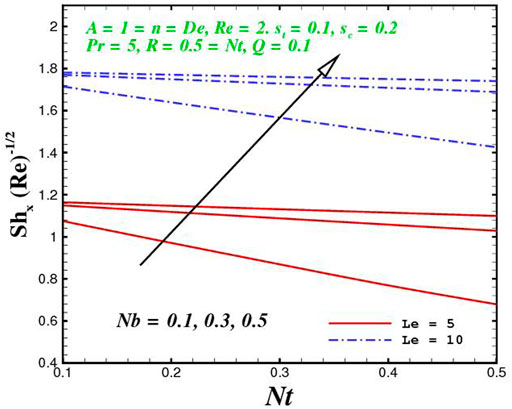
The function of innovative quantities on flow profile pictures is investigated in this section for various values of emerging parameters. Physical changes in temperature, concentration, skin friction, Nussselt and Sherwood, and velocity versus numerous parameters are reviewed in Figures 2–17. The variational curves of velocity towards M are shown in Figure 2. It is evident that velocity dwindle near the center and exhibits a reverse attitude across the walls. In fact, this means that increasing M values strengthens the retarding and Lorentz forces, which has an immediate effect on the fluid dynamics. The diminishing conduct of Sutterby fluid is exposed in Figure 3. De is a rheological term that describes the fluidity of substances under precise flow conditions. The escalation in De assist the delaying flow as witnessed in the paint. Physically, strengthened in De result in shear thickening rheology of the Sutterby fluid as a consequences the fluid flow dwindle. The reverse trend for f′(η) against Reynolds Re is delineated in Figure 4. Physically, uplifting Re, result in denser liquid, as a consequences, depressing the flow rate. The flowing rate through the surface dwindle; Figure 5, addresses the slip A impact on velocity f′(η). The flow structure is depressed with greater values of slip factor. In fact, velocity slip escalates the momentum boundary layer thickness. Figures 6–10), exhibits the temperature conduct via novel parameters. The Prandtl Pr consequences for temperature θ(η), is painted in Figure 6. Since the Prandtl number is inversely related to thermal diffusivity, boosting it cools the flow. This is justified by the fact that an escalation in Pr contracts the thermal boundary layer thickness; Figure 7 outlines the impact of the radiation parameter R on the temperature θ(η). The radiant parameter indicates how much heat transport through conduction contributes to thermal radiation. As an outcome, for increasing R values, there is a distinct rise in temperature curves. Optimizing thermal radiation entails transferring energy into the flow via radiating, which promotes the fluid’s thermal performance. The joint action of Nt and Nb on thermal field is offered in Figure 8. Accelerating Brownian action caused quicker stochastic mobility of nanoparticles in a stream, resulting in an increase in thermal boundary layer thickness and a quicker spike in flow temperature. For increasing Nt values, a similar trend can be seen. As a function of the thermophoresis mechanism, more heated particles near the surface migrate away from hot regions into cold regions, raising temperature there, and the entire system temperature rises. The stratification parameter s_t attributed to temperature variation is indicated graphically in Figure 9. The thermally stratification process induces layer development owing to temperature variations; as the stratification parameter is strengthened, the temperature differential between the wall and the frame of reference declines, and the system’s cools down. Positive values of Q, result in the highest temperature because more heat generated, which strengthens the thermal behavior. When the heat input parameter advances, the boundary layer relating to the temperature field thickens. The uplifting temperature curves can be witnessed from Figure 10. Figures 11–17) show how different flow characteristics can be used to map the decorum of dimensionless concentration. A substantial growth in radiant parameter R, the corresponding concentration of the nanoparticles depressed near the wall, while within the central region, the concentration boundary layer expand as clear from Figure 11. The physics behind the mechanism is that, the radiant parameter escalates the thermal and concentration boundary layer thickness, while adverse reaction happen near the wall of geometry. The influence of heat generation exhibits contrary conduct on concentration sketch ϕ(η). The heat producing/absorbing coefficient, Q, has little significance on the concentration distribution, ϕ(η), since the fluid’s concentration remains unaffected as the heat in the fluid changes. The heat generation coefficient is responsible for increasing the fluid flow’s heat gradient, although it has no effect on the fluid particle concentration levels. The fluid central regime is dwindle, while the concentration layer near the boundaries are little altered is visible in Figure 12. To be more explicit; Figure 11 exhibits the concentration distribution’s descending tendency for positive values of the solutal stratified parameter s_c. The potential difference across wall surface and ambient fluid concentrationC_w − C_∞ drops as the potential difference between c surface wall and ambient fluid concentration upturns, dropping the thickness of the corresponding concentration boundary layer; Figure 14, offerings the dimension of skin friction against magnetic parameter and velocity slip. It is evident from the scenario that surface skin friction expand against velocity slip parameter, while the magnetic field strength weakens the surface skin friction. The shear strength at the wall drops significantly with an expansion in slip parameter when the surface is sufficiently smooth and fluid flows at nanoscales is predicted; Figure 17, reveal the same outcomes. The action of magnetic parameter in the existence of slip parameter is obvious. Magnetic parameter reduces the movement growth, as a result the skin friction diminished; Figure 16, testify that the heat transfer rate is shrink with the Brownian Nb and thermopheretic Nt phenomena in the flow region. This is justified by the fact that greater Brownian motion results in the intensification of large movements of nanoparticles, and consequently heat is transmitted into colder particles. This phenomenon depressed the nanoparticles’ heat transfer rate. While on the other hand, mass transmission rate (Sherwood number) is significantly high with the growth of said phenomena as clear from Figure 17.

FIGURE 1

FIGURE 1. The physical model and coordinate systems.

FIGURE 2

FIGURE 2. f′(η), alteration via M.

FIGURE 3

FIGURE 3. f′(η), alteration via De.

FIGURE 4

FIGURE 4. f′(η), alteration via Re.

FIGURE 5

FIGURE 5. f′(η), alteration via A.

FIGURE 6

FIGURE 6. θ(η), alteration via Pr.

FIGURE 7

FIGURE 7. θ(η), alteration via R.

FIGURE 8

FIGURE 8. θ(η), alteration via Nt.

FIGURE 9

FIGURE 9. θ(η), alteration via S_t.

FIGURE 10

FIGURE 10. θ(η), alteration via Q.

FIGURE 11

FIGURE 11. ϕ(η), alteration via R.

FIGURE 12

FIGURE 12. ϕ(η), alteration via Q.

FIGURE 13

FIGURE 13. ϕ(η)), alteration via S_c.

FIGURE 14

FIGURE 14. $skin{C}_f\sqrt{R{e}_x}$, sketch for frequent values M and A.

FIGURE 15

FIGURE 15. $skin{C}_f\sqrt{R{e}_x}$, sketch for frequent values of A and M.

FIGURE 16

FIGURE 16. $\text{Nusslt}N{u}_x\sqrt{R{e}_x}$, sketch for frequent values of Nb and Nt.

FIGURE 17

FIGURE 17. $\text{Shaerwood}S{h}_x\sqrt{R{e}_x}$, sketch for frequent values of Nb and Nt.

3 Conclusion

The investigation presented in this paper helps us to understand, physically as well as numerically, the aspects of activation energy on magnetized Sutterby nanoliquid subjected to heat generation/absorption through a Darcy porous medium. The well-established Buongiorno model is employed to examine the features of Brownian and thermophoresis diffusion of the nanofluid. The most significant outcomes noted from present research are described as follows.

• g(ζ) nanoliquid temperature deteriorates for larger S₁while it intensifies against Q.

• Positive values (heat generation) of Q, improve the temperature distribution while reverse trend is seen in case of negative values (heat absorption).

• Velocityf′ζ), is increasing function of n, and D_a and dwindle for large M.

• Opposite trend of h(ζ) is detected against N_b (Brownian moment parameter) and N_b (thermophoresis parameter).

• The solutal stratification parameter S₁, Le and γ (Chemical reaction rate) exhibitsdiminishing behavior for concentration of the nanofluid.

• Heat transfer rate is significantly rises with heat generating parameter.

• Large magnetic number reduces the skin friction of the nanofluid.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

There are six authors in this manuscript and each one has contributed properly. The mathematical model has been proposed by SA, all the numerical computations and their graphs have been carried out by UU. The discussion of graphs and their physical interpretation has been given by HK and KSN. The literature review and comparison of the present simulations with the classical data has been established by MY. The final review and amendments in the manuscript has been carried out by NU.

Funding

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, J., Akbar, N. S., and Tripathi, D. (2021). A theoretical investigation on the heat transfer ability of water-based hybrid (Ag–Au) nanofluids and Ag nanofluids flow driven by electroosmotic pumping through a microchannel. Arabian J. Sci. Eng. 46, 2911–2927. doi:10.1007/s13369-020-05265-0

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., and Tripathi, D. (2020). Comparative study on ethylene glycol based Ag-Al 2 O 3 and Al 2 O 3 nanofluids flow driven by electroosmotic and peristaltic pumping: A nano-coolant for radiators. Phys. Scr. 95 (11), 115208. doi:10.1088/1402-4896/abbd6b

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., and Tripathi, D. (2020). Numerical simulation of electrokinetically driven peristaltic pumping of silver-water nanofluids in an asymmetric microchannel. Chin. J. Phys. 68, 745–763. doi:10.1016/j.cjph.2020.10.015

CrossRef Full Text | Google Scholar

Akram, J., Akbar, N. S., and Tripathi, D. (2022). Thermal analysis on MHD flow of ethylene glycol-based BNNTs nanofluids via peristaltically induced electroosmotic pumping in a curved microchannel. Arabian J. Sci. Eng. 47, 7487–7503. doi:10.1007/s13369-021-06173-7

CrossRef Full Text | Google Scholar

Andersson, H. (2002). Slip flow past a stretching surface. Acta Mech. 158, 121–125. doi:10.1007/bf01463174

CrossRef Full Text | Google Scholar

Aziz, A. (2010). Hydrodynamic and thermal slip flow boundary layer over a flat plate with constant heat flux boundary condition. Commun. Non-linear Sci. Numer. Simul. 15, 80–573.

CrossRef Full Text | Google Scholar

Bég, O. A., Bég, T., Khan, W. A., and Uddin, M. J. Multiple slip effects on nanofluid dissipative flow in a converging/diverging channel: A numerical study. Heat. Transf. 51(1) (2022)1040–1061. doi:10.1002/htj.22341

CrossRef Full Text | Google Scholar

Bég, O. A., Uddin, M. J., Bég, T. A., Kadir, A., Shamshuddin, M. D., and Babaie, M. (2020). Numerical study of self-similar natural convection mass transfer from a rotating cone in anisotropic porous media with Stefan blowing and Navier slip. Indian J. Phys. 94(6), 863–877. doi:10.1007/s12648-019-01520-9

CrossRef Full Text | Google Scholar

Buongiorno, J. (2006). Convective transport in nanofluids. J. Heat. Transf. 128 (3), 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Chamkha, A. J., Rashad, A. M., and Al-Meshaiei, E. (2011). Melting effect on unsteady hydromagnetic flow of a nanofluid past a stretching sheet. Int. J. Chem. React. Eng., 9, doi:10.2202/1542-6580.2613

CrossRef Full Text | Google Scholar

Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. Fed. 231, 99–105.

Google Scholar

Daniel, Y. S., Aziz, Z. A., Ismail, Z., and Salah, F. (2017). Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J. Appl. Res. Technol. 15(5), 464–476. doi:10.1016/j.jart.2017.05.007

CrossRef Full Text | Google Scholar

Das, K. (2012). Slip flow and convective heat transfer of nanofluids over a permeable stretching surface. Comput. Fluids 64, 34–42. doi:10.1016/j.compfluid.2012.04.026

CrossRef Full Text | Google Scholar

Effect of heat generation (2012). Effect of heat generation/absorption on stagnation point flow of nanofluid over a surface with convective boundary conditions. Comm. Nonlinear Sci. Num. Simul. 17, 4210–4223.

Google Scholar

El-Hakiem, M. A., and Rashad, A. M. (2007). Effect of radiation on non-Darcy free convection from a vertical cylinder embedded in a fluid-saturated porous medium with a temperature-dependent viscosity. J. porous media 10(2).

CrossRef Full Text | Google Scholar

El-Kabeir, S. M. M., Chamkha, A., and Rashad, A. M. (2010). Heat and mass transfer by MHD stagnation-point flow of a power-law fluid towards a stretching surface with radiation, chemical reaction and Soret and Dufour effects. Int. J. Chem. React. Eng. 8. doi:10.2202/1542-6580.2396

CrossRef Full Text | Google Scholar

El-Kabeir, S. M. M., Rashad, A. M., and Gorla, R. S. R. (2007). Unsteady MHD combined convection over a moving vertical sheet in a fluid saturated porous medium with uniform surface heat flux. Math. Comput. Model. 46 (3-4), 384–397. doi:10.1016/j.mcm.2006.11.010

CrossRef Full Text | Google Scholar

Fang, T., S.YaoZhang, J., and Aziz, A. (2010). Viscous flow over a shrinking sheet with second order slip flow model. Commun. Non-linear Sci. Numer. Simul. 15, 42–831.

CrossRef Full Text | Google Scholar

Fang, T., Zhang, J., and Yao, S. (2009). Slip MHD viscous flow over a stretching sheet–an exact solution. Commun. Non-linear Sci. Numer. Simul. 14, 3731–3737. doi:10.1016/j.cnsns.2009.02.012

CrossRef Full Text | Google Scholar

Hamad, A., and Ferdows, M. (2012). Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing: A lie group analysis. Nonlinear Sci. Numer. simulat. 17, 132–140. doi:10.1016/j.cnsns.2011.02.024

CrossRef Full Text | Google Scholar

Hayat, T., Khan, M., Imtiaz, M., and Alsaedi, A. (2017). Squeezing flow past a Riga plate with chemical reaction and convective conditions. J Molec Liqs 225, 569–576. doi:10.1016/j.molliq.2016.11.089

CrossRef Full Text | Google Scholar

Hayat, T., Muhammad, T., Shehzad, S. A., and Alsaedi, A. (2015). Temperature and concentration stratification effects in mixed convection flow of an Oldroyd-B fluid with thermal radiation and chemical reaction. PloS one 10 (6), 0127646. doi:10.1371/journal.pone.0127646

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayat, T., Qasim, M., and Mesloub, S. (2011). MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Meth Fluid. 66, 963–975. doi:10.1002/fld.2294

CrossRef Full Text | Google Scholar

Kuznetsov, A. V., and Nield, D. A. (2010). Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 49, 243–247. doi:10.1016/j.ijthermalsci.2009.07.015

CrossRef Full Text | Google Scholar

Lin, P., and Ghaffari, A. (2021). Heat and mass transfer in a steady flow of Sutterby nanofluid over the surface of a stretching wedge. Phys. Scr 96(6), 065003. doi:10.1088/1402-4896/abecf7

CrossRef Full Text | Google Scholar

Mahantesh, M., Vajravelu, K., Abel, M. S., and Siddalingappa, M. N. (2012). Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 58, 50–142.

Google Scholar

Mahanthesh, B., Gireesha, B. J., and Gorla, R. S. (2016). Nonlinear radiative heat transfer in MHD three-dimensional flow of water based nanofluid over a non-linearly stretching sheet with convective boundary condition. J Niger. Mathem Soc.35(1) 35, 178–198. doi:10.1016/j.jnnms.2016.02.003

CrossRef Full Text | Google Scholar

Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Ther. Sci. 50 (7), 1326–1332. doi:10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

Mostafa, M., Hayat, T., Pop, I., Asghar, S., and Obaidat, S. (2011). Stagnation point flow of a nanofluid towards a stretching sheet. Int. J. Heat. Mass Transf. 54, 5588–5594. doi:10.1016/j.ijheatmasstransfer.2011.07.021

CrossRef Full Text | Google Scholar

Muhammad, N., Nadeem, S., and Mustafa, T. (2017). Squeezed flow of a nanofluid with Cattaneo–Christov heat and mass fluxes. Results Phys 7, 862–869. doi:10.1016/j.rinp.2016.12.028

CrossRef Full Text | Google Scholar

Nabwey, H. A., Khan, A. W., Rashad, A. M., Mabood, F., and Salah, T. (2022). Power-law nanofluid flow over a stretchable surface due to gyrotactic microorganisms. Mathematics 10 (18), 3285. doi:10.3390/math10183285

CrossRef Full Text | Google Scholar

Nandi, S., Kumbhakar, B., and Sarkar, S. (2022). MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int Commu Heat Mass Transf 130, 105791. doi:10.1016/j.icheatmasstransfer.2021.105791

CrossRef Full Text | Google Scholar

Bachok, N., Ishak, A., and Pop, I. (2012). Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int. J. Heat. Transf. 55, 8122–8128. doi:10.1016/j.ijheatmasstransfer.2012.08.051

CrossRef Full Text | Google Scholar

Prakash, J., Balaji, R., Tripathi, D., Tiwari, A. K., and Sharma, R. K. (2022). “Composite nanofluids flow driven by electroosmosis through squeezing parallel plates in presence of magnetic fields,” in Advancements in nanotechnology for energy and environment (Singapore: Springer Nature Singapore), 273–293.

CrossRef Full Text | Google Scholar

Prakash, J., Sharma, A., and Tripathi, D. (2020). Convective heat transfer and double diffusive convection in ionic nanofluids flow driven by peristalsis and electromagnetohydrodynamics. Pramana 94, 4–17. doi:10.1007/s12043-019-1873-5

CrossRef Full Text | Google Scholar

Ramzan, M., Bilal, M., and Chung, J. D. (2017). Radiative flow of Powell-Eyring magneto-nanofluid over a stretching cylinder with chemical reaction and double stratification near a stagnation point. PloS one 12 (1), 0170790. doi:10.1371/journal.pone.0170790

PubMed Abstract | CrossRef Full Text | Google Scholar

Reddy, S. R. R., Bala Anki Reddy, P., and Rashad, A. M. (2020). Activation energy impact on chemically reacting Eyring–Powell nanofluid flow over a stretching cylinder. Arabian J. Sci. Eng. 45, 5227–5242. doi:10.1007/s13369-020-04379-9

CrossRef Full Text | Google Scholar

Rehman, K. U., Malik, M. Y., Salahuddin, T., and Naseer, M. (2016). Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv. 6 (7), 075112. doi:10.1063/1.4959587

CrossRef Full Text | Google Scholar

Rehman, S. U., Mir, N. A., Farooq, M., Rafiq, N., and Ahmad, S. (2021). Analysis of thermally stratified radiative flow of Sutterby fluid with mixed convection. Proc. Institution Mech. Eng. Part C, 09544062211007887.J of Mech Engg Sci

CrossRef Full Text | Google Scholar

Saleem, N., Munawar, S., Tripathi, D., Afzal, F., and Afzal, D. (2022). Cilia beating modulated radiating ternary nanofluids flow in a corrugated asymmetric channel with electromagnetohydrodynamic and momentum slip. Heat. Transf. 51(8), 7462–7486. doi:10.1002/htj.22652

CrossRef Full Text | Google Scholar

Sutterby, J. L. (1966). Laminar converging flow of dilute polymer solutions in conical sections: Part I. Viscosity data, new viscosity model, tube flow solution. Viscosity data, new viscosity Model., tube Flow. Solut. 12, 63–68. doi:10.1002/aic.690120114

CrossRef Full Text | Google Scholar

Sutterby, J. L. (1965). Laminar converging flow of dilute polymer solutions in conical sections. II. Ii. Trans. Soc. Rheol. 9, 227–241. doi:10.1122/1.549024

CrossRef Full Text | Google Scholar

Tlili, I., Rashad, A. M., Khan, A. W., and el-Hakiem, A. M. A. (2019). Indian J. Pure Appl. Phys. (IJPAP) 57 (10), 773–782.

Tripathi, D., Prakash, J., and Bég, O. A. (2020). Peristaltic pumping of hybrid nanofluids through an asymmetric microchannel in the presence of electromagnetic fields. J. Therm. Sci. Eng. Appl.

Google Scholar

Tripathi, D., Prakash, J., Gnaneswara Reddy, M., and Kumar, R. (2021). Numerical study of electroosmosis-induced alterations in peristaltic pumping of couple stress hybrid nanofluids through microchannel. Indian J. Phys. 95, 2411–2421. doi:10.1007/s12648-020-01906-0

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2012). Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chem. Eng. Sci. 84, 182–187. doi:10.1016/j.ces.2012.08.029

CrossRef Full Text | Google Scholar

Unyong, B., Vadivel, R., Govindaraju, M., Anbuvithya, R., and Gunasekaran, N. (2021). Entropy analysis for ethylene glycol hybrid nanofluid flow with elastic deformation, radiation, non-uniform heat generation/absorption, and inclined Lorentz force effects. Case Stud. Therm Engg 30, 101639. doi:10.1016/j.csite.2021.101639

CrossRef Full Text | Google Scholar

Wang, C. Y. (2002). Flow due to a stretching boundary with partial slip-an exact solution of the Navier-Stokes equation. Chem. Eng. Sci. 57, 7–3745.

CrossRef Full Text | Google Scholar

Wang, C. Y. (2006). Stagnation slip flow and heat transfer on a moving plate. Chem. Eng. Sci. 61, 7668–7672. doi:10.1016/j.ces.2006.09.003

CrossRef Full Text | Google Scholar

Ibrahim, W., Shanker, B., and Mahantesh, M. (2013). MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. Heat. Mass Transf. 56, 1–9. doi:10.1016/j.ijheatmasstransfer.2012.08.034

CrossRef Full Text | Google Scholar

Wu, L. (2008). A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 93, 253103. doi:10.1063/1.3052923

CrossRef Full Text | Google Scholar

Xuan, Y., and Li, Q. (2000). Heat transfer enhancement of nanofluids, int. J. Heat fluid flow 21(1), 58–64.

CrossRef Full Text | Google Scholar

Glossary

x, y Cartesian Coordinates

D_a Darcy

u, v velocity components in x(y) directions

c_p specific heat (JKg⁻¹k⁻¹)

D mass diffusivity

D_b Brownian diffusion coefficient

D_t Thermophoretic diffusion coefficient

T₀ Reference temperature(K)

T_w wall temperature(K)

C₀ Concentration

E Activation energy J)

Q Heat generating absorbing J)

s₁ $\frac{b}{d}$ Thermal stratification

s₂ $\frac{c}{e}$ Solutal stratification

τ_np $\frac{{(\rho c_p)}_p}{{(\rho c_p)}_f}$ Ratio of the nano particle to fluid particle

K Thermal conductivity (Wm⁻¹k⁻¹)

t_w sheer stress on the wall

Dimensionless functions

η similarity variables

h(η) represent the velocity component u

g(η) represent the velocity component v

τ shear stress

Re Reynolds number

Pr Prandtl number

Le Lewis number

Sc Schmidth number

Sh Sherwood number

Nu Nusselt number

Nt Thermophoresis parameter

Nb Brownian motion parameter

Gr_x Grashof number along x − axis

Greek Letters

α Thermal diffusivity

β Sutterby fluid coefficient

γ Chemical reaction

ϵ Sutterby fluid

δ Temperature ratio

μ Viscosity (Nsm⁻²)

ρ Density (Kgm⁻¹)

ν Kinematic viscosity (m⁻²s⁻¹)