Numerical study of magnetized Powell–Eyring hybrid nanomaterial flow with variable heat transfer in the presence of artificial bacteria: Applications for tumor removal and cancer cell destruction

This investigation determined the effectiveness of an exterior magnetic field on bacteria enclosed by thousands of magnetite nanoparticles. Variable thermal conductivity and Joule heating were used in the interstitial nano liquid in which artificial bacteria were swimming in a biotic cell. The unsteady motions of a Powell–Eyring fluid in two dimensions were assumed. The porous extending wall was used as a bent surface shape. To convert the governing non-linear PDEs into non-linear ODEs, suitable transformations were exploited. The homotopy analysis technique (HAM) was utilized to resolve the semi-analytical results of non-linear ODEs. Plots were utilized to investigate the impact of significant parameters of velocity distribution, temperature profile, bacterial density field, nutrient concentration field, skin friction, Nusselt number, and nutrient concentration density. Clinical disease has shown that daring tumors have reduced blood flow. The results of this study showed that augmenting the values of unsteady parameters improved the blood velocity profile. The velocity distribution decreased for higher magnetite volume fraction values, as well as porosity and magnetic parameters. As the concentration of magnetite nanoparticles increased, so did the blood temperature distribution. As a result, the immersion of magnetite nanoparticles improved the physical characteristics of the blood. These findings also demonstrated that magnetic parameters and Eckert number play an essential role in increasing heat transfer rates.

1 Introduction

Radiotherapy and chemotherapy are frequently applied to treat patients with cancer. However, the combination of these treatments may be inadequate to achieve a cure in some cases. Thus, the development of advanced and novel tactics may provide oncologists with additional therapeutic possibilities. A laboratory in Spain recently produced an artificial magnetic bacterium that, when consumed, can trigger a charged magnetism compass to mark and destroy tumors because the compass rotation speed heats and melts tumors. This method is based on hyperthermia caused by magnets, which is an exploratory treatment method in which magneto-nanoparticle-saturated tumors are subjected to a discontinuous magnetic field. This treatment begins by immersing a tumor in iron magneto-nanoparticles. Every cell in the body requires oxygen to function, and tumors cannot grow beyond the size of a sugar pill without it. Thus, tumors produce hormones that permit them to obtain oxygen-rich blood by hijacking surrounding blood vessels. Moreover, because blood arteries grow in tumors in an unorganized and faster manner, they are porous and defective. When ferromagnetic iron nanoparticles are infused into blood circulation, they travel throughout the body, avoiding healthy blood vessels unless they enter the leakages that nourish tumors. Mathuriya et al. (2015)reported that these vaccinated magnetic iron nanomaterials eventually pass through the blood unless they reach a tumor’s blood generator, in which these particles accumulate. Magnetic nanoparticles show potential as a drug conveyance module because of their large surface area, high viability, low toxicity, and volume proportions. Furthermore, magnetic hyperthermia uses magnetic nanoparticles to reduce tumor volume and to target and eliminate malignant cells. Magnetic bio partitioning is useful for detaching a specific atom from a catalog of molecules. One example is the magnetic bio partitioning used to restrict viral RNA for further investigation by polymerase chain reaction. Furthermore, magnetic particles exhibit imaging characteristics, making them useful for multimodal theranostics. These characteristics of magnetic nanomaterials allow simultaneous treatment and diagnostics (Anik et al. (2021). Kong et al. (2014) and Cui et al. (2012) used an unsteady applied magnetic field impact to examine the movement of magnetotactic bacteria (MTB) in a Newtonian fluid. The authors addressed the swimming motion of MTB from a fluid dynamics standpoint in conjunction with an entire three-dimensional Stokes flow. Vincenti et al. (2018) scrutinized the effect of a magnetic field on micro-swimmer suspensions in liquid. Furthermore, Nagaraj et al. (2018) reported on the joint effect of electric and magnetic fields on the synovial fluid in a biological context. Bhatti (2021) recently investigated nanomedicine utilizing suspensions of magnetized gold $\left(Au\right)$ nanoparticles. Afridi et al. (2019) explored the effect of thermal dissipation and entropy formation on the flow of a hybrid nanofluid across a curved sheet. Moreover, it is practical to use a spreading twisted surface for interstitial nanoparticle flow, in which artificial magnetic bacteria swim within biological cells. Shukla et al. (2019) examined the effects of viscoelasticity factors on second-order fluid in carotid artery blood flow. The HAM was used to initiate an entropy creation evaluation of time-dependent second-grade nanoliquid and heat transfer under the influence of a magnetic field. The authors discovered that increasing the second-order viscoelastic and magnetic values increased the entropy production number.

Many studies have proposed strategies for mathematical models within the human body, including the flow of fluid across a curved surface. Several investigators have also considered abdominal fluid flowing through biological cells as a non-Newtonian Powell–Eyring fluid. Saleem and Munawar (2016) examined blood flow via a stenotic artery in a constant magnetic field by assuming that blood within the artery was an Powell–Eyring fluid. Hina et al. (2016) investigated the heat transfer characteristics of a Powell–Eyring fluid in peristaltic flow within a curved channel with compliant walls. According to Riaz et al. (2019), the heat transfer procedure in the human body is a complex process that includes heat movement in tissues, membrane pores, electromagnetic radiation emitted by cell phones, exterior interface, metabolic heat production, and arterial-venous blood circulation. Their research aimed to determine the impact of bioheat and mass transfer in the peristaltic movement of an Powell–Eyring liquid in a three-dimensional rectangular cross section in the context of the human thermoregulation framework and thermotherapy. Hussain et al. (2020) numerically explored flow and explained blood flow behavior through tapered arteries as a non-Newtonian Powell–Eyring fluid. Asha and Sunitha (2018), Gholinia et al. (2019), Mallick and Misra (2019), Sultan et al. (2019), and Basha and Sivaraj (2021) conducted relevant research on this model. In the presence of a magnetic field generated using magnetite $\left({Fe}_3{O}_4\right)$, Yasmin (2022), Alyousef et al. (2023), Yasmin et al. (2023a), Yasmin et al. (2023b), and Yasmin et al. (2023c) performed biomedical investigations of fluid flow and studied nanofluid flow and hybrid nanofluids experimentally and theoretically, with stability analysis in the context of energy storage and other applications.

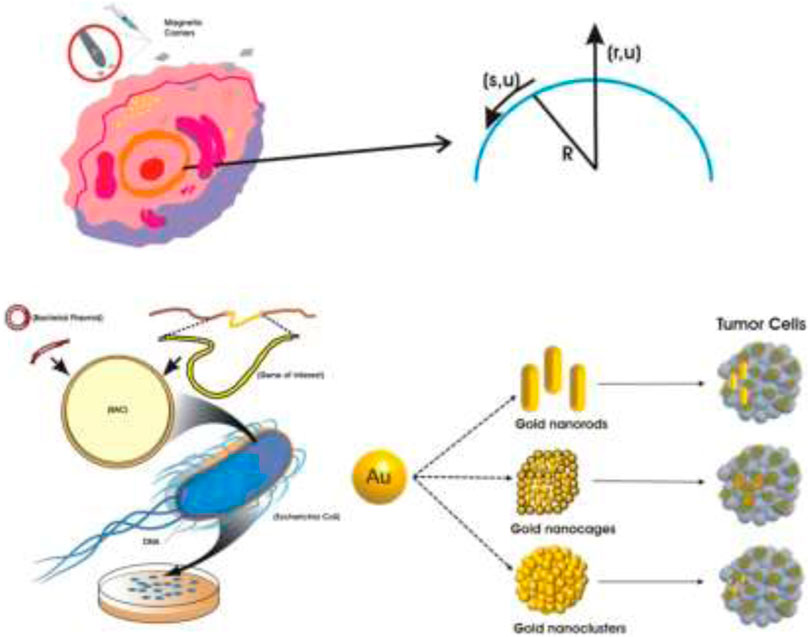
Based on these previous findings, the present study considered the growth of artificial magnetic bacteria in a non-Newtonian Powell–Eyring nanofluid on a stretching curved surface using a porous medium. The variable fluid thermal conductivity of the nanofluid was considered. As shown in Figure 1, curvilinear coordinates were used to model mathematical expressions across the curved biological boundary. This investigation also used magnetite nanoparticles. The temperature, concentration, and velocity of magnetite/blood in biological cells were acquired by the homotopy analysis method (HAM) via MATHEMATICA and depicted in a set of plots. Additionally, different scenarios were developed by varying the impact of dimensionless parameters, and distinct cases were constructed to obtain maximum reference data. The magnetic bacterium function as a magnetically charged compass to mark and abolish tumors by revolving at such a high rate that tumors heat and melt. Section 2 provides the mathematical formulas and all relevant details. Section 3 presents the physical quantities and the solution method, and its convergence with the validation of the results is shown in Sections 4 and 5. Section 6 includes the results and discussion. Finally, Section 7 contains the conclusions.

FIGURE 1

FIGURE 1. Fluid flow configuration and coordinate system.

2 Mathematical formulas

We assumed a two-dimensional unsteady boundary layer Powell–Eyring nanofluid flow on a strained curved surface using a porous medium that was a spiral in a circle with radius $R$ around the curvilinear coordinates. The stretching surface in the $s-direction$ had a velocity $u=U_w$ and was vertical to the $r-direction$. A magnetic field of intensity $B\left(t\right)$ was applied in the vertical direction. The nanofluid was embedded in the porous medium, and its flow behavior in the porous medium was accounted for by using the Brinkman model. The effects of variable thermal conductivity, heat generation/absorption, and joule dissipation were all considered. We used reaction–diffusion equations to explicitly model the dynamics of the bacterial density ${\rho }_n$ and nutrient concentration $n$.

2.1 Formal model and geometry

Figure 1 shows the geometry of the flow problem along with the coordinate system, velocity field, and other details.

2.1.1 Governing equations and boundary conditions after applying assumptions

Navier–Stokes flow is a type of fluid movement in which the spinning speed of the flow, $U_w$, is extremely low and the typical dimension $a$ is slight. The Stokes estimate is commonly used to describe the motion of magnetic bacteria because it ignores the inertial term in the Navier–Stokes equation by using a low Reynolds number. Thus, the Navier–Stokes and continuity equations govern the fluid speed produced by swimming magnetotactic bacteria. The theory of rate mechanisms was utilized to deduce the Powell–Eyring model (1994) to define shear in non-Newtonian flow. The shear tensor in the Powell–Eyring fluid model is given by (Riaz et al. (2019)

$\mathit{\tau }=\mu \nabla \mathit{V}+\frac{1}{{\beta }_1}{\sinh }^{-1}\left(\frac{1}{c_1}\nabla \mathit{V}\right)(1)$

and

${\sinh }^{-1}\left(\frac{1}{c_1}\nabla \mathit{V}\right)\approx \left(\frac{1}{c_1}\nabla \mathit{V}\right)-\frac{1}{6}{\left(\frac{1}{c_1}\nabla \mathit{V}\right)}^3,\hspace{1em}\left|\frac{1}{c_1}\nabla \mathit{V}\right|\ll 1.(2)$

The appropriate governing equations to examine the foregoing fluid flow are as follows:

$\overline{r}\frac{\partial v}{\partial r}+r+R\frac{\partial u}{\partial s}=0,(3)$

$\frac{u^2}{\overline{r}}=\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial r},(4)$

$\begin{array}{c}{\rho }_{nf}\left(\frac{\partial u}{\partial t}+\nu \frac{\partial u}{\partial r}+\frac{R}{\overline{r}}u\frac{\partial u}{\partial s}+u\nu \right)=-\frac{R}{\overline{r}}\frac{\partial p}{\partial s}+\left({\mu }_{nf}+\frac{1}{{\beta }_1{c}_1}\right)\frac{\partial }{\partial r}\left(\frac{\partial u}{\partial r}+\frac{u}{\overline{r}}\right)\\ -\frac{1}{6{\beta }_1{c_1}^3}\frac{\partial }{\partial r}{\left(\frac{\partial u}{\partial r}+\frac{u}{\overline{r}}\right)}^3-{\sigma }_{nf}{B}^2\left(t\right)u-\frac{{\mu }_{nf}}{k_1}u,\end{array}(5)$

${\left(\rho C_p\right)}_{nf}\left(\frac{\partial T}{\partial t}+\nu \frac{\partial T}{\partial r}+\frac{R}{\overline{r}}u\frac{\partial T}{\partial s}\right)=\frac{1}{\overline{r}}\frac{\partial }{\partial r}\left(\overline{r}{k}_{nf}\left(T\right)\frac{\partial T}{\partial r}\right)+{\sigma }_{nf}{B}^2\left(t\right)u^2+Q^{*}\left(T-T_{\infty }\right),(6)$

$\left(\frac{\partial {\rho }_n}{\partial t}+v\frac{\partial {\rho }_n}{\partial r}+\frac{R}{\overline{r}}u\frac{\partial {\rho }_n}{\partial s}\right)=D_n\left(\frac{{\partial }^2{\rho }_n}{\partial r^2}+\frac{1}{\overline{r}}\frac{\partial {\rho }_n}{\partial r}\right)+A\left(n,t\right){\rho }_n,(7)$

$\left(\frac{\partial n}{\partial t}+v\frac{\partial n}{\partial r}+\frac{R}{\overline{r}}u\frac{\partial n}{\partial s}\right)=D_n\left(\frac{{\partial }^{2}n}{\partial r^2}+\frac{1}{\overline{r}}\frac{\partial n}{\partial r}\right)-\frac{A\left(n,t\right)}{Y}{\rho }_n.(8)$

subject to the boundary condition (Elgazery et al., 2022)

$\left.\begin{array}{c}u=U_w=\frac{as}{1-ct},\hspace{1em}v=0,\hspace{0.17em}T=T_w,\hspace{0.17em}{\rho }_n={\left({\rho }_n\right)}_w,\hspace{0.17em}n=n_{w}atr\to 0\\ u\to 0,\hspace{1em}\frac{\partial u}{\partial r}\to 0,\hspace{0.17em}T\to T_{\infty },\hspace{0.17em}{\rho }_n\to {\left({\rho }_n\right)}_{\infty },\hspace{0.17em}n\to n_{\infty },\hspace{0.17em}asr\to \infty \end{array}\right\}.(9)$

Here, $\overline{r}=r+R,B\left(t\right)=\frac{B_0}{\sqrt{1-ct}}$, $Y=\frac{{\left({\rho }_n\right)}_w-{\left({\rho }_n\right)}_{\infty }}{n_w-n_{\infty }}$ is the conversion factor, $A\left(n,t\right)=a\lambda \left(t\right)\frac{n}{\left(K_m+n\right)}$ represents the variable nutrient bacterial growth rate, and $\lambda \left(t\right)=\frac{{\lambda }_0}{1-ct}$ represents the maximum growth rate. In this present discussion, we assume that $n$ is greater than the Monod constant $K_m$ and that $a>0$ and $c\ge 0$ with dimension ${\left(time\right)}^{-1}$.

2.1.2 Similarity transformations and modeled ODEs

Using the following dimensionless similarity transformations (Elgazery et al., 2022),

$\left.\begin{array}{c}\xi =\sqrt{\frac{a}{{\nu }_f\left(1-ct\right)}}r,\hspace{1em}\\ u=\frac{as}{1-ct}{f}^{\prime }\left(\xi \right),\hspace{0.17em}p={\rho }_f{\left(\frac{as}{1-ct}\right)}^{2}P\left(\xi \right),\hspace{0.17em}T=T_{\infty }+\left(T_w-T_{\infty }\right)\theta \left(\xi \right),\\ {\rho }_n={\left({\rho }_n\right)}_{\infty }+\left({\left({\rho }_n\right)}_w-{\left({\rho }_n\right)}_{\infty }\right)\chi \left(\xi \right),\hspace{1em}n=n_{\infty }+\left(n_w-n_{\infty }\right)\omega \left(\xi \right).\end{array}\right\}(10)$

and using the aforementioned dimensionless quantity, the equation of continuity is satisfied, and after pressure elimination the governing Eqs 7–12 can be written as follows:

$\begin{array}{c}\left({\phi }_4+{\alpha }_1\right)\left[f^{IV}+\frac{2f^{‴}}{\overline{\xi }}-\frac{f^{″}}{{\left(\overline{\xi }\right)}^2}+\frac{f^{\prime }}{{\left(\overline{\xi }\right)}^3}\right]-{\phi }_{3}M\left(f^{″}+\frac{f^{\prime }}{\overline{\xi }}\right)-{\phi }_4{\beta }_0\left(f^{″}+\frac{f^{\prime }}{\overline{\xi }}\right)\\ -{\alpha }_2\left[\begin{array}{c}\left({f^{″}}^2+\frac{2f^{\prime }{f}^{″}}{\overline{\xi }}+\frac{{f^{\prime }}^2}{{\left(\overline{\xi }\right)}^2}\right)f^{IV}+\left({f^{″}}^2-\frac{3f^{\prime }{f}^{″}}{\overline{\xi }}-\frac{{f^{\prime }}^2}{{\left(\overline{\xi }\right)}^2}\right))\frac{f^{″}}{{\left(\overline{\xi }\right)}^2}+\frac{3{f^{\prime }}^3}{{\left(\overline{\xi }\right)}^5}\\ +2\left(f^{″}+\frac{f^{\prime }}{\overline{\xi }}\right){f^{‴}}^2+2\left(3{f^{″}}^2+\frac{2f^{\prime }{f}^{″}}{\overline{\xi }}-\frac{{f^{\prime }}^2}{{\left(\overline{\xi }\right)}^2}\right))\frac{f^{‴}}{\overline{\xi }}\end{array}\right]\\ +{\phi }_1\left[\frac{K\left(f{f}^{‴}-f^{\prime }{f}^{″}\right)}{\overline{\xi }}+\frac{K\left(f{f}^{″}-{f^{\prime }}^2\right)}{{\left(\overline{\xi }\right)}^2}-\frac{Kf{f}^{\prime }}{{\left(\overline{\xi }\right)}^3}-\frac{\gamma }{\overline{\xi }}\left(\frac{\xi }{2}{f}^{″}+f^{\prime }\right)-\frac{\gamma }{2}\left(\xi f^{‴}+3f^{″}\right)\right]]=0,\end{array}(11)$

$\begin{array}{c}{\phi }_5\left[\left(1+\beta \theta \right)\left({\theta }^{″}+\frac{{\theta }^{\prime }}{\overline{\xi }}\right)+\beta {\left({\theta }^{\prime }\right)}^2\right]+{\phi }_{3}MPrEc{f^{\prime }}^2\\ +{\phi }_2\mathit{Pr}\left[\left(\frac{Kf}{\overline{\xi }}-\frac{\gamma \xi }{2}\right){\theta }^{\prime }+\frac{Q}{{\phi }_2}\theta \right]=0,\end{array}(12)$

${\chi }^{″}+\frac{\chi }{\overline{\xi }}+Lb\left[(\frac{Kf}{\overline{\xi }}-\frac{\gamma \xi }{2}){\chi }^{\prime }+\lambda \left(\mathrm{\Omega }+\chi \right)\right]=0,(13)$

${\omega }^{″}+\frac{\omega }{\overline{\xi }}+Lb[(\frac{Kf}{\overline{\xi }}-\frac{\gamma \xi }{2}){\omega }^{\prime }+\lambda \left(\mathrm{\Omega }+\chi \right)]=0.(14)$

Similarly, pressure can be expressed as follows:

$\begin{array}{c}P\left(\xi \right)=\frac{\overline{\xi }}{2K}\left({\phi }_4+{\alpha }_1\right)\left[f^{‴}+\frac{f^{″}}{\overline{\xi }}-\frac{f^{\prime }}{{\left(\overline{\xi }\right)}^2}\right]+\frac{{\phi }_1}{2}\left[f{f}^{″}-{f^{\prime }}^2+\frac{f{f}^{\prime }}{\overline{\xi }}-\frac{\overline{\xi }}{K}\gamma \left(\frac{\xi }{2}{f}^{″}+f^{\prime }\right)\right]]\\ -\frac{\overline{\xi }}{2K}\left({\phi }_{3}M+{\phi }_1{\beta }_0\right)f^{\prime }+\frac{\overline{\xi }}{2K}{\alpha }_2{\left(f^{″}+\frac{f^{\prime }}{\overline{\xi }}\right)}^2\left(f^{‴}+\frac{f^{″}}{\overline{\xi }}-\frac{f^{\prime }}{{\left(\overline{\xi }\right)}^2}\right).\end{array}(15)$

subject to the boundary conditions

$\begin{array}{c}{f}^{\prime }\left(0\right)=\theta \left(0\right)=\chi \left(0\right)=\omega \left(0\right)=1,\hspace{1em}f\left(0\right)=0,\\ f^{\prime }\left(\infty \right)=f^{″}\left(\infty \right)=\theta \left(\infty \right)=\chi \left(\infty \right)=\omega \left(\infty \right)=0,\end{array}(16)$

where $\overline{\xi }=\xi +K$, $K=\sqrt{\frac{a}{{\nu }_f\left(1-ct\right)}}R$, $M=\frac{{\sigma }_f{B}_0^2}{{\rho }_{f}a}$, $\mathrm{\Omega }=\frac{{\left({\rho }_n\right)}_w}{{\left({\rho }_n\right)}_w-{\left({\rho }_n\right)}_{\infty }}$, ${\alpha }_1=\frac{{\mu }_f}{{\beta }_1{c}_1}$, ${\alpha }_2=\frac{a^3{s}^2}{{\beta }_1{c}_1^3{\rho }_f{\nu }_f^2{\left(1-ct\right)}^3}$, ${\beta }_0=\frac{{\mu }_f\left(1-ct\right)}{{\rho }_f{k}_{1}a}$, $Lb={\nu }_f/D_n$, $Q=\frac{1-ct}{a{\left(\rho C_P\right)}_f}{Q}^{*}$, and $\mathit{Pr}=\frac{\nu {\left(\rho C_P\right)}_f}{k_0}$ $\left(\mathit{Pr}\approx 21forblood\right).$

2.1.3 Thermo-physical characteristics of nanofluid

The thermo-physical characteristics of an effective nanofluid can be expressed as follows (Mallick and Misra, 2019; Yasmin, 2022; Alyousef et al., 2023):

${\mu }_{nf}={\phi }_1{\mu }_f,{\rho }_{nf}={\phi }_2{\rho }_f,\hspace{1em}{\left(\rho C_P\right)}_{nf}={\phi }_3{\left(\rho C_P\right)}_f,\hspace{0.17em}{\sigma }_{nf}={\phi }_5{\sigma }_f,(17)$

where

$\left.\begin{array}{c}{\phi }_2=\left(1-\varphi \right)+\frac{{\rho }_P}{{\rho }_f}\varphi ,\hspace{1em}{\phi }_3=\left(1-\varphi \right)+\varphi \frac{{\left(\rho C_P\right)}_P}{{\left(\rho C_p\right)}_f}\\ {\phi }_5=\frac{\left({\sigma }_P+2{\sigma }_f+2\varphi \left({\sigma }_P-{\sigma }_f\right)\right)}{\left({\sigma }_P+2{\sigma }_f-\varphi \left({\sigma }_P-{\sigma }_f\right)\right)},\hspace{1em}{\phi }_1={\left(1-\varphi \right)}^{-2.5}\end{array}\right\}.(18)$

Here, the index $f$ represents the base fluid and $P$ refers to the nanoparticles ($F{e}_3{O}_4$). The thermophysical characteristics of magnetite nanoparticles are given in Table 1. Moreover, the nanoliquid variable thermal conductivity can be considered as follows (Yasmin, 2022):

${\kappa }_{nf}\left(T\right)={\phi }_4{\kappa }_0\left(1+\beta \theta \left(\eta \right)\right),(19)$

where ${\phi }_4=\left(\frac{k_P+2k_f+2\varphi \left(k_P-k_f\right)}{k_P+2k_f-\varphi \left(k_P-k_f\right)}\right)$, $k_0$ represents the constant thermal conductivity of the base fluid and $\beta$ is a parameter used for variable thermal conductivity.

TABLE 1

TABLE 1. Thermophysical characteristics of ${Fe}_3{O}_4$ magnetite nanoparticles and blood (Alyousef et al., 2023; Yasmin et al., 2023a).

3 Physical quantities

The physical quantities of concern in the current research are expressed as follows:

$C_f=\frac{{\tau }_w}{{\rho }_f{U}_w^2},\hspace{1em}{Nu}_s=\frac{s{q}_w}{k_f\left(T_w-T_{\infty }\right)},\hspace{0.17em}{Nn}_s=\frac{s{q}_n}{D_n\left(n_w-n_{\infty }\right)},(20)$

where $C_f$ signifies the skin friction, $N{u}_s$ denotes the Nusselt number, and $N{n}_s$ represents the nutrient concentration. Moreover, ${\tau }_w$, $q_w$, and $q_n$ are the surface shear stress, heat flux, and wall nutrient concentration flux, respectively. These are defined as follows:

${\tau }_{rs}={\left[\left({\mu }_{nf}+\frac{1}{\beta c}\right)\left(\frac{\partial u}{\partial r}+\frac{u}{\overline{r}}\right)-\frac{1}{6\beta c^3}{\left(\frac{\partial u}{\partial r}+\frac{u}{\overline{r}}\right)}^3\right]}_{r=R},q_w=-k_{nf}{\left[\frac{\partial T}{\partial r}\right]}_{r=0},\hspace{1em}{q}_s=-D_n.(21)$

These quantities can be written in non-dimensional form as follows:

$\begin{array}{c}{C}_f{\left(R{e}_s\right)}^{1/2}=\left({\phi }_1+{\alpha }_1\right)\left(f^{″}\left(0\right)+\frac{f^{\prime }\left(0\right)}{\overline{\xi }}\right))-{\alpha }_2{\left(f^{″}\left(0\right)+\frac{f^{\prime }\left(0\right)}{\overline{\xi }}\right))}^3,\\ N{u}_s{\left(R{e}_s\right)}^{-1/2}=-\theta /\left(0\right),\\ \hspace{1em}N{n}_s{\left(R{e}_s\right)}^{-1/2}=-\omega /\left(0\right),\end{array}(22)$

where ${\left(R{e}_s\right)}^{1/2}=\sqrt{\frac{a}{{\nu }_f\left(1-ct\right)}}s$ represents the local Reynolds number.

4 Solution methods

To find the solution to the system of Eqs 11–14 under the boundary constraints (16), a HAM (Liao, 2004) approach was used and figures were sketched for convergence. The complete procedure is shown in Eqs 23–45.

The initial guesses were selected as follows:

$f_0\left(\eta \right)=1-e^{-\eta },{\theta }_0\left(\eta \right)=e^{-\eta },{\chi }_0\left(\eta \right)=e^{-\eta },{\omega }_0\left(\eta \right)=e^{-\eta }.(23)$

The linear operators are taken as $L_f,L_{\theta },L_{\chi },{\mathrm{a}\mathrm{n}\mathrm{d}L}_{\omega }$:

$L_f\left(f\right)=f^{‴}-f^{\prime },L_{\theta }\left(\theta \right)={\theta }^{″}-\theta ,L_{\chi }\left(\chi \right)={\chi }^{″}-\chi ,L_{\omega }={\omega }^{″}-\omega ,(24)$

which have the following properties:

$\begin{array}{c}{L}_f\left(c_1+c_2\eta +c_3{e}^{-\eta }+c_4{e}^{\eta }\right)=0,\hspace{1em}{L}_{\theta }\left(c_5{e}^{\eta }+c_6{e}^{-\eta }\right)=0,\\ L_{\chi }\left(c_7{e}^{-\eta }+c_8{e}^{\eta }\right)=0,\hspace{1em}{L}_{\omega }\left(c_9{e}^{-\eta }+c_{10}{e}^{\eta }\right)=0,\end{array}(25)$

where $c_i\left(i=1-10\right)$ are the constants in the general solution.

The resultant non-linear operatives $N_f,N_{\theta },N_{\chi },{\mathrm{a}\mathrm{n}\mathrm{d}N}_{\omega }$ are given as follows:

$\begin{array}{c}{N}_f\left[f\left(\eta ;p\right)\right]=\left({\mathrm{\phi }}_4+{\alpha }_1\right)\left[\frac{{\partial }^{4}f\left(\eta ;p\right)}{\partial {\eta }^4}+\frac{2}{\xi }\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}-\frac{1}{{\xi }^2}\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{{\xi }^3}\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right]\\ -{\phi }_{3}M\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)-{\phi }_4{\beta }_0\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)\\ \begin{array}{c}-{\alpha }_2\left[\begin{array}{c}\left({\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\right)}^2+\frac{2}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}+\frac{2}{{\xi }^2}{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\right)\frac{{\partial }^{4}f\left(\eta ;p\right)}{\partial {\eta }^4}\\ +\left({\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\right)}^2-\frac{3}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}-\frac{2}{{\xi }^2}{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\right)\frac{1}{{\xi }^2}\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\\ +\frac{3}{{\xi }^5}{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^3+2\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right){\left(\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}\right)}^2\\ +2\left(3{\left(\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\right)}^3+\frac{2}{\xi }\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}-\frac{1}{{\xi }^2}{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\right)\frac{1}{\xi }\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}\end{array}\right]\\ {\phi }_1\left[\begin{array}{c}\frac{k}{\xi }\left(f\left(\eta ;p\right)\frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}-\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\right)+\frac{k}{{\xi }^2}\left(f\left(\eta ;p\right)\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}-{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2\right)\\ \frac{k}{{\xi }^3}f\left(\eta ;p\right)\frac{\partial f\left(\eta ;p\right)}{\partial \eta }-\frac{\gamma }{\xi }\left(\frac{\xi }{2}\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}-\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)-\frac{\gamma }{2}\left(\xi \frac{{\partial }^{3}f\left(\eta ;p\right)}{\partial {\eta }^3}+3\frac{{\partial }^{2}f\left(\eta ;p\right)}{\partial {\eta }^2}\right)\end{array}\right],\end{array}\end{array}(26)$

$\begin{array}{c}{N}_{\theta }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right)\right]={\phi }_5\left[\left(1+\beta \frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right)\left(\frac{{\partial }^2\theta \left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right)+\beta {\left(\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right)}^2\right]]-\\ {\phi }_{3}MPrEc{\left(\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right)}^2+{\phi }_2\mathit{Pr}\left[\left(\frac{k_f}{\xi }-\frac{\gamma \xi }{2}\right)\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }+\frac{Q}{{\phi }_2}\theta \left(\eta ;p\right)\right],\end{array}(27)$

$N_{\omega }\left[f\left(\eta ;p\right),\omega \left(\eta ;p\right)\right]=\frac{{\partial }^2\omega \left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial \omega \left(\eta ;p\right)}{\partial \eta }+Lb\left[\begin{array}{c}\left(\frac{K}{\xi }f\left(\eta ;p\right)-\frac{\gamma \xi }{2}\right)\frac{\partial \omega \left(\eta ;p\right)}{\partial \eta }\\ +\lambda \left(\mathrm{\Omega }+\chi \left(\eta ;p\right)\right)\end{array}\right],(28)$

$N_{\chi }\left[f\left(\eta ;p\right),\chi \left(\eta ;p\right)\right]=\frac{{\partial }^2\chi \left(\eta ;p\right)}{\partial {\eta }^2}+\frac{1}{\xi }\frac{\partial \chi \left(\eta ;p\right)}{\partial \eta }+Lb\left[\left(\frac{K}{\xi }f\left(\eta ;p\right)-\frac{\gamma \xi }{2}\right)\frac{\partial \chi \left(\eta ;p\right)}{\partial \eta }+\lambda \left(\mathrm{\Omega }+\chi \left(\eta ;p\right)\right)\right]].(29)$

The fundamental concept of HAM is characterized in Cui et al. (2012), Kong et al. (2014), Mathuriya et al. (2015), and Anik et al. (2021). The zeroth-order problems from Eqs 9–12 are as follows:

$\left(1-p\right)L_f\left[f\left(\eta ;p\right)-f_0\left(\eta \right)\right]=p{\hslash }_f{N}_f\left[f\left(\eta ;p\right)\right],(30)$

$\left(1-p\right)L_{\theta }\left[\theta \left(\eta ;p\right)-{\theta }_0\left(\eta \right)\right]=p{\hslash }_{\theta }{N}_{\theta }\left[f\left(\eta ;p\right),\theta \left(\eta ;p\right)\right],(31)$

$\left(1-p\right)L_{\omega }\left[\omega \left(\eta ;p\right)-{\omega }_0\left(\eta \right)\right]=p{\hslash }_{\omega }{N}_{\omega }\left[f\left(\eta ;p\right),\omega \left(\eta ;p\right)\right],(32)$

$\left(1-p\right)L_{\chi }\left[\chi \left(\eta ;p\right)-{\chi }_0\left(\eta \right)\right]=p{\hslash }_{\chi }{N}_{\chi }\left[f\left(\eta ;p\right),\omega \left(\eta ;p\right),\chi \left(\eta ;p\right)\right].(33)$

The equivalent boundary conditions are as follows:

$\begin{array}{c}{\left.f\left(\eta ;p\right)\right|}_{\eta =0}=0,\hspace{1em}{\left.\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right|}_{\eta =0}=1,\hspace{0.17em}{\left.\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right|}_{\eta \to \infty }=0,\\ {\left.\theta \left(\eta ;p\right)\right|}_{\eta =0}=0,\hspace{1em}{\left.\theta \left(\eta ;p\right)\right|}_{\eta =\infty }=0,\\ \begin{array}{c}{\left.\omega \left(\eta ;p\right)\right|}_{\eta =0}=0,\hspace{1em}{\left.\omega \left(\eta ;p\right)\right|}_{\eta =\infty }=0,\\ {\left.\chi \left(\eta ;p\right)\right|}_{\eta =0}=0,\hspace{1em}{\left.\chi \left(\eta ;p\right)\right|}_{\eta =\infty }=0,\end{array}\end{array}(34)$

where $p\in \left[0,1\right]$ is the imbedding parameter and ${\hslash }_f,{\hslash }_{\theta },{\hslash }_{\omega },\mathrm{a}\mathrm{n}\mathrm{d}{\hslash }_{\chi }$ are used to control the convergence of the solution. When $p=0$ and $p=1$,

$f\left(\eta ;1\right)=f\left(\eta \right),\hspace{1em}\theta \left(\eta ;1\right)=\theta \left(\eta \right),\hspace{0.17em}\omega \left(\eta ;1\right)=\omega \left(\eta \right),\hspace{0.17em}\chi \left(\eta ;1\right)=\chi \left(\eta \right).(35)$

and expanding $f\left(\eta ;p\right),\theta \left(\eta ;p\right),\omega \left(\eta ;p\right),\mathrm{a}\mathrm{n}\mathrm{d}\chi \left(\eta ;p\right)$ in the Taylor’s series about $p=0$,

$\begin{array}{c}f\left(\eta ;p\right)=f_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{f}_m\left(\eta \right)p^m,\\ \theta \left(\eta ;p\right)={\theta }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\theta }_m\left(\eta \right)p^m,\\ \begin{array}{c}\omega \left(\eta ;p\right)={\omega }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\omega }_m\left(\eta \right)p^m,\\ \chi \left(\eta ;p\right)={\chi }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\chi }_m\left(\eta \right)p^m,\end{array}\end{array}(36)$

where

$\begin{array}{c}{f}_m=\frac{1}{m!}{\left.\frac{\partial f\left(\eta ;p\right)}{\partial \eta }\right|}_{p=0},\hspace{1em}{\theta }_m=\frac{1}{m!}{\left.\frac{\partial \theta \left(\eta ;p\right)}{\partial \eta }\right|}_{p=0},\\ {\omega }_m=\frac{1}{m!}{\left.\frac{\partial \omega \left(\eta ;p\right)}{\partial \eta }\right|}_{p=0},\hspace{1em}{\chi }_m=\frac{1}{m!}{\left.\frac{\partial \chi \left(\eta ;p\right)}{\partial \eta }\right|}_{p=0}.\end{array}(37)$

The secondary constraints ${\hslash }_f,{\hslash }_{\theta },{\hslash }_{\omega },{\mathrm{a}\mathrm{n}\mathrm{d}\hslash }_{\chi }$ are selected so that the series (27) converges at $p=1$; substituting $p=1$ in (27), we obtain:

$\begin{array}{c}f\left(\eta \right)=f_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{f}_m\left(\eta \right),\\ \theta \left(\eta \right)={\theta }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\theta }_m\left(\eta \right),\\ \begin{array}{c}\omega \left(\eta \right)={\omega }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\omega }_m\left(\eta \right),\\ \chi \left(\eta \right)={\chi }_0\left(\eta \right)+{\displaystyle \sum }_{m=1}^{\infty }{\chi }_m\left(\eta \right).\end{array}\end{array}(38)$

The $m^{th}-order$ problem satisfies the following:

$\begin{array}{c}{L}_f\left[f_m\left(\eta \right)-{\chi }_m{f}_{m-1}\left(\eta \right)\right]={\hslash }_f{R}_m^f\left(\eta \right),\\ L_{\theta }\left[{\theta }_m\left(\eta \right)-{\chi }_m{\theta }_{m-1}\left(\eta \right)\right]={\hslash }_{\theta }{R}_m^{\theta }\left(\eta \right),\\ \begin{array}{c}{L}_{\omega }\left[{\omega }_m\left(\eta \right)-{\chi }_m{\omega }_{m-1}\left(\eta \right)\right]={\hslash }_{\omega }{R}_m^{\omega }\left(\eta \right),\\ L_{\chi }\left[{\chi }_m\left(\eta \right)-{\chi }_m{\chi }_{m-1}\left(\eta \right)\right]={\hslash }_{\chi }{R}_m^{\chi }\left(\eta \right).\end{array}\end{array}(39)$

The following are the corresponding boundary conditions:

$\begin{array}{c}{f}_m\left(0\right)=f_m^{\prime }\left(0\right)={\theta }_m\left(0\right)={\omega }_m\left(0\right)={\chi }_m\left(0\right)=0,\\ f_m^{\prime }\left(\infty \right)={\theta }_m\left(\infty \right)={\omega }_m\left(\infty \right)={\chi }_m\left(\infty \right)=0.\end{array}(40)$

Here,

$\begin{array}{c}\begin{array}{c}{R}_m^f\left(\eta \right)=\left({\phi }_4+{\alpha }_1\right)\left[f_{m-1}^{⁗}+\frac{2}{\xi }{f}_{m-1}^{‴}-\frac{1}{{\xi }^2}{f}_{m-1}^{″}+\frac{1}{{\xi }^3}{f}_{m-1}^{\prime }\right]\\ -{\phi }_{3}M\left(f_{m-1}^{″}+\frac{1}{\xi }{f}_{m-1}^{\prime }\right)-{\phi }_4{\beta }_0\left(f_{m-1}^{″}+\frac{1}{\xi }{f}_{m-1}^{\prime }\right)\end{array}\\ -{\alpha }_2\left(\begin{array}{c}\left(\begin{array}{c}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{″}{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{⁗}+\frac{2}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{⁗}\\ +\frac{2}{{\xi }^2}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{\prime }{f}_l^{⁗}\end{array}\right)+\\ \left(\frac{1}{{\xi }^2}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{″}{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{″}-\frac{3}{{\xi }^2}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{″}-\frac{2}{{\xi }^4}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{\prime }{f}_l^{″}\right)\\ \begin{array}{c}+\frac{3}{{\xi }^5}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{\prime }{f}_l^{\prime }+2\left({\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{″}{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{‴}{f}_l^{‴}+\frac{1}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{‴}{f}_l^{‴}\right)\\ +2\left(\frac{3}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{″}{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{‴}+\frac{2}{{\xi }^2}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{″}{f}_l^{‴}-\frac{1}{{\xi }^3}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{\displaystyle \sum }_{l=0}^k{f}_{k-l}^{\prime }{f}_l^{‴}\right)\end{array}\end{array}\right)\\ +{\phi }_1\left(\begin{array}{c}\frac{k}{\xi }\left({\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}{f}_k^{‴}-{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{f}_k^{″}\right)+\frac{k}{{\xi }^2}\left({\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}{f}_k^{″}-{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{f}_k^{\prime }\right)\\ -\frac{k}{{\xi }^3}{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}{f}_k^{\prime }-\frac{\gamma }{\xi }\left(\frac{\xi }{2}{f}_{m-1}^{″}-f_{m-1}^{\prime }\right)-\frac{\gamma }{2}\left(\xi f_{m-1}^{‴}+3f_{m-1}^{″}\right)\end{array}\right),\end{array}(41)$

$\begin{array}{c}{R}_m^{\theta }\left(\eta \right)={\phi }_5\left(\left({\theta }_{m-1}^{″}+\frac{1}{\xi }{\theta }_{m-1}^{\prime }\right)+\beta \left({\displaystyle \sum }_{k=0}^{m-1}{\theta }_{m-1-k}^{\prime }{\theta }_k^{″}+\frac{1}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{\theta }_{m-1-k}^{\prime }{\theta }_k^{\prime }\right)+\beta {\displaystyle \sum }_{k=0}^{m-1}{\theta }_{m-1-k}^{\prime }{\theta }_k^{\prime }\right)\\ -{\phi }_{3}MPrEc{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}^{\prime }{f}_k^{\prime }+{\phi }_2\mathit{Pr}\left(\left(\frac{k_f}{\xi }-\frac{\gamma \xi }{2}\right){\theta }_{m-1}^{\prime }+\frac{Q}{{\phi }_2}{\theta }_{m-1}\right),\end{array}(42)$

$R_m^{\omega }\left(\eta \right)={\omega }_{m-1}^{″}+\frac{1}{\xi }{\omega }_{m-1}^{\prime }+Lb\left[\left(\frac{K}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}{\omega }_k-\frac{\gamma \xi }{2}{\omega }_{m-1}^{\prime }\right)+\lambda \left(\mathrm{\Omega }+{\chi }_{m-1}\right)\right],(43)$

$R_m^{\chi }\left(\eta \right)={\chi }_{m-1}^{″}+\frac{1}{\xi }{\chi }_{m-1}^{\prime }+Lb\left[\left(\frac{K}{\xi }{\displaystyle \sum }_{k=0}^{m-1}{f}_{m-1-k}{\chi }_k-\frac{\gamma \xi }{2}{\chi }_{m-1}^{\prime }\right)+\lambda \left(\mathrm{\Omega }+{\chi }_{m-1}\right)\right],(44)$

where

${\chi }_m=\left\{\begin{array}{c}0,\hspace{1em}ifp\le 1,\\ 1,\hspace{1em}ifp>1.\end{array}\right.(45)$

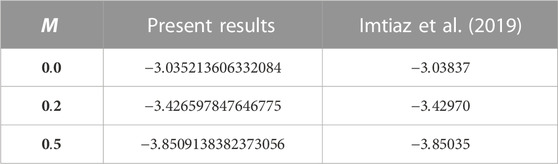
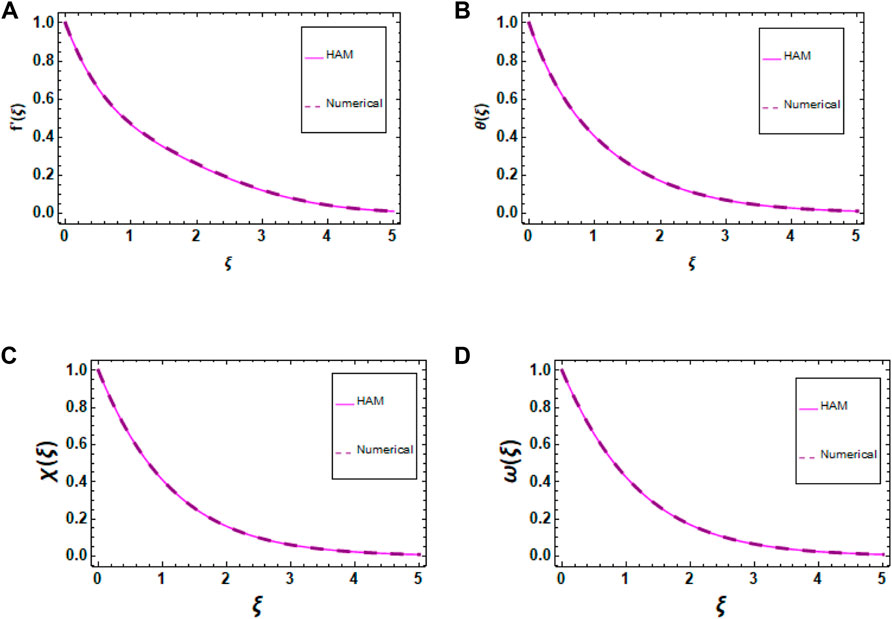
5 Validations of the results

This section shows the result validations graphically and numerically. The results obtained using the semi-analytical HAM method are compared to the numerical (ND-Solved) techniques for temperature $\theta \left(\xi \right)$, pressure $p\left(\xi \right)$, velocity $f^{\prime }\left(\xi \right)$, bacterial density field $\chi \left(\xi \right)$, and nutrient concentration $\omega \left(\xi \right)$.

Table 2(a–d) shows the results of the HAM solutions, numerical solutions, and the absolute errors for temperature $\theta \left(\xi \right)$, pressure $p\left(\xi \right)$, velocity $f^{\prime }\left(\xi \right)$, bacterial density field $\chi \left(\xi \right)$, and nutrient concentration $\omega \left(\xi \right)$. We observed excellent agreement between the results for all profiles. Table 3 shows a comparison between the current and previous results (Elgazery et al., 2022) for skin friction and it was found that both results agreed. Figures 2A–D show comparison between HAM and numerical solutions for the temperature θ(ξ), pressure p(ξ), velocity f′(ξ), the bacterial density field χ(ξ), nutrient concentration ω(ξ). An excellent agreement is found between both results for all profile.

TABLE 2

TABLE 2. Tables 2(a-d).

TABLE 3

TABLE 3. Comparison of skin friction.

FIGURE 2

FIGURE 2. (A–D) Graphical validations of the HAM with numerical methods for $f^{\prime }\left(\xi \right)$, $p\left(\xi \right)$, $\theta \left(\xi \right),$ and $\chi \left(\xi \right)$.

6 Results and discussion

This investigation used HAM to graphically explore the efficacy of numerous governing factors, such as the curvature factor $K$, volume fraction $\varphi$, maximum bacteria growth rate $\lambda$, fluid parameter ${\alpha }_1$, unsteady parameter $\gamma$, magnetic parameter $M$, porosity parameter ${\beta }_0$, non-dimensional bacterial density difference $\mathrm{\Omega }$, non-dimensional generation/absorption coefficient, bioconvection Lewis number $Lb$, and variable thermal conductivity $\beta$, on the temperature $\theta \left(\xi \right)$, pressure $p\left(\xi \right)$, velocity $f^{\prime }\left(\xi \right)$, bacterial density field $\chi \left(\xi \right)$, nutrient concentration $\omega \left(\xi \right)$, Nusselt number, skin friction, and density of nutrient concentration.

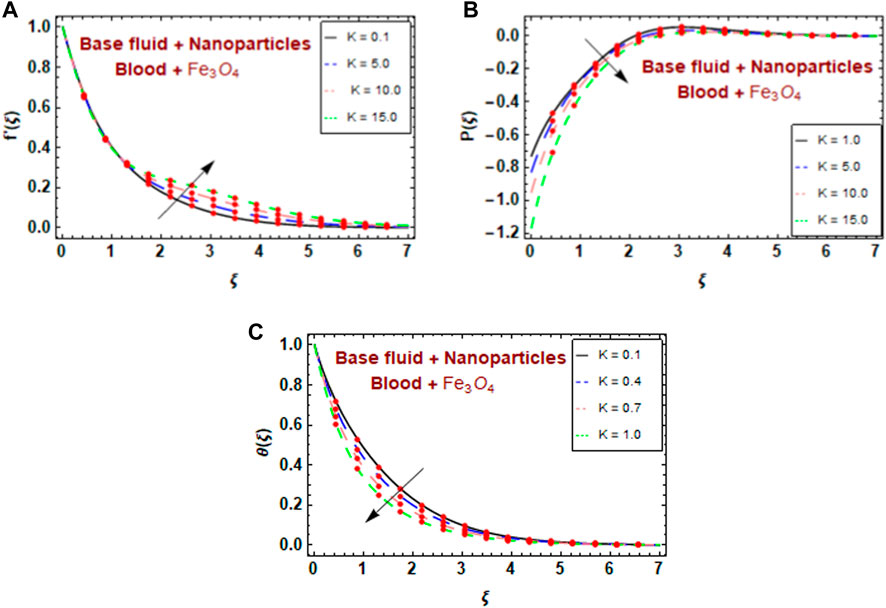
Figures 3A–C show how the curvature factor K affects the velocity $f^{\prime }\left(\xi \right)$, pressure $P\left(\xi \right)$, and temperature $\theta \left(\xi \right)$ curves, in which increases in velocity and decreases in pressure resulted in increased curvature parameter values. Tumor blood flow usually decreases as tumors grow larger; however, mathematical examination predicted that enhancing the curvature parameter would boost tumor blood flow, which may enhance medical treatment.

FIGURE 3

FIGURE 3. (A–C) Variations in $f^{\prime }\left(\xi \right)$, $p\left(\xi \right)$, and $\theta \left(\xi \right)$ for distinct numbers of $K$.

Furthermore, as shown in Figures 4A, B increasing the curvature parameter value increased the radius of the curved surface, which increased the velocity and decreased the pressure. Due to vascular damage, the environment within the tumors became hypoxic, acidic, and nutritionally deficient when heated. These suboptimal environmental changes enhance the tumor cell hyperthermia response, inhibit thermal damage repair, and interfere with the development of thermal tolerance. At high temperatures, the acidic environment enhances the tumor cell response to certain drugs. As shown in Figure 4C, the temperature decreased as the curvature factor increased, and increased with increasing unsteady parameter. In medical treatment, to enhance the tumor cell response to magnetic magnetite nanoparticles, $\gamma$ should be increased, thus increasing the environmental temperature of the nanofluid. Figures 4A, B show increased velocity and decreased pressure with increasing unsteady parameter $\gamma$.

FIGURE 4

FIGURE 4. (A–C) Variations in $f^{\prime }\left(\xi \right)$, $p\left(\xi \right)$, and $\theta \left(\xi \right)$ for distinct numbers of $\gamma$.

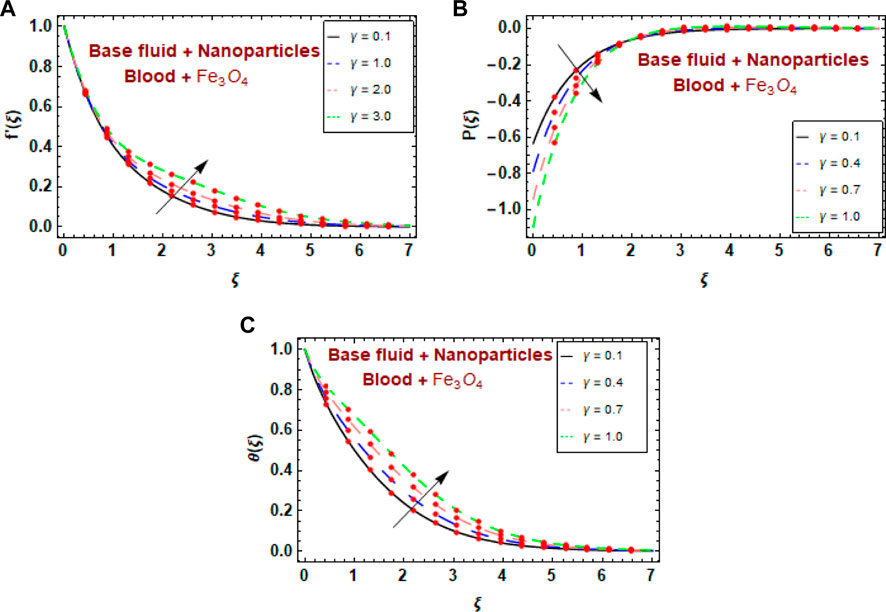
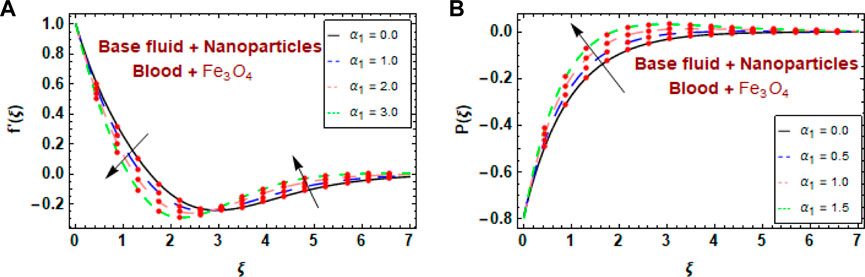
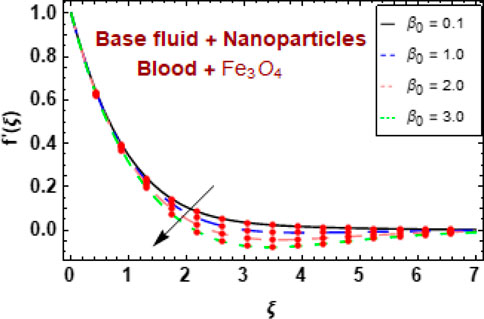
Figures 5A, B show the effect of the fluid parameter ${\alpha }_1$ on velocity and pressure. Figure 5A shows that the blood velocity first decreased and then gradually increased as the fluid parameter value increased. Figure 5B shows that the blood pressure curves increased for large fluid parameter values.

FIGURE 5

FIGURE 5. (A,B) Variations in $f^{\prime }\left(\xi \right)$ and $p\left(\xi \right)$ for distinct numbers of ${\alpha }_1$.

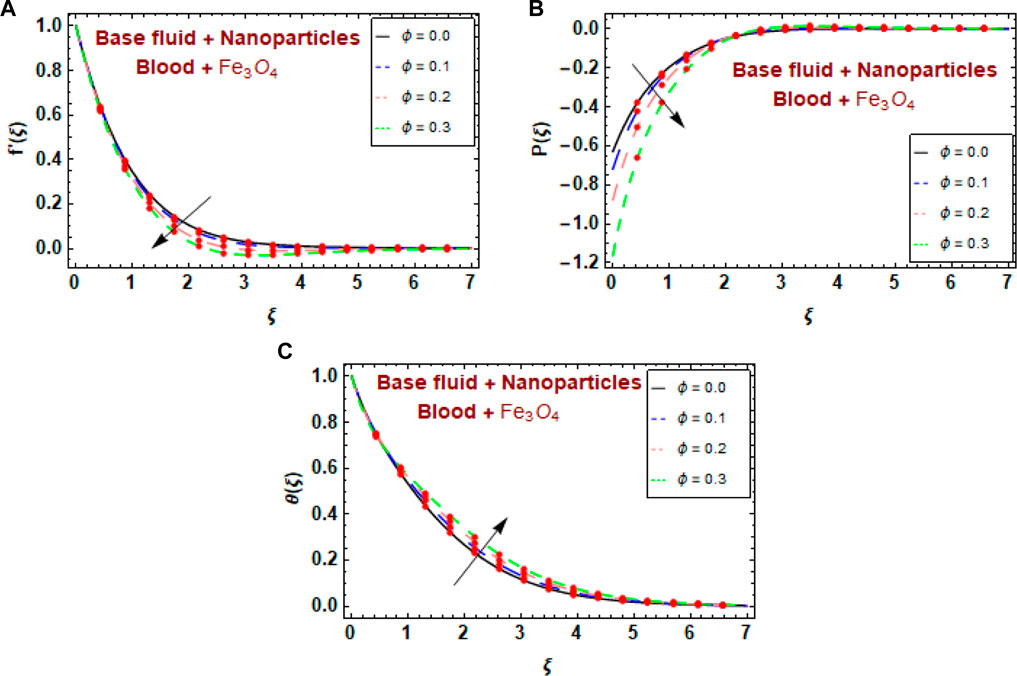
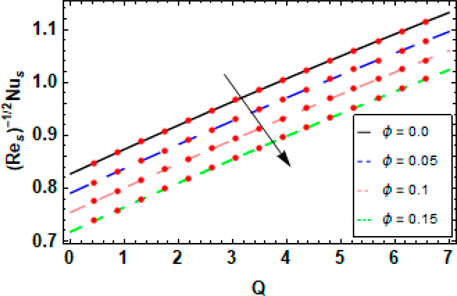
Figures 6A–C show how the magnetite nanoparticle volume fraction parameter $\varphi$ affects the velocity $f^{\prime }\left(\xi \right)$, pressure $P\left(\xi \right)$, and temperature $\theta \left(\xi \right)$ curves. As the volume fraction of magnetite nanoparticles increased, the velocity profile and pressure distribution decreased. The mathematical explanation showed that magnetite nanoparticles reduced blood flow pressure, which is a beneficial outcome in the medical treatment of cancer, thus demonstrating the potential effectiveness of magnetite nanoparticles in medical therapy. As the concentration of magnetite nanoparticles increased, so did the blood temperature distribution. Therefore, passing magnetite nanoparticles through the blood improves its physical properties.

FIGURE 6

FIGURE 6. (A–C) Variations in $f^{\prime }\left(\xi \right)$, $p\left(\xi \right)$, and $\theta \left(\xi \right)$ for distinct numbers of $\varphi$.

The impact of the porosity parameter on blood velocity is shown in Figure 7, in which the blood velocity decreased as the porosity increased. This effect occurred because increasing blood porosity increased the interactions and fraction between the flow and blood cells, resulting in decreased velocity.

FIGURE 7

FIGURE 7. Variations in $f^{\prime }\left(\xi \right)$ for distinct numbers of ${\beta }_0$.

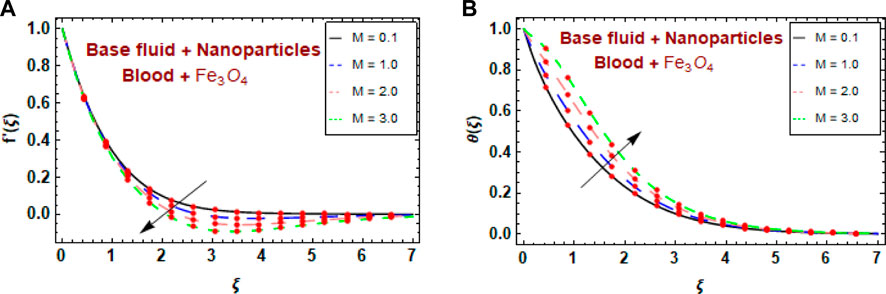
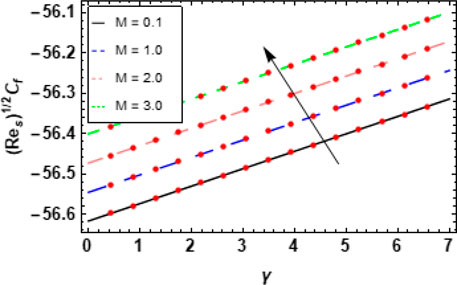
The exploration of the magnetic factor M showed that opposition in artificial magnetic bacteria swimming within the blood flow was a major factor. Figures 8A, B show the effects of M on the velocity $f^{\prime }\left(\xi \right)$ and temperature $\theta \left(\xi \right)$, respectively. When the magnetic factor $M$ increased, $f^{\prime }\left(\xi \right)$ decreased and $\theta \left(\xi \right)$ increased. The changes in magnetite/blood velocity were inversely related to the magnetic factor. Thus, applying a magnetic field to an electrically conducting liquid created a resistive Lorentz force that tended to diminish the fluid flow while increasing the temperature.

FIGURE 8

FIGURE 8. (A,B) Variations in $f^{\prime }\left(\xi \right)$ and $\theta \left(\xi \right)$ for distinct numbers of $M$.

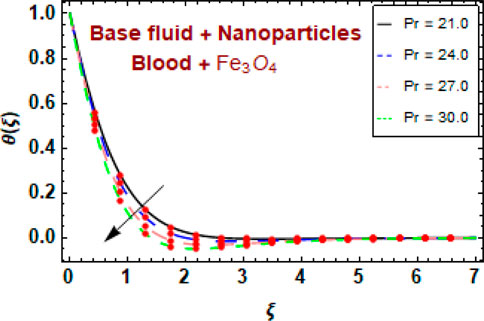
Figure 9 depicts the influence of the Prandtl number $\mathit{Pr}$ on the temperature $\theta \left(\xi \right)$. As $\mathit{Pr}$ increased, the temperature decreased. The thermal boundary layer thickness decreased as the Prandtl number increased. The Prandtl number is the momentum diffusivity/thermal diffusivity ratio and it governs the relative thickening of the momentum and thermal boundary layers in heat transfer.

FIGURE 9

FIGURE 9. Variations in $\theta \left(\xi \right)$ for distinct numbers of $\mathit{Pr}$.

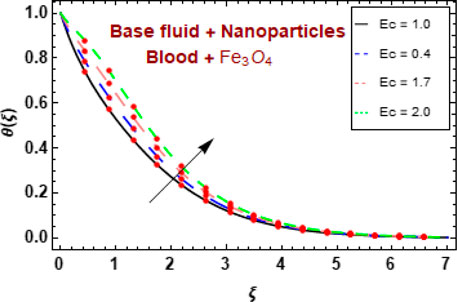
Figure 10 shows the temperature distribution for various Eckert number $Ec$ values. The relationship between heat enthalpy difference and flow kinetic energy is known as the Eckert number $Ec$. Therefore, increasing the Eckert number increases the kinetic energy. Furthermore, temperature is defined as the average kinetic energy. Consequently, the temperature of the fluid increased with increasing Eckert number $Ec$.

FIGURE 10

FIGURE 10. Variations in $\theta \left(\xi \right)$ for distinct numbers of $Ec$.

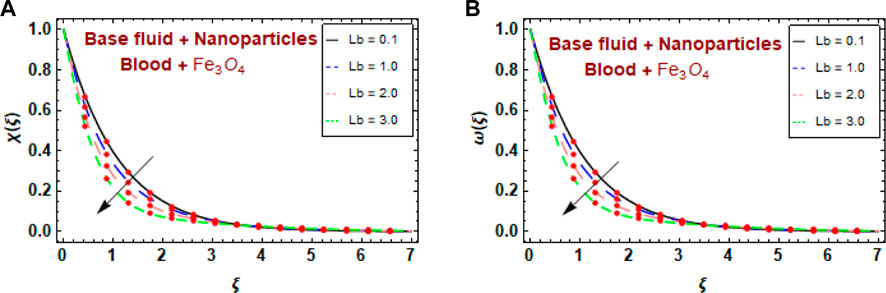
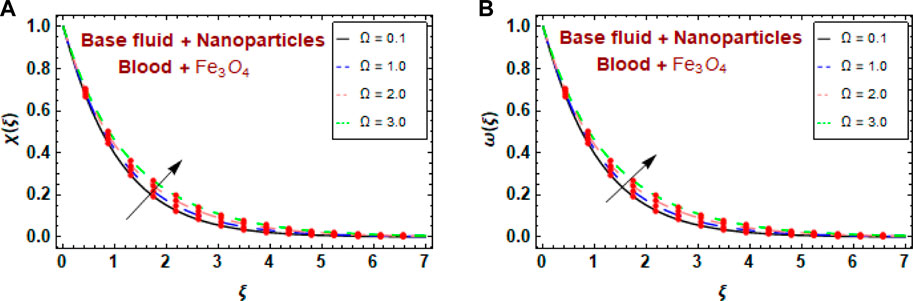
Figures 11A, B show the effect of the bioconvection Lewis number $Lb$ on the bacterial density $\chi \left(\xi \right)$ and nutrient concentration $\omega \left(\xi \right)$, in which both bacterial density and nutrient concentration decreased with increasing bioconvection Lewis number $Lb$.

FIGURE 11

FIGURE 11. (A,B) Variations in $\chi \left(\xi \right)$ and $\omega \left(\xi \right)$ for distinct numbers of $Lb$.

Figures 12A, B show the influence of the bacterial difference density parameter $\mathrm{\Omega }$ on the bacterial density field $\chi \left(\xi \right)$ and nutrient concentration $\omega \left(\xi \right)$. As the $\mathrm{\Omega }$ increased, so did the bacterial density and nutrient concentration.

FIGURE 12

FIGURE 12. (A,B) Variations in $\chi \left(\xi \right)$ and $\omega \left(\xi \right)$ for distinct numbers of $\mathrm{\Omega }$.

The effects of the bacteria maximum growth rate $\lambda$ on the bacterial density and nutrient concentration are shown in Figures 13A, B, in which the bacterial density and nutrient concentration fields improved when the bacterial maximum growth rate increased.

FIGURE 13

FIGURE 13. (A,B) Variations in $\chi \left(\xi \right)$ for distinct numbers of $\lambda$.

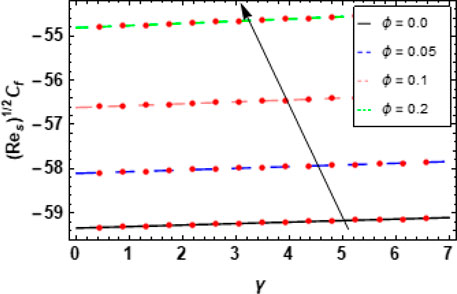
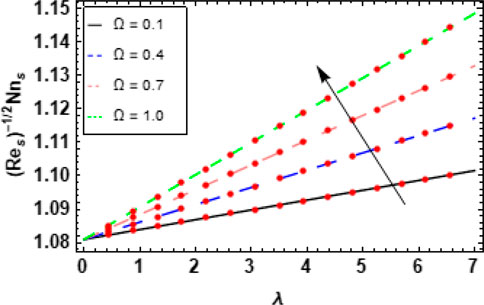
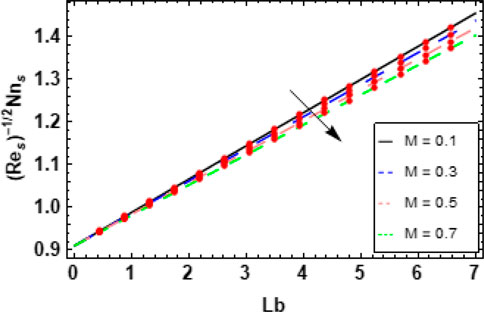
6.1 Skin friction coefficients and Nusselt numbers

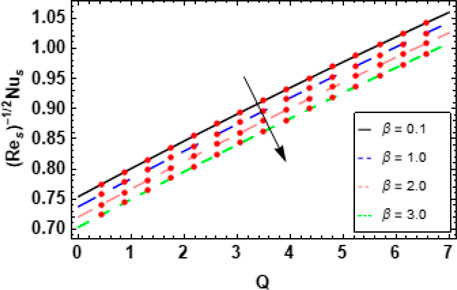
Figures 14, 15 show the effects of the nanoparticle volume fraction $\varphi$ and magnetic factor $M$ on the skin friction coefficient, with mainly significant influences on the unsteady constraint $\gamma$ on skin friction. The skin friction increased with increasing $\varphi$ and $M$.

FIGURE 14

FIGURE 14. Influences of $\gamma$ and $\varphi$ on skin friction.

FIGURE 15

FIGURE 15. Influences of $\gamma$ and $M$ on skin friction.

Figure 16 shows the effects of the volume fraction $\varphi$ and variable thermal conductivity constraint $\beta$ on the Nusselt number. The Nusselt number decreased with increasing $\varphi$. Figure 17 shows the effects of $\beta$ against $Q$ on the Nusselt number distribution. The Nusselt number decreased with increasing $\beta$. Figure 18 shows the variation in the nutrient concentration density because of the bacterial difference density $\mathrm{\Omega }$ and the optimum bacterial growth rate $\lambda$. When both the bacterial difference density and the optimum bacterial growth rate increased, the nutrient concentration density increased. These mathematical outcomes showed that in the medical treatment of cancer using magnetite nanoparticles and artificial bacteria, it is preferable to moderate the bacterial difference density and the bacterial growth rate to increase nutrients in normal cells while decreasing nutrient consumption in tumor cells. Figure 19 also shows the behavior of the nutrient concentration density as a function of the bioconvection Lewis number $Lb$ and the magnetic parameter $M$. The nutrient concentration density value improved as the Lewis number increased but decreased as the magnetic parameter increased. Physically, in medical treatment, increasing the magnetic factor and decreasing the ratio of thermal diffusivity to mass diffusivity are recommended to increase nutrient consumption in normal cells while decreasing nutrient consumption in tumor cells.

FIGURE 16

FIGURE 16. Effects of $Q$ and $\varphi$ on $N{u}_s{\left(R{e}_s\right)}^{-1/2}$.

FIGURE 17

FIGURE 17. Effects of $Q$ and $\beta$ on $N{u}_s{\left(R{e}_s\right)}^{-1/2}$.

FIGURE 18

FIGURE 18. Influences of $\mathrm{\Omega }$ and $\lambda$ on $N{n}_s{\left(R{e}_s\right)}^{-1/2}$.

FIGURE 19

FIGURE 19. Influences of $Lb$ and $M$ on $N{n}_s{\left(R{e}_s\right)}^{-1/2}$.

7 Conclusion

This study aimed to determine the effectiveness of an external magnetic field on bacteria enclosed by thousands of magnetic magnetite nanoparticles. Variable thermal conductivity and Joule heating were used in the interstitial nanofluid, in which artificial bacteria swam in a biological cell. The unsteady motion of a Powell–Eyring fluid in two dimensions was considered. A porous stretching wall was used as a curved surface structure. To convert the governing non-linear PDEs into non-linear ODEs, suitable transformations were exploited. The HAM was used to resolve the semi-analytical results of non-linear ODEs. This mathematical procedure demonstrates unnatural magnetic bacterium that can function like a compass that is magnetically charged to mark and abolish tumors by spinning at such a high rate that tumors heat and melt. We discovered the following:

• The blood velocity improved at higher curvature parameter values and was unsteady when the velocity decreased for large magnetic factor, volume fraction, and porosity parameter values.

• The blood velocity profile began to decrease and then gradually increased with increasing fluid parameter values.

• The mathematical description revealed that magnetite nanoparticles lower blood pressure, which is a beneficial outcome in the clinical consideration of cancer, and demonstrates the effectiveness of magnetite nanoparticles in such medical therapy.

• The mathematical analysis showed that to enhance the reaction of tumor cells to several drugs in an acidic environment, temperatures should be raised by increasing the characteristics of the nearby environment, including the unsteady parameter, Eckert number, magnetite nanoparticles, and magnetic parameters.

• To increase nutrient consumption in normal cells while decreasing nutrient consumption in tumor cells, our mathematical outcomes showed that the bacterial difference density, bacterial growth rate, and Lewis number should be moderated in the medical treatment of cancer using magnetite nanoparticles and artificial bacteria.

• For the intensification of the unsteady parameter, applied magnetic fields should be considered.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made substantial, direct, and intellectual contributions to the work and approved it for publication.

Funding

The project was financed by the Lucian Blaga University of Sibiu through research grant number LBUS-IRG-2022-08.”

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afridi, M. I., Alkanhal, T. A., Qasim, M., and Tlili, I. (2019). Entropy generation in Cu-Al2O3-H2O hybrid nanofluid flow over a curved surface with thermal dissipation. Entropy 21, 941. doi:10.3390/E21100941

CrossRef Full Text | Google Scholar

Alyousef, H. A., Yasmin, H., Shah, R., Shah, N. A., El-Sherif, L. S., and El-Tantawy, S. A. (2023). Mathematical modeling and analysis of the steady electro-osmotic flow of two immiscible fluids: A biomedical application. Coatings 13, 115. doi:10.3390/coatings13010115

CrossRef Full Text | Google Scholar

Anik, M. I., Hossain, M. K., Hossain, I., Mahfuz, A. M. U. B., Rahman, M. T., and Ahmed, I. (2021). Recent progress of magnetic nanoparticles in biomedical applications: A review. Nano Sel. 2, 6, 1146–1186. doi:10.1002/NANO.202000162

CrossRef Full Text | Google Scholar

Asha, S. K., and Sunitha, G. (2018). Effect of joule heating and MHD on peristaltic blood flow of Eyring–Powell nanofluid in a non-uniform channel. J. Taibah Univ. Sci. 13 (1), 155–168. doi:10.1080/16583655.2018.1549530

CrossRef Full Text | Google Scholar

Basha, H. T., and Sivaraj, R. (2021). Entropy generation of peristaltic Eyring–Powell nanofluid flow in a vertical divergent channel for biomedical applications. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 235 (5), 1575–1586. doi:10.1177/09544089211013926

CrossRef Full Text | Google Scholar

Bhatti, M. M. (2021). Biologically inspired intra-uterine nanofluid flow under the suspension of magnetized gold (Au) nanoparticles: Applications in nanomedicine. Invent 6, 28. doi:10.3390/INVENTIONS6020028

CrossRef Full Text | Google Scholar

Cui, Z., Kong, D., Pan, Y., and Zhang, K. (2012). On the swimming motion of spheroidal magnetotactic bacteria. Fluid Dyn. Res. 44 (5), 055508. doi:10.1088/0169-5983/44/5/055508

CrossRef Full Text | Google Scholar

Elgazery, N. S., Elelamy, A. F., Bobescu, E., and Ellahi, R. (2022). How do artificial bacteria behave in magnetized nanofluid with variable thermal conductivity: Application of tumor reduction and cancer cells destruction. Int. J. Numer. Methods Heat Fluid Flow 32 (9), 2982–3006. doi:10.1108/HFF-11-2021-0722

CrossRef Full Text | Google Scholar

Gholinia, M., Hosseinzadeh, K., Mehrzadi, H., Ganji, D. D., and Ranjbar, A. A. (2019). Investigation of MHD Eyring–Powell fluid flow over a rotating disk under effect of homogeneous–heterogeneous reactions. Case Stud. Therm. Eng. 13, 100356. doi:10.1016/J.CSITE.2018.11.007

CrossRef Full Text | Google Scholar

Hina, S., Mustafa, M., Hayat, T., and Alsaedi, A. (2016). Peristaltic flow of powell-eyring fluid in curved channel with heat transfer: A useful application in biomedicine. Comput. Methods Programs Biomed. 135, 89–100. doi:10.1016/J.CMPB.2016.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussain, A., Sarwar, L., Akbar, S., and Nadeem, S. (2020). Mathematical model for blood flow through the stenosed channel. Phys. Scr. 95 (2), 025206. doi:10.1088/1402-4896/AB43FF

CrossRef Full Text | Google Scholar

Kong, D., Lin, W., Pan, Y., and Zhang, K. (2014). Swimming motion of rod-shaped magnetotactic bacteria: The effects of shape and growing magnetic moment. Front. Microbiol. 5, 8. doi:10.3389/FMICB.2014.00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, S. (2004). On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147 (2), 499–513. doi:10.1016/S0096-3003(02)00790-7

CrossRef Full Text | Google Scholar

Mallick, B., and Misra, J. C. (2019). Peristaltic flow of Eyring-Powell nanofluid under the action of an electromagnetic field. Eng. Sci. Technol. Int. J. 22 (1), 266–281. doi:10.1016/J.JESTCH.2018.12.001

CrossRef Full Text | Google Scholar

Mathuriya, A. S., Yadav, K., and Kaushik, B. D. (2015). Magnetotactic bacteria: Performances and challenges. Geomicrobiol. J. 32 (9), 780–788. doi:10.1080/01490451.2014.986694

CrossRef Full Text | Google Scholar

Nagaraj, C., Dinesh, P. A., and Kalavathi, G. K. (2018). Combined effects of electric field and magnetic field on electro hydrodynamic dispersion of macromolecular components in biological bearing. Defect Diffus. Forum 388, 361–377. doi:10.4028/www.scientific.net/ddf.388.361

CrossRef Full Text | Google Scholar

Riaz, A., Ellahi, R., Bhatti, M. M., and Marin, M. (2019). Study of heat and mass transfer in the eyring–powell model of fluid propagating peristaltically through a rectangular compliant channel. Heat. Transf. Res. 50 (16), 1539–1560. doi:10.1615/HEATTRANSRES.2019025622

CrossRef Full Text | Google Scholar

Saleem, N., and Munawar, S. (2016). A mathematical analysis of MHD blood flow of Eyring-Powell fluid through a constricted artery. Int. J. Biomath. 9 (2), 1650027. doi:10.1142/S1793524516500273

CrossRef Full Text | Google Scholar

Shukla, N., Rana, P., and Bég, O. A. (2019). Unsteady MHD non-Newtonian heat transfer nanofluids with entropy generation analysis. Nonlinear Eng. 8 (1), 630–644. doi:10.1515/nleng-2017-0177

CrossRef Full Text | Google Scholar

Sultan, F., Khan, N. A., Qasim, M., and Afridi, M. I. (2019). Numerical simulation of the flow of nano-eyring-powell fluid through a curved artery with time-variant stenosis and aneurysm. Nihon Reoroji Gakkaishi 47 (2), 75–85. doi:10.1678/RHEOLOGY.47.75

CrossRef Full Text | Google Scholar

Vincenti, B., Douarche, C., and Clement, E. (2018). Actuated rheology of magnetic micro-swimmers suspensions: Emergence of motor and brake states. Phys. Rev. Fluids 3 (3), 033302. doi:10.1103/physrevfluids.3.033302

CrossRef Full Text | Google Scholar

Yasmin, H. (2022). Design and research of biomaterials. Coatings 12, 1684. doi:10.3390/coatings12111684

CrossRef Full Text | Google Scholar

Yasmin, H., Giwa, S. O., Noor, S., and Aybar, H. Ş. (2023). Influence of preparation characteristics on stability, properties, and performance of mono- and hybrid nanofluids: Current and future perspective. Machines 11, 112. doi:10.3390/machines11010112

CrossRef Full Text | Google Scholar

Yasmin, H., Giwa, S. O., Noor, S., and Aybar, H. Ş. (2023). Reproduction of nanofluid synthesis, thermal properties and experiments in engineering: A research paradigm shift. Energies 16, 1145. doi:10.3390/en16031145

CrossRef Full Text | Google Scholar

Yasmin, H., Giwa, S. O., Noor, S., and Sharifpur, M. (2023). Experimental exploration of hybrid nanofluids as energy-efficient fluids in solar and thermal energy storage applications. Nanomaterials 13, 278. doi:10.3390/nano13020278

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature

$\left(\mathit{r},\mathit{s}\right)$ curvilinear coordinates

$\left(\mathit{u},\mathit{v}\right)$ velocity components

$\mathit{p}$ pressure

$\mathit{T}$ temperature

$\mathit{R}$ curvature radius

$\mathit{k}$ thermal conductivity

${\mathit{k}}_{\mathbf{1}}$ permeability of the porous medium

$\mathit{t}$ time

$\mathit{n}$ nutrient concentration

${\mathit{D}}_{\mathit{n}}$ nutrient diffusivity

$\mathit{K}$ curvature parameter

$\mathit{Pr}$ Prandtl number

$\mathit{L}\mathit{b}$ bioconvection Lewis number

$\mathit{M}$ magnetic parameter

$\mathit{Q}$ generation/absorption coefficient

Greek terms

${\mathit{\alpha }}_{\mathbf{1}},{\mathit{\alpha }}_{\mathbf{2}}$ fluid parameters

$\mathit{\mu }$ dynamic viscosity

$\mathit{\nu }$ kinematic viscosity

$\mathit{\rho }$ density

${\mathit{\rho }}_{\mathit{n}}$ bacterial density

$\mathit{\beta }$ thermal conductivity parameter

${\mathit{\beta }}_{\mathbf{0}}$ porosity parameter

$\mathit{\gamma }$ unsteady parameter

$\mathrm{\Omega }$ bacterial difference density

$\mathit{\lambda }$ bacteria maximum growth rate

$\mathit{\varphi }$ nanoparticle volume fraction

Subscripts

$\mathit{n}\mathit{f}$ nanofluid

$\mathit{f}$ base fluid

$\mathit{p}$ nanoparticles

$\mathit{w}$ at the curved surface

$\mathit{\infty }$ far from the surface