Darcy–Benard–Oldroyd convection in anisotropic porous layer subject to internal heat generation

1 Introduction

Numerous real-world applications exist for the theoretical and practical analysis of convective heat transfer in porous media. Geothermal energy systems, hydrocarbon reserves, nuclear reactors, medicine, and the chemical industry are among the many examples. Ingham and Pop (2005), Nield and Bejan (2006), Vafai (2005), and Vadasz (2008) have documented the developments in porous medium thermal convection. An essential component of rheological research is the study of the viscoelastic properties of the asthenospheric and mantle components of the Earth (see Lowrie, 2020). Snow systems and the rheology of food transport involve viscoelastic liquids saturated in porous media. Less research has been conducted on Rayleigh–Benard convection in liquids with viscoelastic properties than on thermal convection in a Newtonian fluid (refer to Li and Khayat, 2005).

Due to their coagulated viscosity, polymeric liquids are unaffected by flow and turbulence, whereas Newtonian fluids are affected. Moreover, oscillatory convection is believed to exist as viscoelastic fluids are characterized by their elasticity. According to Kim et al. (2003), the system is unstable due to its elasticity but stable due to its porosity. The oscillatory mode is appropriate for studying convection because convection reduced to supercritical and stable bifurcation forms does not vary with elasticity. However, few authors have investigated oscillatory convection in viscoelastic liquids, and many researchers have not addressed a comparable problem in porous media. Thermal convection in viscoelastic fluids was studied by O’Connell and Budiansky (1977), Griffiths (1987), Rudraiah et al. (1989), Yoon et al. (2004), Malashetty et al. (2006a), and Swamy et al. (2012).

When a porous medium exhibits anisotropy in its mechanical and thermal properties, the flow behavior is significantly altered. The assumption underlying Darcy’s model is that the fluid flow is sufficiently slow for inertial effects to be negligible, and that the fluid complies with the laws of continuum mechanics. If the porous medium is anisotropic, then the medium’s permeability will depend on the flow direction. In other words, the permeability of the porous medium will vary in different orientations. Darcy’s law must be modified to account for the anisotropy of the medium in this instance. This can be accomplished by introducing a permeability tensor that describes the medium’s permeability in various orientations. Numerous applications in the actual world involve anisotropic porous media. Anisotropy results from the incorrect orientation of a solid matrix or the asymmetries of the natural porous medium; it is also a characteristic of porous synthetic materials, such as the fibrous material utilized for insulation and pelleting, both of which are beneficial to chemical engineering processes.

McKibbin et al. (1985) and Storesletten (1998) have exhaustively documented the work pertaining to convection in anisotropic porous media. Govender (2006) described the effects of anisotropy on thermal convection in a porous layer. Malashetty et al. (2006b)presented a study on the effect of a time-periodic modulated temperature field on the stability of a viscoelastic fluid saturated within an anisotropic porous layer. Saravanan and Purusothaman (2009) studied non-Darcian effects in anisotropic porous media. Many pertinent studies on anisotropy have been conducted (Malashetty and Swamy, 2007a; Malashetty and Swamy, 2007b; Malashetty et al., 2009; Sivakumar and Saravanan, 2009; Malashetty and Swamy, 2010; Agarwal et al., 2011; Malashetty et al., 2011; Srivastava et al., 2011; Chandra and Satyamurty, 2012; Swamy et al., 2013; Swamy et al., 2014; Swamy, 2017; Swamy et al., 2019; Capone et al., 2020).

Understanding thermal convection in a porous stratum with internal heat generation is crucial in a variety of natural and artificial systems. The interior of the Earth provides an example of internal heat production. Due to the disintegration of radioactive isotopes and residual heat from the planet’s formation, the Earth’s core is thought to be the source of significant internal heating. This heat production is responsible for the elevated temperature of the Earth’s interior and is one of the driving forces behind plate tectonics and volcanism. Electronic devices, such as computer processors, are another example of internal heat generation. A computer processor’s electronic components generate heat due to the passage of electric current through them. If the generated heat is not effectively dissipated, the processor may malfunction or even fail. To prevent this, electronic devices are frequently equipped with cooling systems, such as heat sinks and fans, to dissipate heat and maintain secure component temperatures. Chemical reactions can also generate heat internally. Due to the exothermic nature of the combustion reaction, for example, heat is produced when fuel is consumed. This internal heat production can be utilized to generate electricity in power facilities or to heat industrial processes.

Internal heat generation results in a nonlinear temperature gradient. A temperature gradient is the temperature change over a specified distance. A nonlinear temperature gradient indicates that the change in temperature over a given distance is not constant. In other terms, the change in temperature is not linear. This refers to the fact that the system or material in question generates its own heat rather than receiving it from an external source. Therefore, thermal convection occurs even though the temperature difference between the lower and upper surfaces is insufficient for convection to begin. Consequently, the production of internal heat is an additional essential mechanism for regulating the onset of convection in the porous layer. Numerous researchers have conducted extensive research on thermal convection in absorbent layers with internal heat generation [refer to (Thirlby, 1970; Mahabaleshwar et al., 2017; Ahmed and Rashed, 2019; Yadav et al., 2021; Enagi et al., 2022; Raju et al., 2022; Upadhya et al., 2022)].

Now, let us see the physical mechanisms involved in the present problem. As a result of the internal heating, a temperature gradient is generated within the porous layer, with the temperature being higher near the heat source and decreasing toward the top surface of the layer. This temperature gradient creates density differences within the viscoelastic liquid, causing it to flow from the heat source toward the top surface. The fluid flow of the viscoelastic liquid is influenced by the anisotropy of the porous layer. If the porous layer is more permeable in one direction than in other directions, the fluid flow will be preferentially directed along the more permeable direction, resulting in anisotropic convection. The properties of the porous medium, such as its porosity, permeability, and tortuosity, also affect the rate of fluid flow and the way in which heat is transferred through the medium. For example, a higher porosity of the porous layer can increase the flow rate of the viscoelastic liquid, while a higher tortuosity can hinder the flow, leading to a slower rate of fluid motion. The viscoelasticity of the liquid can also influence the way in which fluid flow and heat transfer occur within the porous layer. A viscoelastic liquid has both viscous and elastic properties, which can lead to nonlinear behavior in fluid flow and heat transfer. For instance, the elasticity of the liquid can cause it to exhibit oscillatory behavior in response to the temperature gradient, resulting in oscillatory fluid flow and heat transfer. The heating of the bottom surface by an external means can also affect the flow of the viscoelastic liquid. For instance, uniformly heating the bottom surface can generate a temperature gradient that interacts with the temperature gradient generated by the internal heat source, resulting in a more complex flow pattern.

A stability analysis of an Oldroyd-B fluid in a porous medium with the combined influence of anisotropy and the internal heat source is rare. Such investigations are still greatly desired. The primary objective of this study is to determine how the viscoelastic parameters, internal heat generation coefficient, and anisotropy parameters impact the onset criterion of thermal convection and the heat transfer across the layer.

2 Mathematical formulation

A shallow horizontal anisotropic porous layer saturated with Oldroyd-B liquid is considered. The surfaces held at $z=0$ and $z=h$ are regarded as being stress-free and isothermal. The gravitational force $g\equiv \left(\mathrm{0,0},-g\right)$ is acting downward in the direction of the z-axis. The adverse temperature gradient $∆T$ between the two surfaces is maintained by heating the lower surface uniformly. Internal heat generation is considered as an additional source. The temperatures of the solid and liquid phases are assumed to have reached equilibrium. The conservation law of linear momentum is represented by a modified Darcy–Oldroyd model incorporating local time derivatives, Boussinesq approximation, and anisotropy. The convection velocities are expected to be negligible. Thus, the effects of Forchheimer inertia and advection are disregarded. Consequently, the pertinent mathematical model is

$\nabla .\mathbf{v}=0,(1)$

$\left(1+{\mathrm{\Lambda }}_1\frac{\partial }{\partial t}\right)\left(\frac{{\rho }_0}{\epsilon }\frac{\partial \mathbf{v}}{\partial t}+\nabla p-\rho \mathbf{g}\right)=-\mu \left(1+{\mathrm{\Lambda }}_2\frac{\partial }{\partial t}\right)\mathbf{K}\cdot {\mathbf{v}}_D,(2)$

$\gamma \frac{\partial T}{\partial t}+\left(\mathbf{v}\cdot \nabla \right)T=\nabla \cdot \left(\mathbf{\kappa }\cdot \nabla T\right)+Q_I\left(T-T_0\right),(3)$

$\rho ={\rho }_0\left(1-\alpha \left(T-T_0\right)\right),(4)$

where $\mathbf{v}\equiv \left(v_1,v_2,v_3\right)$ denotes the velocity vector, ${\mathbf{v}}_D=\epsilon \mathbf{v}$ is the seepage velocity, ${\mathrm{\Lambda }}_1$ is the stress-relaxation time, ${\mathrm{\Lambda }}_2$ is the strain-retardation time, $\epsilon$ is the porosity, $\mu$ is the viscosity, $\rho$ is the density, $\alpha$ is the thermal expansion coefficient, $\gamma =\left(\epsilon {\left(\rho c\right)}_f+\left(1-\epsilon \right){\left(\rho c\right)}_s\right)/{\left(\rho c\right)}_f$ is the ratio of specific heat capacities, $\mathbf{K}=\left({\mathbf{e}}_{\mathbf{1}}{\mathbf{e}}_{\mathbf{1}}+{\mathbf{e}}_2{\mathbf{e}}_2\right){\mathrm{K}}_1^{-1}+\left({\mathbf{e}}_3{\mathbf{e}}_3\right){\mathrm{K}}_3^{-1}$ and $\mathbf{\kappa }=\left({\mathbf{e}}_{\mathbf{1}}{\mathbf{e}}_{\mathbf{1}}+{\mathbf{e}}_2{\mathbf{e}}_2\right){\kappa }_1+\left({\mathbf{e}}_3{\mathbf{e}}_3\right){\kappa }_3$ denote the anisotropy-induced permeability and thermal diffusivity tensor, respectively, with ${\mathbf{e}}_{\mathbf{1}}{,\mathbf{e}}_{\mathbf{2}},{\mathbf{e}}_{\mathbf{3}}$ being the unit vectors along the x, y, and z-axes, respectively. The last term in Eq. 3 is due to the presence of internal heat generation, where ${\mathcal{Q}}_I$ quantifies the amount of heat generation within the bulk of the porous layer

Because the fluid is at rest in the basic state, we can determine its mass, pressure, and temperature by

${\rho }_b\left(z\right)={\rho }_0\left(1-\alpha ∆T\left(\sin \left(\sqrt{{\mathcal{Q}}_I/k_3}h\left(1-z/h\right)\right)/\sin \left(\sqrt{{\mathcal{Q}}_I/k_3}h\right)\right)\right),(5)$

$p_b\left(z\right)={\rho }_0\mathit{g}\left(z-\left(\alpha ∆T/\sqrt{{\mathcal{Q}}_I/k_3}\right)\left(\cos \left(\sqrt{{\mathcal{Q}}_I/k_3}h\left(1-z/h\right)\right)/\sin \left(\sqrt{{\mathcal{Q}}_I/k_3}h\right)\right)\right),(6)$

$T_b\left(z\right)=T_0+∆T\left(\sin \left(\sqrt{{\mathcal{Q}}_I/k_3}h\left(1-z/h\right)/\sin \left(\sqrt{{\mathcal{Q}}_I/k_3}h\right)\right)\right).(7)$

The stability of the system is studied by imposing the perturbations on the basic state.

$\mathbf{v}={\mathbf{v}}^{\prime },\rho ={\rho }_b\left(z\right)+{\rho }^{\prime },T=T_b\left(z\right)+T^{\prime },(8)$

where prime represents the quantity in the perturbed state. We use Eqs. 5–8 in the governing Eqs. 1–4 and eliminate $p^{\prime }$. Furthermore, assume the flow to be two-dimensional and thus incorporate the stream function such that $\left(u^{\prime },w^{\prime }\right)=\left(\partial /{\partial }_z,-\partial /\partial x\right){\mathrm{\Psi }}^{\prime }$. Then, use $\left(x,z\right)=h\left(x^{*},z^{*}\right),t=\left(h^2/k_3\right)t^{*},\mathrm{\Psi }=k_3{\mathrm{\Psi }}^{*}$ and $T^{\prime }=\left(∆T\right)T^{*}$ to express the equations in the nondimensional form as follows:

$\left(1+{\mathrm{\lambda }}_1\frac{\partial }{\partial t}\right)\left(\frac{1}{\mathrm{Pr}}\frac{\partial }{\partial t}\left({\nabla }^2\mathrm{\Psi }\right)+Ra\frac{\partial T}{\partial x}\right)=-\left(1+{\mathrm{\lambda }}_2\frac{\partial }{\partial t}\right){\nabla }_1^2\mathrm{\Psi },(9)$

$\gamma \frac{\partial T}{\partial t}+f\left(z\right)\frac{\partial \mathrm{\Psi }}{\partial x}-\left(\frac{\partial \mathrm{\Psi }}{\partial x}\frac{\partial T}{\partial z}-\frac{\partial \mathrm{\Psi }}{\partial z}\frac{\partial T}{\partial x}\right)={\nabla }_1^{2}T+R{a}_{I}T,(10)$

where $f\left(z\right)=\sqrt{{Ra}_I}\cos \left(\sqrt{{Ra}_I}\left(1-z\right)\right)/\sin \left(\sqrt{{Ra}_I}\right)$, ${\nabla }_1^2={\partial }^2/{\partial x}^2+\left(1/\xi \right)\left({\partial }^2/{\partial z}^2\right)$, and ${\nabla }_2^2=\eta \left({\partial }^2/{\partial x}^2\right)+{\partial }^2/{\partial z}^2$. $Ra={\rho }_0\alpha g∆T{h}^3/\mu k_3$ denotes the thermal Rayleigh number, $R{a}_I=\mathcal{Q}{h}^2/k_3$ is the internal Rayleigh number, $\mathit{Pr}=\mu h^2/\epsilon {\rho }_0{k}_3{K}_3$ is the Darcy–Prandtl number, ${\lambda }_1={\mathrm{\Lambda }}_1{k}_3/h^2$ is the Deborah number or stress-relaxation parameter, ${\lambda }_2={\mathrm{\Lambda }}_2{k}_3/h^2$ is the strain-retardation parameter, and $\xi =K_1/K_3$ and $\eta =k_1/k_3$ denote mechanical and thermal anisotropy parameters, respectively. Because the boundaries are assumed to be stress-free and isothermal, the relevant boundary conditions are

$\mathrm{\Psi }=D^2\mathrm{\Psi }=T=0\mathrm{a}\mathrm{t}\mathit{z}=\mathrm{0,1}.(11)$

3 Galerkin weighted-residual technique

In the linear stability theory, the imposed perturbations are anticipated to be infinitesimal, and hence, the nonlinear terms in Eqs. 9–11 can be ignored. The normal mode analysis is used to solve the resulting eigenvalue problem. Thus, it is supposed that the infinitesimal perturbations are the periodic waves of form

$\left(\mathrm{\Psi },T\right)=\left(\mathrm{\Psi }\left(z\right),\mathrm{\Theta }\left(z\right)\right)e^{i\left(\omega t+kx\right)},(12)$

where the real variable k is the wavenumber, and the complex variable $\omega$ is the temporal growth rate. It decides whether these tiny-recurrent-perturbations either enlarge or degenerate. In thermal convection, wavenumber is a term used to describe the spatial variation of temperature and fluid flow patterns that arise due to temperature differences within the fluid. Wavenumber is a measure of the number of waves that occur in a given distance. The concept of wavenumber is closely related to the concept of wavelength, which is the distance between successive peaks or troughs of a wave. The wavelength and wavenumber are related by the formula k = 2π/λ, where λ is the wavelength of the wave. This shows that the wavenumber is inversely proportional to the wavelength; that is, waves with shorter wavelengths have larger wavenumbers, and waves with longer wavelengths have smaller wavenumbers.

In natural convection, the spatial variation of temperature and fluid flow patterns can take on different wavelengths, depending on factors such as the geometry of the system, the temperature differences within the fluid, and the properties of the fluid itself. The wavelength of these patterns can be quantified in terms of the wavenumber, and the behavior of natural convection can be analyzed in terms of the relationship between the wavenumber and other parameters such as the Rayleigh number.

On substituting Eq. 12 into linearized Eqs. 9–11, we obtain

$\left(\frac{i\omega }{\mathrm{Pr}}\left(1+i\omega {\lambda }_1\right)\left(D^2-k^2\right)+\left(1+{\lambda }_{2}i\omega \right)\left(\frac{1}{\xi }{D}^2-k^2\right)\right)\mathrm{\Psi }+Ra\left(1+i\omega {\lambda }_1\right)ik\mathrm{\Theta }=0,(13)$

$\left(D^2-\eta k^2-i\omega \gamma +R{a}_I\right)\mathrm{\Theta }-\mathrm{i}kf\left(z\right)\mathrm{\Psi }=0,(14)$

$\mathrm{\Psi }=D^2\mathrm{\Psi }=\mathrm{\Theta }=0\mathrm{a}\mathrm{t}\mathrm{z}=\mathrm{0,1}.(15)$

According to the Galerkin method, we choose

$\left(\mathrm{\Psi }\left(z\right),\mathrm{\Theta }\left(z\right)\right)=\left(A_1{\mathrm{\Psi }}_1\left(z\right),B_1{\mathrm{\Theta }}_1\left(z\right)\right),(16)$

where A₁ and B₁ are constants, and ${\mathrm{\Psi }}_1\left(z\right),{\mathrm{\Theta }}_1\left(z\right)$ are so designated that they satisfy the boundary conditions (15). On multiplying Eqs. 13, 14, respectively, by ${\mathrm{\Psi }}_1\left(z\right),{\mathrm{\Theta }}_1\left(z\right)$ and integrating the resultant equations w. r. t. z between the limits 0 and 1, we acquire

$\left(\frac{i\omega }{\mathrm{Pr}}\left(1+i\omega {\lambda }_1\right)X_0+\left(1+i\omega {\lambda }_2\right)X_1\right)A_1+ikRa\left(1+i\omega {\lambda }_1\right)X_2{B}_1=0,(17)$

$ik{X}_4{A}_1+\left(\left(i\omega \gamma -R{a}_I\right)X_5-X_6\right)B_1=0,(18)$

where $X_0=〈{\mathrm{\Psi }}_1\left(D^2-k^2\right){\mathrm{\Psi }}_1〉$, $X_1=〈{\mathrm{\Psi }}_1\left(\frac{1}{\xi }{D}^2-k^2\right){\mathrm{\Psi }}_1〉$, $X_2=〈{\mathrm{\Psi }}_1{\mathrm{\Theta }}_1〉$, $X_4=〈f\left(z\right){\mathrm{\Theta }}_1{\mathrm{\Psi }}_1〉$, $X_5=〈{\mathrm{\Theta }}_1^2〉,$ and $X_6=〈{\mathrm{\Theta }}_1\left(D^2-\eta k^2\right){\mathrm{\Theta }}_1〉$. The angular brackets denote the integral w. r. t. z between the limits 0 and 1. The requirement for the existence of a non-trivial solution of Eqs. 17 and 18 yield the expression for Rayleigh number:

$Ra=\frac{N_r+i\omega N_i}{k^2{X}_2{X}_4\left(1+{\omega }^2{\lambda }_1^2\right)}.(19)$

Because $\omega ={\omega }_r+i{\omega }_i$, the case ${\omega }_r<0$ specifies a stable state, while ${\omega }_r>0$ corresponds to the unstable mode. A neutral state is attained for ${\omega }_r=0$. The steady-marginal stability can be observed for $\omega =0$ (i.e., ${\omega }_r={\omega }_i=0$), with which Eq. 19 abridges to the expression of stationary Rayleigh number:

${Ra}^{st}=X_1\left({Ra}_I{X}_5+X_6\right)/k^2{X}_2{X}_{4.}(20)$

The trial functions that satisfy the boundary conditions (15) are obviously

$\left({\mathrm{\Psi }}_1\left(z\right),{\mathrm{\Theta }}_1\left(z\right)\right)=\left(\sin \pi z,\sin \pi z\right).$

On using these, one can estimate X₁, X₂, X₄, X₅ and X₆ value and then substituting into Eq. 20 to get

${Ra}^{st}=\frac{{\delta }_1^2}{4{\pi }^2{k}^2}\left(4{\pi }^2-{Ra}_I\right)\left({\delta }_2^2-{Ra}_I\right),(21)$

where ${\delta }_1^2=k^2+{\pi }^2/\xi$ and ${\delta }_2^2=\eta k^2+{\pi }^2$. Eq. 21 is free from viscoelasticity, so it resembles the equation obtained for a viscous Newtonian fluid. The validity of our work can be ascertained through Table 1, wherein we recovered the previous classical results as a special case of Eq. 21

TABLE 1

TABLE 1. Comparison of the present result with the earlier published works.

Now, we discuss the behavior of Eq. 19 with the nonzero growth rate, that is, $\omega \ne 0$. As $Ra$ portrays a physical phenomenon, it should not be imaginary and hence, Eq. 19 admits $N_i=0$ as $\omega \ne 0$. This affords the expression for${\omega }^2$:

${\omega }^2=\frac{X_1\left(X_5\left(\gamma +{\lambda }_1{Ra}_I\right)-{\lambda }_2\left(X_6+X_5{Ra}_I\right)+{\lambda }_1{X}_6\right)-{\mathit{Pr}}^{-1}{X}_0\left(X_6+X_5{Ra}_I\right).}{{\lambda }_1\left({\lambda }_1{\mathit{Pr}}^{-1}{X}_0\left(X_6+X_5{Ra}_I\right)-\gamma {\lambda }_2{X}_1{X}_5\right)}(22)$

The real part of Eq. 19 then symbolizes the expression for the oscillatory Rayleigh number:

${Ra}^{Osc}=\frac{N_r}{k^2{X}_2{X}_4\left(I+{\omega }^2{\lambda }_1^2\right)}.(23)$

To estimate ${Ra}_c^{Osc}$ , we minimize (23) w. r. t. k, after substituting ${\omega }^2\left(>0\right)$ from Eq. 22.

4 Weak nonlinear theory

Nonlinear stability analysis is preferred to measure convection amplitudes and heat transfer. This facilitates comprehension of the physical mechanism with a little mathematical labor. This is a basic step toward grasping the full nonlinearity of the problem. Because the perturbations are assumed to be of finite amplitude, it is reasonable to represent them in the form of a limited Fourier series, as follows:

$\mathrm{\Psi }={\mathrm{A}}_{11}\left(t\right)\sin \left(kx\right)\sin \left(\pi z\right),(24)$

$T=B_{11}\left(t\right)\cos \left(kx\right)\sin \left(\pi z\right)+B_{02}\left(t\right)\sin \left(2\pi z\right).(25)$

The finite amplitudes of A and B subscripts for unsteady nonlinear convection are to be assessed by the dynamics of the system. Using Eqs. 24 and 25 in Eqs. 9 and 10 and comparing the coefficients of like terms, the following fourth-order Lorenz system of autonomous nonlinear differential equations is obtained:

$d/dt\left({\mathrm{A}}_{11},G_1,B_{11},B_{12}\right)=\left({\mathrm{G}}_1,D_1,G_2,D_2\right),(26)$

where

$D_1=-\mathrm{Pr}{\delta }^{-2}\left({\lambda }_1^{-1}\left({\delta }_1^2\left(A_{11}+{\lambda }_2{G}_1\right)+\left({\delta }^2{\mathrm{Pr}}^{-1}{G}_1+Rak{B}_{11}\right)\right)+Rak{G}_2\right),$

$G_2=-{\gamma }^{-1}\left(kf\left(z\right)A_{11}+{\delta }_2^2{B}_{11}-{Ra}_I{B}_{11}+2\pi k{A}_{11}{B}_{02}\right),$

$D_2=-{\gamma }^{-1}\left(\left(4{\pi }^2-{Ra}_I\right)B_{02}-\pi k{A}_{11}{B}_{11}/2\right).$

There is no suitable analytical method to obtain a closed-form solution of the aforementioned system. Thus, a competent numerical technique is recommended. Although it may not be possible to make precise quantitative predictions, there are several qualitative insights that can be gleaned from the available data or theoretical models. As system of Eq. 26 is homogeneously bounded with time, it retains numerous features of the full problem. For ${Ra}_I<\left(0.5\right){\delta }_2^2+2{\pi }^2$, the velocity field possesses a constant negative divergence; that is,

$\nabla \bullet \left(d/dt\left(A_{11},G_1,B_{11},B_{12}\right)\right)=-{\lambda }_1^{-1}\left(\mathrm{Pr}{\lambda }_2{\delta }_1^2{\delta }^{-2}+1\right)-{\gamma }^{-1}\left({\delta }_2^2+4{\pi }^2-2{Ra}_I\right).(27)$

This implies that the system is constrained. In dynamical systems theory, a system is said to be constrained if it is subject to certain limitations or conditions. These constraints can arise due to physical, mathematical, or other reasons. For example, a mechanical system may be constrained by rigid walls or other physical barriers that restrict the motion of its components. When a system is constrained, the possible states that it can occupy are limited to a subset of its phase space. The phase space is the space of all possible states of the system, and it is often represented as a high-dimensional space in which each dimension corresponds to a particular variable or parameter of the system. Because the system is constrained, the phase space paths are drawn toward a set of measure zero or a fixed point. A set of measure zero is a subset of the phase space that has zero volume or probability. In other words, it is a set of states that is extremely unlikely to be reached by the system. A fixed point, on the other hand, is a state of the system that does not change over time. When the phase space paths are drawn toward a set of measure zero or a fixed point, this can result in volume shrinkage in the phase space. This means that the volume of the phase space that is accessible to the system becomes smaller over time as the system is forced to occupy a smaller subset of the phase space due to the constraints. This is revealed by Eq. 28 through the fact that if a set of preliminary points in space fills a volume $V\left(0\right)$ at t = 0, then after time t, the endpoints of the corresponding paths will occupy a region

$V\left(t\right)=V\left(0\right)\exp \left(-\left({\lambda }_1^{-1}\left(\mathrm{Pr}{\lambda }_2{\delta }_1^2{\delta }^{-2}+1\right)-{\gamma }^{-1}\left({\delta }_2^2+4{\pi }^2-{2Ra}_I\right)\right)t\right).(28)$

The larger values of the Darcy–Prandtl number and strain-retardation number and smaller values of the Deborah number and heat-capacities ratio are used to emphasize the exponential deterioration of volume with time.

Upon switching from qualitative exploration, we now look into the existence of an analytical solution. As the finite amplitude instability can be well explored analytically using the truncated model shown in Eqs. 24 and 25, a closed-form solution of Eq. 26 is used for the steady case. The following expression is obtained by Eq. 26 after removing all terms except $A_{11}$:

$\left({\delta }_1^2-Ra{k}^{2}f\left(z\right){\left(\left({\delta }_2^2-{Ra}_I\right)+\left(2{\pi }^2{k}^2/\left({\pi }^2-{Ra}_I/4\right)\right)\left(A_{11}^2/8\right)\right)}^{-1}\right)A_{11}=0.$

The solution $A_{11}=0$ symbolizes the pure conduction state. Thus, the second option guarantees the likelihood of finite amplitude steady convection by offering the value of the finite-amplitude $A_{11}^2/8$ of convective motions in the form

$A_{11}^2/8=\left(\left({\pi }^2-{Ra}_I/4\right)/2{\pi }^2{k}^2\right)\left(Ra{k}^{2}f\left(z\right){\delta }_1^{-2}-\left({\delta }_2^2-{Ra}_I\right)\right).(29)$

Rather than merely defining the onset criterion, the impact of the Rayleigh number can be swiftly documented by analyzing its effect on heat transport. In the study of convection, determining the quantity of heat transported past the layer is of utmost importance. Because the basic state is immobile, heat transfer in this state is limited to conduction. However, as the Rayleigh number exceeds the threshold, convection develops. The Nusselt number is used to describe the convection-heat transport throughout the stratum.

$Nu=1+{\left({\displaystyle {\int }_0^{2\pi /k_c}}\left(\partial T/\partial z\right)dx/{\displaystyle {\int }_0^{2\pi /k_c}}\left(\partial T_b/\partial z\right)dx\right)}_{z=0}$

By using Eqs. 28 and 7, one can obtain

$Nu=1-2\pi \left(\left(\tan \sqrt{{Ra}_I}\right)/\sqrt{{Ra}_I}\right){\left(B_{02}\right)}_{z=0}.$

Substituting the value of $B_{02}$ at $z=0$ gives

$Nu=1-2\pi \left(\frac{\tan \sqrt{{Ra}_I}}{\sqrt{{Ra}_I}}\right)\left(\frac{-\pi k^{2}f\left(0\right)}{\left(\left({\pi }^2-{Ra}_I/4\right)\left({\delta }_2^2-{Ra}_I\right)+2{\pi }^2{k}^2\left(A_{11}^2/8\right)\right)}\left(A_{11}^2/8\right)\right).$

This can be further simplified as

$Nu=1+2{\pi }^2{k}^2\left(A_{11}^2/8\right)/\left(\left({\pi }^2-{Ra}_I/4\right)\left({\delta }_2^2-{Ra}_I\right)+2{\pi }^2{k}^2\left(A_{11}^2/8\right)\right).(30)$

This analysis is valid for Rayleigh numbers close to their threshold value. By including more terms in the Fourier expansion, one can anticipate better outcomes. The Runge–Kutta–Gill method is used to clarify the unsteady Eq. 26. The calculated amplitude values for various time intervals are then used to estimate Nu as a function of t.

5 Results and discussion

The onset of convection refers to the point at which fluid motion due to buoyancy forces begins to occur in a fluid that is initially at rest. This occurs when a fluid is subjected to a temperature difference that is large enough to cause density variations within the fluid, which in turn generate buoyancy forces that drive fluid motion. The onset of convection can be characterized by a critical value of a dimensionless parameter called the Rayleigh number. The Rayleigh number represents the ratio of buoyancy forces to viscous forces in the fluid. For a fluid layer that is initially at rest, the onset of convection occurs when the Rayleigh number exceeds a critical value that is specific to the geometry and boundary conditions of the system. Above this critical value, the buoyancy forces overcome the viscous forces and initiate fluid motion. The critical Rayleigh number can be determined through theoretical analysis or experimental observation. The onset of convection is an important phenomenon in many natural and industrial systems, including geophysical flows, crystal growth, and industrial heat transfer processes. Understanding the onset of convection is important for predicting the behavior of these systems and for designing efficient heat transfer systems.

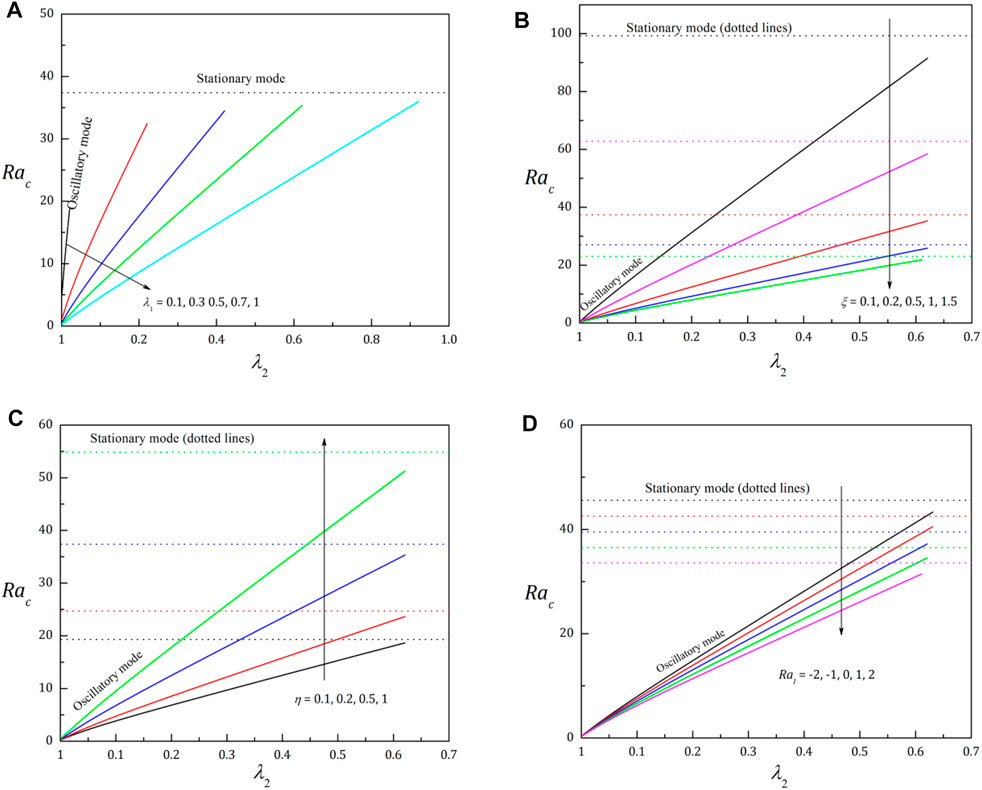
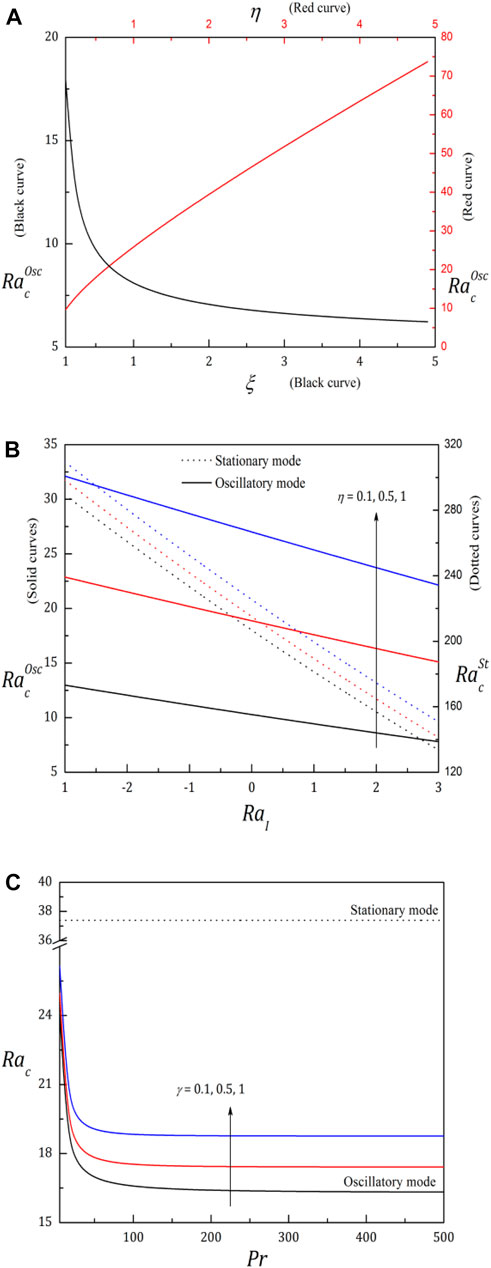
The primary objective of investigating a convection problem is to determine the smallest possible Rayleigh number that demonstrates convection. Fine-tuning the parameters that define the Rayleigh number is advantageous for deferring or accelerating convective motions. This study examines the interaction between variable permeability, thermal diffusivity, and internal heat generation. The point $\left(k_c,R{a}_c\right)$ at which the marginal stability curve reaches the least signifies the convection threshold. The detailed behavior of this critical value is deliberated as a function of the strain-retardation number. Figures 1A–D display the dependence of critical $Ra$ on the strain-retardation parameter ${\lambda }_2$. It has already been mentioned that $R{a}_c^{St}$ is independent of viscoelasticity. This fact is justified by a horizontal dotted line (corresponding to $R{a}_c^{St}$) in Figure 1A, which is invariant with respect to ${\lambda }_2$, ${\lambda }_1$ and located at the higher level. All the $R{a}^{Osc}$ curves lie at the lower level, indicating that the onset of convection is through oscillatory mode. It is observed that $R{a}_c^{Osc}$ increases with ${\lambda }_2$. Thus, the strain-retardation parameter makes the system more stable, but this stabilizing effect is retarded by ${\lambda }_1$ because there is a significant decrease in $R{a}_c^{Osc}$ w.r.t. ${\lambda }_1$. We note that the influence of ${\lambda }_2$ on $R{a}_c^{Osc}$ is constrained to a specific range depending on the value of ${\lambda }_1$. Beyond this range, the oscillatory convection ceases to occur.

FIGURE 1

FIGURE 1. Plot of Ra_c versus ${\lambda }_2$ for varying (A) ${\lambda }_1$, (B) $\xi$, (C) $\eta ,$ and (D) $R{a}_I$.

In Figure 1B, the effect of the mechanical anisotropy parameter, which signifies heterogeneity in the permeability of the porous layer, is expressed. The values of both $R{a}_c^{St}$ and $R{a}_c^{Osc}$ decline with $\xi$. This indicates that the onset of convection can be advanced by increasing the anisotropy in permeability. Figure 1C exhibits the impact of anisotropy in thermal diffusivity on the threshold of convection. It portrays that by choosing larger values for $\eta$, one can enhance the values of $R{a}_c^{St}$ and $R{a}_c^{Osc}$. Hence, stabilization can be achieved through increasing $\eta$. Figure 1D depicts the variation of $R{a}_c$ with the internal Rayleigh number. Convective motions in both steady and oscillatory modes vary considerably with the aid of internal heating. This is revealed through the fact that when $R{a}_I$ is increased, the $R{a}_c$ curves are shifted downward in both stationary and oscillatory cases. This confirms that internal heating favors the onset of convection.

One of the main objectives of the present paper is to analyze the significance of controlling the convection by the anisotropic nature of the porous layer. The detailed behavior of $R{a}_c^{Osc}$ as a function of anisotropy parameters is demonstrated via Figure 2A. The black solid curve with regards to the left-side axis shows that the value of $R{a}_c^{Osc}$ decreases with $\xi$. Therefore, the anisotropy in permeability causes the oscillatory convective motions to occur at the earlier stage. However, note that this destabilization is more sensitive for the small and moderate values of $\xi$. Furthermore, the red curve drawn with reference to the right-side axis makes us aware of the stabilizing role of anisotropic thermal diffusivity. The value of $R{a}_c^{Osc}$ increases almost linearly with $\eta$.

FIGURE 2

FIGURE 2. Plot of Ra_c as a function of (A) $\xi$ and $\eta$, (B) $R{a}_I$ and $\eta$, and (C) Pr and $\gamma$.

The impact of $R{a}_I$, which signifies the strength of the internal heat source, is expressed through the curves in the $\left(R{a}_c,R{a}_I\right)$ plane (see Figure 2B). Both $R{a}_c^{St}$ and $R{a}_c^{Osc}$ plummet with $R{a}_I$. This indicates that onset of convection can be brought forward by increasing the rate of internal heating. The figure also exhibits that these critical curves are shifted upward when we increase the thermal anisotropy parameter. So, the heterogeneity of thermal diffusivity retards the destabilization caused by an internal heat source.

To explore the activity of $R{a}_c$ with respect to the varying Prandtl number, we plot the critical curves in the $\left(R{a}_c,\mathrm{Pr}\right)$ plane in Figure 2C. For smaller values of Pr, there is a swift decrease in the value of $R{a}_c^{Osc}.$ This trend continues up to some specific value of Pr, beyond which $R{a}_c^{Osc}$ becomes independent of Pr. Thus, a destabilizing effect is reported for smaller values of Pr. The dotted horizontal line, which corresponds to the stationary case, shows that $R{a}_c^{St}$ is not influenced by the varying Prandtl number. Furthermore, the value of $R{a}_c^{St}$ is much larger than $R{a}_c^{Osc}$. Another fact that can be noticed through this figure is the enhancement in the values of $R{a}_c^{Osc}$ with respect to the increasing heat capacities ratio. Therefore, the destabilization caused by increasing Pr can be suppressed by $\gamma$. Linear stability analysis, which provided us with a glimpse of the convection threshold, is followed by weak nonlinear stability analysis.

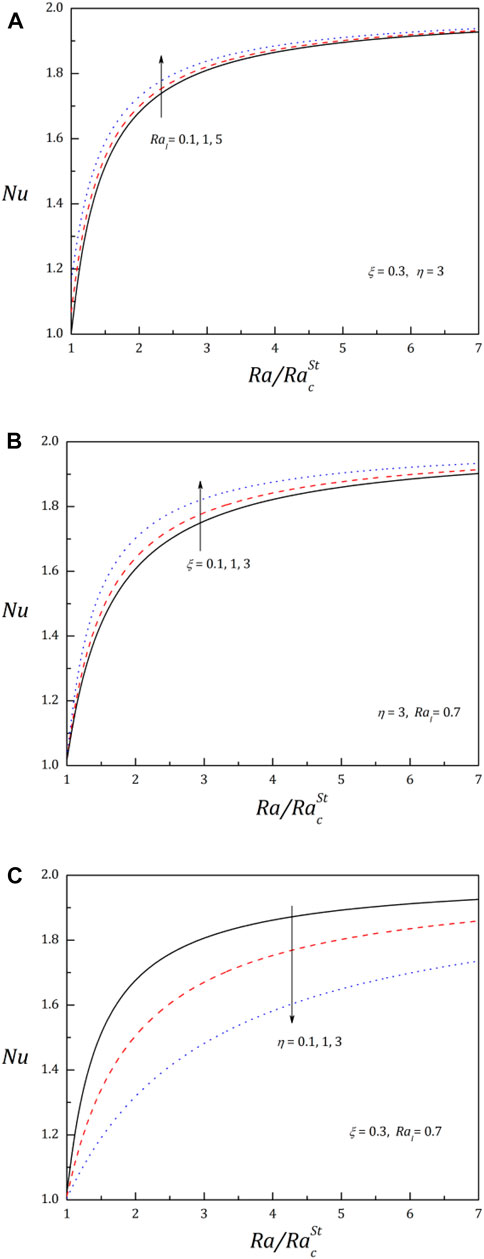
This study helped us to measure the amplitude of convective motions and the amount of heat transfer. The Nusselt number (Nu) that signifies the extent of convective heat transfer is calculated. The control of Rayleigh number over Nu is presented in Figures 3A–C. The value of Nu is found to be 1 at the onset, while as the $R{a}_c$ increases to about three times the value of the critical Rayleigh number, the Nusselt number also increases. Thereafter, Nu becomes less sensitive to $R{a}_c$. Thus, one can conclude that in the vicinity of the onset of convection, the enhancement of heat transfer occurs, and the same magnitude is maintained even after the further increase in $R{a}_c$.

FIGURE 3

FIGURE 3. Plot of Nu against $Ra/R{a}_c^{St}$ for varying (A) $R{a}_I$, (B) $\xi$ and $\eta$, and (C) $\eta$.

From Figures 3A,B, Nu is found to upsurge for the higher $R{a}_I$ and $\xi$. Therefore, heat transport is amplified by introducing an internal source within the porous layer and by choosing the anisotropy in permeability. Furthermore, through Figure 3C, we notice that there is a significant reduction in the value of Nu w.r.t. the thermal anisotropy parameter. The heat transfer across the layer decreases considerably with increasing anisotropy in thermal diffusivity.

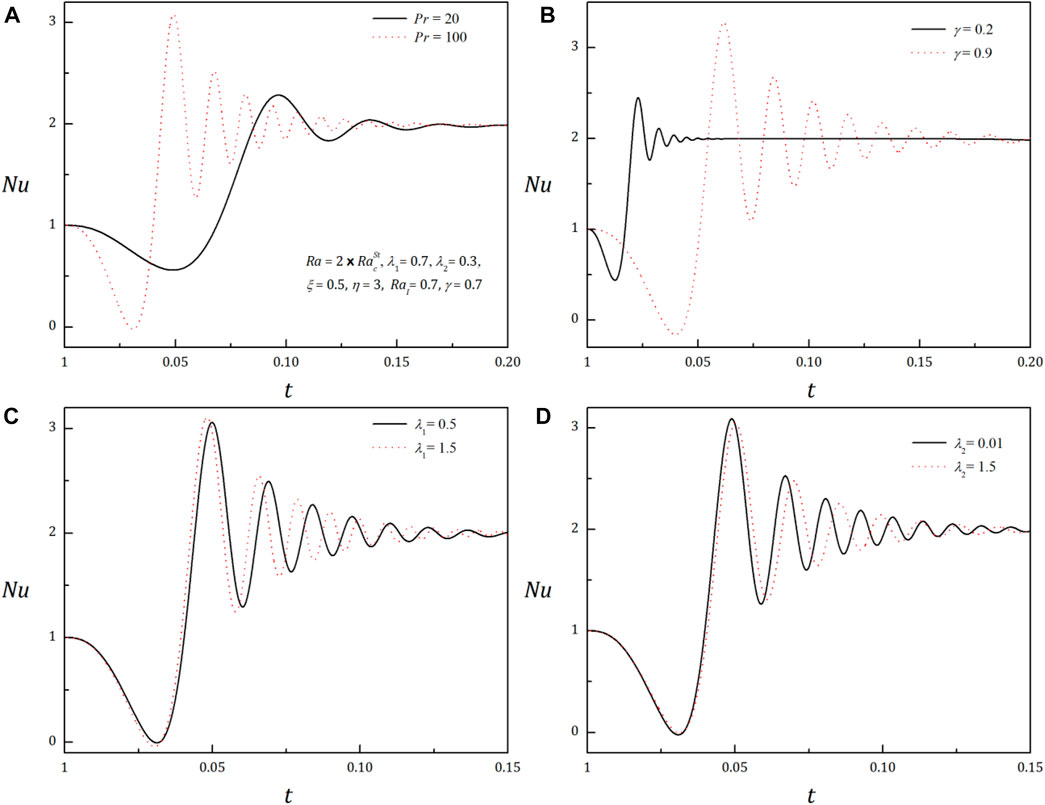
In unsteady finite-amplitude analysis, the fourth-order Lorenz model has been solved numerically using the Runge–Kutta–Gill method. The amplitudes are obtained as the functions of t and then substituted into the expression of Nu. In general, the Nusselt number is a function of several parameters, including the fluid velocity, temperature, and physical properties of the fluid, and it can vary with time during transient heat transfer processes. The behavior of the heat transfer coefficient with respect to time is displayed through the curves in the (Nu, t) plane, as shown in Figures 4A–D. One can observe from these figures that at the onset of natural convection, heat transfer initially occurs through conduction alone, and Nu has a value of 1, which corresponds to purely conductive heat transfer. As the fluid flow starts to develop, convective heat transfer becomes dominant, and the Nusselt number becomes sensitive to time. The behavior of the Nusselt number during this transient phase is oscillatory, with the value of Nu fluctuating about a mean value. This means that the heat transfer coefficient, which is related to the Nusselt number, varies periodically in time, with some oscillations. However, as time progresses, the oscillatory behavior of the Nusselt number starts to decay, and after a short period of time, the heat transfer process reaches a steady state. At this point, the Nusselt number reaches a mean value that is similar to the value of Nu obtained in the steady-state, finite-amplitude case. Thus, in general, these figures display that the behavior of the Nusselt number during a transient heat transfer process is initially oscillatory and sensitive to time but eventually reaches a steady-state mean value. This behavior is a result of the interplay between conduction and convection heat transfer mechanisms during the transient phase of the process.

FIGURE 4

FIGURE 4. Nu versus t for varying (A) Pr, (B) $\gamma$,(C) ${\lambda }_1$, and (D) ${\lambda }_2$

Figures 4A, B depict a considerable enhancement in the value of the heat transfer coefficient with the Prandtl number and the heat capacities ratio. It also shows that the sensitivity of Nu with respect to t increases with increasing Pr and $\gamma$. Figure 4C shows that the amount of convective heat transfer rises with Deborah’s number. However, the strain-retardation parameter shows a decrease in the heat-transfer coefficient (see Figure 4D). This justifies the fact that the influence of retardation time is to inhibit the heat transfer.

6 Conclusion

The aforementioned results support the subsequent conclusions. Due to a competition between thermal diffusion, viscoelastic relaxation, anisotropy in permeability, thermal diffusivity, and internal heat generation, the conduction state degenerated into convective motions via the oscillatory mode. Viscoelasticity, the heat capacity ratio, and the Prandtl number have no effect on stationary convection. Increasing anisotropy in permeability, the coefficient of internal heat generation, and stress-relaxation parameters are associated with an early onset. It has been discovered that anisotropy in thermal diffusivity and heat capacity ratios delays convection. Strain-retardation time reinforces oscillatory case stability. The range of retardation parameter values within which oscillatory convection occurs is determined by the magnitude of the relaxation time. Beyond this range, oscillatory convection ceases, and stationary mode instability is then established. The Prandtl number indicates the effect of destabilization on oscillatory convection. The coefficient of heat transfer increases with the Rayleigh number, the internal Rayleigh number, the Deborah number, the Prandtl number, anisotropy in permeability, and the heat capacity ratio. Increasing values of the strain-retardation parameter and anisotropy in thermal diffusivity indicate an inverse trend. It is possible to promote or inhibit convection in a given system by adjusting the relevant parameters in accordance with practical application. In other words, the onset and intensity of convection can be manipulated by adjusting the system’s controlling parameters, such as temperature gradients, fluid properties, and geometrical factors. Several of the prior results were obtained through the use of special cases. This provides substantial support for the results of the current investigation (Eswaramoorthi et al., 2023).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author contributions

MS, BH, AS: conceptualization, methodology, software, formal analysis, and writing—original draft. AH: writing—original draft, data curation, investigation, visualization, and validation. UK: conceptualization, writing—original draft, writing—review and editing, supervision, and resources. RK: validation, investigation, writing—review and editing, and formal analysis. VK: writing—review and editing, data curation, validation, and resources. All authors contributed to the article and approved the submitted version.

Funding

This work was partially funded by the research center of the Future University in Egypt 2023.

Acknowledgments

The authors would like to express their gratitude to the reviewers for their constructive remarks and insightful suggestions, which have significantly improved the current work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agarwal, S., Bhadauria, B. S., and Siddheshwar, P. G. (2011). Thermal instability of a nanofluid saturating a rotating anisotropic porous medium. Spec. Top. Rev. Porous Media 2 (1), 53–64. doi:10.1615/specialtopicsrevporousmedia.v2.i1.60

CrossRef Full Text | Google Scholar

Ahmed, S. E., and Rashed, Z. Z. (2019). MHD natural convection in a heat generating porous medium-filled wavy enclosures using Buongiorno's nanofluid model. Case Stud. Therm. Eng. 14, 100430. doi:10.1016/j.csite.2019.100430

CrossRef Full Text | Google Scholar

Capone, F., De Luca, R., and Gentile, M. (2020). Thermal convection in rotating anisotropic bidispersive porous layers. Mech. Res. Comm. 110, 103601. doi:10.1016/j.mechrescom.2020.103601

CrossRef Full Text | Google Scholar

Chandra, P., and Satyamurty, V. V. (2012). Effect of anisotropy on natural convective flow through a rectangular porous slab. J. Porous Media 15 (6), 595–605. doi:10.1615/jpormedia.v15.i6.70

CrossRef Full Text | Google Scholar

Eswaramoorthi, S., Loganathan, K., Faisal, M., Botmart, T., and Shah, N. A. (2023). Analytical and numerical investigation of Darcy-Forchheimer flow of a nonlinear-radiative non- Newtonian fluid over a Riga plate with entropy optimization. Ain Shams Eng. J. 14 (3), 101887. doi:10.1016/j.asej.2022.101887

CrossRef Full Text | Google Scholar

Gasser, R. D., and Kazimi, M. S. (1976). Onset of convection in a porous medium with internal heat generation. J. Heat. Transf. 98 (1), 49–54. doi:10.1115/1.3450468

CrossRef Full Text | Google Scholar

Govender, S. (2006). Effect of anisotropy on stability of convection in a rotating porous layer distant from the center of rotation. J. Porous Media 9 (7), 651–662. doi:10.1615/jpormedia.v9.i7.40)

CrossRef Full Text | Google Scholar

Griffiths, R. W. (1987). Effects of earth’s rotation on convection in magma chambers. Earth Planet Sci. Lett. 85, 525–536. doi:10.1016/0012-821x(87)90146-4

CrossRef Full Text | Google Scholar

Horton, C. W., and Rogers, F. T. (1945). Convection currents in a porous medium. J. Al. Phys. 16, 367–370. doi:10.1063/1.1707601

CrossRef Full Text | Google Scholar

Ingham, D. B., and Pop, I. (2005). Transport phenomena in porous media, III. Amsterdam, Netherlands: Elsevier.

Google Scholar

Kim, M. C., Lee, S. B., Kim, S., and Chung, B. J. (2003). Thermal instability of viscoelastic fluids in porous media. Int. J. Heat. Mass Transf. 46, 5065–5072. doi:10.1016/s0017-9310(03)00363-6

CrossRef Full Text | Google Scholar

Lapwood, E. R. (1948). Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44, 508–521. doi:10.1017/s030500410002452x

CrossRef Full Text | Google Scholar

Li, Z., and Khayat, R. E. (2005). Finite-amplitude Rayleigh–Benard convection and pattern selection for viscoelastic fluids. J. Fluid Mech. 529, 221–251. doi:10.1017/s0022112005003563

CrossRef Full Text | Google Scholar

Lowrie, W. (2020). Fundamentals of geophysics. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Mahabaleshwar, U. S., Basavaraja, D., Wang, S., Lorenzini, G., and Lorenzini, E. (2017). Convection in a porous medium with variable internal heat source and variable gravity. Int. J. Heat. Mass Transf. 111, 651–656. doi:10.1016/j.ijheatmasstransfer.2017.04.030

CrossRef Full Text | Google Scholar

Malashetty, M. S., Shivakumara, I. S., Kulkarni, S., and Swamy, M. (2006a). Convective instability of Oldroyd-B fluid saturated porous layer heated from below using a thermal non-equilibrium model. Transp. Porous Med. 62, 123–139. doi:10.1007/s11242-005-1893-0

CrossRef Full Text | Google Scholar

Malashetty, M. S., Siddheshwar, P. G., and Swamy, M. (2006b). Effect of thermal modulation on the onset of convection in a viscoelastic fluid saturated porous layer. Transp. Porous Media 62, 55–79. doi:10.1007/s11242-005-4507-y

CrossRef Full Text | Google Scholar

Malashetty, M. S., Swamy, M. S., and Sidram, W. (2011). Double diffusive convection in a rotating anisotropic porous layer saturated with viscoelastic fluid. Int. J. Therm. Sci. 50, 1757–1769. doi:10.1016/j.ijthermalsci.2011.04.006

CrossRef Full Text | Google Scholar

Malashetty, M. S., and Swamy, M. (2007b). The effect of rotation on the onset of convection in a horizontal anisotropic porous layer. Int. J. Therm. Sci. 46, 1023–1032. doi:10.1016/j.ijthermalsci.2006.12.007

CrossRef Full Text | Google Scholar

Malashetty, M. S., and Swamy, M. (2010). The onset of convection in a binary fluid saturated anisotropic porous layer. Int. J. Therm. Sci. 49, 867–878. doi:10.1016/j.ijthermalsci.2009.12.008

CrossRef Full Text | Google Scholar

Malashetty, M. S., and Swamy, M. (2007a). The onset of convection in a viscoelastic liquid saturated anisotropic porous layer. Transp. Porous Media 67, 203–218. doi:10.1007/s11242-006-9001-7

CrossRef Full Text | Google Scholar

Malashetty, M. S., Tan, W. C., and Swamy, M. (2009). The onset of double diffusive convection in a binary viscoelastic fluid saturated anisotropic porous layer. Phys. Fluids 21 (8), 084101. doi:10.1063/1.3194288

CrossRef Full Text | Google Scholar

McKibbin, R. (1985). “Thermal convection in layered and anisotropic porous media: A review,” in Convective flows in porous media. Editors R. A. Wooding, and I. White (Wellington, NZ: Department of Scientific and Industrial Research), 113–127.

Google Scholar

Nield, D. A., and Bejan, A. (2006). Convection in porous media. New York, NY, United States: Springer.

Google Scholar

Enagi, N. K., Chavaraddi, K. B., Kulkarni, S., and Ramesh, G. K. (2022). Effect of maximum density and internal heating on the stability of rotating fluid saturated porous layer using LTNE model. Heliyon 8, e09620. doi:10.1016/j.heliyon.2022.e09620

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Connell, R. J., and Budiansky, B. (1977). Viscoelastic properties of fluid saturated cracked solids. J. Geophys. Res. 82, 5719–5735. doi:10.1029/jb082i036p05719

CrossRef Full Text | Google Scholar

Raju, C. S. K., Ahammad, N. A., Sajjan, K., Shah, N. A., Yook, S. J., and Kumar, M. D. (2022). Nonlinear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Comm. Heat. Mass 135, 106110. doi:10.1016/j.icheatmasstransfer.2022.106110

CrossRef Full Text | Google Scholar

Rudraiah, N., Kaloni, P. N., and Radhadevi, P. V. (1989). Oscillatory convection in a viscoelastic fluid through a porous layer heated from below. Rheol. Acta 28, 48–53. doi:10.1007/bf01354768

CrossRef Full Text | Google Scholar

Saravanan, S., and Purusothaman, A. (2009). Floquet instability of a gravity modulated Rayleigh–Benard problem in an anisotropic porous medium. Int. J. Therm. Sci. 48, 2085–2091. doi:10.1016/j.ijthermalsci.2009.04.001

CrossRef Full Text | Google Scholar

Sivakumar, T., and Saravanan, S. (2009). Effect of gravity modulation on the onset of convection in a horizontal anisotropic porous layer. AIP Conf. Proc. 1146, 472–478.

CrossRef Full Text | Google Scholar

Srivastava, A. K., Bhadauria, B. S., and Kumar, J. (2011). Magnetoconvection in an anisotropic porous layer using thermal nonequilibrium model. Spec. Top. Rev. Porous Media 2 (1), 1–10. doi:10.1615/specialtopicsrevporousmedia.v2.i1.10

CrossRef Full Text | Google Scholar

Storesletten, L. (1998). “Effects of anisotropy on convective flow through porous media,” in Transport phenomena in porous media (Oxford, United Kingdom: Pergamon Press), 261–283.

CrossRef Full Text | Google Scholar

Swamy, M. S. (2017). Combined effect of thermal modulation and AC electric field on the onset of electrothermoconvection in anisotropic porous layer. Am. J. Heat Transf. 4 (3), 95–114. doi:10.7726/ajhmt.2017.1011

CrossRef Full Text | Google Scholar

Swamy, M. S., Naduvinamani, N. B., and Sidram, W. (2012). Onset of Darcy-Brinkman convection in a binary viscoelastic fluid saturated porous layer. Transp. Porous Med. 94, 339–357. doi:10.1007/s11242-012-0008-y

CrossRef Full Text | Google Scholar

Swamy, M. S., Patil, S., and Pallavi, S. P. (2019). Soret and dufour effect induced double- diffusive reaction-convection in anisotropic porous layer. J. Nanofluids 8, 1329–1337. doi:10.1166/jon.2019.1688

CrossRef Full Text | Google Scholar

Swamy, M. S., Shivakumara, I. S., and Naduvinamani, N. B. (2014). Effect of gravity modulation on electrothermal convection in dielectric fluid saturated anisotropic porous layer. J. Heat. Transf. 136, 032601.

CrossRef Full Text | Google Scholar

Swamy, M. S., Shivakumara, I. S., and Sidram, W. (2013). The onset of convection in a gravity-modulated viscoelastic fluid-saturated anisotropic porous layer. Spec. Top. Rev. Porous Media 4 (1), 69–80. doi:10.1615/specialtopicsrevporousmedia.v4.i1.70

CrossRef Full Text | Google Scholar

Thirlby, R. (1970). Convection in an internally heated layer. J. Fluid Mech. 44, 673–693. doi:10.1017/s0022112070002082

CrossRef Full Text | Google Scholar

Upadhya, S. M., Raju, S. V. S. R., Raju, C. S. K., Shah, N. A., and Chung, J. D. (2022). Importance of entropy generation on Casson, Micropolar and Hybrid magneto-nanofluids in a suspension of cross diffusion. Chin. J. Phys. 77 (2022), 1080–1101. doi:10.1016/j.cjph.2021.10.016

CrossRef Full Text | Google Scholar

Vadasz, P. (2008). Emerging topics in heat and mass transfer in porous media. New York, NY, United States: Springer.

Google Scholar

Vafai, K. (2005). Handbook of porous media. Boca Raton, Florida, United States: Taylor and Francis.

Google Scholar

Yadav, D., Mahabaleshwar, U. S., Wakif, A., and Chand, R. (2021). Significance of the inconstant viscosity and internal heat generation on the occurrence of Darcy Brinkman convective motion in a couple-stress fluid saturated porous medium an analytical solution. Int. Comm. Heat. Mass Transf. 122, 105165. doi:10.1016/j.icheatmasstransfer.2021.105165

CrossRef Full Text | Google Scholar

Yoon, D. Y., Kim, M. C., and Choi, C. K. (2004). The onset of oscillatory convection in a horizontal porous layer saturated with viscoelastic liquid. Transp. Porous Media 55, 275–284. doi:10.1023/b:tipm.0000013328.69773.a1

CrossRef Full Text | Google Scholar