Mixed convection and thermal radiation effects on non-Newtonian nanofluid flow with peristalsis and Ohmic heating

Introduction: This investigation explores the heat and mass transfer properties of a non-Newtonian nanofluid containing graphene nano-powder and ethylene glycol during peristalsis. The rheological characteristics of the nanofluid are determined using the Carreau-Yasuda model, and various factors such as viscous dissipation, Lorentz force, Ohmic heating, and Hall effects are taken into account. Mixed convection and thermal radiation effects are also considered in the analysis, and the problem is mathematically described using the long wavelength and low Reynolds number approximations.

Methods: The resulting nonlinear system is solved using numerical methods to obtain the solutions. The dominant effects of mixed convection and thermal radiation are given particular attention, while the influences of other parameters are discussed in relation to these dominant effects.

Results and Discussion: The results demonstrate that increasing the Brinkman number, heat source, and thermal slip parameter leads to higher nanofluid temperatures. However, the heat transfer rate decreases with a higher Hall parameter. The velocity near the center of the channel increases for higher values of the concentration Grashof and Hall parameters. Furthermore, an increase in the Hall and Brownian motion parameters results in a higher concentration of nanoparticles. These findings have practical implications in various fields, including materials science, chemical engineering, and biomedical engineering.

1 Introduction

Peristaltic flows are a special type of flow generated by continuous waves of area contraction/expansion traveling on the walls of hollow tube-like structures of many living beings. The propagation of such waves propels the fluid confined inside the tube in the direction parallel to the propagation. In fact, peristaltic mechanisms are noted to be one of the very familiar fluid transport structures in the individual body as well as by way of which various fluids are moved over a short distance. In physiology, such flows find their applications in the transport of urine through the urinary tract, of food through the digestive tract, of bile through the bile duct, and in the transport of reproductive cells, etc. The utility of the peristaltic mechanism persuaded engineers to adopt such a mechanism in devising several engineering devices as well, particularly in processes where the constituents to be transported are sensitive/corrosive and are meant to be insulated from direct contact with the external environment. Latham, (1966) provided a pioneering study for the analysis of peristaltic phenomena, followed by Shapiro et al. (1969) who utilized the “long wavelength and low Reynolds number approach” to investigate such flows. Based on the utility of peristaltic flows, literature on the topic grew with time, incorporating analysis of such flows in different flow settings, some of which can be found in (Dobrolyubov and Douchy, 2002; Reddy et al., 2005; Abbasi et al., 2015). It is well established that many of the naturally occurring fluids (e.g., blood, semi-digested food, lava, etc.) are non-Newtonian. This fact makes the flow analysis of such fluids additionally important. Keeping this in mind, the peristaltic movement of non-Newtonian fluids is analyzed via studies (Abbasi et al., 2014; Babu and Narayana, 2016; Abbasi and Shehzad, 2017).

The importance of nanofluids and their utility cannot be overstated by any means. Since the proposal of the novel idea of nanofluids by Choi and Eastman, (1995), scientists and engineers have found numerous ways in which nanofluids enhance the performance of many scientific and engineering processes. Unique and modifiable thermals, as well as chemical properties of nanofluids, make them an ideal substance to achieve high performance in engineering processes such as in modern drug delivery systems, diagnostics and treatments of tumors/cancerous cells, and domestic/industrial heating/cooling systems. IT and automobile industries are some of the areas witnessing considerable advancements due to the use of nanofluids. Buongiorno, (2006) proposed that incorporating the Brownian motion and thermophoresis properties is essential in the flow study of nanofluids. Tiwari and Das, (2007) used effective thermophysical quantities for the analysis of nanofluid transport making use of the two-phase approach. Keeping the two-phase approach in view, several experimental investigations were carried out to propose different empirical relations predicting effective thermophysical quantities that are in close ties with that of experimental results. Some of these relations were specific for specific nanofluids whereas some models were proposed to predict the general behavior of nanofluids (Xue, 2005; Rudyak and Krasnolutskii, 2014; Shehzad et al., 2015).

Hybrid nanofluids are further modifications of nanofluids obtained by mixing more than one different nanosized particle in a base fluid. Mixtures thus obtained possess enhanced and precise thermophysical and chemical properties required for several processes. Recently, the flow analysis of nanofluids under different flow conditions has been reported in a number of studies, some of which are given through references (Izadi et al., 2019; Abbasi et al., 2022; Haq et al., 2022; Kumar and Sharma, 2022; Rehman et al., 2022; Yasmin et al., 2023). Investigations revealed that the addition of nanoparticles beyond a certain fraction of the total volume can perturb the rheological characteristics as well. Mixtures thus obtained act as non-Newtonian fluids of different types. Hence, the flow analysis of non-Newtonian nanofluids becomes important and has been attended in some of the studies given through references (Akbar et al., 2015; Rasheed et al., 2015; Eldabe et al., 2020; Gul et al., 2020; Sharma et al., 2023).

The present study delves into the peristalsis of non-Newtonian nanofluid, taking into account several factors to highlight its novelty. The study incorporates the rheologic properties of the fluid, applying the Carreau-Yasuda model, as well as viscous dissipation. Additionally, it considers the Lorentz force rendered by a uniform magnetic field, Ohmic heating, and Hall effects. The analysis also incorporates the effects of mixed convection, thermal radiation, and porous medium, making it more comprehensive. The mathematical description is obtained using the “long wavelength and low Reynolds number approximations,” and the boundaries adopt the slip condition of velocity and jump condition of temperature. Due to the resulting nonlinear system’s complexity, numerical solutions employing the inherent command in Mathematica are found. The study’s key findings are then briefly outlined at the end, emphasizing its novelty and significance.

2 Problem formulation

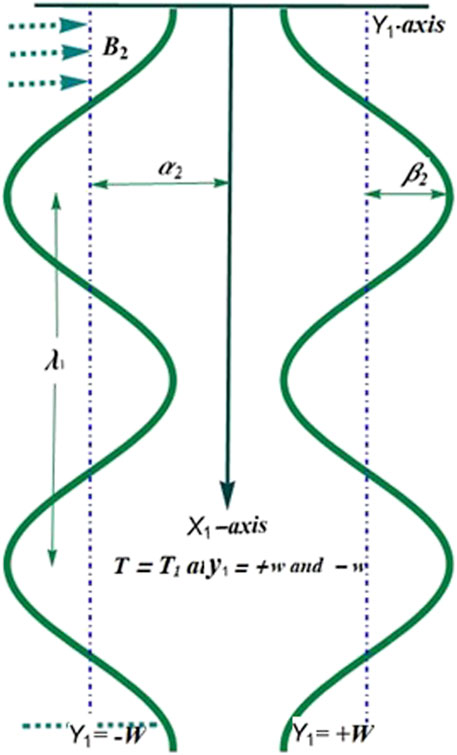
An electrically conducting 2D incompressible peristalsis of Carreau-Yasuda (C-Y) nanofluid is contemplated in a symmetric channel of width $2{\alpha }_2$ and the sinusoidal waves propagate with a wavelength of ${\lambda }_1$ on its walls at constant wave speed $c_1$, as shown in Figure 1. Channel walls are maintained at a constant mass concentration $C_1$ and temperature $T_1$. Rectangular coordinates (${\overline{X}}_1$, ${\overline{Y}}_1$) with the $\overline{Y_1}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$ perpendicular and $\overline{X_1}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$ parallel to the middle line are considered. The flow is affected by an external magnetic field $B_2.$ The geometric description of the wall’s surface is written as:

$\pm \overline{W}\left({\overline{X}}_1,{\overline{t}}_1\right)=\pm \left[{\beta }_2\mathit{cos}\left(\frac{2\pi }{{\lambda }_1}\left({\overline{X}}_1-c_1{\overline{t}}_1\right)\right)+{\alpha }_2\right],(1)$

here ${\lambda }_1$, ${\overline{t}}_1$, $c_1$, ${\alpha }_2$, and ${\beta }_2$ are, respectively, the wavelength time, speed of the wave, width of the wall, and amplitude of the peristaltic waves. $+\overline{W}\left({\overline{X}}_1,{\overline{t}}_1\right)$ and $-\overline{W}\left({\overline{X}}_1,{\overline{t}}_1\right)$ are used for the right and left walls, respectively.

FIGURE 1

FIGURE 1. The geometry of the flow problem.

Thus, the study assumes that the flow is occurring in a symmetric channel of width with sinusoidal waves propagating at a constant wave speed at its walls. The flow is electrically conducting, 2D, and incompressible. The nanofluid being studied follows the Carreau-Yasuda model. Additionally, the channel walls are maintained at a constant mass concentration and temperature, and the flow is affected by an external magnetic field and various assumptions including mixed convection, heat absorption/generation, modified Darcy’s law, thermophoresis diffusion, Ohmic heating, Brownian diffusion, magnetic field/flux, viscous dissipation, and thermal radiation. Therefore, the leading equations for the underlying flow with these assumptions are given as (Shehzad et al., 2015; Gul et al., 2020):

$\frac{\partial {\overline{U}}_1}{\partial {\overline{X}}_1}+\frac{\partial {\overline{V}}_1}{\partial {\overline{Y}}_1}=0,(2)$

$\begin{array}{c}{\rho }_f\left(\frac{\partial {\overline{U}}_1}{\partial {\overline{t}}_1}+{\overline{U}}_1\frac{\partial {\overline{U}}_1}{\partial {\overline{X}}_1}+{\overline{V}}_1\frac{\partial {\overline{U}}_1}{\partial {\overline{Y}}_1}\right)=-\frac{\partial \overline{P}}{\partial {\overline{X}}_1}+\frac{\partial {\overline{S}}_{{\overline{X}}_1{\overline{Y}}_1}}{\partial {\overline{Y}}_1}+\frac{\partial {\overline{S}}_{{\overline{X}}_1{\overline{X}}_1}}{\partial {\overline{X}}_1}\\ +g{\rho }_f{\beta }_T\left(T-T_1\right)+{\overline{R}}_{{\overline{X}}_1}+g{\rho }_f{\beta }_C\left(C-C_1\right)\\ -\frac{{\sigma }_f{B_2}^2}{1+m^2}\left(\overline{U_1}-m\overline{V_1}\right),\end{array}(3)$

$\begin{array}{c}{\rho }_f\left(\frac{\partial {\overline{V}}_1}{\partial {\overline{t}}_1}+{\overline{U}}_1\frac{\partial {\overline{V}}_1}{\partial {\overline{X}}_1}+{\overline{V}}_1\frac{\partial {\overline{V}}_1}{\partial {\overline{Y}}_1}\right)=-\frac{\partial \overline{P}}{\partial {\overline{Y}}_1}+\frac{\partial {\overline{S}}_{{\overline{Y}}_1{\overline{X}}_1}}{\partial {\overline{X}}_1}+\frac{\partial {\overline{S}}_{{\overline{Y}}_1{\overline{Y}}_1}}{\partial {\overline{Y}}_1}\\ -\frac{{\sigma }_f{B_2}^2}{1+m^2}\left(\overline{V_1}+m\overline{U_1}\right)+{\overline{R}}_{{\overline{Y}}_1},\end{array}(4)$

$\begin{array}{c}{\left(\rho C\right)}_f\left(\frac{\partial T}{\partial {\overline{t}}_1}+{\overline{U}}_1\frac{\partial T}{\partial {\overline{X}}_1}+{\overline{V}}_1\frac{\partial T}{\partial {\overline{Y}}_1}\right)=K_f\left(\frac{{\partial }^{2}T}{\partial {{\overline{X}}_1}^2}+\frac{{\partial }^{2}T}{\partial {{\overline{Y}}_1}^2}\right)\\ +\overline{S}.\overline{L}+{\mathrm{\Phi }}_2+\frac{1}{{\sigma }_f}\overline{J}.\overline{J}-\frac{\partial Q_r}{\partial {\overline{Y}}_1}\\ +\tau {\left(\rho C\right)}_f\left\{D_B\left(\frac{\partial C}{\partial {\overline{X}}_1}\frac{\partial T}{\partial {\overline{X}}_1}+\frac{\partial C}{\partial {\overline{Y}}_1}\frac{\partial T}{\partial {\overline{Y}}_1}\right)+\frac{D_T}{T_m}{\left(\left(\frac{\partial T}{\partial {\overline{X}}_1}\right)+\left(\frac{\partial T}{\partial {\overline{Y}}_1}\right)\right)}^2\right\},\end{array}(5)$

$\left(\frac{\partial C}{\partial {\overline{t}}_1}+{\overline{U}}_1\frac{\partial C}{\partial {\overline{X}}_1}+{\overline{V}}_1\frac{\partial C}{\partial {\overline{Y}}_1}\right)=\frac{D_T}{T_m}\left(\frac{{\partial }^{2}T}{\partial {{\overline{Y}}_1}^2}+\frac{{\partial }^{2}T}{\partial {{\overline{X}}_1}^2}\right)+D_B\left(\frac{{\partial }^{2}C}{\partial {{\overline{Y}}_1}^2}+\frac{{\partial }^{2}C}{\partial {{\overline{X}}_1}^2}\right).(6)$

In the above equations, $g$ is the gravitational acceleration, ${\sigma }_f$ is the electric conductivity of nanofluid, ${\overline{S}}_{ij}$ is the extra stress tensor components, $\overline{P}\left(\overline{X_1},\overline{Y_1},{\overline{t}}_1\right)$ is the pressure, C is the concentration, ${\mathrm{\Phi }}_2$ is heat absorption/generation parameter, $\overline{S}.\overline{L}$ is the viscous dissipation, $\overline{J}$ is the current density, $D_B$ is the Brownian motion, $D_F$ is the diffusion coefficient, $D_T$ is the thermophoretic diffusion coefficient, ${\beta }_T$ and ${\beta }_C$ are thermal and concentration expansion coefficients, respectively. The Rosseland approximation leads to the following expression of radiative heat flux $Q_r$

$Q_r=-\frac{16}{3}\frac{{{\sigma }_1}^{*}}{{k_1}^{*}}{T_1}^3\frac{\partial T}{\partial {\overline{Y}}_1}.(7)$

where ${k_1}^{*}$ is the radiative conductivity and ${{\sigma }_1}^{*}$ is Stefan’s constant. The modified Darcy’s law has been employed for porous medium, which satisfies ${\overline{R}}_1=\left({\overline{R}}_{{\overline{X}}_1},{\overline{R}}_{{\overline{Y}}_1},0\right)$:

${\overline{R}}_1=-\frac{{\epsilon }^{*}}{k_1}\mu \left({\gamma }_1^{\prime }\right)\overline{V},(8)$

where, ${\epsilon }^{*}$ and $k_1$ are signified by the porosity and permeability in the case of a porous medium.

For Carreau-Yasuda (C-Y) nanofluid, the extra stress tensor is presented as (Abbasi and Shehzad, 2017; Gul et al., 2020):

$\overline{S}={\overline{A}}_2\mu \left({\gamma }_1^{\prime }\right),(9)$

here $A_2$ and $\mu \left({\mathrm{\gamma }}_1^{\prime }\right)$ denote the first Rivlin-Erickson tensor and apparent viscosity, correspondingly.

$\mu \left({\mathrm{\gamma }}_1^{\prime }\right)={\mu }_{\infty }+\left({\mu }_0-{\mu }_{\infty }\right){\left(1+{\left(\mathrm{\Gamma }{\mathrm{\gamma }}_1^{\prime }\right)}^{{\alpha }_1}\right)}^{\frac{n-1}{{\alpha }_1}},(10)$

in which ${\mu }_{\infty }$, $n$, ${\mu }_0$, and ${\alpha }_1$ notate the infinite share rate, power law index, zero share rate, and non-Newtonian characteristic of C-Y nanofluid, respectively.

Here, the shear rate $\left({\mathrm{\gamma }}_1^{\prime }\right)$ is defined as:

${\mathrm{\gamma }}_1^{\prime }=\sqrt{2\mathrm{t}\mathrm{r}\left({\mathrm{\Pi }}^2\right)}.(11)$

Furthermore, $\mathrm{\Pi }$ is defined as:

$\mathrm{\Pi }=\frac{1}{2}{A}_2\mathrm{a}\mathrm{n}\mathrm{d}{A}_2=\nabla \overline{V}+{\left(\nabla \overline{V}\right)}^T.(12)$

The relationship between fixed frame $\left({\overline{X}}_1,{\overline{Y}}_1,{\overline{t}}_1\right)$ and wave frame $\left({\overline{x}}_1,{\overline{y}}_1\right)$ is given as:

$\left\{\begin{array}{l}\overline{p}\left({\overline{x}}_1,{\overline{y}}_1\right)=\overline{P}\left({\overline{X}}_1,{\overline{Y}}_1,{\overline{t}}_1\right),\\ {\overline{y}}_1={\overline{Y}}_1,{\overline{x}}_1=\overline{X_1}-c_1\overline{t_1,}\\ {\overline{u}}_1\left({\overline{x}}_1,{\overline{y}}_1\right)={\overline{U}}_1\left({\overline{X}}_1,{\overline{Y}}_1,{\overline{t}}_1\right)-c_1,\\ {\overline{v}}_1\left({\overline{x}}_1,{\overline{y}}_1\right)={\overline{V}}_1\left({\overline{X}}_1,{\overline{Y}}_1,{\overline{t}}_1\right).\end{array}\right.(13)$

Utilizing the above-stated transformation to Eqs 2–6, we obtain.

$\frac{\partial {\overline{u}}_1}{\partial {\overline{x}}_1}+\frac{\partial {\overline{v}}_1}{\partial {\overline{y}}_1}=0,(14)$

$\begin{array}{c}{\rho }_f\left(\left({\overline{u}}_1+c_1\right)\frac{\partial {\overline{u}}_1}{\partial {\overline{x}}_1}+{\overline{v}}_1\frac{\partial {\overline{u}}_1}{\partial {\overline{y}}_1}\right)=-\frac{\partial \overline{p}}{\partial {\overline{x}}_1}+\frac{\partial {\overline{s}}_{{\overline{x}}_1{\overline{x}}_1}}{\partial {\overline{x}}_1}+\frac{\partial {\overline{s}}_{{\overline{x}}_1{\overline{y}}_1}}{\partial {\overline{y}}_1}\\ +g{\rho }_f{\beta }_T\left(T-T_1\right)+g{\rho }_f{\beta }_C\left(C-C_1\right)\\ -\frac{{\sigma }_f{B_2}^2}{1+{\left(m\right)}^2}\left(\left({\overline{u}}_1+c_1\right)-m\overline{v_1}\right)-\frac{{\epsilon }^{*}}{k_1}\mu \left({\gamma }_1^{\prime }\right)\left({\overline{u}}_1+c_1\right),\end{array}(15)$

${\rho }_f\left(\left({\overline{u}}_1+c_1\right)\frac{\partial {\overline{v}}_1}{\partial {\overline{x}}_1}+{\overline{v}}_1\frac{\partial {\overline{v}}_1}{\partial {\overline{y}}_1}\right)=-\frac{\partial \overline{p}}{\partial {\overline{y}}_1}+\frac{\partial {\overline{s}}_{{\overline{y}}_1{\overline{x}}_1}}{\partial {\overline{x}}_1}+\frac{\partial {\overline{s}}_{{\mathrm{y}}_1{\overline{y}}_1}}{\partial {\overline{y}}_1}-\frac{{\epsilon }^{*}}{k_1}\mu \left({\gamma }_1^{\prime }\right)\left({\overline{v}}_1\right)-\frac{{\sigma }_f{B_2}^2}{1+{\left(m\right)}^2}\left({\overline{v}}_1+m\left({\overline{u}}_1+c_1\right)\right),(16)$

$\begin{array}{c}{\left({\rho }^C\right)}_f\left(\left({\overline{u}}_1+c_1\right)\frac{\partial T}{\partial {\overline{x}}_1}+{\overline{v}}_1\frac{\partial T}{\partial {\overline{y}}_1}\right)=K_f\left(\frac{{\partial }^{2}T}{\partial {\overline{x}}_1^2}+\frac{{\partial }^{2}T}{\partial {\overline{y}}_1^2}\right)+{\mathrm{\Phi }}_2+\frac{{\sigma }_f{B}_2^2}{1+{\left(m\right)}^2}\left({\overline{v}}_1^2+{\left({\overline{u}}_1^2+c_1\right)}^2\right)+\overline{s}.\overline{L}\\ +\frac{16}{3}\frac{{\sigma }_1^{*}}{k_1^{*}}{T}_1^3\frac{{\partial }^{2}T}{\partial {\overline{y}}_1^2}+\tau {\left({\rho }^C\right)}_f\left\{D_B\left(\frac{\partial \mathrm{C}}{\partial {\overline{x}}_1}\frac{\partial T}{\partial {\overline{x}}_1}+\frac{\partial \mathrm{C}}{\partial {\overline{y}}_1}\frac{\partial T}{\partial {\overline{y}}_1}\right)\right.+\left.\frac{D_T}{T_m}{\left(\left(\frac{\partial T}{\partial {\overline{x}}_1}\right)+\left(\frac{\partial T}{\partial {\overline{y}}_1}\right)\right)}^2\right\},\end{array}(17)$

$\left(\left({\overline{u}}_1+c_1\right)\frac{\partial C}{\partial {\overline{x}}_1}+{\overline{v}}_1\frac{\partial C}{\partial {\overline{y}}_1}\right)=\frac{D_T}{T_m}\left(\frac{{\partial }^{2}T}{\partial {{\overline{y}}_1}^2}+\frac{{\partial }^{2}T}{\partial {{\overline{x}}_1}^2}\right)+D_B\left(\frac{{\partial }^{2}C}{\partial {{\overline{y}}_1}^2}+\frac{{\partial }^{2}C}{\partial {{\overline{x}}_1}^2}\right).(18)$

Using the following dimensionless quantities (Abbasi and Shehzad, 2017; Gul et al., 2020):

$\begin{array}{c}\mathrm{Pr}=\frac{{\mu }_0{C}_f}{K_f},x_1=\frac{{\overline{x}}_1}{{\lambda }_1},y_1=\frac{{\overline{y}}_1}{{\alpha }_2},u_1=\frac{{\overline{u}}_1}{c_1},v_1=\frac{{\overline{v}}_1}{c_1\delta },w=\frac{\overline{W}}{{\alpha }_2},d_1=\frac{{\beta }_2}{{\alpha }_2},p=\frac{{{\alpha }_2}^2\overline{p}}{c_1{\lambda }_1{\mu }_0},\mathrm{R}\mathrm{e}=\frac{{\rho }_f{c}_1{\alpha }_2}{{\mu }_0},\\ \in =\frac{{\alpha }_2^2{\mathrm{\Phi }}_2}{T_1{K}_f},M=\sqrt{\frac{{\sigma }_f}{{\mu }_f}}{B}_2{d}_1,Gc=\frac{{\rho }_f{\beta }_{C}g\left(C-C_1\right){\alpha }_2^2}{{\mu }_0{c}_1},Nr=\frac{16}{3}\frac{{{\sigma }_1}^{*}}{{k_1}^{*}}\frac{{T_1}^3}{K_f},Br=\mathrm{Pr}E,\theta =\frac{T-T_1}{T_1},\\ Gr=\frac{{\rho }_f{\beta }_{T}g\left(T-T_1\right){\alpha }_2^2}{{\mu }_0{c}_1},\tau =\frac{{\left(\rho C\right)}_p}{{\left(\rho C\right)}_f},s_{ij}=\frac{{\alpha }_2{\overline{s}}_{ij}}{c_1{\mu }_0},Nt=\frac{\tau \left(D_T{T}_1\right)}{\nu T_m},Nb=\frac{\tau \left(D_B{C}_1\right)}{\nu },\upsilon =\frac{{\mu }_0}{{\rho }_0},\\ Ec=\frac{c_1^2}{C_f{T}_1},\varphi =\frac{C-C_1}{C_1},u_1=\frac{\partial \psi }{\partial y_1},v_1=-\frac{\partial \psi }{\partial x_1},{\beta }_1=\frac{{\mu }_{\infty }}{{\mu }_0},We=\frac{\mathrm{\Gamma }{c}_1}{{\alpha }_1}.\end{array}(19)$

In the above non-dimensional quantities, $\theta$, $Nb$, $M$, $Nt$, $Nr,$ $\mathrm{R}\mathrm{e}$, $\mathit{Pr}$, $m$, $Ec$, $\alpha$, $Gr$, $\in$, ${\beta }_2$, Gc, $\tau$, and $We$ are the dimensionless temperature, Brownian motion parameter, Hartman number, thermophoresis and thermal radiation parameters, Reynolds number, Prandtl number, Hall parameter, Eckert number, thermal conductivity parameter, thermal Grashof number, heat absorption/generation parameter, dimensionless amplitude, concentration Grashof number, the ratio of specific heats of particles and fluid, and Weissenberg number.

Thus, the dimensionless quantities stated in Eq. 19 yield the satisfaction of the continuity equation, whereas Reynolds number and long wavelength are approximated to be small and long, correspondingly, which results in the following set of equations:

$0=-\frac{\partial p}{\partial x_1}+\frac{\partial s_{x_1{y}_1}}{\partial y_1}-\frac{M^2}{1+{\left(m\right)}^2}\left[1+\frac{\partial \psi }{\partial y_1}\right]-\frac{1}{Da}\frac{\mu \left({\gamma }_1^{\prime }\right)}{{\mu }_0}\left[1+\frac{\partial \psi }{\partial y_1}\right]+Gr\theta +Gc\varphi ,(20)$

$0=\frac{\partial p}{\partial y_1},(21)$

$\begin{array}{c}0=\frac{{\partial }^2\theta }{\partial y_1^2}+Br\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)S_{x_1{y}_1}+\frac{Br{M}^2}{1+{\left(m\right)}^2}{\left(1+\frac{\partial \psi }{\partial y_1}\right)}^2+\in \\ +\mathit{Pr}Nb\left(\frac{\partial \theta }{\partial y_1}\frac{\partial \varphi }{\partial y_1}\right)+Nr\frac{{\partial }^2\theta }{\partial y_1^2}+\mathit{Pr}Nt{\left(\frac{\partial \theta }{\partial y_1}\right)}^2,\end{array}(22)$

$0=\left[\frac{{\partial }^2\varphi }{\partial y_1^2}\right]+\frac{N_t}{N_b}\left[\frac{{\partial }^2\theta }{\partial y_1^2}\right],(23)$

where $Da$ is Darcy’s parameter. Thus, the extra stress tensor (dimensionless) of Carreau-Yasuda nanofluid becomes:

$s_{x_1{y}_1}=\left[1-\frac{\left(n-1\right)\left({\beta }_1-1\right)W{e}^{{\alpha }_1}}{{\alpha }_1}{\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)}^{{\alpha }_1}\right]\frac{{\partial }^2\psi }{\partial y_1^2}=s_{y_1{x}_1}.(24)$

Applying cross-differentiating and substituting the values of $s_{x_1{y}_1}$ and $\mu \left({\gamma }_1^{\prime }\right)$, Eqs 20, 22 yield:

$\begin{array}{c}0=\frac{{\partial }^2}{\partial y_1^2}\left\{\left[1-\frac{\left(n-1\right)\left({\beta }_1-1\right)W{e}^{{\alpha }_1}}{{\alpha }_1}{\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)}^{{\alpha }_1}\right]\left[\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)\right]\right\}-\frac{M^2}{1+{\left(m\right)}^2}\left[\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)\right]+Gc\frac{\partial \varphi }{\partial y_1}\\ -\frac{1}{Da}\frac{\partial }{\partial y_1}\left[1-\frac{\left(n-1\right)\left({\beta }_1-1\right)W{e}^{{\alpha }_1}}{{\alpha }_1}{\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)}^{{\alpha }_1}\right]\left[\frac{{\partial }^2\psi }{\partial y_1^2}\right]+Gr\frac{\partial \theta }{\partial y_1}.\end{array}(25)$

The flow rates in non-dimensional settings in the fixed ${\eta }_2\left(=\frac{\overline{Q_1}}{c_1{d}_1}\right)$ and moving frames $F_2\left(=\frac{{\overline{q}}_1}{c_1{d}_1}\right)$ are presented as:

${\eta }_2=F_2+1,(26)$

where ${\overline{Q}}_1$ and ${\overline{q}}_1$ represent flow ratios in fixed and moving frames, respectively. Additionally, $F_2$ is defined as:

$F_2={\displaystyle \underset{0}{\overset{w}{\int }}}\frac{\partial \psi }{\partial y_1}d{y}_1.(27)$

The slip boundary conditions are vital in many practical situations, especially in scenarios where the contact surfaces are lubed. Hence, the considerations of slip for velocity, temperature, and concentration are accounted for here. The dimensionless form of boundary conditions making use of the stresses defined via Eq. 24 for wall slip is stated as (Abbasi and Shehzad, 2017):

$\begin{array}{l}{\psi }_1=-\frac{F_2}{2}\mathrm{a}\mathrm{t}{y}_1=w_1,{\psi }_1=\frac{F_2}{2}\mathrm{a}\mathrm{t}{y}_1=w_2,\\ \frac{\partial {\psi }_1}{\partial y_1}+\alpha \left[1-\frac{\left(n-1\right)\left({\beta }_1-1\right)W{e}^{{\alpha }_1}}{{\alpha }_1}{\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)}^{{\alpha }_1}\right]\frac{{\partial }^2\psi }{\partial y_1^2}=1,\mathrm{a}\mathrm{t}{y}_1=w_1,\\ \frac{\partial {\psi }_1}{\partial y_1}-\alpha \left[1-\frac{\left(n-1\right)\left({\beta }_1-1\right)W{e}^{{\alpha }_1}}{{\alpha }_1}{\left(\frac{{\partial }^2\psi }{\partial y_1^2}\right)}^{{\alpha }_1}\right]\frac{{\partial }^2\psi }{\partial y_1^2}=1,\mathrm{a}\mathrm{t}{y}_1=w_2.\end{array}(28)$

$\begin{array}{l}\theta +{\gamma }_1\frac{\partial \theta }{\partial y_1}=0,\mathrm{a}\mathrm{t}{y}_1=w_1,\\ \theta -{\gamma }_1\frac{\partial \theta }{\partial y_1}=0,\mathrm{a}\mathrm{t}{y}_1=w_2,\\ \varphi +{\gamma }_2\frac{\partial \varphi }{\partial y_1}=0,\mathrm{a}\mathrm{t}{y}_1=w_1,\\ \varphi -{\gamma }_2\frac{\partial \varphi }{\partial y_1}=0,\mathrm{a}\mathrm{t}{y}_1=w_2.\end{array}(29)$

The non-dimensionless form of a peristaltic wall is described as:

$\begin{array}{l}{w}_1=1+d_1\cos \left(2\pi x_1\right),\\ w_2=-1-d_1\cos \left(2\pi x_1\right),\end{array}(30)$

where ${\gamma }_1$, $\alpha$, and ${\gamma }_2$ denote the thermal, velocity, and concentration of nanofluid slip factors. It is meaningful that the no-slip case for velocity, temperature, and concentration can be reduced from the present condition by substituting ${\gamma }_1=\alpha ={\gamma }_2=0$, using NDSolve (built-in command in Mathematica) to calculate numerical results of Eqs 22, 23, 25 with the above-mentioned boundary conditions Eqs 28, 29.

3 Results and discussion

This section aims to provide graphical results explaining the effects of various flow parameters involved in this study. In this study, we looked at how different parameters affect the distribution of fluid velocity, temperature, concentration, and heat and mass transfer rates in a channel under mixed convection and thermal radiation along with other flow parameters. The relationship among different flow parameters is provided by Eq. 19. We specifically considered the velocity slip parameter, concentration Grashof number, thermal Grashof number, Hartmann number, and Hall parameter, which are commonly used in similar studies. Below, we provide a brief description of these parameters and their typical range for a better understanding for readers:

• The velocity slip parameter measures the difference in velocity between the fluid and the solid surface and characterizes the effect of slip velocity on fluid motion. It ranges from zero to one, where zero represents no-slip and one represents free-slip.

• The concentration Grashof number is a dimensionless parameter that describes buoyancy-driven flow caused by concentration gradients in a fluid. Its typical range is between ${10}^3$ and ${10}^7$.

• The thermal Grashof number is a dimensionless parameter that describes buoyancy-driven flow caused by temperature gradients in a fluid. Similar to the concentration Grashof number, the typical range for thermal Grashof number is between ${10}^3$ and ${10}^7$.

• The Hartmann number is a dimensionless parameter that characterizes the effect of a magnetic field on the motion of an electrically conducting fluid. Its typical range is between 0 and 100.

• The Hall parameter is a dimensionless parameter that describes the influence of the magnetic field on the motion of a conducting fluid and considers the Hall effect. Its typical range is between zero and one.

• For mixed convection, typical parameter ranges are Reynolds number of 10–1,000 and Grashof number of ${10}^3$ and ${10}^6$, whereas for thermal radiation, typical ranges are Rosseland number of 0.1–10 and emissivity of 0.1–0.9.

In the subsequent subsections, the velocity profile, temperature distribution, concentration profile, and heat and mass transfer rates at the boundary are presented and explained.

3.1 Velocity profile

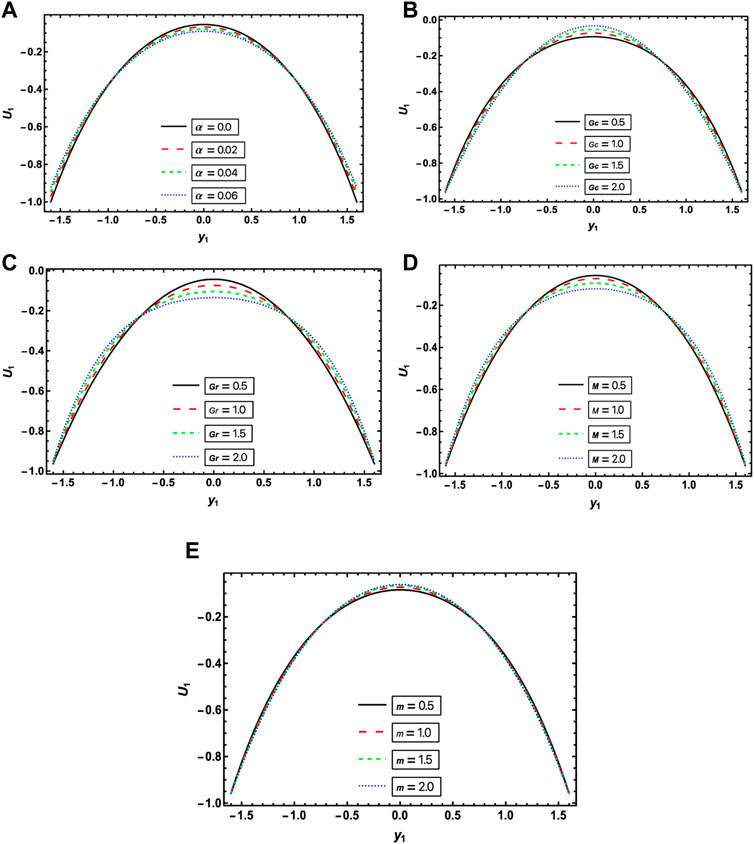
Figures 2A–E interact with the influence of velocity slip parameter $\left(\alpha \right)$, concentration Grashof number $\left(Gc\right)$, thermal Grashof number $\left(Gr\right)$, Hartman number $\left(M\right)$, and Hall parameter $\left(m\right)$ on fluid velocity distribution. Overall, plotting the velocity distribution against the various parameters of mixed convection and thermal radiation can provide insight into how these parameters influence the fluid flow in a peristaltic channel. The influence of $\alpha$ on the velocity profile is projected in Figure 2A. It is observed that the growth in the velocity slip parameter reduces fluid velocity in the middle of the channel and the opposite behavior has been noticed in the left and right walls; Figure 2B represents $u$ via $Gc.$ It is obvious from this figure that fluid velocity raises the larger values of concentration Grashof number in the center of the channel and declines in the upper and lower walls. This is because ‘$Gc$’ with its growing values improves the concentration of nanofluid, which leads to a decline in velocity near the channel. Physically, “mixed convection is useful in nuclear reactor technology and in electronic cooling processes where forced convection is insufficient to dissipate energy.” The velocity profile decreases in the middle of the channel by increasing the thermal Grashof number (see Figure 2C). It is quite evident from Figure 2D that the velocity distribution improves near the walls by increasing the Hartmann number. Figure 2E reports that fluid velocity distribution increases with an increase in ${}^{\prime }{m}^{\prime }$. In this case, the rise in velocity for the larger Hall parameter is caused by less electrical conductivity production that decreases the damping of the magnetic force. In fact, the resistive effect of the applied magnetic field is partially balanced by the Hall effect.

FIGURE 2

FIGURE 2. Velocity distribution with ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nr=1.0,$, $Nt=0.2,Nb=0.3,\mathrm{Pr}=204,Br=0.3,x=0,\in =2.0,{\gamma }_2=0.1,$ for change in (A) $\alpha \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Gc=1.0,Gr=1.0,M=0.5,m=0.5,$ (B,C) $Gr\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\alpha =0.3,Gc=1.0,M=0.5,m=0.5,$ (D) $M\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Gr=1.0,\alpha =0.3,Gc=1.0,m=0.5,$ and (E) $m\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Gr=1.0,\alpha =0.3,Gc=1.0,M=0.5.$

3.2 Temperature profile

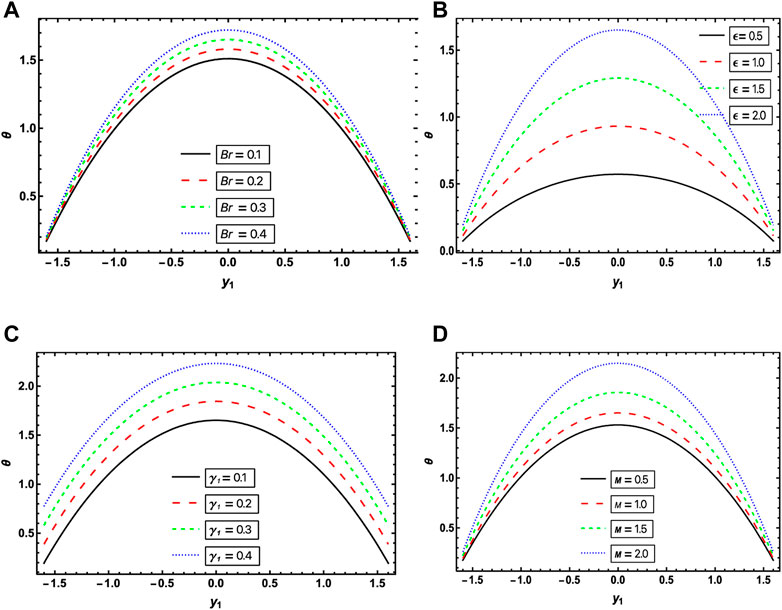
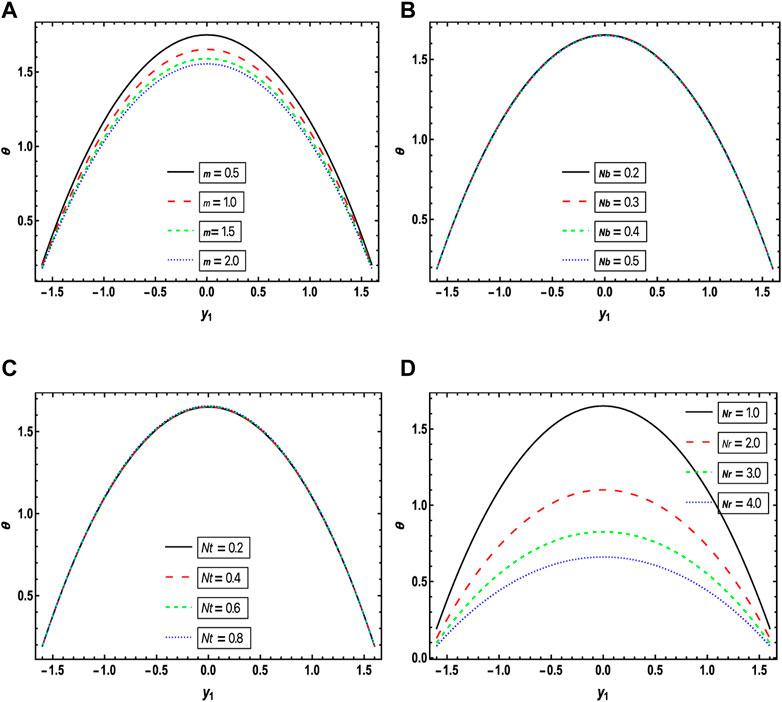
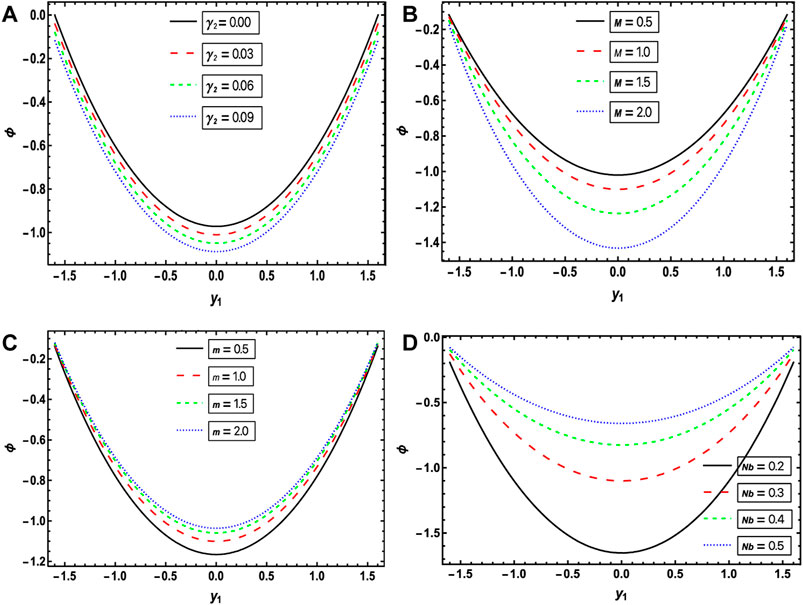
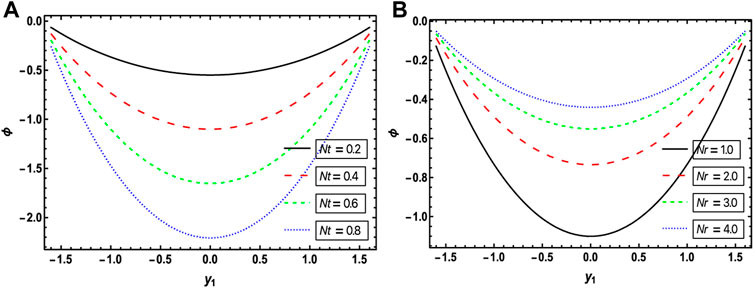
Figures 3, 4 relate to the impact of “Brinkman number $\left(Br\right)$, heat source/sink parameter $\left(\in \right)$, thermal slip parameter $\left({\gamma }_1\right)$, Hartman number $\left(M\right)$, thermophoresis parameter $\left(Nt\right)$, Hall parameter $\left(m\right)$, Brownian motion parameter $\left(Nb\right)$, and thermal radiation parameter $\left(Nr\right)$” on temperature distribution. From Figure 3A, an increment in the magnitude of temperature distribution is witnessed for larger values of the Brinkman number. Physically, the nanofluid warmed up due to friction in the fluid layers, and, hence, the temperature of the fluid improved as the Brinkman number increased. From Figure 3B, an increase in temperature distribution is observed in larger values of the heat source parameter. This reveals that the existence of the heat sink/source parameter produces more heat in the fluid. Figure 3C demonstrates the influence of the thermal slip parameter on temperature distribution. It can be seen that the magnitude of the temperature rises by improving ${\gamma }_1$. The feature of the temperature profile under the impact of the Hartman number is illustrated in Figure 3D. It is noted that the improvement in $M$ enhances the fluid temperature. This is mainly due to Ohmic heating. Figure 4A delineates the influence of the Hall parameter on the temperature profile. It is clear from this figure that the higher values of $m$ significantly reduce the temperature of the fluid. The impact of the bulk magnetic force is diminished by the existence of stronger Hall currents. As a result, the temperature distribution decreased. Figure 4B reveals that the magnitude of fluid temperature dramatically lessens with an increase in Brownian motion parameter. From Figure 4C, it is observed that the magnitude of the temperature increases by improving the thermophoresis parameter. Figure 4D shows that fluid temperature declines for larger values of $Nr.$ since the thermal radiation parameter is inversely proportional to $k_1^{*}.$ Thus, the absorption coefficient decreases with more radiation.

FIGURE 3

FIGURE 3. Temperature distribution with ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nt=0.2,$ $Nr=1.0,Nb=0.3,\mathrm{Pr}=204,Da=1.0,Gc=1.0,Gr=1.0,x=0,{\gamma }_2=0.1,$ for change in (A) $Br\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\gamma }_1=0.1,\in =2.0,M=0.5,$ (B) $\in \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\gamma }_1=0.1,Br=0.3,M=0.5,$ (C) ${\gamma }_1\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\in =2,Br=0.3,M=0.5,$ and (D) $M\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\in =2,Br=0.3,{\gamma }_1=0.1.$

FIGURE 4

FIGURE 4. Temperature distribution with ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,\in =2,$ $Br=0.3,{\gamma }_1=0.1,M=0.5,\mathrm{Pr}=204,Da=1.0,Gc=1.0,Gr=1.0,x=0,{\gamma }_2=0.1,$ for change in (A) $m\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Nb=0.3,Nt=0.2,Nr=1.0,$ (B) $Nb\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}m=0.1,Nt=0.2,Nr=1.0,$ (C) $Nt\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}m=0.1,Nb=0.3,Nr=1.0,$ and (D) $Nr\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}m=0.1,Nb=0.3,Nt=0.2.$

3.3 Concentration profile

Graphical influences of the concentration slip parameter $\left({\gamma }_2\right)$, Hall parameter $\left(m\right)$, thermophoresis parameter $\left(Nt\right)$, Hartmann number $\left(M\right)$, Brownian motion parameter $\left(Nb\right)$, and thermal radiation parameter $\left(Nr\right)$ on nanoparticles concentration are investigated in Figures 5, 6. Figure 5A signifies that the concentration profile declines by increasing the values of ${}^{\prime }{{\gamma }_2}^{\prime }$. In Figure 5B, the concentration of nanoparticles $\left(\varphi \right)$ is illustrated for different values of Hartmann number $M$. It is noted that concentration decreases by improving the values of $M$, and this plot shows the minimum values in the middle of the channel. Alternatively, ${}^{\prime }{\varphi }^{\prime }$ has a contrary behavior against ${}^{\prime }{m}^{\prime }$. An increment in the Hall parameter increases the concentration profile in the middle of the walls of Carreau-Yasuda (C-Y) nanofluid in Figure 5C. The impact of the Brownian motion parameter on concentration distribution is plotted in Figure 5D. It is observed that the concentration of nanoparticles was enhanced for the higher values of $Nb.$ Concentration distribution decreases by enhancing thermophoresis parameter (see Figure 6A). In a physical context, these results show that mass flow increases with increasing temperature because the thermophoretic effect becomes more stable. The viscosity is reduced by this thermophoretic phenomenon. The concentration becomes smaller due to the diffusion of less viscous particles. The rise in concentration is reflected in higher values of ${}^{\prime }{Nr}^{\prime }$ in Figure 6B.

FIGURE 5

FIGURE 5. Concentration distribution with $n=-0.0216,{\beta }_1=0.04971,Nr=1.0,Nt=0.2,$, $\mathrm{Pr}=204,{\alpha }_1=123.84,Da=1.0,\alpha =0.03,Gr-0.1,Gc=1.0,Br=0.3,$ for change in (A) ${\gamma }_2\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}M=0.5,m=0.1,Nb=0.3,$ (B) $M\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\gamma }_2=0.1,m=0.1,Nb=0.3,$ (C) $m\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\gamma }_2=0.1,M=0.5,Nb=0.3,$ and (D) $Nb\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\gamma }_2=0.1,M=0.5,m=0.1.$

FIGURE 6

FIGURE 6. Concentration distribution with ${\alpha }_1=123.84,n=-0.0216,Nb=0.3,m=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,Gr=0.1,Gc=1.0,Br=0.3,Nr=1.0,\in =2.0,{\gamma }_1=0.1,$, for change in (A) $Nt\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Nr=1.0,$ and (B) $Nr\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}Nt=0.2.$

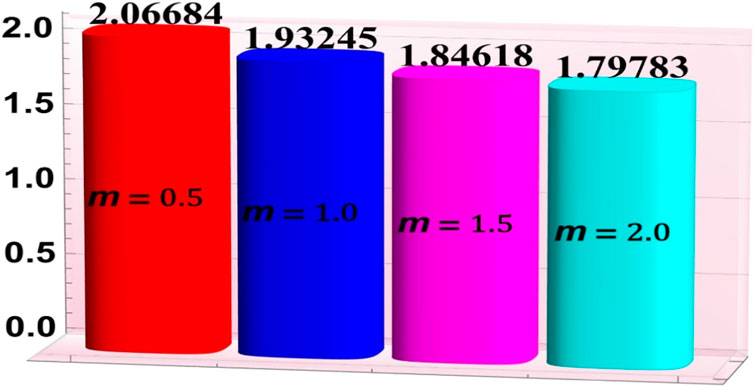
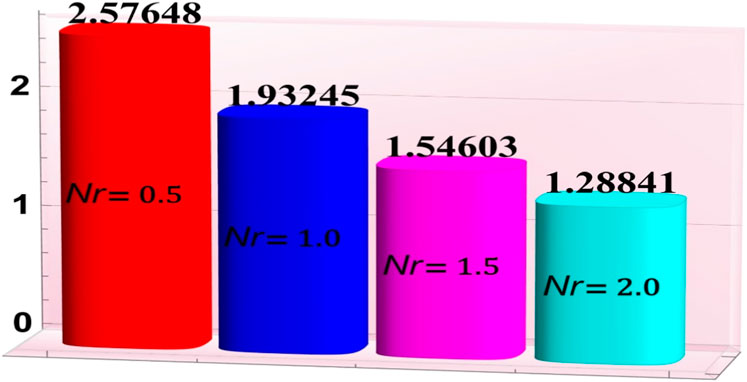
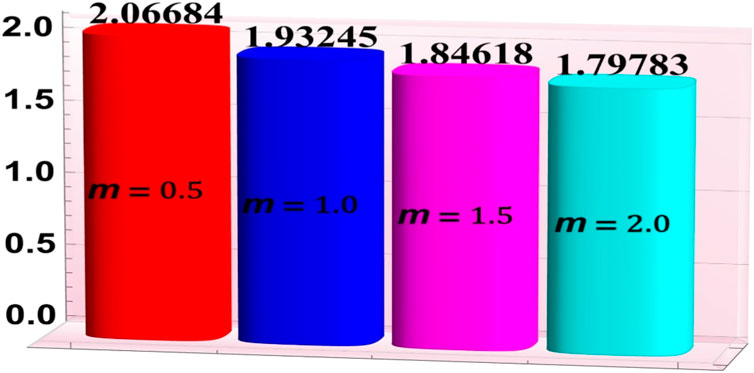
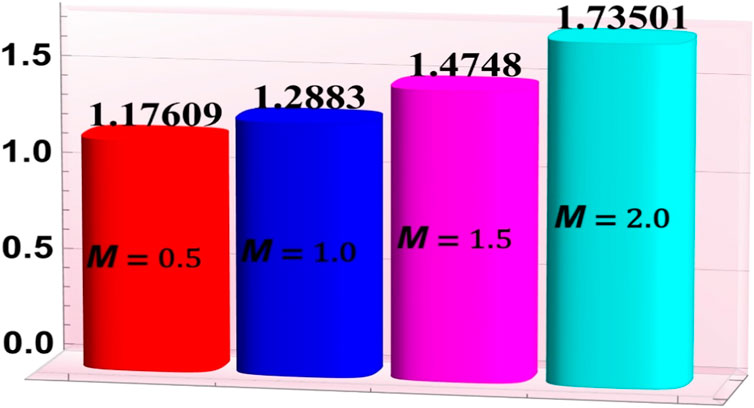
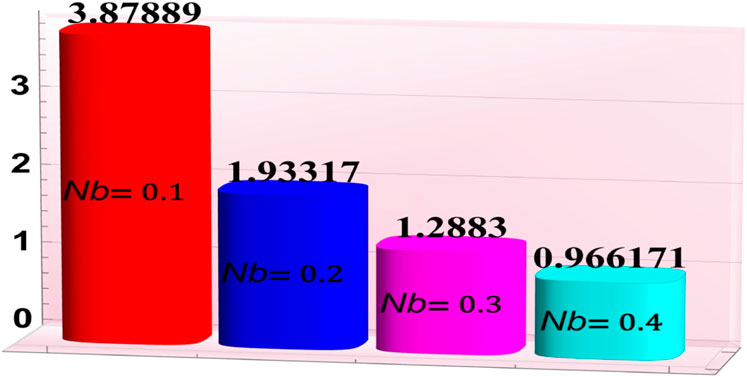
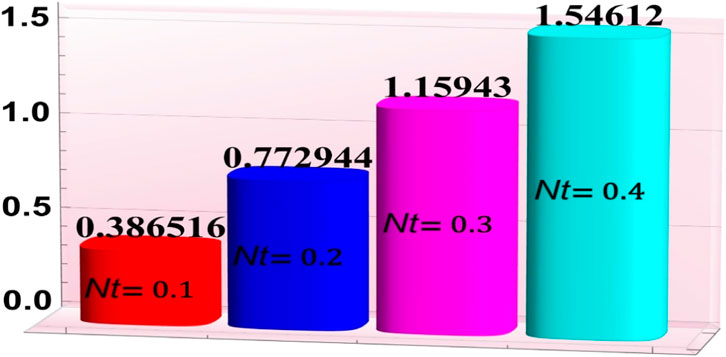
3.4 Heat and mass transfer rates

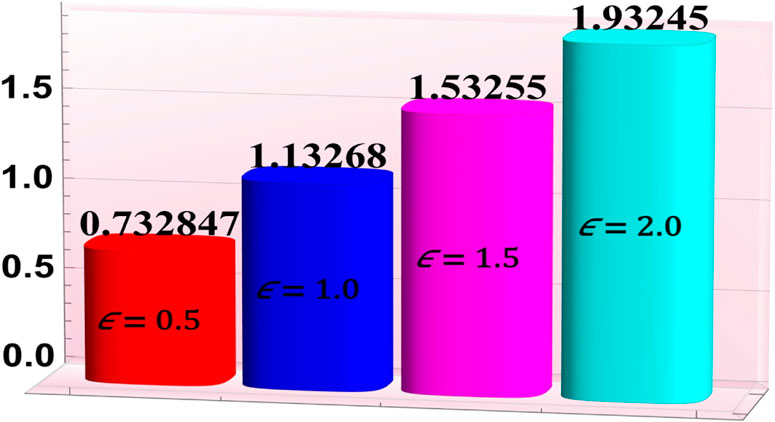
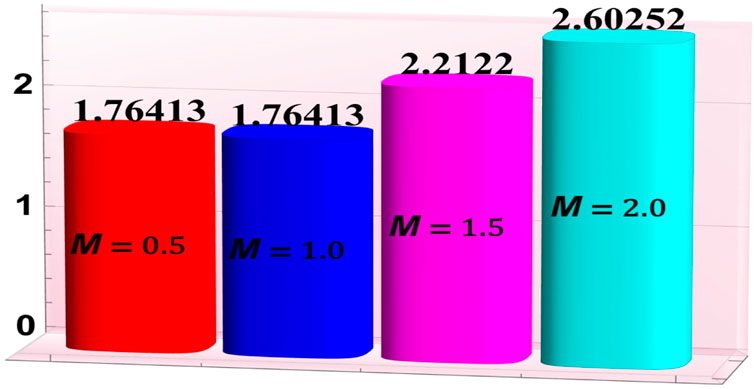
Figures 7–11 have been developed to examine the phenomena of heat “absorption/generation parameter $\left(\in \right)$, Grashof number $\left(Gr\right)$, Hartmann number $\left(M\right)$, Hall parameter $\left(m\right)$, Brownian motion parameter $\left(Nb\right)$, thermophoresis parameter $\left(Nt\right)$, and thermal radiation parameter $\left(Nr\right)$” for heat transfer rates at the wall. Furthermore, Figures 12–15 were used to study the mass transfer rates at the boundary for different values of flow parameters $m,M,Nb,$ and $Nt.$ Figure 7 illustrates that heat transfer at the boundary increases whenever the heat sink/source parameter is enhanced. Heat transfer rates enhance for the higher values of Hartmann number (see Figure 8). In Figure 9, it is noticed that heat transfer rates decline for the higher values of the Hall parameter. Large values of $Nb$ and $Nr$ increase the rates of heat transfer at the boundary (see Figures 10, 11). In Figures 12, 14, increasing the parameter ${}^{\prime }{m}^{\prime }$ and ${}^{\prime }{Nb}^{\prime }$ on the Carreau-Yasuda (C-Y) nanofluid flow results in a decrease in the heat transfer rates. An increase in both Hall and Brownian motion parameters shows a reduction in behavior on the walls. The impact of variations in Hartmann number and thermophoresis parameter on the mass transfer rates $\left({\varphi }^{\prime }\left(w\right)\right)$ at the wall are explored in Figures 13, 15, respectively. These figures indicate that the rates of mass transfer improved for the higher values of $M$ and $Nt.$

FIGURE 7

FIGURE 7. Heat transfer rates for change in “$\in$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,m=1.0,\mathrm{Pr}=204,Da=1.0,Gc=1.0,Br=0.3,x=0,{\gamma }_1=0.1.$

FIGURE 8

FIGURE 8. Heat transfer rates for change in “$M$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,m=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,Br=0.3,x=0,{\gamma }_1=0.1.$

FIGURE 9

FIGURE 9. Heat transfer rates for change in “$m$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,m=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,Gc=1.0,Br=0.3,x=0.$

FIGURE 10

FIGURE 10. Heat transfer rates for change in “$Nb$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nr=1.0,Nt=0.2,m=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,Gc=1.0,Br=0.3,x=0.$

FIGURE 11

FIGURE 11. Heat transfer rates for change in “$Nr$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,m=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,x=0,{\gamma }_1=0.1.$

FIGURE 12

FIGURE 12. Mass transfer rates for change in “$m$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,Da=1.0,\alpha =0.03,Gc=1.0,Br=0.3,x=0,{\gamma }_1=0.1.$

FIGURE 13

FIGURE 13. Mass transfer rates for change in “$M$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,Nt=0.2,Nr=1.0,\mathrm{Pr}=204,Da=1.0,\alpha =0.03,Gc=1.0,Br=0.3,{\gamma }_1=0.1.$

FIGURE 14

FIGURE 14. Mass transfer rates for change in “$Nb$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,m=1.0,Nt=0.2,Nr=1.0,\mathrm{Pr}=204,Da=1.0,Gc=1.0,Br=0.3,x=0,{\gamma }_1=0.1.$

FIGURE 15

FIGURE 15. Mass transfer rates for change in “$Nt$” when ${\alpha }_1=123.84,n=-0.0216,{\beta }_1=0.04971,Nb=0.3,M=1.0,Nr=1.0,\mathrm{Pr}=204,Gc=1.0,Br=0.3,x=0,{\gamma }_2=0.1.$

4 Conclusion

This research investigated the properties of heat and mass transfer in the case of a non-Newtonian nanofluid under peristaltic motion, with a focus on the influence of mixed convection and thermal radiation effects. Key findings are as follows:

• Both mixed convection and thermal radiation had significant impacts on the behavior of the nanofluid.

• A rise in the Brinkman number led to a rise in temperature distribution, highlighting the significance of mixed convection effects.

• The heat transfer rate decreased with a higher Hall parameter, indicating the importance of mixed convection effects.

• An enhancement in the thermal radiation parameter led to a reduction in temperature profiles, while the concentration profile decreased with an increase in the concentration slip parameter and Hartmann number, highlighting the importance of thermal radiation effects.

• A rise in the Hall parameter and Brownian motion parameter resulted in an increase in the concentration of nanoparticles.

• Intensification in the Hartmann number and thermal radiation parameter led to an increase in the mass transfer rates.

• Overall, the study provided insights into the mixed effects of mixed convection and thermal radiation on the heat and mass transfer characteristics of non-Newtonian nanofluids and can have practical implications in a choice of engineering applications.

The findings of this study can have practical implications in several areas. One such area is the field of biomedical engineering, where the understanding of heat and mass transfer during peristalsis is crucial in the design of drug delivery systems. The use of non-Newtonian nanofluids in drug delivery can have significant benefits, such as improved drug solubility, increased drug loading capacity, and controlled release of drugs. However, the thermal and mechanical stresses experienced by the nanofluid during peristalsis can affect the efficiency and safety of the drug delivery system. The outcomes of these findings can specify insights into the heat and mass transfer characteristics of non-Newtonian nanofluids during peristalsis, which can aid in the design of more efficient and safe drug delivery systems.

In addition, the study can also have implications in the fields of materials science and chemical engineering, where the use of non-Newtonian nanofluids is becoming increasingly prevalent in various industrial applications, such as heat exchangers and cooling systems. The understanding of the effects of viscous dissipation, Lorentz force, Ohmic heating, and Hall effects on the heat and mass transfer characteristics of these nanofluids can aid in the design and optimization of these systems for improved efficiency and reduced energy consumption. Generally, the findings of this study can have positive impacts on the development of drug delivery systems, as well as various industrial applications, leading to improved efficiency, reduced energy consumption, and, potentially, lower costs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, F. M., Alsaedi, A., and Hayat, T. (2014). Peristaltic transport of Eyring-Powell fluid in a curved channel. J. Aerosp. Eng. 27 (6), 04014037. doi:10.1061/(asce)as.1943-5525.0000354

CrossRef Full Text | Google Scholar

Abbasi, F. M., Hayat, T., Ahmad, B., and Chen, B. (2015). Peristaltic flow with convective mass condition and thermal radiation. J. Cent. South Univ. 22, 2369–2375. doi:10.1007/s11771-015-2762-9

CrossRef Full Text | Google Scholar

Abbasi, F. M., and Shehzad, S. A. (2017). Heat transfer analysis for peristaltic flow of Carreau-Yasuda fluid through a curved channel with radial magnetic field. Int. J. Heat Mass Transf. 115, 777–783. doi:10.1016/j.ijheatmasstransfer.2017.08.048

CrossRef Full Text | Google Scholar

Abbasi, F. M., Zahid, U. M., Akbar, Y., and Hamida, M. B. B. (2022). Thermodynamic analysis of electroosmosis regulated peristaltic motion of Fe3O4–Cu/H2O hybrid nanofluid. Int. J. Mod. Phys. B 36, 2250060. doi:10.1142/s0217979222500606

CrossRef Full Text | Google Scholar

Akbar, T., Nawaz, R., Kamran, M., and Rasheed, A. (2015). Magnetohydrodynamic (MHD) flow analysis of second grade fluids in a porous medium with prescribed vorticity. AIP Adv. 5, 117133. doi:10.1063/1.4936184

CrossRef Full Text | Google Scholar

Babu, D. H., and Narayana, P. V. S. (2016). Joule heating effects on mhd mixed convection of a jeffrey fluid over a stretching sheet with power law heat flux: A numerical study. J. Magnetism Magnetic Mater. 412, 185–193. doi:10.1016/j.jmmm.2016.04.011

CrossRef Full Text | Google Scholar

Buongiorno, J. (2006). Convective transport in nanofluids. J. Heat Transf. 128, 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles ASME. Int. Mech. Eng. Congr. Expo., 12–17.

Google Scholar

Dobrolyubov, A. I., and Douchy, G. (2002). Peristaltic transport as the travelling deformation waves. J. Theor. Biol. 219, 55–61. doi:10.1016/s0022-5193(02)93107-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Eldabe, N. T., Moatimid, G. M., Abouzeid, M. Y., ElShekhipy, A. A., and Abdallah, N. F. (2020). A semianalytical technique for MHD peristalsis of pseudo plastic nanofluid with temperature-dependent viscosity: Application in drug delivery system. Heat Transfer-Asian Res. 49, 424–440. doi:10.1002/htj.21619

CrossRef Full Text | Google Scholar

Gul, M., Abbasi, F., Shehzad, S. A., and Shafee, A. (2020). Entropy generation for peristaltic motion of Carreau’s fluid with mixture of ethylene glycol and boron-nitride nanoparticles. Phys. Scr. 95, 035212. doi:10.1088/1402-4896/ab49f8

CrossRef Full Text | Google Scholar

Haq, I., Bilal, M., Ameer Ahammad, N., Ghoneim, M. E., Ali, A., and Weera, W. (2022). Mixed convection nanofluid flow with heat source and chemical reaction over an inclined irregular surface. ACS Omega 7 (34), 30477–30485. doi:10.1021/acsomega.2c03919

PubMed Abstract | CrossRef Full Text | Google Scholar

Izadi, M., Oztop, H. F., Sheremet, M. A., Mehryan, S. A. M., and Abu-Hamdeh, N. (2019). Coupled FHD–MHD free convection of a hybrid nanoliquid in an inversed T-shaped enclosure occupied by partitioned porous media. Part A Appl. 76, 479–498. doi:10.1080/10407782.2019.1637626

CrossRef Full Text | Google Scholar

Kumar, S., and Sharma, K. (2022). Entropy optimized radiative heat transfer of hybrid nanofluid over vertical moving rotating disk with partial slip. Chin. J. Phys. 77, 861–873. doi:10.1016/j.cjph.2022.03.006

CrossRef Full Text | Google Scholar

Latham, T. W. (1966). MS thesis. Cambridge, England: MIT.Fluid motion in a peristaltic pump

Google Scholar

Rasheed, A., Nawaz, R., Khan, S. A., Hanif, H., and Wahab, A. (2015). Numerical study of a thin film flow of fourth grade fluid. Int. J. Numer. Methods Heat Fluid Flow 25 (4), 929–940. doi:10.1108/hff-06-2014-0188

CrossRef Full Text | Google Scholar

Reddy, M. V. S., Mishra, M., Sreenadh, S., and Rao, A. R. (2005). Influence of lateral walls on peristaltic flow in a rectangular duct. J. fluids Eng. 127, 824–827. doi:10.1115/1.1994876

CrossRef Full Text | Google Scholar

Rehman, A., Khan, W., Abdelrahman, A., Jan, R., Khan, M. S., and Galal, A. M. (2022). Influence of Marangoni convection, solar radiation, and viscous dissipation on the bioconvection couple stress flow of the hybrid nanofluid over a shrinking surface. Front. Mater. 9, 964543. doi:10.3389/fmats.2022.964543

CrossRef Full Text | Google Scholar

Rudyak, Y., and Krasnolutskii, S. L. (2014). Dependence of the viscosity of nanofluids on nanoparticle size and material. Phys. Lett. A 378, 1845–1849. doi:10.1016/j.physleta.2014.04.060

CrossRef Full Text | Google Scholar

Shapiro, A. H., Jaffrin, M. Y., and Weinberg, S. L. (1969). Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 37, 799–825. doi:10.1017/s0022112069000899

CrossRef Full Text | Google Scholar

Sharma, B. K., Kumar, A., Gandhi, R., Bhatti, M. M., and Mishra, N. K. (2023). Entropy generation and thermal radiation analysis of EMHD jeffrey nanofluid flow: Applications in solar energy. Nanomaterials 13, 544. doi:10.3390/nano13030544

PubMed Abstract | CrossRef Full Text | Google Scholar

Shehzad, S. A., Abbasi, F. M., Hayat, T., and Alsaadi, F. (2015). Model and comparative study for peristaltic transport of water based nanofluids. J. Mol. Liq. 209, 723–728. doi:10.1016/j.molliq.2015.05.058

CrossRef Full Text | Google Scholar

Tiwari, R. K., and Das, M. K. (2007). Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 50, 2002–2018. doi:10.1016/j.ijheatmasstransfer.2006.09.034

CrossRef Full Text | Google Scholar

Xue, Q. Z. (2005). Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter. 368, 302–307. doi:10.1016/j.physb.2005.07.024

CrossRef Full Text | Google Scholar

Yasmin, H., Giwa, S. O., Noor, S., and Sharifpur, M. (2023). Thermal conductivity enhancement of metal oxide nanofluids: A critical review. Nanomaterials 13, 597. doi:10.3390/nano13030597

PubMed Abstract | CrossRef Full Text | Google Scholar