Investigation of fluid flow pattern in a 3D meandering tube

Several types of meandering channels and their mathematical simulation have been proposed and discussed widely in the open literature. In the present study, the impact of a novel meandering tube geometry on streamwise vortices and pressure losses have been determined. Using a simplified Poiseuille flow simulation approach with a sinusoidal wavy meandering tube of non-uniform radius, the onset flow separation, vertex formation, and the impact of Reynolds number on field variables and stream function has been analyzed. Moreover, the linear stability theory has been implemented to trace the vertex formation. A decrease in wavelength leads to flow separation near the tube’s surface, but the flow becomes rectilinear with a sudden disturbance caused by the meander, becoming independent of vertex generating centrifugal forces. Novel insights are provided on the impact of meandering tube geometry on fluid flow and potential applications for enhancing flow conditions are suggested.

1 Introduction

The escalation process of heat and species transport in different flow phases with practical significance is an interesting and important subject in thermodynamics and fluid mechanics. Both the formation of fluid mixtures and changes in the functional thermophysical characteristics of the fluids fall within the category of escalation processes (Bergles and Webb, 1985; Jensen et al., 1997; Ligrani et al., 2003). Integrated heat exchangers that operate at low Reynolds numbers in case of laminar flows are treated specially for improved mixing (Webb and Bergles, 1981). It is often accepted that improved mixing may be achieved by driving a laminar-turbulent transformation under difficult conditions or by inserting vortex generators, which are efficient but have a substantial drag cost (Fiebig, 1995a; Fiebig, 1995b; Jacobi and Shah, 1995; Fiebig, 1998; Fiebig and Chen, 1999). In most cases, the hydrodynamic stabilities have been used for the transition of laminar flow to turbulent flow and, therefore, transverse grooves are used. However, a novel model has been demonstrated with the most accurate simulations, i.e., to shift laminar states without transiting to turbulent ones by using hydrodynamic instabilities. In this novel model, separating local flow is demonstrated well; the flow is driven by a slight oscillatory component and enters the resonant and stable separated shear layer (Patera and Mikic, 1986) Another type of bifurcation, i.e., centrifugal instability, has been taken into account and it produces simple vortices without suffering from the maximum drag cost associated with conventional vortex generators. Instability can improve vortex generators in limiting vortices decay, which decreases the minimum number of such generators even when the flow is only locally asymptotically stable. Both directly (by establishing a transverse transition) and indirectly (by creating a bypass transition), streamwise vortices can boost heat transfer. In most cases, a three-dimensional flow field has been developed at the end and transverse shear layers with inflection points and rapidly expanding secondary instability are formed (Floryan, 1991). Recent investigations have reported an alternate approach being taken into account of a fluid of higher thermal conductivity used with properly shaped channels while, at the same time, flow pressure being reduced immediately (Mohammadi and Floryan, 2013). This technique has provided an alternative solution to the most common development programs used on macro channels (Xu et al., 2016).

It has been known for nearly 100 years that the rotating shear layers are subjected to centrifugal instabilities. This instability has been taken into account for the situation of simple geometry and canonical flow, providing an example where it is possible to forecast the curvature of lines with ease. Using the flow state between rotating cylinders, Rayleigh introduced the inviscid technique in 1920 and determined the necessary stabilization condition through circulating distribution (Rayleigh, 1917). In 1923, Taylor included the full viscous problem and identified the crucial conditions that emerge as a result of the secondary flow (Taylor, 1923). Similar instability in curved channels was examined by Dean (Dean, 1928). The occurrence of centrifugal instability in the context of boundary layers on concave surfaces was proved by Görtler (Görtler, 1941). If the streamwise velocity distribution is not monotonic (Floryan, 1986), demonstrated that the instability is active in flows over concave as well as convex surfaces. A clear relationship between the streamline curvature and the wall curvature was provided by all of these investigations where the wall curvature was either constant or had been approximated as a constant. As a result, the critical stability condition might be expressed in terms of one parameter.

There are very few theoretical investigations that can pinpoint the starting conditions for flows in complex geometries where the wall curvature varies spatially. However, there are large number of numerical models and experimental studies that offer qualitative data (Gschwind et al., 1995). used a meandering amplitude of the same order of magnitude as the channel height, and (Nishimura et al., 1990; Tatsuo et al., 1990) used a large amplitude compared to the channel height to demonstrate the existence of streamwise vortices attributed to the centrifugal instability in sinusoidal channels. Rush et al. (Rush et al., 1999) has qualitatively identified the additional types of instability for corresponding geometries. Theoretical investigations which employed two-dimensional models were able to identify the effect of flow separation on heat transfer (Metwally and Manglik, 2004; Zhang et al., 2004) and identify the conditions that led to either single or double Hopf bifurcations or self-sustained oscillations (Guzmán et al., 2009). These models failed to identify the formation of the vortices. In their 2012 study, (Sui et al., 2012), took into account a three-dimensional rectangular channel with a very large meandering amplitude and applied numerical simulations to find a complex pattern of Dean’s vortices that changed over time and space. In the case of turbulent flow, consistent structures were found by (Pham et al., 2008). Other types of geometries, such as boundary layer flows over wavy surfaces (Saric and Ali, 1991) and Couette flows over wavy walls (Floryan, 2002), have also been found to demonstrate centrifugal instability. According to recent findings, streamwise vortices may be created by the placement of different triangular surface obstacles (Floryan and Asai, 2011) The transport of heat and fluid flow in various mediums and the studies considered the impact of magnetic fields, chemical reactions, porous media on fluid flow and thermal transport. The studies considered the impact of magnetic fields, chemical reactions, and porous media on fluid flow and thermal transport The results suggest that the addition of tri-hybrid nanoparticles and magnetic dipoles can enhance thermal transportation in Carreau Yasuda liquid, but may decrease the flow profile. This study also investigated the effects of different parameters on the peristaltic motion of hyperbolic tangent fluid in a curved compliant channel, which has potential applications in explaining blood transport dynamics. Numerical solutions and perturbation techniques were used to analyze and evaluate the results (Javed et al., 2021; Naseem et al., 2021; Wang et al., 2022). Different approaches related to the studies of fluid flow in microfluidic systems for biomedical engineering. This study analyzed the behavior of different types of fluids in different channel geometries by taking into account, convective conditions, thermal deposition effect, and chemical reactions. They investigated the impact of various parameters on flow quantities such as velocity, temperature, and concentration. This study also suggest the viability of electro-osmotic pumps for fluid flow in large osteoarticular implants (Hayat et al., 2015; Yasmin et al., 2020a; Yasmin et al., 2020b; Mehmood et al., 2020; Yasmin and Iqbal, 2021; Alyousef et al., 2023).

The main objective of the current analysis is to investigate the three-dimensional structure of the meandering geometries that cause the centrifugal force mechanism to produce streamwise vortices at the lowest possible cost as measured by pressure losses and without the interference of the traveling wave instability. This is the first comprehensive analysis of three-dimensional flow in a meandering tube that takes all potential instabilities into consideration. The new information would provide an accurate mathematical simulation for engineers and be a reasonable foundation upon which they may construct small heat exchangers that operate in the laminar flow domain. The study is divided into three main parts, specifically: i) mathematical modeling of flow in the meandering tube; ii) calculating the flow losses related to the meandering tube; and iii) identifying the geometric and flow characteristics that cause the centrifugal instability to predominate. The source in engineering procedures might be a mechanical pressure gradient. In this study, we look at the pressure gradient-driven (Poiseuille flow) flow of viscous fluid in a meandering tube with waves that is made up of fixed walls. A lot of interest has been shown in the flow of viscous fluid in a wavy meandering tube due to its applications in engineering and biological sciences, including regarding the development of muddy waves in river channels, the generation of wind waves on water and sandbanks in deserts, the movement of melting slides, rocket boosters, and the evaporation of film in burning chambers. Furthermore, physiologists and technicians have often attempted to create and explain blood and urine flow in terms of meandering channels (tubes).

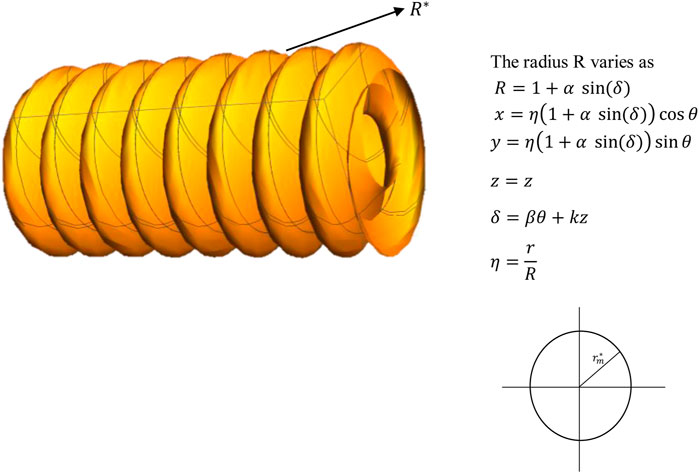
2 Geometry of the problem

The flow of a viscous fluid in a meandering tube, whose geometry is shown in Figure 1, is the main focus of this paper.

FIGURE 1

FIGURE 1. Geometry of the meandering tube under consideration and flow regime with coordinate$x$-axis.

The tube of variable radius is taken, whose radius is determined by $R^{*}=r_m^{*}\left(1+\alpha \mathit{sin}\delta \right)$. The polar coordinate system $\left(r,\theta ,z\right)$ is connected to the Cartesian coordinate system $\left(x,y,z\right)$ for this particular problem in such a way that $x=\eta \left(1+\alpha \sin \delta \right)\cos \theta ,y=\eta \left(1+\alpha \sin \delta \right)\sin \theta ,z=z$ where $\delta =\beta \theta +kz$ and $=\frac{r}{R}$ . Note that $x,y,z,$ and $\eta$ are dimensionless variables.

3 Governing equations

In order to express the current problem in proper coordinates, it is appropriate to choose a suitable coordinate system for the simulated problem. The well-established relationship between the Cartesian coordinates $\left(x^{*},y^{*},z^{*}\right)$ and cylindrical ones $\left(r^{*},\theta ,z^{*}\right)$ has been presented above. For the meandering, we took the following transformation to define a tube of non-uniform radius $\left(R^{*}\right)$ as:

$R^{*}=r_m^{*}\left(1+\alpha \mathit{Sin}\delta \right)where\delta =\beta \theta +k^{*}{z}^{*}$

where $r_m^{*}$ is the mean radius of the tube while “$\alpha$” represents the dimensionless amplitude, “$\beta$” represents the number of helixes starts, and “$k^{*}$” represents the wave number in the axial direction of the wall of the tube.

The governing equations are non-dimensionalized by introducing dimensionless variables and the length is non-dimensionalized by $r_m^{*}$ (mean radius), the velocity components ($u^{*},v^{*},w^{*})$ by ${\upsilon }^{*}/r_m^{*}$, the static pressure by ${\rho }^{*}{\left({\upsilon }^{*}/r_m^{*}\right)}^2$, ${\nabla }^{*2}$ by $1/r_m^{*2}$, and $\left({\mathbf{V}}^{*}\bullet {\nabla }^{*}\right)$ by ${\upsilon }^{*}/r_m^{*2}$.

Note that the asterisk “*” represents the dimensional quantities and ${\upsilon }^{*}$ and ${\rho }^{*}$ are kinematic viscosity and density of the fluid, respectively. The governing equations in cylindrical coordinates $\left(r^{*},\theta ,z^{*}\right)$ are:

Continuity equation, $r^{*}$, $\theta ,$ and $z^{*}$- components of Navier-Stokes equations in cylindrical coordinates $\left(r^{*},\theta ,z^{*}\right)$ are given as:

$\frac{\partial }{\partial r^{*}}\left(r^{*}{u}^{*}\right)+\frac{\partial }{\partial \theta }{v}^{*}+r^{*}\frac{\partial }{\partial z^{*}}{w}^{*}=0(1)$

$\left({\mathbf{V}}^{*}\bullet {\nabla }^{*}\right)u^{*}-\frac{v^{*2}}{r^{*}}=-\frac{1}{{\rho }^{*}}\frac{\partial P^{*}}{\partial r^{*}}+{\upsilon }^{*}\left({\nabla }^{*2}{u}^{*}-\frac{u^{*}}{r^{*2}}-\frac{2}{r^{*2}}\frac{\partial v^{*}}{\partial \theta }\right)(2)$

$\left({\mathbf{V}}^{*}\bullet {\nabla }^{*}\right)v^{*}-\frac{u^{*}{v}^{*}}{r^{*}}=-\frac{1}{{\rho }^{*}{r}^{*}}\frac{\partial P^{*}}{\partial \theta }+{\upsilon }^{*}\left({\nabla }^{*2}{v}^{*}-\frac{v^{*}}{r^{*2}}-\frac{2}{r^{*2}}\frac{\partial u^{*}}{\partial \theta }\right)(3)$

$\left({\mathbf{V}}^{*}\bullet {\nabla }^{*}\right)w^{*}=-\frac{1}{{\rho }^{*}}\frac{\partial P^{*}}{\partial z^{*}}+{\upsilon }^{*}{\nabla }^{*2}{w}^{*}(4)$

${\mathbf{V}}^{*}\bullet {\nabla }^{*}=u^{*}\frac{\partial }{\partial r^{*}}+\frac{1}{r^{*}}{v}^{*}\frac{\partial }{\partial \theta }{+w}^{*}\frac{\partial }{\partial z^{*}}(5)$

${\nabla }^{\ast 2}=\frac{1}{r^{*}}\frac{\partial }{\partial r^{*}}\left(r^{*}\frac{\partial }{\partial r^{*}}\right)+\frac{1}{r^{*2}}\frac{{\partial }^2}{\partial {\theta }^2}+\frac{{\partial }^2}{\partial z^{*2}}(6)$

The no slip boundary conditions at the wall and the symmetry conditions at the center of the meandering tube are given as:

$u^{*}=v^{*}=w^{*}=0at{r}^{*}=R^{*}\mathrm{a}\mathrm{n}\mathrm{d}{u}^{*}=v^{*}=0,w^{*}=U^{*}\mathrm{a}\mathrm{t}{r}^{*}=0(7)$

where $U^{*}$ represents stream velocity at the center of the meandering tube.

By using the dimensionless variables as defined above, the continuity Eq. 1 is transformed as:

$\frac{\partial }{r_m^{*}\partial \frac{r^{*}}{r_m^{*}}}{r}_m^{*}\left(\frac{r^{*}}{r_m^{*}}\right)\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)\frac{u^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}+\frac{\partial }{\partial \theta }\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)\frac{v^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}+r_m^{*}\left(\frac{r^{*}}{r_m^{*}}\right)\frac{\partial }{r_m^{*}\partial \frac{z^{*}}{r_m^{*}}}\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)\frac{w^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}=0(8)$

From above definitions of dimensionless variables, we have:

$\frac{u^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}=v_r,\frac{v^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}=v_{\theta },\frac{w^{*}}{\left(\frac{{\upsilon }^{*}}{r_m^{*}}\right)}=v_z,r=\frac{r^{*}}{r_m^{*}},z=\frac{z^{*}}{r_m^{*}}(9)$

where $v_r$, $v_{\theta }$, and $v_z$ represent the dimensionless velocity components in r, $\theta ,$ and z directions, respectively:

$\frac{\partial }{\partial r}\left(r{v}_r\right)+\frac{\partial }{\partial \theta }{v}_{\theta }+r\frac{\partial }{\partial z}{v}_z=0(10)$

$\left(\mathbf{V}\bullet \nabla \right)v_r-\frac{1}{r}{v}_{\theta }^2=-\frac{\partial P}{\partial r}+{\nabla }^2{v}_r-\frac{v_r}{r^2}-\frac{2}{r^2}\frac{\partial v_{\theta }}{\partial \theta }(11)$

$\left(\mathbf{V}\bullet \nabla \right)v_{\theta }+\frac{v_r{v}_{\theta }}{r}=-\frac{1}{r}\frac{\partial P}{\partial \theta }+{\nabla }^2{v}_{\theta }-\frac{v_{\theta }}{r^2}+\frac{2}{r^2}\frac{\partial v_r}{\partial \theta }(12)$

$\left(\mathbf{V}\bullet \nabla \right)v_z=-\frac{\partial P}{\partial z}+{\nabla }^2{v}_z(13)$

$\mathbf{V}\bullet \nabla =\frac{r_m^{\ast 2}}{{\upsilon }^{*}}\left({\mathbf{V}}^{*}\bullet {\nabla }^{*}\right)(14)$

${\nabla }^2=r_m^{\ast 2}{\nabla }^{\ast 2}(15)$

Where Eqs. 10–13 represent the dimensionless form of continuity and components of Navier-Stokes equations, respectively.

The dimensionless form of no slip boundary conditions at the wall and the symmetry conditions at the center of the meandering tube are obtained as:

$v_r=v_{\theta }=v_z=0atr=R\mathrm{a}\mathrm{n}\mathrm{d}{v}_r=v_{\theta }=0,v_z=Re\mathrm{a}\mathrm{t}r=0$

where $Re=\frac{{\rho }^{*}{U}^{*}{r}_m^{*}}{{\upsilon }^{*}}$ represents the Reynolds number.

4 Modal problem

The velocity vector ${\mathit{V}}_b$ for the modeled problem is decomposed as ${\mathit{V}}_b={\mathit{V}}_0+{\mathit{V}}_1$ where the velocity ${\mathit{V}}_0$, pressure $P_0$, the total volume flow rate $Q_0$, the stream function ${\psi }_0$, and the vorticity function ${\xi }_0$ for the fully developed flow in a straight duct (circular pipe) becomes purely radial in a pipe. The solution is obtained from the continuity equation, $\eta$, $\theta$, and $z$ momentum equations. Note that the fluid flow is directed in the direction along positive $z$-axis. The velocity field and other field quantities for fluid motion in the meandering tube are approximated as:

$\begin{array}{ll}\hfill {\mathit{V}}_b={\mathit{V}}_0+{\mathit{V}}_1=& \left[0,0,w_0\left(\eta \right)\right]+\left[u_1\left(\eta ,\theta ,z\right),v_1\left(\eta ,\theta ,z\right),w_1\left(\eta ,\theta ,z\right)\right]P_b=P_0\left(\eta \right)\hfill \\ \hfill & +P_1\left(\eta ,\theta ,z\right){\psi }_b={\psi }_0\left(\eta \right)+{\psi }_1\left(\eta ,\theta ,z\right)Q_b=Q_0\left(\eta \right)+Q_1\left(\eta ,\theta ,z\right){\xi }_b={\xi }_0\left(\eta \right)+{\xi }_1\left(\eta ,\theta ,z\right)\hfill \end{array}$

${\mathit{V}}_0\left(\eta ,\theta ,z\right)=\left[u_0\left(\eta ,\theta ,z\right),{\mathit{v}}_0\left(\eta ,\theta ,z\right),w_0\left(\eta ,\theta ,z\right)\right]=\left[0,0,Re\left(1-{\eta }^2\right)\right],P_0=-4Rez+c_0,Q_0=\frac{\pi Re}{2},{\psi }_0=-\frac{{\eta }^2}{2}Re\left(1-\frac{{\eta }^2}{2}\right)+c_{1}and{\xi }_0=2\eta Re$

Further, the velocity vector ${\mathit{V}}_b=\left[u_b,v_b,w_b\right]$ needs to be determined; therefore, an appropriate approximation technique is used to get this part of velocity ${\mathit{V}}_b$.

5 Solution of the problem

Next, our aim is to determine the solution of dimensionless Eqs. (10 - 16). As these equations have a parameter $\alpha$ which may be a small quantity in many practical problems, we therefore consider the case of small amplitude waviness, i.e.; $\alpha \to 0$ and the flow domain has been regularized for the radial coordinate of the form when $\eta =\frac{r}{R}$ where $R=1+\alpha \sin \left(\delta \right)$ where $\delta =\beta \theta +kz$ (the tube or its wall is located at $\eta =1$ for this new variable), and the dimensionless governing equations are transformed from $\left(r,\theta ,z\right)$ to $\left(\eta ,\theta ,z\right)$ such that the dimensionless continuity and Navier-Stokes Eqs. (10-13) in cylindrical coordinates $\left(r,\theta ,z\right)$ take the form below:

$\left(1+\alpha \mathit{sin}\delta \right)u_b+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{\partial w_b}{\partial z}+\frac{\partial v_b}{\partial \theta }+\eta \frac{\partial u_b}{\partial \eta }+\alpha \mathit{sin}\delta \frac{\partial v_b}{\partial \theta }+\alpha \eta \mathit{sin}\delta \frac{\partial u_b}{\partial \eta }-\alpha \eta \mathit{cos}\delta \beta \frac{\partial v_b}{\partial \eta }+k\eta \alpha \eta \mathit{cos}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{\partial w_b}{\partial z}=0(18)$

$\begin{array}{c}-\eta {\left(1+\alpha \mathit{sin}\delta \right)}^3{v_b}^2-{\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{u}_b}{\partial {\theta }^2}+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3\frac{\partial P_b}{\partial \eta }-2{\alpha }^2{\beta }^2\eta {\cos }^2\delta \frac{\partial u_b}{\partial \eta }-\alpha {\beta }^2\eta \mathit{sin}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{\partial u_b}{\partial \eta }+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{u}_b\frac{\partial u_b}{\partial \eta }\hfill \\ +{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{w}_b\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial u_b}{\partial z}-k\alpha \eta \mathit{cos}\delta \frac{\partial u_b}{\partial \eta }\right)+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2{v}_b\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial u_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial u_b}{\partial \eta }\right)+2\left(1+\alpha \mathit{sin}\delta \right)\hfill \\ \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial u_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial u_b}{\partial \eta }\right)+\alpha \beta \eta \mathit{cos}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{u}_b}{\partial \eta \partial \theta }-{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3\left(\frac{\partial u_b}{\partial \eta }+\eta \frac{{\partial }^2{u}_b}{\partial {\eta }^2}\right)+\alpha \beta \eta \mathit{cos}\delta \hfill \\ \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{u}_b}{\partial \eta \partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{{\partial }^2{u}_b}{\partial {\eta }^2}\right)-{\left(\eta +\alpha \eta \mathit{sin}\delta \right)}^2({\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{u}_b}{\partial z^2}+\frac{1}{2}k\alpha \eta (k\left(3\alpha +\alpha \mathit{cos}\delta +2\sin \delta \right)\frac{\partial u_b}{\partial \eta }\hfill \\ +2\cos \delta \left(-2\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{u}_b}{\partial \eta \partial z}+k\alpha \eta \mathit{cos}\delta \frac{{\partial }^2{u}_b}{\partial {\eta }^2}\right)))=0\hfill \end{array}(19)$

$\begin{array}{c}-\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2{v}_b+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^3{u}_b{v}_b-{\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{v}_b}{\partial {\theta }^2}+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial P_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial P_b}{\partial \eta }\right)-2\left(1+\alpha \mathit{sin}\delta \right)\hfill \\ \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial u_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial u_b}{\partial \eta }\right)-2{\alpha }^2{\beta }^2\eta {\mathit{cos}}^2\delta \frac{\partial v_b}{\partial \eta }-\alpha {\beta }^2\eta \mathit{sin}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{\partial v_b}{\partial \eta }+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{u}_b\frac{\partial v_b}{\partial \eta }+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{w}_b\hfill \\ \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial v_b}{\partial z}-k\alpha \eta \mathit{cos}\delta \frac{\partial v_b}{\partial \eta }\right)+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2{v}_b\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial v_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial v_b}{\partial \eta }\right)+\alpha \beta \eta \mathit{cos}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{v}_b}{\partial \eta \partial \theta }\hfill \\ -{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3\left(\frac{\partial v_b}{\partial \eta }+\eta \frac{{\partial }^2{v}_b}{\partial {\eta }^2}\right)+\alpha \beta \eta \mathit{cos}\delta \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{v}_b}{\partial \eta \partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{{\partial }^2{v}_b}{\partial {\eta }^2}\right)-{\left(\eta +\alpha \eta \mathit{sin}\delta \right)}^2\hfill \\ ({\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{v}_b}{\partial {\eta }^2}+\frac{1}{2}k\alpha \eta (k\left(3\alpha +\alpha \mathit{cos}\delta +2\mathit{sin}\delta \right)\frac{\partial v_b}{\partial \eta }+2\mathit{cos}\delta \left(k\alpha \eta \mathit{cos}\delta \frac{{\partial }^2{v}_b}{\partial {\eta }^2}-2\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{v}_b}{\partial \eta \partial z}\right)))=0\hfill \end{array}(20)$

$\begin{array}{c}-{\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{w}_b}{\partial {\theta }^2}+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial P_b}{\partial z}-k\alpha \eta \mathit{cos}\delta \frac{\partial p_b}{\partial \eta }\right)-2{\alpha }^2{\beta }^2\eta {\mathit{cos}}^2\delta \frac{\partial w_b}{\partial \eta }-\alpha {\beta }^2\eta \mathit{sin}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{\partial w_b}{\partial \eta }\hfill \\ +{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{u}_b\frac{\partial w_b}{\partial \eta }+{\eta }^2{\left(1+\alpha \mathit{sin}\delta \right)}^3{w}_b\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial w_b}{\partial z}-k\alpha \eta \mathit{cos}\delta \frac{\partial w_b}{\partial \eta }\right)+\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2{v}_b\left(\left(1+\alpha \mathit{sin}\delta \right)\frac{\partial w_b}{\partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{\partial w_b}{\partial \eta }\right)\hfill \\ +\alpha \beta \eta \mathit{cos}\delta \left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{w}_b}{\partial \eta \partial \theta }-\eta {\left(1+\alpha \mathit{sin}\delta \right)}^2\left(\frac{\partial w_b}{\partial \eta }+\eta \frac{{\partial }^2{w}_b}{\partial {\eta }^2}\right)+\alpha \beta \eta \mathit{cos}\delta \left(\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{w}_b}{\partial \eta \partial \theta }-\alpha \beta \eta \mathit{cos}\delta \frac{{\partial }^2{w}_b}{\partial {\eta }^2}\right)-{\left(\eta +\alpha \eta \mathit{sin}\delta \right)}^2\hfill \\ ({\left(1+\alpha \mathit{sin}\delta \right)}^2\frac{{\partial }^2{w}_b}{\partial z^2}+\frac{1}{2}k\alpha \eta (k\left(3\alpha +\alpha \mathit{cos}2\delta +2\mathit{sin}\delta \right)\frac{\partial w_b}{\partial \eta }+2\mathit{cos}\delta \left(k\alpha \eta \mathit{cos}\delta \frac{{\partial }^2{w}_b}{\partial {\eta }^2}-2\left(1+\alpha \mathit{sin}\delta \right)\frac{{\partial }^2{w}_b}{\partial \eta \partial z}\right)))=0\hfill \end{array}(21)$

Similarly, the dimensionless Eq. 16 has transformed (by introducing $\eta =\frac{r}{R}$; $R=1+\alpha \sin \delta$ where $\delta =\beta \theta +kz$) into the following form:

$u_b=v_b=w_b=0\mathrm{a}\mathrm{t}\eta =1\mathrm{a}\mathrm{n}\mathrm{d}{u}_b=v_b=0,w_b=Re\mathrm{a}\mathrm{t}\eta =0(22)$

In the case of small amplitude waviness, i.e., $\alpha \to 0$, the velocity components, i.e., $u_b,v_b$, and $w_b$ in ${\eta }_{,}\theta$, and z-directions, respectively, and the pressure term $P_b$ are expanded in a series of $\alpha$ as:

$u_b={\widehat{\mathcal{u}}}_0+\alpha {\widehat{\mathcal{u}}}_1+O\left({\alpha }^2\right),v_b={\widehat{v}}_0+\alpha {\widehat{v}}_1+{O(\alpha }^2),w_b={\widehat{w}}_0+\alpha {\widehat{w}}_1+{O(\alpha }^2)\mathrm{a}\mathrm{n}\mathrm{d}{P}_b={\widehat{P}}_0+\alpha {\widehat{P}}_1+O\left({\alpha }^2\right)(23)$

where $u_0={\widehat{u}}_0,v_0={\widehat{v}}_0,w_0={\widehat{w}}_0,and{P}_0={\widehat{P}}_0$ and they are determined previously for the fully developed flow in straight duct.

The values of $u_b,v_b,w_b$, and $P_b$ are substituted from Eq. 23 into the equations of continuity, motion, and the relevant boundary conditions, i.e., Eqs. 18–21 which are described by means of (${\eta }_{,}\theta ,z$), and terms of the same order of $\alpha$ are collected on each side of these equations.

6 Results and discussion

The solution of the zeroth-order system, which is obtained by putting value from Eq. 23 into Eqs 18–21 and equating like powers of ${\alpha }^0$ on both sides of them, is given below:

${\widehat{u}}_0={\widehat{\mathit{v}}}_0=0,{\widehat{w}}_0=Re\left(1-{\eta }^2\right),{\widehat{P}}_0=-4Rez+c_0,{\widehat{Q}}_1=\frac{\pi Re}{2},{\psi }_0={\widehat{\psi }}_0=-\frac{{\eta }^2}{2}Re\left(1-\frac{{\eta }^2}{2}\right)+c_{1}and{\widehat{\xi }}_0=2\eta Re(24)$

Note that the solution in Eq. 24 for the fully developed flow in a straight duct has been reported in F.M. White (White and Majdalani, 2006) and Schlichting (Schlichting and Kestin, 1961).

Similarly, the first-order system is obtained by equating like powers of ${\alpha }^1$ on both sides of Eqs 18–21 and then by substituting Eq. 24 into them. The unknowns in this system are further expressed by the following series:

$\begin{array}{c}{\widehat{\psi }}_1=f_a\left(\eta \right)\mathit{sin}\delta +f_b\left(\eta \right)\mathit{cos}\delta ,{\widehat{w}}_1=f_c\left(\eta \right)\mathit{sin}\delta +f_d\left(\eta \right)\mathit{cos}\delta ,{\widehat{u}}_1=\frac{1}{\eta }\left(\frac{\partial {\widehat{\psi }}_1}{\partial \theta }-\frac{1}{2}kRe{\eta }^4\mathit{cos}\delta \right),\hfill \\ {\widehat{v}}_1=-\frac{\partial {\widehat{\psi }}_1}{\partial \eta }-\frac{1}{\beta }k\eta {\widehat{w}}_1,f_a\left(\eta \right)={\displaystyle \sum _{p=0}^{\infty }}{a}_p{\eta }^p,f_b\left(\eta \right)={\displaystyle \sum _{p=0}^{\infty }}{b_p\eta }^p,f_c\left(\eta \right)={\displaystyle \sum _{p=0}^{\infty }}{c_p\eta }^{p}and{f}_d\left(\eta \right)={\displaystyle \sum _{p=0}^{\infty }}{d}_p{\eta }^p\hfill \end{array}$

where the functions $f_a,f_b,f_c$, and $f_d$ depend only on $\eta$ and the coefficients $a_p,b_p,c_p$, and $d_p$ are obtained by substituting the series into the first-order system. The coefficients of the above series are:

$a_0=0,a_1=0,a_2=0,a_3=0,a_4=\frac{12kRe+5kRe{\beta }^2}{2\beta \left(12+{\beta }^2\right)},a_5=\frac{54kRe\beta }{\left(12+{\beta }^2\right)\left(15+2{\beta }^2\right)},a_6=-\frac{2Re\beta \left(-576k+15k^3+2k^3{\beta }^2\right)}{\left(6+{\beta }^2\right)\left(12+{\beta }^2\right)\left(15+2{\beta }^2\right)},a_7=-\frac{2kRe\beta \left(-72000+k^2\left(2523+358{\beta }^2\right)\right)}{\left(6+{\beta }^2\right)\left(12+{\beta }^2\right)\left(15+2{\beta }^2\right)\left(21+4{\beta }^2\right)},$

$a_8=\frac{1}{\left(6+{\beta }^2\right)\left(12+{\beta }^2\right)\left(15+2{\beta }^2\right)\left(21+4{\beta }^2\right)\left(24+5{\beta }^2\right)}\left\{2kRe\beta \left(15552000+5k^4\left(315+102{\beta }^2+8{\beta }^4\right)-k^2\left(72\left(8409+1234{\beta }^2\right)+5{Re}^2\left(315+102{\beta }^2+8{\beta }^4\right)\right)\right)\right\}$

Moreover, the coefficients $a_I$ are recursively obtained as:

$\begin{array}{ll}\hfill a_{I+4}& =\frac{1}{\left(I+4\right)\left({\beta }^2+3\right)-3{\beta }^2}\{\left[\left(I+3\right)\left\{\left(I+1\right)\left(I+2\right)+1\right\}-1\right]a_{I+3}-kRe\left(I-1\right)b_I-k^2\left(I+1\right)a_{I+2}+kRe\left(I+1\right)b_{I+2}\hfill \\ \hfill & +kRe\left(I+1\right)b_{I+1}-\frac{k}{\beta }\left({\beta }^2+3\right)c_{I+2}+\frac{k}{\beta }\left\{\left(I+1\right)\left(I+3\right)+1\right\}{c}_{I+1}-\frac{k^3}{\beta }{c}_I+\frac{k^{2}Re}{\beta }{d}_I-\frac{k^{2}Re}{\beta }{d}_{I-2}\}\hfill \end{array}$

For $I=\mathrm{5,6,7},\dots \dots$

Furthermore, the coefficients of the second series in the expression of ${\widehat{\psi }}_1$ are obtained as:

$b_0=0,b_1=0,b_2=0,b_3=0,b_4=0,b_5=0,b_6=-\frac{2k^2{\mathrm{R}\mathrm{e}}^2\beta }{\left({\beta }^2+6\right)\left({\beta }^2+12\right)},b_7=-\frac{2k^2{\mathrm{R}\mathrm{e}}^2\beta \left(2523+358{\beta }^2\right)}{\left({\beta }^2+6\right)\left({\beta }^2+12\right)\left(2{\beta }^2+15\right)\left(4{\beta }^2+21\right)},$

$b_8=\frac{1}{\left({\beta }^2-36\right)\left({\beta }^2+6\right)\left({\beta }^2+12\right)\left(2{\beta }^2+15\right)\left(4{\beta }^2+21\right)\left(5{\beta }^2+24\right)}\left\{2k^2{\mathrm{R}\mathrm{e}}^2\beta \left(21580668+2489292{\beta }^2-105021{\beta }^4-762{\beta }^6+8{\beta }^8+10k^2\left(\beta -6\right)\left(\beta +6\right)\left(15+2{\beta }^2\right)\left(21+4{\beta }^2\right)\right)\right\},$

The recursive formula for $b_I$ is obtained as:

$b_{I+4}=\frac{1}{\left({\beta }^2+3\right)\left(I+4\right)-3{\beta }^2}\left\{-kRe\left(I+1\right)a_{I+2}+kRe\left(I-1\right)a_I+\left[\left(I+3\right)\left\{\left(I+1\right)\left(I+2\right)+1\right\}-1\right]b_{I+3}-k^2\left(I+1\right)b_{I+2}-\frac{k}{\beta }\left({\beta }^2+3\right)d_{I+2}+\frac{k}{\beta }\left\{\left(I+1\right)\left(I+3\right)+1\right\}{d}_{I+1}+\frac{k^3}{\beta }{d}_I\right\}$

For $I=\mathrm{5,6,7},\dots \dots$

$c_0=0,c_1=0,c_2=-2Re,c_3=0,c_4=0,c_5=0,c_6=0,c_7=0,$

The recursive formula for $c_I$ is obtained as:

$c_{I+2}=\frac{1}{{\left(I+2\right)}^2-{\beta }^2}\left\{2R\mathrm{e}\beta b_I+k^2{c}_I-kR\mathrm{e}{d}_I+kR\mathrm{e}{d}_{I-2}\right\}$

For $I=\mathrm{6,7,8},\dots \dots$

$d_0=0,d_1=0,d_2=-2Re,d_3=0,d_4=0,d_5=0,d_6=\frac{4k{\mathrm{R}\mathrm{e}}^2{\beta }^2}{\left({\beta }^2-36\right)\left({\beta }^2+12\right)},d_7=\frac{108k{\mathrm{R}\mathrm{e}}^2{\beta }^2}{\left({\beta }^2-49\right)\left({\beta }^2+12\right)\left(2{\beta }^2+15\right)},$

And the recursive formula for $d_I$ is obtained as:

$d_{I+2}=\frac{1}{{\left(I+2\right)}^2-{\beta }^2}\left\{-2R\mathrm{e}\beta a_I+k^2{c}_I+kR\mathrm{e}{c}_I+kR\mathrm{e}{c}_{I-2}\right\}$

For $I=\mathrm{6,7,8},\dots \dots$

Figure 2, Figure 3, Figure 4, Figure 5 describe the impact of meanders on the formation and behavior of vortices in the flow, producing complex patterns of stream contours. Vortices form near the wall of the tube and interact with the fluid flow. In Figure 6, fluid flow patterns are affected in several ways with variation in the number of helixes. As the number of helixes increases, the amplitude of the meanders increases, leading to more complex flow patterns with multiple recirculation zones near the wall of the tube. This also causes an increase in the pressure drop and the overall mixing in the flow.

FIGURE 2

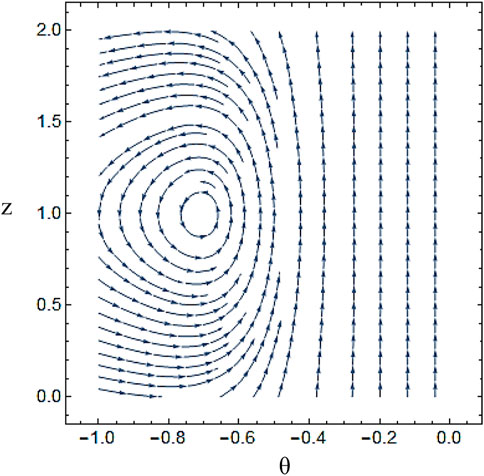
FIGURE 2. The stream lines are drawn by using $u_b$ and $w_b$ (components of velocity) and the stream contours are graphed for Re = 10, ß = 1, z = 1, and k = 10 in the domain 0 ≤ θ ≤ 2, −1 ≤ η ≤ 0 at the lower portion of the tube.

FIGURE 3

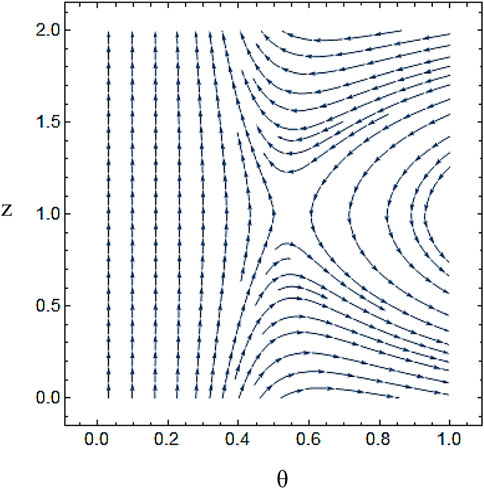
FIGURE 3. The stream lines are drawn by using $u_b$ and $w_b$ (components of velocity) and the stream contours are graphed for Re = 10, ß = 1, z = 1, and k = 10 in the domain 0 ≤ θ ≤ 2, 0 ≤ η ≤ 1 at the upper portion of the tube.

FIGURE 4

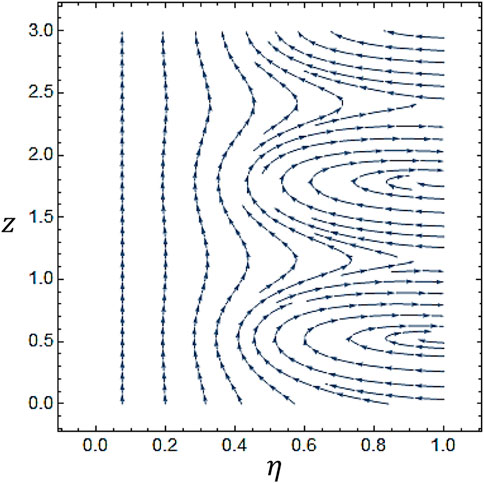
FIGURE 4. The stream lines are drawn by using $v_b$ and $w_b$ (components of velocity) and the stream contours are graphed for Re = 100, ß = 1, z = 1, and k = 0.1 in the domain 0 ≤ θ ≤, 0 ≤ η ≤ 1 at the upper portion of the tube.

FIGURE 5

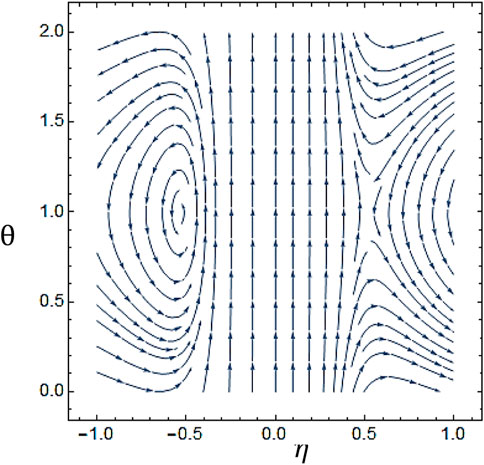
FIGURE 5. The stream lines are drawn by using $u_b$ and $w_b$ (components of velocity) and the stream contours are graphed for Re = 10, ß = 1, z = 1, and k = 10 in the domain 0 ≤ θ ≤ 2, −1 ≤ η ≤ 1 of the whole tube.

FIGURE 6

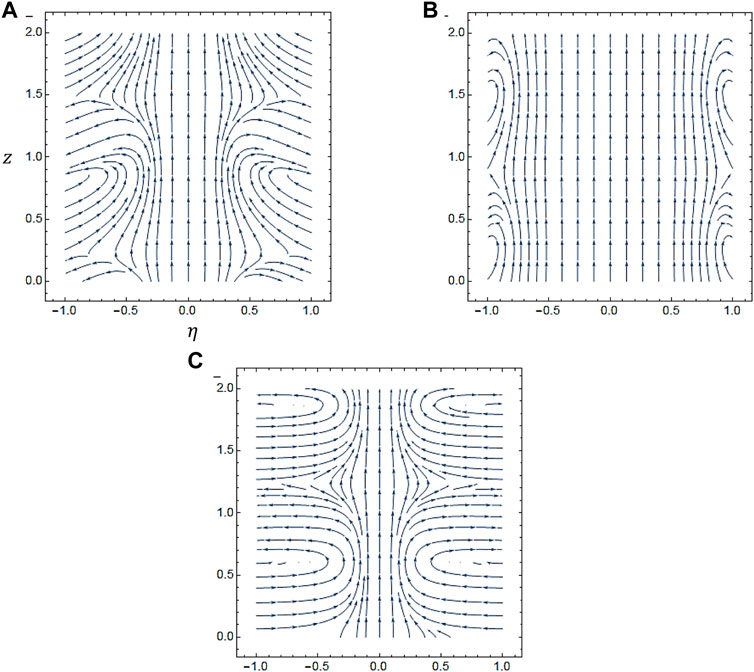
FIGURE 6. The stream lines are drawn by using $v_b$ and $w_b$ (components of velocity) and the stream contours are graphed for Re = 100, θ = 1, k = 5, (A) ß = 2, (B) ß = 5, and (C) ß = 0.1 in the domain 0 ≤ z ≤ 2, −1 ≤ η ≤ 1 of the whole tube.

7 Conclusion

In a meandering tube, streamwise vortices can improve the transportation of heat and species mass in a transverse direction. To create these vortices, a specific meandering wavelength is required, which can be measured using linear instability theory. Short wavelengths cause flow separation, while long wavelengths result in a rectilinear stream resembling a flat plate. Shear-driven instability also contributes to vortex formation. The effect of a steady laminar flow in a meandering tube with small amplitude wavy walls was studied. The governing equations were constructed using the continuity equation and Navier-Stokes equations with no slip boundary conditions. Suppositions were made to simplify the complex non-linear problem, including linear instabilities, uniform thermal characteristics, and laminar flow conditions. The equations were further simplified using available dimensionless variables and new transformations. The perturbation and power series approaches were used to solve the equations with the help of Mathematica, and the velocity profiles and stream contours were graphed using standard codes and definitions.

The flow in a meandering tube becomes unstable due to centrifugal impact, which results in the formation of streamwise vortices. This research has focused on identifying the lowest meandering amplitude that can create these vortices with minimal pressure loss. Two primary forms of vortex instability have been studied, with the most effective parameter being better for creating vortex instability than centrifugal instability. The meandering geometry that is most successful in producing vortices does not encourage traveling wave instability, which can delay the onset of laminar-turbulent transition. By using the reduced geometry model approach, the findings can be applied to various types of meandering tubes.

Further investigations can be conducted through experiments, simulations, and new applications. Experiments can provide valuable insights into the complex nature of the flow using advanced techniques like PIV, LDV, and HWA to measure velocities, turbulence, and vortices. Numerical simulations using CFD techniques can also be performed to investigate flow behavior, providing detailed information on velocity, pressure, and vortices, and help optimize tube design.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The mathematical model has been proposed by DK, all the numerical computations and their graphs have been carried out by SI. The discussion of graphs and their physical interpretation has been given by DK and SI. The literature review and comparison of the present simulations with the classical data has been established by NU. The final review and amendments in the manuscript has been carried out by KN.

Funding

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alyousef, H. A., Yasmin, H., Shah, R., Shah, N. A., El-Sherif, L. S., and El-Tantawy, S. A. (2023). Mathematical modeling and analysis of the steady electro-osmotic flow of two immiscible fluids: A biomedical application. Coatings 13 (1), 115. doi:10.3390/coatings13010115

CrossRef Full Text | Google Scholar

Bergles, A. E., and Webb, R. L. (1985). A guide to the literature on convective heat transfer augmentation. Ames, Iowa: Iowa State University College of Engineering.

Google Scholar

Dean, W. R. (1928). Fluid motion in a curved channel. Proc. R. Soc. Lond. Ser. A, Contain. Pap. a Math. Phys. Character 121, 402–420.

Google Scholar

Fiebig, M., and Chen, Y. (1999). “Heat transfer enhancement by wing-type longitudinal vortex generators and their application to finned oval tube heat exchanger elements,” in Heat transfer enhancement of heat exchangers (Dordrecht: Springer), 79–105.

CrossRef Full Text | Google Scholar

Fiebig, M. (1995). Embedded vortices in internal flow: Heat transfer and pressure loss enhancement. Int. J. Heat Fluid Flow 16, 376–388. doi:10.1016/0142-727x(95)00043-p

CrossRef Full Text | Google Scholar

Fiebig, M. (1995). Vortex generators for compact heat exchangers. J. Enhanc. Heat Transf. 2, 1–20. doi:10.1615/jenhheattransf.v24.i1-6.10

CrossRef Full Text | Google Scholar

Fiebig, M. (1998). Vortices, generators and heat transfer. Chem. Eng. Res. Des. 76, 108–123. doi:10.1205/026387698524686

CrossRef Full Text | Google Scholar

Floryan, J. M., and Asai, M. (2011). On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23, 104101. doi:10.1063/1.3644694

CrossRef Full Text | Google Scholar

Floryan, J. M. (2002). Centrifugal instability of Couette flow over a wavy wall. Phys. fluids 14, 312–322. doi:10.1063/1.1416185

CrossRef Full Text | Google Scholar

Floryan, J. M. (1986). Görtler instability of boundary layers over concave and convex walls. Phys. fluids 29, 2380–2387. doi:10.1063/1.865531

CrossRef Full Text | Google Scholar

Floryan, J. M. (1991). On the Görtler instability of boundary layers. Prog. Aerosp. Sci. 28, 235–271. doi:10.1016/0376-0421(91)90006-p

CrossRef Full Text | Google Scholar

Görtler, H. (1941). Instabilität laminarer Grenzschichten an konkaven Wänden gegenüber gewissen dreidimensionalen Störungen. ZAMM-Journal Appl. Math. Mechanics/Zeitschrift für Angewandte Math. und Mech. 21, 250–252. doi:10.1002/zamm.19410210408

CrossRef Full Text | Google Scholar

Gschwind, P., Regele, A., and Kottke, V. (1995). Sinusoidal wavy channels with Taylor-Goertler vortices. Exp. Therm. fluid Sci. 11, 270–275. doi:10.1016/0894-1777(95)00056-r

CrossRef Full Text | Google Scholar

Guzmán, A. M., Cárdenas, M. J., Urzúa, F. A., and Araya, P. E. (2009). Heat transfer enhancement by flow bifurcations in asymmetric wavy wall channels. Int. J. Heat Mass Transf. 52, 3778–3789. doi:10.1016/j.ijheatmasstransfer.2009.02.026

CrossRef Full Text | Google Scholar

Hayat, T., Iqbal, M., Yasmin, H., Alsaadi, F. E., and Gao, H. (2015). Simultaneous effects of Hall and convective conditions on peristaltic flow of couple-stress fluid in an inclined asymmetric channel. Pramana 85, 125–148. doi:10.1007/s12043-014-0888-1

CrossRef Full Text | Google Scholar

Jacobi, A. M., and Shah, R. K. (1995). Heat transfer surface enhancement through the use of longitudinal vortices: A review of recent progress. Exp. Therm. Fluid Sci. 11, 295–309. doi:10.1016/0894-1777(95)00066-u

CrossRef Full Text | Google Scholar

Javed, M., Imran, N., Arooj, A., and Sohail, M. (2021). Meta-analysis on homogeneous-heterogeneous reaction effects in a sinusoidal wavy curved channel. Chem. Phys. Lett. 763, 138200. doi:10.1016/j.cplett.2020.138200

CrossRef Full Text | Google Scholar

Jensen, M. K., Bergles, A. E., and Shome., B. (1997). The literature on enhancement of convective heat and mass transfer. J. Enhanc. Heat Transf. 4, 1–6. doi:10.1615/jenhheattransf.v4.i1.10

CrossRef Full Text | Google Scholar

Ligrani, P. M., Oliveira, M. M., and Blaskovich, T. (2003). Comparison of heat transfer augmentation techniques. AIAA J. 41, 337–362. doi:10.2514/2.1964

CrossRef Full Text | Google Scholar

Mehmood, O. U., Qureshi, A. A., Yasmin, H., and Uddin, S. (2020). Thermo-mechanical analysis of non Newtonian peristaltic mechanism: Modified heat flux model. Phys. A Stat. Mech. its Appl. 550, 124014. doi:10.1016/j.physa.2019.124014

CrossRef Full Text | Google Scholar

Metwally, H. M., and Manglik, R. M. (2004). Enhanced heat transfer due to curvature-induced lateral vortices in laminar flows in sinusoidal corrugated-plate channels. Int. J. Heat Mass Transf. 47, 2283–2292. doi:10.1016/j.ijheatmasstransfer.2003.11.019

CrossRef Full Text | Google Scholar

Mohammadi, A., and Floryan, J. M. (2013). Groove optimization for drag reduction. Phys. Fluids 25, 113601. doi:10.1063/1.4826983

CrossRef Full Text | Google Scholar

Naseem, T., Nazir, U., and Sohail, M. (2021). Contribution of Dufour and Soret effects on hydromagnetized material comprising temperature-dependent thermal conductivity. Heat. Transf. 50 (7), 7157–7175. doi:10.1002/htj.22222

CrossRef Full Text | Google Scholar

Nishimura, T., Yano, K., Yoshino, T., and Kawamura, Y. (1990). Occurrence and structure of Taylor–Goertler vortices induced in two-dimensional wavy channels for steady flow. J. Chem. Eng. Jpn. 23, 697–703. doi:10.1252/jcej.23.697

CrossRef Full Text | Google Scholar

Patera, A. T., and Mikic, B. B. (1986). Exploiting hydrodynamic instabilities. Resonant heat transfer enhancement. Int. J. heat mass Transf. 29, 1127–1138. doi:10.1016/0017-9310(86)90144-4

CrossRef Full Text | Google Scholar

Pham, M. V., Plourde, F., and Doan, S. K. (2008). Turbulent heat and mass transfer in sinusoidal wavy channels. Int. J. Heat Fluid Flow 29 (5), 1240–1257. doi:10.1016/j.ijheatfluidflow.2008.04.002

CrossRef Full Text | Google Scholar

Rayleigh, L. (1917). On the dynamics of revolving fluids. Proc. R. Soc. Lond. Ser. A, Contain. Pap. a Math. Phys. Character 93, 148–154.

Google Scholar

Rush, T. A., Newell, T. A., and Jacobi, A. M. (1999). An experimental study of flow and heat transfer in sinusoidal wavy passages. Int. J. heat mass Transf. 42, 1541–1553. doi:10.1016/s0017-9310(98)00264-6

CrossRef Full Text | Google Scholar

Saric, W. S., and Ali, B. (1991). “Görtler vortices with periodic curvature,” in Boundary layer stability and transition to turbulence (Berlin, Germany: Springer), 37–42.

Google Scholar

Schlichting, H., and Kestin, J. (1961). Boundary layer theory. New York: McGraw-Hill.

Google Scholar

Sui, Y., Teo, C. J., and Lee, P. S. (2012). Direct numerical simulation of fluid flow and heat transfer in periodic wavy channels with rectangular cross-sections. Int. J. Heat Mass Transf. 55, 73–88. doi:10.1016/j.ijheatmasstransfer.2011.08.041

CrossRef Full Text | Google Scholar

Tatsuo, N., Shinichiro, M., Shingho, A., and Yuji, K. (1990). Flow observations and mass transfer characteristics in symmetrical wavy-walled channels at moderate Reynolds numbers for steady flow. Int. J. Heat Mass Transf. 33, 835–845. doi:10.1016/0017-9310(90)90067-5

CrossRef Full Text | Google Scholar

Taylor, G. I. (1923). VIII. Stability of a viscous liquid contained between two rotating cylinders. Philosophical Trans. R. Soc. Lond. Ser. A, Contain. Pap. a Math. or Phys. Character 223, 605–615.

Google Scholar

Wang, F., Sohail, M., Nazir, U., El-Zahar, E. R., Park, C., and Jabbar, N. (2022). An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial. Nanotechnol. Rev. 11 (1), 1620–1632. doi:10.1515/ntrev-2022-0100

CrossRef Full Text | Google Scholar

Webb, R. L., and Bergles, A. E. (1981). Performance evaluation criteria for selection of heat transfer surface geometries used in low Reynolds number heat exchangers. Ames, Iowa: Iowa State University College of Engineering.

Google Scholar

White, F. M., and Majdalani, J. (2006). Viscous fluid flow. New York: McGraw-Hill, 433–434.

Google Scholar

Xu, M., Lu, H., Gong, L., Chai, J. C., and Duan, X. (2016). Parametric numerical study of the flow and heat transfer in microchannel with dimples. Int. Commun. Heat Mass Transf. 76, 348–357. doi:10.1016/j.icheatmasstransfer.2016.06.002

CrossRef Full Text | Google Scholar

Yasmin, H., and Iqbal, N. (2021). Convective mass/heat analysis of an electroosmotic peristaltic flow of ionic liquid in a symmetric porous microchannel with soret and dufour. Math. Problems Eng. 2021, 1–14. doi:10.1155/2021/2638647

CrossRef Full Text | Google Scholar

Yasmin, H., Iqbal, N., and Hussain, A. (2020). Convective heat/mass transfer analysis on johnson-segalman fluid in a symmetric curved channel with peristalsis: Engineering applications. Symmetry 12 (9), 1475. doi:10.3390/sym12091475

CrossRef Full Text | Google Scholar

Yasmin, H., Iqbal, N., and Tanveer, A. (2020). Engineering applications of peristaltic fluid flow with hall current, thermal deposition and convective conditions. Mathematics 8 (10), 1710. doi:10.3390/math8101710

CrossRef Full Text | Google Scholar

Zhang, J., Kundu, J., and Manglik, M. (2004). Effect of fin waviness and spacing on the lateral vortex structure and laminar heat transfer in wavy-plate-fin cores. Int. J. Heat Mass Transf. 47, 1719–1730. doi:10.1016/j.ijheatmasstransfer.2003.10.006

CrossRef Full Text | Google Scholar

Nomenclature