Calculation method for holding prestress of corroded prestressed anchor cable in long-term operation slope

Due to the rich water in the weathered layer of the free section, the prestressed anchor cable of the long-term operating slope is severely corroded and its mechanical properties are deteriorated, affecting the stability of the slope. Based on a certain number of long-term operation highway anchor cable excavation tests, the author found that the free section of the anchor cable orifice was seriously corroded. Currently, there is very little research on the relationship between the holding capacity of anchor cables and the degree of corrosion of the free section of the cable, and the research is mainly focused on the life of the anchor section. Therefore, the constitutive relationship of the cable body is established on the basis of corrosion force coupled statistical damage mechanics, and the relationship between the degree of corrosion of the cable body and the holding prestress of the operating slope anchor cables is derived using the load transfer method. The rationality of prestressed anchor cables on highway slopes during the operation period was verified by actual measurement. This study has positive significance for long-term stability analysis of slopes.

1 Introduction

Tension type prestressed anchor cables are widely used in transportation, land and resources, railways, industrial and civil buildings, water conservancy and hydropower projects, and other industries. The prestressed anchor cable is bonded to the grouting body through the steel strand to form an anchor solid, and a certain length of unbonded free section is set to apply prestress, thereby playing an active role in reinforcing the slope (Shi et al., 2019; Lin et al., 2020; Wang L. Q. et al., 2023).

For engineering slopes that have been reinforced with prestressed anchor cables for a long time, the prestress held by the landslide will decrease over time as the operation time increases after the anchor cable reinforcement is completed. The current research mainly focuses on the stress relaxation effect of the cable body caused by the creep of the rock mass in the anchoring section of the prestressed anchor cable (Jiang et al., 2014; Chen G. et al., 2018). However, for the prestressed anchor cable in hard rock areas, the creep effect of the rock mass in the anchoring section is weak, and this factor is not the main reason for the anchor cable to hold the prestress (stress relaxation) (Fan et al., 2015).

The authors conducted anchor opening testing, prestressed anchor cable holding capacity testing, and anchor cable full length excavation tests on multiple operating highways and cutting slope points in Guangdong, China. The main types of slope strata are carbonaceous mudstone, quartz sandstone, granite, and fused tuff. In some slope points, even if the anchor section is located in moderately weathered hard rock stratum, the prestress held by the anchor cable still suffers from a loss of 30%–50%. The impact of construction quality factors is not considered for the time being, and the steel strands at the anchor head section often suffer from severe corrosion when the loss ratio is large. Many scholars have done some valuable engineering research on the corrosion of anchor cables during the operation period. He et al. (2010) studied the stress distribution characteristics of the anchor section of the anchor cable based on summarizing the corrosion damage laws of steel strands. Zheng et al. (2010) studied the variation of physical and mechanical parameters of the reinforcement under the influence of corrosion. Deng et al. (2014) focused on the impact of cable rust expansion on anchor solids in the anchoring section, and proposed a prediction model for anchor cable life. Jiang et al. (2014) and Fu et al. (2021) considered the damage and failure of the anchor section caused by the corrosion and expansion of rock bolts in the process of studying the long-term reliability of slopes. Li and Liu (2016) studied the effect of cable corrosion on the performance of the anchoring interface. However, during the anchor opening inspection and the full length excavation test, the author found that the corrosion of the shallow free section of the anchor cable is the most serious, and the corrosion of the anchor section is relatively rare. Rust in the free section reduces the force transmission performance of the anchor cable, and it is unable to transmit the anchoring force to the orifice reaction structure (lattice beam), which is intuitively manifested as a reduction in the holding prestress of the anchor cable. In practical engineering, the mechanical properties of rock masses can decrease due to precipitation cycles, temperature, and alternating disturbances (Li and Chen, 2022; Wang et al., 2022; Wang Y. et al., 2023). If the anchor cable does not have sufficient prestress, it is difficult to prevent cracks in the rock mass due to weathering and deformation, and the passive support force of the prestressed anchor cable is usually considered as a safety reserve in engineering. Therefore, the proportion of holding prestress has received great attention in practical engineering. At present, some scholars and experts have established models for the overall pull-out resistance of anchor cables (including passive support force) and the reduction of anchor cable prestress caused by soft rock creep (Shi et al., 2019; Yang et al., 2022). However, there are relatively few mechanical model studies on the reduction of prestress caused by reinforcement corrosion in hard rock formations. In order to effectively prevent disasters caused by slope instability and collapse, and guide corresponding engineering construction, it is necessary to explore the mechanical mechanisms of relevant aspects and establish corresponding mechanical models.

In order to explore the mechanism by which corrosion in the free section affects the holding prestress of anchor cables, a mechanical model for calculating the holding prestress of anchor cables under corrosion conditions of hard rock and non soft rock slopes is established. Based on statistical damage mechanics, a new tensile constitutive model of steel strands considering the interaction of corrosion and force is derived, and the constitutive model and load transfer method are applied to the mechanical analysis of the corroded free section of anchor cables. In the analysis of the application of the model to field tests, it was found that the calculated results were relatively close to the measured values, verifying the rationality of the model.

2 Rust force statistical damage constitutive equation

To simplify the analysis, the following assumptions are made.

(1) Only consider uniform corrosion of steel strands;

(2) The shear stress in the anchoring section of the anchor cable is uniformly distributed on the surface of the steel strand;

(3) This model only considers the effect of anchor cable corrosion on maintaining pre-stress of the anchor cable, without considering the interaction with other factors. It is applicable to the corrosion of steel strands in the free section of the anchor cable in hard rock slopes.

After a series of chemical and electrochemical actions, steel strands can form rust. Rust has poor mechanical properties, is relatively loose, and basically has no bearing capacity. It is assumed that the actual bearing capacity cross-sectional area of the steel strand decreases, causing damage.

$\eta =\frac{g^o-g}{g^o}(1)$

Where, $\eta$ is the corrosion rate, which is a dimensionless percentage, $g^o$ is the weight of the steel strand before corrosion, and $g$ is the weight of the steel strand after corrosion.

The research by Luo and Li (2008) shows that the physical and mechanical properties of unbonded steel strands affected by normal corrosion have decreased to varying degrees, as shown in Table 1 below.

TABLE 1

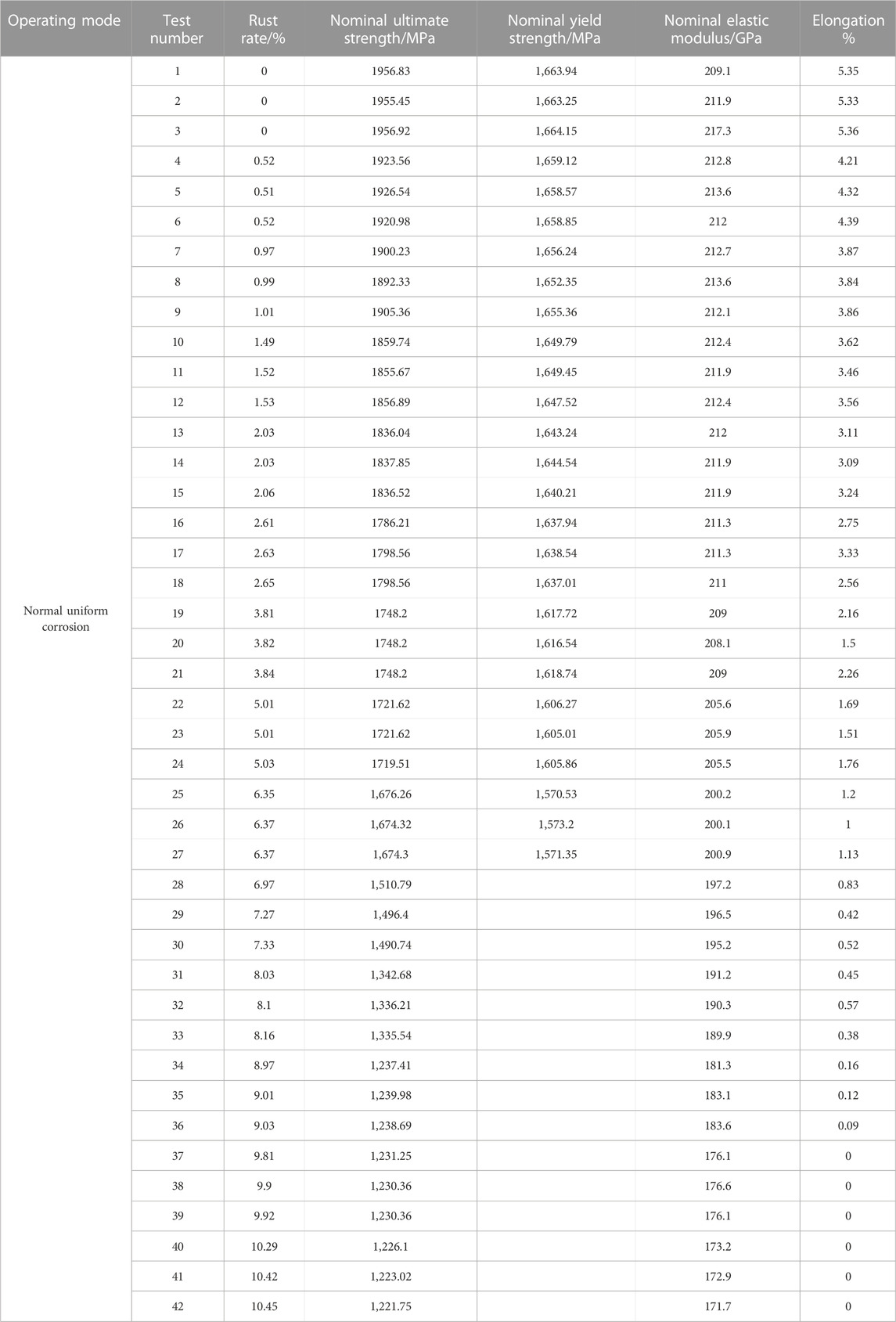
TABLE 1. Change trend of physical and mechanical parameters of unbonded free section steel strands with different corrosion rates.

From Table 1, it can be seen that under normal uniform corrosion, the physical and mechanical parameters of the steel strand are negatively correlated with the corrosion rate, which is caused by damage caused by corrosion. The actual engineering design is often conservative and generally does not place the steel strand in a relatively plastic tensile state, but rather requires a certain safety reserve. In order to reflect the impact of the combined action of corrosion and force, damage factors can be introduced. Therefore, the damage discussed in this article refers to the process that under the combined action of corrosion and force, the internal micro elements of the steel strand cable or tendon become unable to withstand stress, and the effective cross-sectional area decreases.

The damage of solid materials is usually defined by the following formula (Liu et al., 2018):

$D=\frac{A_D}{A_{total}}(2)$

Where, $D$ is the damage factor, it is a dimensionless parameter, $A_D$ is the cross-sectional area of the loss, and $A_{total}$, is the total cross-sectional area of the material.

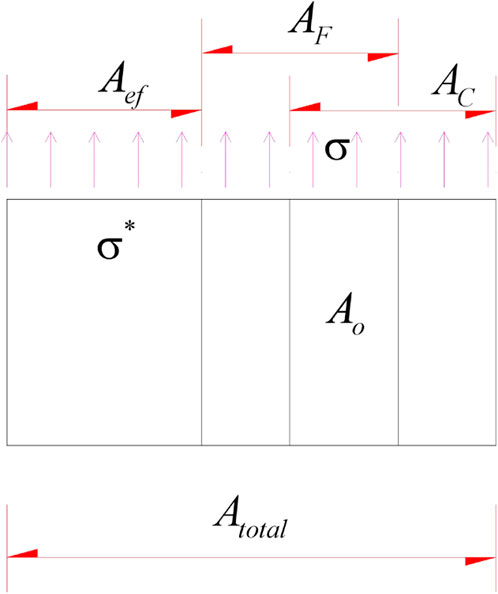
Under corrosion conditions, the unbonded free section steel strand is damaged by the combined action of external force and corrosion, as shown in Figure 1.

FIGURE 1

FIGURE 1. Damage distribution mode of steel strand during tension.

The steel strand is subjected to tensile load, and the total tensile stress and total area borne by the cross section micro element are $\sigma$ and $A_{total}$, the undamaged part bears effective shear stress ${\sigma }^{*}$ and cross-sectional area carrying effective stress $A_{ef}$, and the areas of corrosion, pullout load, and common damage are $A_C$, $A_F$ and $A_o$.

At a certain corrosion rate, the corrosion damage area is $A_C$, so the damage expression caused by corrosion is (Liu et al., 2018):

$D_c=\frac{A_C}{A_{total}}(3)$

After corrosion, the damage area caused by tensile load is $A_F$, and the damage area caused by both corrosion and tensile load is $A_F$. Therefore, the damage expression caused by pure tensile load is:

$D_F=\frac{A_F-A_o}{A_{total}-A_C}(4)$

The total damage caused by corrosion and load is defined as the cumulative damage caused by both minus the common damage caused by their intersection, and the expression is:

$D=\frac{A_F+A_C-A_o}{A_{total}}(5)$

The expression of the total damage factor obtained is:

$D=D_C+D_F-D_C{D}_F(6)$

From a mesoscopic perspective, material damage leads to loss of cross-sectional area, resulting in a reduction in macroscopic mechanical properties, which is essentially caused by the destruction of material microelements. Therefore, the damage factor can also be defined by counting the number of micro element failures, as shown in the following equation.

$D=\frac{n}{N}(7)$

Where, n is the number of damaged micro elements, and N is the total number of micro elements of the steel strand.

Taking the corrosion rate as the strength index, it is assumed that the microcracks and microelements of the steel strand under the influence of corrosion follow the Weibull probability distribution (Chen S. et al., 2018). The expression of the probability distribution density function of the Weibull distribution is:

$\mathrm{\Phi }\left(\eta \right)=\frac{b}{a}{\left(\frac{\eta }{a}\right)}^{b-1}\exp \left[-{\left(\frac{\eta }{a}\right)}^b\right](8)$

Where, $a$ and $b$ are model parameters of Weibull distribution, reflecting the brittleness and morphology of the model curve.

As the corrosion rate changes, the number of micro cracks and micro elements in the steel strand that are damaged is:

$n={\displaystyle {\int }_0^{\eta }}N\mathrm{\Phi }\left(\eta \right)d\eta =N\left(1-\exp \left[-{\left(\frac{\eta }{a}\right)}^b\right]\right)(9)$

Therefore, the expression of the damage factor caused by pure corrosion is:

$D_C=1-\exp \left[-{\left(\frac{\eta }{a}\right)}^b\right](10)$

Macroscopically, damage can be characterized as a loss of modulus, so the formula can also be written as:

$D_C=\frac{E_{r\eta }}{E_{\eta =0}}=1-\exp \left[-{\left(\frac{\eta }{a}\right)}^b\right](11)$

Where, $E_r$ is the elastic modulus after corrosion damage, and $E_{\eta =0}$ is the elastic modulus when the corrosion rate is equal to 0.

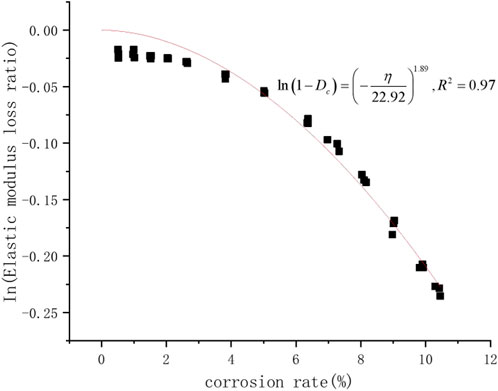
Based on the data in Table 1, a scatter plot (see Figure 2) of the corrosion rate damage evolution law can be drawn to verify the rationality of the formula.

FIGURE 2

FIGURE 2. Evolution law of the damage along with the corrosion rate.

It can be seen from Figure 2 that this figure can better describe the evolution of steel strands with corrosion rate, which indicates that the law of micro element failure of steel strand section under corrosion obeys Weibull probability distribution.

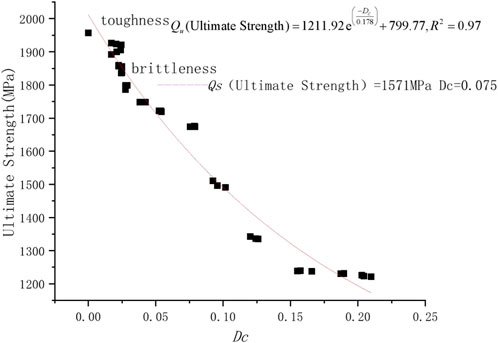
With the evolution of corrosion damage, the rule between the tensile ultimate strength of steel strands and corrosion damage can be obtained through nonlinear regression analysis (see Figure 3).

FIGURE 3

FIGURE 3. Ultimate strength of steel strands under different degrees of corrosion damage.

It can be seen from Figure 3 that the ultimate strength of corroded steel strands decreases exponentially with the evolution of corrosion damage factors. When the corrosion damage of the steel strand reaches a certain degree, the ultimate strength value tends to converge and tend to be gentle. This is because as the degree of corrosion increases, the initial damage increases under load, and the internal micro cracks and pores become larger, making it more prone to low stress instability and expansion. Under normal corrosion conditions, the ultimate strength approaches or even equals the yield strength. Under local corrosion damage conditions, the yield strength of steel strands also decreases with the ultimate strength.

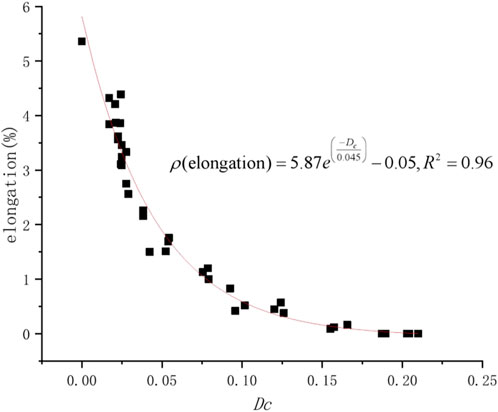
As can be seen from Figure 4, as the corrosion damage evolves, the elongation of the steel strand decreases exponentially, and the brittleness of the material increases as the corrosion damage evolves.

FIGURE 4

FIGURE 4. Ultimate strength of steel strands under different degrees of corrosion damage.

Load action is also an important factor that affects the mechanical properties of steel strands in corroded environments. It is assumed that under tensile load, with strain as the strength index, the strength of the microelement obeys a uniform distribution, as shown in the following equation.

$\mathrm{\Phi }\left(\epsilon \right)=\frac{1}{a_F}(12)$

$a_F$ is a model parameter that reflects the uniformity of the distribution of microelements under tensile load.

Eq. 13 considers the location parameter $c_F$, which can reflect the condition that the elastic modulus of the tensile elastic section of the steel strand is not damaged due to force. As the strain increases, the number of microelements that fail is:

$n={\displaystyle {\int }_{c_F}^{\epsilon }}N\mathrm{\Phi }\left(\epsilon \right)d\epsilon =N\frac{\epsilon -c_F}{a_F}(13)$

Where, $c_F$ is the strain threshold for force induced damage.

Combining Eqs. 13 and Eqs 6, 7 obtain Eq. 14:

$D=\left\{\begin{array}{c}1-\exp \left[{\left(-\frac{\eta }{a}\right)}^b\right],\epsilon \le c_F\\ 1-\exp \left[{\left(-\frac{\eta }{a}\right)}^b\right]\left(1-\frac{\epsilon -c_F}{a_F}\right),\epsilon >c_F\end{array}\right.(14)$

Based on the assumption of strain equivalence, the Constitutive equation acting on the damaged material is equivalent to the effect produced by the effective force on the nondestructive material, the expression is as follows (Chen G. et al., 2018):

$\sigma =E_{\eta =0}\left(1-D\right)\epsilon (15)$

Combining Eqs. 14, 15, the stress-strain relationship (constitutive model) of the steel strand can be obtained as follows:

$\sigma =\left\{\begin{array}{c}{E}_{\eta =0}\exp \left[{\left(-\frac{\eta }{a}\right)}^b\right]\epsilon ,\epsilon \le c_F\\ E_{\eta =0}\exp \left[{\left(-\frac{\eta }{a}\right)}^b\right]\left(1-\frac{\epsilon -c_F}{a_F}\right)\epsilon ,\epsilon >c_F\end{array}\right.(16)$

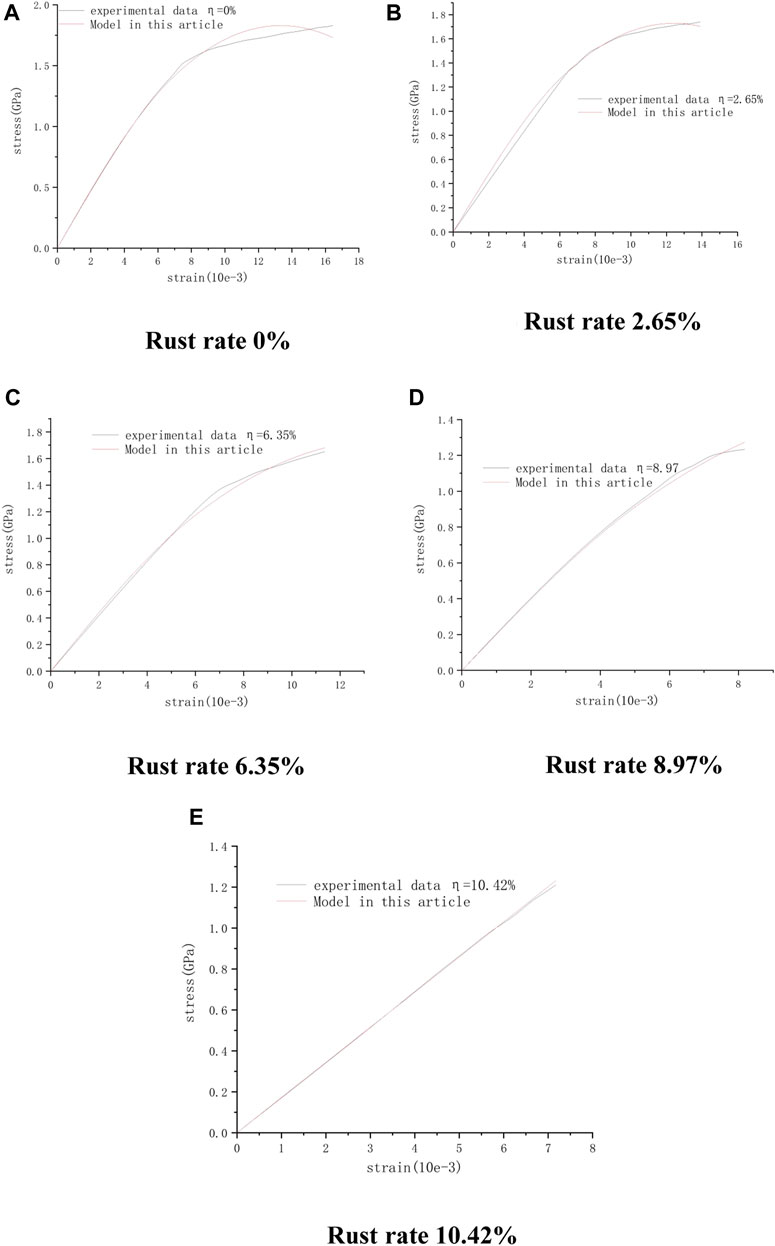
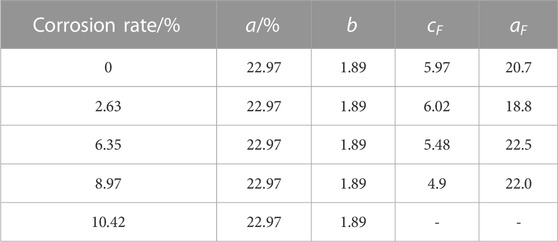
Select tensile test data of steel strands with normal corrosion rates of 0%, 2.63%, 6.35%, 8.97%, and 10.42% to verify the rationality of Formula (16). See Figure 2; Figure 5 for relevant model parameters and curves.

FIGURE 5

FIGURE 5. Comparison of model and test data.

It can be seen from Figure 5 that the derived model agrees well with the experimental data. The model can better reflect the constitutive relationship of steel strands under the combined action of corrosion and force damage. In practical engineering, the unbonded free section of steel strands is prone to corrosion and corrosion during highway slope operation, resulting in loss of cross-sectional area, resulting in a decrease in the holding prestress of the anchor cable, and affecting the long-term stability of the slope.

3 Calculation method of anchor cable holding prestress based on damage statistical theory and load transfer method

The tendons of anchor bolts and anchor cables are usually in an elastic state under working conditions. The elastic situation in the constitutive model derived in this paper can be used in the load transfer analysis of corroded prestressed anchor bolts (cables). On the anchored micro segment, assuming that the interfacial shear stress on the micro segment is uniformly distributed, it can be obtained based on the force balance of the micro segment (Li and Stillborg, 1999):

$dp\left(x\right)+\pi d\tau dx=0(17)$

Where, $d$ is the diameter of the anchor rod; $P\left(x\right)$ The axial force at a certain rod length, and $\tau$ is the shear stress between the reinforcement and the anchor body.

The magnitude of the axial force is related to the strain of the steel strand, as shown in the formula.

$P\left(x\right)=E_{cable}\pi d^2\frac{\epsilon \left(x\right)}{4}(18)$

Where, $E_{cable}$ is the elastic modulus of the steel strand, which is related to factors such as corrosion rate is ε(x) the strain value along the length of the anchor cable.

In the free section of the anchor cable, $\tau =0$, it can be seen by substituting Formula (17) that the axial force of the anchor cable in the free section is:

$P\left(l_f\right)=E_{cable}\pi d^2\frac{\epsilon \left(x=l_f\right)}{4}(19)$

Where, $l_f$ is the length of the free section.

It is assumed that the deformation of the steel strands of the anchor cable is coordinated, there is $\epsilon \left(x=l_f\right)=\epsilon \left(x=0\right)$ at the boundary between the free section and the anchor section, and the strains at both ends are equal. Under the same strain, after corrosion damage to the unbonded free section steel strand, the elastic modulus $E_{cable}$ decreases under the combined action of force and corrosion, which is reflected in a decrease in the anchor head holding capacity on the macro level.

The shear stress and shear displacement of the anchoring section of the anchor cable follow the following constitutive relationship:

$\tau =Ku(20)$

Where, $K$ is the interfacial shear stiffness, and if the anchor cable at the anchor section is not corroded, this value is not affected. Parameter $u$ is the shear displacement between the cable body and the grouting body.

From the geometric equation of the steel strand, it can be obtained that:

$\epsilon =\frac{du}{dx}(21)$

From Eqs. 18–21, it can be obtained that:

$\frac{d^{2}u}{{dx}^2}=-\frac{4}{E_{cable}d}Ku(22)$

Since the elastic modulus of the anchor cable does not decrease due to corrosion during the pre tensioning and post tensioning periods, taking $E_{cable}=215\mathrm{G}\mathrm{P}\mathrm{a}$, the general solution expression can be obtained by solving the differential equation as follows:

$u=C1e^{\left(x\sqrt{\frac{4K}{E_{cable}d}}\right)}+C2e^{\left(-x\sqrt{\frac{4K}{E_{cable}d}}\right)}(23)$

Where, $C1,C2$ are undetermined coefficients.

The expression for the axial force distribution of the anchoring section along the rod length can be obtained from the above various methods as follows:

$P\left(x\right)=\frac{E_{cable}\pi d^2}{4}\left[C1\sqrt{\frac{4K}{E_{cable}d}}{e}^{\left(x\sqrt{\frac{4K}{E_{cable}d}}\right)}-C2\sqrt{\frac{4K}{E_{cable}d}}{e}^{\left(-x\sqrt{\frac{4K}{E_{cable}d}}\right)}\right]=M\left[C1{Ne}^{\left(xN\right)}-C2{Ne}^{\left(-xN\right)}\right](24)$

After tensioning the anchor cable, there is a boundary condition of $P\left(x=0\right)=P_{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}}$ at the junction of the free section and the anchor section, and there is a boundary condition of $P\left(x=l_r\right)=0$ at the end of the anchor section. Therefore, the specific solution expression of the above equation is:

$P\left(x\right)=\frac{P}{\left(1-e^{2l_{r}N}\right)}{e}^{xN}-\frac{P{e}^{2l_{r}N}}{\left(1-e^{2l_{r}N}\right)}{e}^{-xN}(25)$

Considering the stress transfer characteristics of the free section of the anchor cable, the expression for the axial force distribution along the length of the anchor cable is shown in the following equation.

$\left\{\begin{array}{l}P=P\left(x=0\right),\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ P\left(x\right)=\frac{P}{\left(1-e^{2l_{r}N}\right)}{e}^{xN}-\frac{P{e}^{2l_{r}N}}{\left(1-e^{2l_{r}N}\right)}{e}^{-xN},0<x\le l_r,\mathrm{A}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.(26)$

If the free section of the anchor cable is corroded during highway operation, the formula can be rewritten as follows:

$\left\{\begin{array}{l}P\left(x=0\right)=P\left(1-D\right),\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ P\left(x\right)=\frac{P}{\left(1-e^{2l_{r}N}\right)}{e}^{xN}-\frac{P{e}^{2l_{r}N}}{\left(1-e^{2l_{r}N}\right)}{e}^{-xN},0<x\le l_r,\mathrm{A}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.(27)$

In addition to the decrease in the elastic modulus, the relative increase in the nominal diameter of the corroded reinforcement in the free section under the same strain also affects the force transmission performance of the anchor cable. The expression for the nominal diameter of the steel strand under corrosion is:

$d_m=\sqrt{\left(n-1\right)\eta +1d}(28)$

Where, n is the volume expansion rate of the corroded steel bar, and research shows that this value is usually 2–4. $\eta$ is the reinforcement corrosion rate, calculated based on the weight loss of the reinforcement section. The expression can be seen from the previous formula, where n = 3 is taken (Xu et al., 2015).

Combining Eq. 28, Eq. 19, Eq. 27 can be rewritten as:

$\left\{\begin{array}{c}P\left(x=0\right)=P\left(1-D\right)\frac{d}{d_m},\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ P\left(x\right)=\frac{P}{\left(1-e^{2l_{r}N}\right)}{e}^{xN}-\frac{P{e}^{2l_{r}N}}{\left(1-e^{2l_{r}N}\right)}{e}^{-xN},0<x\le l_r,\mathrm{A}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.(29)$

The combination of Eq. 29 and Eq. 14 can determine the distribution of axial stress in the corroded free section of the anchor cable along the length of the rod. The calculation results are shown in Figure 6.

FIGURE 6

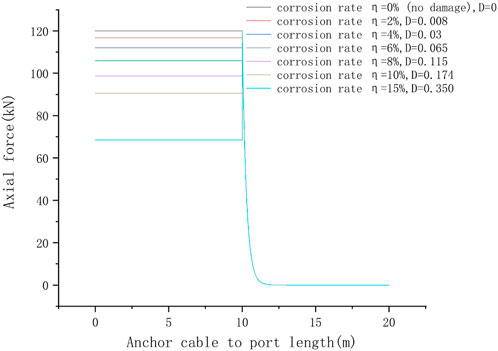
FIGURE 6. Distribution curve of axial stress of corroded/non corroded anchor cables along the length of the rod in the free section.

As can be seen from Figure 5, there is a negative correlation between the corrosion rate of steel strands in the free section and the magnitude of the axial force in the free section. This is because under the influence of corrosion, the free segment steel strand is damaged, and a portion of the load-bearing microelement is damaged. On the macro level, it is reflected in the decrease in the elastic modulus of the steel strand, so that the axial force of the free segment is less than that of the non-corroded anchor segment under the same strain. The anchor cable provides tensile force by anchoring into the stratum with good engineering geological conditions, and acts on the potential sliding mass at the orifice to strengthen the engineering slope. Therefore, corrosion of the free section of the anchor cable means that the axial force at the orifice decreases, and the reinforcement effect of the anchor cable becomes poor, affecting the overall stability of the engineering slope.

4 Engineering verification and case analysis

During the operation period, the entire Shanwei Longgang section of the expressway - Shenhai Expressway needs to be reconstructed and expanded. In order to provide design basis for the designers of the reconstruction and expansion project, the author conducted anchor opening inspection, anchor cable holding force test, and full-length excavation test for No. 2-one to three anchor cables at the edge of the secondary slope that will be expanded and excavated on a fully to moderately weathered fused tuff slope (see Figure 7).

FIGURE 7

FIGURE 7. Photos of on-site inspection and excavation.

From Figure 7, it can be seen that the shallow free section of the anchor head (0∼2 m along the depth of the anchor cable axis) has a relatively serious degree of corrosion. This is because the free section of the anchor cable is located in a soil like weathered layer, and is affected by environmental factors such as groundwater, surface water infiltration, and oxygen. In addition, the long grouting length of the free section makes it difficult to ensure that it is as dense as the anchor section, resulting in sufficient contact between the free section steel strand and water and air, resulting in corrosion.

During the construction period, the prestressed anchor cable is tensioned, and its prestress is provided by the frictional resistance between the anchor body and the stratum, and transmitted to the slope reaction structure (lattice beam) through the steel strand, which plays a role in strengthening the engineering slope. Fused tuff is hard rock, and relevant data shows that the rock is dense and hard (Bao, 1985), with a uniaxial saturated compressive strength of 68.8–241.4 MPa. The survey data of this section of expressway shows that the uniaxial saturated compressive strength of Ignimbrite is 76.9 MPa. The classification standard of engineering rock hardness is specified in the Standard for Classification of Engineering Rock Masses (Ministry of Water Resources of the Ministry of Water Resources of the People’s Republic of China, 2014). The rocks on the slope of this study are typical hard rocks. When the anchor section is located in moderately weathered rock stratum, there is basically no rheological effect, which can provide a large anchoring force. However, after a certain service life, the free section anchor cable body is corroded, the force transmission performance is reduced, and the holding prestress of the anchor cable is reduced. In Guangdong region, four to six bundles of anchor cables are commonly used in highway slope engineering. In order to increase the active support force of soft rock highway slopes, 6 strands of anchor cables are usually used. For hard rock highway slopes, the tensioning pre-stress of four to five anchor cables can meet the design requirements, so more economical anchor cable specifications and sizes were selected in the design. Generally speaking, the diameter of four to five anchor cables is 130 mm, and the diameter of 6 anchor cables is 150 mm.

The authors determined that the corrosion rate of the free section steel strand was 13% by cutting the anchor cable at a distance of 0∼2 m, cleaning and chemical composition analysis. The holding prestress test results of this anchor cable are shown in Table 2 below. In Table 2, the percentage of retained prestress refers to the percentage of retained prestress and design prestress value of the current anchor cable, while the prestress loss rate refers to the percentage of lost prestress and design prestress value of the anchor cable.

TABLE 2

TABLE 2. Test results of holding prestress of no. 2–one to three anchor cable.

Considering the actual testing results, the corrosion of steel strands is mainly concentrated in the shallow free section of the orifice, so during the transfer of anchoring force to the ground, a sudden drop occurs near the free section of the orifice corrosion. Eq. 29 can be adjusted as follows:

$\left\{\begin{array}{l}P=P\left(x=0\right)\left(1-D\right)\frac{d}{d_m}=P\left(x=0\right)\exp \left[-{\left(\frac{\eta }{a}\right)}^b\right]\frac{d}{d_m},\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ P=P\left(x=0\right),\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{d}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ P\left(x\right)=\frac{P}{\left(1-e^{2l_{r}N}\right)}{e}^{xN}-\frac{P{e}^{2l_{r}N}}{\left(1-e^{2l_{r}N}\right)}{e}^{-xN},0<x\le l_r\mathrm{A}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.(30)$

In order to verify the validity of the established model, the corrosion rate of the free section steel strand is 13% and substituted into the first formula in Eq. 30 Referring to relevant data, it is taken that n = 3 (Xu et al., 2015), and the steel strand is in the elastic state. From Table 3, a = 2, b = 3, and c = 4, it is calculated that the holding force of the anchor cable is 300.8 kN, the holding prestress ratio is 64%, and the loss prestress ratio is 36%. The calculated result of the derived expression is relatively close to the measured value, and the calculated result of holding prestress is slightly greater than the measured value by 4%, which indicates that the derived expression has certain rationality. The reason for the slightly larger calculation result is that the calculation method in this article does not consider the loss of holding prestress caused by other factors (such as prestress loss caused by clamping pieces, prestress loss caused by sequential tensioning, etc.).

TABLE 3

TABLE 3. Model parameters.

5 Conclusion

(1) Based on statistical damage mechanics, a tensile constitutive model of steel strand under the combined action of corrosion and force is established, and the validity of the model is verified. The model can accurately analyze the prestress loss of prestressed anchor cable in hard rock slope due to corrosion of free section.

(2) When corrosion occurs in the free section of the anchor cable, which leads to a decrease in the modulus and physical and mechanical parameters of the reinforcement, weakening the force transmission performance, and preventing the effective transmission of anchoring force to the reaction structure (grid beam) on the surface slope.

(3) Through the actual measurement of the highway reconstruction and expansion project, the results show that the predicted prestress bearing force of the calculation model is close to the actual data, which proves the validity and rationality of the calculation model. The overall stability evaluation of engineering slopes and landslides after treatment has important positive significance.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: ZY; methodology: ZY and SC; software: BN and YX; validation: HL; Data curation: HL and QZ; writing—original draft preparation, ZY and SL; writing—review and editing: YY and QT. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by Science and Technology Project of Hebei Education Department (QN2023060), and National Pre-research Funds of Hebei GEO University in 2023 (KY202305) and Funding for the Science and Technology Innovation Team Project of Hebei GEO University (KJCXTD-2021-08).

Conflict of interest

Authors ZY, BN, HL, QZ, QT, and SL were employed by Guangdong Huadu Transport Technology Co., Ltd. Author YX was employed by Guangdong Provincial Freeway Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, Y. N. (1985). Structural characteristics and genetic significance of fused tuff with different occurrences in Zhejiang. Zhejiang Land Resour. (1), 15–24.

Google Scholar

Chen, G., Chen, T., Chen, Y., Huang, R., and Liu, M. (2018a). A new method of predicting the prestress variations in anchored cables with excavation unloading destruction. Eng. Geol. 241, 109–120. doi:10.1016/j.enggeo.2018.05.015

CrossRef Full Text | Google Scholar

Chen, S., Qiao, C., Ye, Q., and Khan, M. (2018b). Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution. Environ. earth Sci. 77 (3), 108. doi:10.1007/s12665-018-7297-6

CrossRef Full Text | Google Scholar

Deng, D. P., Li, L., Zhao, L. H., and Liu, J. H. (2014). Prediction of the service life of prestressed anchor rods (cables) based on rust expansion cracking. J. Geotechnical Eng. 36 (8), 1464–1472. doi:10.11779/CJGE201408012

CrossRef Full Text | Google Scholar

Fan, Q., Zhu, H., and Gen, J. (2015). Monitoring result analyses of high slope of five-step ship lock in the Three Gorges Project. J. Rock Mech. Geotechnical Eng. 7 (2), 199–206. doi:10.1016/j.jrmge.2015.02.007

CrossRef Full Text | Google Scholar

Fu, G., Deo, R., Ji, J., and Kodikara, J. (2021). Failure assessment of reinforced rock slopes subjected to bolt corrosion considering correlated multiple failure modes. Comput. Geotechnics 132, 104029. doi:10.1016/j.compgeo.2021.104029

CrossRef Full Text | Google Scholar

He, S. M., Wang, Q. C., and Luo, Y. (2010). The effect of steel strand corrosion on the load transfer characteristics of prestressed anchor cables. J. Sichuan Univ. Eng. Sci. Ed. 42 (1), 1–4. doi:10.15961/j.jsuese.2010.01.022

CrossRef Full Text | Google Scholar

Jiang, S. H., Li, D. Q., Zhang, L. M., and Zhou, C. B. (2014). Time-dependent system reliability of anchored rock slopes considering rock bolt corrosion effect. Eng. Geol. 175, 1–8. doi:10.1016/j.enggeo.2014.03.011

CrossRef Full Text | Google Scholar

Li, C., and Stillborg, B. (1999). Analytical models for rock bolts. Int. J. Rock Mech. Min. Sci. 36 (8), 1013–1029. doi:10.1016/S1365-1609(99)00064-7

CrossRef Full Text | Google Scholar

Li, F. M., and Liu, Z. G. (2016). The effect of cable corrosion on the anchoring performance of anchor cable structures. Chin. J. Highw. Eng. 29 (2), 23–31. doi:10.19721/j.cnki.1001-7372.2016.02.004

CrossRef Full Text | Google Scholar

Li, W., and Chen, W. H. (2022). Linear crack initiation analysis on rock surface under the combined action of sub-elevated temperature stress and fracture air-vapor pressure. Theortical Appl. Fract. Mech. 122, 103582. doi:10.1016/j.tafmec.2022.103582

CrossRef Full Text | Google Scholar

Lin, C., Li, T., Zhao, L., Zhang, Z., Niu, Z., Liu, X., et al. (2020). Reinforcement effects and safety monitoring index for high steep slopes: A case study in China. Eng. Geol. 279, 105861. doi:10.1016/j.enggeo.2020.105861

CrossRef Full Text | Google Scholar

Liu, X. S., Tan, Y. L., Ning, J. G., Lu, Y. W., Gu, Q. H., and Lu, Y. (2018). Mechanical properties and damage constitutive model of coal in coal-rock combined body. Int. J. Rock Mech. Min. Sci. 110, 140–150. doi:10.1016/j.ijrmms.2018.07.020

CrossRef Full Text | Google Scholar

Luo, X. Y., and Li, Z. (2008). Study on the mechanical properties of unbonded prestressed steel strands after corrosion. J. Railw. 142 (02), 108–112. doi:10.3321/j.issn:1001-8360.2008.02.021

CrossRef Full Text | Google Scholar

Ministry of Water Resources of the Ministry of Water Resources of the People's Republic of China (2014). GB/T 50218-2014, standard for engineering rock mass classification. Ministry of housing and urban rural development of the Ministry of housing and urban-rural development. China: General Administration of Quality Supervision, Inspection and Quarantine of the China.

Google Scholar

Shi, K., Wu, X., Liu, Z., and Dai, S. (2019). Coupled calculation model for anchoring force loss in a slope reinforced by a frame beam and anchor cables. Eng. Geol. 260 (3), 105245. doi:10.1016/j.enggeo.2019.105245

CrossRef Full Text | Google Scholar

Wang, L. Q., Xiao, T., Liu, S. L., Zhang, W. G., Yang, B. B., and Chen, L. C. (2023a). Quantification of model uncertainty and variability for landslide displacement prediction based on Monte Carlo simulation. Gondwana Res., doi:10.1016/j.gr.2023.03.006

CrossRef Full Text | Google Scholar

Wang, Y., Cao, Z., Li, P., and Yi, X. (2023b). On the fracture and energy characteristics of granite containing circular cavity under variable frequency-amplitude fatigue loads. Theor. Appl. Fract. Mech. 125, 103872. doi:10.1016/j.tafmec.2023.103872

CrossRef Full Text | Google Scholar

Wang, Y., Song, Z. Y., Mao, T. Q., and Zhu, C. (2022). Macro–meso fracture and instability behaviors of hollow-cylinder granite containing fissures subjected to freeze–thaw–fatigue loads. Rock Mech. Rock Eng. 55, 4051–4071. doi:10.1007/s00603-022-02860-5

CrossRef Full Text | Google Scholar

Xu, G., Bao, H., Wang, Q., and Xu, L. L. (2015). Study on the volume expansion rate of steel corrosion in concrete structures. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 43 (9), 105–109. doi:10.13245/j.hust.150920

CrossRef Full Text | Google Scholar

Yang, Z., Chen, S., Sun, J. L., Zheng, Y. B., Li, L. F., and Yuan, Y. (2022). Bar load-displacement curve model based on statistical damage mechanics. Front. Earth Sci. 10. doi:10.3389/feart.2022.1001777

CrossRef Full Text | Google Scholar

Zheng, J., Zeng, H. H., and Zhu, B. Z. (2010). Experimental study on the influence of corrosion on the mechanical properties of anchor cable. J. rock Mech. Eng. 29 (12), 2469–2474.

Google Scholar