Research on explosive damage effects of tungsten fiber-reinforced Zr-based bulk metallic glass matrix composite shell

1 Introduction

Explosive fragmentation projectiles rely on the explosion of the explosive to drive the metal shell to break and scatter, thereby generating high-speed fragments to damage the enemy. Therefore, the quantity, mass, and velocity of the fragments are important indicators that affect the destructive power of the projectile (Zhao et al., 2020). The shell is the source of fragment production, making it the most important component that affects the damage caused by explosive projectiles (Goto et al., 2008). Currently, the most commonly used material for shell is steel (Zhu et al., 2017; Wang et al., 2018; Li et al., 2021; Du et al., 2022a; Elshenawy et al., 2022), but due to different requirements for explosive fragmentation projectiles in different situations, more research is needed to develop shell materials to expand their application range.

Zr-based bulk metallic glasses are high-strength materials with a tendency to ignite, making them potential candidates for use as shell materials for explosive projectiles (Zhou et al., 2018; Yang et al., 2021; Shen et al., 2022; Cai et al., 2023). However, Zr-based bulk metallic glasses have low toughness and require fibers to enhance toughness for use as explosive projectile shells. Dandliker et al. (Dandliker et al., 1998) found that tungsten fibers have good interface wetting with Zr-based bulk metallic glasses through experimental research, and can be used as a reinforcing phase. The experiment proved that the compression strength of tungsten fiber reinforced Zr-based bulk metallic glasses matrix composite (WF/Zr-MG) is about 2,200 MPa, with a fracture strain of more than 14% (Zhang et al., 2013; Chen et al., 2017; 2020; Zhang et al., 2021; Du et al., 2022b), meeting the performance requirements for explosive projectiles. Compared with traditional steel materials, WF/Zr-MG has two advantages. Firstly, WF/Zr-MG is highly combustible, resulting in better damage effects from the fragments produced during the explosion (Du et al., 2016; Zhou et al., 2023). Secondly, WF/Zr-MG can be designed and modified by adjusting the fiber volume fraction or layout according to demand. However, no relevant research on the application of WF/Zr-MG as an explosive projectile shell has been seen so far.

Therefore, this study used the same size WF/Zr-MG shell for explosive experiments and compared it with traditional 40CrMnSiB steel. The explosive experiment was used to analyze the damage range and destructive power of WF/Zr-MG.

2 Setup of experiments and analysis of experimental results

2.1 Setup of experiments

Taking into account the aspect ratio of the shell of an explosive projectile, a simulated explosive shell with an outer diameter of 40 mm, height of 80 mm, and thickness of 4 mm was designed. The shell was made of WF/Zr-MG and 40CrMnSiB, as shown in Figure 1. The average weight of WF/Zr-MG and 40CrMnSiB shells is 613.0 g and 276.4 g, respectively, with densities of 16.93 g/cm³ and 7.63 g/cm³.

FIGURE 1

FIGURE 1. Shells made of (A) WF/Zr-MG, (B) 40CrMnSiB.

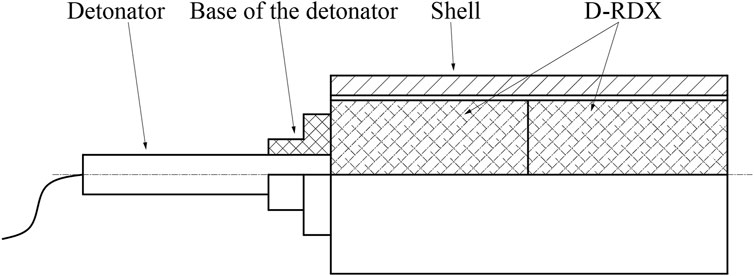
D-RDX (Desensitized- Royal demolition explosive) is used in the experiment, and the explosive column is shown in Figure 2. The dimensions of the explosive column were ∅30 mm × 40 mm, with a mass of 45 ± 0.1 g and a density of 1.62 ± 0.05 g/cm³ for each column. The projectile is shown in Figure 3, consisting of two columns of D-RDX placed within the shell. A detonator is placed at one end of the D-RDX column. The detonator is connected to the D-RDX column through a base of the detonator, ensuring that the detonator and D-RDX column are aligned steadily.

FIGURE 2

FIGURE 2. D-RDX.

FIGURE 3

FIGURE 3. Schematic of projectile.

The setup of the experiment is shown in Figure 4, with the shell height from the ground at 45 cm. To analyze the effect of the explosive shock wave on the range of the explosion and the formation and distribution of shell fragments for different shells, three 1 m × 1.25 m×2 mm 2A12 aluminum alloy targets are arranged around the shell to track the trajectory and quantity of fragments. The aluminum alloy targets are placed at distances of 3 m, 5 m, and 8 m from the shell, and are not obstructed by each other, ensuring the validity of the test results.

FIGURE 4

FIGURE 4. Setup of the experiment.

2.2 Analysis of experimental results

Four experiments were conducted, including two WF/Zr-MG shells (No. 1# and 2#) and two 40CrMnSiB shells (No. 3# and 4#). The aluminum alloy targets show that the explosion of the WF/Zr-MG shell resulted in a higher number of fragments compared to the explosion of the 40CrMnSiB shell, as shown in Figure 5 and Figure 6.

FIGURE 5

FIGURE 5. Fragments on the target at the distance of (A) 3 m, (B) 5 m, (C) 8 m penetrated by 2# shell.

FIGURE 6

FIGURE 6. Fragments on the target at the distance of (A) 3 m, (B) 5 m, (C) 8 m penetrated by 4# shell.

Furthermore, Figure 7 presents the magnified images of the fragments that penetrated the target plate at 3 m by the 2# and 4# shells, which indicates that the fragments produced by the WF/Zr-MG shell after the explosion are denser compared to those produced by the 40CrMnSiB shell. In addition, the fragments produced by the WF/Zr-MG shell have a smaller average size but a larger aspect ratio compared to those produced by the 40CrMnSiB shell.

FIGURE 7

FIGURE 7. Detailed of fragments on the target at the distance of 3 m penetrated by (A) 2# shell and (B) 4# shell.

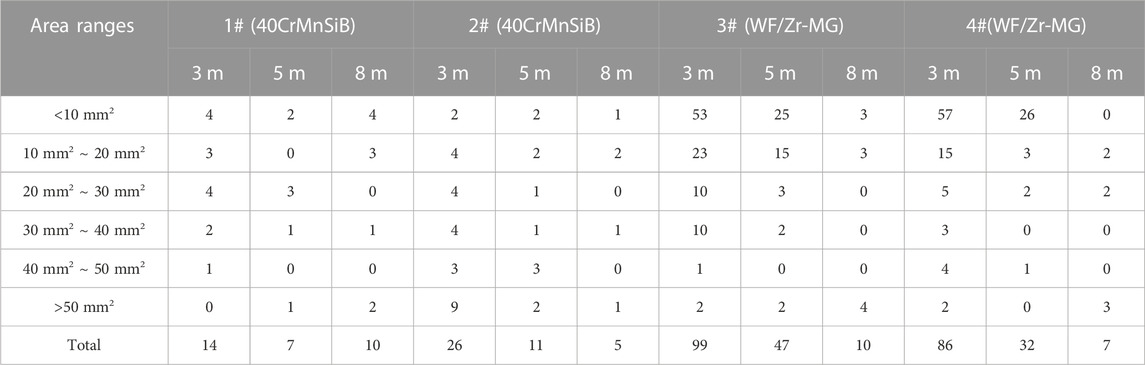
To further analyze the characteristics of the fragments generated after the explosion of the two materials, a statistical analysis of the number of perforations on the targets was conducted, and the dimensions of the perforations were measured. Table 1 presents the quantity of perforations in different area ranges on all targets, as well as the total number of perforations.

TABLE 1

TABLE 1. Quantity in different area ranges and total number of perforations on targets.

Table 1 indicates that the number of perforations on the targets at 3 m and 5 m distances after the explosion of the WF/Zr-MG shells is significantly higher than that of the 40CrMnSiB shells, while the number of perforations on the target at an 8 m distance is comparable to that of the 40CrMnSiB shells. Additionally, from Figures 5, 6, it can be observed that the distribution range of fragments generated by the WF/Zr-MG shells on the target plates at 3 m, 5 m, and 8 m distances is larger than that of the 40CrMnSiB shells.

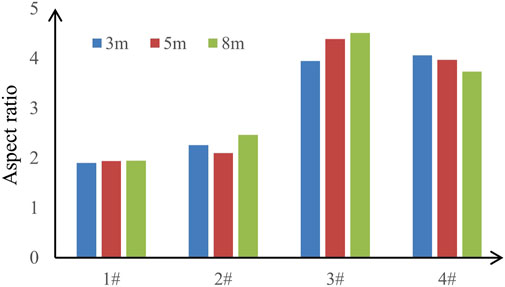
According to the dimensions of the perforations on the targets, the aspect ratio of the fragments generated by the four shells is calculated. The average aspect ratio of the fragments, as calculated from all the aluminum alloy targets, is presented in Figure 8. It can be observed from Figure 8 that the average aspect ratio of the fragments generated by the 40CrMnSiB shell is approximately 2, while the average aspect ratio of the fragments generated by the WF/Zr-MG shell is approximately 4, twice that of the fragments generated by the 40CrMnSiB shell.

FIGURE 8

FIGURE 8. Average aspect ratio of the fragments.

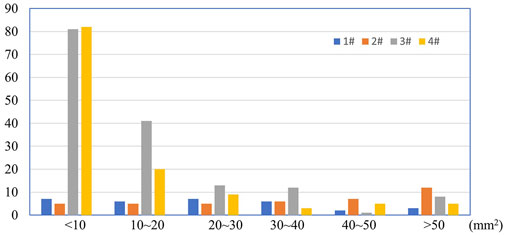
To further compare and analyze the quantity of fragments produced by the two materials after the explosion, the number of perforations on the target plates at distances of 3 m, 5 m, and 8 m was combined, as shown in Figure 9. From Figure 9, it can be observed that the number of fragments with perforations smaller than 20 mm² generated by the WF/Zr-MG shells is significantly higher than those produced by the 40CrMnSiB steel shell after the explosion. The quantity of fragments with perforations ranging from 20 to 30 mm² generated by the WF/Zr-MG shells is also greater than those produced by the 40CrMnSiB steel shell, approximately twice as many. The number of fragments with perforations larger than 30 mm² generated by both the WF/Zr-MG shells and the 40CrMnSiB steel shell is relatively equal. The statistical results from Figure 9 reveal that the WF/Zr-MG shells produce a large quantity of small-sized fragments, while the quantity of large-sized fragments is comparable to that of the 40CrMnSiB steel shell. Therefore, WF/Zr-MG is more suitable for applications requiring the generation of small-sized fragments in explosive ammunition compared to 40CrMnSiB steel.

FIGURE 9

FIGURE 9. Area of the bullet hole.

When facing heavily armored targets, large-sized fragments often play a deterministic role compared to small-sized fragments. Therefore, it is necessary to compare the ability of WF/Zr-MG and 40CrMnSiB steel materials to produce large-sized fragments. As shown in Table 1, for 1# and 2# 40CrMnSiB steel shells, a total of 3 and 12 fragments with perforation areas larger than 50 mm² were observed on three target plates, while for 3# and 4# WF/Zr-MG shells, a total of 8 and 5 fragments with perforation areas larger than 50 mm² were observed on three target plates. This indicates that the quantity of large-sized fragments generated by WF/Zr-MG steel shells and 40CrMnSiB shells is comparable. However, when looking at the number of individual fragments, among all the perforations, the largest area of fragments produced by the 40CrMnSiB steel shell is approximately 128 mm², while the largest perforation area produced by the WF/Zr-MG shell is 168 mm², as shown in Figure 10 and Figure 11. Therefore, from the perspective of the largest mass of fragments, it is found that the WF/Zr-MG is capable of producing larger fragments than the 40CrMnSiB steel shell, thus possessing greater penetration capability.

FIGURE 10

FIGURE 10. Large bullet holes caused by the fragmentation of 40CrMnSiB steel shell. (A) the largest bullet hole from the 1# shell, (B) the largest bullet hole from the 2# shell.

FIGURE 11

FIGURE 11. Large bullet holes caused by the fragmentation of WF/Zr-MG shell. (A) the largest bullet hole from the 3# shell, (B) the largest bullet hole from the 4# shell.

Therefore, from the experimental results, it can be concluded that WF/Zr-MG has a higher number of fragments and destructive power than the 40CrMnSiB in a small range as a warhead shell. In a far distance range, its number of fragments and destructive power are comparable to those of 40CrMnSiB.

3 Explosive fracture mechanism of WF/Zr-MG shell

From Figure 7, Figure 10, and Figure 11, it can be observed that the shapes of the fragments generated after the explosion of the WF/Zr-MG shell differ from those generated after the explosion of the 40CrMnSiB shell. The majority of fragments produced by the 40CrMnSiB shell explosion have an elliptical shape with a relatively small aspect ratio, while the majority of fragments produced by the WF/Zr-MG shell explosion are rectangular with a larger aspect ratio. This demonstrates that the WF/Zr-MG shell and the 40CrMnSiB shell have different fracture modes under explosive loading conditions, leading to the generation of different fragment shapes.

WF/Zr-MG material is a unidirectional fiber-reinforced composite, making it anisotropic. Experimental results confirm that the compressive strength along the fiber direction of WF/Zr-MG material is approximately 2 GPa, the tensile strength along the fiber direction is approximately 1 GPa, and the tensile strength perpendicular to the fiber direction is only 253 MPa (Zhang et al., 2014). Due to the lower tensile strength in the perpendicular fiber direction of WF/Zr-MG, the material experiences rapid circumferential fracture under the action of explosive loading. As the explosive load continues to apply, the fractured WF/Zr-MG material is subjected to tensile stress along the fiber direction that exceeds its tensile strength, resulting in material fracture. Since the material has lower strength perpendicular to the fiber direction and the explosive load is high, circumferential fracture occurs easily, leading to the formation of multiple cracks. On the other hand, the high tensile strength along the fiber direction results in smaller fractions of fractures in that direction, resulting in the generation of fragments with a larger aspect ratio, as shown in Figure 12.

FIGURE 12

FIGURE 12. WF/Zr-MG fragments embedded in protective steel plate.

3.1 Theoretical calculation of shell breaking under dynamic pressure

Assuming the material density ${\rho }_0$ remains constant during the expansion process of the shell, the motion equation and continuity equation can be respectively expressed as follows (Wang, 2019):

$\frac{\partial {\sigma }_r}{\partial r}-\upsilon \frac{{\sigma }_{\theta }-{\sigma }_r}{r}={\rho }_0\frac{d{v}_r}{dt}(1)$

$\frac{\partial v_r}{\partial r}+\upsilon \frac{v_r}{r}=0(2)$

where ${\sigma }_{\theta }$ and ${\sigma }_r$ represent the instantaneous stress of an arbitrary infinitesimal element within the shell, $r$ represents the instantaneous radius of a particular point inside the shell, as illustrated in Figure 13. $\upsilon$ is the shape factor of the shell, which, for the cylindrical shell used in this experiment, is determined by $\upsilon =1$.

FIGURE 13

FIGURE 13. The stress state on an infinitesimal element within a cylindrical shell.

The yield condition of the material can be expressed as follows:

${\sigma }_{\theta }-{\sigma }_r=\lambda {\sigma }_y(3)$

In the equation, ${\sigma }_y$ represents the yield limit of the material, $\lambda$ denotes the calculation coefficient. In this calculation, the Tresca criterion is employed; therefore $\lambda =1$, which implies ${\sigma }_{\theta }-{\sigma }_r={\sigma }_y$.

Substituting Equation 3 into Equation 1 and integrating with respect to $r$, while $r=a$, ${\sigma }_r=-p$, where $p$ represents the pressure of the explosive products inside the shell, the following equation can be obtained:

${\sigma }_r=-p+{\sigma }_y\ln \frac{r}{a}+{\rho }_0\left(a\ddot{a}+{\dot{a}}^2\right)\ln \frac{r}{a}+{\rho }_0\left(\frac{a^2{\dot{a}}^2}{2r^2}-\frac{{\dot{a}}^2}{2}\right)(4)$

The initial pressure on the surface within the shell is equal to the average pressure of the gas products at the moment of instantaneous explosion of the explosive.

$p_0=\frac{0.5{\rho }_e{D}_e^2}{\gamma +1}(5)$

The pressure variation experienced by the surface within the shell follows the expansion behaviour of the explosive products

$p=p_0{\left(\frac{a_0}{a}\right)}^{2\gamma }(6)$

In the equation, $a_0$ represent the initial inner radius of the shell, $a$ represent the inner radius of the shell during expansion. ${\rho }_e$ and $D_e$ represent the density and detonation velocity of the explosive, $\gamma$ represents the adiabatic index of the explosive. For the D-RDX used in this experiment, the density is ${\rho }_e$ = 1.65 g/cm³, the detonation velocity is $D_e$ = 8,180 m/s, and the adiabatic index is $\gamma =1.26$ (Wang, 2019). Based on these parameters, the initial pressure inside the shell during the explosion of the explosive in this experiment can be calculated to be $p_0$ = 24.4 GPa.

Based on Taylor’s assumption (Taylor, 1963; Held, 2010) that radial cracks can only be stretched circumferentially on the outer surface of the shell, the boundary condition ${\sigma }_{\theta }=k{\sigma }_B$ can be obtained, where $k$ is the fracture coefficient and ${\sigma }_B$ is the material’s tensile strength,

${\sigma }_{\mathrm{r}}=k{\sigma }_{\mathrm{B}}-\lambda {\sigma }_{\mathrm{y}}(7)$

According to the end effect theory, when the explosive detonates, as the expands of the shell, it undergoes plastic deformation and forms fragments when the internal pressure $P$ drops to the yield limit of the material. When the shell is completely broken, the boundary condition is $r=a_f$ and ${\sigma }_r=-P_f$, where $a_f$ is the expansion radius of the shell at the moment of fragmentation, and $p_f$ is the critical pressure for shell fragmentation. Substituting Equation 7 into Equation 4, it can be derived that

$p_f=\lambda {\sigma }_y-k{\sigma }_B(8)$

Equation 8 demonstrates that, the failure of a monolith is not only influenced by the material’s yield limit but also by its strength limit. Furthermore, consideration must be given to the monolith’s shape and its corresponding yield conditions. According to the Taylor critical stress fracture criterion, when the shell is completely fractured, $k$ is determined as.

$k=\left(\lambda -1\right)\frac{{\sigma }_y}{{\sigma }_B}(9)$

Combining Eq.8 and 6, and the Tresca criterion, the expansion radius of a shell material at the moment of fragmentation can be expressed as

$a_f=a_0{\left[\frac{p_0}{{\sigma }_{\mathrm{y}}}\right]}^{1/2\gamma }(10)$

Based on the relevant experimental results, the yield strength of 40CrMnSiB steel and WF/Zr-MG are 850 MPa and 253 MPa (Zhang et al., 2014), respectively. Therefore, the fracture diameters of the 40CrMnSiB steel shell and the WF/Zr-MG shell can be calculated as 60.62 mm and 98.07 mm, respectively.

Under the action of explosive loads, the warhead shell expands outward. Assuming that the initial shell radius and wall thickness of the expansion are $a_0$ and ${\delta }_o$, respectively, according to the law of constant volume for the shell:

${\left(a_f+\delta \right)}^2-a_f^2={\left(a_0+{\delta }_o\right)}^2-a_0^2(11)$

The thickness of the shell at the moment of rupture will be:

$\delta =\sqrt{{\left({\delta }_0+a_0\right)}^2+a_0^2\left({\epsilon }^2-1\right)}-a_0\epsilon (12)$

where

$\epsilon ={\left[\frac{E{\rho }_e\left(\gamma -1\right)}{{\sigma }_y}\right]}^{1/2\gamma }(13)$

$\epsilon$ is the ratio of the radius at the moment of shell rupture:

Mott and Linfoot (Mott and Linfoot, 1943) proposed that the energy W required per unit area of shell thickness at the moment when a crack is formed is:

$W=\frac{1}{24}{\rho }_0{v}_0^2\frac{l_2^3}{a_f^2}(14)$

Based on experimental results, the value of W for most metallic materials ranges from 14.7 to 168 J/cm². It should be noted that due to the extensive use of modern advanced materials, their material properties have significantly improved, and the corresponding critical energy value for crack failure, W may exceed this range. The determination of the specific value of W can be accomplished through experimental and theoretical methods (Wang, 2019).

$W=\frac{E\left(2\gamma -1\right)\left[{\left(1+\beta \right)}^{\frac{\gamma -1}{\gamma }}-1\right]}{\delta l\left(\gamma -1\right)\left[{\left(1+\beta \right)}^{\frac{2\gamma -1}{\gamma }}-1\right]}\left[1-{\left(\frac{a_0}{a_i}\right)}^{2\left(\gamma -1\right)}\right](15)$

In the equation, $E$ is Gauney constant, $E=4015778{\mathrm{m}}^2{/\mathrm{s}}^2$ (Wang, 2019), $\beta =C/M$ represents the mass ratio of the explosive to the shell, ${\alpha }_i$ represents the radius of the shell during the expansion process, and l represents the calculated effective length of the warhead. With the known parameters of the shell and the value of W, once the initial velocity v₀ of the fragments is obtained, the average width l₂ of the warhead fragments can be determined.

Although the theoretical calculation formulas mentioned above are commonly employed to calculate fragment sizes generated by homogeneous materials during shell explosions, WF/Zr-MG is a heterogeneous material. However, due to its unidirectional fiber reinforcement, the WF/Zr-MG shell experiences only radial forces during the explosive propulsion process, rendering the fibers inactive. Consequently, for analytical purposes, WF/Zr-MG can be treated as a homogeneous material.

According to Eq. 14 and 15, the average width of fragments from the 40CrMnSiB steel shell after expansion is 1.01 mm, while that of the WF/Zr-MG shell is 0.67 mm. Compared to 40CrMnSiB steel shells, WF/Zr-MG shells have better fragmentation effects and are more likely to tear and break under the expansive force of the shock wave. However, relative to 40CrMnSiB steel, the WF/Zr-MG shells have a shorter expansion time under the shock wave and initial fragment velocities will be smaller.

3.2 Calculation of initial velocity of fragments

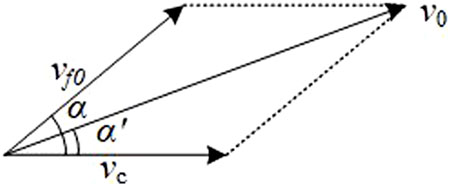
According to the theory of terminal effect (Wang, 2019), the classical Gruneisen formula does not include relevant parameters such as the strength of materials used of the shell, it is not suitable for calculating the initial velocity of the composite shell in this case. The influence of the shell material mainly manifests in plastic deformation. A shell with good plasticity does not rupture even when its inner radius expands to the maximum critical radius under the action of explosion products, and thus can achieve greater acceleration. On the other hand, a shell with poor plasticity will rupture before it reaches its maximum velocity under the action of the explosion products. Relevant literature suggests that the initial velocity model of a shell fragment at the moment of rupture can be expressed as follows (Wang et al., 2015; Wang, 2019):

$v_0=\sqrt{\frac{2}{2+\beta }\left[\frac{{\mathrm{D}}_e\beta }{8}\right]\left(1-\frac{a_0^4}{a_f^4}\right)-\frac{S_{0}A{Y}_s}{M{a}_0}\cdot \ln \frac{a_f}{a_0}}(16)$

Here, $A$ is a constant, $S_0$ is the inner surface area of the shell, $a_0$ and $a_f$ are the initial inner radius and critical fracture expansion inner radius of the shell, respectively, and $Y_s$ is the dynamic tensile strength of the shell.

Compared to the 40CrMnSiB shell, the radial tensile strength of WF/Zr-MG is lower. During the expansion of the explosive gases, the WF/Zr-MG shell experiences a faster fragmentation rate and shorter acceleration time of the fragments, resulting in a lower initial velocity. After calculation, the initial velocities of the two types of shells are as follows: the initial velocity of the 40CrMnSiB steel shell fragment is 1,332 m/s, while that of the WF/Zr-MG shell fragment is 908 m/s.

The storage capability and flight performance of the fragments are related to factors such as the shape, mass, and windward area of the fragments. Relevant empirical formulas suggest that (Wang et al., 2015; Wang, 2019):

$V=V_0\exp \left(-\frac{C_x{\rho }_{0}K}{2m_f^{1/3}}R\right)(17)$

Here, $V_0$ is the initial velocity of the fragment, $C_x$ is the air resistance coefficient, which can be determined based on the shape of the fragment collected from experiments. The fragments resulting from 40CrMnSiB shells tend to form irregular shapes, while the fragments resulting from WF/Zr-MG shells tend to be composed of shattered long strip-shaped tungsten fibers and bonding phases. Wang performed curve fitting of the $C_x$ values for different fragment shapes, determining a $C_x$ value of 1.3 for regular rectangular or diamond-shaped fragments and 1.5 for irregular fragments. Therefore, a value of 1.5 is chosen for the fragments resulting from 40CrMnSiB shells, while a value of 1.3 is chosen for WF/Zr-MG shells. ${\rho }_0$ is the air density, $R$ is the flight attenuation distance of the fragment, $K$ is the shape coefficient of the fragment, which is 4.5 × 10⁻³ for 40CrMnSiB steel fragments and 3.3 × 10⁻³ for WF/Zr-MG fragments, and $m_{\mathrm{f}}$ is the mass of the calculated fragment. The attenuation law of the formed fragment velocity with distance for the two types of shell materials can be calculated as shown in Figure 14.

FIGURE 14

FIGURE 14. Decay of flight velocity of fragments.

4 Discussion

4.1 Damage criterion of fragments on light armored vehicles

The probability of damage to a vehicle by fragments is determined by a linear probability distribution function and a penetration fragment density criterion, which can be expressed as follows (Wang, 2019):

$\mathrm{P}=\left\{\begin{array}{l}0\left(\epsilon \left(r\right)=0\right)\\ \frac{\epsilon \left(r\right)}{\epsilon \left(c\right)}\left(0<\epsilon \left(r\right)<\epsilon \left(c\right)\right)\\ 1\left(\epsilon \left(r\right)>\epsilon \left(c\right)\right)\end{array}\right.(18)$

Here, $\epsilon \left(c\right)$ is the damage criterion for warheads against typical targets. According to relevant literature, the damage criterion for fragments against light armored vehicles is 4–8 pieces/m² (Wang et al., 2017). In this case, the damage criterion is taken as $\epsilon \left(c\right)=6\text{ pieces}/{\mathrm{m}}^2$. By substituting Eq. 7 and 8 into formula Eq. (9), we get the damage criterion of the 40CrMnSiB shells (Eq. 10) and the WF/Zr-MG shells Eq. 11 (Wang, 2019)

$\mathrm{P}=\left\{\begin{array}{l}0\left(47.2e^{-\frac{\mathrm{R}}{2.54}}+0.8=0\right)\\ \frac{47.2e^{-\frac{\mathrm{R}}{2.54}}+0.8}{6}\left(0<\epsilon \left(r\right)<6\right)\\ 1\left(47.2e^{-\frac{\mathrm{R}}{2.54}}+0.8>6\right)\end{array}\right.(19)$

$\mathrm{P}=\left\{\begin{array}{l}0\left(223e^{-\frac{\mathrm{R}}{3}}-8.84=0\right)\\ \frac{223e^{-\frac{\mathrm{R}}{3}}-8.84}{6}\left(0<\epsilon \left(r\right)<6\right)\\ 1\left(223e^{-\frac{\mathrm{R}}{3}}-8.84>6\right)\end{array}\right.(20)$

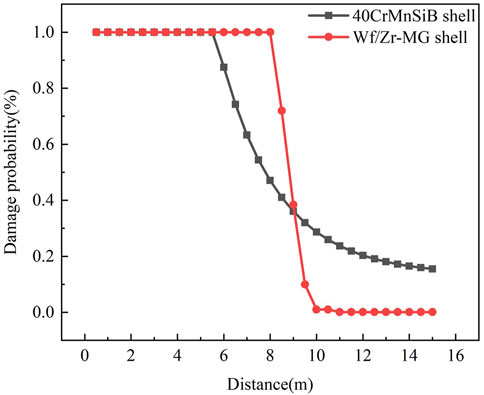
According to Eq. 10 and 11, the probability of damage to light armored vehicles by 40CrMnSiB shells and WF/Zr-MG shells can be calculated, as shown in Figure 15. It can be seen from Figure 15 that the determined damage range of 40CrMnSiB shells to armored vehicles is 6 m, while that of WF/Zr-MG shells is 8 m. Therefore, the determined damage range of WF/Zr-MG shells to light armored vehicles is 33% higher than that of 40CrMnSiB shells.

FIGURE 15

FIGURE 15. Damage criterion of the 40CrMnSiB shells and the WF/Zr-MG shells.

4.2 Effective interception radius

The corresponding circular radius $R_0$, which represents the effective interception, is referred to as the interception radius. The meaning of $R_0$ is as follows: On the circumference of this radius, the targets are intercepted, with an average of one fragment hitting each intercepted target.

When considering the projectile velocity $v_c$, the dynamic initial velocity $v_0$ of the fragments is (Wang, 2019):

$v_0=\sqrt{v_{f0}^2+v_c^2+2v_{f0}{v}_c\cos \alpha }(21)$

where is $\alpha$ is the angle between the projectile velocity $v_c$ and the fragment velocity $v_{f0}$, as shown in Figure 16.

FIGURE 16

FIGURE 16. Synthesis of fragment initial velocity.

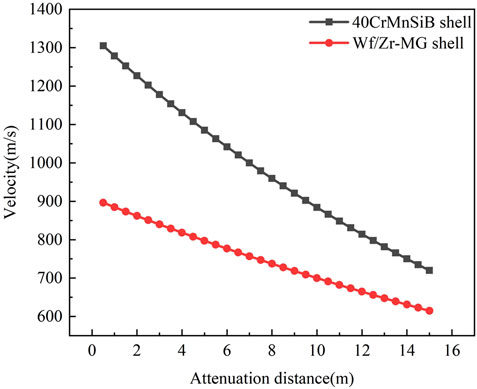
Considering air resistance, the velocity of the fragments during motion decays exponentially, as follows:

$v=v_0{e}^{-\xi R}(22)$

In the equation, $\xi$ represents the velocity decay coefficient, $R$ denotes the flight distance, and represents the initial dynamic velocity of the fragments. The coefficient $\xi$ can be expressed as:

$\xi =\frac{C_D\overline{s}{\rho }_{a}gR}{2m_p}(23)$

where $m_p$ represents the mass of the fragments, $C_D$ represents the air resistance coefficient during fragment flight, $\overline{s}$ represents the frontal area of the fragments, and ${\rho }_a$ represents the air density.It can be set

$H=\frac{2}{C_D{\rho }_{a}gK}(24)$

The coefficient H, commonly referred to as the conformal coefficient, is primarily determined by the shape of the fragments and greatly influences their ability to retain velocity. For irregular steel fragments, H is approximately 230. Finally, we obtain (Wang, 2019)

$v=v_0{e}^{\left(-\frac{R}{H{m}_p^{1/3}}\right)}(25)$

Assuming that the target intercepted by the shell is an incoming aircraft and the projectile’s terminal velocity is 700 m/s, we can calculate the effective interception radius of different weight fragments for both the 40CrMnSiB and WF/Zr-MG shells based on Eqs 23–25, as shown in Figure 17. From Figure 17, it can be observed that under the same conditions, using WF/Zr-MG material as the shell results in an approximately 20% higher effective interception radius compared to the 40CrMnSiB shell.

FIGURE 17

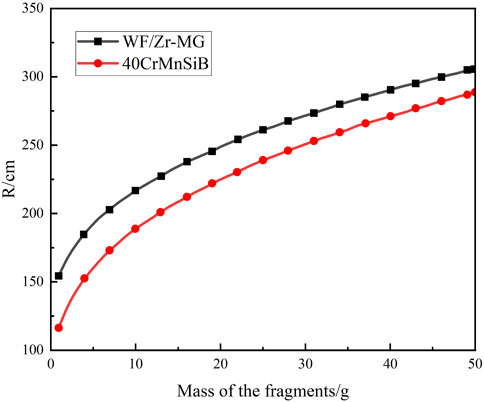
FIGURE 17. Effective interception radius of 40CrMnSiB and WF/Zr-MG shell with different weights of fragments.

5 Conclusion

This study conducted static blast experiments using WF/Zr-MG shells and theoretically calculated the fragment velocity and destructive power under explosion conditions. A comparison was made with traditional 40CrMnSiB steel shells, and the following conclusions were drawn:

(1) As a warhead shell, the WF/Zr-MG shells produce more fragments on targets at a distance of 3 m and 5 m than 40CrMnSiB steel shells, and produce the same amount of fragments on targets at a distance of at 8 m as 40CrMnSiB steel shells. The WF/Zr-MG shell generates the highest number of fragments smaller than 10 mm². Additionally, the fragments produced by the WF/Zr-MG shell differ in shape from those generated by the 40CrMnSiB shell, with the aspect ratio of WF/Zr-MG fragments being approximately twice that of 40CrMnSiB fragments.

(2) Theoretical calculations demonstrate that the lower transverse tensile strength of WF/Zr-MG results in lower initial velocities and smaller fragment sizes. Due to the fracture characteristics of WF/Zr-MG, it generates a higher number of fragments, resulting in approximately 25% higher damage to armored vehicles and around a 20% larger interception range for airborne targets when used as a shell material.

(3) The experimental results have demonstrated that the fragments produced by WF/Zr-MG exhibit superior damage ability compared to 40CrMnSiB. Therefore, WF/Zr-MG can be applied for the shell of explosive fragmentation projectiles.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

BX: conceptualization, methodology, investigation, writing-original draft; CD: methodology, writing and editing; ZD: validation, resources; HF: resources and methodology; ZZ: resources and methodology; FZ: methodology. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundations of China (Grant No. 12102201).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, A. H., Zhou, G., Li, P. W., Ding, D. W., An, Q., Zhou, G. J., et al. (2023). Mechanical properties for a series of zr-based bulk metallic glasses. J. Alloy. Compd. 938, 168579. doi:10.1016/j.jallcom.2022.168579

CrossRef Full Text | Google Scholar

Chen, G., Hao, Y., Chen, X., and Hao, H. (2017). Compressive behaviour of tungsten fibre reinforced zr-based metallic glass at different strain rates and temperatures. Int. J. Impact Eng. 106, 110–119. doi:10.1016/j.ijimpeng.2017.03.017

CrossRef Full Text | Google Scholar

Chen, S., Li, W. Q., Zhang, L., Fu, H. M., Li, Z. K., Zhu, Z. W., et al. (2020). Dynamic compressive mechanical properties of the spiral tungsten wire reinforced zr-based bulk metallic glass composites. Compos. Part B Eng. 199, 108219. doi:10.1016/j.compositesb.2020.108219

CrossRef Full Text | Google Scholar

Dandliker, R. B., Conner, R. D., and Johnson, W. L. (1998). Melt infiltration casting of bulk metallic-glass matrix composites. J. Mater. Res. 13 (10), 2896–2901. doi:10.1557/JMR.1998.0396

CrossRef Full Text | Google Scholar

Du, C., Du, Z., Wang, K., Dai, W., Gao, G., Zhu, Z., et al. (2022a). Effect of tungsten fiber diameter on the dynamic compression properties of tungsten fiber/zr-based bulk metallic glasses matrix composite. Int. J. Impact Eng. 164, 104185. doi:10.1016/j.ijimpeng.2022.104185

CrossRef Full Text | Google Scholar

Du, X., Liu, J., Shi, Y., and Liu, D. (2022b). The study on laser composite processing of pre-controlled crack in low carbon steel. J. Manuf. Process. 76, 79–92. doi:10.1016/j.jmapro.2022.01.062

CrossRef Full Text | Google Scholar

Du, Z., Du, C., Zhu, Z., and Xiang, X. (2016). Discrepancy between blood gas concentration measurements and carbon dioxide removal rate. Rare Metal. Mat. Eng;45(05):1308–1309. doi:10.1007/s00134-016-4397-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Elshenawy, T., Zaky, M. G., and Elbeih, A. (2022). Experimental and numerical studies of fragmentation shells filled with advanced hmx-plastic explosive compared to various explosive charges. Braz. J. Chem. Eng. 40, 481–492. doi:10.1007/s43153-022-00267-x

CrossRef Full Text | Google Scholar

Goto, D. M., Becker, R., Orzechowski, T. J., Springer, H. K., Sunwoo, A. J., and Syn, C. K. (2008). Investigation of the fracture and fragmentation of explosively driven rings and cylinders. Int. J. Impact Eng. 35 (12), 1547–1556. doi:10.1016/j.ijimpeng.2008.07.081

CrossRef Full Text | Google Scholar

Held, M. (2010). Fragment mass distribution of he projectiles. Propellants Explos. Pyrotech. 15 (6), 254–260. doi:10.1002/prep.19900150606

CrossRef Full Text | Google Scholar

Li, W., Chen, Z., Wang, X., and Li, W. (2021). Research on the intermediate phase of 40crmnsib steel shell under different heat treatments. Def. Technol. 17 (3), 1032–1041. doi:10.1016/j.dt.2020.06.009

CrossRef Full Text | Google Scholar

Mott, N. F., and Linfoot, E. H. (1943). A theory of fragmentation. China: BRISTOL UNIV BRISTOL United Kingdom. (Reprinted.

Google Scholar

Shen, G., Li, W., Ma, Z., Zhao, S., Liu, D., Zhao, H., et al. (2022). Mechanical size effect and serrated flow of various zr-based bulk metallic glasses. Intermetallics 151, 107737. doi:10.1016/j.intermet.2022.107737

CrossRef Full Text | Google Scholar

Taylor, G. I. (1963). Fragmentation of tubular bombs: Science papers of sir g i taylor. London: Cambridge University Press. (Reprinted.

Google Scholar

Wang, S. (2019). Terminal effects. Beijing: Science Press. (In Chinese)

Google Scholar

Wang, S., Han, X., and Wang, X. (2017). Research on evaluation method of comprehensive power of high explosive warhead and its application. Acta Armamentarii 38 (7), 1249. doi:10.3969/j.issn.1000-1093.2017.07.001

CrossRef Full Text | Google Scholar

Wang, X., Wang, S., and Ma, F. (2018). Experimental study on the expansion of metal cylinders by detonation. Int. J. Impact Eng. 114, 147–152. doi:10.1016/j.ijimpeng.2017.12.017

CrossRef Full Text | Google Scholar

Wang, X., Wang, S., Xu, Y., and Hu, S. (2015). The energy conversion and fragment initial velocity model of metal cylinder driven by detonation. Acta Armamentarii 36 (8), 1417.

Google Scholar

Yang, W., Liu, Y., Hua, N., Pang, S., Li, Y., Liaw, P. K., et al. (2021). Formation and properties of biocompatible ti-based bulk metallic glasses in the ti–cu–zr–fe–sn–si–ag system. J. Non-Cryst. Solids. 571, 121060. doi:10.1016/j.jnoncrysol.2021.121060

CrossRef Full Text | Google Scholar

Zhang, B., Fu, H., Li, Z., Zhu, Z., Zhang, H., and Hu, Z. (2014). Anisotropic tensile properties of tungsten fiber reinforced zr based metallic glass composites. Mater. Sci. Eng. A 619, 165–170. doi:10.1016/j.msea.2014.09.084

CrossRef Full Text | Google Scholar

Zhang, B. Y., Chen, X. H., Wang, S. S., Lin, D. Y., and Hui, X. D. (2013). High strength tungsten wire reinforced zr-based bulk metallic glass matrix composites prepared by continuous infiltration process. Mater. Lett. 93, 210–214. doi:10.1016/j.matlet.2012.11.086

CrossRef Full Text | Google Scholar

Zhang, Z., Kong, J., Liu, X., Song, X., and Dong, K. (2021). Preparation, microstructure and mechanical properties of tungsten fiber reinforced laalcuni metallic glass matrix composites. Intermetallics 132, 107139. doi:10.1016/j.intermet.2021.107139

CrossRef Full Text | Google Scholar

Zhao, C., Wang, S., Guo, C., Liu, D., and Ma, F. (2020). Experimental study on fragmentation of explosive loaded steel projectile. Int. J. Impact Eng. 144, 103610. doi:10.1016/j.ijimpeng.2020.103610

CrossRef Full Text | Google Scholar

Zhou, D., Hou, B., Li, B., Zhang, S., Dai, L., and Li, Y. (2018). A comparative study of the rate effect on deformation mode in ductile and brittle bulk metallic glasses. Intermetallics 96, 94–103. doi:10.1016/j.intermet.2018.01.020

CrossRef Full Text | Google Scholar

Zhou, F., Du, C., Cheng, C., Xu, L., Du, Z., Gao, G., et al. (2023). Penetration performance and fragmentation mechanism behind target of tungsten fibre/zirconium-based bulk metallic glass matrix composite rod. Int. J. Refract. Metals Hard Mater. 112, 106160. doi:10.1016/j.ijrmhm.2023.106160

CrossRef Full Text | Google Scholar

Zhu, J., Li, W., Wang, X., and Li, W. (2017). Effect of tempering temperature on expansion and fracture mechanism of 40crmnsib steel cylinder shell. Int. J. Impact Eng. 107, 38–46. doi:10.1016/j.ijimpeng.2017.05.007

CrossRef Full Text | Google Scholar