- 1Department of Mathematics, Amrita School of Engineering, Amrita Vishwa Vidyapeetham, Bengaluru, India
- 2Department of Studies in Mathematics, Davangere University, Davangere, India
- 3Department of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Bangi, Selangor, Malaysia
- 4Department of Computer Science and Mathematics, Lebanese American University, Byblos, Lebanon
- 5Department of Mathematics and Social Sciences, Sukkur IBA University, Sukkur, Sindh, Pakistan
- 6Department of Mechanical Engineering and University Centre for Research and Development, Chandigarh University, Mohali, Punjab, India
- 7Mechanical Engineering Department, College of Engineering, King Saud University, Riyadh, Saudi Arabia
- 8Department of Mechanical Engineering, University of West Attica, Athens, Greece
- 9Mechanical Engineering, Future University in Egypt, New Cairo, Egypt
- 10Department of Mathematics, CVR College of Engineering, Rangareddy, India
This study examines the effects of a porous media and thermal radiation on Casson-based nano liquid movement over a curved extending surface. The governing equations are simplified into a system of ODEs (ordinary differential equations) using the appropriate similarity variables. The numerical outcomes are obtained using the shooting method and Runge-Kutta Fehlbergs fourth-fifth order (RKF-45). An analysis is conducted to discuss the impact of significant nondimensional constraints on the thermal and velocity profiles. The findings show that the rise in curvature constraint will improve the velocity but diminish the temperature. The increased values of the modified Hartmann number raise the velocity, but a reverse trend is seen for increased porosity parameter values. Thermal radiation raises the temperature, while modified Hartmann numbers and the Casson factor lower the velocity but raise the thermal profile. Moreover, the existence of porous and solid fractions minimizes the surface drag force, and radiation and solid fraction components enhance the rate of thermal dispersion. The findings of this research may have potential applications in the design of heat exchangers used in cooling electronic devices like CPUs and GPUs, as well as microscale engines such as microturbines and micro-heat engines.
1 Introduction
Fluid flow past a curved stretching sheet (CSS) is a classical fluid mechanics problem with numerous applications in engineering and physics. Investigating nanofluid flow over curved stretched sheets has become an attractive field of study due to its many useful applications, such as cooling in electronic devices, heat exchangers, processing of materials, solar collectors, synthesis of polymers, and microelectronic devices. The behavior of the fluid in this scenario depends on several factors, including the geometry of the surface, the velocity of the stretching motion, and the properties of the fluid itself. Madhukesh et al. (Madhukesh et al., 2021) investigated the Newtonian heating (NH) and non-Fourier heat flux (NFHF) effect on the CSS in the presence of HNF (hybrid nanofluid). Multiple slippages on hydro-magnetic dissipative fluid across a CSS were addressed by Aihem et al. (Duraihem et al., 2023) and discussed their enhanced thermal and mass transmission properties. The impact of Cross dispersion on MHD Casson liquid movement along a CSS was inspected by Lakshmi et al. (Lakshmi et al., 2022). Sakkaravarthi et al. (Sakkaravarthi and Reddy, 2023) made a numerical investigation on entropy formation over a CHNF circulation over CSS. Simulation and theoretical inquiry on CNF over a CSS with the impact of a magnetic field and chemical processes were examined by Kumar et al. (Varun Kumar et al., 2022).
An electromagnetic actuator is a tool used in fluid mechanics to produce an effective liquid motion. A planar surface known as the Riga plate (RP) comprises alternating permanent magnets and electrodes. The magnetic field on the RP is not uniform, producing a Lorentz force that propels the fluid flow. In 1999, Gailitis and Lielausis (Gailitis and Lielausis, 1961) presented the electromagnetic actuator’s basic theory for the first time. In contrast to typical techniques, they showed that employing electrodes and permanent magnets on a Riga plate may considerably increase the fluid flow rate and mixing capabilities. The advantage of employing an electromagnetic actuator to produce liquid flow is that it can do so without the need for mechanical actuators or movable components, which may be costly and prone to failure. Consequently, it is a viable solution for various practical purposes such as improving the exchange of heat, combining, and liquid flow. Asogwa et al. (Asogwa et al., 2022) examined analytical approaches to cross-diffusion and convection effects in the presence of CF over a porous RP. Hussain et al. (Hussain et al., 2022) investigated the impact of the Navier slip on an upward RP with CF displacement. Madhukesh et al. (Madhukesh et al., 2022a) investigated TPD and heat generation of Newtonian NF in an RP. Alshehri as al. (Mohammed Alshehri et al., 2021). Investigated Buoyancy implications in a Micropolar solution over an upward RP.
A nanofluid is a liquid with individual nanoparticles suspended in a solvent. Increased transfer of heat efficiency is a significant benefit of nanofluids over more traditional fluids. Increased thermal conductivity due to nanoparticles in the base fluid makes nanofluids excellent for thermal transfer medium. Nanofluids remain an intriguing field of study because of their revolutionary effects on a wide range of businesses and technology. The use of the change of variables approaches in the hydrothermal investigation of MHD compressing nanofluid circulation in parallel plates was studied by Zabihi et al. (Zabihi et al., 2022). Rizk et al. (Rizk et al., 2022) assessed the influence of the KKL correlation hypothesis on the production of thermal energies in a nanofluid comprising GO and ZnO dissolved in water passing via a permeable vertically spinning substrate. Shah et al. (Shah et al., 2021) researched mesoscopic modelling for magnetized nanofluid movement inside a porous three-dimensional tank. Ullah et al. (Ullah et al., 2022) scrutinized a magnetized 2D nanofluid that included blood, Go, and ZnO nanoparticles and moved via a perforated tube. The computational estimation of mixed convective entropy optimized in Darcy-Forchheimer circulation of Cross nanofluids via an upward plane plate with inconsistent heat source/sink was explored by Hussain et al. (Hussain et al., 2023).
When non-Newtonian behavior and nanofluids are combined, the result is a non-Newtonian nanofluid. Non-Newtonian fluids have a viscosity that varies as a function of the shear or stress rate. The temperature, nanoparticle concentration, and nanoparticle kind may impact this behavior. Khan et al. (Khan et al., 2023) investigated the effects of irregular heat source/sink on the aiding and opposing movements of the Eyring-Powell liquid on wall jet nanoparticles. Alharbi et al. (Alharbi et al., 2022) assessed the influence of viscous dissipation and Coriolis impacts on the mass and heat transmission evaluation of the 3D non-Newtonian flow of liquids. Khan et al. (Khan S. et al., 2021) investigated the study of the movement of a non-Newtonian liquid through a stretching/shrinking permeable material while considering the transmission of heat and mass. Some of the noticeable works on non-Newtonian fluids are found in (Algehyne et al., 2023; Alsulami et al., 2023).
The Casson nanofluid (CNF) idea is built on the assumption that the Casson equation governs liquid circulation and particle motion, a rheological model that explains the momentum behavior of non-Newtonian liquids. The Casson model considers yield stress and plastic solution viscosity, essential factors in various real-world scenarios such as blood circulation, coating layout, and liquid processing. Because of its improved thermal conductivity and specific heat capacity, CNF can considerably improve a fluid’s ability to transmit temperature. Nanoparticles can also affect the fluid’s rheological properties, such as viscosity and yield stress. Madhukesh et al. (Madhukesh et al., 2023) used the Cattaneo–Christov theory to investigate the heat transport of an MHD CMNF (Casson—Maxwell nanofluid) between two porous discs. Mabood et al. (Mabood et al., 2020) studied the free convective movement of time-dependent CNF in a permeable stretched surface. Madhukesh et al. (Madhukesh et al., 2022b) scrutinized the circulation of MHD MCNF in the presence of permeable discs using CCHF and slip impacts. Rasheed et al. (Rasheed et al., 2022) considered the homotopic solutions for the unsteady MHD CNF in a vertical cylinder with viscous dissipation impacts. The exact solution of a CF using Prabhakar-fractional simulations while also experiencing the effects of magnetohydrodynamic and sinusoidal thermal conditions was examined by Raza et al. (Raza et al., 2023).
Because of its temperature, a body emits a specific sort of electromagnetic radiation known as thermal radiation (TR). This radiation is formed by the thermal movement of the molecules and atoms inside the body, and it can go freely into space as there is no requirement for a medium to conduct it. The Stefan-Boltzmann equation describes the relationship between the temperature of a blackbody (an idealized object that absorbs all radiation incident on it) and the intensity of the thermal radiation it emits. Thermal radiation has important practical applications in various fields, including engineering, physics, astronomy, electronics, and energy conversion. Lone et al. (Lone et al., 2022) inspected MHD micropolar nanofluid hybrids circulating across a flat surface exposed to TR and mixed convection. Khan et al. (Khan U. et al., 2021) inspected the nonlinear T-R-influenced entropy production in the presence of NF with mixed convection effects. Naqvi et al. (Raza Shah Naqvi et al., 2022) examined numerical simulations to study the movement of hybrid nanofluids while considering the consequences of TR and entropy formation. Ramesh et al. (Ramesh et al., 2023) scrutinized the hybrid-based CNT movement over a rotating sphere object in the presence of T-R and TPD. Magnetite-based liquid nanofluid three-dimensional layer movement involving non-linear TR and couple stress responses were studied by Ullah et al. (Ullah et al., 2021). The thermal study of slip and magnetohydrodynamic consequences for unstable sheet extending was investigated by Benos et al. (Benos et al., 2019).
The liquid and porous medium’s features affect the rheological behavior of a fluid moving through them. When a non-Newtonian fluid, like a CNF, travels through a porous media, the pores’ porosity, permeability, size, and shape can all impact how the fluid behaves. There has been a rise in interest in CNF flowing through porous media in recent years because of its potential applications in various industries, including increased oil recovery and geothermal energy generation. Understanding Casson nanofluid behavior is crucial for optimizing these processes since the characteristics of the porous medium can significantly impact how they behave. Alrehili et al. (Alrehili et al., 2022) made a numerical investigation of linear radiation and Soret impacts on MHD CNF over a vertical surface with a porous medium. Rallabandi et al. (Rallabandi, 2022) investigated the CNF flow over an inclined permeable stretched surface. Yogeesha et al. (Yogeesha et al., 2022) studied the Dufour and Soret effects to evaluate the dusty TNF circulation across an unstable stretched sheet. Raza et al. (Raza et al., 2022) inspected the activation energy, magnetic field, and binary chemical reaction impact on NF- and HNF through a porous area. Shoaib et al. (Shoaib et al., 2022) made soft computing to investigate the thermal energy’s effects on the MHD CF as it passes over a porous material with an inclined non-linear surface.
The RKF-45, or Runge Kutta Fehlberg 4th 5th order, is a numerical method employed to solve complex systems of differential equations governing fluid flow problems. Many problems arise from simple laminar to complex turbulent flows in fluid mechanics. In mathematics, many of these situations may be modelled using ordinary differential equations, partial differential equations, or a hybrid of the two. Due to its high order accuracy and flexible step size capacity, RKF-45 is a popular numerical approach for modelling fluid dynamics. RKF-45 continuously controls the step size to reach the required level of precision while minimizing computational cost by calculating two estimates of the solution with varying orders of accuracy. The algorithm of the RKF-45 method is in detail given in (Mathews and Fink, 2004), and solving the differential equations using the RKF-45 algorithm was explained in (Abell and Braselton, 2000). Some works that implemented and used the RKF-45 algorithm are provided in (Sarris et al., 2002; Arifeen et al., 2021; Madhukesh et al., 2022b; Yogeesha et al., 2022; Hussain et al., 2023; Madhukesh et al., 2023).
The consider examination originality comes from its emphasis on the as-yet-unstudied subject of Casson-based nanofluid flow over a CSS in the presence of a porous medium and thermal radiation effects. In today’s energy-conscious world, this study has the potential to help create more effective and sustainable thermal energy systems. Overall, studying the fluid flow past a CSS is an important area of research in fluid mechanics, with a significant impact on the development of microscale machines, including microfluidic devices, microscale engines, microsensors, and microscale reactors.
2 Mathematical formulation of the problem
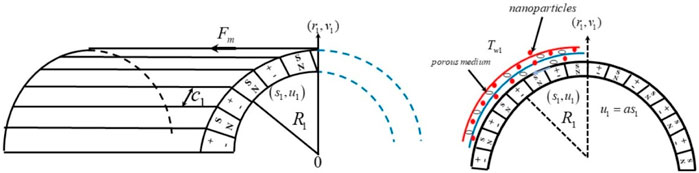
As schematically seen in Figure 1, the flow pattern under study is a two-dimensional, incompressible, non-Newtonian Casson nanofluid flowing over a curved Riga surface. The radius of the curved surface is represented by
in Eq. 4, the term
The respective boundary conditions for the consider model are
Furthermore, to ease the analysis of the consider investigation, the following similarity variables are introduced as [see (Abbas et al., 2020; AdnanZaidi et al., 2020)]:
Therefore, with the help of the above similarity variables stated in Eqs 1, 6 is satisfied and Eqs 2, 3 take the following form as:
here,
Moreover, to eliminate the pressure terms in Eqs 7, 8, we get
After utilizing the similarity variables, the energy Eq. 4 reduces to the form as:
with simplified boundary conditions are
in aforesaid Eqs 9–11, the term
The important engineering quantities and its reduced form [see (Abbas et al., 2020; AdnanZaidi et al., 2020)]:
Hence,
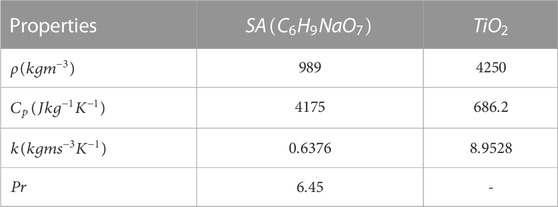
The thermophysical properties of nanofluid are given as follows [see (Khan et al., 2018; Alwawi et al., 2019)].
The effective thermophysical characteristics of nanofluid are given as follows [see (Acharya et al., 2019)]
3 Numerical method and code validation
The higher order and two-point boundary conditions in the governing equations for the fluid flow over the curved Riga surface make them challenging to solve analytically. We must transform these into first-order differential equations to achieve a numerical solution. Applying appropriate transformations will allow the higher-order differential equations to be represented as a set of first-order differential equations. Let us take,
with the boundary constraints become
The Runge-Kutta Fehlberg 45-order approach was then used to solve the transformed Eq. 19 numerically and (20) as well as the boundary conditions (21). Since the boundary conditions contain unknowns, we employed a shooting technique to find the solution that meets the conditions at infinity. Further, utilised a step size of 0.001 and set the error tolerance to 10–6 to achieve accurate findings. By substituting appropriate values for the dimensionless variables and using the thermophysical properties of the nanofluid (see Table 1) solutions are obtained. We discovered that our findings were in strong accord with prior work (Sajid et al., 2010), demonstrating the accuracy and dependability of our numerical method (see Table 2).
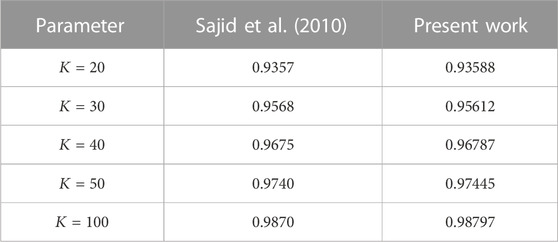
TABLE 2. Comparison of
4 Results and discussion
The purpose of this section is to describe how significant dimensionless parameters affect the temperature and velocity profiles. The RKF-45 method and shooting approach are used to numerically solve the reduced ODEs and boundary conditions acquired in the previous section. The acquired data are shown as graphs to illustrate the impact of various dimensionless parameters on the motion and temperature fields. Also, a discussion of the important technical variables that may have an impact on the system’s flow and thermal transfer characteristics is included in this section. The current study offers useful insights for designing and optimising industrial applications employing Casson-based nanofluid movements over curved surfaces by taking these parameters into account.
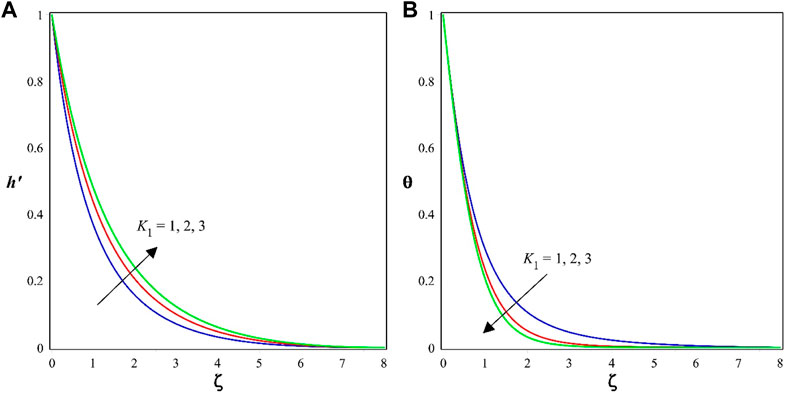
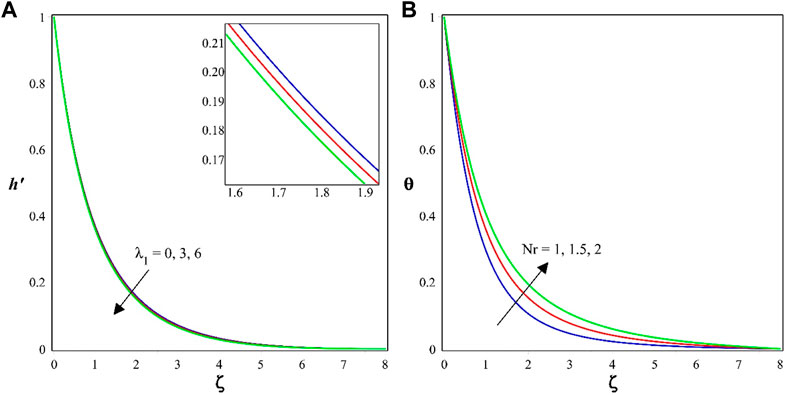
Figures 2A, B show the impact of
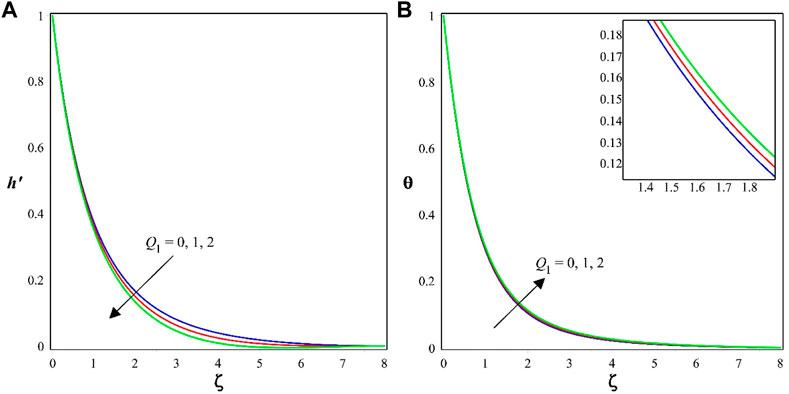
Figure 3A, B display the variation of
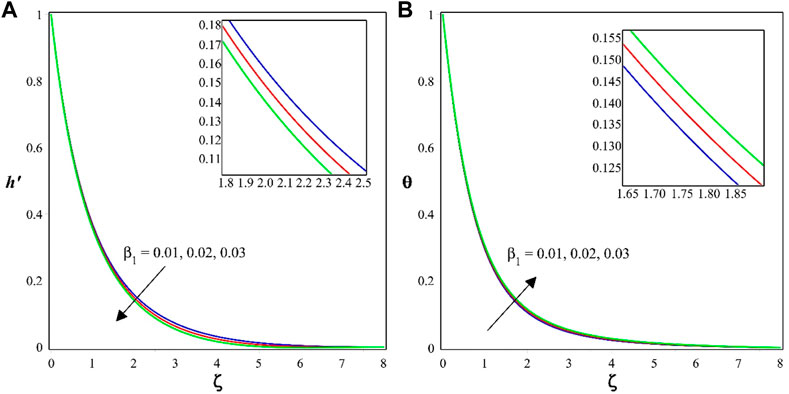
The effect of the porosity constraint
The consequence of the Casson parameter
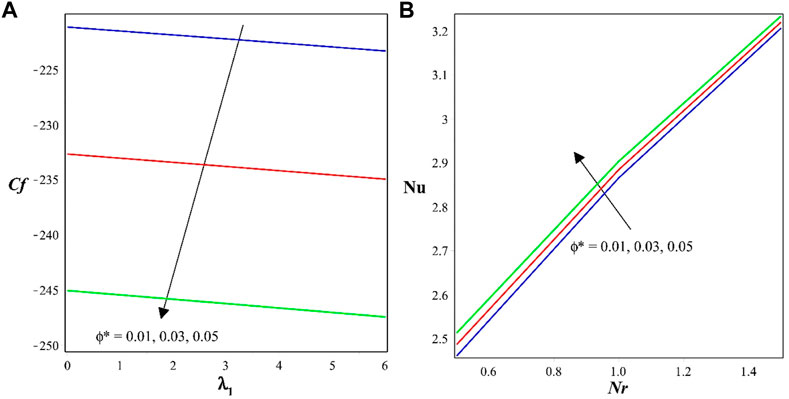
Figure 6A represents the effect of skin friction on the porous parameter
5 Final remarks
The present study investigates Casson-based nanofluid movement over a curved stretching surface in the presence of porous medium and thermal radiation effects. The ODEs and BCs are obtained by applying suitable similarity constraints to the PDEs. The numerical calculations are done with the aid of RKF-45 and shooting techniques. The outcomes are visualized using a graphical representation. The discussions on important dimensionless constraints are presented. The main conclusions of the study are as follows:
❖ The improvement in the modified Hartman number and porosity factors will decrease the velocity. An increase in these components indicates stronger magnetic impacts and increased permeability. As a result, the velocity of the flow of nanofluid reduces.
❖ With an increase in the curvature parameter, the velocity rises but the temperature decreases. The surface becomes increasingly curved when the curvature parameter is increased. This causes higher liquid flow along the curved surface, which causes velocity to go up. The temperature, on the other hand, falls as the liquid moves more and releases heat owing to the increasing surface area.
❖ Thermal radiation and modified Hartmann numbers will improve the temperature. Thermal radiation and modified Hartmann numbers facilitates the distribution of heat from liquid to the surrounding and improves the thermal distribution due to strong magnetic effects.
❖ The Casson factor will decline the velocity but improve the thermal profile. The rise in Casson factor will denotes the higher yield stress and more resistance to flow of the liquid. This results in decrease in velocity and improved thermal profile.
❖ The surface drag force reduces with increase in the values of porous and solid fractions. Porous medium act as a barrier and slows down the fluid flow and adding of solid particles also influence on the surface drag force by increasing thickness of momentum boundary layer.
❖ The rate of thermal distribution advances with radiation and solid fraction factors. Heat transport is facilitated by radiation, and the thermal distribution is improved by the presence of solid fractions, which encourage better mixing and dispersion of thermal energy.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, AH, BS, KN, KV, and JM; methodology, KN, KV, and JM; software, KN, KV, and JM; validation, KN, KV, and JM; formal analysis, KN, KV, and JM; investigation, UK, JS, and IS; resources, IS; data curation, AH, BS, UK, JS, and IS; writing—original draft preparation, AH, BS, UK, JS, IS, and E-SS; writing—review and editing, AH, BS, UK, JS, IS, and E-SS; visualization, E-SS; supervision, E-SS; project administration, E-SS; funding acquisition, E-SS. All authors contributed to the article and approved the submitted version.
Funding
This work was funded by the Researchers Supporting Project number (RSP2023R33), King Saud University, Riyadh, Saudi Arabia.
Acknowledgments
The authors are thankful for the support of Researchers Supporting Project number (RSP2023R33), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, N., Malik, M. Y., and Nadeem, S. (2020). Transportation of magnetized micropolar hybrid nanomaterial fluid flow over a Riga curface surface. Comput. Methods Programs Biomed. 185, 105136. doi:10.1016/j.cmpb.2019.105136
Abell, M. L., and Braselton, J. P. (2000). Differential equations with maple V. Cambridge, Massachusetts, United States: Academic Press.
Acharya, N., Maity, S., and Kundu, P. K. (2019). Framing the hydrothermal features of magnetized TiO2–CoFe2O4 water-based steady hybrid nanofluid flow over a radiative revolving disk. Multidiscip. Model. Mater. Struct. 16, 765–790. doi:10.1108/mmms-08-2019-0151
AdnanZaidi, S. Z. A., Khan, U. N., Chu, Y. M., Mohyud-Din, S. T., Chu, Y.-M., Khan, I. K. S., et al. (2020). Impacts of freezing temperature based thermal conductivity on the heat transfer gradient in nanofluids: applications for a curved Riga surface. Molecules 25, 2152. doi:10.3390/molecules25092152
Ahmad, S., Nadeem, S., and Muhammad, N. (2019). Boundary layer flow over a curved surface imbedded in porous medium. Commun. Theor. Phys. 71, 344. doi:10.1088/0253-6102/71/3/344
Algehyne, E. A., Abdelmohsen, S. A. M., Gowda, R. J. P., Kumar, R. N., Abdelbacki, A. M. M., Gorji, M. R., et al. (2023). Mathematical modeling of magnetic dipole effect on convective heat transfer in Maxwell nanofluid flow: single and multi-walled carbon nanotubes. Waves Random Complex Media 33, 489–504. doi:10.1080/17455030.2022.2125598
Alharbi, K. A. M., Ullah, A., Ikramullah, , , Fatima, N., Khan, R., Sohail, M., et al. (2022). Impact of viscous dissipation and coriolis effects in heat and mass transfer analysis of the 3D non-Newtonian fluid flow. Case Stud. Therm. Eng. 37, 102289. doi:10.1016/j.csite.2022.102289
Alrehili, M. F., Goud, B. S., Reddy, Y. D., Mishra, S. R., Lashin, M. M. A., Govindan, V., et al. (2022). Numerical computing of Soret and linear radiative effects on MHD Casson fluid flow toward a vertical surface through a porous medium: finite element analysis. Mod. Phys. Lett. B 36, 2250170. doi:10.1142/s0217984922501706
Alsulami, M. D., Naveen Kumar, R., Punith Gowda, R. J., and Prasannakumara, B. C. (2023). Analysis of heat transfer using Local thermal non-equilibrium conditions for a non-Newtonian fluid flow containing Ti6Al4V and AA7075 nanoparticles in a porous media. ZAMM - J. Appl. Math. Mech./ Zeitschrift Für Angewandte Math. Und Mech. 103, e202100360. doi:10.1002/zamm.202100360
Alwawi, F. A., Alkasasbeh, H. T., Rashad, A. M., and Idris, R. (2019). Natural convection flow of Sodium Alginate based Casson nanofluid about a solid sphere in the presence of a magnetic field with constant surface heat flux. J. Phys. Conf. Ser. 1366, 012005. doi:10.1088/1742-6596/1366/1/012005
Arifeen, S. U., Haq, S., Ghafoor, A., Ullah, A., Kumam, P., and Chaipanya, P. (2021). Numerical solutions of higher order boundary value problems via wavelet approach. Adv. Differ. Equ. 2021, 347. doi:10.1186/s13662-021-03495-6
Asogwa, K. K., Alsulami, M. D., Prasannakumara, B. C., and Muhammad, T. (2022). Double diffusive convection and cross diffusion effects on Casson fluid over a Lorentz force driven Riga plate in a porous medium with heat sink: an analytical approach. Int. Commun. Heat Mass Transf. 131, 105761. doi:10.1016/j.icheatmasstransfer.2021.105761
Benos, L. Th., Mahabaleshwar, U. S., Sakanaka, P. H., and Sarris, I. E. (2019). Thermal analysis of the unsteady sheet stretching subject to slip and magnetohydrodynamic effects. Therm. Sci. Eng. Prog. 13, 100367. doi:10.1016/j.tsep.2019.100367
Duraihem, F. Z., Devi, R. L. V. R., Prakash, P., Sreelakshmi, T. K., Saleem, S., Durgaprasad, P., et al. (2023). Enhanced heat and mass transfer characteristics of multiple slips on hydro-magnetic dissipative Casson fluid over a curved stretching surface. Int. J. Mod. Phys. B, 2350229. doi:10.1142/s0217979223502296
Gailitis, A., and Lielausis, O. (1961). On a possibility to reduce the hydrodynamic resistance of a plate in aelectro-lyte. Appl. Magnetohydrodyn. 12, 143–146.
Hayat, T., Qayyum, S., Imtiaz, M., and Alsaedi, A. (2018). Double stratification in flow by curved stretching sheet with thermal radiation and joule heating. J. Therm. Sci. Eng. Appl. 10, 021010. doi:10.1115/1.4037774
Hussain, S. M., Khan, U., Zaib, A., Ishak, A., and Sarris, I. E. (2023). Numerical computation of mixed convective entropy optimized in Darcy-Forchheimer flow of Cross nanofluids through a vertical flat plate with irregular heat source/sink. Tribol. Int. 187, 108757. doi:10.1016/j.triboint.2023.108757
Hussain, S. M., Sharma, R., and Alrashidy, S. S. (2022). Numerical study of Casson nanofluid flow past a vertical convectively heated Riga-plate with Navier’s slip condition. AIP Conf. Proc. 2435, 020002. doi:10.1063/5.0083603
Khan, A., Khan, D., Khan, I., Ali, F., ul Karim, F., and Imran, M. (2018). MHD flow of sodium alginate-based casson type nanofluid passing through A porous medium with Newtonian heating. Sci. Rep. 8, 8645. doi:10.1038/s41598-018-26994-1
Khan, S., Selim, M. M., Khan, A., Ullah, A., Abdeljawad, T., Ikramullah,, , et al. (2021a). On the analysis of the non-Newtonian fluid flow past a stretching/shrinking permeable surface with heat and mass transfer. Coatings 11, 566. doi:10.3390/coatings11050566
Khan, U., Zaib, A., Ishak, A., Sherif, E.-S. M., Sarris, I. E., Eldin, S. M., et al. (2023). Analysis of assisting and opposing flows of the Eyring-Powell fluid on the wall jet nanoparticles with significant impacts of irregular heat source/sink. Case Stud. Therm. Eng. 49, 103209. doi:10.1016/j.csite.2023.103209
Khan, U., Zaib, A., Khan, I., and Nisar, K. S. (2021b). Entropy generation incorporating γ-nanofluids under the influence of nonlinear radiation with mixed convection. Crystals 11, 400. doi:10.3390/cryst11040400
Lakshmi, K. B., Sugunamma, V., Tarakaramu, N., Sivakumar, N., and Sivajothi, R. (2022). Cross-dispersion effect on magnetohydrodynamic dissipative Casson fluid flow via curved sheet. Heat. Transf. 51, 7822–7842. doi:10.1002/htj.22668
Lone, S. A., Alyami, M. A., Saeed, A., Dawar, A., Kumam, P., and Kumam, W. (2022). MHD micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal radiation. Sci. Rep. 12, 17283. doi:10.1038/s41598-022-21255-8
Mabood, F., Yusuf, T. A., and Sarris, I. E. (2020). Entropy generation and irreversibility analysis on free convective unsteady mhd casson fluid flow over a stretching sheet with soret/dufour in porous media. STRPM 11, 595–611. doi:10.1615/specialtopicsrevporousmedia.2020033867
Madhukesh, J. K., Naveen Kumar, R., Punith Gowda, R. J., Prasannakumara, B. C., Ramesh, G. K., Ijaz Khan, M., et al. (2021). Numerical simulation of aa7072-aa7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: a non-fourier heat flux model approach. J. Mol. Liq. 335, 116103. doi:10.1016/j.molliq.2021.116103
Madhukesh, J. K., Prasannakumara, B. C., Kumar, R. S. V., Rauf, A., and Shehzad, S. A. (2022b). Flow of hydromagnetic micropolar-casson nanofluid over porous disks influenced by cattaneo-christov theory and slip effects. JPM 25, 35–49. doi:10.1615/jpormedia.2021039254
Madhukesh, J. K., Ramesh, G. K., Shehzad, S. A., Chapi, S., and Prabhu Kushalappa, I. (2023). Thermal transport of MHD Casson–Maxwell nanofluid between two porous disks with Cattaneo–Christov theory. Numer. Heat. Transf. Part A Appl., 1–16. doi:10.1080/10407782.2023.2214322
Madhukesh, J. K., Varun Kumar, R. S., Punith Gowda, R. J., Prasannakumara, B. C., and Shehzad, S. A. (2022a). Thermophoretic particle deposition and heat generation analysis of Newtonian nanofluid flow through magnetized Riga plate. Heat. Transf. 51, 3082–3098. doi:10.1002/htj.22438
Mathews, J. H., and Fink, K. D. (2004). Numerical methods using MATLAB. Upper Saddle River, NJ, USA: Pearson Prentice Hall.
Mohammed Alshehri, A., Huseyin Coban, H., Ahmad, S., Khan, U., and Alghamdi, W. M. (2021). Buoyancy effect on a micropolar fluid flow past a vertical Riga surface comprising water-based SWCNT–MWCNT hybrid nanofluid subject to partially slipped and thermal stratification: cattaneo–christov model. Math. Problems Eng. 2021, 1–13. doi:10.1155/2021/6618395
Rallabandi, S. R. (2022). Finite element solutions of non-Newtonian dissipative Casson fluid flow past a vertically inclined surface surrounded by porous medium including constant heat flux, thermal diffusion, and diffusion thermo. Int. J. Comput. Methods Eng. Sci. Mech. 23, 228–242. doi:10.1080/15502287.2021.1949407
Ramesh, G. K., Madhukesh, J. K., Ali Shah, N., and Yook, S.-J. (2023). Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alexandria Eng. J. 64, 969–979. doi:10.1016/j.aej.2022.09.026
Rasheed, H. U., Khan, Z., El-Zahar, E. R., Shah, N. A., Islam, S., and Abbas, T. (2022). Homotopic solutions of an unsteady magnetohydrodynamic flow of Casson nanofluid flow by a vertical cylinder with Brownian and viscous dissipation effects. Waves Random Complex Media 0, 1–14. doi:10.1080/17455030.2022.2105979
Raza, A., Khan, U., Almusawa, M. Y., Hamali, W., and Galal, A. M. (2023). Prabhakar-fractional simulations for the exact solution of Casson-type fluid with experiencing the effects of magneto-hydrodynamics and sinusoidal thermal conditions. Int. J. Mod. Phys. B 37, 2350010. doi:10.1142/s0217979223500108
Raza, Q., Qureshi, M. Z. A., Khan, B. A., Kadhim Hussein, A., Ali, B., Shah, N. A., et al. (2022). Insight into dynamic of mono and hybrid nanofluids subject to binary chemical reaction, activation energy, and magnetic field through the porous surfaces. Mathematics 10, 3013. doi:10.3390/math10163013
Raza Shah Naqvi, S. M., Waqas, H., Yasmin, S., Liu, D., Muhammad, T., Eldin, S. M., et al. (2022). Numerical simulations of hybrid nanofluid flow with thermal radiation and entropy generation effects. Case Stud. Therm. Eng. 40, 102479. doi:10.1016/j.csite.2022.102479
Rizk, D., Ullah, A., Ikramullah,, , Elattar, S., Alharbi, K. A. M., Sohail, M., et al. (2022). Impact of the KKL correlation model on the activation of thermal energy for the hybrid nanofluid (GO+ZnO+Water) flow through permeable vertically rotating surface. Energies 15, 2872. doi:10.3390/en15082872
Sajid, M., Ali, N., Javed, T., and Abbas, Z. (2010). Stretching a curved surface in a viscous fluid. Chin. Phys. Lett. 27, 024703. doi:10.1088/0256-307x/27/2/024703
Sakkaravarthi, K., and Reddy, P. B. A. (2023). Entropy generation on Casson hybrid nanofluid over a curved stretching sheet with convective boundary condition: semi-analytical and numerical simulations. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 237, 465–481. doi:10.1177/09544062221119055
Sarris, I. E., Lekakis, I., and Vlachos, N. S. (2002). Natural convection in a 2d enclosure with sinusoidal upper wall temperature. Numer. Heat. Transf. Part A Appl. 42, 513–530. doi:10.1080/10407780290059675
Shah, Z., Kumam, P., Ullah, A., Khan, S. N., and Selim, M. M. (2021). Mesoscopic simulation for magnetized nanofluid flow within a permeable 3D tank. IEEE Access 9, 135234–135244. doi:10.1109/access.2021.3115599
Shoaib, M., Kausar, M., Nisar, K. S., Asif Zahoor Raja, M., and Morsy, A. (2022). Impact of thermal energy on MHD casson fluid through a forchheimer porous medium with inclined non-linear surface: a soft computing approach. Alexandria Eng. J. 61, 12211–12228. doi:10.1016/j.aej.2022.06.014
Ullah, A., Ikramullah,, , Selim, M. M., Abdeljawad, T., Ayaz, M., Mlaiki, N., et al. (2021). A magnetite–water-based nanofluid three-dimensional thin film flow on an inclined rotating surface with non-linear thermal radiations and couple stress effects. Energies 14, 5531. doi:10.3390/en14175531
Ullah, I., Ullah, A., Selim, M. M., Khan, M. I., Saima,, , Khan, A. A., et al. (2022). Analytical investigation of magnetized 2D hybrid nanofluid (GO + ZnO + blood) flow through a perforated capillary. Comput. Methods Biomechanics Biomed. Eng. 25, 1531–1543. doi:10.1080/10255842.2021.2021194
Varun Kumar, R. S., Gunderi Dhananjaya, P., Naveen Kumar, R., Punith Gowda, R. J., and Prasannakumara, B. C. (2022). Modeling and theoretical investigation on Casson nanofluid flow over a curved stretching surface with the influence of magnetic field and chemical reaction. Int. J. Comput. Methods Eng. Sci. Mech. 23, 12–19. doi:10.1080/15502287.2021.1900451
Yogeesha, K. M., Megalamani, S. B., Gill, H. S., Umeshaiah, M., and Madhukesh, J. K. (2022). The physical impact of blowing, Soret and Dufour over an unsteady stretching surface immersed in a porous medium in the presence of ternary nanofluid. Heat. Transf. 51, 6961–6976. doi:10.1002/htj.22632
Zabihi, A., Akinshilo, A. T., Rezazadeh, H., Ansari, R., Sobamowo, M. G., and Tunc, C. (2022). Application of variation of parameter’s method for hydrothermal analysis on MHD squeezing nanofluid flow in parallel plates. Comput. Methods Differ. Equations 10, 580–594. doi:10.22034/cmde.2021.41296.1794
Keywords: curved stretching sheet, Riga plate, casson nanofluid, thermal radiation, porous medium
Citation: Nagaraja KV, Vinutha K, Madhukesh JK, Khan U, Singh Chohan J, Sherif E-SM, Sarris IE, Hassan AM and Shanker B (2023) Thermal conductivity performance in sodium alginate-based Casson nanofluid flow by a curved Riga surface. Front. Mater. 10:1253090. doi: 10.3389/fmats.2023.1253090
Received: 04 July 2023; Accepted: 04 August 2023;
Published: 17 August 2023.
Edited by:
Noor Saeed Khan, University of Education Lahore, PakistanReviewed by:
Ali Zabihi, Rowan University, United StatesAsad Ullah, University of Lakki Marwat, Pakistan
Copyright © 2023 Nagaraja, Vinutha, Madhukesh, Khan, Singh Chohan, Sherif, Sarris, Hassan and Shanker. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ahmed M. Hassan, YWhtZWQuaGFzc2FuLnJlc0BmdWUuZWR1LmVn
 K. V. Nagaraja
K. V. Nagaraja K. Vinutha
K. Vinutha J. K. Madhukesh
J. K. Madhukesh Umair Khan
Umair Khan Jasgurpreet Singh Chohan6
Jasgurpreet Singh Chohan6 El-Sayed M. Sherif
El-Sayed M. Sherif Ioannis E. Sarris
Ioannis E. Sarris Ahmed M. Hassan
Ahmed M. Hassan