- 1Ningbo Cigarette Factory, China Tobacco Zhejiang Industrial Co., Ltd., Ningbo, China
- 2Department of Civil Engineering, Zhejiang University, Hangzhou, China
The shrinkage characteristic of porous materials is an important consideration in the drying process, as it can significantly impact the texture of the dried product and energy utilization. This phenomenon is influenced by numerous factors, including the structure of the cells, drying conditions, and the glass transition temperature. To gain a deeper understanding of the drying process, it is necessary to develop theoretical models that account for the simultaneous heat and mass transfer processes at the cellular level, as well as simulation tools to analyze the associated changes in drying morphology. In this paper, we highlight several key factors affecting shrinkage during the drying of porous materials, and also outline drying modeling, morphological simulation, and drying technology design considerations to provide guidance for improving the drying quality of porous materials as well as energy conversion efficiency.
1 Introduction
Drying is one of the oldest unit operations, which is performed by applying heat to the material, resulting in diffusion of moisture inside the material to its surface and then the diffusion of moisture from the surface to the air, both of which occur simultaneously (Ekechukwu, 1999; Akpinar and Bicer, 2005). The process of drying is widely used to preserve materials by minimizing physical and chemical changes, reducing their water activity and extending their shelf life during storage. Also, the lower weight and volume of the dried product reduces transportation and storage costs (Dadali et al., 2007; Doymaz and Ismail, 2011).
Porous materials usually have a high initial moisture content and porosity. The evaporation of water during the drying process is often accompanied by significant volume changes and tissue shrinkage (Dissa et al., 2010; El Tabbal et al., 2020). The deformation in the material drying process directly affects the heat and mass transfer pattern of the material, which in turn affects the drying efficiency, the selection and design of the drying machine, the energy consumption of the drying process and the final product quality (Masters, 1996; Lelièvre et al., 2012). Porous materials undergo many physical and chemical changes during the drying process, and moisture migration and temperature distribution have a great impact on the drying shrinkage characteristics. Such as, Joardder et al. (Joardder et al., 2015) showed that the migration of bound water within the tissue during drying has a significant effect on the shrinkage of the material. Golpour et al. (2017) showed that the percentage shrinkage of the material increased with the increase in drying temperature. Therefore, the study of the factors affecting the shrinkage characteristics in the drying process is crucial for gaining a better understanding of this process and designing more effective drying technologies.
Drying models are essential tools for understanding the behavior of drying processes, designing and constructing effective drying systems, and reducing the associated experimental costs and time investment (Babu et al., 2018; Inyang et al., 2018). Currently available drying models can be categorized as macro-scale models, micro-scale models, and multi-scale models. The macro-scale model represents the overall drying characteristics (Çakmak and Yıldız, 2011), while the micro-scale model considers tissue deformation and local distribution of water at the cellular level (Prawiranto et al., 2020). The multi-scale model couples the macroscopic model and the microscopic model (Dias et al., 2022; Welsh et al., 2022). Drying performance is affected by various factors including drying parameters, dryer type, and properties of the drying material. Therefore, drying models are crucial for predicting ideal drying conditions and optimizing the drying process to enhance product quality.
Morphological modeling of porous materials has proven to be a useful tool for predicting composite indicators of plants under different drying conditions. For example, it can quantify the degree of drying curl (Hong et al., 2005), estimate the photosynthetic production potential (Bernard and McQuillan, 2018; Cieslak et al., 2022), and determine the leaf area index (Wang et al., 2013). Such computational analysis tools provide valuable insights for evaluating the drying process, selecting suitable plant varieties, designing effective drying technologies, and reducing shrinkage in dried products. By leveraging these tools, researchers can optimize the drying process and produce high-quality dried products that meet the needs of various industries.
Traditional drying techniques for porous materials include atmospheric pressure hot air drying (Doymaz and Pala, 2002), freeze drying (Shukla, 2011; Kurapova et al., 2016; Kurapova et al., 2017), supercritical drying (Baudron et al., 2019), solar drying (Pirasteh et al., 2014) and microwave drying (Cao et al., 2017). Each of these techniques has its own characteristics, such as atmospheric pressure hot air drying is easy to operate and low cost, vacuum drying is suitable for heat-sensitive materials, freeze drying can maintain the microstructure of porous materials, supercritical drying is suitable for highly fragile materials, and microwave drying can significantly reduce the drying time. However, a single drying technology has limitations such as long drying time and excessive energy consumption, which leads to poor quality of dried products. In order to improve the drying efficiency and quality of porous materials, hybrid drying technology has been widely used in the drying of porous materials (Menon et al., 2020; Hii et al., 2021). Hybrid drying techniques for porous materials include hot air-vacuum drying (Zhao et al., 2014), freezing-microwave drying (Sickert et al., 2023), supercritical-hot air drying (Siddiqui et al., 2023), vacuum-microwave drying (González-Cavieres et al., 2021) and freezing-supercritical drying (Wang et al., 2019). By combining different drying methods, these techniques aim to achieve a more efficient and gentle drying process. Porous materials have attracted much attention due to their high specific surface area, diverse pore structures and tunable chemical and physical properties. Hybrid drying techniques combine the advantages of each while maintaining the unique properties of porous materials, enabling porous materials to exhibit superior performance in areas such as catalysis, separation, adsorption, sensors, and energy storage. Therefore, the selection of appropriate drying techniques is essential to maintain these advantages of porous materials.
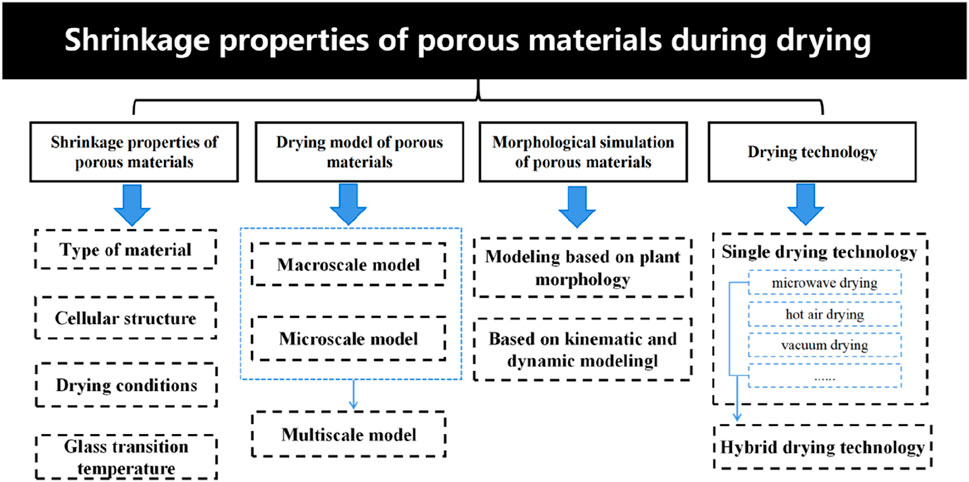
This paper focuses on analyzing the primary factors that influence the shrinkage properties of porous materials, including cell structure, drying conditions, and glass transition temperature. The study will review the available drying models and morphological simulations for porous materials, as well as the various drying techniques currently in use. Figure 1 represents a summary diagram of the review of this paper. By understanding these key factors, we can inform the development of more effective methods for drying porous materials to minimize shrinkage and optimize the quality of the final product.
2 Shrinkage properties of porous materials
The shrinkage property of porous materials is worth considering in the drying property. The transport of water from the cellular location to the surrounding environment during the drying of porous materials leads to irregular volume changes, and this volume reduction is usually defined as shrinkage of the material (Khan and Karim, 2017). Material shrinkage is a common physical phenomenon that affects energy consumption, process selection and design, drying efficiency, and the quality of the final product. (Masters, 1996). Therefore, it is of theoretical and practical value to study the shrinkage characteristics of porous materials during drying. The shrinkage of porous materials during drying depends on many factors, including the type of material, cellular structure, drying conditions, and mechanical properties of the material.
2.1 The effect of different types of materials on shrinkage properties
Different types of porous materials have different shrinkage characteristics in the drying process. Porous materials are mainly divided into microporous (pores <2 nm), mesoporous (2–50 nm), and macroporous (>50 nm) types according to pore size (Nimmo, 2004; Zdravkov et al., 2007), each showing different shrinkage in drying (Ishizaki et al., 2013; Hu et al., 2023). Microporous materials have a low shrinkage rate during drying due to very small pores and slow migration and evaporation of water. Shrinkage occurs mainly at the microscopic level of the material and the overall size change may not be significant. Mesoporous materials evaporate water more quickly from larger pores when drying, which can lead to more pronounced macroscopic shrinkage. Due to the heterogeneous nature of the pore structure, shrinkage may result in uneven changes in the material structure, such as cracking or deformation. Macroporous materials evaporate water rapidly due to their large pores, which leads to rapid and significant macroscopic shrinkage. Under rapidly drying conditions, macroporous materials may develop large internal stresses, leading to cracking or structural damage. Porous materials can be categorized into organic and inorganic porous materials based on the source or manufacturing method (Pal and Bhaumik, 2013). Organic porous materials may exhibit a higher degree of flexibility and elasticity during drying, thereby reducing the risk of cracking. Inorganic porous materials may be more fragile during drying and prone to cracking or structural damage. Porous materials can be categorized based on surface area as low surface area porous materials, medium surface area porous materials, and high surface area porous materials (Kovler and Zhutovsky, 2006; Zdravkov et al., 2007; Lowell et al., 2012). High-surface-area materials may experience greater internal stresses upon loss of moisture due to surface tension within the pores, resulting in more significant shrinkage. Medium surface area materials may have better structural stability during drying compared to high surface area materials. A low surface area usually means that the pores are larger or fewer in number, so these materials may exhibit less shrinkage during drying.
2.2 The effect of cell structure on material shrinkage
The structural stiffness of cellular tissues can prevent shrinkage during drying, and the structural stiffness often depends on the distribution and transport mechanism of water inside cells (Barati and Esfahani, 2012). The water transport rate is related to cell size, direction, and type of cell water in the sample (Halder et al., 2011). The porous materials generally contain free water (FW) and bound water (BW) (Khan et al., 2017a; Khan and Karim, 2017), as shown in Figure 2. FW exists in intercellular space, and BW can be divided into loosely bound water (LBW) and strongly bound water (SBW) based on fluidity. Bound water present in cells is called LBW, while cell wall water is called SBW.
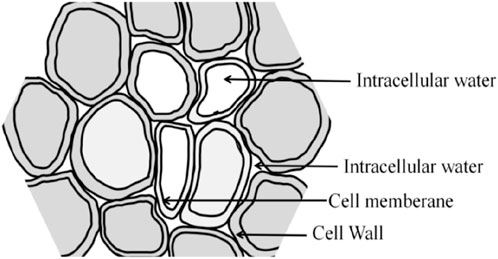
FIGURE 2. General water distribution within the porous materials (Khan et al., 2017a; Khan and Karim, 2017).
According to reports, the migration of FW has a limited impact on material shrinkage, while the migration of BW during drying has a strong effect on material shrinkage. Joardder et al. (2015) indicated that migration of LBW resulted in cell shrinkage, pore formation, and cell structure collapse, while migration of SBW resulted in deformation of the entire material structure. Khan et al. (2018a) found that vacuum-steam pulsed blanching (VSPB) could enhance the transfer of water within the material structure. Subsequently, Wang et al. (2021) used VSPB to treat carrots, and the results showed that the content of BW in carrot tissues decreased with the increase of blanching times. The migration of water in the material cells can promote the drying process and improve efficiency, energy saving, and emission reduction for the drying industry.
Understanding the period at which cell membranes break is also crucial, as this knowledge can be used to design more efficient drying systems. Halder et al. (2011) believed that the cell membrane of the material tissue collapsed simultaneously in a certain period of drying, thus resulting in the deformation of the whole tissue. In contrast, Khan et al. (2017b), Khan et al. (2018b) and Luo et al. (2021) have found that cell membranes rupture at different stages of the drying process. The main factors of cell rupture depend on the rate of heat energy penetration and the pressure gradient generated in the cell tissue.
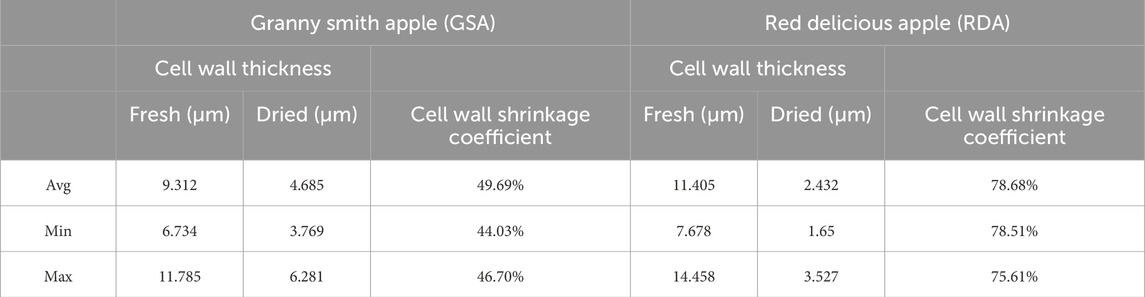
In addition, tissue shrinkage depends on the characteristics of the cell walls of the tissue (Haman and Konstankiewicz, 2000). Joardder et al. (2015) studied the cell wall characteristics of the Granny Smith Apple (GSA) and Red Delicious Apple (RDA) under convection drying. Table 1 displays the cell wall thickness for GSA and RDA in both fresh and dry states. The table reveals that the cell walls of RDA are thicker when they are fresh, while dried RDA cell walls show a greater degree of contraction than those of GSA. This suggests that RDA contains more bound water within its cell walls compared to GSA, resulting in a greater energy requirement for drying due to the thicker cell walls. Karunasena et al. (2014a) presented Scanning Electron Microscopy (Kovler and Zhutovsky, 2006) images of apples at varying stages of drying, shown in Figure 3. It can be observed from Figure 3 that the shape and size of the cells gradually change with the decrease of water content during the drying process, and cell wall wrinkling and cell contraction can be observed. The quality of dried food, especially physical properties such as porosity, shrinkage, and microstructure, is significantly affected by cell wall characteristics.

FIGURE 3. SEM images of apple cells at different stages of dryness: (A) X/X0 = 1, (B) X/X0 = 0.5, (C) X/X0 = 0.2, and X/X0 = 0.1. Reproduced from ref (Karunasena et al., 2014a). with permission the Elsevier Ltd. All rights reserved. Copyright 2014.
2.3 Effect of drying conditions on material shrinkage
The shrinkage of materials in the drying process is affected by drying parameters (drying temperature, drying airspeed, and relative humidity of drying air), among which drying temperature and drying air speed are the most important drying parameters that affect the shrinkage of materials (Mugi and Chandramohan, 2021; Shahmirzadi et al., 2021). These drying parameters will be discussed below.
The drying temperature plays an important role in increasing the drying speed and thus saving energy. Numerous studies have shown (Proietti et al., 2018; Shi et al., 2021) that the drying temperature has a significant effect on the shrinkage of the material. Zzaman et al. (2021) applied immersion pre-treatments and different drying temperatures to improve the overall quality of pineapple slices. The results showed that higher drying temperatures greatly enhanced the drying rate, which helped to maintain the physicochemical characteristics of the glass. Kalantari et al. (2023) studied the effect of different parameters (drying temperature, drying airspeed) of a convection hot air dryer on the drying characteristics of thinly sliced pears. Figure 4 represents the variation of surface shrinkage of pear slices with drying temperature and air velocity during drying. It is obvious from the figure that the percentage of pear layer shrinkage increases with the increase of drying temperature and air wind speed. The main reason for this phenomenon could be the decrease in viscoelastic stress within the cells due to the loss of water, which reduces the pressure between the internal cellular tissues (Süfer and Palazoğlu, 2019; Joudi-Sarighayeh et al., 2022). Different drying temperatures have different effects on the shrinkage rate of materials, and the choice of drying temperature is not the higher the better. McMinn and Magee (McMinn and Magee, 1997) and Wang and Brennan (Wang and Brennan, 1995) showed that potato tissues shrink less at high temperatures (70°C) than at low temperatures (40°C). This phenomenon may be due to the shell hardening effect occurring in the material at high temperatures leading to the transport of water, which ultimately controls the shrinkage of the material (Mahiuddin et al., 2018). Therefore, drying temperature is an important influencing factor for material shrinkage, and choosing the right drying temperature is crucial for drying rate as well as energy saving.
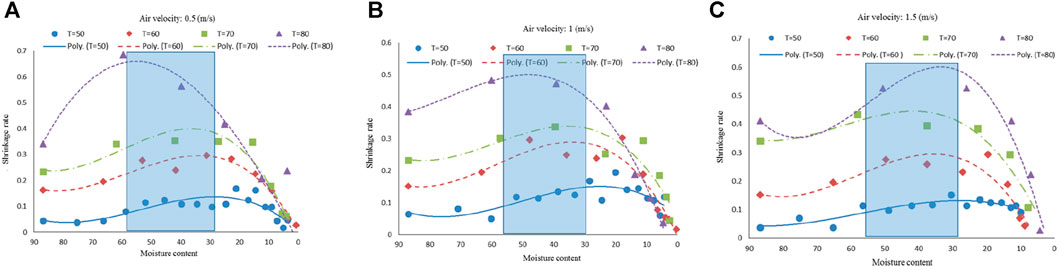
FIGURE 4. Variation of shrinkage rate versus moisture content during drying with different temperatures (T) obtained from experimental data. Reproduced from ref (Kalantari et al., 2023), with permission the Wiley Periodicals LLC. Copyright 2022.
The drying air velocity is also another important factor affecting the shrinkage of materials during the drying process (Ziari et al., 2022). Taghinezhad et al. (2020a) used the heat-mass transfer coupled with a stress-strain mathematical model to analyze the thermal and moisture stress profiles of apple slices at different air speeds (drying temperature of 60 C). The results of the study showed that the greater the hot-air velocity corresponds to the greater the drying stress (thermal and moisture stress), resulting in greater drying shrinkage deformation. The relevant literature (Taghinezhad et al., 2020b; Mugi and Chandramohan, 2021) has similar conclusions. This phenomenon may be because the boundary layer as the surface resistance of the material decreases with increasing air velocity, which results in relatively flat moisture within the tissue leading to low internal stresses and eventually leading to uniform shrinkage of the material at lower drying air velocities.
Related studies have shown that the drying temperature has a greater effect on the shrinkage of porous materials than the drying air speed (Nguyen et al., 2018; Wu et al., 2019). Therefore, it is very important to consider the drying temperature for the dried products.
2.4 Effect of glass transition temperature on material shrinkage
The glass transition temperature (Tg) is very important in the processing of materials, especially during the drying process. The temperature at which the amorphous water of the porous material changes from the rubbery state to the glassy state during the drying process is called the glass transition temperature (Tg) (Champion et al., 2000). In the glassy state, the high viscosity of the matrix leads to extremely slow molecular mobility (Joardder et al., 2018). Therefore, Tg can be used as a reference parameter for characterizing the quality, stability, and safety of food systems (Roos, 1995).
The shrinkage process of the material during drying is theoretically explained by the glass transition temperature (Shishehgarha et al., 2002; Katekawa and Silva, 2007). Ishibashi et al. (2022) demonstrated the non-size moisture content and Tg of radish and potato tested using DSC at drying temperatures below 40°C and 50°C, respectively, as shown in Figure 5 (Nguyen et al., 2018). The maximum glass transition temperatures of radish and potato are 24.9°C and 53.8°C, respectively. Since the drying temperature (<50°C) of radish is lower than Tg, the shrinkage deformation of radish is not affected by the glass transition. On the contrary, the Tg of potatoes was higher than the drying temperature in the later stages of drying, which indicates that potatoes gradually vitrify locally as drying proceeds. Finally, this author concluded that the glass transition phenomenon in the potato core significantly reduces the shrinkage rate. When the drying temperature of the material is higher than Tg, the material remains in a rubbery state. The material has a higher molecular mobility and higher rubber-like shrinkage compared to the glassy material. Therefore, when the drying temperature is lower than Tg, the material appears in a high viscosity state and this phenomenon leads to a reduction in shrinkage of the glassy state (Sappati et al., 2017).
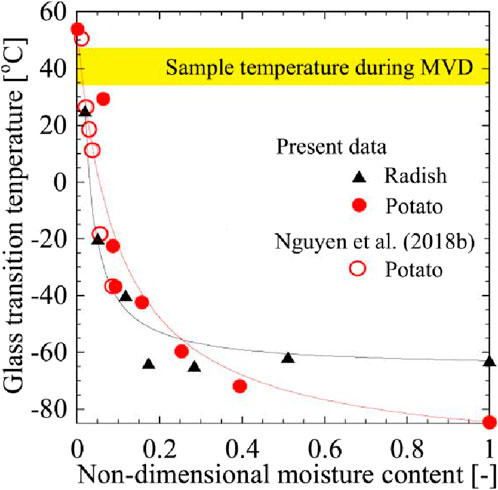
FIGURE 5. Relationship between and non-dimensional moisture content. Reproduced from ref (Nguyen et al., 2018). with permission the Elsevier Ltd. All rights reserved. Copyright 2022.
3 Drying model for porous materials
Drying of porous materials is a very complex operation that requires a lot of effort and time. Experimentation is the backbone of the drying technology research and development process. However, relying solely on experimental drying practices without considering the mathematical considerations of drying kinetics can significantly reduce the efficiency of the dryer and increase production costs (Wehbe et al., 2009; Tao et al., 2021).
The currently available drying models can be classified using the scale approach (Omolola et al., 2015; Onwude et al., 2016a; Ertekin and Firat, 2017), which are macro-scale models, micro-scale models, and multi-scale models, as detailed in Figure 6. Macroscale models treat the material as a continuum and do not consider the interactions between materials internally (Mutuli et al., 2020). Microscale models treat tissues as heterogeneous, with complex cellular structures represented by geometric models (Rahman et al., 2018). Microscale models can provide tissue deformation and local distribution of moisture at the cellular level, while macroscale models can represent the overall drying characteristics (Ahmad et al., 2021). Therefore, to predict the whole drying process of porous materials, the macroscopic model and the microscopic model can be coupled, and the coupled model is also the multiscale model.
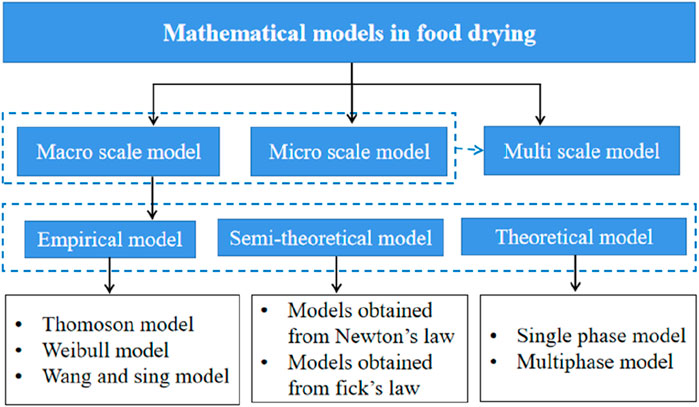
FIGURE 6. Classification of mathematical models in Porous material drying (Omolola et al., 2015; Onwude et al., 2016a; Ertekin and Firat, 2017).
3.1 Macroscale model
The general assumptions of the macroscopic model are as follows: (1) the porous material is considered a continuum, meaning that the material’s properties do not change when the material’s internal organization is subdivided. (2) Mass transfer within the solid occurs by diffusion and water evaporation occurs only between the material surface-air, so there is no phase change within the material (Shahari et al., 2016; Castro et al., 2018). This class of model is used to characterize the drying of porous materials, including drying time, mass and heat transfer, and energy consumption (Alam, 2014; Mutuli and Mbuge, 2015; Tzempelikos et al., 2015).
The theoretical models can be divided into single-phase model and multiphase model. The single-phase model assumes that diffusion drives moisture migration, but only considers mass transfer and conduction as energy transfer mechanisms without accounting for other important drying properties (Rahman et al., 2015; Kumar et al., 2016). The multi-phase model considers the coupled three-phase mass and heat transfer of liquid water, gas, and solid in the drying of porous materials. Thus it can provide a relatively realistic understanding of the heat and mass transfer process (Gulati and Datta, 2015; Papasidero et al., 2015).
Semi-theoretical models are generally obtained based on the solution of Fick’s second law and the variation of its simplified form. They are developed by relying on physical phenomena that occur during experiments, so they are easier to apply and have fewer assumptions. The empirical model and semi-theoretical model have similar characteristics (Erbay and Icier, 2010).
Empirical and semi-theoretical models are largely dependent on experimental data and offer restricted insights into product drying characteristics (Erbay and Icier, 2010; Janjai et al., 2011). Theoretical models not only consider the external and internal resistance of water transfer but also the shrinkage rate, geometry, porosity, and conductivity of materials (Defraeye and Verboven, 2017; Joardder and Karim, 2019). However, there are many limitations to assumptions.
3.2 Microscale model
The micro-scale model can include the transport phenomena of different components at the microscopic scale, such as cell walls, cell membranes, cell vacuoles, pores, etc. The model accounts for the anisotropy of the material, and since the geometric model indicates the cell structure of the material, its organization changes as it is subdivided (Van Liedekerke et al., 2011; Lemus-Mondaca et al., 2017). To better understand the potential phenomena leading to water loss of materials, Fanta et al. (Fanta et al., 2014) established a micro-scale water transport model combined with the microstructure deformation and calculated the effective conductivity of pear skin tissue. The results show that the membrane has the greatest influence on the surface macroscopic water conductivity. Karunasena et al. (2014b) established a meshless particle microscopic model through smooth particle fluid dynamics (SPH) and discrete element method (Dadali et al., 2007), which can deal with the extreme deformation of cell tissues during drying. Rahman (Rahman, 2018) established a micro-scale drying model based on real cell geometry to study the effects of drying conditions on the horizontal transport and deformation of porous material cells. Gao et al. (2021) used the locally exact homogenization theory to reveal the influence of the transfer mechanism of heat conduction at the microscopic interfaces of porous materials on the material properties. Chai et al. (2019) established a micro-scale heat transfer analysis model based on thermal parameters and boundary conditions of composites using Abaqus finite element analysis software. The local temperature distribution of composites under different heat transfer conditions was analyzed by this model.
In the development of existing microscale models, many of the assumptions of microscale models are based on the circular cell structure and lack the assumptions of real cell shape. As a result, the relationship between the space between cells and the transport process during the drying process is not strong, which leads to inaccurate prediction results. Therefore, it is necessary to develop a model based on plant microstructure to correctly analyze the transport process.
3.3 Multiscale model
Multi-scale modeling is a comprehensive method combining macro - and micro-scale. It can describe macroscopic scale phenomena by physical properties obtained in the microscopic environment, and at the same time consider the uncertain influence within micro-organization (Fish et al., 2021). Coupling geometric features at the micro-scale with conservation equations at the macro scale shows great potential in predicting the depth and precision of material properties (Li et al., 2022). Multi-scale models have been widely used in various research fields because of their advantages of inferring macroscopic properties from micro-scale structures (He et al., 2019; Tian et al., 2021). The drying of porous materials can be regarded as a phenomenon of heat and mass transfer coupled with multiple physical fields, which is very suitable for multi-scale modeling (Farid, 2019).
Multi-scale modeling is an effective method to better understand the water migration in tissues and the mechanical properties of porous materials during drying. Sano et al. (2019) predicted sample shrinkage, surface deformation, and effective water diffusion during isothermal drying by using a moving boundary model that considered the reduction of microstructure volume of food materials during drying. Welsh et al. (2021a) developed a multi-scale drying model for apple drying, which considered the effective water diffusivity when water distribution was uneven during the drying process. In this work, predetermined temperatures are used to determine microscale mean diffusion coefficients. Subsequently, the author (Welsh et al., 2021b; Welsh et al., 2023) further extended the multi-scale modeling method by considering the effects of cell rupture in the micro-scale domain as well as in the macro-scale, overcoming the dependence of the previous model on the mean diffusion coefficient and predetermined temperature. It provides a new insight for considering the heterogeneous distribution of water by using the change of microstructure. Sinha and Bhargav, (2022) established a physics-based transfer model to predict the temperature, moisture content, and shrinkage rate in the drying process of low-temperature air. And the author also improved the model through an artificial neural network (Lelièvre et al., 2012) model. Gao et al. (2021) established a multi-scale model to simulate heat transfer in the drying process of granular materials. The results show that the simulation of isothermal particles is closer to the experimental data than that of non-isothermal particles. Lu et al. (2021) used a three-dimensional particle model to consider intraparticle heat transfer, the interaction between particles, interphase momentum, heat transfer, and other multi-scale phenomena. The research results showed that particle shape, particle size, and operating conditions all had an impact on biomass pyrolysis. Such studies provide some insights into the pyrolysis kinetics of biomass.
As the model scale decreases, the accuracy of the multi-scale model increases gradually. However, the simplicity and generality of the model are often at odds with the approximation of the real micro-structure. Multi-scale models often have a complex solution process, which is the biggest challenge in the development of multi-scale models. Therefore, promoting the development of multi-scale modeling should focus on reducing the modeling difficulty and computational cost, and then meet the requirements of different accuracies in different studies.
4 Morphological simulation of porous materials
Porous materials have complex physiological features, geometric morphology, and optical properties. Therefore, the morphological modeling and visualization of porous materials remain one of the most challenging tasks in the simulation of realistic natural scenes. The work related to the simulation of plant leaves is mainly divided into computer graphics modeling and biological modeling.
4.1 Computer graphics modeling
The more representative approaches in computer graphics modeling are Lindenmayer systems (L-systems), image-based modeling, and particle systems, respectively.
The L-system was proposed by the American biologist Aristid Lindenmayer in 1968 (Lindenmayer, 1968). The method consists of a syntactic system of string rewriting rules. The rules replace each character in the string with the subsequent symbol in parallel, which in turn produces the next string, and the process iterates (Bernard and McQuillan, 2023). In the L-system, each string describes a step in the simulation. Also, each character may have one or more rewriting rules, and each rewriting rule is useful for modeling and simulating plants. The main function of this method is to describe plant topology or plant growth processes using a formal language approach (Prusinkiewicz, 1999).
The image-based modeling is mainly based on the plant pictures provided by the user. Quan et al. (2006) proposed a semi-automatic leaf modeling method to model plant leaves. The method first creates a point cloud using plant images taken from different angles provided by the user. Then, the individual leaves are segmented using the image information. Finally, the segmentation is manually refined to avoid errors due to overlapping leaves. This method is more dependent on the image attributes provided by the user.
The venation pattern of the particle system is established mainly through the particle distribution track. Rodkaew et al. (2004) proposed a particle transport algorithm to simulate the complex vein structure. The algorithm randomly applies particles to the blade, each of which has energy, and points each particle toward the target through transmission rules. When particles get close to each other, they bond to each other to form trajectories that create vein patterns.
4.2 Biological modeling
The curl deformation of plant leaves during drying has a great influence on the transportation, preservation, and quality of processed products. For the modeling of plant leaves, relevant researchers use various modeling methods to analyze the overall geometric structure of leaves, including veins and leaves.
For vein modeling, Hong et al. (2005) proposed an interactive modeling method to establish the three-dimensional skeleton of the vein. The method is based on leaf scanning images, interactive construction and modeling of the skeleton, and automatic generation of membrane mesh. Figure 7 shows the morphological changes of blade aging simulated by this method. The main disadvantage of this method is that it is highly dependent on the leaf attributes provided by the user and neglects the biological and physical principles in the process of plant deformation.

FIGURE 7. Leaf aging process simulation (clockwise sequence) Reproduced from ref (Hong et al., 2005). with permission the John Wiley & Sons, Ltd. Copyright 2005.
By taking into account the biology and physics of plant growth or dehydration, the researchers created a more realistic two-dimensional simulation of leaf veins. Kim and Kim, (2017) designed a contour-based method to model leaf veins. This method can use the growth information detected in the binary image of leaves to model the growth of leaf veins. Runions et al. (2017) modeled the growth process of leaf veins through the biological drive method. Alsweis et al. (2017) proposed a biologically motivated method to simulate the generation of different levels of blade pulse systems. Figure 8 Shows simulations of various leaf types using this method, including different vein patterns and complex leaf shapes. However, these simulations are simulations on a two-dimensional plane.

FIGURE 8. Various types of leaves simulated by biologically motivated method. Reproduced from ref (Alsweis et al., 2017). with permission the John Wiley & Sons, Ltd. Copyright 2016.
The 3D morphological modeling of plants can more accurately analyze the morphological structure and deformation of plants (Marshall-Colon et al., 2017; Louarn and Song, 2020). However, due to the complex morphological structure of plants, 3D modeling of plants is still a challenging issue (Zhao et al., 2019; Yang et al., 2020). The relevant researchers (Duan et al., 2016; Apolo-Apolo et al., 2020) realized 3D modeling of wheat leaves through skeleton-driven methods, which also combined the curling and twisting characteristics of wheat leaves. Although the main topological structure of the blade is retained, the simulation of the three-dimensional morphological characteristics of the blade requires many control points, especially the crimp and twist characteristics of the blade (Fang et al., 2016).
For blade deformation simulation, many studies have made many attempts to improve the efficiency of deformation simulation. Xiao and Chen, (2011) based on the observation of shrinkage stress field, which can simulate the morphology of leaves after drying well. However, the biological principles were not considered. In addition, the article showed that the greater the aspect ratio of different leaves, the greater their curvature after drying. Similar conclusions were found in related literature (Shi et al., 2021; Manishimwe et al., 2022). Jeong et al. (2013) proposed the principle of a two-layer mass-spring model, in which both the leaf vein and leaf flesh models are two-layered. Since the leaf vein and flesh models contain many masses and springs, it leads to a more complicated calculation of this algorithm. Liu et al. (2018) developed a model based on Fick’s law and stress-strain relationship to illustrate the leaf curl pattern. The simulation results showed that the curling deformation of leaves was more pronounced for thickened leaves or high drying temperatures. Sun et al. (2021) proposed an algorithm for simulating dehydration crinkle deformation of plant leaves based on cellular dynamics and time-varying external forces.
5 Drying process for porous materials
5.1 Drying technology
Different drying techniques can be used for material dehydration, such as microwave drying (MD), hot air drying (AD), vacuum drying (VD), freeze-drying (FD), infrared drying (ID), etc.
Microwave drying technology allows for rapid evaporation of water during the drying process of materials, which provides shorter drying times and thus reduced energy consumption during the drying process compared to other drying methods. Compared to hot air drying, products dried by this technique have the advantages of greater shrinkage, faster water absorption, and lower rehydration capacity (Maskan, 2001). Related studies have shown that microwave output power has a significant effect on the drying time as well as the drying rate (Soysal, 2004; Ozkan et al., 2007). The drying rate of the product increases with the increase of microwave output power. On the contrary, the color of the product after drying is not related to the microwave output power. In summary, microwave drying technology offers significant advantages in terms of speed, energy efficiency and quality retention, but it also faces challenges in terms of cost, technical complexity and safety.
The biggest advantage of hot air drying technology is the controllability of the drying process. This technology allows artificial control of process parameters such as drying temperature, drying time, and air velocity during the drying process (Onwude et al., 2016b). Hot air drying can cause degradation or deformation of the material due to the high temperature applied to the material (Orikasa et al., 2008). The drying temperature in hot air drying affects the drying time, shrinkage rate, and color of the product (Zhang et al., 2017; Senadeera et al., 2020).
Freeze-drying techniques require very low pressure or high vacuum to produce good drying rates. Due to the low-temperature conditions, most deterioration and microbial reactions are prevented, resulting in a high-quality product (Ciurzynska and Lenart, 2011; Kurapova et al., 2012). In addition, the solid state of water in the tissue during freeze-drying protects the main structure and shape of the product, which in turn leads to a reduction in shrinkage (Ratti, 2001). Despite its many advantages, freeze-drying is considered to be the most expensive of all drying techniques.
The main advantages of the infrared drying process are fast heating, fast drying speed, uniform product temperature, high controllability of drying process parameters, eco-friendliness, etc. (Nowak and Lewicki, 2004; Kocabiyik and Tezer, 2009) At the same time, the technology also has some limitations, such as the low penetration depth of infrared radiation (Erdogdu et al., 2015) and the long infrared exposure time that hurts the final product color (Wang et al., 2014).
Vacuum drying is characterized by high drying rates and lower drying temperatures. These features provide better sensory and nutritional properties to the product (Wu et al., 2007). However, vacuum drying can lead to shrinkage of the product during drying, resulting in low porosity and brittleness (Arévalo-Pinedo and Murr, 2006; Karam et al., 2016).
5.2 Hybrid drying technology
Hybrid drying technology is a combination of two or more different drying processes. By combining the advantages of different drying methods and reducing the limitations of each method. This results in lower energy requirements and shorter drying times, while maintaining product quality attributes such as flavor, nutrition, aroma, texture, color, (Ai et al., 2022; Maftoonazad et al., 2022; Zhang et al., 2022) etc., Hybrid drying techniques have been shown to have lower energy consumption (Acar et al., 2022; Qu et al., 2022).
5.2.1 Microwave-assisted drying technology
Microwave-assisted drying often used in industrial production are microwave-assisted hot air drying, microwave vacuum drying, and microwave freeze-drying, respectively. Due to the advantages of traditional hot air drying such as low investment cost and ease of operation, it is used in 85% of industrial drying operations. But there are some limitations of hot air drying. However, some limitations of hot air drying, such as long drying time and high drying temperature can lead to the loss of some nutritional values of the product (Gamboa-Santos et al., 2014), dramatic changes in product structure after drying (Gao et al., 2022), and changes in product color and flavor (Huang et al., 2023). Microwave drying accelerates the transfer of moisture from the inside to the outside of the product, greatly reducing the drying time. Therefore, microwave-assisted hot air drying can overcome the limitations of long drying time in hot air drying, and thus improve the drying rate and quality. Geetha, (2022) indicated that microwave-assisted hot air drying retained most of the bioactive molecules of the samples and reduced the loss of volatiles during drying, thus reducing the loss of nutritional value of the product. Gaikwad et al. (2022) showed that microwave hot air drying exhibited higher drying rates and shorter drying times relative to other drying methods, and no swelling was observed on the samples.
Vacuum drying has a long drying time due to the absence of hot air. On the contrary, the microwave is the most efficient way to transfer energy and is the shortest drying time of all drying systems. Therefore, microwave vacuum dryers can improve the drying rate and quality of products. Liu et al. (2023) used a microwave vacuum dryer to dry garlic slices and investigated the effects of microwave power, vacuum, and temperature on the drying characteristics and quality of garlic slices. Studies have shown that compared to hot air drying, microwave vacuum drying can increase the drying rate, improve the quality of dried garlic chips, and consume less energy than vacuum freeze drying. Ishibashi et al. (2022) developed a novel in situ measurement method for microwave vacuum drying that avoids the removal of samples from the vacuum drying chamber. It was found that decreasing the moisture content increased the drying rate when potato and radish samples reached a critical moisture content before they were dried.
The main limitation of freeze drying is the limited heat transfer rate and the absence of a constant drying period. Since water is frozen rather than liquid, this results in a poor heat transfer rate from the outside to the inside of the frozen material. In contrast, microwaves heat the material in a volumetric manner to avoid this localization. Therefore, microwave freeze drying can avoid the limitations of a single drying technique. Li et al. (2022) showed that microwave freeze drying reduced the drying time by 14.29%–35.71% compared to conventional hot air drying. In addition, microwave freeze-dried products were superior to hot air drying in terms of color, water/oil absorption capacity, and solubility. Chen et al. (2023) conducted drying for pineapple slices and showed that microwave freeze drying saved 34.5% of energy consumption and 33.3% of drying time compared to vacuum freeze drying.
5.2.2 Infrared radiation-assisted drying technology
Infrared drying uses infrared radiation as a heat source, thereby increasing the drying temperature and promoting the evaporation of moisture from the product. Infrared radiation has been widely used for drying materials in combination with other drying processes.
Compared with traditional drying methods, the infrared-assisted hot air drying method increases the drying rate of the product while reducing the energy consumption required to dry the product (Onwude et al., 2019; Huang et al., 2022). Jeevarathinam et al. (2022) designed an infrared-assisted hot air dryer for drying turmeric tablets. The results of the study showed that the drying rate of infrared-assisted hot air drying was twice as high as that of infrared drying and hot air drying. Chen et al. (2022) showed that IR-assisted freeze-drying shortens drying time and retains more flavor of quinoa compared to freeze-drying. In contrast to the steaming method, IR-assisted freeze-drying did not destroy the crystalline structure of the starch in raw quinoa and thus could maintain the paste state of the quinoa samples well. Li et al. (2022) created a novel combined drying technique, infrared-assisted tilted tray air impingement drying (IR-TTAID), for drying kiwifruit slices. Compared with TTAID, IR-TTAID reduces the drying time of products by 35.71%–58.33% and energy consumption by 5.96%–27.92% and also obtains higher quality dried products. Zhu et al. (2021) used infrared-assisted spout bed drying for whole peanut fruit (IR-SBD) and compared it with hot air drying and infrared drying. The results showed that the drying time of IR-SBD was reduced by 66% and 32% compared to HD and ID, respectively. The fatty acid content in IR-SBD dried samples was reduced by 4.07% compared to fresh peanut samples.
5.2.3 Solar-assisted drying technology
Since solar energy is a renewable, green, and clean energy source, it is one of the most important applications of solar energy. However, solar dryers are virtually unusable under cloudy skies and have limited control over drying conditions. To overcome this limitation, solar dryers are combined with other energy sources. The technology is called Hybrid Solar Dryer. Hybrid solar drying technology can combine the advantages of solar energy to improve the quality as well as the speed of drying the product.
In recent years, solar drying has been complemented by various traditional drying technologies (Kuan et al., 2019; Hao et al., 2022), such as heat pumps, microwaves, and vacuums. Gu et al. (2022) proposed a novel solar-assisted heat pump (SAPH) for drying grain in grain silos. The operating cost of SAPH grain drying was reduced from $5.57/ton to $1.43/ton compared to conventional dryers. Roratto et al. (2021) developed a hybrid solar vacuum dryer to dry food. This dryer uses solar collectors to provide electrical energy and conductive multiple flash drying (KMFD) for food dehydration. This technology allows you to obtain high-quality dry and crisp products in a short time. Yahya et al. (2017) developed a hybrid solar fluidized bed dryer to dry rice. The dryer uses solar collectors and a heat exchanger with a biomass furnace to heat the drying air.
6 Conclusion
In this paper, the main factors affecting the shrinkage characteristics of porous materials are discussed, the drying theory and deformation simulation of porous materials are summarized, and the drying techniques used in industrial drying products are summarized. The following conclusions can be drawn:
1) The water migration within the cell structure and the characteristics of the cell wall have a great influence on tissue shrinkage. Compared with drying wind speed and drying humidity, drying temperature has more influence on the drying shrinkage of materials. When the drying temperature is lower than the Tg, the material appears in a high-viscosity state, which ultimately leads to the reduction of shrinkage.
2) Relative to macro-scale models and micro-scale models, multi-scale models are an effective approach in drying models. However, the biggest challenge in the development of multi-scale models today is to reduce the modeling difficulty and computational cost, and thus meet the requirements of different accuracy in different studies.
3) Most studies of computer graphics simulation have focused on plant growth simulation. On the contrary, many studies have simulated the deformation of the plant drying process by biological modeling. However, there is a lack of simulation of the drying deformation of porous materials from a mechanical point of view.
4) Different drying techniques for porous materials each have their pros and cons. Hot air drying is easy and cheap but might deform some materials. Microwave drying is quick and saves energy, yet can dry materials unevenly. Freeze drying preserves material structure, ideal for sensitive materials, but it is slow and uses a lot of energy. Infrared drying is fast and efficient, with good quality control, but faces issues with even heating, cost, and safety. Vacuum drying works well for heat-sensitive materials at lower temperatures, though it is expensive. Overall, choosing the right drying technology needs to be based on the specific characteristics of the porous material and the needs of the application.
According to the characteristics and properties of dried products, the influencing factors of porous materials in the drying process are studied, and the selection of suitable drying theory and drying equipment is a decisive factor affecting the storage of dried products as well as energy utilization.
Author contributions
JL: Conceptualization, Writing–review and editing. YH: Conceptualization, Writing–original draft. MG: Writing–original draft. JT: Conceptualization, Data curation, Formal Analysis, Writing–review and editing. GW: Conceptualization, Writing–original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
Authors JL and JT were employed by China Tobacco Zhejiang Industrial Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Acar, C., Dincer, I., and Mujumdar, A. (2022). A comprehensive review of recent advances in renewable-based drying technologies for a sustainable future. Dry. Technol. 40 (6), 1029–1050. doi:10.1080/07373937.2020.1848858
Ahmad, F., Rahimi, A., Tsotsas, E., Prat, M., and Kharaghani, A. (2021). From micro-scale to macro-scale modeling of solute transport in drying capillary porous media. Int. J. Heat. Mass Transf. 165, 120722. doi:10.1016/j.ijheatmasstransfer.2020.120722
Ai, Z., Mowafy, S., and Liu, Y. (2022). Comparative analyses of five drying techniques on drying attributes, physicochemical aspects, and flavor components of Amomum villosum fruits. Lwt 154, 112879. doi:10.1016/j.lwt.2021.112879
Akpinar, E. K., and Bicer, Y. (2005). Modelling of the drying of eggplants in thin-layers. Int. J. Food Sci. Technol. 40 (3), 273–281. doi:10.1111/j.1365-2621.2004.00886.x
Alam, M. S. (2014). Modeling of thin layer drying kinetics of grape juice concentrate and quality assessment of developed grape leather. Agric. Eng. Inter CIGR J. 16 (2), 196–207.
Alsweis, M., Deussenn, O., and Liu, J. (2017). Simulation and visualization of adapting venation patterns. Comput. Animat Virt. W 28 (2), e1723. doi:10.1002/CAV.1723
Apolo-Apolo, O. E., Pérez-Ruiz, M., Martínez-Guanter, J., and Egea, G. (2020). A mixed data-based deep neural network to estimate leaf area index in wheat breeding trials. Agronomy 10 (2), 175. doi:10.3390/agronomy10020175
Arévalo-Pinedo, A., and Murr, F. E. (2006). Kinetics of vacuum drying of pumpkin (Cucurbita maxima): modeling with shrinkage. J. Food Eng. 76 (4), 562–567. doi:10.1016/j.jfoodeng.2005.06.003
Babu, A., Kumaresan, G., Raj, V. A. A., and Velraj, R. (2018). Review of leaf drying: mechanism and influencing parameters, drying methods, nutrient preservation, and mathematical models. Renew. Sust. Energ Rev. 90, 536–556. doi:10.1016/j.rser.2018.04.002
Barati, E., and Esfahani, J. (2012). Mathematical simulation of convective drying: spatially distributed temperature and moisture in carrot slab. Int. J. Therm. Sci. 56, 86–94. doi:10.1016/j.ijthermalsci.2012.01.003
Baudron, V., Gurikov, P., Smirnova, I., and Whitehouse, S. (2019). Porous starch materials via supercritical-and freeze-drying. Gels 5 (1), 12. doi:10.3390/gels5010012
Bernard, J., and McQuillan, I. (2018). “New techniques for inferring L-systems using genetic algorithm,” in Bioinspired Optimization Methods and Their Applications: 8th International Conference, BIOMA, Paris, France, May 16-18, 2018, 13–25.
Bernard, J., and McQuillan, I. (2023). Stochastic L-system inference from multiple string sequence inputs. Soft Comput. 27 (10), 6783–6798. doi:10.1007/s00500-022-07683-8
Çakmak, G., and Yıldız, C. (2011). The drying kinetics of seeded grape in solar dryer with PCM-based solar integrated collector. Food Bioprod. Process 89 (2), 103–108. doi:10.1016/j.fbp.2010.04.001
Cao, X., Zhang, M., Fang, Z., Mujumdar, A. S., Jiang, H., Qian, H., et al. (2017). Drying kinetics and product quality of green soybean under different microwave drying methods. Dry. Technol. 35 (2), 240–248. doi:10.1080/07373937.2016.1170698
Castro, A., Mayorga, E., and Moreno, F. (2018). Mathematical modelling of convective drying of fruits: a review. J. Food Eng. 223, 152–167. doi:10.1016/j.jfoodeng.2017.12.012
Chai, Y., Liang, S., Zhou, Y., Lin, L., and Fu, F. (2019). 3D microscale heat transfer model of the thermal properties of wood-metal functional composites based on the microstructure. Materials 12 (17), 2709. doi:10.3390/ma12172709
Champion, D., Le Meste, M., and Simatos, D. (2000). Towards an improved understanding of glass transition and relaxations in foods: molecular mobility in the glass transition range. Trends Food Sci. Technol. 11 (2), 41–55. doi:10.1016/S0924-2244(00)00047-9
Chen, B.-L., Lin, G.-S., Amani, M., and Yan, W.-M. (2023). Microwave-assisted freeze drying of pineapple: kinetic, product quality, and energy consumption. Case Stud. Therm. Eng. 41, 102682. doi:10.1016/j.csite.2022.102682
Chen, K., Zhang, M., Bhandari, B., and Chen, J. (2022). Instant quinoa prepared by different cooking methods and infrared-assisted freeze drying: effects of variables on the physicochemical properties. Food Chem. 370, 131091. doi:10.1016/j.foodchem.2021.131091
Cieslak, M., Khan, N., Ferraro, P., Soolanayakanahally, R., Robinson, S. J., Parkin, I., et al. (2022). L-system models for image-based phenomics: case studies of maize and canola. silico Plants 4 (1), diab039. doi:10.1093/insilicoplants/diab039
Ciurzynska, A., and Lenart, A. (2011). Freeze-drying-application in food processing and biotechnology-a review. Pol. J. Food Nutr. Sci. 61 (3), 165–171. doi:10.2478/v10222-011-0017-5
Dadali, G., Demirhan, E., and Özbek, B. (2007). Color change kinetics of spinach undergoing microwave drying. Dry. Technol. 25 (10), 1713–1723. doi:10.1080/07373930701590988
Defraeye, T., and Verboven, P. (2017). Convective drying of fruit: role and impact of moisture transport properties in modelling. J. Food Eng. 193, 95–107. doi:10.1016/j.jfoodeng.2016.08.013
Dias, B. S., Navalho, J. E., and Pereira, J. C. (2022). Multi-scale modeling and simulation of IR radiative drying for coil coating processes. Dry. Technol. 40 (16), 3466–3482. doi:10.1080/07373937.2022.2055055
Dissa, A., Desmorieux, H., Savadogo, P., Segda, B., and Koulidiati, J. (2010). Shrinkage, porosity and density behaviour during convective drying of spirulina. J. Food Eng. 97 (3), 410–418. doi:10.1016/j.jfoodeng.2009.10.036
Doymaz, İ., and Ismail, O. (2011). Drying characteristics of sweet cherry. Food Bioprod. process. 89 (1), 31–38. doi:10.1016/j.fbp.2010.03.006
Doymaz, I., and Pala, M. (2002). Hot-air drying characteristics of red pepper. J. Food Eng. 55 (4), 331–335. doi:10.1016/S0260-8774(02)00110-3
Duan, T., Chapman, S., Holland, E., Rebetzke, G., Guo, Y., and Zheng, B. (2016). Dynamic quantification of canopy structure to characterize early plant vigour in wheat genotypes. J. Exp. Bot. 67 (15), 4523–4534. doi:10.1093/jxb/erw227
Ekechukwu, O. (1999). Review of solar-energy drying systems I: an overview of drying principles and theory. Energ Convers. Manage 40 (6), 593–613. doi:10.1016/S0196-8904(98)00092-2
El Tabbal, G., Dangla, P., Vandamme, M., Bottoni, M., and Granet, S. (2020). Modelling the drying shrinkage of porous materials by considering both capillary and adsorption effects. J. Mech. Phys. Solids 142, 104016. doi:10.1016/j.jmps.2020.104016
Erbay, Z., and Icier, F. (2010). A review of thin layer drying of foods: theory, modeling, and experimental results. Crit. Rev. Food Sci. Nutr. 50 (5), 441–464. doi:10.1080/10408390802437063
Erdogdu, S. B., Eliasson, L., Erdogdu, F., Isaksson, S., and Ahrné, L. (2015). Experimental determination of penetration depths of various spice commodities (black pepper seeds, paprika powder and oregano leaves) under infrared radiation. J. Food Eng. 161, 75–81. doi:10.1016/j.jfoodeng.2015.03.036
Ertekin, C., and Firat, M. Z. (2017). A comprehensive review of thin-layer drying models used in agricultural products. Crit. Rev. Food Sci. 57 (4), 701–717. doi:10.1080/10408398.2014.910493
Fang, W., Feng, H., Yang, W., Duan, L., Chen, G., Xiong, L., et al. (2016). High-throughput volumetric reconstruction for 3D wheat plant architecture studies. J. Innov. Opt. Heal Sci. 9 (05), 1650037. doi:10.1142/s1793545816500371
Fanta, S. W., Abera, M. K., Aregawi, W. A., Ho, Q. T., Verboven, P., Carmeliet, J., et al. (2014). Microscale modeling of coupled water transport and mechanical deformation of fruit tissue during dehydration. J. Food Eng. 124, 86–96. doi:10.1016/j.jfoodeng.2013.10.007
Farid, M. (2019). Heat and mass transfer in food processing. Handbook of farm, dairy and food machinery engineering. Amsterdam, Netherlands: Elsevier, 439–460.
Fish, J., Wagner, G. J., and Keten, S. (2021). Mesoscopic and multiscale modelling in materials. Nat. Mater 20 (6), 774–786. doi:10.1038/s41563-020-00913-0
Gaikwad, P. S., Sunil, C., Negi, A., and Pare, A. (2022). Effect of microwave assisted hot-air drying temperatures on drying kinetics of dried black gram papad (Indian snack food): drying characteristics of black gram papad. Appl. Food Res. 2 (2), 100144. doi:10.1016/j.afres.2022.100144
Gamboa-Santos, J., Megías-Pérez, R., Soria, A. C., Olano, A., Montilla, A., and Villamiel, M. (2014). Impact of processing conditions on the kinetic of vitamin C degradation and 2-furoylmethyl amino acid formation in dried strawberries. Food Chem. 153, 164–170. doi:10.1016/j.foodchem.2013.12.004
Gao, M., Wan, K., Miao, Z., He, Q., Xue, S., and Dong, X. (2022). Hot-air drying shrinkage process of lignite and its cracking mechanism. Fuel 316, 123187. doi:10.1016/j.fuel.2022.123187
Gao, M., Yang, B., Huang, Y., and Wang, G. (2021a). Effects of general imperfect interface/interphase on the in-plane conductivity of thermal composites. Int. J. Heat. Mass Tran 172, 121213. doi:10.1016/j.ijheatmasstransfer.2021.121213
Gao, X., Lu, L., Shahnam, M., Rogers, W. A., Smith, K., Gaston, K., et al. (2021b). Assessment of a detailed biomass pyrolysis kinetic scheme in multiscale simulations of a single-particle pyrolyzer and a pilot-scale entrained flow pyrolyzer. Chem. Eng. J. 418, 129347. doi:10.1016/j.cej.2021.129347
Geetha, P. (2022). Effect of microwave assisted hot air drying (MAHD) on volatiles of Moringa oleifera Lam. Pharma Innovation J. 11, 2878.
Golpour, I., Nejad, M. Z., Chayjan, R. A., Nikbakht, A. M., Guiné, R. P., and Dowlati, M. (2017). Investigating shrinkage and moisture diffusivity of melon seed in a microwave assisted thin layer fluidized bed dryer. J. Food Meas. Charact. 11, 1–11. doi:10.1007/s11694-016-9365-5
González-Cavieres, L., Perez-Won, M., Tabilo-Munizaga, G., Jara-Quijada, E., Díaz-Álvarez, R., and Lemus-Mondaca, R. (2021). Advances in vacuum microwave drying (vmd) systems for food products. Trends Food Sci. Tech. 116, 626–638. doi:10.1016/j.tifs.2021.08.005
Gu, X., Dai, J., Li, H., and Dai, Y. (2022). Experimental and theoretical assessment of a solar assisted heat pump system for in-bin grain drying: a comprehensive case study. Renew. Energ 181, 426–444. doi:10.1016/j.renene.2021.09.049
Gulati, T., and Datta, A. K. (2015). Mechanistic understanding of case-hardening and texture development during drying of food materials. J. Food Eng. 166, 119–138. doi:10.1016/j.jfoodeng.2015.05.031
Halder, A., Datta, A. K., and Spanswick, R. M. (2011). Water transport in cellular tissues during thermal processing. Aiche J. 57 (9), 2574–2588. doi:10.1002/aic.12465
Haman, J., and Konstankiewicz, K. (2000). Destruction processes in the cellular medium of a plant-theoretical approach. Int. Agrophys 14 (1). doi:10.1109/AIEEPAS.1953.4498693
Hao, W., Liu, S., Lai, Y., Wang, M., and Liu, S. (2022). Research on drying Lentinus edodes in a direct expansion heat pump assisted solar drying system and performance of different operating modes. Renew. Energ 196, 638–647. doi:10.1016/j.renene.2022.07.034
He, Z., Wang, G., and Pindera, M.-J. (2019). Multiscale homogenization and localization of materials with hierarchical porous microstructures. Compos Struct. 222, 110905. doi:10.1016/j.compstruct.2019.110905
Hii, C. L., Ong, S. P., Yap, J. Y., Putranto, A., and Mangindaan, D. (2021). Hybrid drying of food and bioproducts: a review. Dry. Technol. 39 (11), 1554–1576. doi:10.1080/07373937.2021.1914078
Hong, S. M., Simpson, B., and Vg Baranoski, G. (2005). Interactive venation-based leaf shape modeling. Comput. Animat Virt. W 16 (3-4), 415–427. doi:10.1002/cav.88
Hu, B., Cheng, Y., and Pan, Z. (2023). Classification methods of pore structures in coal: a review and new insight. Gas. Sci. Eng. 110, 204876. doi:10.1016/j.jgsce.2023.204876
Huang, X., Li, Y., Zhou, X., Wang, J., Zhang, Q., Yang, X., et al. (2022). Prediction of apple slices drying kinetic during infrared-assisted-hot air drying by deep neural networks. Foods 11 (21), 3486. doi:10.3390/foods11213486
Huang, Y., Sun, Y., Lu, T., and Chen, X. (2023). Effects of hot-air drying on the bioactive compounds, quality attributes, and drying and color change kinetics of coffee leaves. J. Food Sci. 88 (1), 214–227. doi:10.1111/1750-3841.16431
Inyang, U. E., Oboh, I. O., and Etuk, B. R. (2018). Kinetic models for drying techniques—food materials. Adv. Chem. Eng. 8 (02), 27–48. doi:10.4236/aces.2018.82003
Ishibashi, R., Numata, T., Tanigawa, H., and Tsuruta, T. (2022). In-situ measurements of drying and shrinkage characteristics during microwave vacuum drying of radish and potato. J. Food Eng. 323, 110988. doi:10.1016/j.jfoodeng.2022.110988
Ishizaki, K., Komarneni, S., and Nanko, M. (2013). Porous materials: process technology and applications. Berlin, Germany: Springer science and business media.
Janjai, S., Lamlert, N., Mahayothee, B., Bala, B., Precoppe, M., and Muller, J. (2011). Thin layer drying of peeled longan (Dimocarpus longan Lour.). Food Sci. Technol. Res. 17 (4), 279–288. doi:10.3136/fstr.17.279
Jeevarathinam, G., Pandiselvam, R., Pandiarajan, T., Preetha, P., Krishnakumar, T., Balakrishnan, M., et al. (2022). Design, development, and drying kinetics of infrared-assisted hot air dryer for turmeric slices. J. Food Process Eng. 45 (6), e13876. doi:10.1111/jfpe.13876
Jeong, S., Park, S. H., and Kim, C. H. (2013). Simulation of morphology changes in drying leaves. Comput. Graph. Forum 32, 204–215. doi:10.1111/cgf.12009
Joardder, M. U., Brown, R. J., Kumar, C., and Karim, M. (2015). Effect of cell wall properties on porosity and shrinkage of dried apple. Int. J. Food Prop. 18 (10), 2327–2337. doi:10.1080/10942912.2014.980945
Joardder, M. U., and Karim, M. (2019). Development of a porosity prediction model based on shrinkage velocity and glass transition temperature. Dry. Technol. 37 (15), 1988–2004. doi:10.1080/07373937.2018.1555540
Joardder, M. U., Kumar, C., and Karim, M. (2018). Prediction of porosity of food materials during drying: current challenges and directions. Crit. Rev. Food Sci. Nutr. 58 (17), 2896–2907. doi:10.1080/10408398.2017.1345852
Joudi-Sarighayeh, F., Abbaspour-Gilandeh, Y., Kaveh, M., and Hernández-Hernández, J. L. (2022). The optimization of the physical–thermal and bioactive properties of pumpkin slices dried in a hybrid microwave–convective dryer using the response surface method. Agronomy 12 (10), 2291. doi:10.3390/agronomy12102291
Kalantari, D., Naji-Tabasi, S., Kaveh, M., Azadbakht, M., Majnooni, M., Khorshidi, Y., et al. (2023). Drying kinetics and shrinkage rate of thin-sliced pears in different drying stages. J. Food Process Eng. 46 (3), e14264. doi:10.1111/jfpe.14264
Karam, M. C., Petit, J., Zimmer, D., Djantou, E. B., and Scher, J. (2016). Effects of drying and grinding in production of fruit and vegetable powders: a review. J. Food Eng. 188, 32–49. doi:10.1016/j.jfoodeng.2016.05.001
Karunasena, H., Senadeera, W., Brown, R. J., and Gu, Y. (2014a). Simulation of plant cell shrinkage during drying–A SPH–DEM approach. Eng. Anal. Bound Elem. 44, 1–18. doi:10.1016/j.enganabound.2014.04.004
Karunasena, H., Senadeera, W., Brown, R. J., and Gu, Y. (2014b). A particle based model to simulate microscale morphological changes of plant tissues during drying. Soft Matter 10 (29), 5249–5268. doi:10.1039/c4sm00526k
Katekawa, M. E., and Silva, M. A. (2007). On the influence of glass transition on shrinkage in convective drying of fruits: a case study of banana drying. Dry. Technol. 25 (10), 1659–1666. doi:10.1080/07373930701590863
Khan, M. I. H., Joardder, M., Kumar, C., and Karim, M. (2018a). Multiphase porous media modelling: a novel approach to predicting food processing performance. Crit. Rev. Food Sci. Nutr. 58 (4), 528–546. doi:10.1080/10408398.2016.1197881
Khan, M. I. H., and Karim, M. (2017). Cellular water distribution, transport, and its investigation methods for plant-based food material. Food Res. Int. 99, 1–14. doi:10.1016/j.foodres.2017.06.037
Khan, M. I. H., Nagy, S. A., and Karim, M. (2018b). Transport of cellular water during drying: an understanding of cell rupturing mechanism in apple tissue. Food Res. Int. 105, 772–781. doi:10.1016/j.foodres.2017.12.010
Khan, M. I. H., Wellard, R. M., Mahiuddin, M., and Karim, M. A. (2017a). “Cellular level water distribution and its investigation techniques,” in Intermittent and nonstationary drying technologies: principles and applications (United States of America: CRC Press), 193–210. doi:10.4324/9781351251303
Khan, M. I. H., Wellard, R. M., Nagy, S. A., Joardder, M., and Karim, M. (2017b). Experimental investigation of bound and free water transport process during drying of hygroscopic food material. Int. J. Therm. Sci. 117, 266–273. doi:10.1016/j.ijthermalsci.2017.04.006
Kim, D., and Kim, J. (2017). Procedural modeling and visualization of multiple leaves. Multimed. Syst. 23, 435–449. doi:10.1007/s00530-016-0503-z
Kocabiyik, H., and Tezer, D. (2009). Drying of carrot slices using infrared radiation. Int. J. Food Sci. Technol. 44 (5), 953–959. doi:10.1111/j.1365-2621.2008.01767.x
Kovler, K., and Zhutovsky, S. (2006). Overview and future trends of shrinkage research. Mater Struct. 39, 827–847. doi:10.1617/s11527-006-9114-z
Kuan, M., Shakir, Y., Mohanraj, M., Belyayev, Y., Jayaraj, S., and Kaltayev, A. (2019). Numerical simulation of a heat pump assisted solar dryer for continental climates. Renew. Energ 143, 214–225. doi:10.1016/j.renene.2019.04.119
Kumar, C., Joardder, M., Farrell, T. W., and Karim, M. (2016). Multiphase porous media model for intermittent microwave convective drying (IMCD) of food. Int. J. Therm. Sci. 104, 304–314. doi:10.1016/j.ijthermalsci.2016.01.018
Kurapova, O. Y., Golubev, S., Ushakov, V., and Konakov, V. (2017). Stabilization of cubic zirconia based solid solutions obtained by cryochemical techniques: thermodynamic and kinetic factors. Rev. Adv. Mater Sci. 48 (2).
Kurapova, O. Y., Konakov, V., Golubev, S., Ushakov, V., and Archakov, I. Y. (2012). Cryochemical methods for manufacturing nanosized ceramics and ceramic precursor powders with low agglomeration degree: a review. Rev. Adv. Mater Sci. 32, 112–132.
Kurapova, O. Y., Nechaeva, D., Ivanov, A., Golubev, S., Ushakov, V., and Konakov, V. (2016). Thermal evolution of the microstructure of calcia stabilized zirconia precursors manufactured by cryochemical technique. Rev. Adv. Mater Sci. 47 (1-2), 95–104.
Lelièvre, D., Nicolas, V., Glouannec, P., and Ploteau, J. P. (2012). “Numerical modelling of heat and mass transfer in porous materials during drying and shrinkage,” in COMSOL conference, Newton, Massachusetts, October 3-5 2012.
Lemus-Mondaca, R. A., Vega-Gálvez, A., Zambra, C. E., and Moraga, N. O. (2017). Modeling 3D conjugate heat and mass transfer for turbulent air drying of Chilean papaya in a direct contact dryer. Heat. Mass Transf. 53, 11–24. doi:10.1007/s00231-016-1799-0
Li, J., Deng, Y., Xu, W., Zhao, R., Chen, T., Wang, M., et al. (2022a). Multiscale modeling of food thermal processing for insight, comprehension, and utilization of heat and mass transfer: a state-of-the-art review. Trends Food Sci. Tech. 131, 31–45. doi:10.1016/j.tifs.2022.11.018
Li, L., Chen, J., Bai, D., Xu, M., Cao, W., Ren, G., et al. (2022b). Physicochemical, pasting properties and in vitro starch digestion of Chinese yam flours as affected by microwave freeze-drying. Foods 11 (15), 2324. doi:10.3390/foods11152324
Li, M., Ai, Z., Xiao, H., Mowafy, S., Pei, Y., and Liu, Y. (2022c). Improvement of drying efficiency and physicochemical quality of kiwifruit slices using infrared-assisted tilted tray air impingement drying. Dry. Technol. 41, 1159–1170. doi:10.1080/07373937.2022.2125526
Lindenmayer, A. (1968). Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. J. Theor. Biol. 18 (3), 280–299. doi:10.1016/0022-5193(68)90079-9
Liu, C., Guo, X., and Wang, L. (2018). Experiment on and simulation of moisture transfer and rolling deformation during leaf drying. Dry. Technol. 36 (14), 1653–1661. doi:10.1080/07373937.2017.1421219
Liu, J., Liu, Y., Li, X., Zhu, J., Wang, X., and Ma, L. (2023). Drying characteristics, quality changes, parameters optimization and flavor analysis for microwave vacuum drying of garlic (Allium sativum L.) slices. LWT 173, 114372. doi:10.1016/j.lwt.2022.114372
Louarn, G., and Song, Y. (2020). Two decades of functional–structural plant modelling: now addressing fundamental questions in systems biology and predictive ecology. Ann. Bot-London 126 (4), 501–509. doi:10.1093/aob/mcaa143
Lowell, S., Shields, J. E., Thomas, M. A., and Thommes, M. (2012). Characterization of porous solids and powders: surface area, pore size and density. Berlin, Germany: Springer Science and Business Media.
Lu, L., Gao, X., Shahnam, M., and Rogers, W. A. (2021). Simulations of biomass pyrolysis using glued-sphere CFD-DEM with 3-D intra-particle models. Chem. Eng. J. 419, 129564. doi:10.1016/j.cej.2021.129564
Luo, J., Li, M., Zhang, Y., Zheng, M., and Ming Ling, C. (2021). The low-field NMR studies the change in cellular water in tilapia fillet tissue during different drying conditions. Food Sci. Nutr. 9 (5), 2644–2657. doi:10.1002/fsn3.2221
Maftoonazad, N., Dehghani, M. R., and Ramaswamy, H. S. (2022). Hybrid microwave-hot air tunnel drying of onion slices: drying kinetics, energy efficiency, product rehydration, color, and flavor characteristics. Dry. Technol. 40 (5), 966–986. doi:10.1080/07373937.2020.1841790
Mahiuddin, M., Khan, M. I. H., Kumar, C., Rahman, M. M., and Karim, M. (2018). Shrinkage of food materials during drying: current status and challenges. Compr. Rev. Food Sci. F. 17 (5), 1113–1126. doi:10.1111/1541-4337.12375
Manishimwe, A., Ntirugulirwa, B., Zibera, E., Nyirambangutse, B., Mujawamariya, M., Dusenge, M. E., et al. (2022). Warming responses of leaf morphology are highly variable among tropical tree species. Forests 13 (2), 219. doi:10.3390/f13020219
Marshall-Colon, A., Long, S. P., Allen, D. K., Allen, G., Beard, D. A., Benes, B., et al. (2017). Crops in silico: generating virtual crops using an integrative and multi-scale modeling platform. Front. Plant Sci. 8, 786. doi:10.3389/fpls.2017.00786
Maskan, M. (2001). Drying, shrinkage and rehydration characteristics of kiwifruits during hot air and microwave drying. J. Food Eng. 48 (2), 177–182. doi:10.1016/S0260-8774(00)00155-2
Masters, K. (1996). Deposit-free spray drying: dream or reality. Proc. Tenth Int. Dry. Symp. IDS 96, 52–60.
McMinn, W., and Magee, T. (1997). Physical characteristics of dehydrated potatoes—Part I. J. Food Eng. 33 (1-2), 37–48. doi:10.1016/S0260-8774(97)00039-3
Menon, A., Stojceska, V., and Tassou, S. A. (2020). A systematic review on the recent advances of the energy efficiency improvements in non-conventional food drying technologies. Trends Food Sci. Technol. 100, 67–76. doi:10.1016/j.tifs.2020.03.014
Mugi, V. R., and Chandramohan, V. (2021). Shrinkage, effective diffusion coefficient, surface transfer coefficients and their factors during solar drying of food products–A review. Sol. Energy 229, 84–101. doi:10.1016/j.solener.2021.07.042
Mutuli, G. P., Gitau, A. N., and Mbuge, D. O. (2020). Convective drying modeling approaches: a review for herbs, vegetables, and fruits. Biosyst. Eng. 45, 197–212. doi:10.1007/s42853-020-00056-9
Mutuli, G. P., and Mbuge, D. (2015). Drying characteristics and energy requirement of drying cowpea leaves and jute mallow vegetables. Agric. Eng. Inter CIGR J. 17 (4), 265–272.
Nguyen, T. K., Mondor, M., and Ratti, C. (2018). Shrinkage of cellular food during air drying. J. Food Eng. 230, 8–17. doi:10.1016/j.jfoodeng.2018.02.017
Nimmo, J. R. (2004). Porosity and pore size distribution. Encycl. Soils Environ. 3 (1), 295–303. doi:10.1016/B978-0-12-409548-9.05265-9
Nowak, D., and Lewicki, P. P. (2004). Infrared drying of apple slices. Innov. Food Sci. Emerg. 5 (3), 353–360. doi:10.1016/j.ifset.2004.03.003
Omolola, A. O., Jideani, A. I. O., Kapila, P. F., and Jideani, V. A. (2015). Optimization of microwave drying conditions of two banana varieties using response surface methodology. Food Sci. Tech. 35, 438–444. doi:10.1590/1678-457X.6700
Onwude, D. I., Hashim, N., Abdan, K., Janius, R., and Chen, G. (2019). The effectiveness of combined infrared and hot-air drying strategies for sweet potato. J. Food Eng. 241, 75–87. doi:10.1016/j.jfoodeng.2018.08.008
Onwude, D. I., Hashim, N., and Chen, G. (2016b). Recent advances of novel thermal combined hot air drying of agricultural crops. Trends Food Sci. Technol. 57, 132–145. doi:10.1016/j.tifs.2016.09.012
Onwude, D. I., Hashim, N., Janius, R. B., Nawi, N. M., and Abdan, K. (2016a). Modeling the thin-layer drying of fruits and vegetables: a review. Compr. Rev. Food Sci. F. 15 (3), 599–618. doi:10.1111/1541-4337.12196
Orikasa, T., Wu, L., Shiina, T., and Tagawa, A. (2008). Drying characteristics of kiwifruit during hot air drying. J. Food Eng. 85 (2), 303–308. doi:10.1016/j.jfoodeng.2007.07.005
Ozkan, I. A., Akbudak, B., and Akbudak, N. (2007). Microwave drying characteristics of spinach. J. Food Eng. 78 (2), 577–583. doi:10.1016/j.jfoodeng.2005.10.026
Pal, N., and Bhaumik, A. (2013). Soft templating strategies for the synthesis of mesoporous materials: inorganic, organic–inorganic hybrid and purely organic solids. Adv. Colloid Interface Sci. 189, 21–41. doi:10.1016/j.cis.2012.12.002
Papasidero, D., Manenti, F., and Pierucci, S. (2015). Bread baking modeling: coupling heat transfer and weight loss by the introduction of an explicit vaporization term. J. Food Eng. 147, 79–88. doi:10.1016/j.jfoodeng.2014.09.031
Pirasteh, G., Saidur, R., Rahman, S., and Rahim, N. (2014). A review on development of solar drying applications. Renew. Sust. Energy Rev. 31, 133–148. doi:10.1016/j.rser.2013.11.052
Prawiranto, K., Carmeliet, J., and Defraeye, T. (2020). Identifying in silico how microstructural changes in cellular fruit affect the drying kinetics. Soft Matter 16 (43), 9929–9945. doi:10.1039/d0sm00749h
Proietti, N., Adiletta, G., Russo, P., Buonocore, R., Mannina, L., Crescitelli, A., et al. (2018). Evolution of physicochemical properties of pear during drying by conventional techniques, portable-NMR, and modelling. J. Food Eng. 230, 82–98. doi:10.1016/j.jfoodeng.2018.02.028
Prusinkiewicz, P. (1999). A look at the visual modeling of plants using L-systems. Agronomie 19 (3-4), 211–229. doi:10.1007/BFb0033200
Qu, H., Masud, M., Islam, M., Khan, M. I. H., Ananno, A. A., and Karim, A. (2022). Sustainable food drying technologies based on renewable energy sources. Crit. Rev. Food Sci. Nutr. 62 (25), 6872–6886. doi:10.1080/10408398.2021.1907529
Quan, L., Tan, P., Zeng, G., Yuan, L., Wang, J., and Kang, S. B. (2006). Image-based plant modeling. ACM Siggraph, 599–604. doi:10.1145/1179352.1141929
Rahman, M., Mustayen, A., Mekhilef, S., and Saidur, R. (2015). The optimization of solar drying of grain by using a genetic algorithm. Int. J. Green Energy 12 (12), 1222–1231. doi:10.1080/15435075.2014.890106
Rahman, M. M. (2018). Microscale modelling of cellular level transport and deformation during food drying. Australia: Queensland University of Technology. doi:10.1016/j.ces.2018.04.060
Rahman, M. M., Kumar, C., Joardder, M. U., and Karim, M. (2018). A micro-level transport model for plant-based food materials during drying. Chem. Eng. Sci. 187, 1–15. doi:10.1016/j.ces.2018.04.060
Ratti, C. (2001). Hot air and freeze-drying of high-value foods: a review. J. Food Eng. 49 (4), 311–319. doi:10.1016/S0260-8774(00)00228-4
Rodkaew, Y., Chongstitvatana, P., Siripant, S., and Lursinsap, C. (2004). “Modeling plant leaves in marble-patterned colours with particle transportation system,” in 4th International workshop on functional-structural plant models, Montpellier, France, 7-11 June 2004, 391–397.
Roos, Y. H. (1995). Glass transition-related physicochemical changes in foods: chemical and rheological changes during phase transition in food. Food technol-Chicago 49 (10), 97–102. doi:10.1177/108201329500100209
Roratto, T. B., Monteiro, R. L., Carciofi, B. A., and Laurindo, J. B. (2021). An innovative hybrid-solar-vacuum dryer to produce high-quality dried fruits and vegetables. Lwt 140, 110777. doi:10.1016/j.lwt.2020.110777
Runions, A., Tsiantis, M., and Prusinkiewicz, P. (2017). A common developmental program can produce diverse leaf shapes. New Phytol. 216 (2), 401–418. doi:10.1111/nph.14449
Sano, Y., Kubota, S., Kawarazaki, A., Kawamura, K., Kashiwai, H., and Kuwahara, F. (2019). Mathematical model for coffee extraction based on the volume averaging theory. J. Food Eng. 263, 1–12. doi:10.1016/j.jfoodeng.2019.05.025
Sappati, P. K., Nayak, B., and van Walsum, G. P. (2017). Effect of glass transition on the shrinkage of sugar kelp (Saccharina latissima) during hot air convective drying. J. Food Eng. 210, 50–61. doi:10.1016/j.jfoodeng.2017.04.018
Senadeera, W., Adiletta, G., Önal, B., Di Matteo, M., and Russo, P. (2020). Influence of different hot air drying temperatures on drying kinetics, shrinkage, and colour of persimmon slices. Foods 9 (1), 101. doi:10.3390/foods9010101
Shahari, N., Jamil, N., and Rasmani, K. (2016). Comparative study of shrinkage and non-shrinkage model of food drying. J. Phys. Conf. Ser. 738, 012087. doi:10.1088/1742-6596/738/1/012087
Shahmirzadi, M. R., Gholampour, A., Kashani, A., and Ngo, T. D. (2021). Shrinkage behavior of cementitious 3D printing materials: effect of temperature and relative humidity. Cem. Concr. Comp. 124, 104238. doi:10.1016/j.cemconcomp.2021.104238
Shi, P.-J., Li, Y.-R., Niinemets, Ü., Olson, E., and Schrader, J. (2021b). Influence of leaf shape on the scaling of leaf surface area and length in bamboo plants. Trees 35, 709–715. doi:10.1007/s00468-020-02058-8
Shi, S., Feng, J., An, G., Kong, B., Wang, H., Pan, N., et al. (2021a). Dynamics of heat transfer and moisture in beef jerky during hot air drying. Meat Sci. 182, 108638. doi:10.1016/j.meatsci.2021.108638
Shishehgarha, F., Makhlouf, J., and Ratti, C. (2002). Freeze-drying characteristics of strawberries. Dry. Technol. 20 (1), 131–145. doi:10.1081/DRT-120001370
Shukla, S. (2011). Freeze drying process: a review. Int. J. Pharm. Sci. Res. 2 (12), 3061. doi:10.13040/ijpsr.0975-8232.2(12).3061-68
Sickert, T., Bergmann, R., Christoph, J., and Gaukel, V. (2023). A time-saving approach to parameter studies in microwave-assisted freeze drying. Processes 11 (10), 2886. doi:10.3390/pr11102886
Siddiqui, S. A., Bahmid, N. A., Asif, Z., and Shah, M. A. (2023). Consumers left at the mercy of chefs for potency, consistency, safety and regulation—the edibles industry of cannabinoids—a critical review. Int. J. Food Sci. Technol. 58 (10), 5433–5448. doi:10.1111/ijfs.16603
Sinha, A., and Bhargav, A. (2022). A simplified modelling approach for predicting shrinkage and sensitive material properties during low temperature air drying of porous food materials. J. Food Eng. 317, 110732. doi:10.1016/j.jfoodeng.2021.110732
Soysal, Y. (2004). Microwave drying characteristics of parsley. Biosyst. Eng. 89 (2), 167–173. doi:10.1016/j.biosystemseng.2004.07.008
Süfer, Ö., and Palazoğlu, T. K. (2019). A study on hot-air drying of pomegranate: kinetics of dehydration, rehydration and effects on bioactive compounds. J. Therm. Anal. Calorim. 137, 1981–1990. doi:10.1007/s10973-019-08102-1
Sun, X., Fu, J., Chen, T., and Dong, Y. (2021). Wrinkle and curl distortion of leaves using plant dynamic. Graph Models 118, 101118. doi:10.1016/j.gmod.2021.101118
Taghinezhad, E., Kaveh, M., Jahanbakhshi, A., and Golpour, I. (2020a). Use of artificial intelligence for the estimation of effective moisture diffusivity, specific energy consumption, color and shrinkage in quince drying. J. Food Process Eng. 43 (4), e13358. doi:10.1111/jfpe.13358
Taghinezhad, E., Kaveh, M., Jahanbakhshi, A., and Golpour, I. (2020b). Use of artificial intelligence for the estimation of effective moisture diffusivity, specific energy consumption, color and shrinkage in quince drying. J. Food Process Eng. 43 (4), e13358. doi:10.1111/jfpe.13358
Tao, Y., Li, D., Chai, W. S., Show, P. L., Yang, X., Manickam, S., et al. (2021). Comparison between airborne ultrasound and contact ultrasound to intensify air drying of blackberry: heat and mass transfer simulation, energy consumption and quality evaluation. Ultrason. Sonochem 72, 105410. doi:10.1016/j.ultsonch.2020.105410
Tian, L., Wang, G., Zhao, H., Yuan, M., Peng, Y., and Chen, J. (2021). A novel multiscale semi-analytical approach for thermal properties of fuzzy fiber reinforced composites. Compos Struct. 275, 114424. doi:10.1016/j.compstruct.2021.114424
Tzempelikos, D. A., Vouros, A. P., Bardakas, A. V., Filios, A. E., and Margaris, D. P. (2015). Experimental study on convective drying of quince slices and evaluation of thin-layer drying models. Eng. Agric. Environ. Food 8 (3), 169–177. doi:10.1016/j.eaef.2014.12.002
Van Liedekerke, P., Ghysels, P., Tijskens, E., Samaey, G., Roose, D., and Ramon, H. (2011). Mechanisms of soft cellular tissue bruising. A particle based simulation approach. Soft Matter 7 (7), 3580–3591. doi:10.1039/c0sm01261k
Wang, H., Karim, M., Vidyarthi, S. K., Xie, L., Liu, Z.-L., Gao, L., et al. (2021). Vacuum-steam pulsed blanching (VSPB) softens texture and enhances drying rate of carrot by altering cellular structure, pectin polysaccharides and water state. Innov. Food Sci. Emerg. 74, 102801. doi:10.1016/j.ifset.2021.102801
Wang, L., Zhang, M., Fang, Z., and Xu, B. (2014). Application of intermediate-wave infrared drying in preparation of mushroom chewing tablets. Dry. Technol. 32 (15), 1820–1827. doi:10.1080/07373937.2014.949347
Wang, N., and Brennan, J. (1995). Changes in structure, density and porosity of potato during dehydration. J. Food Eng. 24 (1), 61–76. doi:10.1016/0260-8774(94)P1608-Z
Wang, X., Li, L., and Chai, W. (2013). Geometric modeling of broad-leaf plants leaf based on B-spline. Math. Comp. Model Dyn. 58 (3-4), 564–572. doi:10.1016/j.mcm.2011.10.064
Wang, Z., Xu, J., Wang, P., Zhang, Y., You, J., and Li, C. (2019). Noncloggingly sieving sub-6 nm nanoparticles of noble metals into conductive mesoporous foams with biological nanofibrils. ACS Nano 14 (1), 828–834. doi:10.1021/acsnano.9b07923
Wehbe, N., Sanchez, A. B., Dalmon, J., Guilhaume, N., Homs, N., Li, Y., et al. (2009). Characterisation and modelling of metal deposition in catalytic composite membranes. Rev. Adv. Mater Sci. 21, 57–74.
Welsh, Z., Simpson, M., and Karim, A. (2022). “A multiscale model to determine homogenized diffusivity for convective drying of food material,” in Proceedings of the 22nd international drying symposium (IDS) (USA: Worcester Polytechnic Institute). doi:10.1016/j.jfoodeng.2020.110252
Welsh, Z. G., Khan, M. I. H., and Karim, M. (2021a). Multiscale modeling for food drying: a homogenized diffusion approach. J. Food Eng. 292, 110252. doi:10.1016/j.jfoodeng.2020.110252
Welsh, Z. G., Simpson, M. J., Khan, M. I. H., and Karim, A. (2021b). A multiscale approach to estimate the cellular diffusivity during food drying. Biosyst. Eng. 212, 273–289. doi:10.1016/j.biosystemseng.2021.10.017
Welsh, Z. G., Simpson, M. J., Khan, M. I. H., and Karim, M. (2023). Generalized moisture diffusivity for food drying through multiscale modeling. J. Food Eng. 340, 111309. doi:10.1016/j.jfoodeng.2022.111309
Wu, L., Orikasa, T., Ogawa, Y., and Tagawa, A. (2007). Vacuum drying characteristics of eggplants. J. Food Eng. 83 (3), 422–429. doi:10.1016/j.jfoodeng.2007.03.030
Wu, X.-F., Zhang, M., and Li, Z. (2019). Dehydration modeling of Cordyceps militaris in mid-infrared-assisted convection drying system: using low-field nuclear magnetic resonance with the aid of ELM and PLSR. Dry. Technol. 37, 2072–2086. doi:10.1080/07373937.2018.1555843
Xiao, H., and Chen, X. (2011). Modeling and simulation of curled dry leaves. Soft Matter 7 (22), 10794–10802. doi:10.1039/c1sm05998j
Yahya, M., Fudholi, A., and Sopian, K. (2017). Energy and exergy analyses of solar-assisted fluidized bed drying integrated with biomass furnace. Renew. Energ 105, 22–29. doi:10.1016/j.renene.2016.12.049
Yang, W., Feng, H., Zhang, X., Zhang, J., Doonan, J. H., Batchelor, W. D., et al. (2020). Crop phenomics and high-throughput phenotyping: past decades, current challenges, and future perspectives. Mol. Plant 13 (2), 187–214. doi:10.1016/j.molp.2020.01.008
Zdravkov, B., Čermák, J., Šefara, M., and Janků, J. (2007). Pore classification in the characterization of porous materials: a perspective. Open Chem. 5 (2), 385–395. doi:10.2478/s11532-007-0017-9
Zhang, M., Bhandari, B., and Fang, Z. (2017). Handbook of drying of vegetables and vegetable products. United States: CRC Press.1351648713
Zhang, Y., Yuan, C., Ding, J., Zhuang, Y., Li, Y., Wang, C., et al. (2022). A novel method for low-cost and rapid preparation of nanoporous phenolic aerogels and its performance regulation mechanism. Rev. Adv. Mater Sci. 61 (1), 817–828. doi:10.1515/rams-2022-0262
Zhao, C., Zhang, Y., Du, J., Guo, X., Wen, W., Gu, S., et al. (2019). Crop phenomics: current status and perspectives. Front. Plant Sci. 10, 714. doi:10.3389/fpls.2019.00714
Zhao, D., An, K., Ding, S., Liu, L., Xu, Z., and Wang, Z. (2014). Two-stage intermittent microwave coupled with hot-air drying of carrot slices: drying kinetics and physical quality. Food bioprocess Tech. 7, 2308–2318. doi:10.1007/s11947-014-1274-1
Zhu, K., Li, L., Ren, G., Duan, X., Cao, W., and Qiu, C. (2021). Efficient production of dried whole peanut fruits based on infrared assisted spouted bed drying. Foods 10 (10), 2383. doi:10.3390/foods10102383
Ziari, H., Fazaeli, H., Kang, V., Olyaei, S. J., and Ziari, M. A. (2022). Evaluation of effects of temperature, relative humidity, and wind speed on practical characteristics of plastic shrinkage cracking distress in concrete pavement using a digital monitoring approach. Int. J. Pavement Res. Technol. 15 (1), 138–158. doi:10.1007/s42947-021-00016-2
Keywords: porous materials, energy conversion efficiency, shrinkage property, drying model, morphological simulation, drying technology
Citation: Li J, Huang Y, Gao M, Tie J and Wang G (2024) Shrinkage properties of porous materials during drying: a review. Front. Mater. 11:1330599. doi: 10.3389/fmats.2024.1330599
Received: 31 October 2023; Accepted: 08 February 2024;
Published: 21 February 2024.
Edited by:
Ayrat Gizzatov, Aramco Americas: Aramco Research Center-Boston, United StatesReviewed by:
Hongkui Zheng, University of California, Irvine, United StatesWei Zuo, Wuhan University of Science and Technology, China
Copyright © 2024 Li, Huang, Gao, Tie and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mengyuan Gao, ODI3Nzg1ODI0QHFxLmNvbQ==; Jinxin Tie, dGllamlueGluQHpqdG9iYWNjby5jb20=
 Jie Li1
Jie Li1 Mengyuan Gao
Mengyuan Gao