Orbital character and electron correlation effects on two- and three-dimensional Fermi surfaces in KFe2As2 revealed by angle-resolved photoemission spectroscopy

Introduction

In contrast to the d-wave superconducting gaps in the high-T_c cuprate superconductors, experimental results on most of the iron-pnictide superconductors have indicated that superconducting gaps are nodeless and on the entire Fermi surfaces (FSs) [1]. However, some of the iron pnictide superconductors show signatures of the nodes in the superconducting gaps. For example, thermal conductivity measurements of isovalent substituted system BaFe₂(As_{1 − x}P_x)₂ [2] and the electron doped systems Ba(Fe_{1 − x}Co_x)₂As₂ and Ba(Fe_{1 − x}Ni_x)₂As₂ [3] in the superconducting state have shown signature of line nodes. According to the theories of spin fluctuation-mediated superconductivity, line nodes may appear when the pnictogen height becomes small [4, 5], the hole FS of d_xy character around the zone center disappears and nesting between hole and electron FSs becomes weakened. (Here, x and y are referred to the direction of the nearest neighbor Fe atoms). The hole FSs of these systems exhibit strong three-dimensionality [6–8], resulting in poor nesting between the hole and electron FSs.

The end member compound of K-doped BaFe₂As₂ (K-Ba122) system, KFe₂As₂, with a low T_c of ~4 K [9] also shows signature of line nodes in penetration depth [10], thermal conductivity [11], and nuclear quadrupole resonance (NQR) measurements [12]. In fact, a recent laser angle-resolved photoemission (ARPES) study of KFe₂As₂ has revealed a superconducting gap with “octet-line nodes” on the middle hole FS (ζ FS) [13]. The observed nodes and a clear FS sheet dependence in the superconducting-gap size were well explained by a calculation with spin-fluctuation mechanism. However, the result is in strong contrast to the optimally doped K-Ba122 [14], while this is consistent with the evolution of the gaps as a function of K doping [15]. Such a doping dependence in the superconducting gap may be related to the change in the FS topology. In going from the optimally [15, 16] to the overdoped region [17, 18] in K-Ba122 system, the electron pockets around the zone corner are replaced by small hole pockets surrounding the zone corner in a clover shape.

If the spin fluctuations are dominant in the pairing mechanism in KFe₂As₂, orbital dependent mass renormalization would be observed as a signature of spin fluctuations. So far, strong mass renormalization has been observed from the electronic specific heat coefficient γ as large as ~70–100 mJ/K² mol [12, 19]. Also, both the ARPES [18] and dHvA studies [20, 21] have indicated the enhancement of the electron masses compared to those predicted by the band-structure calculation.

Although three hole FSs (α, β, and ζ) have been clearly resolved in our previous ARPES study [18], the mass renormalization factor for each FS has not been clarified yet. In the present study, in order to reveal the orbital dependent mass renormalization in the iron-based superconductors, we have performed an ARPES study of KFe₂As₂ using high-quality single crystals. We have determined the orbital character of the FSs by polarization dependent measurements and have revealed strongly orbital dependent correlation effects.

Experiment and Band-Structure Calculation

ARPES measurements were performed at beamline 5–4 of Stanford Synchrotron Radiation Lightsource (SSRL) and at BL10.0.1 of Advanced Light Source (ALS). Scienta SES-R4000 electron analyzers and linearly polarized light were used at both beamlines. The typical energy resolutions were 10 meV at SSRL and 20 meV at ALS, respectively. Single crystals of KFe₂As₂ were grown from a self-flux method. Resistivity measurements on some of the grown crystals showed the residual resistivity ratio of ~600. Samples were cleaved in situ and measured at a temperature of 15 K in a pressure better than 5 × 10⁻¹¹ Torr. We have performed the measurements at photon energies from hν = 14 to 40 eV. The in-plane (k_X, k_Y) and out-of-plane (k_Z) momentum are expressed in units of π/a and 2π/c, respectively, where a = 3.864 Å and c = 13.87 Å. Here, the X and Y axes point toward the Fe-As bond direction, while the x and y axes are rotated by 45° from the X-Y coordination. The electronic band structure of KFe₂As₂ was calculated within the local density approximation (LDA) by using the full potential LAPW (FLAPW) method. We used the program codes TSPACE [22] and KANSAI-06. The experimental crystal structure [23] including the atomic position z_As of As (pnictogen height) was used for the calculation.

Results and Discussion

Band dispersions for a cut along the diagonal of the two-dimensional Brillouin zone (BZ) taken with hν = 25 eV [18] and 30 eV are shown in Figures 1A,B. All the energy bands predicted by the calculation (Figure 1C) are observed. While three bands (α, β, and ζ) form hole FSs around the zone center, the ε band forms small hole FSs around the zone corner. The structure around 0.15 eV below E_F in Figure 1A is z² band shown in Figure 1C, which has a strong three dimensionality [18]. Another hole-like band crossing E_F near the zone center is a surface state [18]. While the ζ band is nearly degenerated with the α band at hν = 25 eV, these bands are separated at hν = 30 eV, indicating three-dimensionality of the band dispersions. Note that the order of the α, β, and ζ bands from the zone center is different between theory and experimental data. We shall describe the present assignment of the band dispersions based on the matrix-element effect data as below.

FIGURE 1

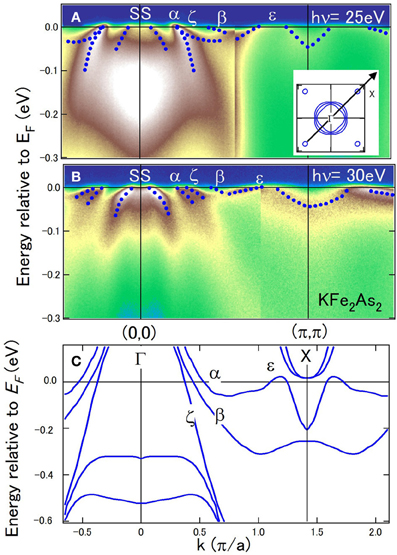
Figure 1. Band dispersions of KFe₂As₂ in the zone diagonal direction. (A,B) ARPES spectra taken at hν = 25 eV [18] and 30 eV, respectively, corresponding to k_z = 6.5 and 7.0 (2π/c). SS denotes surface states. (C) Band dispersions predicted by band-structure calculation.

FS mapping in k_X-k_Y plane is shown in Figures 2A,B. By assuming the inner potential V₀ = 13.0 eV (Figures 2A,B) approximately represent k_X-k_Y planes including the Γ and the Z point, respectively. All the three hole FSs around the center of the 2D BZ have been clearly resolved and small hole FSs appear around the BZ corner due to heavy hole doping. In Figure 2B, the surface states near the zone center form ridge-like structures extending to the k_X and k_Y directions, causing the peculiar cross-like intensity distribution [18]. We found that the middle hole FS (ζ) has different shape between the Γ and the Z point, indicating strong three dimensionality.

FIGURE 2

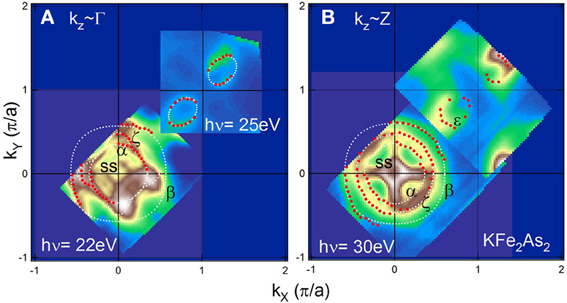
Figure 2. FSs of KFe₂As₂ observed by ARPES. ARPES intensity at E_F mapped in the k_X-k_Y plane taken at different photon energies corresponding to k_z ~ Γ (A) and k_z ~ Z (B). Red dots indicate k_F positions determined by the peak positions of momentum distribution curves (MDC's) and white dotted lines indicate FSs deduced from the k_F positions.

In Figure 3, we compare the FSs obtained by ARPES with the band-structure calculation. As seen in (Figures 3A,B), the sizes of the observed α and β FSs do not show appreciable change with k_z. On the other hand, the shape of the ζ FS significantly changes between k_z ~ Γ and Z. While the ζ FS has a diamond-like cross-section for k_z ~ Γ and is nearly degenerate with the α FS in the zone diagonal direction, it has a circular cross-section for k_z ~ Z. Such a change is seen in the inner-most calculated hole FS in Figures 3C,D.

FIGURE 3

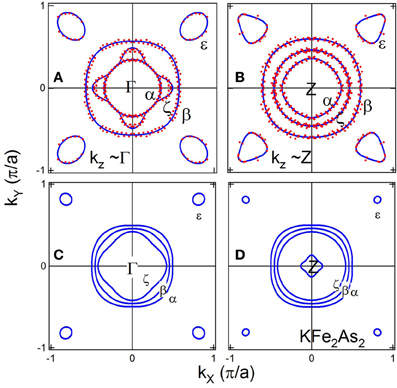
Figure 3. Comparison of FSs obtained by ARPES and those predicted by band-structure calculation. (A,B) FSs determined by ARPES. k_F positions in Figure 2 have been symmetrized in the first BZ. (C,D) FSs given by the band-structure calculation. A small FS around the Z point comes from a three-dimensional d_z2 band.

In order to determine the orbital character of the FSs, we have investigated the polarization dependence of the ARPES intensity as shown in Figure 4. FS mapping shown in (Figures 4A,B) indicates clear polarization dependence in the intensity distribution for each FS. We have simulated the intensity distribution by using the following assumptions. Based on the result of the band-structure calculation, we assume that three orbitals xy, yz, and zx constitute the FSs. We refer to the three band as xy, yz, and zx band according to the orbital character of the band with momentum in the zone diagonal k_x (// k_X + k_Y) direction. Using the angle θ around the Γ point, the orbital character of the xy, zx, and yz band can be approximately expressed by |xy>, cosθ |zx> + sinθ |yz> and -sinθ |zx> + cosθ |yz>, respectively. By assuming the dipole approximation of the transition matrix element |< i|ε · r|f >|², where |i>, |f >, and ε are the initial state, the final state, and the polarization vector, respectively, one can predict the intensity distribution. For example, when |i >=|xy>, ε //x and |f > is a wave function of a free electron, the transition matrix element |< i|ε · r|f >|² is proportional to k²_y in the lowest order in k.

FIGURE 4

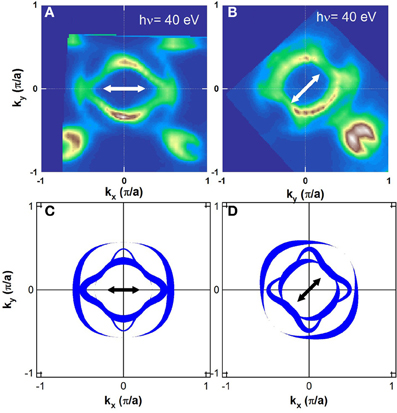
Figure 4. Polarization dependence of the FS mapping for KFe₂As₂. (A,B) Measured ARPES intensity at E_F in the k_X-k_Y plane taken at hν = 40 eV (k_z ~ Γ). Electric vectors are shown by arrows. (C,D) Simulation of the ARPES intensity distribution corresponding to (A,B). Shapes of FSs have been taken from Figure 2. By assuming certain orbital character for each FS, intensity distribution has been simulated and is shown by thickness of the curves (For details, see the text).

Figures 4C,D are the results of the intensity simulations of the FSs whose shapes have been determined by the present experimental data. Here, we assign the inner, middle, and outer FSs to the yz, xz, and xy-band, respectively, so that we can reproduce the experimental intensity distribution. This assignment of the orbital character is different from the band-structure calculation where the inner, middle, and outer FSs have xz, xy, and yz orbital character, respectively. However, the present ARPES result is consistent with the previous ARPES result of Co-Ba122 [24] and the theoretical prediction of LDA+DMFT [25], which indicate the energy inversion of the xy and yz/xz bands due to orbital-dependent correlation effect. This trend is also consistent with an ARPES result of LiFeAs [26]. That is, the xy band in most strongly affected by electron correlation and is shifted upward relative to the other bands.

Another discrepancy from the band-structure calculation is the inversion of the yz and xz bands in the k_X (k_Y) direction. In the result of the band-structure calculation, the inner FS has xz character (in the k_X direction) with rounded-square shape around the Γ point and becomes circular around the Z point because of hybridization with the z² orbital. In the present ARPES result, such a character has been observed in the middle ζ FS. According to the angular-dependent magnetoresistance oscillations, such a rounded-square FS is also bigger than a circular hole FS [27]. The observed inversion of the xz, yz bands is consistent with the ARPES result of Co-Ba122 [24] and the LDA+DMFT calculation for KFe₂As₂ [25].

In the dHvA study, the sizes of the hole FSs are found to be smaller than those predicted by band-structure calculations [9]. We have determined the cross-sectional area of the FSs as listed in Table 1 together with those of the dHvA measurements and the band-structure calculation. The cross-sectional areas for the α and ζ FSs observed by ARPES are close to those obtained by the dHvA result and are smaller than the band-structure calculation. On the other hand, the area of the β and ε FSs determined by ARPES are much larger than the calculation results. The total hole count from the observed FSs yields the hole FS volume of 61% of the BZ, indicating a deviation from the value of 50% expected from the chemical composition, because most of the FSs observed by ARPES are nearly 10–20% larger than those observed by dHvA. The deviation of the FS volume implies that there is excess hole doping of 0.11 per Fe atom at the sample surface. Nevertheless, the surface effect is not so serious as those in 1111 system where excess 0.5–0.6 holes per Fe are doped [28], and one can still discuss mass renormalization from the present result.

TABLE 1

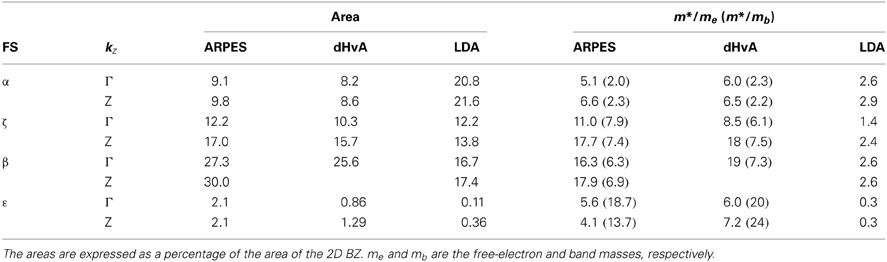
Table 1. Cross-sectional areas and effective masses of FSs of KFe₂As₂ determined by ARPES and dHvA experiment [20, 21].

The effective masses determined by ARPES are compared with those derived from the dHvA measurements and the band-structure calculation in Table 1. For all the FSs, the effective mass ratio m*/m_e, where m_e is the free electron mass, determined by ARPES is in good agreement with those obtained by dHvA. For the hole FSs around the zone center, the outer β and middle ζ FSs show large renormalization factor of m*/m_b ~6–7, while the inner α FS has a smaller factor m*/m_b ~2. The strong mass enhancement for the β and ζ band may be due to the fact that the orbitals are directed to the Fe-As bond direction, causing the enhancement of electron correlation effects. Particularly, according to LDA+DMFT calculation [19, 25], a larger mass renormalization is expected in the xy band than those of the yz/xz bands. Thus, the observed mass enhancement factors indicate moderate to strong electron correlation. From the effective masses m* listed in Table 1, the electronic specific heat coefficient γ is calculated to be γ~90 mJ/molK², which is close to γ = 103 mJ/molK² estimated from specific heat measurements [19].

The penetration depth [10] and thermal conductivity [11] measurements of KFe₂As₂ suggest that line nodes exist in the superconducting gap. Particularly, recent thermal conductivity result [29] has been interpreted based on the d-wave symmetry in KFe₂As₂. Because the small hole FSs around the zone corner are too small to account for the linear temperature dependence of the superfluid density [10], the node should be on the zone-centered hole FSs. In fact, the “octet-node” has been observed in the ζ hole FS by the laser ARPES study [13]. Based on the spin-fluctuation-mediated model calculation, the octet node can be interpreted as vertical nodes with A_1g gap symmetry, which originates from the 3z²−r² orbital character of the ζ hole FS. Such octet nodes may not contradict with the observation of the node on the small hole pockets in Ba_0.1K_0.9Fe₂As₂ [30], if the vertical nodal line with A_1g gap symmetry rapidly shifts in the momentum space with hole doping. On the other hand, a small-angle neutron scattering measurement on KFe₂As₂ has suggested the existence of a horizontal node [31]. One should note that both the vertical and horizontal nodes [32–34] can be realized in the region of the FS with 3z²−r² orbital character. In the present work, we revealed that the ζ FS has a strong three-dimensionality compared to the other FSs, implying a significant amount of the 3z²−r² character in the ζ FS.

Conclusion

We have performed an ARPES study of KFe₂As₂ to investigate orbital-dependent correlation effects. The orbital character of each FS is determined by the polarization dependence of the ARPES intensity. The value of the electron mass renormalization for each band indicates orbital-dependent correlation effects and is consistent with the dHvA result [20, 21] and the DMFT calculation [25]. Particularly, the β and ζ FS show large mass enhancement of m*/m_b ~ 6–7. Only the middle hole FS ζ shows a clear three-dimensionality, suggestive of 3z²−r² orbital character, which may be related to the “octet nodes” [13]. The precise determination of the orbital dependent mass renormalization in the present study would give constraint on the pairing mechanism with line nodes.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to K. Kuroki, R. Arita, H. Fukazawa, T. Terashima and M. Kimata for enlightening discussions. Thanks are also due to K. Haule for showing us the result of LDA-DMFT calculations prior to publication. This work was supported by the Japan-China-Korea A3 Foresight Program and a Grant-in-Aid for Young Scientist (B) (22740221) from the Japan Society for the Promotion of Science. SSRL is operated by the US DOE Office of Basic Energy Science Divisions of Chemical Sciences and Material Sciences. ALS is supported by the U.S. DOE (Contract No. DE-AC02-05CH11231).

References

1. Ding H, Richard P, Nakayama K, Sugawara K, Arakane T, Sekiba Y, et al. Observation of Fermi-surface-dependent nodeless superconducting gaps in Ba_0.6K_0.4Fe₂As₂. Europhys Lett. (2008) 83:47001. doi: 10.1209/0295-5075/83/47001

CrossRef Full Text

2. Hashimoto K, Yamashita M, Kasahara S, Senshu Y, Nakata N, Tonegawa S, et al. Line nodes in the energy gap of superconducting BaFe₂(As_1−xP_x)₂ single crystals as seen via penetration depth and thermal conductivity. Phys Rev B (2010) 81:220501. doi: 10.1103/PhysRevB.81.220501

CrossRef Full Text

3. Reid JP, Tanatar MA, Luo XG, Shakeripour H, Doiron-Leyraud N, Ni N, et al. Nodes in the gap structure of the iron arsenide superconductor Ba(Fe_1−xCo_x)₂As₂ from c-axis heat transport measurements. Phys Rev B (2010) 82:064501. doi: 10.1103/PhysRevB.82.064501

CrossRef Full Text

4. Kuroki K, Usui H, Onari S, Arita R, Aoki H. Pnictogen height as a possible switch between high-T_c nodeless and low-T_c nodal pairings in the iron-based superconductors. Phys. Rev. B (2009) 79:224511. doi: 10.1103/PhysRevB.79.224511

CrossRef Full Text

5. Ikeda H, Arita R, Kuneš J. Phase diagram and gap anisotropy in iron-pnictide superconductors. Phys Rev B (2010) 81:054502. doi: 10.1103/PhysRevB.81.054502

CrossRef Full Text

6. Yoshida T, Nishi I, Ideta S, Fujimori A, Kubota M, Ono K, et al. Two-Dimensional and Three-Dimensional Fermi surfaces of superconducting BaFe₂(As_1−xP_x)₂ and their nesting properties revealed by angle-resolved photoemission spectroscopy. Phys Rev Lett. (2011) 106:117001. doi: 10.1103/PhysRevLett.106.117001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

7. Malaeb W, Yoshida T, Fujimori A, Kubota M, Ono K, Kihou K, et al. Three-Dimensional electronic structure of superconducting iron pnictides observed by angle-resolved photoemission spectroscopy. J Phys Soc Jpn. (2009) 78:123706. doi: 10.1143/JPSJ.78.123706

CrossRef Full Text

8. Vilmercati P, Fedorov A, Vobornik I, Manju U, Panaccione G, Goldoni A, et al. Evidence for three-dimensional Fermi-surface topology of the layered electron-doped iron superconductor Ba(Fe_1−xCo_x)₂As₂. Phys Rev B (2009) 79:220503. doi: 10.1103/PhysRevB.79.220503

CrossRef Full Text

9. Terashima T, Kimata M, Satsukawa H, Harada A, Hazama K, Uji S, et al. Resistivity and upper critical field in KFe₂As₂ single crystals. J Phys Soc Jpn. (2009) 78:063702. doi: 10.1143/JPSJ.78.063702

CrossRef Full Text

10. Hashimoto K, Serafin A, Tonegawa S, Katsumata R, Okazaki R, Saito T, et al. Evidence for superconducting gap nodes in the zone-centered hole bands of KFe₂As₂ from magnetic penetration-depth measurements. Phys Rev B (2010) 82:014526. doi: 10.1103/PhysRevB.82.014526

CrossRef Full Text

11. Dong JK, Zhou SY, Guan TY, Zhang H, Dai YF, Qiu X, et al. Quantum criticality and nodal superconductivity in the FeAs-Based superconductor KFe₂As₂. Phys Rev Lett. (2010) 104:087005. doi: 10.1103/PhysRevLett.104.087005

CrossRef Full Text

12. Fukazawa H, Yamada Y, Kondo K, Saito T, Kohori Y, Kuga K, et al. Possible multiple gap superconductivity with line nodes in heavily hole-doped superconductor KFe₂As₂ studied by 75As nuclear quadrupole resonance and specific heat. J Phys Soc Jpn. (2009) 78:083712. doi: 10.1143/JPSJ.78.083712

CrossRef Full Text

13. Okazaki K, Ota Y, Kotani Y, Malaeb W, Ishida Y, Shimojima T, et al. Octet-Line node structure of superconducting order parameter in KFe₂As₂. Science (2012) 337:1314. doi: 10.1126/science.1222793

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Shimojima T, Sakaguchi F, Ishizaka K, Ishida Y, Kiss T, Okawa M, et al. Orbital-Independent superconducting gaps in iron pnictides. Science (2011) 332:564. doi: 10.1126/science.1202150

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Malaeb W, Shimojima T, Ishida Y, Okazaki K, Ota Y, Ohgushi K, et al. Abrupt change in the energy gap of superconducting Ba_1−xK_xFe₂As₂ single crystals with hole doping. Phys Rev B (2012) 86:165117. doi: 10.1103/PhysRevB.86.165117

CrossRef Full Text

16. Zabolotnyy VB, Inosov DS, Evtushinsky DV, Koitzsch A, Kordyuk AA, Sun GL, et al. (π, π) electronic order in iron arsenide superconductors. Nature (2009) 457:569. doi: 10.1038/nature07714

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

17. Sato T, Nakayama K, Sekiba Y, Richard P, Xu YM, Souma S, et al. Band structure and Fermi surface of an extremely overdoped iron-based superconductor KFe₂As₂. Phys Rev Lett. (2009) 103:047002. doi: 10.1103/PhysRevLett.103.047002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

18. Yoshida T, Nishi I, Fujimori A, Yi M, Moore R, Lu DH, et al. Fermi surfaces and quasi-particle band dispersions of the iron pnictides superconductor KFe₂As₂ observed by angle-resolved photoemission spectroscopy. J Phys Chem Solids (2011) 72:465. doi: 10.1016/j.jpcs.2010.10.064

CrossRef Full Text

19. Hardy F, Böhmer AE, Aoki D, Burger P, Wolf T, Schweiss P, et al. Evidence of strong correlations and coherence-incoherence crossover in the iron pnictide superconductor KFe₂As₂. Phys Rev Lett. (2013) 111:027002. doi: 10.1103/PhysRevLett.111.027002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

20. Terashima T, Kimata M, Kurita N, Satsukawa H, Harada A, Hazama K, et al. Fermi surface and mass enhancement in KFe₂As₂ from de Haas–van Alphen effect measurements. J Phys Soc Jpn. (2010) 79:053702. doi: 10.1143/jpsj.79.053702

CrossRef Full Text

21. Terashima T, Kurita N, Kimata M, Tomioka M, Tsuchiya S, Imai M, et al. Fermi surface in KFe₂As₂ determined via de Haas–van Alphen oscillation measurements. Phys Rev B (2013) 87:224512. doi: 10.1103/PhysRevB.87.224512

CrossRef Full Text

22. Yanase A. FORTRAN Program for Space Group. 1st ed. Shokabo, Tokyo (1985).

23. Rozsa S, Schuster HUZ. Crystal-structure of KFe₂As₂, KCo₂As₂, KRh₂As₂ and KRh₂P₂. Naturforsch B (1981) 36:1668.

24. Zhang Y, Chen F, He C, Zhou B, Xie BP, Fang C, et al. Orbital characters of bands in the iron-based superconductor BaFe_1.85Co_0.15As₂. Phys Rev B (2011) 83:054510. doi: 10.1103/PhysRevB.83.054510

CrossRef Full Text

25. Yin ZP, Haule K, Kotliar G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat Mater. (2011) 10:932. doi: 10.1038/nmat3120

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

26. Lee G, Ji HS, Kim Y, Kim C, Haule K, Kotliar G, et al. Orbital selective fermi surface shifts and mechanism of high T_c superconductivity in correlated AFeAs (A=Li, Na). Phys Rev Lett. (2012) 109:177001. doi: 10.1103/PhysRevLett.109.177001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

27. Kimata M, Terashima T, Kurita N, Satsukawa H, Harada A, Kodama K, et al. Quasi-Two-Dimensional fermi surfaces and coherent interlayer transport in KFe₂As₂. Phys Rev Lett. (2010) 105:246403. doi: 10.1103/PhysRevLett.105.246403

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Nishi I, Ishikado M, Ideta S, Malaeb W, Yoshida T, Fujimori A, et al. Angle-resolved photoemission spectroscopy study of PrFeAsO_0.7: comparison with LaFePO. Phys Rev B (2011) 84:014504. doi: 10.1103/PhysRevB.84.014504

CrossRef Full Text

29. Reid J-Ph, Tanatar MA, Juneau-Fecteau A, Gordon RT, René de Cotret S, Doiron-Leyraud N, et al. Universal heat conduction in the iron arsenide superconductor KFe₂As₂: evidence of a d-Wave State. Phys Rev Lett. (2012) 109:087001. doi: 10.1103/PhysRevLett.109.087001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

30. Xu N, Richard P, Shi X, van Roekeghem A, Qian T, Razzoli E, et al. Possible nodal superconducting gap and Lifshitz transition in heavily hole-doped Ba_0.1K_0.9Fe₂As₂. Phys Rev B (2013) 88:220508. doi: 10.1103/PhysRevB.88.220508

CrossRef Full Text

31. Kawano-Furukawa H, Bowell CJ, White JS, Heslop RW, Cameron AS, Forgan EM, et al. Gap in KFe₂As₂ studied by small-angle neutron scattering observations of the magnetic vortex lattice. Phys Rev B (2011) 84: 024507. doi: 10.1103/PhysRevB.84.024507

CrossRef Full Text

32. Graser S, Kemper AF, Maier TA, Cheng HP, Hirschfeld PJ, Scalapino DJ. Spin fluctuations and superconductivity in a three-dimensional tight-binding model for BaFe₂As₂. Phys Rev B (2010) 81:214503. doi: 10.1103/PhysRevB.81.214503

CrossRef Full Text

33. Suzuki K, Usui H, Kuroki K. Possible Three-Dimensional nodes in the s± superconducting gap of BaFe₂(As_1−xP_x)₂. J Phys Soc Jpn. (2011) 80:013710. doi: 10.1143/JPSJ.80.013710

CrossRef Full Text

34. Suzuki K, Usui H, Kuroki K. Spin fluctuations and unconventional pairing in KFe₂As₂. Phys Rev B (2011) 84:144514. doi: 10.1103/PhysRevB.84.144514

CrossRef Full Text