- 1Institute for Mathematics, Freie Universität Berlin, Berlin, Germany
- 2Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin, Germany
We make use of supersymmetric quantum mechanics (SUSY QM) to find three sets of conditions under which the problem of a planar quantum pendulum becomes analytically solvable. The analytic forms of the pendulum's eigenfuntions make it possible to find analytic expressions for observables of interest, such as the expectation values of the angular momentum squared and of the orientation and alignment cosines as well as of the eigenenergy. Furthermore, we find that the topology of the intersections of the pendulum's eigenenergy surfaces can be characterized by a single integer index whose values correspond to the sets of conditions under which the analytic solutions to the quantum pendulum problem exist.
1. Introduction
The quantum pendulum problem has a venerable history stretching back to the early days of quantum mechanics. First tackled by Condon in 1928 [1] in its planar variety, the quantum pendulum has since turned up in a number of research areas of atomic, molecular and optical physics, ranging from spectroscopy to the stereodynamics of molecular collisions to the manipulation of matter by external electric, magnetic and optical fields. Although both the planar and the full-fledged 3D spherical pendular varieties possess analytic asymptotic states [2–10], the planar case has been explored with particular tenacity [11–19], apparently because of its prototypical character, dwarfed only by that of few other systems such as of the harmonic oscillator.
The planar quantum pendulum or planar hindered rotor problem has been extensively employed to model internal molecular rotation and molecular torsion in spectroscopy [20–22] and coherent control [23–25] as well as molecular orientation and alignment in spectroscopy and photodissociation dynamics [14, 26]. However, unlike the spherical pendulum, the planar pendulum has not been used so far to treat molecules subject to combined fields [27–32].
The spherical quantum pendulum in combined fields has been the subject of a recent study based on supersymmetric quantum mechanics (SUSY QM) [33, 34], which resulted in finding an analytic solution to the problem for a particular class of states (the stretched states) and a particular ratio of the dimensionless parameters that characterize the strengths of the external fields that restrict the system's motion to to and fro pendular librations [35, 36]. A follow-up study [37] revealed a close kinship between the conditions under which an analytic solution is obtained and the topology of the intersections of the eigenenergy surfaces spanned by the dimensionless parameters.
In this study, we seek—and find—analytic solutions for three sets of conditions that render the planar quantum pendulum problem (corresponding to a planar rotor subject to combined fields) analytically solvable and investigate the relationship between these sets of conditions and the topology of the planar pendulum's eigenenergy surfaces. We also make use of the analytic eigenfunctions to find the observables of interest—such as the expectation values of the angular momentum squared and of the orientation and alignment cosines as well as of the eigenenergy—likewise in analytic form.
The Hamiltonian of the planar quantum pendulum problem has the general form
where is the angular momentum and rotational constant with I the moment of inertia. Note that in what follows we will assume B = 1, which is equivalent to dividing all energies by B. In the Hamiltonian of Equation (1) the potential
is restricted to the lowest two Fourier terms and −π ≤ θ ≤ π is a periodic coordinate. Since the cosθ and cos2θ terms generate, respectively, oriented (single-arrow-like) and aligned (double-arrow-like) states, we term the two interactions orienting and aligning. Their strengths are characterized, respectively, by the dimensionless parameters η ≥ 0 and ζ ≥ 0. For η = ζ = 0, the Hamiltonian of Equation (1) becomes that of a planar rotor.
This paper is organized as follows: In section 2 we present, in turn, the cases of a purely orienting interaction, purely aligning interaction and of a combined orienting and aligning interaction and identify a condition for the intersections—genuine or avoided—of the eigenenergy surfaces. We find that the topology of the intersections can be characterized by a single topological index. In section 3, we present three sets of conditions that lead to an analytic solution of the quantum pendulum problem and find that these conditions correspond to particular values of the topological index. In section 4, we provide a summary of the present work and discuss its connections to related work.
2. Eigenproperties
2.1. Pure Orienting Interaction: η > 0 & ζ = 0
When the planar rotor interacts with an external field solely via the orienting interaction, the Schrödinger equation for Hamiltonian of Equation (1), (H − E)ψ = 0, becomes isomorphic with the Mathieu equation [38]
whose characteristic values λ for the interaction parameter q = −2η and coordinate are related to the eigenenergies E by λ = 4E, cf. the classic work on the quantum pendulum [1, 11] and also Friedrich et al. and Leibscher and Schmidt [14, 19]. Then the required 2π periodicity, ψ(θ + 2π) = ψ(θ), of the problem in the original coordinate transforms into a π periodicity, ψ(x + π) = ψ(x), in the Mathieu coordinate. Hence, the admissible solutions to the Schrödinger equation for Hamiltonian (1) with ζ = 0 are only the even-order Mathieu cosine elliptic, ce2r(θ/2; −2η), or sine elliptic, se2r+2(θ/2; −2η), functions. Table 1 lists the Fourier representations of these states (see the 1st and 4th rows) as well as the relationships between Mathieu functions with q positive and negative (the latter needed here) that are obtained upon substituting x → (π/2 − x) or θ → (π − θ) [4, 5, 39]. In Table 1 and in what follows the characteristic values λ are referred to as a and b for the even (ce) and odd (se) parity eigenfunctions, respectively.
The energy levels and wavefunctions for a pure orienting interaction are exemplified in the left panel of Figure 1 for η = 12.5. While the states below the barrier qualitatively resemble those of a harmonic oscillator, the states above the barrier approach those of a free rotor, with (nearly) degenerate pairs of states of even and odd parity (with respect to θ = 0).
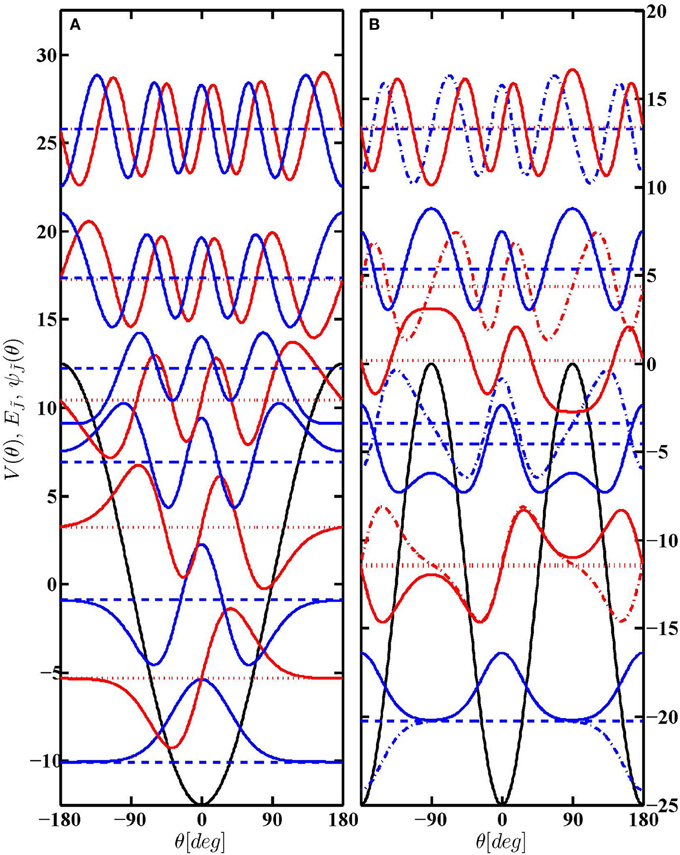
Figure 1. Eigenenergies and eigenfunctions pertaining to Hamiltonian of Equation (1). Left panel (A): purely orienting interaction with η = 12.5, ζ = 0. Right panel (B): purely aligning interaction with η = 0, ζ = 25, where the tunneling doublets can be understood as zeroth-order intersection, κ = 0, see section 2.3. Wavefunctions of even and odd parity (with respect to θ = 0) are drawn in blue and red, respectively. In the right panel, full versus dash-dotted curves are used to distinguish between even and odd parity (with respect to θ = π/2).
The dependence of the eigenenergies E of the lowest 11 states on the orienting interaction parameter η is shown in Figure 2. In the field-free limit, η → 0, the wavefunctions become those of a free planar rotor (i.e., cer(x) → cos (rx) or ser(x) → sin (rx) for r ≠ 0 and ce0(x) → 1/); the corresponding energy levels approach a quadratic energy progression. In the strong field limit, η → ∞, the eigenproperties become those of a harmonic angular oscillator (harmonic librator), which exhibits a linear progression of equidistant energy levels and a zero-point energy. The asymptotic expansion of the characteristic values, Equation (20.2.30) of Abramovitz and Stegun [4], yields the harmonic librator eigenenergies
where v = 0, 1, 2, … is the harmonic librator quantum number and the librator quantum.
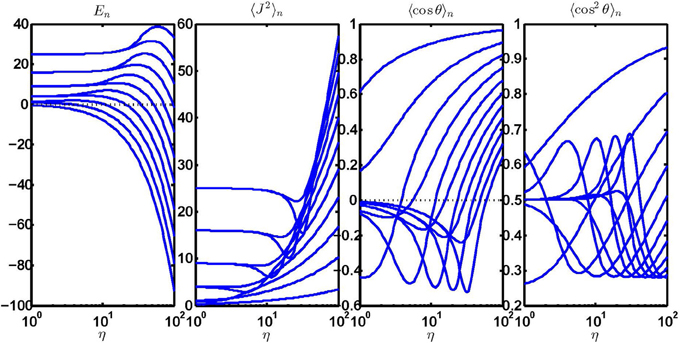
Figure 2. Eigenproperties of the planar quantum pendulum subject to a purely orienting interaction as a function of the interaction parameter η. The four panels show the eigenergies and the expectation values of the squared angular momentum, 〈J2〉, orientation cosine, 〈cos θ〉, and alignment cosine, 〈cos2 θ〉.
In Figure 2 we also show the expectation values of the angular momentum squared, 〈J2〉, and the directional characteristics of the states, the orientation cosine, 〈cos θ〉, and the alignment cosine, 〈cos2 θ〉, as functions of the orientation parameter η for ζ = 0. Except for the lowest states of each symmetry (i.e., ce0 and se0), the states exhibit the Stern wrong-way orientation/alignment effect [14]: they become first anti-oriented, 〈cos θ〉 → −1, or anti-aligned, 〈cos2 θ〉 → 0, at low η, before conforming to the direction of the orienting field at large η.
2.2. Pure Aligning Interaction: η = 0 & ζ > 0
Next, we consider the case when the planar rotor interacts with the external field solely via the aligning interaction, i.e., ζ > 0 and η = 0. Also in this case, the corresponding Schrödinger equation is isomorphic with the Mathieu equation (3) but here the characteristic values λ for a scaled interaction parameter q = −ζ/4 and coordinate x = θ are related to the eigenenergies E via λ = E + ζ/2, see also Friedrich et al. and Leibscher and Schmidt [14, 19]. Hence, the required 2π periodicity, ψ(θ + 2π) = ψ(θ), is satisfied for all four classes of Mathieu functions, i.e., for even- and odd-order Mathieu cosine-elliptic and sine-elliptic functions: ce2r(θ; −ζ/4), se2r+1(θ; −ζ/4), ce2r+1(θ; −ζ/4), and se2r+2(θ; −ζ/4), which are ordered here according to their increasing eigenenergy. Table 1 lists these along with their symmetry and transformation properties for negative values of q. The corresponding eigenenergies as a function of the parameter ζ are displayed in Figure 3.
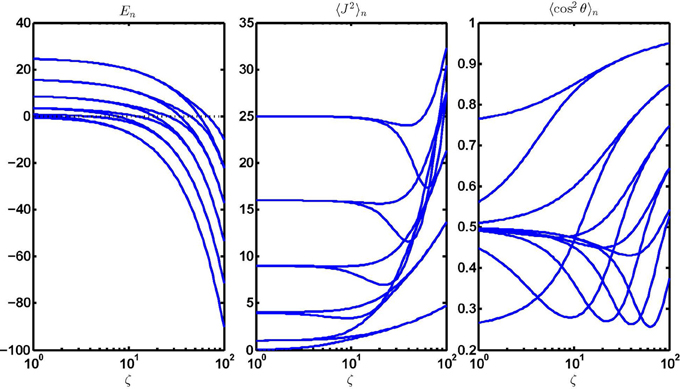
Figure 3. Eigenproperties of the planar quantum pendulum subject to a purely aligning interaction as a function of the interaction parameter ζ. The three panels show the eigenenergies and the expectation values of the squared angular momentum 〈J2〉 and alignment cosine 〈cos2 θ〉. Note that the orientation cosine vanishes identically.
In the field-free limit, ζ → 0, the eigenfunctions become trigonometric functions, see above, with the eigenenergies forming a quadratic progression. In the harmonic librator limit, the asymptotic expansion of the characteristic values, Equation (20.2.30) of Abramovitz and Stegun [4], yields an equidistant energy spectrum
with a harmonic librator quantum and quantum number v = 0, 1, 2, …
The energy levels and wavefunctions for a purely aligning interaction (ζ > 0 and η = 0) are exemplified in the right panel of Figure 1 for ζ = 25; their energies are also given in Table 2. Below the barrier, the levels a2r / b2r+1 and a2r+1/b2r+2 (for r ≥ 0) form pairwise near-degenerate tunneling doublets in the harmonic librator limit, split by tunneling through the equatorial barrier. Hence the members of a given tunneling doublet correlate either with the even eigenfunctions ce of odd order and the odd eigenfunctions se of even order or with the even eigenfunctions ce of even order and the odd eigenfunctions se of odd order. The tunneling splitting in the harmonic librator limit, as obtained from Equation (20.2.31) of Abramovitz and Stegun [4], becomes
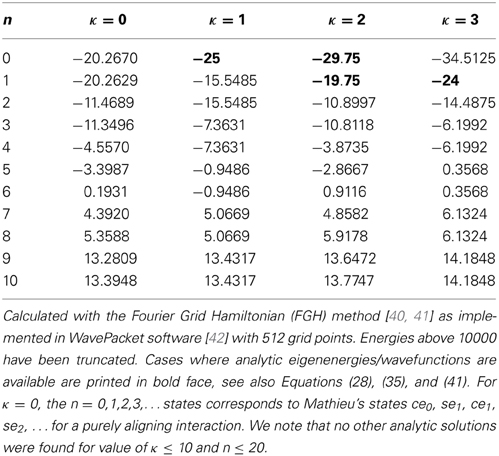
Table 2. Eigenenergies for the Hamiltonian of Equation (1) with ζ = β2 = 25 and η = κβ, as also displayed in Figure 1 (right panel) and in Figures 7–9.
The unbound states exhibit a free-rotor pairing of the levels a2r / b2r and a2r+1 / b2r+1 (for r > 0) are pairwise degenerate in the field free limit. Right above the maximum of the potential, Vmax = 0, there is a single intermediate state at energy E6 = 0.1931 (for the present example pertaining to ζ = 25), which is also listed in Table 2. We note that also the energy splittings of pairs of states well above the barrier converge to zero for increasing ζ.
In Figure 3 we also show the expectation values of the angular momentum squared, 〈J2〉, and the directional characteristic, the alignment cosine, 〈cos2 θ〉, as a function of the alignment parameter ζ for η = 0. Again, all states except for the lowest even and odd states (ce0 and se1) exhibit the Stern effect. Note that the orientation 〈cos θ〉 vanishes identically for η = 0.
2.3. Combined Orienting and Aligning Interactions: η > 0 & ζ > 0
The potential of Hamiltonian (Equation 1) exhibits two kinds of minima:
(a) a global minimum for η + 2ζ > 0 at θ = 0 where the potential V(θ) can be approximated by
yielding bound states with energy levels
and vibrational quanta .
(b) a local minimum for 2ζ > η at θ = π in whose vicinity the potential can be approximated by
yielding bound states with energy levels
and vibrational quanta .
We note that the maximum, , of the potential for the combined orienting and aligning interaction is located at ; its position shifts with decreasing η toward θ = π/2 and with increasing η toward θ = π. However, in order for that to be the case, η must not exceed 2ζ, as there would be neither a maximum nor a local minimum at θ = π.
One can also use Equations (8) and (10) to find a relationship between the interaction parameters η and ζ at the loci of the intersection of the Ev0 and Evπ energy levels. For 2ζ » η the vibrational quanta become approximately equal, and the condition, Ev0 = Evπ, for the degeneracy of levels localized around the global and local minima
yields
with κ the difference of the quantum numbers
The index κ thus defines combinations of the interaction parameters η and ζ at which the eigenenergy surfaces spanned by η and ζ intersect. Figure 4 shows the eigenenergies of a planar rotor subject to the combined orienting and aligning interactions as a function of η for a fixed ζ = 25. The dashed lines (from bottom to top) indicate, respectively, the global minimum at −(ζ + η), the local/secondary minimum at −(ζ − η), and the maximum at of the potential of Equation 2. Also shown are the values of the topological index κ: depending on whether κ is even or odd, the corresponding intersections are found to be, respectively, avoided or genuine. This alternating pattern of avoided and genuine crossings follows from the symmetries of the intersecting states, as described in section 3. Figure 5 shows the eigenenergy surfaces spanned by the parameters η and ζ pertaining to the lowest six eigenstates of a planar rotor subject to the combined interactions. As one can see, at ζ = 0 or η = 0, the energy surfaces correspond to the Mathieu cases for the purely orienting or purely aligning interactions described above and shown in Figures 2, 3. For ζ ≥ 0 and η ≥ 0, the eigenenergy surfaces exhibit the said intersections, which are found to occur exactly at the loci predicted by Equation (12) for a given κ. As Equation (13) is state-independent, the number of intersections an energy surface partakes in is equal to the label n of the corresponding eigenstate: the lowest energy surface, with n = 0, is thus not involved in any intersection; the first excited state surface, with n = 1, is involved in a first-order (κ = 1) intersection (between nearest doublets); the second excited state surface, with n = 2, is involved both in a first-order (κ = 1) genuine intersection (between nearest doublets) and in a second-order (κ = 2) avoided intersection (between second nearest doublets), etc. Consequently, at the loci of the κ-th order intersections given by Equation (12), we find an energy level pattern with κ single states at the bottom, followed by all other states which are doubly degenerate. In contrast, there are no degeneracies arising anywhere in between these intersection loci.
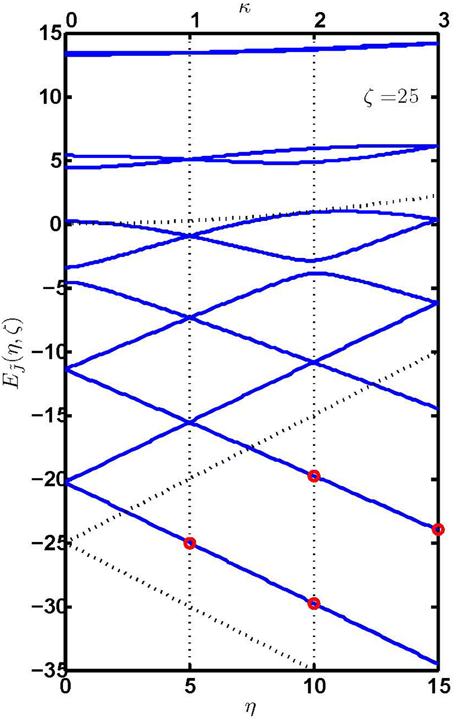
Figure 4. Eigenenergies of a planar rotor subject to the combined orienting and aligning interactions as a function of η for a fixed ζ = 25. The dotted lines indicate (from bottom to top), respectively, the global minimum at −(ζ + η), the local/secondary minimum at −(ζ − η), and the maximum at . Also shown are the values of the index κ which defines the loci of the intersections. For κ even, the intersections are avoided, for κ odd they are genuine. The red circles indicate the four cases for which analytic solutions have been found via SUSY, see section 3.
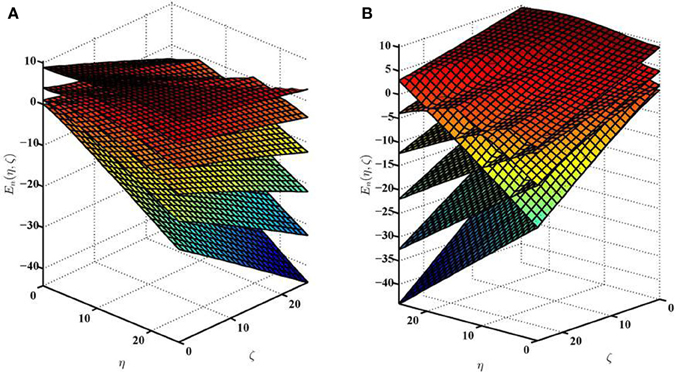
Figure 5. Views of the lowest six eigenenergy surfaces, n = 0, 1, 2, 3, 4, 5, of Hamiltonian (Equation 1) for a planar quantum pendulum subject to combined orienting and aligning interactions. The energy surfaces are shown as functions of the parameters η and ζ that characterize the strengths of, respectively, the orienting and aligning interaction. Panels (A) and (B) show the eigensurfaces from different perspectives.
The intersections of the eigenenergy surfaces are visualized in Figure 6 which shows the energy differences (gaps) between adjacent eigenenergy surfaces. The dashed line at η = 2ζ marks the boundary of the condition η ≤ 2ζ at which the potential exhibits both a maximum, , and a local minimum. By substituting the condition for the intersection loci, Equation (12), we obtain
which is independent of either of the interaction parameters but only reflects the way in which they combine at the intersections. The full lines correspond to various values of the topological index κ and thus of Vmax. Therefore, the dashed line crosses the κ = 1 line where the energy of the lowest doublet (states 1 and 2) coincides with the maximum of the potential; only a single state (state n = 0) lies below that energy. Analogously, the dashed line crosses the κ = 2 line where the energy of the lowest doublet (states n = 2 and n = 3) coincides with Vmax (and two single states, 0 and 1, lie below that energy), etc.
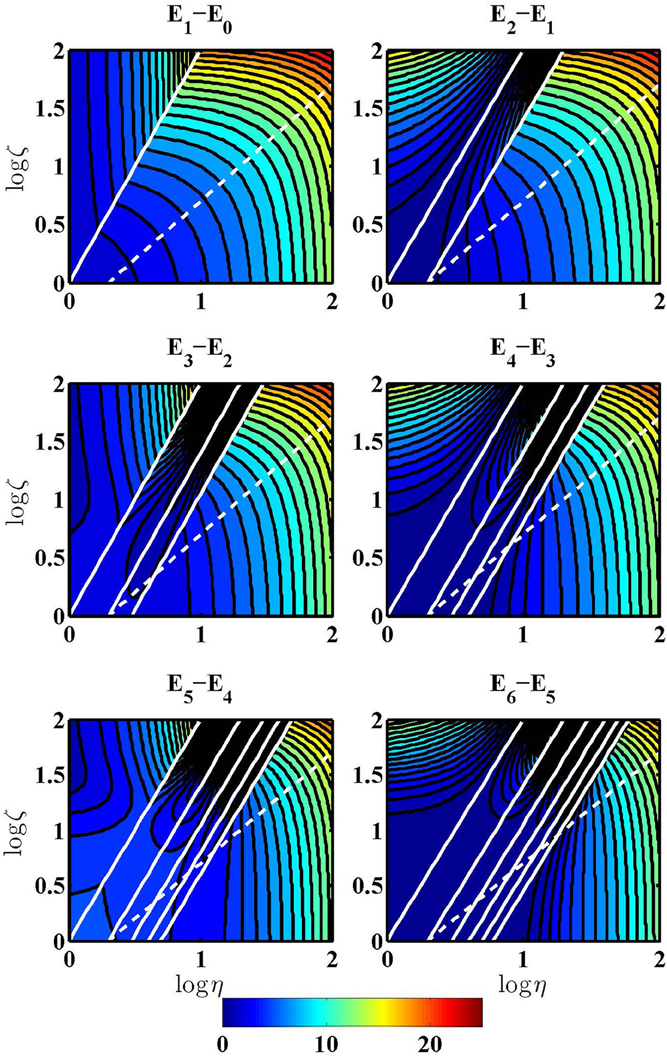
Figure 6. Energy differences (gaps) between adjacent eigenenergy surfaces of Hamiltonian (Equation 1) for a planar quantum pendulum subject to combined fields. The energy gaps are shown as functions of the parameters η and ζ that characterize the strengths of, respectively, the orientation and alignment interactions. White lines indicate the loci of the κ-th order intersection of adjacent surfaces, see Equation (12). The dashed line at η = 2ζ marks the boundary above which the potential exhibits both a maximum and a local minimum, see section 2.3.
In the right panels of Figure 6, the zero gap (darkest blue color) extends along the odd κ lines all the way down to the field-free limit, whereas, in the left panels, the energy gaps along the even κ lines increase slightly when approaching the field-free limit. Thereby the even and odd lines connect, respectively, to the genuine and avoided intersections of the planar rotor levels in the field-free limit, cf. Figure 5. Note that the planar case differs in this respect from the spherical case where all intersections are avoided, cf. Figure 3 of ref. [37].
3. Supersymmetry of the Planar Quantum Pendulum
Supersymmetric quantum mechanics [33, 34] is based on the concept of superpartner Hamiltonians with corresponding Schrödinger equations
where the symmetry of the construction ensures that
which serves to establish relations between the eigenvalues, E(1), E(2), and eigenfunctions, ψ(1),ψ(2) of the superpartner Hamiltonians H1, H2, of Equation (15). For the usual choice of the constant ϵ being the H1 ground state energy, ϵ = E(1)0, this leads to
i. e., the SUSY partner Hamiltonians are isospectral, where the intertwining operators A (or A†) convert the eigenfunctions of H1 (or H2) into those of H2 (or H1), at the same time lowering (or raising) the respective quantum numbers by one; only the ground state eigenfunction of H1 lacks a partner state but is annihilated by the intertwining operator, Aψ(1)0 = 0. In contrast, other choices of ϵ give often rise to a partial or complete breakdown of the degeneracy of the energy levels of H1 and H2 [33, 34], as encountered in some of the cases studied below.
For applications to SUSY QM in the position representation, the standard choice of the intertwining operators is
which leads to the following expressions for superpartner Hamiltonians
where the supersymmetric partner potentials V1 and V2 are related to the superpotential W(θ) via Riccati-type equations
For a nodeless ground state wavefunction, ψ(1)0, this allows to directly calculate the superpotential from a known ground state wavefunction
which can be inverted to obtain an analytic expression for the wavefunction provided the superpotential is known
While this yields non-singular superpotentials for the standard choice of the ground state, ϵ = E(1)0, singularities of the superpotentials are encountered when choosing an excited state, ϵ = En(1) with n > 0, where the singularities arise at the zeros of the excited state wavefunctions. As a result, the partner Hamiltonians H1 and H2 are no longer isospectral [33, 34], see also our results in sections 3.2 and 3.3.
Throughout what follows we make use of the following Ansatz for the superpotential
which is an extension (γ term added) of the Ansatz employed in refs. Lemeshko et al. [35, 36] for the case of the spherical pendulum. Note that the α term alone is related to the Rosen-Morse I superpotential whereas a combination of the α and γ terms bears similarity with the Pöschl-Teller I superpotential, cf. Cooper et al. [33].
Then Equation (23) yields the following expressions for the SUSY partner potentials
By identifying the potential of Equation (2) for the quantum rotor subject to the combined interactions with V1 = W2 − W′ + ϵ, we obtain:
In order for the first two terms on the right-hand side of Equation (24) to vanish, one of the following three conditions must be fulfilled: (A) α = 0 and γ = 0; or (B) α = −1/2 and γ = ±1/2; or (C) α = −1 and γ = 0. Below, we will discuss cases A through C in turn and show that each is connected with a particular ratio of η to ζ and, therefore, with a particular topology of the eigenenergy surfaces, namely case A with κ = 1, case B with κ = 2, and case C with κ = 3.
The knowledge of the superpotential W makes it possible to construct the supersymmetric partner potential V2 = W2 + W′ + ϵ, which—apart from the singular terms proportional to cscθ—differs from V1 in that the interaction parameter η is effectively reduced by 2β. This makes the partner potential V2 less asymmetric than the original potential V1.
Furthermore, using Equation (22) one can derive an analytic expression for the wavefunction from the superpotential W pertaining to the energy eigenvalue ϵ as obtained from Equation (25). For the particular superpotential introduced by Equation (23), the wavefunction takes the form
We note that identifying the potential of Equation 2 with V2 = W2 + W′ + ϵ furnishes no new superpotentials and thus no new analytic wavefunctions.
3.1. First-Order Intersections or κ = 1
For α = γ = 0 the superpotential of Equation 23 simplifies to
and Equation (25) yields the following expressions for the interaction parameters and the energy in terms of the parameter β of Equation (23),
In this case (case A), Equation (26) yields an eigenfunction of the original Hamiltonian H1
which exhibits a pronounced maximum at θ = 0, i. e., at the global minimum of the potential, and decays quickly for larger values of the angle θ. Since ψ(1)ϵ is nodeless, we conclude that it corresponds to the ground state wavefunction ψ(1)ϵ = ψ(1)0 pertaining to the ground-state energy ϵ = E(1)0.
The supersymmetric partner potentials obtained from Equation (25) are
i. e., V2(θ) = V1(θ ± π), as illustrated in Figure 7. Hence, apart from a trivial interchange of the global and local minima, the partner potentials are identical and the ground state wavefunction of H2 becomes
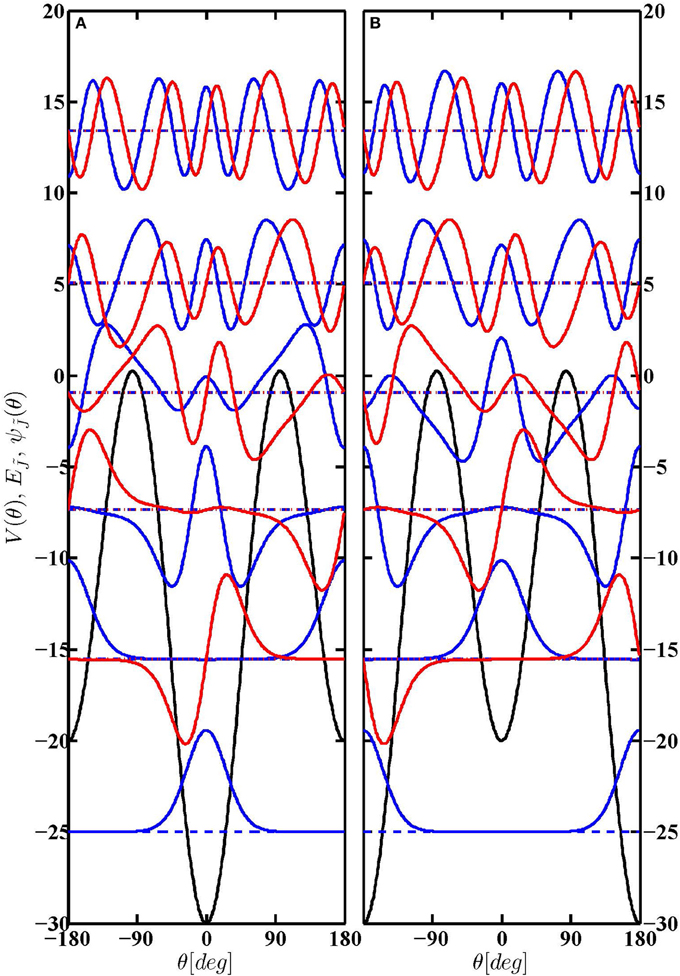
Figure 7. Superpartner potentials V1 (A) and V2 (B), eigenenergies (dashed lines) and eigenfunctions (full curves) of Hamiltonian (Equation 1) with η = 5, ζ = 25, i.e., a first-order intersection with κ = 1, see section 3.1.
Although the SUSY partner Hamiltonians are completely isospectral, see also Table 2, one should not conclude that SUSY is broken [33] here, because the ground state wavefunctions ψ(1)0(θ) and ψ(2)0(θ) pertaining to both SUSY partner Hamiltonians H1 and H2 can nonetheless be annihilated by the intertwining operator A and its adjoint A†:
In contrast, there is a one-to-one pairing of all higher eigenstates, n > 0, which we checked numerically
where the odd parity of the intertwining operators A and A† implies a pairing of even eigenstates of H1 with odd ones of H2 and vice versa, see also Figure 7.
The relation between η and ζ established in Equation (28) implies that for case A, the topological index κ = 1. Hence the case A Hamiltonian gives rise to one single eigenstate while all its higher eigenstates occur as doublets. This we corroborated by a numerical solution to the Schrödinger equation for the case A Hamiltonian, whose results for (η, ζ) = (5, 25) are presented in Table 2. As can also be seen in Figure 7, the n-th doublet is comprised of a state with n nodes near the global minimum (θ = 0) and a state with n − 1 nodes near the local minimum (θ = π), which is in agreement with Equations (12) and (13), thus rationalizing the occurrence of the first-order intersections characterized by κ = 1.
We note that the harmonic oscillator-like states centered at θ = 0 and at θ = π with quantum numbers v0 and vπ differing by one are of different parity. Hence, their coupling due the potentials V1,2, which are of even parity, has to vanish, and hence these pairs of eigenstates are exactly degenerate. This contrasts with the case of a purely aligning interaction (κ = 0), discussed in section 2.2, where we found a small but finite tunneling splitting.
3.2. Second-Order Intersections or κ = 2
For α = −1/2, γ = ±1/2 the superpotential (Equation 23) becomes
and Equation (25) yields the following expressions for the interaction strength parameters and for the energy in terms of β,
From Equation (26) we obtain the case B eigenfunctions for the original potential V1
Again, ψ(1)ϵ+ is nodeless, corresponding to the ground state ψ(1)0 with energy ϵ+ = E(1)0 which we will refer to as case B.1. However, ψ(1)ϵ− exhibits a node at θ = 0 and hence corresponds to the first excited state ψ(1)1 with energy ϵ− = E(1)1 which we will refer to as case B.2.
The SUSY partner potentials for cases B.1 and B.2 take the form
Note that V−2(θ) = V+2(θ ± π) and that the orientation field (∝cos θ) is absent both in V+2 and in V−2. In the vicinity of θ = 0, the former potential can be locally approximated by 1/2 − β2cos2 θ which is—apart from an energy shift of 1/2—identical with our κ = 0 case, i.e., the case of a pure alignment interaction discussed in section 2.2. This is also reflected by the numerical values shown in Table 2, i. e., −19.75 − 0.5 = −20.25, which is quite close to −20.26 or −20.27 found numerically for κ = 0.
Figure 8 shows the potentials V1 and V+2 along with the corresponding wavefunctions. The ground and first excited states of V1, see Equation (36), are found to be single states below the secondary minima. Both of them are annihiliated by the respective intertwining operators, A±≡ d/dθ + W±, pertaining to the superpotential W+ for case B.1 and W− for case B.2,
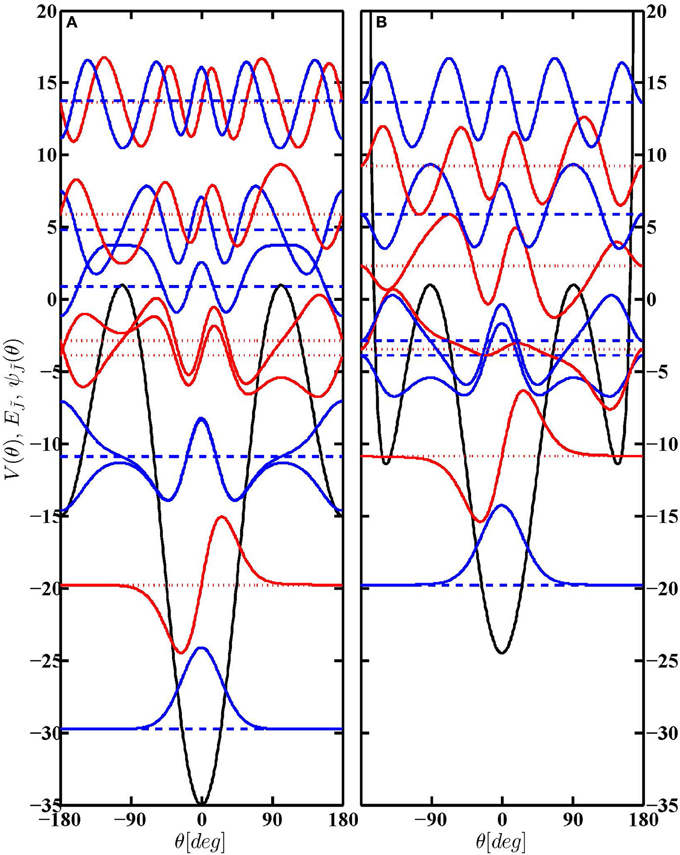
Figure 8. Superpartner potentials V1 (A) and V+2 (B), eigenenergies (dashed lines) and eigenfunctions (full curves) of Hamiltonian (Equation 1) with η = 10, ζ = 25 for a second-order intersection, κ = 2, see section 3.2.
However, when A+ acts on ψ(1)1, one obtains
i. e., an analytic expression for the ground state wavefunction of the SUSY partner potential V+2 at energy . All higher states, n > 1, of V1 occur in nearly-degenerate tunneling pairs as long as they are bound (below the maxima of V1). Like in the case of a purely aligning interaction (section 2.2), these states are followed by a single state (here at an energy of 0.9116) near the energetic barrier at Vmax = 1, whereas all unbound states form nearly-degenerate free-rotor-like pairs. In general, for case B we observe that many but not all of the states of V1 with n > 1 have SUSY partner states of V2 at the same energies and vice versa. Furthermore, there are no intertwining relations, such as Equation (33) in section 3.1, for the wavefunctions any more. We note that, in general, the superpartner potentials (Equation 37) are not expected to yield isospectral Hamiltonians because of the singularities in W and V2, which arise from the cscθ term. However, it is known that in some such cases an accidental degeneracy between the spectra of H1 and H2 (at least partly) remains due to spatial symmetry, as explained in Chapter 12 of Cooper et al. [33].
The relation between η and ζ established by Equation (35) implies that for case B the topological index κ = 2. Hence the case B Hamiltonian gives rise to two single eigenstates while all its higher eigenstates occur as doublets, see also the numerical data for (η, ζ) = (10, 25) presented in Table 2 and Figure 8. It can also be gleaned from Figure 8 that the n-th doublet is comprised of a state with n + 1 nodes near the global minimum (θ = 0) and another state with n − 1 nodes near the local minimum (θ = π), in agreement with Equations (12) and (13), thereby rationalizing the occurrence of the second-order intersections characterized by κ = 2. In contrast to case A and the concomitant first-order intersections, we note that the harmonic oscillator-like states centered at θ = 0 and at θ = π with quantum numbers v0 and vπ differing by two are of same parity. Hence, their coupling induced by the (even-parity) potentials V1,2 does not necessarily vanish, and the eigenstates occur in nearly degenerate pairs with a finite energy splitting. However, these splittings converge to zero for increasing parameter β as the harmonic librator limit is approached.
3.3. Third-Order Intersections or κ = 3
For α = −1, γ = 0 the superpotential (Equation 23) becomes
and so Equation (25) yields the following expressions for the interaction parameters and the energy in terms of the coefficient β
Upon substituting from Equation (41) into (26), we obtain the case C eigenfunction (corresponding to energy ϵ) of the original Hamiltonian H1
which has a node at θ = 0, i.e., pertains to the first excited state ψ(1)ϵ = ψ(1)1 with energy ϵ = E(1)1.
The corresponding supersymmetric partner potentials for case C take the form
i. e., the prefactor of the orientation field (∝cosθ) is effectively reduced from 3β in V1 to β in V2. The left panel of Figure 9 displays the large difference, of 6β, in the well depths at the global and local minima of the original potential V1. It accommodates three single states below the local minima which cannot have SUSY partner states because the wells of V2 are much too shallow; however, only the middle one of the three states is annihilated by the intertwining operator
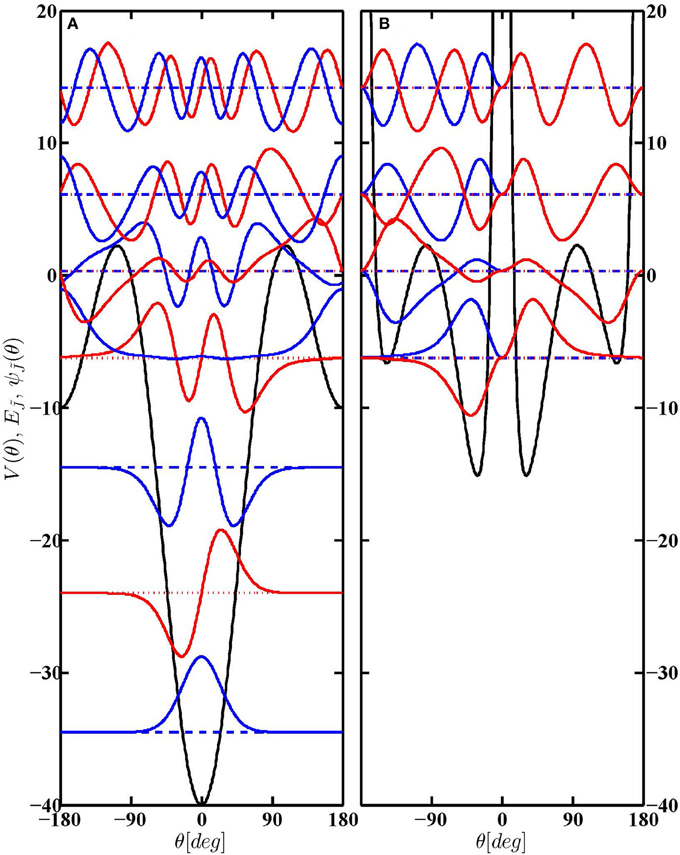
Figure 9. Superpartner potentials V1 (A) and V2 (B), eigenenergies (dashed lines) and eigenfunctions (full curves) of Hamiltonian (Equation 1) with η = 15, ζ = 25 for a third-order intersection, κ = 3, see section 3.3.
All higher states, n > 2, of V1 occur in degenerate pairs with SUSY partner states for V2 at exactly the same energies. However, there are no intertwining relations for their wavefunctions. As we have already noted in section 3.2, the superpartner potentials (Equation 43) do not necessarily yield isospectral Hamiltonians because of the singularities in W and V2. At any rate, we find that in case C, H1 and H2 are isospectral, except for the lowest three states which are absent for H2.
The relation between η and ζ established by Equation (41) implies that for case C the topological index κ = 3. Hence the case C Hamiltonian gives rise to three single eigenstates while all its higher eigenstates occur as doublets, see also the numerical data for (η, ζ) = (15, 25) presented in Table 2. As can be also seen in Figure 9, the n-th doublet arises from a state with n + 2 nodes near the global minimum (θ = 0) and another state with n−1 nodes near the local minimum (θ = π). This is in agreement with Equations (12) and (13), thus rationalizing the occurrence of the third-order intersections, κ = 3. We note that the harmonic oscillator-like states centered at θ = 0 and θ = π with quantum numbers v0 and vπ differing by three are of different parity. Hence, their coupling induced by the (even parity) potentials V1,2 has to vanish, and the eigenstates occur in exactly degenerate pairs without a tunneling splitting.
A special case of case C is the free rotor, which arises for β = 0. Although its analytic eigenenergies, E(1)n = n2, and eigenfunctions ∝sin nθ, ∝cos nθ are well-known, it is nevertheless instructive to discuss the free rotor case from the SUSY point of view, see also Cooper et al. [33].
The case C superpotential (Equation 40) reduces to
and the wavefunction (Equation 42) simplifies to
with a corresponding energy E(1)1 = 1. According to Equation (43), the vanishing potential, V1 = 0, of the free rotor has the following SUSY partner
which has bound states at energies E(2)n = (n + 2)2, i.e., again the three lowest states of the original (free rotor) potential with eigenenergies E(1)0,1,2 = 0, 1, 1 lie below the minimum, Vmin(2) = 2, of the partner potential which, therefore, cannot have SUSY partner states.
The SUSY procedure can be repeated, i.e., one can find a new superpotential such that V2 = W22 − W′2 + ϵ which yields
whose partner potential, V3 = W22 + W′2 + ϵ, evaluates to
This procedure can be repeated to yield the n-th potential
and the n-th superpotential
for the free-rotor case. The eigenenergy
pertains to the ground state for states with n ≥ 2 and to the first excited state for n = 1. As a result, the corresponding Hamiltonians Hn are isospectral, except that, starting with H2, each subsequent Hamiltonian has one level (two bound states) less than the previous one. For H1, as many as one state with n = 0 and two states with n = 1 are lacking, i.e., H2 has two levels (three bound states) less that H1.
We note that the free-rotor superpotential (Equation 51) is closely related to the Rosen-Morse I superpotential of Cooper et al. [33], which is likewise shape invariant. This accounts for the exact solvability of the free-rotor problem.
4. Conclusions and Outlook
We undertook a mutually complementary analytic and computational study of the planar quantum rotor subject to combined orienting and aligning interactions, characterized, respectively, by dimensionless parameters η and ζ. We considered a full range of interaction strengths, which convert, jointly or separately, the planar rotor into a planar hindered rotor or a planar quantum pendulum or a planar harmonic librator (angular harmonic oscillator), depending on the values of η and ζ. Following upon our previous study of the corresponding problem in 3D (spherical rotor/pendulum), we were concerned with the topology of the eigenenergy surfaces spanned by the interaction parameters η and ζ as well as with the supersymmetry of the planar eigenproblem as a means for identifying its analytic solutions.
Topology. We found that the loci of all the intersections that arise among the eigenenergy surfaces of the planar quantum pendulum are accurately rendered by a simple formula, Equation (12). The formula is accurate despite the fact that its derivation was based on two rather crude approximations, namely a harmonic approximation of the combined orienting and aligning potentials and the approximate equality of the vibrational quanta in Equations (8) and (10) for 2ζ » η. Furthermore, since the equation for the loci, Equation (12), and the definition, Equation (13), of the topological index κ are independent of the eigenstate, the energy levels exhibit a general pattern that only depends on the values of κ: for each κ, there are κ single states, followed, in ascending order, by all other states which are doubly degenerate. This energy level pattern reflects the fact that above the local minimum, states can be bound by both the local () and global minima (θ = 0) whereas below the local minimum states can only be bound by the global minimum. Since the energy difference between the global and local minima increases linearly with κ, the number of single states bound solely by the global minimum increases with κ as well (in fact is equal to κ). States bound by both the global and local minima that lie below the maximum of the potential, Equation (14), occur as doublets. Interestingly, the above eigenenergy level pattern persists even for such values of κ ≈ 10 (2ζ < η) where no local minima occur. And finally, the intersections are found to be genuine for odd κ and avoided for even κ. This is due to the fact that for even κ, the intersecting levels are of same parity and thus can be coupled by the combined interactions potential which is of even parity. For odd κ, the intersecting states are of opposite parity and so cannot be coupled by the even-parity potential.
Supersymmetry. By invoking supersymmetric quantum mechanics (SUSY QM), we have identified three sets of conditions (cases A, B and C) under which the eigenproblem for the Hamiltonian of Equation 1 pertaining to the planar quantum pendulum can be solved analytically. As it turns out, each of the cases implies a certain ratio of the interaction parameters η and ζ and, thereby, a certain value of the topological index κ. This made it possible to identify each case with a particular topology: case A with κ = 1, case B with κ = 2, and case C with κ = 3. Whereas cases A and B.1 furnish the ground-state wavefunctions, cases B.2 and C furnish the first excited-state wavefunctions. The free planar rotor has been identified as a subcase of case C, one which exhibits shape invariance and therefore analytic solvability for all states.
By making use of the analytic wave functions, we evaluated, likewise in analytic form, the observables of interest, such as the expectation values of the angular momentum squared, the orientation and alignment cosines, and the corresponding eigenenergy. These are summarized in Table 3. By virtue of the SUSY QM apparatus, we constructed for each potential V1 its supersymmetric partner potential V2 and for cases A and B.1 found the V2 ground-state wave functions in analytic form. Apart from the singularities introduced by the terms proportional to csc θ, the main difference between V1 and V2 is that the orienting field (η) is effectively reduced by 2β, which tends to decrease the well depth of the global minimum while increasing the well depth of the local/secondary minimum. This reduced asymmetry of V2 compared with V1 is the deeper reason why (a certain number of) single states (which are always localized around the global minimum) present in V1 are absent in V2. However, while in standard SUSY QM [33, 34] only one state is eliminated upon the transition from V1 to V2, our present analysis shows that the planar pendulum problem somewhat deviates from this pattern. In our case A (κ = 1), we find strictly isospectral (no state eliminated) partner Hamiltonians although SUSY is not broken. In case B (κ = 2), there is one state eliminated, as expected, but a one-on-one correspondence between higher eigenstates of V1 and V2 is incomplete. In case C (κ = 3), we find that the transition to V2 eliminates no less than the lowest three states! We came across a similar pattern when inspecting Figure 12.1 of Cooper et al. [33] for the harmonic oscillator, where it is loosely attributed to the spatial symmetry of the problem. It is therefore likely that our findings about the planar quantum pendulum are related to the symmetry (parity) of the problem and the resulting degeneracy patterns as well. Clearly, more work needs to be done here, with the ultimate goal of developing a theory that combines supersymmetry and spatial symmetry, SUSY + SY = SUSYSY.

Table 3. Superpotentials, W, interaction parameters, η and ζ, wave functions, ψ, normalization factors, N, orientation cosines, 〈cosθ〉, alignment cosines 〈cos2θ〉, the expectation values of the angular momentum squared, 〈J2〉, and the eigenenergies, ϵ, for the four cases that yield an analytic solution to the eigenproblem of Hamiltonian (1).
Last but not least, we note that it has not escaped our notice that our cases A, B, and C are equivalent to the spherical pendulum problem studied in Lemeshko et al. [36] for m = −, m = 0, and m = , respectively. However, despite this similarity, there is an important difference: in the 3D, spherical case, the polar angle is only defined on a half-circle (0 ≤ θ ≤ π), with repercussions for symmetry (e.g., all crossings of the eigenenergy surfaces in 3D are avoided). In our forthcoming paper, we revisit the spherical pendulum case.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
Support by the Deutsche Forschungsgemeinschaft (DFG) through grants SCHM 1202/3-1 and FR 3319/3-1 is gratefully acknowledged.
References
1. Condon EU. The physical pendulum in quantum mechanics. Phys Rev. (1928) 31:891–894. doi: 10.1103/PhysRev.31.891
2. Meixner J, Schäfke FW. Mathieusche Funktionen und Sphäroidfunktionen. Berlin: Springer (1954). doi: 10.1007/978-3-662-00941-3
6. von Meyenn K. Rotation of diatomic-dipole molecules in strong electric fields. Z Phys. (1970) 231:154–160.
7. Slenczka A, Friedrich B, Herschbach D. Pendular alignment of paramagnetic molecules in uniform magnetic fields. Phys Rev Lett. (1994) 72:1806. doi: 10.1103/PhysRevLett.72.1806
8. Friedrich B, Herschbach D. Polarization of molecules induced by intense laser fields. J Phys Chem. (1995) 99:15686. doi: 10.1021/j100042a051
9. Friedrich B, Herschbach D. Polarizability interaction in molecules and double-well tunneling. Z Phys D. (1996) 36:221. doi: 10.1007/BF01426407
10. Härtelt M, Friedrich B. Directional states of symmetric-top molecules produced by combined static and radiative electric fields. J Chem Phys. (2008) 128:224313. doi: 10.1063/1.2929850
11. Nielsen H. The torsion oscillator-rotator in the quantum mechanics. Phys Rev. (1932) 40:445–456. doi: 10.1103/PhysRev.40.445
12. Pradhan T, Khare AV. Plane pendulum in quantum mechanics. Am J Phys. (1973) 41:59–66. doi: 10.1119/1.1987121
13. Cook GP, Zaidins CS. The quantum point-mass pendulum. Am J Phys. (1986) 54:259–261. doi: 10.1119/1.14640
14. Friedrich B, Pullman DP, Herschbach DR. Alignment and orientation of rotationally cool molecules. J Phys Chem. (1991) 95:8118–8129. doi: 10.1021/j100174a021
15. Baker GL, Blackburn JA, Smith HJT. The quantum pendulum: small and large. Am J Phys. (2002) 70:525–531. doi: 10.1119/1.1456069
16. Baker GL, Blackburn JA. The Pendulum: A Case Study in Physics. Oxford: Oxford University Press (2005).
17. Dimeo RM. Visualization and measurement of quantum rotational dynamics. Am J Phys. (2003) 71:885–893. doi: 10.1119/1.1538575
18. Doncheski MA, Robinett RW. Wave packet revivals and the energy eigenvalue spectrum of the quantum pendulum. Annal Phys. (2003) 308:578–598. doi: 10.1016/S0003-4916(03)00171-4
19. Leibscher M, Schmidt B. Quantum dynamics of a plane pendulum. Phys Rev A. (2009) 80:12510. doi: 10.1103/PhysRevA.80.012510
20. Herschbach DR. Tables for the Internal Rotation Problem. Cambridge, MA: Department of Chemistry, Harvard University (1957).
21. Herschbach DR. Tables of Mathieu integrals for the internal rotation problem. J Chem Phys. (1957) 27:975. doi: 10.1063/1.1744025
22. Herschbach DR. Calculation of energy levels for internal torsion and over-all rotation. III. J Chem Phys. (1959) 31:91. doi: 10.1063/1.1730343
23. Ramakrishna S, Seideman T. Torsional control by intense pulses. Phys Rev Lett. (2007) 99:103001. doi: 10.1103/PhysRevLett.99.103001
24. Parker SM, Ratner MA, Seideman T. Coherent control of molecular torsion. J Chem Phys. (2011) 135:224301. doi: 10.1063/1.3663710
25. Madsen CB, Madsen LB, Viftrup SS, Johansson MP, Poulsen TB, Holmegaard L, et al. Manipulating the torsion of molecules by strong laser pulses. Phys Rev Lett. (2009) 102:073007. doi: 10.1103/PhysRevLett.102.073007
26. Friedrich B, Herschbach DR. On the possibility of orienting rotationally cooled polar molecules in an electric field. Z Phys D. (1991) 18:153. doi: 10.1007/BF01437441
27. Friedrich B, Slenczka A, Herschbach DR. Spectroscopy of pendular molecules in strong parallel electric and magnetic fields. Can J Phys. (1994) 72:897. doi: 10.1139/p94-118
28. Friedrich B, Slenczka A, Herschbach DR. Hybridization of rotor states in parallel electric and magnetic fields. Chem Phys Lett. (1994) 221:333. doi: 10.1016/0009-2614(94)00362-9
29. Slenczka A, Friedrich B, Herschbach DR. Pendular alignment of paramagnetic molecules in uniform magnetic fields. Phys Rev Lett. (1994) 72:1806. doi: 10.1103/PhysRevLett.72.1806
30. Friedrich B, Herschbach D. Manipulating molecules via combined static and laser fields. J Phys Chem A. (1999) 103:10280. doi: 10.1021/jp992131w
31. Friedrich B, Nahler NH, Buck U. The pseudo-first-order stark effect and the orientation of HXeI molecules. J Mod Opt. (2003) 50:2677. doi: 10.1080/09500340308233593
32. Poterya V, Votava O, Farnik M, Oncak M, Slavicek P, Buck U, et al. Generation and orientation of organoxenon molecule HÐXeÐCCH in the gas phase. J Chem Phys. (2008) 128:104313. doi: 10.1063/1.2837656
33. Cooper F, Khare A, Sukhatme U. Supersymmetry and quantum mechanics. Phys Rep. (1995) 251:267. doi: 10.1016/0370-1573(94)00080-M
34. Sukumar CV. Supersymmetric quantum mechanics of one-dimensional systems. J Phys A. (1985) 18:2917. doi: 10.1088/0305-4470/18/15/020
35. Lemeshko M, Mustafa M, Kais S, Friedrich B. Supersymmetric factorization yields exact solutions to the molecular Stark-effect problem for stretched states. Phys Rev A. (2011) 83:043415. doi: 10.1103/PhysRevA.83.043415
36. Lemeshko M, Mustafa M, Kais S, Friedrich B. Supersymmetry identifies molecular Stark states whose eigenproperties can be obtained analytically. New J Phys. (2011) 13:063036. doi: 10.1088/1367-2630/13/6/063036
37. Schmidt B, Friedrich B. Topology of surfaces for molecular Stark energy, alignment, and orientation generated by combined permanent and induced electric dipole interactions. J Chem Phys. (2014) 140:064317. doi: 10.1063/1.4864465
38. Mathieu E. Le mouvement vibratoire d'une membrane de forme elliptique. J Math Pures Appl. (1868) 13:137–203.
39. Gutierrez-Vega JC, Rodriguez-Dagnino RM, Meneses-Nava MA, Chavez-Cerda S. Mathieu functions, a visual approach. Am J Phys. (2003) 71:233–242. doi: 10.1119/1.1522698
40. Meyer R. Trigonometric interpolation method for one–dimensional quantum–mechanical–problems. J Chem Phys. (1970) 52:2053–2059. doi: 10.1063/1.1673259
41. Marston CC, Balint-Kurti GG. The Fourier grid Hamiltonian method for bound state Eigenvalues and Eigenfunctions. J Chem Phys. (1989) 91:3571–3576. doi: 10.1063/1.456888
42. Schmidt B, Lorenz U. Wave Packet 4.9: A Matlab Program Package for Quantum Mechanical Wave Packet Propagation and Time-Dependent Spectroscopy (2013). Available online at: http://sourceforge.net/projects/wavepacket/
Keywords: orientation, alignment, planar rotor/pendulum, molecular Stark effect, combined fields, supersymmetry, Mathieu equation
Citation: Schmidt B and Friedrich B (2014) Supersymmetry and eigensurface topology of the planar quantum pendulum. Front. Physics 2:37. doi: 10.3389/fphy.2014.00037
Received: 04 April 2014; Accepted: 03 June 2014;
Published online: 23 June 2014.
Edited by:
Sabre Kais, Purdue University, USAReviewed by:
Arghavan Safavi-Naini, Massachusetts Institute of Technology, USAGerrit C. Groenenboom, Radboud University Nijmegen, Netherlands
Copyright © 2014 Schmidt and Friedrich. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bretislav Friedrich, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, D-14195 Berlin, Germany e-mail:YnJldGlzbGF2LmZyaWVkcmljaEBmaGktYmVybGluLm1wZy5kZQ==
 Burkhard Schmidt
Burkhard Schmidt Bretislav Friedrich
Bretislav Friedrich