Stable time integration suppresses unphysical oscillations in the bidomain model

1. Introduction

The bidomain model, formulated mathematically by Tung in 1978 [1], is a popular model for describing the electrical activity in the heart. This model treats the heart as two superimposed domains (intracellular and extracellular) that are formally separated by the cell membrane. The model consists of ordinary differential equations (ODEs) describing the electrical properties of the cell membrane, coupled to partial differential equations (PDEs) that describe the electrical conductance in the two domains. The most common formulation of the model is in terms of three primary variables, the transmembrane potential, the extracellular potential, and a vector of states that describe the dynamic electrical properties of the cell membrane. Simplified models such as the monodomain model are also widely used by the research community, but the bidomain model is considered the most accurate and general continuum-based model of cardiac tissue electrophysiology.

The bidomain model can be challenging to solve. For example, it usually includes a stiff, non-linear ODE model describing the average electrical behavior of individual heart cells over volume elements [2], and rapid dynamics and steep gradients in the solution lead to strict resolution requirements in space and time. For example, in Potse and Vinet [3], two billion variables are used. For reasons such as these, the numerical solution of the bidomain model has been studied by numerous researchers; see, e.g., Vigmond et al. [4] for a detailed review of this topic.

First-order methods for solving the bidomain model have been proposed many times in the literature. For example, the forward Euler (FE) method has been used frequently; see e.g., Muzikant et al. [5], Sambelashvili and Efimov [6], ten Tusscher and Panfilov [7], and Tranquillo et al. [8]. An investigation of the stability of FE applied to the bidomain model was performed in Puwal and Roth [9]. To combat the disadvantages of explicit methods such as FE while retaining the implementational simplicity of first-order methods, first-order semi-implicit methods were investigated in Keener and Bogar [10] and Whiteley [11]. Although first-order methods can be easily implemented and analyzed, a comparison in Sundnes et al. [12] of a first- and a second-order method showed that the second-order method gives a better approximation of the conduction velocity. We therefore focus mainly on the use of second-order methods.

The first example of a second-order method for the bidomain model, based on Strang splitting [13], was presented in Sundnes et al. [12]. After splitting the PDEs from the ODEs, the PDEs were integrated in time with the Crank–Nicolson (CN) method. This method has also been used to integrate the PDEs resulting from various first-order splitting methods; see e.g., Whiteley [11] and Qu and Garfinkel [14].

The CN method is one of the simplest implicit second-order methods to implement. However, it has relatively poor error-damping properties that may result in simulations with unphysical oscillations [11]. To overcome this limitation, we investigate a second-order method based on Strang splitting and a second-order L-stable singly diagonally implicit Runge–Kutta (SDIRK2) method (see e.g., [15]) to integrate the PDEs. L-stability is an enhanced numerical stability property designed to maximally damp high-frequency oscillations in numerical solutions. Although the individual SDIRK2 steps are more computationally expensive than those of CN, the computational cost of solving the ODEs is generally non-negligible, and the overall increase in acceptable step sizes from using the SDIRK2 method as the PDE solver may ultimately lead to a favorable tradeoff.

The paper is organized as follows. The model equations and the numerical methods used, in particular the operator-splitting method used for splitting the ODEs and PDEs along with the numerical methods for the PDEs, are described in section 2. Numerical results that verify second-order convergence of the SDIRK2 method and provide comparisons to the CN and backward Euler (BE) methods are presented in section 3. Finally, a discussion of the results is given in section 4.

2. Models and Methods

2.1. Bidomain Model

For simplicity, we consider an isolated heart with no coupling to a surrounding bath. The problem formulation and numerical methods described may easily be extended to include such further coupling. The bidomain model then reads

$\begin{array}{cc}\chi C_m\frac{\partial v}{\partial t}+\chi I_{\text{ion}}(s,v,t)=\nabla ·\left({\sigma }_i\nabla v\right)+\nabla ·\left({\sigma }_i\nabla u_e\right),& (1\text{a})\end{array}$

$\begin{array}{cc}0=\nabla \text{}·\text{}\left({\sigma }_i\nabla v\right)+\nabla ·\text{}\left(\left({\sigma }_i+{\sigma }_e\right)\nabla u_e\right)\text{},& (1\text{b})\end{array}$

$\begin{array}{cc}\frac{\partial s}{\partial t}=f(s,v,t),& (1\text{c})\end{array}$

with boundary conditions

$\begin{array}{l}\widehat{n}·\left({\sigma }_i\nabla v+{\sigma }_i\nabla u_e\right)=0,\\ \widehat{n}·\left({\sigma }_e\nabla u_e\right)=0,\end{array}$

where v is the transmembrane potential, u_e is the extracellular potential, and s is a vector of cellular states such as gating variables and ionic concentrations. The function f(s, v, t) is a non-linear function describing cellular dynamics, I_ion(s, v, t) is the ionic current per cell membrane area, and σ_i and σ_e are extracellular and intracellular conductivity tensors, respectively. The quantity χ is the area of the cell membrane per unit volume, and C_m is the capacitance of the cell membrane per unit area. Finally, $\widehat{n}$ is the unit outward normal. See e.g., Sundnes et al. [2], for further details on the bidomain model.

2.2. Fractional-Step Methods

The bidomain model is difficult to solve as a fully coupled system because the discretized system is typically large and strongly non-linear. However, the PDEs of the bidomain equation are linear in v and u_e when the I_ion term is removed. This suggests the use of operator-splitting methods as a natural way to divide the solution process in order to reduce the complexity of each sub-problem to more manageable levels. The basic idea is to separate the solution of the non-linear ODEs of the cell model from that of the linear PDEs. One family of operator-splitting methods is the so-called fractional-step methods, to which the first-order Godunov and second-order Strang splitting methods belong; see e.g., Hundsdorfer and Verwer [16]. We describe a general formulation of fractional-step methods, based on a parameter Θ, where the Godunov and Strang splitting methods are obtained as special cases for Θ = 1 and Θ = 1/2, respectively. The key step in applying a fractional-step method to the bidomain equations is to treat the non-linear term χI_ion(v, s) and the diffusive terms in (1a) separately; see e.g., Sundnes et al. [2] for details. This split results in two sub-systems to be solved for each time step. One is a system of ODEs describing cellular reactions and the ionic current,

$\begin{array}{cc}\frac{\partial s}{\partial t}=f(v,s,t),& (2\text{a})\end{array}$

$\begin{array}{cc}\frac{\partial v}{\partial t}=-\frac{1}{C_m}{I}_{\text{ion}}(v,s),& (2\text{b})\end{array}$

and the other is the linear PDE system describing electrical conductance

$\begin{array}{cc}\chi C_m\frac{\partial v}{\partial t}=\nabla ·({\sigma }_i\nabla v)+\nabla ·({\sigma }_i\nabla u_e),& (3\text{a})\end{array}$

$\begin{array}{cc}0=\nabla ·({\sigma }_i\nabla v)+\nabla ·\left(({\sigma }_i+{\sigma }_e)\nabla u_e\right).& (3\text{b})\end{array}$

One step of the splitting method to advance from time tⁿ to time t^{n + 1} = tⁿ + Δt involves the solution of the two sub-systems (denoted A and B) and consists of three phases.

1. Using the solution at time tⁿ as the initial condition, solve sub-system A for tⁿ < t ≤ t^{n + Θ} := tⁿ + ΘΔt.

2. Using the solution of phase 1 as the initial condition, solve sub-system B for tⁿ < t ≤ t^{n + 1}.

3. Using the solution of phase 2 as the initial condition, solve sub-system A for t^{n + Θ} < t ≤ t^{n + 1}.

In principle, either system (2) or (3) may be used as sub-system A, with the other as sub-system B. In practice, however, the quality of a numerical solution may vary significantly for different choices of A and B. In this paper, we used the linear PDE system (3) as system B, and compare the performance of the CN and SDIRK2 numerical schemes for integrating this system. For comparison, we also used Godunov splitting with the BE method to integrate the PDEs.

2.3. Solving the Sub-Systems

The fractional-step method outlined above yields second-order convergence for Θ = 1/2 provided each of the phases 1, 2, and 3 are solved with (at least) second-order accuracy. A second-order method was presented in Sundnes et al. [12] that applied a third-order SDIRK method for the ODEs (2) and the CN method for the PDEs (3). This method was shown to give second-order convergence, but in some cases it suffered from instabilities, likely due to the use of the CN method in phase 2. Accordingly, we wish to see the effect of replacing CN with a more stable method.

2.4. Method of Lines

The focus of this study is on the time discretization of the PDEs (3). Using the method of lines, we apply a spatial discretization (specifically, a finite element method) to transform the PDE system (3) into an ODE system and then investigate a number of different time-discretization methods. The FE method is used for the time discretization of the cell model ODEs (2). The FE method is first order and hence the overall operator-splitting method formally becomes first order. However, the cell model ODE systems are stiff enough that the time step of explicit methods are dictated by stability rather than accuracy, and the time step required for stability of the FE method renders highly accurate numerical solutions. The errors from this part of the solution algorithm are therefore sub-dominant, and we observe second-order convergence for the overall solution, as demonstrated in section 3.

To apply the finite element method, we introduce an appropriate function space V_h, with basis functions φ_j, j = 1, 2,…,M. The unknown fields v and u_e are then approximated as linear combinations of the basis functions

$\begin{array}{cc}v={\displaystyle \sum _{j=1}^M{v}_j}{\phi }_j,u_e={\displaystyle \sum _{j=1}^M{u}_j}{\phi }_j,& (4)\end{array}$

where v_j, u_j are time-dependent coefficients and φ_j are appropriate (spatial) basis functions. To simplify the notation, we introduce the bilinear forms

$\begin{array}{l}{a}_i(\eta ,\psi )={\displaystyle {\int }_{\Omega }{\sigma }_i}\nabla \eta ·\nabla \psi dx,\\ a_{i+e}(\eta ,\psi )={\displaystyle {\int }_{\Omega }({\sigma }_i+{\sigma }_e)}\nabla \eta ·\nabla \psi dx.\end{array}$

A weak form of (3) is thus

$\begin{array}{cc}\chi C_m\frac{d}{dt}{\displaystyle {\int }_{\Omega }v}\psi dx=-a_i(v,\psi )-a_i(u_e,\psi ),& (5a)\end{array}$

$\begin{array}{cc}{a}_i(v,\psi )+a_{i+e}(u_e,\psi )=0,& (5b)\end{array}$

and is to be satisfied for all choices ψ ∈ V, where v is some suitable function space. By inserting the approximation (4) into (5) and using the basis functions φ_j, j = 1, 2,…,M, as test functions ψ (i.e., Galerkin's method [16]), we get a linear system of differential-algebraic equations (DAEs) of the form

$\begin{array}{cc}\left[\begin{array}{c}\chi C_{m}A\frac{dv}{dt}\\ 0\end{array}\right]=-\left[\begin{array}{cc}{A}_i& A_i\\ A_i& A_{i+e}\end{array}\right]\left[\begin{array}{c}v\\ u_e\end{array}\right],& (6)\end{array}$

where v, u_e are the vectors of time-dependent coefficients v_i, u_i and the sub-matrices have elements given by

$\begin{array}{l}A(j.k)={\displaystyle {\int }_{\Omega }{\phi }_j}{\phi }_{k}dx,\\ A_i(j,k)={\displaystyle {\int }_{\Omega }{\sigma }_i}\nabla {\phi }_j·\nabla {\phi }_{k}dx,\\ A_{i+e}(j,k)={\displaystyle {\int }_{\Omega }({\sigma }_i+{\sigma }_e)}\nabla {\phi }_j·\nabla {\phi }_{k}dx.\end{array}$

The remainder of this paper focuses on the solution of (6). See e.g., Ascher et al. [15], for an introduction to DAEs and their solution.

2.5. Solution of (6) by the θ-Rule

For completeness, we now specify the algorithm commonly used to solve the DAEs (6). The method is a standard θ-rule, which yields the trapezoidal rule for θ = 1/2 that corresponds to the CN method for (3) and the BE method for θ = 1. We apply a θ-rule to the differential part of (6) and introduce u^{n + θ}_e as an approximation to u_e at time tⁿ + θΔt. This gives the linear system

$\begin{array}{l}\begin{array}{cc}\begin{array}{l}\left[\begin{array}{cc}\chi C_{m}A+\theta \Delta t{A}_i& \Delta t{A}_i\\ \Delta t{A}_i& \frac{\Delta t}{\theta }{A}_{i+e}\end{array}\right]\left[\begin{array}{c}{v}^{n+1}\\ u_e^{n+\theta }\end{array}\right]\\ =\left[\begin{array}{c}(\chi C_{m}A-(1-\theta )\Delta t{A}_i)v^n\\ -\frac{\Delta t(1-\theta )}{\theta }{A}_i{v}^n\end{array}\right],\end{array}& (7)\end{array}\end{array}$

where we have scaled the second block row by Δt/θ to obtain a symmetric system for solution by a conjugate-gradient (CG) iterative solver. An alternative derivation of this block system, based on first discretizing the system in time and then in space, is found in Sundnes et al. [2, 12]. A detailed study of alternative splitting methods, with particular focus on the effects of matrix lumping and the choice of numerical quadrature, is found in Krishnamoorthi et al. [17].

2.6. Solution of (6) by the SDIRK2 Method

As mentioned, numerical experiments show that the method based on (7) is stable for large Δt when θ = 1 but may suffer from significant step-size restrictions to reduce unphysical oscillations when θ = 1/2. Because numerical experiments presented in Sundnes et al. [12] suggest that the second-order method gives a better approximation of the conduction velocity, we examine second-order fractional-step methods (Θ = 1/2) but with better stability properties for the PDE solver. In particular, we expect the L-stability property to be relevant in suppressing unphysical oscillations due to its strong damping properties. SDIRK methods are arguably the simplest possible L-stable methods. The simplest SDIRK method is BE, and it is also L-stable. SDIRK methods can be viewed as combining steps similar to the case where θ = 1 in order to produce higher order. We consider the L-stable, two-stage, second-order SDIRK method (SDIRK2) defined by the Butcher tableau

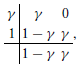
with $\gamma =(2-\sqrt{2})/2$; see e.g., Ascher and Petzold [15] for an explanation of the Butcher tableau for specifying Runge–Kutta methods. For a general initial-value problem dy/dt = f(t, y), y(t⁰) = y⁰, this method advances a known approximate solution yⁿ at time t = tⁿ to a new approximate solution y^{n + 1} at time t = t^{n + 1} by means of the iteration

$\begin{array}{l}{Y}^{(1)}-\Delta t\gamma f(t^{n,\gamma },Y^{(1)})=y^n,\\ y^{n+1}-\Delta t\gamma f(t^{n+1},y^{n+1})=y^n+\Delta t(1-\gamma )f(t^{n,\gamma },Y^{(1)}),\end{array}$

where t^n,γ = tⁿ + γΔt.

Because (6) is a DAE system, application of the SDIRK2 method is slightly more complicated, but it is made easier by the fact that (6) is linear. Applied to this system, the first stage of the SDIRK2 method requires solving the block system

$\left[\begin{array}{cc}\chi C_{m}A+\gamma \Delta t{A}_i& \gamma \Delta t{A}_i\\ \gamma \Delta t{A}_i& \gamma \Delta t{A}_{i+e}\end{array}\right]\left[\begin{array}{c}{v}^{(1)}\\ u_e^{(1)}\end{array}\right]=\left[\begin{array}{c}\chi C_{m}A{v}^n\\ 0\end{array}\right]$

to find the values Y⁽¹⁾ = (v⁽¹⁾, u⁽¹⁾_e). As before, we have scaled the second row (but now by γΔt) to obtain a symmetric system. The second stage involves solving the system

$\begin{array}{l}\left[\begin{array}{cc}\chi C_{m}A+\gamma \Delta t{A}_i& \gamma \Delta t{A}_i\\ \gamma \Delta t{A}_i& \gamma \Delta t{A}_{i+e}\end{array}\right]\left[\begin{array}{c}{v}^{n+1}\\ u_e^{n+1}\end{array}\right]\hfill \\ =\left[\begin{array}{c}\chi C_{m}A{v}^n-(1-\gamma )\Delta t(A_i{v}^{(1)}+A_i{u}_e^{(1)})\\ 0\end{array}\right],\hfill \end{array}$

to find the approximations y^{n + 1} = (v^{n + 1}, u^{n + 1}_e) at the next time step. The linear systems to be solved are similar to those for the θ-rule. The fact that these linear systems have identical coefficient matrices is exploited to improve the efficiency of the SDIRK2 method [18]. Specifically, for a given method and constant Δt, the coefficient matrix is in fact constant throughout the simulation. Thus, it can be factored once at the beginning of each simulation and subsequent linear system solves at each step consist of only forward and backward substitutions. Because the SDIRK2 method requires two such solves per step, it is asymptotically twice as expensive as CN or BE for advancing (6). This does not imply, however, that the overall cost for solving the bidomain model is twice as expensive when using SDIRK2 because the solution of (6) represents only part of the overall solution process.

2.7. Stability Analysis

We now utilize a von Neumann stability analysis, see e.g., Strikwerda [19], for the CN and SDIRK2 methods applied to the bidomain model in the context of operator splitting. For this purpose and in light of (3), we consider the one-dimensional heat Equation $\frac{\partial u}{\partial t}=k\frac{{\partial }^{2}u}{\partial x^2}$ on the interval [−L, L], where k = $k=\frac{\sigma }{\chi C_m}$. Piecewise linear functions are used as basis functions in the finite element method.

A von Neumann stability analysis yields expressions for the amplification factor G(φ), where $\widehat{u}$^{n+ 1}(ω) = G(φ)$\widehat{u}$ⁿ(ω), φ = ω Δx, and $\widehat{u}$ⁿ(ω) is the Fourier transform of uⁿ. For the CN method,

$\begin{array}{cc}{G}_{CN}(\phi )=\frac{1+2c^2-r{s}^2}{1+2c^2+r{s}^2},& (8)\end{array}$

whereas for the SDIRK2 method,

$\begin{array}{cc}{G}_{SDIRK2}(\phi )=\frac{(1+2c^2)\left(1+2c^2+2r(2\gamma -1)s^2\right)}{{\left(1+2c^2+2r\gamma s^2\right)}^2},& (9)\end{array}$

where $c=\cos (\frac{\phi }{2})$, $s=\sin (\frac{\phi }{2})$, $r=k\frac{\Delta t_{\text{PDE}}}{{(\Delta x)}^2}$, Δt_PDE is the time step used in (3), Δx is the (uniform) mesh spacing, and $\omega =\frac{n\pi }{L}$ is the wave number, for n = 1, 2,…,N, with $N=\frac{L}{\Delta x}$.

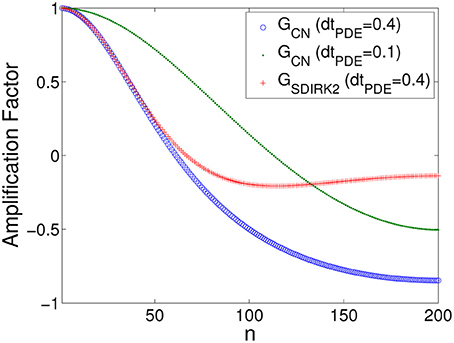
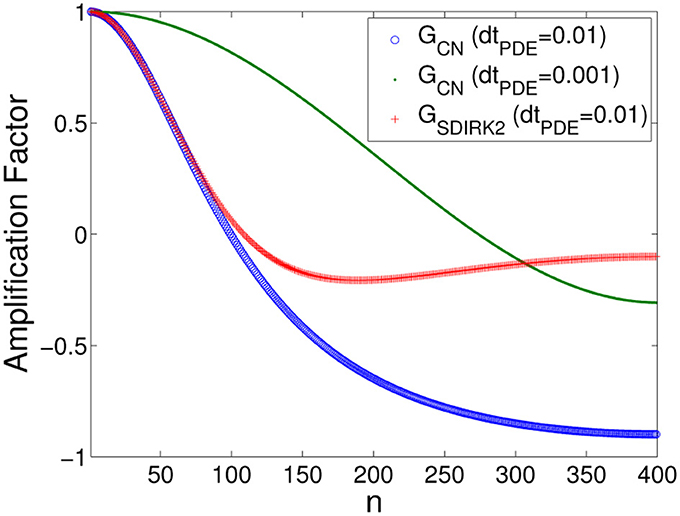
It can be shown that |G_CN(φ)| ≤ 1 and |G_SDIRK2(φ)| ≤ 1 for all φ, Δt > 0; therefore both CN and SDIRK2 methods are unconditionally linearly stable. However, if G(φ) ≳ −1, then the oscillatory components are propagated as weakly damped oscillations in time. G_CN ≳ −1 if rs² is large, i.e., if φ ≈ ±π and r is large. However, G_SDIRK ≳ −1 if and only if $\left(4{\gamma }^2{s}^2\right)r^2+\left(8(1+2c^2)\gamma -2(1+2c^2)\right)r+\frac{2{(1+2c^2)}^2}{s^2}\approx 0$. This condition is generally harder to satisfy, and therefore, SDIRK2 rarely generates sustained oscillations.

We can further identify the relationships of the simulation parameters with the size of the oscillations generated by CN. In particular, Δt_PDE and the conductivity values have a direct relationship with the size of the oscillations; i.e., larger values of these parameters lead to larger oscillations. Conversely, C_m, χ, and Δx have an inverse relationship with the size of the oscillations; i.e., smaller values of these parameters lead to larger oscillations. From this analysis, there is no information about the relationship between the time step Δt_ODE used for the ODEs and the size of the oscillations. However, empirically we do not observe any relationship, nor would we expect one provided the ODE integration is stable. A summary of the relationships of the different simulation parameters with the size of the unphysical oscillations appears in Table 1.

TABLE 1

Table 1. Relationship of parameters with size of unphysical oscillations.

3. Results

We now study aspects of simulations of the bidomain model when using the SDIRK2 method as the PDE solver in an operator-splitting method. We consider the order of convergence, accuracy, stability, and efficiency of the SDIRK2 method compared to the CN and BE methods. For the numerical experiments in one dimension, the direct solver MUMPS [20] is used to solve the associated linear systems. For the numerical experiments in two and three dimensions, a CG iterative solver with a block Jacobi preconditioner is used. All of the numerical results were generated within the Chaste software environment [21].

3.1. Order of Convergence

Because extremely fine spatial and temporal resolutions are required to produce a highly accurate reference solution for convergence testing, we consider a simple one-dimensional problem. The bidomain model was solved for a one-cm spatial interval [0, 1], and reference solutions were generated for two cell models, the Luo–Rudy phase 1 (LR1) model [22] and the model of Courtemanche et al. [23], with the initial condition

$\begin{array}{l}v(t=0,x)=v_0+100(1-\text{sin}(x)),\\ s(t=0,x)=s_0,\\ u_e(t=0,x)=0,\end{array}$

where v₀ and s₀ are the resting values for v and s, respectively, for the particular cell model. We use the (Chaste default) values χ = 1400/cm, C_m = 1 μF/cm², σ_i = 1.75 mS/cm, and σ_e = 7 mS/cm and simulate the model for t ∈ [0, 5] ms.

A reference solution for each bidomain simulation described below was computed with Chaste using the semi-implicit method [11] with Heun's method as the ODE solver. Successive solutions were computed by halving the time step and doubling the number of spatial mesh points until four or more matching digits were obtained at 21 equally spaced points in the temporal interval and 101 equally spaced points in the spatial interval, for a total of 2121 comparison points. The resolutions required for the reference solutions were Δt = 5 · 10⁻⁸ ms, Δx = 1/30 000 cm for the LR1 cell model and Δt = 5 · 10⁻⁷ ms, Δx = 1/20, 000 cm for the cell model of Courtemanche et al.

Numerical experiments were performed to determine the order of convergence using the SDIRK2 method to solve (3). The error is computed for each numerical experiment by computing the absolute error of the solution at x = 0.5 cm relative to the reference solution. The order of convergence is computed from

$p=\frac{\log ({ϵ}_1/{ϵ}_2)}{\log (\Delta t_1/\Delta t_2)},$

where Δt₁ and Δt₂ are two successive step size choices and ϵ₁ and ϵ₂ are the corresponding errors. Table 2 confirms the second-order convergence of the SDIRK2 method.

TABLE 2

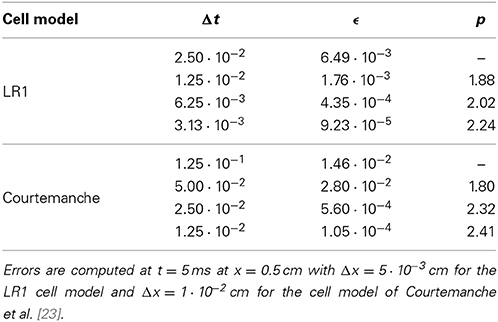
Table 2. Convergence results for the SDIRK2 method applied as the PDE solver for the bidomain model.

3.2. Unphysical Oscillations

We observed unphysical oscillations in different situations, including different spatial dimensions, i.e., from one to three, different mesh sizes, different cell models, i.e., LR1 [22], Courtemanche et al. [23], Maleckar et al. [24], Noble et al. [25], Nygren et al. [26], Winslow et al. [27], and ten Tusscher et al. [28], and different initial conditions, i.e., continuous initial conditions (with stimulus) and discontinuous initial conditions. We now present two different scenarios in which unphysical oscillations are exhibited.

3.2.1. Scenario I: coarse time step

Scenario I is similar to a numerical experiment in Whiteley [11]. The spatial domain is [0, 0.5] × [0, 0.5] cm, discretized uniformly with a spatial resolution of Δx = Δy = 0.0025 cm with N = 40, 401 nodes and 80, 000 triangles. We use Δt_PDE = 0.4 ms, Δt_ODE = 0.01 ms, χ = 1400/cm, C_m = 1 μF/cm², and the LR1 cell model. The tissue fibers are taken to be parallel and aligned with the x-axis, yielding diagonal conductivity tensors σ_i = diag(σ^f_i, σ_iⁿ), σ_e = diag(σ^f_e, σ_eⁿ), with σ^f_i = σ^f_e= 2.63 mS/cm, σ_iⁿ = 0.263 mS/cm, and σ_eⁿ = 1.087 mS/cm. A stimulus with amplitude of −50, 000 μA/cm³ and duration of 2 ms is applied to the lower left-hand corner region [0, 0.1] × [0, 0.1] cm, causing an excitation wave to spread across the domain. The simulation duration is 20 ms. Unphysical oscillations can be generated in three dimensions similarly.

For comparison purposes, we generated a reference solution with Δx = Δy = 0.001 cm, Δt_PDE = 0.01 ms, and Δt_ODE = 0.001 ms. Figure 1A shows a time series plot of the reference solution at the spatial point (0.125, 0.125). The oscillations in the solution produced using CN at the spatial point (0.125, 0.125) are displayed in Figure 1B. These oscillations are attenuated during the plateau phase, at which point the solution looks more physically reasonable. The corresponding plots for SDIRK2 and BE can be seen in Figures 1C, D, respectively.

FIGURE 1

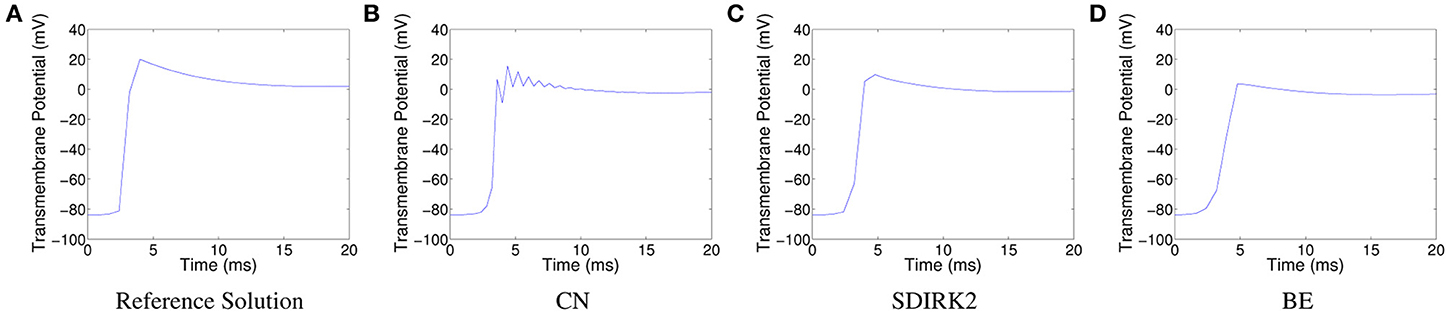
Figure 1. Plots of the transmembrane potential at the spatial point (0.125, 0.125) and t ∈ [0, 20] ms for Scenario I: (A) reference solution, (B) CN solution, (C) SDIRK2 solution, and (D) BE solution.

In Figure 2A, the reference solution is displayed on [0, 0.5] × [0, 0.25] cm. The corresponding solution produced by CN is displayed in Figure 2B. Unphysical oscillations can be seen across the action potential wavefront. The corresponding plots for SDIRK2 and BE are displayed in Figures 2C, D, respectively. There are obvious inaccuracies in all the solutions because of the relatively coarse meshes, but it is also clear that neither the SDIRK2 nor BE methods exhibit unphysical oscillations.

FIGURE 2

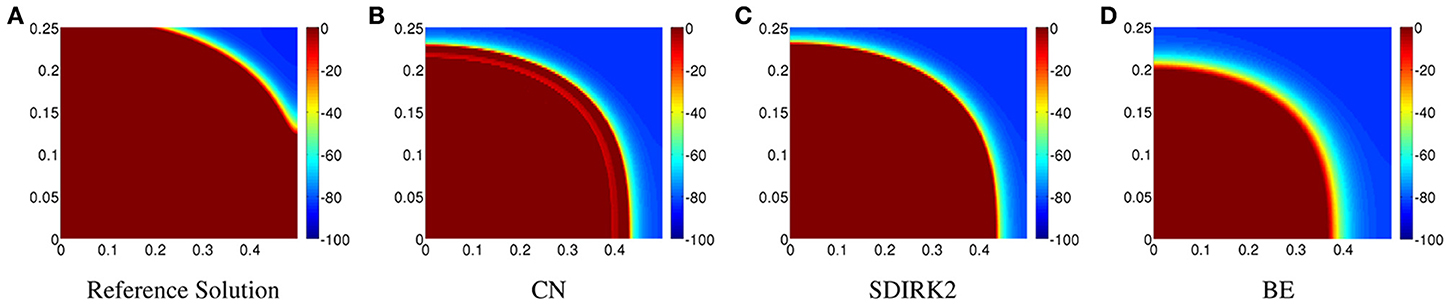
Figure 2. Plots of the transmembrane potential on [0, 0.5] × [0, 0.25] cm at t = 8 ms for Scenario I: (A) reference solution, (B) CN solution, (C) SDIRK2 solution, and (D) BE solution.

All other things being equal, one way to decrease the oscillations for CN is to decrease Δt_PDE. The oscillations in the solution produced using CN with Δt_PDE = 0.3 ms at the spatial point (0.125, 0.125) are displayed in Figure 3A. The corresponding plots for Δt_PDE = 0.2 ms and Δt_PDE = 0.1 ms can be seen in Figures 3B, C, respectively. As can be seen, suppression of unphysical oscillations to visual accuracy requires the use of Δt_PDE = 0.1 ms.

FIGURE 3

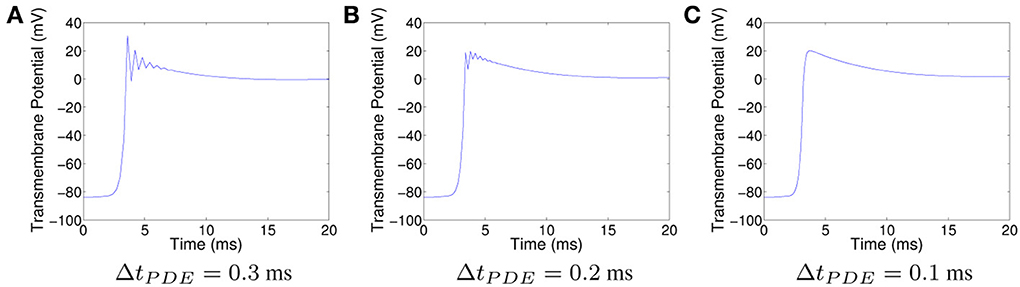
Figure 3. Plots of the transmembrane potential at the spatial point (0.125, 0.125) and t ∈ [0, 20] ms for Scenario I using CN and: (A) Δt_PDE = 0.3 ms, (B) Δt_PDE = 0.2 ms, and (C) Δt_PDE = 0.1 ms.

These observations can be understood in terms of the amplification factors of the methods. For the purposes of analysis, in Equations (8) and (9), we let σ = 0.263, L = 0.5, Δx = 0.0025, and N = 0.5/0.0025 = 200, with φ = φ(n) = ω(n)Δx = $\frac{n\pi }{L}\Delta x$. The CN and SDIRK2 amplification factors as a function of wave number index n are shown in Figure 4. The amplification factor of the BE method behaves similarly to that of the SDIRK2 method (details omitted). Figure 4 shows that although both methods have similar damping properties at low wave numbers for Δt_PDE = 0.4 ms, at high wave numbers (as n → N), G_CN(φ) → −1⁺ (weak damping) whereas G_SDIRK(φ) → 0 (strong damping). CN has better damping properties using Δt_PDE = 0.1 ms.

FIGURE 4

Figure 4. CN and SDIRK2 amplification factors from Equations (9) and (10) for Scenario I.

3.2.2. Scenario II: fine time step

In Scenario II, the spatial domain is [0, 0.4] × [0, 0.4] cm, discretized uniformly with a spatial resolution of Δx = Δy = 1 · 10⁻³ cm with N = 160, 801 nodes and 320, 000 triangles. We use Δt_PDE = 1 · 10⁻² ms and Δt_ODE = 1 · 10⁻³ ms. We use χ = 1400/cm, C_m = 1 μF/cm², the LR1 cell model, and conductivities 2.63 mS/cm along the fiber in both the intracellular and extracellular conductivity tensors, 0.263 mS/cm perpendicular to the fiber in the intracellular conductivity tensor, and 1.087 mS/cm in the extracellular conductivity tensor. A discontinuous initial condition with v₀ = 100 mV on [0, 0.004] × [0, 0.032] cm and v₀ = −83, 853 mV otherwise is used, causing an excitation wave to spread across the square. A simulation duration of 2 ms suffices to capture the behavior of interest. Unphysical oscillations can be generated in three dimensions similarly.

For comparison purposes, we generated a reference solution with Δx = Δy = 5 · 10⁻⁴ cm, Δt_PDE = 1 · 10⁻³ ms, and Δt_ODE = 1 · 10⁻⁴ ms; it is shown in Figure 5A. The oscillations in the solution produced using CN at the spatial point (0.004, 0.032) are displayed in Figure 5B. The corresponding plots for SDIRK2 and BE are displayed in Figures 5C, D, respectively.

FIGURE 5

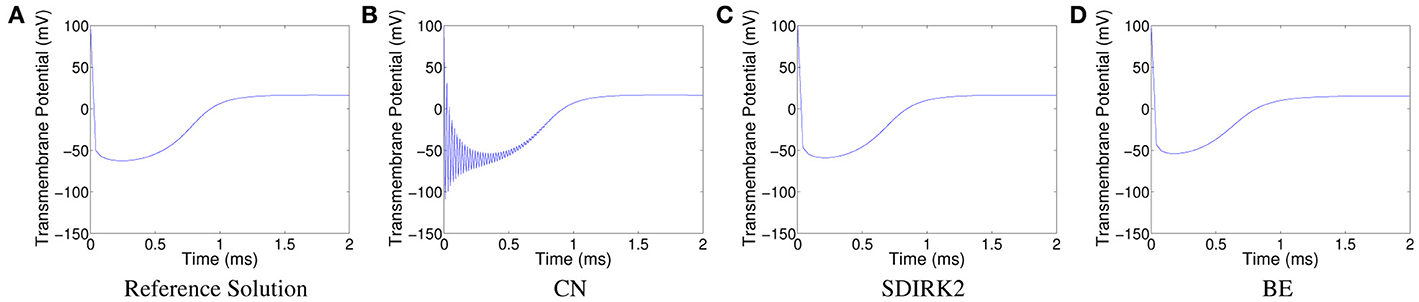
Figure 5. Plots of the transmembrane potential at the spatial point (0.004, 0.032) and t ∈ [0, 2] ms for Scenario II: (A) reference solution, (B) CN solution, (C) SDIRK2 solution, and (D) BE solution.

In Figure 6A, the reference solution is displayed on [0, 0.2] cm × [0, 0.1] cm. The solution produced by CN is displayed in Figure 6B. The corresponding plots for SDIRK2 and BE are shown in Figures 6C, D, respectively. The SDIRK2 and BE solutions agree well with the reference solution.

FIGURE 6

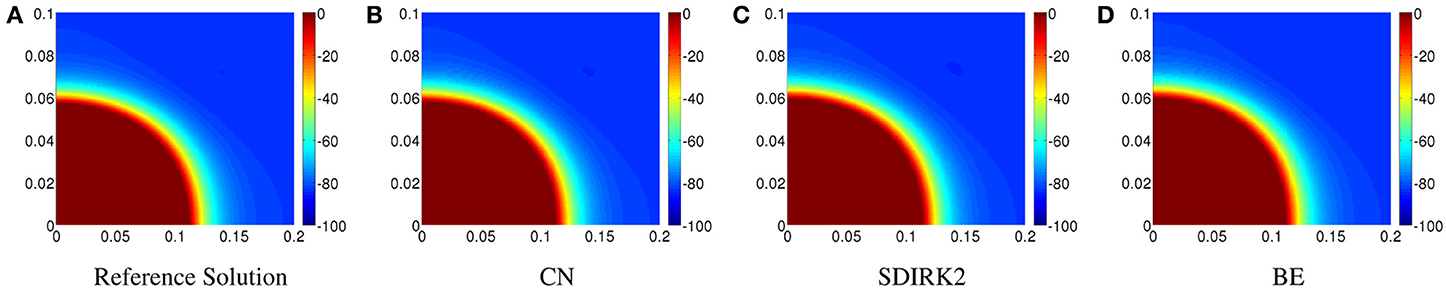
Figure 6. Plots of the transmembrane potential on [0, 0.2] × [0, 0.1] cm at t = 2 ms for Scenario II: (A) reference solution, (B) CN solution, (C) SDIRK2 solution, and (D) BE solution.

Unphysical oscillations can be seen around the location of the discontinuity. The initial solution is displayed on [0, 0.05] cm × [0, 0.05] cm in Figure 7A. The oscillations in the solution produced using CN at time 0.1 ms are displayed in Figure 7B. The corresponding plots at time 0.2 ms and 0.5 ms can be seen in Figures 7C, D, respectively.

FIGURE 7

Figure 7. Plots of the transmembrane potential on [0, 0.05] × [0, 0.05] cm using CN for Scenario II at: (A) t = 0.1 ms, (B) t = 0.2 ms, and (C) t = 0.5 ms.

All things being equal, one way to decrease the oscillations for CN is to decrease Δt_PDE. The oscillations in the solution produced using CN with Δt_PDE = 5 · 10⁻³ ms at the spatial point (0.004, 0.032) are displayed in Figure 8A. The corresponding plots for Δt_PDE = 2 · 10⁻³ ms and Δt_PDE = 1 · 10⁻³ ms can be seen in Figures 8B, C, respectively. As can be seen, suppression of unphysical oscillations to visual accuracy requires the use of Δt_PDE = 1 · 10⁻³ ms. A solution with approximately the same accuracy can be obtained using the SDIRK2 method with a Δt_PDE ten times as large. Such an increase in time step would more than offset the additional cost of using the SDIRK2 method as the PDE solver.

FIGURE 8

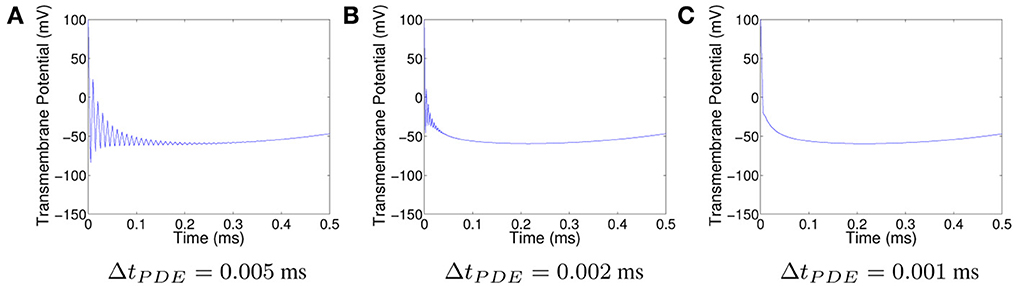
Figure 8. Plots of the transmembrane potential at the spatial point (0.125, 0.125) and t ∈ [0, 0.5] ms for Scenario II using CN and: (A) Δt_PDE = 0.005 ms, (B) Δt_PDE = 0.002 ms, and (C) Δt_PDE = 0.001 ms.

As in Scenario I, these observations can be understood in terms of the amplification factors of the methods. In Equations (8) and (9), we let σ = 2.63, L = 0.4, Δx = 0.001, and N = 0.4/0.001 = 400, where φ = φ(n) = ω(n)Δx = $\frac{n\pi }{L}\Delta x$. The CN and SDIRK2 amplification factors as a function of wave number index n are given in Figure 9, again showing that for Δt_PDE = 0.01 ms as n → N, G_CN(φ) → −1⁺ whereas G_SDIRK(φ) → 0. CN has better damping properties using Δt_PDE = 0.001 ms.

FIGURE 9

Figure 9. CN and SDIRK2 amplification factors from Equations (9) and (10) for Scenario II.

4. Discussion

We have investigated numerical methods within a commonly used operator-splitting technique for solving the bidomain model. Specifically, we have considered a two-stage, second-order, L-stable SDIRK2 method to solve the split linear PDE system (3) as an alternative to the popular CN and BE methods. The BE method is L-stable and widely used for solving the bidomain model, but previous studies have indicated that second-order methods based on the CN method are more efficient than first-order methods [12]. However, as demonstrated in Whiteley [11], the poor damping properties of CN may lead to unphysical oscillations for certain combinations of spatial and temporal resolutions. Although such oscillations are normally transient, they may lead to solver divergence and failure in the context of operator splitting and strongly non-linear cell models.

We have applied von Neumann stability analysis to explain the oscillations seen in Whiteley [11] in terms of the amplification factor of the numerical method. Furthermore, the stability analysis revealed qualitative relations between model parameters and the magnitude of unphysical oscillations. The stability analysis confirms the superior damping properties of the L-stable SDIRK method, and it predicts that weakly damped oscillations do not generically occur for this method. Numerical experiments confirm this result, and switching from CN to SDIRK2 is observed to be effective for suppressing unphysical oscillations.

When solving the bidomain model with operator-splitting methods, the total CPU time is the sum of the time spent on solving the ODE systems in (2) and the PDEs in (3). The relative time spent on each part varies with the numerical methods used and, in particular, with the choice of cell model. However, when optimal-order PDE solvers are applied, the ratio is independent of mesh size [29]. The great variability in cell models used makes it generally difficult to quantify the contribution of each part, but both typically make a significant contribution to the total CPU time. Because the matrices in (6) are constant in time and therefore assembled only once, the CPU time for the PDE step is dominated by solving linear systems. The CN and BE methods require one linear solve per time step, while the SDIRK2 method requires two. If there were no other computational costs associated with solving the bidomain model, one step of a fractional-step method using the SDIRK2 method would be twice as costly as one using CN or BE. However, this upper bound is generally not sharp. Suppose for instance that when using the CN method as the PDE solver, α% of the total CPU time is spent on solving (3), and the rest is spent on (2). The cost of the fractional-step method using SDIRK2 relative to CN is then 100 + α%. Depending on the choice of cell model, α may vary from almost negligible to well above 50, and these variations affect the relative overall cost of using the SDIRK2 method. However, in Scenarios I and II above we saw that removing the oscillations when using the CN method required time step reductions on the order of 4–10, yielding much larger CPU times than those required when using the SDIRK2 method.

In conclusion, use of the SDIRK2 method within a fractional-step method represents a robust alternative to using the popular CN method for solution of the bidomain model. Being a method of second order, the accuracy is comparable to the CN method. The computational cost of the SDIRK2 step is greater than that of CN. However, the cost of the overall solver may be dominated by other factors such as solving the ODEs, in particular for large, complicated, or stiff cell models. Preliminary efficiency estimates indicate that the use of CN results in a slightly more efficient method when strict error tolerances are used because unphysical oscillations are not normally observed. However, such error tolerances may not always be necessary to obtain useful data in practice. In such cases, the data can be more efficiently obtained using the SDIRK2 method proposed. Overall, the added robustness of SDIRK2 comes with a relatively small computational cost while at the same time eliminating the possibility that unfortunate parameter combinations lead the solver to generate unphysical oscillations and potentially fail.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Tung, L. A Bi-domain Model for Describing Ischemic Myocardial D-C Potentials. Cambridge: Massachusetts Institute of Technology (1978).

2. Sundnes, J, Lines, GT, Cai, X, Nielsen, BF, Mardal, KA, and Tveito, A. Computing the Electrical Activity in the Heart. Berlin: Springer-Verlag (2006).

3. Potse, M, and Vinet, A. Large-scale integrative modeling of the human heart. In: HPCS 2008. Quebec (2008).

4. Vigmond, EJ, dos Santos, RW, Prassl, AJ, Deo, M, and Plank, G. Solvers for the cardiac bidomain equations. Prog Biophys Mol Biol. (2008) 96:3–18. doi: 10.1016/j.pbiomolbio.2007.07.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

5. Muzikant, AL, Hsu, EW, Wolf, PD, and Henriquez, CS. Region specific modeling of cardiac muscle: comparison of simulated and experimental potentials. Ann Biomed Eng. (2002) 30:867–83. doi: 10.1114/1.1509453

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

6. Sambelashvili, A, and Efimov, IR. Dynamics of virtual electrode-induced scroll-wave reentry in a 3D bidomain model. Am J Physiol Heart Circ Physiol. (2004) 287:H1570–81. doi: 10.1152/ajpheart.01108.2003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

7. ten Tusscher, KHWJ., and Panfilov, AV. Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol. (2006) 291:H1088–100. doi: 10.1152/ajpheart.00109.2006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

8. Tranquillo, JV, Franz, MR, Knollmann, BC, Henriquez, AP, Taylor, DA, and Henriquez, CS. Genesis of the monophasic action potential: role of interstitial resistance and boundary gradients. Am J Physiol Heart Circ Physiol. (2004) 286:H1370–81. doi: 10.1152/ajpheart.00803.2003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

9. Puwal, S, and Roth, BJ. Forward euler stability of the bidomain model of cardiac tissue. IEEE Trans Biomed Eng. (2007) 54:951–3. doi: 10.1109/TBME.2006.889204

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

10. Keener, JP, and Bogar, K. A numerical method for the solution of the bidomain equations in cardiac tissue. Chaos (1998) 8:234–41. doi: 10.1063/1.166300

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Whiteley, JP. An efficient numerical technique for the solution of the monodomain and bidomain equations. IEEE Trans Biomed Eng. (2006) 53:2139–47. doi: 10.1109/TBME.2006.879425

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

12. Sundnes, J, Lines, GT, and Tveito, A. An operator splitting method for solving the bidomain equations coupled to a volume conductor model for the torso. Math Biosci. (2005) 194:233–48. doi: 10.1016/j.mbs.2005.01.001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

13. Strang, G. On the construction and comparison of difference schemes. SIAM J Numer Anal. (1968) 5:506–17. doi: 10.1137/0705041

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Qu, Z, and Garfinkel, A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans Biomed Eng. (1999) 46:1166–8. doi: 10.1109/10.784149

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Ascher, UM, and Petzold, LR. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM) (1998).

16. Hundsdorfer, W, and Verwer, J. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations. Berlin: Springer-Verlag (2003). doi: 10.1007/978-3-662-09017-6

CrossRef Full Text

17. Krishnamoorthi, S, Sarkar, M, and Klug, WS. Numerical quadrature and operator splitting in finite element methods for cardiac electrophysiology. Int J Numer Meth Biomed Eng. (2013) 29:1243–66. doi: 10.1002/cnm.2573

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

18. de Sturler, E. Inner-outer methods with deflation for linear systems with multiple right hand sides. In: Householder Symposium XIII, Proceedings of the Householder Symposium on Numerical Algebra. Pontresina (1996). p. 193–196.

19. Strikwerda, J. Finite Difference Schemes and Partial Differential Equations. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM) (2004).

20. MUMPS: A Parallel Sparse Direct Solver (2012). Available online at: http://graal.ens-lyon.fr/MUMPS/index.php?page=home

21. Pitt-Francis, J, Pathmanathan, P, Bernabeu, MO, Bordas, R, Cooper, J, Fletcher, AG, et al. Chaste: a test-driven approach to software development for biological modelling. Comput. Phys Commun. (2009) 180:2452–71. doi: 10.1016/j.cpc.2009.07.019

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

22. Luo, C, and Rudy, Y. A model of ventricular cardiac action potential. Circ Res. (1991) 68:1501–26. doi: 10.1161/01.RES.68.6.1501

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

23. Courtemanche, M, Ramirez, RJ, and Nattel, S. Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am J Physiol. (1998) 275:H301–21.

Pubmed Abstract | Pubmed Full Text

24. Maleckar, MM, Greenstein, JL, Trayanova, NA, and Giles, WR. Mathematical simulations of ligand-gated and cell-type specific effects on the action potential of human atrium. Prog Biophys Mol Biol. (2008) 98:161–70. doi: 10.1016/j.pbiomolbio.2009.01.010

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Noble, D, Noble, SJ, Bett, GC, Earm, YE, Ho, WK, and So, IK. The role of sodium-calcium exchange during the cardiac action potential. Ann N Y Acad Sci. (1991) 639:334–53. doi: 10.1111/j.1749-6632.1991.tb17323.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

26. Nygren, A, Fiset, C, Firek, L, Clark, JW, Lindblad, DS, Clark, RB, et al. Mathematical model of an adult human atrial cell: the role of K+ currents in repolarization. Circ Res. (1998) 82:63–81. doi: 10.1161/01.RES.82.1.63

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

27. Winslow, RL, Rice, J, Jafri, S, Marbán, E, and Rourke, BO. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, II model studies. Circ Res. (1999) 84:571–86. doi: 10.1161/01.RES.84.5.571

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. ten Tusscher, KHWJ, and Panfilov, AV. Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol. (2006) 291:H1088–100. doi: 10.1152/ajpheart.00109.2006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Sundnes, J, Nielsen, BF, Mardal, KA, Cai, X, Lines, GT, and Tveito, A. On the computational complexity of the bidomain and the monodomain models of electrophysiology. Ann Biomed Eng. (2006) 34:1088–97. doi: 10.1007/s10439-006-9082-z

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text