- Department of Meteorology, University of Reading, Reading, UK
The drag and momentum fluxes produced by gravity waves generated in flow over orography are reviewed, focusing on adiabatic conditions without phase transitions or radiation effects, and steady mean incoming flow. The orographic gravity wave drag is first introduced in its simplest possible form, for inviscid, linearized, non-rotating flow with the Boussinesq and hydrostatic approximations, and constant wind and static stability. Subsequently, the contributions made by previous authors (primarily using theory and numerical simulations) to elucidate how the drag is affected by additional physical processes are surveyed. These include the effect of orography anisotropy, vertical wind shear, total and partial critical levels, vertical wave reflection and resonance, non-hydrostatic effects and trapped lee waves, rotation and nonlinearity. Frictional and boundary layer effects are also briefly mentioned. A better understanding of all of these aspects is important for guiding the improvement of drag parametrization schemes.
1. Introduction
The atmosphere above the boundary layer is almost invariably characterized by positive static stability, supporting the propagation of internal gravity waves, where buoyancy is the main restoring force. Related waves exist over a wide range of horizontal scales, from ≈1 km, where the waves are non-hydrostatic, to ≈10 km, where they are approximately hydrostatic, through to ≈100 km, where rotation of the Earth becomes important (inertia-gravity waves), up to ≈1000 km, where the variation of the Coriolis parameter with latitude must be taken into account (Rossby-gravity waves) [1]. One of the key permanent sources for these waves is the Earth's orography, although other transient sources exist, for example, thermal contrasts between the continents and oceans, or atmospheric convection [2].
If these orographically generated waves (hereafter called mountain waves, for simplicity, although the term is often reserved for mesoscale waves) are able to propagate energy away from their sources (i.e., they are not evanescent), they exert a drag force on the mountains that generate them. In turn, by Newton's 3rd law, those mountains must exert an equal and opposite force on the atmosphere. However, while drag on the orography must obviously be exerted at the surface, the reaction force on the atmosphere may be distributed in space, and often acts at high altitudes. For mountain waves whose energy propagates vertically, the levels where the reaction force is exerted are given by Eliassen-Palm's theorem [3], or its extension to 3D flow by Broad [4].
Since the horizontal scales of the shortest mountain waves (primarily those unaffected by rotation) are smaller than current grid spacings in global weather and climate prediction models, these waves cannot be represented explicitly and so must be parametrized, because they affect the resolved flow [5, 6]. Perceived overestimations in the intensity of westerly winds in mid-latitudes were initially alleviated by adopting a so-called “envelope orography” [7, 8], whereby the surface elevation in mountainous areas is artificially increased by a certain amount. But a mountain wave drag parametrization was recognized by Palmer et al. [9] as a more physically satisfactory way of correcting this bias. Since then, increasingly sophisticated drag parametrizations have been developed and incorporated in large-scale models [10–19].
Drag not only decelerates the global atmospheric circulation, but, via thermal wind balance, it also has an impact on temperatures in the stratosphere at high latitudes. The formation of polar stratospheric clouds, which have an important role in ozone depletion, is very sensitive to those temperatures [20], and therefore to the drag representation. Additionally, it has been shown recently that the Brewer-Dobson circulation in the stratosphere, which ascends at the tropics and descends at the poles, contributing to the transport of ozone and other chemical species, is partially driven by mountain waves, although its primary forcing is believed to be non-orographic gravity waves [21].
On the other hand, mountain wave drag integrated globally determines the torque exerted on the Earth by the atmosphere and vice-versa, which affects the angular momentum budget of the atmosphere [22, 23]. This budget may be evaluated independently using series of the duration of day [24, 25]. There are known imbalances in the global angular momentum budget as simulated by numerical models, and this may be caused by errors in drag parametrizations [26–28]. The total terrain-induced drag may be split into three components: 1. drag associated with mountain waves, 2. drag associated with low-level blocking caused by stratification effects, and 3. turbulent form drag. There is the possibility, not only that the total drag is incorrectly estimated, but also that errors in each of these 3 components partially compensate.
For all these reasons, a fundamental understanding of mountain wave drag is of the utmost importance for the reliability of the models used to forecast the weather, reproduce the present climate, and especially predict future climate scenarios, on which important political decisions are based.
Several field campaigns to investigate flow over mountains have taken place over the last decades, for example: ALPEX [29, 30], PYREX [31], MAP [32, 33] and T-REX [34, 35]. These campaigns were generally carried out by large consortia, an exception being the smaller-scale campaign in the island of Madeira reported by Miranda et al. [36]. While they contributed decisively to advance our knowledge about orographic flows, and included pressure measurements that allowed obtaining rough estimates of mountain wave drag, their success in this respect was limited, because of the limited available data sampling and complexity of real-world conditions (see also [37]). This hampered a more detailed comparison with theory, numerical simulations and lab experiments, which tend to assume much more idealized conditions.
There have been numerous reviews about flow over mountains [38–45], some on mountain wave drag parametrization [46–48], and also a few on the dependence of the resolved drag on numerical model resolution [33, 49], but none focused specifically on how the drag is affected by different physical processes. The present contribution aims to fill that gap, trying to show how accumulated knowledge, primarily from theory and numerical simulations, helps us understand the behavior of mountain wave drag.
Despite having grown rapidly only over the last 30 years, the subject has become too vast to cover entirely in a single review paper. Therefore, I decided to omit here studies focused on the effects of moisture, phase transitions and precipitation, radiation, and mean flow unsteadiness. Numerical aspects of mountain wave simulations, such as resolution dependence, and aspects directly linked with parametrization, are also, to a large extent, overlooked. I apologize in advance for failing to acknowledge several excellent investigations, even in the research areas that are covered here, and also for my probable bias toward theory.
The remainder of this paper comprises: an introduction to mountain wave drag in its simplest form in section 2, followed by an overview of the impact on the drag of various physical effects. Section 3 deals with orography anisotropy, section 4 addresses vertical wind shear, and in sections 5 and 6 the effects of total and partial critical levels are reviewed. Section 7 deals with partial wave reflection and resonance in layered atmospheres, in section 8 non-hydrostatic effects and trapped lee waves are mentioned, followed by rotation in section 9, and specifically nonlinear effects in section 10. To conclude, section 11 presents a brief overview of boundary layer effects. The paper ends with a summary of some open questions and possible future directions in the field.
2. General Framework for Linearized Mountain Waves
To understand how different physical processes affect mountain wave drag it is useful to formulate first the mountain wave problem in its most basic form. Consider the inviscid, adiabatic, non-rotating, steady, linearized equations of motion with the Boussinesq approximation:
Here (U, V) is the mean incoming wind velocity (which is assumed to depend only on height z), (u, v, w) is the velocity perturbation associated with the waves, p is the pressure perturbation, ρ0 is a reference constant density, b0 = gθ/θ0 is the buoyancy (where g is the acceleration of gravity, θ is a potential temperature perturbation and θ0 is a reference constant potential temperature), and N2 = (g/θ0)dΘ/dz is the static stability (where Θ is the mean potential temperature, assumed to depend only on z). These five equations for the five unknowns u, v, w, p and b0 may be combined into a single equation for w,
which must be solved subject to appropriate boundary conditions.
If the waves are forced by an isolated mountain, w (and all other perturbation variables) must decay to zero as x → ±∞ and y → ±∞. Additionally, the flow must follow the terrain elevation at the surface, i.e., in the linearized approximation
where h(x, y) is the surface elevation and (U0, V0) = (U, V)(z=0) is the mean incoming wind velocity at the surface. The waves must also either decay to zero as z → +∞, or their energy must propagate upward (the so-called radiation boundary condition).
Differentiating (1) with respect to x and (2) with respect to y, adding the two equations and using also (5) to eliminate u and v, an equation for p expressed in terms of w is obtained:
In the linearized approximation, the pressure drag force exerted on the mountain is given in general by:
where Dx and Dy are the drag components along the x and y direction, respectively. An important related quantity is the vertical flux of horizontal momentum associated with the waves,
It can be shown using (1, 2, 7), integrating by parts and using also the horizontal boundary conditions at x, y → ±∞ that:
which basically expresses Newton's 3rd law.
If the mountain is isolated and the flow perturbations decay to zero horizontally away from it, h, w and p may be expressed as Fourier integrals, viz.
where ĥ, ŵ and are the corresponding Fourier transforms, , and (k, l) is the horizontal wavenumber vector. When (13) is inserted into (6), that equation becomes:
which is sometimes called the Taylor-Goldstein equation. The lower boundary condition (7) can then be written as:
From (8, 13, 14), it can be shown that:
On the other hand, using (12) and (14), it is possible to express (9) in wavenumber space,
and also (10) as:
where the asterisk denotes complex conjugate. Treating the wave problem using Fourier analysis is particularly convenient, because the criteria determining whether the waves are vertically propagating of evanescent must be specified in wavenumber space.
2.1. Drag for Hydrostatic Flow with Constant Wind and Static Stability
If the flow is hydrostatic and both N and (U, V) = (U0, V0) are constant, all terms within square brackets in (15) vanish except the first one, which becomes constant. The analytical solution to that equation is then
where
is the vertical wavenumber of the waves and it has been assumed that N2 > 0, hence N > 0 is real. Note that, for hydrostatic flow m is always real, which means that all waves propagate vertically. Equation (21) already implies that the wave energy propagates upward, since the condition for the vertical component of the group velocity to be positive is that m and Uk + Vl have the same sign [50].
If the solution (20) is inserted into (17) and that equation is used in (18), then
where (21) has also been employed. If, additionally, the orography h(x, y) is assumed to have a height of O(h0) and a width of O(a) (see Figure 1), (k, l) may be made dimensionless using a as (k', l') = (ak, al), and ĥ using both a and h0 as ĥ′ = ĥ/(h0 a2), in terms of which (22) becomes:
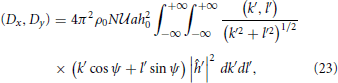
where 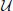 = (U2 + V2)1/2 is the magnitude of the incoming wind velocity and ψ is the angle it makes with the x direction, defined by:
= (U2 + V2)1/2 is the magnitude of the incoming wind velocity and ψ is the angle it makes with the x direction, defined by:
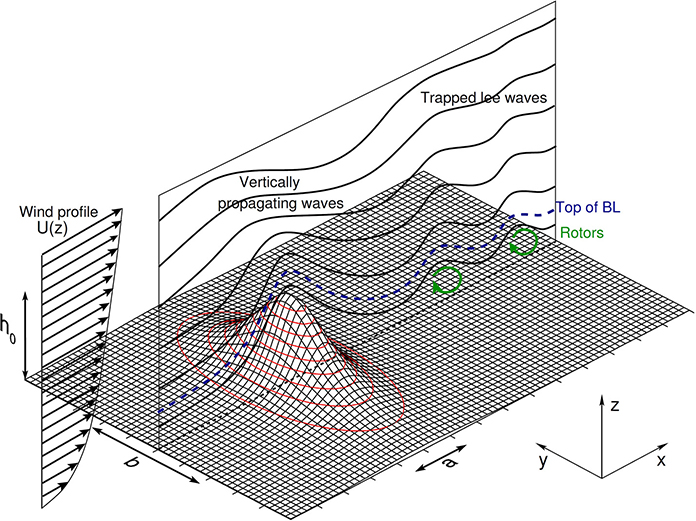
Figure 1. Schematic diagram of mountain waves for a flow with ψ = 0. a and b are the mountain half-widths along x and y (for an axisymmetric mountain b = a) and h0 is the mountain height. Marked in the figure are flow streamlines (thick black lines), the boundary layer top (dashed blue line) and rotors (curved green arrows, see section 8). Note that throughout most of this paper, except in section 11, the boundary layer is neglected and a free-slip boundary condition is assumed at the surface.
In (23) the integral is dimensionless, and its numerical value depends only on the wind direction and shape of the orography. The drag therefore scales as ρ0N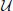 ah20 as is well known [51]. In the case of a circular bell-shaped mountain,
ah20 as is well known [51]. In the case of a circular bell-shaped mountain,
the value of the drag in any direction is the same, and from (23), taking ψ = 0 without any loss of generality, the value of the integral is evaluated to be 1/(16π), so the drag is given by:
It should be noted that, for vertically propagating waves, the horizontal wavelength and amplitude of the dominant waves can be estimated from the corresponding orography width a and height h0, respectively. This implies that ã = Na/U quantifies non-hydrostatic effects (the flow is highly non-hydrostatic when ã ≤ O(1) and is hydrostatic when ã ≫ 1), while = Nh0/U quantifies flow nonlinearity (conditions are approximately linear for ≪ 1 and nonlinear when is of O(1) or larger). The effects of rotation can also be estimated in a similar way: if fa/U ≪ 1 (where f is the Coriolis parameter) then rotation is negligible, while for fa/U of O(1) or larger, it substantially affects the waves. In the present section it was assumed from the outset that ≪ 1 and fa/U ≪ 1, and in this subsection in particular also that ã ≫ 1. These assumptions will be relaxed in the following sections.
3. Orography Anisotropy
In general, the orography that generates mountain waves is not axisymmetric. A useful limit, representative of elongated mountain ranges, is that of 2D orography (say, aligned in the y direction), where (1–8), (15–17) and (20, 21) in the preceding section remain valid, provided that ∂n (…)/∂yn = 0 (for any n = 1, 2, 3, …) and l = 0 are imposed on them, since the flow is now independent of y. In that case, the Fourier transforms should be understood as being 1D (only taken along x) instead of 2D. The drag, on the other hand, must be defined per unit length along y, and is given by:
or
as an integral in physical or in wavenumber space, respectively. Following a procedure similar to that used in the preceding section, it can be shown that this drag scales as ρ0NUh20 and, for a bell-shaped mountain ridge,
(where now ĥ′ = ĥ/(h0a)), the drag takes the form
While the drag on an axisymmetric mountain is aligned with the incoming wind, the drag on a 2D ridge is always perpendicular to the ridge (and only depends on the wind in that direction, as shown by (30)). The considerably more realistic case of flow over a mountain with an elliptical horizontal cross-section, with a generic form h(x, y) = h[(x/a)2 + (y/b)2], was considered by Phillips [51], where b is the width of the mountain along y (see Figure 1). This kind of geometry is relevant, because it can be used to represent more accurately the anisotropy of real orography. This approach is adopted in each model grid box in the drag parametrizations of weather forecast models at the European Centre for Medium-Range Weather Forecasts (ECMWF) [15] and UK Meteorological Office [17]. Using (23) it can be shown that, for this geometry, the two components of the drag take the form
where
γ = a/b is the aspect ratio of the mountain and ĥ is now normalized as ĥ′ = ĥ/(h0ab). G is a coefficient that describes the variation of the surface elevation in the radial direction.
In (31) the drag components are aligned with the main axes of the elliptical mountain. The components aligned with the mean incoming wind and perpendicular to it are [51]
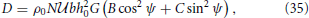
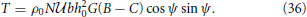
Graphs of these two quantities normalized by ρ0N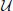 bh20 (D3 and T3, respectively) are presented in Figure 2 as functions of γ and ψ. Clearly, the only situations with γ ≠ 1 where the drag is aligned with the incoming wind are when this wind is aligned with the principal axes of the mountain (ψ = 0o or ψ = 90o). Otherwise, the drag is oblique to both the incoming wind and the principal axes of the mountain.
bh20 (D3 and T3, respectively) are presented in Figure 2 as functions of γ and ψ. Clearly, the only situations with γ ≠ 1 where the drag is aligned with the incoming wind are when this wind is aligned with the principal axes of the mountain (ψ = 0o or ψ = 90o). Otherwise, the drag is oblique to both the incoming wind and the principal axes of the mountain.
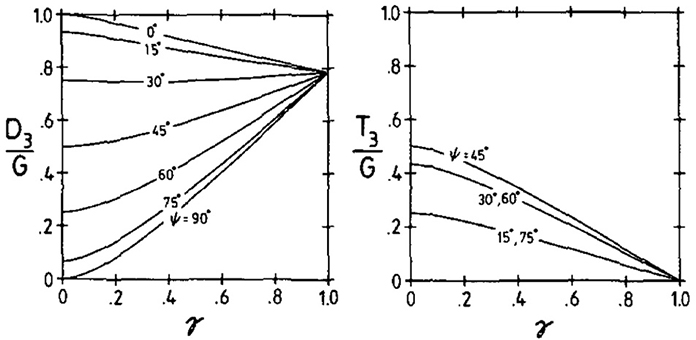
Figure 2. Normalized drag components parallel (D3) and perpendicular (T3) to the incoming wind as a function of ψ and γ (see curve labels for details). Reproduced from Figure 8 of Phillips [51]. © American Meteorological Society. Used with permission.
Hines [54] showed that the contribution to the drag given by wavenumbers within a small angular range surrounding the direction perpendicular to the mountain is overwhelmingly dominant for elongated mountains with aspect ratios γ < 1/3. For that reason, he suggested that the drag be approximated as perpendicular to the major axis of the mountain in those cases, and as receiving contributions from two wavenumber directions symmetrical with respect to the incoming wind otherwise. This allowed the derivation of analytical drag expressions (involving an explicit evaluation of approximated forms for (33,34)). These ideas were used by Scinocca and McFarlane [55] to develop a General Circulation Model (GCM) drag parametrization.
Bauer et al. [56] and Wells et al. [57] studied the interaction of orography anisotropy with flow nonlinearity also assuming elliptical mountains, concluding that flow perpendicular to the major axis of the mountain is substantially more nonlinear than flow parallel to that axis. Wells et al. [57], in particular, found that the dependence of the drag on flow direction is quite well captured by linear theory, but its value is typically underestimated for flow across the mountain (and overestimated for flow along it). Wells et al. [57] additionally explored the effect of weak rotation (fa/U ≈ 0.1), which was shown to introduce a lateral asymmetry in flow over symmetric mountains, but otherwise did not affect much the pressure distribution or the drag. Epifanio and Durran [58] further investigated the joint effects of orography anisotropy and nonlinearity, showing that in flow across an elongated 3D mountain the drag may only be approximated accurately by the drag in flow across an infinite 2D ridge for relatively weak nonlinearity, whereas finite anisotropy becomes much more important for strongly nonlinear flow.
4. Incoming Wind Shear
Blumen and McGregor [59]'s pioneering study used linear theory to calculate the drag over a 2D and an approximately axisymmetric mountain, both for an incoming flow with horizontal shear and for a two-layer atmosphere with positive vertical wind shear and lower static stability in the bottom layer, and no shear and higher stability in the top layer. They found that the drag increased relative to its constant-wind and constant-stability reference value due to horizontal shear, was higher for flow over a 2D mountain than for flow over a 3D mountain, and was an oscillating function of the lower layer height. Blumen and McGregor [59] interpreted this as due to interference between waves transmitted and reflected at the interface between the two layers (see section 7 below), but did not systematically explore the behavior of the drag with the flow parameters.
An important measure of the wind shear in the incoming wind profile is the Richardson number
which quantifies the opposing effects of shear and stratification in destabilizing and stabilizing the flow, respectively. In the cases addressed next Ri > 1/4, which corresponds to dynamically stable (i.e., non-turbulent) flow.
Smith [52] developed a linear model for lee cyclogenesis, where he assumed a unidirectional wind profile with constant negative shear,
where U0 > 0 and α < 0 are constants, and as a by-product calculated mountain wave drag for hydrostatic, non-rotating flow over a 2D bell-shaped ridge (29), yielding
where, from (38), Ri = N2/α2, and the drag is normalized here by the corresponding unsheared reference value (30). Equation (39) shows that the drag decreases from its unsheared value as Ri decreases, until it vanishes at Ri = 1/4, where the flow is expected to become dynamically unstable. Grisogono [60] used linear theory conjugated with a WKB approximation [61] to calculate additional wind profile effects on the surface drag exerted by flow over a 2D ridge, finding that the drag increases for a wind profile with negative curvature at the surface, but decreases instead for positive curvature.
Grubišić and Smolarkiewicz [62] developed linear and numerical calculations of hydrostatic unidirectional negatively sheared flow (38) over an axisymmetric mountain that extended those of Smith [52] to 3D orography. They obtained a semi-analytical formula for the surface drag,
(normalized by (26)), which predicts that the drag is independent of the sign of the shear rate (a property that actually also applies to (39)) and that the drag at Ri = 1/4 is non-zero (reducing to Dx/D0x = 4/(3π)), in contrast with the 2D case. Figure 3 (left panel) shows the variation of the drag with Ri from (40) and from numerical simulations by Grubišić and Smolarkiewicz [62] and Teixeira et al. [50]. The agreement is good down to quite low values of Ri. Grubišić and Smolarkiewicz [62] also found that nonlinear effects become important at progressively lower values of the dimensionless mountain height as Ri decreases.
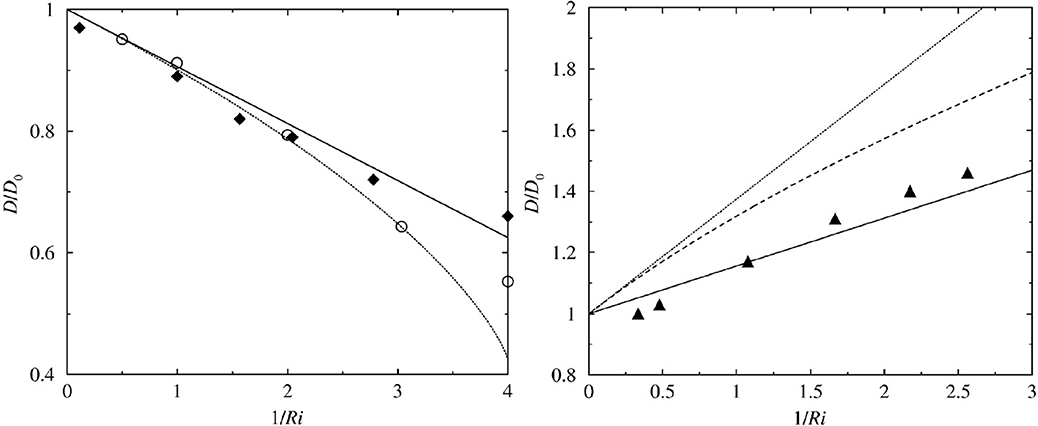
Figure 3. Normalized drag as a function of Ri. Left: drag for wind profile (38) as given by (42) (solid line), from (40) (dotted line), and from numerical simulations (symbols). Right: drag for wind profile (41) as given by (43) (solid line), from Grisogono [60] (dashed line), from the corresponding high-Ri asymptotic limit (dotted line), and from numerical simulations (symbols). Reproduced from Figures 1, 7 of Teixeira et al. [50]. © American Meteorological Society. Used with permission.
For the same kind of wind profile (38), but for flow over a 2D ridge, Wang and Lin [63] investigated the interaction between shear and nonlinear effects for various flow quantities, using high values of Ri. They found that the drag could exceed by a large amount the linear estimate (39), taking normalized values larger than 2 or 3. For = O(1) and Ri > 300, negative shear was found to enhance the drag more than positive shear, but for higher this relation was reversed. Curiously, Wang and Lin [63] found that, in contrast with Grubišić and Smolarkiewicz [62], nonlinear effects become important at lower values of as Ri increases. But the range of Ri and they considered was much higher: Ri > 20 and > 0.8, while in Grubišić and Smolarkiewicz [62] Ri ≤ 9 and ≤ 0.3, which perhaps explains the difference.
Teixeira et al. [50] developed a linear, hydrostatic model based on the WKB approximation to evaluate effects on the surface drag of generic, relatively slowly-varying wind profiles. They aimed to explain why in flow with constant shear over a 3D mountain the drag decreases with Ri (as in [52] or [62]), whereas for a directional shear flow where the wind turns with height at a constant rate keeping a constant magnitude, expressed as:
(where β is a constant), the drag increases instead as Ri decreases, as originally shown by Miranda [64] and confirmed by Valente [65]. Teixeira et al. [50] found that only a 2nd-order WKB approximation is able to capture shear corrections to the surface pressure that are asymmetric with respect to the obstacle, and thus that modify the drag. Figure 3 shows the drag for hydrostatic flow over an axisymmetric mountain for the wind profiles (38) and (41), respectively, which is given by WKB theory [50] as:
respectively. Although in (41) the wind turns with height, and so does the drag in numerical simulations for sufficiently low Ri, this is not captured by (43). However, the behavior of the drag component aligned with the surface wind (Dx) is reproduced quite accurately. It is easy to show that (40) asymptotically approaches (42) as Ri → ∞.
Teixeira and Miranda [66] addressed the simpler case of flow over a 2D ridge, where for the linear wind profile (38) the drag was found to vary with Ri as:
which is clearly the asymptotic limit of (39) as Ri → ∞. For wind profiles with curvature, Teixeira and Miranda [66] obtained results qualitatively in agreement with those of Grisogono [60].
Teixeira and Miranda [67] extended these calculations to flow over mountains with an elliptical horizontal cross section, such as assumed by Phillips [51], obtaining corrections to the drag due to wind profile effects that are in a form suitable to be implemented in the ECMWF drag parametrization [15]. These corrections, like those in Teixeira et al. [50] and Teixeira and Miranda [66], do not depend on the detailed shape of the orography, a property that relies on the hydrostatic assumption. The impact of these corrections on the drag at the global scale and on the integrated torque exerted by mountains on the atmosphere was evaluated using reanalysis meteorological data and orography representative of the real mountain ranges around the world by Miranda et al. [68]. They found that positive corrections to the drag may be important in localized regions such as Antarctica, perhaps contributing to a slight alleviation of the westerly bias exhibited by the drag torque.
More recently, Tang et al. [69] extended the model of Teixeira et al. [50] to a non-Boussinesq atmosphere. They showed using hydrostatic linear theory with a 2nd order WKB approximation that, for constant-shear flow over an axisymmetric mountain, the drag behavior depends on the sign of the shear. Figure 4 reproduces their results, for the linear wind profile with directional shear
showing that the drag, which in the Boussinesq approximation is given by:
(as shown originally by Teixeira et al. [50]), decreases more slowly with Ri when the shear is negative and faster when the shear is positive.
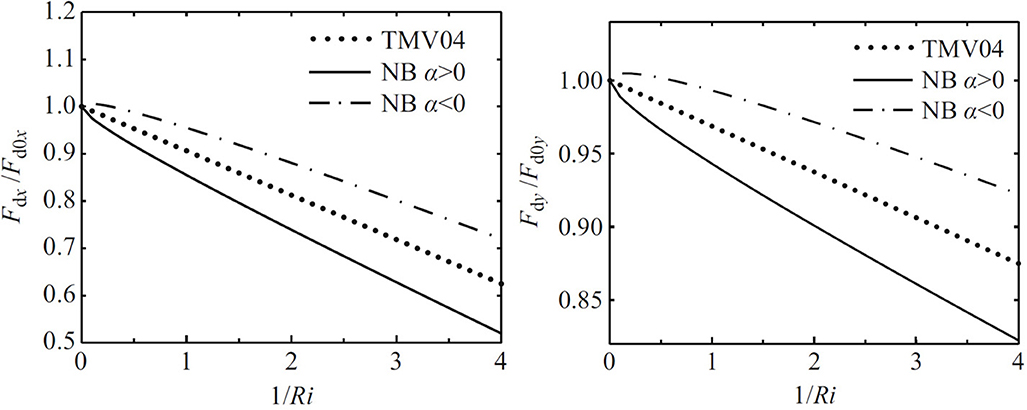
Figure 4. Normalized x (left) and y (right) components of the drag as a function of Ri for the wind profile (45). The solid and dash-dotted lines correspond to non-Boussinesq calculations (with different signs of α – see legend), and the dotted line is the original Boussinesq result (46). Reproduced from Figure 1 of Tang et al. [69] with kind permission from Springer Science and Business Media.
5. Total Critical Levels
A total critical level (also sometimes called 2D or unidirectional critical level) may be defined as a level in the atmosphere where the Taylor-Goldstein Equation (15) has a singularity for all wavenumbers in the mountain wave spectrum at the same time. This can occur when either (U, V) = 0 in flow over 3D orography, or when U = 0 in a flow which may have directional shear over 2D orography for which l = 0. Eliassen and Palm [3] have shown that for low-amplitude 2D mountain waves that propagate vertically, the vertical flux of horizontal momentum only varies at these critical levels, where the reaction force to the drag exerted on the mountain acts on the atmosphere. Eliassen-Palm's theorem does not, however, specify in which way this momentum flux varies, or the value of that force.
Booker and Bretherton [70] were the first to undertake that task. They found that, for linear flow, the momentum flux is always absorbed by critical levels, being attenuated by the factor
where Ric is Ri at the critical level zc. This means that, unless Ric is of O(1), there will be total absorption of the wave momentum flux, by a process which does not depend on viscosity and can be captured in an inviscid framework.
Booker and Bretherton's results were for low-amplitude waves. In the case of larger-amplitude, nonlinear mountain waves, Breeding [71] showed that total critical levels behave in a similar way to that predicted from linear theory (i.e., leading to nearly total momentum flux absorption) for Ric ≥ 5, but reflect a substantial amount of wave energy when 0.25 < Ri < 1. They estimated the amount of reflection as 35% for Ric = 0.53 and 7% for Ric = 2.12, but were unable to establish a relation between the reflection coefficient and the wave amplitude (i.e., nonlinearity).
As a mountain wave, or an internal gravity wave in general, propagates toward a critical level, the magnitude of the associated horizontal velocity fluctuations increases indefinitely in the inviscid linear approximation [70]. This would necessarily lead to dynamical instability. Through linearized calculations including viscosity, Fritts and Geller [72] derived criteria for the viscous stabilization of critical levels, whereby this kind of instability is prevented. They concluded that the flow is stabilized if the viscous length scale associated with the critical levels is somewhat larger than the depth of the layer that becomes unstable in inviscid conditions. From this general criterion, they inferred that internal gravity waves should be stabilized by viscosity only at heights above 130 km. They pointed out, however, that if the atmosphere is turbulent, an eddy viscosity replaces the molecular viscosity in the definition of the viscous length scale, and so waves in the troposphere become typically stable at critical levels. Figure 5 shows the variation of the wave momentum flux at a critical level from viscous and inviscid theory.
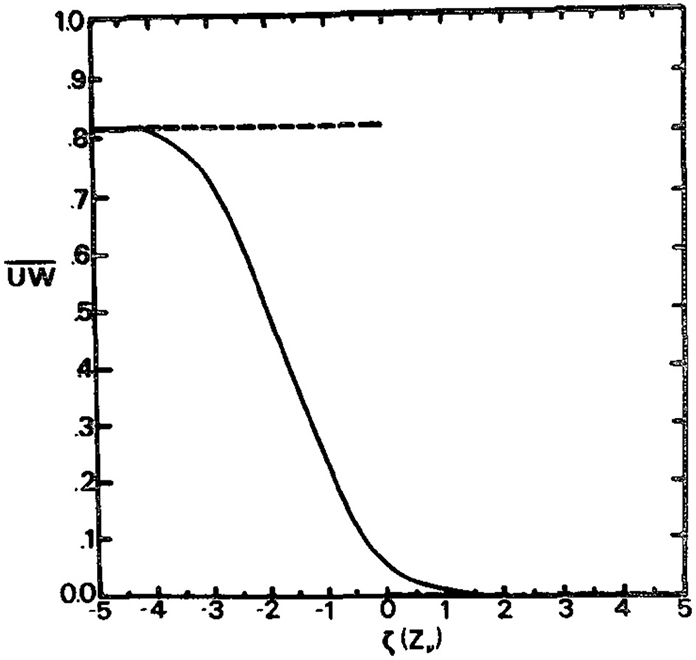
Figure 5. Profile of the momentum flux in a region containing a total critical level (at ζ = 0, where ζ = (k|α|/ν)1/3 z is height scaled by the viscous length scale, with ν being viscosity) for high Ric. Solid line: Viscous theory, dashed line: inviscid theory. Reproduced from Figure 4 of Fritts and Geller [72]. © American Meteorological Society. Used with permission.
Clark and Peltier [73] and Scinocca and Peltier [74] used the concept of wave reflection at a total critical level to explain the occurrence of downslope windstorms and high-drag states in 2D mountain waves. Scinocca and Peltier focused particularly on the effect of the Richardson number at the critical level Ric. (see section 7).
McFarlane [11] developed a drag parametrization based on results from linear theory, where the effect of wave saturation was taken into account in flows with directional shear. The distribution of stress with height was calculated by prescribing that the wave amplitude be limited due to wave breaking associated with the decay of density with height, or critical levels, which they defined as the levels where the wind becomes zero in the direction of the surface wind. This definition, which is independent of the orography orientation and thus not strictly consistent, nevertheless allows directional shear flows to be treated using the conceptual framework of total critical levels.
Grubišić and Smolarkiewicz [62] extended the work of Booker and Bretherton [70] by camputing the wave momentum flux absorption at a critical level for waves generated by a 3D mountain. For a mean incoming flow with the form (38), they obtained the following attenuation factor
where the difference from (47) results from the factor (k2 + l2)/k2. This implies that waves with a wavenumber vector perpendicular to the mean flow (k = 0 and l ≠ 0) are totally absorbed, no matter how low Ric is, whereas the attenuation of waves with wavenumber vectors parallel to the mean flow (l = 0) is similar to that of 2D waves.
Following Lindzen and Tung [75], but carrying out a more systematic exploration of parameter space, [76, 77] used linear theory to address wave ducting, and its implications for downslope windstorms, in flow over 2D mountains. They treated cases where both Ric > 0.25, and thus the critical level absorbs upward propagating waves in accordance with (47), and cases where Ric < 0.25, where the waves are unattenuated, but instead amplified by the critical level, in what has been termed “overreflection” [75].
Lott [78] addressed trapped lee wave absorption at the critical level that exists at the surface due to the no-slip boundary condition. Using a linear model including viscosity, he concluded that absorption of wave momentum at the surface is insignificant for Ric < 0.25 at high Reynolds number Re, leading to long-lived trapped lee waves, whereas it becomes progressively higher as Ric increases for Ric > 0.25. Lott [78] also found that wave absorption for Ric > 0.25 is always smaller than predicted by both inviscid critical-level theory and simplified models that represent friction as a Rayleigh damping (e.g., [49]).
6. Partial Critical Levels in Flow Over 3D Mountains
Partial critical levels (also called 3D or directional critical levels) are levels in flow with directional shear over 3D mountains where the Taylor-Goldstein Equation (15) becomes singular, but not for all wavenumbers in the wave spectrum simultaneously. Mathematically, they are defined by the condition
implying that the mean incoming wind (U, V) and the horizontal wavenumber of the waves (k, l) are perpendicular. Unlike total critical levels, which affect the whole wave spectrum at a single well-defined height, the height of partial critical levels depends on the azimuthal angle of the wavenumber. For this reason, these critical levels only exist for 3D orography, which contains wavenumbers with a range of orientations.
Using linear theory, Grimshaw [79] derived for the first time an expression for the momentum flux absorption at partial critical levels. The attenuation of the momentum flux in the absence of rotation for a linear wind profile expressed by:
where V0 and β are constants, was given by:
Equation (48) can be viewed as a particular case of (51) when the flow is unidirectional (V0 = β = 0).
Shutts [80] noted that most drag parametrizations assume that the wave momentum flux is associated with a single monochromatic wave, following [11]. He tried to improve that situation by calculating the wave momentum flux in flows with directional shear over 3D mountains using hydrostatic linear theory. He developed a practical approach to compute the momentum flux over anisotropic orography, described in the spectral domain, including a selective critical-level absorption effect. Shutts [80] and Shutts and Gadian [81] supported this approach by calculating the momentum flux for idealized flow with constant directional shear over an axisymmetric mountain (a particular case of (50)) and also for a wind that turns with height, (41). They assumed that Ric ≫ 1, and thus that all momentum flux is totally absorbed at critical levels (see also [82]). Shutts and Gadian [81] also carried out numerical simulations that showed that the momentum flux (and the drag) can be substantially underestimated by linear theory, and can exit laterally from the domain at high levels due to spreading of the wave pattern away from its source (see Figure 6), even for hydrostatic flow. This has implications for drag parametrizations, which typically adopt a single-column approach.
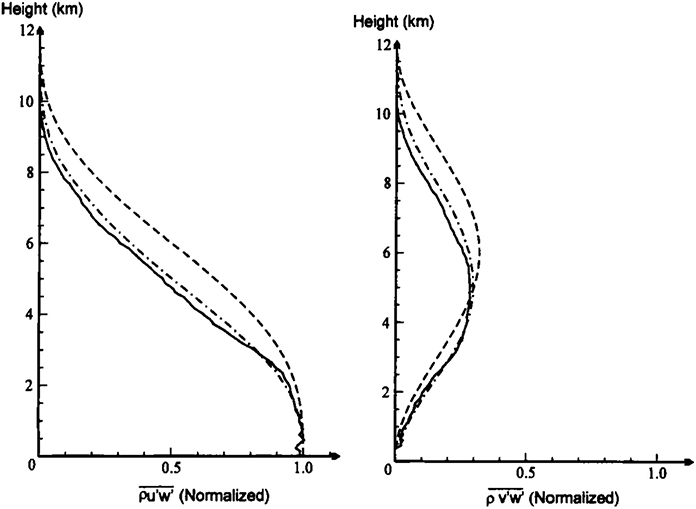
Figure 6. Normalized momentum fluxes as a function of height for the wind profile (41) at very high Ri. Dashed line: infinite-area linear solution, dash- dotted line: linear solution taking into account the finite domain extent, solid line: numerical simulations. Reproduced from Figure 12 of Shutts and Gadian [81]. Copyright © 1999 Royal Meteorological Society.
Concurrently, Broad [4] used linear theory to generalize the Eliassen-Palm theorem [3] to flows with directional shear over 3D orography. The extended theorem states that:
This implies that the momentum flux divergence d(Mx, My)/dz, which corresponds to the drag exerted on the atmosphere, is perpendicular to the wind at each height, and that the momentum flux (Mx, My) will not change unless the wind turns. This result places a strong constraint on the momentum flux profiles, which is of key importance for including directional shear effects in drag parametrizations. Broad [83] also considered the question of whether gravity waves in a directionally sheared flow break or not. This question was prompted by the fact that, before they reach a unidirectional critical level, finite-amplitude waves always overturn, since their amplitude tends to grow without bound before being dissipated. In directionally sheared flows, due to the nature of partial critical levels, this effect would be expected to be weaker. Using linear theory conjugated with ray tracing to clarify this issue, Broad [83] concluded that wave breaking always occurs. This depletes the momentum flux above wave breaking zones, qualitatively in the same way as critical level absorption in the linear analysis of Shutts and Gadian [81]. However, Broad's flow overturning condition was formulated in Fourier space, which seems questionable.
Doyle and Jiang [84] reported observations of mountain waves over the south-western French Alps during the MAP campaign. These waves were of relatively small amplitude, and were embedded in a large-scale flow with substantial directional shear. They observed that the amplitude of the waves decreased rapidly with height (by about 50%) in a layer with directional shear where the wind turned by about 90o. This provided the first experimental support for the prediction by linear theory (e.g., [80, 81]) of momentum flux absorption by partial critical levels in flow with directional shear, highlighting the importance of representing this effect in drag parametrizations.
Using hydrostatic linear theory conjugated with a 3rd-order WKB approximation, Teixeira and Miranda [85] developed calculations of the momentum fluxes associated with mountain waves for generic (albeit slowly-varying) wind profiles over axisymmetric mountains, at values of Ri of O(1). Unlike Shutts [82] and Shutts and Gadian [81] (for Ric ≫ 1), Teixeira and Miranda [85] found that wave absorption at critical levels at low Ri is not total, but rather the attenuation factor is:
where the subscript c denotes values taken at the critical level. This further generalizes (51) to generic wind profiles with relatively high Ri (although actually it has good accuracy down to Ri ≥ 0.5). For the wind profile (50), (53) is the asymptotic limit of (51) for Ri → ∞. Figure 7 shows the normalized momentum flux for the wind profile (41), given by Teixeira and Miranda [85] as:
at a height where the wind has turned by an angle of 180o, and therefore the momentum flux has been filtered for the whole of the wave spectrum. Teixeira and Miranda [85] found that the momentum fluxes normalized by the surface drag in the absence of shear, like the surface drag, do not depend on the detailed shape of the orography, and may be expressed as 1D integrals, while the momentum flux divergence, which corresponds to the drag acting on the atmosphere, has a closed analytical form for generic wind profiles.
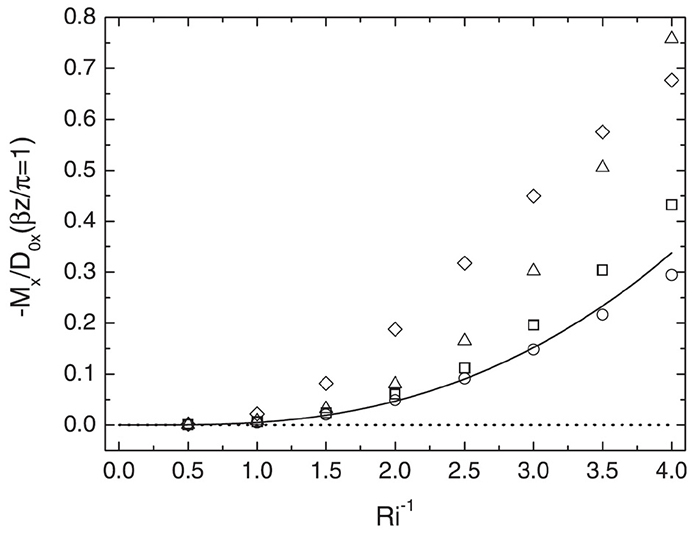
Figure 7. Normalized momentum flux at the height βz/π = 1 as a function of Ri for the wind profile (41). Solid line: (54), dashed line: Ri ≫ 1 limit (total absorption), symbols: numerical simulations for different values of : circles: 0.01, squares: 0.1, triangles: 0.2, diamonds: 0.5. Reproduced from Figure 5 Teixeira and Miranda of [85]. © American Meteorological Society. Used with permission.
Xu et al. [86] used linear theory, conjugated with linear wind profiles and orography similar to those considered by Teixeira and Miranda [85] to show that the wave momentum flux turns with height in the same direction as the mean incoming wind, but by a smaller angle, and the vertical divergence of the momentum flux always vanishes at the surface, pointing perpendicularly to the left (right) of a mean flow that backs (veers) with height. This divergence was found to attain a maximum at a height proportional to the wind speed at the surface and inversely proportional to the shear intensity, of higher magnitude for large wind turning angles and low Ri. These findings are consistent with the results of Teixeira and Miranda [85], but had not been explicitly stated by them. Using nonlinear numerical simulations of the same flow for = 0.0125, 0.625, 1.25 and 2.5, [87] showed that, when = 0.625 the momentum fluxes are enhanced by nonlinear effects. For = 1.25, low- and high-drag states are produced for different wind-turning angles, depending on whether flow over the mountain or flow around the mountain (with lee vortices) are preferred.
Very recently, Teixeira and Yu [88] extended the model of Teixeira and Miranda [85] to mountains with an elliptical horizontal cross-section, bringing it one step closer to a concrete parametrization proposal. They also developed the necessary theory for the situation where the wind turns non-monotonically with height or by an angle larger than 180o, where there is more than one critical level per wavenumber of the wave spectrum. It is then necessary to split the atmosphere into various layers, and express either the momentum flux or its divergence as a function of the momentum flux at the bottom of each layer.
7. Partial Wave Reflection and Resonance
Since their first systematic recordings [89], downslope windstorms are known to be associated with high-drag states, where the drag is several times larger than expected from linear theory. High-drag states are thought to be caused by resonance associated with vertical wave reflection with constructive interference at sharp variations in atmospheric parameters.
Peltier and Clark [90] found that, for constant wind profiles, high-drag states can be explained by processes incorporated in Long's nonlinear wave model of flow over 2D mountains (see section 10). Other nonlinear effects, intrinsically related to the wind variation with height, could only be reproduced by numerical simulations (e.g., highly nonlinear trapped lee waves). Peltier and Clark [90] introduced the concept of wave amplification by reflection at self-induced (wave-overturning) critical levels, suggesting it as the key mechanism behind high-drag states. In order to investigate this issue further, Clark and Peltier [73] carried out numerical simulations with an incoming flow of the form
where d is the depth of the shear layer surrounding the critical level. In these simulations, where the Richardson number Ric = N2d2/U20 was kept above 0.25, resonant drag enhancement corresponding to constructive interference between upward and downward propagating waves below zc was observed for:
where n is an integer number and λz = 2πU0/N is the hydrostatic vertical wavelength of internal gravity waves in the constant-wind layer near the surface. Figure 8 displays the variation of the drag with zc/λz, clearly showing the spacing of λz between maxima, which is twice the value expected from linear resonance theory (see below).
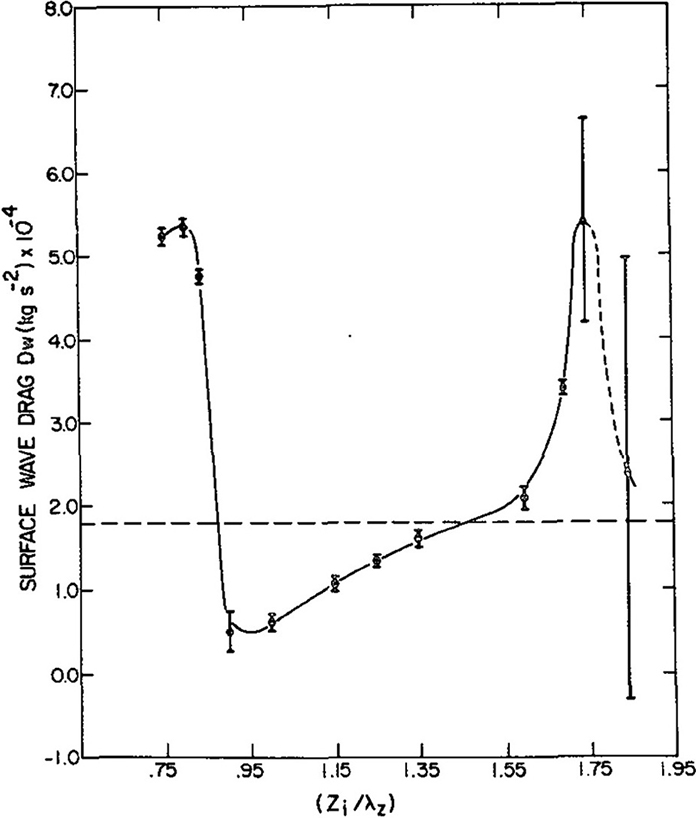
Figure 8. Drag obtained from numerical simulations as a function of zc/λz (denoted here by zi/λz). Reproduced from Figure 5 of Clark and Peltier [73]. © American Meteorological Society. Used with permission.
Smith [91] developed a different “hydraulic” approach, using a hydrostatic version of Long's equation to simulate flow over a 2D mountain for a constant upstream wind profile, with a “dead layer” downstream of the mountain, where the flow is turbulent, well-mixed (and therefore unstratified), and approximately quiescent on average. This model was able to predict the altitude of the well-mixed layer, the strength of the winds at the surface beneath that layer, and the mountain wave drag, which is given by:
where H0 denotes the height of the streamline upstream of the mountain that will divide to contain the well-mixed layer downstream of the mountain, and H1 is the depth of the accelerated layer beneath the well-mixed layer.
Bacmeister and Pierrehumbert [92] evaluated the merits of the theories of Clark and Peltier [73] and of Smith [91] through a number of numerical experiments of nonlinear flow over 2D mountains also with the wind profile (55), reaching the conclusion that Smith's hydraulic theory works better than the theory of Clark and Peltier. They criticized this latter theory for not justifying the phase of the reflected wave that leads to resonance, and found that the height of the critical level for which high-drag states occur depends on , in agreement with Smith's theory (in what was termed “resonance shift”). They additionally showed that high-drag states are possible for low values of , but take a long time to stabilize.
Although Smith's theory is believed to be the most satisfactory to date, other possible explanations for high-drag states have been explored. Durran [93], Wang and Lin [63], and Leutbecher [94] investigated the role played by static stability discontinuities in the establishment of high-drag states and downslope windstorms through wave ducting, and tested the accuracy of their representation by linear theory. Wang and Lin [63] for flow over 2D mountains and Leutbecher [94] for flow over an axisymmetric mountain showed that, when N is higher in the bottom layer and lower in the top layer, drag maxima (as well as wind intensity maxima) exist for:
where n is an integer and z1 is the height of the discontinuity in N, while for the opposite distribution of N maxima occur instead for z1 = (n/2) λz. Durran [95] showed that large drag amplification, and more severe underestimation of it by linear theory (by a factor of 3 or 4), occurs when the static stability is higher in the bottom layer than in the top one. He concluded that in such multi-layer configurations nonlinear effects may become relevant for ≥ 0.3, which is substantially lower than for an atmosphere with constant parameters. For = 0.67, 0.83, and 1, Wang and Lin [63] confirmed that the location of the drag maxima as a function of z1 is roughly unchanged, but their magnitude increases and the detailed variation of the drag with z1 is modified. In 3D flow, Leutbecher [94] found that the drag maxima become less pronounced, especially for high values of z1, because of directional wave dispersion.
Scinocca and Peltier [74] assessed the importance of the Richardson number at the critical level Ric in the establishment of high-drag states for the wind profile (55). They found that high-drag states take longer to achieve as Ric decreases, and may even be prevented for low Ric > 1/4, if is small enough. They also found that the steady-state high-drag states become insensitive to Ric for 0.625 ≤ ≤ 0.85, and attributed resonance shift to the different values of Ric used by previous authors, rather than to nonlinear effects.
Using a piecewise-linear wind profile qualitatively similar to (55), Wang and Lin [76, 77] studied the implications of wave ducting for downslope windstorms and high-drag states. They found that, at least in the linear regime, wave reflections at the shear discontinuities existing below and above the critical level (whose intensity is controlled by Ric) rather than at the critical level itself determine the wave response, with wind and drag maxima at the surface attained when (58) is fulfilled, where now z1 is the height of the lowest shear discontinuity. They explained some of the discrepancies observed between previous studies on high-drag states (namely [73] and [92]) by the use of zc instead of z1 as a key flow parameter. Wang and Lin [77] also showed how nonlinear high-drag states (with a spacing of λz rather than λz/2 as a function of z1) are selected from the linear ducted wave modes through modification of the static stability profile by the wave flow perturbations.
Miranda and Valente [97] treated the same kind of situation, but for flow over an axisymmetric mountain. concluding that the drag amplification is much more modest than for 2D mountains, and the spacing of high-drag states as a function of the critical level height is consistent with linear theory, rather than with Smith's theory, being (1/2) λz. The occurrence of resonance shift was also seen to be much reduced. As in Leutbecher [94], these effects are attributable to directional wave dispersion. Using linear theory and for the same wind profile over both 2D and axisymmetric mountains, Teixeira et al. [96] derived analytical expressions for the drag, the former of which can be written as:
with drag maxima occurring for (58), and being enhanced as Ric decreases. In weakly-nonlinear flow ( = 0.5), high drag-states were found to become much less sensitive to Ric (in agreement with [74]), and to occur for higher values of z1 (consistently with [94]) (see Figure 9). While in flow over an axisymmetric mountain, the locations of drag maxima were found to be accurately predicted by linear theory, in 2D flow intermediate maxima tended to disappear, confirming the results of Miranda and Valente [97]. For the same 2D flow as considered by Teixeira et al. [96], Teixeira and Miranda [98] showed that wave breaking for Rec < 9/4 behaves differently from wave breaking in an atmosphere with constant parameters, occurring not directly over the mountain, but in regions displaced both vertically and horizontally upstream and downstream.
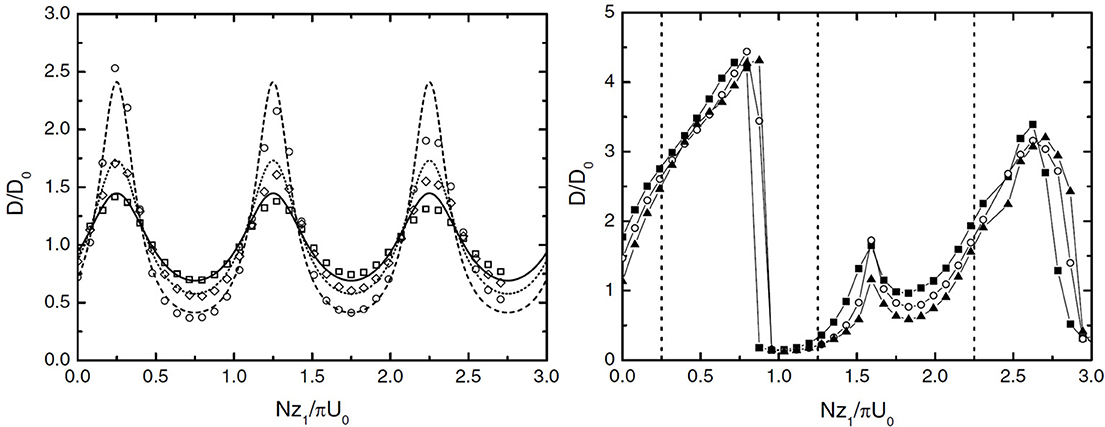
Figure 9. Drag normalized by (30) as a function of Nz1/(πU0). Left: linear flow. Lines: linear theory, symbols: numerical simulations. Solid line and squares: Ric = 2, dotted line and diamonds: Ric = 1, dashed line and circles: Ric = 0.5. Right: Numerical simulations for = 0.5. Squares: Ric = 2, circles: Ric = 1, triangles: Ric = 0.5. Reproduced from Figures 1, 5 of Teixeira et al. [96]. Copyright © 2005 Royal Meteorological Society.
Teixeira et al. [100] showed that differences in the drag behavior for wind profiles where the wind varies linearly near the surface and is constant aloft depend (in hydrostatic conditions) on whether critical levels exist, and are located above or below the shear discontinuity. When a large fraction of the wave spectrum has a critical level below the shear discontinuity, the drag behaves relatively similarly as if the lower layer extended indefinitely. Otherwise, the drag undergoes oscillations due to resonant constructive and destructive interference of reflected waves.
Wells and Vosper [99] identified a wave and drag amplification mechanism by parametric resonance, when the profile of the Scorer parameter
varies sinusoidally with a wavelength of half the basic vertical hydrostatic wavelength. For flow over a 2D ridge, they showed that this could lead to an underestimation of the drag by linear theory by a factor of about 2.5 (see Figure 10). Teixeira et al. [101] developed a perturbation model to explain this drag amplification, showing that the drag behavior at resonance depends on the phase of the oscillation of the Scorer parameter, and also crucially on the representation of dissipative processes.
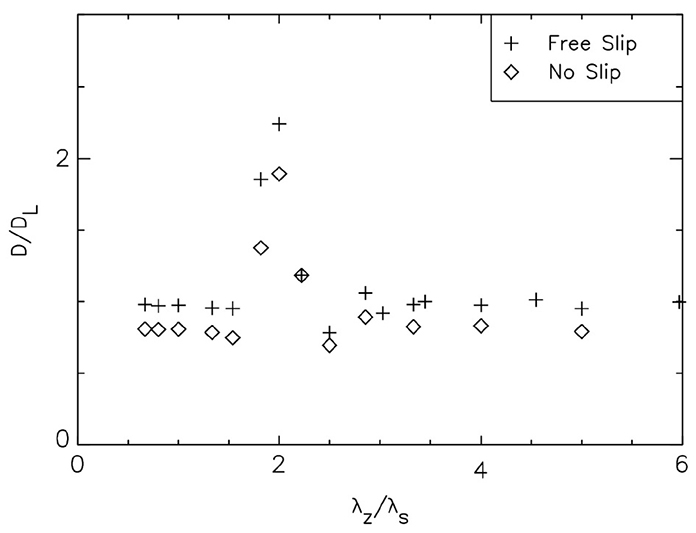
Figure 10. Drag normalized by its reference value for constant l0 as a function of λz/λs, where λs is the wavelength of the vertical oscillation of the Scorer parameter. See legend for details. Reproduced from Figure 9 of Wells and Vosper [99]. © Crown Copyright 2010. Published by John Wiley & Sons, Ltd.
8. Non-Hydrostatic Effects and Trapped Lee Waves
Non-hydrostatic effects (which occur when ã ≲ O(1)) lead to mountain wave dispersion, which tends to weaken the drag in a flow with constant wind and static stability [1]. However, when in a unidirectional flow the Scorer parameter decreases with height, non-hydrostatic effects promote the propagation of trapped lee waves near the surface, which may increase the drag.
Following Wurtele et al. [102], Keller [103] used linear theory to evaluate the accuracy of the hydrostatic approximation in flow over a 2D ridge with a linearly increasing incoming wind velocity (i.e., (38) with α > 0) either extending indefinitely, or in a layer with lower static stability, topped by a semi-infinite layer with no shear and higher static stability. He concluded that the momentum flux is substantially reduced by non-hydrostatic effects and its contributions are shifted downstream from the mountain due to wave trapping near the surface. The momentum flux was shown to depend on the lower layer height and Ri within it (as [100] would confirm later for hydrostatic flow). Sharman and Wurtele [104] treated essentially the same situation, but for flow with positive or negative shear extending indefinitely over 3D mountains of varying aspect ratio. They found that the drag over elongated mountains perpendicular to the flow does not change much for γ < 1/3. The drag also tended to become lower as the flow became more non-hydrostatic for negative shear while for positive shear and the same ã the drag was higher, a behavior they attributed to the existence of trapped lee waves.
Lott [105] calculated the drag associated with trapped lee waves using a 2D numerical linear model. Despite the intrinsic non-hydrostaticity of these waves, their associated drag was shown to be reasonably estimated using the hydrostatic reference value. However, Lott also found that the momentum flux profile was very different from that associated with vertically propagating waves, decaying with altitude in the absence of dissipation, because the assumptions behind Eliassen-Palm's theorem are not satisfied, and a substantial fraction of the wave momentum exits the computational domain through the leeward boundary. Broad [106] explained this variation with height of the momentum flux, showing that it is associated with a decrease of the dynamic pressure across the mountain because of the downstream wave train. He proposed an expression to replace the Eliassen-Palm theorem in those circumstances,
where W is the amplitude of the trapped lee waves far downstream of the obstacle.
In a pioneering study, Bretherton [107] systematically analyzed the drag produced by trapped lee waves, departing from Bernoulli's equation, but he assumed a rigid-lid upper boundary condition, which is not very realistic in the atmosphere. This limitation was removed by Smith [108] who generalized the trapped lee wave drag expression derived by Bretherton to an unbounded atmosphere, yielding
where the index of the sum j is over all trapped lee wave modes and kj (j = 1, 2,..) are the corresponding resonant wavenumbers. This expression is quite powerful, as it does not assume any specific form for the atmospheric profiles, other than that the integral in (62) must converge.
For practical applications, it is useful to explore the drag behavior for more specific atmospheric profiles. Tutiś [109] calculated trapped lee wave solutions in an atmosphere where the Scorer parameter l0 follows a hyperbolic-secant profile. She concluded that linear theory gives good predictions for the wavelength and drag associated with those waves, but the wave amplitude is underestimated. Unfortunately, Tutis used a rigid-lid upper boundary condition in her calculations, which is not very realistic. Adopting a two-layer model with higher Scorer parameter in a lower layer and lower Scorer parameter aloft (following [110]), Teixeira et al. [111] explicitly evaluated the drag associated with waves trapped in the lower layer and waves propagating in the upper layer, obtaining the following expression for the former drag component when the wind velocity is constant:
where m1 = (l21 − k2)1/2, n2 = (k2 − l22)1/2, l1 and l2 are the Scorer parameters in the lower and upper layers, respectively, and H is the height of the lower layer. DL normalized by (30), is plotted in Figure 11 (left). Teixeira et al. [112] considered a similar problem, but for the two-layer atmosphere of Vosper [113] instead, where the lower layer is neutral (l1 = 0), and there is a temperature inversion between the two layers, represented by a jump in potential temperature, which is quantified by a Froude number Fr. They found that in that case the trapped lee wave drag is due to interfacial waves propagating at the inversion, which have only one mode, being given by:
where kL is the resonant wavenumber of the trapped lee waves. Figure 11 (right) presents (64) normalized by (30) using the static stability of the upper layer.
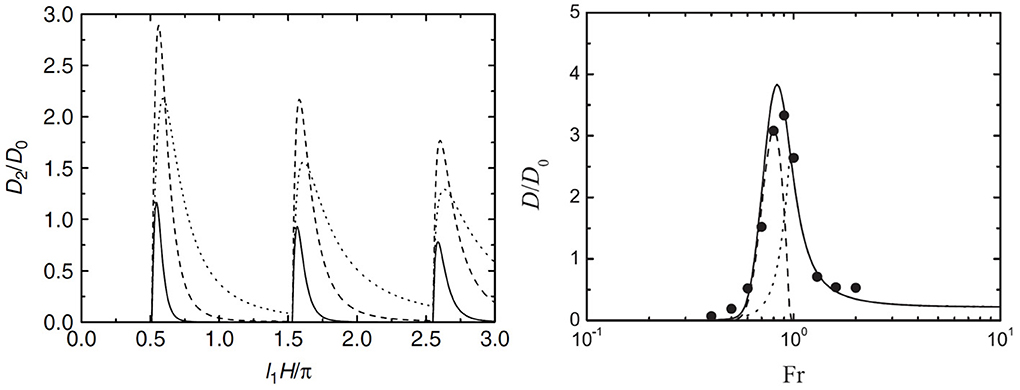
Figure 11. Left: trapped lee wave drag (here denoted by D2) normalized by (30) as a function of l1H/π. Solid line: l1a = 10, dashed line: l1a = 5, dotted line: l1 a = 2. Reproduced from Figure 6 of Teixeira et al. [111]. Copyright © 2012 Royal Meteorological Society. Right: Drag normalized by (30) as a function of Fr for l2H = 0.5 and l2a = 1. Solid line: total drag, dotted line: internal gravity wave drag, dashed line: trapped lee wave drag, all from theory; symbols: numerical simulations. Reproduced from Figure 9 of Teixeira et al. [112]. © American Meteorological Society. Used with permission.
Interesting effects occur when trapped lee waves generated by more than one mountain interact. Vosper [114] studied gravity wave drag on two consecutive 3D mountains using a linear numerical model. He concluded that, when non-hydrostatic effects are unimportant, the drag behaves qualitatively as predicted by Grisogono et al. [115] for flow over 2D ridges (see section 9). When the atmospheric profiles permit the propagation of trapped lee waves, the drag is strongly enhanced when the waves from an upstream mountain interfere constructively with those from a downstream one. Drag extrema can then be produced even when the mountains are quite far apart. Grubišić and Stiperski [116] pursued a similar kind of investigation on lee wave interference and resoance, but for pairs of 2D ridges, and using numerical simulations. They found that the appearance of constructive or destructive interference between trapped lee waves generated by each mountain depends both on the separation between them and the ratio of their heights. As expected, constructive and destructive interference lead to high- and low-drag states, respectively. Stiperski and Grubišić [117] added surface friction to the problem addressed by Grubišić and Stiperski [116], finding that the important parameter to quantify the drag modulation with distance between the two mountains is the ratio of valley width to the wavelength of the trapped lee waves. However, in contrast with inviscid simulations, the wavelength of the velocity perturbation associated with the waves is shorter than the wavelength associated with the pressure perturbation, which is the one that controls drag behavior.
An important phenomenon associated with trapped lee waves is rotors, which are vortices with their axes of rotation aligned with the mountains, where the flow reverses direction at the surface (see Figure 1). These structures were investigated by Doyle and Durran [118] using 2D high-resolution numerical simulations. They found that increasing the roughness length in their model decreased the drag, because it tended to shift the point of boundary-layer separation upstream, and therfore reduce the extent of the lee-side (negative) pressure anomaly. A significant correlation between trapped lee wave drag, as given by linear theory, and the occurrence of rotors, as described in the regime diagram of Vosper [113], was found by Teixeira et al. [112]. That link deserves more detailed investigation.
9. Effects of Rotation
9.1. f-Plane Approximation
For orography with larger width, fa/U = O(1), and the effects of the Earth's rotation may influence mountain waves. The extension of (15) to an atmosphere with an f−plane approximation is:
Note that (65) assumes d2U/dz2 = d2V/dz2 = 0, since this is the only choice consistent with steady-state flow. In a rotating atmosphere, thermal-wind balance implies that vertical shear necessarily corresponds to a mean horizontal temperature gradient, so the potential temperature is no longer steady, because of temperature advection, unless the flow is unidirectional. Consequently, it can be shown (see [119]) that it is only consistent to assume that N is independent of time and of horizontal position if d2U/dz2 = d2V/dz2 = 0.
Jones [120] used an equation equivalent to (65) for unidirectional flow (V = 0) to investigate the interaction of inertia-gravity waves with critical levels. He noted that two types of critical levels, where (65) becomes singular, exist: similar to those in non-rotating flow, where U = 0 (or in general Uk + Vl = 0), and inertial critical levels, where Uk = ±f (or in general Uk + Vl = ±f). Jones found that in rotating flow it is the wave angular momentum, rather than the linear momentum, that is conserved in the vertical away from critical levels. He also concluded that absorption of momentum by critical levels differs only slightly between cases with and without rotation. This result was confirmed by Grimshaw [79], provided that f/N ≪ 1 (which is typically satisfied in the atmosphere). Broad [4]'s generalization of the Eliassen-Palm theorem to 3D flow mentioned in section 6 substantiated these ideas further. The expression valid for rotating flow is still given by (52), but with Mx and My redefined as:
where δ and ζ are the fluid parcel (or streamline) displacements along x and y associated with the waves (an analogous result had been derived previously for 2D rotating flow by Eliassen [121]).
Wurtele et al. [122, 123] revisited the problem addressed by Jones [120] using numerical simulations of flow over 2D mountains. They found that while linear theory predicts absorption of a monochromatic wave at levels where |Uk| = f, in nonlinear flow there is also partial reflection. They further showed that both the horizontal and vertical velocity perturbations diverge at these inertial critical levels, making the momentum flux diverge as well. However, for waves with a continuous spectrum, this singular behavior is avoided because each wavenumber has a different inertial critical level, and so momentum absorption is well predicted by linear theory. Wurtele et al. [123] also found that, for positively sheared flow, the drag and wave momentum flux produced by a monochromatic wave may oscillate in time, with no steady state attained. Shutts [124] explored further a similar problem using linear theory, but for flow over an axisymmetric mountain, finding that, for a monochromatic wave, only the u and v velocity perturbations diverge at the inertial critical level, while w does not (in contrast with [122]).
Another relevant aspect of rotation is how it affects the surface drag. Using linear theory and considering unsheared hydrostatic flow over a 2D bell-shaped ridge, Smith [125] found that mountain wave drag decreases as fa/U increases, being reduced to half of its non-rotating value for fa/U = 0.63 (see Figure 12). While Smith's drag formula can only be expressed analytically in terms of Bessel functions, Miranda and James [126] obtained a closed expression for the drag in entirely similar conditions, but for flow over an axisymmetric bell-shaped mountain (25), namely
which shows that the drag decreases exponentially for large fa/U. On the other hand, Grisogono et al. [115] used linear theory to examine the effects of rotation in flow over a double bell-shaped mountain. They derived an expression for the drag as a function of the mountain separation and fa/U, where a is the width of the first mountain, noting that, when f ≠ 0, the drag displays slight oscillations as the ridge spacing varies, with a wavelength that decreases as fa/U increases, due to wave interference. In the same vein, Teixeira et al. [127] derived asymptotic formulae, expressed in terms of elementary functions, for the mountain wave drag in flow over 2D mountains, when non-hydrostatic effects and rotation are important, but treated as relatively weak. They showed that these approximations are especially accurate for the full range of ã and fa/U when there is a well-defined hydrostatic and non-rotating limit (i.e., f/N ≪ 1), which is typically the case.
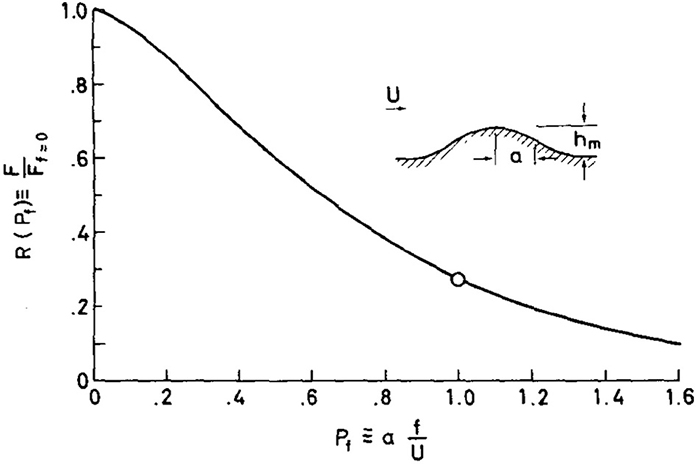
Figure 12. Drag normalized by (30) as a function of fa/U for flow over a bell-shaped ridge. Reproduced from Figure 1 of Smith [125]. © American Meteorological Society. Used with permission.
Using hydrostatic numerical simulations of flow with uniform N and U over elliptical mountains, Ólafsson and Bougeault [128] and Ólafsson [129] separately analyzed the effects of rotation and surface friction on orographic drag. They found that for low the drag is reduced as fa/U increases but for > 1.4 (blocked flow regime), rotation instead increases the drag, which means that rotation may extend the range of usefulness of linear theory. Additionally they showed that in the non-blocked regime ( = O(1)), the mountain exerts a cyclonic couple on the flow, and the drag oscillates in time (due to wave breaking), whereas in the blocked regime (large ) it exerts an anti-cyclonic couple instead. Petersen et al. [130] investigated how upstream wind direction influences the flow across a large meridionally-oriented elliptical mountain (representative of Greenland), finding that the drag force and the wake pressure deficit are larger when the flow is from the southwest than when it is from the northwest. For a similar situation, Doyle et al. [131] examined the sensitivity of wave breaking to terrain slope. They confirmed the result of Ólafsson and Bougeault [128] that the drag is reduced by rotation for = 0.5, but instead increased by rotation for = 1.5.
The interaction of rotation with shear also has consequences for the surface drag. In his theory of lee cyclogenesis, Smith [52] showed that quasi-geostrophic flow with constant negative shear and a critical level ((38) with U0 > 0 and α < 0) generates a baroclinic standing wave train on the lee of a 2D ridge. He evaluated the drag exerted by this kind of lee wave as:
where k* = f/(Nzc) is the corresponding resonant wavenumber. Following a similar approach, Martin and Lott [132] addressed the synoptic response to mountain waves generated by the passage of fronts over orography, and the corresponding absorption of wave momentum flux by directional critical levels. They concluded that the drag exerted by the orography on the flow acts to the left of the wind in a cold front case and to the right of the wind in a warm front case, extending the results of Xu et al. [86] (see section 6) to rotating flow.
9.2. Beta-Plane Approximation
When the horizontal scale of the mountains is even larger, the variation of the Coriolis parameter with latitude becomes important in the dynamics of orographic waves, which are now Rossby-gravity waves, or simply Rossby waves when the stratification becomes of secondary importance. While the effect of rotation in its simplest form decreases the drag (as was seen in the preceding subsection), the beta effect increases it again.
Janowitz [133] calculated the drag produced by barotropic Rossby waves in a single-layer flow with a rigid-lid upper boundary condition over a generic isolated mountain. He noted that the drag increases with increasing β = df/dy, and also that the effects of stratification are negligible for this upper boundary condition, because for typical values of the atmospheric parameters no internal (trapped) wave modes are excited.
McCartney [134] studied inertial Taylor columns on a beta plane, using a two-layer model of flow over a cylindrical mountain. He noted that for eastward flow there was an extensive meandering wake downstream of the mountain, composed of a train of Rossby-gravity waves, and explicitly calculated the associated drag. Bannon [135] did essentially the same, but for single-layer flow over a Gaussian axisymmetric mountain. Thompson and Flierl [136] revisited the problem of one-layer flow over a cylindrical mountain, finding that for eastward flow the barotropic Rossby wave drag can be much larger than predicted by quasi-geostrophic theory, being given by:
where D00 = ρ0f0UR2H, f0 is a constant reference Coriolis parameter, R is the radius of the mountain, H is the height of the fluid layer and J1 is the Bessel function of the first kind of order 1.
Teixeira and Grisogono [137] calculated the drag associated with internal Rossby-gravity waves, by considering a continuously stratified atmosphere flowing over an elliptical mountain. They showed that this drag is especially important for mountains that are aligned meridionally, much larger than the drag given by models where f is constant, substantially larger the the drag produced by internal gravity waves (see Figure 13), and comparable to the barotropic Rossby wave drag calculated by Thompson and Flierl [136], (70). A more explicit link between these two types of drag is currently missing.
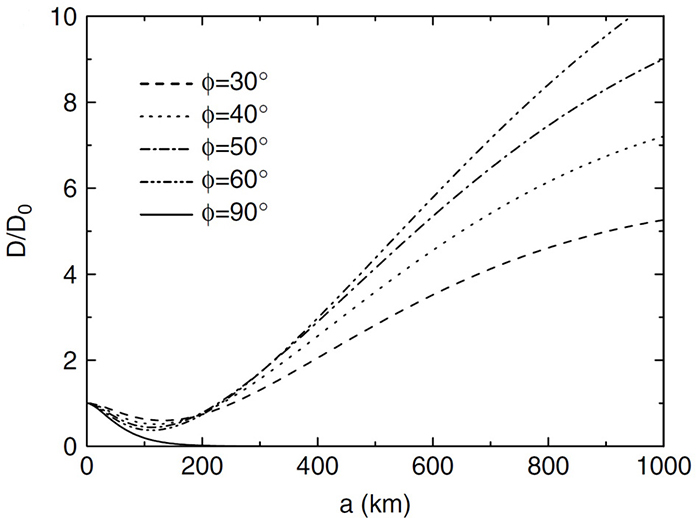
Figure 13. Drag normalized by (31) as a function of the mountain width in the zonal direction for γ = 0.25 and latitudes (ϕ) between 30o and 90o (see legend for details). Reproduced from Figure 3 of Teixeira and Grisogono [137]. Copyright © 2008 Royal Meteorological Society.
10. Nonlinear Effects
Nonlinear effects in mountain waves become important roughly when ≳ O(1). Linear theory, as expressed by (15) or (65), is then not valid anymore, and an alternative method of solution (generally, numerical simulations) must be adopted. There are cases where further progress is possible analytically, however.
Long [138] derived an equation for stratified flow over a 2D obstacle in non-rotating conditions, which is valid for waves of arbitrary amplitude (if the flow remains steady):
where δ = z − z0 is the vertical displacement of a streamline relative to its upstream undisturbed position z0. When U2 ρ is constant to a good approximation, (71) reduces to:
Equation (72) is remarkable because, while describing nonlinear waves, it is linear (and with constant coefficients if N/U is also constant). Long [138] applied (71) and (72) to cases of fluid bounded above by a rigid lid. Huppert and Miles [139] and Miles and Huppert [140] implemented a radiation boundary condition at the upper and downstream limits of the domain, obtaining solutions to (72) for waves generated by mountains with a semi-elliptical vertical cross-section, and arbitrary shape but relatively small amplitude. Miles and Huppert [140] calculated the drag for a number of orography forms, including a bell-shaped ridge (29), yielding
correct up to second order in , showing that the drag is underestimated by linear theory. They also found that, even in hydrostatic conditions, the drag is not invariant to flow reversal for asymmetric mountains.
Lilly and Klemp [141] investigated further the effects of terrain shape and asymmetry using a hydrostatic version of Long's equation, namely
They found that the nonlinear lower and upper (radiative) boundary conditions have a strong influence on the wave structure at large amplitudes, and the drag is significantly enhanced for mountains with a gentle windward slope and a steep leeward slope. Miller and Durran [142] assessed the sensitivity of downslope windstorms to orography asymmetry using numerical simulations for various atmospheric profiles, finding it to be more important in the case of two-layer flow without a critical level or wave breaking than for flows beneath a critical level or beneath breaking waves. Miller and Durran [142] also calculated the drag in a single-layer atmosphere using Long's equation, showing that although the drag is super-linear when the mountain is symmetric or has a steep lee slope, it is sub-linear when the upstream slope is the steepest one.
The use of numerical simulations proved to be particularly valuable for exploring the highly nonlinear flow regimes where wave breaking and flow blocking or splitting occur (and thus Long's equation is not valid anymore). Clark and Peltier [143] performed pioneering numerical simulations of flow over a 2D ridge with constant upstream U and N. They found that while for low the wave drag and momentum flux profile agree with the predictions of linear theory, above a certain threshold there is convective instability, the drag is dramatically enhanced, and the momentum flux profile is strongly divergent (in contrast with what is expected from the Eliassen-Palm theorem), due to wave breaking. In simulations of high-drag states using a hydrostatic primitive equation model, Stein [144] found that the dimensional drag exerted on a 2D ridge varies proportionally to 2 in the quasi-linear regime, proportionally to a power of larger than 2 in the high-drag regime coinciding with wave breaking, and proportionally to 1.3 in the blocked flow regime. Using a similar model setup to address transient upstream flow effects, Garner [145] showed that, while the upstream wind weakens gradually as increases, there is a sudden increase in the downslope wind speed at the onset of wave breaking, accompanied by drag enhancement, despite the fact that upstream changes in the flow only become important for much higher . Garner [145] additionally improved Smith [91]'s formula for the drag in high-drag states, obtaining
where α = 2.2, or
where β = 1/8, when upstream effects become important.
While trying to clarify whether breaking mountain waves decelerate the local mean flow, Durran [146] showed that zones of flow deceleration in the vicinity of the mountain are compensated by zones of flow acceleration. Thus he suggested that information both about the horizontal and vertical flux of wave momentum need to be parametrized, and the momentum fluxes associated with trapped lee waves should be considered a potentially important source of low-level drag (as was seen in section 8). Mayr and Gohm [147] revisited the problem of flow over two successive 2D mountains, for = 0.05, 0.51, 1.01, and 1.52, showing that the differing steepness of the upwind and downwind slopes caused by the separating valley strengthens nonlinear effects, and for wide enough valleys two wave breaking regions can form above both peaks, which causes a sharp increase of the drag (by more than a factor of 3 above the linear estimate).
Highly nonlinear flow over 3D mountains (where no equivalent to Long's equation has been derived) was also simulated numerically by various authors. Smolarkiewicz and Rotunno [148] noted that the conditions for flow reversal on the windward side of a 3D obstacle in inviscid non-rotating flow for ≈ 1 are predicted with some accuracy by linear theory [149] in the case of axisymmetric mountain, but less so for mountains with different horizontal aspect ratios. Smolarkiewicz and Rotunno [148] also calculated the drag for an axisymmetric mountain, showing that a maximum several times higher than the linear estimate occurs at ≈ 2. Miranda and James [126] studied more systematically the drag dependence on (Figure 14, left), finding that the flow is well described by linear theory for < 0.5, for 1 < < 2 it enters the wave-breaking regime, with quasi-periodic oscillations of the drag and an average maximum attained for ≈ 1.3, and for 2 < < 5 it is characterized by streamline splitting around the mountain, a vortex pair on its lee side, and decreasing drag. They concluded that the use of 2D drag estimates may severely overestimate the drag when the flow is in this last regime. Ólafsson and Bougeault [150] carried out analogous simulations of flow over an elliptical mountain of aspect ratio 5 for 0.500 < < 6.818, showing that for low the linear predictions of flow stagnation aloft (leading to wave breaking) and of stagnation at the surface (leading to flow splitting) [149] are accurate, but for higher wave breaking occurs mostly at the edges of the mountain, not over its axis of symmetry. Using an essentially similar setup, Bauer et al. [56] explored more systematically the dependence of the flow on the horizontal aspect ratio of the mountain, finding that, when γ decreases, the threshold for the onset of wave breaking, vortex formation and windward stagnation decreases. The interval of where high-drag states occur, which is centered around ≈ 1, was seen to widen as γ decreases (see Figure 14, right). For a similar flow, Doyle et al. [131] examined the sensitivity of wave breaking to terrain slope, concluding that that the normalized drag shows a stronger dependence on terrain slope for = 0.5 than for = 1.5, and becomes saturated beyond = 1.5, probably because this dimensionless mountain height is sufficiently high to produce wave breaking regardless of the slope.
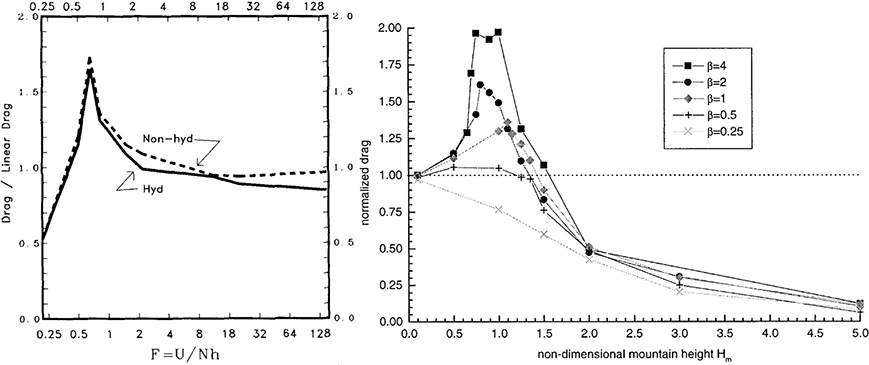
Figure 14. Left: drag in flow over an axisymmetric bell-shaped mountain normalized by its linear hydrostatic value (solid line) and by its linear non-hydrostatic value (dashed line) as a function of −1. Reproduced from Figure 1 of Miranda and James [126]. Copyright © 1992 Royal Meteorological Society. Right: normalized drag in flow over an elliptical Gaussian mountain for different β = 1/γ (see legend) as a function of (here denoted by Hm). Reproduced from Figure 15 of Bauer et al. [56]. © American Meteorological Society. Used with permission.
For flows in the splitting regime, the laboratory experiments of strongly stratified flow past axisymmetric obstacles of Vosper et al. [151] revealed that the wave amplitude decreases, while the drag coefficient increases as increases, reaching values between 2.8 and 5.4 times larger than in the neutral flow limit (depending on obstacle shape) when > 4. A major contribution to the total drag (about 25%) resulted from a separated wake with vortex shedding, rather than from gravity waves.
Eckermann et al. [152] evaluated the dependence of the momentum fluxes on for flow over 3D obstacles, essentially confirming the findings of Ólafsson and Bougeault [150] and Bauer et al. [56] for the surface drag. They additionally showed that the drag vacillates for flow across an elongated obstacle in the 0.7 ≤ < 3 range, due to cyclical buildup and breakdown of wave activity, with the amplitude of these vacillations decreasing as increases. At > 2 − 3, Eckermann et al. [152] noted that the drag decreased smoothly proportionally to −1/3 to values lower than 1, and the dimensional drag approached a constant value at high , a constraint they suggested implementing in drag parametrizations.
Concerning the variation of the wave momentum flux with height due to wave breaking, Lindzen [153] formulated the concept of supersaturation of vertically propagating internal gravity waves, which has proved influential in drag parametrization schemes [46]. The underlying idea is that gravity waves, including mountain waves, tend to increase their amplitude as they propagate upward in the atmosphere, due to the decrease of density with height (a non-Boussinesq effect). In practice, when waves reach a saturated state which corresponds to the onset of wave breaking, their amplitude must be limited. This determines the wave momentum flux distribution (and consequently the drag force on the atmosphere) for finite-amplitude waves. Unfortunately, Lindzen's treatment was limited to monochromatic waves. Kim and Mahrt [154] reported measurements of the momentum flux associated with mountain waves in wave breaking regions from the ALPEX campaign. They attributed the momentum flux divergence in one of the observations to directional wind shear. Using ideas from [11], they then generalized the wave saturation theory of Lindzen [153] to vertically varying mean flows, finding that the wave momentum fluxes from the extended model show good agreement with observations from ALPEX.
11. Boundary Layer Effects
Most of the results described above (except essentially those on lee wave rotors in section 8) assumed frictionless flow and a free-slip boundary condition at the surface. A few studies specifically addressing boundary layer effects are mentioned next.
Richard et al. [155] investigated the effect of friction in downslope windstorms over 2D orography using a hydrostatic numerical model with a turbulent kinetic energy parametrization, finding that it delays the onset of strong surface winds and prevents the downstream propagation of the zone of maximum wind speed. The drag in the corresponding high-states was seen to be established over a longer time interval, with a somewhat lower steady value than in inviscid flow (see Figure 15). Ólafsson and Bougeault [128] similarly found that in flow over 3D elliptical mountains the drag is substantially reduced by surface friction for < 3, with a suppression of wave breaking and high-drag states (as Jiang et al. [156] corroborated later). Peng and Thompson [157] further investigated this effect using a non-hydrostatic numerical model. They hypothesized that the observed reduction in the mountain wave amplitude is due to reduction in the slope of the boundary layer top, and that flow over the mountain outside the boundary layer, including its wave drag, may be reproduced by replacing the terrain elevation with the boundary layer elevation. They found that this effect becomes less pronounced for high because the boundary layer depth occupies then a lower fraction of the relevant flow depth. This was later confirmed by Jiang et al. [156].
Figure 15. Time evolution of the drag for simulations of flow over 2D orography using free-slip and no-slip lower boundary conditions (see curve labels details). Reproduced from Figure 4 of Richard et al. [155]. © American Meteorological Society. Used with permission.
Belcher and Wood [158] and Athanassiadou [159] investigated the relation between form and wave drag in stably stratified flow over 2D hills, using the linear model of Hunt et al. [160] with the added effect of stable stratification. They showed that the form drag first increases with stability due to increased shear in the boundary layer, but for higher stability it decreases due to boundary layer thinning. The wave drag, which for weak stratification is smaller than the form drag, increases with stratification, eventually becoming dominant. Belcher and Wood [158] concluded that the reduction of the wave drag relative to its inviscid value is due to the downstream shift that turbulence in the boundary layer imposes on the pressure distribution outside the boundary layer.
Vosper and Brown [161] investigated the effect of small-scale hills on orographic gravity wave drag and flow blocking produced by 2D and 3D mountains using numerical simulations. They found that corrugations can significantly reduce the amplitude of the mountain waves generated by the broader mountain, and suppress the unsteadiness of the wake. This was seen to be associated with a significant reduction of the total drag compared to the sum of the contributions from the two orography scales, by a factor of more than 30%. Steeneveld et al. [162] showed that a (realistic) parametrization of drag produced by small-scale orography as partly gravity wave drag instead of drag entirely due to turbulence improved various performance indicators in a forecast model, namely: cyclone filling rates and boundary layer depths, particularly in quite stable conditions.
Nappo and Chimonas [163] used linear theory to study momentum flux absorption at a critical level within a stably stratified boundary layer, comparing it to frictional drag. They found that gravity wave drag could be comparable, or even larger than frictional drag, and hence should be taken into account in boundary layer drag parametrizations. Grisogono [60] used linear theory conjugated with a WKB approximation to evaluate the dissipative effect of turbulence in the boundary layer (represented through a constant eddy diffusivity) on the momentum flux profile. He found that the momentum flux decreases exponentially with height due to this effect.
Jiang et al. [164] investigated the absorption of trapped lee waves due to boundary layers, using linear theory and numerical simulations, finding that they decay exponentially with downstream distance. This decay rate was seen to increase with surface roughness (higher momentum flux), but to decrease as the heat flux increases. Trapped lee wave absorption was therefore found to be maximized for stable boundary layers (in accordance with [78]). Smith [165] developed a hydrostatic 3D linear model to represent the absorption of mountain waves by boundary layers, using a bulk approach including a Rayleigh damping coefficient to represent friction. He showed that variations in the boundary layer thickness reduce the mountain wave amplitude (in agreement with [157]), the pressure drag, and even more severely the wave momentum flux, confirming that part of the pressure drag is due to boundary layer friction.
Using a mesoscale model with boundary layer parametrizations and analytical models, Jiang et al. [156] showed that the boundary layer tends to reduce the wave drag by up to 60% and the momentum flux above the boundary layer by up to 80%, and slightly delay the onset of wave breaking. They further showed that these effects are stronger over rougher surfaces and for slower boundary layer flow. Jiang and Doyle [166] found that mountain waves, and in particular the wave drag, exhibit substantial diurnal variation in response to changes in boundary layer depth and stability. During daytime, a convective boundary layer weakens the mountain waves and reduces the surface drag by up to 90%, whereas during nighttime, when the boundary layer is shallow, the drag may increase to several times its free-slip value. This latter phenomenon, which might be due to waves propagating in thin inversion layers existing near the surface (cf. [111, 112]), still awaits a deeper understanding.
12. Concluding Remarks
As was seen in this review, the physical processes affecting mountain wave drag are so numerous, varied and complex, that it is hopeless to include all of them in drag parametrizations. However, it is still useful to study these processes in order to better understand them fundamentally, assess their practical relevance and also the feasibility of parametrizing them. The following list of open questions is by no means exhaustive, being largely dictated by personal preference. It is geared toward a fundamental understanding of mountain wave drag, and the development of simple models useful for parametrization.
Concerning the effect of wind profile shear on the surface drag, results obtained using the WKB approximation [50, 66, 67] have the limitation that they are expressed locally in terms of derivatives of the wind velocity at the surface. The drag behavior is quite sensitive to the particular height where these derivatives are evaluated (which must lie outside the boundary layer, since the theory on which they are based is inviscid). It would be useful to develop an approach where the drag was instead expressed in terms of some integral property of the wind profile, and also where faster variations of the atmospheric parameters, which lead to wave reflections and other non-local effects, could be accommodated.
Critical levels, both total and partial, still need to be better understood, namely the circumstances under which they change from absorbing to reflecting. Perhaps this could be clarified, at least for flow over 2D orography, through the use of weakly-nonlinear theory, more specifically adopting Long's equation including de effect of wind shear. This approach would probably also be able to shed some light on the behavior of nonlinear downslope windstorms, in particular the weakening of intermediate drag maxima in 2D flows with critical levels [73]. Although weakly nonlinear theory has already been applied to 3D problems [58], it would be interesting to develop a model similar to that of Smith [91] for downslope windstorms over 3D mountains, something that has not been done until now.
Although a generic expression for trapped lee wave drag analogous to (62) has been derived by Gregory et al. [16], the dependence of trapped lee wave drag on input flow parameters for simple atmospheric profiles, as investigated by Teixeira et al. [111], [112] for 2D moutains, has not been extended to 3D orograpy, but that is necessary since in real mountains 3D effects are important. It would also be useful to extend the calculations of trapped lee wave drag to more realistic atmospheric profiles, where the windspeed and static stability are not limited to be piecewise constant, as in Teixeira et al. [111, 112] but are, for example, linear, as in Keller [103] or Shutts [80], or even more general.
Despite the fact that the drag produced by mountain waves affected by the Earth's rotation is not as relevant for drag parametrization (because it is fully resolved), the predictions of this drag from simple models that account for barotropic Rossby waves [136] or internal Rossby-gravity waves [137] have not been verified against numerical simulations. A connection between the first approach (where the drag does not depend on stratification) and the second one (which is an extension of the theory of smaller-scale mountain waves to a beta-plane) needs to be established. It would be useful to know how accurately these two disparate approaches represent the drag in realistic flows.
Finally, there is still much to learn about intrinsically nonlinear effects, such as wave breaking in directionally sheared flows. While the linear analysis of Broad [83] has shed some light on this issue, further clarification about when and how wave energy is dissipated in such flows over 3D mountains of realistic height is crucial for the improvement of drag parametrization schemes. Currently, the representation of the momentum flux depletion with height that forces the deceleration of the large-scale atmospheric circulation is based on a monochromatic wave formulation (which does not represent the effects of critical level filtering by directional wind shear). An approach akin those suggested by Shutts and Gadian [81], Teixeira and Miranda [85] and Teixeira and Yu [88], or an extension of it to higher wave amplitudes, would improve consistency with current treatments of the surface drag in parameterizations (e.g., [15]).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author acknowledges the financial support of the Portuguese Science Foundation (FCT) under Grant PTDC/CTE-ATM/122501/2010 and of the European Commission, under Marie Curie Career Integration Grant GLIMFLO, contract PCIG13-GA-2013-618016.
References
2. Lin YL. Mesoscale Dynamics. Cambridge: Cambridge University Press (2007). doi: 10.1017/CBO9780511619649
3. Eliassen A, Palm E. On the transfer of energy in stationary mountain waves. Geofys Publ. (1960) 22:1–23.
4. Broad AS. Linear theory of momentum fluxes in 3-D flows with turning of the mean wind with height. Q J R Meteor Soc. (1995) 121:1891–1902. doi: 10.1002/qj.49712152806
5. Clark TL, Miller MJ. Pressure drag and momentum fluxes due to the Alps. II: representation in large-scale atmospheric models. Q J R Meteor Soc. (1991) 117:527–52. doi: 10.1002/qj.49711749906
7. Wallace JM, Tibaldi S, Simmons AJ. Reduction of systematic forecast errors in the ECMWF model through the introduction of an envelope orography. Q J R Meteor Soc. (1983) 109:683–717. doi: 10.1002/qj.49710946202
8. Tibaldi S. Envelope orography and maintenance of the quasi-stationary circulation in the ECMWF global models. Adv Geophys. (1986) 29:339–74. doi: 10.1016/S0065-2687(08)60045-X
9. Palmer TN, Shutts GJ, Swinbank R. Alleviation of a systematic westerly bias in general circulation and numerical weather prediction models through an orographic gravity wave drag parametrization. Q J R Meteor Soc. (1986) 112:1001–39. doi: 10.1002/qj.49711247406
10. Chouinard C, Béland M, McFarlane N. A simple gravity wave drag parametrization for use in medium-range weather forecast models. Atmos-Ocean (1986) 24:91–110. doi: 10.1080/07055900.1986.9649242
11. McFarlane NA. The effect of orographically excited gravity-wave drag on the general circulation of the lower stratosphere and troposphere. J Atmos Sci. (1987) 44:1775–1800. doi: 10.1175/1520-0469(1987)044<1775:TEOOEG>2.0.CO;2
12. Baines PG, Palmer TN. Rationale for a New Physically Based Parametrization of Sub-Grid Scale Orographic Effects. European Centre for Medium-Range Weather Forecasts (1990).
13. Kim YJ, Arakawa A. Improvement of orographic gravity wave parameterization using a mesoscale gravity wave model. J Atmos Sci. (1995) 52:1875–902. doi: 10.1175/1520-0469(1995)052<1875:IOOGWP>2.0.CO;2
14. Sarin VB, Forichon M, Treut HL. Parameterization and influence of the orographic gravity-wave drag in the LMD-GCM. Math Comput Modelling (1996) 24:71–84. doi: 10.1016/0895-7177(96)00108-2
15. Lott F, Miller MJ. A new subgrid-scale orographic drag parametrization: its formulation and testing. Q J R Meteor Soc. (1997) 123:101–27. doi: 10.1002/qj.49712353704
16. Gregory D, Shutts GJ, Mitchell JR. A new gravity-wave-drag scheme incorporating anisotropic orography and low-level wave breaking. Impact upon the climate of the UK Meteorological Office Unified Model. Q J R Meteor Soc. (1998) 124:463–93. doi: 10.1002/qj.49712454606
17. Webster S, Brown AR, Cameron DR, Jones CP. Improvements to the representation of orography in the Met Office Unified Model. Q J Roy Meteor Soc. (2003) 129:1989–2010. doi: 10.1256/qj.02.133
18. Kim YJ, Doyle JD. Extension of an orographic-drag parametrization scheme to incorporate orographic anisotropy and flow blocking. Q J R Meteor Soc. (2005) 131:1893–921. doi: 10.1256/qj.04.160
19. Garner ST. A topographic drag closure built on an analytical base flux. J Atmos Sci. (2005) 62:2302–15. doi: 10.1175/JAS3496.1
20. Solomon S. Stratospheric ozone depletion: a review of concepts and history. Rev Geophys. (1999) 37:275–316. doi: 10.1029/1999RG900008
21. Okamoto K, Sato K, Akiyoshi H. A study on the formation and trend of the Brewer-Dobson circulation. J Geophys Res. (2011) 116:D10117. doi: 10.1029/2010JD014953
23. Egger J, Weickmann K, Hoinka KP. Angular momentum in the global atmospheric circulation. Rev Geophys. (2007) 45:RG4007. doi: 10.1029/2006RG000213
24. Wolf WL, Smith RB. Length-of-day changes and mountain torque during El Niño. J Atmos Sci. (1987) 44:3656–60. doi: 10.1175/1520-0469(1987)044<3656:LODCAM>2.0.CO;2
25. del Rio RA, Gambis D, Salstein DA. Interannual signals in length of day and atmospheric angular momentum. Ann Geophys. (2000) 18:347–64. doi: 10.1007/s005850050894
26. Madden RA, Speth P. Estimates of Atmospheric Angular momentum, friction, and mountain torques during 1987-1988. J Atmos Sci. (1995) 52:3681–94. doi: 10.1175/1520-0469(1995)052<3681:EOAAMF>2.0.CO;2
27. Huang HP, Sardeshmukh P, Weickmann K. The balance of global anglular momentum in a long-term atmospheric data set. J Geophys Res. (1999) 104:2031–40. doi: 10.1029/1998JD200068
28. Egger J, Hoinka KP. The annual cycle of the axial angular momentum of the atmosphere. J Clim. (2005) 18:757–771. doi: 10.1175/JCLI-3290.1
29. Hafner TA, Smith RB. Pressure drag on the European Alps in relation to synoptic events. J Atmos Sci. (1985) 42:562–75. doi: 10.1175/1520-0469(1985)042<0562:PDOTEA>2.0.CO;2
30. Davies HC, Pichler H. Mountain meteorology and ALPEX. Meteor Atmos Phys. (1990) 43:3–4. doi: 10.1007/BF01028104
31. Bougeault P, Benech B, Bessemoulin P, Carissimo B, Clar AJ, Pelon J, et al. PYREX: a summary of findings. Bull Am Meteor Soc. (1997) 78:637–50. doi: 10.1175/1520-0477(1997)078<0637:PASOF>2.0.CO;2
32. Rotunno R, Houze RA. Lessons on orographic precipitation from the mesoscale alpine programme. Q J R Meteor Soc. (2007) 133:811–30. doi: 10.1002/qj.67
33. Smith RB, Doyle JD, Jiang QF, Smith SA. Alpine gravity waves: lessons from MAP regarding mountain wave generation and breaking. Q J R Meteor Soc. (2007) 133:917–36. doi: 10.1002/qj.103
34. Grubišić V, Doyle JD, Kuettner J, Mobbs S, Smith RB, Whiteman CD, et al. The terrain-induced rotor experiment: a field campaign overview including observational highlights. Bull Am Meteor Soc. (2008) 89:1513–33. doi: 10.1175/2008BAMS2487.1
35. Doyle JD, Grubišić V, Brown WOJ, Wekker SFJD, Dornbrack A, Jiang QF, et al. Observations and numerical simulations of subrotor vortices during T-REX. J Atmos Sci. (2009) 66:1229–1249. doi: 10.1175/2008JAS2933.1
36. Miranda PMA, Ferreira JJ, Thorpe AJ. Gravity-wave drag produced by Madeira. Q J R Meteor Soc. (1999) 125:1341–57. doi: 10.1002/qj.1999.49712555612
37. Vosper SB, Mobbs SD. Lee waves over the English lake district. Q J R Meteor Soc. (1996) 122:1283–1305. doi: 10.1002/qj.49712253404
38. Queney P. The problem of air flow over mountains: a summary of theoretical studies. Bull Am Meteor Soc. (1948) 29:16–26.
39. Smith RB. The influence of mountains on the atmosphere. Adv Geophys. (1979) 21:87–230. doi: 10.1016/S0065-2687(08)60262-9
40. Baines PG. Upstream blocking and airflow over mountains. Ann Rev Fluid Mech. (1987) 19:75–97. doi: 10.1146/annurev.fl.19.010187.000451
41. Smith RB. Hydrostatic airflow over mountains. Adv Geophys. (1989) 31:1–41. doi: 10.1016/S0065-2687(08)60052-7
42. Durran DR. Mountain waves and downslope winds. In: Blumen W, editor. Atmospheric Processes over Complex Terrain. American Meteorological Society (1990). p. 59–81.
43. Wurtele MG, Sharman RD, Datta A. Atmospheric lee waves. Ann Rev Fluid Mech. (1996) 28:429–76. doi: 10.1146/annurev.fl.28.010196.002241
44. Durran DR. Lee waves and mountain waves. In: Holton J, Curry J, Pyle J, editors. Encyclopedia of the Atmospheric Sciences. Academic Press (2003). p. 1161–69. doi: 10.1016/B0-12-227090-8/00202-5
45. Smith RB. Stratified flow over topography. In: Grimshaw R, editor. Environmental Stratified Flows. Kluwer Academic Publishers (2003). p. 119–159. doi: 10.1007/0-306-48024-7-5
46. Kim YJ, Eckermann SD, Chun HY. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models - Survey article. Atmos–Ocean (2003) 41:65–98. doi: 10.3137/ao.410105
47. Kim YJ, Hogan TF. Response of a global atmospheric forecast model to various drag parametrizations. Tellus A (2004) 56:472–84. doi: 10.1111/j.1600-0870.2004.00087.x
48. Lott F, Millet C. The representation of gravity waves in atmospheric general circulation models (CGMs). In: Pinchon AL, Blanc E, Hauchecorne A, editors. Infrasound Monitoring for Atmospheric Studies. Springer (2009). p. 685–699.
49. Smith RB, Doyle JD, Brown AR, Webster S. Sensitivity of resolved mountain drag to model resolution for MAP case-studies. Q J R Meteor Soc. (2006) 132:1467–87. doi: 10.1256/qj.05.67
50. Teixeira MAC, Miranda PMA, Valente MA. An analytical model of mountain wave drag for wind profiles with shear and curvature. J Atmos Sci. (2004) 61:1040–54. doi: 10.1175/1520-0469(2004)061<1040:AAMOMW>2.0.CO;2
51. Phillips DS. Analytical surface pressure and drag for linear hydrostatic flow over three-dimensional elliptical mountains. J Atmos Sci. (1984) 41:1073–84. doi: 10.1175/1520-0469(1984)041<1073:ASPADF>2.0.CO;2
52. Smith RB. Further development of a theory of lee cyclogenesis. J Atmos Sci. (1986) 43:1582–602. doi: 10.1175/1520-0469(1986)043<1582:FDOATO>2.0.CO;2
53. Smith RB. Linear theory of stratified flow past an isolated mountain in isosteric coordinates. J Atmos Sci. (1988) 45:3889–96. doi: 10.1175/1520-0469(1988)045<3889:LTOSFP>2.0.CO;2
54. Hines CO. A modeling of atmospheric gravity waves and wave drag generated by isotropic and anisotropic terrain. J Atmos Sci. (1988) 45:309–322. doi: 10.1175/1520-0469(1988)045<0309:AMOAGW>2.0.CO;2
55. Scinocca JF, McFarlane NA. The parametrization of drag induced by stratified flow over anisotropic orography. Q J R Meteor Soc. (2000) 126:2353–93. doi: 10.1002/qj.49712656802
56. Bauer MH, Mayr GJ, Vergeiner I, Pichler H. Strongly nonlinear flow over and around a three-dimensional mountain as a function of the horizontal aspect ratio. J Atmos Sci. (2000) 57:3971–3991. doi: 10.1175/1520-0469(2001)058<3971:SNFOAA>2.0.CO;2
57. Wells H, Vosper SB, Ross AN, Brown AR, Webster S. Wind direction effects on orographic drag. Q J R Meteor Soc. (2008) 134:689–701. doi: 10.1002/qj.247
58. Epifanio CC, Durran DR. Three-dimensional effects in high-drag-state flows over long ridges. J Atmos Sci. (2001) 58:1051–65. doi: 10.1175/1520-0469(2001)058<1051:TDEIHD>2.0.CO;2
59. Blumen W, McGregor CD. Wave drag by three-dimensional mountain lee-waves in nonplanar shear flow. Tellus (1976) 4:287–98. doi: 10.1111/j.2153-3490.1976.tb00678.x
60. Grisogono B. Dissipation of wave drag in the atmospheric boundary layer. J Atmos Sci. (1994) 51:1237–43. doi: 10.1175/1520-0469(1994)051<1237:DOWDIT>2.0.CO;2
61. Bender CM, Orszag SA. Advanced Mathematical Methods for Scientists and Engineers. New York, NY: Springer (1999). doi: 10.1007/978-1-4757-3069-2
62. Grubišić V, Smolarkiewicz PK. The effect of critical levels on 3D orographic flows: linear regime. J Atmos Sci. (1997) 54:1943–60. doi: 10.1175/1520-0469(1997)054<1943:TEOCLO>2.0.CO;2
63. Wang TA, Lin YL. Effects of shear and sharp gradients in static stability on two-dimensional flow over an isolated mountain ridge. Meteor Atmos Phys. (2000) 75:69–99. doi: 10.1007/s007030070017
64. Miranda PMA. Gravity Waves and Wave Drag in Flow Past Three-Dimensional Isolated Mountains. PhD dissertation, University of Reading (1991).
65. Valente MA. Effects of Directional Wind Shear on Orographic Gravity Wave Drag. PhD dissertation, University of Reading (2000).
66. Teixeira MAC, Miranda PMA. The effect of wind shear and curvature on the gravity wave drag produced by a ridge. J Atmos Sci. (2004) 61:2638–43. doi: 10.1175/JAS3282.1
67. Teixeira MAC, Miranda PMA. A linear model of gravity wave drag for hydrostatic sheared flow over elliptical mountains. Q J R Meteor Soc. (2006) 132:2439–58. doi: 10.1256/qj.05.220
68. Miranda PMA, Martins JPA, Teixeira MAC. Assessing wind profile effects on the global atmospheric torque. Q J R Meteor Soc. (2009) 135:807–14. doi: 10.1002/qj.393
69. Tang JY, Tang J, Wang Y. Analytical investigation on 3D non-Boussinesq mountain wave drag for wind profiles with vertical variations. Appl Math Mech. (2007) 28:317–25. doi: 10.1007/s10483-007-0305-z
70. Booker JR, Bretherton FP. The critical layer for internal gravity waves in a shear flow. J Fluid Mech. (1967) 27:513–39. doi: 10.1017/S0022112067000515
71. Breeding RJ. A non-linear investigation of critical levels for internal atmospheric gravity waves. J Fluid Mech. (1971) 50:545–63. doi: 10.1017/S0022112071002751
72. Fritts DC, Geller MA. Viscous stabilization of gravity wave critical level flows. J Atmos Sci. (1976) 33:2276–84. doi: 10.1175/1520-0469(1976)033<2276:VSOGWC>2.0.CO;2
73. Clark TL, Peltier WR. Critical level reflection and the resonant growth of nonlinear mountain waves. J Atmos Sci. (1984) 41:3122–34. doi: 10.1175/1520-0469(1984)041<3122:CLRATR>2.0.CO;2
74. Scinocca JF, Peltier WR. On the Richardson number dependence of nonlinear critical-layer flow over localized topography. J Atmos Sci. (1991) 48:1560–72. doi: 10.1175/1520-0469(1991)048<1560:OTRNDO>2.0.CO;2
75. Lindzen RS, Tung KK. Banded convective activity and ducted gravity waves. Mon Wea Rev. (1976) 104:1602–17. doi: 10.1175/1520-0493(1976)104<1602:BCAADG>2.0.CO;2
76. Wang TA, Lin YL. Wave ducting in a stratified shear flow over two-dimensional mountains. Part I: general linear criteria. J Atmos Sci. (1999) 56:412–36. doi: 10.1175/1520-0469(1999)056<0412:WDIASS>2.0.CO;2
77. Wang TA, Lin YL. Wave ducting in a stratified shear flow over a two-dimensional mountain. Part II: implications for the development of high-drag states for severe downslope windstorms. J Atmos Sci. (1999) 56:437–52. doi: 10.1175/1520-0469(1999)056<0437:WDIASS>2.0.CO;2
78. Lott F. The reflection of a stationary gravity wave by a viscous boundary layer. J Atmos Sci. (2007) 64:3363–71. doi: 10.1175/JAS4020.1
79. Grimshaw R. Internal gravity waves: critical layer absorption in a rotating fluid. J Fluid Mech. (1975) 70:287–304. doi: 10.1017/S0022112075002030
80. Shutts G. Gravity-wave drag parametrization over complex terrain: the effect of critical-level absorption in directional wind-shear. Q J R Meteor Soc. (1995) 121:1005–21. doi: 10.1002/qj.49712152504
81. Shutts GJ, Gadian A. Numerical simulations of orographic gravity waves in flows which back with height. Q J R Meteor Soc. (1999) 125:2743–65. doi: 10.1002/qj.49712555920
82. Shutts GJ. Stationary gravity-wave structure in flows with directional wind shear. Q J R Meteor Soc. (1998) 124:1421–42.
83. Broad AS. Do orographic gravity waves break in flows with uniform wind direction turning with height. Q J R Meteor Soc. (1999) 125:1695–714. doi: 10.1002/qj.49712555711
84. Doyle JD, Jiang QF. Observations and numerical simulations of mountain waves in the presence of directional wind shear. Q J R Meteor Soc. (2006) 132:1877–905. doi: 10.1256/qj.05.140
85. Teixeira MAC, Miranda PMA. On the momentum fluxes associated with mountain waves in directionally sheared flows. J Atmos Sci. (2009) 66:3419–33. doi: 10.1175/2009JAS3065.1
86. Xu X, Wang Y, Xue M. Momentum flux and flux divergence of gravity waves in directional shear flows over three-dimensional mountains. J Atmos Sci. (2012) 69:3733–44. doi: 10.1175/JAS-D-12-044.1
87. Xu X, Xue M, Wang Y. Gravity wave momentum flux in directional shear flows over three-dimensional mountains: linear and nonlinear numerical solutions as compared to linear analytical solutions. J Geophys Res. (2013) 118:7670–81. doi: 10.1002/jgrd.50471
88. Teixeira MAC, Yu CL. The gravity wave momentum flux in hydrostatic flow with directional shear over elliptical mountains. Eur J Mech B Fluids (2014). 47:16–31. doi: 10.1016/j.euromechflu.2014.02.004
89. Lilly DK. A severe downslope windstorm and aircraft turbulence event induced by a mountain wave. J Atmos Sci. (1978) 35:59–77. doi: 10.1175/1520-0469(1978)035<0059:ASDWAA>2.0.CO;2
90. Peltier WR, Clark TL. The evolution and stability of finite-amplitude mountain waves. Part II: surface wave drag and severe downslope windstorms. J Atmos Sci. (1979) 36:1498–1529. doi: 10.1175/1520-0469(1979)036<1498:TEASOF>2.0.CO;2
91. Smith RB. On severe downslope winds. J Atmos Sci. (1985) 42:2597–603. doi: 10.1175/1520-0469(1985)042<2597:OSDW>2.0.CO;2
92. Bacmeister JT, Pierrehumbert RT. On high-drag states of nonlinear stratified flow over an obstacle. J Atmos Sci. (1988) 45:63–80. doi: 10.1175/1520-0469(1988)045<0063:OHDSON>2.0.CO;2
93. Durran DR. Another look at downslope windstorms. Part I: the development of analogous to supercritical flow in an infinitely deep, continuously stratified fluid. J Atmos Sci. (1986) 43:2527–43. doi: 10.1175/1520-0469(1986)043<2527:ALADWP>2.0.CO;2
94. Leutbecher M. Surface pressure drag for hydrostatic two-layer flow over axisymmetric mountains. J Atmos Sci. (2001) 58:797–807. doi: 10.1175/1520-0469(2001)058<0797:SPDFHT>2.0.CO;2
95. Durran DR. Two-layer solutions to Long's equation for vertically propagating mountain waves: how good is linear theory? Q J R Meteor Soc. (1992) 118:415–33. doi: 10.1002/qj.49711850502
96. Teixeira MAC, Miranda PMA, Argaín JL, Valente MA. Resonant gravity-wave drag enhancement in linear stratified flow over mountains. Q J R Meteor Soc. (2005) 131:1795–814. doi: 10.1256/qj.04.154
97. Miranda PMA, Valente MA. Critical level resonance in three-dimensional flow past isolated mountains. J Atmos Sci. (1997) 54:1574–88. doi: 10.1175/1520-0469(1997)054<1574:CLRITD>2.0.CO;2
98. Teixeira MAC, Miranda PMA. Linear criteria for gravity-wave breaking in resonant stratified flow over a ridge. Q J R Meteor Soc. (2005) 131:1815–20. doi: 10.1256/qj.04.155
99. Wells H, Vosper SB. The accuracy of linear theory for predicting mountain-wave drag: implications for parametrization schemes.
100. Teixeira MAC, Miranda PMA, Argaín JL. Mountain waves in two-layer sheared flows: critical level effects, wave reflection and drag enhancement. J Atmos Sci. (2008) 65:1912–26. doi: 10.1175/2007JAS2577.1
101. Teixeira MAC, Argaín JL, Miranda PMA. The importance of friction in mountain wave drag amplification by Scorer parameter resonance. Q J R Meteor Soc. (2012) 138:1325–37. doi: 10.1002/qj.1874
102. Wurtele MG, Sharman RD, Keller TL. Analysis and simulations of a troposphere-stratosphere gravity wave model. Part I. J Atmos Sci. (1987) 44:3269–81. doi: 10.1175/1520-0469(1987)044<3269:AASOAT>2.0.CO;2
103. Keller TL. Implications of the hydrostatic assumption on atmospheric gravity waves. J Atmos Sci. (1994) 51:1915–29. doi: 10.1175/1520-0469(1994)051<1915:IOTHAO>2.0.CO;2
104. Sharman RD, Wurtele MG. Three-dimensional structure of forced gravity waves and lee waves. J Atmos Sci. (2004) 61:664–81. doi: 10.1175/1520-0469(2004)061<0664:TSOFGW>2.0.CO;2
105. Lott F. Linear mountain drag and averaged pseudo-momentum flux profiles in the presence of trapped-lee waves. Tellus A (1998) 50:12–25. doi: 10.1034/j.1600-0870.1998.00002.x
106. Broad AS. Momentum flux due to trapped lee waves forced by mountains. Q J R Meteor Soc. (2002) 128:2167–73. doi: 10.1256/003590002320603593
107. Bretherton FP. Momentum transport by gravity waves. Q J R Meteor Soc. (1969) 95:213–43. doi: 10.1002/qj.49709540402
108. Smith RB. The generation of lee waves by the Blue Ridge. J Atmos Sci. (1976) 33:507–19. doi: 10.1175/1520-0469(1976)033<0507:TGOLWB>2.0.CO;2
109. Tutiś V. Trapped lee waves: a special analytical solution. Meteor Atmos Phys. (1992) 50:189–95. doi: 10.1007/BF01026016
110. Scorer RS. Theory of waves in the lee of mountains. Q J R Meteor Soc. (1949) 75:41–56. doi: 10.1002/qj.49707532308
111. Teixeira MAC, Argaín JL, Miranda PMA. Drag produced by trapped lee waves and propagating mountain and propagating mountain waves in a two-layer atmosphere. Q J R Meteor Soc. (2013) 139:964–81. doi: 10.1002/qj.2008
112. Teixeira MAC, Argaín JL, Miranda PMA. Orographic drag associated with lee waves trapped at an inversion. J Atmos Sci. (2013) 70:2930–47. doi: 10.1175/JAS-D-12-0350.1
113. Vosper SB. Inversion effects on mountain lee waves. Q J R Meteor Soc. (2004) 130:1723–48. doi: 10.1256/qj.03.63
114. Vosper S. Gravity-wave drag on two mountains. Q J R Meteor Soc. (1996) 22:993–9. doi: 10.1002/qj.49712253211
115. Grisogono B, Pryor SC, Keislar RE. Mountain wave drag over double bell-shaped orography. Q J R Meteor Soc. (1993) 119:199–206.
116. Grubišić V, Stiperski I. Lee-wave resonances over double bell-shaped obstacles. J Atmos Sci. (2009) 66:1205–28. doi: 10.1175/2008JAS2885.1
117. Stiperski I, Grubišić V. Trapped lee wave interference in presence of surface friction. J Atmos Sci. (2011) 68:918–36. doi: 10.1175/2010JAS3495.1
118. Doyle JD, Durran DR. The dynamics of mountain-wave-induced rotors. J Atmos Sci. (2002) 59:186–201. doi: 10.1175/1520-0469(2002)059<0186:TDOMWI>2.0.CO;2
119. Inverarity GW, Shutts GJ. A general, linearized vertical structure equation for the vertical velocity: properties, scalings and special cases. Q J R Meteor Soc. (2000) 126:2709–24. doi: 10.1002/qj.49712656906
120. Jones WL. Propagation of internal gravity waves in fluids with shear flow and rotation. J Fluid Mech. (1967) 30:439–48. doi: 10.1017/S0022112067001521
122. Wurtele MG, Datta A, Sharman RD. The propagation of gravity-inertia waves and lee waves under a critical level. J Atmos Sci. (1996) 53:1505–23. doi: 10.1175/1520-0469(1996)053<1505:TPOGWA>2.0.CO;2
123. Wurtele MG, Datta A, Sharman RD. The propagation of a gravity-inertia wave in a positively sheared flow. J Atmos Sci. (2000) 57:3703–15. doi: 10.1175/1520-0469(2000)057<3703:TPOAGI>2.0.CO;2
124. Shutts G. A linear model of back-sheared flow over an isolated hill in the presence of rotation. J Atmos Sci. (2001) 58:3293–311. doi: 10.1175/1520-0469(2001)058<3293:ALMOBS>2.0.CO;2
125. Smith RB. The influence of the Earth's rotation on mountain wave drag. J Atmos Sci. (1979) 36:177–80. doi: 10.1175/1520-0469(1979)036<0177:TIOTER>2.0.CO;2
126. Miranda PMA, James IN. Non-linear three dimensional effects on the wave drag: splitting flow and breaking waves. Q J R Meteor Soc. (1992) 118:1057–81. doi: 10.1002/qj.49711850803
127. Teixeira MAC, Miranda PMA, Cardoso RM. Asymptotic gravity wave drag expressions for non-hydrostatic rotating flow over a ridge. Q J R Meteor Soc. (2008) 134:271–6. doi: 10.1002/qj.196
128. Ólafsson H, Bougeault P. The effect of rotation and surface friction on orographic drag. J Atmos Sci. (1997) 54:193–210. doi: 10.1175/1520-0469(1997)054<0193:TEORAS>2.0.CO;2
129. Ólafsson H. The impact of flow regimes on asymmetry of orographic drag at moderate and low Rossby numbers. Tellus A (2000) 54:365–79. doi: 10.1034/j.1600-0870.2000.00765.x
130. Petersen GN, Kristjansson JE, Ólafsson H. The effect of upstream wind direction on atmospheric flow in the vicinity of a large mountain. Q J R Meteor Soc. (2005) 131:1113–28. doi: 10.1256/qj.04.01
131. Doyle JD, Shapiro MA, Jiang Q, Bartels D. Large-amplitude mountain wave breaking over Greenland. J Atmos Sci. (2005) 62:3106–26. doi: 10.1175/JAS3528.1
132. Martin A, Lott F. Synoptic responses to mountain gravity waves encountering directional critical levels. J Atmos Sci. (2007) 64:828–48. doi: 10.1175/JAS3873.1
133. Janowitz GS. The barotropic Rossby wave drag due to an isolated topography. J Atmos Sci. (1977) 34:802–5. doi: 10.1175/1520-0469(1977)034<0802:TBRWDD>2.0.CO;2
134. McCartney MS. Inertial Taylor columns on a beta plane. J Fluid Mech. (1975) 68:71–95. doi: 10.1017/S0022112075000699
135. Bannon PR. Rotating barotropic flow over finite isolated topography. J Fluid Mech. (1980) 101:281–306. doi: 10.1017/S0022112080001668
136. Thompson L, Flierl GR. Barotropic flow over finite isolated topography: steady solutions on the beta-plane and the initial value problem. J Fluid Mech. (1993) 250:553–86. doi: 10.1017/S0022112093001569
137. Teixeira MAC, Grisogono B. Internal wave drag in stratified flow over mountains on a beta plane. Q J R Meteor Soc. (2008) 134:11–19. doi: 10.1002/qj.188
138. Long RR. Some aspects of the flow of stratified fluids, a theoretical investigation. Tellus (1953) 5:42–58. doi: 10.1111/j.2153-3490.1953.tb01035.x
139. Huppert HE, Miles JW. Lee waves in a stratified flow. Part 3. Semi-elliptical obstacle. J Fluid Mech. (1969) 35:481–96. doi: 10.1017/S0022112069001236
140. Miles JW, Huppert HE. Lee waves in a stratified flow. Part 4. Perturbation approximation. J Fluid Mech. (1969) 35:497–525. doi: 10.1017/S0022112069001248
141. Lilly DK, Klemp JB. The effects of terrain shape on nonlinear hydrostatic mountain waves. J Fluid Mech. (1979) 95:241–61. doi: 10.1017/S0022112079001452
142. Miller PP, Durran DR. On the sensitivity of downslope windstorms to the asymmetry of the mountain profile. J Atmos Sci. (1991) 48:1457–73. doi: 10.1175/1520-0469(1991)048<1457:OTSODW>2.0.CO;2
143. Clark TL, Peltier WR. On the evolution and stability of finite-amplitude mountain waves. J Atmos Sci. (1977) 34:1715–30. doi: 10.1175/1520-0469(1977)034<1715:OTEASO>2.0.CO;2
144. Stein J. Investigation of the regime diagram of hydrostatic flow over a mountain with a primitive equation model. Part I: Two-dimensional flows. Mon Wea Rev. (1992) 120:2962–76. doi: 10.1175/1520-0493(1992)120<2962:IOTRDO>2.0.CO;2
145. Garner ST. Permanent and transient upstream effects in nonlinear stratified flow over a ridge. J Atmos Sci. (1995) 52:227–46. doi: 10.1175/1520-0469(1995)052<0227:PATUEI>2.0.CO;2
146. Durran DR. Do breaking mountain waves decelerate the local mean flow? J Atmos Sci. (1995) 52:4010–32. doi: 10.1175/1520-0469(1995)052<4010:DBMWDT>2.0.CO;2
147. Mayr GJ, Gohm A. 2D airflow over a double bell-shaped mountain. Meteor Atmos Phys. (2000) 72, 13–27. doi: 10.1007/s007030050002
148. Smolarkiewicz PK, Rotunno R. Low Froude number flow past three-dimensional obstacles. Part II: upwind flow reversal zone. J Atmos Sci. (1990) 47:1498–1511. doi: 10.1175/1520-0469(1990)047<1498:LFNFPT>2.0.CO;2
149. Smith RB. Mountain-induced stagnation points in hydrostatic flow. Tellus A (1989) 41:270–4. doi: 10.1111/j.1600-0870.1989.tb00381.x
150. Ólafsson H, Bougeault P. Nonlinear flow past an elliptic mountain ridge. J Atmos Sci. (1996) 53:2465–89. doi: 10.1175/1520-0469(1996)053<2465:NFPAEM>2.0.CO;2
151. Vosper SB, Castro IP, Snyder WH, Mobbs SD. Experimental studies of strongly stratified flow past three-dimensional orography. J Fluid Mech. (1999) 390:223–49. doi: 10.1017/S0022112099005133
152. Eckermann S, Lindeman J, Broutman D, Ma J, Boybeyi Z. Momentum fluxes of gravity waves generated by variable Froude number flow over three-dimensional obstacles. J Atmos Sci. (2010) 67:2260–78. doi: 10.1175/2010JAS3375.1
153. Lindzen RS. Supersaturation of vertically propagating internal gravity waves. J Atmos Sci. (1988) 45:705–11. doi: 10.1175/1520-0469(1988)045<0705:SOVPIG>2.0.CO;2
154. Kim J, Mahrt L. Momentum transport by gravity waves. J Atmos Sci. (1992) 49:735–48. doi: 10.1175/1520-0469(1992)049<0735:MTBGW>2.0.CO;2
155. Richard E, Mascart P, Nickerson E. The role of surface friction in downslope windstorms. J Appl Meteor. (1989) 28:241–51. doi: 10.1175/1520-0450(1989)028<0241:TROSFI>2.0.CO;2
156. Jiang Q, Smith RB, Doyle JD. Impact of the atmospheric boundary layer on mountain waves. J Atmos Sci. (2008) 65:592–608. doi: 10.1175/2007JAS2376.1
157. Peng MS, Thompson WT. Some aspects of the effect of surface friction on flows over mountains. Q J R Meteor Soc. (2003) 129:2527–57. doi: 10.1256/qj.02.06
158. Belcher SE, Wood N. Form and wave drag due to stably stratified turbulent flow over low ridges. Q J R Meteor Soc. (1996) 122:863–902. doi: 10.1002/qj.49712253205
159. Athanassiadou M. Wave and form drag: their relation in the linear gravity wave regime. Tellus A (2003) 55:173–80. doi: 10.1034/j.1600-0870.2003.00016.x
160. Hunt JC, Leibovich S, Richards KJ. Turbulent shear flows over low hills. Q J R Meteor Soc. (1988) 114:1435–70. doi: 10.1002/qj.49711448405
161. Vosper SB, Brown AR. The effect of small-scale hills on orographic drag. Q J R Meteor Soc. (2007) 133:1345–52. doi: 10.1002/qj.101
162. Steeneveld GJ, Holtslag AAM, Nappo CJ, de Wiel BJHV, Mahrt L. Exploring the possible role of small-scale terrain drag on stable boundary layers over land. J Appl Meteor Climatol. (2008) 47:2518–30. doi: 10.1175/2008JAMC1816.1
163. Nappo CJ, Chimonas G. Wave exchange between the ground surface and a boundary-layer critical level. J Atmos Sci. (1992) 49:1075–91. doi: 10.1175/1520-0469(1992)049<1075:WEBTGS>2.0.CO;2
164. Jiang Q, Doyle JD, Smith RB. Interaction between trapped waves and boundary layers. J Atmos Sci. (2006) 63:617–33. doi: 10.1175/JAS3640.1
165. Smith RB. Interacting mountain waves and boundary layers. J Atmos Sci. (2007) 64:594–607. doi: 10.1175/JAS3836.1
Keywords: mountain waves, drag, momentum flux, stratification, wind shear, coriolis force, nonlinearity, non-hydrostatic effects
Citation: Teixeira MAC (2014) The physics of orographic gravity wave drag. Front. Phys. 2:43. doi: 10.3389/fphy.2014.00043
Received: 12 March 2014; Accepted: 19 June 2014;
Published online: 11 July 2014.
Edited by:
Gert-Jan Steeneveld, Wageningen University, NetherlandsReviewed by:
Simon Henri Chabrillat, Belgian Institute for Space Aeronomy, BelgiumIvana Stiperski, University of Innsbruck, Austria
Copyright © 2014 Teixeira. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miguel A. C. Teixeira, Department of Meteorology, University of Reading, Earley Gate, PO Box 243, Reading RG6 6BB, UK e-mail:bS5hLnRlaXhlaXJhQHJlYWRpbmcuYWMudWs=
 Miguel A. C. Teixeira
Miguel A. C. Teixeira