- 1Department of Mathematics and Statistics, University of Cyprus, Nicosia, Cyprus
- 2Department of Mathematics, Aristotle University of Thessaloniki, Thessaloniki, Greece
This paper is a review on some recent works on the Liouville integrability of a large class of Lotka-Volterra systems.
1. Introduction
The Lotka-Volterra equations were discovered independently by Alfred Lotka and Vito Volterra around 1925. Volterra was trying to make sense of the fact that the predator fish increased in numbers after WWI. This question was posed to him by his son-in-law Umberto D'Ancona a marine biologist who collected data of fish catches in the Adriatic for the years during and after the war. Volterra proposed the following simple system to model the interaction between predator and prey fish
where a, b, c, d > 0. This system and its generalizations to n dimensions is one of the most basic models in population dynamics. The variable x denotes the density of prey fish while y is the density of predator fish. Note that if there are no predators (y = 0) then x grows at a constant rate ẋ = ax, the so called Malthusian law of population. Volterra made the assumption that the interaction between predator and prey fish depends on both x and y, hence the Malthusian law is modified by subtracting a term bxy. Note that he did not take into account a possible death of prey fish due to other causes. Similarly, the density of the predator fish increases at a rate proportional to both x and y, i.e., a factor dxy. Assuming that they die at the rate ẏ = −cy we get the second equation. The same model was also derived by Lotka [1] in the context of chemical reaction theory.
Note that the vector field vanishes at the origin (0, 0) and at the point . The origin is saddle point while the second point is a center, i.e., it corresponds to a periodic solution. It is not difficult to produce a constant of motion. We multiply the first equation by and the second by and then we add the result. We obtain
This equation is equivalent to
Therefore the function
is a constant of motion. The function H is actually a Hamiltonian. By defining the Poisson bracket on ℝ2 by {x, y} = xy we produce the following Hamiltonian formulation
The Lotka-Volterra equations generalize from two to n species. The most general form of the equations is
where xi denotes the density of the ith species, εi is its intrinsic growth (or decay) rate and the matrix A = (aij) is called the interaction matrix. We consider Lotka-Volterra equations without linear terms (εi = 0), i.e., the population of the ith species stays constant if there is no interraction with other species. We also assume that the matrix of interaction coefficients A = (aij) is skew-symmetric. This assumption places the problem in the context of the so called conservative Lotka-Volterra systems.
These systems can be written in Hamiltonian form using the Hamiltonian function
Hamilton's equations take the form with quadratic functions
From the skew symmetry of the matrix A = (aij) it follows that the Schouten-Nijenhuis bracket [π, π] vanishes identically:
The bivector field π is an example of a diagonal Poisson structure.
The Poisson tensor (2) is Poisson isomorphic to the constant Poisson structure defined by the constant matrix A, see [2]. If k = (k1, k2 …, kn) is a vector in the kernel of A then the function
is a Casimir of π. Indeed for an arbitrary function g the Poisson bracket {f, g} is
If the matrix A has rank r then there are n − r functionally independent Casimirs. This type of integral can be traced back to Volterra [3]; see also [2, 4, 5].
The most famous special case of Lotka-Volterra system is the KM system (also known as the Volterra system) defined by
where x0 = xn + 1 = 0. It was first solved by Kac and van-Moerbeke [6], using a discrete version of inverse scattering due to Flaschka [7]. In Moser [8] Moser gave a solution of the system using the method of continued fractions, and in the process he constructed action-angle coordinates. Lax pairs of the system can be found in Moser [8], Damianou [9]. Equations (3) can be considered as a finite-dimensional approximation of the Korteweg-de Vries (KdV) equation. This system has a close connection with the Toda lattice,
In fact, a transformation of Hénon connects the two systems:
The Lotka-Volterra system forms the basis for many models used today in the analysis of population dynamics. It has other applications in Physics, e.g., laser Physics, plasma Physics (as an approximation to the Vlasov-Poisson equation), and neural networks. It appears also in computer science, e.g., communication networks, see [10]. Lotka-Volterra systems have been studied extensively, see e.g., [4, 11–14]. The Darboux method of finding integrals of finite dimensional vector fields and especially for various types of Lotka-Volterra systems has been used by several authors, e.g., [15–20].
2. Hamiltonian Structure
There is a symplectic realization of the Lotka-Volterra system which goes back to Volterra. For simplicity we write the equations in the form
where the matrix A = (ajk) is a fixed skew-symmetric matrix. In Fernandes and Oliva [21] the Hamiltonian formulation is obtained based on Volterra's work using a symplectic realization from R2n ↦ Rn. Volterra defined the variables
(which he called quantity of life) and
for i = 1, 2, …, n. Now, the variables are doubled and the Volterra's transformation is:
where
The Hamiltonian in these (q, p) coordinates becomes
The vector field (4) can be written as
for i = 1, 2, …, n, where the bracket {·,·} is the standard symplectic on ℝ2n, that is:
All others are equal to zero. This system has n integrals given by
One checks that indeed
Moreover, {Ij, Jk} = ajk. The corresponding Poisson bracket produced by the transformation (5) in the x coordinates is
This observation gives a another proof that the bracket (2) is indeed Poisson.
3. Bogoyavlensky-Volterra Systems
We now describe the construction of the generalized Volterra systems of Bogoyavlensky (see [22, 23]). In this first construction the matrix A is not skew-symmetric but we include the details for completeness.
Let 𝔤 be a simple Lie algebra, with 𝔤 = n, and let Π = {ω1,ω2, …,ωn} be a Cartan-Weyl basis for the simple roots in 𝔤. There exist unique positive integers ki such that
where k0 = 1 and ω0 is the minimal negative root. We consider the Lax pair:
where
Let 𝔥 ⊂ 𝔤 be the Cartan subalgebra. For every root ωa ∈ 𝔥* there is a unique Hωa ∈ 𝔥 such that ω(h) = β(Hωa, h), for all h ∈ 𝔥, where β denotes the Killing form. Also, β induces an inner product on 𝔥* by setting 〈ωa, ωb〉 = β(Hωa, Hωb), and we define
With these choices, the Lax pair above is equivalent to the system of o.d.e.'s
To obtain a Lotka-Volterra type system one introduces a new set of variables by
Note that xij ≠ 0 iff there exists an edge in the Dynkin diagram for the Lie algebra 𝔤 connecting the vertices ωi and ωj. System (7), in the variables xij, takes the form
which is a Lotka-Volterra type system.
For example the following system is an open version of a Bn system:
The Hamiltonian formulation of these systems, Lax pairs and master symmetries were considered by Kouzaris [24]. There is also a Lax pair in Damianou and Fernandes [25]. The system in our example has two integrals of motion, one of degree 2 and one of degree 4. The quadratic integral is
The fourth degree invariant is
4. More Bogoyavlensky's Type Systems
Bogoyavlensky in [22, 23] and [5] has generalized the KM-system in the following way,
with periodic condition xn + i = xi. We will denote this system with B(n, p). All the results in this section, except the bihamiltonian pair follow [5]. The system has a Lax pair of the form
where L = X + λM and A = b − λMp + 1. The matrix X has the form xi, i − p = xi for p + 1 ≤ i ≤ n and xi, i + n − p = xi for 1 ≤ i ≤ p. The matrix M is defined by mi, i + 1 = mn, 1 = 1. The matrix b is diagonal with entries bii = −(xi + xi + 1 + … + xi + p).
Example 1. Let us consider the system B(6, 2), i.e., n = 6, p = 2. The equations of motion become
We have
Let p(x) = det(L − xI) be the characteristic polynomial of L. Then the coefficient of x3 is of the form H λ2 + F2, where H = x1 + x2 + x3 + x4 + x5 + x6 is the Hamiltonian and F2 = x1x3x5 + x2x4x6. On the other hand the constant term of p(x) has the form F3 λ2 + F4, where F3 = x1x2x4x5 + x1x3x4x6 + x2x3x5x6 and F4 = x1x2x3x4x5x6.
By examining the eigenvectors of the coefficient matrix of (11) we can see that the functions C1 = x2x5, C2 = x1x4, C3 = x2x4x6 and C4 = x1x3x5 are all Casimirs of the corresponding quadratic Poisson structure. Therefore we have a rank 2 Poisson bracket and the system is clearly integrable. It is easy to see that the functions F2, F3, F4 can be expressed as functions of C1, C2, C3, C4.
Now restrict this system on the invariant submanifold x5 = x6 = 0. We obtain the system
This system is integrable. It has two Casimirs F1 = x1x4 = C2 and .
Example 2. Similarly, the quadratic Poisson structure π2 associated to the system B(5, 2), i.e.,
has a single Casimir x1x2x3x4x5. The system is Hamiltonian with Hamiltonian function
and it has as additional first integral the function
Define the Poisson tensor π0 as follows:
It is easy to check that π0 is compatible with π2 and that we have a bihamiltonian pair
The function H is the Casimir of bracket π0.
More generally, if n = 2p + 1, then we can define a (skew-symmetric) tensor field π0 with non-zero entries π0[i, i + n − p − 1] = −1 for 1 ≤ i ≤ p + 1 and π0[i, i + n − p] = 1 for 1 ≤ i ≤ p. The associated quadratic Poisson structure π2 to the system (10) and π0 are compatible and they form a bihamiltonian pair.
Restricting on the submanifold x5 = 0 we obtain the system
This system is integrable with second integral given by x1x4(x2 + x3), i.e., the restriction of F on the submanifold.
Example 3. Restricting the B(7, 2) on the submanifold x4 = x6 = x7 = 0 and renaming x5 → x4 results in the following system
The additional integral is F = x4(x1 + x2).
Example 4. Restricting the B(7, 3) on the submanifold x5 = x6 = x7 = 0 results in the following system
The Poisson matrix in this example is symplectic. The system is integrable since it has two constants of motion and . Note that
is also a first integral.
5. Generalized Volterra Systems
We recall the following procedure from Damianou [26]. Let 𝔤 be any simple Lie algebra equipped with its Killing form 〈· | ·〉. One chooses a Cartan subalgebra 𝔥 of 𝔤 and a basis Π of simple roots for the root system Δ of 𝔥 in 𝔤. The corresponding set of positive roots is denoted by Δ+. To each positive root α one can associate a triple (Xα, X−α, Hα) of vectors in 𝔤 which generate a Lie subalgebra isomorphic to 𝔰𝔩2(ℂ). The set (Xα, X−α)α∈Δ+ ∪ (Hα)α∈Π is a basis of 𝔤, called a root basis. Let Π = {α1, …, αℓ} and let Xα1, …, Xαℓ be the corresponding root vectors in 𝔤. Define
To find the matrix B we use the following procedure. For each i, j form the vectors . If αi + αj is a root then include a term of the form aiaj in B. We make B skew-symmetric by including the corresponding negative root vectors aiaj[X−αi, X−αj]. Finally, we define the system using the Lax equation = [L, B]. For a root system of type An we obtain the KM system.
If a system is of type ADE we can define the system in the following alternative way. Consider the Dynkin diagram of 𝔤 and define a Lotka–Volterra system by the equations
where the skew-symmetric matrix mij for i < j is defined to be mij = 1 if vertex i is connected with vertex j and 0 otherwise. For i > j the term mij is defined by skew-symmetry. Note that if we replace one of the mij for i < j from +1 to −1 we may end up with an inequivalent system. In our definition, the upper part of the matrix (mij) consists only of 0 and 1. However, it is possible to define for each connected graph 2m systems, where m is the number of edges, by assigning the ±1 sign to each edge. Of course, some of these systems will be isomorphic. One more observation: there are several inequivalent ways to label a graph and therefore the association between graphs and Lotka–Volterra systems is not always a bijection. The number of distinct labellings of a given unlabeled simple graph G on n vertices is known to be
Example 5. (D4 system) By examining the Dynkin diagram of the simple Lie algebra of type D4 we obtain the system
One can obtain the same equations in the following way. Define the matrix L using the root vectors of a Lie algebra of type D4
and
Then the Lax equation = [L, B] is equivalent to (18). We note that
are integrals of motion for the system. In fact
Also, the associated quadratic Poisson structure to the system (18) has two Casimirs F1 = x1x4 and F2 = x1x3. It turns out that det(L) = (F1 + F2)2.
We have
We can find the Casimirs by computing the kernel of the matrix
The two eigenvectors with eigenvalue 0 are (1, 0, 0, 1) and (1, 0, 1, 0). We obtain the two Casimirs F1 = x11x02x03x14 = x1x4 and F2 = x11x02x13x04 = x1x3.
In Charalambides et al. [27] the algorithm was generalized as follows. Consider a subset Φ of Δ+ such that Π ⊂ Φ ⊂ Δ+. The Lax matrix is easy to construct
Here we use the following enumeration of Φ which we assume to have m elements. The variables aj correspond to the simple roots αj for j = 1, 2, …, ℓ. We assign the variables aj for j = ℓ + 1, ℓ + 2, …, m to the remaining roots in Φ. To construct the matrix B we use the following algorithm. Consider the set Φ ∪ Φ− which consists of all the roots in Φ together with their negatives and let Ψ = {α + β | α, β ∈ Φ ∪ Φ−, α + β ∈ Δ+}. Define
where cij = ±1 if αi + αj ∈ Ψ with αi, αj ∈ Φ ∪ Φ− and 0 otherwise. In all eight cases in A3 we are able to make the proper choices of the sign of the cij so that we can produce a Lax pair. This method produces a Lax pair in all but five out of sixty four cases in A4. However, when we allow the cij to take the complex values ±i we are able to produce a Lax pair in all 64 cases. By using Maple we were able to check that all these examples in A3 and A4 are in fact Liouville integrable. We will not attempt to prove the integrability of these systems in general due to the complexity of their definition.
This algorithm for certain subsets Φ recovers well known integrable systems. For example for Φ = Π, the simple roots of the root system An, and ci, i+1 = 1 for i = 1, 2, …, n − 1 we obtain the KM system while for Φ = Π ∪ {αn + 1}, the simple roots and the highest root, the choice of the signs ci, i + 1 = 1 for i = 1, 2, …, n − 1 and c1, n + 1 = cn, n + 1 = −1 produces the periodic KM system.
Example 6. For the root system of type A3 if we take Φ = {α1, α2, α3, α1 + α2} then
In this example the variables ai for i = 1, 2, 3 correspond to the three simple roots α1, α2, α3 and the variable a4 to the root α1 + α2. We obtain the following Lax pair:
Using the substitution xi = 2a2i, the system defined by the Lax equation = [L, B] is transformed to the following Lotka-Volterra system.
This system is integrable. There exist two functionally independent Casimir functions F1 = x1x3 = det L and F2 = x1x2x4. The standard quadratic Poisson bracket (2) is defined by the relations {xi, xj} = ri,jxixj where r1,2 = r2,3 = r3,4 = r2,4 = − r1,4 = 1 and r1,3 = 0. One can find the Casimirs by computing the kernel of the skew symmetric matrix A = (ri,j)1 ≤ i,j ≤ 4. The additional integral is the Hamiltonian H = x1 + x2 + x3 + x4 = trL2.
Example 7. Let Φ = {α1, α2, α3, α1 + α2, α2 + α3}. Its associated Lax equation = [B, L] with
and
is equivalent to the following equations of motion
Note that the system is not Lotka-Volterra. It is Hamiltonian with Hamiltonian function H = (a21 + a22 + a23 + a24 + a25). The system has Poisson matrix
of rank 4. The determinant C = (a1a3 − a4a5)2 of L is the Casimir of the system. The trace of L3 gives the additional constant of motion
Since the three constants of motion are evidently independent, the system is Liouville integrable.
6. Subsets Φ Giving Rise to Lotka Volterra Systems
In Evripidou [28] Evripidou classified all subsets of the positive roots containing the simple roots which give rise to Lotka Volterra systems via the transformation xi = 2a2i. He also explicitly described each system associated with this subsets.
Theorem 1. The only choices for the subset Φ of Δ+ so that the corresponding generalized Volterra systems, under the substitution xi = 2a2i, are transformed into Lotka-Volterra systems are the following five.
(1) Φ = Π,
(2) Φ = Π ∪ {α2 + α3 + … + αn − 1},
(3) Φ = Π ∪{α1 + α2 + … + αn − 1},
(4) Φ = Π ∪{α2 + α3 + … + αn},
(5) Φ = Π ∪{α1 + α2 + … + αn}.
We outline the proof of this theorem. First one proves the theorem for the special case where Φ is the subset of the positive roots containing the simple roots and only one extra root. This is done by explicitly writing down the matrix [B, L] and setting equal to zero the coefficients of the root vectors corresponding to roots not appearing in Φ. We end up with a linear system of the signs ci, j, which in order to have a solution, the extra root αn + 1 ∈ Φ must be of the form αn + 1 = αk + αk + 1 + … + αm with k ≤ 2 and m ≥ n − 1. Since subsystems of Lotka-Volterra systems are also Lotka-Volterra systems, the proof of theorem 1 is a case by case verification of all of the 16 possible subsets Φ containing the simple roots and roots in
Below we describe the corresponding Lotka-Volterra systems.
Case (1) gives rise to the KM system while case (5) gives rise to the periodic KM system.
Case (2) corresponds to the Lax equation = [L, B] with L matrix
The skew symmetric matrix B is defined using the method described in the previous section.
After substituting xi = 2a2i for i = 1, …, n + 1, the Lax pair L, B becomes equivalent to the following equations of motion:
It is easily verified that for n even, the rank of the corresponding Poisson matrix is n and the function f = x2x3 … xn − 1xn + 1 is the Casimir of the system, while for n odd, the rank of the Poisson matrix is n − 1 and the functions f1 = x1x3 … xn = and f2 = x2x3 … xn − 1xn + 1 are the Casimirs.
Case (3) corresponds to the Lax pair whose Lax matrix L is given by
with an + 1 = α1 + … + αn − 1. The upper triangular part of the skewsymmetric matrix B is
After substituting xi = 2a2i for i = 1, …, n + 1, we obtain the following equivalent equations of motion:
For n even, the rank of the Poisson matrix is n and the function f = x1x2 … xn − 1xn + 1 is the Casimir, while for n odd, the rank of the Poisson matrix is n − 1 and the functions f1 = x1x3x5 … xn = and f2 = x1x2 … xn − 1xn + 1 are Casimirs.
The system obtained in case (4) turns out to be isomorphic to the one in case (3). In fact, the change of variables un + 1 − i = −xi for i = 1, 2, …, n and un + 1 = − xn + 1 in case (3) gives the corresponding system of case (4).
7. Poisson Brackets with Prescribed Casimirs
In Damianou and Petalidou [29] by constructing the Poisson brackets for the periodic Toda starting from the well-known Casimirs we observed the surprising appearance of the Volterra system. We first review the basic construction in Damianou and Petalidou [29].
Suppose dim M = 2n. Let f1, …, f2n−2k be smooth functions on M, functionally independent on a dense open set. Let ω0 be an almost symplectic form on M such that the associate bivector field Λ0 satisfies:
where Xfi = Λ#0(dfi). Note that f is the Pfaffian of ({fi, fj}0). Consider the (2n − 2)-form
where σ is a 2-form on M satisfying:
The operator δ is defined by δ = ∗ d ∗, where * is the standard star operator.
(ii) The 2-form σ is a section of 2 D° of maximal rank where D° is the annihilator of the distribution D generated by the vector fields of Xf1, …, Xf2n − 2k.
Finally, g = iΛ0σ. Then Φ corresponds to a Poisson tensor field Λ on M with orbits of dimension at most 2k for which f1, …, f2n − 2k are Casimir functions. Precisely, Λ = Λ#0(σ) and the associated bracket of Λ on C∞(M) is given, for any h1, h2 ∈ C∞(M), by
Conversely, if Λ is a Poisson tensor on (M, ω0) of rank at most 2k on an open and dense subset 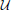 of M, then there are 2n − 2k functionally independent smooth functions f1, …, f2n − 2k on
of M, then there are 2n − 2k functionally independent smooth functions f1, …, f2n − 2k on 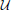 and a suitable 2-form σ on M such that ΨΛ = −iΛΩ and {·, ·} is of the form (19).
and a suitable 2-form σ on M such that ΨΛ = −iΛΩ and {·, ·} is of the form (19).
Similar results hold when M is an odd-dimensional manifold. One may establish a similar formula for the Poisson brackets on C∞(M) with the prescribed properties. For this construction, we assume that M is equipped with a suitable almost cosymplectic structure (ϑ0, Θ0) and with the volume form . In Damianou and Petalidou [29] we showed how one obtains the An Volterra bracket starting from the An Lie Poisson bracket of the periodic Toda lattice. The algorithm can of course be generalized to any complex simple Lie algebra.
8. From AN-Periodic Toda to Volterra Lattice
In this section we describe the An-Toda to An-Volterra case. We begin with the linear Poisson structure ΛT associated with the periodic Toda lattice of n particles. This Poisson structure has two well-known Casimir functions. Using formula (19) we construct another Poisson structure having the same Casimir invariants with ΛT. It turns out that this structure decomposes as a direct sum of two Poisson tensors one of which (involving only the a variables in Flaschka's coordinates) is the quadratic Poisson bracket of the Volterra lattice.
The periodic Toda lattice of n particles (n ≥ 2) is the system of ordinary differential equations on ℝ2n which in Flaschka's [7] coordinates (a1, …, an, b1, …, bn) takes the form
This system is Hamiltonian with respect to the nonstandard Lie-Poisson structure
on ℝ2n and it has as Hamiltonian the function . ΛT is of rank 2n − 2 on 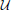 = {(a1, …, an, b1, …, bn) ∈ ℝ2n / and it admits two Casimir functions:
= {(a1, …, an, b1, …, bn) ∈ ℝ2n / and it admits two Casimir functions:
We consider on ℝ2n the standard symplectic form , its associated Poisson tensor , and the corresponding volume element = da1 ∧ db1 ∧ … ∧ dan ∧ dbn. The Hamiltonian vector fields of C1 and C2 with respect to Λ0 are
So, D = 〈XC1, XC2〉 and
The family of 1-forms (σ1, …, σn − 1, σ′1, …, σ′n − 1),
provides, at every point (a, b) ∈ 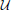 , a basis of D°(a, b). The section of maximal rank σT of 2 D° →
, a basis of D°(a, b). The section of maximal rank σT of 2 D° → 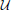 , which corresponds to ΛT, via the isomorphism Λ#0, and verifies (18), is written, in this basis, as
, which corresponds to ΛT, via the isomorphism Λ#0, and verifies (18), is written, in this basis, as
Now, we consider on ℝ2n the 2-form
It is a section of 2 D° whose rank depends on the parity of n; if n is odd, its rank is 2n − 2 on  , while, if n is even, its rank is 2n − 4 almost everywhere on ℝ2n. Also, after a long computation, we can confirm that it satisfies (18). Thus, its image via Λ#0, i.e., the bivector field
, while, if n is even, its rank is 2n − 4 almost everywhere on ℝ2n. Also, after a long computation, we can confirm that it satisfies (18). Thus, its image via Λ#0, i.e., the bivector field
defines a Poisson structure on ℝ2n with symplectic leaves of dimension at most 2n − 2, when n is odd, that has C1 and C2 as Casimir functions. (When n is even, Λ has two more Casimir functions.) We remark that (ℝ2n, Λ) can be viewed as the product of Poisson manifolds (ℝn, ΛV) × (ℝn, Λ′), where
The Poisson tensor ΛV is the quadratic Poisson structure associated to the periodic Volterra lattice
on ℝn and it has C2 as unique Casimir function, when n = 2k + 1 is odd.
It is well known that (21) is a completely integrable system that admits a bihamiltonian formulation, [30–32], and a Lax pair representation [8, 9, 33]. ΛV is compatible with the cubic Poisson tensor field Q on ℝn whose components are the functions
and we have that
Also, (21) can be written in the form = [B, L], where
and
The functions det L = 2C1/22 and TrL2k are first integrals of (21).
Some other An-type Lotka-Volterra systems: We remark that to each 2-form σ′ which is a linear combination of 2-forms of type σ′i ∧ σ′j corresponds, via Λ#0, a diagonal quadratic Poisson structure whose a Casimir is the function C2 and whose Hamiltonian system associated to H = a1 + … + an is of the form (4). For example, if n = 5 and σ′ = 3 σ′1 ∧ σ′2 + σ′1 ∧ σ′3 + σ′1 ∧ σ′4 − 2 σ′2 ∧ σ′4 + σ′3 ∧ σ′4,
and the Hamiltonian vector field Λ#(dH) corresponds to the system
The integrability of the Lotka-Volterra systems obtained by the above procedure is an open problem.
We close with the following observation. Beginning with the standard Poisson bracket for the periodic Toda lattice corresponding to a complex simple Lie algebra 𝔤 and by repeating the procedure of this section we produce new Lotka-Volterra systems associated with 𝔤. Establishing the integrability of these systems is also an open problem.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lotka AJ. Undamped oscillations derived from the law of mass action. J Am Chem Soc. (1920) 42, 1595–9. doi: 10.1021/ja01453a010
2. Hernandez-Bermejo B, Fairen V. Separation of variables in the Jacobi identities, Phys Lett A (2000) 271, 258-63. doi: 10.1016/S0375-9601(00)00375-3
3. Volterra V. Leçons sur la théorie mathématique de la lutte pour la vie, (1931) Paris: Gauthier-Villars.
4. Plank M. Hamiltonian structures for the n-dimensional Lotka-Volterra equations. J Math Phys. (1995) 36, 3520–34. doi: 10.1063/1.530978
5. Bogoyavlensky OI. Integrable Lotka-Volterra systems. Regul Chaotic Dyn. (2008) 13, 543–56. doi: 10.1134/S1560354708060051
6. Kac M, van Moerbeke P. On an explicit soluble system of nonlinear differential equations related to certain Toda lattices. Adv Math. (1975) 16, 160–9. doi: 10.1016/0001-8708(75)90148-6
7. Flaschka H. On the Toda lattice II. Inverse scattering solution. Progr Theor Phys. (1974) 51, 703–16. doi: 10.1143/PTP.51.703
8. Moser J. Three integrable Hamiltonian systems connected with isospectral deformations. Adv Math. (1975) 16, 197–220. doi: 10.1016/0001-8708(75)90151-6
9. Damianou PA. The Volterra model and its relation to the Toda lattice. Phys Lett A (1991) 155, 126–32. doi: 10.1016/0375-9601(91)90578-V
10. Antoniou P, Pitsillides A. “Congestion control in autonomous decentralized networks based on the Lotka-Volterra competition model,” In: ICAAN 2009 19th International Conference on Artificial Neural Networks, (Limassol, Cyprus), pp. 14–7, (2009).
11. Ballesteros A, Blasco A Musso F. Integrable deformations of LotkaVolterra systems Phys Lett A (2011) 375, 3370-4. doi: 10.1016/j.physleta.2011.07.055
12. Goriely A. Integrability and Nonintegrability of Dynamical Systems, Singapore: World Scientific Publishing, (2001).
13. Hernandez-Bermejo B, Fairen, V. Hamiltonian structure and Darboux theorem for families of generalized Lotka-Volterra systems. J Math Phys. (1998) 39, 6162–74. doi: 10.1063/1.532621
14. Plank M. Bi-Hamiltonian systems and Lotka-Volterra equations: a three-dimensional classification. Nonlinearity (1996) 9, 887–96. doi: 10.1088/0951-7715/9/4/004
15. Cairó L, Feix MR. Families of invariants of the motion for the Lotka-Volterra equations: the linear polynomial family. J Math Phys. (1992) 33, 2440–55. doi: 10.1063/1.529614
16. Cairó L, Llibre J. Darboux integrability for 3D Lotka-Volterra systems. J Phys A Math Gen. (2000) 33, 2395–406. doi: 10.1088/0305-4470/33/12/307
17. Labrunie S. On the polynomial first integrals of the (a, b, c) Lotka-Volterra system. J Math Phys. (1996) 37, 5539–50. doi: 10.1063/1.531721
18. Maciejewski AJ, Przybylska M. Darboux polynomials and first integrals of natural polynomial Hamiltonian systems. Phys Lett A (2004) 326, 219–26. doi: 10.1016/j.physleta.2004.04.034
19. Moulin-Ollagnier J. Polynomial first integrals of the Lotka-Volterra system. Bull Sci Math. (1997) 121, 463–76.
20. Moulin-Ollagnier J. Rational integration of the Lotka-Volterra system. Bull Sci Math. (1999) 123, 437–66. doi: 10.1016/S0007-4497(99)00111-6
21. Fernandes RL, Oliva WM. “Hamiltonian dynamics of the Lotka-Volterra equations,” In: International Conference on Differential Equations, Lisboa 1995 (River Edge, NJ: World Sci. Publ.) (1998) pp. 327–34.
22. Bogoyavlensky OI. Five constructions of integrable Hamiltonian systems. Acta Appl Math. (1988) 13, 227–66.
23. Bogoyavlensky OI. Intergrable discretizations of the KdV equation. Phys Lett A (1988) 134, 34–8. doi: 10.1016/0375-9601(88)90542-7
24. Kouzaris SP. Multiple Hamiltonian structures and Lax pairs for Bogoyavlensky–Volterra systems. J Nonlinear Math Phys. (2003) 10, 431–50. doi: 10.2991/jnmp.2003.10.4.2
25. Damianou PA, Fernandes RL. From the Toda lattice to the Volterra lattice and back. Rep Math Phys. (2002) 50, 361–78. doi: 10.1016/S0034-4877(02)80066-0
26. Damianou PA. “Lotka-Volterra systems associated with graphs,” In: Sixth Workshop Group Analysis of Differential Equations and Integrable Systems (2013), 30–44.
27. Charalambides SA, Damianou PA, Evripidou CA. On generalized Volterra systems. arXiv:1305.7329, (2013).
28. Evripidou CA. Applications of Root Systems in Geometry and Physics. Ph.D. dissertation, University of Cyprus (2014).
29. Damianou PA, Petalidou F. Poisson brackets with prescribed Casimirs. Can J Math. (2012) 64, 991–1018. doi: 10.4153/CJM-2011-082-2
30. Penskoï AV. Canonically conjugate variables for the Volterra system with periodic boundary conditions. Mat Zametki. (1998) 68 115–28. (English translation: Math. Notes. (1998) 64 98–109.) doi: 10.1007/BF02307200
31. Veselov AP, Penskoï AV. On algebro-geometric Poisson brackets for the Volterra lattice. Reg Chaot Dyn. (1998), 3, 3–9. doi: 10.1070/rd1998v003n02ABEH000066
32. Falqui G, Pedroni M. Gel'fand-Zakharevich systems and algebraic integrability: The Volterra lattice revised. Reg Chaot Dyn. (2005) 10, 399–412. doi: 10.1070/RD2005v010n04ABEH000322
Keywords: Lotka-Volterra equations, integrable systems, poisson geometry, integrable models, hamiltonian systems.
Citation: Damianou PA and Petalidou F (2014) On the liouville intergrability of Lotka-Volterra systems. Front. Phys. 2:50. doi: 10.3389/fphy.2014.00050
Received: 01 June 2014; Accepted: 28 July 2014;
Published online: 19 August 2014.
Edited by:
Oleg N. Kirillov, Helmholtz-Zentrum Dresden-Rossendorf, GermanyReviewed by:
Petre Birtea, West University of Timisoara, RomaniaMark Levi, Pennsylvania State University, USA
Igor Mencattini, Universidade de São Paulo, Brazil
Copyright © 2014 Damianou and Petalidou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pantelis A. Damianou, Department of Mathematics and Statistics, University of Cyprus, PO Box 20537, Nicosia 1678, Cyprus e-mail:ZGFtaWFub3VAdWN5LmFjLmN5
 Pantelis A. Damianou
Pantelis A. Damianou Fani Petalidou
Fani Petalidou